第10章 简单线性回归分析思考与练习参考答案
应用回归分析课后习题参考答案_全部版__何晓群_刘文卿

第一章回归分析概述1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
回归思考与练习参考答案

第18章Logistic回归思考与练习参考答案一、最佳选择题1. Logistic回归与多重线性回归比较,( A )。
A.logistic回归的因变量为二分类变量B.多重线性回归的因变量为二分类变量C.logistic回归和多重线性回归的因变量都可为二分类变量D.logistic回归的自变量必须是二分类变量E.多重线性回归的自变量必须是二分类变量2. Logistic回归适用于因变量为( E )。
A.二分类变量B.多分类有序变量C.多分类无序变量D.连续型定量变量E.A、B、C均可3. Logistic回归系数与优势比OR的关系为( E )。
A.0等价于OR>1 B.0等价于OR<1 C.=0等价于OR=1 D.<0等价于OR<1 E.A、C、D均正确4. Logistic回归可用于( E )。
A.影响因素分析B.校正混杂因素C.预测D.仅有A和C E.A、B、C均可5. Logistic回归中自变量如为多分类变量,宜将其按哑变量处理,与其他变量进行变量筛选时可用( D )。
A.软件自动筛选的前进法B.软件自动筛选的后退法C.软件自动筛选的逐步法D.应将几个哑变量作为一个因素,整体进出回归方程E.A、B、C均可二、思考题1. 为研究低龄青少年吸烟的外在因素,研究者采用整群抽样,在某中心城区和远城区的初中学校,各选择初一年级一个班的全部学生进行调查,并用logistic回归方程筛选影响因素。
试问上述问题采用logistic回归是否妥当?答:上述问题采用logistic回归不妥当,因为logistic回归中参数的极大似然估计要求样本结局事件相互独立,而研究的问题中低龄青少年吸烟行为不独立。
2. 分类变量赋值不同对logistic回归有何影响? 分析结果一致吗?答:(1)若因变量交换赋值,两个logistic回归方程的参数估计绝对值相等,符号相反;优势比互为倒数,含义有所区别,实质意义一样;模型拟合检验与回归系数的假设检验结果相同。
回归分析的基本知识点及习题

模型评估:线性 回归模型的评估 通常使用R方值、 调整R方值、残 差图等指标进行
评估。
参数估计与求解
最小二乘法:通过最小化误差的平 方和来估计线性回归模型的参数
梯度下降法:通过迭代更新参数, 使得损失函数最小化,从而得到最 优解
添加标题
添加标题
添加标题
添加标题
最大似然估计法:基于似然函数的 最大值来估计参数,使得观测到的 数据出现的概率最大
原理:通过引入 一个小的正则化 项来改进最小二 乘法的估计,以 减少过拟合和增 加模型的稳定性。
目的:在回归分析 中,岭回归分析用 于处理自变量之间 高度相关的情况, 通过加入正则化项 来减少过拟合,提 高模型的预测精度。
应用场景:岭回 归分析广泛应用 于统计学、机器 学习和数据分析 等领域,尤其在 处理共线性数据 问题时表现出色。
感谢您的观看
汇报人:
梯度下降法:通过 迭代更新参数来最 小化损失函数
牛顿-拉夫森方法 :利用泰勒级数展 开来求解参数
模型评估与优化
模型的准确性评估:通过比较实际值与预测值来评估模型的预测能力。
模型的可靠性评估:检查模型是否具有足够的稳定性和可靠性。
模型的优化方法:通过调整模型参数或改变模型结构来提高模型的预测能力和可 靠性。
假设:满足线性关系、误差项独立同分布、误差项无偏、误差项无自相关等假设。 模型建立:基于历史数据,通过最小二乘法等估计方法确定自变量和因变量的关系。 模型评估:通过残差分析、决定系数、调整决定系数等方法评估模型的拟合优度。
参数估计与求解
最小二乘法:通过 最小化误差的平方 和来估计参数
最大似然估计法: 基于似然函数的最 大值来估计参数
模型的适用性:确定模型是否适用于特定的数据集和问题类型。
统计学一元线性回归课后习题答案

(1)绘制运送距离和运送时间的散点图,判断二者之间的关系形 态 (2)计算线性相关系数,说明两个变量之间的关系强度。 (3)利用最小二乘法求出估计的回归方程,并解释回归系数的实 际意义。
(1)绘制产量与生产费用的散点图,判断二者之间的关系形态。
产量与生产费用 200 180 160 140 120 100 80 60 40 20 0 0 20 40 60 80 产量 100 120 140 160 系列1
费用
产量和费用存在正的线性相关系数
2)计算产量与生产费用之间的线性相关系数。
1、提出假设:H0: ;H1: 0
2、计算检验的统计量
t r n 2 ~t( n 2 ) 2 1 r
1 2 2 t 0 . 9 2 0 2 7 . 4 3 5 4 5 3 t(12-2)=2.2281 2 10 . 9 2 0 2
根据显著性水平=0.05,查t分布表得t(n2)=2.2281由于t=7.435453>t(12-2)=2.2281, 拒绝H0,产量与生产费用之间存在着显著的正线性 相关关系
(1)绘制运送距离和运送时间的散点图,判断二者之间的关系形态
6.0 5Байду номын сангаас0
运送时间(天)
4.0 3.0 2.0 1.0 0.0 0 200 400 600 800 1000 运送距离(公里) 1200 1400 1600
根据图表显示,二者可能存在正线性相关关系
(2)计算线性相关系数,说明两个变量之间的关系强度
第10章 简单线性回归分析案例辨析及参考答案

,=0.698。经检验,贫血患者治疗后的血红蛋白增加量与治疗有 关。
正常人均数:=20.21+7.78×0=20.21 患 者均数:=20.21+7.78×1=27.99 截距与两样本均数的差值相等。分别进行回归方程的方差分析与回 归系数的t检验,得F=17.112,t=4.137。回归系数的t检验结果与两样 本均数的t检验结果完全一致。以上结果说明,t检验的结果可以转化为
Quadratic .9941206.902 2 14.000 60.78810.805-.292
Cubic
.9982575.942 3 13.000 81.857 3.490 .447-.023
Growth .924 182.200 1 15.000 4.539 .034
The independent variable is 年龄。
上述曲线类型依次为线性、二次、三次多项式曲线和生长曲线,由 拟合结果可知,曲线拟合效果较好,进一步得到曲线图(案例图101):
(3)选择合理的模型,列出回归方程。以女孩身高二次曲线为
例,方程如下: 多项式曲线: (4)统计预测:预测19岁女孩身高为60.788+10.805×18-
0.292×182=160.7,与实际趋势相符。其他预测方法相同。
案例10-2 贫血患者的血清转铁蛋白研究。第6章例6-1中,为研究 某种新药治疗贫血患者的效果,将20名贫血患者随机分成两组,一组用 新药,另一组用常规药物治疗,测得血红蛋白增加量(g/L)见表6-1。 问新药与常规药治疗贫血患者后的血红蛋白增加量有无差别?
张医生用检验比较新药与常规药治疗贫血患者后的血红蛋白增加 量,计算得:
第11章 多重线性回归分析思考与练习参考答案

第11章多重线性回归分析思考与练习参考答案一、最佳选择题1.逐步回归分析中,若增加自变量的个数,则(D)。
A.回归平方和与残差平方和均增大B.回归平方和与残差平方和均减小C.总平方和与回归平方和均增大D.回归平方和增大,残差平方和减小E.总平方和与回归平方和均减小2.下面关于自变量筛选的统计学标准中错误的是(E)。
A.残差平方和(SS残差)缩小B.确定系数(R)增大2C.残差的均方(MS残差)缩小D.调整确定系数(Rad)增大2E.Cp统计量增大3.多重线性回归分析中,能直接反映自变量解释因变量变异百分比的指标为(C)。
A.复相关系数B.简单相关系数C.确定系数D.偏回归系数E.偏相关系数4.多重线性回归分析中的共线性是指(E)。
A.Y关于各个自变量的回归系数相同B.Y关于各个自变量的回归系数与截距都相同C.Y变量与各个自变量的相关系数相同D.Y与自变量间有较高的复相关E.自变量间有较高的相关性5.多重线性回归分析中,若对某一自变量的值加上一个不为零的常数K,则有(D)。
A.截距和该偏回归系数值均不变B.该偏回归系数值为原有偏回归系数值的K 倍C.该偏回归系数值会改变,但无规律D.截距改变,但所有偏回归系数值均不改变E.所有偏回归系数值均不会改变二、思考题1.多重线性回归分析的用途有哪些?答:多重线性回归在生物医学研究中有广泛的应用,归纳起来,可以包括以下几个方面:定量地建立一个反应变量与多个解释变量之间的线性关系,筛选危险因素,通过较易测量的变量估计不易测量的变量,通过解释变量预测反应变量,通过反应变量控制解释变量。
2.多重线性回归模型中偏回归系数的含义是什么?答:偏回归系数的含义是:在控制其他自变量的水平不变的情况下,该自变量每改变一个单位,反应变量平均改变的单位数。
3.请解释用于多重线性回归参数估计的最小二乘法的含义。
答:最小二乘法的含义是:残差的平方和达到最小。
4.如何判断和处理多重共线性?答:如果自变量之间存在较强的相关,则存在多重共线性。
人教版选修【1-2】1.1《回归分析的基本思想及其初步应用》习题及答案

数学·选修1-2(人教A版)1.1回归分析的基本思想及其初步应用►达标训练1.下列结论正确的是( )①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.A.①② B.①②③C.①②④ D.①②③④解析:根据函数关系、相关关系、回归关系的概念可知选C.答案:C2.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是()A.总偏差平方和 B.残差平方和C.回归平方和 D.相关指数R2答案:B3.下表是某工厂6~9月份用电量(单位:万度)的一组数据:月份x 6789用电量y 653 2由散点图可知,用电量y与月份x间有较好的线性相关关系,其线性回归直线方程是错误!=-1。
4x+a,则a等于( )A.10.5 B.5。
25C.5。
2 D.14。
5解析:答案:D4.(2013·广东四校联考)某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元)423 5销售额y(万元)49263954根据上表可得回归方程错误!=错误!x+错误!中的错误!为9.4,据此模型预报广告费用为6万元时销售额为()A.63。
6万元 B.65.5万元C.67.7万元 D.72.0万元答案:B5.设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n 个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如右图),以下结论正确的是()A.直线l过点(错误!,错误!)B.x和y的相关系数为直线l的斜率C.x和y的相关系数在0到1之间D.当n为偶数时,分布在l两侧的样本点的个数一定相同答案:A6.两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( ) A.模型1:相关指数R2为0。
98B.模型2:相关指数R2为0。
统计学一元线性回归课后习题答案 ppt课件

2)=2.2281由于t=7.435453>t(12-2)=2.2281,
拒绝H0,产量与生产费用之间存在着显著的正线性
相关关系
统计学一元线性回归课后习题答案
11.2 学生在期末考试之前用于复习的时间(单位:小时)和考 试分数(单位:分)之间是否有关系?为研究这一问题,一位 研究者抽取了由8名学生构成的一个随机样本,取得的数据如 下:
81444968681133169213057950372ssr提出假设提出假设人均消费水平不人均人均消费水平不人均gdpgdp乊间的线性关系丌显著线性关系丌显著计算检验统计量计算检验统计量f确定显著性水平确定显著性水平005005并根据分子自由度并根据分子自由度11和分母自和分母自由度7722找出临界值找出临界值ff661661作出决策
人均GDP为5 000元时,人均消费水平95%的
置信区间为[1990.7491统5计,学一2元5线6性5回.4归6课3后9习9题]答案
解:根据前面的计算结果,已知n=7,t(7-2)=2.5706
n
se
yiy ˆi2
i 1
SSE305795.034361159.007
n2 n2
5
预测区间为
2 2 7 8 .1 0 7 8 2 .5 7 0 6 * 6 1 1 5 9 .0 0 71 + 1 5 0 0 0 4 5 1 5 .5 7 1 4 2
复习 时间X
考试 分数Y
20 16 34 23 27 32 18 22 64 61 84 70 88 92 72 77
统计学一元线性回归课后习题答案
要求:(1)绘制复习时间和考试分数的散点图,判断二者之 间的关系形态。
分数
100 90 80 70 60 50 40 30 20 10 0
思考与练习答案(预测)

思考与练习答案(预测)第⼀章思考与练习1.预测是指什么举例说明预测的作⽤。
答:预测是指根据客观事物的发展趋势和变化规律对特定的对象未来发展的趋势或状态做出科学的推测与判断。
预测可以为决策提供必要的未来信息,是进⾏决策的基础。
如在产品的销售⽅⾯,通过对顾客类型、市场占有份额、物价变动趋势、新产品开发等⽅⾯的预测,可以对市场销售起促进作⽤。
⼜如在⽣产⽅⾯,通过对原材料需求量、材料成本及劳动⼒成本的变动趋势以及材料与劳动⼒的可⽤量的变动趋势等⽅⾯的预测,便于企业对⽣产和库存进⾏计划,并在合理的成本上满⾜销售的需求2.预测有哪些基本原理预测有什么特点影响预测精确度的最主要的因素是什么如何提⾼预测的精确度答:预测的基本原理包括:系统性原理、连贯性原理、类推原理、相关性原理、概率推断原理。
预测的特点:⼀⽅⾯我们可以根据预测的基本原理,利⽤适当的预测⽅法对未来进⾏预测,因此预测是可能的;另⼀⽅⾯由于各种社会现象和⾃然现象的随机性以及⼈们认识能⼒的有限性等原因,因此不存在绝对准确的预测。
影响预测精确度的主要因素包括:预测资料的分析和预处理,预测问题的分析与认识、预测⽅法的选择和运⽤、预测结果的分析和处理等。
因此,要提⾼预测的精确度,需要从以上⼏个⽅⾯认真对待,从⽽为决策者提供可靠的未来信息。
3.叙述预测的基本步骤。
答:预测的基本步骤为;(1)确定预测⽬标;(2)收集、整理有关资料;(3)选择预测⽅法;(4)建⽴预测模型;(5)评价预测模型;(6)利⽤模型进⾏预测;(7)分析预测结果。
4.为什么要对收集的资料进⾏分析和预处理如何鉴别异常数据对异常数据应如何处理答:在预测⼯作中,所收集的资料是进⾏预测的基础,相关资料的缺少或数据的异常都会导致所建⽴的预测模型不准确,从⽽直接影响到预测的结果,所以需要对数据的异常情况进⾏鉴别与分析。
鉴别异常数据可采⽤图形观察法有统计滤波法。
异常数据处理的主要⽅法包括:剔除法、还原法、拉平法、⽐例法等。
第10章:定量预测5-因果关系分析法

ˆ Y t 1
=Yt(1+A%+B%+C%+D%+· · · · · · · · · · · · · · )
• 表示t+1期预测对象的预测值;表示t期预测对象的 实际值;A%表示预测对象受第一个因素影响的程 度;B%表示预测对象受第二个因素影响的程度; 以此类推。例如:见下页
• 例1: 已知某空调制造公司2006年销售中央 空调750套。市场调研人员通过对历史统计 资料的研究估计出,未来各因素影响销售 量的程度为:商品质量的提高和价格的降 低可使销量增加30%;国家经济政策的变 动(如紧缩)可能使销量减少10%;由于 规格不全而失去部分顾客,可能使未来销 量减少5%;居民收入的增加可能使未来销 量增加20%;同类产品的竞争可能使销量 减少8%,预测2007年企业空调的销售量?
• 4 变量遗漏问题 当回归结果与经济理论不一致时,重要变量 的遗漏可能是最主要的原因。 比如:有一个大学生进行需求预测,根据收 集到的历史资料进行回归后得到的预测方程为: Q=7.8+3.42P,价格系数为正值,并在统计上显 著。对这样的一个结果,我们认为不合常理,一 个解释是:价格一直上涨,但收入和人口数也增 加,价格和收入、人口呈现正相关,所以3.42反 映收入和人口增加而导致需求的增加。因此,为 了分别找出这些影响,全面合理的解释因变量的 变化,就需要在回归方程中增加新的变量。
解决方法:对自变量之间是否存在高度相关 进行检验,从方程中取消一个高度相关的 自变量。 多重共线性举例说明: SPSS的多重共线性诊断功能 Collinearty Diagnostics 数据10-2
• 我们曾经收集1985-2005年粮食产量(因变量)、 耕地面积、劳动人口等9个变量的数据,分别进 行一元回归。可决系数R2结果如下表(一般认为 可决系数大于0.7效果较好,否则效果较差。)
一元线性回归习题答案

一元线性回归习题答案一元线性回归是统计学中常用的一种回归分析方法,用于研究两个变量之间的关系。
在实际应用中,我们常常需要根据给定的数据集来建立一元线性回归模型,并通过该模型来预测或解释变量之间的关系。
本文将通过一些习题来解答一元线性回归的相关问题。
假设我们有一组数据集,包含了自变量x和因变量y的取值。
我们的目标是建立一个线性回归模型,用于预测y在给定x值时的取值。
首先,我们需要计算相关系数r来衡量x和y之间的线性关系强度。
相关系数的取值范围为-1到1,接近1表示正相关,接近-1表示负相关,接近0表示无相关。
接下来,我们可以使用最小二乘法来估计回归方程的参数。
最小二乘法的基本思想是通过最小化误差平方和来确定回归方程的参数。
回归方程的一般形式为y = a + bx,其中a为截距,b为斜率。
我们可以通过计算公式来求解a和b的值。
在实际计算中,我们可以使用统计软件或编程语言来进行计算。
例如,使用Python中的scikit-learn库可以很方便地进行一元线性回归分析。
以下是一个使用Python进行一元线性回归的示例代码:```pythonimport numpy as npfrom sklearn.linear_model import LinearRegression# 定义自变量和因变量的取值x = np.array([1, 2, 3, 4, 5])y = np.array([2, 4, 6, 8, 10])# 将自变量转换为二维数组X = x.reshape(-1, 1)# 创建线性回归模型model = LinearRegression()# 拟合数据model.fit(X, y)# 输出回归方程的参数print("截距a =", model.intercept_)print("斜率b =", model.coef_)```运行以上代码,我们可以得到回归方程的参数值。
第10章-简单线性回归分析思考与练习参考答案

第10章 简单线性回归分析思考与练习参考答案一、最佳选择题1.如果两样本的相关系数21r r =,样本量21n n =,那么( D )。
A. 回归系数21b b = B .回归系数12b b < C. 回归系数21b b > D .t 统计量11r b t t = E. 以上均错2.如果相关系数r =1,则一定有( C )。
A .总SS =残差SSB .残差SS =回归SSC .总SS =回归SSD .总SS >回归SS E.回归MS =残差MS3.记ρ为总体相关系数,r 为样本相关系数,b 为样本回归系数,下列( D )正确。
A .ρ=0时,r =0B .|r |>0时,b >0C .r >0时,b <0D .r <0时,b <0 E. |r |=1时,b =14.如果相关系数r =0,则一定有( D )。
A .简单线性回归的截距等于0B .简单线性回归的截距等于Y 或XC .简单线性回归的残差SS 等于0D .简单线性回归的残差SS 等于SS 总E .简单线性回归的总SS 等于05.用最小二乘法确定直线回归方程的含义是( B )。
A .各观测点距直线的纵向距离相等B .各观测点距直线的纵向距离平方和最小C .各观测点距直线的垂直距离相等D .各观测点距直线的垂直距离平方和最小E .各观测点距直线的纵向距离等于零二、思考题1.简述简单线性回归分析的基本步骤。
答:① 绘制散点图,考察是否有线性趋势及可疑的异常点;② 估计回归系数;③ 对总体回归系数或回归方程进行假设检验;④ 列出回归方程,绘制回归直线;⑤ 统计应用。
2.简述线性回归分析与线性相关的区别与联系。
答:区别:(1)资料要求上,进行直线回归分析的两变量,若X 为可精确测量和严格控制的变量,则对应于每个X 的Y 值要求服从正态分布;若X 、Y 都是随机变量,则要求X 、Y 服从双变量正态分布。
直线相关分析只适用于双变量正态分布资料。
回归分析练习题及参考答案
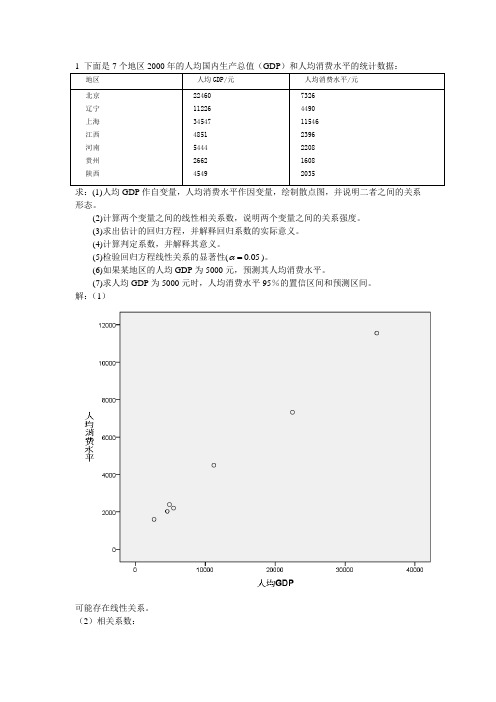
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
2024-2025年北师大版数学选择性必修第一册7.1.1-1.2一元线性回归(带答案)

第七章统计案例§1一元线性回归1.1 直线拟合1.2 一元线性回归方程必备知识基础练知识点一直线拟合1.下表提供了某厂利用节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.(1)(2)从散点图中可以看出,甲产品的产量和相应的生产能耗近似呈什么关系?(3)如果甲产品的产量为7吨,预测相应的生产能耗的吨数.知识点二一元线性回归方程2.[多选题]已知一组样本点(x i,y i),其中i=1,2,3,…,30,根据最小二乘法求得的回归方程是y=bx+a,则下列说法正确的是( )A.回归方程y=bx+a经过点(x,y )B.至少有一个样本点落在回归直线y=bx+a上C.对所有的x i(i=1,2,3,…,30),预报变量bx i+a的值一定与y i有误差D.若y=bx+a的斜率b>0,则变量x与y正相关3.已知变量x,y之间的一组数据如下表所示:若根据表中数据得出y+0.76x,则表中a的值为________.4.某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到的数据如下表所示:(1)(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?关键能力综合练一、选择题1.一位母亲记录了自己儿子3~9岁的身高数据(略),由此建立的身高与年龄的线性回归方程为Y=7.19X+73.93,用这个方程预测这个孩子10岁时的身高,则正确的叙述是( )A.身高一定是145.83 cmB.身高在145.83 cm以上C.身高在145.83 cm左右D.身高在145.83 cm以下2.下表显示出样本中y随x变化的一组数据,由此判断它最可能是( )A.C.指数函数模型D.对数函数模型3.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得回归方程为y=0.67x+54.9.若已知x1+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=( ) A.75 B.155.4C.375 D.466.24.某青少年成长关爱机构为了调研所在地区青少年的年龄与身高状况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1 000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列选项中对该样本描述错误的是( )A.据样本数据估计,该地区青少年的身高与年龄成正相关B.所抽取数据中,5 000名青少年的平均身高约为145 cmC.直线L的斜率的值近似等于样本中青少年平均身高每年的增量D.从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上5.已知变量x与y负相关,且由观测数据算得样本平均数x=4,y=5.6,则由该观测的数据算得的线性回归方程可能是( )A.y=0.4x+4 B.y=1.2x+0.7C.y=-0.6x+8 D.y=-0.7x+8.2二、填空题6.[易错题]某公司过去五个月的广告费支出x(单位:万元)与销售额y(单位:万元)之间有下列对应数据:且回归方程为y =6.5x +17.5,则下列说法:①销售额y 与广告费支出x 正相关;②丢失的数据(表中▲处)为30;③该公司广告费支出每增加1万元,销售额一定增加6.5万元;④若该公司下月广告费投入7万元,则销售额估计为60万元.其中,说法正确的是________.7.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的回归直线方程:∧y=0.254x +0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.8.[双空题]为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间X(单位:h )与当天投篮命中率Y 之间的关系:小李这56号打6小时篮球的投篮命中率为________.三、解答题9.记录某产品的单价x(元)与销售量y(件)的数据如下表所示:其中(1)已知y 与x 具有线性相关关系,求出y 关于x 的线性回归方程;(2)预测当单价为12元时,该产品的销售量.学科素养升级练1.[多选题]某企业节能降耗技术改造后,在生产某产品过程中记录的产量x (吨)与相应的生产能耗y (吨)的几组对应数据如表,现发现表中有个数据看不清,已知线性回归方程为∧y=6.3x +6.8,下列说法正确的是( )A .B .回归直线∧y =6.3x+6.8必经过样本点(4,★)C .回归系数6.3的含义是产量每增加1吨,相应的生产能耗一定增加6.3吨D .据此模型预测产量为7吨时,相应的生产能耗为50.9吨2.[学科素养——数据分析]某地随着经济的发展,居民收入逐年增长,该地一银行连续五年年底的储蓄存款情况如下表所示:为了计算方便,工作人员将上表的数据进行了处理,令t=x-2014,z=y-5,得到下表:(1)求z关于t(2)通过(1)中的方程,求出y关于x的线性回归方程;(3)用所求线性回归方程预测到2024年年底,该地此银行储蓄存款额可达到多少?§1一元线性回归1.1 直线拟合1.2 一元线性回归方程必备知识基础练1.解析:(1)由题中所给数据,可得散点图如图所示.(2)从散点图可以发现甲产品的产量和相应的生产能耗近似呈线性关系.(3)甲产品的产量为7吨时,相应的生产能耗大约为5吨.2.解析:线性回归方程y =bx +a 经过样本中心点(x ,y ),故A 正确;样本点可能都不在回归直线上,故B 错误;样本点可能在直线y =bx +a 上,即可以存在x i 对应的预报变量bx i +a 与y i 没有误差,故C 错误;若y =bx +a 的斜率b >0,则样本点的分布从左至右上升,变量x 与y 正相关,故D 正确.故选AD.答案:AD3.解析:由题意,可知x =14(5+6+7+8)=6.5.由回归直线过样本点的中心(x ,y ),得y =0.26+0.76x =0.26+0.76×6.5=5.2,由y =14(4+5+5.4+a )=5.2,解得a =6.4.答案:6.44.解析:(1)x =8+8.2+8.4+8.6+8.8+96 =8.5, y =90+84+83+80+75+686=80,=80+20×8.5=250,∴y 关于x 的线性回归方程为y =-20x +250.(2)设工厂获得的利润为L 万元,则L =(x -4)(-20x +250)=-20(x -8.25)2+361.25,∴预测把单价定为8.25元时,工厂获得最大利润,最大利润为361.25万元.关键能力综合练1.解析:由线性回归方程可得Y 0=7.19×10+73.93=145.83,所以预测这个孩子10岁时的身高在145.83 cm 左右.答案:C2.解析:画出散点图(图略),可以得到这些样本点在某一条直线上或该直线附近,故最可能是线性函数模型.答案:A3.解析:由题意,可得x =1505=30,代入回归方程中,可得y =0.67×30+54.9=75,所以y 1+y 2+y 3+y 4+y 5=5×y =375,故选C .答案:C4.解析:在给定范围内,随着年龄的增加,年龄越大身高越高,故该地区青少年的身高与年龄成正相关,故A 正确;用样本数据估计总体可得平均数大约是145 cm ,故B 正确;根据直线斜率的意义可知斜率的值近似等于样本中青少年平均身高每年的增量,故C 正确;各取一人具有随机性,根据数据做出的点可能在直线附近,不一定在直线上,故D 错误.故选D .答案:D5.解析:因为变量x 与y 负相关,所以b<0,排除A 、B 选项;将x =4,y =5.6代入检验即可得到C 是正确选项,故选C .答案:C6.解析:由回归方程为y =6.5x +17.5,可知b =6.5,则销售额y 与广告费支出x 正相关,所以①是正确的;设丢失的数据为a ,由表中的数据可得x =5,y =220+a 5,把点(5,220+a 5 )代入回归方程,可得220+a 5=6.5×5+17.5,解得a =30,所以②是正确的;该公司广告费支出每增加1万元,销售额应平均增加6.5万元,所以③不正确;若该公司下月广告费投入7万元,则销售额估计为y =6.5×7+17.5=63万元,所以④不正确.答案:①②7.解析:由题意知,[0.254(x +1)+0.321]-(0.254x +0.321)=0.254.答案:0.2548.解析:小李这5天的平均投篮命中率Y - =15×(0.4+0.5+0.6+0.6+0.4)=0.5,X - =3,∧b =0.110 =0.01,∧a =Y - -∧bX - =0.5-0.03=0.47. ∴线性回归方程为Y =0.01X +0.47,则当X 0=6时,Y 0=0.53.∴预测小李该月6号打6小时篮球的投篮命中率为0.53.答案:0.5 0.539.解析:(1)由题意,得x =15(6+7+8+9+10)=8, y =15(55+48+44+38+25)=42,∴b=1 610-5×8×42330-5×82 =-7,a =42-(-7)×8=98, ∴y 关于x 的线性回归方程为y =-7x +98.(2)当x =12时,y =-7×12+98=14,即当单价为12元时,该产品的销售量约为14件.学科素养升级练1.解析:设看不清的数字为a ,计算x - =15 ×(2+3+4+5+6)=4,y - =15×(19+25+a +38+44)=126+a 5 ,代入线性回归方程∧y =6.3x +6.8中,得126+a 5=6.3×4+6.8,解得a =34,所以y - =32,所以看不清的数据★的值为34,A 正确;又回归直线∧y=6.3x +6.8过样本点(4,32),所以B 错误;回归系数6.3的含义是产量每增加1吨,相应的生产能耗预测增加6.3吨,所以C 错误;x =7时,∧y=6.3x +6.8=6.3×7+6.8=50.9,所以据此模型预测产量为7吨时,相应的生产能耗为50.9吨,D 正确.故选AD .答案:AD2.解析:(1)t - =3,z - =2.2,所以z 关于t 的线性回归方程为∧z=1.2t -1.4. (2) ∧z=1.2t -1.4, 代入t =x -2014,z =y -5,得∧y-5=1.2(x -2014)-1.4, 即∧y=1.2x -2 413.2. 故y 关于x 的线性回归方程为∧y=1.2x -2 413.2. (3)由(1)中的线性回归方程,预测到2024年年底,该地此银行储蓄存款额可达到1.2×2024-2 413.2=15.6(千亿元).。
应用回归分析第四版课后习题答案_全_何晓群_刘文卿

实用回归分析第四版第一章回归分析概述1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i=0 。
证明:∑∑+-=-=niiiniXYYYQ12121))ˆˆ(()ˆ(ββ其中:即: ∑e i =0 ,∑e i X i =02.5 证明0ˆβ是β0的无偏估计。
证明:)1[)ˆ()ˆ(1110∑∑==--=-=ni i xxi n i i Y L X X X Y n E X Y E E ββ )] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==1010)()1(])1([βεβεβ=--+=--+=∑∑==i xx i ni i xx i ni E L X X X nL X X X n E 2.6 证明 证明:)] ()1([])1([)ˆ(102110i i xxi ni ixx i ni X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑== 222212]1[])(2)1[(σσxx xx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7 证明平方和分解公式:SST=SSE+SSR证明:2.8 验证三种检验的关系,即验证: (1)21)2(r r n t --=;(2)2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 01ˆˆˆˆi i i i iY X e Y Y ββ=+=-())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSESSR )Y ˆY Y Y ˆn1i 2ii n1i 2i +=-+-=∑∑==0100ˆˆQQββ∂∂==∂∂证明:(1)ˆt======(2)2222201111 1111ˆˆˆˆˆˆ()()(())(()) n n n ni i i i xxi i i iSSR y y x y y x x y x x Lβββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xxLSSRF tSSE nβσ∴===-2.9 验证(2.63)式:2211σ)L)xx(n()e(Varxxii---=证明:0112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i ii i i ii ixx xxixxe y y y y y yy x y y x xx x x xn L n Lx xn Lβββσσσσ=-=+-=++-+---=++-+-=--其中:222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxixxiniixxiiiniiiiiiiiLxxnLxxnyLxxyCovxxynyCovxxyCovyyCovxxyyCov-+=-+=--+=-+=-+∑∑==2.10 用第9题证明是σ2的无偏估计量证明:2221122112211ˆˆ()()()22()111var()[1]221(2)2n ni ii in niii i xxE E y y E en nx xen n n Lnnσσσσ=====-=---==----=-=-∑∑∑∑第三章2ˆ22-=∑neiσ1.一个回归方程的复相关系数R=0.99,样本决定系数R 2=0.9801,我们能判断这个回归方程就很理想吗? 答:不能断定这个回归方程理想。
人教版高考数学总复习第一部分考点指导第十章第三节变量的相关性与一元线性回归模型列联表与独立性检验

i1
,其中 (yi yi )2 是残差平
(yi y)2
i1
i1
方和,R2 越大,残差平方和_越__小__,模型的拟合效果_越__好__.R2 越小,残差平方和
_越___大__,模型的拟合效果__越__差___.
5.列联表与独立性检验
(1)关于分类变量 X 和 Y 的抽样数据的 2×2 列联表:
【解析】选 C.因为 χ2=5,根据临界值表知 P(χ2≥3.841) =0.05,P(χ2≥6.635) =0.01,
故有 95%以上的把握认为“X 和 Y 有关系”.
4.(回归方程的性质)(多选题)在统计中,由一组样本数据(x1,y1),(x2,y2),…, (xn,yn)利用最小二乘法得到两个变量的经验回归方程为 = x+ ,,那么下列说法 正确的是( ) A.样本相关系数 r 不可能等于 1
X YY=0Y=1合计 X=0 a b a+b X=1 c d c+d
合计a+c b+dn=a+b+c+d
n(ad-bc)2
计算随机变量 χ2=
,利用 χ2 的取值推断
(a+b)(c+d)(a+c)(b+d)
分类变量 X 和 Y_是__否__独__立__的方法称为 χ2 独立性检验.
(2)独立性检验【3】 基于小概率值 α 的检验规则: 当 χ2≥xa 时,推断 H0 不成立,即认为 X 和 Y 不独立,该推断犯错误的概率不超过 α; 当 χ2<xa 时,没有充分证据推断 H0 不成立,可以认为 X 和 Y 独立. 利用 χ2 的取值推断分类变量 X 和 Y 是否独立的方法称为 χ2 独立性检验,简称独立 性检验.
x0 1 3 4 y 2.2 4.3 4.8 6.7
一元线性回归模型(习题与解答)

资料来源:总统经济报告,1997,CPI 指数见表 B-60,第 380 页;S&P 指数见表 B-93,第 406 页。
$x +μ $ +β ⑶ yt = α t t $x +μ $+β $t = α ⑷ y t t $x $+β ⑸ yt = α t $x $+β $t = α ⑹ y t $x +μ $+β $t ⑺ yt = α t $x +μ $+β $t $t = α ⑻ y t t = 1,2, L , n t = 1,2, L , n t = 1,2, L , n t = 1,2, L , n t = 1,2, L , n t = 1,2, L , n
(二)基本证明与问答类题型
2
2-4.对于一元线性回归模型,试证明: (1) E ( y i ) = α + β xi (2) D( y i ) = σ
2
(3) Cov( y i , y j ) = 0
i≠ j
2-5.参数估计量的无偏性和有效性的含义是什么?从参数估计量的无偏性和有效性证明过 程说明, 为什么说满足基本假设的计量经济学模型的普通最小二乘参数估计量才具有无偏性 和有效性? 2-6.对于过原点回归模型 Yi =
3
或债券的收益率;rm 表示有价证券的收益率(用市场指数表示,如标准普尔 500 指数) ;t 表示时间。在投资分析中,β1 被称为债券的安全系数β,是用来度量市场的风险程度的, 即市场的发展对公司的财产有何影响。依据 1956~1976 年间 240 个月的数据,Fogler 和 Ganpathy 得到 IBM 股票的回归方程;市场指数是在芝加哥大学建立的市场有价证券指数:
统计学一元线性回归课后习题答案

人均消费水平
10000 8000 6000 4000 2000 0 0 10000 20000 人均GDP 30000 40000 系列1
产量和生产费用之间存在着正的线性相关关系
(2)计算两个变量之间的线性相关系数,说明两个变量之 间的关系强度。
r
2 2 n n x x y y 2 2
说明两个变量之间高度相关
(3)利用最小二乘法求出估计的回归方程,并解释回归系数的实际 意义。
n n n x x y iy i i i 1 1 1 i i ˆ i 1 2 n n 2 n x x i i i 1 1 i
11.4 设SSR=36,SSE=4,n=18 要求:1)计算判定系数R^2并解释其意义
S S R S S R 3 6 R 0 . 9 S S TS S TS S E4 0
2
回归直线对观测值的拟合程度为0.9,说明变量Y的 变异性中有90%是由自变量x引起的。 2)计算估计标准误差s
2 x x 0 n 2 x x i i 1
置信区间为
ˆ y t n 2 ) s 0 2( e 1 n
5 0 0 0 4 5 1 5 . 5 7 1 4 1 2 2 7 8 . 1 0 7 8 2 . 5 7 0 6 * 6 1 1 5 9 . 0 0 7 7 1 3 6 2 5 1 2 7 . 2 9
n
ˆ y ˆx 0 1
将表中数据代入公式得:
{
=0.003585 =0.118129
∴y=0.118129 + 0.003585x
y关于x的回归方程为y=0.118129 + 0.003585x表示运输距离每增加1公里, 运送时间平均增加 0.003585天。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章 简单线性回归分析
思考与练习参考答案
一、最佳选择题
1.如果两样本的相关系数21r r =,样本量21n n =,那么( D )。
A. 回归系数21b b = B .回归系数12b b < C. 回归系数21b b > D .t 统计量11r b t t = E. 以上均错
2.如果相关系数r =1,则一定有( C )。
A .总SS =残差SS
B .残差SS =回归
SS
C .总SS =回归SS
D .总SS >回归SS E.
回归MS =残差MS
3.记ρ为总体相关系数,r 为样本相关系数,b 为样本回归系数,下列( D )正确。
A .ρ=0时,r =0
B .|r |>0时,b >0
C .r >0时,b <0
D .r <0时,b <0 E. |r |=1时,b =1
4.如果相关系数r =0,则一定有( D )。
A .简单线性回归的截距等于0
B .简单线性回归的截距等于Y 或X
C .简单线性回归的残差SS 等于0
D .简单线性回归的残差SS 等于SS 总
E .简单线性回归的总SS 等于0
5.用最小二乘法确定直线回归方程的含义是( B )。
A .各观测点距直线的纵向距离相等
B .各观测点距直线的纵向距离平方和最小
C .各观测点距直线的垂直距离相等
D .各观测点距直线的垂直距离平方和最小
E .各观测点距直线的纵向距离等于零
二、思考题
1.简述简单线性回归分析的基本步骤。
答:① 绘制散点图,考察是否有线性趋势及可疑的异常点;② 估计回归系数;③ 对总体回归系数或回归方程进行假设检验;④ 列出回归方程,绘制回归直线;⑤ 统计应用。
2.简述线性回归分析与线性相关的区别与联系。
答:区别:
(1)资料要求上,进行直线回归分析的两变量,若X 为可精确测量和严格控制的变量,则对应于每个X 的Y 值要求服从正态分布;若X 、Y 都是随机变量,则要求X 、Y 服从双变量正态分布。
直线相关分析只适用于双变量正态分布资料。
(2)应用上,说明两变量线性依存的数量关系用回归(定量分析),说明两变量的相关关系用相关(定性分析)。
(3)两个系数的意义不同。
r 说明具有直线关系的两变量间相互关系的方向与密切程度,b 表示X 每变化一个单位所导致Y 的平均变化量。
(4)两个系数的取值范围不同:-1≤r ≤1,∞<<∞-b 。
(5)两个系数的单位不同:r 没有单位,b 有单位。
联系:
(1)对同一双变量资料,回归系数b 与相关系数r 的正负号一致。
b >0时,r >0,均表示两变量X 、Y 同向变化;b <0时,r <0,均表示两变量X 、Y 反向变化。
(2)回归系数b 与相关系数r 的假设检验等价,即对同一双变量资料,r b t t =。
由于相关系数r 的假设检验较回归系数b 的假设检验简单,故在实际应用中常以r 的假设检验代替b 的假设检验。
(3)用回归解释相关:由于决定系数2
R =SS 回 /SS 总 ,当总平方和固定时,回归平方和的大小决定了相关的密切程度。
回归平方和越接近总平方和,则2
R 越接近1,说明引入相关的效果越好。
例如当r =0.20,n =100时,可按检验水准0.05拒绝H 0,接受H 1,认为两变量有相关关系。
但2
R =(0.20)2=0.04,表示回归平方和在总平方和中仅占4%,说明两变量间的相关关系实际意义不大。
3. 决定系数与相关系数的意义相同吗?如果不一样,两者关系如何?
答:现将相关系数、决定系数与Y 的总变异的关系阐释如下:假如在一回归分析中,回归系数的变异数回归SS =9,而Y 的总变异数总SS =13,则
决定系数2
R =回归SS / 总SS =9/14=0.642 9/1,相关系数R =0.801 8
即将决定系数表示为一比值关系,当总SS = l 时,则回归SS = 0.642 9,我们可以采用直角三角形的“勾股定理”图示决定系数与相关系数的关系,如练习图10-1所示。
练习图10-1 相关系数、决定系数与总变异的关系
三、计算题
1. 以例10-1中空气一氧化氮(NO)为因变量,风速(X4)为自变量,采用统计软件完成如下分析:
(1)试用简单线性回归方程来描述空气中NO浓度与风速之间的关系。
(2)对回归方程和回归系数分别进行假设检验。
(3)绘制回归直线图。
(4)根据以上的计算结果,进一步求其总体回归系数的95%置信区间。
(5)风速为1.50 m/s时,分别计算个体Y值的95%容许区间和Y的总体均数的95%置信区间,并说明两者的意义。
解:运用SPSS进行处理,主要分析结果如下:
(1)简单线性回归方程、假设检验结果及总体回归系数的95%置信区间如下:
(2)方差分析结果:
(3)回归直线如练习图10-2。
练习图10-2 回归直线图
2. 教材表10-8为本章例10-1回归分析的部分结果,依次为X 、Y 、Y 的估计值(Y ˆ)与残差(e ),请以相关分析考察四者之间的关系,以回归分析考察Y ˆ与X 、Y 与Y ˆ、Y 与Y
Y ˆ-、Y Y ˆ-与X 之间的关系,并予以解释。
教材表10-8 案例分析中回归分析的部分结果
解:主要分析结果:
(1)四者之间的相关系数
** Correlation is significant at the 0.01 level (2-tailed).
(2)四个变量间的回归系数 因变量
自变量
截距 回归系数 t
P
Y ˆ X
-0.136 0.159 456.016 0.000 Y
Y
ˆ 1.005 0.001 6.457 0.000 Y
Y
Y ˆ- 0.088
0.999
3.394 0.003 Y
Y ˆ- X
0.000 014 7 0.000 010 5
0.000
1.000
Y
ˆ与X 呈完全正相关关系,回归系数t 检验结果P =0.000,表明Y ˆ的变异可由X 完全解释。
Y 与Y
ˆ的相关系数与Y 与X 的相关系数相同,表明正是由于X 的影响引起Y 的变异,Y 与Y
ˆ关系即体现了Y 与X 的变化关系。
Y 与Y
Y ˆ-体现了扣除X 的影响后,Y 与残差仍呈正相关关系。
Y
Y ˆ-与X 呈零相关关系,表明扣除了X 的影响,回归方程的残差与X 不再有相关或回归关系。
(张岩波 郝元涛)。
