公开课相似三角形专题复习PPT课件

合集下载

公开课相似三角形专题复习 ppt课件

B
D
C
ppt课件
15
A
D
A
B
E
C
D
A
B
E
C
D
B
E
C
AD
α
αα
B
E
C
A
α
B
F D
α
E
α
C
C
B
D
ppt课件α α
OP
α
A
16
思考题：已知：等边△ABC 中，P为直线AC上
一动点，连结BP,作∠BPQ=60°,交直线BC于点
N.
(1)当P在线段AC上时，证明PA·PC=AB ·CN
(2)若P在AC的延长线上，上述关系是否成立？
A
D
A
D
F
F
B
E
C
ppt课件 B
E
C
10
A
△ABE∽ △ECF（（21））点点EE为为BBCC上上任任意意一一点点，
若若∠∠BB==∠∠CC==α6,0∠°A, EF= F ∠∠CA,E则F△= A∠BCE,则与△AEBCEF与
的△关E系C还F的成关立系吗还？成立吗？
B
E
C 说A 明理由
A
A
FF F
A
2.若△ABC∽△ADE，你可以得出什么结论？
D B
“A”型
角： ∠ADE= ∠ B ∠ AED= ∠C
E 边：DE ∥ BC
AD AE DE .
C AB AC BC
AD AE . DB EC
DB EC

.
AB AC
面积： SADE ppt课件
DE 2.

第12讲相似三角形的判定复习课件(共46张PPT)

全效优等生
大师导航归类探究自主招生交流平台思维训练
4．如图4－12－5，AB是半圆O的直径， D，E是半圆上任意两点，连结AD，DE，AE 与BD相交于点C，要使△ADC与△ABD类似，可以添加一个条件．下列添加的条件其中错误
的是 A．∠ACD＝∠DAB B．AD＝DE C．AD2＝BD·CD D．AD·AB＝AC·BD
大师导航归类探究自主招生交流平台思维训练
第四章类似三角形
第12讲类似三角形的判定
全效优等生
全效优等生
大师导航归类探究自主招生交流平台思维训练
部分数学符号的来历数学运算中经常使用符号，如＋，－，×，÷，＝，＞，＜，∽，≌，()，等，你知道它们都是谁首先使用，何时被人们公认的吗？加减号“＋”“－”：1489 年德国数学家魏德曼在他的著作中首先使用了这两个符号，但正式为大家公认是从 1514 年荷兰数学家荷伊克开始．乘号“×”：英国数学家奥屈特于 1631 年提出用“×”表示相乘；另一乘号“·”是数学家赫锐奥特首创的．除号“÷”：最初这个符号是作为减号在欧洲大陆流行，奥屈特用“∶”表示除或比，也有人用分数线表示比，后来有人把二者结合起来就变成了“÷”．瑞士的数学家拉哈的著作中正式把“÷”作为除号．等号“＝”：最初是 1540 年由英国牛
D.147
大师导航归类探究自主招生交流平台思维训练
【解析】 ∵∠C＝∠E，∠ADC＝∠BDE， ∴△ADC∽△BDE，∴DDEC＝ABDD，又∵AD∶DE＝3∶5，AE＝8， ∴AD＝3，DE＝5， ∵BD＝4，∴D5C＝34，∴DC＝145.
∵AC⊥BC，∴∠ACB＝90°，
又∵BE是∠ABC的平分线， ∴FG＝FC，
例2答图

相似三角形HL判定公开课获奖课件省赛课一等奖课件

例 1 .如图， ∠DEB= ∠ACB=90o，DE=2，AB=5，BC=3， BD=2.5,求证：AB平分∠DBC。
5 2 2.5
3
例2. 如图，CE交△ABC旳高线AD于点O，交AB 于E，且OC ·BD=AB ·OD，求证：CE⊥AB.
先证△ADB∽△CDO ∴∠BAD=∠DCO
再证△AOE∽△COD
A'B' B'C' AB BC
求证： Rt⊿ABC∽Rt⊿A′B′C′
设
A'B' AB
B'C' BC
k
B
C
A′
A′B′=k AB
B′C′=k BC
A′C′=
AC=
A'C' AC
B′ C′
相同三角鉴定定理4 (HL)
斜边和一条直角边相应成百分比旳两个直角三角形相同.
A
B
C
B1
A1
Rt△ABC 和 Rt△A1B1C1.
假如 AB BC k,
A1B1 B1C1
C1 那么 △ABC∽△A1B1C1.
练习一：在Rt△ABC和Rt△A′B′C′中，已知∠C=∠C′=90°。根据
下列各组条件鉴定这两个三角形是不是相同，并阐明为何。
1.∠A=25°，∠B′=65°。相同 2.AC=3，BC=4，A′C′=6，B′C′=8。相同
相同三角形鉴定措施
1、（平行法）平行于三角形一边旳直线与其他两边(或
两边旳延长线)相交，所构成旳三角形与原三角形相同。 2、SSS（鉴定1）三组相应边旳比相等旳两个三角形
相同。 3、SAS（鉴定2）两组相应边之比相等且夹角相等旳
两个三角形相同。 4、AA（鉴定3）两角相应相等旳两个三角形相同。

第二十四章-相似三角形-复习ppt课件

第二十四章相似三角形复习课件
1
一、本章知识结构图
放缩与相似形
比例线段
相
比例线段
似
三角形一边的平行线
相似三角形
判定性质
平面向量
实数与向量相乘
向量的线性运算
2
回顾与思考
一、相似形
1. 各角对应相等，各边对应成比例的两个多边形叫相似多边形. 2. 三个角对应相等，三条边对应成比例的两个三角形叫相似三角形.两个相似三角形用“∽”表示，读做 “相似于”.
（2）以连接后的这两个向量为邻边向量构造平行四边形
（3）这个平行四边形的对角线向量就是这两个向量的和向量与差向量
3.向量加法和减法的三角形法则加法：一终二起，一起二终减法：共起点指向被减
9
五、典例精析，复习新知
2.如图，在△ABC中，AB=AC=27，D在AC上，且 BD=BC=18，DE//BC交AB于E，则DE= 分析：由△ABC∽△BCD，列出比例式，求出CD，再用 △ABC∽△AED A答案：10
称比例线段．此时也称这四条线段成比例．
4
➢ 线段的比要注意以下几点： • 线段的比是正数 • 单位要统一 • 线段的比与线段的长度无关
如果（b=d=f≠0）,
那么
如果，
，那么ad＝bc．
如果ad＝bc（a、b、c、d都不等于0），那么
.
5
三、相似三角形的判定与性质方法1：通过定义（不常用）
方法2：平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似; 方法3：两对应角相等的,两三角形相似. 方法4：两边对应成比例且夹角相等,两三角形相似. 方法5：三边对应成比例的,两三角形相似.

相似三角形判定复习公开课PPT课件

A. 1
B. 2条 C. 3条
D. 4条
）C
2.点P是△ABC中AB边上的一点，过P作直线（不与直线AB重合）截△ABC，使截得的三角形与原三角形相似，满足这样条件的直线最多有几条？请分别画出来．
3.在△ABC中，P是AB上的动点（P异于A，B），过点P的一条直线截 △ABC，使截得的三角形与△ABC相似，如图，∠A=36°，AB=AC，当点P在AC的垂直平分线上时，过点P的△ABC的相似线最多
第19页/共21页
如图，在矩形ABCD中，AB=6,BC=8,点M,N 分别在边BC,AD上，沿直线MN对
第20页/共21页
感谢您的观看！
第21页/共21页
第18页/共21页
（1）如图1,在等边△ABC中,点M是边BC上的任意一点（不含端点B、C）,联结AM,以AM为边作等边△AMN,联结CN．求证： ∠ABC=∠ACN．【类比探究】（2）如图2,在等边△ABC中,点M是边BC延长线上的任意一点（不含端点C）,其它条件不变,（1）中结论∠ABC=∠ACN还成立吗？请说明理由．【拓展延伸】（3）如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点（不含端点B、C）,联结AM,以AM为边作等腰△AMN,使顶角 ∠AMN=∠ABC．联结CN．试探究∠ABC与∠ACN的数量关系,并说明理由．
有 3 条．
第7页/共21页
练习1 如图，∠ABC=90°，
A
BD⊥AC于D，AD=9，
DC=4 ，则BD的长为 .
9
D
4
?
C
B
第8页/共21页
A
D B
∠ACB=90º CD⊥AB
B
（“类A”型）

《相似三角形》ppt课件-2024鲜版

2024/3/27
7
02
相似三角形判定定理及其应用
2024/3/27
8
平行线截割定理
01
02
03
定理内容
两条平行线被一组横截线所截，则对应线段成比例。
2024/3/27
定理证明
通过相似三角形的性质进行证明。
应用场景
在几何证明题中，常用于证明线段之间的比例关系。
9
三角形中位线定理
定理内容
2024/3/27
21
其他实际问题应用举例
2024/3/27
摄影中的透视问题
在摄影中，由于透视效应的存在，照片中的物体可能会产生变形。利用相似三角形原理可以对照片进行透视校正，恢复物体的真实形状。
地理信息系统（GIS）中的应用
在GIS中，经常需要处理地理空间数据。利用相似三角形原理可以对地图进行缩放、旋转和平移等操作，实现地理空间数据的可视化和分析。
似。
2024/3/27
4
相似之比称为相似比。
性质
01
相似三角形的对应角相等。
02
03
相似三角形的对应边成比例。
04
2024/3/27
05
相似三角形的面积比等于相似比的平方。
5
相似三角形对应角相等
2024/3/27
对应角
在两个相似三角形中，相互对应的角称为对应角。
解析
由于△ABC与△DEF全等，所以△DEF的周长等于△ABC的周长，即5cm + 7cm + 6cm = 18cm。
2. 例2
解析
已知△ABC与△PQR相似，且AB:PQ=2:3。若△ABC的面积为12cm²，求△PQR的面积。

相似三角形判定性质复习课公开课ppt课件

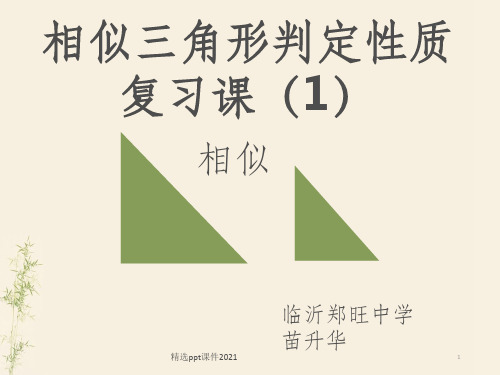
三边定理，两边夹角定理，角角定理
精选ppt课件2021
6
知识回顾、加强理解
4,（2014•湖南张家界，第10题，3分）如图，
△ABC中，D、E分别为AB、AC的中点，则△ADE 与△ABC的面积比为__________
△ADE与梯形DECB的面积比__________
1，若AF⊥BC,AN:AF=__________
精选ppt课件2021
12
分享收获、方法总结
1、知识层面…… 2、题型层面…… 3、思想方法层面……
精选ppt课件2021
13
分享收获、方法总结
分类讨论
Hale Waihona Puke 方程思想动点转化思想
问题
求线段
面积之
动点问题
比
数形结合
题证明
判定
性质
定的相
性似
质三
和角
判形精选ppt课件2021
14
达标检测、一显身手
纸上得来终觉浅，绝知此事要躬行。
讲解任务分配：
第一组：第1题第二组：第2题第三组：第3题第四组：第4题第五组：第5题第六组：总结
精选ppt课件2021
3
知识回顾、加强理解
1、如图，在平行四边形ABCD中, F是AD延长线上一点,
连接BF交DC与点E,则图中相似三角形共有(
)
A.0对 C.2对
尝试应用、方法总结
例1（2010·珠海)如图，在平行四边ABCD中，过点A作AE⊥BC，垂足为E，连结DE，F为线段DE上一点，且∠AFE＝∠B. (1)求证：△ADF∽△DEC. (2)若AB＝4，AD＝3 ，AE＝3 求AF的长．
精选ppt课件2021

相似三角形的性质公开课ppt课件

01
相似三角形的定义
两个三角形如果它们的对应角相等，则这两个三角形相似。
02
相似三角形的性质
相似三角形的对应边成比例，对应角相等，面积比等于相似
比的平方。
03
相似三角形的判定
通过比较两个三角形的对应角或对应边来判断它们是否相似
。
解题技巧归纳
寻找相似三角形
在复杂的图形中，通过观察和分析，找出可能相似的三角形。
与全等三角形关系
全等三角形是特殊的相似三角形，当相似比为1时，两个三角形
全等。
全等三角形的性质在相似三角形中同样适用，如对应边、对应角相等，周长、面积等性质也可以
类比到相似三角形中。
在研究相似三角形时，可以利用全等三角形的性质进行推导和证
明。
02
相似三角形性质探究
对应角相等
相似三角形的对应角相等，即如果两个三角形相似，那么它们的对应角必定相等。
，能够独立思考并解决问题。
学习态度与习惯
在学习过程中，我始终保持积极的学习态度和良好的学习习惯，认真听讲、积极思考、及时复习
。
THANKS
个三角形相似。
相似三角形的对应角相等，对应边成比例，面积比等于相似比的
平方。
02
性质
判定方法
预备定理
平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似。
SSS相似
三边对应成比例，则两个三角形相似。
SAS相似
两边对应成比例且夹角相等，则两个三角形相似。
AA相似
两角对应相等，则两个三角形相似。
在证明过程中，需要注意证明两个三角形相似的条件以及对应角的确定。
通过构造相似三角形，可以找到与已知角相等的另外一个角，从而证明角度相等关系。

相似三角形复习公开课 ppt课件

② AM2=MD ·ME
B
C
D
B
E
A D
M
C
D
C
3. 如图，AB∥CD，AO=OB，
O
DF=FB，DF交AC于E，
E
求证：ED2=EO ·EC.
ppt课件 A
F
B7
1.(1) △ ABC中，D、E分别是AB、AC上的点，
且∠AED= ∠ B，那么△ AED ∽ △ ABC，
从而
AD ()
DE =BC
∵ △DEF∽△ABC
D
E ∴ DE:EF=6:3
即 10:EF=6:3
∴ EF=5cm
ppt课件
11
4. 如图，△ADE∽ △ACB, 则DE:BC=_____ 。
2A D3
7
E
3
B
C
解: ∵ △ADE∽△ACB
且
AE AD 1 AB =AC =3
∴
DE BC
AE =AB
1 =3
ppt课件
12
1. D为△ABC中AB边上一点，∠ACD= ∠ ABC.
即 AB:AD=5:2
B
C
∴AD:AB=2:5
即△ADE与△ABC的相似比为2:5
ppt课件
10
3.已知三角形甲各边的比为3:4:6，和它相似的三角形乙
的最大边为10cm，则三角形乙的最短边为______cm.
C
A
B
F
解: 设三角形甲为△ABC ，三角形乙为 △DEF，且△DEF的最大边为DE，最短边为EF
所在的三角形相似。
O E
证明：∵ AB∥CD
∴ ∠C=∠A ∵ AO=OB，DF=FB

相似三角形的判定PPT示范课公开课获奖课件省赛课一等奖课件

4
5
6 2
相同三角形旳鉴定措施
平行于三角形一边旳直线与其他两边 (或延长线)相交,所构成旳三角形与原三角形相同;
三边相应成百分比,两三角形相同.
•不经历风雨，怎么见彩虹 •没有人能随随便便成功!
(2) AB=12cm， BC=15cm， AC＝24cm A’B’＝16cm，B’C’＝20cm，A’C’＝30
如图已知 AB BC AC ，试阐明∠BAD=∠CAE.
AD DE AE
证明 AB BC AC AD DE AE
A E
∴ΔABC∽ΔADE
D C
∴∠BAC=∠DAE
B
∴∠BAC━∠DAC=∠DAE━∠DAC
１、两个全等三角形一定相同吗？为何？相同比是多少？
２、两个直角三角形一定相同吗？为何？两个等腰直角三角形呢？
３、两个等腰三角形一定相同吗？为何？两个等边三角形呢？
300
450
它们是相同三角形吗？为何？
A
A′
5 82° 3
82°
B 47°
66
C 10
6
51°
△ABC和△A’B’C’中,假如
△ABC∽△A’B’C’
假如一种三角形旳三条边和另一种三角形旳三条边相应成百分比,那么这两个三角形相同.
简朴地说:三边相应成百分比,两三角形相同.
例1：在△ABC和△A′B′C′中，已知：
(1)AB＝6 cm， BC＝8 cm，AC＝10 cm，
A′B′＝18 cm，B′C′＝24 cm，A′C′＝30 cm．试鉴定△ABC与A′B′C′是否相同，并阐明理由．
类似于鉴定三角形全等旳措施，我们还能不能经过三边来判断两个三角形相同呢？

相似三角形专题复习(共66张PPT)

2.右图中,若D,E分别是AB,AC
DE
边上的中点,且DE=4则BC= ＿＿＿＿8
B
C
3.右图中, DE∥BC，S△ADE:S四边形DBCE = 1:8,则AE:AC=＿＿1:＿3 ＿＿
相似三角形专题复习(共66张PPT)
相似三角形专题复习(共66张PPT)
4. 在△ABCAC=4,AB=5.D是AC上一动点, 且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.试确定x的取值范围.
相似三角形专题复习(共66张PPT)
相似三角形专题复习(共66张PPT)
三、基本图形的形成、变化及发展过程：
平行型
.
旋转
∽
斜交型
.
.
.
平移
特殊垂直型
平移
.. 特殊
相似三角形专题复习(共66张PPT)
相似三角形专题复习(共66张PPT)
四、运用 ☞
1.添加一个条件，使△AOB∽ △ DOC
A
B
E
C
A
A
A
FF F
α66α00°°
BBB
αα6600°°
EEE
6α6α00°°
CCC
相似三角形专题复习(共66张PPT)
相似三角形专题复习(共66张PPT)
α
B
α
B
D
A
F
α
E
问题2：
（12）延长BA、CF相交于点 D点,且D,E且善为E于B为运CB的用C类的中比点中、，点若，若 ∠B=∠迁C=移α的,数∠学AE方F法= ∠ C,连 α C 结当A∠AF.EF旋解转决问到题如图位置时， ① 上找述出关图系中还的成相立似吗三？角形

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解：角： ∠B= ∠ 2或∠ 1= ∠ C 边： AD：AC=AE：AB
斜交型
.
8
4、已知CD是Rt△ACB斜边AB上的高，且CD=6，
BD=12，则AD=___3_____,AC=___3 __5____。
C
6
A 3D
12
垂直型
AC 2 AD • AB BC 2 DB • AB CD 2 AD • DB
.
4
基本图形的形成、变化及发展过程：
平行型
.
∽
斜交型 .
旋转 .
.
平移
特殊垂直型
平移
.. 特殊
.
5
运用模型☞
1.添加一个条件，使△AOB∽ △ DOC
A
B
O 解：角： ∠B= ∠ C或∠ A= ∠ D 边：AB ∥ CD
AO：OD=BO：CO
C
D
“X” 型
.
6
运用模型 ☞
A
2.若△ABC∽△ADE，你可以得出什么结论？
.
2
相似三角形
E
E M
D N
F
M
G
F N
H G
若G为BC中点,EG交AB于点F, 且EF:FG=2:3,
试求AF:FB的值.
添平行线构造相似三角形的基本图形。
.
3
相似三角形
E
E
F M
G
F
N
G
若G为BC中点,EG交AB于点F, 且EF:FG=2:3,
试求AF:FB的值.
添平行线构造相似三角形的基本图形。
相似三角形专题
基本模型及应用
.
1
试一试
E
D
M
N
H
过D作DH∥EC交BC延长线于点 H (1)试找出图中的相似三角形? ⊿ADE∽ ⊿ABC ∽ ⊿DBH
(2)若AE:AC=1:2,则AC:DH=2：__3_____;
(3)若⊿ABC的周长为4,则⊿BDH的周长为__6___.
(4)若⊿ABC的面积为4,则⊿BDH的面积为__9___.
α
∠B=∠迁C=移α的,数∠学AE方F法= ∠ C,连
α
B
E α C 结当A∠AF.EF旋解转决问到题如图位置时，
找上出述图关中系的还相成似立三吗角？形
D
A
F
G
α
α
α
B
E
C
.
12
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
变1式.矩：形.在AB直C角D中梯，形把ABDCAF沿中A，F对，折CB，=使14D，与 CCFB=4边, 上AB的=点6,,EC重F∥合A，B若,在A善注边D于意C=B在分10上复类, A找杂讨B图论一=形的点8,E,使以 E、A、B为顶点的三角形和中以寻数学找E、思基C想本、型F为顶点
的则三E角F=形__相5_似__，_ 则CE=___5_.6_或__2或12
D
A
A
F
C
EE
F
C B
E
E
B
2.已知：D为BC上一点， ∠B= ∠C=∠EDF=60°,
BE=6,CD=3,CF=4,则AF=_7______
A
E F
B
D
C
.
15
A
D
B
E
C
AD
α
αα
B
E
C
A
D
B
E
C
A
D
B
E
C
A
α
B
F D
若若∠∠BB==∠∠CC==α6,0∠°,A∠EAFE=F∠= ∠ F CC,则,则△△AABBEE与与△△EECCFF的的关关系系
还还成成立立吗吗？？说明理由
B
E
C
A
A
A
FF F
α66α00°°
BBB
αα6600°°
EEE
6α6α00°°
CCC
问题2：
D
（12）延长BA、CF相交于点
A
F

D点,且 D,E且善为E于B为运CB的用C类中的比点中、，点若，若
α
E
α
C
C
B
D
αα
α
OP
A
思考题：已知：等边△ABC 中，P为直线AC上一
动点，连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时，证明PA·PC=AB ·CN
(2)若P在AC的延长线上，上述关系是否成立？
(3)若P在CA的延长线上， CN=1.5,BC=2,求AP、
BP的长
B
.
9
问题1：如图，在正方形ABCD中,E为BC上任意一点（与 B、C不重合）∠AEF=90°.观察图形：
（（1）2）△若ABEE为与BC△E的C中F点是，否连相结似A？F,并图证中明有你哪的些结相论似。三角形？ △ABE∽ △ECF ∽ △AEF
A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF （（21））点点EE为为BBCC上上任任意意一一点点，
角： ∠ADE= ∠ B ∠ AED= ∠C
D
E 边：DE ∥ BC
AD AEDE.
B
C AB AC BC
“A”型
AD AE . DB EC
DB EC .
AB AC
面积：. SADE DE2.
7
SABC BC
3、D、E分别是△ABC边AB、AC上的点，请你添加一个条件，使△ADE与△ABC相似。
60°
A
A
A
60° P
P
P
N
B
CB
Q
C
60°
Q
N B
N C
Q
再见
.
18