生产车间名工人加工零件数件如下
《统计学原理》综合练习题解读

《统计学原理》综合练习题及解答概述、调查、整理一、判断题1.社会经济统计的研究对象是社会经济现象总体的数量方面。
2.统计调查过程中采用的大量观察法,是指必须对研究对象的所有单位进行调查。
3.全面调查包括普查和统计报表。
4.统计分组的关键问题是确定组距和组数。
5.在全国工业普查中,全国企业数是统计总体,每个工业企业是总体单位。
6.我国的人口普查每十年一次,因此它是一种连续性调查研究方法。
7.对全同各大型钢铁生产基地的生产情况进行调查,以掌握全国钢铁生产的基本情况。
这种调查属于非全面调查。
8.对某市工程技术人员进行普查,该市工程技术人员的工资收入水平是数量标志。
9.对我国主要粮食作物产区进行调查,以掌握全国主要粮食作物生产的基本情况,这种调查是重点调查。
10.我国人口普查的总体单位和调查单位都是每一个人,而填报单位是户。
二、单项选择题1.设某地区有670家工业企业,要研究这些企业的产品生产情况,总体单位是()。
A.每个工业企业 B.670家工业企业 C.每件新产品 D.全部工业产品2.某市工业企业2003年生产经营成果年报呈报时间规定在2004年1月31日,则调查时限为()。
A.一日 B.一个月 C.一年 D.一年零一个月3.在全国人口普查中,()。
A.男性是品质标志 B.人的年龄是变量C.人口的平均寿命是数量标志 D.全国人口是统计指标4.某机床厂要统计该企业的自动机床的产量和产值.上述两个变量是()。
A.二者均为离散变量 B.二者均为连续变量C.巴前者为连续变量,后者为离散变量D.前者为离散变量,后者为连续变量5.下列调查中,调查单位与填报单位一致的是()。
A.企业设备调查 B.人口普查 C.农村耕地调查 D.工业企业现状调查6.抽样调查与重点调查的主要区别是()。
A.作用不同 G.组织方式不同C.灵活程度不同 D.选取调查单位的方法不同7.下列调查属于不连续调查的是()。
A.每月统计商品库存额 B.每月统计产品产量C.每月统计商品销售额 D.每季统计进出口贸易额8.全面调查与非全面调查的划分是以()。
统计学原理计算题及参考答案

1、某生产车间30名工人日加工零件数(件)如下: 30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 3447 33 43 38 42 32 34 38 46 43 39 35 要求:(1)根据以上资料分成如下几组:25—30,30—35,35—40,40—45,45—50,计算各组的频数和频率,编制次数分布表;(2) 根据整理表计算工人平均日产零件数。
(20分)则工人平均劳动生产率为:17.38301145===∑∑fxf x(2)当产量为10000件时,预测单位成本为多少元?(15分)xbx a y n x b n y a x x n y x xy n b c 5.2808010703125.232105.26151441502520250512503210128353)(222-=+==+=⨯+=-=-=-=--=-⨯⨯-⨯=--=∑∑∑∑∑∑∑因为,5.2-=b ,所以产量每增加1000件时,即x 增加1单位时,单位成本的平均变动是:平均减少2.5元 (2)当产量为10000件时,即10=x 时,单位成本为55105.280=⨯-=c y 元>课程的测试,甲班平均成绩为81分,标准差为9.5分;乙班的成绩分组资料如下: 计算乙班学生的平均成绩,并比较甲.乙两班哪个班的平均成绩更有代表性? 解:乙班学生的平均成绩∑∑=fxf x ,所需的计算数据见下表:75554125===∑∑fxf x (比较甲.乙两班哪个班的平均成绩更有代表性,要用变异系数σν的大小比较。
)甲班%65.207549.1549.152405513200)(2======-=∑∑xff x x σνσσ%73.11815.9===xσνσ 从计算结果知道,甲班的变异系数σν小,所以甲班的平均成绩更有代表性。
计算(1)产品产量总指数及由于产量增长而增加的总成本.(2)总成本指数及总成本增减绝对额. 解;(1)产品产量总指数为: %42.1112102342106351120605010060%10550%102100%12000==++=++⨯+⨯+⨯=∑∑qp qkp 由于产量增长而增加的总成本:∑∑=-=-242102340000qp q kp(2)总成本指数为:%62.10721022660501006046120011==++++=∑∑qp qp总成本增减绝对额:∑∑=-=-162102260011qp q p. 解:商品流转次数c=商品销售额a/库存额bba c =商品销售额构成的是时期数列,所以67.23837163276240200==++==∑na a 库存额b 构成的是间隔相等的时点数列,所以33.533160327545552453224321==+++=+++=b b b b b 第二季度平均每月商品流转次数475.433.5367.238===ba c 第二季度商品流转次数3*4.475=13.4251. 2008年某月份甲、乙两市场某商品价格和销售量、销售额资料如下:试分别计算该商品在两个市场上的平均价格. 解:甲市场的平均价格为:04.123270033220027001507001080007350011009007001100137900120700105==++=++⨯+⨯+⨯==∑∑fxf x乙市场的平均价格为74.1172700317900700800120031790013795900120960001051260009590096000126000==++=++++==∑∑xM M x。
统计学复习资料

一、判断正误1、统计研究的对象是客观现象总体的数量特征及其联系,而非有关某一个体的具体情况。
( )2、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
( )3、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
( )4、已知各期环比增长速度为3%、2%、7%和5%,则相应的定基增长速度的技术方法为3%×2%×7%×5%—100%。
( )5、两个有密切联系的属于不同总体的总量指标之比是动态相对指标。
( )6、用价格作同度量的销售量指数∑10q p /∑00q p ,其分子分母之差∑10q p - ∑00q p 是表示报告期比基期一共增加或减少的销售量。
( )7、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
( )8、数量指标作为同度量因素,时期一般固定在基期( )9、发展水平就是动态数列中的每一项具体指标数值,它只能表现为绝对数。
( ) 10、定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于相应各个环比增长速度乘积。
( ) 二、单项选择题1、抽样调查与重点调查的主要区别是( )。
A.作用不同 B.组织方式不同 C.灵活程度不同 D.选取调查单位的方法不同2、在全国人口普查中( )。
A .男性是品质标志 B.人的年龄是变量 C .人口的平均寿命是数量标志 D.全国人口是统计指标3、某机床厂要统计该企业的自动机床的产量和产值,上述两个变量是( )。
A.二者均为离散变量 B.二者均为连续变量C.前者为连续变量,后者为离散变量D.前者为离散变量,后者为连续变量4、下列调查中,调查单位与填报单位一致的是( )。
A.企业设备调查B.人口普查C.农村耕地调查D.工业企业现状调查 5、下列分组中哪个是按品质标志分组( )。
统计学练习与作业(内)2013

第三章统计整理1、某生产车间20名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求:根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50,计算出各组的频数和频率,整理编制次数分布表。
第四章总量指标与相对指标4.1某空调厂2003年产量资料如表4—1所示。
表4—1 某空调厂产量表单位:万台的单位成本计划降低5.2%,实际降低6.4%。
试运用各类相对指标对该厂2003年的空调生产情况进行分析。
第5章平均指标与变异度指标5.1某百货公司6月份前6天的销售额数据(万元)如下:276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。
5.3已知某集团下属各企业的生产资料如下:试计算该集团生产平均计划完成百分比5.4 某电子产品某电子产品企业工人日产量资料如下表:试根据表中资料计算工人日产量的平均数、中位数和众数,并判断该分布数列的分布状态。
5.5一位投资者持有一种股票,2001-2004年的收益率分别为4.5%,2.1%,25.5%和1.9%。
要求计算该投资者在这4年内的平均收益率。
5.6 一种产品需要人工组装,现有两种可供选择的组装方法。
为检验哪种方法更好,随机抽取6名工人,让他们分别用两种方法组装,测试在相同的时间内组装的产品数量。
得到第一种组装方式组装的产品平均数量是127件,标准差为5件。
第二种组装方式组装的产品数量(单位:件)如下:129,130,131,127,128,129。
要求:1) 计算第二种组装方式组装产品的平均数和标准差。
2)如果让你选择一种组装方式,你会选择哪种?5.7一家公司在招收职员时,首先要通过两项能力测试。
在A项测试中,其平均分数是100分,标准差是15分;在B项测试中,其平均分数是400分,标准差是50分。
统计学原理计算题(公式)复习资料

《统计学原理》复习资料(计算部分)一、 编制分配数列(次数分布表) 统计整理公式a) 组距=上限-下限 b) 组中值=(上限+下限)÷2c) 缺下限开口组组中值=上限-1/2邻组组距 d) 缺上限开口组组中值=下限+1/2邻组组距1.某班40名学生统计学考试成绩分别为:57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61要求:⑴ 根据上述资料按成绩分成以下几组:60分以下,60~70分,70~80分,80~90分,90~100分,整理编制成分配数列。
⑵ 根据整理后的分配数列,计算学生的平均成绩。
解:分配数列成绩(分) 学生人数(人) 频率(%) 60以下 4 10 60—70 6 15 70—80 12 30 80—90 15 37.5 90—100 3 7.5 合计 40 100平均成绩 55465675128515953307076.754040xf x f⨯+⨯+⨯+⨯+⨯====∑∑(分)或 5510%6515%7530%8537.5%957.5%76.75fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑(分)2.某生产车间40名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 33 43 38 42 32 25 30 46 29 34 38 46 43 39 35 40 48 33 27 28要求:⑴ 根据以上资料分成如下几组:25~30,30~35,35~40,40~45,45~50,整理编制次数分布表。
⑵ 根据整理后的次数分布表,计算工人的平均日产量。
(作业10P 1) 解:次数分布表日加工零件数(件) 工人数(人)频率(%)25—307 17.5 30—35 8 20 35—40 9 22.5 40—45 10 25 45—50 6 15 合计 40100平均日产量 27.5732.5837.5942.51047.56150037.54040xf x f⨯+⨯+⨯+⨯+⨯====∑∑ 件或 27.517.5%32.520%37.522.5%42.525%47.515%37.5fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑ 件二、 算术平均数和调和平均数的计算 加权算术平均数公式 xfx f=∑∑(常用) fx x f=⋅∑∑(x 代表各组标志值,f 代表各组单位数,ff∑代表各组的比重)加权调和平均数公式 m x m x=∑∑ (x 代表各组标志值,m 代表各组标志总量)分析: m x mx=总产量工人平均劳动生产率(结合题目)总工人人数从公式可以看出,“生产班组”这列资料不参与计算,是多余条件,将其删去。
统计学练习(内)2013答案
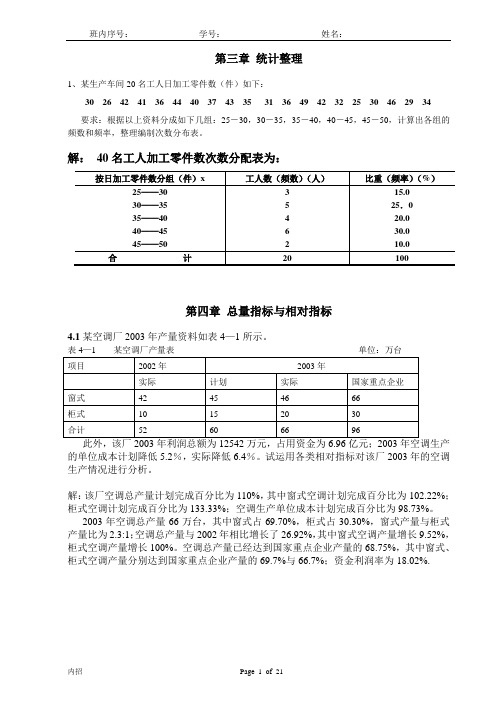
第三章统计整理1、某生产车间20名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求:根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50,计算出各组的频数和频率,整理编制次数分布表。
解:40名工人加工零件数次数分配表为:第四章总量指标与相对指标4.1某空调厂2003年产量资料如表4—1所示。
的单位成本计划降低5.2%,实际降低6.4%。
试运用各类相对指标对该厂2003年的空调生产情况进行分析。
解:该厂空调总产量计划完成百分比为110%,其中窗式空调计划完成百分比为102.22%;柜式空调计划完成百分比为133.33%;空调生产单位成本计划完成百分比为98.73%。
2003年空调总产量66万台,其中窗式占69.70%,柜式占30.30%,窗式产量与柜式产量比为2.3:1;空调总产量与2002年相比增长了26.92%,其中窗式空调产量增长9.52%,柜式空调产量增长100%。
空调总产量已经达到国家重点企业产量的68.75%,其中窗式、柜式空调产量分别达到国家重点企业产量的69.7%与66.7%;资金利润率为18.02%.第5章 数据的分布特征的测度5.1 某百货公司6月份前6天的销售额数据(万元)如下: 276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。
解:67.2716310238252257297276=+++++==∑nx x i(万元)排序:238 252 257 276 297 310不存在O U L M 25.300 Q 5.248Q 5.266===e M解:2000年甲种自行车的平均单位成本=210*0.4+230*0.45+250*0.15=225 (元/辆)5.3已知某集团下属各企业的生产资料如下:试计算该集团生产平均计划完成百分比 解:列表计算如下该集团生产平均计划完成百分比%57.103420435==∑∑=xm m X5.4 某电子产品某电子产品企业工人日产量资料如下表:试根据表中资料计算工人日产量的平均数、中位数和众数,并判断该分布数列的分布状64.84848660428001121332211===++++++=∑∑==ni ini iinnn f f xf f f f x f x f x f x x60=L 70=U 260=f1401=-f 1501=+f 10=i代入公式65.2173910)150260()140260(15026070)()(111=⨯-+---=⨯-+---=+-+i f f f f f f U M o651026020026607021=⨯--=⨯--=+∑i f S fU M mm e651026020026606021=⨯-+=⨯-+=-∑i f S fL M m m e5.5 一位投资者持有一种股票,2001-2004年的收益率分别为4.5%,2.1%,25.5%和1.9%。
统计学练习与作业(内)2013

第三章统计整理1、某生产车间20名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求:根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50,计算出各组的频数和频率,整理编制次数分布表。
第四章总量指标与相对指标4.1某空调厂2003年产量资料如表4—1所示。
表4—1 某空调厂产量表单位:万台的单位成本计划降低5.2%,实际降低6.4%。
试运用各类相对指标对该厂2003年的空调生产情况进行分析。
第5章平均指标与变异度指标5.1某百货公司6月份前6天的销售额数据(万元)如下:276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。
5.3已知某集团下属各企业的生产资料如下:试计算该集团生产平均计划完成百分比5.4 某电子产品某电子产品企业工人日产量资料如下表:试根据表中资料计算工人日产量的平均数、中位数和众数,并判断该分布数列的分布状态。
5.5一位投资者持有一种股票,2001-2004年的收益率分别为4.5%,2.1%,25.5%和1.9%。
要求计算该投资者在这4年内的平均收益率。
5.6 一种产品需要人工组装,现有两种可供选择的组装方法。
为检验哪种方法更好,随机抽取6名工人,让他们分别用两种方法组装,测试在相同的时间内组装的产品数量。
得到第一种组装方式组装的产品平均数量是127件,标准差为5件。
第二种组装方式组装的产品数量(单位:件)如下:129,130,131,127,128,129。
要求:1) 计算第二种组装方式组装产品的平均数和标准差。
2)如果让你选择一种组装方式,你会选择哪种?5.7一家公司在招收职员时,首先要通过两项能力测试。
在A项测试中,其平均分数是100分,标准差是15分;在B项测试中,其平均分数是400分,标准差是50分。
统计学试题

0907《统计学原理》试题及答案一、单选题(每小题2分,共12分)1、构成统计总体的个别事物称为(c )。
A.调查总体 B。
调查单位 C。
总体单位 D。
标志值2、某市工业企业2007年生产经营成果年报呈报时间规定在2008年1月31日,则调查期限为( B )。
A、一日B、一个月C、一年D、一年零一个月3、全面调查和非全面调查的划分依据是( B )。
A、调查组织规模的大小B、调查对象所包括的单位是否完全C、最后取得的调查资料是否全面D、调查时间是否连续4、直接反映总体规模大小的指标是( A )。
A、总量指标B、相对指标C、平均指标D、变异指标5、抽样误差是指( C ).A、调查中所产生的登记性误差 B调查中所产生的系统性误差C、随机的代表性误差 D计算过程中产生的误差6、如果变量X和变量Y之间的相关系数为1,说明两个变量之间存在( C ).A、微弱相关关系B、显著相关关系C、完全相关关系D、没有相关关系二、多项选择题(2×4=8分)1、在对工业企业生产设备调查中(BCE )。
A、全部的工业企业是调查对象B、工业企业的全部生产设备是调查对象C、每台设备是调查单位D、每台设备是调查单位也是填报单位E、每个工业企业是填报单位2、下列分组哪些是按品质标志分组( BCDE )。
A、职工按工龄分组B、科技人员按职称分组C、人口按民族分组D、企业按经济类型分组E、人口按地区分组3、计算变异指标可以(BDE )。
A、反映总体各单位标志值分布的集中趋势B、反映总体各单位标志值分布的离中趋势C、分析现象之间的依存关系D、衡量平均数代表性的大小E、说明现象变动的均匀性或稳定程度4、总指数的两种计算形式是( BC )。
A、个体指数 B综合指数 C平均指数 D定基指数 E环比指数三、判断题(2×5=10分)1、统计工作的研究对象是客观现象总体的数量方面。
(√)2、变异指标和平均指标从不同侧面反映了总体的特征,因而标志变异指标数值越大,则平均指标的代表性就越高,反之平均指标的代表性就越低。
统计学原理作业2答案(新)

《统计学原理》作业(二)(第四章)一、判断题1、总体单位总量和总体标志总量是固定不变的,不能互相变换。
(×)2、相对指标都是用无名数形式表现出来的。
(×)3、能计算总量指标的总体必须是有限总体。
(×)4、按人口平均的粮食产量是一个平均数。
(×)5、在特定条件下,加权算术平均数等于简单算术平均数。
(√)6、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
(×)7、国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
(×)8、总量指标和平均指标反映了现象总体的规模和一般水平。
但掩盖了总体各单位的差异情况,因此通过这两个指标不能全面认识总体的特征。
(√)9、用相对指标分子资料作权数计算平均数应采用加权算术平均法。
(×)10、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
(√)二、单项选择1、总量指标数值大小(A)A、随总体范围扩大而增大B、随总体范围扩大而减小C、随总体范围缩小而增大D、与总体范围大小无关2、直接反映总体规模大小的指标是(C)A、平均指标B、相对指标C、总量指标D、变异指标3、总量指标按其反映的时间状况不同可以分为(D)A、数量指标和质量指标B、实物指标和价值指标C、总体单位总量和总体标志总量D、时期指标和时点指标4、不同时点的指标数值(B)A、具有可加性B、不具有可加性C、可加或可减D、都不对5、由反映总体各单位数量特征的标志值汇总得出的指标是(B)A、总体单位总量B、总体标志总量C、质量指标D、相对指标6、计算结构相对指标时,总体各部分数值与总体数值对比求得的比重之和(C)A、小于100%B、大于100%C、等于100%D、小于或大于100%7、相对指标数值的表现形式有( D )A、无名数B、实物单位与货币单位C、有名数D、无名数与有名数8、下列相对数中,属于不同时期对比的指标有(B)A、结构相对数B、动态相对数C、比较相对数D、强度相对数9、假设计划任务数是五年计划中规定最后一年应达到的水平,计算计划完成程度相对指标可采用(B)A、累计法B、水平法C、简单平均法D、加权平均法10、按照计划,今年产量比上年增加30%,实际比计划少完成10%,同上年比今年产量实际增长程度为(D)。
《统计学原理》作业[二]参考答案解析[新]
![《统计学原理》作业[二]参考答案解析[新]](https://img.taocdn.com/s3/m/525b641f647d27284a735102.png)
《统计学原理》作业(二)(第四章)一、判断题1、总体单位总量和总体标志总量是固定不变的,不能互相变换。
(×)2、相对指标都是用无名数形式表现出来的。
(×)3、按人口平均的粮食产量是一个平均数。
(×)4、在特定条件下,加权算术平均数等于简单算术平均数。
(√)5、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
(×)6、国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
(×)7、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
(√)二、单项选择1、总量指标数值大小(A)A、随总体范围扩大而增大B、随总体范围扩大而减小C、随总体范围缩小而增大D、与总体范围大小无关2、直接反映总体规模大小的指标是(C)A、平均指标B、相对指标C、总量指标D、变异指标3、总量指标按其反映的时间状况不同可以分为(D)A、数量指标和质量指标B、实物指标和价值指标C、总体单位总量和总体标志总量D、时期指标和时点指标4、由反映总体各单位数量特征的标志值汇总得出的指标是(B)A、总体单位总量B、总体标志总量C、质量指标D、相对指标5、计算结构相对指标时,总体各部分数值与总体数值对比求得的比重之和(C)A、小于100%B、大于100%C、等于100%D、小于或大于100%6、相对指标数值的表现形式有 ( D )A、无名数B、实物单位与货币单位C、有名数D、无名数与有名数7、下列相对数中,属于不同时期对比的指标有(B)A、结构相对数B、动态相对数C、比较相对数D、强度相对数8、假设计划任务数是五年计划中规定最后一年应达到的水平,计算计划完成程度相对指标可采用(B)A、累计法B、水平法C、简单平均法D、加权平均法9、按照计划,今年产量比上年增加30%,实际比计划少完成10%,同上年比今年产量实际增长程度为(D)。
统计学复习资料

一、判断正误1、统计研究的对象是客观现象总体的数量特征及其联系,而非有关某一个体的具体情况。
( )2、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
( )3、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
( )4、已知各期环比增长速度为3%、2%、7%和5%,则相应的定基增长速度的技术方法为3%×2%×7%×5%—100%。
( )5、两个有密切联系的属于不同总体的总量指标之比是动态相对指标。
( )6、用价格作同度量的销售量指数∑10q p /∑00q p ,其分子分母之差∑10q p - ∑00q p 是表示报告期比基期一共增加或减少的销售量。
( )7、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
( )8、数量指标作为同度量因素,时期一般固定在基期( )9、发展水平就是动态数列中的每一项具体指标数值,它只能表现为绝对数。
( ) 10、定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于相应各个环比增长速度乘积。
( ) 二、单项选择题1、抽样调查与重点调查的主要区别是( )。
A.作用不同 B.组织方式不同 C.灵活程度不同 D.选取调查单位的方法不同2、在全国人口普查中( )。
A .男性是品质标志 B.人的年龄是变量 C .人口的平均寿命是数量标志 D.全国人口是统计指标3、某机床厂要统计该企业的自动机床的产量和产值,上述两个变量是( )。
A.二者均为离散变量 B.二者均为连续变量C.前者为连续变量,后者为离散变量D.前者为离散变量,后者为连续变量 4、下列调查中,调查单位与填报单位一致的是( )。
A.企业设备调查B.人口普查C.农村耕地调查D.工业企业现状调查 5、下列分组中哪个是按品质标志分组( )。
统计学计算题

2004年1月1、从一批零件中抽取200件进行测验,其中合格品188件。
要求:(1)计算该批零件合格率的抽样平均误差;(2)以95.45%(t =2)的可靠程度对该批零件的合格率作出区间估计。
p=94% μp 20006.094.0)1(⨯=-=n p p =0.0168 Δp ==⨯pt μ0.0336 p ±Δp =0.94±0.0336 即90.64%---97.36%2、以95.45%的概率保证,该批零件合格率在90.64%---97.36%之间。
2、某商场三种商品的价格和销售量资料如下:商品 计量单位价格(元) 销售量基期 报告期 基期 报告期A B C个 双 公斤30 20 2335 22 25100 200 150120 160 150要求: (1)计算价格总指数; (2)分析价格变动对销售额的绝对影响额。
(1)价格总指数==∑∑0111p q p q ==⨯+⨯+⨯⨯+⨯+⨯1025011470231502016030120251502216035120111.90%(2)销售量对销售收入的影响额为 :=-∑∑0111pq p q 11470-10250=1220元即由于价格的增加,使销售额增加了1220元。
3、某地区1984年平均人口数为120万人.1995年人口变动情况如下: 月份 1 2 5 9 11 次年1月 月初人数 122 125 132 147 151 157计算: (1)1995年平均人口数 (2)1984年—1995年该地区人口的平均增长速度(3)假设从1995年起该地区人口以9‰的速度增长,到2008年该地区人口数量将达到什么水平?(1)1995年的人口=∑--++++++ff a a f a a f a a n n n 11232121222=224312215715122151147421471323213212512125122++++⨯++⨯++⨯++⨯++⨯+=139.42(万人)(2)1984—1995年人口平均增长速度:112042.139111-=-x =1.37%(3)到2008年的人口数量为:===130)009.1(42.139)(n n x a a 156.64(万人)4、甲、乙两班同时对《统计学原理》课程进行测试,甲班平均成绩为70分,标准差为9.0分;乙班的成绩分组资料如下:按成绩分组 学生人数(人)60以下 60-70 70-80 80-90 90-1002 6 25 12 5计算乙班学生的平均成绩,并比较甲、乙两班哪个班的平均成绩更有代表性? 据题意列计算表如下:组中值x 学生人数 f xf x 2f 55 2 110 6050 65 6 390 25350 75 25 1875 140625 85 12 1020 8670095 5 475 45125 合计 50 3870 303850∴ 乙班学生的平均成绩 503870==∑∑fxf x =77.4(分)乙班学生成绩的标准差==-=-∑∑∑∑222)4.77(50303850)(fxf ffx 9.29(分) 又因为 甲班标准差系数709==xv σ甲=0.1286; 乙班标准差系数4.7729.9==x v σ甲=0.120所以,乙班学生的平均成绩更具有代表性。
电大职业技能实训平台形成性考核《统计学原理》参考答案

一、判断题、社会经济统计工作的研究对象是社会经济现象总体的数量方面。
(√)、统计调查过程中采用的大量观察法,是指必须对研究对象的所有单位进行调查。
( ×) 、全面调查包括普查和统计报表。
(×)、统计分组的关键是确定组限和组距(×)、在全国工业普查中,全国企业数是统计总体,每个工业企业是总体单位。
(×)、我国的人口普查每十年进行一次,因此它是一种连续性调查方法。
(×)、对全国各大型钢铁生产基地的生产情况进行调查,以掌握全国钢铁生产的基本情况。
这种调查属于非全面调查。
(√)、对某市工程技术人员进行普查,该市工程技术人员的工资收入水平是数量标志。
(√)、对我国主要粮食作物产区进行调查,以掌握全国主要粮食作物生长的基本情况,这种调查是重点调查。
(√)、我国人口普查的总体单位和调查单位都是每一个人,而填报单位是户。
(√ )二、单项选择题、设某地区有家工业企业,要研究这些企业的产品生产情况,总体单位是()、每个工业企业;、家工业企业;、每一件产品;、全部工业产品、某市工业企业年生产经营成果年报呈报时间规定在年月日,则调查期限为()。
、一日、一个月、一年、一年零一个月、在全国人口普查中()。
、男性是品质标志、人的年龄是变量、人口的平均寿命是数量标志、全国人口是统计指标、某机床厂要统计该企业的自动机床的产量和产值,上述两个变量是()。
、二者均为离散变量、二者均为连续变量、前者为连续变量,后者为离散变量、前者为离散变量,后者为连续变量、下列调查中,调查单位与填报单位一致的是()、企业设备调查、人口普查、农村耕地调查、工业企业现状调查、抽样调查与重点调查的主要区别是()。
、作用不同、组织方式不同、灵活程度不同、选取调查单位的方法不同、下列调查属于不连续调查的是()。
、每月统计商品库存额、每旬统计产品产量、每月统计商品销售额、每季统计进出口贸易额、全面调查与非全面调查的划分是以()、时间是否连续来划分的、最后取得的资料是否完全来划分的、调查对象所包括的单位是否完全来划分的、调查组织规模的大小划分的、下列分组中哪个是按品质标志分组()、企业按年生产能力分组、产品按品种分组、家庭按年收入水平分组、人口按年龄分组三、多项选择题、总体单位是总体的基本组成单位,是标志的直接承担者。
电大《统计学原理》形考册参考答案(二)(重新订正)

《统计学原理》形成性考核册参考答案<二)<第四章)一、判断题1、总体单位总量和总体标志总量是固定不变的,不能互相变换。
< ×)2、相对指标都是用无名数形式表现出来的。
< ×)3、按人口平均的粮食产量是一个平均数。
< ×)4、在特定条件下,加权算术平均数等于简单算术平均数。
<√)5、用总体部分数值与总体全部数值对比求得的相对指标。
说明总体内部的组成状况,这个相对指标是比例相对指标。
<×)b5E2RGbCAP6、国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
< ×)7、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
< √)二、单项选择题1、总量指标数值大小<A )A、随总体范围扩大而增大B、随总体范围扩大而减小C、随总体范围缩小而增大D、与总体范围大小无关2、直接反映总体规模大小的指标是<C )A、平均指标B、相对指标C、总量指标D、变异指标3、总量指标按其反映的时间状况不同可以分为< D )A、数量指标和质量指标B、实物指标和价值指标C、总体单位总量和总体标志总量D、时期指标和时点指标4、由反映总体各单位数量特征的标志值汇总得出的指标是< B )A、总体单位总量B、总体标志总量C、质量指标D、相对指标5、计算结构相对指标时,总体各部分数值与总体数值对比求得的比重之和<C )A、小于100%B、大于100%C、等于100%D、小于或大于100%6、相对指标数值的表现形式有 <D)A、无名数B、实物单位与货币单位C、有名数D、无名数与有名数7、下列相对数中,属于不同时期对比的指标有< B )A、结构相对数B、动态相对数C、比较相对数D、强度相对数8、假设计划任务数是五年计划中规定最后一年应达到的水平,计算计划完成程度相对指标可采用<B )A、累计法B、水平法C、简单平均法D、加权平均法9、按照计划,今年产量比上年增加30%,实际比计划少完成10%,同上年比今年产量实际增长程度为< D)。
计算题:2010.12电大统计练习

--
要求计算:<1>三种商品销售量总指数; <2>销售量变化对销售收入的影响 额。
2010.12.期末总复习计算题
1.某班40名学生某课程成绩分别为: 68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81 按学校规定:60分以下为不及格,60─70分为及 格,70─80分为中,80─90分为良,90─100分为优。 要求: ⑴ 将学生的考核成绩分组并编制一张考核成绩 次数分配表; (2)指出分组标志及类型及采用的分组方法; (3)计算本班学生的考核平均成绩并分析本班学生 考核况。
4.某厂三个车间一季度生产情况如下:计算: ⑴一季度三个车间产量平均计划完成百分比; ⑵一季度三个车间产量平均单位成本。 计划完成 实际产 单位产成本 (元/件) 百分比 量 (%) (件) 95 190 12 第一车间 104 308 15 第二车间 110 250 8 第三车间 车间
5.2006年某月甲、乙两市场某商品价格, 销售量和销售额资料如下:
6..某企业工业总产值1998年—2000年平均发 展速度是1.02,2001---2004年平均发展速 度是1.06,2005年比2004年增长8%,试求 1998---2005年的平均增长速度。
指数计算题练习:
1.某企业生产甲、乙两种产品,基期和报告 期的产量单位成本资料如下表:
产 产 品 基期 甲 乙 1000 3000 量(件) 单位成本(元/件) 报告期 基期 1100 4000 10 8 报告期 12 7
• 试比较哪个企业的工人平均日产量更具代表性?
统计学原理计算题期末练习参考答卷
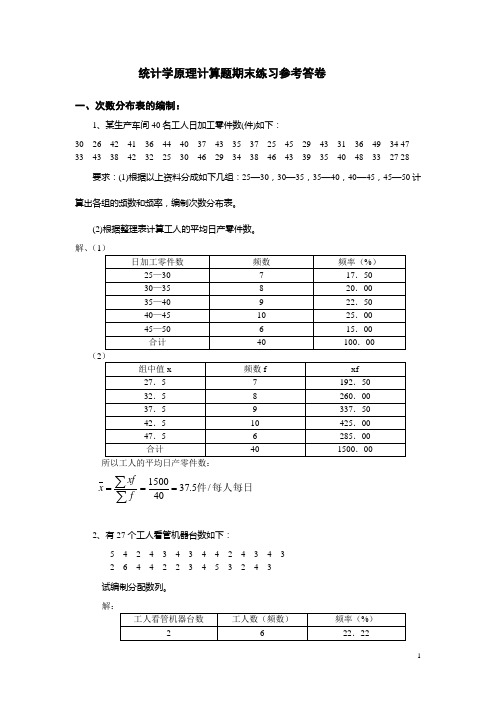
统计学原理计算题期末练习参考答卷一、次数分布表的编制:1、某生产车间40名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 33 43 38 42 32 25 30 46 29 34 38 46 43 39 35 40 48 33 27 28 要求:(1)根据以上资料分成如下几组:25—30,30—35,35—40,40—45,45—50计算出各组的频数和频率,编制次数分布表。
(2)根据整理表计算工人的平均日产零件数。
解、(1(2所以工人的平均日产零件数:每人每日件/5.37401500===∑∑fxf x2、有27个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3 试编制分配数列。
二、平均指标、相对指标、变量指标的计算1.某车间有甲、乙两个生产小组,甲组平均每个工人的日产量为22件标准差为3.5件;计算乙组每个工人的平均日产量,并比较甲、乙两生产小组哪个组的日产量更有代表性? 解:)/(171001700人件乙===∑∑f xf x ())(65.21007022件乙==-=∑∑ff x x σ。
又因为:)/(22人件甲=x )(5.3件甲=σ 1591.0225.3===甲甲甲x σν 1559.01765.2===乙乙乙x σν 即:甲ν>乙ν 因此乙组的平均数更具代表性。
2、某局15个企业99年某产品的单位成本资料如下:试计算该产品的平均单位产品成本。
解:由于组距式分组,故采用组中值计算:∑∑∑∑⨯==ffx f xf x =11×22%+13×40%+15×38%=2.42+5.2+5.7=13.32(元/件)3、 已知某局20个企业的有关统计资料如下:试计算产值的平均计划完成程度。
统计学原理复习

统计学原理计算题练习第 1 页 共 6 页统计学原理计算题练习1.某生产车间30名工人日加工零件数(件)如下:(学习指导P300—1,下同)30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35要求:(1)根据以上资料分成如下向组:25—30,30—35,35—40,40—45,45—50,计算出各组频数和频率,编制次数分布表。
(2)根据整理表计算工人平均日产零件数。
2.某公司下属50个企业,生产同种产品,某月对产品质量进行调查,得资料;要求计算该产品的平均合格率。
(P279—1345. 1990试问哪一个市场农产品的平均价格较高?并说明原因。
6.7(P168—21(P166—18(P165—13(P164—10)8.某企业甲、乙两个车间,甲车间平均每个工人日加工零件数65件,标准差11件;乙车间工人日加工零件数资料:计算乙车间工人加工零件的平均数和标准差,并比较甲、乙两车间哪个车间的平均日加工零9.某工厂有2000个工人,用简单随机不重复方法抽出100个工人作为样本,计算出平均工资560元,标准差32.45元。
要求:(1)计算抽样平均误差; (2)以95.45%(t=2)的可靠性估计该厂工人的月平均工资区间。
(P295—5)10.某乡有5000农户,按随机原则重复抽取100户调查,得平均每户年纯收入12000元,标准差2000元。
要求:(1)以95%的概率(t=1.96)估计全乡平均每户年纯收入的区间。
(2)以同样概率估计全乡农户所纯收入总额的区间范围(P179—14)11.为了解某城市分体式空调的零售价格,随机抽取若干个商场中的40台空调,平均价格为3800元,样本标准差400元。
要求:(1)计算抽样平均误差;(2)以99.73%(t=3)的可靠性估计该城市分体式空调的价格区间。
某生产车间40名工人的日加工零件...

某生产车间40名工人的日加工零件数(件)如下:
30 26 42 41 36 44 40 37 43 35 37 25
45 29 43
31 36 49 34 47 33 43 48 42 32 25 30
46 29 34
38 46 43 39 35 40 48 33 27 28
(1)根据以上数据分成如下5组:25~30,30~35,35~40,40~45,45~50,绘制频数分布表,频数分布直方图和折线图;
(2)求工人的平均日加工零件数(取整数).
解:(1)根据以上数据分成如下5组:25~30,30~35,35~40,40~45,45~50,各组人数为:9,8,8,9,6;
(2)工人的平均日加工零件数为:
(30+26+42+41+36+44+40+37+43+35+37+25+45+29+4 3+31+36+49+34+47+33+43+48+42+32+25+30+46+29+34+3 8+46+43+39+35+40+48+33+27+28)=37(个).
分析:首先分析数据,可得:5组中各组人数为:9,8,8,9,6;据此可绘制频数分布表,频数分布直方图和折线图;根据平均数的求法,可得工人的平均日加工零件数是37.
点评:本题考查了频数分布表,频数分布直方图和折线图的画法;熟练掌握平均数的求法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
企业数(个)
合格品数量(件)
70—80 80—90—100 90
10 25 15
25500
59500 34200
计合20个企业,1999
50年甲种车的单位成本分组资料如下:计算平均单位成本
119200
/辆)
企业数(个)
各组产量占总产量的比重(
200-220 240 220-240-260
日加工零件数(件)
工人数(人)
以下607Байду номын сангаас 60—70—80 90
80—10090—
5 9 12 1410
(03-01金)计算题(每小题10分,共50分)
1.某工厂有2000个工人,用简单随机不重复方法抽出100个工人作为样本,计算出平均工资差32.45元。要求:(1)计算抽样平均误差;(2)以95.45%(t=2)的可靠性估计该厂工人的月平均工资区间。
(3)由此例说明误差范围与概率度之间的关系。(15分)
(04-01).1、采用简单重复抽样的方法,抽取一批零件中的200件作为样本,其中合格品为(1)计算该批零件合格率的抽样平均误差(2)以95.45%的概率保证程度对该零件的合格率进行区间估计=2)
(04-07)2、从某年级字生中按简单随机抽样方式抽取50名学生,对某公共课的考试成绩进行检查,得知其平均分数为75.6分,样本标准差10分,试以95.45%的概率保证程度推断全年级学生的考试成绩的区间范围。如果其它条件不变,将允许误差缩小一半,应抽取多少名学生检查?
(04-07)1.某生产车间30名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 3846 43 39 35
要求:(1)根据以上资料分成如下向组:25—30,30—35,35—40,40—各组频数和频率,编制次数分布表。(2)根据整理表计算工人平均日产零件数。2.某公司下属50个企业,生产同种产品,某月对产品质量进行调查,得资料;要求计算该产品的平均合格率。3.某自行车公司下属甲种车单位成本(元4、某企业产品的有关资料如下:试分别计算企业该企业产品(03-01)6. 1990年某月份甲、乙两农贸市场某农产品价格和成交量、成交额资料如下:品种甲乙丙合计试问哪一个市场农产品的平均价格较高5.已知某局20按计划完成百分比分组(04-01)4.甲、乙两班同时参加《统计学原理》课程的测试,甲班平均成绩为的成绩分组资料如下:计算乙班学生的平均成绩,并比较甲、乙两班哪个班的平均成绩更有代表性?8某企业甲、乙两个车间,甲车间平均每个工人日加工零件数数资料:计算乙车间工人加工零件的平均数和标准差,并比较甲、乙两车间哪个车间的平均日加工零件数更有代表性?
学习时数(小时)
学习成绩(分)
4 6 7 10 13
40
60 50 70 90
要求:建立学习成绩(Y)倚学习时间(X)的直线回归方程—1995年个人消费支出和收入资料如下:
年份
个人收入
消费支出
1992
225
202
56元,标200元380元,样本8500小时,68.27的概率18件。要求(
要求:((01-07)4、某部门所属∑x=30、8∑y=961、要求:(1)计算全员劳动生产率与销售利润之间的相关系数,并分析相关的密切程度和方向。(2)建立销售利润倚全员劳动生产率变化的直线回归方程。5.某部门所属20个企业的可比产品成本降低率(%)与销产利润(万元)的调查资料整理如下(比产品成本降低率,y代表销售利润):=∑x109,8∑x要求:(1)建立销售利润倚可比产品成本降低率的直线回归方程,预测可比产品成本降低率为润为多少万元?((04-07)6、根据某地区历年人均收入(元)(下:y=260 n=9∑x=546∑要求:(1)计算以商品销售额为因变量的直线回归方程;并解释回归系数的含义(2)若2003年人均收入为(04-01)7、某部门5个企业产品销售额和销售利润资料如下:企业编号1 2 3 4 5试计算产品销售额与利润额的相关系数(04-07)1某公司销售的三种商品的销售额及价格变动资料如下:(04-01)2、某商店三种商品的销售资料如下:?商品甲乙丙试计算:(13.某集团公司销售的三种商品的销售额及价格提高幅度资料如下:试求价格总指数和销售额总指数。商品种类
(%)
企业数(个)实际产值(
90以下100 90——110 100110以上
4 68
57 5 126 4 1847
计合
43520
70分,标准差为11件;乙车间工人日加工零件
按成绩分组学生人数(人)
60以下2
6 70—6025 70—80
12 90 80—5
100
90—
65件,标准差
445,计算(元24 50028 56048 000万)万9.分;乙
3.某乡有5000农户,按随机原则重复抽取100户调查,得平均每户年纯收入12000元,标准差要求:(1)以95%的概率(t=1.96)估计全乡平均每户年纯收入的区间。
(2)以同样概率估计全乡农户所纯收入总额的区间范围
3.为了解某城市分体式空调的零售价格,随机抽取若干个商场中的40台空调,平均价格为准差400元。要求:(1)计算抽样平均误差;(2)以99.73%(t=3)的可靠性估计该城市分体式空调的价格区间。
5 12 3
40
45 15
98年99年的平均单位产品成本。
产品
年产量(件)98单位成本(元/件)
99年成本总额
甲乙丙
25 1500 28 1020980 32
价格(元/斤)
甲市场成交额(万元)
乙市场成交量
1.2 1.4 1.5
1.2 2.8 1.5
2
1 1
5.5
4
?并说明原因。个企业的有关统计资料如下:试计算产值的平均计划完成程度。
3、从某年级字生中按简单随机抽样方式抽取100名学生,对某公共课的考试成绩进行检查,及格的有人,试以95.45%的概率保证程度推断全年级学生的及格率区间范围。如果其它条件不变,将允许误差缩小一半,应抽取多少名学生检查?
2.某企业生产一批日光灯管,随机重复抽取400只作使用寿命试验。测试结果,平均寿命为本标准差为300小时,400只中发现10只不合格。求平均数的抽样平均误差和成数的抽样平均误差。2.某洗衣机厂随机抽选100台洗衣机进行质量检验,发现有5台不合格。试计算:(1)以证程度推断这批洗衣机的合格率。(2)若概率保证程度提高到95.45%,则这批洗衣机的合格率将怎样变化?
1.某企业第二季度产品产量与单位成本资料如下:要求:(2.已知五位同学统计学的学习时间与成绩分数如下表所示:(02-07)3.某地区1992
月份
产量(千件)单位成本(元)
4 5 6
3 73
69 4 5 68
1)配合回归方程,指出产量每增加1000件时单位成本平均变动多少?(2)产量为8000—10000件时,单位成本的区间是多少元。
