Newton分形的原理及Matlab实现
MATLAB计算方法迭代法牛顿法二分法实验报告

完美WORD格式姓名实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理 (1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2a b x -=。
否则,继续判断是否0)()(<∙x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 7.0软件四、 结果预测(1)11x =0.09033 (2)5x =0.09052 (3)2x =0,09052 五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x的近似根。
要求误差不超过3105.0-⨯。
MATLAB程序(牛顿法及线形方程组)

MATLAB 程序1、图示牛顿迭代法(M 文件)文件名:newt_gfunction x = new_g(f_name,x0,xmin,xmax,n_points)clf,hold off% newton_method with graphic illustrationdel_x = 0.001;wid_x = xmax - xmin; dx = (xmax - xmin)/n_points;xp = xmin:dx:xmax; yp = feval(f_name,xp);plot(xp,yp);xlabel('x');ylabel('f(x)');title('newton iteration'),hold onymin = min(yp); ymax = max(yp); wid_y = ymax-ymin;yp = 0. * xp; plot(xp,yp)x = x0; xb = x+999; n=0;while abs(x-xb) > 0.000001if n > 300 break; endy=feval(f_name,x); plot([x,x],[y,0]);plot(x,0,'o')fprintf(' n = % 3.0f, x = % 12.5e, y = % 12.5e \ n', n, x, y);xsc = (x-xmin)/wid_x;if n < 4, text(x,wid_y/20,[num2str(n)]), endy_driv = (feval(f_name,x + del_x) - y)/del_x;xb = x;x = xb - y/y_driv; n = n+1;plot([xb,x],[y,0])endplot([x x],[0.05 * wid_y 0.2 * wid_y])text( x, 0.2 * wid_y, 'final solution')plot([ x ( x - wid_x * 0.004)], [0.01 * wid_y 0.09 * wid_y])plot([ x ( x + wid_x * 0.004)], [0.01 * wid_y 0.09 * wid_y])传热问题假设一个火炉是用厚度为0.05m 的砖单层砌成的。
matlab牛顿拉夫逊法与快速分解法的实现

一、概述MATLAB是一种强大的数学软件工具,它提供了许多优秀的数值计算和数据分析功能。
其中,牛顿拉夫逊法和快速分解法是两种常用的数值计算方法,它们在解决非线性方程组和矩阵分解等问题中具有重要的应用价值。
本文将介绍如何在MATLAB中实现这两种方法,并对它们的优缺点进行详细分析。
二、牛顿拉夫逊法的实现1. 算法原理牛顿拉夫逊法是一种用于求解非线性方程组的迭代算法。
它利用函数的一阶和二阶导数信息来不断逼近方程组的解,直到满足精度要求为止。
算法原理可以用以下公式表示:公式1其中,x表示解向量,F(x)表示方程组的函数向量,J(x)表示方程组的雅可比矩阵,δx表示解的更新量。
通过不断迭代更新x,最终得到方程组的解。
2. MATLAB代码实现在MATLAB中,可以通过编写函数来实现牛顿拉夫逊法。
以下是一个简单的示例代码:在这段代码中,首先定义了方程组的函数向量和雅可比矩阵,然后利用牛顿拉夫逊法进行迭代更新,直到满足精度要求为止。
通过这种方式,就可以在MATLAB中实现牛顿拉夫逊法,并应用于各种实际问题。
三、快速分解法的实现1. 算法原理快速分解法是一种用于矩阵分解的高效算法。
它利用矩阵的特定性质,通过分解为更小的子问题来加速计算过程。
算法原理可以用以下公式表示:公式2其中,A表示要分解的矩阵,L和U分别表示矩阵的下三角和上三角分解。
通过这种分解方式,可以将原始矩阵的计算量大大减小,提高求解效率。
2. MATLAB代码实现在MATLAB中,可以利用内置函数来实现快速分解法。
以下是一个简单的示例代码:在这段代码中,利用MATLAB内置的lu函数进行LU分解,得到矩阵的下三角和上三角分解。
通过这种方式,就可以在MATLAB中实现快速分解法,并应用于各种矩阵计算问题。
四、方法比较与分析1. 算法复杂度牛顿拉夫逊法和快速分解法在计算复杂度上有所不同。
牛顿拉夫逊法的迭代次数取决于所求解问题的非线性程度,通常需要较多的迭代次数。
matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码二分法(Bisection Method)是一种寻找函数零点的数值计算方法。
该方法的基本思想是:首先确定一个区间[a, b],使得函数在这个区间的两个端点处的函数值异号,然后将区间逐步缩小,直到找到一个区间[a', b'],使得函数在这个区间的中点处的函数值接近于零。
以下是使用MATLAB实现二分法的示例代码:```matlabfunction [x, iter] = bisection(f, a, b, tol)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function has the same sign at the endpoints of the interval');enditer = 0;while (b - a) / 2 > tolc=(a+b)/2;fc = f(c);if fc == 0break;endif sign(fc) == sign(fa)a=c;fa = fc;elseb=c;fb = fc;enditer = iter + 1;endx=(a+b)/2;end```牛顿法(Newton's Method)是一种用于寻找函数零点的数值计算方法。
该方法的基本思想是:通过迭代来逼近函数的零点,每次迭代通过函数的切线来确定下一个近似值,直到满足收敛条件。
以下是使用MATLAB实现牛顿法的示例代码:```matlabfunction [x, iter] = newton(f, df, x0, tol)iter = 0;while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);iter = iter + 1;endx=x0;end```黄金分割法(Golden Section Method)是一种用于寻找函数极值点的数值计算方法。
newton迭代matlab代码_概述及解释说明

newton迭代matlab代码概述及解释说明1. 引言1.1 概述本文将介绍并详细解释Newton迭代算法在MATLAB中的代码实现。
Newton 迭代算法是一种用于求解方程根和优化问题的数值迭代算法,其基本原理是通过不断逼近函数的零点或最小值点来获得解。
本文将从算法的概述、原理介绍、迭代过程以及算法适用性分析等方面对Newton迭代算法进行全面的阐述。
1.2 文章结构文章将按照以下顺序展开对Newton迭代算法的讲解和说明:- 引言:对本文的主题和内容进行简要介绍,并给出文章的结构安排。
- Newton迭代算法概述:包括原理介绍、迭代过程和算法适用性分析三个部分,对Newton迭代算法的基本概念和应用领域进行阐述。
- MATLAB代码实现解释说明:详细说明了使用MATLAB编写Newton迭代算法代码的背景信息和相关工具介绍,然后逐步解释代码实现的步骤,并通过示例与结果分析来更好地理解代码部分。
- 应用案例和拓展讨论:通过具体案例一(求解方程根)和案例二(系统优化问题求解)来展示Newton迭代算法的实际应用,并在拓展讨论部分探讨改进Newton迭代算法的研究方向和方法。
- 结论与展望:对整篇文章进行总结回顾,并展望未来更高效、更准确的数值迭代算法发展趋势。
1.3 目的本文的目的是通过对Newton迭代算法在MATLAB中代码实现的详细解释,帮助读者更好地理解该算法的原理和应用,并提供相应的代码示例和结果分析。
同时,通过应用案例和拓展讨论,引发读者对于改进Newton迭代算法及其未来发展方向的思考。
通过阅读本文,读者可以具备一定程度上运用Newton迭代算法解决实际问题的能力,并对当前数值迭代算法领域的研究方向有一定了解。
2. Newton迭代算法概述:2.1 原理介绍:Newton迭代算法是一种用于数值逼近解的迭代方法,可以用于求解非线性方程的根、优化问题等。
该算法基于牛顿-拉弗森方法,其基本思想是通过不断逼近函数曲线上的某点来寻找函数零点或极值点。
[matlab二分法程序代码]matlab牛顿迭代法程序代码
![[matlab二分法程序代码]matlab牛顿迭代法程序代码](https://img.taocdn.com/s3/m/5cd37268a0116c175f0e48ea.png)
[matlab二分法程序代码]matlab牛顿迭代法程序代码篇一: matlab牛顿迭代法程序代码牛顿迭代法主程序:function?[k,x,wuca,yx]?=?newtonk=1;yx1=fun;yx2=fun1;x1=x0-yx1/yx2;while?abs>tolx0=x1;yx1=fun;yx2=fun1;k=k+1;x1=x1-yx1/yx2;endk;x=x1;wuca=abs/2;yx=fun;end分程序1:function?y1=funy1=sqrt-tan;end分程序2:function????y2=fun1%函数fun的导数y2=x/)-1/) );end结果:[k,x,wuca,yx]?=?newtonk?=8x?=0.9415wuca?=4.5712e-08yx?=-3.1530e-14[k,x,wuca,yx]?=?newtonk?=243x?=NaNwuca?=NaNyx?=NaN篇二: 二十个JA V A程序代码1百分制分数到等级分数package pm;public class SwitchTest {//编写程序,实现从百分制分数到等级分数的转换////>=90 A// 80~89 B// 70~79 C// 60~69 D// public static void main {int s=87;switch{case 10 :System.out.println;break; case 9 :System.out.println;break; case 8 :System.out.println;break;case 7 :System.out.println;break;case 6 :System.out.println;break; default :System.out.println;break; }}}2成法口诀阵形package pm;public class SwitchTest{public static void main{for{for{System.out.print+”\t”); }System.out.println;}}}3华氏和摄氏的转换法package pm;import java.util.Scanner;public class SwitchTest {public static void main {Scanner sc=new Scanner;while {System.out.println;String s = sc.next.trim;if ) {//做摄氏向华摄的转换System.out.println;double db = sc.nextDouble; double db2 = + 32;System.out.println;} else if ) {//做华摄向摄氏的转换System.out.println;double db = sc.nextDouble; double db2 = * 5 / 9;System.out.println + “C”); }else if){ break;}}}}package pm;import java.util.Scanner;public class SwitchTest{public static void main {Scanner sc=new Scanner;boolean flag=true;while {System.out.println; String str = sc.nextLine.trim; if || str.endsWith) {//做摄氏向华摄的转换30cString st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = + 32;System.out.println;} else if || str.endsWith) {//做华摄向摄氏的转换String st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = * 5 / 9;System.out.println + “C”); }else if){flag=false;}}}}4三个数的最大数package pm;public class SwitchTest {public static void main {int a=1,b=2,c=3,d=0;d=a>b?a:b;d=a>b?:;System.out.println;}}5简单计算器的小程序package one;import java.awt.BorderLayout;import java.awt.GridLayout;import java.awt.event.ActionEvent; import java.awt.event.ActionListener;import javax.swing.JButton;import javax.swing.JFrame;import javax.swing.JPanel;import javax.swing.JTextField;public class Jsq implements ActionListener {private JFrame frame;private JButton[] bus;private JTextField jtx;private JButton bu;private char[] strs;private String d_one = ““;private String operator;public static void main { new Jsq;}/* 利用构造进行实例化*/ public Jsq { frame = new JFrame; jtx = new JTextField; bus = new JButton[16]; strs = “789/456*123-0.+=“.toCharArray; for { bus[i] = new JButton; bus[i].addActionListener; } bu = new JButton; bu.addActionListener; init; } /* GUI 初始化*/ public void init { JPanel jp1 = new JPanel; jp1.add; jp1.add; frame.add; } /* 事件的处理*/ public void actionPerformed { /*获取输入字符*/ String conn = arg0.getActionCommand; /*清除计算器内容*/ if ) { JPanel jp2 = new JPanel; jp2.setLayout); for { jp2.add; } frame.add; frame.pack; frame.setLocation; frame.setVisible; frame.setDefaultCloseOperation;d_one = ““; operator = ““; jtx.setText; return; } /*暂未实现该功能*/if){ return; } /*记录运算符,保存运算数字*/ if ) != -1) { if && ““.equals)) return; d_one = jtx.getText; operator = conn; jtx.setText; return; } /*计算结果*/ if ) { if && ““.equals)) return; double db = 0; if ) { db = Double.parseDouble + Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble - Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble * Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble / Double.parseDouble); jtx.setText; } d_one = db + ““; return; }//界面显示jtx.setText + conn);}}6三角形图案package pm;public class SwitchTest{public static void main{int n=5;for{for{System.out.print;}for{System.out.print;}System.out.println;}}}7输出输入的姓名package pm;import java.util.Scanner;public class SwitchTest{public static void main{String name=null;Scanner sca=new Scanner ; char firstChar; do{System.out.println; name=sca.nextLine; firstChar=name.charAt;}while);System.out.println;}}8一小时倒计时小程序package pm;import javax.swing.JFrame;import javax.swing.JLabel;import javax.swing.JPanel;public class SwitchTest {private JFrame frame;private JLabel jl1;private JLabel jl2;private JLabel jl3;/*主方法*/public static void main {new SwitchTest.getTime;}/*倒计时的主要代码块*/private void getTime{long time=1*3600;long hour =0 ;long minute =0 ;long seconds=0;while{hour=time/3600;minute=/60;seconds=time-hour*3600-minute*60; jl1.setText;jl2.setText;jl3.setText;try {Thread.sleep;} catch {e.printStackTrace;}time--;}}/*构造实现界面的开发GUI */ public SwitchTest{frame = new JFrame;jl1 = new JLabel;jl2 = new JLabel;jl3 = new JLabel;init;}/*组件的装配*/private void init{JPanel jp=new JPanel;jp.add;jp.add;jp.add;frame.add;frame.setVisible;frame.setLocation;frame.setSize;frame.setDefaultCloseOperation; } }9棋盘图案public class Sjx{public static void main{int SIZE=19;for{if{System.out.print;//两个空格}else{System.out.print);//两个空格}}System.out.println;// System.out.print:);for{System.out.print;//一个空格}else{System.out.print+” “);//一个空格}for{System.out.print;//两个空格}System.out.println;}}}10数组输出唐诗package day04;public class ArrayTest {public static void main{char[][] arr=new char[4][7];String s=“朝辞白帝彩云间千里江陵一日还两岸猿声啼不住轻舟已过万重山”; for{for{arr[i][j]=s.charAt;}for{for{System.out.print;}System.out.println;}}}11找出满足条件的最小数package day02;public class Fangk{public static void main{// for{// int q=i/1000;// int b=i/100%10;// int s=i/10%10;// int g=i%10;// if{ // System.out.println; // break; // }// }loop1: for{loop2: for{if{continue loop2;}for{for{if{ System.out.println); break loop1;}}}}}}} Min Number12判断一个数是否是素数package day02;public class Fangk{ public static void main{ int num=14;boolean flag=true;for{flag=false;break;}}if{System.out.println; }else{System.out.println; }}}////////////////////////////////////////////////////////////////////// package day04;import java.util.Scanner;public class A1{public static void main{int n;Scanner sca=new Scanner;System.out.println; n=sca.nextInt;if){System.out.println; }else{System.out.println;}public static boolean isPrimeNumber{ for{if{return false;}}return true;}}13一个数倒序排列package day02;public class Daoxu{public static void main{ int olddata=3758;int newdata=0;while{for{newdata=newdata*10+olddata%10; olddata=olddata/10; }System.out.println;}}}14将一个整数以二进制输出package day04;import java.util.Scanner; public class ArrayTest { public static void main{ int n; Scanner s=new Scanner; System.out.println; n=s.nextInt; for{if)!=0){System.out.print;}else{System.out.print;}if%8==0){System.out.print;}}}}15矩形图案package day02;public class Fangk {public static void main{ int m=5,n=6; for{System.out.print;}System.out.println;for{System.out.print;for{System.out.print; }System.out.print;System.out.println;}for{System.out.print;}}}16猜数字package day02;import java.util.Scanner;public class Csz {public static void main {Scanner s = new Scanner; int num = * 1000); int m=0; for{System.out.println; m=s.nextInt;if{System.out.println;}else if{System.out.println;}else{System.out.println; break;}if{System.out.println; }}if{System.out.println; }}}17.HotelManagerpackage hotel;import java.util.Scanner;public class HotelManager {private static String[][] rooms;// 表示房间public static void main {rooms = new String[10][12];String comm;// 表示用户输入的命令for {for {rooms[i][j] = “EMPTY”;}}//while {System.out.println;Scanner sca = new Scanner; System.gc;comm = sca.next;if ) {search;} else if ) {int roomNo = sca.nextInt;String name = sca.next;in;} else if ) {int roomNo = sca.nextInt;out;} else if ) {System.out.println;break;} else {System.out.println; }}}private static void out {if-1][-1])){ System.out.println;} return; } rooms[-1][-1]=“EMPTY”; System.out.println; private static void in { if-1][-1])){ System.out.println;return;}rooms[-1][-1]=name;System.out.println;}private static void search {for {//打印房间号for {if {System.out.print + “ “); } else {System.out.print + “ “); }}//打印房间状态System.out.println;for {System.out.print;}System.out.println;}}}18.StudentManagerpackage day05.student_manager;import java.util.Scanner;public class StudentManager {static int[][] scores=new int[6][5];static String[] students={“zhangsan”,”lisi”,”wangwu”,”zhaoliu”,”qianqi”,”liuba”}; static String[] courses={“corejava”,”jdbc”,”servlet”,”jsp”,”ejb”};public static void main {for{for{scores[i][j]=*100);}}Scanner s=new Scanner; String comm;while{System.out.println; comm=s.next;if){String para=s.next; avg;}else if){String course=s.next; sort;}else if){String student=s.next; String course=s.next; get;}else if){break;}else{System.out.println; }}}//main end!public static void avg{int sIndex=-1;//int cIndex=-1; for{ if){ sIndex=i; } } if{ for{ if){ cIndex=i; } } } if{ System.out.println; return; } double avg=0.0; if{ for{ avg+=scores[sIndex][i]; } avg/=scores[sIndex].length; System.out.println; }else{ for{ avg+=scores[i][cIndex]; } avg/=scores.length; System.out.println; } } public static void sort{ int[] courseScore=new int[scores.length]; if){//如果求总分的排名//求出每个学生的总分,将成绩存放在courseScore数组中for{ int studentSum=0; for{ studentSum+=scores[i][j]; }courseScore[i]=studentSum; } }else{//如果不是求总分排名int cIndex=-1; for{//找到这门课程的下标if){ cIndex=i; } } if{//如果是一门有效的课程//把scores数组中这一列的值放到courseScore数组中!for{ courseScore[i]=scores[i][cIndex]; } }else{//如果不是一门有效的课程System.out.println; return; } } String[] studentCopy=new String[students.length]; System.arraycopy; for{ for{ if{ int temp=courseScore[i]; courseScore[i]=courseScore[j]; courseScore[j]=temp; String stemp=studentCopy[i];studentCopy[i]=studentCopy[j]; studentCopy[j]=stemp; } } } int order=1; System.out.println; for{ if{ order--; }else{ order=i+1;} System.out.print;System.out.print;System.out.println;order++;}}public static void get{int sIndex=-1;int cIndex=-1;for{if){sIndex=i;}}if{System.out.println;return;}if){//如果求总分int studentSum=0;for{studentSum+=scores[sIndex][j];}System.out.println; return;}for{if){cIndex=i;}}if{System.out.println;return;}System.out.println;}}19.Fivepackage hotel;import java.util.Scanner;/*** 首先在程序第一次运行的时候,构建出棋盘,切以后* 不能再从新构建,知道结束,所以将其放到静态代码块中。
用Matlab编写二分法和Newton迭代法求解非线性函数
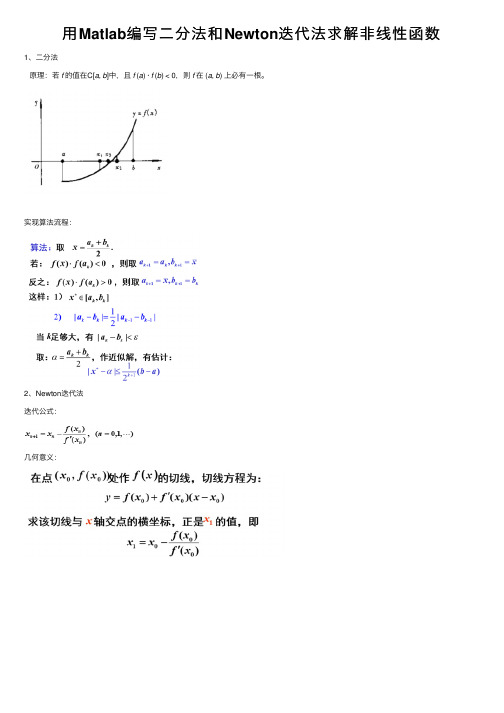
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理:若f的值在C[a, b]中,且f (a) · f (b) < 0,则f在 (a, b) 上必有⼀根。
实现算法流程:2、Newton迭代法迭代公式:⼏何意义:3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值:12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间:[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥,请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值:p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数:48 %⽅程近似解:p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
非线性方程组求解的牛顿迭代法用MATLAB实现

****1. 二元函数的newton 迭代法理论分析设),(y x f z =在点),(00y x 的某一邻域内连续且有直到2阶的连续偏导数,),(00h y h x ++为该邻域内任意一点,则有⎥⎦⎤⎢⎣⎡∂∂+∂∂+≈++==00),(),(),(),(0000y y x x y x f y k y x f xh y x f k y h x f 其中 0x x h -=,0y -=y k 于是方程0),(=y x f 可近似表示为0),(),(),(k =⎥⎦⎤⎢⎣⎡∂∂+∂∂+==k k y y x x k y x f y k y x f x h y x f 即 0),()(),()(),(y k =-+-+k k k k k x k k y x f y y y x f x x y x f同理,设y)g(x,z =在点),(00y x 的某一邻域内连续且有直到2阶的连续偏导数,),(00h y h x ++为该邻域内任意一点,亦有⎥⎦⎤⎢⎣⎡∂∂+∂∂+≈++==00),(),(),(),(0000y y x x y x g y k y x g x h y x g k y h x g其中0x x h -=,0y -=y k 于是方程0),(g =y x 可近似表示为0),(),(),(k =⎥⎦⎤⎢⎣⎡∂∂+∂∂+==k k y y x x k y x g y k y x g x h y x g 即 0),(g )(),()(),(y k =-+-+k k k k k x k k y x y y y x g x x y x g于是得到方程组⎩⎨⎧=-+-+=-+-+0),(g )(),()(),(0),()(),()(),(y k y k k k k k k x k k k k k k k x k k y x y y y x g x x y x g y x f y y y x f x x y x f****求解这个方程组,当0),(),(),(),(≠-k k y k k x k k y k k x y x g y x f y x f y x g 时),(),(),(),(),(),(),(),(k k y k k x k k y k k x k k y k k k k y k k k y x g y x f y x f y x g y x f y x g y x g y x f x x --+=),(),(),(),(),(),(),(),(y k k y k k x k k y k k x k k x k k k k x k k k y x g y x f y x f y x g y x g y x f y x f y x g y --+=从而⎪⎪⎩⎪⎪⎨⎧--+=--+=),(),(),(),(),(),(),(),(y ),(),(),(),(),(),(),(),(k k y k k x k k y k k x k k x k k k k x k k k k k y k k x k k y k k x k k y k k k k y k k k y x g y x f y x f y x g y x g y x f y x f y x g y y x g y x f y x f y x g y x f y x g y x g y x f x x (1) 记符号),(),(),(),(g ),(k k x k k k k x k k y x x x y x g y x f y x f y x g fg f k k -=- ),(),(),(),(),(k k y k k k k y k k y x yy y x f y x g y x g y x f gf fg k k -=-),(),(),(),(),(k k y k k x k k y k k x y x y x y x y x g y x f y x f y x g g f f g k k -=-于是(1)式可改写为⎪⎪⎩⎪⎪⎨⎧--+=--+=),(),(),(),(g k k k k k k k k y x y x y x y x x x k y x y x y x y x y y k g f f g fg f y y g f f g gf fg x x (2)迭代公式为:⎪⎪⎩⎪⎪⎨⎧--+=--+=++),(),(1),(),(1k g k k k k k k k k y x y x y x y x x x k k y x y x y x y x y y k gf fg fg f y yg f f g gf fg x x (3) 通过迭代公式(3)可以迭代出当 ,2,1=k 时,),(k k y x 的值,当δ≤++)1,1(yk xk (0>δ为给定的误差控制项)时,原方程组的根即为),(k k y x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Newton分形的原理及Matlab实现
作者:张健徐聪全付勇智
来源:《电脑知识与技术》2009年第24期
摘要:详细推导了复平面上Newton迭代法的原理和计算公式,用MATLAB编制程序实现了Newton迭代算法,得到了一些奇异、绚丽的分形图形。
对《数学实验》课程有一定的参考价值。
关键词:Newton迭代法;分形;Matlab;数学实验
中图分类号:TP312文献标识码:A文章编号:1009-3044(2009)24-6997-03
The Principles of Newton Fractal and it's Realization Using MATLAB
ZHANG Jian, XU Cong-quan, FU Yong-zhi
(Department of Basic Courses, Southwest Forestry College, Kunming 650224, China)
Abstract: The Principles and formulas of Newton fractal was explained,fractal graphics of Newton iteration was created using Matlab.
Key words: newton iteration; fractal; Matlab; mathematical experimental
分形是非线性科学的一个重要分支,应用于自然科学和社会科学的众多领域。
其中,分形图形以其奇异、绚丽多彩的特点,广泛应用于纺织印染、广告设计、装潢设计、计算机美术教学等领域[1]。
很多分形图形都是用迭代的方式实现的,Newton迭代法就是其中的一种。
由Newton迭代法产生的分形图形称为Newton分形[2]。
很多文献都对Newton分形进行了介绍,但都没有详细的计算公式和算法说明,读者很难编制相应程序。
本文详细介绍了复平面上Newton迭代法的原理和计算公式,设计了相应的实现算法,并用Matlab编制程序实现了Newton分形的绘制,生成了一些奇异、瑰丽的分形图形。
由于国内高校《数学实验》课程大多采用Matlab软件,同时很少涉及分形图形的实验,因此,Newton分形的Matlab实现可以丰富《数学实验》课程的内容,对数学类、计算机类、艺术类学生和教师有一定的参考价值。
1 Newton迭代法
17世纪,牛顿创立了一种依靠简单迭代计算求方程f(x)=0的根的方法[3]:
任取一点x0,利用公式(1)进行迭代,若存在,则序列xt收敛于方程f(x)=0在x0附近的一个根。
我们把复数z应用到公式(1)上,就得到了复平面上的Newton迭代公式:
现在,取一个较简单的函数f(z)=zn-1,则f(z)的一阶导数f’(z)=nzn-1,代入公式(2)得:
根据复数的三角表示式,可记zt为:
zt=xt+iyt=|zt|(cosθ+isinθ) (4)
其中,称为复数zt的模,θ为复数zt的辐角的主值,-π≤θ≤π。
辐角主值θ的计算方法如下[1]:
由复变函数知识可知:
将(5)、(6)两式代入(3)得:
即有:
(8)
式(8)就是编写程序时需要的迭代计算公式。
2 Newton分形的生成算法
在复平面上取定一个窗口,将此窗口均匀离散化为有限个点,将这些点记为初始点z0,按公式(8)进行迭代。
其中,大多数的点都会很快收敛到方程f(z)=zn-1的某一个零点,但也有一些点经过
很多次迭代也不收敛。
为此,可以设定一个正整数M和一个很小的数δ,若果当迭代次数小于M 时,就有两次迭代的两个点的距离小于δ,即
则认为z0是收敛的,即点z0被吸引到方程f(z)=zn-1=0的某一个根上;反之,当迭代次数达到了M,而|zt+1-zt|>δ时,则认为点z0是发散(逃逸)的。
这就是逃逸时间算法的基本思想。
当点z0比较靠近方程f(z)=zn-1的根时,迭代过程就很少;离得越远,则迭代次数越多甚至不收敛[2]。
由此设计出函数f(z)=zn-1的Newton分形生成算法步骤如下:
1)设定复平面窗口范围,实部范围为[a1,a2],虚部范围为[b1,b2],并设定最大迭代步数M和判断距离δ;
2)将复平面窗口均匀离散化为有限个点,取定第一个点,将其记为z0,然后按公式(8)进行M 次迭代。
每进行一次迭代,按公式(9)判断迭代前后的距离是否小于δ,如果小于δ,根据当前迭代的次数M选择一种颜色在复平面上绘出点z0;如果达到了最大迭代次数M而迭代前后的距离仍然大于δ,则认为z0是发散的,选择白色(也可换为其他颜色)在复平面上绘出点z0。
3)在复平面窗口上取定第二个点,将其记为z0,按第(2)步的方法进行迭代和绘制。
直到复平面上所有点迭代完毕。
3 Matlab程序设计
Matlab是由MathWorks公司与1984年推出的数学软件,原意为“矩阵实验室”。
Matlab以其强大的功能和良好的开放性、面向问题性、易学易用等特点,越来越被广大科研人员和工程计算人员以及高校学生和老师所重视[4]。
国内外《数学实验》课程大多采用Matlab软件作为计算工具,为此,我们使用Matlab编制了绘制Newton分形的程序。
程序由3个函数组成:
1)主函数newton.m:
function f = newton(n)
m=13;%迭代次数
a1=-2;%复平面窗口实部范围
a2=2;
b1=-1.5; %复平面窗口虚部范围
b2=1.5;
delta=0.01 %收敛判定距离
hold on
for i = a1:0.02:a2
for j =b1:0.02:b2
%对每一个点,调用迭代函数,返回收敛时间(即判断为收敛时的迭代次数M) f=f_iterat(i,j,n,m,delta);
if f > 0%用7种颜色(不含白色)绘制收敛点
switch rem(f,7) %求f除以7的余数
case 0
plot(i,j,'b.')%蓝色
case 1
plot(i,j,'c.')%青色
case 6
plot(i,j,'y.')%黄色
end
end
end
hold off
2)Newton迭代函数f_iterat.m:
%参数说明:(x,y)为点的实部与虚部,n为方程的幂次,m为最大迭代次数,delta为收敛判断距离
function f=f_iterat(x,y,n,m,delta)
delta = 0.01;%收敛判断距离
f=0; %赋初值为0,表示发散
for i = 1:m
p = sqrt(x*x+y*y);%计算复数的模
seta = f_arg(x,y); %计算复数的辐角
x2=((n-1)*p*cos(seta)+p^(1-n)*cos((1-n)*seta))/n;%实部
y2=((n-1)*p*sin(seta)+p^(1-n)*sin((1-n)*seta))/n;%虚部
dis = sqrt((x2-x)^2+(y2-y)^2); %计算迭代前后两点的距离
if dis < delta %收敛
f=i; %返回收敛时间
break%结束循环
end
x=x2;
y=y2;
end
其中,函数f_arg(x,y)为计算复数z=x+iy的辐角主值θ的函数,根据公式(5)不难写出。
4 实验结果
在MATLAB命令窗口中,输入“>> newton(3)”或“>> newton(4)”,即可绘制出函数f(z)=z3-1
或f(z)=z4-1对应的Newton分形的图形:
在图1中,白色区域表示发散点所组成的区域,彩色区域为收敛点组成的区域。
收敛区域内的点,由于收敛时间的不同,所呈现的颜色不同,构成了一幅五彩斑斓、奇异复杂的图形。
输入其他的n,则可绘制出函数f(z)=zn-1对于的Newton分形,举例如下:
5 结论
用VB、VC等程序设计语言编写的Newton分形生成程序需要两个窗口:绘图窗口和参数窗口,然后要建立绘图窗口到参数窗口之间的映射[5-6]。
而用MATLAB编制的程序直接在参数窗口(复平面窗口)中绘图,所编制的程序简单易懂,所绘制的图形奇异瑰丽、绚丽多彩,体现了数学、计算机、艺术三者的结合,学生有很大的吸引力,对有关专业的教师、学生以及分形爱好者有一定的参考作用。
而且,只要稍微改动迭代参数,如迭代次数M、判断距离?啄、复窗口范围等,所得到的图形会出现很多意想不到的变化,很适合做为理工科《数学实验》课程的内容。
参考文献:
[1] 秦宣云,任波.逃逸时间法生成Julia集的算法分析和具体实现[J].计算机工程与应
用,2007,43(5):30-32.
[2] 李水根.分形[M].北京:高等教育出版社,2004:20-30.
[3] 孙博文.分形算法与程序设计[M].北京:科学出版社,2004:61-91.
[4] 曾建军,李世航,王永国等.MATLAB语言与数学建模[M].合肥:安徽大学出版社,2005:1-30.
[5] 姜卓睿,宋中山,苏斌.基于重根牛顿迭代法和比较算法实现的分形图形的研究 [J].电脑开发与应用,2008;21(7):12-13.
[6] 吴运兵,李勇.牛顿迭代法在分形图形生成上的应用研究[J].西安科技大学学
报,2005,25(3):365-367.。
