几何基础
初一几何入门基础知识

初一几何入门基础知识
初一几何入门基础知识包括以下几个方面:
1. 几何图形的基本概念:几何图形包括点、线、面、体等基本元素,这些元素可以用来描述错综复杂的世界。
几何图形分为立体图形和平面图形两大类。
2. 直线的性质:直线是几何学中的一个基本概念,表示点在空间内沿相同或相反方向运动的轨迹。
在平面解析几何中,直线由一个二元一次方程表示,可以通过联立方程组求两条直线的交点。
直线的倾斜角或斜率可以用来表示平面上直线的倾斜程度。
3. 射线和线段:射线是直线上的一点和它一旁的部分组成的图形,而线段是由两个端点确定的连续或不连续的图线。
线段有特定的性质,例如两点之间线段最短。
4. 角的定义和性质:角是由两条射线组成的图形,有公共端点。
角的大小取决于两条边张开的程度,可以用角度制、弧度制等度量单位来衡量。
角可以分为锐角、直角、钝角、平角、周角等不同类型,它们之间存在余角、补角和对顶角等关系。
5. 几何图形的分类:几何图形可以分为立体图形和平面图形两大类。
立体图形包括柱体、锥体和球体等,平面图形包括圆形、多边形等。
以上是初一几何入门基础知识的主要内容,这些知识是进一步学习几何的基础。
在学习过程中,学生需要掌握这些概念的定义、性质和应用,以及如何使用这些知识解决实际问题。
同时,也需要通过大量的练习和实践来加深对几何知识的理解和掌握。
小升初几何基础知识点总结

小升初几何基础知识点总结一、点、线、面的基本概念1. 点:点是最基本的几何图形,没有长度、宽度和高度,只有位置,用字母标记。
2. 直线:由无数个相邻的点组成,无限延伸,两点确定一条直线。
3. 线段:是直线的一部分,有固定的长度。
4. 射线:是一个端点和它在同一侧直线上的所有点组成的全体。
二、角的概念和性质1. 角的概念:两条线段共同端点为顶点,分别位于这两条线段的两侧的两条射线组成的图形。
2. 角的度量:用度来表示角的大小,一个圆共360度。
3. 角的种类:锐角、直角、钝角。
4. 角的性质:相邻角、对顶角、、补角、同位角等。
三、平行线和平行四边形1. 平行线:在一个平面内,不相交且在同一方向的直线称为平行线。
2. 平行线的性质:平行线上的平行线,平行线上的平行线等于90度,直线被平行线截断时,对应角相等。
3. 平行四边形:对边平行的四边形,对角相等。
四、三角形1. 三角形:是由三条线段相互连接而成的简单的封闭图形。
2. 三角形的角:内角和为180度,外角等于其对边内角的和。
3. 三角形的性质:等边三角形的三边相等,等腰三角形的两边相等,直角三角形的一个角为90度。
4. 三角形的分类:按边长分为等边三角形、等腰三角形、普通三角形;按角度分为直角三角形、锐角三角形、钝角三角形。
五、四边形1. 四边形:是由四条线段相互连接而成的封闭图形。
2. 四边形的性质:内角和为360度。
3. 四边形的分类:矩形、正方形、平行四边形、菱形、梯形。
六、圆的概念1. 圆:一个平面内到一个固定点的距离恒定为r的所有点的集合。
2. 圆的性质:圆上任意一点到圆心的距离相等。
3. 圆的周长和面积计算公式:周长C = 2πr,面积S = πr²。
总结:以上是小升初几何基础知识点的总结,掌握这些知识点对于学生来说是非常重要的,这也是他们在学习几何课程中的基础。
希望学生能够通过学习,牢固掌握这些知识点,为之后的学习打下坚实基础。
几何基础知识

几何基础知识1.同角或等角的余角相等,同角或等角的补角相等(余角和补角)2.如果两个角是对等角,那么这两个角相等(对等角定义,要素)3.同位角相等,两条直线平行(同位角定义)4.内错角相等,两条直线平行(内错角定义)5.同旁内角互补,两条直线平行(同旁内角定义)注:不平行的两条直线也有同位角,内错角,同旁内角6.平行线性质:两条直线平行,同位角相等,内错角相等,同旁内角互补7.用尺规做线段和角的方法。
、8.三角形(定义)性质:a三角形任意两边之和大于第三边b三角形任意两边之差小于第三边9.等腰三角形,等边三角形,正三角形定义(顶角,腰,底边,底角)10.a三角形内角和是180度b直角三角形的两个锐角互余(锐角三角形,直角三角形,钝角三角形,直角边定义)11.在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线12.在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线13.三角形的三条角平分线交于一点,三条中线交于一点。
等腰三角形的顶角角平分线和底边的中线是重合的。
14.从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高(三角形的三条高所在的直线交于一点,锐角在内部,直角在直角顶点,钝角在外部)15.图形的全等:两个能够重合的图形称为全等图形(全等图形的形状和大小都)16.全等三角形的对应边相等,对应角相等。
全等符号是什么?分别表示什么?(全等三角形面积一定相等,但是面积相等不一定是全等三角形)17.a三边对应相等的两个三角形全等,简写“边边边”或“SSS”b两角和他们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”c两角和其中一角的对边对应相等的两个三角形全等,简写“角角边”或“AAS”d两边和他们的夹角对应相等的两个三角形全等,简写“边角边”或“SAS”注:两边及其中一边的对角对应相等,两个三角形不一定全等。
几何基础

献给爱好平面几何的每一个读者:(来源:luoqq330501)(一)欧几里德几何原本公设:公设1:任意一点到另外任意一点可以画直线。
公设2:一条有限线段可以继续延长。
公设3:以任意点为心及任意的距离可以画圆。
公设4:凡直角都彼此相等。
公设5:同平面内一条直线和另外两条直线相交,若在某一侧的两个内角和小于二直角的和,则这二直线经无限延长后在这一侧相交。
(二)几何五大模型(1)等积变换模型1、等底等高的两个三角形面积相等2、两个三角形高相等,面积比等于它们的底之比3、两个三角形底相等,面积比等于它的的高之比(2)共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(3)蝴蝶定理模型任意四边形与四边形、长方形、梯形,连接对角线所成四部分的比例关系是一样的(4)相似三角形模型相似三角形:形状相同,但大小不同的三角形相似三角形的一切对应线段的长度成比例,且这个比例等于它们的相似比相似三角形的面积比等于它们相似比的平方(5)燕尾定理模型燕尾定理,在△ABC中,D、E、F为BC、CA、AB 上点,AD、BE、CF 交于同一点O,则有S△AOB:S△AOC=S△BDO:S△CDO=BD:CDS△AOC:S△BOC=S△AFO:S△BFO=AF:BFS△BOC:S△BOA=S△CEO:S△AEO=EC:AE(三)(1)有一条公共边的三角形叫做共边三角形。
共边定理:设直线AB与PQ交于点M,则S△PAB/S△QAB=PM/QM特殊地:当PQ∥AB时,易知△PAB与△QAB的高相等,从而S△PAB=S△QAB反之,S△PAB=△QAB,则PQ∥AB(2)角平分线定理在△ABC中,BD平分∠ABC,则AD:DC=AB:BC(3)分角定理在△ABC中,D是BC或其延长线上的一点,连结AD,则有BD/CD=(sin∠BAD/sin ∠CAD)*(AB/AC)。
数学几何基础知识

数学几何基础知识几何学是数学的一个分支,研究空间和图形的形状、大小、相互关系及其性质。
它是数学中的一门重要学科,应用广泛,涉及到许多实际问题的解决。
本文将介绍一些数学几何的基础知识和概念。
一、点、线和面在几何学中,最基本的元素是点、线和面。
点:点是最基本的几何元素,没有大小和形状,可以用来表示物体的位置。
线:两个点之间的直线称为线段,线段可以延伸到无穷远。
在几何学中,直线也是由无数个点组成的。
面:面由无数个点和线组成,可以看作是一个平面或者一个曲面。
面可以有形状和大小。
二、几何图形几何图形是由点、线和面组成的具有特定形状的图形。
1. 点和线:在平面上,最简单的几何图形是点和线段。
这些图形可以用来表示平面上的位置和距离。
2. 三角形:三角形是由三条线段组成的图形。
它有三个顶点、三条边和三个内角。
3. 四边形:四边形是由四条线段组成的图形。
它有四个顶点、四条边和四个内角。
4. 圆形:圆形是由一个圆心和一条半径组成的图形。
圆的直径是通过圆心的两个点之间的线段。
5. 多边形:多边形是由多条线段组成的图形。
它有多个顶点、多条边和多个内角。
三、几何性质几何学有许多重要的性质和定理,这些性质和定理可以帮助我们解决几何问题。
1. 平行线和垂直线:平行线是在同一平面上永不相交的直线。
垂直线是形成90度角的直线。
2. 同位角和内错角:同位角是指两条平行线被一条横线切割形成的对应角,它们是相等的;内错角是指两条平行线被一条横线切割形成的内侧相对角,它们是补角。
3. 相似三角形:如果两个三角形的对应角相等,对应边成比例,则这两个三角形是相似的。
4. 距离和角度:在几何学中,我们可以使用距离和角度来度量物体之间的关系。
四、几何计算几何学也涉及到一些计算问题,例如计算图形的面积、周长和体积等。
1. 长方形的面积和周长:长方形的面积可以通过将其宽度乘以长度得到,周长可以通过将两倍的宽度和两倍的长度相加得到。
2. 三角形的面积:三角形的面积可以通过将底边乘以高度再除以2得到。
几何原本-第一卷几何基础

命题1.35
• 命题:在同底上且在相同的二平行线之间的平行 四边形面积相等;
Hanjing shanxi jincheng
命题1.36-41
• 命题1.36、在等底上且在相同的二平行线之间的平行四边 形面积相等; • 命题1.37、同底等高的三角形面积相等; • 命题1.38、等底等高的三角形面积相等; • 命题1.39、有共同底边位于同侧面积相等的三角形的令两 点的连线平行于底边; • 命题1.40、等底并在同一边的面积相等的三角形,定点的 连线平行于底边; • 命题1.41、如果一个平行四边形与三角形同底边,并同一 顶点连线平行与底边,那么平行四边形的面积是三角形的 两倍;
Hanjing shanxi jincheng
命题1.13-15
• 命题1.13、两条直线相交,邻角是两个直角或者 其和为180度; • 命题1.14、平面上两条不在一边的射线过任意直 线上一点,所成的邻角之和若等于两个直角的 和,那么这两条射线构成一条直线; • 命题1.15、两直线相交对顶角相等;
Hanjing shanxi jincheng
定义
• 定义1.18、 半圆:是直径与被它切割的圆弧围成 的图形,半圆的圆心与原圆心相同;
Hanjing shanxi jincheng
定义
• 定义1.19、 直线图形是由线段首位顺次相接围成 的。 三角形是由三条线段围成的, 四边形是由四条线段围成的, 多边形是由四条以上线段围成的; • 定义1.20、三角形中,三条变相等称为等边三角 形,两条变相等称等腰三角形,三边都不相等称 不等边三角形;
Hanjing shanxi jincheng
命题1.16-17
• 命题16:任意三角形,其任意一边的延长线所形 成的外角大于任意不相邻的内角;
初中数学几何知识点归纳

初中数学几何知识点归纳一、几何基础知识1. 点、线、面- 点:没有大小,只有位置。
- 线:由无数个点组成,有长度,没有宽度。
- 面:由无数条线组成,有长度和宽度。
2. 直线、射线、线段- 直线:无限延伸,没有端点。
- 射线:有一个端点,向一个方向无限延伸。
- 线段:有两个端点,长度有限。
3. 角- 邻角:有共同顶点和边的两个角。
- 对顶角:两条射线共享一个公共点,形成的两个角。
- 平行线:在同一平面内,永不相交的两条直线。
二、平面图形1. 三角形- 等边三角形:三条边长度相等。
- 等腰三角形:至少有两条边长度相等。
- 直角三角形:有一个90度的角。
- 钝角三角形:有一个大于90度的角。
- 锐角三角形:所有角都小于90度。
2. 四边形- 正方形:四条边长度相等,四个角都是直角。
- 长方形:对边平行且相等,四个角都是直角。
- 平行四边形:对边平行。
- 梯形:至少有一组对边平行。
3. 圆- 圆心:圆的中心点。
- 半径:圆心到圆上任意一点的距离。
- 直径:通过圆心的最长线段,等于半径的两倍。
三、几何图形的性质1. 三角形的性质- 内角和:三角形内角和为180度。
- 海伦公式:已知三边长度,可以计算三角形的面积。
2. 四边形的性质- 正方形的性质:对角线相等且互相平分。
- 长方形的性质:对角线相等且互相平分。
- 平行四边形的性质:对角线互相平分。
3. 圆的性质- 圆周率:圆的周长与直径的比值,用π表示。
- 圆的面积:π乘以半径的平方。
四、几何图形的计算1. 面积计算- 三角形面积:底乘高除以2。
- 四边形面积:长乘宽(正方形和长方形);梯形的上下底之和乘高除以2。
- 圆的面积:π乘以半径的平方。
2. 周长计算- 三角形周长:三边之和。
- 四边形周长:四边之和(正方形和长方形);梯形的上下底之和加上两腰之和。
- 圆的周长:2π乘以半径。
3. 体积计算- 圆柱体积:底面积乘以高。
- 圆锥体积:1/3乘以底面积乘以高。
小学数学的几何基础知识

小学数学的几何基础知识几何学是数学的一个分支,主要研究空间与图形及其属性之间的关系。
在小学阶段,学生开始接触几何基础知识,这些知识不仅为后续学习打下坚实的基础,而且在生活中也有广泛的应用。
本文将介绍小学数学中的几何基础知识,包括点、线、面、图形等概念,以及相关的性质和运用。
一、点、线、面的基本概念在几何学中,点、线、面是最基本的概念。
1. 点:点是几何学的基本要素,它是没有长度、宽度和高度的,一般用大写字母表示,如A、B等。
2. 线:线是由无数个点连成的无限细长的对象,它没有宽度,但有长度,用小写字母表示,如a、b等。
3. 面:平面是由无数个点连成的无限大的对象,它没有厚度,但有长度和宽度。
用大写字母表示,如P、Q等。
二、图形的分类和性质在小学数学中,常见的图形主要包括点、线段、射线、直线、角、三角形、四边形等。
1. 点:点是最简单的图形,它没有长度和宽度。
一个点可以用一支尖笔在纸上画出来。
2. 线段:线段是由两个端点和连接它们的线段组成的,可以用直尺在纸上画出来。
线段的长度可以通过测量得到。
3. 射线:射线由一个起点和一个方向组成,可以用直尺和直角器在纸上画出来。
射线没有终点,可以无限延伸。
4. 直线:直线是由无数个点连成的,没有起点和终点,可以无限延伸,用直尺和直角器在纸上画出来。
5. 角:角是由两条射线的公共端点组成的。
角可以分为锐角、直角、钝角和平角四种类型。
6. 三角形:三角形是由三条线段组成,它有三个顶点和三条边。
7. 四边形:四边形是由四条线段组成的图形,它有四个顶点和四条边。
三、图形的运用几何学的概念和原理在生活中有广泛的应用。
1. 导航和地图:在导航和地图中,我们需要理解和运用几何概念,如平行、垂直、角度等,以确定最短路径或确定方向。
2. 建筑设计:建筑师在设计建筑物时需要使用几何知识,如平面图、立体图、比例等,以确保建筑物的结构稳定和美观。
3. 工程测量:工程师需要使用几何知识进行测量,如直线距离、角度、比例等,以确保工程的准确性和可行性。
几何数学入门基础知识点

几何数学入门基础知识点
1. 什么是点呀?嘿,点就像一颗小小的星星,在那安安静静地待着,只有位置没有大小呢!比如纸上的一个小黑点。
你说是不是很神奇呀?
2. 线呀,那可是直直的家伙哟!就像无尽的道路一样,能向两端无限延伸呢!像画在纸上的一条直线。
哇塞,想想就觉得好厉害呢!
3. 面呢,那可不一样啦!它就像一块大大的平板呀,可以平平地铺在那。
就好像桌面一样平平整整的。
不是很有意思吗?
4. 三角形啊,它有三个角呢!就像一个稳固的小架子,可牢固啦!看那路边的三角形指示牌。
多特别呀!
5. 圆形,多可爱呀!圆圆的就像天上的月亮一样,完美无缺呢!比如家里的盘子就是圆形的嘛。
是不是很形象呀?
6. 正方形也很有趣哟!四四方方的,整整齐齐的,就像一个小盒子的面。
像魔方的一个面那样规矩。
是不是呀?
7. 长方形呢,长长的样子,不就像我们的书本吗?长长的直直的。
嘿嘿,很容易想到吧?
8. 角度也很重要哦!那可是衡量转弯的关键呢。
就好比开门的时候,门转动的角度。
神奇吧?
9. 平行呀,两条线永远不相交,就像两个人永远平行地走,不会碰到一起。
像铁轨那样平行。
好特别呀!
我觉得这些几何数学入门基础知识点真的好有意思呀,它们是几何世界的基石,让我们能更好地理解和探索这个奇妙的世界呢!。
几何基础必学知识点

几何基础必学知识点以下是几何基础的必学知识点:1. 点、线、面:点是几何图形的最基本单位,没有长度、宽度和高度;线由两个点组成,没有宽度;面由多条线组成,有长度和宽度。
2. 角:两条射线共享同一个端点形成的几何图形称为角。
角的大小通过其开口的程度来衡量,以度或弧度表示。
3. 三角形:有三条线段组成的多边形。
三角形的属性包括边长、角度、高度、面积等。
4. 直角三角形:一种有一个90度角的三角形。
5. 相似三角形:两个三角形的对应角度相等,对应边的比值相等。
6. 同位角:两条平行线被一条横切线交叉时,对应的角称为同位角,它们的大小相等。
7. 圆:由一条曲线和一个固定点组成的几何图形。
圆的属性包括半径、直径、弧长、扇形等。
8. 多边形:由多条线段组成的几何图形。
常见的多边形有三角形、四边形、五边形、六边形等。
9. 平行线:在同一平面上,永远不会相交的两条线称为平行线。
10. 垂直线:两条线相交时,且相交角为90度,称为垂直线。
11. 空间几何:涉及三维空间中的几何图形和关系。
例如,立方体、球体、棱柱等。
12. 向量:有大小和方向的量。
在几何中用箭头表示,箭头的长度表示向量的大小,箭头的方向表示向量的方向。
向量可以用于描述平移、旋转等几何变化。
13. 三角函数:三角函数是角的函数,包括正弦、余弦、正切等。
14. 坐标系:用来表示几何图形在平面或空间中位置的系统。
常见的坐标系有直角坐标系和极坐标系。
以上是几何基础的一些必学知识点,掌握这些知识可以帮助理解和解决各种几何问题。
数学课几何基础

数学课几何基础在学习数学的过程中,几何是一个非常重要的分支。
几何学以空间和形状为研究对象,通过推理和证明,探索各种几何性质和定理。
本文将介绍数学课上关于几何基础的内容,帮助读者更好地理解和应用几何知识。
一、几何基本概念几何学中有一些基本概念是我们在学习几何时需要了解的。
首先是点、线和面的概念。
点是几何学的基本单位,它没有大小和形状。
线由无限多个点组成,线没有宽度,只有长度。
面是由无限多条线组成的,面有长度和宽度。
在几何学中,我们还需要了解边、角和多边形的概念。
边是连接两个点的线段,角是由两条线段的端点组成的,它可以用来衡量两条线段之间的夹角。
多边形是由多个线段连接而成的,其中最常见的是三角形和四边形。
二、几何图形的分类在几何学中,图形可以根据它的属性和特征进行分类。
最常见的几何图形分类有以下几种:1. 点、线和面:点是几何图形的基本单位,线由多个点连接而成,面是由多个线段闭合形成的。
2. 二维图形:二维图形是指面积有限的图形,例如矩形、正方形、圆等。
3. 三维图形:三维图形是指具有长度、宽度和高度的图形,例如立方体、圆柱体、金字塔等。
4. 同位图形:同位图形是指具有相同形状但大小不同的图形,例如相似三角形。
5. 共圆图形:共圆图形是指所有的图形都与同一个圆相切或相交。
三、几何运算在几何学中,我们可以通过一系列的几何运算来研究和解决各种几何问题。
几何运算包括以下一些基本操作:1. 直线的垂直平分线:通过一个点,可以画出与已知直线垂直且平分已知直线的直线。
2. 两条直线的交点:当两条直线相交时,它们会在一个点上相交,我们称之为交点。
3. 两条平行线的切线:当两条平行线之间有一条直线与之相交时,与这两条平行线相交的线段称为切线。
4. 线段的垂直平分线:通过一个线段,可以画出与该线段垂直且平分该线段的线段。
以上仅是几何运算的一小部分,通过这些运算我们可以更好地理解几何图形之间的关系,解决各类几何问题。
四、几何定理与性质在几何学中,有很多重要的定理和性质可以帮助我们解决各种几何问题。
(完整版)解析几何基础知识汇总

解析几何基础知识5.0≤d <|r 1-r 2|(r 1≠r 2)⇔两圆内含6.椭圆一、椭圆的定义和方程 1.椭圆的定义平面内到两定点F 1、F 2的距离的和等于常数2a (大于|F 1F 2|=2c )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦点.定义中特别要注意条件2a >2c ,否则轨迹不是椭圆;当2a =2c 时,动点的轨迹是线段;当2a <2c 时,动点的轨迹不存在。
2.椭圆的方程(1)焦点在x 轴上的椭圆的标准方程:x 2a 2+y 2b2=1(a >b >0).(2)焦点在y 轴上的椭圆的标准方程:y 2a 2+x 2b2=1(a >b >0).二、椭圆的简单几何性质(a 2=b 2+c 2)标准方程 x 2a 2+y 2b 2=1(a >b >0)y 2a 2+x 2b 2=1(a >b >0) 图 形性 质范围-a ≤x ≤a -b ≤y ≤b-b ≤x ≤b -a ≤y ≤a对称性 对称轴:x 轴,y 轴 对称中心:坐标原点顶点A 1(-a,0),A 2(a,0)B 1(0,-b ),B 2(0,b ) A 1(0,-a ),A 2(0,a ) B 1(-b,0),B 2(b,0)性 质轴长轴A 1A 2的长为2a短轴B 1B 2的长为2b焦距 |F 1F 2|=2c 离心率 e =ca∈(0,1) a ,b ,c 的关系c 2=a 2-b 28.抛物线(1)抛物线的概念平面内与一定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线(定点F 不在定直线l 上)。
定点F 叫做抛物线的焦点,定直线l 叫做抛物线的准线。
方程()022>=p pxy 叫做抛物线的标准方程。
注意:它表示的抛物线的焦点在x 轴的正半轴上,焦点坐标是F (2p ,0),它的准线方程是2p x -= ;(2)抛物线的性质一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式:px y 22-=,py x 22=,py x 22-=.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下表: [一次项的字母定轴(对称轴),一次项的符号定方向(开口方向)]标准方程22(0)y pxp =>22(0)y px p =->22(0)x py p =>22(0)x pyp =->图形焦点坐标 (,0)2p (,0)2p -(0,)2p(0,)2p -准线方程 2p x =-2p x =2p y =-2p y =范围 0x ≥ 0x ≤ 0y ≥ 0y ≤对称性 x 轴 x 轴 y 轴 y 轴 顶点 (0,0) (0,0) (0,0) (0,0) 离心率1e = 1e =1e = 1e =说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径;(2)抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,没有渐近线;(3)注意强调p 的几何意义:是焦点到准线的距离。
数学几何的基础知识

数学几何的基础知识数学几何是数学的一个分支,研究空间形状、大小、位置以及它们之间的关系。
了解数学几何的基础知识对我们理解空间的结构和解决实际问题具有重要意义。
本文将介绍数学几何的基础概念和相关定理。
一、点、直线和平面在数学几何中,最基本的概念是点、直线和平面。
点是没有大小和形状的,它只有位置;直线是由无数个点组成,具有无限延伸的特性;平面是由无数个直线组成,具有二维的特性。
二、角度角度是数学几何中常见的概念,它由两条射线构成,有大小和方向。
角度的度量单位通常使用度(°)或弧度(rad)。
常见的角度类型包括锐角、直角、钝角和平角。
三、三角形三角形是由三条线段组成的图形,它是几何中最基本的形状之一。
三角形的内角和等于180°,根据边长和角度的不同,可以分为等边三角形、等腰三角形、直角三角形等多种类型。
四、四边形四边形是由四个线段组成的图形,它包括多种类型,如矩形、正方形、菱形等。
四边形的性质和关系可以用于解决实际问题,如计算面积、判断平行性等。
五、圆圆是由一个确定的中心点和到该中心点距离相等的所有点组成的图形。
圆的重要性质包括半径、直径、弧长和面积等。
圆的几何关系在很多实际应用中都有着重要的作用。
六、立体几何立体几何研究的是三维空间中的图形和物体。
常见的立体图形包括球体、圆柱体、锥体和立方体等。
立体几何的基本概念和计算方法在建筑、工程等领域有广泛应用。
七、相似与全等数学几何中的相似和全等是重要的概念。
两个图形如果形状相同且大小相等,则它们是全等的;如果两个图形形状相同但大小不同,则它们是相似的。
相似和全等的判定方法可以通过比较边长、角度等几何属性来实现。
八、向量向量是用于描述空间中的方向和大小的量。
向量有起点和终点,可以通过终点减去起点得到。
向量的加法、减法和数量乘法等运算在几何中有广泛的应用。
九、三角函数三角函数是数学几何中的重要工具。
常见的三角函数包括正弦、余弦和正切等,它们以角度作为自变量,返回与该角度相关的数值。
几何原本》第一卷《几何基础》

《几何原本》第一卷《》23条定义1、点是没有部分的2、线只有长度而没有宽度3、一线的两端是点4、直线是它上面的点一样地平放着的线5、面只有长度和宽度6、面的边缘是线7、平面是它上面的线一样地平放着的面8、平面角是在一平面内但不在一条直线上的两条相交线相互的倾斜度.9、当包含角的两条线都是直线时,这个角叫做直线角.10、当一条直线和另一条直线交成邻角彼此相等时,这些角的每一个叫做直角,而且称这一条直线垂直于另一条直线。
11、大于直角的角叫钝角。
12、小于直角的角叫锐角13、边界是物体的边缘14、图形是一个边界或者几个边界所围成的15、圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等。
16、这个点(指定义15中提到的那个点)叫做圆心。
17、圆的直径是任意一条经过圆心的直线在两个方向被圆截得的线段,且把圆二等分。
18、半圆是直径与被它切割的圆弧所围成的图形,半圆的圆心与原圆心相同。
(暂无注释,可能是接着17的)19、直线形是由线段围成的,三边形是由三条线段围成的,四边形是由四条线围成的,多边形是由四条以上线段围成的。
20、在三边形中,三条边相等的,叫做等边三角形;只有两条边相等的,叫做等腰三角形;各边不等的,叫做不等边三角形.21、此外,在三边形中,有一角是直角的,叫做直角三角形;有一个角是钝角的,叫做钝角三角形;有三个角是锐角的,叫做锐角三角形。
22、在四边形中,四边相等且四个角是直角的,叫做正方形;角是直角,但四边不全相等的,叫做长方形;四边相等,但角不是直角的,叫做菱形;对角相等且对边相等,但边不全相等且角不是直角的,叫做斜方形;其余的四边形叫做不规则四边形.23、平行直线是在同一个平面内向两端无限延长不能相交的直线.五条1、等于同量的量彼此相等;2、等量加等量,其和相等;3、等量减等量,其差相等;4、彼此能重合的物体是全等的;5、整体大于部分。
五条公设1、过两点能作且只能作一;2、(有限直线)可以无限地延长;3、以任一点为圆心,任意长为半径,可作一圆;4、凡是直角都相等;5、同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线经无限延长后在这一侧一定相交。
几何基础知识

几何基础知识几何学是数学的一个重要分支,研究几何图形的形状、大小、相对位置等属性。
在几何学中,有一些基础知识是我们必须掌握的,这些知识不仅在学校的数学课程中重要,也在日常生活中有着实际应用。
本文将介绍一些几何基础知识,以帮助读者更好地理解和应用这些概念。
一. 平面几何1. 点、线、面和角在几何学中,点是最基本的概念,它没有长、宽、高,只有位置坐标。
点可以连接成线,线是由无数个点组成的。
两条线相交形成一个角,角的大小可以用度数来度量。
面是由无数个点和线组成的,它是一个平坦的二维空间。
2. 多边形多边形是由直线段相连而形成的封闭图形。
常见的多边形有三角形、四边形和五边形等。
每个多边形都有内角和外角,内角的和加起来总是等于180度。
3. 圆形圆形是一个封闭的曲线,由与圆心距离相等的所有点组成。
圆心到圆上任意一点的距离称为半径,圆周上任意两点之间的距离称为弧长,半径的两倍称为直径。
二. 空间几何1. 空间坐标系空间几何使用三维坐标系来描述物体的位置。
三维坐标系由三条相互垂直的轴组成,通常用x、y和z来表示。
物体的位置可以用一个有序三元组来表示,其中每个元素分别对应x、y和z轴上的坐标值。
2. 立体图形立体图形是由平面图形沿某一方向延伸而成的图形。
常见的立体图形有立方体、圆柱体和球体等。
立体图形有面积和体积两个重要的属性。
面积是指立体图形的表面积,体积是指立体图形所占据的空间大小。
3. 投影投影是指物体在不同位置或角度下在平面上形成的影子。
在空间几何中,我们常常需要计算物体的投影。
平行投影是指物体的投影与原物体平行,透视投影则是物体的投影与原物体在一个点上。
三. 角度与距离的计算1. 三角函数三角函数是几何学中一组重要的函数,包括正弦、余弦和正切等。
三角函数可以帮助我们计算两个角之间的关系,以及在给定角度情况下的边长比值。
2. 相似三角形相似三角形是指两个三角形的对应角度相等,对应边长成比例。
相似三角形的出现使得角度与距离的计算变得更加简便,通过已知的一些长度和角度信息,我们可以推导出未知的边长或角度。
初二几何基础知识点总结

初二几何基础知识点总结一、直线和角1. 直线的概念直线是由无穷多个排列在一起的点所组成的,它是没有端点的。
2. 角的概念两条射线有一个公共起点A,则可围绕这个公共起点转动其中一根射线去覆盖另一根射线就形成了角,称为∠A。
3. 角的种类(1) 锐角:小于90度的角。
(2) 直角:等于90度的角。
(3) 钝角:大于90度但小于180度的角。
(4) 平角:等于180度的角。
4. 角的性质(1) 对顶角相等:若两条直线AB和CD相交,在相交点O处分别作AE和CF是两个对顶角,则∠A = ∠C。
(2) 同位角相等:AB与CD是两条平行线,交BC和AD于E和F,则∠A = ∠E,∠B = ∠F。
(3) 互补角:两个角的和等于90度。
(4) 补角:两个角的和等于180度。
二、三角形1. 三角形的定义三角形是由三条线段所围成的闭合图形。
2. 三角形的分类(1) 根据角度分:锐角三角形、直角三角形、钝角三角形。
(2) 根据边长分:等腰三角形、等边三角形、不等边三角形。
3. 三角形的性质(1) 三角形内角和等于180度。
(2) 等边三角形三个角相等。
(3) 等腰三角形的两个底角相等。
(4) 直角三角形的两条腰的平方和等于斜边的平方。
4. 三角形的勾股定理在直角三角形中,斜边的平方等于两条直角边的平方和。
三、平行线和相交线1. 平行线若两条直线和平面上第三条直线的交角分别等于180度,则这两条直线互为平行线。
2. 平行线的性质(1) 平行线的性质和角的对应角、同位角等有关。
(2) 平行线的性质和平行线与交线夹角、对应角等有关。
3. 相交线平面内直线AB和CD相交于点O,则AO、BO、CO、DO共同围成四个角,一对一对的角互相等。
四、多边形1. 多边形的概念多边形是由三条或三条以上的线段相连成的闭合图形。
2. 多边形的分类(1) 分为三角形、四边形、五边形、六边形等。
(2) 分为凹多边形和凸多边形。
3. 多边形的性质(1) 内角和:n边形的内角和等于180×(n-2)度。
几何基础:几何概念与简单证明的基本知识

几何基础:几何概念与简单证明的基本知识2023年最新人教版初二数学专项训练一、代数基础代数是数学中的一个重要分支,主要研究数的运算、代数式和代数方程等。
在初二数学中,代数是非常重要的一部分。
下面我们将从基本概念和基本运算、一元一次方程组的解法等方面进行介绍。
(一)基本概念和基本运算1.代数式:用运算符号(加、减、乘、除等)把数或表示数的字母连接而成的式子称为代数式。
2.方程:含有未知数的等式称为方程。
3.方程的解:使方程左右两边相等的未知数的值称为方程的解。
4.一元一次方程:只含有一个未知数,且未知数的次数为1,且含未知数项的系数不为0的整式方程。
(二)一元一次方程组的解法5.代入消元法:通过消元,将方程组转化为一元一次方程进行求解。
6.【例1】解方程组:2x + y = 5, 3x - y = 10解:将两方程相加得:5x = 15,即x = 3。
将x = 3代入第一个方程得:y = -1。
所以,方程组的解为:x = 3, y = -1。
7.加减消元法:通过消元,将方程组转化为一元一次方程进行求解。
8.【例2】解方程组:3x + 2y = 10, x + 3y = 15解:将两方程相减得:-2x + y = 5。
将y = 5代入第二个方程得:x = 0。
所以,方程组的解为:x = 0, y = 5。
二、几何基础几何是数学中的一个重要分支,主要研究形状、大小、距离和角度等概念。
在初二数学中,几何是非常重要的一部分。
下面我们将从基本概念和基本运算、简单的几何证明等方面进行介绍。
(一)基本概念和基本运算9.点:在几何中,点是一个基本元素,表示位置。
10.线:由无数个点组成,有长度和方向。
11.平面:由无数条线组成,有大小和形状。
12.角:由两条线或射线相交而形成。
13.三角形:由三条线段首尾相连而成。
14.矩形:由四条线段组成,其对角相等且互相垂直。
15.圆形:由一条线段围绕一个中心点旋转而成。
(二)简单的几何证明16.演绎推理:根据已知条件和已学定理,推导出结论。
高中立体几何基础知识点全集(图文并茂)
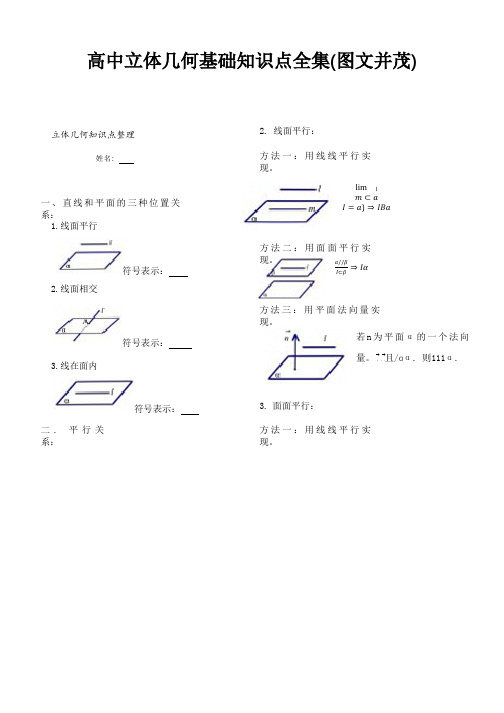
高中立体几何基础知识点全集(图文并茂)立体几何知识点整理 2. 线面平行:姓名: 方法一:用线线平行实现。
一、直线和平面的三种位置关系:1.线面平行lim lm⊂aI=a}⇒IBa符号表示:2.线面相交方法二:用面面平行实现。
α//βI⊂β⇒Iα符号表示:3.线在面内符号表示:方法三:用平面法向量实现。
若n为平面α的一个法向量。
⃗⃗且/ɑα.则111α. 3. 面面平行:二. 平行关系:方法一:用线线平行实现。
1. 线线平行:方法一:用线面平行实现。
lIIaI ⇒lIm方法二:用面面平行实现。
方法三:用线面垂直实现。
1//rm∥m'l. m=β且相交 ⇒α∥βl',m'cα且相交方法二:用线面平行实现。
1/1am//α ⇒α∥β 1. m ⊂β且相交)三.垂直关系:1.线面垂直:若/⊥α,m⊥α,则|∥m.方法四:用向量方法:若向量i 和向量 ⃗共线且1. m 不重合,则|//m 。
方法一:用线线垂直实现。
IA方法二:用面面垂直实现。
2.面面垂直:方法一:用线面垂直实现。
方法二:计算所成二面角为直角。
3. 线线重直:方法一:用线面垂直实现。
方法二:三重线定理及其逆定理。
方法三:用向量方法:若向量/和向量⃗的数量积为0,则/⊥m.三.夹角问题。
(一)异面直线所成的角:(1) 范围: (0°,90°](2)求法:方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)(计算结果可能是其补角)方法二:向量法。
转化为向量的夹角(二)线面角(1)定义:直线/ 上任取一点P(交点除外),作PO⊥α于O,连结AO,则AO为斜线PA 在面α内的射影,∠PAO(图中θ)为直线t与面α所成的角。
(2)范围: [0°.90°]当θ=0°时, 1cα或1//α当θ=90°时, 1⊥α(3)求法:方法一:定义法。
初中数学中的几何学基础

初中数学中的几何学基础概述:几何学是数学的一个重要分支,它研究空间、形状和大小之间的关系。
在初中阶段,学生们将接触到几何学的基础知识,包括平面几何和立体几何。
本文将详细介绍初中数学中的几何学基础,包括平面几何中的点、线、面及其性质,以及立体几何中的体积、表面积等内容。
一、平面几何1. 点、线、面的定义和性质在平面几何中,点是最基本的概念,它没有长度、宽度和高度。
线是由一组点组成的,它有无限多个点,并且没有宽度。
面是由一组线组成的,它有无限多个点和线,并且没有厚度。
点、线、面有各自独特的性质,如点没有方向,线没有端点等。
2. 直线、射线和线段直线是一条无限延伸的线,没有端点。
射线是起点固定且延伸方向唯一的线段,有一个端点。
线段是有两个端点的线,长度是有限的。
3. 角的概念和性质角是由两条射线共享一个端点组成的,可以用度数或弧度来表示。
角的性质有很多,如同一直角的两个角互为补角,同一直径上的两个角互为对顶角等。
4. 三角形、四边形和多边形三角形是由三条线段组成的图形,有不同的分类和性质,如锐角三角形、钝角三角形等。
四边形是由四条线段组成的图形,有不同的分类和性质,如矩形、平行四边形等。
多边形是由多条线段组成的图形,有不同的分类和性质,如五边形、六边形等。
5. 相似和全等的概念相似是指两个图形的形状相似,但大小可能不同。
全等是指两个图形的形状和大小完全相同。
相似和全等的判断方法和性质有一定的规律和准则。
二、立体几何1. 立体图形的分类和性质在立体几何中,我们会接触到各种立体图形,如球体、圆柱体、长方体等。
每种立体图形都有自己独特的性质和特点,如球体的表面积和体积的计算方法,圆柱体的侧面积和体积的计算方法等。
2. 体积和表面积的计算体积是指立体图形所占据的三维空间的大小,可以通过公式来计算。
不同立体图形的体积计算方法不同,并且需要根据给定的条件进行推导和运用。
表面积是指立体图形的全部外部面积之和,也可以通过公式来计算,每种立体图形都有相应的表面积计算公式。
几何基础 连续公理

几何基础连续公理1. 什么是几何基础?几何基础是数学中关于空间和形状的研究,它是许多数学分支的基础。
几何基础包括点、线、面以及它们之间的关系和性质。
在几何基础中,连续公理是一个重要的概念。
2. 连续公理的定义连续公理是几何中的一个公理系统,它描述了点、线、面的连续性。
连续公理基于欧几里德几何学的基本原理,它假设空间是连续的,不存在间断。
连续公理可以简单地定义为:连续公理:通过两点之间可以作一条直线。
根据这个公理,我们可以推导出许多几何基础的性质和定理。
3. 连续公理的应用3.1 点的连续性根据连续公理,我们可以得出点的连续性定理:在空间中的任意两个点,都可以找到一条直线将它们连接起来。
这个定理是理解几何学中点之间的关系和空间结构的基础。
3.2 线的连续性连续公理还可以应用于线的连续性。
通过连续公理,我们可以得出线的连续性定理:一条直线上的任意两点,都可以通过该直线上的其他点连接起来。
这个定理在几何学中被广泛应用,例如证明线段的长度等性质。
3.3 面的连续性在几何学中,面是由一组互相连接的点和线构成的。
根据连续公理,我们可以推导出面的连续性定理:通过一个面上的任意两点,都可以找到一条曲线将它们连接起来。
这个定理对于理解几何学中的平面结构和面的性质至关重要。
4. 连续公理的推广连续公理不仅适用于欧几里德几何学,它还可以应用于其他几何理论中。
例如,非欧几里德几何学和拓扑学中都有对连续公理的推广和应用。
4.1 非欧几里德几何学中的连续公理在非欧几里德几何学中,连续公理也适用,但需要进行适当的修改。
例如,在双曲几何中,连续公理可以定义为:通过两点之间可以作一条拟直线。
这个公理描述了双曲几何学中的连续性。
4.2 拓扑学中的连续公理连续公理在拓扑学中也有着重要的地位。
拓扑学是研究空间和连续性的学科,它通过连续公理来定义拓扑空间和连续映射。
在拓扑学中,连续公理是定义点的连续性的基础。
5. 总结连续公理是几何基础中的一个重要概念,它描述了点、线、面的连续性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斯坦纳点S(经过△ABC三个顶点的所有椭圆中达到最小面积的那个椭圆可称作斯坦纳椭圆,它恰以△ABC重心为其中心;而斯坦纳椭圆与△ABC外接圆的第四个交点正是斯坦纳点。过△ABC的三个顶点分别作其第一布洛卡三角形(它必与△ABC反相似)相应边的平行线,三线必交汇于外接圆上一点,它就是△ABC的斯坦纳点)
第一拿破仑点(在任意一个三角形的三条边上分别向外做出三个等边三角形,则这三个等边三角形的中心也构成一个等边三角形。这个由三个等边三角形中心构成的三角形称外拿破仑三角形。外拿破仑三角形顶点与原三角形最远的对应顶点分别连线,三线共点)
第二拿破仑点(在任意一个三角形的三条边上分别向内侧做出三个等边三角形,则这三个等边三角形的中心也构成一个等边三角形。这个等边三角形 称内拿破仑三角形。内拿破仑三角形的三个中心点分别与原三角形的对应顶点连线,三线共点)
S△AOB:S△AOC=S△BDO:S△CDO=BD:CD
S△AOC:S△BOC=S△AFO:S△BFO=AF:BF
S△BOC:S△BOA=S△CEO:S△AEO=EC:AE
(三)(1)有一条公共边的三角形叫做共边三角形。
共边定理:设直线AB与PQ交于点M,则S△PAB/S△QAB=PM/QM
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)
5. 以重心为起点,以三角形三顶点为终点的三向量之和等于零向量
(2)三角形外心定理
过三角形各顶点的圆叫做三角形的外接圆,三角形外接圆的圆心叫三角形的外心。这个三角形叫做这个圆的内接三角形。三角形有且只有一个外接圆
界心(设D、E、F分别在△ABC的三边BC、CA、AB上,若AD、BE、CF把△ABC的周界分成两条等长的折线,则AD、BE、CF三线共点)
陪位重心(AD、BE、CF为三角形的中线,D、E、F分别在BC、CA、AB上,若角BAD=角DAC,角CBE=角EBA,角ACF=角FCB,则AD、BE、CF三线共点)
阿波罗尼斯点(三角形三个旁切圆共切于一个圆,每个切点与三角形最远的顶点连线,三线共点)
斯俾克点J(三角形ABC中,D,E,F分别为BC,AC,AB的中点,G,I为三角形的重心与内心,过D,E,F分别作此三角形内切圆切点三角形对应三边的垂线,三线共点,称斯俾克点。 斯俾克点是三角形线框重心,同时是三个旁切圆的根心,也是中点三角形DEF的内心,而中点三角形与原三角形关于重心G是1:2位似的,有GJ=0.5IG。过D,E,F分别作对应的三角形ABC三个旁切圆切点所构成的三角形三边的垂线,它们交于一点,分别记作J1,J2,J3,称其为原三角形的旁斯俾克点。J是三角形J1J2J3的垂心,四个斯俾克点恰好构成垂心组。三角形J1J2J3的三条高的垂足为三角形ABC三边中点D,E,F )
献给爱好平面几何的每一个读者:
(来源:luoqq330501)
(一)欧几里德几何原本公设:
公设1:任意一点到另外任意一点可以画直线。
公设2:一条有限线段可以继续延长。
公设3:以任意点为心及任意的距离可以画圆。
公设4:凡直角都彼此相等。
公设5:同平面内一条直线和另外两条直线相交,若在某一侧的两个内角和小于二直角的和,则这二直线经无限延长后在这一侧相交。
九点圆心V(三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共圆。通常称这个圆为九点圆,九点圆是一个更一般的定理:垂心四面体12点共球(各棱的中点,各棱相对于对棱的垂心)的一个特例。当一个顶点被压入所对面时,12点的共球就退化为9点共圆)
费尔巴哈点(内切圆和九点圆的公切点)
三角形的三条高(所在直线)交于一点,该点叫三角形的垂心。锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点;钝角三角形的垂心在三角形外。三角形只有一个垂心。
垂心性质:
1、三角形三个顶点,三个垂足,垂心这7个点可得到6个四点圆
2、三角形外心O、重心G和垂心H三点共线,且OG:GH=1:2(此直线称为三角形的欧拉线)
3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍
4、垂心分每条高线的两部分乘积相等
5、垂心定理:ΔABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交AB于点F ,则CF⊥AB
证明:连接DE
∵∠ADB=∠AEB=90度
∴A、B、D、E四点共圆
∴∠ADE=∠ABE
(1).三角形重心定理
三角形三条边的中线交于一点,该点叫三角形的重心。三中线交于一点可用燕尾定理证明。
重心性质:
1、重心到顶点的距离与重心到对边中点的距离之比为2:1(即重心分线段1:2)
2、重心和三角形任意两顶点组成的3个三角形面积相等(即重心到三条边的距离与三条边的长成反比)
3、重心到三角形3个顶点距离的平方和最小
7、内心到三角形三边距离相等
(5)三角形旁心定理
三角形的旁切圆(与三角形的一边和其他两边的延长线相切的圆)的圆心叫三角形的旁心
旁心性质:
1、三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点即为三角形的旁心
2、每个三角形都有三个旁切圆,因而有三个旁心,且一定在三角形外
3、旁心到三边延长线的距离相等
(二)几何五大模型
(1)等积变换模型
1、等底等高的两个三角形面积相等
2、两个三角形高相等,面积比等于它们的底之比
3、两个三角形底相等,面积比等于它的的高之比
(2)共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
威毕特点(△ABC两边AB、AC各向外作正方形ABDE、ACFG,若AP垂直BC于P,则AP、BF、CD共点)
伪垂心(设AD、BE、CF为△ABC的三条高,D、E、F关于三边中点的对称点为D'、E'、F',则AD'、BE'、CF'三线共点)
奈格尔点N(△ABC 具有边长 a = |BC|, b = |CA|,和 c = |AB|,设TA,TB,TC分别是三旁切圆和三条边的切点。直线 ATA,BTB,CTC 共点 。另外一种方法构造TA,从点 A 出发沿着三角形 ABC 的边走到半周长位置,得到 TB 和 TC。奈格尔点也被称为平分周长点(界心)(奈格尔点、内心和重心三点共线。内心是中点三角形的奈格尔点。奈格尔点是反补三角形的重心)
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
外心坐标:((c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c)
5、外心到三顶点的距离相等
(3)三角形垂心定理
外心性质:
1、三角形的三条边的垂直平分线交于一点,该点即为该三角形的外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
内心性质:
1、三角形的三条内角平分线交于一点。该点即为三角形的内心
2、直角三角形的内心到边的距离等于两直角边的和减去斜边的差的一半
3、P为ΔABC所在空间中任意一点,点0是ΔABC内心的充要条件是:向量P0=(a×向量PA+b×向量PB+c×向量PC)/(a+b+c)
4、O为三角形的内心,A、B、C分别为三角形的三个顶点,延长AO交BC边于N,则有AO:ON=AB:BN=AC:CN=(AB+AC):BC
5、(欧拉定理)⊿ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI^2=R^2-2Rr
6(内角平分线分三边长度关系)△ABC中,0为内心,∠A 、∠B、 ∠C的内角平分线分别交BC、AC、AB于Q、P、R,则BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b
∵∠EAO=∠DAC ∠AEO=∠ADC
∴ΔAEO∽ΔADC
∴AE/AO=AD/AC
∴ΔEAD∽ΔOAC
∴∠ACF=∠ADE=∠ABE
又∵∠ABE+∠BAC=90度
∴∠ACF+∠BAC=90度
∴CF⊥AB
(4)三角形内心定理
与三角形各边都相切的圆叫做三角形的内切圆,三角形内切圆的圆心叫三角形的内心。这个三角形叫做圆的外切三角形。三角形有且只有一个内切圆。
附:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
类似重心(在一个三角形中,类似中线是一个三条特殊直线。他们分别是三条中线(顶点和对边中点的连线),关于相应角的平分线的反射。这三条类似中线交于三角形内部一点,称为三角形的类似重心或莱莫恩点,三角形的莱莫恩点和三角形的内接三角形的类似重心重合。类似重心是三角形的重心的等角共轭点)
布洛卡点(已知P为△ABC内一点,若角PAB=角PBC=角PCA=a,则P为布洛卡点,a为布洛卡角)
垂极点(D、E、F是三角形ABC三点在任一直线L上的投影,则D、E、F到对边BC、AC、AB的垂线共点。若一条直线与△ABC的外接圆相交,则其垂极点是两个交点处西摩松线的交点。若直线经过外心,则其垂极点在△ABC的九点圆上)
