第三章方位投影
工程制图 第三章 投影法及点线面投影

与三个投影面都倾斜
一般位置平面
工程图学基础/机械设计制图
平面对三投影面均倾斜 — 一般位置平面
V
平面相于投影面W 的位置可归纳为 几类?
H
工程图学基础/机械设计制图 Nhomakorabea一般位置平面的投影
投影特性: 三个投影都为类似形。
b c
a b a
b
c
a
c
工程图学基础/机械设计制图
V W V W
H
V
d′
B C c D d
O
c
b
b H
两直线相交吗? 不相交!
为什么? 交点不符合一个点的投影规律!
工程图学基础/机械设计制图
b′ V 1′ ′ 3(4 ′) c′ d′ 2 ′Ⅳ Ⅰ B ′ a A ⅢⅡ D C a 4 d
● ● ● ● ● ● ● ● ● ●
c′ a′ X a c
′ 3(4 ′)
即: AC : CB = ac : cb
B C A a c b b c a c A B C C B b A
a
工程图学基础/机械设计制图 4. 相交二直线的投影也必然相交,交点的投影必是 其投影的交点。
F
B A E b a e f a c k d C K B D
A
b
5. 两平行直线的投影仍然互相平行,且其长度之比投 影后保持不变。
投影面平行线 侧平线(平行于W面)
水平线(平行于H面) 统称特殊位置直线 正垂线(垂直于V面) 投影面垂直线 侧垂线(垂直于W面) 铅垂线(垂直于H面)
垂直于某一投影面
与三个投影面都倾斜的直线
一般位置直线
工程图学基础/机械设计制图 1)投影面平行线
第三章投影法的概念
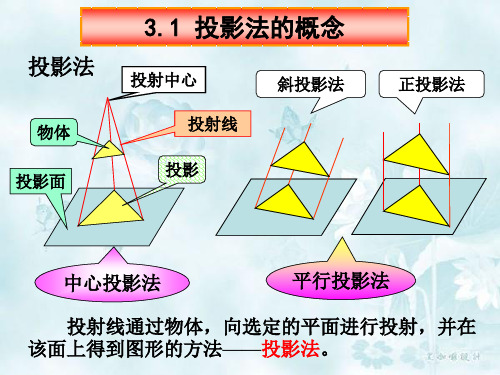
第二节 三视图的形成及投影规律
二、三视图的关系及投影规律
1、位置关系 物体的三个视图按规定展开,摊平在同一平面上以后,具有明确的位置 关系,主视图在上方,俯视图在主视图的正下方,左视图在主视图的正右 方。 2、投影关系 三视图之间的投影对应关系可以归纳为: 主视、俯视长对正(等长)。 主视、左视高平齐(等高)。 俯视、左视宽相等(等宽)。 这就是“三等”关系,简单地说就是“长对正,高平齐,宽相等”。对 于任何一个物体,不论是整体,还是局部,这个投影对应关系都保持不变 (图3-7)。 “三等”关系反映了三个视图之间的投影规律,是我们看图、画图和检 查图样的依据。
Y
ay
a●
Y ay
四、点的投影规律:
V a
●
X ax
Z
az
A
●
O
●a W
a● H
ay Y
① aa⊥OX轴 aa⊥OZ轴
② aax= aaz=y =Aa(A到V面的距离) aay= aaz =x =Aa(A到W面的距离) aax= aay =z =Aa (A到H面的距离)
五、 点的坐标
如图3-11所示,点的坐标值的意义如下: A点到W面的距离Aa″=aaY=a′aZ=OaX,以坐标x标记。 A点到V面的距离Aa′=aaX=a″aZ=OaY,以坐标y标记。 A点到H面的距离Aa=a′aX=a″aY=OaZ,以坐标z标记。 由于x坐标确定空间点在投影面体系中的左右位置,y坐标确定空间点在投影面体系 中的前后位置。z坐标确定点在投影面体系中的高低位置,因此,点在空间的位置 可以用坐标x、y、z确定。
一、平面的投影特性
⒈ 平面对一个投影面的投影特性
平行
垂直
地图投影第三章方位投影

长半径和纬线方向一致,短半径与经线方 向一致,且等于微圆半径r,又因自投影中 心,纬线扩大程度越来越大,所以变形 椭圆的长半径也越来越长,椭圆越来越扁。 常用来做两极的投影。
横轴方位投影 ——等距
经纬线形状
中央经线为直线,其它经线是对 称于中央经线的曲线。中央纬线 为直线,其它纬线是对称于中央 纬线的曲线。在中央经线上纬线 间隔相等。在中央纬线上经线间 隔相等。
从区域所在的地理位置来说,两极地区和南、北半球图采 用正轴方位投影;赤道附近地区和东、西半球图采用横轴 方位投影;其他地区和水、陆半球图采用斜轴方位投影。
横轴、斜轴方位投影变形分布规律
投影面在p点与地球面相切,过新极点p可做许多大圆, 命名为垂直圈,再作垂直于垂直圈的各圈,命名为等高圈。 这样垂直圈相当于地理坐标系的经线圈,等高圈相当于纬 线圈,等高圈和垂直圈投影后的形式和变形分布规律和正 轴方位投影时,情况完全一致。
3 21ቤተ መጻሕፍቲ ባይዱ
七. 球心投影(日晷投影)
4 3
21
八. 方位投影的分析和应用
方位投影的差别是取决于纬圈或等高圈投影半径p
的形式,而ρ的具体形式是取决于变形性质或透
视条件。
4
根据方位头因的长度比、面积比和角度最大变形的
公式来看,在正轴投影中,它们是纬度3 φ的函数, 在斜轴和横轴投影中,它们是天顶距Z的函数1
方位投影变形性质的图形判别
方位投影经纬线形式具有共同的特征,判别时先看构成形 式(经纬线网),判别是正轴、横轴、斜轴方位投影。
正轴投影,纬线为以投影中心为圆心的同心圆,经线为放 射状直线,夹角相等。横轴投影,赤道与中央经线为垂直 的直线,其他经纬线为曲线。斜轴投影,除中央经线为直 线外,其余的经纬线均为曲线。
工程制图03基本体的三视图讲解

二、回转体
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两底面组成。
圆柱面是由直线AA1绕与
它平行的轴线OO1旋转而成。
直线AA1称为母线。 圆柱面上与轴线平行的任
a
c
一直线称为圆柱面的素线。
(b)
⑵ 圆柱体的三视图
b
⑶ 轮廓圆线柱素面线的的俯投视影图与积曲聚面成的一 ⑷个两示可圆圆 个 。见柱, 方性面在 向的上另 的判取两 轮断点个廓视素图线上的分投别影以表
部分,弄清各部分的形状和它们的相对位 置及组合形式,分别画出各部分的投影。
例:画出所给叠加体的三视图。
立板 肋板
分解形体
叠加方式
底板和立板右面平齐叠加
底板
肋板与底板和立板对称叠加
投影作图 分块画图 ①底板 ②立板 ③肋板
看得见的线画实线 看不见的线画虚线
表面平齐, 应无线。
三、已知两视图,求作第三视图。
主视俯视长相等且对正 主视左视高相等且平齐 左 俯视左视宽相等且对应
长对正
高平齐
左
宽相等 三等关系
上 右
下 长对正
后
右
前
高平齐
上
后
前
下
3.三视图之间的方位对应关系
主视图反映:上、下 、左、右 俯视图反映:前、后 、左、右 左视图反映:上、下 、前、后
3.2 基本体的形成及其三视图
常见的基本几何体
⒈ 分析投影,想象出物体的形状。 ⒉ 根据投影规律及“三等”关系,画出第三视图
㈠ 投影分析
圆柱轮廓素线 直线 平面
⒈ 视图上图线的意义
① 一个平面的投影
② 面与面的交线
③ 回转体轮廓素线 的投影
方位投影

面积变形为零的投影。为满足这个条件,必须使变形椭圆的最大长度比a与最小长度比b互为倒数,即a=1/b 或b=1/a,这样才能使微分圆投影前后保持面积不变。因此,变形椭圆的长轴越长,其短轴就越小,与投影前的 圆形相比,其视觉变形就越大,即“非正形”。等积投影具有以下特点:①所有的面状要素投影前后面积保持不 变,因此可以直接在等积投影图上进行面积量算;②角度变形大,等积投影适用于对面积要求较高的自然地图和 社会经济地图,如行政区划图、土地利用类型图等。但不适用于制作航海、航空、军事等对方向精度要求较高的 地图。
用途
以平面作为投影面,使平面与地球相切(或相割),将地球面上的经纬线投影到平面上所得到的图形。由于投 影面与地球面的关系位置不同,又分为正轴方位投影、横轴方位投影和斜轴方位投影。正轴方位投影是投影平面 与地轴垂直(即投影平面切于极点,设以φ0表示切点的纬度,φ0=90°);横轴方位投影是投影平面与地轴平行 (投影平面与地球面相切于赤道,φ0=0°);斜轴方位投影是投影平面与地轴斜交(投影平面与地球面相切点的纬 度,小于90°,大于0°,0°<0<90°)。正轴投影的经纬线形状比较简单,称为标准。纬线为同心圆,经线为同 心圆的半径,经线间的夹角等于相应的经度差。纬线半径ρ随纬度φ的变化而变化,即ρ是纬度的函数,一般用 ρ=f(φ)式表达。故正轴方位投影的一般公式为:ρ=f(φ),δ=λ,δ为投影平面上经线夹角,λ为地球面上 经线间的夹角。
方位投影
分为非透视方位投影和透视方位投影
01 概念
03 地图投影
目录
02 用途 04 分类
方位投影分为非透视方位投影和透视方位投影。前者按变形性质又分为等角、等积和任意(包括等距离)投 影;后者随视点位置不同又分为正射、外心、球面和球心投影。方位投影的特点是:在投影平面上由投影中心向 各方向的方位角与实地相等。这种投影适用于区域轮廓大致为圆形的地图。
第3章 投影基础
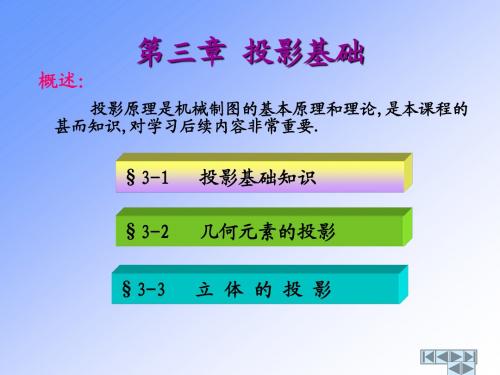
例2 已知A点在B点的右10毫米、前6毫米、上12毫米,求A点的 投影。 Z a 12 a
b X 10 b 6 a
b
O
YW
YH
§3.2.2
一、直线
b′
直线的投影
Z
b″
a′
X
a″
YW
b
a
YH
图2-18 直线的投影
二、直线的投影
1.三种位置直线 平行于某一个投影面而对另外两个 投影面平行线:
k1 k′ d1
l2
d′
X O X
d′
O
d
d k l2 l1
k
c
图2-26 求直线上点的投影
c
例2 已知线段AB的投影图,试将AB分成1:2两段,求分点C 的投影。 b c a X b
O
c
a
[例3] 已知直线AB和M点的正面投影和水平投影,问 M点是否在直线上?
Z
解:分析:AB为侧 平线,M在直线上 ,必在直线AB的同 面投影上,并满足 定比规律。 作图: 方法一 分割线段成定比 方法二 画第三投影
1.平面内取点
Z
b′ e′ a′ c′
X
b″
a″
e″
c″
YW
a c e b
YH
图2-39 平面内取点
取属于平面的点,要取自属于该平面的已知直线
平面上取点
b
e
d
B E D C
c
a c
a
d
A
e b
2.平面内取线
Z
a′ c′ m′ 1′ b′ c n 2 a 1 b
YH
a″ n′ 2′
a′
(a′)b′
第三章 方位投影

三、透视方位投影
(一).透视方位投影 一 透视方位投影 利用透视法把地球表 面投影到平面上的方法 称为透视投影。 称为透视投影。 透视方位投影的点光 源或视点位于垂直于投 影面的地球直径及其延 长线上, 长线上,由于视点位置 不同, 不同,因而有不同的透 视方位投影。
• 透视方位投影的一般公 式推导 由相似三角形Q’A’O及qAO 有(图3-12,46)
在方位投影投影中,极点(或天顶)均投 影为点(投影中心点),投影中心点至任 意点的方位角无变形。 1.等变形线——与等高圈一致为同心圆 •
切方位
割方位
图04-14
2.等高圈长度比μ2 的变化规律 3.方位投影的应用 (1)等角方位投影, (2)各大洲图常采用斜轴等面积方位投影。其投影中心常 取以下位置:
五、双重方位投影
Z KR ( D + KR ) Sin K ρ= Z D + KRCos K
Z (1 + β )1 + βCos K µ1 = Z ( β + Cos ) SinZ K
Z (1 + β ) Sin K µ2 = z ( β + Cos ) SinZ k
六、方位投影变形分析及其应用
第三章
方位投影
学习目标与要求 1.掌握方位投影的一般公式及其分类 2.掌握等角、等面积、等距离方位投影的坐标与 变形公式 3.掌握透视方位投影的特点 4.掌握方位投影的变形规律及应用 • 学习重点 1.掌握方位投影的基本概念以及公式 2.掌握方位投影的变形分析 3.掌握方位投影的应用 • 学习难点 1. 方位投影概念及公式意义 2. 方位投影的变形规律 •
非透视方位投影是借 助于透视投影的方式, 助于透视投影的方式, 而附加上一定的条件, 而附加上一定的条件, 如加上等角、等积、 如加上等角、等积、等 距等条件所构成的投影。 距等条件所构成的投影。 在这类投影中有等角方 位投影、 位投影、等距方位投影 和等积方位投影。 和等积方位投影。
建筑工程技术《第3章 投影基本知识》

第三章投影的基本知识3.1 投影的形成与分类一、投影的概念产生投影必须具备:1、光线——投影线;2、形体——只表示物体的形状和大小,而不反映物体的物理性质;3、投影面——影子所在的平面。
投影三要素:投影线;物体;投影面。
二、投影的分类投影分为两种:中心投影和平行投影。
1、中心投影法——由点光源产生放射状的光线,使形体产生投影,叫做中心投影。
2、平行投影法——当点光源向无限远处移动时,光线与光线之间的夹角逐渐变小,直至为0,这时光线与光线互相平行,使形体产生的投影,叫做平行投影。
平行投影又分为正投影和斜投影。
正投影是投影线与投影面垂直的投影。
正投影具有作图简单,度量方便的特点,被工程制图广泛应用,其缺点是直观性较差,投影图的识读较难。
标高投影是带有数字的正投影图。
投影线与投影面倾斜的投影称为斜投影,这种投影直观性较好,但视觉效果没有中心投影图逼真。
三、平行投影的特性定比性;积聚性;类似性;平行性;度量性;3 2 三面投影图一、投影面的设置三面投影的必要性。
由于三面投影图能唯一的确定形体的形状,因此,作形体投影图时,应建立三面投影体系,即水平投影面(H)、正立投影面V、和侧立投影面W。
形体在三面投影体系中的投影,称作三面投影图。
二、三面投影图的形成及展开规则1、水平投影图水平投影面用字母H表示,形体的水平投影反映形体的长度和宽度。
2、正面投影图正立投影面用字母V表示,形体的正面投影反映了形体的长度和高度,如图所示。
3、侧面投影图侧立投影面用字母W表示,形体的侧立投影反映了形体的高度和宽度。
三、三面投影图的特性作形体投影图时,形体的位置不变,展开后,同时反映形体长度的水平投影和正面投影左右对齐——长对正,同时反映形体高度的正面图和侧面图上下对齐——高平齐,同时反映形体宽度的水平投影和侧面投影前后对齐——宽相等。
“长对正、高平齐、宽相等”是形体三面投影图的规律,无论是整个物体,还是物体的局部都符合这条规律。
第3章12第2节方位投影PPT课件

光源置于无穷远——正射方位投影 属于任意投影
光源置于另一极——平射方位投影 投影图上的角度可与实际球面上相应的角度相等
属于等角投影
(一)投影条件
原理:投影面与地球椭球面切于极点, 将光源置于另一极进行几何投影
条件:使投影图上的角度与实际球面 上相应的角度相等。
(一)投影条件
原理:投影面与地球椭球面切于极点, 将光源置于另一极进行几何投影
三、等积方位投影
(一) 投影条件 (二) 变形规律 (三) 用途
投影条件
原理:投影面与地 球椭球面切于极点, 数学解析法进行投 影
条件:使投影图上 的面积与实际球面 上相应的面积相等
正轴等积方位投影极坐标公式
球冠面积 PAB=2RH = 2*R*R(1-cosZ)
=4R2sin2 (Z/2)
极坐标 ρ=f(Z) δ=λ
平面直角坐标 x=ρcosδ y=ρsinδ
变形分布规律
投影中心是没有变形的点,以投影中心 向外变形逐渐增大,等变形线呈同心圆 状分布
变形分布规律
方位投影的特性:在方位投影,过投影 中心的球面上的大圆弧均投影为直线, 从中心到任何点的方位角没有变形
等变形线和方位角
第二节 方位投影
一、方位投影 二、平射方位投影(等角方位投影) 三、等积方位投影 四、等距投影
一、方位投影
构成原理 一般公式 变形分布规律 用途
构成原理
投影面为平面,投影面切或割地球表面。
正方位
φ=900
横方位 切点纬度φ φ= 00
斜方位
00<φ<900
方位投影
Байду номын сангаас轴
横轴
斜轴
一般公式
第三章 投影的基本知识
第三章投影的基本知识§3-1投影及其特性§3-2正投影图及其特性§3-3基本形体的投影§3-4组合形体的投影投影法的基本概念一、投影的基本概念二、投影法分类把空间形体表示在平面上,是以投影法为基础的。
投影法源出于日常生活中光的投射成影这个物理现象。
例如,当电灯光照射室内的一张桌子时,必有影子落在地板上;如果把桌于搬到太阳光下,那么,必有影子落在地面上。
§3-1投影及其特性假设要画出一个房屋形体的图形(图a),可在形体前面设置一个光源S (例如电灯),在光线的照射下,形体将在它背后的平面P 上投落一个灰黑的多边形的影。
这个影能反映出形体的轮廓,但表达不出形体各部分的形状。
假设光源发出的光线,能够透过形体而将各个顶点和各根侧棱都在平面P上投落它们的影,这些点和线的影将组成一个能够反映形体各部分形状的图形(图b),这个图形称为形体的投影。
光源S称为投射中心。
投影所在的平面P称为投影面。
连接投射中心与形体上各点的直线称为投射线。
通过一点的投射线与投影面P相交,所得交点就是该点在平面P上的投影。
作出形体投影的方法,称为投影法。
S投影中心投射线A空间点投影ba投影面P B空间点投影的基本概念投影三条件:①投影中心及投射线②投影面(不通过投影中心)③表达对象(空间几何元素或几何形体)投影——通过表达对象的一系列投射线与投影面的交点的总和。
投影法——获得投影的方法。
投影法的分类:投影中心投影平行投影斜投影正投影斜投影正投影投影面P中心投影中心投影法S 投射中心cba投射线A CB表达对象投影中心S 距投影面P 有限远中心投影法当投影中心S距投影面P为有限远时,所有的投射线都从投影中心一点出发(如同人眼观看物体或电灯照射物体),这种投影方法称为中心投影法。
用中心投影法获得的投影通常能反应表达对象的三维空间形态,立体感强,但度量性差。
这种图习惯上称之为透视图。
分析上图,我们可以得到中心投影的两条基本特性:1)直线的投影,在一般情况下仍为直线;2)点在直线上,则该点的投影必位在该直线的投影上。
机械制图第3章-基本几何体

b' A
ABC是水平面,在俯视图的上各反个映投影均为类似形。 实两形个。侧侧 棱棱面C面为ca""S一A般C为位侧置垂平其面面棱侧,。面面另△投S影AsC”为a侧”垂c”面,
a
s B c b"
重影为一直线。
b
Y
正三棱锥的投影
16
V
a' X
Z s'
S
s"
W
b'
Ca"
A
c"
a
s B c b"
b
Y
正三棱锥的投影
d
X
a
d” a”b” c”
Cb
c
22 Y
2)圆柱表面上取点
已知圆柱表面上的点M及N正面投影a’、 b’、m′和n′,求 它们的其余两投影。
b’ a’
(b”) a”
b
a
在圆柱表面上取点
23
2、圆锥体
1) 圆锥的投影
圆锥表面由圆锥面和底圆组成。它是一母线绕与它相交
的轴线回转而成。
Z
如图所示,圆锥轴 线垂直H面,底面为水 平面,它的水平投影 反映实形,正面和侧 面投影重影为一直线。
成的平面。 讨论的问题:截交线的分析和作图 。
32
一、 平面立体的截切
1、平面截切的基本形式
截断面 截交线
截平面
截交线与截断面
33
截交线的性质:
• 截交线是一个由直线组成的封闭的平面多边形,其 形状取决于平面体的形状及截平面相对平面体的截
切位置。 •平面立体的截交线是一个多边形,它的顶点是平 面立体的棱线或底边与截平面的交点。截交线的每 条边是截平面与棱面的交线。 • 共有性:截交线既属于截平面,又属于立体表面。
方位投影的概念

方位投影的概念方位投影,这听起来是不是有点像一种神秘的魔法呢?其实啊,它就是地图投影的一种类型。
咱就把地球想象成一个大皮球,这皮球上有各种各样的图案和标记,就像地球表面有山川河流、城市乡村一样。
现在呢,我们想要把这个皮球上的图案平平整整地画在一张纸上,这可不容易啊,就好像要把一个鼓鼓囊囊的大包裹里的东西,一点不皱巴地铺在一个小盒子里一样难。
方位投影做的就是这个事儿,它是想办法把地球这个球面上的东西,投影到一个平面上。
方位投影有好多有趣的特点呢。
它有点像那种从一个固定的点去看整个地球的感觉。
比如说,你站在一个高塔上,然后向四周看,你看到的东西在你的视野里的样子,就有点像方位投影在平面上展现地球的样子。
这个固定的点就像是投影的中心,从这个中心往外,把地球表面的东西映射到平面上。
那它具体是怎么做到的呢?这就像是把地球表面的每一个小部分,都像是捏橡皮泥一样,按照一定的规则,把它们拉到平面上。
不过这个规则可不像我们捏橡皮泥那么随意。
有些方位投影会让靠近中心的地方变形比较小,越往边缘呢,变形就越大。
这就好比你在一个池塘里扔了一颗石子,涟漪从中心往外扩散,中心的水波很整齐,可是到了边缘就变得比较乱了。
再比如说,有一种方位投影就像是聚光灯打在地球上的某个点上,以这个点为中心进行投影。
在这种投影下,如果这个点是北极点,那北极附近的地区就会在平面上看起来比较准确,形状和实际的比例比较接近。
可是离北极越远的地方,就像那些靠近赤道的地方,就会被拉得变形比较厉害。
这就像你在拍照的时候,你把焦点对在一个近处的花朵上,那花朵很清晰,背后的风景就变得模糊而且变形了。
方位投影在很多地方都有用呢。
航海的时候就经常会用到。
你想啊,船员们在茫茫大海上,他们需要知道自己的位置,还需要知道周围的岛屿、大陆在哪里。
方位投影的地图就像是他们的指南针一样。
虽然它可能有些变形,但是只要船员们知道这个投影的规则,他们就能根据地图找到自己要去的地方。
2方位投影
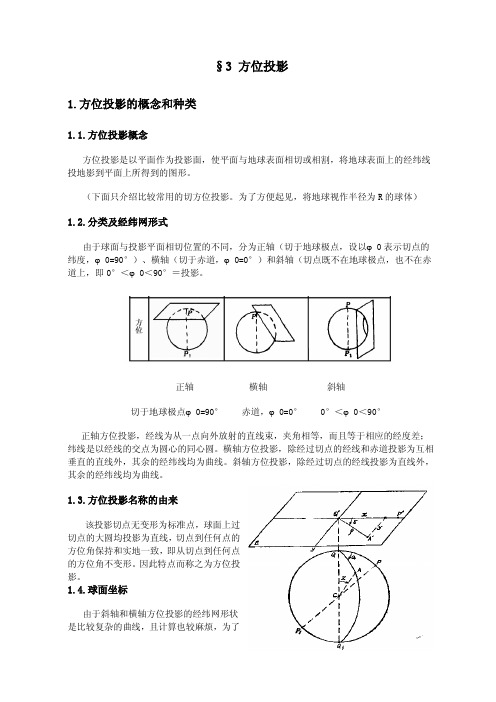
根据上述变形公式,计算出本投影的各种变形值,列于表 2-2 中。 由表 2-2 看出,这种投影沿垂直圈方向长度比不断缩小,沿等高圈方向长度比不断增大; 在一点上,垂直圈长度比与等高圈长度比互为倒数。投影中心附近变形小,离中心点愈远, 变形愈大。图 2-24 是用斜轴等积方位投影绘制的陆半球图。图上表示出角度最大变形,其 等变形线呈同心圆状分布。
2
R sin z
cos12 Z
2
1 2 sec2
sin
2
Z 2 Z 2
P 1 2 sec4
1 2 1 2
0
即 μ1=μ2,因此这种投影具有等角性质,故又称等角方位投影。 用正轴平射方位投影绘制北(南)半球图时,先画一圆,它的半径等于按比例缩小了的 地球直径,这个圆代表赤道。然后引两条互相垂直的直径,并按规定的经线间隔将圆周等分, 各等分点与圆心的连线就是经线。以经线交点为圆心,按纬线半径公式所求得的数值为半径 画圆(计算纬线半径时,要将地球半径 R 按比例缩小),即为各条纬线。 如果是绘制横轴和斜轴投影,则须按下列步骤进行: 1)确定球面坐标极,其地理坐标为 0,λ0; 2)将各经纬线交叉点的地理坐标( ,λ)换算成球面坐标(Z,ψ); 3)计算平面极坐标(ρ,δ)和平面直角坐标(x,y); 4)连接相同经度的各点、相同纬度的各点构成经纬线网。
方位投影球面和平面上的微分线段
球面上微分弧长
由于垂直圈和等高圈投影后成正交,故其长度比 μ1、μ2 为最大、最小长度比,因而面 积比和角度最大变形公式为:
从公式可以看出,方位投影的变形公式都是 z 的函数,如果 z 不变,则变图 2-21 切方位 投影等变形线分布形值不变。这就是说,在同一等高圈上各点的各种变形数值均各自相等, 等变形线(变形值相等的各点连线)是与等高圈一致的同心圆。 图上同心圆是等变形线,箭头所指方向为变形增加的方向。投影中心是没有变形的点, 从投影中心向四周变形逐渐增大。 方位投影的中心,也就是投影平面与地球相切的点,没有变形;过投影中心球面上的大 圆弧投影为直线,而且从中心到任何点的方位角没有变形。因此,这种投影被称为方位投影。
房屋建筑构造与识图课件第3章 三面正投影图的形成及特性

3.1 点、直线、平面的投影
➢2.直线上点的投影 直线上点的投影,必在直线的同面投影上;直线段上的点分割直线段之比,在 投影后仍保持不变。如下图所示,C是直线AB上的点,C点投影在直线AB的同面 投影上,且有AC∶CB=ac∶cb= a'c'∶c'b'= a''c''∶c''b''。
直线上点的投影
两直线交叉
3.1 点、直线、平面的投影
3.1.3 平面的投影 三点确定一个三角形平面,将三点的同名投影用直线两两相连,就得到平面的同 名投影,如下图所示。平面的投影一般仍为平面,特殊情况下投影可为一直线。
平面的同名投影
3.1 点、直线、平面的投影
当平面垂直于投影面时,其投影重合成直线,具有积聚性,如图(a)所示; 当平面平行于投影面时,其投影反映平面实形,如图(b)所示; 当平面倾斜于投影面时,其投影类似原平面,如图(c)所示。
直线的同名投影
3.1 点、直线、平面的投影
当直线垂直于投影面时,其投影重合为一点,具有积聚性,如图 (a)所示; 当直线平行于投影面时,其投影反映线段实长,ab=AB,如图 (b)所示; 当直线倾斜于投影面时,其投影比空间线段短,ab=AB cos α,如图(c)所示。
(a)
(b)
(c)
直线对一个投影面的投影特性
侧垂线
3.1 点、直线、平面的投影
投影面垂直线特性:垂直于那个投影面,在那个投影面上的投影积聚成一个点, 而另外两个投影面上的投影平行于投影轴且反映实长。
正垂线
铅垂线
侧垂线
3.1 点、直线、平面的投影
3)一般位置直线 直线与三个投影面都处于倾斜位置,称为一般位置直线。一般位置直线的三个 投影仍为直线;三个投影都倾斜于投影轴;投影长度小于直线的真长;投影与 投影轴的夹角,不反映直线对投影面的倾角,如下图所示。
3.机械制图第三章三投影面及三视图

下
后 左 右
前
关于方位的进一步说明(图574)
关于方位的进一步说明
从前向后看
主视图
从左向右看
左视图
从上向下看
俯视图
§3-2-3 正投影的三个特性
1.实形性(真实性): 直线或平面平行于投影面,直线的投影反映实长; 平面的投影反映其真实形状。
2.积聚性: 直线或平面垂直于投影面,直线在投影面上的投影 积聚为一个点;平面的投影积聚为一条直线。
上 左
Z
右
W 左视图
上 后 下 前
X
下
YW
H 俯视图
后
左 前
右
YH
物体左右间的距离称为“长”,上下间的距离称为 “高”,前后间 的距离称为“宽”。二维的平面图形只反映两个方向的尺寸,从图中可 以看出,主视图反映物体的长度和高度;俯视图反映物体的长度和宽度; 左视图反映物体的高度和宽度。 物体不仅有长、宽、高三个方向的尺寸,还有上、下、左、右、前、 后六个方位。主视图反映上、下、左、右四个方位;俯视图反映左、右、 前、后四个方位;左视图反映上、下、前、后四个方位。
左 下 H 俯视图 后 左 前
右
后 下
前
右
零件的三视图画法(图354)
V 主视图 上 左 右 后 W 左视图
上
前
下 H 俯视图
后
下
左
右
前
注意
作图时,从反应实形和形状特征明显的视图画起!
零件的三视图画法(图353)
V 主视图 上 W 左视图 上
左 下 H 俯视图 后
右
后 下
前
左 前
右
零件的三视图画法(图352)
§3-2 三投影面体系及三视图
第3章 第3讲方位投影及其应用讲解

地图学
Cartography
第三章 地图投影原理及方位投影
第3讲 方位投影及其应用
回顾
地图投影:将地球椭球面投影到平面上。
各种各样的地图投影,满足不同的需求!
地球椭球面 B , L
x,y
地图平面
地图投影
2
内容 3 地图方位投影
3.1 球面坐标系 3.2 方位投影的概念及一般公式 3.3 透视方位投影 3.4 等角、等积、等距方位投影
?C D
? ??
6
3.2 方位投影的概念及一般公式
地球:球体, 半径R
方位投影: 将一个平面切于或割于地球某一点或一 部分,再将球面投影到此平面上。
7
纬线为圆 经线为直线
切点为极点
切方位投影:平面与球相切。 割方位投影:平面与球相割。
9
正方位投影: 平面切于极点或垂直于地轴 割于某一纬线的;
?
RtgZ
sin a
? ?? ?
? 2 ? sec Z
? ?
p ? sec3 Z
?
?
sin ? ? tg 2 Z
2
2
? ??
18
19
球心方位投影特性: 大圆线投影成直线。 球心投影又称 日晷投影 。该投影不可能作半球图, 也不适合作一般用途的地图。古代常用来作天体图, 现在主要用来作航海图。 在球心投影地图上,连接航线始、终点的直线即 为航行的最短距离。但领航极为不便,所以该投影 图常与等角投影图配合使用。 在军事上,球心投影常用来制作无线电定位图。
?
?1
? ?
2
? 2 ? ? 1 ?? 13
? 方位投影的方位角与实地相等。 ? ? a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
方 位 投 影
正射投影 透视投影 外心投影 球面投影 球心投影 纬线——一组同心圆 正轴 经线——交于投影中心的直 线束,夹角不变 非透视投影 横轴 等高圈——同心圆 斜轴 垂直圈——同心圆半径,夹 角不变
方位投影——又称平面投影
RZ C
式中C为积分常数。因Z = 0 时, = 0,故C = 0。 于是:
RZ
22
等距离方位投影的变形公式:
长度比为:
1 1 2
R sin Z Z sin Z
面积比为:
P 1 2 Z sin Z
a,b
最大角度变形为:
sin
2
投影中心: 平面和球面相切的一点 用圆球体代替椭球体:M=N=R B,L
投影中心
1. 方位投影分类
根据投影面和地球球体相切位置不同 当投影面切于地球极点时,为正轴投影。 当投影面切于赤道时,为横轴方位投影。 当投影面切于既不在极点也不在赤道时,斜轴方位投影。
2、正轴方位投影
投影中心为极点,纬线为同心 圆,经线为同心圆的半径,两 条经线间的夹角与实地相等。
由此得到直角坐标公式为:
x cos
LR sin Z cos D R cos Z
y sin
LR sin Z sin 4 D R cos Z
变形公式为:
d L( D cos Z R) RdZ ( D R cos Z )2 3 L 2 R sin Z D R cos Z
P 2
41
当Zk=0,即投影面切在投影中心,则有:
k 2R
Z 2Rtg 2
Z sec 2
2
对于正轴投影,只要在等角方位投影一般公式 中以 代,以90- 代 Z 即可,有:
k )tg (45 ) 2 2 k 2 2 cos (45 )sec (45 ) 2 2 2 R cos 2 (45
经纬线形式
中央经线为直线,其它经线是对称于 中央经线的凹向曲线;中央纬线为直 线,其它纬线是对称于中央纬线的凸 向曲线。 在中央经线上纬线间隔自投影中心向 外逐渐减小在中央纬线上经线间隔自 投影中心向东、向西方向逐渐减小。
横轴等面积方位投影
变形分布规律
投影中心无变形,离投影中心愈远角度、长度变形增大 。 20
Q
d
Q’
d
d
R 2 sin ZdZ
Z
D RdZ A
C
B
d
D’ A’
C’ B’
最大角度变形为:
2 a b ab
球面微分梯形在平面上的投影
sin
或
tg (45
4
)
1 2
(6-5)
12
d d m Rd (90 ) Rd
d n rd R sin(90 )
Zk k tan R sin Z k 2
或
Zk k 2 R cos 2
2
40
等角方位投影的一般公式为:
x cos
2 R cos 2
y sin Zk Z sec 2 2 2 0
Zk Z tan 2 2
1 2 cos 2
经纬线形式
中央经线为直线,其它经纬 线均是曲线。 在中央经线上纬线间隔相等。
变形分布规律
斜轴等距离方位投影
投影中心无变形,离开投影中心愈远角度、长 度变形增大,面积变形、角度变形都不大 。
28
§3-4 透视方位投影
透视方位投影的概念
透视方位投影是方位投影的特殊情 况。它是用透视的原理来确定 = f(Z)的函数关系。
4
A′
Z 投影变形公式为: 2 R tan 2 d 2 Z 1 sec
RdZ
1
2 2 Z 2 sec R sin Z 2 2 Z P sec 2
§3-6 球面投影(等角方位投影)
等角方位投影的条件:
1、 2分别为垂直圈 和等高圈的长度比
1 2
P mn
d
R 2 sin(90 )d
mn sin 2 mn
m和n分别是经纬线长度比
方位投影的特征
由投影中心到任何一点的方位角保持与实地相等(无变形)。
14
§3-2
等面积方位投影
等面积方位投影(Lambert)的条件:
P 1 2
移项积分,得:
30
§3-4 透视方位投影
Q 'O qA QA qO
' '
A′
有如下的一些关系: Q ' A'
Q 'O R D
qA R sin Z qO R cos Z D
带入上式:
4
P
3
Z
2
1
LR sin Z D R cos Z
§3-4 透视方位投影
LR sin Z D R cos Z
此投影为波斯托于1581年所创.又称波斯托投影。
正轴等距离方位投影
25
正轴等距方位投影
经纬线形状
纬线投影后为同心圆,经线投影为交于纬线圆 心的直线束,经线投影后保持正长,所以投影 后的纬线间距相等。
变形分布规律
球面上的微圆投影为椭圆,且误差椭圆的长半 径和纬线方向一致,短半径与经线方向一致, 且等于微圆半径r,又因自投影中心,纬线扩大 程度越来越大,所以变形椭圆的长半径也越来 越长,椭圆越来越扁。
42
正轴等角方位投影
43
横轴等角方位投影
44
斜轴等角方位投影
45
§ 3.7 球心投影(日晷投影)
对于球心投影而言,D=0,L=R,因此有:
LR sin Z D R cos Z
A′
R tan Z
3 投影变形公式为:
d 1 sec2 Z RdZ 2 sec Z R sin Z
Q
d
Q’
d
Z
D RdZ A
C
B
d
D’ A’
C’ B’
长度比为:
球面微分梯形在平面上的投影
AD ' d 1 AD RdZ D ' C d d 2 DC rd R cos(90 Z )d R sin Z
11
面积比为:
P ab 1 2
d 1 RdZ R sin Z
2
2
C R 2 cos Z
式中C为积分常数,因Z= 0时, = 0,故C = R2。 于是:
2 2R2 (1 cos Z )
整理后开方得:
2 R sin
Z 2
15
等面积方位投影的变形公式:
长度比为:
2 1
D 3 D Q Q
A A A A 2 A’ 1 A’ 3 2 A’ 4 3 A’ 1 4
A 4
4 A
3 2 1
根据投影面与地球的相对位置(即投影中心Q的纬度2 0)的不同 1 分类:
图6-6 透视方位投影
1)正轴( 0 = 90°)
2)斜轴( 0 <0 < 90°)
3) 横轴( 0 = 0°)
1
1
L2 ( D cos Z R) P 12 ( D R cos Z )3
最大角度变形公式为:
sin
2
a b ab
x cos
LR sin Z cos D R cos Z
LR sin Z sin y sin D R cos Z
或
0
按公式 得:
d RdZ R sin Z
移项积分后,得:
ln ln tan
或
Z ln k 2
Z k tan 2
注意:Z=0 Z=90是否可用 39
要求系数 k,可指定某等高圈Zk上的长度比2(k)=1,有:
2( k )
即
k 1 R sin Z k
P 12 cos Z
a tan(45 ) sec Z 4 b
(a)以北极为中心的正射投影
(b)以赤道为中心的正射投影
(c)以北纬45度为中心的正射投影
§3-6 球面投影(等角方位投影)
对于等角方位投影而言,D=R,L=2R,因此有:
LR sin Z D R cos Z 2 R 2 sin Z 2 R sin Z R(1 cos Z ) 1 cos Z
等变形线都是以投影中心为圆
心的同心圆。 包括等角、等积、
等距三种变形性质,主要用于 制作两极地区图。
概念:方位投影是以平面作为投影面,使平面与地球
表面相切或相割,将球面上的经纬线投影到平面上所 得到的图形。 投影平面上,由投影中心(平面与球面相切的点,或 平面与球面相割的割线圆心点)向各个方向的方位角 与实地相等,等变形线是以投影中心为圆心的同心圆, 切点或相割的割线无变形。适合制作形状大致为圆形 区域的地图。
第三章 方位投影
3.1 方位投影的种类和基本原理 3.2 等面积方位投影
3.3 等距离方位投影
3.4 透视方位投影的种类和一般公式
3.5 正射投影
3.6 球面投影(等角方位投影)
3.7 球心投影(日晷投影)
3.8 方位投影的分析和应用
§ 3.1方位投影的种类和基本原理
