期权的希腊字母(ppt 38)
期权希腊字母

期权希腊字母 — 风险度量指标: THETA的说明
如下面例子所示,期权越接近到期,时间价值损失越 快。Theta用以测量每天期权价格大约的下降幅度。在下 面例子中,Theta约等于期权的价格变化。
期权希腊字母 — 风险度量指标: THETA计算器
Theta的数值通常为负值,其绝对值会随时间消逝而 变大, 也就是说愈接近到期日,权证的时间价值消失的 速度会愈快,最后到期时权证的时间价值应等于0。
期权希腊字母 — 风险度量指标: DELTA看跌期权/卖权PUT
对于看跌期权来说,Delta的变动范围为-1至0,而且 标的资产价格越低,Delta就越小。“平值”看跌期权Delta 为-0.5。从另一个角度来说,Delta的绝对值可以被认为是 看跌期权到期时为“实值”的可能性。
期权希腊字母 — 风险度量指标: DELTA的说明
Delta值的运用-Delta中性套期保值 (Delta Hedging)
如果投资者希望对冲期权或期货头寸的风险,Delta 就是套期保值比率。只要使头寸的整体 Delta值保持为0. 就建立了一个中性的套期策略。
期权希腊字母 — 风险度量指标:GAMMA
Gamma是指Delta的变化率,即给定标的资产价格发 生变化时Delta的变化率。(译注:就是为底层资产价格变 动一个单位时Delta的变动量)。Gamma在“平值”的时候最 大,在期权价格向“实值”或“虚值”变化的时候逐渐变小。 如下所示,期权价格的变化(到期之前)用一条曲线表示, 而不是直线。Delta是指曲线上任意一点的变化,而 Gamma则描述了delta的变化或者称之为曲线的曲率。对 于微积分的爱好者来说,Gamma是二阶导数。对于设法 对冲投资组合的交易员来说,理解Gamma至关重要。
期权价值敏感性——希腊字母汇总

第三章 期权敏感性(希腊字母)顾名思义,期权敏感性是指期权价格受某些定价参数的变动而变动的敏感 程度,本章主要介绍期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标,这些敏感性指标也称作希腊值(Greeks )。
每一个希腊值刻画了某个特定风险,如果期权价格对某一参数的敏感性为 零,可以想见,该参数变化时给期权带来的价格风险就为零。
实际上,当我们 运用期权给其标的资产或其它期权进行套期保值时,一种较常用的方法就是分 别算出保值工具与保值对象两者的价值对一些共同的变量(如标的资产价格、 时间、标的资产价格的波动率、无风险利率等)的敏感性,然后建立适当数量 的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动 能相互抵消,也就是说让套期保值组合对该参数变化的敏感性变为零,这样就 能起到消除相应风险的套期保值的目的。
本章将主要介绍 Delta 、Gamma 、Vega 、Theta 、Rho 五个常用希腊字母。
符号风险因素 量化公式Gamma Γ标的证券价格变化 Delta 变化/标的证券价格变化 Vega ν波动率变化 权利金变化/波动率变化Theta Θ到期时间变化 权利金变化/到期时间变化 本章符号释义:T 为期权到期时间S 为标的证券价格, S 0 为标的证券现价, S T 为标的证券行权时价格K 为期权行权价格σ 为标的证券波动率r 为无风险利率π t 为资产组合在 t 时刻的价值N () 为标准正态分布的累积密度函数,可以查表或用计算机(如 Excel)求得N()为标准正态分布的密度函数,N()=-x2''2第一节Delta(德尔塔,∆)1.1定义Delta衡量的是标的证券价格变化对权利金的影响,即标的证券价格变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Delta×标的证券价格变化1.2公式从理论上,Delta准确的定义为期权价值对于标的证券价格的一阶偏导。
「期权系列」期权的风险管理利器—希腊字母
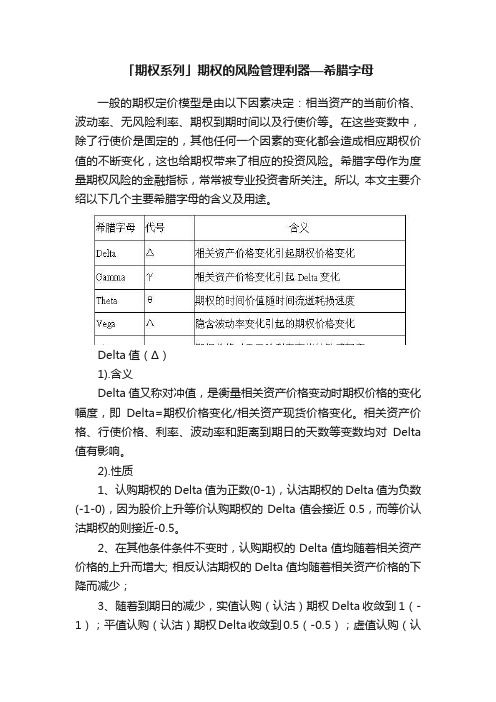
「期权系列」期权的风险管理利器—希腊字母一般的期权定价模型是由以下因素决定:相当资产的当前价格、波动率、无风险利率、期权到期时间以及行使价等。
在这些变数中,除了行使价是固定的,其他任何一个因素的变化都会造成相应期权价值的不断变化,这也给期权带来了相应的投资风险。
希腊字母作为度量期权风险的金融指标,常常被专业投资者所关注。
所以, 本文主要介绍以下几个主要希腊字母的含义及用途。
Delta值(Δ)1).含义Delta值又称对冲值,是衡量相关资产价格变动时期权价格的变化幅度,即Delta=期权价格变化/相关资产现货价格变化。
相关资产价格、行使价格、利率、波动率和距离到期日的天数等变数均对Delta 值有影响。
2).性质1、认购期权的Delta值为正数(0-1),认沽期权的Delta值为负数(-1-0),因为股价上升等价认购期权的Delta值会接近0.5,而等价认沽期权的则接近-0.5。
2、在其他条件条件不变时,认购期权的Delta值均随着相关资产价格的上升而增大; 相反认沽期权的Delta值均随着相关资产价格的下降而减少;3、随着到期日的减少,实值认购(认沽)期权Delta收敛到1(-1);平值认购(认沽)期权Delta收敛到0.5(-0.5);虚值认购(认沽)期权Delta收敛到0;3).应用Delta均值常用于中性套期保值,如果投资者想要对冲掉期权仓位风险,Delta值就是套期保值比率。
若头寸的Delta值持续为0,就建立了一个中性套期策略。
简单来讲,以做空认购期权为例假设一份长期认购期权的delta是0.8,则卖掉一份认购期权需要买入delta(0.8)份股票来做对冲,达到套期保值的效果。
Gamma 值(γ)1).含义Gamma值反映期权价格对delta值的影响程度,即delta变化量与期货价格变化量之比。
另外的,现在的Delta值将约等于之前的Delta值加上或减去Gamma 值。
2).性质1、对于长仓,无论认购期权或是认沽期权的gamma值均为正值。
详解期权的希腊字母

标的价格变化一单位的时,Delta值变化多少
波动率
Vega
波动率变化一单位间减少一单位时,期权合约的价格减少多少
无风险利率
Rho
无风险利率每变化一单位,期权合约的价格变化多少
期权合约的希腊值
本次内容:
• 为什么期权交易要用到希腊字母? • 希腊字母体现的是什么关系? • 希腊字母的取值是什么含义? • 使用希腊字母时需要注意什么问题?
期权的杠杆率是多少?
• 你问的是哪个合约的杠杆率? • 你问的是成本杠杆率还是收益杠杆率? • 你问的是啥时候的杠杆率? • 你问杠杆率想干啥?
期权价格变化非线性特征
期权价格变化非线性特征
本次内容:
• 为什么期权交易要用到希腊字母? • 希腊字母体现的是什么关系? • 希腊字母的取值是什么含义? • 使用希腊字母时需要注意什么问题?
详解股指期权的希腊字母
本次内容:
• 为什么期权交易要用到希腊字母? • 希腊字母体现的是什么关系? • 希腊字母的取值是什么含义? • 使用希腊字母时需要注意什么问题?
本次内容:
• 为什么期权交易要用到希腊字母? • 希腊字母体现的是什么关系? • 希腊字母的取值是什么含义? • 使用希腊字母时需要注意什么问题?
• 实际使用时,gamma所代表的是 标的价格涨速(真实波动)对期 权价格的影响
期权合约的希腊值
Vega:说不清的价格变化都在这里
• Vega的含义是波动率变化一单 位时,期权合约的价格变化多 少
• 实际使用的时候,波动率用的 是隐含波动率,而隐含波动率 是用市场价反推出来的,其实 隐含波动率不仅仅是波动率
期权合约的希腊值
Theta:时间价值是怎么折损的?
期权中希腊字母的含义

H F = H Ae
− rT ∗
标的资产为股票指数
−( r − q )T ∗
标的资产为外汇
− r −rf T ∗
(
)
Greeks
11
Theta——定义 定义
1. Theta是期权价值对时间的偏导数,度量了期权价值 是期权价值对时间的偏导数, 是期权价值对时间的偏导数 随时间衰减的速度
股价:Delta, Gamma 股价: 到期时间: 到期时间:Theta 波动率: 波动率:Vega 无风险利率: 无风险利率:Rho
Greeks
3
Delta
1. Delta是期权价值对标的资产价格的偏导数,度量了 是期权价值对标的资产价格的偏导数, 是期权价值对标的资产价格的偏导数 期权价值对标的资产价格变化的敏感性
卖权
买权
Greeks
24
Rho——外汇期权 外汇期权
1. 外汇期权涉及本币利率与外币利率,因此,有两个 外汇期权涉及本币利率与外币利率,因此, rho,一个对应于本币利率 见上一页 ,另一个对应 见上一页), ,一个对应于本币利率(见上一页 于外币利率
买权
rho c = −Te
卖权
− rf T
S0 N ( d1 )
Gamma与到期时间的关系 与到期时间的关系
in the money at the money out of the money
Greeks
19
Delta, Theta, Gamma的关系 的关系
1. 从BSM方程容易推导出三者的关系 方程容易推导出三者的关系
2. 如果投资组合是 如果投资组合是Delta中性的,则 中性的, 中性的
2. 基金经理常常创建合成期权进行投资组合保险 3. 期权合成技术——动态复制 动态复制 期权合成技术
希腊字母在期权中的应用

希腊字母在期权中的应用在衡量期权组合风险的时候,若用希腊字母来表示期权的风险指标,原本繁多复杂的期权交易和持仓就会显得简洁明了。
在交易中,投资者不仅要关注做多做空多少手不同的期权合约,而且还要注意所有持仓的Delta、Gamma等参数。
选择策略以最简单的买入标的和单腿策略为例,预计标的价格上涨,想要做多Delta,有买入期货、买入看涨期权和卖出看跌期权三种方法,但预计标的价格上涨的同时波动率下跌,即需要做多Delta、做空Vega,那么卖出看跌期权则是相对有利的策略。
对冲期权对于同一个品种的期货和期权,希腊字母都可以直接相加减。
当投资者利用跨式策略、价差策略、蝶式策略等多腿策略来交易期权时,有时候固定的策略并不能完美贴合投资者的交易需求,此时就可以根据叠加后的希腊字母总和去对冲存在风险的部分。
例如,当预计市场有重大消息披露、标的价格可能有大幅变化、波动率将会变大时,通常可以利用买入平值跨式期权策略来做多波动率。
比如说,当豆粕期货1901合约价格为3111元/吨时,同时买入行权价为3100元/吨的看涨期权和看跌期权构建买入跨式期权策略。
可以看到这个策略中,两个期权的Delta并没有完全对冲掉,还存在一小部分方向上的风险,当标的价格下跌时,会对这个跨式组合策略造成不利影响。
此时可以做空0.073倍的期货,得到-0.073个Delta,使得期权部位的总Delta为零。
管理持仓由于希腊字母可以直接相加减,当持有的期权合约类型、行权价、数量等各不相同时,可以通过计算持仓部位的希腊字母来管理持仓风险。
因此,即使持仓的头寸繁多复杂,利用希腊字母的叠加,持仓的风险状况就会变得更直观明了,分析起来也更方便。
下面以铜期权2018年9月21日收盘时的风险参数为例,假设同时持有数量不一、行权价不同的若干期权,结果如下表所示:那么仓位全部的风险参数总和计算如下:仓位的风险指标汇总如下:每新增或者减少一个期权,都能很清楚地观察到仓位变化。
期权风险指标--希腊字母

Delta值概述期权的风险指标通常用希腊字母来表示,包括:delta值、gamm值、theta 值、vega值、rho值等。
Delta值(S),又称对冲值:是衡量标的资产价格变动时,期权价格的变化幅度。
用公式表示:Delta=期权价格变化/期货价格变化所谓Delta ,是用以衡量选择权标的资产变动时,选择权价格改变的百分比,也就是选择权的标的价值发生变动时,选择权价值相应也在变动。
公式为:Delta =外汇期权费的变化/外汇期权标的即期汇率的变化关于Delta值,可以参考以下三个公式:1.选择权Delta加权部位二选择权标的资产市场价值x选择权之Delta值;2.选择权Delta加权部位x各标的之市场风险系数=Delta风险约当金额;加权部位价值=选择权Delta加权部位价值+现货避险部位价值。
二、Delta值的特性Delta具有以下特性:买权的Delta 一定要是正值;卖权的Delta 一定要是负值;Delta 数值的范围介乎0到1之间;价平选择权的Delta为;Delta 数值可以相加,假设投资组合内两个选择权的Delta数值分别为及,整个组合的Delta数值将会是。
对于看涨期权来说,期货价格上涨(下跌),期权价格随之上涨(下跌),二者始终保持同向变化。
因此看涨期权的delta为正数。
而看跌期权价格的变化与期货价格相反,因此,看跌期权的delta为负数。
风险指标的正负号均是从买入期权的角度来考虑的。
|因此,交易者一定要注意期权的指标与部位的指标之区别。
对于delta,期权部位的符号如下表。
表1期权部位的delta值部位看涨期权看跌期权多头+ -空头- +期权的delta值介于-1到1之间。
对于看涨期权,delta的变动范围为0 到1,深实值看涨期权的delta趋增至1,平值看涨期权delta为,深虚值看涨期权的delta则逼近于0。
对于看跌期权,delta变动范围为-1到0,深实值看跌期权的delta趋近-1,平值看跌期权的delta 为,深虚值看跌期权的delta 趋近于0。
期权价值敏感性希腊字母

期权价值敏感性希腊字母公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]第三章期权敏感性(希腊字母)顾名思义,期权敏感性是指期权价格受某些定价参数的变动而变动的敏感程度,本章主要介绍期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标,这些敏感性指标也称作希腊值(Greeks)。
每一个希腊值刻画了某个特定风险,如果期权价格对某一参数的敏感性为零,可以想见,该参数变化时给期权带来的价格风险就为零。
实际上,当我们运用期权给其标的资产或其它期权进行套期保值时,一种较常用的方法就是分别算出保值工具与保值对象两者的价值对一些共同的变量(如标的资产价格、时间、标的资产价格的波动率、无风险利率等)的敏感性,然后建立适当数量的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动能相互抵消,也就是说让套期保值组合对该参数变化的敏感性变为零,这样就能起到消除相应风险的套期保值的目的。
本章将主要介绍Delta、Gamma、Vega、Theta、Rho五个常用希腊字母。
符号风险因素量化公式Delta 变化/标的证券价格变化GammaΓ化Vegaν波动率变化权利金变化/波动率变化ThetaΘ到期时间变化权利金变化/到期时间变化本章符号释义:T 为期权到期时间S 为标的证券价格,0S 为标的证券现价,T S 为标的证券行权时价格K 为期权行权价格 r 为无风险利率σ 为标的证券波动率 t π 为资产组合在t 时刻的价值()N 为标准正态分布的累积密度函数,可以查表或用计算机(如 Excel)求得'()N为标准正态分布的密度函数,22'()x N -=第一节 Delta (德尔塔,∆)定义Delta 衡量的是标的证券价格变化对权利金的影响,即标的证券价格变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Delta ×标的证券价格变化公式从理论上,Delta 准确的定义为期权价值对于标的证券价格的一阶偏导。
期权的希腊字母

Gamma——欧式股票期权
Gamma与到期时间的关系
Delta, Theta, Gamma的关系
从BSM方程容易推导出三者的关系
如果投资组合是Delta中性的,则
如果Theta是较大的正数,Gamma就是很大的负数, 因此,Theta可以作为Gamma的替代指标使用
Vega
Vega是期权的价值对标的资产波动率的偏导数,度 量了期权价值对标的资产波动率的敏感性
上图有助于理解动态复制技术
曲线表示卖权与标的股票价格的关系 切线的斜率表示卖权的Delta 截距表示复制投资组合在无风险资产上的投资额
随着股价的涨跌,切线的位置和方向将发生改变,其 斜率与截距都将发生变化
因此,动态复制需要经常性地调整头寸
2. 投资组合保险(股票+卖权)包含两个头寸 • 股票头寸:
股价:Delta, Gamma 到期时间:Theta 波动率:Vega 无风险利率:Rho
Delta
Delta是期权价值对标的资产价格的偏导数,度量了 期权价值对标的资产价格变化的敏感性
图示
Delta——欧式股票期权
利用BS公式,可以推导出 Delta与股价的关系
1
X
Delta——欧式股票期权
动态复制在理论上虽然是“自融资策略”,但是,由于 存在交易成本,实际上不可能是“自融资策略”。基金 经理必须在交易成本与复制效果之间进行平衡
定义:建立对冲工具头寸,使得对冲工具头寸与要保 护的头寸的Delta等于零
Delta中性:资产(或者组合)的Delta等于零
动态对冲
由于资产的Delta通常是时间的函数,因此,为了实现 对冲目标,通常必须动态调整对冲工具头寸的数量
例子:BSM随机微分方程的推导
期权中希腊字母的含义讲解

1. 股指期权
? ? ? c ? e? qT N d1
2. 外汇期权
? ? ? c ? e? rf T N d1
3. 期货期权
? ? ? c ? e? rT N d1
4. 股票远期
? p ? e? qT N ?d1 ?? 1 ? ? ? p ? e? rf T N d1 ? 1 ? p ? e? rT N ?d1 ?? 1
BS 采用Delta 对冲方法,建立起包含期权的 Delta 中性 头寸
Greeks
9
Delta对冲——使用期货
1. 实践中,对冲工具多选用期货
期货流动性好、交易成本低
2. 符号
期货到期时间:T * Delta 对冲需要的标的资产头寸:H A Delta 对冲需要的期货头寸:H F
3. 期货的Delta:
19
Delta, Theta, Gamma的关系
1. 从BSM 方程容易推导出三者的关系
?? ?t
? rS ?? ?S
?
1?
2
2S 2
? 2? ?S 2
?
r?
? ? rS ? ? 1 ? 2S 2? ? r?
2
2. 如果投资组合是Delta 中性的,则
? ? 1 ? 2S 2? ? r?
2
如果Theta 是较大的正数, Gamma 就是很大的负数, 因此, Theta 可以作为 Gamma 的替代指标使用
股价: Delta, Gamma 到期时间: Theta 波动率: Vega 无风险利率: Rho
Greeks
3
Delta
1. Delta 是期权价值对标的资产价格的偏导数,度量了 期权价值对标的资产价格变化的敏感性
趣谈期权有关的希腊字母

趣谈期权有关的希腊字母趣谈期权有关的希腊字母!Delta, Gamma, Vega和Theta当我们理解期权价值与其影响因素的敏感性时,可以作这样比喻。
股票期权作为股票的“孩子”,其脾气秉性自然受三方面的影响:一是自身“基因”的制约,比如:权利属性(认购还是认沽)、行权价(K)、到期时间(T);二是“父母亲”的言传身教:股价(S)、股价的波动率(Sigma);三是社会大环境的熏陶:无风险收益率(r)。
那么一份股票期权的价格(V)究竟是如何被这些因素所影响的呢?换而言之,股票价格上涨1%,或者股价波动率上升1%,作为孩子的期权的“脾气”变化多少呢?为了回答这个问题,我们就必须认识五个“希腊字母”了。
毫不夸张地说,这五个希腊字母就是期权价格变化的生命源泉,也是“孩子”与“父母”的纽带。
这五个希腊字母就叫做Delta,Gamma,Vega,Theta和Rho。
先让我们来认识第一个希腊字母——Delta。
1. Delta是什么?期权是标的资产的衍生产品。
两者之间就像是“父子”一样,父亲的一举一动无时无刻不在影响着孩子的行为。
父亲的这种影响力就是Delta。
以50ETF为例,当ETF价格发生变化时,期权价格也会随之改变。
ETF与期权之间的价格关系可以用Delta来刻画:当ETF价格变化0.001元时,对期权价格的影响就是0.001*Delta元。
认购期权是“乖孩子”,当“父亲”ETF价格上涨的时候,认购期权价格也会上涨,认购期权的Delta大于零;而“坏孩子”认沽期权则恰恰相反,当ETF 价格上涨时,认沽期权的价格反而是下跌的,它的Delta小于零。
2. Delta在投资中的两个简单应用一个是对冲作用。
如果我们有着如下对冲组合:由Delta份ETF空头和1份期权多头组成。
当ETF价格变化0.001元时,Delta份ETF 空头价格会变化-0.001*Delta元,1份期权合约价格会变化0.001*Delta元。
期权的希腊字母(ppt 38)

X
Theta——欧式股票期权
Theta与时间的关系
in the money at the mone来自 out of the money
Gamma
1. Gamma是期权的Delta对标的资产价格的偏导数, 也是期权价值对标的资产价格的二阶偏倒数
2 S S 2
2. Gamma度量了期权Delta对标的资产价格变化的敏 感性,也度量了期权价值对标的资产价格的凸性
F0 S0erT erT
期货合约的Delta v.s. 远期合约的Delta
Delta对冲——使用期货
4. Delta对冲需要的期货头寸
标的资产不分红
H F H AerT
标的资产为股票指数
H F H AerqT
标的资产为外汇
H F H Aerrf T
Theta——定义
1. Theta是期权价值对时间的偏导数,度量了期权价值 随时间衰减的速度
X
Vega——与到期时间的关系
in the money at the money out of the money
Rho
1. Rho是期权价值对无风险利率的偏导数,度量了期权 价值对利率变化的敏感性
rho r
2. 标的股票不支付红利的欧式期权
买权
rhoc XTerT N (d2 )
卖权
rho p XTerT N (d2 )
t 1 S2 2
3. Gamma中性与Gamma对冲
由于标的资产及其远期、期货合约的Gamma都等于零, 因此,不能用来改变投资组合的Gamma
要改变投资组合的Gamma,必须使用那些价格与标的 资产价格呈非线性关系的工具,例如期权
Gamma——欧式股票期权
期权价值敏感性——希腊字母

第三章 期权敏感性(希腊字母)顾名思义,期权敏感性是指期权价格受某些定价参数的变动而变动的敏感程度,本章主要介绍期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标,这些敏感性指标也称作希腊值(Greeks )。
每一个希腊值刻画了某个特定风险,如果期权价格对某一参数的敏感性为零,可以想见,该参数变化时给期权带来的价格风险就为零。
实际上,当我们运用期权给其标的资产或其它期权进行套期保值时,一种较常用的方法就是分别算出保值工具与保值对象两者的价值对一些共同的变量(如标的资产价格、时间、标的资产价格的波动率、无风险利率等)的敏感性,然后建立适当数量的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动能相互抵消,也就是说让套期保值组合对该参数变化的敏感性变为零,这样就能起到消除相应风险的套期保值的目的。
本章将主要介绍Delta 、Gamma 、Vega 、Theta 、Rho 五个常用希腊字母。
符号风险因素 量化公式Gamma Γ 标的证券价格变化 Delta 变化/标的证券价格变化 Vega ν 波动率变化 权利金变化/波动率变化 Theta Θ到期时间变化 权利金变化/到期时间变化本章符号释义:T 为期权到期时间S 为标的证券价格,0S 为标的证券现价,T S 为标的证券行权时价格K 为期权行权价格 r 为无风险利率σ 为标的证券波动率 t π 为资产组合在t 时刻的价值()N 为标准正态分布的累积密度函数,可以查表或用计算机(如 Excel)求得'()N 为标准正态分布的密度函数,22'()x N -=第一节 Delta (德尔塔,∆)1.1 定义Delta 衡量的是标的证券价格变化对权利金的影响,即标的证券价格变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Delta ×标的证券价格变化1.2 公式从理论上,Delta 准确的定义为期权价值对于标的证券价格的一阶偏导。
期权对冲中的希腊字母

“希腊字母”期权的风控体系期权产品是目前国际衍生品市场的重要组成部分。
因其独特的优势和丰富的内涵,期权在国际市场上迅猛发展,应用日益广泛,在风险管理、产品构建等方面发挥着举足轻重的作用。
随着投资热情的高涨,期权交易的风险管理问题也日益突出,如何准确地度量和合理控制期权头寸的风险对投资者至关重要。
著名的Black-Scholes期权定价模型中,期权的价格受多种因素影响,包括标的价格、标的波动率、到期时间、行权价格以及无风险利率。
如何量化各类风险,较为准确地估计持仓损益,进行合理有效的风险管理和投资决策非常重要。
由Black-Scholes模型衍生出的希腊字母体系则是这样一套风险管理工具,该体系将期权头寸风险分解成若干风险组成部分,包括标的价格风险、时间风险、波动率风险和利率风险,并用希腊字母估计当其他风险条件不变时,一个单位的某种风险变动所造成的期权的价值变化。
通过量化每一种风险类型的风险暴露,投资者就可以将期权风险管理转化为希腊字母的管理。
Delta看多就买看涨期权,看空就买看跌期权。
这是刚接触期权的投资者的笼统看法。
假设大盘涨了10点,看涨期权价值会涨多少呢,同样是10点吗? Delta就是用来回答这个问题的。
Delta表示在其他因素保持不变的情况下,一单位标的资产价格的变化所引起的期权价值的变化。
Delta反映了标的价格单位变化给期权投资者带来的收益或亏损。
例如投资者持有一手看涨期权,Delta值为0.5,表示在一定的标的价格变化区间内,期权的价值的变化幅度约为标的价格变化幅度的50%,具体来讲,若标的价格上涨1点,期权价值将上升约0.5点,投资者持有该看涨期权将获利约0.5点,反之若标的价格下降1点,投资者将损失约0.5点。
由Delta的定义可以推导出Delta的一些性质:(1)看涨期权多头的Delta值为正,表示看涨期权价值和标的价格同方向变动;看跌期权多头的Delta值为负,表示看跌期权价值同标的价格反方向变动;期权空头的Delta值与期权多头的Delta值符号相反。
期权的定价和希腊字母

期权
权证
一般独立
经常嵌入
期权卖方
券商
履约价数量较多,期限 履约价一般只有一个,
一般不长于1年
期限也较长(1,2年
)
做市商者
发行量 交易方向
专业做市者(期货自营 券商 商)
不固定 可以买,也可以做空
固定 只能买或者不做
路漫漫其悠远
保证金 成本 保证金追加 每日结算 强行平仓 风险
期货与期权或对比一览表 期货
种类:
买权(看涨期权):持有人拥有购买标的资产的权利; 卖权(看跌期权):持有人拥有出售标的资产的权利; 奇异期权。
到期日:
欧式(主流):到期日(或者到期的一段特定时间)才可以执行权利; 美式(非主流):到期日以前(含到期日)均可以执行权利。 百慕大式,以色列式,俄罗斯式……
行权价格:执行价格,既定价格或者履约价格。 标的资产:
买方
卖方
从卖方买入买权
将买权卖给买方
支出权利金
获得权利金
有权利向卖方以约定价格买入 有义务将目标资产卖给买权持
标的资产
有人
主动(有权利没有义务)
比如:股票
路漫漫其悠远
被动(有义务没有权利)
买权的极限值:
最高:K=0,T→∞,买权的价格C=标的资产的价格S; 最低:K→∞,T→0,买权的价格C=0.
期权价格 卖权
路漫漫其悠远
买权 市场价格
衡量标的资产价格变动的风险-delta(Δ)
delta=期权变动/标的资产价格的变动 N(d1)/N(-d1) 买权的delta为正值(大于0,小于1);卖权的delta为负值(大于-1,小 于0);平价期权的delta的绝对值为0.5。 随着标的资产价格上涨买权的delta趋近于1,卖权的delta趋近0,随着标 的资产价格的下跌,买权的delta趋近与0,卖权的delta趋近与-1.(相当于自 动加减仓位)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
in the money at the money out of the money
中国最庞大的数据库下载
Gamma
1. Gamma是期权的Delta对标的资产价格的偏导数, 也是期权价值对标的资产价格的二阶偏倒数
2 S S 2
2. Gamma度量了期权Delta对标的资产价格变化的敏 感性,也度量了期权价值对标的资产价格的凸性
中国最庞大的数据库下载
Vega
1. Vega是期权的价值对标的资产波动率的偏导数,度 量了期权价值对标的资产波动率的敏感性
Vega
2. Vega中性与Vega对冲
由于标的资产及其远期、期货合约的Vega都等于零, 因此,不能用来改变投资组合的Vega 要改变投资组合的Vega ,必须使用那些Vega不等于 零的工具,例如期权
第7章
期权的希腊字母
教学内容
1. Delta 2. Theta 3. Gamma 4. Vega 5. Rho 6. Portfolio Insurance
中国最庞大的数据库下载
希腊字母
1. 希腊字母度量期权的风险,用于期权头寸的风险管理
期权做市商 金融机构地期权交易员
2. 期权价值的决定因素包括股价、到期时间、波动率、 无风险利率以及执行价格,其中易变的因素有四个:
3. 例子:BSM随机微分方程的推导
1个单位衍生工具空头, f 份股票 S
BS采用Delta对冲方法,建立起包含期权的Delta中性 头寸
中国最庞大的数据库下载
Delta对冲——使用期货
1. 实践中,对冲工具多选用期货
期货流动性好、交易成本低
2. 符号
期货到期时间:T * Delta对冲需要的标的资产头寸:H A Delta对冲需要的期货头寸:H F
中国最庞大的数据库下载
Delta——其它欧式期权
1. 股指期权
c eqT N d1
2. 外汇期权
p eqT N d1 1
c erfT N d1
3. 期货期权
c erT N d1
4. 股票远期
p erfT N d1 1 p erT N d1 1
f S KerTt
1
中国最庞大的数据库下载
Delta——线性
考虑一个期权投资组合,其中所有期权的标的资产都 是同一种资产,则,组合的Delta等于每种期权的 Delta的线性和
n
wii i 1
其中,wi 表示组合包含第I中期权的数量
中国最庞大的数据库下载
3. 期货的Delta:
F0 S0erT erT
期货合约的Delta v.s. 远期合约的Delta
中国最庞大的数据库下载
Delta对冲——使用期货
1. Delta对冲需要的期货头寸
标的资产不分红
HF H AerT
标的资产为股票指数
HF H AerqT
标的资产为外汇
Delta对冲
中国最庞大的数据库下载
1. 定义:建立对冲工具头寸,使得对冲工具头寸与要保 护的头寸的Delta等于零
Delta中性:资产(或者组合)的Delta等于零
2. 动态对冲
由于资产的Delta通常是时间的函数,因此,为了实现 对冲目标,通常必须动态调整对冲工具头寸的数量
欧式股票期权的Gamma
c
p
N (d1 )
S0 T
中国最庞大的数据库下载
Gamma——欧式股票期权
Gamma与股价的关系
X
中国最庞大的数据库下载
Gamma——欧式股票期权
Gamma与到期时间的关系
in the money at the money out of the money
t 1 S2 2
3. Gamma中性与Gamma对冲
由于标的资产及其远期、期货合约的Gamma都等于零, 因此,不能用来改变投资组合的Gamma
要改变投资组合的Gamma,必须使用那些价格与标的 资产价格呈非线性关系的工具,例如期权
中国最庞大的数据库下载
Gamma——欧式股票期权
中国最庞大的数据库下载
Delta, Theta, Gamma的关系
1. 从BSM方程容易推导出三者的关系
t
rS
S
1
22S22 S 2来自rrS 1 2S 2 r
2
2. 如果投资组合是Delta中性的,则
1 2S2 r
2
如果Theta是较大的正数,Gamma就是很大的负数, 因此,Theta可以作为Gamma的替代指标使用
H F H Aerrf T
中国最庞大的数据库下载
Theta——定义
1. Theta是期权价值对时间的偏导数,度量了期权价值 随时间衰减的速度
t
2. 与股价呈随机波动不同,距离到期的时间是一个完全 确定的量,无需进行对冲
中国最庞大的数据库下载
Theta——欧式股票期权
Delta——欧式股票期权
1. 利用BS公式,可以推导出
c N d1
p N d1 1 0
2. Delta与股价的关系
1
X
中国最庞大的数据库下载
S(0)
Delta——欧式股票期权
Delta与到期时间的关系
at the money in the money out of the money
1. 欧式股票期权的Theta
买权
c
S0 N (d1 )
2T
rXerT N (d2 )
卖权
p
S0 N (d1 )
2T
rXerT N (d2 )
中国最庞大的数据库下载
Theta——欧式股票期权
Theta与股价的关系
X
中国最庞大的数据库下载
Theta——欧式股票期权
股价:Delta, Gamma 到期时间:Theta 波动率:Vega 无风险利率:Rho
中国最庞大的数据库下载
Delta
1. Delta是期权价值对标的资产价格的偏导数,度量了 期权价值对标的资产价格变化的敏感性
S
2. 图示
中国最庞大的数据库下载
S(0)
