正余弦定理和数列测试题
正弦定理和余弦定理

正弦定理和余弦定理一、选择题1.(2017·哈尔滨模拟)在△ABC中,AB=3,AC=1,B=30°,△ABC的面积为32,则C=( )A.30°B.45°C.60°D.75°解析法一∵S△ABC=12·AB·AC·sin A=32,即12×3×1×sin A=32,∴sin A=1,由A∈(0°,180°),∴A=90°,∴C=60°.故选C.法二由正弦定理,得sin BAC=sin CAB,即12=sin C3,sin C=32,又C∈(0°,180°),∴C=60°或C=120°.当C=120°时,A=30°,S△ABC =34≠32(舍去).而当C=60°时,A=90°,S△ABC =32,符合条件,故C=60°.故选C.答案 C2.在△ABC中,角A,B,C对应的边分别为a,b,c,若A=2π3,a=2,b=233,则B等于( )A.π3B.5π6C.π6或5π6D.π6解析∵A=2π3,a=2,b=233,∴由正弦定理a sin A=b sin B可得,sin B =b a sin A =2332×32=12.∵A =2π3,∴B =π6.答案 D3.(2017·成都诊断)在△ABC 中,cos 2B 2=a +c2c (a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( ) A.等边三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形解析 因为cos 2B 2=a +c2c,所以2cos 2B 2-1=a +c c -1,所以cos B =ac ,所以a 2+c 2-b 22ac =ac ,所以c 2=a 2+b 2.所以△ABC 为直角三角形. 答案 B4.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,则“a >b ”是“cos 2A <cos 2B ”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件D.既不充分也不必要条件解析 因为在△ABC 中,a >b ⇔sin A >sin B ⇔sin 2A >sin 2B ⇔2sin 2A >2sin 2B ⇔1-2sin 2A <1-2sin 2B ⇔cos 2A <cos 2B .所以“a >b ”是“cos 2A <cos 2B ”的充分必要条件. 答案 C5.(2016·山东卷)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =c ,a 2=2b 2(1-sin A ),则A =( )A.3π4B.π3C.π4D.π6解析 在△ABC 中,由b =c ,得cos A =b 2+c 2-a 22bc =2b 2-a 22b 2,又a 2=2b 2(1-sin A ),所以cos A =sin A ,即tan A =1,又知A ∈(0,π),所以A =π4,故选C. 答案 C 二、填空题6.(2015·重庆卷)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cos C =-14,3sin A =2sin B ,则c =________.解析 由3sin A =2sin B 及正弦定理,得3a =2b ,又a =2,所以b =3,故c 2=a 2+b 2-2ab cos C =4+9-2×2×3×⎝ ⎛⎭⎪⎫-14=16,所以c =4. 答案 47.(2017·江西九校联考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若角A ,B ,C 依次成等差数列,且a =1,b =3,则S △ABC =________. 解析 因为角A ,B ,C 依次成等差数列,所以B =60°.由正弦定理,得1sin A =3sin 60°,解得sin A =12,因为0°<A <180°,所以A =30°或150°(舍去),此时C =90°,所以S △ABC =12ab =32.答案328.(2016·北京卷)在△ABC 中,A =2π3,a =3c ,则bc=________. 解析 在△ABC 中,a 2=b 2+c 2-2bc ·cos A , 将A =2π3,a =3c 代入,可得(3c )2=b 2+c 2-2bc ·⎝ ⎛⎭⎪⎫-12,整理得2c 2=b 2+bc .∵c ≠0,∴等式两边同时除以c 2, 得2=⎝ ⎛⎭⎪⎫b c 2+b c ,可解得b c=1. 答案 1 三、解答题9.(2015·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC 的面积为315,b -c =2,cos A =-14.(1)求a 和sin C 的值; (2)求cos ⎝⎛⎭⎪⎫2A +π6的值.解 (1)在△ABC 中,由cos A =-14,可得sin A =154.由S △ABC =12bc sin A =315,得bc =24,又由b -c =2,解得b =6,c =4. 由a 2=b 2+c 2-2bc cos A ,可得a =8. 由a sin A=c sin C,得sin C =158. (2)cos ⎝ ⎛⎭⎪⎫2A +π6=cos 2A ·cos π6-sin 2A ·sin π6=32(2cos 2A -1)-12×2sin A ·cos A =15-7316. 10.(2015·全国Ⅱ卷)在△ABC 中,D 是BC 上的点,AD 平分∠BAC ,BD =2DC . (1)求sin Bsin C; (2)若∠BAC =60°,求∠B . 解 (1)由正弦定理得ADsin B =BDsin ∠BAD,AD sin C=DC sin ∠CAD.因为AD 平分∠BAC ,BD =2DC ,所以sin B sin C =DC BD =12. (2)因为∠C =180°-(∠BAC +∠B ),∠BAC =60°,所以 sin C =sin (∠BAC +∠B )=32cos B +12sin B .由(1)知2sin B =sin C ,所以tan B =33, 即∠B =30°.11.(2017·郑州调研)在△ABC 中,sin 2A ≤sin 2B +sin 2C -sin B sin C ,则A 的取值范围是( ) A.⎝⎛⎦⎥⎤0,π6B.⎣⎢⎡⎭⎪⎫π6,π C.⎝⎛⎦⎥⎤0,π3D.⎣⎢⎡⎭⎪⎫π3,π 解析 由已知及正弦定理有a 2≤b 2+c 2-bc , 由余弦定理可知a 2=b 2+c 2-2bc cos A ,于是b 2+c 2-2bc cos A ≤b 2+c 2-bc ,∴cos A ≥12,在△ABC 中,A ∈(0,π). 由余弦函数的性质,得0<A ≤π3. 答案 C12.在△ABC 中,三个内角A ,B ,C 所对的边分别为a ,b ,c ,若S △ABC =23,a +b =6,a cos B +b cos Ac=2cos C ,则c =( )A.27B.4C.2 3D.3 3解析 ∵a cos B +b cos Ac =2cos C ,由正弦定理,得sin A cos B +cos A sin B =2sin C cos C , ∴sin(A +B )=sin C =2sin C cos C ,由于0<C <π,sin C ≠0,∴cos C =12,∴C =π3,∵S △ABC =23=12ab sin C =34ab ,∴ab =8,又a +b =6,解得⎩⎨⎧a =2,b =4或⎩⎨⎧a =4,b =2,c 2=a 2+b 2-2ab cos C =4+16-8=12,∴c =23,故选C. 答案 C13.(2015·全国Ⅰ卷)在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是________.解析 如图所示,延长BA 与CD 相交于点E ,过点C 作CF ∥AD 交AB 于点F ,则BF <AB <BE .在等腰三角形CBF 中,∠FCB =30°,CF =BC =2, ∴BF =22+22-2×2×2cos 30°=6- 2. 在等腰三角形ECB 中,∠CEB =30°,∠ECB =75°,BE =CE ,BC =2,BE sin 75°=2sin 30°,∴BE =2 12×6+24=6+ 2. ∴6-2<AB <6+ 2. 答案 (6-2,6+2)14.设f (x )=sin x cos x -cos 2⎝ ⎛⎭⎪⎫x +π4.(1)求f (x )的单调区间;(2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若f ⎝ ⎛⎭⎪⎫A 2=0,a =1,求△ABC 面积的最大值.解 (1)由题意知f (x )=sin 2x 2-1+cos ⎝⎛⎭⎪⎫2x +π22=sin 2x 2-1-sin 2x 2=sin 2x -12.由-π2+2k π≤2x ≤π2+2k π,k ∈Z,可得-π4+k π≤x ≤π4+k π,k ∈Z ; 由π2+2k π≤2x ≤3π2+2k π,k ∈Z, 可得π4+k π≤x ≤3π4+k π,k ∈Z.所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤-π4+k π,π4+k π(k ∈Z);单调递减区间是⎣⎢⎡⎦⎥⎤π4+k π,3π4+k π(k ∈Z).(2)由f ⎝ ⎛⎭⎪⎫A 2=sin A -12=0,得sin A =12,由题意知A 为锐角,所以cos A =32. 由余弦定理a 2=b 2+c 2-2bc cos A , 可得1+3bc =b 2+c 2≥2bc ,即bc ≤2+3,且当b =c 时等号成立.因此12bc sin A ≤2+34.所以△ABC 面积的最大值为2+34.。
高三数学正弦定理试题答案及解析

高三数学正弦定理试题答案及解析1.在四边形ABCD中,AD⊥CD,AD=5,AB=7,∠BDA=60º,∠CBD=15º,求BC长.【答案】4【解析】利用已知条件及正余弦定理,即可求得BC的长.试题解析:在ΔABCD中,由余弦定理得AB2=AD2+BD2-2AD•BDcos60º,即BD2-5BD-24=0,解得BD=8.(6分)在ΔBCD中,由正弦定理得:.(12分)【考点】解三角形,正弦定理,余弦定理2.在中,内角A,B,C所对应的边分别为,若,则的值为()A.B.C.1D.【答案】D【解析】由正弦定理得:,又,所以选D.【考点】正弦定理3.如图,在平面四边形中,.(1)求的值;(2)若,,求的长.【答案】(1) (2)【解析】试题分析:(1)题目已知三角形的三条边,利用的余弦定理即可得到该角的余弦值.(2)利用(1)问得到的的余弦结合正余弦之间的关系即可求的该角的正弦值,再利用正余弦之间的关系即可得到,而与之差即为,则利用正弦的和差角公式即可得到角的正弦值,再利用三角形的正弦定理即可求的边长.(1)由关于的余弦定理可得,所以.(2)因为为四边形内角,所以且,则由正余弦的关系可得且,再由正弦的和差角公式可得,再由的正弦定理可得.【考点】三角形正余弦定理正余弦之间的关系与和差角公式4.在△ABC中,内角A,B,C所对的边分别为a,b,c,其中A=120°,b=1,且△ABC的面积为,则=()A.B.C.2D.2【答案】D【解析】S=bcsin120°=,即c×=,∴c=4,∴a2=b2+c2-2bccos120°=21,△ABC∴a=,∴由等比例性质得==2.5.△ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cosB=1,a=2c,则C=()A.或 B. C.或 D.【答案】B【解析】∵cos(A-C)+cosB=1,∴cos(A-C)-cos(A+C)=1,2sinA·sinC=1.又由已知a=2c,根据正弦定理,得sinA=2sinC,∴sinC=,∴C=或.∵a>c,∴A>C,∴C=.6.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC,则sinA-cos(B+)的最大值为()A.B.2C.D.2【答案】D【解析】由正弦定理得sinCsinA=sinAcosC.因为0<A<π,所以sinA>0,从而sinC=cosC.又cosC≠0,所以tanC=1,又0<C<π,故C=,于是sinA-cos(B+)=sinA-cos(π-A)=sinA+cosA=2sin(A+),又0<A<,所以<A+<,从而当A+=,即A=时,2sin(A+)取最大值2.7.已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c=.(1)若sinC=,求sinA的值;(2)设f(C)=sinCcosC-cos2C,求f(C)的取值范围.【答案】(1)(2)(-1,]【解析】解:(1)由正弦定理得=,∴sinA===.(2)在△ABC中,由余弦定理,得c2=b2+a2-2bacosC,∴3=b2+4-4bcosC,即b2-4cosC·b+1=0,由题知关于b的一元二次方程应该有解,令Δ=(4cosC)2-4≥0,得cosC≤- (舍去)或cosC≥,∴0<C≤.∴f(C)=sin2C-=sin(2C-)- (-<2C-≤),∴-1<f(C)≤.故f(C)的取值范围为(-1,].8.在中,已知,且.(1)求角和的值;(2)若的边,求边的长.【答案】(1),;(2).【解析】(1)利用并结合两角差的余弦公式求出,然后再结合的范围求出的值,利用三角形的内角和定理得到,最后再利用两角和的正弦公式求出的值;(2)在(1)的基础上直接利用正弦定理求出的长度.(1)由,,得且,可得,,,,,在中,,;(2)在中,由正弦定理得:,.【考点】1.两角和与差的三角函数;2.内角和定理;3.正弦定理9.(2013•湖北)在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.(1)求角A的大小;(2)若△ABC的面积S=5,b=5,求sinBsinC的值.【答案】(1)(2)【解析】(1)由cos2A﹣3cos(B+C)=1,得2cos2A+3cosA﹣2=0,即(2cosA﹣1)(cosA+2)=0,解得(舍去).因为0<A<π,所以.(2)由S===,得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故.又由正弦定理得.10.在中,角对的边分别为,已知.(1)若,求的取值范围;(2)若,求面积的最大值.【答案】(1);(2)【解析】(1)在中,角对的边分别为,已知,且.由正弦定理可用一个角B表示出b,c的值.再根据三角函数角的和差化一公式,以及角B范围.求出最值,再由三角形的三边的关系即可得到结论.(2)由,可得到三角形边b,c与角A的余弦值的关系式,即可得角A的正弦值.再由余弦定理通过放缩以及三角形的面积公式即可得到结论.(1),(2分)(4分).(6分)(2),(8分)(10分)当且仅当时的面积取到最大值为. . (12分)【考点】1.正余弦定理.2.三角形的面积公式.3.不等式的基本公式.3.最值的求法.11.在中,角所对的边分别为,点在直线上.(1)求角的值;(2)若,且,求.【答案】(1)角的值为;(2).【解析】(1)由正弦定理先化角为边,得到;再由余弦定理求得,所以角的值为;(2)先用二倍角公式化简,再结合正弦函数的性质可求角,由正弦定理知.试题解析:(1)由题得,由正弦定理得,即.由余弦定理得,结合,得.(2)因为因为,且所以所以,.【考点】正余弦定理、二倍角公式.12.设函数.(1)求的值域;(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若,求a的值.【答案】(1);(2).【解析】(1)根据两角和的余弦公式展开,再根据二倍角公式中的降幂公式展开,然后合并同类项,利用进行化简;利用三角函数的有界性求出值域.(2)若,,得到角的取值,方法一:可以利用余弦定理,将已知代入,得到关于的方程,方法二:利用正弦定理,先求,再求角C,然后利用特殊三角形,得到的值.试题解析:(1)4分因此的值域为[0,2]. 6分(2)由得,即,又因,故. 9分解法1:由余弦定理,得,解得. 12分解法2:由正弦定理,得. 9分当时,,从而; 10分当时,,又,从而. 11分故a的值为1或2. 12分【考点】两角和的余弦公式、二倍角公式、余弦定理、正弦定理.13.在锐角中,角、、所对的边分别为、、,若,且,则的面积为()A.B.C.D.【答案】A【解析】,,,又是锐角三角形,.选A.14.△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB.(1)求B;(2)若b=2,求△ABC面积的最大值。
正弦定理和余弦定理

正弦定理和余弦定理一、选择题1.在△ABC中,C=60°,AB=3,BC=2,那么A等于( ).A.135° B.105° C.45° D.75°2.已知a,b,c是△ABC三边之长,若满足等式(a+b-c)(a+b+c)=ab,则角C的大小为( ).A.60° B.90° C.120° D.150°3.在△ABC中,角A,B,C所对应的边分别为a,b,c,若角A,B,C依次成等差数列,且a=1,b=3,则S△ABC =().A. 2 B. 3 C.32D.24.在△ABC中,AC=7,BC=2,B=60°,则BC边上的高等于().A.32 B.332 C.3+62 D.3+3945.在△ABC中,角A、B、C的对边分别为a、b、c,且a=λ,b=3λ(λ>0),A=45°,则满足此条件的三角形个数是( ) A.0 B.1 C.2 D.无数个6.已知△ABC的面积为32,AC=3,∠ABC=π3,则△ABC的周长等于().A.3+ 3 B.3 3 C.2+ 3 D.33 2二、填空题7.如图,△ABC中,AB=AC=2,BC=23,点D在BC边上,∠ADC=45°,则AD的长度等于________.8.已知△ABC的三边长成公比为2的等比数列,则其最大角的余弦值为________.9.在Rt△ABC中,C=90°,且A,B,C所对的边a,b,c满足a+b=cx,则实数x的取值范围是________.10.若AB=2,AC=2BC,则S△ABC的最大值________.三、解答题11.在△ABC中,内角A,B,C的对边分别为a,b,c.已知cos A=23,sin B=5cos C.(1)求tan C的值;(2)若a=2,求△ABC的面积.12.在△ABC中,角A,B,C的对边分别为a,b,c,点(a,b)在直线x(sin A-sin B)+y sin B=c sin C 上.(1)求角C的值;(2)若a2+b2=6(a+b)-18,求△ABC的面积.13.在△ABC中,角A,B,C的对边分别为a,b,c.已知A=π4,b sin⎝⎛⎭⎪⎫π4+C-c sin⎝⎛⎭⎪⎫π4+B=a.(1)求证:B-C=π2;(2)若a=2,求△ABC的面积.。
第6讲 正弦定理和余弦定理

第6讲 正弦定理和余弦定理一、选择题1.(2016·哈尔滨模拟)在△ABC 中,AB =3,AC =1,B =30°,△ABC 的面积为32,则C =( ) A.30°B.45°C.60°D.75°解析 法一 ∵S △ABC =12·AB ·AC ·sin A =32, 即12×3×1×sin A =32,∴sin A =1,由A ∈(0°,180°),∴A =90°,∴C =60°.故选C.法二 由正弦定理,得sin B AC =sin C AB ,即12=sin C 3,sin C =32,又C ∈(0°,180°),∴C =60°或C =120°. 当C =120°时,A =30°,S △ABC =34≠32(舍去).而当C =60°时,A =90°,S △ABC =32,符合条件,故C =60°.故选C. 答案 C2.在△ABC 中,角A ,B ,C 对应的边分别为a ,b ,c ,若A =2π3,a =2,b =233,则B 等于( ) A.π3B.5π6C.π6或5π6D.π6解析 ∵A =2π3,a =2,b =233,∴由正弦定理a sin A =b sin B 可得, sin B =b a sin A =2332×32=12.∵A =2π3,∴B =π6. 答案 D3.(2017·成都诊断)在△ABC 中,cos 2B 2=a +c2c (a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( )A.等边三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形 解析 因为cos 2B2=a +c2c ,所以2cos 2B2-1=a +c c -1,所以cos B =ac ,所以a 2+c 2-b 22ac =ac ,所以c 2=a 2+b 2.所以△ABC 为直角三角形. 答案 B4.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,则“a >b ”是“cos 2A < cos 2B ”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件D.既不充分也不必要条件解析 因为在△ABC 中,a >b ⇔sin A >sin B ⇔sin 2A >sin 2B ⇔2sin 2A >2sin 2B ⇔1-2sin 2A <1-2sin 2B ⇔cos 2A <cos 2B .所以“a >b ”是“cos 2A <cos 2B ”的充分必要条件. 答案 C5.(2016·山东卷)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =c ,a 2=2b 2(1-sin A ),则A =( ) A.3π4B.π3C.π4D.π6解析 在△ABC 中,由b =c ,得cos A =b 2+c 2-a 22bc =2b 2-a 22b 2,又a 2=2b 2(1-sin A ),所以cos A =sin A ,即tan A =1,又知A ∈(0,π),所以A =π4,故选C. 答案 C二、填空题6.(2015·重庆卷)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cos C =-14,3sin A =2sin B ,则c =________.解析 由3sin A =2sin B 及正弦定理,得3a =2b ,又a =2,所以b =3,故c 2=a 2+b 2-2ab cos C =4+9-2×2×3×⎝ ⎛⎭⎪⎫-14=16,所以c =4.答案 47.(2017·江西九校联考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若角A ,B ,C 依次成等差数列,且a =1,b =3,则S △ABC =________. 解析 因为角A ,B ,C 依次成等差数列,所以B =60°.由正弦定理,得1sin A =3sin 60°,解得sin A =12,因为0°<A <180°,所以A =30°或150°(舍去),此时C =90°,所以S △ABC =12ab =32.答案 328.(2016·北京卷)在△ABC 中,A =2π3,a =3c ,则bc =________. 解析 在△ABC 中,a 2=b 2+c 2-2bc ·cos A ,将A =2π3,a =3c 代入,可得(3c )2=b 2+c 2-2bc ·⎝ ⎛⎭⎪⎫-12,整理得2c 2=b 2+bc .∵c ≠0,∴等式两边同时除以c 2,得2=⎝ ⎛⎭⎪⎫b c 2+bc ,可解得b c =1.答案 1 三、解答题9.(2015·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC 的面积为315,b -c =2,cos A =-14. (1)求a 和sin C 的值; (2)求cos ⎝ ⎛⎭⎪⎫2A +π6的值.解 (1)在△ABC 中,由cos A =-14, 可得sin A =154.由S △ABC =12bc sin A =315,得bc =24,又由b -c =2,解得b =6,c =4. 由a 2=b 2+c 2-2bc cos A ,可得a =8. 由a sin A =c sin C ,得sin C =158.(2)cos ⎝ ⎛⎭⎪⎫2A +π6=cos 2A ·cos π6-sin 2A ·sin π6 =32(2cos 2A -1)-12×2sin A ·cos A =15-7316.10.(2015·全国Ⅱ卷)在△ABC 中,D 是BC 上的点,AD 平分∠BAC ,BD =2DC . (1)求sin B sin C ;(2)若∠BAC =60°,求∠B . 解 (1)由正弦定理得AD sin B =BD sin ∠BAD ,AD sin C =DCsin ∠CAD .因为AD 平分∠BAC ,BD =2DC ,所以sin B sin C =DC BD =12. (2)因为∠C =180°-(∠BAC +∠B ),∠BAC =60°, 所以sin C =sin(∠BAC +∠B )=32cos B +12sin B .由(1)知2sin B =sin C ,所以tan B =33,即∠B =30°.11.(2017·广州调研)已知锐角三角形的边长分别为1,3,x ,则x 的取值范围是( ) A.(8,10) B.(22,10) C.(22,10)D.(10,8)解析 因为3>1,所以只需使边长为3及x 的对角都为锐角即可,故⎩⎪⎨⎪⎧12+x 2>32,12+32>x 2,即8<x 2<10.又因为x >0,所以22<x <10. 答案 B12.在△ABC 中,三个内角A ,B ,C 所对的边分别为a ,b ,c ,若S △ABC =23,a +b =6,a cos B +b cos Ac=2cos C ,则c =( )A.27B.4C.2 3D.3 3解析 ∵a cos B +b cos Ac =2cos C ,由正弦定理,得sin A cos B +cos A sin B =2sin C cos C , ∴sin(A +B )=sin C =2sin C cos C ,由于0<C <π,sin C ≠0,∴cos C =12,∴C =π3. ∵S △ABC =23=12ab sin C =34ab ,∴ab =8,又a +b =6,⎩⎪⎨⎪⎧a =2,b =4或⎩⎪⎨⎪⎧a =4,b =2,c 2=a 2+b 2-2ab cos C =4+16-8=12, ∴c =23,故选C. 答案 C13.(2015·全国Ⅰ卷)在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是________.解析 如图所示,延长BA 与CD 相交于点E ,过点C 作CF ∥AD 交AB 于点F ,则BF <AB <BE .在等腰三角形CBF 中,∠FCB =30°,CF =BC =2, ∴BF =22+22-2×2×2cos 30°=6- 2.在等腰三角形ECB 中,∠CEB =30°,∠ECB =75°, BE =CE ,BC =2,BE sin 75°=2sin 30°, ∴BE = 212×6+24=6+ 2.∴6-2<AB <6+ 2. 答案 (6-2,6+2) 14.设f (x )=sin x cos x -cos 2⎝ ⎛⎭⎪⎫x +π4. (1)求f (x )的单调区间;(2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若f ⎝ ⎛⎭⎪⎫A 2=0,a =1,求△ABC 面积的最大值.解 (1)由题意知f (x )=sin 2x2-1+cos ⎝ ⎛⎭⎪⎫2x +π22=sin 2x 2-1-sin 2x 2=sin 2x -12.由-π2+2k π≤2x ≤π2+2k π,k ∈Z,可得-π4+k π≤x ≤π4+k π,k ∈Z ; 由π2+2k π≤2x ≤3π2+2k π,k ∈Z,可得π4+k π≤x ≤3π4+k π,k ∈Z .所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤-π4+k π,π4+k π(k ∈Z ); 单调递减区间是⎣⎢⎡⎦⎥⎤π4+k π,3π4+k π(k ∈Z ).(2)由f ⎝ ⎛⎭⎪⎫A 2=sin A -12=0,得sin A =12,由题意知A 为锐角,所以cos A =32.由余弦定理a 2=b 2+c 2-2bc cos A , 可得1+3bc =b 2+c 2≥2bc ,即bc≤2+3,且当b=c时等号成立.因此12bc sin A≤2+34.所以△ABC面积的最大值为2+34.。
正弦定理和余弦定理-高考数学一轮复习基础练习试题训练

4.7 正弦定理和余弦定理A 组 基础题组1.在△ABC 中,a,b,c 分别为角A,B,C 所对的边,若a,b,c 成等差数列,∠B=30°,△ABC 的面积为32,则b=( )A.1+√32B.1+√3C.2+√32D.2+√3答案 B 由条件知12acsin B=32,得ac=6,又a+c=2b,则由余弦定理得b 2=a 2+c 2-2accos B=(a+c)2-2ac-√3ac,即b 2=4b 2-12-6√3,解得b 1=b 2=1+√3.2.如图,正三棱锥P-ABC 的所有棱长都为4.点D,E,F 分别在棱PA,PB,PC 上,则满足DE=EF=3,DF=2的△DEF 的个数是( )A.1B.2C.3D.4答案 C 令PD=x,PE=y,PF=z,则{x 2+x 2-xy =9,x 2+x 2-zy =9,x 2+x 2-xz =4,当x=z 时,{x =x =2,x =1+√6,当x≠z 时,有两解.3.(2017浙江镇海中学模拟)在△ABC 中,BC=2,AC=2√2,则A 的最大值是( ) A.30° B.45° C.60° D.90° 答案 B 由余弦定理,知cos A=x 2+8-42x ×2√2=14√2(x +4x )≥√22(当且仅当c=2时,取等号),故A 的最大值为45°,故选B.4.(2017浙江台州调研)在△ABC 中,内角A,B,C 的对边分别为a,b,c,已知a=1,2b-√3c=2acos C,sin C=√32,则△ABC 的面积为( ) A.√32 B.√34 C.√32或√34 D.√3或√32答案 C 由正弦定理知,2sin B-√3sin C=2sin Acos C,又sin B=sin(A+C)=sin Acos C+cos Asin C,所以cos A=√32,故A=30°.因为sin C=√32,所以C=60°或C=120°.当C=60°时,B=90°,由x sin x =xsin x,得c=√3,故S=12×√3×1×1=√32;当C=120°时,B=30°,此时b=a=1,故S=12×1×1×sin 120°=√34.故选C.5.(2018杭州高三期末)设点P 在△ABC 的BC 边所在的直线上从左到右运动,设△ABP 与△ACP 的外接圆面积之比为λ,当点P 不与B,C 重合时( )A.λ先变小再变大B.当M 为线段BC 中点时,λ最大C.λ先变大再变小D.λ是一个定值答案 D 设△ABP 与△ACP 的外接圆半径分别为r 1,r 2,则2r 1=xx sin∠xxx ,2r 2=xxsin∠xxx ,因为∠APB+∠APC=180°,所以sin∠APB=sin∠APC,所以x 1x 2=xxxx ,所以λ=x 12x 22=xx 2xx 2.故选D.6.已知a,b,c 分别为△ABC 的内角A,B,C 所对的边,其面积满足S △ABC =14a 2,则xx 的最大值为( ) A.√2-1 B.√2C.√2+1D.√2+2答案 C 根据题意,有S △ABC =14a 2=12bcsin A,应用余弦定理,可得b 2+c 2-2bccos A=2bcsin A,令t=xx ,于是t 2+1-2tcos A=2tsin A.于是2tsin A+2tcos A=t 2+1,所以2√2sin (x +π4)=t+1x ,从而t+1x ≤2√2,解得t的最大值为√2+1.7.(2017浙江测试)在△ABC 中,内角A,B,C 所对的边分别是a,b,c,若a=2√3,C=π3,tan A=34,则sinA= ,b= . 答案 35;4+√3解析 由tan A=34得sin A=35,cos A=45,由正弦定理,得c=sin xsin x a=5,又sin B=sin(A+C)=sin Acos C+cos Asin C,∴b=acos C+ccos A=4+√3.8.(2017浙江名校协作体)已知在△ABC 中,内角A,B,C 所对的边分别为a,b,c,S 为△ABC 的面积.若a=4,b=5,C=2A,则c= ,S= . 答案 6;15√74解析 由题意可知,x sin x =x sin x =x sin(π-3x )=xsin3x , 所以asin 3A=bsin A, 即4(3sin A-4sin 3A)=5sin A, 整理得7=16sin 2A, 从而cos 2A=916,即cos A=34.由正弦定理得,c=sin xsin x ·a=2cos A·a=6. ∴S=12bcsin A=12×5×6×√74=15√74. 9.(2018杭州七校高三联考)设△ABC 的三个内角A 、B 、C 所对的边依次为a 、b 、c,若△ABC 的面积为S,且S=a 2-(b-c)2,则sin x1-cos x = . 答案 4解析 因为△ABC 的面积为S,且S=a 2-(b-c)2=a 2-b 2-c 2+2bc=12bc·sin A, 所以由余弦定理可得-2bc·cos A+2bc=12bc·sin A, 所以4-4cos A=sin A, 所以sin x1-cos x =4-4cos x1-cos x =4.10.(2017浙江稽阳联谊学校联考)在△ABC 中,内角A,B,C 所对的边分别为a,b,c,已知csin A=√3acos C,则C= ;若c=√31,△ABC 的面积为3√32,则a+b= .答案π3;7解析 由正弦定理可得sin Csin A=√3sin Acos C, 因为sin A≠0,所以tan C=√3,所以C=π3. 由12absin C=3√32,得ab=6.又由余弦定理得(√31)2=a 2+b 2-2abcos C=(a+b)2-3ab, 所以a+b=7.11.(2017浙江台州质量评估)已知在△ABC 中,内角A,B,C 的对边分别为a,b,c,且b=√2a,√3cos B=√2cos A,c=√3+1,则△ABC 的面积为 . 答案√3+12解析 由√3cos B=√2cos A,得 √3·x 2+x 2-x 22xx =√2·x 2+x 2-x 22xx, 又b=√2a,c=√3+1,所以上式可化简为a 2=√3-√3+1c 2=2, 所以a=√2,b=2. 所以cos B=x 2+x 2-x 22xx=√22,所以sin B=√1-cos 2B =√22.故△ABC 的面积S=12acsin B=12×√2×(√3+1)×√22=√3+12. 12.(2017浙江宁波期末)已知△ABC 的三边分别为a,b,c,且a 2+c 2=b 2+ac,则边b 所对的角B 为 ;此时,若b=2√3,则xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ 的最大值为 . 答案π3;6+4√3解析 由余弦定理得cos B=x 2+x 2-x 22xx =12,∴B=π3,由正弦定理得c=x sin xsin x=4sin C. ∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =bccos A=8√3sin Ccos A,又C=2π3-A,∴xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =8√3(√32cos x +12sin x )cos A=12cos 2A+4√3·sin Acos A=6(1+cos 2A)+2√3sin 2A=6+4√3sin (2x +π3).∵0<A<2π3,∴π3<2A+π3<5π3,故当2A+π3=π2,即A=π12时,xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·xx ⃗⃗⃗⃗⃗⃗⃗⃗⃗ 有最大值,最大值为6+4√3.13.(2017浙江金华十校调研)在△ABC 中,内角A,B,C 所对的边分别为a,b,c,若2cos 2B=4cos B-3. (1)求角B 的大小;(2)若S △ABC =√3,asin A+csin C=5sin B,求b.解析 (1)2cos 2B-4cos B=-3⇒4cos 2B-4cos B+1=0,所以cos B=12,故B=π3.(2)S △ABC =√3=12acsin B ⇒ac=4. 由asin A+csin C=5sin B 得a 2+c 2=5b,由b 2=a 2+c 2-2accos B 得b 2-5b+4=0,解得b=1或4. 又a 2+c 2=5b≥2ac=8,所以b≥85,所以b=4.14.(2017湖州期末)在锐角△ABC 中,内角A,B,C 所对的边分别是a,b,c.已知sin Asin C=34,b 2=ac. (1)求角B 的值;(2)若b=√3,求△ABC 的周长.解析 (1)由b 2=ac 得,sin 2B=sin Asin C, 因为sin Asin C=34,所以sin 2B=34,因为sin B>0, 所以sin B=√32,因为三角形ABC 为锐角三角形,所以B=π3. (2)已知b=√3,则3=a 2+c 2-2accos π3 =a 2+c 2-ac=(a+c)2-3ac, 所以a+c=2√3,所以三角形ABC 的周长为3√3.15.已知f(x)=sin x·(cos x+sin x)-1,x∈R. (1)求函数f(x)的单调递减区间;(2)在锐角△ABC 中,内角A,B,C 所对的边分别为a,b,c,已知f(A)=0,a=1,求a 2+b 2+c 2的取值范围. 解析 (1)f(x)=sin xcos x+sin 2x-1=12sin 2x+1-cos2x2-1=√22sin (2x -π4)-12.令π2+2kπ≤2x -π4≤2kπ+3π2(k∈Z),得3π8+kπ≤x≤kπ+7π8(k∈Z).故函数f(x)的单调递减区间为[3π8+kπ,7π8+kπ](k∈Z).(2)由f(A)=0得sin (2x -π4)=√22.∵A∈(0,π2),∴2A -π4∈(-π4,3π4),∴2A -π4=π4,∴A=π4. 易得bc=(x sin x )2sin Bsin C=2sin Bsin C=cos(B-C)-cos(B+C)=cos(B-C)-cos(π-A)=√22+cos(B-C),又在锐角△ABC 中,A=π4,故B-C∈(-π4,π4),bc∈(√2,1+√22], 又cos A=x 2+x 2-x 22xx,∴b 2+c 2-a 2=√2bc, ∴a 2+b 2+c 2=√2bc+2∈(4,3+√2].B 组 提升题组1.(2018金华东阳二中高三调研)在△ABC 中,角A,B,C 所对的边分别为a,b,c,若3bcos A=ccos A+acos C,则tan A 的值是( )A.-2√2B.-√2C.2√2D.√2 答案 C 在△ABC 中,由余弦定理得ccos A+acos C=c×x 2+x 2-x 22xx +a×x 2+x 2-x 22xx=b.所以3bcos A=ccos A+acos C=b, 两边约去b,得3cos A=1,所以cos A=13>0,所以A 为锐角,且sin A=√1-cos 2A =2√23,因此,tan A=sin xcos x =2√2.2.若满足条件AB=√3,C=π3的三角形ABC 有两个,则边BC 的长的取值范围是( ) A.(1,√2) B.(√2,√3) C.(√3,2)D.(√2,2)答案 C 设BC=a,∵C=π3,AB=√3, 由正弦定理得xx sin x =xx sin x ,即√3√32=x sin x ,∴sin A=x 2. 由题意得,当A∈(π3,2π3)且A≠π2时,满足条件的△ABC 有两个,∴√32<x2<1,解得√3<a<2,即BC 的取值范围是(√3,2).3.(2017浙江镇海中学模拟)在锐角△ABC 中,内角A,B,C 的对边分别是a,b,c,且acos B+bcos A=c 2,C=π3,则a+b 的取值范围是( ) A.[1,2] B.(1,2]C.[√3,2]D.(√3,2]答案 D 由正弦定理,知sin Acos B+sin Bcos A=sin C·c,即sin(A+B)=csin C,所以c=1. 又x sin x =x sin x =xsin x ,所以a+b=(sin xsin x +sin xsin x )·c=√3sin x +sin (23π-x )]=√3(32sin x +√32cos x )=2sin (x +π6).因为{0<x <π2,0<23π-x <π2,所以π6<A<π2, 所以π3<A+π6<2π3,所以a+b∈(√3,2],故选D.4.(2017浙江绍兴质量检测)在△ABC 中,内角A,B,C 所对的边分别为a,b,c,已知A=π4,b=√6,△ABC 的面积为3+√32,则c= ,B= .答案 1+√3;π3解析 由三角形的面积公式,知3+√32=12×√6×√22×c,所以c=1+√3.由正弦定理得,sin x sin x =xx ,即sin (34π-x )sin x=x x ,所以√6·(√22cos x +√22sin x )=(1+√3)sin B, 所以√3cos B=sin B,即tan B=√3,所以B=π3.5.(2017浙江杭州二模)设a,b,c 分别为△ABC 的内角A,B,C 的对边,且S △ABC =12c 2.若ab=√2,则a 2+b 2+c 2的最大值是 . 答案 4解析 由S △ABC =12c 2,知12absin C=12c 2,所以c 2=√2sin C;由c 2=a 2+b 2-2abcos C,可知a 2+b 2=c 2+2abcos C=√2sin C+2√2cos C. 所以a 2+b 2+c 2=2√2(sin C+cos C)=4sin (x +π4)≤4,当且仅当C=π4时,取等号.故a 2+b 2+c 2的最大值为4.6.已知在△ABC 中,M,N 分别为AC,AB 的中点,|AB|∶|AC|=2∶3,当△ABC 在上述条件下变化时,若|BM|≤λ|CN|恒成立,则λ的最小值为 . 答案 78解析 设角A,B,C 的对边分别为a,b,c,不妨设c=2,b=3,a=x(1<x<5).易求得|BM|2=x 22+x 22-x 24,从而|BM|=√2x 2-12.同理,|CN|=√2x 2+142,∴λ≥√2x 2-12x 2+14(1<x<5),从而λ≥78.7.已知△ABC 的面积为1,∠A 的平分线交对边BC 于D,AB=2AC,且AD=kAC,k∈R,则当k= 时,边BC 的长度最短. 答案2√105解析 由题可设在△ABC 中,内角A,B,C 所对的边分别是a,b,c,则c=2b,AD=kb.由角平分线定理知,S △ACD =13=12sin x2·kb 2,又1=12b·2b·sin A,两式联立,消去b 2,得cos x 2=34k.又a 2=b 2+(2b)2-2×b×2bcos A=b 2(5-4cos A)=5-4cos x sin x,所以a 2sin A+4cos A=5,利用辅助角公式,知√x 4+16sin(A+φ)=5(tan x =4x 2),所以a 4+16≥25,即a 2≥3(当sin x =35,cos x =45时,取等号),此时cos x2=√1+cos x 2=3√1010,故k=43cosx 2=25√10.8.(2018浙江,13,6分)在△ABC 中,角A,B,C 所对的边分别为a,b,c.若a=√7,b=2,A=60°,则sin B= ,c= . 答案√217;3 解析 本题考查正弦定理、余弦定理. 由x sin x =x sin x 得sin B=xx sin A=√217, 由a 2=b 2+c 2-2bccos A,得c 2-2c-3=0,解得c=3(舍负).9.(2017杭州四校期中)在△ABC 中,内角A,B,C 的对边分别为a,b,c,已知cos 2A+32=2cos A.(1)求角A 的大小;(2)若a=1,求△ABC 的周长l 的取值范围. 解析 (1)由题意得2cos 2A+12=2cos A, 即4cos 2A-4cos A+1=0, ∴(2cos A -1)2=0,∴cos A=12.又∵0<A<π, ∴A=π3.(2)根据正弦定理x sin x =x sin x =xsin x ,得b=√3sin B,c=√3sin C,∴l=1+b+c=1+√3(sin B+sinC),∵A=π3,∴B+C=2π3,∴l=1+√3sin x +sin (2π3-B )]=1+2sin (x +π6),∵0<B<2π3,∴π6<B+π6<5π6,∴l∈(2,3].10.在△ABC 中,内角A,B,C 所对的边分别是a,b,c,已知c=2,C=π3. (1)若△ABC 的面积等于√3,求a,b;(2)若sin C+sin(B-A)=3sin 2A,求△ABC 的面积. 解析 (1)在△ABC 中,由余弦定理及三角形面积公式得 {4=x 2+x 2-ab,√3=12ab ×√32,即{4=x 2+x 2-ab,xx =4,解得a=b=2. (2)3sin 2A=sin C+sin(B-A) =sin(B+A)+sin(B-A),化简得6sin Acos A=2sin Bcos A,又A 为△ABC 的内角,所以cos A≠0,所以sin B=3sin A, 即b=3a,由余弦定理可得a 2=47,故△ABC 的面积S=12absin C=3a 2×√34=3√37. 11.(2017温州中学月考)在△ABC 中,角A,B,C 所对的边分别是a,b,c,且 a=2,2cos 2x +x2+sin A=45.(1)若满足条件的△ABC 有且只有一个,求b 的取值范围; (2)当△ABC 的周长取最大值时,求b 的值. 解析 由2cos2x +x2+sin A=45,得1+cos(B+C)+sin A=45,所以sin A-cos A=-15,又0<A<π,且sin 2A+cos 2A=1,所以{sin x =35,cos x =45.(1)若满足条件的△ABC 有且只有一个,则有a=bsin A 或a≥b, 则b 的取值范围为(0,2]∪{103}. (2)设△ABC 的周长为l,则l=a+b+c. 由正弦定理得l=a+xsin x(sin B+sin C) =2+103[sin B+sin(A+B)]=2+103(sin B+sin Acos B+cos Asin B) =2+2(3sin B+cos B) =2+2√10sin(B+θ),其中θ为锐角,且sin θ=√1010,cos θ=3√1010,所以l max =2+2√10,且当cos B=√1010,sin B=3√1010时取到. 此时b=xsin x sin B=√10.。
高三数学余弦定理试题答案及解析

高三数学余弦定理试题答案及解析1.在中,内角所对的边分别是.已知,,则的值为 .【答案】.【解析】∵,由正弦定理可知,,又∵,∴,∴.【考点】正余弦定理解三角形.2.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-sin A)cos B=0.(1)求角B的大小;(2)若a+c=1,求b的取值范围.【答案】(1)(2)≤b<1【解析】(1)由已知得-cos(A+B)+cos Acos B-sin A cos B=0,即有sin Asin B-sin Acos B=0.因为sin A≠0,所以sin B-cos B=0.又cos B≠0,所以tan B=.又0<B<π,所以B=.(2)由余弦定理,有b2=a2+c2-2accos B.因为a+c=1,cos B=,有b2=32+.又0<a<1,于是有≤b2<1,即有≤b<1.3.在中,内角A,B,C所对应的边分别为,若则的面积()A.3B.C.D.【答案】C【解析】因为所以由余弦定理得:,即,因此的面积为选C.【考点】余弦定理4.(12分)(2011•陕西)叙述并证明余弦定理.【答案】见解析【解析】先利用数学语言准确叙述出余弦定理的内容,并画出图形,写出已知与求证,然后开始证明.方法一:采用向量法证明,由a的平方等于的平方,利用向量的三角形法则,由﹣表示出,然后利用平面向量的数量积的运算法则化简后,即可得到a2=b2+c2﹣2bccosA,同理可证b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC;方法二:采用坐标法证明,方法是以A为原点,AB所在的直线为x轴建立平面直角坐标系,表示出点C和点B的坐标,利用两点间的距离公式表示出|BC|的平方,化简后即可得到a2=b2+c2﹣2bccosA,同理可证b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC.解:余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍;或在△ABC中,a,b,c为A,B,C的对边,有a2=b2+c2﹣2bccosA,b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC.证法一:如图,====b2﹣2bccosA+c2即a2=b2+c2﹣2bccosA同理可证b2=c2+a2﹣2cacosB,c2=a2+b2﹣2abcosC;证法二:已知△ABC中A,B,C所对边分别为a,b,c,以A为原点,AB所在直线为x轴建立直角坐标系,则C(bcosA,bsinA),B(c,0),∴a2=|BC|2=(bcosA﹣c)2+(bsinA)2=b2cos2A﹣2bccosA+c2+b2sin2A=b2+c2﹣2bccosA,同理可证b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC.点评:此题考查学生会利用向量法和坐标法证明余弦定理,以及对命题形式出现的证明题,要写出已知求证再进行证明,是一道基础题.5.如图所示,位于东海某岛的雷达观测站A,发现其北偏东,与观测站A距离海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北的C处,且,已知A、C两处的距离为10海里,则该货船的船速为海里/小时___________.【答案】【解析】由已知,所以,,由余弦定理得,,故(海里),该货船的船速为海里/小时.【考点】三角函数同角公式,两角和与差的三角函数,余弦定理的应用.6.△各角的对应边分别为,满足,则角的范围是( )A.B.C.D.【答案】A【解析】由得:,化简得:,同除以得,,即,所以,故选.【考点】余弦定理.7.在△ABC中,内角A,B,C所对的边分别是a,b,c,若a=4,A=,则该三角形面积的最大值是( )A.2B.3C.4D.4【答案】C【解析】由余弦定理得:a2=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc bc≤16,∴S=bcsinA≤×16×sin=4.8.在中,角,,所对的边分别为为,,,且(1)求角;(2)若,,求,的值.【答案】(1);(2)【解析】(1)将已知利用正弦二倍角公式展开,因为,约去,得的值,进而求;(2)已知三角形的面积和,不难想到,得,又根据余弦定理得,联立求即可.试题解析:(1)由已知,∴,∵,∴,∴.(2)由余弦定理,又, 10分由解得 13分【考点】1、正弦二倍角公式;2、三角形面积公式;3、余弦定理.9.已知外接圆的半径为,且.,从圆内随机取一个点,若点取自内的概率恰为,则的形状为( )A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形【答案】B【解析】由题意得所以.在三角形AOB中,由于,所以由余弦定理得,即,所以,的形状为等边三角形.【考点】几何概型概率,余弦定理10.在△ABC中,角A,B,C的对边分别为a,b,c.已知(1)求角A的大小;(2)若,△ABC的面积为,求.【答案】(1);(2)【解析】(1)三角恒等变换是以三角基本关系式,诱导公式,和、差、倍角等公式为基础的,三角变换的常见策略有:(1)发现差异;(2)寻找联系;(3)合理转化、概括.由题知,将展开,得,移项合并得,注意到,可求,进而求角A的大小;(2)由(1)知,结合△ABC的面积为,不难想到①,得关系;又根据,利用余弦定理得②,联立求.试题解析:(1)∵,∴可得,∴. 4分∵,可得.∴. 7分=∴,解得bc=8.① 10分(2)由(1)得.∵S△ABC由余弦定理,得, 12分即.②将①代入②,可得. 14分【考点】1、两角差的余弦公式;2、诱导公式;3、余弦定理.11.已知△ABC的角A、B、C所对的边分别是a、b、c,设向量m=(a,b),n=(sinB,sinA),p=(b-2,a-2).(1)若m∥n,求证:△ABC为等腰三角形;(2)若m⊥p,边长c=2,角C=,求△ABC的面积.【答案】(1)见解析(2)【解析】(1)证明:∵m∥n,∴asinA=bsinB,即a·=b·,其中R是△ABC外接圆半径,∴a=b.∴△ABC为等腰三角形.(2)解:由题意可知m·p=0,即a(b-2)+b(a-2)=0.∴a+b=ab.由余弦定理可知,4=a2+b2-ab=(a+b)2-3ab,即(ab)2-3ab-4=0,∴ab=4(舍去ab=-1),∴S=absinC=×4×sin=.12.△ABC中,角A,B,C所对的边分别为a,b,c,若C=,3a=2c=6,则b的值为( ) A.B.C.-1D.1+【答案】D【解析】因为3a=2c=6,所以a=2,c=3,由余弦定理知cos C=,即cos===,得b=1+.13.如果一个钝角三角形的边长是三个连续自然数,那么最长边的长度为()A.3B.4C.6D.7【答案】B【解析】设出三边的长度,然后由余弦定理,使其最长边所对的角的余弦值小于0即可得到边长的取值范围,再结合边长是自然数得到解.设三角形的三边长分别为n-1,n,n+1(n>1),则n+1对的角θ为钝角,由余弦定理得cosθ= ,所以(n-1)2+n2<(n+1)2,解得0<n<4,所以n=2,3.当n=2时,三边长为1,2,3,1+2=3,不符合题意.当n=3时,三边长为2,3,4,符合题意.故最长边的长度为4.14.已知函数的图像经过点.(1)求的值;(2)在中,、、所对的边分别为、、,若,且.求.【答案】(1)(2)sinB=【解析】(1)f(x)的图像经过点,带入函数得到关于的三角等式,再利用常见三角函数值与的范围即可求出的值.(2)利用三角形关于C角的余弦定理与题目已知式子结合即可得出C角的余弦值,进而得到C角的正弦值(三角形内角的正弦值都为正数),再把带入函数解析式即可得到A角的余弦,利用余弦与正弦的关系得到A角的正弦值,而三角形三个角和为180度,则B角的正弦利用和差角公式即可用A,C两个角的正余弦值来表示,进而得到B角的余弦值.试题解析:(1)由题意可得,即. 2分,,,. 5分(2),, 7分. 8分由(1)知,.,, 10分又,. 12分【考点】三角函数的图象与性质,三角恒等变换余弦定理15.在△ABC中,AB=5,AC=3,BC=7,则∠BAC=( )A.B.C.D.【答案】C【解析】由余弦定理有:.所以.【考点】余弦定理.16.在△ABC中,AB=2,AC=3,BC=4,则角A,B,C中最大角的余弦值为________.【答案】-【解析】根据三角形的性质:大边对大角,由此可知角A最大,由余弦定理得cos A==-17.已知的重心为G,内角A,B,C的对边分别为a,b,c,若,则角A为()A.B.C.D.【答案】A【解析】∵,∴,∴,∴,∴,∴.【考点】1.向量的运算;2.余弦定理.18.在△ABC中,∠ACB=60°,sin A∶sin B=8∶5,则以A,B为焦点且过点C的椭圆的离心率为________.【答案】【解析】设BC=m,AC=n,则=,m+n=2a,(2c)2=m2+n2-2mn cos 60°,先求得m=a,n=a,代入得4c2=a2,e=.19.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且23cos2A+cos 2A=0,a=7,c=6,则b=________.【答案】5【解析】由23cos2A+cos 2A=23cos2A+2cos2A-1=0,∴cos2A=,则cos A=.由a2=b2+c2-2bc cos A,得:72=b2+62-12b×,解之得b=5(舍去负值).20.在△ABC中,AB=2,AC=3,BC=4,则角A,B,C中最大角的余弦值为().A.-B.-C.D.【答案】A【解析】根据三角形的性质:大边对大角,由此可知角A最大,由余弦定理得cos A===-.21.在△中,,,,则△的面积等于()A.B.C.或D.或【答案】D【解析】由余弦定理,代入各值整理可得,解得,三角形面积,所以面积为或【考点】1.余弦定理;2.三角形的面积公式。
余弦定理40道基础题必练题含详解

利用余弦定理可求 ab 的值,从而可求三角形的面积.
【详解】
因为 C 120 ,故 c2 a2 b2 2ab cos120 a2 b2 ab ,
而 a b2 c2 4 ,故 c2 a2 b2 2ab 4 a2 b2 ab ,
故 ab 4 ,故三角形的面积为 1 ab sin120 3 4 3 ,
由余弦定理可得: cos A b2 c2 a2 16 36 28 1
2bc
246 2
又 A 0, 所以 A
3
故选:C
4.C
【分析】
答案第 1页,总 21页
利用余弦定理即可求解. 【详解】
在 ABC 中,若 b2 c2 a2 2bc ,
所以 cos A b2 c2 a2 2bc 2 ,
【详解】
依题意,由正弦定理得 c2 2a bb a b a ,
c2 2ab b2 a2 ab , a2 b2 c2 ab , a2 b2 c2 1 ,
2ab
2
即 cos C 1 .由于 0 C ,
2 所以 C 2 .
3
故选:C
3.C
【分析】
由余弦定理求解可得结果. 【详解】
则C ( )
A. 6
B.
或
2
33
C. 2 3
D.
6
或
5 6
3.在 ABC 中,若 AC 4 , AB 6 , BC 2 7 ,则 A ( )
A. 6
B.
4
C.
3
4.在 ABC 中,若 b2 c2 a2 2bc ,则 A ( )
D.
2
A. 90
B.150
C.135
正弦定理和余弦定理习题及答案

正弦定理和余弦定理测试题一、选择题:1.在△ABC中,a=15,b=10,A=60°,则 cos B=() 22226 A.-3 B.3C.-3D.6 32.在△ABC中,内角A,B,C的对边分别是a,b,c.若 a2-b2=3bc,sin C=23sin B,则A=()A.30°B.60°C.120°D.150°3.E,F是等腰直角△ABC斜边AB上的三平分点,则tan ∠ECF =()16233A. 27B. 3C.3D.4.△中,若-lg c ==-lg 2且∈ 0,π,则△ABC4ABC lg a lgsin B B2的形状是 ()A.等边三角形 B .直角三角形 C .等腰三角形 D .等腰直角三角形5.△ABC中,a、b、c分别为∠A、∠B、∠C的对边,假如a、b、c 成等差数列,∠ B=30°,△ ABC的面积为,那么 b 为()A.1+ 3B.3+ 3 C.3+ 3D.2+ 3 36.已知锐角A是△ABC的一个内角,a、b、c是三角形中各内角的对应边,若 sin2-cos2=1,则 ()A A2A.b+c=2a B .b+c<2a C.b+c≤2a D.b+c≥2a7、若ABC的内角A知足sin 2A 2,则 sin A cos A 3A.153 B.153C.5D.5338、假如A1 B1C1的三个内角的余弦值分别等于A2 B2C2的三个内角的正弦值,则A.A1B1C1和A2B2C2都是锐角三角形B.A1B1C1和A2 B2C2都是钝角三角形C.A1 B1C1是钝角三角形,A2 B2C2是锐角三角形D.A1B1C1是锐角三角形,A2 B2C 2是钝角三角形9、VABC的三内角A,B,C所对边的长分别为 a, b, c 设向量ur r ur rp (a c, b) , q (b a, c a) ,若 p // q ,则角C的大小为(A)(B)(C)(D)233 6210、已知等腰△ABC的腰为底的 2 倍,则顶角A的正切值是()A.3B. 3C.15D.15 28711、ABC的内角 A、B、C的对边分别为a、b、c,若 a、b、c 成等比数列,且 c2a ,则 cosBA .1B.3C .24 44D.2312、在△ABC中,角A、B、C的对边分别为a、b、c, A=, a= 3 , b=1,3则 c=(A)1(B)2(C)3—1(D)3二、填空题:13 、在ABC中,若sin A:sin B :sin C5:7:8 ,则B的大小是___________.14、在 ABC中,已知a 3 3,=,=°,则=.b 4 A30sinB415、在△ ABC中,已知 BC=12,A=60°, B=45°,则 AC=16、已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边 BC上的中线 AD的长为.三、解答题:11 17。
高三数学正弦定理试题答案及解析

高三数学正弦定理试题答案及解析1.在中,,则的面积等于___ __.【答案】【解析】由余弦定理得:.所以.【考点】解三角形.2.在中,的对边分别为且成等差数列.(1)求的值;(2)求的范围.【答案】(1);(2)【解析】(1)先利用等差中项的定义找出等量关系,再利用三角恒等变换化简求解;(2)先由(1)得,从而代入,转化为只含A的三角函数,利用三角公式将其化为的形式,再注意到,进而转化成三角函数求值域问题求解.试题解析:(1)由正弦定理得,,即:,.又在中,,.(2),所以,的范围是.【考点】1.等差数列的性质;2.正弦定理;3.三角函数的图象和性质.3.如图,为测量山高,选择和另一座山的山顶为测量观测点.从点测得点的仰角,点的仰角以及;从点测得.已知山高,则山高________.【答案】150【解析】根据题意,在中,已知,易得:;在中,已知,易得:,由正弦定理可解得:,即:;在中,已知,易得:.【考点】1.空间几何体;2.仰角的理解;3.解三角形的运用4.若的内角满足,则的最小值是 .【答案】【解析】由已知及正弦定理可得,,当且仅当即时等号成立.【考点】正弦定理与余弦定理.5.在△ABC中,2sin2=sinA,sin(B-C)=2cosBsinC,则=____________.【答案】【解析】2sin2=sinA⇔1-cosA=sinA⇔sin=,又0<A<π,所以<A+<,所以A+=,所以A=.再由余弦定理,得a2=b2+c2+bc①将sin(B-C)=2cosBsinC展开,得sinBcosC=3cosBsinC,所以将其角化边,得b·=3··c,即2b2-2c2=a2②将①代入②,得b2-3c2-bc=0,左右两边同除以bc,得-3×-1=0,③解③得=或=(舍),所以==.6.在△ABC中,角A,B,C所对应的边分别为a,b,c且c=3,a=2,a=2bsin A,则△ABC的面积为________.【答案】【解析】由题意知,bsin A=1,又由正弦定理得:bsin A=2sin B,故解得sin B=,所以△ABC的面积为acsin B=.7.设函数f(x)=cos+2cos2,x∈R.(1)求f(x)的值域;(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若f(B)=1,b=1,c=,求a的值.【答案】(1)[0,2] (2)1或2【解析】(1)f(x)=cos xcos -sin xsin +cos x+1=-cos x-sin x+cos x+1=cos x-sin x+1=sin+1,因此f(x)的值域为[0,2].(2)由f(B)=1得sin+1=1,即sin=0,又因0<B<π,故B=.方法一由余弦定理b2=a2+c2-2accos B,得a2-3a+2=0,解得a=1或2.方法二由正弦定理=,得sin C=,C=或.当C=时,A=,从而a==2;当C=时,A=,又B=,从而a=b=1.故a的值为1或2.8.已知分别为三个内角A、B、C的对边,若,则=_________.【答案】【解析】【考点】正弦定理和余弦定理.9.设函数.(1)求的值域;(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若,求a的值.【答案】(1);(2).【解析】(1)根据两角和的余弦公式展开,再根据二倍角公式中的降幂公式展开,然后合并同类项,利用进行化简;利用三角函数的有界性求出值域.(2)若,,得到角的取值,方法一:可以利用余弦定理,将已知代入,得到关于的方程,方法二:利用正弦定理,先求,再求角C,然后利用特殊三角形,得到的值.试题解析:(1)4分因此的值域为[0,2]. 6分(2)由得,即,又因,故. 9分解法1:由余弦定理,得,解得. 12分解法2:由正弦定理,得. 9分当时,,从而; 10分当时,,又,从而. 11分故a的值为1或2. 12分【考点】两角和的余弦公式、二倍角公式、余弦定理、正弦定理.10.已知向量,设函数(1)求函数的单调递增区间;(2)在中,角、、的对边分别为、、,且满足,,求的值.【答案】(1);(2)【解析】(1)利用数量积的坐标表示,先计算,然后代入中,利用正弦的二倍角公式和降幂公式,将函数解析式化为,然后利用复合函数的单调性和正弦函数的单调区间,求出函数的单调递增区间;(2)三角形问题中,涉及边角混合的式子,往往进行边角转换,或转换为边的代数式,或转换为三角函数问题处理.将利用正弦定理转换为,同时结合已知和余弦定理得,,从而求,进而求的值.试题解析:(1)令 6分所以所求增区间为 7分(2)由,, 8分,即 10分又∵, 11分 12分【考点】1、正弦定理;2、余弦定理;3、三角函数的图象和性质.11.的三个内角A,B,C所对的边分别为,则()A.B.C.D.【答案】B【解析】根据正弦定理可知,即,所以,选B.12.在ABC中,sin(C-A)=1,sinB=.(1)求sinA的值;(2)设AC=,求ABC的面积.【答案】(1)(2)【解析】(1)∵sin(C-A)=1且A,B,C为三角形之内角,∴C-A=,又C+A=-B,∴A=-∴sinA=sin(-)=(cos-sin),∴sin2A =(cos2+sin2-2sin cos)即,又,∴(2)如图,由正弦定理得∴,又∴13.已知函数.(1)求函数的最小正周期;(2)在中,若的值.【答案】(1)(2)【解析】(1)要得到的最小正周期,必须对进行化简,首先观察与之间的关系,可以发现,故利用诱导公式(奇变偶不变符号看象限)把,再利用正弦的倍角公式即可得到函数的最简形式,利用周期即可得到最小正周期.(2)把带入(1)得到的中,化简即可求的C角的大小,A角已知,所以可以求的C,A两个角的正弦值,利用正弦定理可得所求比值即为A,C两个角的正弦之比,带入即可求出.试题解析:(1)因为,所以函数的最小正周期为 6分(2)由(1)得,,由已知,,又角为锐角,所以,由正弦定理,得 12分【考点】诱导公式正弦定理周期正弦倍角公式14.在三棱锥中,,,,则与平面所成角的余弦值为.【答案】【解析】作PO⊥面ABC,垂足为O,连结AO,BO,CO,∴∠PBO是PB与面ABC所成的角,因,∴≌≌,∴AO=BO=CO,∴O是△ABC的外心,由正弦定理知,===12(R为△ABC外接圆半径),∴R=6,∴在Rt△POB中,∠BPO=30,∴∠PBO=,其余弦值为.【考点】1.正弦定理;2.线面角.15.已知函数.(1)若,求的取值范围;(2)设△的内角A、B、C所对的边分别为a、b、c,已知为锐角,,,,求的值.【答案】(1) (2)【解析】(1)首先利用正弦和差角公式展开,再利用正余弦的二倍角与辅助角公式化简,得到,则从x的范围得到的范围,再利用正弦函数的图像得到的取值范围,进而得到的取值范围.(2)把带入第(1)问得到的解析式,化简求值得到角A,再利用角A的余弦定理,可以求出a的值,再根据正弦定理,可以求的B角的正弦值,再利用正余弦之间的关系可以求的A,B的正余弦值,根据余弦的和差角公式即可得到的值.试题解析:(1).4分∵,∴,.∴. .7分(2)由,得,又为锐角,所以,又,,所以,. .10分由,得,又,从而,.所以, 14分【考点】三角形正余弦定理正余弦和差角与倍角公式正弦函数图像16.在△ABC中,A、B、C所对的边分别是a、b、c,且bcosB是acosC、ccosA的等差中项.(1)求B的大小;(2)若a+c=,b=2,求△ABC的面积.【答案】(1)B=(2)【解析】(1)由题意,得acosC+ccosA=2bcosB.由正弦定理,得sinAcosC+cosAsinC=2sinBcosB,即sin(A+C)=2sinBcosB.∵A+C=π-B,0<B<π,∴sin(A+C)=sinB≠0.∴cosB=,∴B=.(2)由B=,得=,即=,∴ac=2.∴S=acsinB=.△ABC17.已知函数,的最大值为2.(1)求函数在上的值域;(2)已知外接圆半径,,角所对的边分别是,求的值.【答案】(1);(2).【解析】本题主要考查三角函数的最值问题、函数的单调性、正弦定理等基础知识,同时考查运算转化能力和计算能力.第一问,利用最大值为,可以解出m的值,利用两角和的正弦公式化简,根据函数定义域求的值域;第二问,利用第一问的表达式,化简,再利用正弦定理将角转化成边,由,从而得到的值.试题解析:(1)由题意,的最大值为,所以. 2分而,于是,. 4分在上递增.在递减,所以函数在上的值域为; 5分(2)化简得. 7分由正弦定理,得, 9分因为△ABC的外接圆半径为.. 11分所以 12分【考点】1.两角和的正弦公式;2.正弦定理;3.三角函数值域.18.设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为()A.直角三角形B.锐角三角形C.钝角三角形D.不确定【答案】A【解析】由正弦定理,得sinBcosC+cosBsinC=sin2A,则sin(B+C)=sin2A,由三角形内角和定理及互为补角的诱导公式,得sin(B+C)=sin2A=1,所以A=,故选A.19.△ABC的内角A、B、C所对的边分别为a、b、c.若B=2A,a=1,b=,则c等于()(A)2 (B)2 (C) (D)1【答案】B【解析】由正弦定理,得=,∵B=2A,a=1,b=,∴==,∵sinA≠0,∴cosA=得A=,B=,C=.∴c==2.故选B.20.△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为()A.2+2B.+1C.2-2D.-1【答案】B【解析】由正弦定理知c==2.又sinA=sin(π-B-C)=sin(B+C)=sinBcosC+cosBsinC=,所以△ABC的面积S=bcsin A=+1.故选B.21.在中,角、、所对的边分别为、、,若,则为()A.B.C.D.【答案】B【解析】由于,故,所以,由正弦定理可得,故选B.【考点】1.二倍角公式;2.正弦定理22.在△ABC中,内角A,B,C所对的边分别是a,b,c,若C=120°,c=a,则() A.a>b B.a<bC.a=b D.a与b的大小关系不能确定【答案】C【解析】因为sin 120°=sin A,所以sin A=,则A=30°=B,因此a=b23.设△ABC的内角A,B,C所对的边分别为a,b,c且cos A=,cos B=,b=3,则c=________.【答案】【解析】因为cos A=,cos B=,所以sin A=,sin B=.由正弦定理得,即,所以a=.由余弦定理得b2=a2+c2-2accos B,即9=+c2-2c,解得c= (负值舍去).24.△ABC的三个内角A,B,C的对边分别a,b,c,且a cos C,b cos B,c cos A成等差数列,则角B等于()A.30°B.60°C.90°D.120°【答案】B【解析】由题意,得2b cos B=a cos C+c cos A,根据正弦定理可得2sin B cos B=sin A cos C+cos A sin C,即2sin B cos B=sin(A+C)=sin B,解得cos B=,所以B=60°25.在△ABC中,内角A,B,C所对的边分别是a,b,c.已知8b=5c,C=2B,则cos C等于________.【答案】【解析】先用正弦定理求出角B的余弦值,再求解.由,且8b=5c,C=2B,所以5c sin 2B=8c sin B,所以cos B=.所以cos C=cos 2B=2cos2B-1=.26.在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2cos B-sin(A-B)sin B+cos(A+C)=-.(1)求cos A的值;(2)若a=4,b=5,求向量在方向上的投影.【答案】(1)-(2)【解析】(1)由2cos2cos B-sin(A-B)sin B+cos(A+C)=-,得[cos(A-B)+1]cos B-sin(A-B)sin B-cos B=-,∴cos(A-B)cos B-sin(A-B)sin B=-.则cos(A-B+B)=-,即cos A=-.(2)由cos A=-,0<A<π,得sin A=,由正弦定理,有,所以,sin B=.由题知a>b,则A>B,故B=,根据余弦定理,有(4)2=52+c2-2×5c×,解得c=1或c=-7(舍去).故向量在方向上的投影为||cos B=.27.如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登800米方到达C处,则索道AC的长为______米.【答案】400【解析】如题图,在△ABD中,BD=400米,∠ABD=120°.因为∠ADC=150°,所以∠ADB=30°.所以∠DAB=180°-120°-30°=30°.由正弦定理,可得所以,得AD=400 (米).在△ADC中,DC=800米,∠ADC=150°,由余弦定理,可得AC2=AD2+CD2-2×AD×CD×cos∠ADC=(400)2+8002-2×400×800×cos 150°=4002×13,解得AC=400(米).故索道AC的长为400米.28.在△ABC中,角A,B,C对应的边分别是a,b,c.已知cos 2A-3cos(B+C)=1.(1)求角A的大小;(2)若△ABC的面积S=5,b=5,求sin B sin C的值.【答案】(1)A=(2)【解析】(1)由cos 2A-3cos(B+C)=1,得2cos2A+3cos A-2=0,即(2cos A-1)(cos A+2)=0,解得cos A=或cos A=-2(舍去).因为0<A<π,所以A=,(2)由S=bc sin A=bc·=bc=5,得bc=20.又b=5,知c=4.由余弦定理得a2=b2+c2-2bc cos A=25+16-20=21,故a=.又由正弦定理得sin B=sin A,sin C=sin A.∴sin B·sin C=sin2A=×=.29.在△ABC中,∠ABC=,AB=,BC=3,则sin ∠BAC=().A.B.C.D.【答案】C【解析】在△ABC中,由余弦定理得AC2=BA2+BC2-2BA·BC cos ∠ABC=()2+32-2××3cos =5.∴AC=,由正弦定理得sin ∠BAC=.30.已知函数f(x)=sin x cos x+cos 2x-,△ABC三个内角A,B,C的对边分别为a,b,c,且f(B)=1.(1)求角B的大小;(2)若a=,b=1,求c的值.【答案】(1)B=,(2)c=1【解析】(1)因为f(x)=sin 2x+cos 2x=sin ,所以f(B)=sin =1,又∈,所以2B+=,所以B=(2)法一由余弦定理b2=a2+c2-2ac cos B得c2-3c+2=0,所以c=1,或c=2.法二由正弦定理得sin A=,所以A=或A=,当A=时,C=,所以c=2;当A=时,C=,所以c=1.31.类比正弦定理,如图,在三棱柱ABC-A1B1C1中,二面角B-AA1-C,C-BB1-A,B-CC1-A的平面角分别为α,β,γ,则有________.【答案】==【解析】根据正弦定理得==,即==,而AA1=BB1=CC1,且EF·BB1=SBB1C1C,DF·CC1=SAA1C1C,DE·AA1=SAA1B1B,因此==32.在△ABC中,A=120°,AB=5,BC=7,则的值为().A.B.C.D.【答案】D【解析】由余弦定理,得BC2=AB2+AC2-2AB·AC·cos A,即72=52+AC2-10AC·cos 120°,∴AC=3.由正弦定理,得==.33.设锐角的三内角、、所对边的边长分别为、、,且,,则的取值范围为().A.B.C..D.【答案】A【解析】要求的范围,首先用正弦定理建立一个关系,,从而,因此我们只要确定出的取值范围,就可求出的取值范围了,,从而,又,,所以有,,所以.【考点】正弦定理,锐角三角形的判定.34.在中,角所对的边分别为,已知,(1)求的大小;(2)若,求的周长的取值范围.【答案】(1);(2).【解析】(1)本小题的突破口主要是抓住条件可使用正弦定理,得到,然后利用三角函数即可求得;(2)本小题首先通过正弦定理把三边用角表示出来,,然后把周长的问题转化为三角函数的值域求解问题;当然本小题也可采用余弦定理建立三边之间的关系,然后根据基本不等式求得,再根据三角形中两边之和大于第三边可得,于是,又,所以求得周长范围为.试题解析:(1)由条件结合正弦定理得,从而,∵,∴ 5分(2)法一:由正弦定理得:∴,, 7分9分∵ 10分∴,即(当且仅当时,等号成立)从而的周长的取值范围是 12分法二:由已知:,由余弦定理得:(当且仅当时等号成立)∴(,又,∴,从而的周长的取值范围是 12分【考点】1 正弦定理;2 余弦定理;3 基本不等式35.在中,角所对的边分别为满足,,, 则的取值范围是 .【答案】【解析】∵,∴,∴,∴为钝角,∵,∴,∴,∵,∴,,∴,∵,,∴,,∴.【考点】1.向量的数量积;2.余弦定理;3.正弦定理;4.三角函数的值域.36.已知中,角的对边分别为,且满足.(I)求角的大小;(Ⅱ)设,求的最小值.【答案】(I);(Ⅱ)当时,取得最小值为0.【解析】(I)利用正弦定理或余弦定理,将已知式化为:,再利用三角函数相关公式(两角和的正弦公式、诱导公式等),结合三角形内角和定理将其化简,即可求得角的大小;(Ⅱ)由已知及平面向量的数量积计算的坐标公式,可得的函数关系式:.由(I),,从而,只需求函数的最小值即可.试题解析:(I)由正弦定理,有, 2分代入得. 4分即.. 6分,. 7分. 8分(Ⅱ), 10分由,得. 11分所以,当时,取得最小值为0. 12分【考点】1.利用正弦定理、余弦定理解三角形;2.平面向量的数量积运算;3.三角函数的最值.37.已知a,b,c分别为△ABC的三个内角A,B,C的对边,=(sinA,1),=(cosA,),且∥.(1)求角A的大小;(2)若a=2,b=2,求△ABC的面积.【答案】(1);(II)△ABC的面积为或.【解析】(1)根据向量平行的坐标运算解答;(2)由(1)得出角A的大小,利用正弦定理计算,计算角大小,然后利用三角形中计算角,根据三角形面积公式解答即可.试题解析:(1) 4分(2)由正弦定理可得,,或. 6分当时,; 9分当时,. 11分故,△ABC的面积为或. 12分【考点】平面向量的坐标运算、正弦定理、解三角形、三角形面积公式.38.的角的对边分别为,已知.(Ⅰ)求角;(Ⅱ)若,,求的值.【答案】(Ⅰ) ;(Ⅱ) .【解析】(Ⅰ)先根据正弦定理将已知表达式:,全部转化为边的关系,然后根据余弦定理求出角的余弦值,结合特殊角的三角函数值以及三角形的内角求角;(Ⅱ)先根据三三角形的面积公式求出,然后根据余弦定理的变形,求得,将已知的与代入此式可解得.试题解析:(1)根据正弦定理,原等式可转化为:, 2分, 4分∴. 6分(Ⅱ),∴, 8分, 10分∴. 12分【考点】1.正弦定理;2.余弦定理及其变形;3.解三角形;4.三角形的面积公式;5.特殊角的三角函数值39.在中,角的对边分别为,已知.(1)求的值;(2)若,求和的值.【答案】(1);(2),;【解析】(1)本小题主要通过正弦定理得边角互化把条件转化为,然后利用余弦定理化简可得;(2)本小题通过展开得,然后根据正弦定理求得,.试题解析:(1)由正弦定理得由余弦定理得故 6分(2)故13分【考点】1.正弦定理;2.余弦定理.40.在中,角的对边分别为,,.(Ⅰ)求的值;(Ⅱ)求的值.【答案】(Ⅰ).(Ⅱ).【解析】(Ⅰ)根据已知条件,建立的方程组即可得解.(Ⅱ)应用余弦定理可首先.进一步应用正弦定理即得.试题解析:(Ⅰ)由和可得, 2分所以, 3分又所以. 5分(Ⅱ)因为,,由余弦定理可得 7分,即. 9分由正弦定理可得 11分, 12分所以. 13分【考点】正弦定理、余弦定理的应用,三角形面积.41.在△中,角的对边分别为,若,则等于.【答案】【解析】因为,,,所以,,由正弦定理得,.【考点】,三角函数同角公式,正弦定理.42.已知的三个内角满足,则角的取值范围是.【答案】.【解析】设的外接圆的半径为,则三个内角、、的对边分别为、、,由于,则有,即,故有,由余弦定理得,,当且仅当的时候,上式取等号,,,即角的取值范围是.【考点】正弦定理与余弦定理、基本不等式43.在中,内角的对边分别为.已知.(Ⅰ)求的值;(Ⅱ)若为钝角,,求的取值范围.【答案】(Ⅰ)3(Ⅱ)【解析】(I)由正弦定理,设则所以………………4分即,化简可得又,所以因此……………….6分(II)由得由题意,…10分……………………………………12分【考点】正余弦定理解三角形点评:正弦定理,余弦定理,,,两定理可以实现三角形中边与角的互相转化44.如图,在某港口处获悉,其正东方向20海里处有一艘渔船遇险等待营救,此时救援船在港口的南偏西据港口10海里的处,救援船接到救援命令立即从处沿直线前往处营救渔船.(Ⅰ) 求接到救援命令时救援船据渔船的距离;(Ⅱ)试问救援船在处应朝北偏东多少度的方向沿直线前往处救援?(已知).【答案】 (Ⅰ) 接到救援命令时救援船据渔船的距离为海里.(Ⅱ)救援船应沿北偏东的方向救援.【解析】本题考查正弦定理、余弦定理在三角形中的应用,注意方位角与计算的准确性,考查计算能力.(Ⅰ):△ABC中,求出边长AB,AC,∠CAB,利用余弦定理求出BC,即可求接到救援命令时救援船据渔船的距离;(Ⅱ)△ABC中,通过正弦定理求出sin∠ACB的值,结合已知数据,得到∠ACB即可知道救援船在C处应朝北偏东多少度的方向沿直线前往B处救援.解:(Ⅰ) 由题意得:中,,……………3分即,所以接到救援命令时救援船据渔船的距离为海里. (6)(Ⅱ)中, ,,由正弦定理得即………9分,,故救援船应沿北偏东的方向救援. …………… 12分45.在中,,,则 ( )A.B.C.或D.或【答案】C【解析】由正弦定理,,故B>A,所以或,选C46.在中,若,则角B为()A.B.C.D.【答案】B【解析】因为,所以.47.在△中,内角、、的对边分别为、、,已知,,,则.【答案】【解析】因为由正弦定理可知,得到sinB=,由于b<a,因此48.(本小题满分14分)中,角A,B,C的对边分别是且满足(1)求角B的大小;(2)若的面积为为,求的值;【答案】(1). ⑵a+c=.【解析】本试题主要是考查了解三角形中正弦定理和余弦定理的综合运用,求解边和角的关系,同时也考查了三角形面积公式的运用。
考点17 正余弦定理(讲解)(解析版)
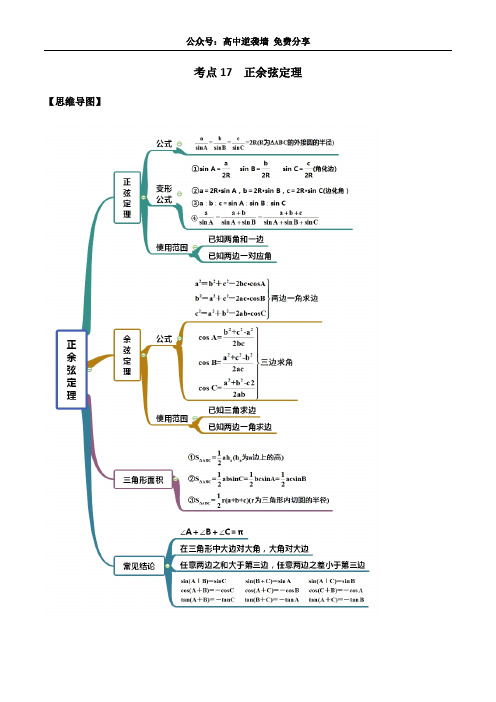
考点17 正余弦定理【思维导图】【常见考法】考法一:正余弦定理选择1.ABC ∆中,角,,A B C 所对的边分别为,,a b c.若3,60a b A ===︒,则边c = 。
【答案】4【解析】2222cos a c b cb A =+-213923cos60c c ⇒=+-⨯⨯︒,即2340c c --=,解得4c =或1c =-(舍去).2.在ABC中,2c =,75A =︒,45B =︒,则ABC 的外接圆面积为 。
【答案】4π 【解析】因为在ABC 中,75A =︒,45B =︒,所以60C =︒,又c =r,则21sin c r C ===,因此ABC 的外接圆面积为214S r ππ==.3.在△ABC 中,A =60°,asin sin sin a b cA B C++++等于 。
【解析】由正弦定理a b c sinA sinB sinC ==,a sinA=3∴sinA ,sinB ,sinC 则a b c sinA sinB sinC ++++=)3sinA sinB sinC sinA sinB sinC ++++=34.在△ABC 中,cos C2=55,BC =1,AC =5,则AB = 。
【答案】4 2【解析】因为cos C =2cos 2C2-1=2×⎝ ⎛⎭⎪⎫552-1=-35,所以c 2=a 2+b 2-2ab cos C =1+25-2×1×5×⎝ ⎛⎭⎪⎫-35=32,∴c =AB =42。
5.在△ABC 中,BC =2,AB =4,cos C =-14,则AC 的值为( ) 【答案】3【解析】△ABC 中,a =BC =2,c =AB =4,cos C =-14,∴c 2=a 2+b 2-2ab cos C ,即16=4+b 2-4b ×⎝ ⎛⎭⎪⎫-14,化简得b 2+b -12=0,解得b =3或b =-4(不合题意,舍去),∴b =AC =3.考法二:边角互换1.在△ABC 中,若a =2bsinA ,则角B 等于 。
高一数学正弦定理试题答案及解析

高一数学正弦定理试题答案及解析1. .若DABC中,,那么=()A.B.C.D.【答案】A【解析】由正弦定理得,设【考点】正弦定理,余弦定理2.在中,角对的边分别为,且.(1)求的值;(2)若,求的面积.【答案】(1);(2).【解析】(1)已知,根据正弦定理和合比定理求的值;(2)由余弦定理得出的值,再根据三角形的面积公式可求出的面积.试题解析:(1)因为,由正弦定理,得,∴;(2)∵,由余弦定理得,即,所以,解得或(舍去),所以.【考点】1、正弦定理;2、余弦定理;3、三角形面积公式.3.在△ABC中,AB=A=45°,C=60°,则BC= .【答案】.【解析】如图,根据正弦定理,,解得.【考点】正弦定理,特殊角的三角函数.4.中,已知,则三角形的形状为 .【答案】等腰或直角三角形【解析】中,,利用余弦定理把用边表示出来,带入原式得整理得,分组分解因式提取公因式,得,三角形的形状为等腰或直角三角形【考点】正余弦定理,三角形形状的判定5.已知圆心角为120°的扇形AOB的半径为1,C为弧的中点,点D,E分别在半径OA,OB上.若,则的最大值是 .【答案】【解析】在△COD中,由余弦定理得CD2=1+OD2-OD,同理在△EOC、△DOE中,由余弦定理分别得CE2=1+OE2-OE,DE2=OE2+OD2+OD·OE,代入整理得,由基本不等式得,所以,解得,即OD+OE的最大值是.【考点】正余弦定理,基本不等式.6.在△中,角,,所对的边分别为,,.(1)若,求角;(2)若,,且△的面积为,求的值.【答案】(1)(2)【解析】(1)将已知应用正弦定理转化为纯角的关系,并用将角C用角A,B表示,再注意到,从而可求得角A的三角函数值,从而得到角A的大小;(2)由于和△的面积为,可将用含量a的代数式表示出来,再由应用余弦定理就可将用含a的代数式表示,最后注意到,从而就可得到关于a的一个一元方程,解此方程就可得到a的值.试题解析:(1),由正弦定理可得.即.即,.注:利用直接得同样给分(2),的面积为,.,①由余弦定理,②由①,②得:,化简得,,(2)或解:由得①由得②由①,②得:,即,,..【考点】1.正弦定理和余弦定理;2.三角形的面积.7.在△ABC中,角A、B、C的对边分别为,∠A、∠B、∠C的大小成等差数列,且(1)若,求∠A的大小;(2)求△ABC周长的取值范围.【答案】(1)(2)【解析】(1)先由A,B,C成等差数列得,再利用正弦定理得,最后根据范围求出∠A的大小;(2)先由正弦定理得到,设周长为y,则y=,然后通过定义域,求出函数的值域,最后写出周长的取值范围.试题解析:(1)∵A,B,C成等差数列,∴解得又∵,,∴∴又∵∴(2)∵∴设周长为y,则∵∴∴∴∴周长的取值范围是【考点】等差数列的定义和性质;三角函数的恒等变换及化简求值;正弦定理的应用.8.在中,角、、所对的边分别为、、,满足.(1)求角;(2)求的取值范围.【答案】(1)(2)【解析】(1)要求角,只能从入手,利用正弦定理,将角化为边,得,进而可得三边关系,利用余弦定理即可求角.(2)从入手,欲找三边关系,用正弦定理将其化简为,将(1)的结论利用起来,代入,同时将代入,使得中只含有,进而根据,讨论的范围.试题解析:(1)根据正弦定理有:,化简得,根据余弦定理有, 所以.(2)根据正弦定理将化简,同时将(1)代入,化简为因为,,所以.故,的取值范围是【考点】正弦定理的应用(角化边);余弦定理;正弦差角;辅助角公式求范围.9.在△ABC中,角A,B,C的对边分别为,,,且.(1)求角的值;(2)若角,边上的中线=,求的面积.【答案】(1);(2).【解析】(1)首先可将条件中变形为,再利用正弦定理进行边角互化可得,再由中,可将等式继续化简为,从而;(2)由(1)及条件可得是等腰三角形,从而,再由边上的中线=,若设,则,可考虑在中采用余弦定理,即有,从而可进一步求得的面积:.试题解析:(1)∵,∴,由正弦定理得, 2分即, 4分∵,∴,∴,又∵,∴,∴; 7分(2)由(1)知,∴,, 8分设,则,又∵在中,由余弦定理:得即, 12分故. 14分【考点】1.三角恒等变形;2.正余弦定理解三角形.10.△ABC中,若,,则等于()A.B.C.D.2【答案】D【解析】由正弦定理得,a="2R" sin A,b=2RsinB,c=2RsinC,所以, .【考点】正弦定理的应用.11.若的三角,则A、B、C分别所对边=()A. B. C. D.【答案】C【解析】由及得,再由正弦定理得。
高三数学余弦定理试题答案及解析

高三数学余弦定理试题答案及解析1.在△ABC中,角A,B,C所对边的长分别为a,b,c.已知a+c=2b,sinB=sinC,则cosA=.【答案】【解析】因为sinB=sinC,由正弦定理得:,由余弦定理得:【考点】正余弦定理2.已知的三个内角所对的边分别为.若△的面积,则的值是。
【答案】4【解析】得得。
【考点】三角形面积公式、余弦定理、商数关系.3.某人先向正东方向走了x km,然后他向右转150°,向新的方向走了3 km,结果他离出发点恰好为km,那么x的值为()A.B.2C.2或D.3【答案】C【解析】根据余弦定理可得:()2=x2+32-2×3x×cos(180°-150°),即x2-3x+6=0.∴x=2或.4.如图,某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是()A.5(+) km B.5(-) kmC.10(-) km D.10(+) km【答案】C【解析】由题意,知∠BAC=60°-30°=30°,∠ABC=30°+45°=75°,∠ACB=180°-75°-30°=75°,∴AC=AB=40×=20(km).由余弦定理,得BC2=AC2+AB2-2AC·AB·cos∠BAC =202+202-2×20×20×cos30°=800-400=400(2-),∴BC===10 (-1)=10(-)(km).5.在中,三个内角A,B,C所对的边分别是a,b,c,且.(1)求角的大小;(2)求的取值范围.【答案】(1);(2).【解析】(1)根据余弦定理的推论,代入到条件中可得,所以有,进一步根据角B的范围求出B 的大小;(2)由(1)知:所以把化成只含角一个变量的三角函数,利用三角函数的最值求解.解:(1)由余弦定理可得:,即由得 5分(2)由得, 6分. 9分∵,∴, 10分∴, 11分∴的取值范围为. 12分【考点】1、余弦绽理及其推论;2、两角各与差的三角函数公式;3、三角函数的最值问题.6.(13分)(2011•天津)在△ABC中,内角A,B,C的对边分别为a,b,c,已知.(Ⅰ)求cosA的值;(Ⅱ)的值.【答案】(Ⅰ)(Ⅱ)【解析】(I)利用三角形中的等边对等角得到三角形三边的关系;利用三角形的余弦定理求出角A的余弦.(II)利用三角函数的平方关系求出角A的正弦,利用二倍角公式求出角2A的正弦,余弦;利用两个角的和的余弦公式求出的值.解:(I)由B=C,可得所以cosA==(II)因为所以=点评:本题考查三角形的余弦定理、考查三角函数的平方关系、考查两角和的余弦公式.7.在中,角A,B,C的对边分别为若,则角B的值为()A.B.C.D.【答案】D【解析】由得.故选.【考点】余弦定理的应用.8.(2013•浙江)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB=b.(Ⅰ)求角A的大小;(Ⅱ)若a=6,b+c=8,求△ABC的面积.【答案】(1)(2)【解析】(Ⅰ)由2asinB=b,利用正弦定理得:2sinAsinB=sinB,∵sinB≠0,∴sinA=,又A为锐角,则A=;(Ⅱ)由余弦定理得:a2=b2+c2﹣2bc•cosA,即36=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,∴bc=,又sinA=,则S=bcsinA=.△ABC9.在△ABC中,BC=,AC=1,以AB为边作等腰直角三角形ABD(B为直角顶点,C、D两点在直线AB的两侧).当变化时,线段CD长的最大值为.【答案】3【解析】设,,则在三角形BCD中,由余弦定理可知,在三角形ABC中,由余弦定理可知,可得,所以,令,则,当时等号成立.【考点】解三角形10.在△中,角、、所对的边长分别为、、,且.(1)若,,求的值;(2)若,求的取值范围.【答案】(1)或;(2).【解析】(1)已知两边,要求第三边,最好能求出已知两边的夹角,然后用余弦定理可求得,而由已知条件可得,从而可知,即,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为的形式,然后利用正弦函数的知识解决问题,,首先用二倍角公式,降幂公式把二次式化为一次式,再利用两角和的正弦公式把两个三角函数化为一个三角函数,,接下来我们只要把作为一个整体,求出它的范围,就可借助于正弦函数求出的取值范围了.试题解析:(1)在△中,.所以.,所以. 3分由余弦定理,得.解得或. 6分(2). 9分由(1)得,所以,,则. ∴.∴.∴的取值范围是. 12分【考点】(1)余弦定理;(2)二倍角公式与降幂公式,三角函数的取值范围11.在△ABC中,角A,B,C的对边分别为a,b,c,C=,a=5,△ABC的面积为10.(1)求b,c的值;(2)求cos的值.【答案】(1)c=7(2)=absinC,即10=b·5sin,解得b=8. 【解析】(1)由已知,C=,a=5,因为S△ABC由余弦定理可得:c2=25+64-80cos=49,所以c=7.(2)由(1)有cosB=,由于B是三角形的内角,易知sinB=,所以cos=cosBcos+sinBsin=.12.在锐角△ABC中,角A、B、C所对的边长分别为a、b、c.向量m=(1,cosB),n=(sinB,-),且m⊥n.(1)求角B的大小;(2)若△ABC面积为10,b=7,求此三角形周长.【答案】(1)(2)20【解析】(1)m·n=sinB-cosB,∵m⊥n,∴m·n=0,∴sinB-cosB=0.∵△ABC为锐角三角形,∴cosB≠0,∴tanB=.∵0<B<,∴B=.=acsinB=ac,由题设ac=10,得ac=40.由72=a2+c2-2accosB,得(2)∵S△ABC49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,∴三角形周长是20.13.在△ABC中,a=,b=1,c=2,则A=________.【答案】60°【解析】由余弦定理,得cosA=,∵0<A<π,∴A=60°14.在△ABC中,a、b、c分别为角A、B、C所对的边,若a=2bcosC,则此三角形一定是________三角形.【答案】等腰【解析】因为a=2bcosC,所以由余弦定理得a=2b·,整理得b2=c2,故此三角形一定是等腰三角形.15.设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为()A.4∶3∶2B.5∶6∶7C.5∶4∶3D.6∶5∶4【答案】D【解析】因为a,b,c为连续的三个正整数,且A>B>C,可得a=c+2,b=c+1;①又因为3b=20acosA,由余弦定理可知cosA=,则3b=20a·,②联立①②,化简可得7c2-13c-60=0,解得c=4或c=-(舍去),则a=6,b=5.又由正弦定理可得,sinA∶sinB∶sinC=a∶b∶c=6∶5∶4.故应选D.16.在△ABC中,a、b、c分别是角A、B、C的对边,B=,且sinA∶sinC=3∶1,则b∶c的值为.【答案】【解析】sinA∶sinC=a∶c=3∶1,∴a=3c.由余弦定理cos==,∴=,7c2=b2,∴=7,∴=.17.在△ABC中,AC=,BC=2,∠B=60°,则△ABC的面积等于.【答案】【解析】设角A、B、C的对边分别为a、b、c,由余弦定理,cosB==,即=,∴c2-2c-3=0,∴c=3或c=-1(舍).∴S=acsinB=.△ABC18.在△ABC中,a、b、c分别为角A、B、C的对边,若m=(sin2,1),n="(-2,cos" 2A+1),且m⊥n.(1)求角A的度数;(2)当a=2,且△ABC的面积S=时,求边c的值和△ABC的面积.【答案】(1) π (2)C=B【解析】解:(1)由于m⊥n,所以m·n=-2sin2+cos 2A+1=1-2cos2+2cos2A-1=2cos2A-cosA-1=(2cosA+1)(cosA-1)=0.所以cosA=-或1(舍去),即角A的度数为π.(2)由S=及余弦定理得tanC=,∴C==B.又由正弦定理=得c=2,所以△ABC的面积S=acsinB=.19.在中,、、分别是角A、B、C所对的边,,则的面积S=______.【答案】【解析】由角A的余弦定理得,因为,所以三角形ABC为直角三角形,则,故填.【考点】余弦定理勾股定理面积=2,则b等20.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=1,B=45°,S△ABC于()A.5B.25C.D.5【答案】A【解析】∵S=ac sin B=2,∴×1×c×sin 45°=2.∴c=4.∴b2=a2+c2-2ac cos B=1+32-2×1×4×cos 45°.∴b2=25,b=5.21.△ABC中内角A,B,C的对边分别为a,b,c,已知a=b cos C+c sin B.(1)求B;(2)若b=2,求△ABC面积的最大值.【答案】(1)B=(2)+1【解析】(1)由已知及正弦定理,得sin A=sin B cos C+sin C sin B,①又A=π-(B+C),故sin A=sin(B+C)=sin B cos C+cos B sin C.②由①,②和C∈(0,π)得sin B=cos B.又B∈(0,π),所以B=.(2)△ABC的面积S=ac sin B=ac.由已知及余弦定理,得4=a2+c2-2ac cos.又a2+c2≥2ac,故ac≤,当且仅当a=c时,等号成立.因此△ABC面积的最大值为+1.22.在△ABC中,a、b、c分别为角A、B、C的对边,4sin2-cos 2A=.(1)求角A的度数;(2)若a=,b+c=3,求△ABC的面积.【答案】(1)A=60°.(2)【解析】(1)∵B+C=π-A,即=,由4sin2-cos 2A=,得4cos2-cos 2A=,即2(1+cos A)-(2cos2A-1)=,整理得4cos2A-4cos A+1=0,即(2cos A-1)2=0.∴cos A=,又0°<A<180°,∴A=60°.(2)由A=60°,根据余弦定理cos A=,得=.∴b2+c2-bc=3,①又b+c=3,②∴b2+c2+2bc=9. ③①-③得bc=2. ④解②④得或∴S=×1×2×sin 60°=.△ABC23.如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A.+1B.2+2C.-1D.2-2【答案】D【解析】分别过点作的垂线,垂足分别为,连结,设,则=,等腰梯形的周长,令则,所以,,所以,当即, ,此时, ,因为为双曲线的焦点,点在双曲线上,所以实轴长.故选D.【考点】1、双曲线的定义;2、余弦定理;3、二次函数的最值问题.24.在△ABC中,角A,B,C所对的边分别为a,b,c.若,,,则()A.B.C.D.【答案】D【解析】∴,由余弦定理得,,所以.【考点】1、诱导公式;2、余弦定理.25.已知三角形的一边长为4,所对角为60°,则另两边长之积的最大值等于 .【答案】16【解析】设三角形的边长为其中,则,即,所以,即,当且仅当时取等号,所以两边长之积的最大值等于16.【考点】余弦定理的应用,基本不等式.26.在⊿ABC中,三边所对的角分别为A,B,C,若,则角C为()A.30°B.45°C.150°D.135°【答案】B【解析】由余弦定理得,,又,∴.【考点】余弦定理.27.在△的内角、、的对边分别为、、,若,,,则 .【答案】【解析】由余弦定理可知.【考点】余弦定理.28.在中,设内角的对边分别为,向量,向量,若(1)求角的大小;(2)若,且,求的面积.【答案】(1);(2)16【解析】(1)先计算的坐标,由得关于的方程,再利用辅助角公式化为,则,然后根据,得范围,从而求值,进而确定;(2)在中,,确定,另外两边的关系确定,所以利用余弦定理列方程求,再利用求面积.试题解析:(1)又因为,故,∴;(2)由余弦定理得,即,解得,∴,∴.【考点】1、向量的模;2、向量运算的坐标表示;3、余弦定理.29.在中,,,,则的面积为().A.B.C.D.【答案】D.【解析】因为为三角形的内角,所以,所以三角形的面积,选D.【考点】三角形面积公式.30.在中,角所对的边分别为满足,,,则的取值范围是 .【答案】【解析】由得,得为钝角,故,由正弦定理可知:,,所以.【考点】正余弦定理,辅助角公式.31.已知△ABC的内角A、B、C所对应边分别为a、b、c,若,则角C的大小是_______________(结果用反三角函数值表示)【答案】【解析】,故.【考点】考查余弦定理及运算,属容易题。
高二数学正弦定理试题答案及解析

高二数学正弦定理试题答案及解析1.在△ABC中,、、分别是角、、的对边,且.(Ⅰ)求角的大小;(Ⅱ)若,求△ABC的面积.【答案】(Ⅰ);(Ⅱ)【解析】(Ⅰ)利用正弦定理并化简得,又,所以,因为为三角形的内角,所以.(Ⅱ)将已知条件代入余弦定理得 ac=3,所以.试题解析:(Ⅰ)由正弦定理得将上式代入已知即即∵∵∵为三角形的内角,∴.(Ⅱ)将代入余弦定理得,∴∴.【考点】1.解三角形的正弦定理与余弦定理;2.三角形的面积公式2.已知a,b,c分别为△ABC三个内角A,B,C的对边,a2=b2+c2﹣bc.(Ⅰ)求A;(Ⅱ)若a=2,求bsinB+csinC的最大值.【答案】(Ⅰ);(Ⅱ)2【解析】(Ⅰ)利用余弦定理可解得cosA=,因此A=;(Ⅱ)由正弦定理可知2r==,所以bsinB+csinC=(b2+c2),又b2+c2﹣4=bc≤得b2+c2≤8,所以bsinB+csinC=(b2+c2)≤2,所求的最大值为2.试题解析:(Ⅰ)△ABC中,∵a2=b2+c2﹣bc,∴cosA==,∴A=.(Ⅱ)若a=2,则2r==,∴bsinB+csinC=(b2+c2).∵b2+c2﹣4=bc≤,∴b2+c2≤8,∴(b2+c2)≤2,即bsinB+csinC的最大值为2.【考点】1.正弦定理与余弦定理;2.基本不等式的应用3.在中,角所对的边分别为,已知,(1)求的大小;(2)若,求的取值范围.【答案】(1);(2).【解析】(1)由条件结合正弦定理,构建关于的方程,从而解出的值.(2)求的取值范围,通过正弦定理转化为角或角的三角函数,运用三角函数的知识解决问题,注意角的范围.在三角函数中求式子的取值范围,通常是运用正、余弦定理转化为某个角的三角函数来求范围,很少转化为某条边的代数函数来求范围的.试题解析:(1)由已知条件结合正弦定理有:,从而有:,.(2)由正弦定理得:,,,即:.【考点】1.解三角形;2.三角函数图象与性质.4.在△ABC中,设A、B、C的对边分别为a、b、c,向量,,若(1)求角A的大小;(2)若的面积.【答案】(1);(2)16.【解析】解题思路:(1)利用平面向量的模长公式将条件转化为,再结合角的范围求角A;(2)由正弦定理将边的关系化成角的正弦的关系,进而判定三角形的形状和求三角形的面积.规律总结:以平面向量为载体考查三角函数问题,体现了平面向量的工具性,要灵活选择平面向量知识合理化简,出现三角函数关系式;根据三角函数值求角的,要注意结合所给角的范围;解三角形要根据条件合理选择正弦定理、余弦定理、面积公式.试题解析:(1)又,,,为等腰三角形,.【考点】1.平面向量的模长;2.解三角形.5.中,,,则()A.B.C.D.【答案】C【解析】在中,由正弦定理可得即,所以,因为,,所以为锐角,所以由可得,所以,选C.【考点】正弦定理.6.在中,,则等于A.30°B.60°C.60°或120°D.30°或150【答案】C【解析】由正弦定理得:,∴,∴60°或120°.【考点】正弦定理.7.在中,角A.B.C所对的边分别是..,若,,则等于()A.B.C.D.【答案】B【解析】由正弦定理与题中条件可得即,而为三角形的内角,所以,所以,故选B.【考点】1.正弦定理;2.正弦的二倍角公式.8.辽宁广播电视塔位于沈阳市沈河区青年公园西侧,蜿蜒的南运河带状公园内,占地8000平方米.全塔分为塔座、塔身、塔楼和桅杆四部分.某数学活动小组在青年公园内的A处测得塔顶B处的仰角为45°. 在水平地面上,沿着A点与塔底中心C处连成的直线行走129米后到达D处(假设可以到达),此时测得塔顶B处的仰角为60°.(1)请你根据题意,画出一个ABCD四点间的简单关系图形;(2)根据测量结果,计算辽宁广播电视塔的高度(精确到1米).【答案】305米【解析】由题意知,,可用正弦定理求出或的边长,最后在或中用三角函数求的边长。
正弦定理与余弦定理练习题共3套(附答案)

正弦定理与余弦定理练习第一套正弦定理(一)●作业导航掌握正弦定理,会利用正弦定理求已知两角和任意一边或两边和一边对角的三角形问题.一、选择题(本大题共5小题,每小题3分,共15分)1.已知△ABC 中,a =4,b =43,∠A =30°,则∠B 等于()A .30°B .30°或150°C .60°D .60°或120°2.已知△ABC 中,AB =6,∠A =30°,∠B =120°,则△ABC 的面积为()A .9B .18C .93D .1833.已知△ABC 中,a ∶b ∶c =1∶3∶2,则A ∶B ∶C 等于()A .1∶2∶3B .2∶3∶1C .1∶3∶2D .3∶1∶24.已知△ABC 中,sin A ∶sin B ∶sin C =k ∶(k +1)∶2k (k≠0),则k 的取值范围为()A .(2,+∞)B .(-∞,0)C .(-21,0)D .(21,+∞) 5.在△ABC 中,sin A >sin B 是A >B 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件二、填空题(本大题共5小题,每小题3分,共15分)1.在△ABC 中,若∠B =30°,AB =23,AC =2,则△ABC 的面积是________.2.在△ABC 中,若b =2c sin B ,则∠C =________.3.设△ABC 的外接圆半径为R ,且已知AB =4,∠C =45°,则R =________.4.已知△ABC 的面积为23,且b =2,c =3,则∠A =________.5.在△ABC 中,∠B =45°,∠C =60°,a =2(3+1),那么△ABC 的面积为________.三、解答题(本大题共5小题,每小题6分,共30分)1.在△ABC 中,∠C =60°,BC =a ,AC =b ,a +b =16.(1)试写出△ABC 的面积S 与边长a 的函数关系式.(2)当a 等于多少时,S 有最大值?并求出这个最大值.2.在△ABC 中,已知a 2-a =2(b +c ),a +2b =2c -3,若sin C ∶sin A =4∶13,求a ,b ,c .3.在△ABC 中,求证2tan 2tanBA BA b a b a +-=+-.4.△ABC 中,A 、B 、C 成等差数列,b =1,求证:1<a +c ≤2.5.在一个三角形中,若有一个内角不小于120°,求证:最长边与最短边之比不小于3.参考答案一、选择题(本大题共5小题,每小题3分,共15分)1.D 分析:由正弦定理得,B bA a sin sin =,∴sin B =23sin =aA b ,∴∠B =60°或∠B =120°.2.C 分析:∵∠A =30°,∠B =120°,∴∠C =30°,∴BA =BC =6,∴S △ABC =21×BA ×BC ×sin B =21×6×6×23=93.3.A 分析:由正弦定理得,C cB b A a sin sin sin ==,∴sin A ∶sin B ∶sin C =1∶3∶2=21∶23∶1,∴A ∶B ∶C =30°∶60°∶90°=1∶2∶3.4.D 分析:利用正弦定理及三角形两边之和大于第三边.5.C 分析:A >B ⇔a >b ⇔2Rsin A >2Rsin B ⇔sin A >sin B .二、填空题(本大题共5小题,每小题3分,共15分)1.23或3分析:sin C =23230sin 32=︒,于是,∠C =60°或120°,故∠A =90°或30°,由S △ABC =21×AB ×AC ×sin A ,可得S △ABC =23或S △ABC =3.2.30°或150°分析:由b =2c sin B 及正弦定理C cB B c Cc B b sin sin sin 2sin sin ==得,∴sin C =21,∴∠C =30°或150°.3.22分析:∵c =2R sin C ,∴R =22sin 2=C c.4.60°或120°分析:∵S △ABC =21bc sin A ,∴23=21×2×3sin A ,∴sin A=23,∴∠A =60°或120°.5.6+23分析:∵B bA a sin sin =,∴︒=︒-︒-︒+45sin )6045180sin()13(2b,∴b =4.∴S △ABC =21ab sin C =6+23.三、解答题(本大题共5小题,每小题6分,共30分)1.解:(1)∵a +b =16,∴b =16-aS =21ab sin C =21a (16-a )sin60°=43(16a -a 2)=-43(a -8)2+163(0<a <16)(2)由(1)知,当a =8时,S 有最大值163.2.解:∵sin C ∶sin A =4∶13∴c ∶a =4∶13设c =4k ,a =13k ,则⎪⎩⎪⎨⎧-=++=-38213)4(213132k b k k b kk∵k =133时b <0,故舍去.∴k =1,此时a =13,b =2135-,c =4.3.证明:由正弦定理,知a =2R sin A ,b =2R sin B2tan2tan2cos 2sin 22cos 2sin 2)22sin(22sin()22sin()22sin(sin sin sin sin sin 2sin 2sin 2sin 2B A B A B A B A B A B A B A B A B A B A B A B A B A B A BA BA B R A R B R A R b a b a +-=-++-=--++-++--+--++=+-=+-=+-∴4.证明:∵A 、B 、C 成等差数列,∴2B =A +C ,又A +B +C =π,∴B =3π,A +C =32π.∵b =1,设△ABC 的外接圆半径为R ,∴b =2R sin 3π∴1=2R ·23,∴3R =1.∴a +c =2R sin A +2R sin C =2R (sin A +sin C )=2R [sin(32π-C )+sin C ]=2R (23cos C +23sin C )=23R (21cos C +23sin C )=23R sin(C +6π)=2sin(C +6π)∵A +C =32π,∴0<C <32π∴6π<C +6π<65π∴21<sin(C +6π)≤1∴1<2sin(C +6π)≤2 ∴1<a +c ≤2.5.证明:在△ABC 中,设C ≥120°,则c 最长,令最短边为a ,由正弦定理得A B A A C a c sin )sin(sin sin +==∵A ≤B∴2A ≤A +B ≤180°-C ≤60°∵正弦函数在(0,3π)上是增函数,∴sin(A +B )≥sin2A >0∴A B A a c sin )sin(+=≥A A A A A sin cos sin 2sin 2sin ==2cos A ∴a c≥2cos A ∵2A ≤60° ∴0°<A ≤30°∴cos A ≥cos30°=23∴a c ≥2·23∴a c≥3∴最长边与最短边之比不小于第二套正弦定理练习(二)1.在ABC ∆中,已知角04345,2,,3B c b ===则角A 的值是()A.15°B.75°C.105°D.75°或15°2.ABC ∆中,bsinA<a<b,则此三角形有()A.一解B.两解C.无解D.不确定3.若sin cos cos ,A B CABC a b c==∆则是()A.等边三角形B.有一内角是30°C.等腰直角三角形D.有一内角是30°的等腰三角形4.在ABC ∆中,已知0060,45,8,B C BC AD BC ===⊥于D,则AD 长为()A.4(31)- B.4(3+1)3+3)D.4(33)5.在ABC ∆中,A>B 是sinA>sinB 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在ABC ∆中,060,6,14B b a ===,则A=7.在ABC ∆ABC ∆中,已知cos 2cos 21sin 2sin cos ,cos sin B C A B C C B +=+==求证:b=c 且A=900。
人教B版高中数学必修五 1.1正弦定理和余弦定理(5必修)

1.1正弦定理和余弦定理(数学5必修)1.2应用举例1.3实习作业[基础训练A 组]一、选择题(六个小题,每题5分,共30分)1.在△ABC 中,若0030,6,90===B a C ,则b c -等于()A .1B .1-C .32D .32-2.若A 为△ABC 的内角,则下列函数中一定取正值的是()A .A sinB .A cosC .A tanD .Atan 1 3.在△ABC 中,角A 、B 均为锐角,且,sin cos B A >则△ABC 的形状是()A .直角三角形B .锐角三角形C .钝角三角形D .等腰三角形4.等腰三角形一腰上的高是3,这条高与底边的夹角为060,则底边长=()A .2B .23C .3D .32 5.在△ABC 中,若B a b sin 2=,则A 等于()A .006030或B .006045或C .0060120或D .0015030或6.边长为5,7,8的三角形的最大角与最小角的和是()A .090B .0120C .0135D .0150二、填空题(五个小题,每题6分,共30分)1. 在Rt △ABC 中,C=090,则B A sin sin 的最大值是_______________。
2.在△ABC 中,若=++=A c bc b a 则,222_________。
3.在△ABC 中,若====a C B b 则,135,30,200_________。
4.在△ABC 中,若sin A ∶sin B ∶sin C=7∶8∶13,则C=_____________。
5.在△ABC 中,,26-=AB ∠C=300,则AC+BC 的最大值是________。
三、解答题(四个小题,每题10分,共40分)1. 在△ABC 中,若,cos cos cos C c B b A a =+则△ABC 的形状是什么?2.在△ABC 中,求证:)cos cos (aA bB c a b b a -=-3.在锐角△ABC 中,求证:C B A C B A cos cos cos sin sin sin ++>++。
高三数学正弦定理试题

高三数学正弦定理试题1.在中,内角的对边分别为,且,.(1)求角的大小;(2)设边的中点为,,求的面积.【答案】(1);(2).【解析】(1)利用同角三角函数关系求得sinB的值,利用求得a和c的关系,进而利用正弦定理求得转化成角的正弦,利用两角和公式化简整理求得sinA和cosA的关系,求得tanA的值,进而求得A.(2)利用余弦定理求得c,进而求得b,最后根据三角形面积公式求得答案.试题解析:(1)由,得, 1分又,代入得,由,得, 2分,得, 4分(2), 5分,,则 7分9分【考点】1.正弦定理;2.余弦定理.2.中,分别为角的对边,满足.(Ⅰ)求角的值;(Ⅱ)若,设角的大小为的周长为,求的最大值.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)先已知根据余弦定理可求出角A的余弦值,然后可得到角A的值.(Ⅱ)先根据正弦定理用角B表示出边b,c,然后代入整理成的形式,注意角B的取值范围,再由正弦函数的性质可求最大值试题解析:(Ⅰ)在中,由及余弦定理得而,则;(Ⅱ)由及正弦定理得,同理∴∵∴,∴即时,.【考点】1.正弦定理与余弦定理;2.正弦函数的图象与性质.3.在中,角所对的边分别是,已知.(1)若的面积等于,求;(2)若,,求的面积.【答案】(Ⅰ)2,2(Ⅱ)【解析】(Ⅰ)由,运用余弦定理可得,由的面积等于,运用三角形面积公式可得,,联立即可解得;(Ⅱ)利用三角形内角和定理先将化为,利用诱导公式及两角和与差的正弦公式将上式化为,因为,若,求出A,B关系,利用正弦定理求出关系,结合(Ⅰ)中结果求出,从而求出三角形面积.试题解析:(Ⅰ)由余弦定理及已知条件得又,得 3分联立解得 5分(Ⅱ)由题意得,即,又9分的面积 12分【考点】正弦定理,余弦定理,三角形面积公式,三角变换,运算求解能力4.一艘海轮从处出发,以每小时20海里的速度沿南偏东40°方向直线航行.30分钟后到达处.在处有一座灯塔,海轮在处观察灯塔,其方向是南偏东70°,在处观察灯塔,其方向是北偏东65°,那么、两点间的距离是 .【答案】海里【解析】由已知,图中(海里),所以,,由正弦定理得,,即、两点间的距离是海里.所以答案应填:海里【考点】正弦定理的应用.5.[2014·广西模拟]在△ABC中,角A,B,C的对边分别为a,b,c,ac=3,且a=3bsinA,则△ABC的面积等于()A.B.C.1D.【答案】A【解析】∵a=3bsinA,∴由正弦定理得sinA=3sinBsinA.∴sinB=.∵ac=3,∴△ABC的面积S=acsinB=×3×=,故选A.6.如图所示,为了测量某湖泊两侧间的距离,李宁同学首先选定了与不共线的一点,然后给出了三种测量方案:(的角所对的边分别记为):①测量②测量③测量则一定能确定间距离的所有方案的序号为()A.①②B.②③C.①③D.①②③【答案】D【解析】①测量,因为知道,可求出,由正弦定理可求出;②测量,已知两边及夹角,可利用余弦定理可求出;③测量,因为知道,可求出,由正弦定理可求出,故三种方法都可以.【考点】解三角形.7.已知函数,.(1)求函数的最小正周期和单调递减区间;(2)已知中的三个内角所对的边分别为,若锐角满足,且,,求的面积.【答案】(1)最小正周期为,单调递减区间是,;(2).【解析】(1)首先应用三角函数公式,化简得到,从而得到其最小正周期为,由复合函数的单调性,由解得,函数的单调递减区间是,;(2)由已知,根据,求得.由正弦定理可得;应用余弦定理得:,求得,应用三角形面积计算公式即可得解.解得本题,巧妙地利用“整体观”,确定及,简化了解题过程.试题解析:(1)2分的最小正周期为 3分由得:,,的单调递减区间是, 6分(2)∵,∴,∴ 7分∵,∴.由正弦定理得:,即,∴ 9分由余弦定理得:,即,∴ 11分∴ 12分【考点】三角函数式的化简,三角函数的性质,正弦、余弦定理的应用,三角形面积公式.8.在△ABC中.Sin2A≤sin2B+sin2C-sinBsinC.则A的取值范围是()A.(0,] B.[,)C.(0,] D.[,)【答案】C【解析】由题意及正弦定理得a2≤b2+c2-bc bc≤b2+c2-a2≥1又由余弦定理知2cosA=≥1cosA≥因为角A为三角形内角,所以0<A≤9.在△ABC,内角A,B,C所对的边长分别为a,b,c.asinBcosC+csinBcosA=b且a>b,B= ()A.B.C.D.【答案】A【解析】因为asinBcosC+csinBcosA=b,由正弦定理得sinAsinBcosC+sinCsinBcosA=sinB,而sinB≠0,所以sinAcosC+sinCcosA=,即sin(C+A)=,也即sinB=所以B=或,又a>b,故B=10.△ABC的三内角A,B,C所对边长分别是a,b,c,设向量m=(a+b,sinC),n=(a+c,sinB-sinA),若m∥n,则角B的大小为()A.30°B.60°C.120°D.150°【答案】D【解析】∵m∥n,∴(a+b)(sinB-sinA)-sinC(a+c)=0,由正弦定理有(a+b)(b-a)=c(a+c),即a2+c2-b2=-ac,再由余弦定理得cosB=-,∴B=150°.11.在中,角的对边分别是,且,则等于()A.B.C.D.【答案】D【解析】,所以,.【考点】三角形的内角和,正弦定理.12.在中,内角所对的边分别为,其中,且面积为,则A.B.C.D.【答案】D【解析】利用三角形的面积公式表示出三角形ABC的面积,将sinA与b的值,以及已知面积代入求出c=4,再由b,c及cosA的值,利用余弦定理求出a的长,由a=与sinA的值,利用正弦定理求出三角形外接圆的半径R,利用正弦定理及比例的性质即可求出所求式子的值.【考点】正弦定理.13.在中,角、、所对的边分别为、、.已知.(1)求的大小;(2)如果,,求的值.【答案】(1);(2).【解析】(1)先根据条件结合余弦定理求出的值,从而求出的大小;(2)先利用同角三角函数的基本关系结合角的范围求出的值,最后利用正弦定理求解的值. 试题解析:(1)因为,所以,又因为,所以.(2)解:因为,,所以,由正弦定理,得.【考点】1.正弦定理与余弦定理;2.同角三角函数的基本关系14.在中,角、、所对的边分别为、、.已知.(1)求的大小;(2)如果,,求的面积.【答案】(1);(2).【解析】(1)先根据条件结合余弦定理求出的值,从而求出的大小;(2)先利用已知条件结合同角三角函数的基本关系求出的值,利用正弦定理求出的值,最后利用三角形的面积公式求出的面积.试题解析:(1)因为,所以,又因为,所以;(2)因为,,所以.由正弦定理,得.因为,所以,解得,因为,所以.故的面积.【考点】1.正弦定理与余弦定理;2三角形的面积公式15.在△中,三个内角,,所对的边分别为,,,若,则 .【答案】【解析】由正弦定理,,所以,即,∴【考点】1正弦定理;2余弦定理。
正弦定理和余弦定理习题及答案

正弦定理和余弦定理习题及答案正弦定理和余弦定理 测试题一、选择题:1.在△ABC 中,a =15,b =10,A =60°,则cos B =( )A .-223 B.223 C .-63D.632.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c .若a 2-b 2=3bc ,sin C =23sin B ,则A =( )A .30°B .60°C .120°D .150°3.E ,F 是等腰直角△ABC 斜边AB 上的三等分点,则tan ∠ECF =( )A.1627B.23C.33D.344.△ABC 中,若lg a -lg c =lgsin B =-lg 2且B ∈⎝ ⎛⎭⎪⎫0,π2,则△ABC的形状是( )A .等边三角形B .直角三角形C .等腰三角形D .等腰直角三角形5.△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,如果a 、b 、c 成等差数列,∠B =30°,△ABC 的面积为0.5,那么b 为( )A .1+ 3B .3+ 3 C.3+33D .2+ 36.已知锐角A 是△ABC 的一个内角,a 、b 、c 是三角形中各内角的对应边,若sin 2A -cos 2A =12,则( )A .b +c =2aB .b +c <2ªC .b +c ≤2aD .b +c ≥2a7、若ABC ∆的内角A 满足2sin 23A =,则sin cos A A +=15.15.53 D .53-8、如果111A B C ∆的三个内角的余弦值分别等于222A B C ∆的三个内角的正弦值,则A .111ABC ∆和222A B C ∆都是锐角三角形 B .111A B C ∆和222A B C ∆都是钝角三角形C .111A B C ∆是钝角三角形,222A B C ∆是锐角三角形D .111A B C ∆是锐角三角形,222A B C ∆是钝角三角形9、ABC 的三内角,,A B C 所对边的长分别为,,a b c 设向量(,)p a c b =+,(,)q b a c a =--,若//p q ,则角C 的大小为(A)6π (B)3π (C) 2π (D) 23π10、已知等腰ABC △的腰为底的2倍,则顶角A 的正切值是( ) A.323 C.158D.15720、已知ABC △21,且sin sin 2A B C +=.(I )求边AB 的长;(II )若ABC △的面积为1sin 6C ,求角C 的度数.21、△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知a ,b ,c 成等比数列,.43cos =B(Ⅰ)求cot A +cot C 的值; (Ⅱ)设32BA BC ⋅=,求a +c 的值.22、 某海轮以30海里/小时的速度航行,在A 点测得海面上油井P 在南偏东︒60,向北航行40分钟后到达B 点,测得油井P 在南偏东︒30,海轮改为北偏东︒60的航向再行驶80分钟到达C 点,求P 、C 间的距离.答案1.解析:依题意得0°<B <60°,由正弦定理得a sin A =bsin B得sin B =b sin A a =33,cos B =1-sin 2B =63,选D. 2.解析:由sin C =23sin B 可得c =23b ,由余弦定理得cos A =b 2+c 2-a 22bc =-3bc +c 22bc =32,于是A =30°,故选A. 3.解析:设AC =1,则AE =EF =FB =13AB =23,由余弦定理得CE =CF =AE 2+AC 2-2AC ·AE cos45°=53,所以cos ∠ECF =CE 2+CF 2-EF 22CE ·CF =45,所以tan ∠ECF =sin ∠ECF cos ∠ECF=1-⎝ ⎛⎭⎪⎫45245=34. 答案:D 4.解析:∵lg a -lg c =lgsin B =-lg 2,∴lg a c =lgsin B =lg 22.∴a c =sin B =22. ∵B ∈⎝⎛⎭⎪⎫0,π2,∴B =π4,由c =2a , 得cos B =a 2+c 2-b 22ac=3a 2-b 222a2=22. ∴a 2=b 2,∴a =b . 答案:D5.解析:2b =a +c ,12ac ·12=12⇒ac =2,a 2+c 2=4b 2-4,b 2=a 2+c 2-2ac ·32⇒b 2=4+233⇒b =3+33. 答案:C6.解析:由sin 2A -cos 2A =12,得cos2A =-12, 又A 是锐角,所以A =60°,于是B +C =120°. 所以b +c 2a =sin B +sin C2sin A=2sinB +C2cosB -C23=cosB -C2≤1,b +c ≤2a . 答案:c7.解:由sin2A =2sinAcosA >0,可知A 这锐角,所以sinA +cosA >0, 又25(sin cos )1sin 23A A A +=+=,故选A8.解:111A B C ∆的三个内角的余弦值均大于0,则111A B C ∆是锐角三角形,若222A B C ∆是锐角三角形,由211211211sin cos sin()2sin cos sin()2sin cos sin()2A A A B B B C C C πππ⎧==-⎪⎪⎪==-⎨⎪⎪==-⎪⎩,得212121222A A B B C C πππ⎧=-⎪⎪⎪=-⎨⎪⎪=-⎪⎩,那么,2222A B C π++=,所以222A B C ∆是钝角三角形。
2020年高考文科数学新课标第一轮总复习练习:3-7正弦定理和余弦定理含解析

课时规范练A组基础对点练1.(2016·高考全国卷Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.已知a=5,c=2,cos A=2 3,则b=(D)A. 2B. 3C.2 D.32.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b=(D)A.10 B.9C.8 D.53.钝角三角形ABC的面积是12,AB=1,BC=2,则AC=(B)A.5 B. 5 C.2 D.1解析:∵钝角三角形ABC的面积是12,AB=c=1,BC=a=2,∴S=12ac sin B=12,即sin B=22,当B为钝角时,cos B=-1-sin2B=-2 2,利用余弦定理得AC2=AB2+BC2-2AB·BC·cos B=1+2+2=5,即AC=5,当B为锐角时,cos B=1-sin2B=2 2,利用余弦定理得AC2=AB2+BC2-2AB·BC·cos B=1+2-2=1,即AC=1,此时AB2+AC2=BC2,即△ABC为直角三角形,不合题意,舍去,则AC= 5.故选B.4.在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin A cos C+cos A sin C,则下列等式成立的是(A)A.a=2b B.b=2aC.A=2B D.B=2A5.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且b sin A =3a cos B ,则B =( C ) A.π6 B.π4 C.π3D.π26.(2018·衡阳联考)已知△ABC 的三边长为三个连续的自然数,且最大内角是最小内角的2倍,则最小内角的余弦值是( B ) A.23 B.34 C.56D.710解析:设三边长依次是x -1,x ,x +1,其中x 是自然数,且x ≥2, 令三角形的最小角为A ,则最大角为2A , 由正弦定理,有x -1sin A =x +1sin 2A =x +12sin A cos A , ∴cos A =x +12(x -1),由余弦定理,有cos A =x 2+(x +1)2-(x -1)22x (x +1),∴x +12(x -1)=x 2+(x +1)2-(x -1)22x (x +1),即x +1x -1=x 2+4x x 2+x =x +4x +1, 整理得(x +1)2=(x -1)(x +4), 解得x =5, 三边长为4,5,6, 则cos A =52+62-422×5×6=34.7.(2018·西安模拟)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,且sin 2B =sin 2C ,则△ABC 的形状为( D ) A .等腰三角形 B.锐角三角形 C .直角三角形D.等腰直角三角形解析:因为b cos C +c cos B =a sin A ,所以由正弦定理得sin B cos C +sin C cos B =sin 2A , 所以sin(B +C )=sin 2A , 所以sin A =sin 2A .因为0<A<π,所以sin A≠0,所以sin A=1.所以A=π2.因为sin2B=sin2C,所以由正弦定理得b2=c2.因为b>0,c>0,所以b=c.所以△ABC是等腰直角三角形.综上所述,故选D.8.(2016·高考北京卷)在△ABC中,∠A=2π3,a=3c,则bc=__1__.9.在△ABC中,已知sin A∶sin B=2∶1,c2=b2+2bc,则三内角A,B,C的度数依次是__45°,30°,105°__.10.在△ABC中,A=30°,AB=4,满足此条件的△ABC有两解,则BC边长度的取值范围为__(2,4)__.解析:由正弦定理可得BCsin A=AB sin C,∴BC=AB·sin Asin C=2sin C,∵△ABC有两个解,∴30°<C<150°,且C≠90°,∴12<sin C<1,∴BC=2sin C∈(2,4).11.已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,BD=2,连接CD,则△BDC的面积是152,cos∠BDC=104.解析:如图,取BC中点E,DC中点F,由题意知AE ⊥BC ,BF ⊥CD . 在Rt △ABE 中,cos ∠ABE =BE AB =14, ∴cos ∠DBC =-14,sin ∠DBC =1-116=154.∴S △BCD =12×BD ×BC ×sin ∠DBC =152.∵cos ∠DBC =1-2sin 2∠DBF =-14,且∠DBF 为锐角,∴sin ∠DBF =104. 在Rt △BDF 中,cos ∠BDF =sin ∠DBF =104. 综上可得,△BCD 的面积是152,cos ∠BDC =104.12.四边形ABCD 的内角A 与C 互补,AB =1,BC =3,CD =DA =2. (1)求C 和BD ;(2)求四边形ABCD 的面积. 解析:(1)由题设及余弦定理得BD 2=BC 2+CD 2-2BC ·CD cos C =13-12cos C ,① BD 2=AB 2+DA 2-2AB ·DA cos A =5+4cos C .②由①②得cos C =12,故C =60°,BD =7. (2)四边形ABCD 的面积 S =12AB ·DA sin A +12BC ·CD sin C =⎝ ⎛⎭⎪⎫12×1×2+12×3×2sin 60° =2 3.13.△ABC 中,D 是BC 上的点,AD 平分∠BAC ,BD =2DC .(1)求sin B sin C ;(2)若∠BAC =60°,求∠B . 解析:(1)由正弦定理,得AD sin B =BD sin ∠BAD ,AD sin C =DCsin ∠CAD . 因为AD 平分∠BAC ,BD =2DC , 所以sin B sin C =DC BD =12.(2)因为∠C =180°-(∠BAC +∠B ),∠BAC =60°, 所以sin C =sin(∠BAC +∠B )=32cos B +12sin B. 由(1)知2sin B =sin C ,所以tan B =33,即∠B =30°.B 组 能力提升练1.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,已知8b =5c ,C =2B ,则cos C =( A ) A.725 B.-725 C .±725D.2425解析:由C =2B ,得sin C =sin 2B =2sin B cos B ,由正弦定理及8b =5c ,得cos B =sin C 2sin B =c 2b =45, 所以cos C =cos 2B =2cos 2B -1=2×⎝ ⎛⎭⎪⎫452-1=725.故选A.2.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若b 2+c 2-a 2=3bc ,且b =3a ,则下列关系一定不成立的是( B ) A .a =c B.b =c C .2a =cD.a 2+b 2=c 2解析:由余弦定理,得cos A =b 2+c 2-a 22bc =3bc 2bc =32,则A =30°.又b =3a ,由正弦定理得sin B =3sin A =3sin 30°=32,所以B =60°或120°.当B =60°时,△ABC 为直角三角形,且2a =c ,可知C ,D 成立;当B =120°时,C =30°,所以A =C ,即a =c ,可知A 成立,故选B.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若满足c =2,a cos C =c sin A 的△ABC 有两个,则边长BC 的取值范围是( D )A .(1,2) B.(1,3) C .(3,2)D.(2,2)解析:因为a cos C =c sin A ,由正弦定理得sin A cos C =sin C sin A ,易知sin A ≠0,故tan C =1,所以C =π4.过点B 作AC 边上的高BD (图略),垂足为D ,则BD =22BC ,要使满足条件的△ABC 有两个,则BC >2>22BC ,解得2<BC <2.故选D.4.在△ABC 中,已知2a cos B =c ,sin A sin B ·(2-cos C )=sin 2 C 2+12,则△ABC 为( D ) A .等边三角形 B.钝角三角形 C .锐角非等边三角形D.等腰直角三角形解析:由2a cos B =c ⇒2a ·a 2+c 2-b 22ac =c ⇒a 2=b 2, 所以a =b .因为sin A sin B (2-cos C )=sin 2 C 2+12,所以2sin A sin B (2-cos C )-2+1-2sin 2 C2=0,所以2sin A sin B (2-cos C )-2+cos C =0,所以(2-cos C )(2sin A sin B -1)=0,因为cos C ≠2,所以sin A sin B =12,因为a =b ,所以sin 2 A =12,所以A =B =π4,所以C =π2,所以△ABC 是等腰直角三角形,故选D.5.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a =2,且(2+b )(sin A -sin B )=(c -b )sin C ,则△ABC 面积的最大值为3 .解析:由正弦定理得(2+b )(a -b )=(c -b )c ,即(a +b )·(a -b )=(c -b )c ,即b 2+c 2-a 2=bc ,所以cos A =b 2+c 2-a 22bc =12,又A ∈(0,π),所以A =π3,又b 2+c 2-a 2=bc ≥2bc -4,当且仅当b =c =2时,等号成立,即bc ≤4,故S △ABC =12bc sin A ≤12×4×32=3,则△ABC 面积的最大值为 3.6.(2017·高考全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B =a cos C +c cos A ,则B = π3 .解析:由正弦定理可得2sin B cos B =sin A cos C +sin C cos A =sin(A +C )=sin B ⇒cos B =12⇒B =π3. 7.在△ABC 中,内角A ,B ,C 所对应的边分别为a ,b ,c ,若b sin A -3a cos B =0,且b 2=ac ,则a +cb 的值为__2__.解析:由题意及正弦定理得sin B sin A -3sin A cos B =0,因为sin A ≠0,所以sin B -3cos B =0,所以tan B =3,又0<B <π,所以B =π3.由余弦定理得b 2=a 2+c 2-2ac cos B =a 2+c 2-ac ,即b 2=(a +c )2-3ac ,又b 2=ac ,所以4b 2=(a +c )2,解得a +cb =2.8.(2018·高考北京卷)若△ABC 的面积为34(a 2+c 2-b 2),且∠C 为钝角,则∠B =__60°__;ca 的取值范围是__(2,+∞)__.解析:∵S △ABC =34(a 2+c 2-b 2)=12ac sin B , ∴a 2+c 2-b 22ac =sin B 3, 即cos B =sin B 3,∴sin B cos B =3,∠B =π3, 则c a =sin C sin A =sin ⎝ ⎛⎭⎪⎫2π3-A sin A =32cos A -⎝ ⎛⎭⎪⎫-12·sin A sin A =32·1tan A +12, ∴∠C 为钝角,∠B =π3,∴0<∠A <π6,∴tan A ∈⎝ ⎛⎭⎪⎫0,33,1tan A ∈(3,+∞),故ca ∈(2,+∞).9.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知cos 2B +cos B =1-cos A cos C . (1)求证:a ,b ,c 成等比数列; (2)若b =2,求△ABC 的面积的最大值.解析:(1)证明:在△ABC 中,cos B =-cos(A +C ). 由已知,得(1-sin 2B )-cos(A +C )=1-cos A cos C , ∴-sin 2B -(cos A cos C -sin A sin C )=-cos A cos C , 化简,得sin 2B =sin A sin C . 由正弦定理,得b 2=ac , ∴a ,b ,c 成等比数列. (2)由(1)及题设条件,得ac =4.则cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac ≥2ac -ac 2ac =12,当且仅当a =c 时,等号成立. ∵0<B <π,∴sin B =1-cos 2B ≤ 1-(12)2=32,∴S △ABC =12ac sin B ≤12×4×32= 3. 即△ABC 的面积的最大值为 3.10.(2018·海口调研)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知(a -3b )cos C =c (3cos B -cos A ). (1)求sin Bsin A 的值;(2)若c =7a ,求角C 的大小.解析:(1)由正弦定理,得(sin A -3sin B )cos C =sin C (3cos B -cos A ), ∴sin A cos C +cos A sin C =3sin C cos B +3cos C sin B , 即sin(A +C )=3sin(C +B ),即sin B =3sin A , ∴sin B sin A =3.(2)由(1)知b =3a ,∵c =7a ,∴cos C =a 2+b 2-c 22ab =a 2+9a 2-7a 22×a ×3a =3a 26a 2=12,又C ∈(0,π),∴C =π3.。
高中数学正弦定理与余弦定理习题及详解

高中数学正弦定理与余弦定理习题及详解一、选择题1.在△ABC 中,a 、b 、c 分别是三内角A 、B 、C 的对边,且sin 2A -sin 2C =(sin A -sin B )sin B ,则角C 等于( )A.π6B.π3C.5π6D.2π3 [答案] B[解析] 由正弦定理得a 2-c 2=(a -b )·b ,由余弦定理得cos C =a 2+b 2-c 22ab =12, ∵0<C <π,∴C =π3. 2.(文)(2010·泰安模拟)在△ABC 中,若A =60°,BC =43,AC =42,则角B 的大小为( )A .30°B .45°C .135°D .45°或135°[答案] B[解析] ∵AC ·sin60°=42×32=26<42<43,故△ABC 只有一解,由正弦定理得,42sin B =43sin60°, ∴sin B =22,∵42<43,∴B <A ,∴B =45°. (理)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,A =π3,a =3,b =1,则c =( ) A .1B .2 C.3-1D. 3[答案] B[解析] ∵b sin A =32<1<3,∴本题只有一解. ∵a =3,b =1,A =π3, ∴根据余弦定理,cos A =b 2+c 2-a 22bc =1+c 2-32c =12, 解之得,c =2或-1,∵c >0,∴c =2.故选B.3.在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,若a =2,b =22,且三角形有两解,则角A 的取值范围是( ) A.⎝⎛⎭⎫0,π4 B.⎝⎛⎭⎫π4,π2 C.⎝⎛⎭⎫π4,3π4D.⎝⎛⎭⎫π4,π3[答案] A[解析] 由条件知b sin A <a ,即22sin A <2,∴sin A <22, ∵a <b ,∴A <B ,∴A 为锐角,∴0<A <π4. [点评] 如图,AC =22,以C 为圆心2为半径作⊙C ,则⊙C上任一点(⊙C 与直线AC 交点除外)可为点B 构成△ABC ,当AB 与⊙C 相切时,AB =2,∠BAC =π4,当AB 与⊙C 相交时,∠BAC <π4,因为三角形有两解,所以直线AB 与⊙C 应相交,∴0<∠BAC <π4. 4.(2010·湖南理)在△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c .若∠C =120°,c =2a ,则( )A .a >bB .a <bC .a =bD .a 与b 的大小关系不能确定 [答案] A[解析] ∵∠C =120°,c =2a ,c 2=a 2+b 2-2ab cos C∴a 2-b 2=ab ,又∵a >0,b >0,∴a -b =ab a +b >0,所以a >b . 5.(文)(2010·天津理)在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,若a 2-b 2=3bc ,sin C =23sin B ,则A =( )A .30°B .60°C .120°D .150°[答案] A[解析] 由余弦定理得:cos A =b 2+c 2-a 22bc, ∵sin C =23sin B ,∴c =23b ,∴c 2=23bc ,又∵b 2-a 2=-3bc ,∴cos A =32, 又A ∈(0°,180°),∴A =30°,故选A.(理)(2010·山东济南)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为( )A.π6B.π3C.π6或5π6D.π3或2π3 [答案] D[解析] 由(a 2+c 2-b 2)tan B =3ac 得,a 2+c 2-b 2ac·tan B =3,再由余弦定理cos B =a 2+c 2-b 22ac 得,2cos B ·tan B =3,即sin B =32,∴角B 的值为π3或2π3,故应选D. 6.△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,如果a 、b 、c 成等差数列,∠B =30°,△ABC 的面积为0.5,那么b 为( )A .1+ 3B .3+ 3 C.3+33D .2+ 3[答案] C[解析] 12ac sin B =12,∴ac =2, 又2b =a +c ,∴a 2+c 2=4b 2-4,由余弦定理b 2=a 2+c 2-2ac cos B 得,b =3+33. 7.(2010·厦门市检测)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,若角A 、B 、C 依次成等差数列,且a =1,b =3,则S △ABC 等于( )A. 2B. 3C.32 D .2 [答案] C[解析] ∵A 、B 、C 成等差数列,∴B =60°,∵b sin B =a sin A ,∴sin A =a sin B b =1×323=12, ∴A =30°或A =150°(舍去),∴C =90°,∴S △ABC =12ab =32. 8.(2010·山师大附中模考)在△ABC 中,cos 2B 2=a +c 2c(a 、b 、c 分别为角A 、B 、C 的对边),则△ABC 的形状为( )A .直角三角形B .正三角形C .等腰三角形D .等腰三角形或直角三角形[答案] A [解析] ∵cos 2B 2=a +c 2c ,∴1+cos B 2=sin A +sin C 2sin C, ∴sin C cos B =sin A ,∴sin C cos B =sin(B +C ),∴sin B cos C =0,∵0<B ,C <π,∴sin B ≠0,cos C =0,∴C =π2,故选A. 9.(2010·四川双流县质检)在△ABC 中,tan A =12,cos B =31010,若最长边为1,则最短边的长为( ) A.455B.355C.255D.55[答案] D[解析] 由tan A >0,cos B >0知A 、B 均为锐角, ∵tan A =12<1,∴0<A <π4,cos B =31010>32, ∴0<B <π6,∴C 为最大角, 由cos B =31010知,tan B =13,∴B <A ,∴b 为最短边, 由条件知,sin A =15,cos A =25,sin B =110, ∴sin C =sin(A +B )=sin A cos B +cos A sin B=15×310+25×110=22, 由正弦定理b sin B =c sin C 知,b 110=122,∴b =55. 10.(2010·山东烟台)已知非零向量AB →,AC →和BC →满足⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|·BC →=0,且AC →·BC →|AC →|·|BC →|=22,则△ABC 为( ) A .等边三角形B .等腰非直角三角形C .直角非等腰三角形D .等腰直角三角形[答案] D[解析] ∵AC →·BC →|AC →|·|BC →|=cos ∠ACB =22, ∴∠ACB =45°,又∵⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|·BC →=0, ∴∠A =90°,∴△ABC 为等腰直角三角形,故选D.二、填空题11.(文)判断下列三角形解的情况,有且仅有一解的是________.①a =1,b =2,B =45°;②a =5,b =15,A =30°;③a =6,b =20,A =30°;④a =5,B =60°,C =45°.[答案] ①④[解析] ①一解,a sin B =22<1<2,有一解. ②两解,b ·sin A =152<5<15,有两解; ③无解,b ·sin A =10>6,无解.④一解,已知两角和一边,三角形唯一确定.(理)在锐角△ABC 中,边长a =1,b =2,则边长c 的取值范围是________.[答案] 3<c < 5[解析] 边c 最长时:cos C =a 2+b 2-c 22ab =1+4-c 22×1×2>0, ∴c 2<5.∴0<c < 5.边b 最长时:cos B =a 2+c 2-b 22ac =1+c 2-42c>0, ∴c 2>3.∴c > 3.综上,3<c < 5.12.(2010·上海模拟)在直角坐标系xOy 中,已知△ABC 的顶点A (-1,0),C (1,0),顶点B 在椭圆x 24+y 23=1上,则sin A +sin C sin B的值为________.[答案] 2[解析] 由题意知△ABC 中,AC =2,BA +BC =4,由正弦定理得sin A +sin C sin B =BC +BA AC=2. 13.(文)(2010·沈阳模拟)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,若b 2+c 2=a 2+bc ,且AC →·AB →=4,则△ABC 的面积等于________.[答案] 2 3[解析] ∵b 2+c 2=a 2+bc ,∴cos A =b 2+c 2-a 22bc =12, ∵AC →·AB →=4,∴b ·c ·cos A =4,∴bc =8,∴S =12AC ·AB sin A =12×bc ·sin A =2 3. (理)(2010·北京延庆县模考)在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =c=2b 且sin B =45,当△ABC 的面积为32时,b =________. [答案] 2[解析] ∵a +c =2b ,∴a 2+c 2+2ac =4b 2(1)∵S △ABC =12ac sin B =25ac =32,∴ac =154(2) ∵sin B =45,∴cos B =35(由a +c =2b 知B 为锐角), ∴a 2+c 2-b 22ac =35,∴a 2+c 2=92+b 2(3) 由(1)、(2)、(3)解得b =2.14.(2010·合肥市质检)在△ABC 中,sin A -sin B sin (A +B )=2sin A -sin C sin A +sin B,则角B =________. [答案] π4[解析] 依题意得sin 2A -sin 2B =sin(A +B )(2sin A -sin C )=2sin A sin C -sin 2C , 由正弦定理知:a 2-b 2=2ac -c 2, ∴a 2+c 2-b 2=2ac ,由余弦定理知:cos B =a 2+c 2-b 22ac =22, ∴B =π4. 三、解答题15.(文)(2010·广州六中)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足cos A 2=255,AB →·AC →=3. (1)求△ABC 的面积;(2)若b +c =6,求a 的值.[解析] (1)∵cos A 2=255, ∴cos A =2cos 2A 2-1=35,sin A =45. 又由AB →·AC →=3得,bc cos A =3,∴bc =5,∴S △ABC =12bc sin A =2. (2)∵bc =5,又b +c =6,∴b =5,c =1或b =1,c =5,由余弦定理得a 2=b 2+c 2-2bc cos A =20,∴a =2 5.(理)(2010·山东滨州)已知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角,向量m =(sin A ,sin B ),n =(cos B ,cos A ),且m ·n =sin2C .(1)求角C 的大小;(2)若sin A ,sin C ,sin B 成等差数列,且CA →·(AB →-AC →)=18,求边c 的长.[解析] (1)m ·n =sin A ·cos B +sin B ·cos A =sin(A +B ).在△ABC 中,由于sin(A +B )=sin C .∴m ·n =sin C .又∵m ·n =sin2C ,∴sin2C =sin C ,∴2sin C cos C =sin C .又sin C ≠0,所以cos C =12.而0<C <π,因此C =π3. (2)由sin A ,sin C ,sin B 成等差数列得,2sin C =sin A +sin B ,由正弦定理得,2c =a +b .∵CA →·(AB →-AC →)=18,∴CA →·CB →=18.即ab cos C =18,由(1)知,cos C =12,所以ab =36. 由余弦定理得,c 2=a 2+b 2-2ab cos C=(a +b )2-3ab .∴c 2=4c 2-3×36,∴c 2=36.∴c =6.16.(文)在△ABC 中,已知AB =3,BC =2.(1)若cos B =-36,求sin C 的值; (2)求角C 的取值范围. [解析] (1)在△ABC 中,由余弦定理知,AC 2=AB 2+BC 2-2AB ·BC ·cos B=3+4-2×23×⎝⎛⎭⎫-36=9. 所以AC =3.又因为sin B =1-cos 2B =1-⎝⎛⎭⎫-362=336, 由正弦定理得AB sin C =AC sin B. 所以sin C =AB AC sin B =116. (2)在△ABC 中,由余弦定理得,AB 2=AC 2+BC 2-2AC ·BC cos C ,∴3=AC 2+4-4AC ·cos C ,即AC 2-4cos C ·AC +1=0.由题意知,关于AC 的一元二次方程应该有解,令Δ=(4cos C )2-4≥0,得cos C ≥12,或cos C ≤-12(舍去,因为AB <BC ) 所以,0<C ≤π3,即角C 的取值范围是⎝⎛⎦⎤0,π3. [点评] 1.本题也可用图示法,如图:A 为⊙B 上不在直线BC 上的任一点,由于r =AB =3,故当CA 与⊙B 相切时∠C 最大为π3,故C ∈⎝⎛⎦⎤0,π3. 2.高考命题大题的第一题一般比较容易入手,大多在三角函数的图象与性质、正余弦定理、平面向量等内容上命制,这一部分要狠抓基本原理、公式、基本方法的落实.(理)(2010·东北师大附中、辽宁省实验中学联考)设△ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ,且a cos C +12c =b . (1)求角A 的大小;(2)若a =1,求△ABC 的周长l 的取值范围.[解析] (1)由a cos C +12c =b 得 sin A cos C +12sin C =sin B又sin B =sin(A +C )=sin A cos C +cos A sin C∴12sin C =cos A sin C , ∵sin C ≠0,∴cos A =12, 又∵0<A <π,∴A =π3. (2)解法1:由正弦定理得:b =a sin B sin A =23sin B ,c =23sin C l =a +b +c =1+23(sin B +sin C ) =1+23(sin B +sin(A +B )) =1+2⎝⎛⎭⎫32sin B +12cos B =1+2sin ⎝⎛⎭⎫B +π6 ∵A =π3,∴B ∈⎝⎛⎭⎫0,2π3,∴B +π6∈⎝⎛⎭⎫π6,5π6, ∴sin ⎝⎛⎭⎫B +π6∈⎝⎛⎦⎤12,1. 故△ABC 的周长l 的取值范围是(2,3].解法2:周长l =a +b +c =1+b +c由(1)及余弦定理a 2=b 2+c 2-2bc cos A ,∴b 2+c 2=bc +1,∴(b +c )2=1+3bc ≤1+3⎝⎛⎭⎫b +c 22,∴b +c ≤2,又b +c >a =1,∴l =a +b +c ∈(2,3],即△ABC 的周长l 的取值范围为(2,3].17.(文)△ABC 中内角A 、B 、C 的对边分别为a 、b 、c ,向量m =(2sin B ,-3),n =(cos2B,2cos 2B 2-1)且m ∥n . (1)求锐角B 的大小;(2)如果b =2,求△ABC 的面积S △ABC 的最大值.[分析] (1)问利用平行向量的坐标表示将向量知识转化为三角函数,利用三角恒等变换知识解决;(2)问利用余弦定理与基本不等式结合三角形面积公式解决.[解析] (1)∵m ∥n ,∴2sin B ⎝⎛⎭⎫2cos 2B 2-1=-3cos2B ∴sin2B =-3cos2B ,即tan2B =- 3又∵B 为锐角,∴2B ∈(0,π),∴2B =2π3,∴B =π3. (2)∵B =π3,b =2, ∴由余弦定理cos B =a 2+c 2-b 22ac得, a 2+c 2-ac -4=0又∵a 2+c 2≥2ac ,∴ac ≤4(当且仅当a =c =2时等号成立)S △ABC =12ac sin B =34ac ≤3(当且仅当a =c =2时等号成立), [点评] 本题将三角函数、向量与解三角形有机的结合在一起,题目新疑精巧,难度也不大,即符合在知识“交汇点”处构题,又能加强对双基的考查,特别是向量的坐标表示及运算,大大简化了向量的关系的运算,该类问题的解题思路通常是将向量的关系用坐标运算后转化为三角函数问题,然后用三角函数基本公式结合正、余弦定理求解.(理)(2010·山师大附中模考)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知sin B =513,且a 、b 、c 成等比数列. (1)求1tan A +1tan C的值; (2)若ac cos B =12,求a +c 的值.[解析] (1)依题意,b 2=ac由正弦定理及sin B =513得,sin A sin C =sin 2B =25169. 1tan A +1tan C =cos A sin A +cos C sin C =sin (A +C )sin A sin C =sin B sin A sin C =135. (2)由ac cos B =12知cos B >0,∵sin B =513,∴cos B =1213(b 不是最大边,舍去负值) 从而,b 2=ac =12cos B=13. 由余弦定理得,b 2=(a +c )2-2ac -2ac cos B .∴13=(a +c )2-2×13×⎝⎛⎭⎫1+1213. 解得:a +c =37.。
正弦定理余弦定理练习题及答案(供参考)

正弦定理、余弦定理练习题年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共20题,题分合计100分)1.已知在△ABC中,sin A:sin B:sin C=3:2:4,那么cos C的值为B.D.2.在△ABC中,a=λ,b=λ,A=45°,则满足此条件的三角形的个数是D.无数个3.在△ABC中,b cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形4.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为°°°°5.在△ABC中,=1,=2,(+)·(+)=5+2则边||等于A.C.D.6.在△ABC中,已知B=30°,b=50,c=150,那么这个三角形是A.等边三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形7.在△ABC中,若b2sin2C+c2sin2B=2bc cos B cos C,则此三角形为A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形8.正弦定理适应的范围是△B.锐角△ C.钝角△ D.任意△9.已知△ABC中,a=10,B=60°,C=45°,则c=+(-1) C.(+1)10.在△ABC中,b sin A<a<b,则此三角形有A.一解B.两解C.无解D.不确定11.三角形的两边分别为5和3,它们夹角的余弦是方程5x2-7x-6=0的根,则三角形的另一边长为12.在△ABC中,a2=b2+c2+bc,则A等于°°°13.在△ABC中,,则△ABC是A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形14.在△ABC中,a=2,A=30°,C=45°,则△ABC的面积S△ABC等于A.C.+1D.(+1)15.已知三角形ABC的三边a、b、c成等比数列,它们的对角分别是A、B、C,则sin A sin C 等于+cos2B+sin2B16.在△ABC中,sin A>sin B是A>B的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件17.在△ABC中,b Cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形18.△ABC中,sin2A=sin2B+sin2C,则△ABC为A.直角三角形B.等腰直角三角形C.等边三角形D.等腰三角形19.△ABC中,A=60°,b=1,这个三角形的面积为,则△ABC外接圆的直径为A.B.C.D.20.在△ABC中,,则k为D.(R为△ABC外接圆半径)二、填空题(共18题,题分合计75分)1.在△ABC中,A=60°,C=45°,b=2,则此三角形的最小边长为.2.在△ABC中,= .3.在△ABC中,a∶b∶c=(+1)∶∶2,则△ABC的最小角的度数为.4.在△ABC中,已知sin A∶sin B∶sin C=6∶5∶4,则sec A= .5.△ABC中,,则三角形为_________.6.在△ABC中,角A、B均为锐角且cos A>sin B,则△ABC是___________.7.在△ABC中,若此三角形有一解,则a、b、A满足的条件为____________________.8.已知在△ABC中,a=10,b=5,A=45°,则B= .9.已知△ABC中,a=181,b=209,A=121°14′,此三角形解.10.在△ABC中,a=1,b=1,C=120°则c= .11.在△ABC中,若a2>b2+c2,则△ABC为;若a2=b2+c2,则△ABC为;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为.12.在△ABC中,sin A=2cos B sin C,则三角形为_____________.13.在△ABC中,BC=3,AB=2,且,A= .14.在△ABC中,B=,C=3,B=30°,则A= .15.在△ABC中,a+b=12,A=60°,B=45°,则a= ,b= .16.若2,3,x为三边组成一个锐角三角形,则x的范围为.17.在△ABC中,化简b cos C+c cos B= .18.钝角三角形的边长是三个连续自然数,则三边长为.三、解答题(共24题,题分合计244分)1.已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.2.已知△ABC的三边长a=3,b=4,c=,求三角形的最大内角.3.已知在△ABC中,∠A=45°,a=2,c=,解此三角形.4.在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求AB的长.5.在△ABC中,A最大,C最小,且A=2C,A+C=2B,求此三角形三边之比.6.证明:在△ABC中,.(其中R为△ABC的外接圆的半径)7.在△ABC中,最大角A为最小角C的2倍,且三边a、b、c为三个连续整数,求a、b、c的值.8.如下图所示,半圆O的直径MN=2,OA=2,B为半圆上任意一点,以AB为一边作正三角形ABC,问B在什么位置时,四边形OACB面积最大?最大面积是多少?9.在△ABC中,若sin A∶sin B∶sin C=m∶n∶l,且a+b+c=S,求a.10.根据所给条件,判断△ABC的形状(1)a cos A=b cos B(2)11.△ABC中,a+b=10,而cos C是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.12.在△ABC中,a、b、c分别是角A、B、C的对边,设a+c=2b,A-C=,求sin B的值.13.已知△ABC中,a=1,b=,A=30°,求B、C 和c.14.在△ABC中,c=2,tan A=3,tan B=2,试求a、b及此三角形的面积.15.已知S△ABC=10,一个角为60°,这个角的两边之比为5∶2,求三角形内切圆的半径.16.已知△ABC中,,试判断△ABC的形状.17.已知△ABC的面积为1,tan B=,求△ABC 的各边长.18.求值:19.已知△ABC的面积,解此三角形.20.在△ABC中,a=,b=2,c=+1,求A、B、C及S△.21.已知(a2+bc)x2+2=0是关于x的二次方程,其中a、b、c是△ABC的三边,(1)若∠A为钝角,试判断方程根的情况.(2)若方程有两相等实根,求∠A的度数.22.在△ABC中,(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断△ABC的形状.23.在△ABC中,a>b,C=,且有tan A·tan B=6,试求a、b以及此三角形的面积.24.已知:k是整数,钝角△ABC的三内角A、B、C所对的边分别为a、b、c(1)若方程组有实数解,求k的值.(2)对于(1)中的k值,若且有关系式,试求A、B、C的度数.正弦定理、余弦定理答案一、选择题(共20题,合计100分)1 A 2A3C 4 B 5 C 6D 7A 8 D 9B 10 B 11 B 12C 13C 14C 16. C 17:C 18A 19C 20. A二、填空题(共18题,合计75分)1.2(-1) 23. 45°4. 85.等腰三角形6.:钝角三角形7.a=b sin A或b<a8.60°或120°9无10.11.钝角三角形直角三角形锐角三角形12.等腰三角形13.120°14.或215. 36-1216.<x<17.a18. 2、3、4三、解答题(共24题,合计244分)=B=105°b=2.∠C=120°3.∠B=75°或∠B=15°b=+1,∠C=60°,∠B=75°或b=-1,∠C=120°,∠B=15°4. AB的长为5.:此三角形三边之比为6∶5∶4=6,b=5,c=48.当θ=时,S四边形OACB最大, 最大值为+29.10(1)△ABC是等腰三角形或直角三角形(2)△ABC为等边三角形11△ABC周长的最小值为12.=60°,B2=120°;C1=90°,C2=30°;c1=2,c2=114..15.16.等边三角形17.18.20. A=60°,B=45°,C=75°,S△=21. (1)没有实数根(2)60°22.等腰三角形或直角三角形23.24.(1)k=1,2,3 (2)C=45°,B=15°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修5(1-2)章测试题
一、选择题(共10题,每题5分)
1.三角形的两边分别为5和3,它们夹角的余弦是方程5x 2-7x -6=0的根,则三角形的另一边长为
A.52 B .2 C.16 D.4
2.在△ABC 中,a 2=b 2+c 2+bc ,则A 等于
A.60° B .45° C.120 D.30°
3.如果a 1,a 2,…,a 8为各项都大于零的等差数列,公差d ≠0,则( ).
A .a 1a 8>a 4a 5
B .a 1a 8<a 4a 5
C .a 1+a 8<a 4+a 5
D .a 1a 8=a 4a 5
4.已知方程(x 2-2x +m )(x 2-2x +n )=0的四个根组成一个首项为41
的等差数
列,则|m -n |等于( ).
A .1
B .43
C .21
D . 8
3 5.已知三角形ABC 的三边a 、b 、c 成等比数列,它们的对角分别是A 、B 、C ,则sin A sin C 等于
A.cos 2B
B.1-cos 2B
C.1+cos 2B
D.1+sin 2B
6.若数列{a n }是等差数列,首项a 1>0,a 2 003+a 2 004>0,a 2 003·a 2 004<0,则使前n 项和S n >0成立的最大自然数n 是( ).
A .4 005
B .4 006
C .4 007
D .4 008
7.在△ABC 中,b Cos A =a cos B ,则三角形为
A.直角三角形
B.锐角三角形
C.等腰三角形
D.等边三角形 8.△ABC 中,sin 2A =sin 2B +sin 2C ,则△ABC 为
A.直角三角形
B.等腰直角三角形
C.等边三角形
D.等腰三
角形
9.△ABC 中,A =60°,b =1,这个三角形的面积为,则△ABC 外接圆的直径为
A. B. C. D.
10.在等差数列{a n }中,a n ≠0,a n -1-2n a +a n +1=0(n ≥2),若S 2n -1=38,则n
=( ).
A .38
B .20
C .10
D .9
二、填空题(共6题,每题5分)
11.在△ABC 中,若a 2>b 2+c 2,则△ABC 为;若a 2=b 2+c 2,则△ABC 为 ;若a 2<b 2+c 2且b 2<a 2+c 2且c 2<a 2+b 2,则△ABC 为 .
12.在△ABC 中,sin A =2cos B sin C ,则三角形为 _____________.
13.设f (x )=221
x ,利用课本中推导等差数列前n 项和公式的方法,可求得
f (-5)+f (-4)+…+f (0)+…+f (5)+f (6)的值为 .
14.已知等比数列{a n }中,
(1)若a 3·a 4·a 5=8,则a 2·a 3·a 4·a 5·a 6= .
(2)若a 1+a 2=324,a 3+a 4=36,则a 5+a 6= .
15.在38和2
27之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .
16.在等差数列{a n }中,3(a 3+a 5)+2(a 7+a 10+a 13)=24,则此数列前13项之和为 .
三、解答题(共6题, 每题10分)
17.已知△ABC 中,
,试判断△ABC 的形状.
18.已知△ABC 的面积
,解此三角形.
19.在△ABC 中,a =
,b =2,c=+1,求A 、B 、C 及S △.
20.已知(a 2+bc )x 2+2
=0是关于x 二次方程,其中a 、b 、c 是△ABC
的三边, (1)若∠A 为钝角,试判断方程根的情况.(2)若方程有两相等实根,求∠A 的度数.
21.(1)已知数列{a n }的前n 项和S n =3n 2-2n ,求证数列{a n }成等差数列.
(2)已知a 1,b 1,c 1成等差数列,求证
a c
b +,b a
c +,c
b a +也成等差数列.
22.设{a n }是公比为 q 的等比数列,且a 1,a 3,a 2成等差数列.
(1)求q 的值;
(2)设{b n }是以2为首项,q 为公差的等差数列,其前n 项和为S n ,当n ≥2时,比较S n 与b n 的大小,并说明理由.
23.数列{a n }的前n 项和记为S n ,已知
a 1=1,a n +1=n n 2+S n (n =1,2,3…).
答案
一、选择题
1 B
2C
3C
4C
5.B
6.B
7:C
8A
9C
10. C
二、填空题
11.钝角三角形直角三角形锐角三角形
12.等腰三角形
13. 120°
14.或2
15. 36-12
三、解答题
16.等边三角形
17.
18.
20. A=60°,B=45°,C=75°,S△=
21. (1)没有实数根(2)60°。
