正余弦定理练习题(答案)

合集下载

正弦定理和余弦定理及答案

Байду номын сангаас

, 即

2 ) 3
············· 12 分
12 3 sin sin( ) 3

2 6 3 cos(2 ) 3 3 (0 ) （下同） 3 3
15．（1）因为 (2a c)cos B b cos C ，所以 (2sin A sin C ) cos B sin B cos C ，即 2sin A cos B sin C cos B sin B cos C sin(C B) sin A 而（2）因为
17．（1）在 ABC中 ,由b 2 c 2 a 2 3bc, 得b 2 c 2 a 2 3bc ，所以 cos A
b2 c2 a2 3 . 2bc 2
在ABC 中,因为0 A , 所以 A
又因为 sin A sin B cos 即 sin B 1 cos C.
16. ABC 的三边 a, b, c 满足关系： c 4 2 a 2 b 2 c 2 a 4 a 2b 2 b 4 0 ,角 C 为锐角. ⑴ 求 C 的度数； ⑵ 求函数式 sin A sin B及 sin A cos B 的取值范围.

17．在△ABC 中，角 A， B， C 的对边分别为 a， b， c，且 b 2 c 2 a 2 （1）求角 A，B，C 的大小；（2）若 BC 边上的中线 AM 的长为 7 ，求△ABC 的面积．
0 A 2 5 1 , A , sin A 1, 3 6 6 6 2 6

3 sin A sin B 3 . 2

正余弦定理知识点经典题(有答案)

正余弦定理1.定理内容：（1）正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即2sin sin sin a b cR A B C=== （2）余弦定理：三角形中任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的两倍。

即：2222cos a b c bc A =+-2222cos b a c ac B =+- 2222cos c a b ab C =+-（3）面积定理：111sin sin sin 222ABC S ab C bc A ac B ∆=== 2.利用正余弦定理解三角形：（1）已知一边和两角：（2）已知两边和其中一边的对角：（3）已知两边和它们所夹的角：（4）已知三边：正弦定理1．在△ABC 中，∠A ＝45°，∠B ＝60°，a ＝2，则b 等于( )A.6B. 2C. 3 D ．2 6 2．在△ABC 中，已知a ＝8，B ＝60°，C ＝75°，则b 等于( )A ．4 2B ．4 3C ．4 6 D.3233．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，A ＝60°，a ＝43，b ＝42，则角B 为( )A ．45°或135°B ．135°C ．45°D ．以上答案都不对 4．在△ABC 中，a ∶b ∶c ＝1∶5∶6，则sin A ∶sin B ∶sin C 等于( )A ．1∶5∶6B ．6∶5∶1C ．6∶1∶5D ．不确定解析：选A.由正弦定理知sin A ∶sin B ∶sin C ＝a ∶b ∶c ＝1∶5∶6. 5．在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若A ＝105°，B ＝45°，b ＝2，则c ＝( )A ．1 B.12 C ．2 D.146．在△ABC 中，若cos A cos B ＝ba，则△ABC 是( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形 7．已知△ABC 中，AB ＝3，AC ＝1，∠B ＝30°，则△ABC 的面积为( )A.32B.34C.32或 3D.34或328．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c ＝2，b ＝6，B ＝120°，则a 等于( )A. 6 B ．2 C. 3 D. 29．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若a ＝1，c ＝3，C ＝π3，则A ＝________.10．在△ABC 中，已知a ＝433，b ＝4，A ＝30°，则sin B ＝________.11．在△ABC 中，已知∠A ＝30°，∠B ＝120°，b ＝12，则a ＋c ＝________. 12．在△ABC 中，a ＝2b cos C ，则△ABC 的形状为________．13．在△ABC 中，A ＝60°，a ＝63，b ＝12，S △ABC ＝183，则a ＋b ＋csin A ＋sin B ＋sin C ＝________，c ＝________.14．已知△ABC 中，∠A ∶∠B ∶∠C ＝1∶2∶3，a ＝1，则a －2b ＋csin A －2sin B ＋sin C＝________.15．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________.16．在△ABC 中，b ＝43，C ＝30°，c ＝2，则此三角形有________组解．17．如图所示，货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行，为了确定船位，船在B 点观测灯塔A 的方位角为110°，航行半小时后船到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是多少？18．在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，若a ＝23，sin C 2cos C 2＝14，sin B sin C ＝cos 2A2，求A 、B 及b 、c .19．(2009年高考四川卷)在△ABC 中，A 、B 为锐角，角A 、B 、C 所对应的边分别为a 、b 、c ，且cos 2A ＝35，sin B ＝1010.(1)求A ＋B 的值；(2)若a －b ＝2－1，求a ，b ，c 的值．20．△ABC 中，ab ＝603，sin B ＝sin C ，△ABC 的面积为153，求边b 的长．余弦定理1．在△ABC 中，如果BC ＝6，AB ＝4，cos B ＝13，那么AC 等于( )A ．6B ．2 6C ．3 6D ．4 6 2．在△ABC 中，a ＝2，b ＝3－1，C ＝30°，则c 等于( )A. 3B. 2C. 5 D ．2 3．在△ABC 中，a 2＝b 2＋c 2＋3bc ，则∠A 等于( )A ．60°B ．45°C ．120°D ．150°4．在△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若(a 2＋c 2－b 2)tan B ＝3ac ，则∠B 的值为( )A.π6B.π3C.π6或5π6D.π3或2π35．在△ABC 中，a 、b 、c 分别是A 、B 、C 的对边，则a cos B ＋b cos A 等于( )A ．aB ．bC ．cD ．以上均不对6．如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．由增加的长度决定7．已知锐角三角形ABC 中，|AB →|＝4，|AC →|＝1，△ABC 的面积为3，则AB →·AC →的值为( )A ．2B ．－2C ．4D ．－4 8．在△ABC 中，b ＝3，c ＝3，B ＝30°，则a 为( )A. 3 B ．2 3 C.3或2 3 D ．29．已知△ABC 的三个内角满足2B ＝A ＋C ，且AB ＝1，BC ＝4，则边BC 上的中线AD 的长为________． 10．△ABC 中，sin A ∶sin B ∶sin C ＝(3－1)∶(3＋1)∶10，求最大角的度数．11．已知a 、b 、c 是△ABC 的三边，S 是△ABC 的面积，若a ＝4，b ＝5，S ＝53，则边c 的值为________． 12．在△ABC 中，sin A ∶sin B ∶sin C ＝2∶3∶4，则cos A ∶cos B ∶cos C ＝________.13．在△ABC 中，a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________.14．已知△ABC 的三边长分别为AB ＝7，BC ＝5，AC ＝6，则AB →·BC →的值为________．15．已知△ABC 的三边长分别是a 、b 、c ，且面积S ＝a 2＋b 2－c 24，则角C ＝________.16．(2011年广州调研)三角形的三边为连续的自然数，且最大角为钝角，则最小角的余弦值为________． 17．在△ABC 中，BC ＝a ，AC ＝b ，a ，b 是方程x 2－23x ＋2＝0的两根，且2cos(A ＋B )＝1，求AB 的长．18．已知△ABC 的周长为2＋1，且sin A ＋sin B ＝2sin C .(1)求边AB 的长；(2)若△ABC 的面积为16sin C ，求角C 的度数．19．在△ABC 中，BC ＝5，AC ＝3，sin C ＝2sin A .(1)求AB 的值；(2)求sin(2A －π4)的值．20．在△ABC 中，已知(a ＋b ＋c )(a ＋b －c )＝3ab ，且2cos A sin B ＝sin C ，确定△ABC 的形状．正弦定理1．在△ABC 中，∠A ＝45°，∠B ＝60°，a ＝2，则b 等于( )A.6B. 2C. 3 D ．2 6解析：选A.应用正弦定理得：a sin A ＝b sin B ，求得b ＝a sin Bsin A＝ 6.2．在△ABC 中，已知a ＝8，B ＝60°，C ＝75°，则b 等于( )A ．4 2B ．4 3C ．4 6 D.323解析：选C.A ＝45°，由正弦定理得b ＝a sin Bsin A＝4 6.3．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，A ＝60°，a ＝43，b ＝42，则角B 为( )A ．45°或135°B ．135°C ．45°D ．以上答案都不对解析：选C.由正弦定理a sin A ＝b sin B 得：sin B ＝b sin A a ＝22，又∵a >b ，∴B <60°，∴B ＝45°.4．在△ABC 中，a ∶b ∶c ＝1∶5∶6，则sin A ∶sin B ∶sin C 等于( )A ．1∶5∶6B ．6∶5∶1C ．6∶1∶5D ．不确定解析：选A.由正弦定理知sin A ∶sin B ∶sin C ＝a ∶b ∶c ＝1∶5∶6. 5．在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若A ＝105°，B ＝45°，b ＝2，则c ＝( )A ．1 B.12 C ．2 D.14解析：选A.C ＝180°－105°－45°＝30°，由b sin B ＝c sin C 得c ＝2×sin 30°sin45°＝1.6．在△ABC 中，若cos A cos B ＝ba，则△ABC 是( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形解析：选D.∵b a ＝sin B sin A ，∴cos A cos B ＝sin Bsin A，sin A cos A ＝sin B cos B ，∴sin2A ＝sin2B即2A ＝2B 或2A ＋2B ＝π，即A ＝B ，或A ＋B ＝π2.7．已知△ABC 中，AB ＝3，AC ＝1，∠B ＝30°，则△ABC 的面积为( )A.32B.34C.32或 3D.34或32解析：选D.AB sin C ＝AC sin B ，求出sin C ＝32，∵AB ＞AC ，∴∠C 有两解，即∠C ＝60°或120°，∴∠A ＝90°或30°.再由S △ABC ＝12AB ·AC sin A 可求面积．8．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c ＝2，b ＝6，B ＝120°，则a 等于( )A. 6 B ．2 C. 3 D. 2解析：选D.由正弦定理得6sin120°＝2sin C，∴sin C ＝12.又∵C 为锐角，则C ＝30°，∴A ＝30°， △ABC 为等腰三角形，a ＝c ＝ 2.9．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若a ＝1，c ＝3，C ＝π3，则A ＝________.解析：由正弦定理得：a sin A ＝csin C，所以sin A ＝a ·sin C c ＝12.又∵a ＜c ，∴A ＜C ＝π3，∴A ＝π6.答案：π610．在△ABC 中，已知a ＝433，b ＝4，A ＝30°，则sin B ＝________.解析：由正弦定理得a sin A ＝bsin B⇒sin B ＝b sin A a ＝4×12433＝32.答案：3211．在△ABC 中，已知∠A ＝30°，∠B ＝120°，b ＝12，则a ＋c ＝________.解析：C ＝180°－120°－30°＝30°，∴a ＝c ，由a sin A ＝b sin B 得，a ＝12×sin30°sin120°＝43， ∴a ＋c ＝8 3. 答案：8 312．在△ABC 中，a ＝2b cos C ，则△ABC 的形状为________．解析：由正弦定理，得a ＝2R ·sin A ，b ＝2R ·sin B ，代入式子a ＝2b cos C ，得 2R sin A ＝2·2R ·sin B ·cos C ，所以sin A ＝2sin B ·cos C ，即sin B ·cos C ＋cos B ·sin C ＝2sin B ·cos C ，化简，整理，得sin(B －C )＝0. ∵0°＜B ＜180°，0°＜C ＜180°， ∴－180°＜B －C ＜180°， ∴B －C ＝0°，B ＝C . 答案：等腰三角形13．在△ABC 中，A ＝60°，a ＝63，b ＝12，C=30°则a ＋b ＋csin A ＋sin B ＋sin C＝________，c ＝________.解析：由正弦定理得a ＋b ＋c sin A ＋sin B ＋sin C ＝a sin A ＝63sin60°＝12，又S △ABC ＝12bc sin A ，∴12×12×sin60°×c ＝183，∴c ＝6.答案：12 614．已知△ABC 中，∠A ∶∠B ∶∠C ＝1∶2∶3，a ＝1，则a －2b ＋csin A －2sin B ＋sin C＝________.解析：由∠A ∶∠B ∶∠C ＝1∶2∶3得，∠A ＝30°，∠B ＝60°，∠C ＝90°，∴2R ＝a sin A ＝1sin30°＝2，又∵a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ，∴a －2b ＋c sin A －2sin B ＋sin C ＝2R sin A －2sin B ＋sin Csin A －2sin B ＋sin C ＝2R ＝2.15．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________.解析：依题意，sin C ＝223，S △ABC ＝12ab sin C ＝43，解得b ＝2 3. 答案：2 316．在△ABC 中，b ＝43，C ＝30°，c ＝2，则此三角形有________组解．解析：∵b sin C ＝43×12＝23且c ＝2，∴c <b sin C ，∴此三角形无解．答案：0 17．如图所示，货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行，为了确定船位，船在B 点观测灯塔A 的方位角为110°，航行半小时后船到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是多少？解：在△ABC 中，BC ＝40×12＝20，∠ABC ＝140°－110°＝30°， ∠ACB ＝(180°－140°)＋65°＝105°，所以∠A ＝180°－(30°＋105°)＝45°，由正弦定理得AC ＝BC ·sin ∠ABC sin A＝20sin30°sin45°＝102(km)．即货轮到达C 点时，与灯塔A 的距离是10 2 km.18．在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，若a ＝23，sin C 2cos C 2＝14，sin B sin C ＝cos 2A2，求A 、B 及b 、c .解：由sin C 2cos C 2＝14，得sin C ＝12，又C ∈(0，π)，所以C ＝π6或C ＝5π6.由sin B sin C ＝cos 2A2，得sin B sin C ＝12[1－cos(B ＋C )]，即2sin B sin C ＝1－cos(B ＋C )，即2sin B sin C ＋cos(B ＋C )＝1，变形得 cos B cos C ＋sin B sin C ＝1，即cos(B －C )＝1，所以B ＝C ＝π6，B ＝C ＝5π6(舍去)，A ＝π－(B ＋C )＝2π3.由正弦定理a sin A ＝b sin B ＝csin C，得b ＝c ＝a sin Bsin A ＝23×1232＝2.故A ＝2π3，B ＝π6，b ＝c ＝2.19．(2009年高考四川卷)在△ABC 中，A 、B 为锐角，角A 、B 、C 所对应的边分别为a 、b 、c ，且cos 2A＝35，sin B ＝1010.(1)求A ＋B 的值；(2)若a －b ＝2－1，求a ，b ，c 的值．解：(1)∵A 、B 为锐角，sin B ＝1010，∴cos B ＝1－sin 2B ＝31010.又cos 2A ＝1－2sin 2A ＝35，∴sin A ＝55，cos A ＝255，∴cos(A ＋B )＝cos A cos B －sin A sin B ＝255×31010－55×1010＝22.又0＜A ＋B ＜π，∴A ＋B ＝π4.(2)由(1)知，C ＝3π4，∴sin C ＝22.由正弦定理：a sin A ＝b sin B ＝csin C得5a ＝10b ＝2c ，即a ＝2b ，c ＝5b .∵a －b ＝2－1，∴2b －b ＝2－1，∴b ＝1. ∴a ＝2，c ＝ 5.20．△ABC 中，ab ＝603，sin B ＝sin C ，△ABC 的面积为153，求边b 的长．解：由S ＝12ab sin C 得，153＝12×603×sin C ，∴sin C ＝12，∴∠C ＝30°或150°.又sin B ＝sin C ，故∠B ＝∠C . 当∠C ＝30°时，∠B ＝30°，∠A ＝120°.又∵ab ＝603，a sin A ＝bsin B，∴b ＝215.当∠C ＝150°时，∠B ＝150°(舍去)．故边b 的长为215.余弦定理1．在△ABC 中，如果BC ＝6，AB ＝4，cos B ＝13，那么AC 等于( )A ．6B ．2 6C ．3 6D ．4 6 解析：选A.由余弦定理，得 AC ＝AB 2＋BC 2－2AB ·BC cos B＝ 42＋62－2×4×6×13＝6.2．在△ABC 中，a ＝2，b ＝3－1，C ＝30°，则c 等于( ) A. 3 B. 2 C. 5 D ．2解析：选B.由余弦定理，得c 2＝a 2＋b 2－2ab cos C ＝22＋(3－1)2－2×2×(3－1)cos30° ＝2， ∴c ＝ 2.3．在△ABC 中，a 2＝b 2＋c 2＋3bc ，则∠A 等于( ) A ．60° B ．45° C ．120° D ．150°解析：选D.cos ∠A ＝b 2＋c 2－a 22bc ＝－3bc 2bc ＝－32，∵0°＜∠A ＜180°，∴∠A ＝150°. 4．在△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若(a 2＋c 2－b 2)tan B ＝3ac ，则∠B 的值为( ) A.π6 B.π3 C.π6或5π6 D.π3或2π3解析：选D.由(a 2＋c 2－b 2)tan B ＝3ac ，联想到余弦定理，代入得cos B ＝a 2＋c 2－b 22ac ＝32·1tan B ＝32·cos B sin B .显然∠B ≠π2，∴sin B ＝32.∴∠B ＝π3或2π3.5．在△ABC 中，a 、b 、c 分别是A 、B 、C 的对边，则a cos B ＋b cos A 等于( ) A ．a B ．b C ．c D ．以上均不对解析：选C.a ·a 2＋c 2－b 22ac ＋b ·b 2＋c 2－a 22bc ＝2c 22c＝c .6．如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．由增加的长度决定解析：选A.设三边长分别为a ，b ，c 且a 2＋b 2＝c 2. 设增加的长度为m ，则c ＋m ＞a ＋m ，c ＋m ＞b ＋m ，∴三角形各角均为锐角，即新三角形为锐角三角形．7．已知锐角三角形ABC 中，|AB →|＝4，|AC →|＝1，△ABC 的面积为3，则AB →·AC →的值为( ) A ．2 B ．－2 C ．4 D ．－4解析：选A.S △ABC ＝3＝12|AB →|·|AC →|·sin A＝12×4×1×sin A ， ∴sin A ＝32，又∵△ABC 为锐角三角形，∴cos A ＝12，∴AB →·AC →＝4×1×12＝2.8．在△ABC 中，b ＝3，c ＝3，B ＝30°，则a 为( ) A. 3 B ．2 3 C.3或2 3 D ．2解析：选C.在△ABC 中，由余弦定理得b 2＝a 2＋c 2－2ac cos B ，即3＝a 2＋9－33a ， ∴a 2－33a ＋6＝0，解得a ＝3或2 3. 9．已知△ABC 的三个内角满足2B ＝A ＋C ，且AB ＝1，BC ＝4，则边BC 上的中线AD 的长为________．解析：∵2B ＝A ＋C ，A ＋B ＋C ＝π，∴B ＝π3.在△ABD 中，AD ＝AB 2＋BD 2－2AB ·BD cos B＝ 1＋4－2×1×2×12＝ 3.答案： 310．△ABC 中，sin A ∶sin B ∶sin C ＝(3－1)∶(3＋1)∶10，求最大角的度数．解：∵sin A ∶sin B ∶sin C ＝(3－1)∶(3＋1)∶10， ∴a ∶b ∶c ＝(3－1)∶(3＋1)∶10.设a ＝(3－1)k ，b ＝(3＋1)k ，c ＝10k (k ＞0)， ∴c 边最长，即角C 最大．由余弦定理，得cos C ＝a 2＋b 2－c 22ab ＝－12，又C ∈(0°，180°)，∴C ＝120°. 11．已知a 、b 、c 是△ABC 的三边，S 是△ABC 的面积，若a ＝4，b ＝5，S ＝53，则边c 的值为________．解析：S ＝12ab sin C ，sin C ＝32，∴C ＝60°或120°.∴cos C ＝±12，又∵c 2＝a 2＋b 2－2ab cos C ，∴c 2＝21或61，∴c ＝21或61. 答案：21或6112．在△ABC 中，sin A ∶sin B ∶sin C ＝2∶3∶4，则cos A ∶cos B ∶cos C ＝________. 解析：由正弦定理a ∶b ∶c ＝sin A ∶sin B ∶sin C ＝2∶3∶4，设a ＝2k (k ＞0)，则b ＝3k ，c ＝4k ，cos B ＝a 2＋c 2－b 22ac ＝2k 2＋4k 2－3k 22×2k ×4k ＝1116，同理可得：cos A ＝78，cos C ＝－14，∴cos A ∶cos B ∶cos C ＝14∶11∶(－4)．答案：14∶11∶(－4)13．在△ABC 中，a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________. 解析：∵cos C ＝13，∴sin C ＝223. 又S △ABC ＝12ab sin C ＝43，即12·b ·32·223＝43， ∴b ＝2 3.答案：2 314．已知△ABC 的三边长分别为AB ＝7，BC ＝5，AC ＝6，则AB →·BC →的值为________．解析：在△ABC 中，cos B ＝AB 2＋BC 2－AC 22AB ·BC＝49＋25－362×7×5＝1935， ∴AB →·BC →＝|AB →|·|BC →|·cos(π－B )＝7×5×(－1935) ＝－19.答案：－1915．已知△ABC 的三边长分别是a 、b 、c ，且面积S ＝a 2＋b 2－c 24，则角C ＝________. 解析：12ab sin C ＝S ＝a 2＋b 2－c 24＝a 2＋b 2－c 22ab ·ab 2＝12ab cos C ，∴sin C ＝cos C ，∴tan C ＝1，∴C ＝45°. 答案：45°16．(2011年广州调研)三角形的三边为连续的自然数，且最大角为钝角，则最小角的余弦值为________．解析：设三边长为k －1，k ，k ＋1(k ≥2，k ∈N )，则⎩⎪⎨⎪⎧k 2＋k －12－k ＋12＜0k ＋k －1＞k ＋1⇒2＜k ＜4， ∴k ＝3，故三边长分别为2,3,4，∴最小角的余弦值为32＋42－222×3×4＝78. 答案：7817．在△ABC 中，BC ＝a ，AC ＝b ，a ，b 是方程x 2－23x ＋2＝0的两根，且2cos(A ＋B )＝1，求AB 的长．解：∵A ＋B ＋C ＝π且2cos(A ＋B )＝1，∴cos(π－C )＝12，即cos C ＝－12. 又∵a ，b 是方程x 2－23x ＋2＝0的两根，∴a ＋b ＝23，ab ＝2.∴AB 2＝AC 2＋BC 2－2AC ·BC ·cos C＝a 2＋b 2－2ab (－12) ＝a 2＋b 2＋ab ＝(a ＋b )2－ab＝(23)2－2＝10，∴AB ＝10.18．已知△ABC 的周长为2＋1，且sin A ＋sin B ＝2sin C .(1)求边AB 的长；(2)若△ABC 的面积为16sin C ，求角C 的度数．解：(1)由题意及正弦定理得AB ＋BC ＋AC ＝2＋1，BC ＋AC ＝2AB ，两式相减，得AB ＝1.(2)由△ABC 的面积12BC ·AC ·sin C ＝16sin C ，得BC ·AC ＝13，由余弦定理得cos C ＝AC 2＋BC 2－AB 22AC ·BC＝AC ＋BC 2－2AC ·BC －AB 22AC ·BC ＝12，所以C ＝60°.19．在△ABC 中，BC ＝5，AC ＝3，sin C ＝2sin A .(1)求AB 的值；(2)求sin(2A －π4)的值．解：(1)在△ABC 中，由正弦定理AB sin C ＝BC sin A ，得AB ＝sin C sin ABC ＝2BC ＝2 5. (2)在△ABC 中，根据余弦定理，得cos A ＝AB 2＋AC 2－BC 22AB ·AC ＝255，于是sin A ＝1－cos 2A ＝55. 从而sin 2A ＝2sin A cos A ＝45， cos 2A ＝cos 2 A －sin 2 A ＝35. 所以sin(2A －π4)＝sin 2A cos π4－cos 2A sin π4＝210.20．在△ABC 中，已知(a ＋b ＋c )(a ＋b －c )＝3ab ，且2cos A sin B ＝sin C ，确定△ABC 的形状．解：由正弦定理，得sin C sin B ＝c b. 由2cos A sin B ＝sin C ，有cos A ＝sin C 2sin B ＝c 2b. 又根据余弦定理，得cos A ＝b 2＋c 2－a 22bc ，所以c 2b ＝b 2＋c 2－a 22bc，即c 2＝b 2＋c 2－a 2，所以a ＝b .又因为(a ＋b ＋c )(a ＋b －c )＝3ab ，所以(a ＋b )2－c 2＝3ab ，所以4b 2－c 2＝3b 2，所以b ＝c ，所以a ＝b ＝c ，因此△ABC 为等边三角形．。

根据正弦与余弦原理练习题及答案

根据正弦与余弦原理练习题及答案
以下是一些根据正弦与余弦原理的练题和答案，希望对你的研
究有所帮助：
1. 问题：已知三角形ABC中，角A的度数为30°，BC边长为6，AC边长为10。

求角B的度数和边AB的长度。

答案：根据正弦定理，我们可以得到正弦B的值：sin B = (AB / AC) = (AB / 10)，因此 AB = 10 * sin B。

又由于三角形ABC是直角三角形，我们知道角A + 角B + 角
C = 180°，所以角C = 180° - 30° - B。

根据余弦定理，我们可以得到：
AB^2 = BC^2 + AC^2 - 2 * BC * AC * cos C
将已知的数值代入计算即可得到答案。

2. 问题：已知三角形DEF中，角D的度数为60°，EF边长为8，DF边长为12。

求角E的度数和边DE的长度。

答案：根据正弦定理，我们可以得到正弦E的值：sin E = (DE / DF) = (DE / 12)，因此 DE = 12 * sin E。

同样地，由于三角形DEF是直角三角形，我们知道角D + 角E + 角F = 180°，所以角F = 180° - 60° - E。

根据余弦定理，我们可以得到：
DE^2 = EF^2 + DF^2 - 2 * EF * DF * cos F
将已知的数值代入计算即可得到答案。

请根据以上原理和计算方法，练习更多的题目，加深对正弦与余弦原理的理解和应用能力。

正余弦定理练习题（含答案）

A.6B.2 C.3 D ．26 2．在△ABC 中，已知a ＝8，B ＝60°，C ＝75°，则b 等于( ) A ．42 B ．43 C ．46 D.3233．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，A ＝60°，a ＝43，b ＝42，则角B 为( ) A ．45°或135°B ．135°C ．45°D ．以上答案都不对．以上答案都不对 4．在△ABC 中，a ∶b ∶c ＝1∶5∶6，则sin A ∶sin B ∶sin C 等于( ) A ．1∶5∶6B ．6∶5∶1 C ．6∶1∶5 D ．不确定．不确定解析：选A.由正弦定理知sin A ∶sin B ∶sin C ＝a ∶b ∶c ＝1∶5∶6. 5．在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若A ＝105°，B ＝45°，b ＝2，则c ＝( ) A ．1 B.12 C ．2 D.146．在△ABC 中，若cos A cos B ＝b．已知△ABC 中，AB ＝3，AC ＝1，∠B ＝30°，则△ABC C.32或3 D.34或3、b 、c .若c ＝2，b ＝6，B ＝120°，则a 等于( ) A.6 B ．2 C.3 D.2 9．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若a ＝1，c ＝3，C ＝π3，则A ＝________. 10．在△ABC 中，已知a ＝433，b ＝4，A ＝30°，则sin B ＝________. 11．在△ABC 中，已知∠A ＝30°，∠B ＝120°，b ＝12，则a ＋c ＝________. 12．在△ABC 中，a ＝2b cos C ，则△ABC 的形状为________．13．在△ABC 中，A ＝60°，a ＝63，b ＝12，S △ABC ＝183，则a ＋b ＋csin A ＋sin B ＋sin C ＝________，c ＝________. 14．已知△ABC 中，∠A ∶∠B ∶∠C ＝1∶2∶3，a ＝1，则a －2b ＋csin A －2sin B ＋sin C＝________. 15．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________. 16．在△ABC 中，b ＝43，C ＝30°，c ＝2，则此三角形有________组解．组解．的方向航行，为了确定船位，船在B 点观测灯塔A 的方位角为110°，航行半小时后船到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是多少？的距离是多少？18．在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，若a ＝23，sin C 2cos C 2＝14，sin B sin C ＝cos 2、c ，且cos cos 22A ＝35，sin B ＝1010.(1)求A ＋B 的值；(2)若a －b ＝2－1，求a ，b ，c 的值．的值．20．△ABC 中，ab ＝603，sin B ＝sin C ，△ABC 的面积为153，求边b 的长．的长．1．在△ABC 中，∠A ＝45°，∠B ＝60°，a ＝2，则b 等于( ) a，则△ABC 是( ) A ．等腰三角形 B ．等边三角形 C ．直角三角形 D ．等腰三角形或直角三角形．等腰三角形或直角三角形 7的面积为( ) A.32B.3428．△ABC 的内角A 、B 、C 的对边分别为a 17．如图所示，货轮在海上以40 40 km/h km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°A2，求A 、B 及b 、c . 19．(2009年高考四川卷)在△ABC 中，A 、B 为锐角，角A 、B 、C 所对应的边分别为a 、b，那么26 6 6 ＝3－A.3 B.2 5 c 2＋3bc ＝3A.π B.π C.π或5π D.π或2π ＝3，c A.3 ．23 C.323 3，则边32＝13，则＝a ＋b －c 1为3，则(3－(3∶1023x 为2＝2sin 的面积为1sin ＝5，－π)A.6B.2 3 6 应用正弦定理得：＝，求得＝＝ 6. 42 43 46 D.32＝ 6. 3，42，则角由正弦定理＝得：＝＝2，又∵＝2，则B.1 D.1，由＝得＝2×2×sin 30°sin 30°＝中，若cos A ＝，则△∵＝sin B ，∴cos A ＝sin B ，π. 3A.3 B.3 C.3或3 D.3或3D.＝，求出＝3，∵1AB ，6A.6 C.3 D.2 由正弦定理得6＝2，＝ 2. 3，π，则＝2＝1. A ＝csin C，所以sin A ＝a ·sin C c ＝12. 又∵a ＜c ，∴A ＜C ＝π3，∴A ＝π6. 答案：π610．在△ABC 中，已知a ＝433，b ＝4，A ＝30°，则sin B ＝________. 解析：由正弦定理得a sin A ＝bsin B ⇒sin B ＝b sin A a ＝4×12433＝32. 答案：3211．在△ABC 中，已知∠A ＝30°，∠B ＝120°，b ＝12，则a ＋c ＝________. 解析：C ＝180°－120°－30°＝30°，∴a ＝c ，由a sin A ＝b sin B 得，a ＝12×12×sin30°sin30°sin120°＝43， ∴．在△ABC 中，A ＝60°，a ＝63，b ＝12，S △ABC ＝183，则a ＋b ＋csin A ＋sin B ＋sin C＝________，c ＝________. 解析：由正弦定理得a ＋b ＋c sin A ＋sin B ＋sin C ＝a sin A ＝63sin60°＝12，又S △ABC ＝12bc sin A ，∴12×12×12×sin60°sin60°sin60°××c ＝183， ∴c ＝6. 答案：12 6 14．已知△ABC 中，∠A ∶∠B ∶∠C ＝1∶2∶3，a ＝1，则a －2b ＋csin A －2sin B ＋sin C ＝________. 解析：由∠A ∶∠B ∶∠C ＝1∶2∶3得，∠A ＝30°，∠B ＝60°，∠C ＝90°， ∴2R ＝a sin A ＝1sin30°＝2，又∵a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ， ∴a －2b ＋c sin A －2sin B ＋sin C ＝2R s in A －2sinB ＋sin C sin A －2sin B ＋sin C ＝2R ＝2. 答案：2 15．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________. 解析：由解析：由正弦定理正弦定理得：a sin a ＋c ＝8 3. 答案：83 12．在△ABC 中，a ＝2b cos C ，则△ABC 的形状为________．解析：由正弦定理，得a ＝2R ·sin A ，b ＝2R ·sin B ，代入式子a ＝2b cos C ，得，得 2R sin A ＝2·2·22R ·sin B ·cos C ，所以sin A ＝2sin B ·cos C ，即sin B ·cos C ＋cos B ·sin C ＝2sin B ·cos C ，化简，整理，得sin(B －C )＝0. ∵0°＜B ＜180°，0°＜C ＜180°， ∴－180°＜B －C ＜180°， ∴B －C ＝0°，B ＝C . 答案：答案：等腰三角形等腰三角形13解析：依题意，sin C ＝223，S △ABC ＝12ab s in C ＝43，解得b ＝2 3. 答案：23 16．在△ABC 中，b ＝43，C ＝30°，c ＝2，则此三角形有________组解．组解．解析：∵b sin C ＝＝BC ·sin ∠ABCsin A ＝20sin30°sin45°＝102(km)．即货轮到达C 点时，与灯塔A 的距离是102 2 km. km. 18．在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，若a ＝23，sin C 2cos C 2＝14，sin B sin C ＝cos 2A2，求A 、B 及b 、c . 解：由sin C 2cos C 2＝14，得sin C ＝12，又C ∈(0，π)，所以C ＝π6或C ＝5π6. 由sin B sin C ＝cos 2A2，得，得sin B sin C ＝12[1－cos(B ＋C )]，即2sin B sin C ＝1－cos(B ＋C )，即2sin B sin C ＋cos(B ＋C )＝1，变形得，变形得 cos B cos C ＋sin B sin C ＝1，即cos(B －C )＝1，所以B ＝C ＝π6，B ＝C ＝5π6(舍去)，A ＝π－(B ＋C )＝2π3. 由正弦定理a sin A ＝b sin B ＝csin C ，得，得b ＝c ＝a sin B sin A ＝23×1232＝2. 故A ＝2π3，B ＝π6，b ＝c ＝2. 19．(2009所对应的边分别为a 、b 、c ，且cos cos 22A ＝35，sin B ＝1010.(1)求A ＋B 的值；(2)若a －b ＝2－1，求a ，b ，c 的值．的值． 43×12＝23且c ＝2，∴c <b sin C ，∴此三角形无解．，∴此三角形无解．答案：0 17．如图所示，货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行，为了确定船位，船在B 点观测灯塔A 的方位角为110°，航行半小时后船到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是多少？的距离是多少？解：在△ABC 中，BC ＝40×12＝20，∠ABC ＝140°－110°＝30°，∠ACB ＝(180°－140°140°))＋65°＝105°，所以∠A ＝180°－(30°＋105°105°))＝45°，由正弦定理得AC 年高考四川卷)在△ABC 中，A 、B 为锐角，角A 、B 、C＝10，＝1－sin 2B ＝310. ＝3，∴＝5，25，25×310－5×10＝2. π. 3π2＝＝得5a ＝10b ＝2c 2b ＝5－b ＝2－，∴2＝2－＝2，c ＝ 5. 603×3×sin ＝1，∴∠3，sin A ＝sin B ，∴215. 21，那么6 6 46 AC ＝AB 2＋BC 2－2AB ·BC cos B ＝ 42＋62－2×2×4×4×4×6×6×13＝6. ．在△ABC 中，a ＝2，b ＝3A.3 2 C.5 2(3－2×((32. ＋3bc ＝＝－3bc 2bc ＝－32，：603153＝1153115. 4．在△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若(a 2＋c 2－b 2)tan B ＝3ac ，则∠B 的值为( ) A.π6B.π3C.π6或5π6D.π3或2π3解析：选D.由(a 2＋c 2－b 2)tan B ＝3ac 2－b 22ac ＝32·1tan B ＝32·cos Bsin B . 显然∠B ≠π2，∴sin B ＝32.∴∠B ＝π3或2π3. 5．在△ABC 中，a 、b 、c 分别是A 、B 、C 的对边，则a cos B ＋b cos A 等于( ) A ．a B ．b ＋2m 2＞c 2＋2cm ＋m 2＝(c ＋m )2， ∴三角形各角均为锐角，即新三角形为锐角三角形．∴三角形各角均为锐角，即新三角形为锐角三角形．7．已知锐角三角形ABC 中，|AB →|＝4，|AC →|＝1 ) A ．2 B ．－2 C ．4 D ．－4 解析：选A.S △ABC ＝3＝12|AB →|·|·||AC →|·|·sin sin A＝12×4×4×1×1×1×sin sin A ， ∴sin A ＝32，又∵△ABC 为锐角三角形，为锐角三角形，∴cos A ＝12，∴AB →·AC →＝4×4×1×1×12＝2. 8．在△ABC 中，b ＝3，c ＝3，B ＝30°，则a 为( ) A.3 B ．23 C.3或23 D ．2 解析：选C.在△ABC 中，由余弦定理得b 2＝a 2＋c 2－2ac cos B ，即3＝a 2＋9－33a ， ∴a 2－33a ＋6＝0，解得a ＝3或2 3. 9．已知△ABC π3. 在△ABD 中，中，AD ＝AB 2＋BD 2－2AB ·BD cos B＝ 1＋4－2×2×1×1×1×2×2×12＝ 3. 答案：3 10．△ABC 中，sin A ∶sin B ∶sin C ＝(3－1)∶(3＋1)∶10，求最大角的度数．，求最大角的度数．解：∵sin A ∶sin B ∶sin C ＝(3－1)∶(3＋1)∶10， ∴a ∶b ∶c ＝(3－1)∶(3＋1)∶10. 设a ＝(3－1)k ，b ＝(3＋1)k ，c ＝10k (k ＞0)，，联想到余弦定理，代入得到余弦定理，代入得cos B ＝a 2＋c C ．c D ．以上均不对．以上均不对解析：选C.a ·a 2＋c 2－b 22ac ＋b ·b 2＋c 2－a 22bc ＝2c 22c＝c . 6．如果把．如果把直角三角形直角三角形的三边都增加同样的长度，则这个新的三角形的形状为( ) A ．锐角三角形三角形 B ．直角三角形．直角三角形 C ．钝角三角形．钝角三角形 D ．由增加的长度决定．由增加的长度决定解析：选A.设三边长分别为a ，b ，c 且a 2＋b 2＝c 2. 设增加的长度为m ，则c ＋m ＞a ＋m ，c ＋m ＞b ＋m ，又(a ＋m )2＋(b ＋m )2＝a 2＋b 2＋2(a ＋b )m ，△ABC 的面积为3，则AB →·AC →的值为( 的三个的三个内角内角满足2B ＝A ＋C ，且AB ＝1，BC ＝4，则边BC 上的上的中线中线AD 的长为________．解析：∵2B ＝A ＋C ，A ＋B ＋C ＝π，∴B ＝＝－1，3，＝1ab ＝3，∴＝＝＝11，7，＝－132，43＝1，∴＝22. 1ab 431·32·22＝432 3. 答案：23 ＝＝49＋25－36 19，－19) ±12，又∵＝21或61. 答案：21或61 ，则角1ab ＝＝·1ab4＝78. 答案：723x ＋2＝0的两根，且2cos(A ＋B )＝1，求AB 的长．解：∵A ＋B ＋C ＝π且2cos(A ＋B )＝1，∴cos(π－C )＝12，即cos C ＝－12. 又∵a ，b 是方程x 2－23x ＋2＝0的两根，的两根，∴a ＋b ＝23，ab ＝2. ∴AB 2＝AC 2＋BC 2－2AC ·BC ·cos C＝a 2＋b 2－2ab (－12) ＝a 2＋b 2＋ab ＝(a ＋b )2－ab ＝(23)2－2＝10， ∴AB ＝10. 18．已知△ABC AC ＝2＋1，BC ＋AC ＝2AB ，两式相减，得AB ＝1. (2)由△ABC 的面积12BC ·AC ·sin C ＝AC 2＋BC 2－AB 22AC ·BC＝A C ＋BC 2－2AC ·BC －AB 22AC ·BC ＝12，所以C ＝60°60°. . 19．在△ABC 中，BC ＝5，AC ＝3，sin C ＝2sin A . (1)求AB 的值；的值；(2)求sin(2A －π4)的值．的值．解：(1)在△ABC 中，由正弦定理AB sin C ＝BCsin A ，得AB ＝sin Csin A BC ＝2BC ＝2 5. (2)在△ABC 中，根据余弦定理，得中，根据余弦定理，得cos A ＝AB 2＋AC 2－BC 22AB ·AC ＝255，于是sin A ＝1－cos 2A ＝55. 从而sin 2A ＝2sin A cos A ＝45， cos 2A ＝cos 2 A －sin 2 A ＝35. 所以sin(2A －π4)＝sin 2A cos π4－cos 2A sin π4＝210. 则îïíïìk 2＋k －12－k ＋12＜0k ＋k －1＞k ＋1⇒2＜k ＜4， ∴k ＝3，故三边长分别为2,3,4，∴最小角的∴最小角的余弦余弦值为32＋42－222×2×3×3×817．在△ABC 中，BC ＝a ，AC ＝b ，a ，b 是方程x 2－的周长为2＋1，且sin A ＋sin B ＝2sin C . (1)求边AB 的长；的长； (2)若△ABC 的面积为16sin C ，求角C 的度数．的度数．解：(1)由题意及由题意及正弦定理正弦定理得AB ＋BC ＋＝16sin C ，得BC ·AC ＝13，由余弦定理得cos C＝. sin C ，所以＝，得sin C ＝，。

正弦定理和余弦定理专题试题及答案

正弦定理和余弦定理专题试题及答案1．在△ABC 中，若sin 2A ＋sin 2B ＜sin 2C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形2．在△ABC 中，已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( ) A ．有一解 B ．有两解 C ．无解 D ．有解但解的个数不确定3．已知△ABC 中，内角A ，B ，C 的对边分别为ɑ，b ，c ，若ɑ2＝b 2＋c 2－bc ，bc ＝4，则△ABC 的面积为( ) A.12 B ．1 C.3 D ．24．在△ABC 中，内角A ，B ，C 的对边分别为ɑ，b ，c ，且bsin A ＝3ɑcos B ．则B ＝( ) A.π6 B.π4 C.π3 D.π25．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c.若3a ＝2b ，则2sin 2B －sin 2Asin 2A的值为( )A ．－19B .13C ．1D .726．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，且满足c sin A ＝3a cos C ，则sin A ＋sin B 的最大值是( )A ．1B . 2C . 3D ．37.在△ABC 中,若A=,B=,BC=3,则AC=( )A. B. C.2D.48.在△ABC 中,若a 2+b 2<c 2,则△ABC 的形状是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定9.已知△ABC 的内角A,B,C 的对边分别为a,b,c,且=,则B= ( ) A.B. C. D.10.在△ABC 中,角A,B,C 所对的边长分别为a,b,c.若C=120°,c=a,则 ( )A.a>bB.a<bC.a=bD.a 与b 的大小关系不能确定11．在△ABC 中，已知AB →·AC →＝tan A ，当A ＝π6时，△ABC ＝的面积为________．12．若△ABC 的内角满足sin A ＋2sin B ＝2sin C ，则cos C 的最小值是________．13.△ABC 中,点D 是BC 上的点,AD 平分∠BAC,BD=2DC. (1)求.(2)若∠BAC=60°,求B.14.在△ABC 中,角A,B,C 的对边分别为a,b,c,且bcosC=3acosB-ccosB. (1)求cosB 的值. (2)若·=2,且b=2,求a 和c 的值.15．如图，在△ABC 中，点P 在BC 边上，∠PAC ＝60°，PC ＝2，AP ＋AC ＝4.(1)求∠ACP ；(2)若△APB 的面积是332，求sin ∠BAP .16．在△ABC 中，角A ，B ，C 的对边分别是ɑ，b ，c ，且b 2＝ɑc ＝ɑ2－c 2＋bc. (1)求bsin Bc的值； (2)试判断△ABC 的形状，并说明理由．正弦定理和余弦定理专题试题及答案1．在△ABC 中，若sin 2A ＋sin 2B ＜sin 2C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形答案：C2．在△ABC 中，已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( ) A ．有一解 B ．有两解 C ．无解 D ．有解但解的个数不确定解析：由正弦定理得b sin B ＝csin C，∴sin B ＝bsin Cc＝40×3220＝3＞1.∴角B 不存在，即满足条件的三角形不存在．答案：C3．已知△ABC 中，内角A ，B ，C 的对边分别为ɑ，b ，c ，若ɑ2＝b 2＋c 2－bc ，bc ＝4，则△ABC 的面积为( ) A.12B ．1 C. 3 D ．2 解析：∵ɑ2＝b 2＋c 2－bc ，∴cos A ＝12，∴A ＝π3，又bc ＝4，∴△ABC 的面积为12bcsin A ＝3，故选C.答案：C4．在△ABC 中，内角A ，B ，C 的对边分别为ɑ，b ，c ，且bsin A ＝3ɑcos B ．则B ＝( ) A.π6 B.π4 C.π3 D.π2解析：根据题意结合正弦定理，得sin Bsin A ＝3sin Acos B. 因为sin A ≠0，所以sin B ＝3cos B ，即sin B cos B ＝tan B ＝3，所以B ＝π3. 答案：C5．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c.若3a ＝2b ，则2sin 2B －sin 2A sin 2A的值为( )A ．－19B .13C ．1D .72解析：由正弦定理可得2sin 2B －sin 2A sin 2A ＝2⎝ ⎛⎭⎪⎫sinB sin A 2－1＝2⎝ ⎛⎭⎪⎫b a 2－1，因为3a ＝2b ，所以b a ＝32，所以2sin 2B －sin 2A sin 2A ＝2×⎝ ⎛⎭⎪⎫322－1＝72。

(完整版)正弦定理和余弦定理练习题

【正弦定理、余弦定理模拟试题】一. 选择题：1. 在∆ABC 中，a b B ===︒232245，，，则A 为（）A B C D ....60120603015030︒︒︒︒︒︒或或2. 在∆AB C A a B bB 中，若，则sin cos =∠=（） A BCD ....30456090︒︒︒︒3. 在∆ABC 中，a b c bc 222=++，则A 等于（）A B C D ....604512030︒︒︒︒4. 在∆ABC 中，||||()()AB BC AB BC AB BC →=→=→+→⋅→+→=+12523，，，则边||AC →等于（） A B C D ....5523523523--+5. 以4、5、6为边长的三角形一定是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 锐角或钝角三角形6. 在∆ABC 中，b A a B cos cos =，则三角形为（）A. 直角三角形B. 锐角三角形C. 等腰三角形D. 等边三角形7. 在∆ABC 中，cos cos sin sin A B A B >，则∆ABC 是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 正三角形8. 三角形的两边分别为5和3，它们夹角的余弦是方程57602x x --=的根，则三角形的另一边长为（）A. 52B. 213C. 16D. 4二. 填空题：9. 在∆ABC 中，a b A B +==︒=︒126045，，，则a =_______，b =________10. 在∆ABC 中，化简b C c B cos cos +=___________11. 在∆ABC 中，已知sin :sin :sin ::A B C =654，则cosA =___________12. 在∆ABC 中，A 、B 均为锐角，且cos sin A B >，则∆ABC 是_________三. 解答题：13. 已知在∆ABC 中，∠=︒==A a c 4526，，，解此三角形。

正弦定理与余弦定理练习题共3套（附答案）

正弦定理与余弦定理练习第一套正弦定理（一）●作业导航掌握正弦定理，会利用正弦定理求已知两角和任意一边或两边和一边对角的三角形问题．一、选择题(本大题共5小题，每小题3分，共15分)1．已知△ABC 中，a ＝4，b ＝43，∠A ＝30°，则∠B 等于()A ．30°B ．30°或150°C ．60°D ．60°或120°2．已知△ABC 中，AB ＝6，∠A ＝30°，∠B ＝120°，则△ABC 的面积为()A ．9B ．18C ．93D ．1833．已知△ABC 中，a ∶b ∶c ＝1∶3∶2，则A ∶B ∶C 等于()A ．1∶2∶3B ．2∶3∶1C ．1∶3∶2D ．3∶1∶24．已知△ABC 中，sin A ∶sin B ∶sin C ＝k ∶(k ＋1)∶2k (k≠0)，则k 的取值范围为()A ．(2，＋∞)B ．(-∞，0)C ．(-21，0)D ．(21，＋∞) 5．在△ABC 中，sin A ＞sin B 是A ＞B 的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件二、填空题(本大题共5小题，每小题3分，共15分)1．在△ABC 中，若∠B ＝30°，AB ＝23，AC ＝2，则△ABC 的面积是________．2．在△ABC 中，若b ＝2c sin B ，则∠C ＝________．3．设△ABC 的外接圆半径为R ，且已知AB ＝4，∠C ＝45°，则R ＝________．4．已知△ABC 的面积为23，且b ＝2，c ＝3，则∠A ＝________．5．在△ABC 中，∠B ＝45°，∠C ＝60°，a ＝2(3＋1)，那么△ABC 的面积为________．三、解答题(本大题共5小题，每小题6分，共30分)1．在△ABC 中，∠C ＝60°，BC ＝a ，AC ＝b ，a ＋b ＝16．(1)试写出△ABC 的面积S 与边长a 的函数关系式．(2)当a 等于多少时，S 有最大值？并求出这个最大值．2．在△ABC 中，已知a 2-a ＝2(b ＋c )，a ＋2b ＝2c -3，若sin C ∶sin A ＝4∶13，求a ，b ，c ．3．在△ABC 中，求证2tan 2tanBA BA b a b a +-=+-．4．△ABC 中，A 、B 、C 成等差数列，b ＝1，求证：1＜a ＋c ≤2．5．在一个三角形中，若有一个内角不小于120°，求证：最长边与最短边之比不小于3．参考答案一、选择题(本大题共5小题，每小题3分，共15分)1．D 分析：由正弦定理得，B bA a sin sin =，∴sin B ＝23sin =aA b ，∴∠B ＝60°或∠B ＝120°．2．C 分析：∵∠A ＝30°，∠B ＝120°，∴∠C ＝30°，∴BA ＝BC ＝6，∴S △ABC ＝21×BA ×BC ×sin B ＝21×6×6×23＝93．3．A 分析：由正弦定理得，C cB b A a sin sin sin ==，∴sin A ∶sin B ∶sin C ＝1∶3∶2＝21∶23∶1，∴A ∶B ∶C ＝30°∶60°∶90°＝1∶2∶3．4．D 分析：利用正弦定理及三角形两边之和大于第三边．5．C 分析：A ＞B ⇔a ＞b ⇔2Rsin A ＞2Rsin B ⇔sin A ＞sin B ．二、填空题(本大题共5小题，每小题3分，共15分)1．23或3分析：sin C ＝23230sin 32=︒，于是，∠C ＝60°或120°，故∠A ＝90°或30°，由S △ABC ＝21×AB ×AC ×sin A ，可得S △ABC ＝23或S △ABC ＝3．2．30°或150°分析：由b ＝2c sin B 及正弦定理C cB B c Cc B b sin sin sin 2sin sin ==得，∴sin C ＝21，∴∠C ＝30°或150°．3．22分析：∵c ＝2R sin C ，∴R ＝22sin 2=C c．4．60°或120°分析：∵S △ABC ＝21bc sin A ，∴23＝21×2×3sin A ，∴sin A＝23，∴∠A ＝60°或120°．5．6＋23分析：∵B bA a sin sin =，∴︒=︒-︒-︒+45sin )6045180sin()13(2b，∴b ＝4．∴S △ABC ＝21ab sin C ＝6＋23．三、解答题(本大题共5小题，每小题6分，共30分)1．解：(1)∵a ＋b ＝16，∴b ＝16-aS ＝21ab sin C ＝21a (16-a )sin60°＝43(16a -a 2)＝-43(a -8)2＋163（0＜a ＜16)(2)由(1)知，当a ＝8时，S 有最大值163．2．解：∵sin C ∶sin A ＝4∶13∴c ∶a ＝4∶13设c ＝4k ，a ＝13k ，则⎪⎩⎪⎨⎧-=++=-38213)4(213132k b k k b kk∵k ＝133时b ＜0，故舍去．∴k ＝1，此时a ＝13，b ＝2135-，c ＝4．3．证明：由正弦定理，知a ＝2R sin A ，b ＝2R sin B2tan2tan2cos 2sin 22cos 2sin 2)22sin(22sin()22sin()22sin(sin sin sin sin sin 2sin 2sin 2sin 2B A B A B A B A B A B A B A B A B A B A B A B A B A B A BA BA B R A R B R A R b a b a +-=-++-=--++-++--+--++=+-=+-=+-∴4．证明：∵A 、B 、C 成等差数列，∴2B ＝A ＋C ，又A ＋B ＋C ＝π，∴B ＝3π，A ＋C ＝32π．∵b ＝1，设△ABC 的外接圆半径为R ，∴b ＝2R sin 3π∴1＝2R ·23，∴3R ＝1．∴a ＋c ＝2R sin A ＋2R sin C ＝2R (sin A ＋sin C )＝2R ［sin(32π-C )＋sin C ］＝2R (23cos C ＋23sin C )＝23R (21cos C ＋23sin C )＝23R sin(C ＋6π)＝2sin(C ＋6π)∵A ＋C ＝32π，∴0＜C ＜32π∴6π＜C ＋6π＜65π∴21＜sin(C ＋6π)≤1∴1＜2sin(C ＋6π)≤2 ∴1＜a ＋c ≤2．5．证明：在△ABC 中，设C ≥120°，则c 最长，令最短边为a ，由正弦定理得A B A A C a c sin )sin(sin sin +==∵A ≤B∴2A ≤A ＋B ≤180°-C ≤60°∵正弦函数在(0，3π)上是增函数，∴sin(A ＋B )≥sin2A ＞0∴A B A a c sin )sin(+=≥A A A A A sin cos sin 2sin 2sin =＝2cos A ∴a c≥2cos A ∵2A ≤60° ∴0°＜A ≤30°∴cos A ≥cos30°＝23∴a c ≥2·23∴a c≥3∴最长边与最短边之比不小于第二套正弦定理练习（二）1．在ABC ∆中，已知角04345,2,,3B c b ===则角A 的值是（）A．15°B．75°C．105°D．75°或15°2．ABC ∆中，bsinA<a<b,则此三角形有（）A．一解B．两解C．无解D．不确定3．若sin cos cos ,A B CABC a b c==∆则是（）A．等边三角形B．有一内角是30°C．等腰直角三角形D．有一内角是30°的等腰三角形4．在ABC ∆中，已知0060,45,8,B C BC AD BC ===⊥于D,则AD 长为（）A.4(31)- B.4(3+1)3+3)D.4(33)5．在ABC ∆中，A>B 是sinA>sinB 的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件6．在ABC ∆中，060,6,14B b a ===，则A=7．在ABC ∆ABC ∆中，已知cos 2cos 21sin 2sin cos ,cos sin B C A B C C B +=+==求证：b=c 且A=900。

(完整版)正余弦典型例题及详细答案

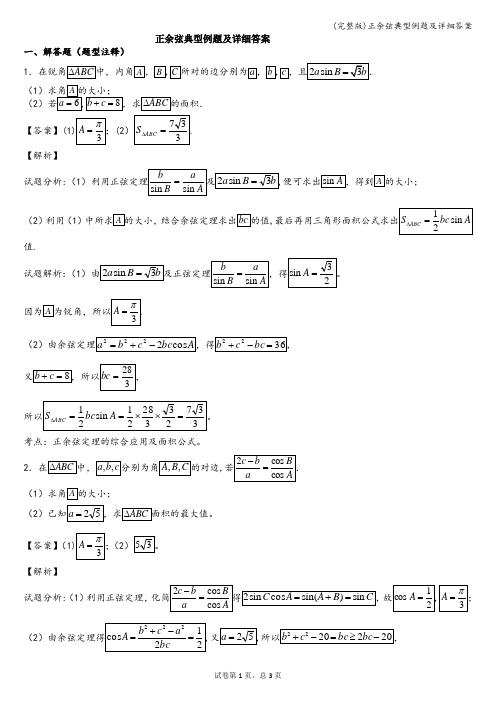
正余弦典型例题及详细答案一、解答题（题型注释）1（1（2【答案】(2【解析】试题分析:（1;（2）利用（1）,值.试题解析：（1（2考点：正余弦定理的综合应用及面积公式。

2,（1（2【答案】（（2【解析】试题分析:（1）利用正弦定理，（2试题解析：(1（2=”考点：解三角形，正余弦定理，基本不等式．3（1(2【答案】（1（2【解析】试题分析：（1）等差数列再由正弦定理6sin(3045)4+=+=，再由正弦定理2245sin60sin7526224b a==⇒=+,,则11sin2(22ABCS ac B∆==⨯2分sin 6032A =4分 120，∴6分 675sin(3045)4+=+=分 245sin 60sin 752322b a b==⇒=2(31)6(31)b -=-，， 10分12分4．已知A 、B 、C 为三角形ABC 的三内角,其对应边分别为a ，b ，c,若有2acosC=2b+c 成立. (1）求A 的大小；（2)ABC 的面积. 【答案】（1（2【解析】试题分析：（1)A 的余弦值，从而求出角A ；（2,,再结合上题中求得的角A试题解析:(1（2)考点：正弦定理，余弦定理，三角形两边一夹角的面积公式,化归与转化的数学思想.。

高考正弦定理和余弦定理练习题及答案

高考正弦定理和余弦定理练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN高考正弦定理和余弦定理练习题及答案一、选择题1. 已知△ABC 中，a ＝c ＝2，A ＝30°，则b ＝( ) A. 3 B. 23 C. 3 3D. 3＋1答案：B解析：∵a ＝c ＝2，∴A ＝C ＝30°，∴B ＝120°. 由余弦定理可得b ＝2 3.2. △ABC 中，a ＝5，b ＝3，sin B ＝22，则符合条件的三角形有( ) A. 1个 B. 2个 C. 3个D. 0个答案：B 解析：∵a sin B ＝102， ∴a sin B <b ＝3<a ＝5， ∴符合条件的三角形有2个．3．(2010·天津卷)在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c .若a 2－b 2＝3bc ，sin C ＝23sin B ，则A ＝( )A ．30°B ．60°C ．120°D ．150°答案：A解析：利用正弦定理，sin C ＝23sin B 可化为c ＝23b . 又∵a 2－b 2＝3bc ，∴a 2－b 2＝3b ×23b ＝6b 2，即a 2＝7b 2，a ＝7b . 在△ABC 中，cos A ＝b 2＋c 2－a 22bc＝b 2＋(23b )2－(7b )22b ×23b ＝32，∴A ＝30°.4．(2010·湖南卷)在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C ＝120°，c ＝2a ，则( )A ．a >bB ．a <bC ．a ＝bD ．a 与b 的大小关系不能确定答案：A解析：由正弦定理，得c sin120°＝asin A ，∴sin A ＝a ·322a＝64>12.∴A >30°.∴B ＝180°－120°－A <30°.∴a >b .5. 如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为( ) A. 518 B. 34 C. 32D. 78答案：D解析：方法一：设三角形的底边长为a ，则周长为5a ， ∴腰长为2a ，由余弦定理知cos α＝(2a )2＋(2a )2－a 22×2a ×2a ＝78.方法二：如图，过点A 作AD ⊥BC 于点D ，则AC ＝2a ，CD ＝a 2，∴sin α2＝14，∴cos α＝1－2sin 2α2＝1－2×116＝78.6. (2010·泉州模拟)△ABC 中，AB ＝3，AC ＝1，∠B ＝30°，则△ABC 的面积等于( )A. 32B. 34C.32或 3D. 32或34答案：D解析：∵sin C 3＝sin B1，∴sin C ＝3·sin30°＝32. ∴C ＝60°或C ＝120°.当C ＝60°时，A ＝90°，S △ABC ＝12×1×3＝32，当C ＝120°时，A ＝30°，S △ABC ＝12×1×3sin30°＝34.即△ABC 的面积为32或34. 二、填空题7．在△ABC 中，若b ＝1，c ＝3，∠C ＝2π3，则a ＝________.答案：1解析：由正弦定理b sin B ＝c sin C ，即1sin B ＝3sin 2π3，sin B ＝12. 又b <c ，∴B ＝π6，∴A ＝π6.∴a ＝1.8．(2010·山东卷)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝2，b ＝2，sin B ＋cos B ＝2，则角A 的大小为________．答案：π6解析：∵sin B ＋cos B ＝2， ∴sin(B ＋π4)＝1.又0<B <π，∴B ＝π4.由正弦定理，知2sin A ＝2sin B ，∴sin A ＝12.又a <b ，∴A <B ，∴A ＝π6.9. (2010·课标全国卷)在△ABC 中，D 为边BC 上一点，BD ＝12DC ，∠ADB ＝120°，AD＝2.若△ADC 的面积为3－3，则∠BAC ＝________.答案：60°解析：S △ADC ＝12×2×DC ×32＝3－3，解得DC ＝2(3－1)，∴BD ＝3－1，BC ＝3(3－1)．在△ABD 中，AB 2＝4＋(3－1)2－2×2×(3－1)×cos120°＝6， ∴AB ＝ 6.在△ACD 中，AC 2＝4＋[2(3－1)]2－2×2×2(3－1)×cos60°＝24－123， ∴AC ＝6(3－1)，则cos ∠BAC ＝AB 2＋AC 2－BC 22AB ·AC＝6＋24－123－9(4－23)2×6×6×(3－1)＝12， ∴∠BAC ＝60°. 三、解答题10. 如图，△OAB 是等边三角形，∠AOC ＝45°，OC ＝2，A 、B 、C 三点共线．(1)求sin ∠BOC 的值； (2)求线段BC 的长．解：(1)∵△AOB 是等边三角形，∠AOC ＝45°， ∴∠BOC ＝45°＋60°， ∴sin ∠BOC ＝sin(45°＋60°) ＝sin45°cos60°＋cos45°sin60° ＝2＋64. (2)在△OBC 中，OC sin ∠OBC ＝BCsin ∠BOC ，∴BC ＝sin ∠BOC ×OCsin ∠OBC＝2＋64×2sin60°＝1＋33. 11. (2010·全国Ⅱ卷)△ABC 中，D 为边BC 上的一点，BD ＝33，sin B ＝513，cos ∠ADC＝35，求AD .解：由cos ∠ADC ＝35>0知B <π2，由已知得cos B ＝1213，sin ∠ADC ＝45，从而sin ∠BAD ＝sin(∠ADC －B ) ＝sin ∠ADC cos B －cos ∠ADC sin B ＝45×1213－35×513＝3365. 由正弦定理得AD sin B ＝BDsin ∠BAD ，AD ＝BD ·sin Bsin ∠BAD＝33×5133365＝25.12. (2010·安徽卷)设△ABC 是锐角三角形，a ，b ，c 分别是内角A ，B ，C 所对边长，并且sin 2A ＝sin ⎝⎛⎭⎫π3＋B sin ⎝⎛⎭⎫π3－B ＋sin 2B . (1)求角A 的值；(2)若AB →·AC →＝12，a ＝27，求b ，c (其中b <c )．解：(1)因为sin 2A ＝⎝⎛⎭⎫32cos B ＋12sin B⎝⎛⎭⎫32cos B －12sin B ＋sin 2B ＝34cos 2B －14sin 2B ＋sin 2B ＝34，所以sin A ＝±32.又A 为锐角，所以A ＝π3.(2)由AB →·AC →＝12，可得cb cos A ＝12.① 由(1)知A ＝π3，所以cb ＝24.②由余弦定理知a 2＝c 2＋b 2－2cb cos A ，将a ＝27及①代入，得c 2＋b 2＝52，③ ③＋②×2，得(c ＋b )2＝100，所以c ＋b ＝10.因此c ，b 是一元二次方程t 2－10t ＋24＝0的两个根．解此方程并由c >b 知c ＝6，b ＝4.。

高中数学必修二 6 4 2 正余弦定理(精练)(含答案)

6.4.2 正余弦定理（精练）【题组一余弦定理】1．（2020·福建宁德市·高一期末）在三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，其中2a =，b =3B π=，则边c 的长为______．【答案】4【解析】因为2a =，b =3B π=，所以2222222cos 222cos3b ac ac B c c π=+-∴=+-⋅⋅⋅，228004c c c c ∴--=>∴=故答案为：42．（2020·上海高一课时练习）在ABC中，若a b c ===，则A =________.【答案】60°【解析】由余弦定理的推论得2222221cos 22b c aA bc +-+-===， 0180A <<，60A ∴=.故答案为：60°3．（2020·长春市第二实验中学高一期中）在ABC 中，若::5:7:8a b c =，则B 的大小是_______. 【答案】3π【解析】::5:7:8a b c =设5a k =，7b k =，8c k =，由余弦定理可得2221cos 22a cb B ac +-==；3B π∴∠=．故答案为：3π． 3．（2020·湖北荆门外语学校高一期中）在ABC 中，内角、、A B C 对应的边分别为ab c 、、，若120,2Ab =︒=，1c =，则边长a 为（）A B C D ．2【答案】A【解析】在ABC 中， 120,2A b =︒=，1c =，所以22212cos 4122172a b c bc A =+-=+-⨯⨯⨯=，a ∴= A.4．（2020·安徽高一期末）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .已知3b =，c =4A π=，则a =（）A ．5 BC ．29D【答案】B【解析】由余弦定理得a ===.故选：B 5．（2020·吉林长春市）在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，::3:2:4a b c =，则cos C 。

(完整版)正弦定理、余弦定理综合训练题含答案

正弦定理、余弦定理综合训练题1．[2016·全国卷Ⅰ] △ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知a ＝5，c ＝2，cos A ＝23，则b ＝( ) A. 2 B.3 C ．2 D ．3[解析] D 由余弦定理得5＝b 2＋4－2×b ×2×23，解得b ＝3或b ＝－13(舍去)，故选D. 2．[2016·全国卷Ⅲ] 在△ABC 中，B ＝π4，BC 边上的高等于13BC ，则sin A ＝( ) A.310 B.1010 C.55 D.31010[解析] D 作AD ⊥BC 交BC 于点D ，设BC ＝3，则有AD ＝BD ＝1，AB ＝2，由余弦定理得AC ＝ 5.由正弦定理得5sin π4＝3sin A，解得sin A ＝3×225＝31010. 3．[2013·新课标全国卷Ⅰ] 已知锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，23cos 2 A ＋cos 2A ＝0，a ＝7，c ＝6，则b ＝( )A ．10B ．9C ．8D ．5[解析] D 由23cos 2A ＋cos 2A ＝0，得25cos 2A ＝1.因为△ABC 为锐角三角形，所以cos A ＝15.在△ABC 中，根据余弦定理，得49＝b 2＋36－12b ·15，即b 2－125b 4．[2016·全国卷Ⅱ] △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若cos A ＝45，cos C ＝513，a ＝1，则b ＝________．[解析] 因为cos A ＝45，cos C ＝513，且A ，C 为三角形的内角，所以sin A ＝35，sin C ＝1213，sin B ＝sin(A ＋C )＝sin A cos C ＋cos A sin C ＝6365.又因为a sin A ＝b sin B ，所以b ＝a sin B sin A ＝2113. －13＝0，解得b ＝5或b ＝－135(舍去)． 5．[2015·全国卷Ⅰ] 已知a ，b ，c 分别是△ABC 内角A ，B ，C 的对边，sin 2B ＝2sin A sin C.(1)若a ＝b ，求cos B;(2)若B ＝90°，且a ＝2，求△ABC 的面积．解：(1)由题设及正弦定理可得b 2＝2ac .又a ＝b ，所以可得b ＝2c ，a ＝2c .由余弦定理可得cos B ＝a 2＋c 2－b 22ac ＝14. (2)由(1)知b 2＝2ac .因为B ＝90°，所以由勾股定理得a 2＋c 2＝b 2.故a 2＋c 2＝2ac ，得c ＝a ＝2，所以△ABC 的面积为1.6．[2015·全国卷Ⅱ] △ABC 中，D 是BC 上的点，AD 平分∠BAC ，BD ＝2D C.(1)求sin ∠B sin ∠C； (2)若∠BAC ＝60°，求∠B.解：(1)由正弦定理得AD sin ∠B ＝BD sin ∠BAD ，AD sin ∠C ＝DC sin ∠CAD. 因为AD 平分∠BAC ，BD ＝2DC ，所以sin ∠B sin ∠C ＝DC BD ＝12. (2)因为∠C ＝180°－(∠BAC ＋∠B )，∠BAC ＝60°，所以sin ∠C ＝sin(∠BAC ＋∠B )＝32cos ∠B ＋12sin ∠B. 由(1)知2sin ∠B ＝sin ∠C ，所以tan ∠B ＝33，即∠B ＝30°. 7．[2014·新课标全国卷Ⅱ] 四边形ABCD 的内角A 与C 互补，AB ＝1，BC ＝3，CD ＝DA ＝2.(1)求C 和BD ；(2)求四边形ABCD 的面积．解：(1)由题设及余弦定理得BD 2＝BC 2＋CD 2－2BC ·CD cos C＝13－12cos C ，①BD 2＝AB 2＋DA 2－2AB ·DA cos A＝5＋4cos C ．②由①②得cos C ＝12，故C ＝60°，BD ＝7. (2)四边形ABCD 的面积S ＝12AB ·DA sin A ＋12BC ·CD sin C ＝⎝⎛⎭⎫12×1×2＋12×3×2sin 60°＝2 3. 8.[2016·山东卷] △ABC 中，角A ，B ，C 的对边分别是a ，b ，c .已知b ＝c ，a 2＝2b 2(1－sin A )，则A ＝( )A.3π4B.π3C.π4D.π6[解析] C ∵b ＝c ，a 2＝2b 2(1－sin A )，∴2b 2sin A ＝b 2＋c 2－a 2＝2bc cos A ＝2b 2cos A ，∴tan A＝1，即A ＝π4. 9.[2015·广东卷] 设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝2，c ＝23，cos A ＝32且b <c ，则b ＝( ) A ．3 B ．22 C ．2 D. 3 [解析] C 由余弦定理得a 2＝b 2＋c 2－2bc cos A ，所以22＝b 2＋(23)2－2×b ×23×32，即b 2－6b ＋8＝0，解得b ＝2或b ＝4.因为b <c, 所以b ＝2.10.[2016·上海卷] 已知△ABC 的三边长分别为3，5，7，则该三角形的外接圆半径等于________．[解析] 利用余弦定理可求得最大边7所对角的余弦值为32＋52－722×3×5＝－12，所以此角的正弦值为32.设三角形外接圆的半径为R ，由正弦定理得2R ＝732，所以R ＝733. 11.[2016·北京卷] 在△ABC 中，∠A ＝2π3，a ＝3c ，则b c＝________．[解析] 由余弦定理a 2＝b 2＋c 2－2bc cos A 可得，3c 2＝b 2＋c 2－2bc cos 2π3，整理得b c 2＋b c－2＝0，解得b c ＝1或b c＝－2(舍去)．12.[2016·浙江卷] 在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知b ＋c ＝2a cos B .(1)证明：A ＝2B ；(2)若cos B ＝23，求cos C 的值．解：(1)证明：由正弦定理得sin B ＋sin C ＝2sin A cos B ，故2sin A cos B ＝sin B ＋sin(A ＋B )＝sin B ＋sin A cos B ＋cos A sin B ，于是sin B ＝sin(A －B )．又A ，B ∈(0，π)，故0＜A －B ＜π，所以B ＝π－(A －B )或B ＝A －B ，因此A ＝π(舍去)或A ＝2B ，所以A ＝2B.(2)由cos B ＝23得sin B ＝53，cos 2B ＝2cos 2B －1＝－19，故cos A ＝－19，sin A ＝459，cos C ＝－cos(A ＋B )＝－cos A cos B ＋sin A sin B ＝2227.。

正弦定理、余弦定理综合训练题含答案

正弦定理余弦定理习题及答案

正余弦定理3、已知a,b,c 分别是△ABC 的三个内角A,B,C 所对的边，若则sinC= . 4、如图，在△ABC 中，若b = 1，c23C π∠=，则a= 。

5、在ABC ∆中，角,,A B C 所对的边分别为a ，b ，c，若a =2b =，sin cos B B +=，则角A 的大小为．6、在∆ABC 中，,,a b c 分别为角,,A B C 的对边，且274sin cos 222B C A +-= （1）求A ∠的度数（2）若a =3b c +=，求b 和c 的值7、在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.8、如图，在△ABC 中，已知3=a ，2=b ，B=45︒ 求A 、C 及c .1.在△ABC 中，已知角B ＝45°，D 是BC 边上一点，AD ＝5，AC ＝7，DC ＝3，求AB ..AB2.在△ABC 中，已知cos A ＝35 ，sin B ＝513 ，求cos C 的值.3、在△ABC 中，已知2cos B sin C ＝sin A ，试判定△ABC 的形状.4..在△ABC 中，若sin A ＝sin B ＋sin Ccos B ＋cos C ，试判断△ABC 的形状.5.在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，求证：a 2－b 2c 2 ＝sin （A －B ）sin C. .6..在△ABC 中，若（a ＋b ＋c ）（b ＋c －a ）＝bc ，并且sin A ＝2sin B cos C ，试判断△ABC 的形状. \1.解：在△ADC 中，cos C ＝AC 2＋DC 2－AD 22AC ·DC ＝72＋32－522×7×3 ＝1114 ，又0＜C ＜180°，∴sin C ＝5314在△ABC 中，AC sin B ＝ABsin C ∴AB ＝sin C sin B AC ＝5314· 2 ·7＝5622.解：∵cos A ＝35 ＜22＝cos45°，0＜A ＜π∴45°＜A ＜90°，∴sin A ＝45∵sin B ＝513 ＜12 ＝sin30°，0＜B ＜π ∴0°＜B ＜30°或150°＜B ＜180° 若B ＞150°，则B ＋A ＞180°与题意不符.∴0°＜B ＜30° cos B ＝1213∴cos （A ＋B ）＝cos A ·cos B －sin A ·sin B ＝35 ·1213 －45 · 513 ＝1665又C ＝180°－（A ＋B ）.∴cos C ＝cos ［180°－（A ＋B ）］＝－cos （A ＋B ）＝－1665 . 3.解：在原等式两边同乘以sin A 得2cos B sin A sin C ＝sin 2A ，由定理得sin 2A ＋sin 2C －sin 2B ＝sin 2A ， ∴sin 2C ＝sin 2B ∴B ＝C 故△ABC 是等腰三角形.4.解：∵sin A ＝sin B ＋sin C cos B ＋cos C，∴cos B ＋cos C ＝sin B ＋sin Csin A ，应用正、余弦定理得a 2＋c 2－b 22ac＋a 2＋b 2－c 22ab ＝b ＋ca ，∴b （a 2c 2－b 2）＋c （a 2－b 2c 2）＝2bc （b ＋c ）， ∴a 2（b ＋c ）－（b ＋c ）（b 2－2bc ＋c 2）＝2bc （b ＋c ）即a 2＝b 2＋c 2故△ABC 为直角三角形.5.证明：由a 2＝b 2＋c 2－2bc cos A . b 2＝a 2＋c 2－2ac cos B 两式相减得a 2－b 2＝c （a cos B －b cos A ）， ∴a 2－b 2c 2 ＝a cos B －b cos A c 2.又a c ＝sin A sin C ，b c ＝sin B sin C ，∴a 2－b 2c 2 ＝sin A cos B －sin B cos A sin C ＝sin （A －B ）sin C解：由已知条件（a ＋b ＋c ）（b ＋c －a ）＝bc 及余弦定理得 cos A ＝b 2＋c 2－a 22bc ＝（a ＋b ＋c ）（b ＋c －a ）2（a ＋b ＋c ）（b ＋c －a ）＝12∴A ＝60°又由已知条件sin A ＝2sin B cos C 得sin （B ＋C ）＝sin （B ＋C ）＋sin （B －C ） ∴sin （C －B ）＝0，∴B ＝C 于是有A ＝B ＝C ＝60°，故△ABC 为等边三角形. 3、【规范解答】由A+C=2B 及180A B C ++=得60B =，由正弦定理得1sin A =得1sin 2A =，由a b <知60A B <=，所以30A =，180C A B =-- 90=，所以sin sin90 1.C ==4、【规范解答】由余弦定理得，222121cos 33a a π+-⨯⨯⨯=，即220a a +-=，解得1a =或2-（舍）。

完整版)正弦定理与余弦定理练习题

完整版)正弦定理与余弦定理练习题1.已知三角形ABC中，a=4，b=43，A=30°，求角B的大小。

解：根据正弦定理，有XXX，即sinB=43/4×sin30°=21.5/4.由此可知B的大小为30°或150°，故选B。

2.已知锐角三角形ABC的面积为33，BC=4，CA=3，求角C的大小。

解：根据面积公式，有33=1/2×4×3×sinC，即sinC=22/3.由此可知C的大小为arcsin(22/3)≈75°，故选A。

3.已知三角形ABC中，a,b,c分别是角A,B,C所对的边，且(2a+c)cosB+bcosC=0，求角B的大小。

解：根据余弦定理，有c^2=a^2+b^2-2abcosC，即cosC=(a^2+b^2-c^2)/(2ab)。

代入已知式中，得(2a+c)cosB-b(a^2+b^2-c^2)/(2ab)=0，化简得(4a^2+2ac-b^2)cosB=2abc。

由此可知cosB=(2abc)/(4a^2+2ac-b^2)。

代入cosine double angle formula，得cos2B=(4a^2b^2c^2)/(4a^2b^2+2a^2c^2-2ab^3+2abc^2-2b^2c^2-b^4)。

由于cos2B≤1，可列出不等式4a^2b^2+2a^2c^2-2ab^3+2abc^2-2b^2c^2-b^4≥4a^2b^2c^2，即b^4-2ab^3+(2ac-2c^2-4a^2)b+6a^2c^2-5a^2b^2≤0.考虑b的取值，当b=0时，不等式显然成立；当b>0时，由于a,b,c均为正数，不等式两边同除以b^4后，得到一个关于x=ac/b^2的一元二次不等式6x^2-5x-2≤0.解得x∈[2/3,1]，即ac/b^2∈[2/3,1]。

由此可知cosB的取值范围为[1/2,√3/2]，故角B的大小为arccos(1/2)≈60°或arccos(√3/2)≈30°，故选B。

正弦定理余弦定理习题及答案

正余弦定理1．在是的（）ABC ∆中，A B >sin sin A B >A ．充分不必要条件 B ．必要不充分条件C ．充要条件 D ．既不充分也不必要条件2、已知关于的方程的两根之和等于两根之积的一半，x 22cos cos 2sin02Cx x A B -⋅+=则一定是（）ABC ∆（A ）直角三角形（B ）钝角三角形（C ）等腰三角形（D ）等边三角形.3、已知a,b,c 分别是△ABC 的三个内角A,B,C 所对的边，若, A+C=2B,则Sin C = .4、如图，在△ABC 中，若b = 1，23C π∠=，则a= 。

5、在ABC ∆中，角,,A B C 所对的边分别为a ，b ，c，若a =，2b =，sin cos B B +=，则角A 的大小为．6、在中，分别为角的对边，且∆ABC ,,a b c ,,A B C 274sin cos 222B C A +-=（1）求的度数A ∠（2）若，求和的值a =3b c +=b c 7、在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.8、如图，在△ABC 中，已知，，B=45︒ 求A 、C 及c .3=a 2=b 1、解：在，因此，选ABC A B ∆>中，2sin 2sin sin sin a b R A R B A B ⇔>⇔>⇔>．C 2、【答案】由题意可知：，从而211cos cos cos 2sin 222C CA B -=⋅⋅=2cos cos 1cos()1cos cos sin sin A B A B A B A B=++=+-AB，又因为所以，所cos cos sin sin 1A B A B +=cos()1A B -=A B ππ-<-<0A B -=以一定是等腰三角形选CABC ∆3、【命题立意】本题考察正弦定理在解三角形中的应用.【思路点拨】由已知条件求出B 、A 的大小，求出C ，从而求出sin .C【规范解答】由A+C=2B 及180A B C ++=得60B =，由正弦定理得1sin A =得1sin 2A =，由a b <知60A B <= ，所以30A = ，180C A B =--90= ，所以sin sin 90 1.C == 4、【命题立意】本题考查解三角形中的余弦定理。

正余弦定理专题练习(含答案)

正余弦定理专题2020.3一、选择题1、在△ABC中，a=1，B=45°，S△ABC=2，则△ABC外接圆的直径为( )A.4B.60C.5D.6【解析】选C.因为由三角形的面积公式得：S=acsin B=×1×c×=2，所以c=4，又因为a=1，cos B=，根据余弦定理得：b2=1+32-8=25，解得b=5.所以△ABC的外接圆的直径为==5.2、在△ABC中，角A，B，C所对的边分别为a，b，c，如果c=a，B=30°，那么角C等于 ( )A.120°B.105°C.90°D.75°【解析】选A.因为c=a，所以sin C=sin A=sin(180°-30°-C)=sin(30°+C)=，即sin C=-cos C.所以tan C=-.又0°<C<180°，所以C=120°.3、在△ABC中，已知sin2A+sin2B-sin Asin B=sin2C，且满足ab=4，则该三角形的面积为( )A.1B.2C.D.【解析】选D.因为sin2A+sin2B-sin Asin B=sin2C，根据正弦定理得a2+b2-ab=c2，由余弦定理得2abcos C=ab，所以cos C=，所以sin C==，4、若△ABC为钝角三角形，三边长分别为2，3，x，则x的取值范围是( )A.(1，)B.(，5)C.(，)D.(1，)∪(，5)【解析】选D.(1)若x>3，则x对角的余弦值<0且2+3>x，解得<x<5.(2)若x<3，则3对角的余弦值<0且x+2>3，解得1<x<.故x的取值范围是(1，)∪(，5).所以S=absin C=×4×=.二、填空题5、在△ABC中，已知A=60°，tan B=，a=2，则c=________. 【解析】因为tan B=，所以sin B=，cos B=.又因为A=60°，所以sin C=sin[180°-(A+B)]=sin(120°-B)=sin 120°cos B-cos 120°sin B=+.由正弦定理，得=，即c===.答案：6、在△ABC中，角A，B，C的对边分别为a，b，c.若(a2+c2-b2)tan B=ac，则角B的度数为________.【解析】由余弦定理，得2accos B·tan B=ac，整理，得sin B=，所以B=60°或120°.答案：60°或120°7、△ABC的内角A，B，C的对边分别是a，b，c且满足acos B-bcos A=c，则△ABC的形状为________.【解析】根据正弦定理，得a=2Rsin A，b=2Rsin B，C=2Rsin C(其中R是△ABC外接圆的半径)，代入acos B-bcos A=c得2Rsin Acos B-2Rsin Bcos A=2Rsin C，所以sin Acos B-sin Bcos A=sin (A+B)，所以sin Acos B-sin Bcos A=sin Acos B+sin Bcos A，所以2sin Bcos A=0，又因为sin B≠0，所以cos A=0，又A∈(0，π)，所以A=，所以该三角形为直角三角形.答案：直角三角形8、在△ABC中，若3b=2asin B，cos A=cos C，则△ABC的形状为________.【解析】由正弦定理知b=2R·sin B，a=2R·sin A，则3b=2a·sin B可化为：3sin B=2sin A·sin B.因为0°<B<180°，所以sin B≠0，所以sin A=，所以A=60°或120°，又cos A=cos C，所以A=C，所以A=60°，所以△ABC为等边三角形.答案：等边三角形9、在△ABC中，a，b，c分别为内角A，B，C所对的边长，a=，b=，1+2cos(B+C)=0，则边BC上的高为________.【解析】由1+2cos(B+C)=0和B+C=π-A，得1-2cos A=0，所以cos A=，sin A=.再由正弦定理，得sin B==.由b<a知B<A，所以B不是最大角，B<，从而cos B==.由上述结果知sin C=sin(A+B)=×=.设边BC上的高为h，则有h=bsin C=.答案：10、在锐角三角形ABC中，a，b，c所对的角分别为A，B，C，A=2B，则的取值范围是________.【解析】在锐角三角形ABC中，A，B，C<90°，即所以30°<B<45°.由正弦定理知：===2cos B∈(，)，故的取值范围是(，).答案：(，)三、解答题11、在△ABC中，a，b，c分别是角A，B， C所对的边且b=6，a=2，A=30°，求ac的值.【解析】由正弦定理=得sin B===.由条件b=6，a=2，b>a知B>A.所以B=60°或120°.(1)当B=60°时，C=180°-A-B=180°-30°-60°=90°.在Rt△ABC中，C=90°，a=2，b=6，c=4，所以ac=2×4=24.(2)当B=120°时，C=180°-A-B=180°-30°-120°=30°，所以A=C，则有a=c=2.所以ac=2×2=12.12、△ABC的内角A，B，C所对的边分别为a，b，c.向量m=(a，b)与n=(cos A，sin B)平行.(1)求A.(2)若a=，b=2，求sin C.【解析】(1)因为m∥n，所以asin B-bcos A=0.由正弦定理，得sin Asin B-sin Bcos A=0，又因为sin B≠0，从而tan A=.由于0<A<π，所以A=.(2)由正弦定理，得=，从而sin B=，又由a>b，知A>B，所以cos B=.故sin C=sin(A+B)=sin(B+)=sin Bcos +cos Bsin=.13、在△ABC中，求证：(1)=.(2)=.【证明】(1)由余弦定理，a2=b2+c2-2bccos A，于是==1-·2cos A=1-·2cos A===.(2)方法一：==·==.方法二：====.14、在△ABC中，已知(a+b+c)(a+b-c)=3ab，且2cos Asin B=sin C，确定△ABC的形状.【解析】由正弦定理得=，由2cos Asin B=sin C，有cos A==.又由余弦定理得cos A=，所以=，即c2=b2+c2-a2，所以a2=b2，所以a=b.又因为(a+b+c)(a+b-c)=3ab，所以(a+b)2-c2=3ab，所以4b2-c2=3b2，即b2=c2.所以b=c，所以a=b=c.15、所以△ABC为等边三角形.已知a，b，c分别为△ABC三个内角A，B，C的对边，+=.(1)求角A的大小.(2)若a=2，△ABC的面积为，求边b，c.【解析】(1)由+=及正弦定理得+=，得，sin Acos B+cos Asin B=2sin Ccos A，即 sin(A+B)=2sin CcosA. 因为sin(A+B)=sin(π-C)=sin C，且sin C≠0，所以，cos A=.又0<A<π，所以，A=.(2)因为△ABC的面积S=bcsin A=bcsin=，所以，bc=4.①由余弦定理得，a2=b2+c2-2bccos A，22=b2+c2-2bccos所以，b2+c2=8，②联立①②解得，b=c=2.16、在△ABC中，角A，B，C的对边分别为a，b，c，且a2-(b-c)2=(2-)bc，sin Asin B=cos2，BC边上的中线AM的长为.(1)求角A和角B的大小.(2)求△ABC的周长.【解析】(1)由a2-(b-c)2=(2-)bc，得a2-b2-c2=-bc所以cos A==.又0<A<π，所以A=.由sin Asin B=cos2，得sin B=，即sin B=1+cos C，则cos C<0，即C为钝角.所以B为锐角，且B+C=，则sin=1+cos C，化简得cos=-1，解得C=，所以B=.(2)由(1)知，a=b，在△ACM中，由余弦定理得AM2=b2+-2b··cos C=b2++=()2，解得b=2，所以a=2.在△ABC中c2=a2+b2-2abcos C=22+22-2×2×2×cos =12，所以c=2.所以△ABC的周长为4+2.。

正余弦定理练习题(含答案)

正弦定理演习题1．在△ABC 中,∠A＝45°,∠B＝60°,a＝2,则b 等于( )A. 6B. 2C. 3 D ．26 2．在△ABC 中,已知a ＝8,B ＝60°,C＝75°,则b 等于( )A ．4 2B ．4 3C ．4 6 D.3233．在△ABC 中,角A.B.C 的对边分离为a.b.c,A ＝60°,a＝43,b ＝42,则角B 为( )A ．45°或135° B．135° C．45° D．以上答案都不合错误4．在△ABC 中,a∶b∶c＝1∶5∶6,则sinA∶sinB∶sinC 等于( )A ．1∶5∶6B ．6∶5∶1C．6∶1∶5 D．不肯定解析：选A.由正弦定理知sinA∶sinB∶sinC＝a∶b∶c＝1∶5∶6. 5．在△ABC 中,a,b,c 分离是角A,B,C 所对的边,若A ＝105°,B＝45°,b＝2,则c ＝( )A ．1 B.12C ．2 D.146．在△ABC 中,若cos A cos B ＝ba,则△ABC 是( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形7．已知△ABC 中,AB ＝3,AC ＝1,∠B＝30°,则△ABC 的面积为( )A.32B.34C.32或3D.34或328．△ABC 的内角A.B.C 的对边分离为a.b.c.若c ＝2,b ＝6,B ＝120°,则a等于( )A.6B ．2C.3D.29．在△ABC 中,角A.B.C 所对的边分离为a.b.c,若a ＝1,c ＝3,C ＝π3,则A＝________.10．在△ABC 中,已知a ＝433,b ＝4,A ＝30°,则sinB ＝________.11．在△ABC 中,已知∠A＝30°,∠B＝120°,b＝12,则a ＋c ＝________. 12．在△ABC 中,a ＝2bcosC,则△ABC 的外形为________．13．在△ABC 中,A ＝60°,a＝63,b ＝12,S△ABC＝183,则a ＋b ＋csinA ＋sinB ＋sinC＝________,c ＝________.14．已知△ABC 中,∠A∶∠B∶∠C＝1∶2∶3,a＝1,则a －2b ＋csin A －2sin B ＋sin C＝________.15．在△ABC 中,已知a ＝32,cosC ＝13,S△ABC＝43,则b ＝________.16．在△ABC 中,b ＝43,C ＝30°,c＝2,则此三角形有________组解．17．如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正南偏向顺时针转到目的偏向线的程度转角)为140°的偏向航行,为了肯定船位,船在B 点不雅测灯塔A 的方位角为110°,航行半小时后船到达C 点,不雅测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是若干？18．在△ABC 中,a.b.c 分离为角A.B.C 的对边,若a ＝23,sin C 2cos C 2＝14,sinBsin C ＝cos2A2,求A.B 及b.c.19．(2009年高考四川卷)在△AB C 中,A.B 为锐角,角A.B.C 所对应的边分离为a.b.c,且cos 2A ＝35,sin B ＝1010.(1)求A ＋B 的值;(2)若a －b ＝2－1,求a,b,c 的值．20．△ABC 中,ab ＝603,sin B ＝sin C,△ABC 的面积为153,求边b 的长．余弦定理演习题1．在△ABC 中,假如BC ＝6,AB ＝4,cosB ＝13,那么AC 等于()A ．6B ．26C ．36D ．462．在△ABC 中,a ＝2,b ＝3－1,C ＝30°,则c 等于()A. 3B.2C. 5 D ．23．在△ABC 中,a2＝b2＋c2＋3bc,则∠A 等于()A ．60° B．45°C．120° D．150° 4．在△ABC 中,∠A.∠B.∠C 的对边分离为a.b.c,若(a2＋c2－b2)tanB ＝3ac,则∠B 的值为()A.π6B.π3C.π6或5π6D.π3或2π35．在△ABC 中,a.b.c 分离是A.B.C 的对边,则acosB ＋bcosA 等于()A ．aB ．bC ．cD ．以上均不合错误6．假如把直角三角形的三边都增长同样的长度,则这个新的三角形的外形为()A ．锐角三角形B ．直角三角形C ．钝角三角形D ．由增长的长度决议7．已知锐角三角形ABC 中,|AB →|＝4,|AC →|＝1,△ABC 的面积为3,则AB →·AC →的值为()A ．2B ．－2C ．4D ．－48．在△ABC 中,b ＝3,c ＝3,B ＝30°,则a 为()A.3B ．23C.3或23D ．29．已知△ABC 的三个内角知足2B ＝A ＋C,且AB ＝1,BC ＝4,则边BC 上的中线AD 的长为________．10．△ABC 中,sinA∶sinB∶sinC＝(3－1)∶(3＋1)∶10,求最大角的度数．11．已知a.b.c 是△ABC 的三边,S 是△ABC 的面积,若a ＝4,b ＝5,S ＝53,则边c 的值为________．12．在△ABC 中,sin A∶sin B∶sin C＝2∶3∶4,则cos A∶cos B∶cos C ＝________.13．在△ABC 中,a ＝32,cos C ＝13,S△ABC＝43,则b ＝________.14．已知△ABC 的三边长分离为AB ＝7,BC ＝5,AC ＝6,则AB →·BC →的值为________．15．已知△ABC 的三边长分离是 a.b.c,且面积S ＝a2＋b2－c24,则角C ＝________.16．(2011年广州调研)三角形的三边为持续的天然数,且最大角为钝角,则最小角的余弦值为________． 17．在△ABC 中,BC ＝a,AC ＝b,a,b 是方程x2－23x ＋2＝0的两根,且2cos(A ＋B)＝1,求AB 的长．18．已知△ABC 的周长为2＋1,且sin A ＋sin B ＝2sin C.(1)求边AB 的长;(2)若△ABC 的面积为16sin C,求角C 的度数．19．在△ABC 中,BC ＝5,AC ＝3,sin C ＝2sin A.(1)求AB 的值;(2)求sin(2A －π4)的值．20．在△ABC 中,已知(a ＋b ＋c)(a ＋b －c)＝3ab,且2cos Asin B ＝sinC,肯定△ABC 的外形．正弦定理1．在△ABC 中,∠A＝45°,∠B＝60°,a＝2,则b 等于( )A. 6B.2C.3D ．26解析：选A.运用正弦定理得：a sinA ＝b sinB ,求得b ＝asinBsinA＝ 6.2．在△ABC 中,已知a ＝8,B ＝60°,C＝75°,则b 等于( )A ．42B ．43C ．46D.323解析：选C.A ＝45°,由正弦定理得b ＝asinBsinA ＝4 6.3．在△ABC 中,角A.B.C 的对边分离为a.b.c,A ＝60°,a＝43,b ＝42,则角B 为( )A ．45°或135° B．135°C．45° D．以上答案都不合错误 a sinA ＝b sinB 得：sinB ＝bsinA a ＝22,又∵a>b,∴B<60°,∴B＝45°. 4．在△ABC 中,a∶b∶c＝1∶5∶6,则sinA∶sinB∶sinC 等于( )A ．1∶5∶6B ．6∶5∶1C ．6∶1∶5D ．不肯定解析：选A.由正弦定理知sinA∶sinB∶sinC＝a∶b∶c＝1∶5∶6. 5．在△ABC 中,a,b,c 分离是角A,B,C 所对的边,若A ＝105°,B＝45°,b＝2,则c ＝( )A ．1 B.12C ．2 D.14解析：选 A.C ＝180°－105°－45°＝30°,由b sinB ＝csinC 得c ＝2×sin 30°sin45°＝1.6．在△ABC 中,若cos A cos B ＝ba,则△ABC 是( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形解析：选D.∵b a ＝sin B sin A ,∴cos A cos B ＝sin Bsin A,sinAcosA ＝sinBcosB,∴sin2A＝sin2B即2A ＝2B 或2A ＋2B ＝π,即A ＝B,或A ＋B ＝π2.7．已知△ABC 中,AB ＝3,AC ＝1,∠B＝30°,则△ABC 的面积为( )A.32B.34C.32或 3 D.34或32解析：选D.AB sinC ＝AC sinB ,求出sinC ＝32,∵AB＞AC,∴∠C 有两解,即∠C＝60°或120°,∴∠A＝90°或30°.再由S△ABC＝12AB·ACsinA 可求面积．8．△ABC 的内角A.B.C 的对边分离为a.b.c.若c ＝2,b ＝6,B ＝120°,则a 等于( )A. 6 B ．2 C. 3 D.26sin120°＝2sinC,∴sinC＝12.又∵C 为锐角,则C ＝30°,∴A＝30°, △ABC 为等腰三角形,a ＝c ＝ 2.9．在△ABC 中,角A.B.C 所对的边分离为a.b.c,若a ＝1,c ＝3,C ＝π3,则A＝________.解析：由正弦定理得：a sinA ＝csinC,所以sinA ＝a·sinC c ＝12.又∵a＜c,∴A＜C ＝π3,∴A＝π6.答案：π610．在△ABC 中,已知a ＝433,b ＝4,A ＝30°,则sinB ＝________.解析：由正弦定理得a sinA ＝bsinB⇒sinB ＝bsinA a ＝4×12433＝32.答案：3211．在△ABC 中,已知∠A＝30°,∠B＝120°,b＝12,则a ＋c ＝________.解析：C ＝180°－120°－30°＝30°,∴a＝c,由a sinA ＝b sinB 得,a ＝12×sin30°sin120°＝43, ∴a＋c ＝8 3. 答案：8312．在△ABC 中,a ＝2bcosC,则△ABC 的外形为________．解析：由正弦定理,得a ＝2R·sinA,b＝2R·sinB, 代入式子a ＝2bcosC,得2RsinA ＝2·2R·sinB·cosC, 所以sinA ＝2sinB·cosC,即sinB·cosC＋cosB·sinC＝2sinB·cosC, 化简,整顿,得sin(B －C)＝0.∵0°＜B ＜180°,0°＜C ＜180°, ∴－180°＜B －C ＜180°, ∴B－C ＝0°,B＝C. 答案：等腰三角形13．在△ABC 中,A ＝60°,a＝63,b ＝12,S△ABC＝183,则a ＋b ＋csinA ＋sinB ＋sinC＝________,c ＝________.解析：由正弦定理得a ＋b ＋c sinA ＋sinB ＋sinC ＝a sinA ＝63sin60°＝12,又S△ABC＝12bcsinA,∴12×12×sin60°×c＝183, ∴c＝6.答案：12 614．已知△ABC 中,∠A∶∠B∶∠C＝1∶2∶3,a＝1,则a －2b ＋csin A －2sin B ＋sin C＝________.解析：由∠A∶∠B∶∠C＝1∶2∶3得,∠A＝30°,∠B＝60°,∠C＝90°,∴2R＝a sinA ＝1sin30°＝2,又∵a＝2Rsin A,b ＝2Rsin B,c ＝2Rsin C,∴a －2b ＋c sin A －2sin B ＋sin C ＝2R sin A －2sinB ＋sin Csin A －2sin B ＋sin C＝2R ＝2.答案：215．在△ABC 中,已知a ＝32,cosC ＝13,S△ABC＝43,则b ＝________.解析：依题意,sinC ＝223,S△ABC＝12absinC ＝43,解得b ＝2 3.答案：2316．在△ABC 中,b ＝43,C ＝30°,c＝2,则此三角形有________组解．解析：∵bsinC＝43×12＝23且c ＝2,∴c<bsinC,∴此三角形无解．答案：017．如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正南偏向顺时针转到目的偏向线的程度转角)为140°的偏向航行,为了肯定船位,船在B 点不雅测灯塔A 的方位角为110°,航行半小时后船到达C 点,不雅测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是若干？解：在△ABC 中,BC ＝40×12＝20,∠ABC＝140°－110°＝30°,∠ACB＝(180°－140°)＋65°＝105°, 所以∠A＝180°－(30°＋105°)＝45°, 由正弦定理得AC ＝BC·sin∠ABC sinA＝20sin30°sin45°＝102(km)．即货轮到达C 点时,与灯塔A 的距离是10 2 km.18．在△A BC 中,a.b.c 分离为角A.B.C 的对边,若a ＝23,sin C 2cos C 2＝14,sinBsin C ＝cos2A2,求A.B 及b.c.解：由sin C 2cos C 2＝14,得sinC ＝12,又C∈(0,π),所以C ＝π6或C ＝5π6.由sin Bsin C ＝cos2A2,得sin Bsin C ＝12[1－cos(B ＋C)],即2sin Bsin C ＝1－cos(B ＋C),即2sin Bsin C ＋cos(B ＋C)＝1,变形得 cos Bcos C ＋sin Bsin C ＝1,即cos(B －C)＝1,所以B ＝C ＝π6,B ＝C ＝5π6(舍去),A ＝π－(B ＋C)＝2π3.由正弦定理a sin A ＝b sin B ＝csin C,得b ＝c ＝a sin Bsin A ＝23×1232＝2.故A ＝2π3,B ＝π6,b ＝c ＝2.19．(2009年高考四川卷)在△ABC 中,A.B 为锐角,角A.B.C 所对应的边分离为a.b.c,且cos 2A ＝35,sin B ＝1010.(1)求A ＋B 的值;(2)若a －b ＝2－1,求a,b,c 的值．解：(1)∵A.B 为锐角,sin B ＝1010,∴cos B＝1－sin2B ＝31010.又cos 2A ＝1－2sin2A ＝35,∴sinA＝55,cos A ＝255,∴cos(A＋B)＝cos Acos B －sin Asin B ＝255×31010－55×1010＝22.又0＜A ＋B ＜π,∴A＋B ＝π4.(2)由(1)知,C ＝3π4,∴sin C＝22.由正弦定理：a sin A ＝b sin B ＝csin C得5a ＝10b ＝2c,即a ＝2b,c ＝5b.∵a－b ＝2－1,∴2b －b ＝2－1,∴b＝1. ∴a＝2,c ＝ 5.20．△ABC 中,ab ＝603,sin B ＝sin C,△ABC 的面积为153,求边b 的长．解：由S ＝12absin C 得,153＝12×603×sin C,∴sin C＝12,∴∠C＝30°或150°.又sin B ＝sin C,故∠B＝∠C.当∠C＝30°时,∠B＝30°,∠A＝120°.又∵ab＝603,a sin A ＝bsin B,∴b＝215.当∠C＝150°时,∠B＝150°(舍去)．故边b 的长为215.余弦定理1．在△ABC 中,假如BC ＝6,AB ＝4,cosB ＝13,那么AC 等于()A ．6B ．26C ．3 6D ．46 解析：选A.由余弦定理,得AC ＝AB2＋BC2－2AB·BCcosB＝42＋62－2×4×6×13＝6.2．在△ABC 中,a ＝2,b ＝3－1,C ＝30°,则c 等于() A. 3 B.2 C. 5 D ．2解析：选B.由余弦定理,得c2＝a2＋b2－2abcosC ＝22＋(3－1)2－2×2×(3－1)cos30° ＝2,∴c＝ 2.3．在△ABC 中,a2＝b2＋c2＋3bc,则∠A 等于() A ．60° B ．45° C ．120° D ．150°解析：选D.cos∠A＝b2＋c2－a22bc ＝－3bc 2bc ＝－32,∵0°＜∠A＜180°,∴∠A＝150°.4．在△ABC 中,∠A.∠B.∠C 的对边分离为a.b.c,若(a2＋c2－b2)tanB ＝3ac,则∠B 的值为()A.π6B.π3C.π6或5π6D.π3或2π3解析：选D.由(a2＋c2－b2)tanB ＝3ac,联想到余弦定理,代入得cosB ＝a2＋c2－b22ac ＝32·1tanB ＝32·cosB sinB .显然∠B≠π2,∴sinB＝32.∴∠B＝π3或2π3.5．在△ABC 中,a.b.c 分离是A.B.C 的对边,则acosB ＋bcosA 等于() A ．a B ．b C ．c D ．以上均不合错误解析：选C.a·a2＋c2－b22ac ＋b·b2＋c2－a22bc ＝2c22c＝c.6．假如把直角三角形的三边都增长同样的长度,则这个新的三角形的外形为()A ．锐角三角形B ．直角三角形C ．钝角三角形D ．由增长的长度决议解析：选A.设三边长分离为a,b,c 且a2＋b2＝c2. 设增长的长度为m,则c ＋m ＞a ＋m,c ＋m ＞b ＋m,又(a ＋m)2＋(b ＋m)2＝a2＋b2＋2(a ＋b)m ＋2m2＞c2＋2cm ＋m2＝(c ＋m)2,∴三角形各角均为锐角,即新三角形为锐角三角形．7．已知锐角三角形ABC 中,|AB →|＝4,|AC →|＝1,△ABC 的面积为3,则AB →·AC →的值为()A ．2B ．－2C ．4D ．－4 解析：选A.S△ABC＝3＝12|AB →|·|AC →|·sinA＝12×4×1×sinA,∴sinA＝32,又∵△ABC 为锐角三角形, ∴cosA＝12, ∴AB →·AC →＝4×1×12＝2. 8．在△ABC 中,b ＝3,c ＝3,B ＝30°,则a 为() A. 3 B ．23C.3或2 3 D ．2解析：选C.在△ABC 中,由余弦定理得b2＝a2＋c2－2accosB,即3＝a2＋9－33a,∴a2－33a ＋6＝0,解得a ＝3或2 3.9．已知△ABC 的三个内角知足2B ＝A ＋C,且AB ＝1,BC ＝4,则边BC 上的中线AD 的长为________．解析：∵2B＝A ＋C,A ＋B ＋C ＝π,∴B＝π3. 在△ABD 中, AD ＝AB2＋BD2－2AB·BDcosB＝1＋4－2×1×2×12＝ 3. 答案：310．△ABC 中,sinA∶sinB∶sinC＝(3－1)∶(3＋1)∶10,求最大角的度数．解：∵sinA∶sinB∶sinC＝(3－1)∶(3＋1)∶10, ∴a∶b∶c＝(3－1)∶(3＋1)∶10.设a ＝(3－1)k,b ＝(3＋1)k,c ＝10k(k ＞0),∴c 边最长,即角C 最大．由余弦定理,得cosC ＝a2＋b2－c22ab ＝－12, 又C∈(0°,180°),∴C＝120°.11．已知a.b.c 是△ABC 的三边,S 是△ABC 的面积,若a ＝4,b ＝5,S ＝53,则边c 的值为________．解析：S ＝12absinC,sinC ＝32,∴C＝60°或120°. ∴cosC＝±12,又∵c2＝a2＋b2－2abcosC,∴c2＝21或61,∴c＝21或61. 答案：21或6112．在△ABC 中,sin A∶sin B∶sin C＝2∶3∶4,则cos A∶cos B∶cos C ＝________.解析：由正弦定理a∶b∶c＝sin A∶sin B∶sin C＝2∶3∶4,设a ＝2k(k ＞0),则b ＝3k,c ＝4k,cos B ＝a2＋c2－b22ac ＝2k 2＋4k 2－3k 22×2k×4k ＝1116, 同理可得：cos A ＝78,cos C ＝－14, ∴cos A∶cos B∶cos C＝14∶11∶(－4)．答案：14∶11∶(－4)13．在△ABC 中,a ＝32,cos C ＝13,S△ABC＝43,则b ＝________. 解析：∵cos C＝13,∴sin C＝223. 又S△ABC＝12absinC ＝43, 即12·b·32·223＝43, ∴b＝2 3.答案：2314．已知△ABC 的三边长分离为AB ＝7,BC ＝5,AC ＝6,则AB →·BC →的值为________．解析：在△ABC 中,cosB ＝AB2＋BC2－AC22AB·BC＝49＋25－362×7×5＝1935, ∴AB →·BC →＝|AB →|·|BC →|·cos(π－B)＝7×5×(－1935) ＝－19.答案：－1915．已知△ABC 的三边长分离是a.b.c,且面积S ＝a2＋b2－c24,则角C ＝________.解析：12absinC ＝S ＝a2＋b2－c24＝a2＋b2－c22ab ·ab 2＝12abcosC,∴sinC＝cosC,∴tanC＝1,∴C＝45°. 答案：45°16．(2011年广州调研)三角形的三边为持续的天然数,且最大角为钝角,则最小角的余弦值为________．解析：设三边长为k －1,k,k ＋1(k≥2,k∈N),则⎩⎪⎨⎪⎧ k2＋k －12－k ＋12＜0k ＋k －1＞k ＋1⇒2＜k ＜4,∴k＝3,故三边长分离为2,3,4,∴最小角的余弦值为32＋42－222×3×4＝78. 答案：7817．在△ABC 中,BC ＝a,AC ＝b,a,b 是方程x2－23x ＋2＝0的两根,且2cos(A ＋B)＝1,求AB 的长．解：∵A＋B ＋C ＝π且2cos(A ＋B)＝1,∴cos(π－C)＝12,即cosC ＝－12. 又∵a,b 是方程x2－23x ＋2＝0的两根,∴a＋b ＝23,ab ＝2.∴AB2＝AC2＋BC2－2AC·BC·cosC＝a2＋b2－2ab(－12) ＝a2＋b2＋ab ＝(a ＋b)2－ab＝(23)2－2＝10,∴AB＝10.18．已知△ABC 的周长为2＋1,且sin A ＋sin B ＝2sin C.(1)求边AB 的长;(2)若△ABC 的面积为16sin C,求角C 的度数．解：(1)由题意及正弦定理得AB ＋BC ＋AC ＝2＋1,BC ＋AC ＝2AB,两式相减,得AB ＝1.(2)由△ABC 的面积12BC·AC·sin C＝16sin C,得BC·AC＝13, 由余弦定理得cos C ＝AC2＋BC2－AB22AC·BC＝AC ＋BC 2－2AC·BC－AB22AC·BC ＝12, 所以C ＝60°.19．在△ABC 中,BC ＝5,AC ＝3,sin C ＝2sin A.(1)求AB 的值;(2)求sin(2A －π4)的值．解：(1)在△ABC 中,由正弦定理AB sin C ＝BC sin A, 得AB ＝sinC sinA BC ＝2BC ＝2 5. (2)在△ABC 中,依据余弦定理,得cos A ＝AB2＋AC2－BC22AB·AC ＝255, 于是sin A ＝1－cos2A ＝55. 从而sin 2A ＝2sin Acos A ＝45, cos 2A ＝cos2A －sin2A ＝35. 所以sin(2A －π4)＝sin 2Acos π4－cos 2Asin π4＝210. 20．在△ABC 中,已知(a ＋b ＋c)(a ＋b －c)＝3ab,且2cos Asin B ＝sinC,肯定△ABC 的外形．解：由正弦定理,得sin C sin B ＝c b. 由2cos Asin B ＝sin C,有cosA ＝sinC 2sin B ＝c 2b. 又依据余弦定理,得cos A ＝b2＋c2－a22bc ,所以c 2b ＝b2＋c2－a22bc, 即c2＝b2＋c2－a2,所以a ＝b.又因为(a ＋b ＋c)(a ＋b －c)＝3ab,所以(a ＋b)2－c2＝3ab,所以4b2－c2＝3b2, 所以b ＝c,所以a ＝b ＝c,是以△ABC 为等边三角形．。

正弦定理余弦定理练习题及答案(供参考)

正弦定理、余弦定理练习题年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共20题，题分合计100分)1.已知在△ABC中,sin A:sin B:sin C=3:2:4,那么cos C的值为B.D.2.在△ABC中，a=λ,b=λ,A=45°,则满足此条件的三角形的个数是D.无数个3.在△ABC中，b cos A=a cos B，则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形4.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x＞1)，则最大角为°°°°5.在△ABC中，=1，=2，（+）·（+）=5+2则边||等于A.C.D.6.在△ABC中，已知B=30°,b=50,c=150，那么这个三角形是A.等边三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形7.在△ABC中，若b2sin2C+c2sin2B=2bc cos B cos C，则此三角形为A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形8.正弦定理适应的范围是△B.锐角△ C.钝角△ D.任意△9.已知△ABC中，a=10,B=60°,C=45°，则c=+（-1） C.（+1）10.在△ABC中，b sin A＜a＜b，则此三角形有A.一解B.两解C.无解D.不确定11.三角形的两边分别为5和3，它们夹角的余弦是方程5x2-7x-6=0的根，则三角形的另一边长为12.在△ABC中，a2=b2+c2+bc，则A等于°°°13.在△ABC中，，则△ABC是A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形14.在△ABC中，a=2，A=30°,C=45°，则△ABC的面积S△ABC等于A.C.+1D.(+1)15.已知三角形ABC的三边a、b、c成等比数列，它们的对角分别是A、B、C，则sin A sin C 等于+cos2B+sin2B16.在△ABC中，sin A＞sin B是A＞B的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件17.在△ABC中，b Cos A=a cos B，则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形18.△ABC中，sin2A=sin2B+sin2C，则△ABC为A.直角三角形B.等腰直角三角形C.等边三角形D.等腰三角形19.△ABC中,A=60°,b=1,这个三角形的面积为,则△ABC外接圆的直径为A.B.C.D.20.在△ABC中，,则k为D.(R为△ABC外接圆半径)二、填空题(共18题，题分合计75分)1.在△ABC中，A=60°，C=45°，b=2，则此三角形的最小边长为.2.在△ABC中，= .3.在△ABC中,a∶b∶c=(+1)∶∶2，则△ABC的最小角的度数为.4.在△ABC中，已知sin A∶sin B∶sin C=6∶5∶4，则sec A= .5.△ABC中，，则三角形为_________.6.在△ABC中，角A、B均为锐角且cos A＞sin B，则△ABC是___________.7.在△ABC中，若此三角形有一解，则a、b、A满足的条件为____________________.8.已知在△ABC中，a=10,b=5,A=45°,则B= .9.已知△ABC中，a=181,b=209,A=121°14′，此三角形解.10.在△ABC中,a=1,b=1,C=120°则c= .11.在△ABC中，若a2＞b2+c2，则△ABC为；若a2=b2+c2，则△ABC为；若a2＜b2+c2且b2＜a2+c2且c2＜a2+b2，则△ABC为.12.在△ABC中，sin A=2cos B sin C，则三角形为_____________.13.在△ABC中，BC=3，AB=2，且，A= .14.在△ABC中，B=,C=3,B=30°，则A= .15.在△ABC中，a+b=12,A=60°，B=45°，则a= ,b= .16.若2,3,x为三边组成一个锐角三角形，则x的范围为.17.在△ABC中，化简b cos C+c cos B= .18.钝角三角形的边长是三个连续自然数，则三边长为.三、解答题(共24题，题分合计244分)1.已知在△ABC中，c=10，A=45°，C=30°，求a、b和B.2.已知△ABC的三边长a=3，b=4，c=，求三角形的最大内角.3.已知在△ABC中，∠A=45°，a=2，c=，解此三角形.4.在四边形ABCD中，BC=a，DC=2a，四个角A、B、C、D度数的比为3∶7∶4∶10，求AB的长.5.在△ABC中，A最大，C最小，且A=2C，A+C=2B，求此三角形三边之比.6.证明：在△ABC中，.（其中R为△ABC的外接圆的半径）7.在△ABC中，最大角A为最小角C的2倍，且三边a、b、c为三个连续整数，求a、b、c的值.8.如下图所示，半圆O的直径MN=2，OA=2，B为半圆上任意一点，以AB为一边作正三角形ABC，问B在什么位置时，四边形OACB面积最大？最大面积是多少？9.在△ABC中，若sin A∶sin B∶sin C=m∶n∶l，且a+b+c=S，求a.10.根据所给条件，判断△ABC的形状（1）a cos A=b cos B(2)11.△ABC中，a+b=10，而cos C是方程2x2－3x－2=0的一个根，求△ABC周长的最小值.12.在△ABC中，a、b、c分别是角A、B、C的对边，设a+c=2b,A－C=,求sin B的值.13.已知△ABC中，a=1,b=,A=30°,求B、C 和c.14.在△ABC中，c=2，tan A=3,tan B=2,试求a、b及此三角形的面积.15.已知S△ABC=10,一个角为60°，这个角的两边之比为5∶2，求三角形内切圆的半径.16.已知△ABC中，，试判断△ABC的形状.17.已知△ABC的面积为1，tan B=,求△ABC 的各边长.18.求值：19.已知△ABC的面积，解此三角形.20.在△ABC中，a=,b=2,c=+1，求A、B、C及S△.21.已知（a2+bc）x2+2=0是关于x的二次方程，其中a、b、c是△ABC的三边，(1)若∠A为钝角，试判断方程根的情况.(2)若方程有两相等实根，求∠A的度数.22.在△ABC中，（a2+b2）sin(A-B)=(a2-b2)sin(A+B)，判断△ABC的形状.23.在△ABC中，a＞b,C=，且有tan A·tan B=6，试求a、b以及此三角形的面积.24.已知：k是整数，钝角△ABC的三内角A、B、C所对的边分别为a、b、c（1）若方程组有实数解，求k的值.（2）对于（1）中的k值，若且有关系式,试求A、B、C的度数.正弦定理、余弦定理答案一、选择题(共20题，合计100分)1 A 2A3C 4 B 5 C 6D 7A 8 D 9B 10 B 11 B 12C 13C 14C 16. C 17：C 18A 19C 20. A二、填空题(共18题，合计75分)1.2（-1） 23. 45°4. 85.等腰三角形6.：钝角三角形7.a=b sin A或b＜a8.60°或120°9无10.11.钝角三角形直角三角形锐角三角形12.等腰三角形13.120°14.或215. 36-1216.＜x＜17.a18. 2、3、4三、解答题(共24题，合计244分)=B=105°b=2.∠C=120°3.∠B=75°或∠B=15°b=+1，∠C=60°，∠B=75°或b=－1，∠C=120°，∠B=15°4. AB的长为5.：此三角形三边之比为6∶5∶4=6,b=5,c=48.当θ=时，S四边形OACB最大, 最大值为+29.10（1）△ABC是等腰三角形或直角三角形（2）△ABC为等边三角形11△ABC周长的最小值为12.=60°,B2=120°；C1=90°，C2=30°；c1=2,c2=114..15.16.等边三角形17.18.20. A=60°，B=45°，C=75°，S△=21. (1)没有实数根(2)60°22.等腰三角形或直角三角形23.24.（1）k=1，2，3 （2）C=45°,B=15°。