高三文科数学第一轮复习经典习题集(含答案)
锁定新高考新课标文科数学一轮总复习练习3.3两角和、差及二倍角公式(含答案详析)

A 组 基础达标(时间: 30 分钟满分: 50 分)若时间有限,建议选讲 3,6,9一、 选择题(每题5 分,共 25 分)π11.( 2014 ·荆州模拟)设sin+θ= ,则 sin 2 θ等于( A )4371A. -B. -991 7C.D.99分析: sin 2 θ=- cosπ π1 2 7+ 2θ =2sin 2+θ-1 = 2 ×-1=- .24392.( 2013·潍坊模拟)化简 2 +cos 2 -sin 21的结果是( C )A. -cos 1B. cos 1C. 3cos 1D. -3cos 12 +cos 2 -sin 21=1-cos 23 +3cos 2分析:2 +cos 2 - ==223cos 2 1 = 3cos 1.3.( 2014 ·北京东城模拟)已知函数f ( x )= cos 2ππ+x - cos 2-x ,则 44π f等于( B )121 1 A.B. - 2233 C.D. -22分析:2π2x + ππ =- π f (x )=cos+ x-sin =-sin 2x ,∴sin =44f6 121- .24. 已知 tan1 cos2 α+sin 2 α+1α= ,则 cos 2α 等于( A )2 A.3 B.63 C. 12 D.2cos 2 α+sin 2 α+12cos 2α+ 2sin α· cos α 分析:cos 2α==2+ 2tan α=3.cos 2α5. ( 2014 ·淄博模拟已)知△ABC 的三个内角知足: sinA = sinCcosB ,则△ ABC 的形状为( B )A. 正三角形B. 直角三角形C. 等腰直角三角形D. 等腰三角形或直角三角形分析: 由 sinA =sin CcosB ,得 sin ( B +C )= sin Ccos B ,于是 sinBcos C +cos BsinC =sin CcosB ,即 sin Bcos C =0 ,∵sin B ≠0 ,∴cos C =0,故 C = 90 °,∴△ABC 为直角三角形 .二、 填空题(每题5 分,共 15 分)1+tan α 16. ( 2013 ·南平模拟)若 = 2 013 ,则 + tan 2 α= 21-tan α cos 2 α013.1+tan 1+ sin 2 α(cos α+sin α)2cos α+ sin α分析:2α==α-sin 2α=cos 2 αcos 2 αcos 2cos α- sin α1+ tan α==2 013.1- tan α7. ( 2013 ·抚顺模拟)若锐角α,β知足(1+3tan α)( 1+ 3tan β)= 4π,则α+β=W.3分析:由( 1 +3tanα)(1+3tanβ)=4,tan α+ tan β可得= 3 ,即 tan (α+β)=3.1 - tan αtan βπ又α+β∈( 0,π),∴α+β=.38.已知α,β均为锐角,且 cos (α+β)= sin (α-β),则 tanα=1W .分析:依据已知条件得cos αcos β-sinαsinβ=sin αcos β-cos αsin β,cosβ(cosα- sinα)+sinβ(cos α-sin α)=0,即( cos β+sinβ)(cos α-sin α)= 0.又α,β为锐角,则 sinβ+ cosβ>0 ,∴cos α-sin α= 0,∴tan α=1.三、解答题(共10 分)12cos 4x-2cos 2 x+9 .( 2014 ·贵州六校联考)化简:2.πsin 2π2tan -x+x441-2sin 2xcos 2x +2分析:原式=(4 分)ππ2sin - x cos 2-x44πcos - x41(1-sin 22x )2=π(8 分)π2sin-x cos-x441cos 22x2=πsin- 2x21=cos 2x. (10 分)2B 组提优操练(时间: 30 分钟满分:50分)若时间有限,建议选讲4,6,9一、选择题(每题 5 分,共 20 分)ππ 3 71.( 2012 ·山东高考)若θ∈,,sin 2 θ=,则 sin θ等于( D )4283 4A.B.5 5C.D.44π π π分析: ∵θ∈ , ,∴2θ∈ , π .4 2 2 ∴cos 2θ=-11 -sin 22 θ=- ,8 ∴sin1- cos 2 θ 3θ=2= .42. ( 2014 ·厦门模拟已)知 tan π 1 π2sin 2 α+sin 2 α α+ = ,且- < α<0 ,则4 2 2πcos α-4等于( A )2 53 5A. -B. -1053 102 5C. -D.510π tan α+1 1 1分析: 由 tanα+ 4 = - = ,得 tanα=- .1 tan α 23π10又- < α<0 ,∴sinα=-.2102sin 2α+sin 2 α 2sin α( sin α+cos α)=2 2sin 2 5故 = 2α=-.π5cos α- 2(sin α+cos α)43.( 2013 ·中山模拟)已知角A 为△ ABC 的内角,且 sin32A =- ,则 sin4A - cos A 等于( A )7 B. -7A.22C.-D.22分析: ∵A 为△ ABC 的内角且 sin2A =2sin3Acos A =- <0 ,4∴sin A>0 ,cos A<0 ,∴sin A -cosA>0.又(sinA - cosA )2= 1 -2sinAcos77 A = . ∴ sin A - cos A =.4 2a b =ad -bc ,若 cos1sin α sin β 334. 定义运算d α= ,=,c7cos α cos β14π 0< β< α< ,则 β等于( D )2π π A.B.12 6π π C.D.43分析: 依题意有 sinαcos β-cos3 3αsin β=sin (α-β)=,又140< β< α< π π,∴0< α- β< ,221 -sin 2(α- β)= 13 1 4 3故 cos (α- β)= ,而 cos α= ,∴sin α= ,14 77 于是 sinβ=sin[ α-(α- β)]=sin αcos ( α- β)-cos αsin (α-β)43 13 1 3 3 3π =× - × 14 = ,故 β= .7 14 7 2 3二、 填空题(每题5 分,共 15 分)5. 若 tanπcos 2 θ 3 W.-θ= 3,则 =41+sin 2 θπ1 -tan θ 1cos 2 θ 分析 : ∵ tan -θ= = 3 , ∴tanθ=-. ∴ =4 1 +tan θ2 1+sin 2 θ1cos 2θ-sin 2 θ1 - tan 2θ1-4 sin 2θ+ 2sin θcos θ+cos2 ===3.θ tan 2θ+ 2tanθ+11-1+14·北大附中模拟)在△中,已知π36. ( 2013cos+A =,则cos 2AABC 4 524 W .的值为25分析: cosππ π 23+A =cos cos A -sin sin A = (cos A - sin A )= ,44 4 25 32>0.∴cos A - sin A =5 ①ππ ∴0<A < ,∴0<2A < .4218,∴sin 2A7由①得 1-sin 2A == .25 25 ∴cos 2A =241- sin 22A = .253x - π1 1 7. ( 2013·衡水调研) x - πcos =- ,则 cos 4x = W .sin44 4 23 π 3π 分析: ∵ sinx - π =- cos +x - π =- cos x - ,4 2 4 4ππ 1 1+ cos 2x -∴cos22 1 x - = ,∴ 2= .4 44π 11 ∴cos 2x - =- ,即 sin 2x =- .2 221 ∴cos 4x =1 -2sin 22x = .2三、 解答题(共 15 分)π8.(7 分)( 2013 ·玉溪模拟)已知函数f ( x )=tan3x + .4(1 )求 f π的值;93πα ππ (2 )设 α∈ π,,若 f + = 2 ,求 cos α- 的值 .2 3 44π ππ π πtan +tan 4 3+ 13 分析: ( 1)f=tan + = = =-2- 3.(29 3 4 1 -tan ππ1- 3tan 43分)α π 3π π(2 )∵f + =tan α+ + =tan (α+π)= tan α=2,3 4 4 4sin α ∴ =2 ,即 sin α= 2cos α. ①cos α又 sin 2 α+cos 2 α= 1 , ②1由①②解得 cos 2α= .(4分)53 π5 2 5∵α∈ π, ,∴cos α=-,sinα=-.2 5 5π=cosαcos π π∴cos α- + sin αsin4445 2 2 5 2=- × + - 5 ×5 2 2310=-.(7 分)109. ( 8 分 )( 2014 ·蒙 阴 模 拟 ) 已 知 f ( x ) = 1+1sin 2x -tan xππ2sin x + ·sin x - .4 4(1 )若 tanα=2 ,求 f (α)的值;(2 )若 x ∈ π π , ,求 f (x )的取值范围 .12 22)+ π x + π分析: ( 1 )f ( x )=( sin x + sin xcosx 2sinx +4· cos 41 -cos 2x1π=2 + sin 2x +sin 2x +2 2 1 12x -cos 2x )+ cos2x = + (sin2 211= (sin 2x +cos 2x )+.(2 分)22∵tan α=2,∴sin 2 α= 2sin αcos α 2tan α 4== ,sin 2α+cos 2 α tan 2 α+1 5 coscos 2 α-sin 2α 1- tan 2α 32 α= = =- .sin 2 α+ cos 2α 1+ tan 2α512 α+cos1 3∴f ( α)= (sin 2α)+ = .(4 分)22 511 2π 1 (2 )由( 1)得 f (x )= (sin 2x +cos2x )+ = sin 2x + + .22 2 4 2 (6 分)由 x ∈ π π5 π π 5 π 12 , 2 ,得 ≤ 2x + ≤ .12 4 4故-2 2x + π()≤ 2 + 1≤ sin, 2 4 ≤ 1 ,则0 ≤ f x2 ∴f ( x )的取值范围是 0 ,2 +12.(8 分)。
2019-2020年高三一轮复习第一次检测 数学文试题 含答案

2019-2020年高三一轮复习第一次检测 数学文试题 含答案一、选择题:本大题共15个小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知是实数集,2{|1},{|1}M x N y y x =<==,则( )A .B . C. D .2.命题“所有不能被2整除的整数都是奇数“的否定( )A 所有能被2整除的整数都是奇数B 所有不能被2整除的整数不都是奇数C 存在一个能被2整除的整数不都是奇数D 存在一个不能被2整除的整数不是奇数3.是纯虚数,则( )A .B .C .D . 4.若幂函数的图象经过点,则其定义域为( )A. B. C.D. 5. 已知是定义在上的奇函数,当时,的图象如图所示,那么不等式的解集是( ) A. B.C. D.6.设)5lg(lg ,2lg ,22lg ===c b a 则的大小关系( ) (A ) (B ) (C ) (D )7.双曲线的渐近线与抛物线相切,则该双曲线的离心率等于((A ) (B ) (C ) (D )8.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是,其中P n 为预测人口数,P 0为初期人口数,k 为预测年内增长率,n 为预测期间隔年数.如果在某一时期有-1<k <0,那么这期间人口数( )A .呈上升趋势B .呈下降趋势C .摆动变化D .不变9.若实数满足12()a y y y R >---∈恒成立,则函数的单调减区间为( ) 55(,)(3,)(,)(,2)22A B C D +∞+∞-∞-∞ 10.已知向量,把向量绕坐标原点O 按逆时针方向旋围θ角得到向量,则下列说法不正确...的为( ) A . B .||||||OA OB OA OB +>-u u u r u u u r u u u r u u u rC .D .、在方向上的投影相等11.若圆锥的主视图(正视图)是一个边长为的等边三角形,则该圆锥的表面积为( ).A. B. C. D.12. 满足对任意的实数都有且,则=++++)2015()2016()5()6()3()4(f(1)f(2)f f f f f f Λ( )A.1006B. 2016C.xxD. 100813. 若,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A.和内B.和内C.和内D.和内 14. 定义在R 上的奇函数满足,当时,,又 ,则集合等于( ) A. B.C. D.15.已知凸函数的性质定理“对于定义域内的任意自变量,都有1212...1[()()...()]()n n x x x f x f x f x f n n++++++≤”成立。
2019届高三文科数学第一轮复习五套训练题含答案

2019届高三文科数学第一轮复习训练题第一轮复习训练题练习一1.下列各式的运算结果为纯虚数的是( )A .2(1)i i + B .2(1)i i - C .2(1)i + D .(1)i i +2.如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( ) A.14 B.π8 C.12 D.π43.已知{a n }是公差为1的等差数列,S n 为{a n }的前n 项和,若S 8=4S 4,则a 10=( ) A .172 B .192C .10D .12 4.已知向量()1,2a =-,(),1b m =,若向量a b +与a 垂直,则m = .5.已知曲线C 1的参数方程为45cos ,55sin x t y t =+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ.(1)把C 1的参数方程化为极坐标方程;(2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).6.已知等差数列{a n }的前n 项和为S n ,等比数列{b n }的前n 项和为T n ,a 1=-1,b 1=1,a 2 + b 2 =2.(1)若a 3 + b 3 = 5,求{b n }的通项公式;(2)若T 3=21,求S 3.7.已知,,a b c 分别为ABC △内角,,A B C 的对边,2sin 2sin sin B A C =.(1)若a b =,求cos B ;(2)设90B ∠=,且a =ABC △的面积.8.如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,1AB =BC =AD ,∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为四棱锥P-ABCD 的体积.9.某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人的本年(Ⅱ)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”. 求P (B )的估计值;(Ⅲ)求续保人本年度的平均保费估计值.D PAB C2019届高三文科数学第一轮复习训练题第一轮复习训练题练习二1.设()()12i i a ++的实部与虚部相等,其中a 为实数,则a =( )A .3-B .2-C .2D .32.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( ). A .13 B . 12 C . 23 D . 563.设首项为1,公比为23的等比数列{a n }的前n 项和为S n ,则( ). A .S n =2a n -1 B .S n =3a n -2 C .S n =4-3a n D .S n =3-2a n 4.设向量()1x x +,a =,()12,b =,且⊥a b ,则x = .5.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,sin cos c C c A =-.(1)求A ;(2)若2a =,△ABC b ,c .6.已知{}n a 是公差为3的等差数列,数列{}n b 满足12111==3n n n n b b a b b nb +++=1,,. (1)求{}n a 的通项公式;(2)求{}n b 的前n 项和.7.已知曲线C :22149x y +=,直线l :222x t y t=+⎧⎨=-⎩(t 为参数).(Ⅰ)写出曲线C 的参数方程,直线l 的普通方程;(Ⅱ)过曲线C 上任一点P 作与l 夹角为o 30的直线,交l 于点A ,求||PA 的最大值与最小值.8.如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的点. (Ⅰ)证明:PB // 平面AEC ;(Ⅱ)设AP=1,AD =3,三棱锥P -ABD 的体积V =43,求A 点到平面PBC 的距离.(Ⅲ)补充:设AP=1,AD =3,三棱锥P -ABD 的体积V =43,求A 点到平面PBD 的距离.9.某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得分A 地区用户满意评分的频率分布直方图和B 地区用户满意度评分的频数分布表.区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).2019届高三文科数学第一轮复习训练题第一轮复习训练题练习三 1.设11z i i=++,则|z |=( )A .21B .22C .23D .22.如果3个正数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( ) A .310 B .15 C .110 D .1203.若将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期后,所得图像对应的函数为( ) A .π2sin 24y x ⎛⎫=+⎪⎝⎭ B .π2sin 23y x ⎛⎫=+ ⎪⎝⎭B .C .π2sin 24y x ⎛⎫=-⎪⎝⎭ D .π2sin 23y x ⎛⎫=- ⎪⎝⎭4.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .已知sin sin (sin cos )0B A C C +-=,a=2,C=( ) A .π12B .π6C .π4D .π35.数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为( )A .3690B .3660C .1845D .1830 6.已知两个单位向量a ,b 的夹角为60°,c =ta +(1-t )b .若b ·c =0,则t =______. 7.在直角坐标系xOy 中,直线1C :x =-2,圆2C :()()22121x y -+-=,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.(I )求1C ,2C 的极坐标方程;(II )若直线3C 的极坐标方程为()4R πθρ=∈,设2C 与3C 的交点为M ,N ,求2C MN ∆的面积.8.已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5=-5. (1)求{a n }的通项公式; (2)求数列21211n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和.9.如图,直三棱柱111ABC A B C -中,D ,E 分别是AB ,1BB 的中点.(Ⅰ)证明:1//BC 平面1ACD ;(Ⅱ)设12AA AC CB ===,AB =1C A DE -的体积.1A2019届高三文科数学第一轮复习训练题第一轮复习训练题练习四1.212i1i +(-)=( )A .11i 2--B .11+i 2-C .11+i 2D .11i 2-2.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( ).A .12B .13C .14D .16 3.ABC △的内角A B C ,,的对边分别为a b c ,,.已知a =,2c =,2cos 3A =,则b =( ) A .BC .2D .34.函数f (x )=cos(ωx +φ)的部分图像如图所示,则f (x )的单调递减区间为( ) A .13(,),44k k k Z ππ-+∈ B .13(2,2),44k k k Z ππ-+∈ C .13(,),44k k k Z -+∈ D .13(2,2),44k k k Z -+∈5.已知向量a ,b 夹角为45°,且||1a =,|2|10a b -=,则||b =________. 6.数列{a n }中,a 1=2,a n +1=2a n ,S n 为{a n }的前n 项和,若S n =126,则n = . 7.已知等比数列{}a 中,113a =,公比13q =.(1)n S 为{}n a 的前n 项和,证明:12n n a S -=;(2)设31323log log log n n b a a a =+++,求数列n b 的通项公式.8.在直角坐标系xOy 中,曲线1C 的参数方程为⎩⎨⎧+==,sin 1,cos t a y t a x t (为参数,)0>a .在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线θρcos 4:2=C .(Ⅰ)说明1C 是哪一种曲线,并将1C 的方程化为极坐标方程; (Ⅱ)直线3C 的极坐标方程为0αθ=,其中0α满足2tan 0=α,若曲线1C 与2C 的公共点都在3C 上,求a .9.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB =90°,112AC BC AA ==,D 是棱AA 1的中点.(I) 证明:平面BDC 1⊥平面BDC ;(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.BAC DB 1C 1 A 12019届高三文科数学第一轮复习训练题第一轮复习训练题练习五 1.复数32iz i-+=+的共轭复数是( )A .2i +B .2i -C .1i -+D .1i --2.在一组样本数据(1x ,1y ),(2x ,2y ),…,(n x ,n y )(2n ≥,1x ,2x ,…,n x 不 全相等)的散点图中,若所有样本点(i x ,i y )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为( ) A .-1 B .0C .12D .13.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ=( ). A .45-B .35-C .35D .454.设函数ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则 ( ) A .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π4x =对称 B .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π2x =对称 C .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减,其图象关于直线π4x =对称 5. 已知a 与b 为两个不共线的单位向量,k 为实数,若向量+a b 与向量k -a b 垂直,则k = .6.等比数列{}n a 的前n 项和为n S ,若3230S S +=,则公比q =________. 7.在直角坐标系xOy 中,曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩(θ为参数),直线l 的参数方程为4,1,x a t y t =+⎧⎨=-⎩(t 为参数).(1)若1a =-,求C 与l 的交点坐标;(2)若C 上的点到l 的a .8.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg ), 其频率分布直方图如下:旧养殖法箱产量/kg(1)记A 表示事件“旧养殖法的箱产量低于50kg”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖(32()()()()()n ad bc K a b c d a c b d -=++++9.如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD .(Ⅰ)证明:P A ⊥BD ;(Ⅱ)若PD =AD=1,求棱锥 D-PBC 的高.箱产量/kg新养殖法2019届高三文科数学第一轮复习训练题第一轮复习训练题练习一答案1.下列各式的运算结果为纯虚数的是( C )A .2(1)i i + B .2(1)i i - C .2(1)i + D .(1)i i + 2.如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( B ) A.14 B.π8 C.12 D.π43.已知{a n }是公差为1的等差数列,S n 为{a n }的前n 项和,若S 8=4S 4,则a 10=( B ) A .172 B .192C .10D .12 4.已知向量()1,2a =-,(),1b m =,若向量a b +与a 垂直,则m = .7 5.已知曲线C 1的参数方程为45cos ,55sin x t y t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ.(1)把C 1的参数方程化为极坐标方程;(2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).解:(1)将45cos ,55sin x t y t=+⎧⎨=+⎩消去参数t ,化为普通方程(x -4)2+(y -5)2=25,即C 1:x 2+y 2-8x -10y +16=0. 将cos ,sin x y ρθρθ=⎧⎨=⎩代入x 2+y 2-8x -10y +16=0得ρ2-8ρcos θ-10ρsin θ+16=0.所以C 1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0. (2)C 2的普通方程为x 2+y 2-2y =0.由2222810160,20x y x y x y y ⎧+--+=⎨+-=⎩解得1,1x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩所以C 1与C 2交点的极坐标分别为π4⎫⎪⎭,π2,2⎛⎫ ⎪⎝⎭.6.已知等差数列{a n }的前n 项和为S n ,等比数列{b n }的前n 项和为T n ,a 1=-1,b 1=1,a 2 + b 2 = 2.(1)若a 3 + b 3 = 5,求{b n }的通项公式;(2)若T 3=21,求S 3. 解析:(1)设{a n }的公差为d ,{b n }的公比为q ,则a n = -1+(n -1)d ,b n = q n -1 错误!未找到引用源。
高三数学(文科)第一轮复习测试试题及答案12 Word版含答案

广州市高考数学(文科)一轮复习测试题本试题卷共页,六大题小题。
全卷满分分。
考试用时分钟。
一、选择题:本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的..的值为()....【答案】【解析】因为,所以选..命题“,”的否定是().,.,.,.,【答案】【解析】全称命题的否定式特称命题,所以原命题的否定为,,选..阅读右面的程序框图,运行相应的程序,则输出的值为()....【答案】【解析】第一次循环,;第二次循环,;第三次循环,;第四次循环,,此时满足条件,输出,选..已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是(). `.【答案】【解析】由三视图可知,该几何体是一个半径分别为和的同心圆柱,大圆柱内挖掉了小圆柱。
两个圆柱的高均为.所以几何体的体积为,选..已知幂函数是定义在区间上的奇函数,则()....【答案】【解析】因为幂函数在上是奇函数,所以,所以,所以,选..已知、两点分别在两条互相垂直的直线和上,且线段的中点为,则线段的长为()....【答案】【解析】直线的斜率为,的斜率为。
因为两直线垂直,所以,所以。
所以直线方程,中点。
则,在直角三角形中斜边的长度,所以线段的长为,选..已知数列{}满足,且,则的值是(). . .【答案】【解析】由,得,即,解俯视图正视图侧视图。
高三文科数学第一轮复习资料

第一章集合与常用逻辑用语第一节集合☆☆☆2017考纲考题考情☆☆☆自|主|排|查1.集合的含义与表示方法(1)集合的含义:研究对象叫做元素,一些元素组成的总体叫做集合。
集合中元素的性质:确定性、无序性、互异性。
(2)元素与集合的关系:①属于,记为∈;②不属于,记为∉。
(3)集合的表示方法:列举法、描述法和图示法。
(4)常用数集的记号:自然数集N,正整数集N*或N+,整数集Z,有理数集Q,实数集R。
2.集合间的基本关系A B或B A3.集合的基本运算1.认清集合元素的属性(是点集、数集或其他情形)和化简集合是正确求解集合问题的两个先决条件。
2.易忘空集的特殊性,在写集合的子集时不要忘了空集和它本身。
3.运用数轴图示法易忽视端点是实心还是空心。
4.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性\”而导致解题错误。
5.记住以下结论(1)若集合A中有n个元素,则其子集的个数为2n,真子集的个数为2n-1。
(2)A∪B=A⇔B⊆A;A∩B=A⇔A⊆B。
小|题|快|练一、走进教材1.(必修1P12B组T4改编)满足{0,1}⊆A{0,1,2,3}的集合A的个数为()A.1 B.2C.3 D.4【解析】由题意得A可为{0,1},{0,1,2},{0,1,3}。
故选C。
【答案】 C2.(必修1P12B组T1改编)已知集合A={0,1,2},集合B满足A∪B ={0,1,2},则集合B有个。
【解析】由题意知B⊆A,则集合B有8个。
【答案】8二、双基查验1.已知集合M={-1,0,1},N={0,1,2},则M∪N=()A.{-1,0,1} B.{-1,0,1,2}C.{-1,0,2} D.{0,1}【解析】M∪N表示属于M或属于N的元素构成的集合,故M∪N={-1,0,1,2}。
故选B。
【答案】 B2.设集合M={≥0,x∈R},N={2<1,x∈R},则M∩N=() A.[0,1]B.[0,1)C.(0,1] D.(0,1)【解析】∵x2<1,∴-1<x<1。
新高考数学文科一轮总复习课时练习14.2古典概型(含答案详析)

第2讲古典概型1.从 {1,2,3,4,5} 中随机选用一个数为a,从 {1,2,3} 中随机选用一个数为b,则 b>a 的概率是 ()43A. 5B.521C.5D.52. (2011 年浙江 )从装有 3 个红球、 2 个白球的袋中任取 3 个球,则所取的 3 个球中至罕有 1 个白球的概率是 ()1339A. 10B.10C.5D.103.羊村村长慢羊羊决定从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊去割草,则喜羊羊和美羊羊恰巧只有一只被选中的概率为()3634A. 10B.7C.5D.54.若以连续掷两次骰子分别获得的点数m, n 作为点 P 的横、纵坐标,则点P(m, n)落在直线 x+ y= 5 下方的概率为 ()1111A. 6B.4C.12D.95.在一次教师联欢会上,到会的女教师比男教师多12 人,从到会教师中随机精选一人表演节目.假如每位教师被选到的概率相等,并且选到男教师的概率为9 ,那么参加此次联20欢会的教师共有()A. 360 人 B .240 人C. 144 人D. 120 人6. (2013 年安徽 )若某企业从五位大学毕业生甲、乙、丙、丁、戍中录取三人,这五人被录取的时机均等,则甲或乙被录取的概率为()2239A. 3B.5C.5D.107.从含有 2 件正品和 1 件次品的3 件产品中每次任取 1 件,每次拿出后再放回,连续取两次,则两次拿出的产品中恰巧有一件次品的概率是________.8.连掷两次骰子获得的点数分别为m 和 n,设向量a= (m, n)与向量b= (1,- 1)的夹π的概率是 ________.角为θ,则θ∈ 0,29. (2012 年广东揭阳学业水平测试)某产品按行业生产标准分红8 个等级,等级系数ξ挨次为 1,2,, 8,此中ξ≥5为标准 A,ξ≥ 3 为标准 B,产品的等级系数越大表示产品的质量越好,已知某厂履行标准 B 生产该产品,且该厂的产品都切合相应的履行标准.从该厂生产的产品中随机抽取30 件,相应的等级系数构成一个样本,数据以下:353385563463475348538343447567该行业规定产品的等级系数ξ≥ 7 的为一等品,等级系数5≤ ξ<7 的为二等品,等级系数3≤ ξ<5 的为三等品.(1)试分别预计该厂生产的产品的一等品率、二等品率和三等品率;(2)从样本的一等品中随机抽取 2 件,求所抽得 2 件产品等级系数都是8 的概率.10. (2013 年天津一模)某中学一、二、三年级分别有普法志愿者36 人、 72 人、 54人,用分层抽样的方法从这三个年级抽取一个样本,已知样本中三年级志愿者有 3 人.(1)分别求出样本中一、二年级志愿者的人数;(2)用 A i (i= 1,2 )表示样本中一年级的志愿者,a i(i = 1,2, )表示样本中二年级的志愿者,现从样本中一、二年级的全部志愿者中随机抽取 2 人,①用以上志愿者的表示方法,用列举法列出上述全部可能状况,②抽取的 2 人在同一年级的概率.第2讲 古典概型1.D 2.D3.C4.A 分析:试验是连续掷两次骰子. 故共包括 6×6= 36(个 )基本领件. 事件“点 P(m ,n)落在直线 x + y = 5 下方”,包括 (1,1) , (1,2), (2,1), (1,3) , (2,2), (3,1)共 6 个基本领件, 故 p = 6 =1.36 65.D分析: 设到会男教师 x 人,则女教师为x +12 人,由条件知,x= 9,x + x +12 20∴ x = 54,∴ 2x + 12= 120.应选 D.6.D4分析: 2 件正品记为 a , b ,次品记为 c ,则有放回地连续取两次的基本领件有 (a , 7.9b), (a , c), (b , c), (b , a),(c ,a), (c , b), (a , a),( b , b), (c , c)共 9 个.记“恰巧有一件次品”为事件 A ,则 A 含有的基本领件数为4 个.∴ P(A)= 4.9 7 分析: ∵cos θ= m - n π8.12 2· m 2 +n 2, θ∈ 0,2 ,∴ m ≥ n ,知足条件 m = n 的概率为 6 = 1, 366m>n 的概率与 m<n 的概率相等,∴ m>n 的概率为 1 1 5 2× 1-6 = 12,∴知足 m ≥ n 的概率为 p = 1+ 5 =76 12 12.9. 解: (1)由样本数据知, 30 件产品中等级系数ξ≥ 7 有 6 件,即一等品有 6 件,二等品有 9 件,三等品有 15 件.∴样本中一等品的频次为6= 0.2,故预计该厂生产的产品的一等品率为 0.2;930二等品的频次为 30= 0.3,故预计该厂生产的产品的二等品率为0.3;三等品的频次为15= 0.5,故预计该厂生产的产品的三等品的频次为0.5.30(2)样本中一等品有 6 件,此中等级系数为 7 的有 3 件,等级系数为 8 的也有 3 件,记等级系数为 7 的 3 件产品分别为C 1, C 2, C 3,等级系数为 8 的 3 件产品分别为 P 1, P 2, P 3.则从样本的一等品中随机抽取 2 件的全部可能为:(C 1,C 2) ,(C 1,C 3 ),(C 2 ,C 3),(P 1,P 2 ),( P 1,P 3),(P 2,P 3),( C 1,P 1),(C 1,P 2), (C 1, P 3) ,(C 2, P 1), (C 2, P 2),( C 2,P 3), (C 3, P 1), (C 3,P 2),( C 3, P 3),共 15 种.记从“一等品中随机抽取2 件, 2 件等级系数都是 8”为事件 A , 则 A 包括的基本领件有 (P 1, P 2), (P 1, P 3), (P 2, P 3)共3 种,故所求的概率 P(A)=3=1. 15510. 解: (1)依题意,分层抽样的抽样比为 3 = 154 18.∴在一年级抽取的人数为36× 1= 2(人 ).18在二年级抽取的人数为72× 1= 4(人 ). 18 2人和 4人.因此一、二年级志愿者的人数分别为(2)①用 A 1, A 2 表示样本中一年级的2 名志愿者,用 a 1, a 2,a 3, a 4 表示样本中二年级的 4 名志愿者.则抽取 2 人的状况为 A 1A 2,A 1a 1,A 1a 2,A 1a 3,A 1a 4,A 2a 1,A 2a 2,A 2a 3,A 2a 4,a 1a 2,a 1a 3,a 1a 4,a 2a 3,a 2a 4, a 3a 4,共 15 种.②抽取的 2 人在同一年级的状况是A1A2, a1a2, a1a3,a1a4, a2 a3, a2a4,a3a4,共 7 种.∵每一种状况发生的可能性都是等可能的,7∴抽取的 2 人是同一年级的概率为15.。
高三数学(文科)第一轮复习测试试题及答案10 Word版含答案

广州市高考数学(文科)一轮复习测试题
本试卷分第卷和第卷两部分,第卷第至第页,第卷第至第页,共分.考试时间长分钟.
第Ⅰ卷(选择题共分)
一、选择题(共小题,每小题分,共分)在每小题列出的四个选项中,选出符合题目要求
的一项.
.已知集合,,则
()()()()
【答案】
【.解析】因为,所以,选.
.在复平面内,复数对应的点位于
()第一象限()第二象限()第三象限()第四象限
【答案】
【.解析】,,对应的点的坐标为,所以在第二象限,选.
.已知圆的方程为,则圆心坐标为
()()()()
【答案】
【.解析】圆的标准方程为,所以圆心坐标为,选.
.设函数则
()()()()
【答案】
【.解析】,所以,选.
.一个几何体的三视图如图所示,该几何体的体积是
()()()()
【答案】
【.解析】由三视图可知,该几何体是一个平放的直三棱柱,棱柱的底面为等腰直角三角形,棱柱的高为,所以该几何体的体积为,选.
.执行如图所示的程序框图,输出的值为
()()()()
【答案】
【.解析】由程序框图可知,当时,满足条件,即,所以该程序是求
的程序,所以,选.。
新高考数学文科一轮总复习课时练习3.7抽象函数(含答案详析)

第7讲 抽象函数1. (2010 年陕西 )以下四类函数中,有性质“对随意的x>0 , y>0,函数 f(x)知足 f(x + y)= f(x)f( y)”的是 ( )A .幂函数B .对数函数C .指数函数D .余弦函数 f(a - 3)+ f(9- a 2)<0. 则 a 的取值2.已知定义域为 (- 1,1)的奇函数 y = f(x)是减函数,且范围是 ( )A . (3, 10)B . (2 2,3)C . (22, 4) D . (-2,3)3.已知函数 f(x)是定义在 R 上的函数且知足 f x + 3=- f(x),若 x ∈ (0,3)时,f(x)= log 2(3x + 1),则 f(2011) =() 2A . 4B .- 2C . 2D . log 271+ f x,则 f(2011) = ()4.已知函数 f(x)知足: f(1)= 2, f(x + 1)= 1- f x1 1A .2B .-3C .-2D.3f x + f y5.给出以下三个等式: f(xy)= f(x)+ f(y),f(x + y)= f(x)f(y),f(x + y)=1- f x f y .以下函数中,不知足此中任何一个等式的是 ()A . f(x)= 3xB .f(x)= sinxC . f(x)= log 2xD . f(x)= tanx6.设 f(x)是定义域为 R 的奇函数,且 f(x + 2)=- f(x),那么以下五个判断:① f(x)的一个周期为 T = 4;② f(x)的图象对于直线 x =1 对称;③ f(2010) = 0;④ f(2011)= 0; ⑤ f(2012) = 0.此中正确的个数有 ( )A .2个B .3个C .4 个D .5个7.对于函数 f(x)定义域中的随意 x 1, x 2(x 1≠ x 2) ,有以下结论:① f(x 1+ x 2)= f(x 1) ·f(x 2 );② f(x 1·x 2)= f( x 1)+ f(x 2 );f x 1 - f x 2 ③x 1- x 2>0;④f x 1+ x 2 <f x 1 + f x 2 .22当 f(x)= x 1时,上述结论中正确结论的序号是 ____________;3 1 x时,上述结论中正确结论的序号是 ____________; 当 f(x)=2当 f(x)= lg x 时,上述结论中正确结论的序号是____________.π8.已知函数 y = f(x)是定义在 R 上的奇函数,且y =f x +2 为偶函数,对于函数y =f(x)有以下几种描绘:① y = f(x)是周期函数;② x = π是它的一条对称轴;③ (- π, 0)是它图象的一个对称中心;π④当 x=时,它必定取最大值.2此中描绘正确的选项是 ________.9.函数 f(x)的定义域 D :{ x|x∈R,且 x≠ 0} ,且知足对于随意x1,x2∈ D.有+ f(x2).(1)求 f(1) 的值;(2)判断 f(x)的奇偶性并证明;(3)假如 f(4)= 1, f(3x+ 1)+ f(2x- 6)≤ 3,且 f(x)在 (0,+∞ )上是增函数,求围.f(x1·x2)= f(x1) x的取值范10.设 f(x) 是定义在 [ - 1,1] 上的奇函数,且对随意a, b∈[ - 1,1],当 a+ b≠ 0 时,都有f a + f ba+ b>0.(1)若 a>b,比较 f( a) 与 f(b)的大小;11(2)解不等式 f x-2<f x-4;(3)2记 P={ x|y= f(x- c)} , Q= { x|y= f(x- c )} ,且 P∩ Q= ?,求 c 的取值范围.第 7 讲 抽象函数1. C 分析: 假定 f(x)= a x ,f(x)f(y)= a x a y = a x + y= f(x +y) .- 1<a - 3<1 ,2.B分析: 由条件得 f(a -3) <f(a 2- 9),即 - 1<a 2- 9<1 , ∴ a ∈ (22,3),应选a - 3> a 2- 9,B.3. C14. C 分析: 方法一,由条件知, f(2) =- 3, f(3) =- ,f(4) =13, f(5) = f(1) = 2,故 f(x + 4)= f(x)(x ∈N * ).1∴ f(x)的周期为 4,故 f(2011) =f(3)=- .2方法二,严格推证以下:f(x + 2)=1+ f x + 1=- 1 ,1- f x + 1 f x ∴ f(x + 4)= f[( x + 2)+ 2]= f(x).即 f(x) 周期为 4.故 f(4k + x)= f(x)( k ∈ N * ).即 f(2011) = f(3)=- 1. 25. B 分析: 选项 A ,知足 f(x + y)= f(x)f(y);选项 C 知足 f(xy)= f( x)+ f(y);f x + f y选项 D ,知足 f(x +y)=.6. C7.③ ①④ ②③ 8.①③9. 解: (1)令 x 1= x 2= 1,有 f(1× 1)= f(1)+ f(1),∴ f(1)= 0.(2) f (x)为偶函数,证明以下:令 x 1= x 2=- 1,有 f[( - 1)× (- 1)] =f(- 1)+ f(- 1),∴ f(- 1)= 0.令 x 1=- 1, x 2= x ,有 f(- x)= f(- 1)+ f(x), ∴ f(- x)= f(x).∴ f(x)为偶函数.(3) f (4× 4)=f(4)+ f(4) = 2, f(16× 4)= f(16)+ f(4) = 3. 由 f(3x + 1)+ f(2x - 6)≤ 3,变形为 f[(3 x + 1)(2x - 6)] ≤ f(64). (*)∵ f(x)为偶函数,∴ f(- x)=f(x)= f(|x|).∴不等式 (*) 等价于 f[|(3x + 1)(2x - 6)|] ≤f(64). 又∵ f(x)在 (0,+∞ )上是增函数,∴ |(3x + 1)(2x - 6)|≤ 64,且 (3x + 1)(2x - 6)≠ 0.解得- 7≤ x<-1或-1 <x<3 或 3<x ≤ 5.3 33∴ x 的取值范围是 x -7≤ x ≤ 5,且 x ≠- 1,且 x ≠ 3 .3 310. 解:设- 1≤ x 1<x 2≤ 1,则 x 1- x 2≠ 0,∴f x 1 + f - x 2 >0.x 1+ -x 2∵ x 1- x 2<0,∴ f(x 1)+ f(- x 2)<0. ∴ f(x 1)< - f(- x 2).又 f(x)是奇函数,∴ f(- x 2)=- f(x 2).∴ f(x 1)< f(x 2).∴ f(x)是增函数.(1)∵ a>b ,∴ f(a)>f(b).1 1 (2)由 f x -2 <f x - 4 ,得- 1≤ x -12≤ 1,1 ≤ 1,1 5 - 1≤ x - ∴- ≤ x ≤ .4241 1 ,x - <x -2 4∴不等式的解集为x-1≤ x ≤5.2 4(3)由- 1≤x - c ≤ 1,得- 1+ c ≤ x ≤ 1+ c , ∴ P = { x|-1+ c ≤ x ≤ 1+c} .由- 1≤ x - c 2≤ 1,得- 1+ c 2≤ x ≤ 1+ c 2,∴ Q = { x|- 1+ c 2≤ x ≤ 1+ c 2} . ∵ P ∩ Q = ?,∴ 1+c<- 1+ c 2 或- 1+ c>1+ c 2, 解得 c>2 或 c<- 1.∴ c 的取值范围是 (-∞,- 1) ∪(2,+∞ ).。
高三文科数学第一轮复习经典题

高三文科数学第一轮复习题一、选择题1.集合P={x|x 2=1},Q={x|mx=1},若Q ⊆P ,则m 等于( ) A .1 B .-1C .1或-1D .0,1或-1 2.已知函数f (x )=x -11定义域为M ,g (x )=ln (1+x )定义域N ,则M ∩N等于( ) A .{x|x>-1} B .{x|x<1} C .{x|-1<x<1} D .φ3.以下有关命题的说法错误的是( )A .命题“若0232=+-x x 则x=1”的逆否命题为“若023,12≠+-≠x x x 则”B .“1=x ”是“”0232=+-x x 的充分不必要条件C .若q p ∧为假命题,则p 、q 均为假命题D .对于命题01,:,01:22≥++∈∀⌝<++∈∃x x R x p x x R x p 均有则使得4.函数x x x f 2)1ln()(-+=的零点所在的大致区间是( ) A .(3,4) B .(2,e ) C .(1,2) D .(0,1)5.函数[)⎪⎩⎪⎨⎧+∞∈--∞∈=,1,log )1,(,32x x x y x 的值域为( ) A .(0,3) B .[0,3] C .(]3,∞- D .[)+∞,06.函数)1(),1|(|log >+=a x y 的图像大致是( )A B C D7. 下列函数中,图像的一部分如右图所示的是( )A .sin()6y x π=+ O xy O y -1 O 1 y -1 O 1 yB .sin(2)6y x π=-C .cos(4)3y x π=-D .cos(2)6y x π=- 8.将函数sin 2y x =的图象向左平移4π个单位,再向上平移1个单位,所得图象的函数解析式是( )A .cos 2y x =B .22cos y x =C .)42sin(1π++=x y D .22sin y x =9.已知函数23)(23+-+=x x ax x f 在R 上是减函数,则a 的取值范围是( ) A .(-∞,-3) B . (-∞,-3)C .(-3,0)D .[-3,0] 10. 已知函数f (221)1x x x x +=-则f (3)=( )A .8B .9C .10D .11二、填空题: 13.若函数f (x )=(x-1)(x-a )为偶函数,则a=___________.11.若=--∈=-)sin(),0,2(35)2cos(a a a πππ则且___________ 12.给出下列命题:①存在实数α,使1cos sin =⋅αα;②存在实数α,使23cos sin =+αα; ③函数)23sin(x y +=π是偶函数; ④8π=x 是函数)452sin(π+=x y 的一条对称轴方程;⑤若βα、是第一象限的角,且βα>,则βαsin sin >;其中正确命题的序号是_______________.三、解答题:13.设条件p :2x 2-3x+1≤0,条件q :x 2-(2a+1)x+a (a+1)≤0,若p ¬是q ¬的必要不充分条件,求实数a 的去值范围.14.已知函数f (x )=ax 3+bx+c (a>0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f /(x)的 最小值为-12,求a,b,c 的值.15.已知函数.2321)3(,2)0(,cos sin cos 2)(2+==+=πf f x x b x a x f 且 (1)求a ,b 的值;(2)求)(x f 的最大值及取得最大值时x 的集合;(3)写出函数)(x f 在[0,π]上的单调递减区间.。
新高考数学文科一轮总复习课时练习15.1随机抽样随机抽样(含答案详析)

第十五章统计第1讲随机抽样1. (2013 年湖南 )某学校有男、女学生各好方面能否存在明显差别,拟从全体学生中抽取是 ()500 名.为认识男女学生在学习兴趣与业余爱100 名学生进行检查,则宜采纳的抽样方法A.抽签法B.随机数法C.系统抽样法D.分层抽样法2.用系统抽样法(按等距离的规则),要从 160 名学生中抽取容量为20 的样本,将160名学生从1~ 160 编号.按编号次序均匀分红20 组 (1~ 8 号, 9~ 16 号,, 153~ 160 号 ),若第 16 组应抽出的号码为125,则第一组中按此抽签方法确立的号码是() A. 7B.5C.4D. 33. (2012 年四川 )交通管理部门为认识灵活车驾驶员(简称驾驶员 )对某新法例的了解情况,对甲、乙、丙、丁四个社区做分层抽样检查.假定四个社区驾驶员的总人数为N,此中甲社区有驾驶员96 人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为()A. 101 B . 808C. 1212D. 20124.为认识参加一次知识比赛的3204 名学生的成绩,决定采纳系统抽样的方法抽取一个容量为 80 的样本,那么整体中应随机剔除的个体数量是()A.2B.3C. 4D. 55.某初级中学有学生270 人,此中一年级108 人,二、三年级各81 人,现要利用抽样方法抽取10 人参加某项检查,考虑采纳简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级挨次一致编号为1,2,, 270,使用系统抽样时,将学生一致随机编号为1,2,, 270,并将整个编号挨次分为10 段,假如抽得号码有以下四种状况:①7,34,61,88,115,142,169,196,223,250 ;② 5,9,100,107,111,121,180,195,200,265 ;③ 11,38,65,92,119,146,173,200,227,254 ;④ 30,57,84,111,138,165,192,219,246,270.对于上述样本的以下结论中,正确的选项是()A.②、③都不可以为系统抽样B.②、④都不可以为分层抽样C.①、④都可能为系统抽样D.①、③都可能为分层抽样6.(2013 年浙江模拟 )学校高中部共有学生2000 名,高中部各年级男、女生人数以下表,已知在高中部学生中随机抽取 1 名学生,抽到高三年级女生的概率是0.18,现用分层抽样的方法在高中部抽取50 名学生,则应在高二年级抽取的学生人数为()高一级高二级高三级A.14 人C.16 人女生人数男生人数B.15 人D.17 人/人/人373327yzx3407. (2012 届广东惠州第三次调研 )为了保证食品安全,现采纳分层抽样的方法对某市场的甲、乙、丙、丁四个厂家生产的奶粉进行检测,若甲、乙、丙、丁四个厂家生产的奶粉分别为 120 袋、 100 袋、 80 袋、 60 袋,已知甲、乙两个厂家抽取的袋数之和为 22 袋,则四个厂家一共抽取 ____________袋.8. (2012 年福建 )一支田径队有男女运动员用分层抽样的方法,从全体运动员中抽出一个容量为是 ________人.98 人,此中男运动员有56 人.按男女比率28 的样本,那么应抽取女运动员人数9.某电视台在一次对收看文艺节目和新闻节目观众的抽样检查中,随机抽取了100 名电视观众,有关的数据以下表所示:文艺节目新闻节目总计20~ 40 岁 /人大于 40 岁/人401518275842总计5545100(1)由表中数据直观剖析,收看新闻节目的观众能否与年纪有关?(2)用分层抽样方法在收看新闻节目的观众中随机抽取 5 名,大于40 岁的观众应当抽取几名?(3)在上述抽取的 5 名观众中任取 2 名,求恰有 1 名观众的年纪为20 至40 岁的概率.10.(2012 年广东韶关第二次调研)某中学在校就餐的高一年级学生有440 名,高二年级学生有460 名,高三年级学生有 500 名.为认识学校食堂的服务质量状况,用分层抽样的方法从中抽取 70 名学生进行抽样检查,把学生对食堂的“服务满意度”与“价钱满意度”都分为 5个等级: 1 级 (很不满意 );2 级 (不满意 );3级 (一般 );4 级 (满意 );5级( 很满意 ),其统计结果以下表 (服务满意度为x,价钱满意度为y):价钱满意度12345111220服务满221341 337884意度414641501231(1)求高二年级共抽取学生人数;(2)求“服务满意度”为 3 时的 5 个“价钱满意度”数据的方差;(3)为提升食堂服务质量,现从x<3 且 2≤ y<4 的全部学生中随机抽取两人征采建议,求起码有一人的“服务满意度”为 1 的概率.第十五章 统 计 第 1 讲随机抽样1.D 2.B 3.B 4. C 分析: 因为 3204= 80×40+ 4,因此应随机剔除 4 个个体,应选 C. 5.D6.B 分析: 因为高中部学生中随机抽取 1 名学生,抽到高三年级女生的概率是0.18,因此x= 0.18,解得 x = 360.因此高一人数为 373+ 327= 700(人 ),高三人数为 360+ 340 2000 = 700( 人 ),因此高二人数为 2000-700- 700= 600(人 ).因此高一、高二、高三的人数比为700∶ 600∶ 700=7∶ 6∶ 7,因此利用分层抽样从高中部抽取50 人,则应在高二抽取的人数为50×6=50× 66+7+7 20= 15(人 ).7. 36x = 28,易得 x = 12.8. 12 分析: 设应抽取的女运动员人数是 x ,则98- 56 98 9. 解: (1)因为大于 40 岁的 42 人中有 27 人收看新闻节目,而 20 至 40 岁的 58 人中,只有 18 人收看新闻节目,故收看新闻节目的观众与年纪有关.5(2)27× 45=3,∴大于 40 岁的观众应抽取 3 名.(3)由题意知,设抽取的 5 名观众中,年纪在 20 岁至 40 岁的为 a 1, a 2,大于 40 岁的为b 1,b 2,b 3,从中随机取 2 名,基本领件有: (a 1,a 2 ),(a 1,b 1) ,(a 1,b 2), (a 1,b 3),(a 2,b 1), ( a 2 ,b 2), (a 2,b 3),(b 1, b 2),(b 1,b 3), (b 2,b 3) ,共 10 个,设恰有 1 名观众年纪在 20至40 岁为事件 A ,则 A 中含有基本领件 6 个: (a 1, b 1), (a 1, b 2), (a 1,b 3) ,(a 2,b 1), (a 2, b 2), ( a 2 , b 3 ),∴P(A)= 6= 3.10 510. 解: (1)共有 1400 名学生,高二级抽取的人数为460×70= 23(人 ). 1400(2)“服务满意度为 3”时的 5 个数据的均匀数为 3+ 7+ 8+8+ 4= 6,2+ 7-6 2+ 2× 8-6 2+ 4-6 252 3- 6 因此方差 s = 5 = 4.4.(3)切合条件的全部学生共 7 人,此中“服务满意度为 2”的 4 人记为 a ,b ,c ,d ,“服务满意度为 1”的 3 人记为 x ,y , z.在这 7 人中抽取 2 人有以下状况: (a ,b),(a ,c),(a ,d), (a ,x), (a ,y),( a , z),( b ,c),( b ,d), (b ,x) ,(b ,y) ,(b ,z) , (c , d), (c , x), (c , y), (c , z), (d , x), (d , y), (d ,z), (x , y), (x , z), (y , z),共 21 种状况.此中起码有一人的“服务满意度为1”的状况有 15 种.因此起码有一人的“服务满意度”为1 的概率为 p =15= 5 .21 7。
(北师大版)2020版高考文科数学一轮复习集合文课后训练题含解析

课后限时集训(一)(建议用时:40分钟)A组基础达标一、选择题1.若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=( )A.4 B.2 C.0 D.0或4A[由题意知方程ax2+ax+1=0只有一个实数解或两个相等的根.当a=0时,方程无实根,则a≠0,Δ=a2-4a=0,解得a=4,故选A.]2.(2019·济南模拟)已知集合A={x|x2+2x-3=0},B={-1,1},则A∪B=( ) A.{1} B.{-1,1,3}C.{-3,-1,1} D.{-3,-1,1,3}C[A={-3,1},B={-1,1},则A∪B={-3,-1,1},故选C.]3.(2019·重庆模拟)已知集合A={0,2,4},B={x|3x-x2≥0},则A∩B的子集的个数为( )A.2 B.3 C.4 D.8C[B={x|0≤x≤3},则A∩B={0,2},故其子集的个数是22=4个.]4.若A={2,3,4},B={x|x=n·m,m,n∈A,m≠n},则集合B中的元素个数是( ) A.2 B.3 C.4 D.5B[当m=2时,n=3或4,此时x=6或8.当m=3时,n=4,此时x=12.所以B={6,8,12},故选B.]5.设A,B是全集I={1,2,3,4}的子集,A={1,2},则满足A⊆B的集合B的个数是( ) A.5 B.4 C.3 D.2B[满足条件的集合B有{1,2},{1,2,3},{1,2,4},{1,2,3,4}共4个.]6.(2019·衡水模拟)已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=( )A.{2,5} B.{3,6} C.{2,5,6} D.{2,3,5,6,8}A[由题意得∁U B={2,5,8},∴A∩∁U B={2,3,5,6}∩{2,5,8}={2,5}.]7.(2019·青岛模拟)设集合A={y|y=2x,x∈R},B={x|x2-1<0},则A∪B=( ) A.(-1,1) B.(0,1)C.(-1,+∞) D.(0,+∞)C[由已知得A={y|y>0},B={x|-1<x<1},则A∪B={x|x>-1}.]二、填空题8.已知集合A ={x |x 2-2 019x +2 018<0},B ={x |x ≥a },若A ⊆B ,则实数a 的取值范围是________.(-∞,1] [A ={x |1<x <2 018},B ={x |x ≥a }, 要使A ⊆B ,则a ≤1.]9.若集合A ={y |y =lg x },B ={x |y =x },则A ∩B =________. {x |x ≥0} [A =R ,B ={x |x ≥0},则A ∩B ={x |x ≥0}.]10.设集合A ={-1,1,2},B ={a +1,a 2-2},若A ∩B ={-1,2},则a 的值为________.-2或1 [由A ∩B ={-1,2}得⎩⎪⎨⎪⎧a +1=-1,a 2-2=2,或⎩⎪⎨⎪⎧a +1=2,a 2-2=-1,解得a =-2或a =1.]B 组 能力提升1.(2019·潍坊模拟)已知集合M ={x |lg x <1},N ={x |-3x 2+5x +12<0},则( ) A .N ⊆M B .∁R N ⊆MC .M ∩N =(3,10)∪⎝ ⎛⎭⎪⎫-∞,-43D .M ∩(∁R N )=(0,3]D [由M ={x |lg x <1}得M ={x |0<x <10};由-3x 2+5x +12=(-3x -4)(x -3)<0得N =x ⎪⎪⎪x <-43或x >3,所以∁R N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-43≤x ≤3,则有M ∩(∁R N )=(0,3],故选D.] 2.(2019·南昌模拟)在如图所示的Venn 图中,设全集U =R ,集合A ,B 分别用椭圆内图形表示,若集合A ={x |x 2<2x },B ={x |y =ln(1-x )},则阴影部分图形表示的集合为( )A .{x |x ≤1}B .{x |x ≥1}C .{x |0<x ≤1}D .{x |1≤x <2}D [由x 2<2x 解得0<x <2,∴A =(0,2),由1-x >0,解得x <1,∴B =(-∞,1),阴影部分图形表示的集合为A ∩(∁U B )={x |1≤x <2},故选D.]3.已知A =[1,+∞),B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪12a ≤x ≤2a -1,若A ∩B ≠∅,则实数a 的取值范围是________.[1,+∞) [由A ∩B ≠∅,得⎩⎪⎨⎪⎧2a -1≥1,2a -1≥12a ,解得a ≥1.]4.已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围是________.(-∞,4] [当B =∅时,有m +1≥2m -1,则m ≤2. 当B ≠∅时,若B ⊆A ,如图.则⎩⎪⎨⎪⎧m +1≥-2,2m -1≤7,m +1<2m -1,解得2<m ≤4.综上,m 的取值范围为m ≤4.]。
高考数学( 文科)一轮复习练习:第三章 导数及其应用 第3讲 含答案

基础巩固题组 (建议用时:40分钟)一、填空题1.函数f (x )=2x 3-6x 2-18x -7在[1,4]上的最小值为________. 解析 f ′(x )=6x 2-12x -18=6(x 2-2x -3) =6(x -3)(x +1),由f ′(x )>0,得x >3或x <-1; 由f ′(x )<0,得-1<x <3,故函数f (x )在[1,3]上单调递减,在[3,4]上单调递增, ∴f (x )min =f (3)=2×27-6×9-18×3-7=-61. 答案 -612.函数f (x )=x 3+3x 2+3x -a 的极值点的个数是________.解析 ∵f ′(x )=3x 2+6x +3=3(x 2+2x +1)=3(x +1)2≥0,∴函数f (x )在R 上单调递增,故f (x )无极值点. 答案 03.(2015·泰州调研)函数f (x )=x 3-3bx +3b 在(0,1)内有极小值,则b 的取值范围是________.解析 由f (x )=x 3-3bx +3b ,得f ′(x )=3x 2-3b .由已知可得f ′(x )=3x 2-3b 在(0,1)上与x 轴有交点,且满足⎩⎨⎧f ′(0)<0,f ′(1)>0,即⎩⎨⎧b >0,3-3b >0.∴0<b <1.∴b 的取值范围是(0,1). 答案 (0,1)4.(2015·扬州模拟)已知f (x )=x 3+3ax 2+bx +a 2在x =-1时有极值0,则a -b =________.解析 由题意得f ′(x )=3x 2+6ax +b ,则 ⎩⎨⎧a 2+3a -b -1=0,b -6a +3=0,解得⎩⎨⎧a =1,b =3或⎩⎨⎧a =2,b =9,经检验当a =1,b =3时,函数f (x )在x =-1处无法取得极值,而a =2,b =9满足题意,故a -b =-7. 答案 -75.(2016·长沙模拟)已知函数f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则实数a 的取值范围是________. 解析 ∵f ′(x )=3x 2+2ax +(a +6), 由已知可得f ′(x )=0有两个不相等的实根, ∴Δ=4a 2-4×3×(a +6)>0,即a 2-3a -18>0. ∴a >6或a <-3.答案 (-∞,-3)∪(6,+∞)6.设a ∈R ,若函数y =e x +ax ,x ∈R 有大于零的极值点,则a 的取值范围是________.解析 ∵y =e x +ax ,∴y ′=e x +a . ∵函数y =e x +ax 有大于零的极值点, 则方程y ′=e x +a =0有大于零的解, ∵x >0时,-e x <-1,∴a =-e x <-1. 答案 (-∞,-1)7.已知函数f (x )=x 3-12x +8在区间[-3,3]上的最大值与最小值分别为M ,m ,则M -m =________.解析 由题意,得f ′(x )=3x 2-12,令f ′(x )=0,得x =±2,又f (-3)=17,f (-2)=24,f (2)=-8,f (3)=-1,所以M =24,m =-8,M -m =32. 答案 328.(2015·苏、锡、常、镇模拟)函数f (x )=ax 3+bx 2+cx +d 在x =0处有极大值1,在x =2处有极小值0,则常数a ,b ,c ,d 分别为________,________,________,________.解析 f ′(x )=3ax 2+2bx +c ,则⎩⎨⎧f (2)=0,f ′(2)=0,f (0)=1,f ′(0)=0,即⎩⎨⎧8a +4b +2c +d =0,12a +4b +c =0,d =1,c =0,解得a =14,b =-34,c =0,d =1.答案 14 34 0 1 二、解答题9.(2016·徐州一检)当a ∈⎝ ⎛⎭⎪⎫-∞,-1e 时,函数f (x )=ax -1+ln x 在区间(0,e)上的最大值为-4,求a 的值.解 由题意f ′(x )=a +1x ,令f ′(x )=0,解得x =-1a .∵a ∈⎝ ⎛⎭⎪⎫-∞,-1e ,∴0<-1a <e ,由f ′(x )>0,解得0<x <-1a,由f ′(x )<0,解得-1a <x <e.从而f (x )的单调增区间为⎝ ⎛⎭⎪⎫0,-1a ,减区间为⎝ ⎛⎭⎪⎫-1a ,e .∴f (x )max =f ⎝ ⎛⎭⎪⎫-1a =-1-1+ln ⎝ ⎛⎭⎪⎫-1a =-4,解得a =-e 2.10.(2015·安徽卷)已知函数f (x )=ax(x +r )2(a >0,r >0).(1)求f (x )的定义域,并讨论f (x )的单调性; (2)若ar =400,求f (x )在(0,+∞)内的极值.解 (1)由题意知x ≠-r ,所求的定义域为(-∞,-r )∪(-r ,+∞). f (x )=ax (x +r )2=axx 2+2rx +r 2,f ′(x )=a (x 2+2rx +r 2)-ax (2x +2r )(x 2+2rx +r 2)2=a (r -x )(x +r )(x +r )4.所以当x <-r 或x >r 时,f ′(x )<0, 当-r <x <r 时,f ′(x )>0.因此,f (x )的单调递减区间为(-∞,-r ),(r ,+∞); f (x )的单调递增区间为(-r ,r ).(2)由(1)的解答可知f ′(r )=0,f (x )在(0,r )上单调递增,在(r ,+∞)上单调递减.因此,x =r 是f (x )的极大值点,所以f (x )在(0,+∞)内的极大值为f (r )=ar (2r )2=a 4r =4004=100.能力提升题组 (建议用时:25分钟)11.已知函数f (x )=-x 3+ax 2-4在x =2处取得极值,若m ,n ∈[-1,1],则f (m )+f ′(n )的最小值是________.解析 对函数f (x )求导得f ′(x )=-3x 2+2ax , 由函数f (x )在x =2处取得极值知f ′(2)=0, 即-3×4+2a ×2=0,∴a =3.由此可得f (x )=-x 3+3x 2-4,f ′(x )=-3x 2+6x , 易知f (x )在(-1,0)上单调递减,在(0,1)上单调递增, ∴当m ∈[-1,1]时,f (m )min =f (0)=-4. 又∵f ′(x )=-3x 2+6x 的图象开口向下, 且对称轴为x =1,∴当n ∈[-1,1]时, f ′(n )min =f ′(-1)=-9. 故f (m )+f ′(n )的最小值为-13. 答案 -1312.(2016·南通调研)若函数f (x )=x 33-a 2x 2+x +1在区间⎝ ⎛⎭⎪⎫12,3上有极值点,则实数a 的取值范围是________.解析 若函数f (x )在区间⎝ ⎛⎭⎪⎫12,3上无极值,则当x ∈⎝ ⎛⎭⎪⎫12,3时,f ′(x )=x 2-ax +1≥0恒成立或当x ∈⎝ ⎛⎭⎪⎫12,3时,f ′(x )=x 2-ax +1≤0恒成立.当x ∈⎝ ⎛⎭⎪⎫12,3时,y =x +1x 的值域是⎣⎢⎡⎭⎪⎫2,103;当x ∈⎝ ⎛⎭⎪⎫12,3时,f ′(x )=x 2-ax +1≥0,即a ≤x +1x 恒成立,a ≤2;当x ∈⎝ ⎛⎭⎪⎫12,3,f ′(x )=x 2-ax +1≤0,即a ≥x +1x 恒成立,a ≥103.因此要使函数f (x )在⎝ ⎛⎭⎪⎫12,3上有极值点,实数 a 的取值范围是⎝ ⎛⎭⎪⎫2,103.答案 ⎝ ⎛⎭⎪⎫2,10313.(2015·太原二模)已知f ′(x )=a (x +1)(x -a )是函数f (x )的导函数,若f (x )在x =a 处取得极大值,则实数a 的取值范围是________.解析 ∵f ′(-1)=f ′(a )=0,∴当a <-1时,x <a 时,f ′(x )<0,f (x )单调递减;a <x <-1时,f ′(x )>0,f (x )单调递增;x >-1时,f ′(x )<0,f (x )单调递减,此时f (x )在x =a 处取得极小值,不符合题意.当-1<a <0时,x <-1时,f ′(x )<0,f (x )单调递减;-1<x <a 时,f ′(x )>0,f (x )单调递增;x >a 时,f ′(x )<0,f (x )单调递减,此时f (x )在x =a 处取得极大值,符合题意.当a >0时,x <-1时,f ′(x )>0,f (x )单调递增;-1<x <a 时,f ′(x )<0,f (x )单调递减;x >a 时,f ′(x )>0,f (x )单调递增,此时f (x )在x =a 处取得极小值,不符合题意.∴实数a 的取值范围是(-1,0). 答案 (-1,0)14.(2015·南京、盐城调研)已知a ∈R ,函数f (x )=a x +ln x -1. (1)当a =1时,求曲线y =f (x )在点(2,f (2))处的切线方程; (2)求f (x )在区间(0,e]上的最小值.解 (1)当a =1时,f (x )=1x +ln x -1,x ∈(0,+∞), 所以f ′(x )=-1x 2+1x =x -1x 2,x ∈(0,+∞).因此f ′(2)=14,即曲线y =f (x )在点(2,f (2))处的切线斜率为14. 又f (2)=ln 2-12,所以曲线y =f (x )在点(2,f (2))处的切线方程为 y -⎝ ⎛⎭⎪⎫ln 2-12=14(x -2),即x -4y +4ln 2-4=0. (2)因为f (x )=ax +ln x -1,所以f ′(x )=-a x 2+1x =x -ax 2,x ∈(0,+∞). 令f ′(x )=0,得x =a .①若a ≤0,则f ′(x )>0,f (x )在区间(0,e]上单调递增,此时函数f (x )无最小值. ②若0<a <e ,当x ∈(0,a )时,f ′(x )<0, 函数f (x )在区间(0,a )上单调递减,当x ∈(a ,e]时, f ′(x )>0,函数f (x )在区间(a ,e]上单调递增,所以当x=a时,函数f(x)取得最小值ln a.③若a≥e,则当x∈(0,e]时,f′(x)≤0,函数f(x)在区间(0,e]上单调递减,所以当x=e时,函数f(x)取得最小值a e.综上可知,当a≤0时,函数f(x)在区间(0,e]上无最小值;当0<a<e时,函数f(x)在区间(0,e]上的最小值为ln a;当a≥e时,函数f(x)在区间(0,e]上的最小值为a e.。
2024届联考高三一轮复习联考(三)全国卷文科数学一轮三数学(全国文)答案

\2)\2
B( )的最大值为 2 ln2i ln2 <o·
:.g(x)<0,即f'(x)<0在(0,+)上恒成立,…………………………………4分
f(x)在(0,+)上单调递减.………………………………………………………………………………5分
N是平行四边形
是平行四边形
是平行四边形
所以平面PBC
即是△A
2
全国卷文科数学答案第2页
由余弦定理,得DM2=MN2+DN22MN·DN·COSLMND—1+4AC2+2X1X2ACXSinB
11sina
=1 X(54COSa)十2X1XACX
42AC
4Cos +sina·…9分-4+ sini a4 i·其中o< <r·
TT3
当a ,即a=x时,DM有最大值:
424
DM长度的最大值为 ·i2分
21.(1)证明:f(u)=x(alnzz1)=axrlnzz2x的定义域为(0,+),
当a=1时,f"(x)=lnx2z.…………………………………………………1分
112
设x()=Inx2r,则g'(r) 2 ·
由g(.r)—0·得 2·当o< <2时·g ( )>o;当 >2时·g ( )<0
h(x)有极大值也是最大值h(e) e·
当0<z<1时,h(x)<0,当z>1时,h(x)>0,且z→+o时,h(x)→0.…………………………………10分
2024-2025学年高三一轮复习联考(三)_全国卷文数(含答案)

2024届高三一轮复习联考(三)全国卷文科数学试题注意事项:1.答卷前,考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回,考试时间为120分钟,满分150分一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}212,1A xx B x x =<<=∣∣,则A B ⋃=()A.[)1,2-B.(),2∞-C.[)1,3- D.[]1,2-2.命题2:,220p x R x x ∀∈+-<的否定p ⌝为()A.2000,220x R x x ∃∈+->B.2,220x R x x ∀∈+-C.2,220x R x x ∀∈+->D.2000,220x R x x ∃∈+-3.3.已知复数2(1i)z =+(i 为虚数单位),则复数z 的虚部为()A.2B.2- C.2iD.2i-4.若函数()222,0,log ,0,x x x f x x x ⎧-=⎨>⎩则()2f f ⎡⎤-=⎣⎦()A.2- B.2 C.3- D.35.已知1sin 62πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭()A.14-B.14C.12-D.126.函数()21x xe ef x x --=+在[]3,3-上的大致图象为()A.B.C. D.7.函数2sin cos21y x x=-+的最小值是()A.3-B.1-C.32- D.12-8.已知数列{}n a的前n项和22nS n n m=-++,且对任意*1,0n nn N a a+∈-<,则实数m 的取值范为是()A.()2,∞-+ B.(),2∞--C.()2,∞+ D.(),2∞-9.已知等比数列()*a满足4221,m nq a a a≠=,(其中,*m n N∈),则91m n+的最小值为()A.6 B.16 C.32 D.210.已知函数()cos3f x xπ⎛⎫=+⎪⎝⎭,若()f x在[]0,a上的值域为11,2⎡⎤-⎢⎥⎣⎦,则实数a的取值范为()A.40,3π⎛⎤⎥⎝⎦B.24,33ππ⎡⎤⎢⎥⎣⎦C.2,3π∞⎡⎫+⎪⎢⎣⎭ D.25,33ππ⎡⎤⎢⎥⎣⎦11.设4sin1,3sin2,2sin3a b c===,则()A.a b c<< B.c b a<<C.c a b<< D.a c b<<12.已矨,,A B C均在球O的球面上运动,且满足3AOBπ∠=,若三棱锥O ABC-体积的最大值为6,则球O的体积为()A.12πB.48πC.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知()(1,,a k b==,若a b⊥,则k=__________.14.已知{}n a是各项不全为零的等差数列,前n项和是n S,且2024S S=,若()2626nS S m=≠,则正整数m=__________.15.设,m n为不重合的直线,,,αβγ为不重合的平面,下列是αβ∥成立的充分条件的有()(只填序号).①,m a m β⊂∥②,,m n n m αβ⊂⊥⊥③,αγβγ⊥⊥④,m m αβ⊥⊥16.已知函数()14sin ,01,2,1,x x x f x x x π-<⎧=⎨+>⎩若关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解,则实数m 的取值集合为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.(12分)已知数列{}n a 满足12122,log log 1n n a a a +==+,(1)求数列{}n a 的通项公式;(2)求(){}32nn a -的前n 项和nS.18.(12分)已知ABC 中,三个内角,,A B C 的对边分别为,,,,cos cos 2cos 4a b c C a A c C b B π=+=.(1)求tan A ;(2)若c =,求ABC 的面积.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,O 是BC 的中点,PB PC ==,22PD BC AB ===.(1)求证:平而PBC ⊥平面ABCD ;(2)求点A 到平面PCD 的距离.20.(12分)已知数列()n a 满足()21112122222326n n n n n a a a a n -+-++++=-⋅+ .(1)求{}n a 的通项公式;(2)若2n an n b a =+,求数列n b 的前n 项和T .21.(12分)已知函数()ln x af x ex x -=-+.(1)当1a =时,求曲线()f x 在点()()1,1f 处的切线方程,(2)当0a 时,证明,()2f x x >+.(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系,xOy 中,直线l的参数方程为2,21,2x a y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为22413sin ρθ=+.(1)求直线l 和曲线C 的直角坐标方程;(2)若曲线C 经过伸缩变换,2,x x y y ⎧=⎪⎨⎪='⎩'得到曲线C ',若直线l 与曲线C '有公共点,试求a 的取值范围.23.[选修4-5:不等式选讲](10分)已知函数()22(0)f x x x t t =++->,若函数()f x 的最小值为5.(1)求t 的值;(2)若,,a b c 均为正实数,且2a b c t ++=,求1412a b c++的最小值.2024届高三一轮复习联考(三)全国卷文科数学参考答案及评分意见1.A【解析】由21x ,即()()110x x -+,解得11x -,所以{}11B xx =-∣,所以{12}A B xx ⋃=-<∣.故选A .2.D 【解析】2,220x x x ∀∈+-<R 的否定为:2000,220x x x ∃∈+-R ,故选D.3.A 【解析】2(1i)2i z =+=,即复数z 的虚部为2,故选A .4.D【解析】()()()222(2)228,8log 83f f -=--⨯-===,故选D.5.C 【解析】因为1sin 62πα⎛⎫-= ⎪⎝⎭,所以2211cos 2cos 2cos 22sin 11366622ππππααπαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=--=--=-=- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故选C.6.A 【解析】()()2e e 1x xf x f x x ---==-+,所以函数()y f x =是奇函数,排除B 选项,又()22e e 215f --=>,排除C ,D 选项,故选A.7.D 【解析】由题意,函数22sin cos212sin 2sin y x x x x =-+=+,令[]sin 1,1t x =∈-,可得221122222y t t t ⎛⎫=+=+- ⎪⎝⎭,当12t =-,即1sin 2x =-时,函数取得最小值,最小值为12-.故选D.8.A【解析】因为10n n a a +-<,所以数列{}n a 为递减数列,当2n 时,()2212(1)2123n n n a S S n n m n n m n -⎡⎤=-=-++---+-+=-+⎣⎦,故可知当2n 时,{}n a 单调递减,故{}n a 为递减数列,只需满足21a a <,即112m m-+⇒-.故选A .9.D【解析】由等比数列的性质,可得()911911918,10102888m n m n m n m n m n n m ⎛⎛⎫⎛⎫+=+=++=+++= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当6,2m n ==时,等号成立,因此,91m n +的最小值为2.故选D.10.B 【解析】()cos 3f x x π⎛⎫=+⎪⎝⎭,结合图象,()f x 的值域是11,,0,2333x a x a πππ⎡⎤-++⎢⎣⎦,于是533a πππ+,解得2433aππ,所以实数a 的取值范围为24,33ππ⎡⎤⎢⎥⎣⎦.故选B.11.B 【解析】设()()2sin cos sin ,x x x xf x f x x x -==',令()()cos sin ,sing x x x x g x x x =-'=-,当()0,x π∈时,()0g x '<,故()g x 在()0,π上递减,()()()00,0g x g f x <=∴<',故()sin xf x x=在()0,π上递减,023π<<< .()()sin3sin232,,2sin33sin232f f ∴<<<,故c b <,()()()sin 2012,sin1,sin22sin1,3sin232sin14sin12ππππππ-<<-<<<-<-<-,故b a <,故c b a <<,故选B.12.C 【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时231133632212O ABC C AOB V V R R --==⨯⨯⨯==,故3R =O 的体积为343R V π==,故选C.13.3-【解析】0a b a b ⊥⇔⋅=,所以()(1,10,3k k ⋅=+==-.14.18【解析】设等差数列{}n a 的首项和公差分别为1,a d ,则2122n d d S n a n ⎛⎫=+- ⎪⎝⎭,所以n S 可看成关于n 的二次函数,由二次函数的对称性及202426,m S S S S ==,可得20242622m++=,解得18m =.15.④【解析】根据线面的位置关系易知,①②③中面α和面β可能相交也可能平行,④:若m α⊥且m β⊥,根据面面平行的判定可知垂直于同一直线的两平面互相平行,故④正确.16.()3,1--【解析】作出函数()f x 的大致图象,如图所示,令()t f x =,则()()()2[]210f x m f x m --+-=可化为()()()221110t m t m t m t --+-=-+-=,则11t =或21t m =-,则关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解等价于()t f x =的图象与直线12,t t t t ==的交点个数之和为5个,由图可得函数()t f x =的图象与直线1t t =的交点个数为2,所以()t f x =的图象与直线2t t =的交点个数为3个,即此时214m <-<,解得31m -<<-.17.【解析】(1)在数列{}n a 中,已知12122log log log 1n n n na a a a ++-==,所以12n na a +=,.即{}n a 是首项为12a =,公比为2的等比数列,所以()1*222n n n a n -=⨯=∈N .(2)由()()32322nn n a n -=-⨯,故()()231124272352322n n n S n n -=⨯+⨯+⨯++-⨯+-⨯ ,所以()()23412124272352322nn n S n n +=⨯+⨯+⨯++-⨯+-⨯ ,则()23123222322n n n S n +⎡⎤-=+⨯+++--⨯⎣⎦,()()()11212433221053212n n n n n ++-=-+⨯--⨯=-+-⋅-,故()110352n n S n +=+-⋅.18.【解析】(1)解法一:由题,cos cos 2cos a A c C b B +=,由正弦定理得,sin2sin cos sin cos B A A C C =+,.3,,sin2sin 2sin 2cos2422C A B C B A A A ππππ⎛⎫⎛⎫=++==-=-=- ⎪ ⎪⎝⎭⎝⎭,所以1cos2sin cos 2A A A -=+,221sin cos sin cos 2A A A A --=22tan 1tan 1tan 12A A A --=+,化简得2tan 2tan 30A A --=,解得tan 3A =或tan 1A =-(舍去).解法二:由题,cos cos 2cos a A c C b B +=,由正弦定理得,2sin2sin2sin2B A C =+,即()()()()2sin2sin sin B A C A C A C A C ⎡⎤⎡⎤=++-++--⎣⎦⎣⎦,即()()sin2sin cos B A C A C =+-,又A B C π++=,故()sin sin A C B +=,所以()2sin cos sin cos B B B A C =-,又0B π<<,故sin 0B ≠,所以()2cos cos B A C =-,又A B C π++=,故()cos cos B A C =-+,化简得sin sin 3cos cos A C A C =,因此tan tan 3A C =且tan 1C =,所以tan 3A =.(2)由(1)知tan 3A =,因此()tan tan tan tan 21tan tan A CB AC A C+=-+=-=-,.所以sin 10A =,sin 5B =2sin 2C =,因为,6sin sin a c a A C==,.所以1125sin 612225ABC S ac B ==⨯⨯= .19.【解析】(1)因为,PB PC O =是BC 的中点,所以PO BC ⊥,在直角POC 中,1PC OC ==,所以PO =,在矩形ABCD 中,1,2AB BC ==,所以DO =,又因为2PD =,所以在POD 中,222PD PO OD =+,即PO OD ⊥.而,,BC OD O BC OD ⋂=⊂平面ABCD ,所以PO ⊥平面ABCD ,而PO ⊂平面PBC ,所以平面PBC ⊥平面ABCD .'(2)由(1)平面PBC ⊥平面ABCD ,且DC BC ⊥,所以DC ⊥平面PBC ,所以DC PC ⊥,即PCD 是直角三角形,因为1PC CD ==,所以13122PDC S =⨯=,又知11212ACD S =⨯⨯= ,PO ⊥平面ABCD ,设点A 到平面PCD 的距离为d ,则A PCD P ACD V V --=,即1133PCD ACD S d S PO ⨯⨯=⨯⨯ ,即1311323d ⨯⨯=⨯⨯所以263d =,所以点A 到平面PCD 的距离为3..20.【解析】(1)由题当1n =时,()111223262a +=-⋅+=,即11a =.()21112122222326n n n n n a a a a n -+-++++=-⋅+ ①当2n 时,()211212222526n n n a a a n --+++=-⋅+ ②.①-②得()()()1223262526212nn n n n a n n n +=-⋅+--⋅-=-⋅,所以21n a n =-..(2)由(1)知,212221n an n n b a n -=+=+-,则()()()()3521212325221n n T n -=++++++++- ()()3521222213521n n -=+++++++++-⋅()()212214121232..1423nn n n n +⨯-+-+-=+=-21.【解析】(1)当1a =时,()()111e ln ,e 1x xf x x x f x x--=-+=-+',所以()()12,11f f '==,.则切线方程为()211y x -=⨯-,.即10x y -+=曲线()f x 在点()()1,1f 处的切线方程为10x y -+=.(2)证明:要证()2f x x >+,即证e ln 2x a x -->,设()eln ,0x aF x x x -=->,即证()2F x >,当0a 时,()()1e 1e ln ,ex a x ax ax F x x F x x x----=-=-='在()0,∞+上为增函数,且()e1x ah x x -=-中,()()0100e 110,1e 1e 10a a h h --=⨯-=-=-->.故()0F x '=在()0,∞+上有唯一实数根0x ,且()00,1x ∈..当()00,x x ∈时,()0F x '<,当()0,x x ∞∈+时,()0F x '>,从而当0x x =时,()F x 取得最小值.由()00F x '=,得001ex ax -=,故()()000001eln 2x aF x F x x x a a x -=-=+->.综上,当0a 时,()2F x >即()2f x x >+.22.【解析】(1)由题2,21,2x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),消去参数t得直线:20l x a -=,.22413sin ρθ=+,即2224cos 4sin ρθθ=+,即曲线C 的直角坐标方程为2214x y +=.(2)由,2,x x y y ⎧=⎪⎨⎪='⎩'得2,,x x y y =⎧⎨=''⎩又2214x y +=,所以()()22214x y +'=',即'2'21x y +=,所以曲线C '的方程是221x y +=,.由1d =得11a -.所以a 的取值范围是[]1,1-.23.【解析】(1)()222f x x x t x x t x t =++-=++-+-,()2222y x x tx x t t t =++-+--=+=+,当2x t -时等号成立,.⋅又知当x t =时,x t -取得最小值,所以当x t =时,()f x 有最小值,此时()min ()25f x f t t ==+=,所以3t =..(2)由(1)知,23a b c ++=,()22141114111162(121)232333a b c a b c a b c ⎛⎫++=++++=++= ⎪⎝⎭,当且仅当333,,824a b c ===时取等号,所以1412a b c ++的最小值为163.。
高三数学(文科)第一轮复习测试试题及答案11 Word版含答案
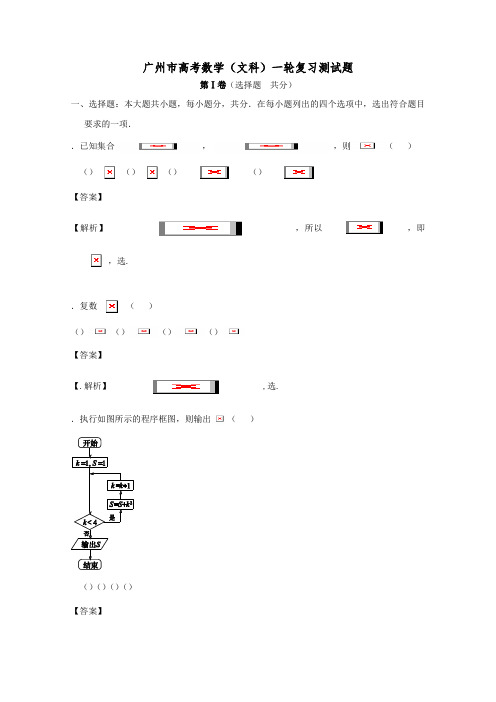
广州市高考数学(文科)一轮复习测试题
第Ⅰ卷(选择题共分)
一、选择题:本大题共小题,每小题分,共分.在每小题列出的四个选项中,选出符合题目
要求的一项.
.已知集合,,则()()()()()
【答案】
【解析】,所以,即
,选.
.复数()
()()()()
【答案】
【.解析】,选.
.执行如图所示的程序框图,则输出()
()()()()
【答案】
【.解析】第一次循环,满足条件,;第二次循环,满足条件,
;第三次循环,满足条件,;第四次循环,不满足条件,输出,选.
.函数的零点个数为()
()()()()
【答案】
【.解析】由,得,令,在坐标系中作出两个函数的图象,由图象可知交点为一个,即函数的零点个数为个,选.
.某四棱锥的三视图如图所示,该四棱锥的体积是()
()()()()
【答案】
【.解析】由三视图可知,四棱锥的高为,底面为直角梯形.其中,所以四棱锥的体积为,选.
.过点作圆的两条切线,,为切点,则()()()()()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础课程教学资料高中数学(文科)高考一轮复习习题集(含答案)目录第一章集合 (1)第一节集合的含义、表示及基本关系 (1)第二节集合的基本运算 (3)第二章函数 (5)第一节对函数的进一步认识 (5)第二节函数的单调性 (9)第三节函数的性质 (13)第三章指数函数和对数函数 (16)第一节指数函数 (16)第二节对数函数 (20)第三节幂函数与二次函数的性质 (24)第四节函数的图象特征 (28)第四章函数的应用 (32)第五章三角函数 (33)第一节角的概念的推广及弧度制 (33)第二节正弦函数和余弦函数的定义及诱导公式 (39)第三节正弦函数与余弦函数的图象及性质 (42)f x A x的图象 (45)第四节函数sin()第六章三角恒等变换 (50)第一节同角三角函数的基本关系 (50)第二节两角和与差及二倍角的三角函数 (53)第七章解三角形 (56)第一节正弦定理与余弦定理 (56)第二节正弦定理、余弦定理的应用 (59)第八章数列 (60)第九章平面向量 (62)第十章算法 (65)第一节程序框图 (65)第二节程序语句 (69)第十一章概率 (73)第一节古典概型 (73)第二节概率的应用 (75)第三节几何概型 (79)第十二章导数 (83)第十三章不等式 (85)第十四章立体几何 (88)第一节简单几何体 (88)第二节空间图形的基本关系与公理 (92)第三节平行关系 (96)第四节垂直关系 (100)第五节简单几何体的面积与体积 (104)第十五章解析几何 (108)第一节直线的倾斜角、斜率与方程 (108)第二节点与直线、直线与直线的位置关系 (111)第三节圆的标准方程与一般方程 (114)第四节直线与圆、圆与圆的位置关系 (117)第五节空间直角坐标系 (121)第十六章圆锥曲线 (123)第一章 集合第一节 集合的含义、表示及基本关系A 组1.已知A ={1,2},B =|x x A ,则集合A 与B 的关系为________. 解析:由集合B =|x x A 知,B ={1,2}.答案:A =B 2.若2,|a a R x x ,则实数a 的取值范围是________.解析:由题意知,2x a 有解,故0a .答案:0a 3.已知集合A =2|21,y yx x x R ,集合B =|28x x ,则集合A 与B的关系是________. 解析:y =x 2-2x -1=(x -1)2-2≥-2,∴A ={y|y ≥-2},∴B A .答案:B A 4.(广东卷改编)已知全集U =R ,则正确表示集合M ={-1,0,1}和N =2|0x x x 关系的韦恩(Venn)图是________.解析:由N=2|0x x x ,得N ={-1,0},则N M .答案:②5.(苏、锡、常、镇四市调查)已知集合A =|5x x ,集合B =|x x a ,若命题“x ∈A ”是命题“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.解析:命题“x ∈A ”是命题“x ∈B ” 的充分不必要条件,∴AB ,∴a <5. 答案:a <56.(原创题)已知m ∈A ,n ∈B ,且集合A ={x |x =2a ,a ∈Z },B ={x |x =2a +1,a ∈Z },又C ={x |x =4a +1,a ∈Z },判断m +n 属于哪一个集合?解:∵m ∈A ,∴设m =2a 1,a 1∈Z ,又∵n ∈B ,∴设n =2a 2+1,a 2∈Z ,∴m +n =2(a 1+a 2)+1,而a 1+a 2∈Z ,∴m +n ∈B .B 组1.设a ,b 都是非零实数,y =a |a |+b |b |+ab|ab |可能取的值组成的集合是________. 解析:分四种情况:(1)a >0且b >0;(2)a >0且b <0;(3)a <0且b >0;(4)a <0且b <0,讨论得y =3或y =-1.答案:{3,-1}2.已知集合A ={-1,3,2m -1},集合B ={3,m 2}.若B ⊆A ,则实数m =________.解析:∵B ⊆A ,显然m 2≠-1且m 2≠3,故m 2=2m -1,即(m -1)2=0,∴m =1.答案:13.设P ,Q 为两个非空实数集合,定义集合P +Q ={a +b |a ∈P ,b ∈Q },若P ={0,2,5},Q ={1,2,6},则P +Q 中元素的个数是________个.解析:依次分别取a =0,2,5;b =1,2,6,并分别求和,注意到集合元素的互异性,∴P +Q ={1,2,6,3,4,8,7,11}.答案:84.已知集合M ={x |x 2=1},集合N ={x |ax =1},若NM ,那么a 的值是________. 解析:M ={x |x =1或x =-1},NM ,所以N =∅时,a =0;当a ≠0时,x =1a =1或-1,∴a =1或-1.答案:0,1,-15.满足{1}A ⊆{1,2,3}的集合A 的个数是________个.解析:A 中一定有元素1,所以A 有{1,2},{1,3},{1,2,3}.答案:36.已知集合A ={x |x =a +16,a ∈Z },B ={x |x =b 2-13,b ∈Z },C ={x |x =c 2+16,c ∈Z },则A 、B 、C 之间的关系是________.解析:用列举法寻找规律.答案:A B =C7.集合A ={x ||x |≤4,x ∈R },B ={x |x <a },则“A ⊆B ”是“a >5”的________.解析:结合数轴若A ⊆B ⇔a ≥4,故“A ⊆B ”是“a >5”的必要但不充分条件.答案:必要不充分条件8.(江苏启东模拟)设集合M ={m |m =2n ,n ∈N ,且m <500},则M 中所有元素的和为________.解析:∵2n <500,∴n =0,1,2,3,4,5,6,7,8.∴M 中所有元素的和S =1+2+22+…+28=511.答案:5119.(北京卷)设A 是整数集的一个非空子集,对于k ∈A ,如果k -1∉A ,且k +1∉A ,那么称k 是A 的一个“孤立元”.给定S ={1,2,3,4,5,6,7,8},由S 的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.解析:依题可知,由S 的3个元素构成的所有集合中,不含“孤立元”,这三个元素一定是相连的三个数.故这样的集合共有6个.答案:610.已知A ={x ,xy ,lg(xy )},B ={0,|x |,y },且A =B ,试求x ,y 的值.解:由lg(xy )知,xy >0,故x ≠0,xy ≠0,于是由A =B 得lg(xy )=0,xy =1.∴A ={x ,1,0},B ={0,|x |,1x}. 于是必有|x |=1,1x=x ≠1,故x =-1,从而y =-1. 11.已知集合A ={x |x 2-3x -10≤0},(1)若B ⊆A ,B ={x |m +1≤x ≤2m -1},求实数m 的取值范围;(2)若A ⊆B ,B ={x |m -6≤x ≤2m -1},求实数m 的取值范围;(3)若A =B ,B ={x |m -6≤x ≤2m -1},求实数m 的取值范围.解:由A ={x |x 2-3x -10≤0},得A ={x |-2≤x ≤5},(1)∵B ⊆A ,∴①若B =∅,则m +1>2m -1,即m <2,此时满足B ⊆A .②若B ≠∅,则⎩⎪⎨⎪⎧ m +1≤2m -1,-2≤m +1,2m -1≤5.解得2≤m ≤3.由①②得,m 的取值范围是(-∞,3].(2)若A ⊆B ,则依题意应有⎩⎪⎨⎪⎧ 2m -1>m -6,m -6≤-2,2m -1≥5.解得⎩⎪⎨⎪⎧ m >-5,m ≤4,m ≥3.故3≤m ≤4,∴m 的取值范围是[3,4]. (3)若A =B ,则必有⎩⎪⎨⎪⎧ m -6=-2,2m -1=5,解得m ∈∅.,即不存在m 值使得A =B . 12.已知集合A ={x |x 2-3x +2≤0},B ={x |x 2-(a +1)x +a ≤0}.(1)若A 是B 的真子集,求a 的取值范围;(2)若B 是A 的子集,求a 的取值范围;(3)若A =B ,求a 的取值范围.解:由x 2-3x +2≤0,即(x -1)(x -2)≤0,得1≤x ≤2,故A ={x |1≤x ≤2},而集合B ={x |(x -1)(x -a )≤0},(1)若A 是B 的真子集,即A B ,则此时B ={x |1≤x ≤ a },故a >2.(2)若B 是A 的子集,即B ⊆A ,由数轴可知1≤a ≤2.(3)若A =B ,则必有a =2第二节 集合的基本运算A 组1.(浙江卷改编)设U =R ,A =|0x x ,B =|1x x ,则A ∩∁U B =____.解析:∁U B ={x |x ≤1},∴A ∩∁U B ={x |0<x ≤1}.答案:{x |0<x ≤1}2.(全国卷Ⅰ改编)设集合A ={4,5,7,9},B ={3,4,7,8,9},全集U =A ∪B ,则集合∁U (A ∩B )中的元素共有________个.解析:A ∩B ={4,7,9},A ∪B ={3,4,5,7,8,9},∁U (A ∩B )={3,5,8}.答案:3x x a a M,则集合M∩N=________.3.已知集合M={0,1,2},N=|2,解析:由题意知,N={0,2,4},故M∩N={0,2}.答案:{0,2}4.(原创题)设A,B是非空集合,定义AⓐB={x|x∈A∪B且x∉A∩B},已知A={x|0≤x≤2},B={y|y≥0},则AⓐB=________.解析:A∪B=[0,+∞),A∩B=[0,2],所以AⓐB=(2,+∞).答案:(2,+∞)5.(湖南卷)某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________.解析:设两项运动都喜欢的人数为x,画出韦恩图得到方程15-x+x+10-x+8=30x=3,∴喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12(人).答案:126.(浙江嘉兴质检)已知集合A={x|x>1},集合B={x|m≤x≤m+3}.(1)当m=-1时,求A∩B,A∪B;(2)若B⊆A,求m的取值范围.m时,B={x|-1≤x≤2},∴A∩B={x|1<x≤2},A∪B={x|x≥-1}.解:(1)当1m,即m的取值范围为(1,+∞)(2)若B⊆A,则1B组1.若集合M={x∈R|-3<x<1},N={x∈Z|-1≤x≤2},则M∩N=________.解析:因为集合N={-1,0,1,2},所以M∩N={-1,0}.答案:{-1,0} 2.已知全集U={-1,0,1,2},集合A={-1,2},B={0,2},则(∁U A)∩B=________.解析:∁U A={0,1},故(∁U A)∩B={0}.答案:{0}3.(济南市高三模拟)若全集U=R,集合M={x|-2≤x≤2},N={x|x2-3x≤0},则M∩(∁U N)=________.解析:根据已知得M∩(∁U N)={x|-2≤x≤2}∩{x|x<0或x>3}={x|-2≤x<0}.答案:{x|-2≤x<0}4.集合A={3,log2a},B={a,b},若A∩B={2},则A∪B=________.解析:由A∩B={2}得log2a=2,∴a=4,从而b=2,∴A∪B={2,3,4}.答案:{2,3,4}5.(江西卷改编)已知全集U=A∪B中有m个元素,(∁U A)∪(∁U B)中有n个元素.若A∩B非空,则A∩B的元素个数为________.解析:U=A∪B中有m个元素,∵(∁U A)∪(∁U B)=∁U(A∩B)中有n个元素,∴A∩B中有m-n个元素.答案:m-n6.(重庆卷)设U={n|n是小于9的正整数},A={n∈U|n是奇数},B={n∈U|n是3的倍数},则∁U(A∪B)=________.解析:U ={1,2,3,4,5,6,7,8},A ={1,3,5,7},B ={3,6},∴A ∪B ={1,3,5,6,7},得∁U (A ∪B )={2,4,8}.答案:{2,4,8}7.定义A ⊗B ={z |z =xy +xy,x ∈A ,y ∈B }.设集合A ={0,2},B ={1,2},C ={1},则集合(A ⊗B )⊗C 的所有元素之和为________.解析:由题意可求(A ⊗B )中所含的元素有0,4,5,则(A ⊗B )⊗C 中所含的元素有0,8,10,故所有元素之和为18.答案:188.若集合{(x ,y )|x +y -2=0且x -2y +4=0}{(x ,y )|y =3x +b },则b =________.解析:由⎩⎪⎨⎪⎧ x +y -2=0,x -2y +4=0.⇒⎩⎪⎨⎪⎧ x =0,y =2.点(0,2)在y =3x +b 上,∴b =2. 9.设全集I ={2,3,a 2+2a -3},A ={2,|a +1|},∁I A ={5},M ={x |x =log 2|a |},则集合M 的所有子集是________.解析:∵A ∪(∁I A )=I ,∴{2,3,a 2+2a -3}={2,5,|a +1|},∴|a +1|=3,且a 2+2a -3=5,解得a =-4或a =2,∴M ={log 22,log 2|-4|}={1,2}.答案:∅,{1},{2},{1,2}10.设集合A ={x |x 2-3x +2=0},B ={x |x 2+2(a +1)x +(a 2-5)=0}.(1)若A ∩B ={2},求实数a 的值;(2)若A ∪B =A ,求实数a 的取值范围.解:由x 2-3x +2=0得x =1或x =2,故集合A ={1,2}.(1)∵A ∩B ={2},∴2∈B ,代入B 中的方程,得a 2+4a +3=0⇒a =-1或a =-3;当a =-1时,B ={x |x 2-4=0}={-2,2},满足条件;当a =-3时,B ={x |x 2-4x +4=0}={2},满足条件;综上,a 的值为-1或-3.(2)对于集合B ,Δ=4(a +1)2-4(a 2-5)=8(a +3).∵A ∪B =A ,∴B ⊆A ,①当Δ<0,即a <-3时,B =∅满足条件;②当Δ=0,即a =-3时,B ={2}满足条件;③当Δ>0,即a >-3时,B =A ={1,2}才能满足条件,则由根与系数的关系得⎩⎪⎨⎪⎧ 1+2=-2(a +1)1×2=a 2-5⇒⎩⎪⎨⎪⎧ a =-52,a 2=7,矛盾.综上,a 的取值范围是a ≤-3. 11.已知函数f (x )=6x +1-1的定义域为集合A ,函数g (x )=lg(-x 2+2x +m )的定义域为集合B .(1)当m =3时,求A ∩(∁R B ); (2)若A ∩B ={x |-1<x <4},求实数m 的值.解:A ={x |-1<x ≤5}.(1)当m =3时,B ={x |-1<x <3},则∁R B ={x |x ≤-1或x ≥3},∴A ∩(∁R B )={x |3≤x ≤5}.(2)∵A ={x |-1<x ≤5},A ∩B ={x |-1<x <4},∴有-42+2×4+m =0,解得m =8,此时B ={x |-2<x <4},符合题意.12.已知集合A ={x ∈R |ax 2-3x +2=0}.(1)若A =∅,求实数a 的取值范围;(2)若A 是单元素集,求a 的值及集合A ;(3)求集合M ={a ∈R |A ≠∅}.解:(1)A 是空集,即方程ax 2-3x +2=0无解.若a =0,方程有一解x =23,不合题意. 若a ≠0,要方程ax 2-3x +2=0无解,则Δ=9-8a <0,则a >98. 综上可知,若A =∅,则a 的取值范围应为a >98. (2)当a =0时,方程ax 2-3x +2=0只有一根x =23,A ={23}符合题意. 当a ≠0时,则Δ=9-8a =0,即a =98时, 方程有两个相等的实数根x =43,则A ={43}. 综上可知,当a =0时,A ={23};当a =98时,A ={43}. (3)当a =0时,A ={23}≠∅.当a ≠0时,要使方程有实数根, 则Δ=9-8a ≥0,即a ≤98. 综上可知,a 的取值范围是a ≤98,即M ={a ∈R |A ≠∅}={a |a ≤98}第二章 函数第一节 对函数的进一步认识A 组1.(江西卷改编)函数y =-x 2-3x +4x 的定义域为________.解析:⎩⎪⎨⎪⎧ -x 2-3x +4≥0,x ≠0,⇒x ∈[-4,0)∪(0,1] .答案:[-4,0)∪(0,1]2.(绍兴第一次质检)如图,函数f (x )的图象是曲线段OAB ,其中点O ,A ,B 的坐标分别为(0,0),(1,2),(3,1),则f (1f (3))的值等于________. 解析:由图象知f (3)=1,f (1f (3))=f (1)=2.答案:23.(北京卷)已知函数f (x )=⎩⎪⎨⎪⎧3x ,x ≤1,-x ,x >1.若f (x )=2,则x =________. 解析:依题意得x ≤1时,3x =2,∴x =log 32;当x >1时,-x =2,x =-2(舍去).故x =log 32.答案:log 324.(黄冈市高三质检)函数f :{1,2}→{1,2}满足f [f (x )]>1的这样的函数个数有________个.解析:如图.答案:15.(原创题)由等式x 3+a 1x 2+a 2x +a 3=(x +1)3+b 1(x +1)2+b 2(x +1)+b 3定义一个映射f (a 1,a 2,a 3)=(b 1,b 2,b 3),则f (2,1,-1)=________.解析:由题意知x 3+2x 2+x -1=(x +1)3+b 1(x +1)2+b 2(x +1)+b 3,令x =-1得:-1=b 3; 再令x =0与x =1得⎩⎪⎨⎪⎧ -1=1+b 1+b 2+b 33=8+4b 1+2b 2+b 3, 解得b 1=-1,b 2=0.答案:(-1,0,-1)6.已知函数f (x )=⎩⎪⎨⎪⎧ 1+1x (x >1),x 2+1 (-1≤x ≤1),2x +3 (x <-1).(1)求f (1-12-1),f {f [f (-2)]}的值;(2)求f (3x -1);(3)若f (a )=32, 求a . 解:f (x )为分段函数,应分段求解.(1)∵1-12-1=1-(2+1)=-2<-1,∴f (-2)=-22+3,又∵f (-2)=-1,f [f (-2)]=f (-1)=2,∴f {f [f (-2)]}=1+12=32.(2)若3x -1>1,即x >23,f (3x -1)=1+13x -1=3x3x -1;若-1≤3x -1≤1,即0≤x ≤32,f (3x -1)=(3x -1)2+1=9x 2-6x +2;若3x -1<-1,即x <0,f (3x -1)=2(3x -1)+3=6x +1.∴f (3x -1)=⎩⎪⎨⎪⎧3x3x -1 (x >23),9x 2-6x +2 (0≤x ≤23),6x +1 (x <0).(3)∵f (a )=32,∴a >1或-1≤a ≤1.当a >1时,有1+1a =32,∴a =2;当-1≤a ≤1时,a 2+1=32,∴a =±22. ∴a =2或±22.B 组1.(广东江门质检)函数y =13x -2+lg(2x -1)的定义域是________. 解析:由3x -2>0,2x -1>0,得x >23.答案:{x |x >23}2.(山东枣庄模拟)函数f (x )=⎩⎪⎨⎪⎧-2x +1,(x <-1),-3,(-1≤x ≤2),2x -1,(x >2),则f (f (f (32)+5))=_.解析:∵-1≤32≤2,∴f (32)+5=-3+5=2,∵-1≤2≤2,∴f (2)=-3,∴f (-3)=(-2)×(-3)+1=7.答案:73.定义在区间(-1,1)上的函数f (x )满足2f (x )-f (-x )=lg(x +1),则f (x )的解析式为________.解析:∵对任意的x ∈(-1,1),有-x ∈(-1,1), 由2f (x )-f (-x )=lg(x +1),① 由2f (-x )-f (x )=lg(-x +1),②①×2+②消去f (-x ),得3f (x )=2lg(x +1)+lg(-x +1), ∴f (x )=23lg(x +1)+13lg(1-x ),(-1<x <1).答案:f (x )=23lg(x +1)+13lg(1-x ),(-1<x <1)4.设函数y =f (x )满足f (x +1)=f (x )+1,则函数y =f (x )与y =x 图象交点的个数可能是________个.解析:由f (x +1)=f (x )+1可得f (1)=f (0)+1,f (2)=f (0)+2,f (3)=f (0)+3,…本题中如果f (0)=0,那么y =f (x )和y =x 有无数个交点;若f (0)≠0,则y =f (x )和y =x 有零个交点.答案:0或无数5.设函数f (x )=⎩⎪⎨⎪⎧2 (x >0)x 2+bx +c (x ≤0),若f (-4)=f (0),f (-2)=-2,则f (x )的解析式为f (x )=________,关于x 的方程f (x )=x 的解的个数为________个.解析:由题意得⎩⎪⎨⎪⎧16-4b +c =c4-2b +c =-2 ⎩⎪⎨⎪⎧b =4c =2, ∴f (x )=⎩⎪⎨⎪⎧2 (x >0)x 2+4x +2 (x ≤0).由数形结合得f (x )=x 的解的个数有3个.答案:⎩⎪⎨⎪⎧2 (x >0)x 2+4x +2 (x ≤0)36.设函数f (x )=log a x (a >0,a ≠1),函数g (x )=-x 2+bx +c ,若f (2+2)-f (2+1)=12,g (x )的图象过点A (4,-5)及B (-2,-5),则a =__________,函数f [g (x )]的定义域为__________.答案:2 (-1,3)7.(天津卷改编)设函数f (x )=⎩⎪⎨⎪⎧x 2-4x +6,x ≥0x +6,x <0,则不等式f (x )>f (1)的解集是________.解析:由已知,函数先增后减再增,当x ≥0,f (x )>f (1)=3时,令f (x )=3, 解得x =1,x =3.故f (x )>f (1)的解集为0≤x <1或x >3.当x <0,x +6=3时,x =-3,故f (x )>f (1)=3,解得-3<x <0或x >3. 综上,f (x )>f (1)的解集为{x |-3<x <1或x >3}.答案:{x |-3<x <1或x >3}8.(山东卷)定义在R 上的函数f (x )满足f (x )=⎩⎪⎨⎪⎧log 2(4-x ), x ≤0,f (x -1)-f (x -2), x >0,则f (3)的值为________.解析:∵f (3)=f (2)-f (1),又f (2)=f (1)-f (0),∴f (3)=-f (0),∵f (0)=log 24=2,∴f (3)=-2.答案:-29.有一个有进水管和出水管的容器,每单位时间进水量是一定的,设从某时刻开始,5分钟内只进水,不出水,在随后的15分钟内既进水,又出水,得到时间x 与容器中的水量y 之间关系如图.再随后,只放水不进水,水放完为止,则这段时间内(即x ≥20),y 与x 之间函数的函数关系是________.解析:设进水速度为a 1升/分钟,出水速度为a 2升/分钟,则由题意得⎩⎪⎨⎪⎧5a 1=205a 1+15(a 1-a 2)=35,得⎩⎪⎨⎪⎧a 1=4a 2=3,则y =35-3(x -20),得y =-3x +95, 又因为水放完为止,所以时间为x ≤953,又知x ≥20,故解析式为y =-3x +95(20≤x≤953).答案:y =-3x +95(20≤x ≤953)10.函数221316f xa x a x .(1)若f x 的定义域为R ,求实数a 的取值范围; (2)若f x 的定义域为[-2,1],求实数a 的值. 解:(1)①若1-a 2=0,即a =±1, (ⅰ)若a =1时,f (x )=6,定义域为R ,符合题意;(ⅱ)当a =-1时,f (x )=6x +6,定义域为[-1,+∞),不合题意.②若1-a 2≠0,则g (x )=(1-a 2)x 2+3(1-a )x +6为二次函数. 由题意知g (x )≥0对x ∈R 恒成立,∴⎩⎪⎨⎪⎧ 1-a 2>0,Δ≤0,∴⎩⎪⎨⎪⎧-1<a <1,(a -1)(11a +5)≤0,∴-511≤a <1.由①②可得-511≤a ≤1. (2)由题意知,不等式(1-a 2)x 2+3(1-a )x +6≥0的解集为[-2,1],显然1-a 2≠0且-2,1是方程(1-a 2)x 2+3(1-a )x +6=0的两个根.∴⎩⎪⎨⎪⎧ 1-a 2<0,-2+1=3(1-a )a 2-1,-2=61-a 2,Δ=[3(1-a )]2-24(1-a 2)>0∴⎩⎪⎨⎪⎧a <-1或a >1,a =2,a =±2.a <-511或a >1∴a =2.11.已知2f x f x x R ,并且当x ∈[-1,1]时,21f x x ,求当21,21x k k kZ 时、f x 的解析式.解:由f (x +2)=f (x ),可推知f (x )是以2为周期的周期函数.当x ∈[2k -1,2k +1]时,2k -1≤x ≤2k +1,-1≤x -2k ≤1.∴f (x -2k )=-(x -2k )2+1.又f (x )=f (x -2)=f (x -4)=…=f (x -2k ),∴f (x )=-(x -2k )2+1,x ∈[2k -1,2k +1],k ∈Z .12.在2008年11月4日珠海航展上,中国自主研制的ARJ 21支线客机备受关注,接到了包括美国在内的多国订单.某工厂有216名工人接受了生产1000件该支线客机某零部件的总任务,已知每件零件由4个C 型装置和3个H 型装置配套组成,每个工人每小时能加工6个C 型装置或3个H 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置,设加工C 型装置的工人有x 位,他们加工完C 型装置所需时间为g (x ),其余工人加工完H 型装置所需时间为h (x ).(单位:h ,时间可不为整数)(1)写出g (x ),h (x )的解析式;(2)写出这216名工人完成总任务的时间f (x )的解析式; (3)应怎样分组,才能使完成总任务的时间最少?解:(1)g (x )=20003x (0<x <216,x ∈N *),h (x )=1000216-x(0<x <216,x ∈N *).(2)f (x )=⎩⎪⎨⎪⎧20003x(0<x ≤86,x ∈N *).1000216-x (87≤x <216,x ∈N *).(3)分别为86、130或87、129.第二节 函数的单调性A 组1.(福建卷改编)下列函数f (x )中,满足“对任意x 1,x 2∈(0,+∞),当12x x 时,都有12f x f x ”的是________.①f (x )=1x②f (x )=(x -1)2 ③f (x )=e x ④f (x )=ln(x +1)解析:∵对任意的x 1,x 2∈(0,+∞),当x 1<x 2时,都有f (x 1)>f (x 2),∴f (x )在(0,+∞)上为减函数.答案:①2.函数f (x )(x ∈R )的图象如右图所示,则函数g (x )=f (log a x )(0<a <1)的单调减区间是________.解析:∵0<a <1,y =log a x 为减函数,∴log a x ∈[0,12]时,g (x )为减函数.由0≤log a x ≤12a ≤x ≤1.答案:[a ,1](或(a ,1))3.函数4154yx x 的值域是________.解析:令x =4+sin 2α,α∈[0,π2],y =sin α+3cos α=2sin(α+π3),∴1≤y ≤2.答案:[1,2] 4.已知函数f (x )=|e x +ae x|(a ∈R )在区间[0,1]上单调递增,则实数a 的取值范围__. 解析:当a <0,且e x +a e x ≥0时,只需满足e 0+ae0≥0即可,则-1≤a <0;当a =0时,f (x )=|e x |=e x 符合题意;当a >0时,f (x )=e x +ae x,则满足f ′(x )=e x -ae x≥0在x ∈[0,1]上恒成立.只需满足a ≤(e 2x )min 成立即可,故a ≤1,综上-1≤a ≤1.答案:-1≤a ≤15.(原创题)如果对于函数f (x )定义域内任意的x ,都有f (x )≥M (M 为常数),称M 为f (x )的下界,下界M 中的最大值叫做f (x )的下确界,下列函数中,有下确界的所有函数是________.①f (x )=sin x ;②f (x )=lg x ;③f (x )=e x ;④f (x )=⎩⎪⎨⎪⎧1 (x >0)0 (x =0)-1 (x <-1)解析:∵sin x ≥-1,∴f (x )=sin x 的下确界为-1,即f (x )=sin x 是有下确界的函数;∵f (x )=lg x 的值域为(-∞,+∞),∴f (x )=lg x 没有下确界;∴f (x )=e x 的值域为(0,+∞),∴f (x )=e x 的下确界为0,即f (x )=e x 是有下确界的函数;∵f (x )=⎩⎪⎨⎪⎧1 (x >0)0 (x =0)-1 (x <-1)的下确界为-1.∴f (x )=⎩⎪⎨⎪⎧1 (x >0)0 (x =0)-1 (x <-1)是有下确界的函数.答案:①③④ 6.已知函数2f xx ,1g xx .(1)若存在x ∈R 使f x b g x ,求实数b 的取值范围;(2)设21F x f x mg xm m 2,且F x 在[0,1]上单调递增,求实数m的取值范围.解:(1)x ∈R ,f (x )<b ·g (x )x ∈R ,x 2-bx +b <0Δ=(-b )2-4b >0b <0或b >4.(2)F (x )=x 2-mx +1-m 2,Δ=m 2-4(1-m 2)=5m 2-4,①当Δ≤0即-255≤m ≤255时,则必需⎩⎪⎨⎪⎧m2≤0-255≤m ≤255-255≤m ≤0.②当Δ>0即m <-255或m >255时,设方程F (x )=0的根为x 1,x 2(x 1<x 2),若m2≥1,则x 1≤0.⎩⎪⎨⎪⎧m 2≥1F (0)=1-m 2≤0m ≥2.若m2≤0,则x 2≤0, ⎩⎪⎨⎪⎧m 2≤0F (0)=1-m 2≥0-1≤m <-255.综上所述:-1≤m ≤0或m ≥2.B 组1.(山东东营模拟)下列函数中,单调增区间是(-∞,0]的是________.①y =-1x②y =-(x -1) ③y =x 2-2 ④y =-|x |解析:由函数y =-|x |的图象可知其增区间为(-∞,0].答案:④2.若函数f (x )=log 2(x 2-ax +3a )在区间[2,+∞)上是增函数,则实数a 的取值范围是________.解析:令g (x )=x 2-ax +3a ,由题知g (x )在[2,+∞)上是增函数,且g (2)>0.∴⎩⎪⎨⎪⎧a 2≤2,4-2a +3a >0,∴-4<a ≤4.答案:-4<a ≤43.若函数f (x )=x +ax (a >0)在(34,+∞)上是单调增函数,则实数a 的取值范围__.解析:∵f (x )=x +a x(a >0)在(a ,+∞)上为增函数,∴a ≤34,0<a ≤916.答案:(0,916]4.(陕西卷改编)定义在R 上的偶函数f (x ),对任意x 1,x 2∈[0,+∞)(x 1≠x 2),有f (x 2)-f (x 1)x 2-x 1<0,则下列结论正确的是________.①f (3)<f (-2)<f (1) ②f (1)<f (-2)<f (3) ③f (-2)<f (1)<f (3) ④f (3)<f (1)<f (-2) 解析:由已知f (x 2)-f (x 1)x 2-x 1<0,得f (x )在x ∈[0,+∞)上单调递减,由偶函数性质得f (2)=f (-2),即f (3)<f (-2)<f (1).答案:①5.(陕西西安模拟)已知函数f (x )=⎩⎪⎨⎪⎧a x (x <0),(a -3)x +4a (x ≥0)满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0成立,则a 的取值范围是________.解析:由题意知,f (x )为减函数,所以⎩⎪⎨⎪⎧0<a <1,a -3<0,a 0≥(a -3)×0+4a ,解得0<a ≤14.6.(宁夏石嘴山模拟)函数f (x )的图象是如下图所示的折线段OAB ,点A 的坐标为(1,2),点B 的坐标为(3,0),定义函数g (x )=f (x )·(x -1),则函数g (x )的最大值为________.解析:g (x )=⎩⎪⎨⎪⎧2x (x -1) (0≤x <1),(-x +3)(x -1) (1≤x ≤3),当0≤x <1时,最大值为0;当1≤x ≤3时, 在x =2取得最大值1.答案:17.(安徽合肥模拟)已知定义域在[-1,1]上的函数y =f (x )的值域为[-2,0],则函数y =f (cos x )的值域是________.解析:∵cosx ∈[-1,1],函数y =f (x )的值域为[-2,0],∴y =f (cos x )的值域为[-2,0].答案:[-2,0]8.已知f (x )=log 3x +2,x ∈[1,9],则函数y =[f (x )]2+f (x 2)的最大值是________.解析:∵函数y =[f (x )]2+f (x 2)的定义域为⎩⎪⎨⎪⎧1≤x ≤9,1≤x 2≤9,∴x ∈[1,3],令log 3x =t ,t ∈[0,1],∴y =(t +2)2+2t +2=(t +3)2-3,∴当t =1时,y max =13.答案:139.若函数f (x )=log a (2x 2+x )(a >0,a ≠1)在区间(0,12)内恒有f (x )>0,则f (x )的单调递增区间为__________.解析:令μ=2x 2+x ,当x ∈(0,12)时,μ∈(0,1),而此时f (x )>0恒成立,∴0<a <1.μ=2(x +14)2-18,则减区间为(-∞,-14).而必然有2x 2+x >0,即x >0或x <-12.∴f (x )的单调递增区间为(-∞,-12).答案:(-∞,-12)10.试讨论函数y =2(log 12x )2-2log 12x +1的单调性.解:易知函数的定义域为(0,+∞).如果令u =g (x )=log 12x ,y =f (u )=2u 2-2u +1,那么原函数y =f [g (x )]是由g (x )与f (u )复合而成的复合函数,而u =log 12x 在x ∈(0,+∞)内是减函数,y =2u 2-2u +1=2(u -12)2+12在u ∈(-∞,12)上是减函数,在u ∈(12,+∞)上是增函数.又u ≤12,即log 12x ≤12,得x ≥22;u >12,得0<x <22.由此,从下表讨论复合函数y =f [g (x )]的单调性:故函数y =2(log 12x )2-2log 12x +1在区间(0,22)上单调递减,在区间(22,+∞)上单调递增.11.(广西河池模拟)已知定义在区间(0,+∞)上的函数f (x )满足f (x 1x 2)=f (x 1)-f (x 2),且当x >1时,f (x )<0.(1)求f (1)的值;(2)判断f (x )的单调性;(3)若f (3)=-1,解不等式f (|x |)<-2.解:(1)令x 1=x 2>0,代入得f (1)=f (x 1)-f (x 1)=0,故f (1)=0.(2)任取x 1,x 2∈(0,+∞),且x 1>x 2,则x 1x 2>1,由于当x >1时,f (x )<0, 所以f (x 1x 2)<0,即f (x 1)-f (x 2)<0,因此f (x 1)<f (x 2), 所以函数f (x )在区间(0,+∞)上是单调递减函数.(3)由f (x 1x 2)=f (x 1)-f (x 2)得f (93)=f (9)-f (3),而f (3)=-1,所以f (9)=-2.由于函数f (x )在区间(0,+∞)上是单调递减函数,由f (|x |)<f (9),得|x |>9,∴x >9或x <-9.因此不等式的解集为{x |x >9或x <-9}.12.已知:f (x )=log 3x 2+ax +b x ,x ∈(0,+∞),是否存在实数a ,b ,使f (x )同时满足下列三个条件:(1)在(0,1]上是减函数,(2)在[1,+∞)上是增函数,(3)f (x )的最小值是1.若存在,求出a 、b ;若不存在,说明理由.解:∵f (x )在(0,1]上是减函数,[1,+∞)上是增函数,∴x =1时,f (x )最小,log 31+a +b 1=1.即a +b =2.设0<x 1<x 2≤1,则f (x 1)>f (x 2).即x 12+ax 1+b x 1>x 22+ax 2+bx 2恒成立.由此得(x 1-x 2)(x 1x 2-b )x 1x 2>0恒成立. 又∵x 1-x 2<0,x 1x 2>0,∴x 1x 2-b <0恒成立,∴b ≥1.设1≤x 3<x 4,则f (x 3)<f (x 4)恒成立.∴(x 3-x 4)(x 3x 4-b )x 3x 4<0恒成立. ∵x 3-x 4<0,x 3x 4>0,∴x 3x 4>b 恒成立.∴b ≤1.由b ≥1且b ≤1可知b =1,∴a =1.∴存在a 、b ,使f (x )同时满足三个条件.第三节 函数的性质A 组1.设偶函数f (x )=log a |x -b |在(-∞,0)上单调递增,则f (a +1)与f (b +2)的大小关系为________.解析:由f (x )为偶函数,知b =0,∴f (x )=log a |x |,又f (x )在(-∞,0)上单调递增,所以0<a <1,1<a +1<2,则f (x )在(0,+∞)上单调递减,所以f (a +1)>f (b +2).答案:f (a +1)>f (b +2)2.(广东三校模拟)定义在R 上的函数f (x )既是奇函数又是以2为周期的周期函数,则f (1)+f (4)+f (7)等于________.解析:f (x )为奇函数,且x ∈R ,所以f (0)=0,由周期为2可知,f (4)=0,f (7)=f (1),又由f (x +2)=f (x ),令x =-1得f (1)=f (-1)=-f (1)⇒f (1)=0,所以f (1)+f (4)+f (7)=0.答案:03.(山东卷改编)已知定义在R 上的奇函数f (x )满足f (x -4)=-f (x ),且在区间[0,2]上是增函数,则f (-25)、f (11)、f (80)的大小关系为________.解析:因为f (x )满足f (x -4)=-f (x ),所以f (x -8)=f (x ),所以函数是以8为周期的周期函数,则f (-25)=f (-1),f (80)=f (0),f (11)=f (3),又因为f (x )在R 上是奇函数,f (0)=0,得f (80)=f (0)=0,f (-25)=f (-1)=-f (1),而由f (x -4)=-f (x )得f (11)=f (3)=-f (-3)=-f (1-4)=f (1),又因为f (x )在区间[0,2]上是增函数,所以f (1)>f (0)=0,所以-f (1)<0,即f (-25)<f (80)<f (11).答案:f (-25)<f (80)<f (11)4.(辽宁卷改编)已知偶函数f (x )在区间[0,+∞)上单调增加,则满足f (2x -1)<f (13)的x 取值范围是________.解析:由于f (x )是偶函数,故f (x )=f (|x |),由f (|2x -1|)<f (13),再根据f (x )的单调性得|2x -1|<13,解得13<x <23.答案:(13,23) 5.(原创题)已知定义在R 上的函数f (x )是偶函数,对x ∈R ,f (2+x )=f (2-x ),当f (-3)=-2时,f (2011)的值为________.解析:因为定义在R 上的函数f (x )是偶函数,所以f (2+x )=f (2-x )=f (x -2),故函数f (x )是以4为周期的函数,所以f (2011)=f (3+502×4)=f (3)=f (-3)=-2.答案:-26.已知函数y =f (x )是定义在R 上的周期函数,周期T =5,函数y =f (x )(-1≤x ≤1)是奇函数,又知y =f (x )在[0,1]上是一次函数,在[1,4]上是二次函数,且在x =2时函数取得最小值-5.(1)证明:f (1)+f (4)=0;(2)求y =f (x ),x ∈[1,4]的解析式;(3)求y =f (x )在[4,9]上的解析式.解:(1)证明:∵f (x )是以5为周期的周期函数,∴f (4)=f (4-5)=f (-1),又∵y =f (x )(-1≤x ≤1)是奇函数,∴f (1)=-f (-1)=-f (4),∴f (1)+f (4)=0.(2)当x ∈[1,4]时,由题意可设f (x )=a (x -2)2-5(a >0),由f (1)+f (4)=0,得a (1-2)2-5+a (4-2)2-5=0,∴a =2,∴f (x )=2(x -2)2-5(1≤x ≤4).(3)∵y =f (x )(-1≤x ≤1)是奇函数,∴f (0)=0,又知y =f (x )在[0,1]上是一次函数,∴可设f (x )=kx (0≤x ≤1),而f (1)=2(1-2)2-5=-3,∴k =-3,∴当0≤x ≤1时,f (x )=-3x ,从而当-1≤x <0时,f (x )=-f (-x )=-3x ,故-1≤x ≤1时,f (x )=-3x .∴当4≤x ≤6时,有-1≤x -5≤1,∴f (x )=f (x -5)=-3(x -5)=-3x +15.当6<x ≤9时,1<x -5≤4,∴f (x )=f (x -5)=2[(x -5)-2]2-5=2(x -7)2-5.∴f (x )=⎩⎪⎨⎪⎧ -3x +15, 4≤x ≤62(x -7)2-5, 6<x ≤9.B 组1.(全国卷Ⅰ改编)函数f (x )的定义域为R ,若f (x +1)与f (x -1)都是奇函数,则下列结论正确的是________.①f (x )是偶函数 ②f (x )是奇函数 ③f (x )=f (x +2)④f (x +3)是奇函数解析:∵f (x +1)与f (x -1)都是奇函数,∴f (-x +1)=-f (x +1),f (-x -1)=-f (x -1),∴函数f (x )关于点(1,0),及点(-1,0)对称,函数f (x )是周期T =2[1-(-1)]=4的周期函数.∴f (-x -1+4)=-f (x -1+4),f (-x +3)=-f (x +3),即f (x +3)是奇函数.答案:④2.已知定义在R 上的函数f (x )满足f (x )=-f (x +32),且f (-2)=f (-1)=-1,f (0)=2,f (1)+f (2)+…+f (2009)+f (2010)=________.解析:f (x )=-f (x +32)⇒f (x +3)=f (x ),即周期为3,由f (-2)=f (-1)=-1,f (0)=2,所以f (1)=-1,f (2)=-1,f (3)=2,所以f (1)+f (2)+…+f (2009)+f (2010)=f (2008)+f (2009)+f (2010)=f (1)+f (2)+f (3)=0.答案:03.(浙江台州模拟)已知f (x )是定义在R 上的奇函数,且f (1)=1,若将f (x )的图象向右平移一个单位后,得到一个偶函数的图象,则f (1)+f (2)+f (3)+…+f (2010)=________.解析:f (x )是定义在R 上的奇函数,所以f (-x )=-f (x ),将f (x )的图象向右平移一个单位后,得到一个偶函数的图象,则满足f (-2+x )=-f (x ),即f (x +2)=-f (x ),所以周期为4,f (1)=1,f (2)=f (0)=0,f (3)=-f (1)=-1,f (4)=0,所以f (1)+f (2)+f (3)+f (4)=0,则f (1)+f (2)+f (3)+…+f (2010)=f (4)×502+f (2)=0.答案:04.(湖南郴州质检)已知函数f (x )是R 上的偶函数,且在(0,+∞)上有f ′(x )>0,若f (-1)=0,那么关于x 的不等式xf (x )<0的解集是________.解析:在(0,+∞)上有f ′(x )>0,则在(0,+∞)上f (x )是增函数,在(-∞,0)上是减函数,又f (x )在R 上是偶函数,且f (-1)=0,∴f (1)=0.从而可知x ∈(-∞,-1)时,f (x )>0;x ∈(-1,0)时,f (x )<0;x ∈(0,1)时,f (x )<0;x ∈(1,+∞)时,f (x )>0.∴不等式的解集为(-∞,-1)∪(0,1)答案:(-∞,-1)∪(0,1).5.(江西卷改编)已知函数f (x )是(-∞,+∞)上的偶函数,若对于x ≥0,都有f (x +2)=f (x ),且当x ∈[0,2)时,f (x )=log 2(x +1),则f (-2009)+f (2010)的值为________.解析:∵f (x )是偶函数,∴f (-2009)=f (2009).∵f (x )在x ≥0时f (x +2)=f (x ),∴f (x )周期为2.∴f (-2009)+f (2010)=f (2009)+f (2010)=f (1)+f (0)=log 22+log 21=0+1=1.答案:16.(江苏苏州模拟)已知函数f (x )是偶函数,并且对于定义域内任意的x ,满足f (x +2)=-1f (x ),若当2<x <3时,f (x )=x ,则f (2009.5)=________.解析:由f (x +2)=-1f (x ),可得f (x +4)=f (x ),f (2009.5)=f (502×4+1.5)=f (1.5)=f (-2.5)∵f (x )是偶函数,∴f (2009.5)=f (2.5)=52.答案:527.(安徽黄山质检)定义在R 上的函数f (x )在(-∞,a ]上是增函数,函数y =f (x +a )是偶函数,当x 1<a ,x 2>a ,且|x 1-a |<|x 2-a |时,则f (2a -x 1)与f (x 2)的大小关系为________.解析:∵y =f (x +a )为偶函数,∴y =f (x +a )的图象关于y 轴对称,∴y =f (x )的图象关于x =a 对称.又∵f (x )在(-∞,a ]上是增函数,∴f (x )在[a ,+∞)上是减函数.当x 1<a ,x 2>a ,且|x 1-a |<|x 2-a |时,有a -x 1<x 2-a ,即a <2a -x 1<x 2,∴f (2a -x 1)>f (x 2).答案:f (2a -x 1)>f (x 2)8.已知函数f (x )为R 上的奇函数,当x ≥0时,f (x )=x (x +1).若f (a )=-2,则实数a =________.解析:当x ≥0时,f (x )=x (x +1)>0,由f (x )为奇函数知x <0时,f (x )<0,∴a <0,f (-a )=2,∴-a (-a +1)=2,∴a =2(舍)或a =-1.答案:-19.(山东卷)已知定义在R 上的奇函数f (x )满足f (x -4)=-f (x ),且在区间[0,2]上是增函数.若方程f (x )=m (m >0)在区间[-8,8]上有四个不同的根x 1,x 2,x 3,x 4,则x 1+x 2+x 3+x 4=________.解析:因为定义在R 上的奇函数,满足f (x -4)=-f (x ),所以f (4-x )=f (x ),因此,函数图象关于直线x =2对称且f (0)=0.由f (x -4)=-f (x )知f (x -8)=f (x ),所以函数是以8为周期的周期函数.又因为f (x )在区间[0,2]上是增函数,所以f (x )在区间[-2,0]上也是增函数,如图所示,那么方程f (x )=m (m >0)在区间[-8,8]上有四个不同的根x 1,x 2,x 3,x 4,不妨设x 1<x 2<x 3<x 4.由对称性知x 1+x 2=-12,x 3+x 4=4,所以x 1+x 2+x 3+x 4=-12+4=-8. 答案:-810.已知f (x )是R 上的奇函数,且当x ∈(-∞,0)时,f (x )=-x lg(2-x ),求f (x )的解析式.解:∵f (x )是奇函数,可得f (0)=-f (0),∴f (0)=0.当x >0时,-x <0,由已知f (-x )=x lg(2+x ),∴-f (x )=x lg(2+x ),即f (x )=-x lg(2+x ) (x >0).∴f (x )=⎩⎪⎨⎪⎧ -x lg(2-x ) (x <0),-x lg(2+x ) (x ≥0).即f (x )=-x lg(2+|x |)(x ∈R ). 11.已知函数f (x ),当x ,y ∈R 时,恒有f (x +y )=f (x )+f (y ).(1)求证:f (x )是奇函数;(2)如果x ∈R +,f (x )<0,并且f (1)=-12,试求f (x )在区间[-2,6]上的最值. 解:(1)证明:∴函数定义域为R ,其定义域关于原点对称.∵f (x +y )=f (x )+f (y ),令y =-x ,∴f (0)=f (x )+f (-x ).令x =y =0,∴f (0)=f (0)+f (0),得f (0)=0.∴f (x )+f (-x )=0,得f (-x )=-f (x ),∴f (x )为奇函数.(2)法一:设x ,y ∈R +,∵f (x +y )=f (x )+f (y ),∴f (x +y )-f (x )=f (y ).∵x ∈R +,f (x )<0,∴f (x +y )-f (x )<0,∴f (x +y )<f (x ).∵x +y >x ,∴f (x )在(0,+∞)上是减函数.又∵f (x )为奇函数,f (0)=0,∴f (x )在(-∞,+∞)上是减函数.∴f (-2)为最大值,f (6)为最小值.∵f (1)=-12,∴f (-2)=-f (2)=-2f (1)=1,f (6)=2f (3)=2[f (1)+f (2)]=-3.∴所求f (x )在区间[-2,6]上的最大值为1,最小值为-3.法二:设x 1<x 2,且x 1,x 2∈R .则f (x 2-x 1)=f [x 2+(-x 1)]=f (x 2)+f (-x 1)=f (x 2)-f (x 1).∵x 2-x 1>0,∴f (x 2-x 1)<0.∴f (x 2)-f (x 1)<0.即f (x )在R 上单调递减.∴f (-2)为最大值,f (6)为最小值.∵f (1)=-12,∴f (-2)=-f (2)=-2f (1)=1,f (6)=2f (3)=2[f (1)+f (2)]=-3.∴所求f (x )在区间[-2,6]上的最大值为1,最小值为-3.12.已知函数f (x )的定义域为R ,且满足f (x +2)=-f (x ).(1)求证:f (x )是周期函数;(2)若f (x )为奇函数,且当0≤x ≤1时,f (x )=12x ,求使f (x )=-12在[0,2010]上的所有x 的个数.解:(1)证明:∵f (x +2)=-f (x ),∴f (x +4)=-f (x +2)=-[-f (x )]=f (x ),∴f (x )是以4为周期的周期函数.(2)当0≤x ≤1时,f (x )=12x , 设-1≤x ≤0,则0≤-x ≤1,∴f (-x )=12(-x )=-12x .∵f (x )是奇函数,∴f (-x )=-f (x ),∴-f (x )=-12x ,即f (x )=12x .故f (x )=12x (-1≤x ≤1) 又设1<x <3,则-1<x -2<1,∴f (x -2)=12(x -2), 又∵f (x -2)=-f (2-x )=-f [(-x )+2]=-[-f (-x )]=-f (x ),∴-f (x )=12(x -2),∴f (x )=-12(x -2)(1<x <3).∴f (x )=⎩⎪⎨⎪⎧ 12x (-1≤x ≤1)-12(x -2) (1<x <3)由f (x )=-12,解得x =-1.∵f (x )是以4为周期的周期函数.故f (x )=-12的所有x =4n -1(n ∈Z ).令0≤4n -1≤2010,则14≤n ≤50234,又∵n ∈Z ,∴1≤n ≤502(n ∈Z ),∴在[0,2010]上共有502个x 使f (x )=-12.第三章 指数函数和对数函数第一节 指数函数A 组1.(黑龙江哈尔滨模拟)若a >1,b <0,且a b +a -b =22,则a b -a -b 的值等于________.解析:∵a >1,b <0,∴0<a b <1,a -b >1.又∵(a b +a -b )2=a 2b+a -2b +2=8,∴a 2b +a -2b =6,∴(a b -a -b )2=a 2b +a -2b -2=4,∴a b -a -b =-2.答案:-22.已知f (x )=a x +b 的图象如图所示,则f (3)=________.解析:由图象知f (0)=1+b =-2,∴b =-3.又f (2)=a 2-3=0,∴a =3,则f (3)=(3)3-3=33-3.答案:33-3 3.函数y =(12)2x -x 2的值域是________. 解析:∵2x -x 2=-(x -1)2+1≤1,∴(12)2x -x 2≥12.答案:[12,+∞) 4.(山东卷)若函数f (x )=a x -x -a (a >0,且a ≠1)有两个零点,则实数a 的取值范围是________.解析:函数f (x )的零点的个数就是函数y =a x 与函数y =x +a 交点的个数,由函数的图象可知a >1时两函数图象有两个交点,0<a <1时两函数图象有惟一交点,故a >1. 答案:(1,+∞)5.(原创题)若函数f (x )=a x -1(a >0,a ≠1)的定义域和值域都是[0,2],则实数a 等于________.解析:由题意知⎩⎪⎨⎪⎧ 0<a <1a 2-1=0a 0-1=2无解或⎩⎪⎨⎪⎧ a >1a 0-1=0a 2-1=2⇒a =3.答案: 36.已知定义域为R 的函数f (x )=-2x +b 2x +1+a是奇函数.(1)求a ,b 的值; (2)若对任意的t ∈R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求k 的取值范围.解:(1)因为f (x )是R 上的奇函数,所以f (0)=0,即-1+b 2+a=0,解得b =1. 从而有f (x )=-2x +12x +1+a .又由f (1)=-f (-1)知-2+14+a =--12+11+a,解得a =2. (2)法一:由(1)知f (x )=-2x +12x +1+2=-12+12x +1, 由上式易知f (x )在R 上为减函数,又因f (x )是奇函数,从而不等式f (t 2-2t )+f (2t 2-k )<0⇔f (t 2-2t )<-f (2t 2-k )=f (-2t 2+k ).因f (x )是R 上的减函数,由上式推得t 2-2t >-2t 2+k .即对一切t ∈R 有3t 2-2t -k >0,从而Δ=4+12k <0,解得k <-13. 法二:由(1)知f (x )=-2x +12x +1+2,又由题设条件得-2t 2-2t +12t 2-2t +1+2+-22t 2-k+122t 2-k +1+2<0 即(22t 2-k +1+2)(-2t 2-2t +1)+(2t 2-2t +1+2)(-22t 2-k +1)<0整理得23t 2-2t -k >1,因底数2>1,故3t 2-2t -k >0上式对一切t ∈R 均成立,从而判别式Δ=4+12k <0,解得k <-13.B 组1.如果函数f (x )=a x +b -1(a >0且a ≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有________.①0<a <1且b >0 ②0<a <1且0<b <1 ③a >1且b <0 ④a >1且b >0解析:当0<a <1时,把指数函数f (x )=a x 的图象向下平移,观察可知-1<b -1<0,即0<b <1.答案:②2.(保定模拟)若f (x )=-x 2+2ax 与g (x )=(a +1)1-x 在区间[1,2]上都是减函数,则a 的取值范围是________.解析:f (x )=-x 2+2ax =-(x -a )2+a 2,所以f (x )在[a ,+∞)上为减函数,又f (x ),g (x )都在[1,2]上为减函数,所以需⎩⎪⎨⎪⎧ a ≤1a +1>1⇒0<a ≤1.答案:(0,1] 3.已知f (x ),g (x )都是定义在R 上的函数,且满足以下条件①f (x )=a x ·g (x )(a >0,a ≠1);②g (x )≠0;若f (1)g (1)+f (-1)g (-1)=52,则a 等于________. 解析:由f (x )=a x ·g (x )得f (x )g (x )=a x ,所以f (1)g (1)+f (-1)g (-1)=52⇒a +a -1=52,解得a =2或12.答案:2或124.(北京朝阳模拟)已知函数f (x )=a x (a >0且a ≠1),其反函数为f -1(x ).若f (2)=9,则f -1(13)+f (1)的值是________. 解析:因为f (2)=a 2=9,且a >0,∴a =3,则f (x )=3x =13,∴x =-1, 故f -1(13)=-1.又f (1)=3,所以f -1(13)+f (1)=2.答案:2 5.(山东青岛质检)已知f (x )=(13)x ,若f (x )的图象关于直线x =1对称的图象对应的函数为g (x ),则g (x )的表达式为________.解析:设y =g (x )上任意一点P (x ,y ),P (x ,y )关于x =1的对称点P ′(2-x ,y )在f (x )=(13)x 上,∴y =(13)2-x =3x -2.答案:y =3x -2(x ∈R ) 6.(山东卷改编)函数y =e x +e -xe x -e -x的图象大致为________.。
