电力系统各元件的数学模型
电力系统各元件的数学模型

推导过程:从1-1’,2-2’之间等值,将导纳支路拿出去
ZT 1:k
I1 1 I2 k
U2
k
U1
I1
ZT
1 I1
U1
ZT
1:k I2
2 U2
I1
U1 ZT
U2
1’
ZT k
U1 (y10
y) 12
2’
U2
y 12
I2
U1 ZT k
U2 ZT k2
U1 y12
U2 (y20
y) 12
§2.5 电力系统的等值电路
一些常用概念
1. 实际变比 k
k=UI/UII UI、UII :分别为与变压器高、低压绕组实际 匝数相对应的电压。 2. 标准变比kN
• 有名制:归算参数时所取的变比 • 标幺制:归算参数时所取各基准电压之比
3. 非标准变比 k* k*= k /kN=UIIN UI /UII UIN
U
U UB
I S Z
I IB S SB Z ZB
P jQ SB
R jX ZB
P SB R ZB
j
Q SB
P
jQ
j
X ZB
R
jX
§2.5 电力系统的等值电路
2、基准值的选取 1) 基准值的单位与对应有名值的单位相同 2) 各种量的基准值之间应符合电路的基本关系
SB 3 UB IB UB 3 IB ZB
§2.5 电力系统的等值电路
四、电力系统的等值电路制订
1、决定是用有名值,还是用标幺值
容量不相同时 2、变压器的归算问题
电压等级归算
采用Γ型和T型 采用π型—不归算
3、适当简化处理
第二章电力系统各元件的数学模型

试验时小绕组不过负荷,存在归算问题,归算到SN
2) 对于(100/50/100)
2
Pk (12)
P' k (12)
IN 0.5IN
P 4 ' k (12)
2
Pk ( 23)
P' k (23)
IN 0.5IN
P 4 ' k ( 23 )
3) 对于(100/100/50)
2
Pk (13)
P' k (13)
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
一次整循环换位:
A B
C
换位的目的:为了减 少三相参数的不平衡
§2.3 电力线路的参数和数学模型
Xd
§2.1 发电机的数学模型
受限条件
定子绕组: IN为限—S园弧
转子绕组: Eqn ife 励磁电流为限—F园弧 Xd
原动机出力:额定有功功率—BC直线
其它约束: 静稳、进相导致漏磁引起温升—T弧
进相运行时受定 子端部发热限制 受原动机出力限制
定子绕组不超 过额定电流
励磁绕组不超 过额定电流 留稳定储备
2、由短路电压百分比求XT(制造商已归算,直接用)
U U U U 1 k1(%) 2
k(12) (%) k(13) (%) (%) k(23)
XT1
Uk
1(%
)U2 N
100SN
U U U U 1 k2 (%) 2
k(12) (%) k(23) (%) (%) k(13)
第2章 电力系统稳态分析_电力系统各元件的特性和数学模型

第二节 变压器的参数和数学模型
两绕组变压器的 Γ 型等值电路与参数计算公式
2 2 Pk U N Uk % UN ,X T RT 2 SN 100 S N P0 I0 % SN GT 2 ,BT 2 U 100 U N N k U 1 N / U 2 N
~ S (U d jU q )(I d jI q ) (U d I d U q I q ) j(U q I d U d I q )
P U d I d U q I q Q U q I d U d I q
从而
第一节 发电机组的运行特性和数学模型
P0 GT 2 1000 UN
第二节 变压器的参数和数学模型
3. 变比 k 定义为一次额定电压与二次空载电压之比,可由 空载试验测得或由变压器铭牌查得。 安装在高压绕组上; 对应于额定电压的抽头为主抽头,其余抽头的 电压相对额定电压偏离一定值;
变压器的实际变比=对应于实际 抽头位置的一 次电压与二次电压之比。
一型
第二节 变压器的参数和数学模型
特点:
增加传输能力 减少功率损耗
S 3UI
S L 3I 2 Z ZS 2 / U 2
减少电压降落
3ZI Z S/ U dU
类型:
单相、三相 两绕组、三绕组 普通、自耦 普通、有载调压、加压调压
第二节 变压器的参数和数学模型
一、双绕组变压器的参数和数学模型
1 U 1ZT 1 NhomakorabeaYT
ZT 2
2
ZT 3
3
U 3
U 2
第二节 变压器的参数和数学模型
1 电力系统各元件数学模型
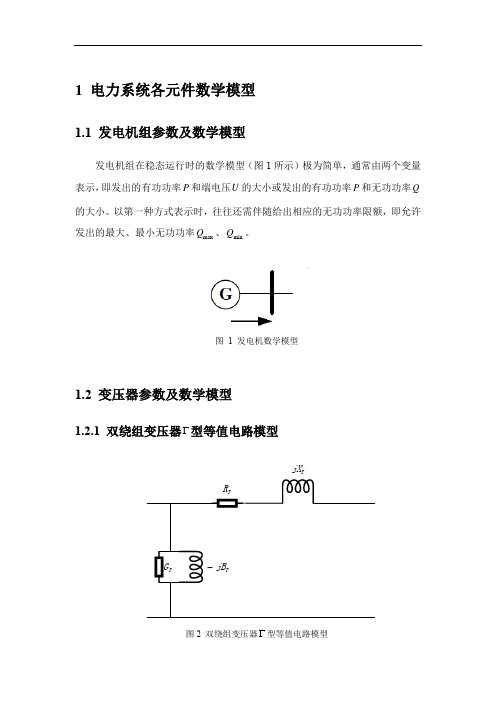
1 电力系统各元件数学模型1.1 发电机组参数及数学模型发电机组在稳态运行时的数学模型(图1所示)极为简单,通常由两个变量表示,即发出的有功功率P 和端电压U 的大小或发出的有功功率P 和无功功率Q 的大小。
以第一种方式表示时,往往还需伴随给出相应的无功功率限额,即允许发出的最大、最小无功功率max Q 、min Q 。
图 1 发电机数学模型1.2 变压器参数及数学模型1.2.1双绕组变压器Γ型等值电路模型TjX 图2 双绕组变压器Γ型等值电路模型双绕组变压器Γ型等值电路模型如图2所示,电路参数通过以下公式计算。
注意,公式中N U 取不同绕组的额定电压,表示将参数归算到相应绕组所在的电压等级(所得所得阻抗/导纳参数都是等值为Y/Y 接线的单相参数);公式中各参数由变压器厂家提供,采用实用单位。
22020210001001000%100k N T Nk NT N T NN T N P U R S U U X S P G U I S B U ⎧∙=⎪⎪⎪%∙=⎪⎪⎨⎪=⎪⎪⎪=∙⎪⎩(1-1) 其中,k P 为短路损耗,k U %为短路电压百分数,0P 为空载损耗,0%I 为空载电流百分数,N U 为归算侧的额定电压,N S 为额定容量 该电路模型一般用于手算潮流中。
1.2.2 双绕组变压器T 型等值电路模型1jX '图 3 双绕组变压器T 型等值电路模型其中,1R 和1X 为绕组1的电阻和漏抗,'2R ,'2X 为归算到1次侧的绕组2 的电阻和漏抗,m R 和m X 为励磁支路的电阻和电抗。
该电路模型一般用于电机学中加深对一二次侧和励磁支路电阻电抗的理解以及手算潮流计算中。
1.2.2 三绕组变压器Z 图4三绕组变压器的等值电路三绕组变压器的等值电路如图3所示,图中,变压器的励磁支路也以导纳表示。
该电路模型一般用于手算潮流计算中。
三绕组变压器的参数计算如下: 电阻:由短路损耗计算()()()1(12)(31)(23)2(23)(12)(31)3(31)(23)(12)121212k k k k k k k k k P P P P P P P P P P P P ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-2) 211222233100010001000k N T Nk N T Nk NT N P U R S P U R S P U R S ⎧∙=⎪⎪⎪∙⎪=⎨⎪⎪∙⎪=⎪⎩(1-3) 其中,k P 为短路损耗,N U 为归算侧的额定电压,N S 为额定容量对于容量比为100/100/50和100/50/100的变压器,厂家提供的短路损耗是小容量绕组达到自身额定电流()/2N I 时的试验数据,计算时应首先将短路损耗折算为对应于变压器额定电流()N I 的值例如,对于100/100/50型变压器,厂家提供的是未经折算的短路损耗'(23)k P -,'(31)k P -,'(12)k P -首先应进行容量归算'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩(1-4) 按新标准,厂家仅提供最大短路损耗max k P ,按以下公式计算电阻:2max (100%)2(50%)(100%)20002k N T N T T P U R S RR ⎧=⎪⎨⎪=⎩(1-5) 其中max k P 为最大短路损耗,N U 为归算侧的额定电压,N S 为额定容量 电抗:由短路电压百分数计算()()()1(12)(31)(23)2(12)(23)(31)3(23)(31)(12)1%%%%21%%%%21%%%%2k k k k k k k k k k k k U U U U U U U U U U U U ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-6) 211222233100100100k N T Nk N T N k NT N U U X S U U X S U U X S ⎧%=⎪⎪⎪%⎪=⎨⎪⎪%⎪=⎪⎩(1-7) 其中,k U %为短路电压百分数,N U 为归算侧的额定电压,N S 为额定容量 注意,厂家提供的短路电压是经过额定电流折算后的数据。
第2章 电力网元件的参数和数学模型

2
2. 电抗
1)单相导线电抗
r Deq 为三相导线间的互几何间距 x0 0.1445lg Deq 0.0157 r ( / km)
Deq 3 D1 D2 D3
r 为导线的计算半径 μr 为导线材料的相对导磁系数,有色金属的相对导磁 系数为1。 在近似计算中,可以取架空线路的电抗为 0.40 / km
2 Pk1U N RT 1 , 2 1000 S N 2 Pk 2U N , 2 1000 S N 2 Pk 3U N 2 1000 S N
RT 2
RT 3
16
•对于100/50/100或100/100/50 首先,将含有不同容量绕组的短路损耗数据归算为额 定电流下的值。
额定容量比为 100/50/100
2)分裂导线线路的电纳
b1 7.58 10 6 (S/km) D lg m req
9
二、电力线路的数学模型
电力线路的数学模型是以电阻、电抗、电纳和电导来表示 线路的等值电路。 1、短线路(<35kv,<100km的架空线路、短电缆线路) 不考虑线路的分布参数特性,只用将线路参数简单地集中 起来的电路表示。
g1 Pg U2 10 3 (S / km)
7
实际上,在设计线路时,已检验了所选导线 的半径是否能满足晴朗天气不发生电晕的要
求,一般情况下可设
g=0
8
4. 电纳 1)单相导线电纳
其电容值为:
C1 0.0241 10 6 D lg m r
最常用的电纳计算公式:
7.58 10 6 (S/km) D lg m r 架空线路的电纳变化不大,一般为 2.85 10 6 S / km b1
3
电力系统各元件的特性和数学模型课件

变压器的主要参数
额定电压
变压器能够长期正常工作的电压值。
额定容量
变压器的最大视在功率,表示变压器的输出 能力。
额定电流
变压器能够长期通过的最大电流值。
效率
变压器传输的功率与输入的功率之比,表示 变压器的能量转换效率。
变压器数学模型
变压器数学模型通常采用传递函数的 形式来表示,可以描述变压器在不同 工作状态下的输入输出关系。
THANKS FOR WATCHING
感谢您的观看
配电系统是电力系统的重要组成部分,主要负责将电能从发电厂或上级电网分配给 终端用户。
配电系统的工作原理包括电压变换、电流变换和功率传输等过程,通过变压器、开 关设备和输配电线路等设备实现。
配电系统通常分为高压配电、中压配电和低压配电三个层次,以满足不同用户的需 求。
配电系统的主要参数
电压
配电系统的电压等级通常在1kV至35kV之间,其 中1kV以下为低压配电,35kV以上为高压配电。
电力系统的控制策略
电力系统的控制策略包括发电机的励磁控 制、调速控制等,这些控制策略对电力系
统的稳定性起着至关重要的作用。
电力系统的运行状态
电力系统的运行状态对稳定性有直接影响 ,如负荷的大小和分布、发电机的出力、 电压和频率等。
外部环境因素
外部环境因素包括自然灾害、战争、恐怖 袭击等,这些事件可能导致电力系统受到 严重干扰,影响其稳定性。
04
负荷:消耗电能的设备或设施。
电力系统元件的分类
一次元件
包括发电机、变压器、输电线路等,是构成电力系统的主体 部分。
二次元件
包括继电器、断路器、测量仪表等,用于控制、保护和监测 电力系统。
电力系统各元件的特性和数学模型

E q
Ixd cos
P ,Q
Eq sin
Q
Ixd
Ixd cos
U
I
Ixd
sin
Eq
cos
U
I I
cos sin
Eq sin
xd
Eq cos
xd
U
P
UI
cos
由此,
Q UI sin
EqU sin
xd
EqU cos
xd
U 2
EqU cos
xd
U2
xd
(2-2)
(2-3)
按每相的绕组数目
双绕组:每相有两个绕组,联络两个电压等级
三绕组:每相有三个绕组,联络三个电压等级,三个绕 组的容量可能不同,以最大的一个绕组的容量为变压器 的额定容量。
类别 普通变 自耦变
高 100% 100% 100% 100%
中 100% 50% 100% 100%
低 100% 100% 50% 50%
1.3 凸极机的稳态相量图和数学模型
11
第一节 发电机组的运行特性和数学模型
12
第一节 发电机组的运行特性和数学模型
13
第一节 发电机组的运行特性和数学模型
稳态分析中的发电机模型
发电机简化为一个节点 节点的运行参数有:
U U G
节点电压:U U u 节点功率:S~ P jQ
S~ P jQ
19
第二节 变压器的参数和数学模型
2.1 变压器的分类:有多种分类方法
按用途:升压变、降压变 按电压类型:交流变、换流变 按三相的磁路系统:
单相变压器、三相变压器 按每相绕组的个数:双绕组,三绕组 按绕组的联结方式:
电力系统各元件的特性和数学模型

电力系统各元件的 特性和数学模型
复功率的规定
•
• 国际电工委员会(IEC)的规定 S U I
j U
•
S U I Ue ju Ie ji UIe j(u i ) UIe j
UI cos j sin
I
u
i
S cos j sin
P jQ
“滞后功率因数 运行”的含义
符号 S φ P Q
电力系统各元件的特性和数学模型
18
双绕组变压器和三绕组变压器
• 双绕组变压器:每相两个绕组,联络两个电压等级
2020/9/7
电力系统各元件的特性和数学模型
6
2.1节要回答的主要问题
• 功角的概念是什么?与功率因数角的区别? • 隐极机的稳态功角特性描述的是什么关系?(由此可
以引申出高压输电网的什么功率传输特性?) • 发电机的功率极限由哪些因素决定?对于隐极机,这
些因素如何体现在机组的运行极限图中?发电机的额 定功率与最大功率有什么关系?发电机能否吸收无功 功率? • 稳态分析中所采用的发电机的数学模型是怎样的?
• 负荷以超前功率因数运行时所吸收的无功功率为 负。——容性无功负荷(负)
• 发电机以滞后功率因数运行时所发出的无功功率为 正。——感性无功电源(正)
• 发电机以超前功率因数运行时所发出的无功功率为 负。——容性无功电源(负)
2020/9/7
ห้องสมุดไป่ตู้
电力系统各元件的特性和数学模型
3
目录
2.1 发电机组的运行特性和数学模型 2.2 变压器的参数和数学模型 2.3 电力线路的参数和数学模型 2.4 负荷的运行特性和数学模型 2.5 电力网络的数学模型 本章小结 习题
电力系统各元件的特性和数学模型

变压器需要承受一定的机械应力,包括自身的重量、运输 过程中的振动以及运行时的电磁力等。因此,变压器需要 有足够的机械强度和稳定性。
数学模型
01 02
电路模型
变压器可以用电路模型表示,其中电压和电流的关系由阻抗和导纳表示 。对于多绕组变压器,需要使用复杂的电路模型来描述各绕组之间的耦 合关系。
。
调相机
主要用于无功补偿和电压调节 ,通过吸收或发出无功功率来
维持电压稳定。
电动机
作为电力系统的负荷,能将电 能转换为机械能。
数学模型
同步发电机
基于电磁场理论和电路理论, 建立电压、电流、功率等变量
的数学关系。
异步发电机
通过分析转子磁场与定子绕组 的相互作用,建立数学模型。
调相机
基于无功功率理论,建立电压 与无功电流之间的数学关系。
05
CATALOGUE
电力电子元件
特性
非线性特性
动态特性
电力电子元件在正常工作状态下表现出非 线性特性,如开关状态下的电压-电流关系 。
电力电子元件的动态特性表现在其工作状 态的快速变化,如开关的快速通断。
时变特性
控制性
由于电力电子元件的工作状态和效率会随 着时间、温度、负载等因素的变化而变化 。
电力系统各元件的 特性和数学模型
contents
目录
• 发电机 • 变压器 • 输电线路 • 配电系统元件 • 电力电子元件
01
CATALOGUE
发电机
特性
01
02
03
04
同步发电机
作为电力系统中的主要电源, 能将机械能转换为电能,具有
稳定的电压和频率输出。
异步发电机
电力系统数学模型与稳定性分析

电力系统数学模型与稳定性分析电力系统是现代社会中不可或缺的基础设施,它承担着电能的生产、传输和分配的重要任务。
为了确保电力系统的安全运行,人们需要对电力系统进行数学建模和稳定性分析。
本文将介绍电力系统数学模型和稳定性分析的基本概念、方法和应用。
一、电力系统数学模型1.1 电力系统的基本组成部分电力系统主要由发电机、变压器、输电线路、配电网和负荷等组成。
发电机用于将机械能转化为电能,变压器用于变换电压,输电线路用于电能的长距离传输,配电网用于将电能分配到各个用户,负荷则表示对电能的需求。
1.2 电力系统的数学模型电力系统的数学模型主要包括节点模型和支路模型。
节点模型是用来描述电力系统中各个节点(发电机、变压器、负荷等)的状态和特性,通常使用节点电压和相角来表示。
支路模型是用来描述电力系统中各个支路(输电线路、变压器等)的传输特性,通常使用支路功率和阻抗来表示。
1.3 节点模型节点模型是电力系统数学模型的核心部分,它描述了电力系统中各个节点的电压和相角的变化规律。
节点模型基于基尔霍夫电流法和基尔霍夫电压法,利用电流平衡和功率平衡等原理建立。
节点模型可以通过节点电压和相角的变化来分析电力系统的稳态和暂态行为。
1.4 支路模型支路模型描述了电力系统中各个支路的传输特性,包括输电线路的电阻、电抗和电导等参数。
支路模型基于欧姆定律和基尔霍夫电压法,利用电压平衡和功率平衡等原理建立。
支路模型可以通过支路功率和阻抗的变化来分析电力系统的稳态和暂态行为。
二、电力系统稳定性分析2.1 稳定性的概念电力系统的稳定性是指系统在外部扰动或内部故障的作用下,能够保持稳定的运行状态。
稳定性分为稳态稳定性和动态稳定性两种。
稳态稳定性是指系统在平衡点附近的行为,动态稳定性是指系统在扰动后恢复稳定的能力。
2.2 稳定性的分析方法稳定性分析的主要方法包括潮流计算、短路计算、暂态稳定性分析和频率稳定性分析等。
潮流计算是用来计算电力系统中各个节点的电压和功率,以确定系统的稳态工作点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ea a Fa I
在时间相位上, 与 I 同相位,则
EEaa滞将后滞于后于I以a 以909°0°电电角角度度,,若所不以计E定a可子写铁成耗负,
a
电抗压降的形式,即
E a jIX a
(2-2)
2.1.1 同步发电机稳态运行的数学模型
将式(2-2)代入式(2-1),可得 Eq U + Ir + jIX + jIX a U + Ir + jIX d
实验二:闭合导体回路和载流线圈 间有相对运动时,亦可引起电磁感 应现象
实验三:闭合导体回路中有电流强 度可改变的载流线圈时,同样可引 起电磁感应现象
实验四:闭合导体回路和载流线圈 间相对静止,但磁铁棒相对于它们 运动,也可引起电磁感应现象。
实验五:闭合导体回路在均匀磁场 中运动,也能够引起电磁感应现象
总结五个典型实验,可得如下结 论:不管什么原因使穿过闭合导 体回路所包围面积内的磁通量发 生变化,回路中都会出现电流, 这种电流称为感应电流
在磁通量增加和减少的两种情 况下,回路中感应电流的流向 相反
感应电流的大小则取决于穿过 回路中的磁通量变化快慢:变 化越快,感应电流越大;反之 ,就越小
电磁感应原理
电磁感应原理
法拉第电磁感应定律 通过回路中的磁通量发生变化时,在回路中产生的 感应电动势的大小与磁通量随时间的变化率成正比
楞次定律 闭合回路中感应电流的磁场总是反抗回路中磁通量 的变化
电磁问题分析:电磁场 —> 电路 + 磁路
E
F
I
Φ
2.1 同步发电机的数学模型
同步电机的基本构造型式
磁极旋转式:以电枢为定子,磁极为转子 电枢旋转式:以磁极为定子,电枢为转子,应
2.1 同步发电机的数学模型
凸极式(磁极旋转式) 同步电机
转子上有明显凸出的成对磁极 和励磁线圈,当励磁线圈中通 过直流励磁电流后,每个磁极 出现一定的极性,相邻磁极交 替为 N 极和 S 极
由于水轮发电机机的转速较低, 要发出工频电能,发电机的极 数就比较多,做成凸极式结构 工艺上较为简单
2.1 同步发电机的数学模型
电枢反应
电枢磁动势的基波在气隙中所产生的磁场称为电枢反 应 磁动势是电流流过导体所产生磁通量的势力,反映了 电流的磁效应 电枢磁动势是由电枢电流所产生的 如果电枢绕组开路(不闭合),是否有电枢反应?
2.1.1 同步发电机稳态运行的数学模型
隐极机的电压方程:定子绕组的电压方程
用于小容量同步电机
2.1 同步发电机的数学模型
磁极旋转式同步电机
定子:又称为电枢,定子的内圆均匀分布着定子槽,槽内 嵌放着按一定规律排列的三相交流绕组
转子:转子铁心上装有成对磁极,磁极上绕有励磁绕组, 通以直流电流时,会在电机的气隙中形成极性相间的分布 磁场,称为励磁磁场,也称主磁场
气隙:处于电枢内圆和转子磁极之间,气隙的厚度和形状 对电机内部磁场的分布和同步电机的性能具有重要影响
任何通有电流的导线,都可以在其周围产生磁场的 现象,称为电流的磁效应;非磁性金属通以电流, 可产生磁场,其效果与磁铁建立的磁场相同
直线电流的磁场
N
螺线管电流的磁场
环形电流的磁场
S 采用右手定则(安培定则) 判断磁场方向
电磁感应原理
实验一:闭合导体回路与磁棒之间 有相对运动时,可引起电磁感应现 象
感应电动势 当闭合导体回路所包围面积的磁通量变化时,此回 路中就出现感应电流,这意味着该回路中必定存在 电动势,这种直接由电磁感应现象所引起的电动势 叫做感应电动势
在任何电磁感应现象中,只要穿过回路的磁通量变 化,回路中就一定有感应电动势产生
若导体回路是闭合的,感应电动势就会在回路中产生感应 电流;若导线回路不是闭合的,回路中仍然有感应电动势, 但是不会形成电流
2.1.1 同步发电机稳态运行的数学模型
凸极机的电压方程:定子绕组的电压方程
不考虑磁饱和,凸极机负载运行时各物理量之间的关系:
If I
Ff
Fad
0
ad
Eq
E ad
E
Fa
Faq
aq Eaq E ( jIX )
2.1.1 同步发电机稳态运行的数学模型
采用发电机惯例,以输出作为电枢电流的正方向时,
电枢电压方程为 : E0 + E ad +
E aq
I(Ra
+
jX
)
U
(2-3)
不计磁饱和,则
Ead Id
Eaq Iq
2.1 同步发电机的数学模型
隐极式(磁极旋转式) 同步电机
转子上没有凸出的磁极,沿着转 子圆周表面有许多槽,槽中嵌放 着励磁绕组
在转子表面约1/3部分没有开槽, 构成所谓大齿,是磁极的中心区
在大容量高转速汽轮发电机中, 转子圆周线速度很高,为了减小 转子本体及 转子上各部件所承 受的离心力,大型汽轮发电机的 转子通常为细长的隐极式圆柱体
式中,Xd(= Xσ+Xa)称为隐极机的同步电抗,是表征 电枢漏磁场和电枢反应这两个效应的综合参数 隐极同步发电机的等效电路由励磁电动势和同步阻 抗r+ jXd串联组成,其中Eq表示主磁场的作用,Xd表 示电枢反应和电枢漏磁场的作用
2.1.1 同步发电机稳态运行的数学模型
双反应原理
考虑到凸极机的气隙不均匀,把电枢反应分成直轴和交 轴电枢反应分别进行处理,称为双反应原理 凸极机极面下气隙较小,两极之间气隙较大,因此, 如图所示,直轴下单位面积的气隙磁导Λd 要比交轴 下单位面积的气隙磁导Λq 大
电气工程基础—系统篇 2013-2014-2
任课教师:褚晓东 Email: Tel.: 81696127 (office),13573122659
电力系统模型:物理系统的数学抽象
电力系统模型:物理系统的数学抽象
第2章 电力系统各元件的数学模型
同步发电机 变压器 输电线路 负荷
电流的磁效应
不考虑磁饱和,隐极机负载运行时各物理量之间的关系:
If
Ff
0
Eq
I
Fa
a
Ea
E
E ( jIX )
2.1.1 同步发电机稳态运行的数学模型
采用发电机惯例,以输出作为电枢电r + jX ) U
(2-1)
电枢反应电动势Ea正比于电枢反应磁通Φa,不计磁饱和,Φa 又正比于电枢磁动势Fa和电枢(定子)电流I,即
