第5章克里格法
GIS空间分析原理与方法

GIS空间分析原理与方法学院:资源与环境学院专业:地理信息系统班级:2011010班姓名:李松青学号:201101014GIS空间分析原理与方法地理信息系统是地理空间数据处理、分析的重要手段和平台。
在计算机软硬件的支持下,对整个或部分地球表层(包括大气层)空间中的有关地理分布数据进行采集、储存、管理、运算、分析、显示和描述的技术系统。
地理信息系统的核心是功能是空间分析。
空间分析使GIS超越一般空间数据库、信息系统和地图制图系统,不仅能进行海量空间数据中隐藏的模式、关系和趋势,挖掘出对科学决策具有指导意义的信息,从而解决复杂的地学应用问题,进行地学综合研究。
以下是对本册内容的总结:第一章地理空间数据源分析与GIS本章简要回顾了20世纪50年代以来地理空间数据处理与建模领域,探讨了GIS 环境下空间分析的基本框架。
1.地理空间数据处理与建模1.1数量地理学讲述了数量地理学的发展、与传统地理学的比较及其地理分析模拟方法(地理系统分析,随机数学方法,地理系统数学模拟)。
1.2 地理信息系统主要介绍了GIS的概念与功能1.3 地理计算介绍了地理计算的概念与地理计算的模型和方法2.地理空间数据挖掘2.1 地理空间数据挖掘概述介绍了数据挖掘的概念、发展及其体系结构2.2 地理空间数据立方体介绍了数据立方体的基本思想与数据立方体概念所涉及的维度类型(非空间维度,空间-非空间维度,空间-空间维度),度量值(数值度量,空间度量)和成员属性2.3 联机分析处理技术介绍了OLAP概念以及与地理空间数据立方体的关系。
2.4 地理空间数据挖掘典型方法地理空间数据挖掘主要方法有:地理空间统计方法,地理空间聚类方法,地理空间关联分析,地理空间分类与预测分析,异常值分析3.GIS环境下的空间分析3.1 空间分析概念介绍了空间分析的概念与本质特征,空间分析的研究对象与目标3.2 空间分析的萌芽与发展介绍了空间分析的发展过程3.3 GIS与空间分析介绍了GIS与空间分析的关系以及地理信息系统未能大量引入专业空间分析模块的原因。
0fm

储层建模Reservoir Modeling 吴胜和金振奎黄沧钿陈崇河编著石油工业出版社内容提要本书系统地阐述了储层建模的基本理论、方法和技术。
从提高建模精度的角度出发,强调应用高分辨率层序地层学及地质概念模式约束建模过程,倡导等时建模、成因控制相建模以及相控建模的基本原则,并系统地介绍了确定性建模与随机建模的基本原理、各种方法技术及其地质适用性,从实用出发系统介绍了目前国际上储层建模的主要软件。
本书可供从事石油地质、开发地质及油藏工程等工作的科研人员参考,也可作为油气地质专业研究生的教学参考书。
前言随着油气田勘探开发的不断深入,储层研究以建立定量的三维储层地质模型为目标,这是储层研究向更高阶段发展的体现。
科学的油藏评价、油藏工程管理以及三维油藏模拟均要求三维储层地质模型,即储层属性的三维定量分布模型。
储层三维建模是国外80年代中后期开始发展起来的储层表征新领域。
十多年来,这一学科领域的发展十分迅速,数学地质及计算机工作者致力于发展各种建模方法特别是各种随机模拟方法,而储层地质工作者则研究各种建模方法的地质适用性,并力求改进方法以建立符合地质实际的三维储层地质模型。
本书作者近年来一直致力于储层建模的教学和科研工作,曾对多种油气储层类型,包括冲积扇、河流、扇三角洲、辫状河三角洲、正常三角洲、滨岸相、潮坪相等储层进行过三维建模研究,并与美国、挪威、法国、英国、澳大利亚等国家的相关专家进行广泛的交流。
为了使更多的油气地质工作者了解并掌握储层建模方法并切实应用于油气田勘探开发实际,有必要系统介绍储层建模的基本理论、方法和技术。
全书共分五章,第一章储层建模概论,介绍储层建模的目的意义、储层模型类型、储层建模流程及建模策略,论述了确定性建模与随机建模、等时建模、成因控制储层相建模以及相控建模的基本原则;第二章储层地质模式,介绍三维储层建模所必须了解的各种沉积环境的储层结构模式;第三章确定性建模技术,介绍三种主要的确定性建模方法,即储层地震地层学方法、储层沉积学方法及地质统计学克里格方法;第四章随机建模技术,介绍了随机模拟的基本原理、算法和随机模型,以及主要的随机模拟方法及其地质适用性,包括标点过程、序贯高斯模拟、截断高斯模拟、序贯指示模拟、分形模拟等;第五章储层建模软件,介绍目前国际上主要的储层建模软件。
巫师加强版——狩魔猎人图文攻略第五章尾声(二)

巫师加强版——(狩魔猎⼈) 图⽂攻略第五章+尾声(⼆) 1.旅⼈之⽯(伊格尼、伊格尼、阿尔德) 2.矮⼈的箱⼦:B i f u n c t i o n a l A l l o y a n d S t e e l F i b e r R e c i l c u l a t o r. 3.旅⼈之⽯(阿尔德,伊格尼,阿尔德) 4. A g n e s o f G l a n v i l l e’s c h e s t:魔法公式、最佳基质、第五要素、⽉亮符⽯和M a g i c F o r m u l a 5.旅⼈之⽯(阿尔德,阿尔德,伊格尼) 6.圣乔治的坟墓:渥都符⽯、圣乔治的坟墓:渥都符⽯、圣乔治的连祷 主线任务 第五章的故事发展,很⼤程度上取决于第四章任务4.107⾃由精灵中所做的选择 进⼊堤防即激活任务5.108甜美的复仇 如果你做出的决定是帮助精灵为⾃由⽽战,在这⾥就会从卓尔坦那⾥接到任务5.109燃烧的希望。
如果你决定保持中⽴,卓尔坦会给你任务5.124在炽热的天空下,如果你⽀持骑⼠团,卓尔坦就不爱搭理了,和他进⾏简短对话后,得到任务5.126清静之⽕。
除了以上任务,还会从国王弗尔泰斯特那⾥得到任务5.110吸⾎妖鸟殿下。
任务4.95护甲、任务4狩魔猎⼈的秘密也会在此章继续 任务5.109燃烧的希望H o p e B u r n s B r i g h t 如果在前章中,你⽀持松⿏党⼀⽅,可以接到这个任务 阶段1卓尔坦 和卓尔坦对话,他会让你帮忙营救难民。
到⽼维吉玛去 阶段2难民 在⽼维吉玛再次遇到卓尔坦(图33.2) 阶段3另⼀群难民 在⼩巷中找到⼀群难民(图33.9) 阶段4医院 在平⾏的⼩巷中找到另⼀群难民(图33.17) 阶段5吸⾎妖鸟 进⼊医院(图33.5)后,⼀个警卫告诉你吸⾎妖鸟出现在塔楼上(图33.21),正在杀⼈ 阶段6去找夏妮 在塔楼下杀死变异⼈,他被误当作了吸⾎妖鸟 阶段7防卫 回到医院(图33.5)。
空间分析要点

空间分析要点(参考)第一章1、空间对象的属性大致可分为两类:一是空间要素属性是指与空间(时间)位置相关的属性,主要包括:空间对象的位置、大小、形状、速度、事件发生的时间。
二是非空间要素属性,也称描述属性,是指与空间位置无关或无直接关系的属性:如颜色、密度、质地等等。
2、空间分析的目的就是根据空间对象的属性进行分析,探求空间对象的时空分布规律、发生原因及发展规律。
3、空间对象的类型:按空间维数分类,大致可分为四类0维空间对象:有位置无长度的对象,如:居民点、地图中的城市、地震的震中位置。
1维空间对象:有长度的对象,一般由两个或多个0维目标组成,如:道路、河流。
2维空间对象:有面积的空间对象,如土地使用的类型、湖泊。
3维空间对象:具有体积的空间对象,如地下的矿体、大坝、隧道等。
根据空间对象的连续性,可分为两类:连续型的空间对象:在空间中连续分布的对象,如:某区域的地球化学元素分布,大气污染物浓度、海水的盐度。
离散型的空间对象:在空间中不连续分布的对象,如:城市中商业网点的分布,道路与河流,建筑物。
4、空间实体之间存在复杂的空间关系,主要可包括:距离关系、方位关系、拓扑关系、空间相关、空间关联、空间配置、空间过程、空间尺度5、空间要素模型:前GIS系统中数据组织的基本方式。
点要素,线要素,面要素。
6、空间的主要内容:空间位置空间分布:同类空间对象的群体定位信息,包括分布、趋势、对比等内容空间形态:空间对象的几何形态空间距离:空间物体的接近程度空间关系:空间对象的相关关系,包括拓扑、方位、相似、相关等空间过程7、空间的主要方法:(1)基于地图的空间图形分析,如GIS中的缓冲区、叠加分析、数字高程模型、数字地面模型等;(2)空间动力学分析,有城市扩张模型(驱动力等)、空间价格竞争模型(区位优势)、空间择位模型(中心地等);(3)空间信息分析,是指根据数据或统计方法建立的模型,如空间聚类、空间自相关、回归模型等。
克里金法

1n 2n nn 1
1 1 , 1 0
1 2 , n
( x1 , x) ( x , x) 2 D ( xn , x ) 1
克里格估计方差也可以写 为
2 K i ( xi , x) ( x, x) i 1 n
也可以将克立格方程组和估计方差用变异函数写成上述矩阵形 式。令
11 12 21 22 K n1 n 2 1 1
i 1
的偏导数,并令其为0,得克里格方程组
n F 2 j c( xi , x j ) 2c( xi , x) 2 0 i j 1 n F 2( 1) 0 i i 1
K D
K D 2 T K D ( x, x)
1
克里格方法根据不同的条件以及需要可以选择不同的估值 方法,常用的克里格方法主要有普通克里格法,泛克里格法, 协同克里格法,对数克里格法和指示克里格法等。其中以普通 克里格法为最基本的估值方法,在推估法的实际运用中也占有 重要地位。简单克里格法只是在变量满足二阶平稳并且均值m 已知条件下的一种特例。
假设在待估计点(x)的临域内共有n个实测点,即x1, x2,…,xn,其样本值为。那么,普通克里格法的插值公式为
Z ( x ) i Z ( x i )
* i 1
n
i 为权重系数,表示各空间样本点处的观测值对估值的影响度或者贡
献程度。 显然,克里格估值的关键问题就是在于求解 i 的值,同时根据估值 的基本原则,即无偏性和估计方差最小(最优性)的要求,具体就是要满 足以下条件:
【最新精选】组织行为学目录

第一章组织行为学的对象与性质1、组织:2、行为: 3、人的行为的特点:3、组织行为学: 4、组织行为学的研究对象: 5、研究范围: 6、研究方法: 7、研究目的: 8、对管理者的意义和作用: 9、组织行为学的学科性质与特点: 10、边缘性主要表现为两个方面:11、两重性的主要表现: 12、行为规律的模式:13、文化的主要功能:第二章组织行为学的研究方法1、研究方法的特征: 2、四个步骤和六步循环系统: 3、案例研究法: 4、观察法: 5、心理测验法:信度、效度6、调查法:。
1)面谈法2)电话调查法: 3)问卷调查法:四种形式:选择法,是否法,计分法,等级排列法8、实验法: 实验室实验法, 现场实验法, 准实验法第三章个体差异与管理1、感觉: 2、知觉:3、社会知觉: 4、社会知觉包括: 5、自我知觉6、知觉过程和影响因素7、影响知觉的因素:1)客观因素。
2)主观因素。
8、造成错误知觉的思想方法主要有下列四种:(1)知觉防御。
(2)首因效应(成见)。
(3)晕轮效应。
(4)投射。
9、领导者对被领导者的认知假设:10、X理论:美国社会心理学家道格拉斯·麦克里格。
(1)领导者对被领导者的看法:(2)相应的领导方式与领导行为:11、Y理论:(1)领导者对被领导者的看法:(2)相应的领导方式和领导行为:12、海德的归因理论13、归因论所研究的基本问题有下列三个方面:14、价值观价值观、价值观体系。
15、价值观的地位:。
16、价值观分类: 17、美国组织行为学家史布兰格(E.Spranger)把人的价值观分为下列六类;按不同行为方式来划分,组织行为学家格雷夫斯(F.W.Graves)归纳为以下七类18、我国企业经营管理价值观经历了三个阶段:七、态度:态度:(二)三个层次:认知,情感,意向(三)特性:(四)工作态度:(五)组织认同感:它包括三个部分:(六)工作参与度:(八)改善这组织认同感与工作参与度的方法:八、个性(一)定义:(二)个性的性质:1、组合性。
地理统计学

第二章预备知识1.频数:在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数n A称为事件A发生的频数2.频率: 比值n A/n称为事件A发生的频率,并记为f n(A)=n A/n.3.统计特征数包括:平均数、离散数、形态数第三章统计分析1.回归分析(1)概念:对具有高度相关关系的现象,根据其相关的形态,建立一个适宜的数学模型(回归方程),来近似地反映变量之间的一般变化关系,以便于进行估计或预测的统计方法。
(2)回归分析的主要内容和步骤①对问题进行分析,确定自变量和因变量②建立回归模型③检验④利用回归模型,根据自变量去估计、预测因变量(3)一元回归系数由最小二乘法估计(4)一元线性回归模型的显著性检验——F 检验法。
F越大,模型的效果越佳2.多元线性回归模型(可能考大题,看作业,ppt第三章75页以后)第七章地统计插值1.克立格法(1)概念:是建立在变异函数理论及结构分析基础上,在有限区域内对区域化变量的取值进行无偏最优估计的一种方法(2)克立格估计量(公式):估计的好坏取决于权重系数λi(3)性质:①无偏性②最优性2.普通克里格法(1)Z(x)为区域化变量,满足二阶平稳假设或本征假设,其数学期望为m,为未知常数(2)普通克立格是条件无偏(3)点普通克里格法的计算(考大题,ppt第七章,32到37页)第四章区域化变量理论1.区域化变量(1)横向:所有实现的集合纵向:随机变量的集合(2)区域化变量Z(x)具有两方面的含义:①观测前——随机场②观测后——实现(3)性质:结构性、随机性(4)各向同性:区域化变量如果在各个方向上的性质变化(变异)相同各向异性:若在各个方向上变异不同2.协方差函数(满足二阶平稳假设)(曲线凹形递减)(1)性质①C(0) = Var*Z(x)+ ≥0,即先验方差不能小于零②C(h) =C(-h) ,即C(h)对h=0的直线对称,是一个偶函数③|C(h)| ≤C(0) ,即协方差函数绝对值小于等于先验方差④|h|→∞时,C(h) →0,或写作C(∞) =0,即当空间距离很大时,协方差函数值很小⑤C(h)必须是一个非负定函数,即由C(x i-x j)构成的协方差函数矩阵必须是非负定矩阵3.变异函数(满足二阶平稳假设)(曲线凸形递增)(考大题,ppt第四章62、68页例题)(1)性质①γ(0) = 0,即在h=0时,变异函数为零②γ(h) = γ(-h) ,即γ(h)对h=0的直线对称,是一个偶函数③γ(h) ≥0,即研究现象的变异性只能大于或等于零④|h|→∞时, γ(h) →C(0),或写作γ(∞) =C(0),即当空间距离很大时,变异函数值接近先验方差⑤[- γ(h)]必须是一个条件非负定函数,即由[- γ(x i-x j)]构成的变异函数矩阵必须是条件非负定矩阵4.协方差函数与变异函数的关系(1)下图解:红色曲线(递增)是变异函数,另一条(递减)是协方差函数变异函数与协方差函数值变化相反,先验方差等于协方差和变异函数之和a称为变程(2)变程a的意义①变程a表示区域化变量从存在空间相关状态(当|h| <a时)转向不存在空间相关状态(当|h|≥a时)的转折点②变程a的大小反映区域化变量影响范围的大小,或说反映该变量自相关范围的大小(3)跃迁现象:当h超过某一数值(变程a)后,γ(h)稳定于C(0)(4)基台值:γ(∞)极限值(γ(∞) =γ(a) = C(0))基台值的大小反映区域化变量变化幅度的大小,即反映区域化变量在研究范围内变异的强度(5)空间相关性越大,协方差函数越大,变异函数越小(6)协方差函数和变异函数实质是计算误差,确切的说是估计误差的函数变异函数曲线图也是误差的曲线分布图(7)块金效应(下图,牢记此图)C0: 表示h很小时,两点间观测值的变化。
第四章 块体模型-5

第四章Block Modeling 块体模型综述这一节将介绍在 Surpac块体模型中使用的术语和基本概念。
什么是Surpac块体模型?当前矿业软件中通行的概念是将块体模型与地质统计学相结合,是应用数学方法对品位分布进行建模,由于品位分布是在资源中受地质因素控制而明显存在的,从而形成一定约束条件下的品位模型。
块体模型的精度取决于块体模型的结构和属性。
在资源储量估算中,利用块体模型可以准确地进行资源量和品级报告。
Surpac 块体模型是数据库的一种格式,意味着其结构不仅可以存储和操作数据,还能修补来自于数据中的信息,这是和传统的数据库不同的地方,存储数据的时候更像内插替换一个值,而不是度量一个值。
另外一个主要的不同在于这个值具有空间参照性。
第三个不同在于块模型在打开的时候完全放在了内存中,实现了动态操作,如画等值线等属性,当然同时对内存也提出了较高的要求。
例如在地质数据库中,特征值都是和空间位置相联系的,然而,空间位置却不是和特征值有必要关系的。
块模型的部分空间是块的组成部分,每一个都和一个记录相联,这个记录是以空间为参照的,每个点的信息可以通过空间点来修改而并不仅仅是取决于其精确测量,空间参照就是一些额外的操作,对数据库的容量进行操作和查询,空间操作的方式是 INSIDE 和 ABOVE,在实体和表面文件中可以用,对于外部和下部空间的操作使用非逻辑操作,例如 NOT INSIDE 或者 NOT ABOVE。
块模型包含了一些组件:模型空间Model Space模型空间是指立体体积,在块模型术语里其中什么都不存在。
在建立的模型空间属性都是有条件的属性,这些属性可以是指定的,有序的,间隔的,可以是比率,也可以是字符,是数值,特征值可以通过别的属性值由计算得出,这些属性值都可以进行报告输出和可视化浏览。
∙约束限制就是对空间操作符和物体的逻辑组合,可以用来控制对块的选择,对信息加以修复,或者对其进行内插值。
地统计学知识点

地统计学知识点第一章概论1.地统计学:以区域化变量理论为基础、以变异函数为主要工具,研究在空间分布上既有随机性和结构性,或空间相关和依赖性的自然现象的科学2.地统计学发展:1951年南非克里金和西舍尔提出克里金法20世纪60年代(1962年)法国马特隆提出地统计学概念出版《应用地统计学论》,该书中第一次阐明了地统计学原理,地统计学诞生1977年美国Parker博士将地统计学概念引入中国4.地统计学研究内容: P3-4空间估值(定义)、局部不确定性预测、随机模拟、多点地统计学(该方法产生于石油领域)5.地统计学适用范围6.地统计学应用领域(地质、土壤、生态、环境、气象)第二章地统计学基础1.总体抽取样本的四种方案(理解如何抽取样本):随机抽样、机械抽样、分层抽样、分组抽样2.随机变量的数字特征(各定义) P15-21a)集中性度量(平均数):算数平均值、中数、众数、数学期望b)离散性度量(离散数):极差、离差、方差、协方差、矩、变异函数c)形态度量(形态数):偏度、峰度期望:设C是常数,则有E(C)=C设X是一个随机变量,C是常数,则有E(CX)=CE(X)设X、Y为两个随机变量,则有E(X+Y)=E(X)+E(Y)设X,Y是相互独立的随机变量,则有E(XY)=E(X)E(Y)方差:设C是常数,则有D(C)=0设X是一个随机变量,C是常数,则有D(CX)=C2D(X) D(C+X)=D(X)设X、Y为两个随机变量,则有D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}若X,Y是相互独立的随机变量,则有D(X+Y)=D(X)+D(Y)协方差:3.相关关系:指事物之间的关系数值存在着一定的依存关系,即某一现象在其发展变化中,当数量上为一确定值时,与之有联系的其他现象可以有若干个数值与之对应,但这些值按某种规律在一定范围内进行波动。
4.特点:一个变量的取值不能由另一个变量唯一确定,也不能用函数形式给予描述,但并不是无规律可行的。
克里格方法(Kriging)

精选完整ppt课件
3
克里格法
01 Z(p)为区域Ω上随机过程,p∈Ω; Ω上有n个测点(样本点),
zi z(pi)在 p i处的测值,则 p 0 处的最优线性估计为
n
zˆ0 i zi i1
02 最小化非测点 p 0 处的估值方差 0 2E[z(0zˆ0)2],可推导出克里
2
基本概念
01 变差函数:Z(p)为一随机过程,Z(p)在p,p+h两点处的值之差 的方差之半定义为Z(p)在p方向上的变差函数,记为
(h)1V[az((rp)z(ph)]
2 变差函数描述了区域化变量的空间结构性。 (h)只依赖于h。
02 协方差函数:随机过程Z(p) 在p1、p2处的两个随机变量Z(p1) 和Z(p2)的二阶混合中心矩,即 Cov{Z(p1), Z(p2)}=E[Z(p1)*Z(p2)]-E[Z(p1)]*E[Z(p2)],记 为 C(p1, p2) 整个区域中,Z(p)的协方差函数存在且相同,即只依赖于h Cov{Z(p),Z(p+h)} ≜C(h); 当h=0时,C(0)=Var{Z(x)},x
n
i1
n j1
1 B'(hij)
B'(hij) k
0
精选完整ppt课件
6
优化测点分布的克里格方程组
由(h)=C(0)B(h),可得 C(h)=C(0)(1-B(h))
设 ce(h)1B(h) ,则上式可表示为
c(h)c(0)ce(h)
令 c(0)e 将上述式子代入克里格方程组可得与C(0)无关的克里 格方程组和克里格方差,如下
g(i)
,表明网格节点上的较大估值方差变大了,
克里格法Kriging——有公式版

克里格法(Kriging)——有公式版二、克里格法(Kriging)克里格法(Kriging)是地统计学的主要内容之一,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法;从插值角度讲是对空间分布的数据求线性最优、无偏内插估计一种方法。
克里格法的适用条件是区域化变量存在空间相关性。
克里格法,基本包括普通克里格方法(对点估计的点克里格法和对块估计的块段克里格法)、泛克里格法、协同克里格法、对数正态克里格法、指示克里格法、折取克里格法等等。
随着克里格法与其它学科的渗透,形成了一些边缘学科,发展了一些新的克里金方法。
如与分形的结合,发展了分形克里金法;与三角函数的结合,发展了三角克里金法;与模糊理论的结合,发展了模糊克里金法等等。
应用克里格法首先要明确三个重要的概念。
一是区域化变量;二是协方差函数,三是变异函数一、区域化变量当一个变量呈空间分布时,就称之为区域化变量。
这种变量反映了空间某种属性的分布特征。
矿产、地质、海洋、土壤、气象、水文、生态、温度、浓度等领域都具有某种空间属性。
区域化变量具有双重性,在观测前区域化变量Z(X)是一个随机场,观测后是一个确定的空间点函数值。
区域化变量具有两个重要的特征。
一是区域化变量Z(X)是一个随机函数,它具有局部的、随机的、异常的特征;其次是区域化变量具有一般的或平均的结构性质,即变量在点X 与偏离空间距离为h的点X+h处的随机量Z(X)与Z(X+h)具有某种程度的自相关,而且这种自相关性依赖于两点间的距离h与变量特征。
在某种意义上说这就是区域化变量的结构性特征。
二、协方差函数协方差又称半方差,是用来描述区域化随机变量之间的差异的参数。
在概率理论中,随机向量X与Y的协方差被定义为:区域化变量在空间点x 和x+h处的两个随机变量Z(x) 和Z(x+h) 的二阶混合中心矩定义为Z(x) 的自协方差函数,即区域化变量Z(x) 的自协方差函数也简称为协方差函数。
克里格法Kriging——有公式版

克里格法(Kriging)——有公式版二、克里格法(Kriging)克里格法(Kriging)是地统计学的主要内容之一,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法;从插值角度讲是对空间分布的数据求线性最优、无偏内插估计一种方法。
克里格法的适用条件是区域化变量存在空间相关性。
克里格法,基本包括普通克里格方法(对点估计的点克里格法和对块估计的块段克里格法)、泛克里格法、协同克里格法、对数正态克里格法、指示克里格法、折取克里格法等等。
随着克里格法与其它学科的渗透,形成了一些边缘学科,发展了一些新的克里金方法。
如与分形的结合,发展了分形克里金法;与三角函数的结合,发展了三角克里金法;与模糊理论的结合,发展了模糊克里金法等等。
应用克里格法首先要明确三个重要的概念。
一是区域化变量;二是协方差函数,三是变异函数一、区域化变量当一个变量呈空间分布时,就称之为区域化变量。
这种变量反映了空间某种属性的分布特征。
矿产、地质、海洋、土壤、气象、水文、生态、温度、浓度等领域都具有某种空间属性。
区域化变量具有双重性,在观测前区域化变量Z(X)是一个随机场,观测后是一个确定的空间点函数值。
区域化变量具有两个重要的特征。
一是区域化变量Z(X)是一个随机函数,它具有局部的、随机的、异常的特征;其次是区域化变量具有一般的或平均的结构性质,即变量在点X 与偏离空间距离为h的点X+h处的随机量Z(X)与Z(X+h)具有某种程度的自相关,而且这种自相关性依赖于两点间的距离h与变量特征。
在某种意义上说这就是区域化变量的结构性特征。
二、协方差函数协方差又称半方差,是用来描述区域化随机变量之间的差异的参数。
在概率理论中,随机向量X与Y的协方差被定义为:区域化变量在空间点x 和x+h处的两个随机变量Z(x) 和Z(x+h) 的二阶混合中心矩定义为Z(x) 的自协方差函数,即区域化变量Z(x) 的自协方差函数也简称为协方差函数。
第5章克里格法PPT课件

实际研究中常常会需要获取研究区内研究对象大于某一给定阈值的概率分布,即要获知研究区内任一点x处随机变量Z(x)的概率分布。 还会碰到采样数据中存在特异值的问题。(特异值是指那些比全部数值的均值或中位数高的多的数值,其既非分析误差所致,也非采样方法等人为误差引起,而是实际存在于所研究的总体之中)。 指示克立格法就是为解决上述问题而发展起来的一种非参数地统计学方法。 指示克立格法不必去掉重要而实际存在的高值数据的条件下处理各种不同现象,并能够给出某点x处随机变量Z(x)的概率分布。
二、线性克里金法
1、简单克里金法
设区域化变量Z(x)满足二阶平稳假设,其数学期望为常数m,协方差函数C(h)和变异函数γ (h)存在且平稳。 现要估计中心点在x0 的待估块段V 的均值Z(x), Z(x)表达式为 由于 E[Z(x)]=m已知 令 Y(x)=Z(x)-m 则 E[Y(x)]=E[Z(x)-m]= E[Z(x)]-m=0 待估块段新待估值
(3)Z(x)的泛克里金法估计
求出函数F对n个权系数λi的偏导数,并令其为0,和无偏性条件联立建立如下方程组。 整理得估计Z (x)的泛克里金方程组:
泛克里金方程组可用矩阵表示为: 其中
(3)Z(x)的泛克里金法估计
从泛克里金方程组可得以下两等式: 将等式带入估计方差公式可得泛克里金方差,记为: 用变异函数γ(h)表示如下:
或 普通克里金方程组用矩阵形式表达为: 或 权重系数 或 普通克里金估计方差用矩阵表达为: 或
2、普通克里金法
普通克里金计算示例: 设某一区域气温数据满足二阶平稳假设,协方差函数和变异函数存在,拟合的变异函数模型为球状模型,如下所示。 数据如下,点的空间分布如图所示。现用普通克里金方法根据已知五个点的气温数据估算0点处的气温值。
地质统计学(6)_普通克里格法-cjg2011

在无偏性条件 数法。 令:
i 1
n
i
1 下,要使得估计方差最小,从而求得诸权
系数λ i , (i=1,2,…,n),这是一个求条件极值的问题,要用拉格朗日乘
n F 2 i 1 ,为n个权系数λ 和μ 的(n+1)元函数。 i i 1
2 E
-2 μ是拉格朗日乘数。求出F对λ i , (i=1,2,…,n)以及F对μ的偏导数,并
(7)指示克里格——处理非参数(类型参数)的区域化变量时
3. 克里格法的使用信息及应用条件 信息: ① 一组数据; ② 空间构形(坐标); ③ 结构信息(变差函数模型)。
线性 平稳
条件: ① 二阶平稳(本征)假设、线性估计量——普通克里格
线性非 平稳
② 平稳条件不满足,仍采用线性估计量——泛克里格
E(Y ) i E (Yi ) i E ( Z i m) 0
V i 1 i 1 n n
E(YV )
1 V
V
E[Y ( x)]dx 0 E (YV ) E(YV )
2 的表达式: E
2 2 为了求出λi,使得 E E YV YV 最小,首先需求出
i 1 j 1
1 2 V
1 C ( x , y ) d x d y 2 i V V V i 1
n n i 1
n
C ( x , x)dx C ( x , x )
V i i 1 j 1 i j i j
n
n
2 所以: E C (V ,V ) 2 i C ( xi ,V ) i j C ( xi , x j ) i 1 j 1
(1)无偏性条件
地统计学简介

一般克里格法(Ordinary Kriging)、 泛克里格法(Universal Kriging)、 指示克里格法(Indicator Kriging) 析取克里格法(Disjunctive Kriging)、 协同克里格法(Cokriging)等。
• 地统计学理论两大学派: • ①以G.Matheron为首旳“枫丹白露地统计学派”,开展以正态假设为基
础旳克立格法研究,提出了多元地统计学旳思想,形成了涉及简朴克 立格、一般克立格、泛克立格、析取克立格等在内旳一套理论和措施 。因为克立格法计算中,需要利用实际样品数据求取区域化变量理论 模型旳若干参数,因而称为“参数地统计学”; • ②觉得首旳“斯坦福地统计学派”,发展无需对数据分布作任何假设旳 指示克立格法、概率克立格法和迅速条件模拟等一套措施,同步考虑 怎样使用“软”数据问题,称为“非参数地统计学”。
3、在生态学中旳应用
① 生态学变量空间变异性旳定量描述和解释。 ② 生物特征旳估计。 ③ 生态学研究对象旳时空变化规律分析,及不同有关研究对象旳时空
动态及耦合关系分析。
4、在环境学中旳应用
① 土壤环境研究 地统计学中旳变异函数和克立格插值技术是进行重金属空间构造分
析、模拟和估值旳主要工具,经过描述和模拟污染物旳空间分布特征以 及估算未采样点旳取值,揭示出污染物在空间上旳分布迁移趋势。 ② 水环境研究
2、在土壤学中旳应用
• 在土壤学试验设计和采样方法中旳应用 • 分析土壤特征旳空间变异规律,可有效
指导土壤采样数目、样点分布、采样密度 及采样方法旳拟定。
• 在土壤质量管理方面旳应用 • 地统计学提供了利用已知取样点旳数据
矿体储量计算方法
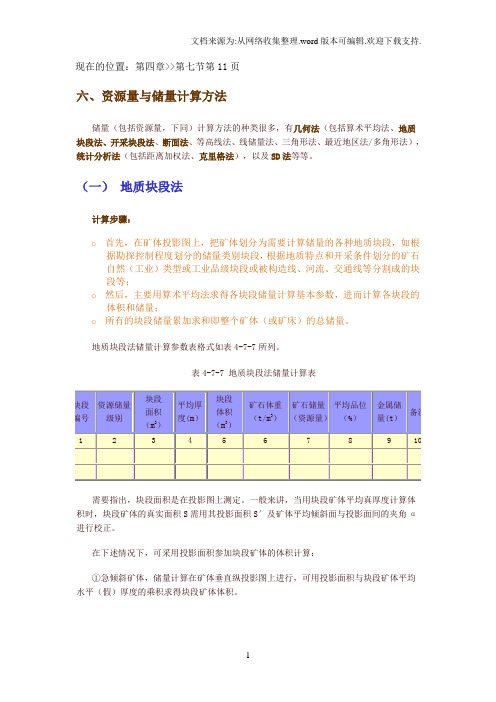
现在的位置:第四章>>第七节第11页六、资源量与储量计算方法储量(包括资源量,下同)计算方法的种类很多,有几何法(包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法),统计分析法(包括距离加权法、克里格法),以及SD法等等。
(一)地质块段法计算步骤:o首先,在矿体投影图上,把矿体划分为需要计算储量的各种地质块段,如根据勘探控制程度划分的储量类别块段,根据地质特点和开采条件划分的矿石自然(工业)类型或工业品级块段或被构造线、河流、交通线等分割成的块段等;o然后,主要用算术平均法求得各块段储量计算基本参数,进而计算各块段的体积和储量;o所有的块段储量累加求和即整个矿体(或矿床)的总储量。
地质块段法储量计算参数表格式如表4-7-7所列。
表4-7-7 地质块段法储量计算表块段编号资源储量级别块段面积(m2)平均厚度(m)块段体积(m3)矿石体重(t/m3)矿石储量(资源量)平均品位(%)金属储量(t)备注12345678910需要指出,块段面积是在投影图上测定。
一般来讲,当用块段矿体平均真厚度计算体积时,块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。
在下述情况下,可采用投影面积参加块段矿体的体积计算:①急倾斜矿体,储量计算在矿体垂直纵投影图上进行,可用投影面积与块段矿体平均水平(假)厚度的乘积求得块段矿体体积。
图4-7-3 在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图; (c)、(d)—立体图1—矿体块段投影; 2—矿体断面及取样位置②水平或缓倾斜矿体,在水平投影图上测定块段矿体的投影面积后,可用其与块段矿体的平均铅垂(假)厚度的乘积求得块段矿体体积。
优点:适用性强。
地质块段法适用于任何产状、形态的矿体,它具有不需另作复杂图件、计算方法简单的优点,并能根据需要划分块段,所以广泛使用。
当勘探工程分布不规则,或用断面法不能正确反映剖面间矿体的体积变化时,或厚度、品位变化不大的层状或脉状矿体,一般均可用地质块段法计算资源量和储量。
概率论与数理统计第五章课后习题及参考答案

概率论与数理统计第五章课后习题及参考答案概率论与数理统计第五章课后习题及参考答案1.用切比雪夫不等式估计下列各题的概率.(1)废品率为03.0,1000个产品中废品多于20个且少于40个的概率;(2)200个新生儿中,男孩多于80个而少于120个的概率(假设男孩和女孩的概率均为5.0).解:(1)设X 为1000个产品中废品的个数,则X ~)1000,03.0(B ,有30)(=X E ,1.29)(=X D ,由切比雪夫不等式,得)3040303020()4020(-<-<-=<<-="X" )103010(<-<-="X" 709.010<="" bdsfid="71" p="" x="">1.2912=-≥.(2)设X 为200个新生儿中男孩的个数,则X ~)200,5.0(B ,有100)(=X E ,50)(=X D ,由切比雪夫不等式,得)10012010010080()12080(-<-<-=<<-="X" )2010020(<-<-="X" 8<="" bdsfid="77" p="" x="">7205012=-≥.2.一颗骰子连续掷4次,点数总和记为X ,估计)1810(<<="">解:设i X 为该骰子掷第i 次出现的点数,则61)(==k X P i ,6,,2,1 =i ,6,,2,1 =k .27)654321(61)(=+++++=i X E ,691)654321(61)(2222222=+++++=i X E ,35)]([)()(22=-=i i i X E X E X D ,4,3,2,1=i .因为4321X X X X X +++=,且1X ,2X ,3X ,4X 相互独立,故有14)(=X E ,335)(=X D .由切比雪夫不等式,得)1418141410()1810(-<-<-=<<-<-="X" )<="" bdsfid="88" p="" x="">414(<-=X P 271.0433512=-≥.3.袋装茶叶用及其装袋,每袋的净重为随机变量,其期望值为100g ,标准差为10g ,一大盒内装200袋,求一盒茶叶净重大于5.20kg 的概率.解:设i X 为一袋袋装茶叶的净重,X 为一盒茶叶的净重,由题可知∑==2001i i X X ,100)(=i X E ,100)(=i X D ,200,,2,1 =i .因为1X ,2X ,…,200X 相互独立,则20000)()(2001==∑=i i X E X E ,20000)()(2001==∑=i i X D X D .)()(20500)()(()20500(2001X D X E X D X E X P X P i i ->-=>∑=)1020020000205001020020000(?->?-=X P )2251020020000(>?-=X P 由独立同分布的中心极限定理,1020020000?-X 近似地服从)1,0(N ,于是0002.0)5.3(1)2251020020000(=Φ-≈>?-X P .4.有一批建筑用木桩,其80%的长度不小于3m .现从这批木桩中随机取出100根,试问其中至少有30根短于3m 的概率是多少?解:设X 为100根木桩中短于3m 的根数,则由题可知X ~)2.0,100(B ,有20)(=X E ,16)(=X D ,由棣莫弗—拉普拉斯定理,得)30(1)30(<-=≥X P X P )42030(1)()((1-Φ-=-Φ-=X D X E X 0062.0)5.2(1=Φ-=.5.某种电器元件的寿命服从均值为100h 的指数分布.现随机选取16只,设它们的寿命是相互独立的.求这16只元件寿命总和大于1920h 的概率.解:设i X 为第i 只电器元件的寿命,由题可知i X ~)01.0(E ,16,,2,1 =i ,且1X ,2X ,…,16X 相互独立,则100)(=i X E ,10000)(=i X D .记∑==161i i X X ,则1600)()(161==∑=i i X E X E ,160000)()(161==∑=i i X D X D .))()(1920)()(()1920(X D X E X D X E X P X P ->-=>)400160019204001600(->-=X P )8.04001600(>-=X P ,由独立同分布的中心极限定理,1600-X 近似地服从)1,0(N ,于是2119.0)8.0(1)8.04001600(=Φ-=>-X P .6.在数值计算中中,每个数值都取小数点后四位,第五位四舍五入(即可以认为计算误差在区间]105,105[55--??-上服从均匀分布),现有1200个数相加,求产生的误差综合的绝对值小于03.0的概率.解:设i X 为每个数值的误差,则i X ~)105,105(55--??-U ,有0)(=i X E ,1210)(8-=i X D ,1200,,2,1 =i .从而0)()(12001==∑=i i X E X E ,61200110)()(-===∑i i X D X D .由独立同分布的中心极限定理,X 近似地服从)10,0(6-N ,于是)03.0(<="" bdsfid="123" p="">()(03.0)()((X D X E X D X E X P -≤-=12101200003.0121012000(44--?-≤?-=X P 9974.01)3(2=-Φ=.7.某药厂断言,该厂生产的某药品对医治一种疑难的血液病治愈率为8.0.医院检验员任取100个服用此药的病人,如果其中多于75个治愈,就接受这一断言,否则就拒绝这一断言.(1)若实际上此药对这种病的治愈率是8.0,问接受这一断言的概率是多少?(2)若实际上此药对这种病的治愈率是7.0,问接受这一断言的概率是多少?解:设X 为100个服用此药的病人中治愈的个数,(1)由题可知X ~)8.0,100(B ,则80)(=X E ,16)(=X D ,由棣莫弗—拉普拉斯定理,得)75(1)75(≤-=>X P X P 48075(1))()((1-Φ-=-Φ-=X D X E X 8944.0)25.1(=Φ=.(2)由题可知X ~)7.0,100(B ,则70)(=X E ,21)(=X D ,由棣莫弗—拉普拉斯定理,得)75(1)75(≤-=>X P X P 217075(1)()((1-Φ-=-Φ-=X D X E X 1379.0)09.1(1=Φ-=.8.一射手在一次射击中,所得环数的分布律如下表:X678910P 05.005.01.03.05.0求:(1)在100次射击中环数介于900环与930环之间的概率是多少?(2)超过950环的概率是多少?解:设X 为100次射击中所得的环数,i X 为第i 次射击的环数,则∑==1001i i X X ,15.9)(=i X E ,95.84)(2=i X E ,2275.1)]([)()(22=-=i i i X E X E X D ,100,,2,1 =i .由1X ,2X ,…,100X 相互独立,得915)()(1001==∑=i i X E X E ,75.122)()(1001==∑=i i X D X D .由独立同分布的中心极限定理,75.122915-X 近似地服从)1,0(N ,于是(1))930900(≤≤X P ))()(930)()()()(900(X D X E X D X E X X D X E P -≤-≤-=75.12291593075.12291575.122915900(-≤-≤-=XP )75.1221575.122915(≤-=X P 823.01)35.1(2=-Φ≈.(2))950(>X P ))()(950)()((X D X E X D X E X P ->-=75.122915950)()((->-=X D X E X P 001.0)1.3(1=Φ-≈.9.设有30个电子元件1A ,2A ,…,30A ,其寿命分别为1X ,2X ,…,30X ,且且都服从参数为1.0=λ的指数分布,它们的使用情况是当i A 损坏后,立即使用1+i A (29,,2,1 =i ).求元件使用总时间T 不小于350h 的概率.解:由题可知i X ~)1.0(E ,30,,2,1 =i ,则10)(=i X E ,100)(=i X D .记∑==301i i X T ,由1X ,2X ,…,30X 相互独立,得300)()(301==∑=i i X E T E ,3000)()(301==∑=i i X D T D .))()(350)()(()350(T D T E T D T E T P T P ->-=>30103003503010300(?->?-=T P )91.03010300(>?-≈T P ,由独立同分布的中心极限定理,3010300?-T 近似地服从)1,0(N ,于是1814.0)91.0(1)91.03010300(=Φ-=>?-T P .10.大学英语四级考试,设有85道选择题,每题4个选择答案,只有一个正确.若需要通过考试,必须答对51道以上.试问某学生靠运气能通过四级考试的概率有多大?解:设X 为该学生答对的题数,由题可知X ~41,85(B ,则25.21)(=X E ,9375.15)(=i X D ,85,,2,1 =i .由棣莫弗—拉普拉斯中心极限定理,近似地有9375.1525.21-X ~)1,0(N ,得)8551(≤≤X P ))()(85)()()()(51(X D X E X D X E X X D X E P -≤-≤-=)9375.1525.21859375.1525.219375.1525.2151(-≤-≤-=X P 0)45.7()97.15(=Φ-Φ=.即学生靠运气能通过四级考试的概率为0.。
petrel中文操作手册(6-9章)

第六章相建模(FaciesModeling)6.1 Petrel2010版本中相建模技术的大发展Petrel相建模(Facies Modeling)现有方法主要包括:多点地质统计学相模拟、基于目标的河流相模拟,基于像元的序贯指示模拟、截断高斯模拟,带趋势的截断高斯模拟,指示克里金模拟、神经网络方法,用于详细表征相带分布特征的确定性和随机性相建模技术,而且可以交互使用。
同时用户可以导入自己的算法和人工赋值的方法,建立沉积相模型。
Petrel2010在原有版本基础上对相建模方法做了较大的改进,主要体现在以下四个方面:1)全新的MPS多点统计相模拟算法在Petrel2010版本中,引进了多点地质统计学相模拟方法,该方法的引进改变了过去传统的两点统计地质学方法,而发展为多点地质学,解决了过去两点统计关系上变差函数的不足,特别是对储层非均质性描述上的不足,多点统计地质学能够充分描述复杂几何形状砂体的空间连续性和变异性。
多点统计地质学是建立在多个点的相关关系上,它在解决描述空间变量的连续性和变异性方面得到越来越广泛的应用。
斯坦福大学的Journel教授曾指出多点地质统计学是今后地质统计学发展的方向,它的优势已越来越显著。
2)基于快速傅立叶变换的高斯模拟算法一种新的新的高斯模拟算法在Petrel 2010.1.中被引用,这种算法与GSLIB的序贯随机模拟方式不同。
A 它比SGS运算速度提高了很多B 它不是序贯算法C 它可以并行运算D 它可以进行快速的协同模拟设定如同上面提到的,这种高斯算法不同于序贯模拟的序贯算法,允许并行计算,采用的算法是傅立叶变换算法,这种算法具有快速、并行、在大的范围变程内优选最合理的变程等优点,这种算法的界面与序贯高斯模拟算法有些类似。
3)进一步改进克里金算法在2010.1版本中引用了新的克里金算法,这是完全不同于标准GSLIB 克里金的一种设计,其搜索性能和并行运算都有很大改进。
克里金可以沿网格方向、也可以沿海平面进行插值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、简单克里金法
• 在满足以下两个条件时,Yv*是Y(V)的线性、无偏、最优估计量。
(1)无偏性 由于
所以 则 Yv* 不需要任何条件即是Y(V)的无偏估计量。 (2)最优性
在满足无偏条件下,可推导估计方差公式为:
.
1、简单克里金法
• 为使估计方差最小,需对上式求λi的偏导数并令其为0
• 整理得简单克里金方程组:
• 设在待估块段V附近有n个样点xi(i=1,2,…n),其观测值为Z(xi) (i=1,2,…n),则观 测值新变量为:Y(xi)=Z(xi)-m
• Y(V)的估计值Yv*是Y(xi) (i=1,2,…n)的线性组合,则
则估计Z(V)的问题转化为估计Y(V)的问题
目标:找出一组权重系数 i (i 1,2, , n),使得Yv*成为Y(V) 的线性、无偏、最优估计量
主要类型: 简单克里金法 普通克里金法 Ordinary Kriging 泛克里金法 Universal Kriging 对数正态克里金法 Logistic Normal Kriging 指示克里金法 Indicator Kriging 概率克里金 Probability Kriging 析取克里金法 Disjuctive Kriging 协同克里金法 Co-Krigin.g
.
2、普通克里金法
• 设区域化变量Z(x)满足二阶平稳假设,其数学期望为m,为未知常数,协方 差函数C(h)和变异函数γ(h)存在且平稳。现要估计中心点在x0的待估块段V的 均值,即
• 设待估块段V附近有n个样点xi(i =1,2,…,n),其观测值为Z(xi) (i =1,2,…,n),待 估块段V的真值是估计邻域内n个信息值的线性组合,即
• 还会碰到采样数据中存在特异值的问题。(特异值是指那些比全部数值的均值 或中位数高的多的数值,其既非分析误差所致,也非采样方法等人为误差引起 ,而是实际存在于所研究的总体之中)。
• 指示克立格法就是为解决上述问题而发展起来的一种非参数地统计学方法。
• 指示克立格法不必去掉重要而实际存在的高值数据的条件下处理各种不同现象 ,并能够给出某点x处随机变量Z(x)的概率分布。
2、克里金估计量
• 设x为研究区域内任一点
待估点的估计 值
克里金估计量
权重系数
n
Z
* v
(
x)
iZ (xi )
i 1
待估点影响范围内的有效样本值
显然,估计的好坏 取决于权重系数λi
i的求解
(1)无偏估计
E[Z
* v
(
x)
Z
v
(x)]0 Nhomakorabea(2)最优估计
Var[Z
* v
(
x)
Z. v
( x)]
E[
Z
* v
• 成立。这k+1个子式称为无偏性条 件。
.
(3)Z(x)的泛克里金法估计
• 2)最优性条件
• 在满足无偏性条件下,用Z*(x)估计 Z(x)的泛克里金估计方差为:
• 将无偏性条件带入得
• 要求出在满足无偏性的条件下使得 估计方差最小的权系数λi(i =1,2,…,n),需根据拉格朗日乘数 法原理,建立拉格朗日函数F。
C(h)和变异函数γ (h)存在且平稳。 现要估计中心点在x0 的待估块段V 的均值
ZV(x), ZV(x)表达式为
Zv (x )
1
v
v Z(x )dx
• 由于
E[Z(x)]=m已知
•令
Y(x)=Z(x)-m
•则
E[Y(x)]=E[Z(x)-m]= E[Z(x)]-m=0
• 待估块段新待估值
.
1、简单克里金法
第五章 克里金法
主讲人:
.
提纲
一.克里金法概述 二.线性克里金法
1. 简单克里金 2. 普通克里金 3. 泛克里金法
三.非线性克里金法
1. 对数正态克里金法 2. 指示克里金法 3. 析取克里金法
四.协同克里金法
.
一、克里金法概述
1、克里金法概念及种类
概念:又称为空间局部估计或空间局部插值法,克里金法是建立在变异函数理论 及结构分析基础上,在有限区域内对区域化变量的取值进行线性无偏最优估 计的一种方法。
• 所谓泛克里金法,就是在漂移的形式E[Z(x)]=m(x),和非平稳随机函数Z(x)的 协方差函数C(h)或变异函数γ(h)为已知的条件下,一种考虑到有漂移的无偏线 性估计量的地统计学方法,这种方法属于线性非平稳地统计学范畴。
.
(1)漂移和涨落
• 漂移:非平稳区域化变量Z(x)的数学
期望,在任一点x上的漂移就是该点 上区域化变量Z(x)的数学期望。
.
(3)Z(x)的泛克里金法估计
• 求出函数F对n个权系数λi的偏导 数,并令其为0,和无偏性条件 联立建立如下方程组。
• 泛克里金方程组可用矩阵表示为:
• 其中
• 整理得估计Z (x)的泛克里金方 程组:
.
(3)Z(x)的泛克里金法估计
• 从泛克里金方程组可得以下两等式: • 将等式带入估计方差公式可得泛克里金方差,记为:
.
1、简单克里金法
• 简单克里金法计算示例:
• 设某一区域气温数据满足二阶平稳假设,协方差函数和变异函数存在,所有采 样数据的均值为16.08度,并将均值作为此区域化变量的数学期望值,将所有 采样数据剔除数学期望值后拟合的变异函数模型为球状模型,如下所示。
• 现用简单克里金方法根据五个已知点的气温数据来估算0点处的气温值
.
(2)非平稳区域化变量的协方差函数和变异函数
• 1)基本假设
• 假设Z(x)的增量[Z(x)-Z(y)]具有非平稳的数学期望[m(x)-m(y)]和非平稳的方差 函数,即假设下式存在:
• 2)协方差函数和变异函数 • 当Z(x)=m(x)+R(x)时,Z(x)的协方差函数C(x,y)为:
• Z(x)的变异函数γ(x,y)为:
• 现要求出权重系数λi(i =1,2,…,n),使Z*V(x)为ZV(x)的无偏估计量,且估计方 差最小。
.
2、普通克里金法
(1)无偏性条件 由于
若要满足无偏性条件,需
,则无偏性条件为:
即在权系数之和为1的条件下估计量是无偏的。
(2)最优性条件
即估计方差最小条件,在满足无偏性条件下,有如下估计方差公式
.
三、非线性克里金法
• 1、对数正态克里金法
• 如果区域化变量经对数变换后是正态分布或近正态分布,则对区域化变量进 行精确估计的地统计学方法称为对数正态克立格法。
• 设区域化变量Z(x)服从对数正态分布,在待估点周围有n个样点xi(i =1,2,…,n), 其观测值为Z(xi) (i =1,2,…,n),区域化变量经对数变换后新变量为:Y(x)= lnZ(x),Y(x)为正态分布。假定Y(x)满足二阶平稳假设,数学期望为m,协方 差函数C(h)和变异函数γ(h)存在且平稳。
• 涨落:对于有漂移的区域化变量
Z(x),假设可分解为漂移和涨落两 部分,
• 漂移经常用邻域模型来研究。可表达 为:在给定的以点x为中心的邻域内 的任一点,其漂移m(x)可用如下函数 表示。
• 式中,m(x) = E[Z(x)]为点x处的漂 移,R(x)称为涨落。
式中,fl(x)为一已知函数;al为未知系数 m(x)通常采用多项式形式,在二维条件 下,漂移可看成坐标x,y的函数。
.
(3)Z(x)的泛克里金法估计
• 设Z(x)为一非平稳区域化变量,其 数学期望为m(x),协方差函数为 C(x,y)且已知,则
• 已知n个样品点xi(i =1,2,…,n),其 观测值为Z(xi) (i =1,2,…,n),现要 用这些样品点估计邻域内任一点x 的值Z(x),Z(x)的泛克里金估计量 为:
• 若选择多个阈值则需重复以上 步骤。
.
3、析取克里金法
• 析取克立格法:假设已知任意区域化变量(Z, Z)及(Z0, Z)二维概 率分布条件下,对待估点的值或待估点值超过给定阈值的概率进行估 计的一种非线性地统计方法。
• 估值步骤: 设区域化变量Z(x)在待估点x0周围有n个样点xi(i =1,2,…,n),其观测 值为Z(xi) (i =1,2,…,n),
(
x)
Zv
( x)]2
min
3、克里金法估值过程
(1)数据检查 (2)模型拟合 (3)模型诊断 (4)模型比较
.
二、线性克里金法
• 当区域化变量Z(x)的E[Z(x)]=m已知,则称 为简单克里金法
• 若Z(x)的E[Z(x)]未知,则称为普通克里金法
.
1、简单克里金法
• 设区域化变量Z(x)满足二阶平稳假设,其数学期望为常数m,协方差函数
• 用变异函数γ(h)表示如下:
.
(4)泛克里金法计算示例
• 设某一区域气温是非平稳的区域化变量,在南北方向(空间坐标的y方向)上 存在线性漂移,即 。若已知其涨落满足二阶平稳假设,并且拟合的协方差函数 模型为球状模型,如下所示。
• 现用表5-1所示数据,利用泛克里金法根据已知五个点的气温数据来估算0点处 的气温值。
• 基于对数变换后的采样点数据Y(xi) (i =1,2,…,n),计算实验变异函数并进行变 异函数模型的拟合和选择,然后利用简单克立格或普通克立格估计待估点x处 的值Y*(x)。
• 由于估计值Y(x)是对数变换后的数值,因此对估计所得Y*(x)需进行反变换。
.
2、指示克里金法
• 实际研究中常常会需要获取研究区内研究对象大于某一给定阈值的概率分布, 即要获知研究区内任一点x处随机变量Z(x)的概率分布。
要求出在满足无偏性条件 下使得估计方差最小的权系数λi(i =1,2,…,n), 这 是个求条件极值问题。
