常用的函数曲线
经济数学微积分经济学中的常用函数

在时间 T 内的总费用 E 为
1 Q E C1Tq C 2 2 q
1 Q 其中 , C1Tq 为贮存费,C 2 为进货费用 . 2 q
八、戈珀兹 (Gompertz) 曲线
戈珀兹 曲线是指数函数
y ka
bt
在经济预测中,经常使用该曲线.
k
初始期 发展期
饱和期
当 lg a 0 , 0 b 1 时,图形如上页所示.
由图可见,曲线当t 0 且无限增大时,
其无限与直线 y k 接近 , 且始终位于该直
线 下方. 在产品销售预测中,当预测销售量充
分接近到 k 值时,表示该产品在商业流通中将
达到市场饱和 .
练习题
1.设需求函数由 P+Q=1 给出,(1)求总收益 函数 P;(2)若售出 1/3 单位,求其总收益。
该点的横坐标称为供需平衡价格 .
供需平衡点 供需平 衡价格
Q0
E
P0
三、生产函数 生产函数刻画了一定时期内各生产
要素的投入量与产品的最大可能产量之
间的关系.一般说来,生产要素包括资金
和劳动力等多种要素 .为方便起见,我
们暂时先考虑只有一个投入变量,而其
他投入皆为常量的情况 .
例 2 设投入 x 与产出 g ( x ) 间的函数关系为
成本是生产一定数量产品所需要的
各种生产要素投入的价格或费用总额,
它由固定成本与可变成本两部分组成.
C总 C固 C可变
支付固定生产 要素的费用 支付可变生产 要素的费用
总 成 本 固 定 成 本 可 变 成 本 平 均 成 本 产量 产量
C ( Q ) C 1 C 2 (Q ) 即C AC Q Q Q
03第三节常用经济函数

03 第三节常用经济函数常用经济函数是经济学中用来描述经济变量之间关系的数学模型。
这些函数可以用来分析经济发展、预测经济趋势、制定经济政策等。
下面介绍几种常用的经济函数及其含义。
一、消费函数消费函数是指消费者在某一时期内消费的商品或服务的数量与收入之间的函数关系。
通常表示为C=f(Y),其中C表示消费,Y表示收入。
消费函数曲线是一条向右上方倾斜的曲线,表示随着收入的增加,消费也会增加。
但在达到一定收入后,消费增长速度会逐渐减缓,甚至出现零增长或负增长。
二、投资函数投资函数是指企业在某一时期内进行的投资数量与资本存量之间的函数关系。
通常表示为I=f(K),其中I表示投资,K表示资本存量。
投资函数曲线是一条向右上方倾斜的曲线,表示随着资本存量的增加,投资也会增加。
但在达到一定资本存量后,投资增长速度会逐渐减缓,甚至出现零增长或负增长。
三、总供给函数总供给函数是指某一时期内,企业愿意且有能力提供的商品和服务的总量与价格水平之间的函数关系。
通常表示为Y=f(P),其中Y表示总供给,P表示价格水平。
总供给函数曲线是一条向右下方倾斜的曲线,表示随着价格水平的提高,总供给会减少。
但在达到一定价格水平后,总供给增长速度会逐渐减缓,甚至出现零增长或负增长。
四、总需求函数总需求函数是指某一时期内,消费者愿意且有能力购买的商品和服务的总量与价格水平之间的函数关系。
通常表示为Y=f(P),其中Y表示总需求,P表示价格水平。
总需求函数曲线是一条向右下方倾斜的曲线,表示随着价格水平的提高,总需求会减少。
但在达到一定价格水平后,总需求增长速度会逐渐减缓,甚至出现零增长或负增长。
五、菲利普斯曲线菲利普斯曲线是指通货膨胀率与失业率之间的函数关系。
通常表示为π=f(u),其中π表示通货膨胀率,u表示失业率。
菲利普斯曲线是一条向右下方倾斜的曲线,表示随着失业率的降低,通货膨胀率会上升。
但在达到一定失业率后,通货膨胀率增长速度会逐渐减缓,甚至出现零增长或负增长。
五大基本函数图像及性质

五大基本函数图像及性质基本函数是数学中最常用的函数,它们能够描述和表示曲线的性质和特征。
常见的基本函数包括指数函数、对数函数、三角函数、双曲函数和偏微分函数。
二、指数函数指数函数是指一类具有指数表达形式的函数,可以用来描述数据之间的相对关系。
指数函数的图像以指定点作为原点,从原点开始上升或下降,通过控制变量取值范围来表示函数值的变化程度。
三、对数函数对数函数是一类定义在正数域上的函数,它的值由底数和指数决定,即形如ax的形式。
它的图形是一条从有限正数到有穷大的抛物线,图像的斜率代表了变化的程度。
四、三角函数三角函数是描述在给定区间内某物体运动的函数,它的图像主要由正弦函数、余弦函数和正切函数构成。
它们的图像是以某一定点为原点,其值随着x变化而循环变化,斜率可以表示变化的程度。
五、双曲函数双曲函数是一类定义在实数域上的函数,它的值由变量的决定,其图像可以表现为一条弯曲的曲线,它的斜率也可以表示变化的程度。
六、偏微分函数偏微分函数是一类关于一元变量的函数,它表示函数在某一点处的切线斜率,其图像表示函数在某一点处的变化率。
综上所述,基本函数是数学中最常用的函数,它们通过控制变量取值范围来表示函数值的变化程度。
常见的基本函数包括指数函数、对数函数、三角函数、双曲函数和偏微分函数,它们的图像由指定点作为原点,其值随x的变化而变化,并代表函数值的变化程度。
指数函数是一类具有指数表达形式的函数,它的图像从原点开始上升或下降,可以用来描述数据之间的相对关系。
而对数函数是定义在正数域上的函数,它的图形是从有限正数到有穷大的抛物线,斜率代表了变化的程度。
三角函数是描述在给定区间内某物体运动的函数,它们的图像以某一定点为原点,其值随着x变化而循环变化,斜率可以表示变化的程度。
而双曲函数是一类定义在实数域上的函数,它的图像是一条弯曲的曲线,斜率也可以表示变化的程度。
最后,偏微分函数是关于一元变量的函数,它的图像表示函数在某一点处的变化率。
一些常用函数的曲线图及应用简说

一、正弦余弦曲线: 正弦曲线公式为:A 为波幅(纵轴),ω为(相位矢量)角频率=2PI/T ,T 为周期,t 为时间(横轴), θ为相位(横轴左右)。
周期函数:正余弦函数可用来表达周期函数。
例如,正弦和余弦函数被用来描述简谐运动,还可描述很多自然现象,比如附着在弹簧上的物体的振动,挂在绳子上物体的小角度摆动。
正弦和余弦函数是圆周运动一维投影。
三角函数在一般周期函数的研究中极为有用。
这些函数有作为图像的特征波模式,在描述循环现象比如声波或光波的时候很有用。
每一个信号都可以记为不同频率的正弦和。
1、函数y=sinx 的图象:叫做正弦曲线。
第一步:在直角坐标系的x 轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x 轴的交点A 起把圆分成n (这里n=12)等份。
把x 轴上从0到2π这一段分成n (这里n=12)等份。
(预备:取自变量x 值—弧度制下角与实数的对应)。
第二步:在单位圆中画出对应于角6,0π,3π,2π,…,2π的正弦线正弦线(等价于“列表” ).把角x 的正弦线向右平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” )。
第三步:连线。
用光滑曲线把正弦线的终点连结起来,就得到正弦函数y=sinx ,x ∈[0,2π]的图象。
根据终边相同的同名三角函数值相等,把上述图象沿着x 轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx ,x ∈R 的图象.把角x (x ∈R )的正弦线平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点的轨迹就是正弦函数y=sinx 的图象。
2、余弦函数y=cosx 的图象:叫做余弦曲线。
根据诱导公式,可以把正弦函数y=sinx的图象向左平移2π单位即得余弦函数y=cosx的图象。
3、用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0)、(2π,1)、(π,0)、(23π,-1)、(2π,0)。
常用函数图像
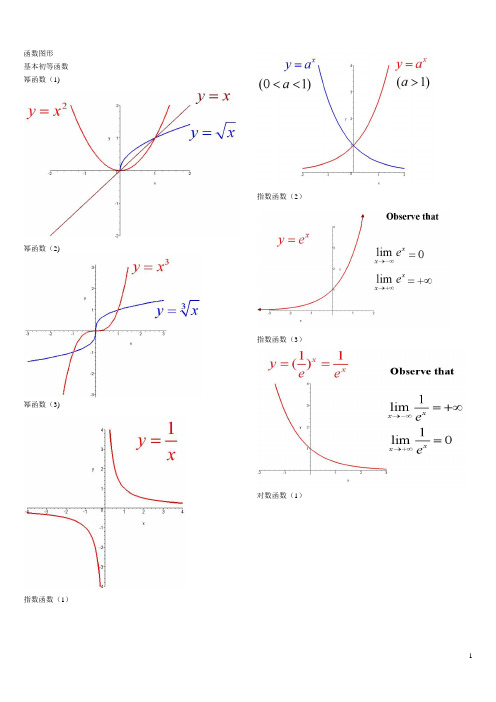
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)三角函数(3)对数函数(2)三角函数(4)三角函数(1)三角函数(5)三角函数(2)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4)y = [1/x](1) y = [1/x](2) y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x) y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)等价无穷小 (x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本) ^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了。
常用曲线函数图例

1. 碟形弹簧圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t2 . 叶形线.笛卡儿坐标方程:a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3. 螺旋线(Helical curve)圆柱坐标(cylindrical)方程: r=ttheta=10+t*(20*360)z=t*34. 蝴蝶曲线球坐标方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 85. 渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=06. 螺旋线.笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t7. 对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t+0.0001)8. .球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*209. 双弧外摆线卡迪尔坐标方程: l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)10. 星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*36012. 圆内螺旋线采用柱座标系方程:theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=014. 太阳线15. 费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做16. Talbot 曲线卡笛尔坐标方程:theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b17. 4叶线18. Rhodonea 曲线采用笛卡尔坐标系方程:theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta19. 抛物线笛卡儿坐标方程:x =(4 * t)y =(3 * t) + (5 * t ^2)z =020. 螺旋线圓柱坐标方程:r = 5theta = t*1800z =(cos(theta-90))+24*t21. 三叶线圆柱坐标方程:a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)22. 外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=023. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)24. 长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)25. 长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)26. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))]27. 概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)28. 箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)29. 阿基米德螺线柱坐标a=100theta = t*400r = a*theta30. 对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)31. 蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x32. tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)y = (exp(x)+exp(0-x))/234. 双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))36. 一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+137. 八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 038. 螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t39. 圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 040. 封闭球形环绕曲线rho=2theta=360*tphi=t*360*1041. 柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 042. 蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)theta = t*360r=10+(8*sin(theta))^244. 椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)theta = t*360r=10+(3*sin(theta*2.5))^246. 另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^247. 改一下就成为空间感更强的花曲线了theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^248. 螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*1249. 甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*1650. 鼓形线r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*1051 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*1053.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)54. 蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*2055. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)57.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*1058.碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+2459.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360) z=10*cos(t*360*5)63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10) y=2*sin(t*360*10)+sin(t*180*10) z=t*664.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8) y=3*sin(t*360*8)-1.5*sin(t*480*8) z=t*865.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)66. ufo (漩涡线)球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*569.圆柱齿轮廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
二次函数的曲线和方程

二次函数的曲线和方程二次函数是数学中一个重要的概念,在数学和科学领域中有很广泛的应用。
它的曲线形状独特,方程形式简洁明了。
本文将从曲线的形状和方程的解析等方面进行分析和讨论。
一、曲线的形状二次函数的曲线通常呈现出一个开口向上或者开口向下的抛物线形状。
开口的方向取决于二次函数中二次项的系数的正负性。
当二次项系数大于0时,抛物线开口向上;当二次项系数小于0时,抛物线开口向下。
二、方程形式二次函数的标准方程形式为 f(x) = ax^2 + bx + c,其中a、b、c为常数,且a ≠ 0。
其中,a决定了抛物线的形状,b决定了抛物线的位置,c决定了抛物线的纵向平移。
三、顶点和对称轴二次函数的曲线都有一个特殊的点,称为顶点。
顶点的横坐标为 -b/2a,纵坐标为 f(-b/2a) = -Δ/4a,其中Δ = b^2 - 4ac为判别式。
对于开口向上的抛物线,顶点是曲线的最低点,对应着最小值;对于开口向下的抛物线,顶点是曲线的最高点,对应着最大值。
同时,二次函数的对称轴是通过顶点的一条线,方程为 x = -b/2a。
四、零点和方程的解析零点就是使得二次函数等于0的x值。
求解二次函数的零点可以通过因式分解、配方法、求根公式等方法进行。
当判别式Δ大于0时,函数有两个不同的实数根;当Δ等于0时,函数有两个相等的实数根;当Δ小于0时,函数没有实数根,但可能有复数根。
五、对称性二次函数具有轴对称性,即以对称轴为中心,对于对称轴上任意点(x, y),也存在对称点(x', y')。
其中,x' = 2p - x,y' = y,p为对称轴的x坐标。
六、平移变换利用平移变换,可以将二次函数的曲线在坐标系中进行上下平移、左右平移。
上下平移即在二次函数的方程中将c的值进行更改,左右平移即在二次函数的方程中将b的值进行更改。
平移后,曲线的形状和顶点位置保持不变,只是位置发生变化。
总结:通过以上对二次函数曲线和方程的讨论,我们可以得出以下结论:二次函数的曲线呈现出独特的抛物线形状,方程的形式简单清晰;二次函数的曲线有顶点和对称轴,顶点确定了曲线的最值,对称轴确定了曲线的位置;二次函数的方程可以通过求解零点来解析函数的根;二次函数具有轴对称性;平移变换可以改变二次函数的位置。
高中常用函数性质及图像汇总

高中常用函数性质及图像一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
(二)一次函数 1、一次函数的定义一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。
当0b =时,一次函数y kx =,又叫做正比例函数。
⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当0b =,0k ≠时,y kx =仍是一次函数.⑶当0b =,0k =时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数.2、正比例函数及性质一般地,形如y=kx(k 是常数,k ≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数一般形式 y=kx (k 不为零) ① k 不为零 ② x 指数为1 ③ b 取零当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时,•直线y=kx 经过二、四象限,从左向右下降,即随x 增大y 反而减小.(1) 解析式:y=kx (k 是常数,k ≠0) (2) 必过点:(0,0)、(1,k )(3) 走向:k>0时,图像经过一、三象限;k<0时,•图像经过二、四象限 (4) 增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小 (5) 倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴3、一次函数及性质一般地,形如y=kx +b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式 y=kx+b (k 不为零) ① k 不为零 ②x 指数为1 ③ b 取任意实数一次函数y=kx+b 的图象是经过(0,b )和(-kb,0)两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)(1)解析式:y=kx+b(k 、b 是常数,k ≠0) (2)必过点:(0,b )和(-kb,0) (3)走向: k>0,图象经过第一、三象限;k<0,图象经过第二、四象限 b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限 ⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限 ⇔⎩⎨⎧><0b k 直线经过第一、二、四象限 ⇔⎩⎨⎧<<0b k 直线经过第二、三、四象限(4)增减性: k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.(5)倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴. (6)图像的平移: 当b>0时,将直线y=kx 的图象向上平移b 个单位;当b<0时,将直线y=kx 的图象向下平移b 个单位.4、一次函数y=kx +b 的图象的画法.根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b ),.即横坐标或纵坐标为0的点.b>0b<0 b=0k>0经过第一、二、三象限经过第一、三、四象限 经过第一、三象限图象从左到右上升,y 随x 的增大而增大k<0经过第一、二、四象限经过第二、三、四象限 经过第二、四象限图象从左到右下降,y 随x 的增大而减小5、正比例函数与一次函数之间的关系一次函数y=kx +b 的图象是一条直线,它可以看作是由直线y=kx 平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移) 6、正比例函数和一次函数及性质 正比例函数一次函数概 念一般地,形如y=kx(k 是常数,k ≠0)的函数叫做正比例函数,其中k 叫做比例系数一般地,形如y=kx +b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数.当b=0时,是y=kx ,所以说正比例函数是一种特殊的一次函数.自变量 围 X 为全体实数 图 象 一条直线 必过点(0,0)、(1,k )(0,b )和(-kb,0)走 向k>0时,直线经过一、三象限; k<0时,直线经过二、四象限k >0,b >0,直线经过第一、二、三象限 k >0,b <0直线经过第一、三、四象限 k <0,b >0直线经过第一、二、四象限 k <0,b <0直线经过第二、三、四象限增减性 k>0,y 随x 的增大而增大;(从左向右上升) k<0,y 随x 的增大而减小。
考研数学常用曲线方程

考研数学中,曲线方程是一个重要的知识点,它涉及到函数、极限、导数、积分等多个数学分支。
以下是一些考研数学中常用的曲线方程:1. **直线方程**:- 一般形式:\( ax + by + c = 0 \)- 斜截式:\( y = mx + b \)(其中\( m \) 是斜率,\( b \) 是截距)2. **圆的方程**:- 一般形式:\( (x - h)^2 + (y - k)^2 = r^2 \)(其中\( (h, k) \) 是圆心坐标,\( r \) 是半径)- 参数方程:\( x = h + r\cos\theta \),\( y = k + r\sin\theta \)(其中\( \theta \) 是参数)3. **椭圆的方程**:- 一般形式:\( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)(其中\( a \) 是半长轴,\( b \) 是半短轴)4. **双曲线的方程**:- 一般形式:\( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \)(其中\( a \) 是实轴半长,\( b \) 是虚轴半长)5. **抛物线的方程**:- 一般形式:\( y^2 = 4ax \) 或\( x^2 = 4ay \)(其中\( a \) 是焦点到准线的距离)6. **正弦曲线**:- 一般形式:\( y = a\sin(x - b) \)(其中\( a \) 是振幅,\( b \) 是相位)7. **余弦曲线**:- 一般形式:\( y = a\cos(x - b) \)(其中\( a \) 是振幅,\( b \) 是相位)8. **指数衰减曲线**:- 一般形式:\( y = a e^{-bx} \)(其中\( a \) 是初值,\( b \) 是衰减系数)9. **对数增长曲线**:- 一般形式:\( y = a + b\ln(x) \)(其中\( a \) 是截距,\( b \) 是增长率)10. **多项式曲线**:- 一般形式:\( y = ax^n + bx^{n-1} + \ldots + k \)(其中\( a, b, \ldots, k \) 是多项式系数,\( n \) 是最高次项)这些曲线方程在考研数学中经常出现,掌握它们对于解决实际问题和理解数学概念至关重要。
正弦函数的图象

正弦函数的图象
正弦函数曲线是一种二次函数, 它表示振动或周期运动物体的物理量和它相关的位置、速度与时间之间的变化关系. 它是几何学中最常用的函数之一, 它与余弦函数具有相同的
属性. 由于正弦函数的基本性质, 它的图形具有一定的特点.
首先, 正弦函数的图形是一个周期性的曲线,它的周期是指函数值重复在相同的值域
上的次数。
其次,正弦函数的曲线是对称的,即它的图中有一条对称轴,且具有周期性,
它值的正负值可以能够在曲线图中相互交替出现。
此外, 正弦函数的曲线有两个极点,即
函数值最大(1)和最小(-1)时的位置。
当以x轴为横轴表示时,y轴上的正弦函数的曲线可以用下面的公式来表示:y=sin x, 其中的x是x轴的变量(时间),y代表函数值(位置和速度)。
当x从0到2π(360度)变化时,正弦函数曲线会沿着一定的规律从最大值开始,直到x变化到270 度时,正弦函数值变为最小值(-1),然后从270度开始,沿着同样的规律正弦函数值变为最大值(1),以此类推,直到x变为360度时,再从最大值(1)开始重复变化。
因此,正弦函数的图象是一条有规律的曲线,它是一条对称的曲线,有两个极点, 它
的变化是一个有规律的周期性运动。
在数学中,正弦函数的分析有助于我们理解振动及周
期性运动的物理量和它们相关的位置、速度及时间的变化关系。
对勾函数绝对精确

对勾函数绝对精确
介绍
对勾函数是指在一个坐标系中,符号为“√”的函数曲线。
它是
一种常用的数学函数,被广泛应用于各个领域,如数学、物理、工
程等。
特点
对勾函数具有以下几个特点:
- 区域限制:该函数的定义域一般为非负实数集合,即x≥0。
- 增长特性:对勾函数曲线是单调递增的,也就是说,随着自
变量x的增加,函数值也随之增加。
- 无极限:对勾函数在x=0处取得最小值,随着自变量的增加,函数值逐渐增大但不会趋近于无穷大。
- 水平渐进线:当x趋近于无穷大时,对勾函数的图像逐渐靠
近y轴,但永远不会达到y轴。
应用领域
对勾函数在各个领域有广泛的应用,包括但不限于以下几个方面:
- 数学:对勾函数是指数函数的一种特例,被用于解决各种数
学问题,如求根、方程求解等。
- 物理:对勾函数在物理学中经常被用于描述物体运动的速度、加速度等相关问题。
- 工程:对勾函数在工程实践中常用于对数据进行处理与分析,如信号处理、图像识别等。
数学表示
对勾函数的数学表示为:
f(x) = √x
其中,f(x)表示对勾函数,√x表示x的平方根。
总结
对勾函数作为一种常见的数学函数,具有特定的特点和应用领域。
在数学、物理、工程等领域中,对勾函数被广泛使用,可以用
于解决各种问题和分析数据。
熟悉对勾函数的特性和数学表示对于
进一步探索和应用该函数非常重要。
1-6经济学中的常用函数

练习题答案
1 2 1. R = Q − Q , R( ) = ; 2 9 2. R = 0.11Q − 0.4 , P (15) = 0.0025, P (12) = 0.0034, P ( 20) = 0.0017, R(10) = 0.044, R(12) = 0.041, R(15) = 0.037; 3.C = C (Q ) = 200000 + 1000Q;
在时间 T 内的总费用 E 为
1 Q E = C1Tq + C 2 2 q 1 Q 为贮存费, 其中 , C1Tq 为贮存费, C 2 为进货费用 . 2 q
八、戈珀兹 (Gompertz) 曲线 戈珀兹 曲线是指数函数 y = ka
bc
在经济预测中,经常使用该曲线 在经济预测中,经常使用该曲线.
k
初始期 发展期
饱和期
0 当 lg a < 0 , < b < 1 时,图形如上页所示 . 且无限增大时, 由图可见 ,曲线当 t > 0 且无限增大时, 其无限与直线 y = k 接近 ,且始终位于该直
下方. 在产品销售预测中, 线 下方 在产品销售预测中,当预测销售量充 分接近到 k 值时,表示该产品在商业流通中 值时, 将达到市场饱和 .
平均收益为 100 Q − 3 Q AP ( Q ) = P ( Q ) = . 4
六、利润函数 利润是生产中获得的总收益与投入的 总成本之差。 总成本之差。即
L(Q ) = R(Q ) − C (Q )
例 5 设某种商品的总成本为C (Q) = 20 + 2Q + 0.5Q ,
2
万元, 若每售出一件该商品的收入是 20 万元, 求生产 10 件的总利润. 件的总利润.
3次函数曲线-概念解析以及定义

3次函数曲线-概述说明以及解释1.引言1.1 概述概述在数学中,三次函数是一种常见的多项式函数,其最高次项的指数为3。
三次函数的一般形式可以表示为y = ax^3 + bx^2 + cx + d,其中a、b、c和d都是实数,并且a不等于0。
三次函数曲线通常呈现出一种典型的"弓形"形状,有时可能具有一个局部极值点或者一个拐点。
它们在图像上的走势和特点在多个领域中都有重要的应用,例如物理学、经济学和计算机图形学等。
理解和掌握三次函数曲线的特点对于解决实际问题和进行进一步的数学研究都是非常重要的。
本文将围绕三次函数曲线展开讨论,首先介绍三次函数的基本定义和性质,然后探讨三次函数曲线的图像特点以及如何进行函数图像的变换和分析。
接下来,我们将进一步研究三次函数曲线的局部极值点和拐点的性质,并举例说明在实际问题中的应用。
最后,我们将总结所讨论的内容,并展望一些可能的研究方向。
通过研究和理解三次函数曲线的性质和特点,我们可以更好地应用它们解决实际问题,并且有助于我们对数学的深入理解和进一步研究。
接下来,我们将详细介绍本文的组织结构和目的。
1.2 文章结构2. 正文在本文中,我们将着重研究3次函数曲线。
通过对这种特殊类型的函数曲线进行深入的分析和研究,我们可以更好地理解它们的数学性质和应用。
本文的正文部分将分为三个要点来探讨3次函数曲线所涉及的关键概念和性质。
2.1 第一要点在第一要点中,我们将首先介绍3次函数曲线的基本定义和表达形式。
我们将学习如何根据给定的系数,利用函数表达式来绘制3次函数曲线的图像。
此外,我们还将讨论3次函数曲线的对称性和奇偶性,并探索其在数学和科学领域中的实际应用。
2.2 第二要点在第二要点中,我们将进一步研究3次函数曲线的性质和特征。
我们将通过对曲线的导数和导数变化率的分析,探讨曲线的增减性和凸凹性。
此外,我们还将介绍曲线的转折点和拐点,并讨论这些特殊点对曲线整体形状的影响。
常见的函数曲线

常见的函数曲线
常见的函数曲线包括:
1. 抛物线:抛物线是二次函数 f(x) = ax2 + bx + c 的图形形状,其中a、
b、c是常数,a的符号决定了抛物线的弯曲程度,如果a>0,则曲线向上弯曲,如果a<0,则曲线向下弯曲。
2. 指数函数:指数函数是用来表达指数增长和指数衰减的数学函数,一般表示为 y=a^x,其中a为一个正数常数,取值范围一般为0-100之间,可表示曲线的下凹程度。
3. 对数函数:对数函数是一类数学函数,它们以x的对数形式表示,常用来表示指数函数的导数,可用来分析以指数形式发展的量的变化情况。
4. 幂函数:幂函数是一类数学函数,通常以x的幂次形式表示,常用来分析某个量以指数形式发展变化的过程,可用来分析幂函数具有的不同特性。
5. 正弦函数:正弦函数也被称作“摆线函数”,它主要用来描述江潮、化浪和振荡周期性现象,例如天气、风力和海浪等,正弦函数具有周期不变的特性。
6. 双曲函数:双曲函数是一类变换函数,是两个单方向延伸的正弦函数的组合。
一般双曲函数的图形以反抛物线的形状呈现,并且可以调节反抛物线的下凹程度来表示函数的特性。
7. 多项式函数:多项式函数是一类极坐标函数,它的图形以右倾的多边形的形状呈现,常用来表示正多项式函数,也可以用来拟合不同曲线。
8. 常数函数:常数函数是一类特殊的一元函数,其性质与参数无关,它的函数曲线呈现为一条水平直线,它可以用来描述一些商业中的概念,如均值数、中位数等。
常见函数曲线

常见函数曲线
一、正
1、线性函数曲线:该函数曲线的斜率在任意点都是一致的,函数类型为y=kx+b,k 为斜率,b为y轴截距。
在x-y平面上,它的图形就是一条直线。
2、二次函数曲线:该函数曲线的图形是在 x-y 平面它的函数解析式为y=ax²+bx+c,其中a,b,c都是常数。
3、三次函数曲线:该曲线的函数解析式为y=ax³+bx²+cx+d,其中a,b,c,d都是常数。
它是一条非常曲折,复杂的曲线。
其在x=0处折点,在x=±√-b/(3a)处取极值点,其取值区间为[-∞,∞]。
4、指数函数曲线:它的函数解析式为y = a^x (a为常数),该曲线一般会趋近于y 轴,因此横坐标取值范围为[-∞,∞],纵坐标取值范围为[0,∞]。
5、三角函数曲线:它的常见函数形式有正弦函数y=sin(x),余弦函数y=cos(x),正切函数y=tan(x),反正弦函数y=arctan(x),反余弦函数y = arccos(x).它在x轴上常有周期性变化,随着x增大,y 也会伴着特殊的变化状态。
二、负
2、抛物线:它是一条双曲抛物线,它的函数解析式为y=ax²+bx+c (a,b,c 为常数),横坐标取值范围为[-∞,∞],纵坐标取值范围为[-∞,∞]。
它的左右两端无边界极点,x=0处取得一个最高点,可以看到抛物线开口向上,斜率随着x增大而逐渐变小,趋近于x轴。
三角函数的双曲线解释

三角函数的双曲线解释在数学中,三角函数是一组基本的函数,其与三角形的边长和角度之间的关系密切相关。
而与三角函数密切相关的是双曲函数,它们是三角函数的扩展形式,并在许多领域中都有着广泛的应用。
一、正弦函数及其双曲线解释正弦函数是最基本的三角函数之一,它表示角度与对应的正弦值之间的关系。
正弦函数的图像可以表示为一个周期性的波状曲线。
然而,当我们考虑到角度可以取任意实数值时,我们需要引入双曲正弦函数来进行解释。
双曲正弦函数的图像是一个无界的波状曲线,与正弦函数的图像相似。
二、余弦函数及其双曲线解释余弦函数是另一个常见的三角函数,它表示角度与对应的余弦值之间的关系。
余弦函数的图像也是一个周期性的波状曲线。
但是,当我们考虑到角度可以取任意实数值时,我们需要引入双曲余弦函数来进行解释。
双曲余弦函数的图像是一个对称的波状曲线,与余弦函数的图像相似。
三、正切函数及其双曲线解释正切函数是三角函数中的另一个重要函数,它表示角度与对应的正切值之间的关系。
正切函数的图像可以表示为一个周期性的波状曲线,且在某些角度上取无穷大或无穷小的值。
当我们考虑到角度可以取任意实数值时,我们需要引入双曲正切函数来进行解释。
双曲正切函数的图像是一个无界的波状曲线,与正切函数的图像相似。
四、反三角函数及其双曲线解释除了常见的正弦、余弦和正切函数,我们还有反三角函数,用于表示给定三角函数值所对应的角度。
对于三角函数来说,我们有反正弦、反余弦和反正切函数。
当我们考虑到三角函数的值可以取任意实数值时,我们需要引入双曲反三角函数来进行解释。
双曲反三角函数的图像与常见的反三角函数的图像类似,但它们的定义域和值域有所不同。
综上所述,通过引入双曲函数,我们可以更全面地解释三角函数及其在实数域上的性质。
双曲函数在物理学、工程学和其他科学领域中有着广泛的应用,能够描述许多实际问题中的变化和波动。
对于理解和应用三角函数,以及相关领域中的问题求解和建模,双曲函数的理解和运用都是至关重要的。
cotx的曲线

cotx的曲线
cotx函数是三角函数中的一种,与sinx、cosx、tanx等一样,cotx
也拥有一个特殊的图像,其图像总体来说有很多相似点和差异点。
一、cotx图像的对称性
cotx的图像具有y轴对称性质,在y轴左右两侧的图像是完全相同的。
二、cotx的渐近线
cotx的渐近线分别为x=π/2+kπ和x=kπ,其中k为任何整数。
这些渐近
线是cotx的不可定义点,cotx会无限靠近这些渐近线却无法达到它们。
cotx的大部分图像都集中在渐近线上下,它们之间形成了一个类似于
正切线的波动区间。
三、cotx的周期性质
cotx的周期是π,也就是说,它的函数取值每个π个单位后会重复一次。
四、cotx的特殊点
cotx有许多特殊的点,例如“次元点”x=π/2,此时函数无定义。
这些特殊点和渐近线使cotx函数的图像显得特别错综复杂,但同时也
充满了许多有趣的数学性质和规律。
通过对cotx函数的研究和分析,
可以深入了解三角函数的基本特性及其应用。
先快后慢的函数曲线

先快后慢的函数曲线函数曲线是数学中的一个重要概念,在数学中,函数曲线有不同的特征和性质。
其中,一种常见的函数曲线类型是先快后慢的函数曲线。
在以下内容中,我将对先快后慢的函数曲线进行详细的介绍。
为了更好地理解这种函数曲线,我将探讨一个具体的实例。
假设我们研究一个人在跑步过程中的速度变化。
在开始跑步时,人的速度会迅速提升,但随着时间的推移,速度的增长逐渐减缓,最终趋于一个极限。
这种速度变化的图形就是一个典型的先快后慢的函数曲线。
为了更加形象地描述这个曲线,我们可以先定义一个函数来表示速度与时间的关系。
假设速度函数为v(t),其中t表示时间。
我们可以假设这个函数是一个二次函数,即v(t) = at^2 + bt + c,其中a、b和c是常数。
在定义函数之后,我们可以通过确定常数a、b和c的值来描绘函数曲线。
在这个例子中,我们可以假设a为正值,以便使速度一开始变快。
然后,我们可以选择b和c的值来决定速度在后期如何变化。
首先,让我们看一下当t接近0时,即刚开始跑步时,速度如何变化。
由于a为正值,t值的平方项将主导函数值的增长,因此速度将迅速提升。
然后,随着时间的推移,t值逐渐增加。
在一些时刻,速度增长的主导因素将从二次项变为线性项,即bt。
这意味着速度的增长将逐渐减缓。
最后,在t值较大的时候,速度的增长几乎可以忽略不计。
函数曲线将趋于水平。
这是因为由于二次项的特性,速度增长将趋向于一个极限值。
通过这个例子,我们可以看到先快后慢的函数曲线的特点。
在开始阶段,函数值的变化较快。
然而,随着自变量的增加,函数值的变化逐渐减慢,最终趋于一个稳定值。
除了二次函数之外,还有许多其他的函数类型可以描述先快后慢的函数曲线。
例如,指数函数和对数函数也常用于描述这种函数曲线。
总的来说,先快后慢的函数曲线是数学中常见的一种曲线类型。
它在许多领域和问题中都有应用,包括物理学、经济学和生物学等。
通过研究这种函数曲线,我们可以更好地理解许多现象中的变化规律。
先快后慢的函数曲线

先快后慢的函数曲线先快后慢的函数曲线是一种常见的数学函数形态,其呈现出前期增长速度快,后期增长速度慢的特点。
这种函数曲线在实际应用中较为普遍,例如描述物理现象中的加速度变化、经济学中的市场需求变化等。
先快后慢的函数曲线通常分为两个部分:增长期和饱和期。
增长期中,函数曲线呈现出前期增长速度快的趋势,可以用指数函数或对数函数等形式进行刻画。
饱和期中,函数曲线逐渐趋于平缓,即增长速度逐渐变慢,可以用幂函数或多项式函数等形式进行刻画。
下面我们将详细介绍这两个部分的数学表示方法以及其实际应用。
1. 增长期增长期通常表现为函数曲线的前期迅速增长。
其基本形式可表示为指数函数或对数函数。
指数函数是一种以指数为自变量的函数形式,通常具有如下形式:y = a*e^(kx)其中a为函数曲线在x=0时的函数值,k为常数,e为自然对数的底数。
指数函数具有前期增长速度很快的特点,随着x的增大,函数曲线上升越来越缓慢。
这种函数曲线常用于描述物理学中的加速度变化、生态学中的物种数量增长等。
对数函数是一种以对数为自变量的函数形式,通常具有如下形式:y = kln(x) + b其中k、b为常数,ln为自然对数运算。
对数函数具有前期增长速度很快的特点,随着x的增大,函数曲线上升越来越缓慢。
这种函数曲线常用于描述经济学中的市场需求变化、化学中的反应过程等。
2. 饱和期饱和期通常表现为函数曲线的后期逐渐逼近水平线,增长速度逐渐变慢的趋势。
其基本形式可表示为幂函数或多项式函数。
幂函数是一种以幂次为自变量的函数形式,通常具有如下形式:y = ax^b其中a、b为常数。
幂函数具有后期增长速度逐渐逼近水平线的特点,常用于描述生态学中物种数量的增长趋势、经济学中市场需求的变化趋势等。
多项式函数是一种以高次幂项为自变量的函数形式,通常具有如下形式:y = ax^n + bx^(n-1) + … + k其中a、b、…、k为常数,n为多项式的最高次幂。
