计算机图形学_有效边表算法源代码
计算机图形学源程序

中点画线法:#include <graphics.h>#include <math.h>#include <conio.h>#include <stdio.h>void MidPoint_Line(int x0,int y0,int x1,int y1,int color); main(){int driver=DETECT,mode;int x0,y0,x1,y1,color;initgraph(&driver,&mode,"");setbkcolor(2);MidPoint_Line(0,0,200,200,1);getch();closegraph();}void MidPoint_Line(x0,y0,x1,y1,color)int x0,y0,x1,y1,color;{ int a,b,delta1,delta2,d,x,y;a=y0-y1;b=x1-x0;d=2*a+b;delta1=2*a;delta2=2*(a+b);x=x0;y=y0;putpixel(x,y,color);while(x<x1){ if(d<0){ x++; y++;d+=delta2;}else{ x++;d+=delta1;}putpixel(x,y,color);}}Bresenham算法:#include <graphics.h>#include <math.h>#include <conio.h>#include <stdio.h>void Bresenham_Line(int x0,int y0,int x1,int y1,int value); main(){int driver=DETECT,mode;int x0,y0,x1,y1,color;initgraph(&driver,&mode,"");setbkcolor(2);Bresenham_Line(0,0,200,200,1);getch();closegraph();}void Bresenham_Line(int x0,int y0,int x1,int y1,int value) {int dx=abs(x0-x1),dy=abs(y0-y1);int d=2*dy-dx;int twody=2*dy,twodydx=2*(dy-dx);int x,y,xend;if (x0>x1){x=x1;y=y1;xend=x0;}else{x=x0;y=y0;xend=x1;}putpixel(x,y,value);while(x<xend){x++;if(d<0)d+=twody;else{y++;d+=twodydx;}putpixel(x,y,value);}}分享到:中点画圆算法(C语言)#include "stdio.h"#include "graphics.h"void circlepoint(int x,int m,int n,int y) {putpixel(x+m,y+n,4);putpixel(y+m,x+n,4);putpixel(y+m,n-x,4);putpixel(x+m,n-y,4);putpixel(m-y,n+x,4);putpixel(m-y,n-x,4);putpixel(m-x,n-y,4);putpixel(m-x,y+n,4);}void midpointcircle(int m,int n,int r) {int x=0;int y=r;int d=1-r;int d1=3;int d2=2-r-r;circlepoint(x,m,n,y);while(x<y){if(d<0){d+=d1;d1+=2;}else{d+=(d1+d2);d1+=2;d2+=2;y--;}x++;circlepoint(x,m,n,y);}}main(){int r,x,y;int drive,mode;drive=DETECT;initgraph(&drive,&mode,"c:\\turboc2");printf("intput the int R and the center of the circle:\n"); scanf("%d%d%d",&x,&y,&r);midpointcircle(x,y,r);getch();} /*程序不足之处请指教*/三次bezer曲线#include"dos.h"#include"bios.h"#include"graphics.h"#include"math.h"main(){int driver,mode,n,i, p1x,p1y,p2x,p2y,p3x,p3y,p4x,p4y;float x,y;double d,d1, f1,f2,f3,f4;driver=DETECT;mode=DETECT;initgraph(&driver,&mode,"d:\\tc3");p1x=150;p1y=150;p2x=300;p2y=180;p3x=400;p3y=160;p4x=250;p4y=50;n=200;d=1.0/n;d1=d;line(150,150,300,180);line(300,180,400,160);line(400,160,250,50);moveto(p1x,p1y);for(i=0;i<=n;i++){f1=(1.0-d1)*(1.0-d1)*(1.0-d1);f2=3.0*d1*(1.0-d1)*(1.0-d1);f3=3.0*d1*d1*(1.0-d1);f4=d1*d1*d1;x=f1*p1x+f2*p2x+f3*p3x+f4*p4x;y=f1*p1y+f2*p2y+f3*p3y+f4*p4y;lineto((int)x,(int)y);d1+=d;}getch();closegraph();}。
计算机图形学课程设计-有效边表填充算法实现

计算机图形学课程设计设计题目改进的有效边表算法对多边形的填充学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名刘柯学生学号201213030112任课教师梅占勇设计(论文)成绩教务处制2015年9 月28 日目录一、设计内容与要求 (3)1.1设计题目 (3)1.2 设计内容 (3)1.3 设计目标 (3)二、总体设计 (3)2.1 多边形的表示 (3)2.2 x-扫描线算法 (4)2.3 改进的有效边表算法 (4)2.3.1 改进的有效边表算法 (4)2.3.2 有效边表 (5)2.3.3 边表 (6)三、详细设计 (8)3.1 改进的有效边表算法的实现 (8)3.2 有效边表算法程序流程图 (9)四、测试结果 (9)五、总结 (15)六、源代码 (15)参考文献 (26)一、设计内容与要求1.1设计题目用改进的有效边表算法实现多边形的填充1.2 设计内容使用OpenGL实现用改进的有效边表算法填充多边形1.3 设计目标参照课本上改进的有效边表算法的思想,实现该算法的C语言代码,并用该算法搭配OpenGL以像素点的方式绘制出给定顶点坐标的多边形。
二、总体设计2.1 多边形的表示在计算机图形学中,多边形有2种重要的表示方法:顶点表示和点阵表示。
顶点表示用多边形的顶点序列来刻画多边形,这种方法直观、几何意义强,占用内存少,应用普遍,但它没有明确指出哪些像素在多边形内,故不能直接用于面着色。
点阵表示用位于多边形内的像素的集合来刻画多边形。
这种表示法虽然失去了许多重要的几何信息,但便于运用帧缓存表示图形,是面着色所需要的图形表示形式。
大多数图形应用系统采用顶点序列表示多边形,而顶点表示又不能直接用于显示,那么就必须有从多边形的顶点表示到点阵表示的转换,这种转换称为多边形的扫描转换或多边形的填充。
即从多边形的顶点信息出发,求出位于其内部的各个像素,并将其颜色值写入帧缓存的相应单元中。
2.2 x-扫描线算法x-扫描线算法的基本思想是,按照扫描线的顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。
计算机图形学代码

四、实验结果抓图与分析1、目标的平移的源程序2、绕任意点旋转的源程序实验一、直线的生成一、实验内容根据提供的程序框架,修改部分代码,完成画一条直线的功能(中点画线法或者Bresenham画线法任选一),只要求实现在第一象限内的直线。
二、算法原理介绍双击直线生成.dsw打开给定的程序,或者先启动VC++,文件(file)→打开工作空间(open workspace)。
打开直线生成view.cpp,按注释改写下列函数:1.void CMyView::OnDdaline() (此为DDA生成直线)2.void CMyView::OnBresenhamline()(此为Bresenham画直线)3.void CMYView::OnMidPointLine()(此为中点画线法)三、程序源代码1.DDA生成直线画法程序:float x,y,dx,dy,k;dx=(float)(xb-xa);dy=(float)(yb-ya);k=dy/dx;x=xa;y=ya;if(abs(k)<1){for (x=xa;x<=xb;x++){pdc->SetPixel(x, int(y+0.5),COLOR);y=y+k;}}if(abs(k)>=1){for(y=ya;y<=yb;y++){pdc->SetPixel(int(x+0.5),y,COLOR);x=x+1/k;}}//DDA画直线结束}2.Bresenham画直线源程序:float b,d,xi,yi;int i;float k;k=(yb-ya)/(xb-xa);b=(ya*xb-yb*xa)/(xb-xa);if(k>0&&k<=1)for(i=0;i<abs(xb-xa);i++){ d=ya+0.5-k*(xa+1)-b;if(d>=0){ xi=xa+1;yi=ya;xa++;ya=ya+0.5;}if(d<0){ xi=xa+1;yi=ya+1;xa++;ya=ya+1.5;}pdc->SetPixel(xi,yi,COLOR); }//BresenHam画直线结束}3.中点画线法源程序:float b,d,xi,yi;int i;float k;k=(yb-ya)/(xb-xa);b=(ya*xb-yb*xa)/(xb-xa);if(k>0&&k<=1)for(i=0;i<abs(xb-xa);i++){ d=ya+0.5-k*(xa+1)-b;if(d>=0){ xi=xa+1;yi=ya;xa++;ya=ya+0.5;}if(d<0){ xi=xa+1;yi=ya+1;xa++;ya=ya+1.5;}pdc->SetPixel(xi,yi,COLOR); }//BresenHam画直线结束}四、实验结果抓图与分析1、DDA生成直线2、Bresenham画直线3、中点画线法实验二、bresenham画圆一、实验内容根据提供的程序框架,修改部分代码,用Bresenham画法画一段圆弧或者画圆。
[VIP专享]计算机图形学 有效边表填充算法实验报告
![[VIP专享]计算机图形学 有效边表填充算法实验报告](https://img.taocdn.com/s3/m/4ea18a9689eb172ded63b7d8.png)
图 2 屏幕显示多边形 3.算法设计: (1)建立 AET 和 BUCKET 类; (2)初始化桶,并在建立桶结点时为其表示的扫描线初始化为带头结点的链表; (3)对每个桶结点进行循环,将桶内每个结点的边表合并为有效边表,并进行有效边表循 环; (4)按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些 交点按 X 值递增的顺序进行排序,配对,以确定填充区间; (5)用指定颜色点亮填充区间内的所有像素,即完成填充工作。 4.源程序: 1)//AET.h class AET { public:
}
Bucket::~Bucket() {
}
3)//TestView.h #include "AET.h"//包含有效边表类 #include "Bucket.h"//包含桶类 #define Number 7//N 为闭合多边形顶点数,顶点存放在整型二维数组 Point[N]中 class CTestView : public CView { 。。。。。。。。。 public:
COLORREF GetColor;//调色板 CPoint Point[7];//定义多边形 Bucket *HeadB,*CurrentB;//桶的头结点和当前结点 AET E[Number],*HeadE,*CurrentE,*T1,*T2;//有效边表的结点 } (4) TestView.cpp #define ROUND(a) int(a+0.5) //四舍五入 CTestView::CTestView() { //设置多边形的 7 个顶点 Point[0]=CPoint(550,400);//P0 Point[1]=CPoint(350,600);//P1 Point[2]=CPoint(250,350);//P2 Point[3]=CPoint(350,50);//P3 Point[4]=CPoint(500,250);//P4 Point[5]=CPoint(600,50);//P5 Point[6]=CPoint(800,450);//P6 }
计算机图形学实验报告及代码

九、作业
课后习题
十、本章小结
在本章中,对计算机图形学的基本概念和研究内容进行了概述,对发展概况和应用领域进行了说明。
第2章计算机图形系统
一、教学目标
通过对本章的学习,要求熟悉计算机图形系统的组成/各种图形显示器、图形输入/输出设备。
二、教学要求
1、了解计算机图形系统的组成;
(5).计算机网络
计算机网络是指将上述四类计算机平台,或者其中某一类通过某种互联技术彼此连接,按照某种通信协议进行数据传输、数据共享、数据处理的多机工作环境。
它的特点是多种计算机相连,可以充分发挥各个机器的性能和特点,以达到很高的性能价格比。
网络图形系统要考虑的关键问题是网络服务器的性能,图形数据的通信、传输、共享以及图形资源的利用问题。
(3).中、小型计算机
一般在特定的部门、单位和应用领域中采用此类环境。它是大型信息系统建立的重要环境,这种环境中信息和数据的处理量是很大的,要求机器有极高的处理速度和极大的存储容量。
(4).大型机
以大型计算机为基础,具有容量庞大的存储器和极强的计算功能,大量的显示终端及
高精度、大幅面的硬拷贝设备。还往往拥有自行开发的、功能齐全的应用软件系统。例如,美国第三大汽车公司(CHRYSLER汽车公司)就拥有庞大的计算机系统来进行计算机辅助设计、实体造型、结构分析、运动模拟、工程和科学计算、项目管理、生产过程控制等。
1.1计算机图形学的研究内容
计算机图形表现形式
(1).线条式(线框架图)
用线段来表现图形,容易反映客观实体的内部结构,如各类工程技术中结构图的表示,机械设计中零件结构图及电路设计中的电路原理图等。具有面模型、色彩、浓淡和明暗层次效应,适合表现客观实体的外形或外貌,如汽车、飞机、轮船等的外形设计以及各种艺术品造型设计等。
有效边表填充算法
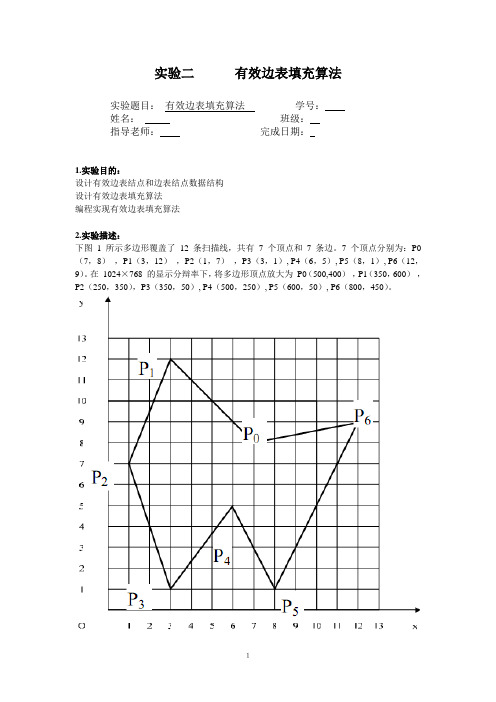
实验二有效边表填充算法实验题目:有效边表填充算法学号:姓名:班级:指导老师:完成日期:1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图1 所示多边形覆盖了12 条扫描线,共有7 个顶点和7 条边。
7 个顶点分别为:P0(7,8),P1(3,12),P2(1,7),P3(3,1), P4(6,5), P5(8,1), P6(12,9)。
在1024×768 的显示分辩率下,将多边形顶点放大为P0(500,400),P1(350,600),P2(250,350),P3(350,50), P4(500,250), P5(600,50), P6(800,450)。
图1示例多边形图2屏幕显示多边形3.算法设计:多边形的有效边表填充算法的基本原理是按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些交点按x值递增的顺序进行排序、配对,以确定填充区间,然后用指定颜色点亮填充区间的所有像素,即完成填充工作。
有效边表填充算法通过访问多边形覆盖区间内的每个像素,可以填充凸、凹多边形和环,已成为目前最为有效的多边形填充算法。
4.源程序:1)//AET.h和AET..cppclass AET{public:AET();virtual ~AET();double x;int yMax;double k; //代替1/kAET *next;}2)//Bucket.h和Bucket.cppclass Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;}3) // TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数,顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
计算机图形学实验有效边表填充算法

实验二2-2一、实验题目给定四个点绘制图4-44所示的不同转角的两个正方形,使用有效边表算法进行填充,填充效果如图4-45所示,注意采用“左闭右开”和“上闭下开”的原则,使得每个正方形的右边界和下边界没有填充。
二、实验思想有效边表填充算法通过维护边表和有效边表,避开了扫描线与多边形所有边求交的复杂运算。
填充原理是按照扫描线从小到大的移动顺序,计算当前扫描线与有效边的交点,然后把这些交点按x值递增的顺序进行排序、配对,以确定填充区间,最后用指定颜色填充区间内的所有像素,即完成填充工作。
三、实验代码void CTestView::GetMaxX()//获得屏幕宽度{CRect Rect;GetClientRect(&Rect);MaxX=Rect.right;}void CTestView::GetMaxY()//获得屏幕高度{CRect Rect;GetClientRect(&Rect);MaxY=Rect.bottom;}void CTestView::ReadPoint()//读入点表函数{//设置第一个正方形的4个顶点int a=160;P1[0]=CP2(MaxX/4-a,MaxY/2+a);//P0P1[1]=CP2(MaxX/4+a,MaxY/2+a);//P1P1[2]=CP2(MaxX/4+a,MaxY/2-a);//P2P1[3]=CP2(MaxX/4-a,MaxY/2-a);//P3//设置第二个正方形的4个顶点int b=ROUND(sqrt(2)*a);P2[0]=CP2(3*MaxX/4,MaxY/2+b);//P0P2[1]=CP2(3*MaxX/4+b,MaxY/2);//P1P2[2]=CP2(3*MaxX/4,MaxY/2-b);//P2P2[3]=CP2(3*MaxX/4-b,MaxY/2);//P3}void CTestView::DrawRect(CDC *pDC,CP2 *P)//绘制正方形函数{CP2 T;CLine line;for(int i=0;i<4;i++)//边循环{if(i==0){line.MoveTo(pDC,P[i]);T=P[0];}else{line.LineTo(pDC,P[i]);;}}line.LineTo(pDC,T);//闭合}void CTestView::OnMENUIFill(){// TODO: Add your command handler code hereCOLORREF FColor;CColorDialog ccd(RGB(255,0,0));if(ccd.DoModal()==IDOK)//调用调色板选取色{FColor=ccd.GetColor();m_Red=GetRValue(FColor);//获得颜色的红色分量m_Green=GetGValue(FColor);//获得颜色的绿色分量m_Blue=GetBValue(FColor);//获得颜色的蓝色分量}RedrawWindow();//刷新屏幕FillRect(P1);//填充正方形1FillRect(P2);//填充正方形2}void CTestView::FillRect(CP2 *P)//填充正方形函数{CFill fill;CPi2 Point[4];for(int i=0;i<4;i++){Point[i].x=P[i].x;Point[i].y=ROUND(P[i].y);Point[i].c=CRGB(double(m_Red)/255.0,double(m_Green)/255.0,double(m_Blue)/255.0);}CDC *pDC=GetDC();fill.SetPoint(Point,4);//填充正方形fill.CreateBucket();fill.CreateEdge();fill.Gouraud(pDC);ReleaseDC(pDC);}四、实验截图。
计算机图形学代码

像素函数56. putpixel() 画像素点函数57. getpixel()返回像素色函数直线和线型函数58. line() 画线函数59. lineto() 画线函数60. linerel() 相对画线函数61. setlinestyle() 设置线型函数62. getlinesettings() 获取线型设置函数63. setwritemode() 设置画线模式函数多边形函数64. rectangle()画矩形函数65. bar() 画条函数66. bar3d() 画条块函数67. drawpoly() 画多边形函数圆、弧和曲线函数68. getaspectratio()获取纵横比函数69. circle()画圆函数70. arc() 画圆弧函数71. ellipse()画椭圆弧函数72. fillellipse() 画椭圆区函数73. pieslice() 画扇区函数74. sector() 画椭圆扇区函数75. getarccoords()获取圆弧坐标函数填充函数76. setfillstyle() 设置填充图样和颜色函数77. setfillpattern() 设置用户图样函数78. floodfill() 填充闭域函数79. fillpoly() 填充多边形函数80. getfillsettings() 获取填充设置函数81. getfillpattern() 获取用户图样设置函数图像函数82. imagesize() 图像存储大小函数83. getimage() 保存图像函数84. putimage() 输出图像函数图形和图像函数对许多图形应用程序,直线和曲线是非常有用的。
但对有些图形只能靠操作单个像素才能画出。
当然如果没有画像素的功能,就无法操作直线和曲线的函数。
而且通过大规模使用像素功能,整个图形就可以保存、写、擦除和与屏幕上的原有图形进行叠加。
编辑本段(一) 像素函数putpixel() 画像素点函数功能:函数putpixel() 在图形模式下屏幕上画一个像素点。
计算机图形学 有效边表填充算法实验报告

实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。
7 个顶点分别为:P0(7, 8), P1(3, 12), P2(1, 7), P3(3, 1), P4(6, 5), P5(8, 1), P6(12, 9)。
在1024×768 的显示分辩率下, 将多边形顶点放大为P0(500,400), P1(350, 600), P2(250, 350), P3(350, 50), P4(500, 250), P5(600, 50), P6(800, 450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:(1)建立AET和BUCKET类;(2)初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表;(3)对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环;(4)按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间;(5)用指定颜色点亮填充区间内的所有像素, 即完成填充工作。
4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
计算机图形学上机代码

glRectf(0.0f, 0.0f, 0.5f, 0.5f); //在右上方绘制一个无镂空效果的正方形
glFlush();
}
E.g.7着色模型
#include <GL/glut.h>
#include <math.h>
const GLdouble Pi = 3.1415926536;
*/
static GLubyte Mask[128];
FILE *fp;
fp = fopen("D:/Mask/Mask.bmp", "rb"); //注意此处的格式fp = fopen("D:/vclx/mask.bmp", "rb");
if( !fp )
exit(0);
if( fseek(fp, -(int)sizeof(Mask), SEEK_END) )
glVertex2f(1.0f, 0.0f); //以上两个点可以画x轴
glVertex2f(0.0f, -1.0f);
glVertex2f(0.0f, 1.0f); //以上两个点可以画y轴
glEnd();
glBegin(GL_LINE_STRIP);
for(x=-1.0f/factor; x<1.0f/factor; x+=0.01f)
0x18, 0xCC, 0x33, 0x18,
0x10, 0xC4, 0x23, 0x08,
0x10, 0x63, 0xC6, 0x08,
0x10, 0x30, 0x0C, 0x08,
0x10, 0x18, 0x18, 0x08,
计算机图形学实验指导(一、二)

电脑图形学实验指导实验一、直线的扫描转换算法实验实验目的掌握中点Bresenham直线扫描转换算法的思想。
实验环境实验内容问题描述:给定两个点的坐标P0(x0,y0),P1(x1,y1),使用中点Bresenham直线扫描转换算法画出连接两点的直线。
中点Bresenham直线扫描转换算法原理见课本。
实验基本步骤首先、使用MFC AppWizard(exe)向导生成一个单文档视图程序框架。
其次、使用中点Bresenham直线扫描转换算法实现自己的画线函数,函数原型可表示如下:void DrawLine(CDC *pDC, int p0x, int p0y, int p1x, int p1y);在函数中,可通过调用CDC成员函数SetPixel来画出扫描转换过程中的每个点。
COLORREF SetPixel(int x, int y, COLORREF crColor );再次、找到文档视图程序框架视图类的OnDraw成员函数,调用DrawLine函数画出不同斜率情况的直线,如下列图:最后、调试程序直至正确画出直线。
实验要求1写出中点Bresenham直线扫描转换算法的程序并在vc6下编译和调试通过,画出具有各种斜率范围的直线(仅使用GDI函数SetPixel函数)。
2按规定的实验格式写出实验报告,包含实验代码〔自己写的画线函数〕,结果〔截图〕。
实验二、多边形填充算法实验实验目的掌握边标志算法或有效边表算法进行多边形填充的基本设计思想。
实验环境实验内容问题描述:给定多边形的顶点的坐标P0(x0,y0),P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4)…使用边标志算法或有效边表算法进行多边形填充。
边标志算法或有效边表算法原理见课本。
实验基本步骤首先、使用MFC AppWizard(exe)向导生成一个单文档视图程序框架。
其次、实现边标志算法或有效边表算法函数,如下:void FillPolygon(CDC *pDC, int px[], int py[], int ptnumb);px:该数组用来表示每个顶点的x坐标py :该数组用来表示每个顶点的y坐标ptnumb:表示顶点个数注意实现函数FillPolygon可以直接通过窗口的DC〔设备描述符〕来进行多边形填充,不需要使用帧缓冲存储。
《计算机图形学》有序边表填充算法资料讲解

《计算机图形学》有序边表填充算法实验报告一、实验目的1、掌握有序边表算法填充多边形区域;2、理解多边形填充算法的意义;3、增强C语言编程能力。
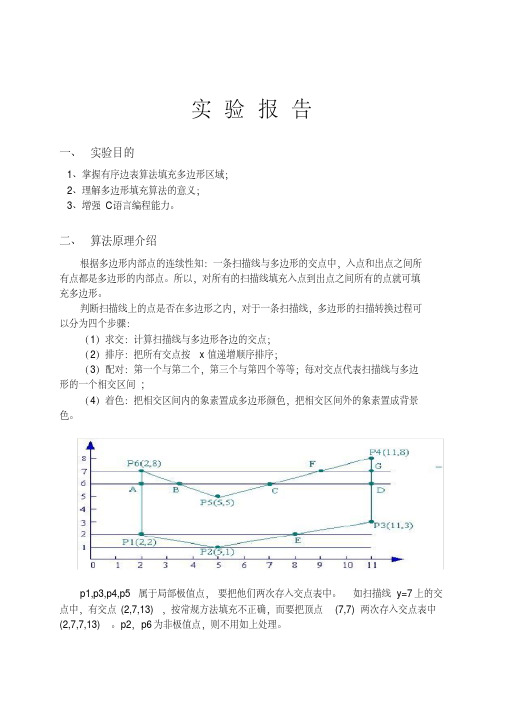
二、算法原理介绍根据多边形内部点的连续性知:一条扫描线与多边形的交点中,入点和出点之间所有点都是多边形的内部点。
所以,对所有的扫描线填充入点到出点之间所有的点就可填充多边形。
判断扫描线上的点是否在多边形之内,对于一条扫描线,多边形的扫描转换过程可以分为四个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把所有交点按x值递增顺序排序;(3)配对:第一个与第二个,第三个与第四个等等;每对交点代表扫描线与多边形的一个相交区间;(4)着色:把相交区间内的象素置成多边形颜色,把相交区间外的象素置成背景色。
p1,p3,p4,p5属于局部极值点,要把他们两次存入交点表中。
如扫描线y=7上的交点中,有交点(2,7,13),按常规方法填充不正确,而要把顶点(7,7)两次存入交点表中(2,7,7,13)。
p2,p6为非极值点,则不用如上处理。
为了提高效率,在处理一条扫描线时,仅对与它相交的多边形的边进行求交运算。
把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中,称此链表为活性边表(AET)。
对每一条扫描线都建立一个与它相交的多边形的活性边表(AET)。
每个AET的一个节点代表一条活性边,它包含三项内容1.x -当前扫描线与这条边交点的x坐标;2.Δx -该边与当前扫描线交点到下一条扫描线交点的x增量;3.ymax -该边最高顶点相交的扫描线号。
每条扫描线的活性边表中的活性边节点按照各活性边与扫描线交点的x值递增排序连接在一起。
当扫描线y移动到下一条扫描线y = y+1时,活性边表需要更新,即删去不与新扫描线相交的多边形边,同时增加与新扫描线相交的多边形边,并根据增量法重新计算扫描线与各边的交点x。
当多边形新边表ET构成后,按下列步骤进行:①对每一条扫描线i,初始化ET表的表头指针ET[i];②将ymax = i的边放入ET[i]中;③使y =多边形最低的扫描线号;④初始化活性边表AET为空;⑤循环,直到AET和ET为空。
计算机图形学课程设计报告报告实验报告

《计算机图形学》实验报告班级计算机科学与技术姓名学号2014 年6 月2 日实验一基本图形生成算法一、实验目的:1、掌握中点Bresenham绘制直线的原理;2、设计中点Bresenham算法;3、掌握八分法中点Bresenham算法绘制圆的原理;4、设计八分法绘制圆的中点Bresenham算法;5、掌握绘制1/4椭圆弧的上半部分和下半部分的中点Bresenham算法原理;6、掌握下半部分椭圆偏差判别式的初始值计算方法;7、设计顺时针四分法绘制椭圆的中点Bresenham算法。
二、实验过程:1、实验描述实验1:使用中点Bresenham算法绘制斜率为0<=k<=1的直线。
实验2:使用中点Bresenham算法绘制圆心位于屏幕客户区中心的圆。
实验3:使用中点Bresenham算法绘制圆心位于屏幕客户区中心的椭圆。
2、实验过程1)用MFC(exe)建立一个单文档工程;2)编写对话框,生成相应对象,设置相应变量;3)在类CLineView中声明相应函数,并在相关的cpp文件中实现;4)在OnDraw()函数里调用函数实现绘制直线、圆、椭圆;5)运行程序,输入相应值,绘制出图形。
三、源代码实验1:直线中点Bresenham算法1.// cline.cpp : implementation file// cline dialogcline::cline(CWnd* pParent /*=NULL*/): CDialog(cline::IDD, pParent){//{{AFX_DATA_INIT(cline)m_x0 = 0;m_y0 = 0;m_x1 = 0;m_y1 = 0;//}}AFX_DATA_INIT}void cline::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(cline)DDX_Text(pDX, IDC_x0, m_x0);DDX_Text(pDX, IDC_y0, m_y0);DDX_Text(pDX, IDC_x1, m_x1);DDX_Text(pDX, IDC_y1, m_y1);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(cline, CDialog)//{{AFX_MSG_MAP(cline)//}}AFX_MSG_MAPEND_MESSAGE_MAP()2、// LineView.hclass CLineView : public CView{public:CLineDoc* GetDocument();..........void Mbline(double,double,double,double); //直线中点Bresenham函数.......}3、// Line.cpp//*******************直线中点Bresenham函数*********************/void CLineView::Mbline(double x0, double y0, double x1, double y1) {CClientDC dc(this);COLORREF rgb=RGB(0,0,255); //定义直线颜色为蓝色double x,y,d,k;x=x0; y=y0; k=(y1-y0)/(x1-x0); d=0.5-k;for(x=x0;x<=x1;x++){dc.SetPixel((int)x,(int)y,rgb);if(d<0){y++;d+=1-k;}elsed-=k;}}4、//LineView.cppvoid CLineView::OnDraw(CDC* pDC){CLineDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data herecline a;a.DoModal();//初始化CLineView::Mbline(a.m_x0,a.m_y0,a.m_x1,a.m_y1); }实验2:圆中点Bresenham算法1、//cricle.cpp// Ccricle dialogCcricle::Ccricle(CWnd* pParent /*=NULL*/): CDialog(Ccricle::IDD, pParent){//{{AFX_DATA_INIT(Ccricle)m_r = 0;//}}AFX_DATA_INIT}void Ccricle::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Ccricle)DDX_Text(pDX, r_EDIT, m_r);//}}AFX_DATA_MAP}2、//CcircleView.hclass CCcircleView : public CView{.......public:CCcircleDoc* GetDocument();void CirclePoint(double,double); //八分法画圆函数void Mbcircle(double); //圆中点Bresenham函数........}3、//CcircleView.cppvoid CCcircleView::OnDraw(CDC* pDC){CCcircleDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCcricle r;r.DoModal();CCcircleView::Mbcircle(r.m_r);//画圆}4、//CcircleView.cpp//*******************八分法画圆*************************************/ void CCcircleView::CirclePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);dc.SetPixel((int)(300+y),(int)(300+x),rgb);dc.SetPixel((int)(300-y),(int)(300+x),rgb);dc.SetPixel((int)(300+y),(int)(300-x),rgb);dc.SetPixel((int)(300-y),(int)(300-x),rgb);}//**************************圆中点Bresenham函数*********************/ void CCcircleView::Mbcircle(double r){double x,y,d;COLORREF rgb=RGB(0,0,255);d=1.25-r;x=0;y=r;for(x=0;x<y;x++){CirclePoint(x,y); //调用八分法画圆子函数if(d<0)d+=2*x+3;else{d+=2*(x-y)+5;y--;}}}实验3:椭圆中点Bresenham算法1、//ellipse1.cpp// Cellipse dialogCellipse::Cellipse(CWnd* pParent /*=NULL*/) : CDialog(Cellipse::IDD, pParent){//{{AFX_DATA_INIT(Cellipse)m_a = 0;m_b = 0;//}}AFX_DATA_INIT}void Cellipse::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Cellipse)DDX_Text(pDX, IDC_EDIT1, m_a);DDX_Text(pDX, IDC_EDIT2, m_b);//}}AFX_DATA_MAP}2、//EllipseView.hclass CEllipseView : public CView{......................public:CEllipseDoc* GetDocument();void EllipsePoint(double,double); //四分法画椭圆void Mbellipse(double a, double b); //椭圆中点Bresenham函数..................}3、//Ellipse.cpp//*****************四分法画椭圆********************************/void CEllipseView::EllipsePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);}//************************椭圆中点Bresenham函数*********************/ void CEllipseView::Mbellipse(double a, double b){double x,y,d1,d2;x=0;y=b;d1=b*b+a*a*(-b+0.25);EllipsePoint(x,y);while(b*b*(x+1)<a*a*(y-0.5))//椭圆AC弧段{if(d1<0)d1+=b*b*(2*x+3);else{d1+=b*b*(2*x+3)+a*a*(-2*y+2);y--;}x++;EllipsePoint(x,y);}d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;//椭圆CB弧段while(y>0){if(d2<0){d2+=b*b*(2*x+2)+a*a*(-2*y+3);x++;}elsed2+=a*a*(-2*y+3);y--;EllipsePoint(x,y);}}4、//EllipseView.cppvoid CEllipseView::OnDraw(CDC* pDC){CEllipseDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCellipse el;el.DoModal();//初始化CEllipseView::Mbellipse(el.m_a, el.m_b);//画椭圆}四、实结果验实验1:直线中点Bresenham算法实验2:圆中点Bresenham 算法实验3:椭圆中点Bresenham 算法实验二有效边表填充算法一、实验目的:1、设计有效边表结点和边表结点数据结构;2、设计有效边表填充算法;3、编程实现有效边表填充算法。
计算机图形学_有效边表算法源代码

#include <stdio.h>#include <malloc.h>#include <gl/glut.h>#include <Windows.h>#define EPSILON 0.000001 //最小浮点数//点结构体struct Point{int x; //x坐标int y; //y坐标};//线结构体struct Line{Point high_point; //高端点Point low_point; //低端点int is_active; //是否为有效边,水平边(0),非水平边(1)double inverse_k; //斜率k的倒数};//边结点struct EdgeNode{double x; //扫描线与边交点的x坐标(边的低端点的x坐标)int y_max; //边的高端点的y坐标ymaxdouble inverse_k; //斜率k的倒数EdgeNode *next; //下一个边结点的指针};//有效边表struct ActiveEdgeTable{int y; //扫描线yEdgeNode *head; //边链表的头指针};//桶结点typedef struct Bucket{int y; //扫描线yEdgeNode *head; //边链表的头指针Bucket *next; //下一个桶的指针} EdgeTable;int compare(Point p1, Point p2);Line* create_lines(Point points[], int n);Point get_lowest_point(Line lines[], int n);Point get_highest_point(Line lines[], int n);void swap(Line &l1, Line &l2);void sort(Line lines[], int n);EdgeTable* create_edge_table(Line lines[], int n);ActiveEdgeTable* init_active_table(EdgeTable *edge_table);void delete_edge(ActiveEdgeTable *active_table, int y_max);void add_edge(ActiveEdgeTable *active_table, EdgeNode edge);ActiveEdgeTable* update_active_table(ActiveEdgeT able *active_table, EdgeTable *edge_table);void DrawPolygon(Point points, int n);void DrawGrid(int x, int y);void Fill(Point points[], int n);void Initial();void Display();int main(int argc, char* argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(400, 300);glutInitWindowPosition(100, 120);glutCreateWindow("Polygon Filling");glutDisplayFunc(Display);Initial();glutMainLoop();return 0;}//比较2个点的高度int compare(Point p1, Point p2){if (p1.y > p2.y)return 1;else if (p1.y == p2.y)return 0;return -1;}//由点数组生成线段数组Line* create_lines(Point points[], int n){Line *lines = (Line*)malloc(n * sizeof(Line));for (int i = 0; i < n; ++i){Point p1 = points[i];Point p2 = points[(i + 1) % n];int result = compare(p1, p2);if (result == 0)lines[i].is_active = 0;elselines[i].is_active = 1;lines[i].high_point = result > 0 ? p1 : p2;lines[i].low_point = result < 0 ? p1 : p2;lines[i].inverse_k = (double)(p2.x - p1.x) / (double)(p2.y - p1.y);}return lines;}//获取线数组中最低的端点Point get_lowest_point(Line lines[], int n){Point lowest_point = lines[0].low_point;for (int i = 1; i < n; ++i){Point low_point = lines[i].low_point;if (compare(lowest_point, low_point) > 0)lowest_point = low_point;}return lowest_point;}//获取线数组中最高的端点Point get_highest_point(Line lines[], int n){Point highest_point = lines[0].high_point;for (int i = 1; i < n; ++i){Point high_point = lines[i].high_point;if (compare(highest_point, high_point) < 0)highest_point = high_point;}return highest_point;}//交换2个Line对象void swap(Line &l1, Line &l2){Line temp = l1;l1 = l2;l2 = temp;}//对线数组进行排序void sort(Line lines[], int n){//先按低端点的y坐标进行升序排序for (int i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; j < n; ++j){if (lines[j].low_point.y < lines[min_index].low_point.y)min_index = j;}swap(lines[i], lines[min_index]);}//再将有序数组按低端点的x坐标升序排列,若x坐标相等,按inverse_k升序for (i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; lines[j].low_point.y == lines[i].low_point.y; ++j){if (lines[j].low_point.x < lines[min_index].low_point.x)min_index = j;}swap(lines[i], lines[min_index]);if (i > 0 && lines[i].low_point.x == lines[i - 1].low_point.x){if (lines[i].is_active == 1 && lines[i - 1].is_active == 1){if (lines[i].inverse_k < lines[i - 1].inverse_k)swap(lines[i], lines[i - 1]);}}}}//创建一个边表EdgeTable* create_edge_table(Line lines[], int n){EdgeTable *edge_table = (EdgeTable*)malloc(sizeof(EdgeTable));edge_table->head = NULL;edge_table->next = NULL;sort(lines, n);Point lowest_point = get_lowest_point(lines, n);Point highest_point = get_highest_point(lines, n);EdgeTable *s = edge_table;for (int i = lowest_point.y; i <= highest_point.y; ++i){Bucket *bucket = (Bucket*)malloc(sizeof(Bucket));bucket->y = i;bucket->next = NULL;bucket->head = (EdgeNode*)malloc(sizeof(EdgeNode));bucket->head->next = NULL;EdgeNode *p = bucket->head;for (int j = 0; j < n; ++j){if (lines[j].is_active == 0)continue;if (lines[j].low_point.y == i){EdgeNode *q = (EdgeNode*)malloc(sizeof(EdgeNode));q->x = lines[j].low_point.x;q->y_max = lines[j].high_point.y;q->inverse_k = lines[j].inverse_k;q->next = NULL;p->next = q;p = q;}}s->next = bucket;s = bucket;}return edge_table;}//从边表中取出第一个不为空的桶初始化有效边表ActiveEdgeTable* init_active_table(EdgeTable *edge_table){ActiveEdgeTable *active_table = (ActiveEdgeTable*)malloc(sizeof(ActiveEdgeTable));active_table->y = edge_table->next->y;active_table->head = (EdgeNode*)malloc(sizeof(EdgeNode));active_table->head->next = NULL;EdgeNode *p = edge_table->next->head;EdgeNode *q = active_table->head;while (p->next != NULL){EdgeNode *s = (EdgeNode*)malloc(sizeof(EdgeNode));s->x = p->next->x;s->y_max = p->next->y_max;s->inverse_k = p->next->inverse_k;s->next = NULL;q->next = s;q = s;p = p->next;}return active_table;}//从有效边表中删除指定y_max的边结点void delete_edge(ActiveEdgeTable *active_table, int y_max){EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if (q->y_max == y_max){p->next = q->next;free(q);}elsep = p->next;}}//将一个边结点按次序添加到有效边表中void add_edge(ActiveEdgeTable *active_table, EdgeNode edge){EdgeNode *t = (EdgeNode*)malloc(sizeof(EdgeNode));t->x = edge.x;t->y_max = edge.y_max;t->inverse_k = edge.inverse_k;t->next = NULL;EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if ((edge.x < q->x) || (edge.x == q->x && edge.inverse_k < q->inverse_k)){p->next = t;t->next = q;return;}p = p->next;}p->next = t;}//更新有效边表,并与边表中对应的桶合并ActiveEdgeTable* update_active_table(ActiveEdgeT able *active_table, EdgeTable *edge_table) {//更新扫描线y++active_table->y;//删除y=ymax的边delete_edge(active_table, active_table->y);//更新边结点的数据EdgeNode *p = active_table->head->next;while (p != NULL){p->x += p->inverse_k;p = p->next;}//找到边表中对应的桶EdgeTable *q = edge_table;while ((q = q->next) != NULL && q->y != active_table->y);//如果找到,则进行合并if (q != NULL){EdgeNode *s = q->head;while ((s = s->next) != NULL){add_edge(active_table, *s);}}return active_table;}//画出多边形的边框void DrawPolygon(Point points[], int n){glBegin(GL_LINE_LOOP);for (int i = 0; i < n; ++i)glVertex2i(points[i].x, points[i].y);glEnd();}//画出x * y的网格void DrawGrid(int x, int y){glBegin(GL_LINES);//横线for (int i = 0; i <= y; ++i){glVertex2d(0, i);glVertex2d(x, i);}//竖线for (i = 0; i <= x; ++i){glVertex2d(i, 0);glVertex2d(i, y);}glEnd();}//用指定的像素大小填充多边形void Fill(Point points[], int n){Line *lines = create_lines(points, n);EdgeTable *edge_table = create_edge_table(lines, n);ActiveEdgeTable *active_table = init_active_table(edge_table);while (active_table->head->next != NULL){EdgeNode *p = active_table->head;int b = -1;while (p->next != NULL){if (b > 0){int left = p->x;int right = p->next->x;//如果不是局部最低点,则进行边界处理if (!(p->x - p->next->x >= -EPSILON && p->x - p->next->x <= EPSILON)){//处理左边界if (!(p->x - left >= -EPSILON && p->x - left <= EPSILON))left += 1;//处理右边界if (p->next->x - right >= -EPSILON && p->next->x - right <= EPSILON)right -= 1;}for (int i = left; i <= right; ++i){glBegin(GL_POINTS);glVertex2d(i, active_table->y);glEnd();glFlush();Sleep(50);}}p = p->next;b = -b;}active_table = update_active_table(active_table, edge_table);}}//初始化窗口,x和y指定窗口的坐标大小void Initial(){glClearColor(1.0f, 1.0f, 1.0f, 1.0f);glMatrixMode(GL_PROJECTION);gluOrtho2D(0.0, 20.0, 0.0, 15.0);}//窗口的显示回调函数void Display(){//使用当前背景色填充窗口glClear(GL_COLOR_BUFFER_BIT);//使用灰色画出网格线glColor3f(0.75f, 0.75f, 0.75f);DrawGrid(20, 14);glFlush();//多边形的顶点坐标Point points[] = { { 3, 1 },{ 6, 5 },{ 8, 1 },{ 12, 9 },{ 7, 8 },{ 3, 12 },{ 1, 7 } };//计算顶点个数int n = sizeof(points) / sizeof(Point);//使用黑色画出多边形的边框glColor3f(0.0f, 0.0f, 0.0f);DrawPolygon(points, n);glFlush();//指定点大小glPointSize(6.0f);//使用红色填充多边形glColor3f(1.0f, 0.0f, 1.0f);Fill(points, n);glFlush();}。
计算机图形学-实验报告2-多边形有效边表填充算法

(9)如果甬结点的扫描线值大于等于有效边表中的结点值ymax,则该边为无效边。
(10)当甬结点不为空则转(6)否则删除甬表和边表的头结点,算法结束。
(11)实验结果及分析:
实验地点
软件实验室
指导教师
(3)动态链表的排序算法
二、实验内容:
三、自定义屏幕二维坐标系,原点位于客户区中心,x轴水平向右为正,y轴垂直向上为正。
四、在屏幕客户区内使用cline类绘制示例多边形边界。
五、设置屏幕背景色为白死,调用windows的颜色对话框选择填充色使用单一颜色填充多边形。
六、使用有效边表填充算法填充示例多边形内部及边界。
(5)对每个甬结点链接的边表,根据x|ymin值的大小进行排序,若x|ymin相等,则按照k由小到大排序。
(6)循环访问每个甬结点,将甬内每个结点的边表合并成有效边表,并循环访问有限边表。
(7)从有效边表中取出扫描线上相邻两条边的结点对进行配对。填充时设置一个逻辑变量binflag,每访问一个结点,把binflag值取反一次,若binflag为真,则把从当前结点的x值开始到下一结点x值结束的区间用指定的颜色填充。
七、实验步骤:
(1)调用颜色对话框读取填充色。
(2)根据示例多边形顶点坐标值,计算扫描线的最大值ScanMax和最小值ScanMin。
(3)用多边形覆盖的扫描线动态建立甬结点。
(4)循环访问多边形的所有顶点,根据边的顶点y值比起点y值高或边的终点y值比起点y值低两种情况,计算每条边的ymin。在甬中寻找与该ymin相对应的甬结点计算该边表示的x|ymin,ymax,k,并依据次链接该边表结点到甬结点。
计算机图形学常用算法及代码大全

2.1.1 生成直线的DDA算法数值微分法即DDA法(Digital Differential Analyzer),是一种基于直线的微分方程来生成直线的方法。
一、直线DDA算法描述:设(x1,y1)和(x2,y2)分别为所求直线的起点和终点坐标,由直线的微分方程得可通过计算由x方向的增量△x引起y的改变来生成直线:也可通过计算由y方向的增量△y引起x的改变来生成直线:式(2-2)至(2-5)是递推的。
二、直线DDA算法思想:选定x2-x1和y2-y1中较大者作为步进方向(假设x2-x1较大),取该方向上的增量为一个象素单位(△x=1),然后利用式(2-1)计算另一个方向的增量(△y=△x·m=m)。
通过递推公式(2-2)至(2-5),把每次计算出的(x i+1,y i+1)经取整后送到显示器输出,则得到扫描转换后的直线。
之所以取x2-x1和y2-y1中较大者作为步进方向,是考虑沿着线段分布的象素应均匀,这在下图中可看出。
另外,算法实现中还应注意直线的生成方向,以决定Δx及Δy是取正值还是负值。
三、直线DDA算法实现:1、已知直线的两端点坐标:(x1,y1),(x2,y2)2、已知画线的颜色:color3、计算两个方向的变化量:dx=x2-x1dy=y2-y14、求出两个方向最大变化量的绝对值:steps=max(|dx|,|dy|)5、计算两个方向的增量(考虑了生成方向):xin=dx/stepsyin=dy/steps6、设置初始象素坐标:x=x1,y=y17、用循环实现直线的绘制:for(i=1;i<=steps;i++){ putpixel(x,y,color);/*在(x,y)处,以color色画点*/x=x+xin;y=y+yin;}五、直线DDA算法特点:该算法简单,实现容易,但由于在循环中涉及实型数的运算,因此生成直线的速度较慢。
//@brief 浮点数转整数的宏实现代码#define FloatToInteger(fNum)((fNum>0)?static_cast<int>(fNum+0.5):static_cast<int>(fNum-0.5))/*!* @brief DDA画线函数** @param pDC [in]窗口DC* @param BeginPt [in]直线起点* @param EndPt [in]直线终点* @param LineCor [in]直线颜色* @return 无*/void CDrawMsg::DDA_DrawLine(CDC *pDC,CPoint &BeginPt,CPoint &EndPt,COLORREF LineCor){l ong YDis = (EndPt.y - BeginPt.y);l ong XDis = (EndPt.x-BeginPt.x);l ong MaxStep = max(abs(XDis),abs(YDis)); // 步进的步数f loat fXUnitLen = 1.0f; // X方向的单位步进f loat fYUnitLen = 1.0f; // Y方向的单位步进f YUnitLen = static_cast<float>(YDis)/static_cast<float>(MaxStep);f XUnitLen = static_cast<float>(XDis)/static_cast<float>(MaxStep);// 设置起点像素颜色p DC->SetPixel(BeginPt.x,BeginPt.y,LineCor);f loat x = static_cast<float>(BeginPt.x);f loat y = static_cast<float>(BeginPt.y);// 循环步进f or (long i = 1;i<=MaxStep;i++){x = x + fXUnitLen;y = y + fYUnitLen;pDC->SetPixel(FloatToInteger(x),FloatToInteger(y),LineCor);}}2.1.2 生成直线的B resenham算法从上面介绍的DDA算法可以看到,由于在循环中涉及实型数据的加减运算,因此直线的生成速度较慢。
扫描线填充算法--有效边表填充算法

代码:draw.cpp//using OpenGL#include "opengl.h"#include <iostream>#include <vector>#include <algorithm>#include <unistd.h>#define PN 6intpoint[N][2]={{40,5},{75,40},{60,70},{35,50},{25,80},{5,30 }};//AEstruct AE{AE(float _x,float _dx,int_ymax){x=_x;dx=_dx;ymax=_ymax;}float x;float dx;int ymax;void operator++(int){x+=dx;}};//AET//which eage is on the rightbool fill_comp(const AE& ae1,const AE& ae2){if(ae1.x<ae2.x){return true;}if(ae1.x==ae2.x&&ae1.dx<ae2.dx){return true;}return false;}void fillline(int y,int x1,int x2){for(int i=x1;i<=x2;i++) drawpoint(i,y);flush();}void fill(){//make k=(x2-x1)/(y2-y1)float k[PN]={0.0};for(inti=0;i!=PN;i++){k[i]=((float)(point[(i+1)%PN][0]-point[i][ 0])/(float)(point[(i+1)%PN][1]-point[i][1]));}//find min and max with selection sort.int min=point[0][1],max=min;for(inti=0;i!=PN;i++){if(point[i][1]>max){max=point[i][1];};;if( point[i][1]<min){max=point[i][1];}}//make scanning line liststd::vector<AE>*ET =new std::vector<AE>[max-min+1];//make ET//for(int i =0; i<PN;++i){//get ymin, ymaxint yminn=point[i][1]<point[(i+1)%PN][1]? i :(i+1)%PN;int ymaxn=point[i][1]>=point[(i+1)%PN][1]? i :(i+1)%PN;AE *tmp =newAE(point[yminn][0],k[i],point[ymaxn][1]);//insert nodeET[point[yminn][1]-min].push_back(*tmp);}//init AETstd::vector<AE> AET;for(int i=0;i!=max-min+1;i++){//insert node from ET to AETfor(int ii=0;ii!=ET[i].size();ii++){//sort with selection sort.AET.insert(std::upper_bound(AET.begin(),AET.end(),ET[i][ii],fill_comp),ET[i][ii]);}//delete y=ymax,"下闭上开"for(intii=0;ii!=AET.size();){if(i+min==AET[ii].ymax){AET.erase(AET.begin()+ii);}else{ii++;}}//draw{bool flag=false;for(int ii=0;ii!=AET.size();ii++){if(flag)fillline(i+min,(int)(AET[ii-1].x+0.5),(int)(AET[ii].x+0.5 ));//if(flag)std::cout<<i+min<<'\t'<<(int)(AET[ii].x+0.5)<<','<<(int)( AET[ii-1].x+0.5)<<'\n';flag=!flag;}}for(int ii=0;ii!=AET.size();ii++){AET[ii]++;} }delete[](ET);}void draw(){drawgrid(0.8,0.8,0.8);setcolor(1,0.5,0.5);fill();draweage(point,PN);}int main(int n,char*avg[]){init(n,avg,"L2");reinit(draw);loop();return0;}opengl.h#include <GL/glut.h>#define N 100#define GRIDSIZE 5int size=N*GRIDSIZE;void init(int argc,char** argv,char*title){//init openGLsize = N * GRIDSIZE;glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);glutInitWindowPosition(10,10);glutInitWindowSize(size, size);glutCreateWindow(title);glClearColor(1.0, 1.0, 1.0, 1.0);//whiteglClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0,0.0,0.0);//blackgluOrtho2D(0, size,0, size);}void reinit(void(*p)()){glutDisplayFunc(p);}void flush(){glFlush();}void loop(){glutMainLoop();}void clear(){glClearColor(1.0, 1.0, 1.0, 1.0);//whiteglClear(GL_COLOR_BUFFER_BIT);}void setcolor(double r,double g,double b){glColor3f(r, g, b);}void drawline(int x1,int y1,int x2,int y2){glBegin(GL_LINES);glVertex2i(x1, y1);glVertex2i(x2, y2);glEnd();flush();}void drawgrid(double r,double g,double b){int i =0;glColor3f(r, g, b);for(i =0;i !=N *GRIDSIZE;i +=GRIDSIZE){drawline(i, 0, i, size);}for(i =0;i !=N *GRIDSIZE;i +=GRIDSIZE){drawline(0, i, size, i);}flush();}void drawpoint(int x,int y){glPointSize((double)GRIDSIZE);glBegin(GL_POINTS);glVertex2i(x * GRIDSIZE, y * GRIDSIZE);glEnd();flush();}void draweage(int p[][2],int pn){if(pn<2)return;setcolor(0,0.8,0.8);for(int i=0;i!=pn-1;i++){drawline(p[i][0]*GRIDSIZE,p[i][1]*GRIDSIZE,p[i+1][0]*GRID SIZE,p[i+1][1]*GRIDSIZE);}drawline(p[pn-1][0]*GRIDSIZE,p[pn-1][1]*GRIDSIZE,p[0][0]* GRIDSIZE,p[0][1]*GRIDSIZE);}运行环境:ubuntu 13.10 + g++ 运行结果:。
《计算机图形学》有序边表填充算法
初始化每条扫面线的边链表 */
/*
建“桶” */
edges[scan]->next=NULL;
}
BuildEdgeList(cnt,pts,edges);
/*
建立有序边表 */
active=(Edge *)malloc(sizeof(Edge));
active->next=NULL;
for(scan=scanmin;scan<=scanmax;scan++) /* 扫描每条扫描线, 求活性表 */
当多边形新边表 ET构成后,按下列步骤进行: ① 对每一条扫描线 i ,初始化 ET表的表头指针 ET[i] ; ② 将 ymax = i 的边放入 ET[i] 中; ③ 使 y = 多边形最低的扫描线号; ④ 初始化活性边表 AET为空; ⑤ 循环,直到 AET和 ET 为空。
将新边表 ET 中对应 y 值的新边节点插入到 AET表。 遍历 AET表,将两两配对的交点之间填充给定颜色值。 遍历 AET表,将 ymax= y 的边节点从 AET表中删除,并将 ymax> y 的各边节点 的 x 值递增 Δx;并重新排序。 y 增加 1。
/* 建立扫描线 scan 的活性边表 , 把活性边结点放入扫描线 scan 的结点指针数组
edges[scan] 中*/
{
Edge *p,*q;
p=edges[scan]->next;
/*
查找当前扫描线对应的 y 桶*/
while(p)
/*y
桶不空 */
{q=p->next;
/*
找到最后一个边结点, 插入 */
*edges[])
/* 把边结点 edge, 放到 lower.y 扫描线所在的边结点指针数组 edges[] 中 */
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <stdio.h>#include <malloc.h>#include <gl/glut.h>#include <Windows.h>#define EPSILON 0.000001 //最小浮点数//点结构体struct Point{int x; //x坐标int y; //y坐标};//线结构体struct Line{Point high_point; //高端点Point low_point; //低端点int is_active; //是否为有效边,水平边(0),非水平边(1)double inverse_k; //斜率k的倒数};//边结点struct EdgeNode{double x; //扫描线与边交点的x坐标(边的低端点的x坐标)int y_max; //边的高端点的y坐标ymaxdouble inverse_k; //斜率k的倒数EdgeNode *next; //下一个边结点的指针};//有效边表struct ActiveEdgeTable{int y; //扫描线yEdgeNode *head; //边链表的头指针};//桶结点typedef struct Bucket{int y; //扫描线yEdgeNode *head; //边链表的头指针Bucket *next; //下一个桶的指针} EdgeTable;int compare(Point p1, Point p2);Line* create_lines(Point points[], int n);Point get_lowest_point(Line lines[], int n);Point get_highest_point(Line lines[], int n);void swap(Line &l1, Line &l2);void sort(Line lines[], int n);EdgeTable* create_edge_table(Line lines[], int n);ActiveEdgeTable* init_active_table(EdgeTable *edge_table);void delete_edge(ActiveEdgeTable *active_table, int y_max);void add_edge(ActiveEdgeTable *active_table, EdgeNode edge);ActiveEdgeTable* update_active_table(ActiveEdgeTable *active_table, EdgeTable *edge_table);void DrawPolygon(Point points, int n);void DrawGrid(int x, int y);void Fill(Point points[], int n);void Initial();void Display();int main(int argc, char* argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(400, 300);glutInitWindowPosition(100, 120);glutCreateWindow("Polygon Filling");glutDisplayFunc(Display);Initial();glutMainLoop();return 0;}//比较2个点的高度int compare(Point p1, Point p2){if (p1.y > p2.y)return 1;else if (p1.y == p2.y)return 0;return -1;}//由点数组生成线段数组Line* create_lines(Point points[], int n){Line *lines = (Line*)malloc(n * sizeof(Line));for (int i = 0; i < n; ++i){Point p1 = points[i];Point p2 = points[(i + 1) % n];int result = compare(p1, p2);if (result == 0)lines[i].is_active = 0;elselines[i].is_active = 1;lines[i].high_point = result > 0 ? p1 : p2;lines[i].low_point = result < 0 ? p1 : p2;lines[i].inverse_k = (double)(p2.x - p1.x) / (double)(p2.y - p1.y);}return lines;}//获取线数组中最低的端点Point get_lowest_point(Line lines[], int n){Point lowest_point = lines[0].low_point;for (int i = 1; i < n; ++i){Point low_point = lines[i].low_point;if (compare(lowest_point, low_point) > 0)lowest_point = low_point;}return lowest_point;}//获取线数组中最高的端点Point get_highest_point(Line lines[], int n){Point highest_point = lines[0].high_point;for (int i = 1; i < n; ++i){Point high_point = lines[i].high_point;if (compare(highest_point, high_point) < 0)highest_point = high_point;}return highest_point;}//交换2个Line对象void swap(Line &l1, Line &l2){Line temp = l1;l1 = l2;l2 = temp;}//对线数组进行排序void sort(Line lines[], int n){//先按低端点的y坐标进行升序排序for (int i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; j < n; ++j){if (lines[j].low_point.y < lines[min_index].low_point.y)min_index = j;}swap(lines[i], lines[min_index]);}//再将有序数组按低端点的x坐标升序排列,若x坐标相等,按inverse_k升序for (i = 0; i < n; ++i){int min_index = i;for (int j = i + 1; lines[j].low_point.y == lines[i].low_point.y; ++j){if (lines[j].low_point.x < lines[min_index].low_point.x)min_index = j;}swap(lines[i], lines[min_index]);if (i > 0 && lines[i].low_point.x == lines[i - 1].low_point.x){if (lines[i].is_active == 1 && lines[i - 1].is_active == 1){if (lines[i].inverse_k < lines[i - 1].inverse_k)swap(lines[i], lines[i - 1]);}}}}//创建一个边表EdgeTable* create_edge_table(Line lines[], int n){EdgeTable *edge_table = (EdgeTable*)malloc(sizeof(EdgeTable));edge_table->head = NULL;edge_table->next = NULL;sort(lines, n);Point lowest_point = get_lowest_point(lines, n);Point highest_point = get_highest_point(lines, n);EdgeTable *s = edge_table;for (int i = lowest_point.y; i <= highest_point.y; ++i){Bucket *bucket = (Bucket*)malloc(sizeof(Bucket));bucket->y = i;bucket->next = NULL;bucket->head = (EdgeNode*)malloc(sizeof(EdgeNode));bucket->head->next = NULL;EdgeNode *p = bucket->head;for (int j = 0; j < n; ++j){if (lines[j].is_active == 0)continue;if (lines[j].low_point.y == i){EdgeNode *q = (EdgeNode*)malloc(sizeof(EdgeNode));q->x = lines[j].low_point.x;q->y_max = lines[j].high_point.y;q->inverse_k = lines[j].inverse_k;q->next = NULL;p->next = q;p = q;}}s->next = bucket;s = bucket;}return edge_table;}//从边表中取出第一个不为空的桶初始化有效边表ActiveEdgeTable* init_active_table(EdgeTable *edge_table){ActiveEdgeTable *active_table = (ActiveEdgeTable*)malloc(sizeof(ActiveEdgeTable));active_table->y = edge_table->next->y;active_table->head = (EdgeNode*)malloc(sizeof(EdgeNode));active_table->head->next = NULL;EdgeNode *p = edge_table->next->head;EdgeNode *q = active_table->head;while (p->next != NULL){EdgeNode *s = (EdgeNode*)malloc(sizeof(EdgeNode));s->x = p->next->x;s->y_max = p->next->y_max;s->inverse_k = p->next->inverse_k;s->next = NULL;q->next = s;q = s;p = p->next;}return active_table;}//从有效边表中删除指定y_max的边结点void delete_edge(ActiveEdgeTable *active_table, int y_max){EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if (q->y_max == y_max){p->next = q->next;free(q);}elsep = p->next;}}//将一个边结点按次序添加到有效边表中void add_edge(ActiveEdgeTable *active_table, EdgeNode edge){EdgeNode *t = (EdgeNode*)malloc(sizeof(EdgeNode));t->x = edge.x;t->y_max = edge.y_max;t->inverse_k = edge.inverse_k;t->next = NULL;EdgeNode *p = active_table->head;while (p->next != NULL){EdgeNode *q = p->next;if ((edge.x < q->x) || (edge.x == q->x && edge.inverse_k < q->inverse_k)){p->next = t;t->next = q;return;}p = p->next;}p->next = t;}//更新有效边表,并与边表中对应的桶合并ActiveEdgeTable* update_active_table(ActiveEdgeTable *active_table, EdgeTable *edge_table) {//更新扫描线y++active_table->y;//删除y=ymax的边delete_edge(active_table, active_table->y);//更新边结点的数据EdgeNode *p = active_table->head->next;while (p != NULL){p->x += p->inverse_k;p = p->next;}//找到边表中对应的桶EdgeTable *q = edge_table;while ((q = q->next) != NULL && q->y != active_table->y);//如果找到,则进行合并if (q != NULL){EdgeNode *s = q->head;while ((s = s->next) != NULL){add_edge(active_table, *s);}}return active_table;}//画出多边形的边框void DrawPolygon(Point points[], int n){glBegin(GL_LINE_LOOP);for (int i = 0; i < n; ++i)glVertex2i(points[i].x, points[i].y);glEnd();}//画出x * y的网格void DrawGrid(int x, int y){glBegin(GL_LINES);//横线for (int i = 0; i <= y; ++i){glVertex2d(0, i);glVertex2d(x, i);}//竖线for (i = 0; i <= x; ++i){glVertex2d(i, 0);glVertex2d(i, y);}glEnd();}//用指定的像素大小填充多边形void Fill(Point points[], int n){Line *lines = create_lines(points, n);EdgeTable *edge_table = create_edge_table(lines, n);ActiveEdgeTable *active_table = init_active_table(edge_table);while (active_table->head->next != NULL){EdgeNode *p = active_table->head;int b = -1;while (p->next != NULL){if (b > 0){int left = p->x;int right = p->next->x;//如果不是局部最低点,则进行边界处理if (!(p->x - p->next->x >= -EPSILON && p->x - p->next->x <= EPSILON)){//处理左边界if (!(p->x - left >= -EPSILON && p->x - left <= EPSILON))left += 1;//处理右边界if (p->next->x - right >= -EPSILON && p->next->x - right <= EPSILON)right -= 1;}for (int i = left; i <= right; ++i){glBegin(GL_POINTS);glVertex2d(i, active_table->y);glEnd();glFlush();Sleep(50);}}p = p->next;b = -b;}active_table = update_active_table(active_table, edge_table);}}//初始化窗口,x和y指定窗口的坐标大小void Initial(){glClearColor(1.0f, 1.0f, 1.0f, 1.0f);glMatrixMode(GL_PROJECTION);gluOrtho2D(0.0, 20.0, 0.0, 15.0);}//窗口的显示回调函数void Display(){//使用当前背景色填充窗口glClear(GL_COLOR_BUFFER_BIT);//使用灰色画出网格线glColor3f(0.75f, 0.75f, 0.75f);DrawGrid(20, 14);glFlush();//多边形的顶点坐标Point points[] = { { 3, 1 },{ 6, 5 },{ 8, 1 },{ 12, 9 },{ 7, 8 },{ 3, 12 },{ 1, 7 } };//计算顶点个数int n = sizeof(points) / sizeof(Point);//使用黑色画出多边形的边框glColor3f(0.0f, 0.0f, 0.0f);DrawPolygon(points, n);glFlush();//指定点大小glPointSize(6.0f);//使用红色填充多边形glColor3f(1.0f, 0.0f, 1.0f);Fill(points, n);glFlush();}。
