杆件内力及内力图的绘制
合集下载
杆件的内力图课件
ห้องสมุดไป่ตู้2
杆件内力图的绘制方法
截面法
定义截面
在杆件上选择一个截面， 该截面可以是垂直于杆件 轴线的平面，也可以是与
杆件轴线平行的平面。
计算截面内力
通过计算或实验得到截面 上的内力，包括轴力、剪
力、弯矩等。
绘制内力图
将截面内力按照一定的比 例尺绘制成图，通常采用 直角坐标系或极坐标系。
积分法
01
02
03
04
杆件内力图的实际应用案例
桥梁结构中的内力图分析
桥梁是内力图分析的重要对象之一，通 过对桥梁结构进行内力图分析，可以确 定桥梁的承载能力、刚度和稳定性等性
能指标。
在进行桥梁内力图分析时，通常需要考 虑多种荷载工况，例如车辆荷载、风荷 载和地震荷载等，以便全面评估桥梁的
安全性和可靠性。
内力图分析在桥梁结构优化设计和维护 保养方面也具有重要意义，可以通过对 桥梁结构进行内力图分析，发现潜在的 结构缺陷和安全隐患，及时采取相应的
内力图与外力图的关系
总结词
内力图和外力图是相互关联的，它们共 同反映了杆件的受力情况。
VS
详细描述
外力图表示杆件所受到的外力的大小和方 向，而内力图则表示杆件内部受力分布情 况。两者之间存在一定的关系，通常情况 下，外力图和内力图是相互匹配的，以确 保杆件在给定边界条件下达到平衡状态。 在分析过程中，需要综合考虑外力、约束 和惯性等影响因素。
定义积分域
选择杆件上的一段或多段 作为积分域，该积分域可 以是直线段、圆弧段或复 杂曲线段。
计算应力分布
根据材料力学和弹性力学 知识，计算出积分域内各 点的应力分布情况。
积分得到内力
将积分域内的应力分布乘 以面积元，并对整个积分 域进行积分，得到整个杆 件的内力。
杆件的内力分析与内力图
F M
y
0 0
C
F l a FS FA l F l a M FA x x l
由其右边分离体的平衡条件同样可得 a FA m F 0
F
y
FB B
FS F FB 0 F l a FS F FB l
A y FA
x
m
m M 切向应力的合力， C A 称为剪力 x m FS x FS m MC 0 M C m M F a x FB l x 0
1 1 FN1
60kN
2
A
30kN
B
x
FN2
2
C
60kN
解：1、计算杆件各段的轴力。 AB 段
X 0
BC 段
FN1 30 0
FN1=30kN
1 30kN
2
X 0
FN2 60 0
FN2= 60kN
+
FN图
2、绘制轴力图。
60kN
| FN |max=60 kN
第三节 扭转和扭矩图
x
Fab l
由剪力、弯矩图知： 在集中力作用点，弯 矩图发生转折，剪力 图发生突变，其突变 值等于集中力的大小， 从左向右作图，突变 方向沿集中力作用的 方向。
Fa l
x
M
三. 弯矩、剪力与分布荷载集度之间的关系及其应用
y O m m x q(x) n n dx F Me x M ( x) m FS(x) m n M(x)+dM(x) C n FS(x)+dFS(x)
1分钟me作功
W ' M e M e (2n 1) 2nMe
杆及杆系的内力及内力图
内力仍可按变形前的原始尺寸来计算。这就是所谓的原始尺寸原理。
end
图中的坐标原点为截面形心, x轴沿杆的轴线并和截面的外向法线同 向，y轴和z轴则分别是截面的形心主惯轴。 内力：
N 引起拉伸或压缩变形,称轴力; Mn 引起扭转变形,称扭矩; Qy和Qz 引起剪切变形,称剪力; My和Mz引起弯曲变形,称弯矩。
0 x1 a 0 x1 a a x2 l
a x2 l
(3)按上述表达式在x 的定义域内作图，即得所求的剪力图和弯矩图，如 图(c)所示。
end
需要指出的是：按照某些工程习惯，常要求弯矩图画在 梁的受拉一侧，以提醒某些脆性材料性材料的梁(如混凝土梁) 常因受拉破坏而需在该侧配置钢筋。
Q2 RA m / l
(a x1 l)
M2 RA x2
m / l x2 m
a x2 l
end
例4-3 作图示的简支梁在均布荷载q作用下的剪力图和弯矩图。
解：
q
1 Q1 RA qx 2 ql qx
A x
B
l
(0 x l)
M
RAx
1 2
qx2
ql 2
1 qlx 1 qx2 (0 x l)
(M
dM
)
0
在上式中略去二阶微量后，得：dM Qdx
所以 dM / dx Q
(4-5)
d 2M / dx2 q
(4-6)
q(x)
P
m
x
dx
(a)
q(x)
M
M+dM
Q
Q+dQ
dx
(b)
以上三式即为梁核所作的Q 、M 图是否正确；
熟练地掌握后，也可在求出反力后，直接利用此关系方便地作出梁的 内力图来。
end
图中的坐标原点为截面形心, x轴沿杆的轴线并和截面的外向法线同 向，y轴和z轴则分别是截面的形心主惯轴。 内力：
N 引起拉伸或压缩变形,称轴力; Mn 引起扭转变形,称扭矩; Qy和Qz 引起剪切变形,称剪力; My和Mz引起弯曲变形,称弯矩。
0 x1 a 0 x1 a a x2 l
a x2 l
(3)按上述表达式在x 的定义域内作图，即得所求的剪力图和弯矩图，如 图(c)所示。
end
需要指出的是：按照某些工程习惯，常要求弯矩图画在 梁的受拉一侧，以提醒某些脆性材料性材料的梁(如混凝土梁) 常因受拉破坏而需在该侧配置钢筋。
Q2 RA m / l
(a x1 l)
M2 RA x2
m / l x2 m
a x2 l
end
例4-3 作图示的简支梁在均布荷载q作用下的剪力图和弯矩图。
解：
q
1 Q1 RA qx 2 ql qx
A x
B
l
(0 x l)
M
RAx
1 2
qx2
ql 2
1 qlx 1 qx2 (0 x l)
(M
dM
)
0
在上式中略去二阶微量后，得：dM Qdx
所以 dM / dx Q
(4-5)
d 2M / dx2 q
(4-6)
q(x)
P
m
x
dx
(a)
q(x)
M
M+dM
Q
Q+dQ
dx
(b)
以上三式即为梁核所作的Q 、M 图是否正确；
熟练地掌握后，也可在求出反力后，直接利用此关系方便地作出梁的 内力图来。
杆件的内力与内力图轴向拉压杆的内力轴力图轴向拉压杆的内力轴
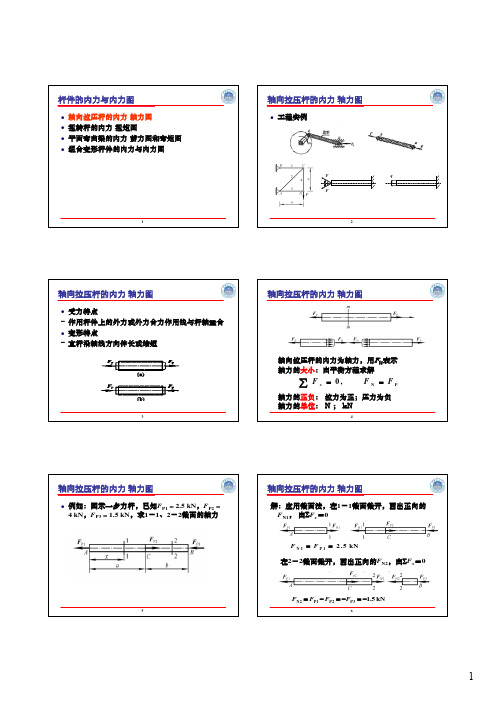
Fθθ34轴向拉压杆的内力轴向拉压杆的内力为轴力，用F N 表示轴力的大小：由平衡方程求解PN ,0F F F x ==∑轴力的正负：拉力为正；压力为负轴力的单位：N ；kN6轴向拉压杆的内力轴力图解：应用截面法，在F N1，由∑F x ＝0kN5.21P 1N ==F F kN5.13P 2P 1P 2N -=-=-=F F F F 在2－2截面截开，画出正向的F N2，由∑F x ＝089= 6 kN = -4 kN轴力图画在受力图正下方；10轴向拉压杆的内力轴力图例2 图示一砖柱，柱高3.5m ，截面尺寸370×370mm 2，柱顶承受轴向力F P ＝60 kN ，砖砌体容重ρ.g ＝18 kN/m 3。
试绘柱的轴力图。
11轴力图应用截面法，由平衡方程求得：kN46.260P y y A g F --=⋅⋅⋅-ρ,kN 6.68)5.3(,kN 60)0N -=-=F ㈠F N /kNy68.66012轴向拉压杆的内力轴力图等截面直杆在上端A 处固定，其受力如图试绘制杆件的轴力图。
kN,10kN,5P2=F l(a)Cl（b）机械传动轴杆件各相邻横截面产生绕杆轴的相对转动ϕ1720扭矩沿轴线的变化规律e21221. 外力偶矩的计算m N ⋅=1146AmN ⋅=3509549n PB m N ⋅=446n D23扭矩的计算m N 350e ⋅-=-=B M m N 700e e ⋅-=--B C M M mN 446e ⋅=D M 扭矩图问题：如将轮A 与轮C 互换，扭矩图如何？哪种布置受力更合理？mN 700max ⋅=轴力图剪力图和弯矩图组合变形杆件的内力与内力图25梁的外力和内力均可仅由静力平衡方程求解27纵向对称面内时，梁的轴线由位于纵向对称面内的直28单跨静定梁的三种基本形式由静力平衡方程无法全部确定梁所有外力和内力29平面弯曲梁的内力剪力图和弯矩图：剪力F S 和弯矩M 求内力的方法：截面法A F R =M MaF A R =30平面弯曲梁的内力剪力图和弯矩图单位；kNN ·m ；kN ·m31截面，并取右段研究221qa -33平面弯曲梁的内力剪力图和弯矩图剪力方程剪力沿梁轴线的变化规律，即F S =F S (x )弯矩方程弯矩沿梁轴线的变化规律，即M=M (x )按比例绘出F S (x )的图线按比例绘出M (x )的图线剪力图和弯矩图受力分析，画受力图，由平衡方程求支座约束力分段列出剪力方程和弯矩方程，标出变量x 的取值根据剪力方程，求各控制面的剪力值，按比例绘剪力图。
第六章 杆件的内力内力图
3.求特殊点内力值，作剪力图和弯矩图。
M a） Ma / l （
例6-11 简支梁受均布载荷作用试写出剪力和弯矩方程，并画
出剪力图和弯矩图。
y
q
解：1．求约束反力 B
x
A x
FAY
FAy＝ FBy＝ ql/2 2．写出剪力和弯矩方程
C
l
FBY
FQ ql / 2
FQ x ＝ql / 2 qx 0 x l
2
（2）求特殊点内力值，画剪力图和弯矩图
x
FQ 0 ＝0
FQ l ＝ql
ql / 2M 0＝0 M l/2 ＝ql 2 / 8 M l ＝ql 2 / 2
M
ql 2 / 8
x
由剪力图、弯矩图可见，最大剪力
和弯矩分别为
FQ max ＝ql
M max＝ql 2 / 2
25
FN1 F1 0
FN1 F1 10kN
FN1 FN2 F2 F2
10
Fx 0
FN 2 F2 F1 0
FN 2 F1 F2 10kN
F1
F3
+ _
10
Fx 0
FN 3 F1 F2 F3 0
FN 3 F1 F2 F3 25kN
剪力和弯矩都可表示为x的函数， FQ = FQ (x) ，M = M (x)。 称为梁的剪力方程和弯矩方程。 一般，剪力方程和弯矩方程是x的分段函数，集中力、集 中力偶、分布力的起点和终点为函数分段点。
剪力、弯矩图：表示剪力、弯矩沿轴线的变化规律的图形。 FQ = FQ (x) ，M = M (x)
压力向下画，最后归零。
第五章 杆件的内力与内力图(陆)
FQ Fp FP a / l FQ Mz
(a≤x≤l)
FPba / l
Mz
例 3： 已知m，求FQ(x)和 Mz (x)。并画出 FQ图和 Mz 图。 m
a
b 解： 1°求支座反力 FRA = FRB = m / l 2°求FQ(x)和 Mz (x)。 AC: FQ(x) = - FRA = - m / l (0＜x＜ a)
3°画 FQ(x)图和 Mz (x)图。 AC: FQ(x) = FRA = FPb / l (0＜x＜ a) Mz (x) = FRAx = FPbx / l (0≤x≤ a) BC: FQ(x) = FRA -FP= FPb / l -FP= -FP a / l (a＜x＜ l)
Mz (x) = FRAx - FP (x -a)= Fpa(l - x) / l FPb / l
60 20 x = 3.6m
Mz 4 =72 ×10-160-160×4 = - 80 KNm
Mz 5 = Mz 4 = - 80 KNm
72
Mz 6 = 72×12 - 160 - 20×10×5 -148×2= 0 FQy
(KN)
当FQ（x）=0时， Mz （x）有极值。 x = 3.6ｍ处， FQ（x）=0 。
1 2m 160KNm 23 20KN 20KN/m 4 5 8m 2m 6
C
B D FRB
BD q = c（＜0） 斜直线（ ） ）
∑MB= 0，FRA= 72 KN. 2°画FQ、M图。
分段 q AC q=0 水平线
CB q = c（＜0） 斜直线（ ） 下凸曲线（ ）
FQ 图 Q
M 图 斜直线（
A
FRA
x
c
(a≤x≤l)
FPba / l
Mz
例 3： 已知m，求FQ(x)和 Mz (x)。并画出 FQ图和 Mz 图。 m
a
b 解： 1°求支座反力 FRA = FRB = m / l 2°求FQ(x)和 Mz (x)。 AC: FQ(x) = - FRA = - m / l (0＜x＜ a)
3°画 FQ(x)图和 Mz (x)图。 AC: FQ(x) = FRA = FPb / l (0＜x＜ a) Mz (x) = FRAx = FPbx / l (0≤x≤ a) BC: FQ(x) = FRA -FP= FPb / l -FP= -FP a / l (a＜x＜ l)
Mz (x) = FRAx - FP (x -a)= Fpa(l - x) / l FPb / l
60 20 x = 3.6m
Mz 4 =72 ×10-160-160×4 = - 80 KNm
Mz 5 = Mz 4 = - 80 KNm
72
Mz 6 = 72×12 - 160 - 20×10×5 -148×2= 0 FQy
(KN)
当FQ（x）=0时， Mz （x）有极值。 x = 3.6ｍ处， FQ（x）=0 。
1 2m 160KNm 23 20KN 20KN/m 4 5 8m 2m 6
C
B D FRB
BD q = c（＜0） 斜直线（ ） ）
∑MB= 0，FRA= 72 KN. 2°画FQ、M图。
分段 q AC q=0 水平线
CB q = c（＜0） 斜直线（ ） 下凸曲线（ ）
FQ 图 Q
M 图 斜直线（
A
FRA
x
c
第六章 杆件的内力与内力图
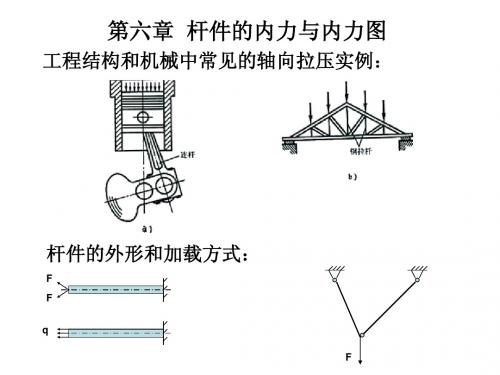
截面法求内力举例：求杆AB段和BC段的内力
FP1=2.5kN A FP1=2.5kN 1 FP2=4kN C FN1 2 FP3=1.5kN
1
2
B
x
Σ X = 0 → FN1 - FP1 = 0
FP1=2.5kN FP2=4kN
FN1=2.5kN
FN2
Σ X = 0 → FN 2 + FP 2 - FP1 = 0
适用于求桁架中某些指定杆件的内力
求 解 要 点
例6-4 试求图中桁架中杆1和杆2的轴力。
Ⅰ Ⅱ
4m 2 1 A Ⅰ 8kN 16kN Ⅱ 16kN 4x3m 16kN FN1 A 8kN 8kN 16kN
B
Σ Fy = 0 FN 1 = -8kN
FN2 B 8kN 16kN
Σ Fy = 0 FN 2 5 = ´ 8kN = 10kN 4
FN2=-1.5kN
6-1-2 轴力图
表示轴力沿杆件轴线方向变化的图形，称为 轴力图（diagram of normal force）。
A
1 B 1Fp2
2 C 2 Fp3
Fp1
Fp1
FN1 FN2 Fp2 FN3
已知Fp1=6kN；Fp2=18kN； Fp3=8kN；Fp4=4kN;试画出 Fp4 图示杆件的轴力图。 3 解：1、计算各段的轴力。 Σ Fx = 0 AB段 FN1 = Fp1 = 6kN
例传动轴如图所示，主动轮A输入功率PA= 36KW，从动轮B、 C、D输出功率分别为 PB= PC =11KW ， PD= 14KW，转速 n = 300r/min。试作该轴的扭矩图。
MeC MeA MeD
先计算外力偶矩
PA 1146 N m n P M eB M eC 9549 B 350 N m n P M eD 9549 D 446 N m n M eA 9549
第五章 杆件的内力与内力图
Mz (x) = m - FRAx = m (l -x ) / l (a ＜ x≤ l ) 3°画 FQy (x)图和 Mz (x)图。
四、剪力、弯矩和荷载集度之间的关系
y FP
q(x) MZ(x) q(x) MZ(x)+d MZ(x) C FQY(x)+d FQY(x) dx
x
x dx
FQY(x)
FRA FQy
(KN)
FRB
60 20 x = 3.6m
Mz6 = 72 ×12 - 160 - 20×10 ×5 = 0
88
当FQY（x）=0时， Mz （x）有极值。
Mz x = 3.6ｍ处， FQY（x）=0 。(KNm)
16 113.6 144
80
即
Mz7 = 72 ×5.6 - 160 - 20×3.6 ×3.6 / 2 = 113.6 KNm
MZ —— 弯矩
A FRA
x
m
C
MZ
m FQY
规 定：
∑FP
FQY 下剪力正, 反之为负
∑M
MZ
MZ
∑M
MZ：
上凹下凸弯矩正, 反之为负
a A
FP1
m m
FP2 B
由∑Fyi=0， FRA- FP1 - FQY =0
x
FRA y A
x
FRB FP1
m
C
得 FQY = FRA- FP1
x = 2m 时 , FN (x) = - 1KN。
3KN
A 2m 3
B 2KN/ m C 2m 2m
D 1KN
FN （KN） 1
规律：没有力作用的杆段，轴力为常数；
分布荷载为常数的杆段，轴力线性变化；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(2) 计算1-1 利用计算剪力和弯矩的规律，由1-1截面左侧外力计
Q1=RA=-2000N(负剪力) M1=RA×200=-400N·m(负弯矩) (3) 计算2-2 利用计算剪力和弯矩的规律，由2-2截面的右侧外力
Q2=q×0.4-RB=-4000N (负剪力) M2=RB×0.4-q×0.4×0.2=2400N·m(正弯矩)
从所作的内力图知，若a>b，则在CB段任一截面上的 剪力值都相等且比AC段的要大，其值｜Qmax｜=Pa/l，最 大弯矩发生在集中力P作用的截面上，其值｜Mmax｜ =Pab/l
如果集中力P作用在梁的跨中，即a=b=l/2
｜Qmax｜=P/2 ｜Mmax｜=Pl/4
【例 7.7】简支梁受集中力偶m作用如图17(a)所示，试画
Q(x)=RA=m/l (a≤x<l) M(x)=RAx-m=m/lx-m(a<x≤l) (3) 画剪力图 从式(a)和式(c)可知，AC段和CB段的剪力为常数m/l， 剪力图是一条在x轴线上侧与x轴平行的直线。剪力图如 图17(b)
【例 7.8】外伸梁受荷载作用如图18(a)所示，试画出梁的
∑Fy=0，RB-Q1=0
Q1=RB=-2P ∑m1(F)= 0，M1-Me=0
M1=Me=Pa 计算结果Q1为负，表明Q1实际方向与图示假设方向 相反，故为负剪力；M1为正，表明M1实际方向与图示假
(3) 求截面2-2
用2-2截面将梁假想地截开，取右段为研究对象，受 力图如图12(c)。由平衡方程求Q2和M2
剪力图和弯矩图的画法与轴力图、扭矩图很相 似，用平行于梁轴的横坐标x表示梁横截面的位置， 用垂直于梁轴的纵坐标表示相应截面的剪力和弯矩。
在土建工程中，习惯上将正剪力画在x轴上方， 负剪力画在x轴的下方；正弯矩画在x轴下方，负弯 矩画在x轴的上方，即把弯矩图画在梁受拉的一侧。
3. 绘制剪力图和弯矩图的步骤
图10
3. 用截面法求指定截面的剪力和弯矩
利用截面法计算指定截面的剪力和弯矩的步骤
（1） （2） 用假想的截面在欲求内力处将梁截成两段，
（3） 画出研究对象的内力图。截面上的剪力和
（4）
【例 1】简支梁如图11(a)所示。已知P1=36kN，P2=30kN， 试求截面I－I
【解】(1)
以整梁为研究对象，受力图如图11(a)。列平衡方程
截面m－m上剪力Q的大小和方向以及弯矩M的
∑Fy=0，NB-Q=0 Q=NB ∑mC(F)= 0，NB·x-M=0 M=NB·x 根据作用力和反作用力的关系，分别以梁的左 段和右段为研究对象求出的Q和M，大小是相等的， 而方向或转向是相反的(图8(b)、(c))。
图8
2. 剪力和弯矩和正负号规定
∑Fy=0，Q2-P=0 Q2=P(正剪力) ∑m2(F)= 0，-M2-P·a/2=0 M2=-Pa/2 (负弯矩)
图11
图12
图12
图12
4. 计算剪力和弯矩的规律
(1) 梁内任一截面上的剪力，其大小等于该截面 左侧(或右侧)梁上所有外力的代数和；梁内任一截面 的弯矩，其大小等于该截面左侧(或右侧)梁上所有外
【例 7.6】简支梁受集中力P作用如图16(a)所示，试画出 梁的剪力图和弯矩图。 【解】(1)
∑mB(F)= 0，-RAl+Pb=0 RA=Pb/l ∑Fy=0，RA+RB-P=0 RB=Pa/l (2) 列剪力方程和弯矩方程 梁在C截面处有集中力P作用，AC段和CB段所受的 外力不同，其剪力方程和弯矩方程也不相同，需分段列 出。取梁左端A
由 ∑Fy=0，Q1+RB-P2=0
得 Q1=P2-RB=(30-26)kN=4kN 由 ∑m1(F)=0，RB×4-P2×2-M1=0 得 M1=RB×4-P2×2=(26×4-30×2)kN·m
=44kN·m 可见，不管选取梁的左段或右段为研究对象，所得 截面I-I
【例 2】外伸梁受载荷作用如图12(a)所示。图中截面1-1 是指从右侧无限接近于支座B。试求截面1-1和截面2-2的
图7
二、 梁的内力-剪力和弯矩
1. 剪力和弯矩
图8(a)为一简支梁，载荷P与支座反力NA和NB是 作用在梁纵向对称面内的平衡力系。现用截面法分 析任一截面m－m上的内力。
梁的横截面上的内力比较复杂，一般存在两个
（1） 剪力Q 相切于横截面的内力。剪力的
（2） 弯矩M 矩。
作用面与横截面垂直的内力偶
由 ∑Fy=0，RA-P1-Q1=0 得 Q1=RA-P1=(40-36)kN=4kN 由 ∑m1(F)=0，M1+P1×1-RA×2=0 得 M1=RA×2-P1×1
=(40×2-36×1)kN·m=44kN·m 计算结果Q1、M1为正，表明Q1、M1实际方向与图示
若取梁的右段为研究对象，受力图如图11(c)所示。
【例7.5】简支梁如图15(a)所示，受均布荷载q作用，试画
【解】(1) 求支座反力
RA=RB=ql/2 (2)
坐标原点取在左端A点处，距原点A为x处的任意截
Q(x)=RA-qx=ql/2-qx(0＜x＜l) M(x)=RAx-qx2/2=ql/2x-qx2/2 (0≤x≤l)
(3)
由式(a)可见，Q(x)是x的一次函数，所以剪力图是一 条斜直线。由式(a)
图13
三、 剪力图和弯矩图
1. 剪力方程和弯矩方程
若以横坐标x表示横截面在梁轴线上的位置，则 各横截面上的剪力和弯矩皆可表示为坐标x的函数，
Q=Q(x) M=M(x) 以上两函数表达了剪力和弯矩沿梁轴线的变化 规律，分别称为梁的剪力方程和弯矩方程
2. 剪力图和弯矩图
为了形象地表示剪力和弯矩沿梁轴的变化规律， 把剪力方程和弯矩方程用其图像表示，称为剪力图 和弯矩图
(1) 正剪力：截面上的剪力使研究对象作顺时针方
向的转动(图7(a)) 负剪力：截面上的剪力使研究对象作逆时针方
向的转动(图7(b)) (2) 弯矩的正负号规定
正弯矩：截面上的弯矩使该截面附近弯成上凹 下凸的形状(图10(a))
(b))
图7
x=0，QA右=ql/2 x=l，QB左=-ql/2 剪力图如图15(b)
由式(b)可见，M(x)是x的二次函数，所以弯矩图是一 条二次抛物线，至少需要确定三个控制截面的弯矩值， 才能描出曲线大致形状。由式(b)
x=0，MA=0 x=l/2，MC=ql2/8 x=l，MB=0 弯矩图如图15(c) 从所作的内力图可知，最大剪力发生在梁端，其值 为｜Qmax｜=ql/2，最大弯矩发生在剪力为零的跨截面， 其值为｜Mmax｜=ql2/8。
(4) 画弯矩图
从式(b)可知，AC段的弯矩是x的一次函数，弯矩图 是一条斜直线，只需确定该段始末两个控制截面的弯矩 值，就能画出该段的弯矩图。由式(b)
x=0，MA=0 x=a，MC=Pab/l 从式(d)可知，CB段的弯矩是x的一次函数，弯矩图 也是一条斜直线，由式(d)
x=a，MC=Pab/l x=l，MB=0
图5
图6
3. 梁的类型
根据梁的支座反力能否全部由静力平衡条件确 定，将梁分为静定梁和超静定梁。静定梁又可分为 单跨静定梁和多跨静定梁
单跨静定梁按支座情况可分三种基本类型： （1） 简支梁梁的一端为固定铰支端，另一端为 活动铰支座(图7(a)) （2） 外伸梁其支座形式和简支梁相同，但梁的 一端或两端伸出支座之外(图7(b)) （3） 悬臂梁梁的一端固定，另一端自由(图 7(c))
(1) 求支座反力 以梁整体为研究对象，根据梁上的荷载和支座
(2) 将梁分段 以集中力和集中力偶作用处、分布荷载的起讫
处、梁的支承处以及梁的端面为界点，将梁进行分
(3) 各段列剪力方程和弯矩方程时，所取的坐标原
点与坐标轴x的正向可视计算方便而定，不必一致。
(4)
先根据剪力方程(或弯矩方程)判断剪力图(或弯 矩图)的形状，确定其控制截面，再根据剪力方程(或 弯矩方程)计算其相应截面的剪力值(或弯矩值)，然 后描点并画出整个全梁的剪力图(或弯矩图)
(2) 左上右下，剪力为正；左顺右逆，弯矩为正。 (3)
【例 3】简支梁受载荷作用如图13所示。已知集中力 P=1000N，集中力偶m=4kN·m，均布载荷q=10kN/m，试 求1-1和2-2 【解】(1) 求支座反力
以整梁为研究对象，受力图如图13所示，由平衡方
∑mB(F)=0，P×750-RA×1000-m+q×500×250=0 RA=(P×750-m+q×500×250)/1000=-2000N ∑Fy=0，RA-P-500q+RB=0 RB=P+500q-RA=8000N
【解】(1) 以整梁为研究对象，受力图如图12(a)。由平衡方程
∑mB(F)=0，RC·a-P×2a-Me=0 RC=(2Pa+Me)/a=（2Pa+Pa）/a=3P ∑mC(F)=0，-RB·a-Pa-Me=0 RB=(-Pa-Me)/a=(-Pa-Pa)/a=-2P
(2) 求截面1-1
用1-1截面将梁假想地截开，取左段为研究对象，受 力图如图12(b)。由平衡方程求Q1和M1
由 ∑mA(F)= 0，RB×6-P1×1-P2×4=0 得 RB=（P1×1+P2×4）/6=26kN 由 ∑mB(F)= 0，P1×5+P2×2-RA×6=0 得 RA=(P1×5+P2×2)/6=40kN (2) 求截面I-I的内力
用I-I截面将梁假想地截开，取左段为研究对象，受 力图如图11(b)
AC
Q(x)=RA=Pb/l (0<x<a) M(x)=RA·x=Pb/lx(0≤x≤a) CB
Q(x)=RA-P=-Pa/l (a<x<l) M(x)=RA·x-P(x-a)=Pa-Pa/lx(a≤x≤l) (3) 画剪力图 从式(a)可知，AC段的剪力为常数Pb/l，剪力图是一 条在x轴线上侧与x轴平行的直线。从式(c)可知，CB段的 剪力为常数-Pa/l，剪力图是一条在x轴线下侧与x轴平行的 直线。画出剪力图如图16(b)