一元方程求根公式
一元方程求根公式
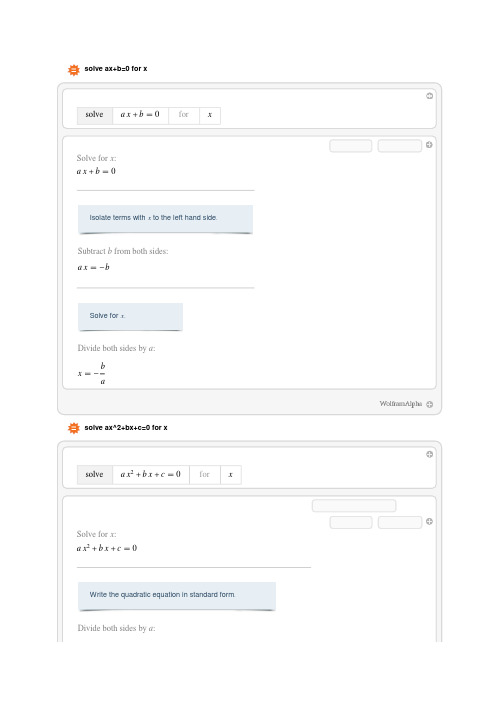
solve ax+b=0 for xIsolate terms with x to the left hand side. Solve for x.solve ax^2+bx+c=0 for xWrite the quadratic equation in standard form.２Solve the quadratic equation by completing the square.Take one half of the coefficient ofx and square it,then add it to both sides.Factor the left hand side.Eliminate the exponent on the left hand side.Look at the first equation:Solve for x.Look at the second equation:Solve for x.solve ax^3+bx^2+cx+d=0 for xLook for a simple substitution that eliminatesthe quadratic term of a x3 b x2 c x d.Write the cubic polynomial on the left hand side in standardWrite the cubic equation in standard form.Change coordinates by substituting y z Κz,whereΚis a constant value that will be determined later.Transform the rational equation into a polynomial equationFind an appropriate value forΚin order to make the coefficients of z2and z4both４Solve for u.Perform back substitution on u154a39a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4.Move everything to the left hand side.Divide by an appropriate factor to make the constant Write 54a3z3 9a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4with a common power.Simplify 54a3z3 9a b c 2b3 27a2d 33a ６Simplify 54a3z3 9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d21 0by making a substitution.Solve for v.Look at the first equation:Perform back substitutionSolve for z.８Perform back substitution on19a b c 2b3 27a2d 33az323a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution onPerform back substitution on3 b2 3a c 3a9a b c 2b3 27a2d 33ay 24a c3 b2c2 4b3d 18a b c d 27a2d21^ 1 3323a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 .Solve for x.Look at the second equation:１０Look at the second equation:3.Perform back substitution on v 1Solve for z.Perform back substitution onz13a1239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for y.Perform back substitution on y 1 2 323 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 31 3a1 239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.Look at the third equation:Perform back substitution on v 1 2 3.Solve for z.Perform back substitution on1z323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution on1y323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 23 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.。
一元二次方程式的求根公式
一元二次方程是形如ax²+bx+c=0的一元二次方程式，求解这种方程的根一直是数学学习中的重点和难点。
幸运的是，数学家们在几个世纪前就已经找到了一元二次方程的求根公式，这个公式被广泛地应用于解决各种实际问题和数学推导中。
一元二次方程的求根公式，也称为根的判别式，是一种能够根据方程系数直接求出方程根的公式。
它的应用在实际生活中非常广泛，例如在物理学和工程学中，用于计算物体的运动轨迹或者建筑结构的稳定性。
而在数学研究中，一元二次方程的求根公式更是作为代数方程的基石，为高阶方程的求解提供了重要的思路。
为了更好地理解一元二次方程的求根公式，我们首先来简单了解一下一元二次方程。
一元二次方程一般写作ax²+bx+c=0，其中a、b、c 分别为方程的系数。
那么，方程的根就是能够使得方程成立的未知数的值，也就是x的值。
而一元二次方程的求根公式就是用来求出这些根的具体数值。
这个公式可以分为求判别式和求根两个部分。
首先求判别式，通过计算Δ=b²-4ac来判断方程的根的情况。
如果Δ大于0，则方程有两个不相等的实根；如果Δ等于0，则方程有两个相等的实根；如果Δ小于0，则方程没有实根。
判别式不仅是用来判断方程根的情况，更重要的是它为我们之后的计算提供了信息。
接着是求根的部分，根据判别式的结果，我们可以直接套用求根公式来求出方程的根。
如果Δ大于0，方程的两个根分别为x1=(-b+√Δ)/2a和x2=(-b-√Δ)/2a；如果Δ等于0，方程的两个根为x1=x2=-b/2a；如果Δ小于0，方程没有实根，但可以求出两个虚根。
通过这样的求根过程，我们可以直观地得出方程的根，并且可以根据判别式的结果对根的情况有一个清晰的认识。
在日常生活和学习中，一元二次方程的求根公式为我们解决各种问题提供了便利。
无论是物理问题中的抛物线运动，还是工程问题中的结构稳定性，都可以通过一元二次方程的求根公式得到精确的解答。
在数学的学习中，理解和掌握一元二次方程的求根公式，不仅有助于我们进一步学习高阶方程和代数方程的解法，更能够帮助我们提高数学建模和分析问题的能力。
一元三次方程万能求根公式
一元三次方程万能求根公式一元三次方程，听上去是不是有点吓人？其实它就像一道数学小题，咱们今天就来聊聊这个“万能求根公式”。
别担心，数学不一定得是严肃的，它也可以轻松有趣，咱们就像聊聊天一样。
想象一下你在海边捡贝壳，偶尔捡到一个特别的，嘿，就是一元三次方程！你心里想：“这玩意儿能干嘛？”其实它的世界大有可为。
这方程的形状就像个有点叛逆的孩子，写成了ax³ + bx² + cx + d = 0。
你一看就觉得，这一堆字母可不是简单的加减乘除呀。
可别急，其实它的背后藏着很多有趣的故事和小秘密。
咱们找找这个“万能求根公式”，听起来像是超能力一样，能让这复杂的方程轻松变得简单。
想象一下，拿出一把万能钥匙，哐当一下，门就开了，问题迎刃而解。
先来个大概念，咱们说的这个公式啊，通常写得有点复杂，但别被吓到。
其实就是为了找出那几个神秘的根，方程的解。
你可以把它看作是方程的好朋友，帮助它找到自己的归属。
想象一下，方程就像一个失落的小孩，根就是它的家，终于找到了可以回去的路。
说到这里，很多小伙伴可能会皱眉头：“这根到底是什么啊？”简单来说，根就是让方程等于零的那些数字。
比如说，咱们用这个公式来求解，可能会得到几个不一样的数字，嘿，这就是它的根。
就像你去找丢失的钥匙，结果翻遍了沙发底下，最后竟然在冰箱里找到了，哈哈，没想到吧？好，咱们再深入一点。
这个公式的确是有点长，像个古老的诗句，但其实它的用法不复杂。
你只需要代入你的系数 a、b、c 和 d，然后一通运算，哗啦啦，结果就出来了。
就像你跟朋友去做一顿丰盛的晚餐，准备食材、调料，然后一气呵成，最后享受美味的过程。
哎呀，光是想象都觉得美好。
很多人可能会觉得，这数学公式太高深，跟自己无缘。
其实啊，生活中到处都有数学的影子。
比如说，你在超市买菜，算算价格，或者打折的时候，看看划不划算，这不就是在做数学吗？一元三次方程也是其中之一，只不过它可能会让你感到一丝神秘感。
一元二次方程求根公式的推导过程
一元二次方程求根公式的推导过程一元二次方程是指形如ax^2 + bx + c = 0的方程，其中a、b、c 是已知实数常数，且a≠0。
它是数学中最基本的二次方程之一，也是最具有代表性的方程之一。
在解一元二次方程时，我们可以借助求根公式进行推导。
首先，我们先回顾一下一元二次方程的一般形式。
任何一元二次方程都可以化为标准形式：x^2 + px + q = 0，其中p和q也是已知实数常数。
为了推导出一元二次方程的求根公式，我们需要通过完成平方的方法将其化为完全平方的形式。
对于一般形式的一元二次方程x^2 + px + q = 0，我们先让其左边加上一个与x无关的常数，使其成为一个完全平方的二次式。
这个常数可以通过平方中项系数一半的平方得到，即：(p/2)^2。
将常数加到方程左边得到：x^2 + px + (p/2)^2 + q - (p/2)^2 = 0。
对右边的式子进行简化，得到：x^2 + px + (p/2)^2 + q -(p^2/4) = 0。
根据平方差公式(a^2 - b^2 = (a+b)(a-b))，我们可以将二次项与常数项相加的式子进行简化。
得到：(x + p/2)^2 + q - (p^2/4) = 0。
再进一步，我们可以将方程左边化为一个完全平方的形式：(x +p/2)^2 = (p^2/4) - q。
接下来，我们对等式两边开根号，得到：x + p/2 = ±√[(p^2/4) - q]。
然后，我们将方程两边都减去 p/2，得到：x = (-p±√[(p^2/4) - q])。
这就是一元二次方程的求根公式，也称为根的判别式。
在求解一元二次方程时，我们只需将方程中的a、b、c分别代入这个公式，即可求得方程的根。
需要注意的是，方程的根可以有两个解、一个解或者无解，这取决于判别式的值。
如果判别式大于零，方程有两个不相等的实数根；如果判别式等于零，方程有两个相等的实数根；如果判别式小于零，则方程无实数根，这时方程的解存在于复数域中。
一元二次方程求根公式
一元二次方程求根公式一元二次方程是数学中常见的一种方程形式，其一般形式为ax^2 + bx + c = 0，其中a、b、c为已知的常数，x为未知数。
解一元二次方程的方法有很多种，其中最常用的方法之一就是利用求根公式来求解。
本文将详细介绍一元二次方程求根公式的推导过程和应用方法。
一、求根公式的推导。
我们先来推导一元二次方程的求根公式。
设一元二次方程为ax^2 + bx + c = 0，我们要求出方程的根。
首先，我们假设方程有两个根x1和x2，那么根据因式分解的性质，我们可以将方程写成(x x1)(x x2) = 0的形式。
展开这个式子得到x^2 (x1 +x2)x + x1x2 = 0。
比较这个式子和原方程ax^2 + bx + c = 0的系数，我们可以得到以下关系：x1 + x2 = -b/a。
x1x2 = c/a。
接下来，我们要解出x1和x2的具体值。
我们可以利用上面的两个关系式来求解。
首先，我们可以将x1表示成-x2，然后代入第二个关系式中，得到x1 = (-b +√(b^2 4ac)) / (2a)，同理可得x2 = (-b √(b^2 4ac)) / (2a)。
这就是一元二次方程的求根公式，也称为根的公式。
二、求根公式的应用。
一元二次方程的求根公式在实际问题中有着广泛的应用。
比如在物理学中，当我们需要求解抛体运动的轨迹方程时，就会遇到一元二次方程。
又比如在工程学中，当我们需要求解某些结构的受力情况时，也会用到一元二次方程的求解。
下面我们通过一个例子来说明一元二次方程求根公式的应用。
例，已知一元二次方程x^2 3x + 2 = 0，求出方程的根。
根据一元二次方程的求根公式，我们可以直接代入a=1，b=-3，c=2，然后带入公式x1 = (-b + √(b^2 4ac)) / (2a)和x2 = (-b √(b^2 4ac)) / (2a)中进行计算。
计算的结果为x1=2，x2=1，所以方程的根为x1=2和x2=1。
数学的魅力_8. 一元n次方程求根公式
Abel:
一元五次以上的代数方程一般来说是 不存在求根公式的. 什么时候存在求根公式呢?
超级天才的出现:
Évariste Galois
Évariste Galois(10.25. 1811-5. 31. 1832)
法国的天才数学家: 莫扎特的天赋, 贝多芬的激情, 拜伦的浪漫. 出生于巴黎南郊小镇, 父亲: 中学校长, 镇长. 母亲: 熟读拉丁文并精通古典文学.
1815年: 进入教会学校读中学.
1817年: 阿贝尔一生的转折点.
数学老师: 好酒如命, 脾气粗暴, 体 罚致死学生被解职, 由比Abel大七 岁的年青教师Holmboe代替.
Holmboe : 最大的贡献, 发掘了Abel的数学才能,
成为Abel的朋友并给予帮助.
Holmboe私下给Abel讲授高等数学, 介绍阅读 Poisson、Gauss以及Lagrange的著作, Abel很快
1789年, 攻占巴士底狱 1794年, 巴黎高师成立 1795年,
巴黎综合理工学院建校
革命狂潮曾指向科学家：
“共和国不需要科学家” “近代化学之父” 拉瓦锡
数学家, 哲学家, 孔多塞
“于断头台就义 欧拉停止了计算和生命”
结果: 院士们变得畏缩, 老态龙钟
Napoléon Bonaparte(1769-1821)
628年:
印度数学家Brahmagupta给 出求根公式
一元三次方程求根
中国唐朝数学家王孝通在626年前后所著的 《缉古算经》中建立了25个三次多项式方 程和提出三次方程实根的数值解法. 波斯数学家欧玛尔·海亚姆(1048-1123)利用圆 锥截面与圆相交的方法构建了三次方程的解法. 他说明了怎样几何方法利用三角法表得到答案.
求根的万能公式(一)
求根的万能公式(一)求根的万能公式1. 二次方程的求根公式•二次方程的一般形式为：ax^2 + bx + c = 0，其中a、b、c是已知实数，a ≠ 0。
•求根公式为：x = (-b ± √(b^2 - 4ac)) / (2a)。
•举例：求解方程2x^2 + 5x - 3 = 0的根。
–根据公式，a = 2, b = 5, c = -3。
–将数值代入公式：•x1 = (-5 + √(5^2 - 42(-3))) / (2*2) = (-5 +√(25 + 24)) / 4 = (-5 + √49) / 4 = (-5 + 7)/ 4 = 2/4 = 。
•x2 = (-5 - √(5^2 - 42(-3))) / (2*2) = (-5 -√(25 + 24)) / 4 = (-5 - √49) / 4 = (-5 - 7)/ 4 = -12/4 = -3。
2. 三次方程的求根公式•三次方程的一般形式为：ax^3 + bx^2 + cx + d = 0，其中a、b、c、d是已知实数，a ≠ 0。
•求根公式为：x = z - b / 3a，其中z是方程的零点，代入公式得到：x = z + m + n，其中m和n为方程求得的虚数根。
•举例：求解方程x^3 - 4x^2 + 5x - 2 = 0的根。
–可以通过观察得到，方程的一个根为x = 2。
–将x = 2代入方程，得到：8 - 16 + 10 - 2 = 0，验证通过。
–使用长除法可以得到另外两个根为x = 1 ± √2i，得到虚数根。
–代入求根公式，得到实数根：x = 2 + 1 - √2i，x = 2 +1 + √2i。
3. 四次方程的求根公式•四次方程的一般形式为：ax^4 + bx^3 + cx^2 + dx + e = 0，其中a、b、c、d、e是已知实数，a ≠ 0。
•求根公式相对复杂，可以转化为解四次方程的问题，或者使用数值解法进行求解。
一元二次方程求根
一元二次方程求根一、一元二次方程求根公式：当Δ=b2-4ac ≥0时, x =−b±√b 2−4ac 2a当Δ=b2-4ac<0时,x 无实数根，但有2个共轭复根只含有一个未知数，并且未知数项的最高次数是2的整式方程叫做一元二次方程。
它的标准形式为: ax 2+bx+c=0(a ≠0)二、一元二次方程解法（直接开平方法、配方法、公式法、因式分解法）1、开平方法形如（X -m ）2=n(n ≥0),可以直接开平方法求解为n m X ±=（1）等号左边是一个数的平方的形式而等号右边是一个常数（2）降次的实质是由一个一元二次方程转化为两个一元一次方程（3）方法是根据平方根的意义开平方2、配方法（1）把原方程化为一般形式（2）方程两边同时除以二次项系数，使二次项系数为1，并把常项移到方程右边（3）方程两边同时加上一次项系数一半的平方（4）把左边配成一个完全平方式，右边化为一个常数（5）进一步直接开平方法求出方程的解3、因式分解法（一移、二分、三转化、四求根）（1）将方程右边化为0（2）方程左边分解为两个一次式的积，令这两个一次式分别为0，得到两个一元一次方程（3）求解这两个一元一次方程三、如何选择一元二次方程组的解法1、看是否可以直接开方解。
2、看是否能用因式分解法解(因式分解的解法中，先考虑提公因式法，再考虑平方公式法，最后考虑十字相乘法)。
3、使用公式法求解。
4、最后再考虑配方法(配方法虽然可以解全部一元二次方程，但有时候解题太麻烦)。
附：一元二次方程解法口诀含有一个未知数，最高指数是二次；整式方程最常见，一元二次方程式；左边二次三项式，右边是零一般式。
方程缺少常数项，求取提取公因式；方程没有一次项，直接开方最合适；方程如果合家欢，十字相乘先去试；分解二次常数项，叉乘求和凑中式；如能做到这一点，十字相乘根求之；否则可以去配方，自然能够套公式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
solve ax+b=0 for x
Isolate terms with x to the left hand side. Solve for x.
solve ax^2+bx+c=0 for x
Write the quadratic equation in standard form.
２
Solve the quadratic equation by completing the square.
Take one half of the coefficient of
x and square it,then add it to both sides.
Factor the left hand side.
Eliminate the exponent on the left hand side.
Look at the first equation:Solve for x.
Look at the second equation:Solve for x.
solve ax^3+bx^2+cx+d=0 for x
Look for a simple substitution that eliminates
the quadratic term of a x3 b x2 c x d.
Write the cubic polynomial on the left hand side in standard
Write the cubic equation in standard form.
Change coordinates by substituting y z Κ
z
,where
Κis a constant value that will be determined later.
Transform the rational equation into a polynomial equation
Find an appropriate value forΚ
in order to make the coefficients of z2and z4both
４
Solve for u.
Perform back substitution on u
1
54a3
9a b c 2b3 27a2d
33a34a c3 b2c2 4b3d 18a b c d 27a2d2
a4
.
Move everything to the left hand side.
Divide by an appropriate factor to make the constant Write 54a3z3 9a b c 2b3 27a2d
33a34a c3 b2c2 4b3d 18a b c d 27a2d2
a4
with a common power.
Simplify 54a3z3 9a b c 2b3 27a2d 33a ６
Simplify 54a3z3 9a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2
1 0by making a substitution.
Solve for v.
Look at the first equation:Perform back substitution
Solve for z.
８
Perform back substitution on
1
9a b c 2b3 27a2d 33a
z
323a
4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1
3 .
Solve for y.
Perform back substitution on
Perform back substitution on
3 b2 3a c 3a9a b c 2b3 27a2d 33a
y 2
4a c3 b2c2 4b3d 18a b c d 27a2d2
1
^ 1 3
323a
9a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2^
1 3 .
Solve for x.
Look at the second equation:
１０
Look at the second equation:
3.
Perform back substitution on v 1
Solve for z.
Perform back substitution on
z
1
3a
1
2
39a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .
Solve for y.
Perform back substitution on y 1 2 32
3 b2 3a c
3a9a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2
^ 1 3
1 3a
1 2
39a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .
Solve for x.
Look at the third equation:
Perform back substitution on v 1 2 3.
Solve for z.
Perform back substitution on
1
z
323a 1 2 39a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1
3 .
Solve for y.
Perform back substitution on
1
y
323a 1 2 39a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2^
1 3 23 b
2 3a c
3a9a b c 2b3 27a2d 33a
4a c3 b2c2 4b3d 18a b c d 27a2d2
^ 1 3 .
Solve for x.。