东南大学丁幼亮工程结构抗震分析- 结构抗震分析模型
东南大学工程结构抗震分析往年真题及答案2

1、试分析剪力墙结构、框架—核心筒结构抗震多道设防的实现途径。
(10分)剪力墙主要表现为连梁和墙肢底层的破坏,连梁由于剪跨比小,梁腹易产生斜裂缝,若其抗剪强度不足,可能产生剪切破坏,连梁一旦破坏,墙肢间失去联系,承载力降低,墙肢底层在竖向荷载和水平荷载下处于剪压受力状态,墙肢剪跨比大,发生弯曲破坏及剪切破坏,墙肢剪跨比小,发生剪切破坏。
剪力墙作为联肢抗震墙,连系梁先屈服,然后墙肢弯曲破坏丧失承载力,当连系梁钢筋屈服并具有延性时,它既可以吸收大量地震能量,又能继续传递弯矩和剪力,对墙肢有一定的约束作用,使抗震墙保持足够的刚度和承载力,延性较好。
如果连系梁出现剪切破坏,按照抗震结构多道设防的原则,只要保证墙肢安全,整个结构就不至于发生严重破坏或倒塌。
框架—核心筒结构是双重结构体系,是由框架和核心筒两个系统组成的,核心筒作为第一道防线,框架作为第二道防线。
在结构中,核心筒在各个方向上都具有较大的抗侧刚度,因此成为结构中的主要抗侧力构件。
在小震作用下,结构整体处于弹性状态,此时核心筒承受绝大部分地震剪力,一般可达总剪力的85 %以上,其刚度大小对结构小震作用下的侧移起控制作用; 在中震及大震作用下,筒体开裂,并且先于框架屈服, 其抗侧刚度降低,所承担的剪力比例有所减小。
而核心筒外围的框架主要承受竖向荷载,并按刚度分配分担相应的剪力,在中震和大震作用下,随着核心筒刚度的降低,框架承担的剪力也相应有所增加。
因此,外框架应具有足够的承载力,以充分发挥框架—核心筒结构的多道抗震防线作用。
框架—核心筒结构具有三道抗震防线:连梁、墙肢或子筒、外框架。
框架—核心筒结构中的各构件设防要求可表述如下:1) 小震作用下,连梁、墙肢或各子筒、外框架均处于弹性状态。
2) 中震作用下,连梁进入塑性,各子筒基本处于弹性状态,外框架也基本保持弹性状态。
震后修复主要集中于耗能连梁。
3) 大震作用下,连梁屈服程度较大,但具有足够的塑性变形能力;各子筒部分进入塑性,但塑性发展程度不大;外框架结构基本保持弹性,少量进入塑性状态。
工程结构抗震与防灾_东南大学_2 第二章结构抗震计算_7 第7讲考虑扭转影响时计算水平地震作用的振型分解反

K zz 0
K zp T
0
KYY
K zp
KY
KY K
(2-104)
式(2-104)表明两个平动之间无耦联
ny
K
zz
K
z
s
(2-105)
s 1
其中: ny 为平行于X轴框架的榀数
K
z
s
为平行于X轴第s榀框架的刚度矩阵
(2-111)
其中: dg (t) 为地面运动加速度的时间历程;
D 为地面运动方向与x轴的夹角。
2.6
振型分解反应谱法
先求解平动-扭转耦联体系的自由振动:
M D K D 0 (2-112)
结构体系的自由度为3n(n为结构的层数),常用 雅可比法求解。
2.6
振型分解反应谱法
其中mmJ i是 第ddiiaaigg楼mJ层11 的mJ22质量mJnn;
(2-102) (2-103)
Ji mi (a2 b2 ) /12
其中: Ji 表示第i层质量对本楼层质心的转动
惯量;a、b分别是本楼层的长短边。
[K2.]6为广义侧振移型刚分度解阵反应谱法
K
坐标原点一般选在各楼层的质心处,如图 2-19所示,坐标轴为一折线形轴,运动方程:
M D(t)CD(t)KDt
M Dg (t)
(2-100)
图2-19计算简图
2.6
振型分解反应谱法
其中: M 为广义质量阵(3n×3n)
M diagm m J (2-101)
2. 结构体系考虑扭转影响的水平地震作用 仍按振型分解法:
高层建筑结构抗震分析和设计若干问题的探讨

高层建筑结构抗震分析和设计若干问题的探讨作者:钱玉林, 丁勇春作者单位:扬州大学建筑科学与工程学院,江苏,扬州,2250091.学位论文丁幼亮带钢塔楼高层建筑的抗震设计方法研究2003近年来,在高层建筑顶部安装钢结构塔楼的建筑结构体系应用日益增多.但是历次地震震害表明,地震作用下屋顶上的塔楼地震反应强烈,即使在主体结构无震害或震害很轻的情况下,屋顶塔楼也会发生严重破坏.目前这种结构体系的抗震设计方法国内研究得较少,更缺乏系统性的研究,以致工程设计上缺乏较为合理的实用设计方法.该文对带钢塔楼高层建筑结构体系的抗震设计方法进行了较为系统的研究,较为深入地研究了动力特性、阻尼计算模型、地震作用计算方法和抗震设计方法.以江苏省电网调度中心为例,采用三维空间有限元模型研究顶部安装钢结构塔楼的高层建筑动力特性.从整体动力特性可以看出,当高层建筑在地震动作用下产生振动时,屋顶钢塔在高层建筑屋顶层振动的激励下,产生二次型振动,发生显著的"鞭梢效应".根据Rayleigh-Ritz法的基本原理,该文给出了带钢塔楼高层建筑动力特性的简化近似计算方法.对于这种主体结构和钢塔组成的组合体系,可以分别求出钢塔和主体结构各自的周期和振型,采用Rayleigh-Ritz法将其进行组合近似求解整体动力特性.讨论了结构动力分析中阻尼计算模型的研究进展,在此基础上研究了非比例阻尼结构体系的动力响应特点.从工程实际应用出发,研究了带钢塔楼的钢筋混凝土高层建筑结构体系等效粘滞阻尼比的计算方法,并采用等效粘滞阻尼比来考虑钢塔楼和主体结构不同阻尼耗能特性的影响.分析表明,带钢塔楼的钢筋混凝土高层建筑进行地震响应计算时,钢塔楼内力标准值需要根据结构的等效粘滞阻尼比进行调整,其余的结构地震响应可不作调整.在总结带钢塔楼高层建筑整体地震作用的计算方法的基础上,采用基于振型分解的结构地震响应时程分析方法分析高阶振型在塔楼地震响应中的贡献,提出了采用振型分解反应谱法和振型分解直接动力分析法时所适宜考虑的振型阶数.该文分析了高层建筑顶部塔楼鞭梢效应产生的本质原因,指出塔楼的鞭梢效应实质上是由于在地震作用下整体结构发生共振产生的,而与塔楼和主体结构自振周期的比值没有直接的联系,并提出了高层建筑顶部塔楼抗震概念设计的基本原则.研究了钢塔楼地震作用的影响因素以及钢塔楼对主体结构地震响应的影响,分别分析了阻尼特性、场地类别、设计地震分组、主体结构质量和刚度、塔楼质量和刚度等因素对塔楼地震作用和主体结构地震作用的影响,在此基础上分别给出了塔楼地震作用和考虑钢塔楼作用的主体结构地震作用的简化计算方法.工程实例计算验证了所提出的简化计算方法的正确性和适用性.总结了带钢塔楼高层建筑的抗震设计方法,并以江苏省电网调度中心为例,采用三维空间有限元程序进行了塔楼与主体结构连接处的局部应力分析.2.期刊论文范勤高层建筑抗震设计中短柱问题的处理-南北桥2008(3)在层高一定的情况下,为提高延性而降低轴压比则会导致柱截面增大,且轴压比越小截面越大;而截面增大导致剪跨比减小,又降低了构件的延性.因此,在高层特别是超高层建筑结构设计中,为满足规程对轴压比限值的要求,柱子的截面往往比较大,在结构底部常常形成短柱甚至超短柱.另外,诸如图书馆的书库、层高较低的储藏室、高层建筑的地下车库等由于使用荷载大,层高较低,在设计中也不可避免地会出现短柱.众所周知,短柱的延性很差,尤其是超短柱几乎没有延性,在建筑遭受本地区设防烈度或高于本地区设防烈度的地震影响时,很容易发生剪切破坏而造成结构破坏甚至倒塌,无法满足"中震可修,一大震不倒"的设计准则.为了避免短柱脆性破坏问题在高层建筑中发生,笔者认为,首先要正确判定短柱,然后对短柱采取一些构造措施或处理,提高短柱的延性和抗震性能. 要求,柱子的截面往往比较大,在结构底部常常形成短柱甚至超短柱.另外,诸如图书馆的书库、层高较低的储藏室、高层建筑的地下车库等由于使用荷载大,层高较低,在设计中也不可避免地会出现短柱.众所周知,短柱的延性很差,尤其是超短柱几乎没有廷性,在建筑遭受本地区设防烈度或高于本地区设防烈度的地震影响时,很容易发生剪切破坏而造成结 破坏甚至倒塌,无法满足"中震可修,一大震不倒"的设计准则.为了避免短柱脆性破坏问题在高层建筑中发生,笔者认为,首先要正确判定短柱,然后对短柱采取一些构造措施或处理,提高短柱的廷性和抗震性能. 要求,柱子的截面往往比较大,在结构底部常常形成短柱甚至超短柱.另外,诸如图书馆的书库、层高较低的储藏室、高层建筑的地下车库等由于使用荷3.学位论文李子杰弹塑性静力与动力分析在高层建筑抗震设计中的应用研究2007我国是一个多地震的国家,目前仍处于地震高发期,因而结构抗震性能的研究具有重要意义。
东南大学《工程结构抗震与防灾》课件

地震作用最大的方向 = -1.040 (度)
东南大学《工程结构抗震与防灾》 课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
各类建筑结构的地震作用
质量和刚度分布明显不对称的结构,应计入双向水平 地震作用下的扭转影响;其他情况,应允许采用调整地 震作用效应的方法计入扭转影响。
8度和9度时的大跨度结构、长悬臂结构,9度时的高 层建筑,应计算竖向地震作用。
第2章 结构抗震计算
§2-1 计算原则 §2-2 地震作用 §2-3 设计反应谱 §2-4 振型分解反应谱法 §2-5 底部剪力法 §2-6 时程分析法 §2-7 竖向地震作用 §2-8 结构抗震验算
东南大学《工程结构抗震与防灾》 课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
结构抗震计算的基本步骤
考虑扭转耦联时的振动周期(秒)、X,Y 方向的平动系数、扭转系数
振型号 周 期 转 角
平动系数 (X+Y) 扭转系数
1 1.5059 178.50 0.65 ( 0.65+0.00 ) 0.35
2 1.3294 0.56 0.37 ( 0.37+0.00 ) 0.63
3 1.1881 89.33 1.00 ( 0.00+1.00 ) 0.00
不规则结构——平面不规则
位移比:在规定的水平力作用下,楼层的最大弹性水平位 移(或层间位移),大于该楼层两端弹性水平位移(或层间 位移)平均值的1.2倍。
东南大学《工程结构抗震与防灾》 课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
不规则结构——平面不规则
凹凸不规则
控制凹凸不规则就是控制房屋局部的外伸长度。 结构平面上的两端相距太远,地震时由于输入相位差容
建筑结构抗震- 结构抗震计算

13
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
例题(1) 例题(1)
例题: 四层钢筋混凝土框架结构, 例题 : 四层钢筋混凝土框架结构 , 已知抗 G4 =831. 6kN 类场地, 震设防烈度为8度(0.20g),Ⅱ类场地,设计 G3 =1039. 6kN 地震分组为第一组, 地震分组为第一组 , 层高和层重力代表值 如图所示。 如图所示。结构的基本周期为0.56s,试用底 G2 =1039. 6kN G1 部剪力法计算多遇地震时的层间地震剪力。 部剪力法计算多遇地震时的层间地震剪力 。 =1122.7kN ( 解: 1)计算结构等效总重力荷载代表值
11
Fn′ = Fn + ∆Fn =
其他各层地震作用: 其他各层地震作用:
Gn Hn
n
∑G H
k k=1
FEk (1−δn ) + δn FEk
k
Fi =
Gi Hi
n
∑G H
k k=1
FEk (1−δn )
k
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
底部剪力法的修正(3) 底部剪力法的修正(3)
(5)计算各层的水平地震作用标准值和层间剪力
16
Fi =
层 4 3 2 1 Σ
HiGi
n
∑H G
k k=1
FEk (1−δn ) Vi = ∑Fk + ∆Fn
k=i
n
k
Gi (kN) 831.6 1039.5 1039.5 1122.7 4033.3
Hi (m) 14.44 11.08 7.72 4.36
17
例题 E3.3.2:一幢六层现浇钢筋混凝土框架房屋,屋顶有局部突出的楼梯间和水箱间,如图 E3.3.1 所示。抗震设防烈度为 8 度,设计基本地震加速度 0.2g,设计地震分组为第一组,Ⅱ 类场地,结构阻尼比为 0.05。基本自振周期 T1 =0.61s。试求各楼层水平地震作用标准值。
工程结构抗震与防灾_东南大学_4 第四章建筑结构基础隔震和消能减震设计_2 第2讲建筑结构隔震设计

图 隔震结构计算简图
分析对比结构隔震与非隔震两种情况下各层最大层 间剪力,宜采用多遇地震下的时程分析。
弹性计算时,简化计算和反应谱分析时宜按隔震支 座水平剪切应变为100%时的性能参数进行计算;当采 用时程分析法时按设计基本地震加速度输入进行计算。
4.2
建筑结构消能减震设计
(3)上部结构水平地震作用计算-水平向减震系数应用
c.当橡胶支座的第二形状系数小于5.0时,应降低平均压应力限值;小于5不 小于4时,降低20%;小于4但不小于3时,降低40%;
d.外径小于300mm的橡胶支座,丙类建筑的平均压应力限值为10MPa。
4.2
建筑结构消能减震设计
(3)隔震支座水平剪力计算
隔震支座的水平剪力应根据隔震层在罕遇地震下的水平剪力按各隔
② 隔震层以上结构的抗震措施
当水平向减震系数为大于0.40时(设置阻尼器为0.38)不应
降低非隔震时的要求;水平向减震系数不大于0.40 (设置阻尼器 为0.38)时,可适当降低抗震规范对非隔震建筑的要求,但烈度 降低不得超过1度,与抵抗竖向地震作用有关的抗震构造措施不 应降低。
4.2
建筑结构消能减震设计
隔震层在罕遇地震下应保持稳定,不宜出现不可恢复变形。 隔震层橡胶支座在罕遇地震的水平和竖向地震同时作用下,拉应力
不应大于1Mpa。 隔震层的平面布置应力求具有良好的对称性。
4.2
建筑结构消能减震设计
(2) 隔震支座竖向承载力验算
抗震规范规定:隔震支座在重力荷载代表值作用下的竖向压应力 设计值不应超过下表列出的限值。
经历相应设计基准期的耐久试验后,刚度、阻尼特性变化不超过初期 值的±20%;徐变量不超过支座橡胶总厚度的0.05倍;
东南大学丁幼亮工程结构抗震分析- 结构抗震分析模型资料

研究生课程《工程结构抗震分析》课件
多点地震动输入问题(2)
引起空间地震动场变化的主要因素
• 行波效应——等效剪切波速
等效剪切波速(m/s) I0
vs>800
0
800≥vs>500
500≥vse>250
250≥vse>150
vse≤150
覆盖层厚度
I1
II
III
IV
0
<5
ቤተ መጻሕፍቲ ባይዱ
研究生课程《工程结构抗震分析》课件
有限元分析时的地震动多点输入(1)
• 大质量法。在地基节点上附属很大的质量(比如质量可以 取结构质量的1E6倍)来带动结构的响应。地基节点在激 励方向不能约束。然后在质量单元上施加适当的力使地基 产生所需加速度,如果质量为1E6,则施加1E6的力将产 生单位加速度。只需为每一荷载步指定时间和相应的力即 可。此方法的优点是可以得到结构的真实响应位移(包括 了地基的平动)。
振动的作用,这种作用称之为科氏耦合效应。
东南大学土木工程学院 丁幼亮
研究生课程《工程结构抗震分析》课件
一致输入时的结构动力方程(7)
多维地震动输入下的结构动力方程
• 当不考虑地面转动角速度和转动角位移时(但地面转动加速 度仍存在),则不存在科氏耦合效应:
MU CU KU M (Ug Xθ) • 目前对地面转动分量(绕竖轴)的观测资料还很少,不足以 应用;对地面摆动分量(绕水平轴)的观测资料则几乎没有。
矩阵通常称
为科氏惯性
耦合矩阵
,
它是因为动
力坐标系相
对于定坐标系作转动运动所引起的。与科氏耦合阵有关的项称
工程结构抗震与防灾_东南大学_2 第二章结构抗震计算_11 第11讲结构截面的抗震验算

式中:
S R RE
(2-204)
R —结构构件承载力设计值;
RE —承载力抗震调整系数 ,按表2-16。
2.10
结构截面的抗震验算
3. 有关系数的确定
①地震作用分项系数的确定
众值烈度下的地震作用,应视为可变作用而 不是偶然作用。这样,根据《建筑结构可靠度 设计统一标准》中确定直接作用(荷载)分项
2.10
结构截面的抗震验算
④承载力调整系数
现阶段大部分结构构件截面抗震验算时,采
用了各有关规范的承载力设计值R 抗震设计
时将地震视为可变荷载,故将相应承载力设计值R
予以提高( RE ),即
RE R / RE 或 RE R / RE
从数值上看, RE 取值范围为0.75~1.0,其实质含
2.10
结构截面的抗震验算
抗震设防两阶段设计步骤的第一阶段做到 “小震不坏”,以多遇地震的水平地震作用标准值, 用线弹性理论求出结构构件的地震作用效应,
再与其他荷载效应组合 得到结构构件内力组
合设计值进行验算。
第二阶段设计,罕遇地震下验算结构的弹塑性变形。
"
因此,结构抗震验算分为截面抗震验算和结构抗震 变形验算两部分。
规范在计算地震作用时,已考虑了地震作用与各种 重力荷载(恒载、活载、雪载等)的组合问题,表2-8 规定了一组组合值系数,形成了抗震设计的重力荷载 代表值(式(2-32))。
规范规定在验算和计算地震作用时(除吊车悬吊
重力外),对重力荷载均采用相同的组合值系数,为了
简化计算
式(2-203)中仅出现风荷载的组合值系数,
系数的方法,规范对水平地震作用: Eh 1.3 ;
东南大学《工程结构抗震与防灾》课件

远震的功率谱
近震的功率谱
(M=7.5,R=104km,峰值加速度186.25cm/s2) (M=6.8,
R=19km,峰值加速东度南3大6学0.《88工c程m结/s构2)抗震与防灾》
课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
地震动频谱特性影响因素——震级和震中距
设计地震分组
第一组 第二组 第三组
I0 0.20 0.25 0.30
I1 0.25 0.30 0.35
场地类别 II
0.35 0.40 0.45
III 0.45 0.55 0.65
IV 0.65 0.75 0.90
东南大学《工程结构抗震与防灾》 课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
国家精品课程《工程结构抗震与防灾》课件
第1章 结构抗震基本知识
§1-1 地震基本知识 §1-2 地震的基本术语 §1-3 地震动特性 §1-4 工程结构的抗震设防 §1-5 建筑场地
东南大学《工程结构抗震与防灾》 课件
东南大学土木工程学院
国家精品课程《工程结构抗震与防灾》课件
第1章 结构抗震基本知识
0.4
200
600
0.2
1004000 Nhomakorabea0
200
-0.2
-100
0
-0.4
-200
-200
-0.60 10 20 30 40 50 60 -3000 10 20 30 40 50 60 -4000 10 20 30 40 50 60
t/s
t/s
t/s
(a)加速度时程
东南大学丁幼亮工程结构抗震分析时程分析法PPT教案学习

(t) 1 y1(t) 2 y2 (t) n yn (t) Y
(26)
式中:
1 2
n
(27)
为振型矩阵。
Y [ y1 y2 yn ]T 第2页/共63页
为振型坐标或广义坐标向量,它是时间的函数。
结构动力响应分析-振型叠加法
将式(26)代入式(25),并注意到i 不随时间变化,得:
结构动力响应分析-直接积分法
(三)Newmark 法
Newmark 法实质上是线性加速度法的推广。其采用如下假设:
tt t [(1 )t tt ]t
(41)
t t
t
tt
[(1 2
)t
tt ]t 2
(42)
其中 和 是按积分精度和稳定性要求而确定的参数。当
1,
1
第27页/共63页
当 t 时,有
t t
t
t 2
t
t 2
t t
(d)
t t
t
tt
t 2 3
t
t 2 6
t t
(e)
由(d)
(e)二式可求得
t t、 t
、
t
t t
与
t
时刻状态向量的关系:
t t
6 t 2
( t t
t )
6 t
t
2t
t t
3 t
( t t
t ) 2第1t 3页/2共t 63t页
时,它就是线性加速度法。
26
结构动力响应分析-直接积分法
由(18)式可解得
t t
1 t 2
( t t
t )
1 t
t
( 1 2
1)t
建筑结构抗震-地震作用
地震反应谱
最大相对位移反应: 最大相对位移反应:
15
Sd = x(t) max =
最大相对速度反应: 最大相对速度反应:
ω ∫0
t 0
1
t
&&g (τ )e−ξω(t −τ ) sin ω(t −τ )dτ x
m ax
& Sv = x(t) max = ∫ &&g (τ )e−ξω(t −τ ) sin ω(t −τ )dτ x
最大绝对加速度反应: 最大绝对加速度反应:
m ax
Sa = &&(t) + &&g (t) x x
m ax
= ω ∫ &&g (τ )e−ξω(t −τ ) sin ω(t −τ )dτ x
0
t
最大反应之间的关系: 最大反应之间的关系:S = ωS = ω2S a v d 意义: 意义:在地面运动 & g (t)确定后,最大地震反应仅由 & x 确定后, 结构自振周期T(圆频率 )和阻尼比ξ决定 决定。 结构自振周期 (圆频率ω)和阻尼比 决定。
t=0时,体系的初始速度 =0时
t=0时,体系的初始位移 =0时
为有阻尼单自由度弹性体系的圆频率。 ω′ = 1−ξ 2ω 为有阻尼单自由度弹性体系的圆频率。 阻尼比ξ=0.05, ω′ = 0.9987ω ≈ 。 阻尼比 , ω 则体系不产生振动,此时ξ称为临界阻尼 当ξ=1, ω′ = 则体系不产生振动,此时 称为临界阻尼 0 比。
2
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
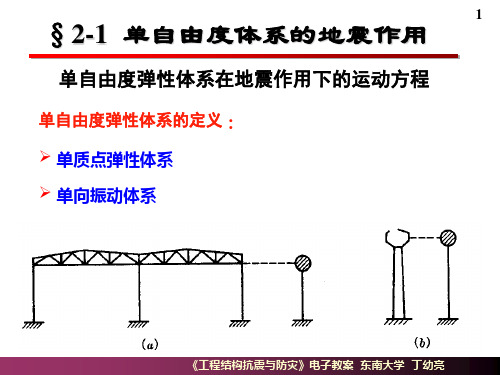
§2-1 单自由度体系的地震作用
单自由度弹性体系在地震作用下的运动方程
建筑结构抗震- 结构抗震计算

➢ 计算原则:总的水平地震作用FEk保持不变,除了顶部 附加的水平地震作用外,剩余的水平地震作用由各层分
担。 顶部地震作用:
FnFnFnnGnHn
F(1 ) F
Ek
n
n Ek
GkHk
其他各层地震作用: k1
GH
F i i
i
n
F (1 )
Ek
n
GkHk
k1
a
11
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
②多质点系存在高振型地震反应,而高振型地震作用
对于各个质点来说有正有负。由此引起的结构底部剪力,
比各质点地震作用绝对值之和要小。
a
6
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
7
基本步骤(2)
步骤1:结构底部水平地震剪力的计算
➢ 基本概念
因此,欲使等效单质点系的底部地震剪力与所代表的
多质点系底部剪力相等,对应单质点系的等效质量应小
a
12
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
13
底部剪力法的修正(4)
突出屋面附属结构地震内力的调整
计算注意点: ➢ 对于T1>1.4Tg的建筑并有突出小屋时,计算的顶部附 加水平地震作用应位于主体房屋的顶部,而不应置于局 部突出小屋的屋顶处。 ➢ 对于顶层带有空旷大房间或轻钢结构的房屋,应视为 结构体系的一部分,采用振型分解反应谱法计算。
a
2
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
3
基本原理(2)
简化思路
➢ 某些多自由度体系的结构,地震作用下的振动以第一
振型为主,可以近似认为作单自由度运动,即原来的多
建筑结构抗震- 结构抗震计算

3
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
基本原理(3) 基本原理(3)
简化思路
在确定这类结构的水平地震作用时, 在确定这类结构的水平地震作用时 , 可以根据其基 本周期确定其总水平地震作用, 本周期确定其总水平地震作用,然后再按照第一振型的 侧移曲线规律来确定结构各楼层的水平地震作用。 侧移曲线规律来确定结构各楼层的水平地震作用。
12
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
底部剪力法的修正(4) 底部剪力法的修正(4)
突出屋面附属结构地震内力的调整
计算注意点: 计算注意点: 的建筑并有突出小屋时, 对于 T1>1.4Tg 的建筑并有突出小屋时 , 计算的顶部附 加水平地震作用应位于主体房屋的顶部, 而不应置于局 加水平地震作用应位于主体房屋的顶部 , 部突出小屋的屋顶处。 部突出小屋的屋顶处。 对于顶层带有空旷大房间或轻钢结构的房屋, 对于顶层带有空旷大房间或轻钢结构的房屋 , 应视为 结构体系的一部分,采用振型分解反应谱法计算。 结构体系的一部分,采用振型分解反应谱法计算。
11
Fn′ = Fn + ∆Fn =
其他各层地震作用: 其他各层地震作用:
Gn Hn
n
∑G H
k k=1
FEk (1−δn ) + δn FEk
k
Fi =
Gi Hi
n
∑G H
k k=1
FEk (1−δn )
k
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮 工程结构抗震与防灾》
底部剪力法的修正(3) 底部剪力法的修正(3)
等效 多自由度体系 单自由度体系 基本自振周期 基本振型 各楼层的 水平地震作用 总水平地震作用
东南大学工程结构抗震分析-二结构抗震概念设计

对地基的影响时,地基承载力取值往往提高33%—50%。
-------------------------------------
目前的抗震设计水平尚未达到真正的科学水平。
要使建筑物具有尽可能好的抗震性能,首先应从大的方面入手,做好 抗震概念设计。如果整体设计没有做好,计算工作再细致,也难免在地震
时建筑物不发生严重的破坏,乃至倒塌。科学辨证观:大处着眼、 小处着手!正确处理整体与局部、宏观与微观的关系!
力特性,一些非结构部件也参与工作,使刚度增加,周期减小。
工程结构抗震分析
2.近似的估算公式 在基于脉动实测的基础上,再忽略房屋高度和层高的影响,可给 出下列更粗略的估算公式: (1)钢筋混凝土框架结构,T1=(0.08~0.10)N; (2)钢筋混凝土框架—剪力墙或框架—筒体结构,T1=(0.06~ 0.08)N; (3)钢筋混凝土剪力墙结构或筒中筒结构,T1=(0.04~0.05)N; (4)钢—钢筋混凝土混合结构,T1=(0.06~0.08)N; (5)高层钢结构,T1=(0.08~0.12)N; 式中,N为地面以上房屋总层数。
古湖床软土上的地震动参数,与硬土上的相比较,加速度峰值约增加4倍, 速度峰值增加5倍,位移峰值增加1.3倍,而反应谱最大反应加速度则增加了9倍多。
工程结构抗震分析
图5 湖泊基床(1-3)和基岩(4-6)加速度对比 ------------------------------------------------------------------------------------------图5中将1985年墨西哥地震中岩层上和湖泊沉积层的相邻点处记录得 到的加速度作了对比,可以看出,由于老湖泊基床沉积层使得这些 峰值加速度增大了5倍。
工程结构抗震与防灾_东南大学_3 第三章建筑结构抗震设计_18 第18讲钢构件的抗震设计

3.4
钢结构房屋震害设计
研究表明:
柱的强度与延性随着轴压比的上升而下降; 相同轴压比下,柱长细比愈大,其弯曲变形能力愈小,易失稳。
λ满足下列直线公式可3-4-11a)
16Mn钢 100(1 ) (3-4-11b)
式(3-4-11)可作为偏心受压柱长细比和轴压比的综合限制公式。
第三章题目
3.4 钢结构房屋抗震设计
23
3.4
钢结构房屋震害设计
三、钢构件与连结的性能及其抗震设计
梁、柱、支撑构件及其节点的合理设计,包括以下方面:
Ⅰ、对于会形成塑性铰的截面,应避免其在未达到塑性弯矩时发生局部失 稳或破坏,同时塑性铰应具有足够的转动能力,以保证体系能形成塑性倒 塌机构; Ⅱ、避免梁、柱构件在塑性铰之间发生局部失稳或整体失稳; Ⅲ、构件之间的连接要设计成能传递剪力与弯矩、并能允许框架构件充分 发挥塑性性能的形式。
工字形柱翼缘外伸部分
13
11
10
9
工字形柱腹板
43
43
43
43
箱形柱壁板
39
37
35
33
注: 表列数值适用于Q235钢,其他钢号应乘以 235 / f ay
3.4
钢结构房屋震害设计
长细比限值: 对8度和9度抗震设防的结构,其长细比限制在60 235 / fay 以
下,7度时为80 235 / fay,6度时则为120 235 / fay 。
72-100
Nb/Af
9度 9
30 72-100
Nb/Af
梁的整体侧向扭转失稳:除按一般要求设置侧向支承外,尚应 在塑性铰处设侧向支承。
3.4
其中:
钢结构房屋震害设计
建筑抗震支吊架地震作用计算方法评述

建筑抗震支吊架地震作用计算方法评述
丁幼亮;梁启慧;朱浩樑;钱东升
【期刊名称】《建筑设计管理》
【年(卷),期】2017(000)011
【摘要】准确计算建筑抗震支吊架的地震作用是其抗震设计的基础问题.本文介绍了建筑抗震支吊架的三种地震作用计算方法——等效侧力法、楼面反应谱法和时程分析法的基本原理和应用现状.从计算精度、计算效率和工程实用性等方面详细阐述了三种计算方法的优势和存在的问题,给出了有待进一步研究的课题.
【总页数】3页(P72-73,90)
【作者】丁幼亮;梁启慧;朱浩樑;钱东升
【作者单位】江苏壹鼎崮机电科技有限公司,南京 210012;东南大学土木工程学院,南京 210096;江苏壹鼎崮机电科技有限公司,南京 210012;东南大学土木工程学院,南京 210096;江苏壹鼎崮机电科技有限公司,南京 210012
【正文语种】中文
【中图分类】TU318
【相关文献】
1.BIM技术在医院建筑抗震支吊架设计中的应用 [J], 李明
2.抗震支吊架地震作用计算方法的适用性研究 [J], 赖光书;丁幼亮;朱浩樑;梁启慧
3.建筑抗震支吊架生产及施工应用现状与展望 [J], 王伟蔚;姜新华;潘邻
4.3种建筑抗震支吊架的力学性能对比探究 [J], 王伟蔚;姜新华;潘邻
5.地震作用下建筑抗震支吊架体系的动力放大系数研究 [J], 董逸轩;丁幼亮;朱浩樑
因版权原因,仅展示原文概要,查看原文内容请购买。
