北师大版七年级数学勾股定理知识点
七年级勾股定理知识点归纳

七年级勾股定理知识点归纳随着数学教育的普及和深入,勾股定理作为数学的基础知识已成为七年级数学必备的知识点之一。
在学习勾股定理时,可能会遇到一些问题和难点。
接下来,我们将对七年级勾股定理的知识点进行全面归纳,希望能够帮助大家更好地掌握这一重要知识点。
勾股定理的基本概念勾股定理,也叫做“毕达哥拉斯定理”,是由古希腊数学家毕达哥拉斯发现的一条基本定理,主要是用于描述直角三角形中各边的关系。
在三角形ABC中,若∠C=90度,则c为斜边,a、b为两条直角边,勾股定理的表达式为:c²=a²+b²。
七年级勾股定理知识点的学习方法1. 熟记勾股定理的公式:c²=a²+b²。
2. 学会判断直角三角形:在判断三角形是否是直角三角形时,需要使用勾股定理。
3. 掌握勾股定理的应用:勾股定理除了用于计算直角三角形的三边之外,还可以用于计算三角形的面积、判定三角形是否为等腰三角形等。
4. 多进行练习:要熟练掌握各种场合下的勾股定理应用,需要多进行习题练习。
勾股定理的推导勾股定理是数学家毕达哥拉斯在公元前五世纪发现的,他使用了古希腊的几何学方法来证明这个定理,被誉为“毕氏定理”。
在勾股定理的推导过程中,一般使用几何分析或代数分析的方法。
几何分析方法:使用几何方法来证明勾股定理,主要是通过画图、观察图形的平移、旋转等,得到三角形的各边的关系,从而证明勾股定理的正确性。
代数分析方法:使用代数方法来证明勾股定理,主要是通过利用代数数量的符号和方程来证明三角形三条边的关系,从而证明勾股定理的正确性。
在学习七年级勾股定理时,可以通过结合几何分析和代数分析的方法,来加深对勾股定理的理解和记忆。
勾股定理的应用举例1. 计算三角形的面积:如果三角形三边已知,则可以用勾股定理求出斜边的长度,进而根据海伦公式(面积=sqrt[p*(p-a)*(p-b)*(p-c)])来计算三角形的面积。
中考数学考点大串讲(北师大版):勾股定理必刷易错30题(解析版)

专题01勾股定理(易错30题3种题型)一、探索勾股定理1.(2023春·辽宁抚顺·八年级统考期末)在ABC 中,5AB AC ,6BC ,D 是BC 的中点,则ABC 的面积为()A .12B .24C .10D .20【答案】A【分析】如图,过A 作AD BC 于,D 证明224,3,CD BD AD AC CD再利用三角形的面积公式可得答案.【详解】解:如图,过A 作AD BC 于,D 5,6AB AC BC ,∴223,4,CD BD AD AC CD ∴116412.22ABC S BC AD 故选A .【点睛】本题考查的是等腰三角形的性质,勾股定理的应用,证明CD BD 是解本题的关键.2.(2023春·山东临沂·八年级校考阶段练习)如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A 、B 、C 、D 的面积分别是3、5、2、3,则最大正方形E 的面积是()A .13B .14C .15D .26【答案】A 【分析】分别设正方形F 、G 、E 的边长为x 、y 、z ,由勾股定理得出29x ,26y ,222z x y ,即最大正方形E 的面积为2z .【详解】解:如图,分别设正方形F 、G 、E 的边长为x 、y 、z ,则由勾股定理得:2358x ,2235y ,222z x y ,即最大正方形E 的面积为:28513z .故选:A .【点睛】本题考查了勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.3.(2023春·辽宁营口·八年级校考阶段练习)如图,在ABC 中,CE 平分ACB 交AB 于点E ,CF 平分ACD ,EF BC ∥,EF 交AC 于点M ,若5CM ,则22CE CF ()A .75B .100C .120D .125【答案】B 【分析】根据角平分线的定义推出ECF △为直角三角形,然后根据勾股定理即可求得222CE CF EF ,进而可求出22CE CF 的值.【详解】解:CE ∵平分ACB ,CF 平分ACD ,12ACE ACB ,12ACF ACD ,即1()902ECF ACB ACD ,EFC 为直角三角形,又EF BC ∥∵,CE 平分ACB ,CF 平分ACD ,ECB MEC ECM ,DCF CFM MCF ,5CM EM MF ,10EF ,由勾股定理可知222100CE CF EF .故选:B .【点睛】本题考查角平分线的定义,直角三角形的判定以及勾股定理的运用,解题的关键是首先证明出ECF △为直角三角形.4.(2023春·安徽合肥·八年级校考期中)在ABC 中,A B C 、、所对的边分别为a b c 、、,且4,5,7a b c ,则ABC 的面积为.【答案】46【分析】作CD AB 于点D ,设AD x ,则7BD x ,先根据2222AC AD BC BD 求出x ,再求出CD ,然后根据三角形的面积公式计算即可.【详解】解:作CD AB 于点D ,设AD x ,则7BD x ,由勾股定理得,2222AC AD BC BD ,∴ 2222547x x ,解得297x =,∴22222986577CD AC AD,∴ABC 的面积为∶1186746227AB CD .故答案为:46.【点睛】本题考查了勾股定理,熟练掌握勾股定理是解答本题的关键.在直角三角形中,如果两条直角边分别为a 和b ,斜边为c ,那么222 a b c .也就是说,直角三角形两条直角边的平方和等于斜边的平方.5.(2023春·海南海口·八年级统考开学考试)如图,在Rt ABC △中,90BAC ,4BC ,分别以AB AC 、为直径作半圆,面积分别记为1S 、2S ,则12S S .【答案】2π【分析】根据半圆面积公式结合勾股定理,知12S S 等于以斜边为直径的半圆面积.【详解】解:2222121111228228AB AC S AB S AC ,所以 2221211288S S AC AB BC ,故答案为:2π.【点睛】此题根据半圆的面积公式以及勾股定理证明:以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积,重在验证勾股定理.6.(2022秋·山东泰安·七年级统考期中)如图,把一块等腰直角三角形零件(ABC ,其中90ACB ),放置在一凹槽内,三个顶点A 、B 、C 分别落在凹槽内壁上,已知90ADE BED ,测得3cm 4cm AD BE ,,该三角形零件的面积为2cm .【答案】12.5/1122/252【分析】先证明ACD CBE ≌得到4cm CD BE ,利用勾股定理求出5cm AC ,再根据三角形面积公式进行求解即可.【详解】解:∵90ACB ,∴90DCA ECB ,∵90ADE BED ,∴90DAC DCA ,∴DAC ECB ,又∵AC CB ,∴ AAS ACD CBE △≌△,∴4cm CD BE ,在Rt ADC 中,由勾股定理得225cm AC AD CD ,∴2112.5cm 2ABC S AC BC △,∴该三角形零件的面积为212.5cm ,故答案为:12.5.【点睛】本题主要考查了全等三角形的性质与判定,勾股定理,证明ACD CBE ≌得到4cm CD BE 是解题的关键.7.(2023春·湖北恩施·八年级统考期中)如图,在55 的正方形网格中,每一个小正方形的顶点为格点,且每一个小正方形的边长为1四边形ABCD 为格点四边形.(1)求AD 的长;(2)仅用无刻度的直尺过点C 作CE AD ,垂足为E ,并简单说明理由.【答案】(1)5(2)见解析【分析】(1)利用勾股定理即可求解;(2)选取格点,,,F H G M ,作射线,MF GH ,两射线的交点为I ,连接CI 交AD 于点E ,则点E 为所求的点.【详解】(1)解:由图可知,AD 是直角边分别为3,4的直角三角形的斜边故22345AD (2)解:选取格点,,,F H G M ,作射线,MF GH ,两射线的交点为I ,连接CI 交AD 于点E ,则点E 为所求的点.取格点,K L ,∵4,3,90IK AL CK DL CKI DLA∴IKC ALD△≌△KIC DAC90DAC ACE KIC ACECE AD【点睛】本题考查了勾股定理、全等三角形的判定与性质.熟记相关数学结论是解题关键.8.(2023春·广西贺州·八年级统考期中)如图,在Rt ABC △中,90C ,AM 是中线,MN AB ,垂足为点N ,求证:222AN BN AC .【答案】见解析【分析】在直角三角形BNM 和ANM 中利用勾股定理可以得到222BN BM MN ,222AN AM MN ,然后得到22222222()()BN AN BM MN AM MN BM AM ;又在直角三角形AMC 中,222AM AC CM ,代入前面的式子中即可得出结论.【详解】解:证明:MN AB ∵于N ,222BN BM MN ,222AN AM MN 2222BN AN BM AM ,又90C ∵,222AM AC CM 22222BN AN BM AC CM ,又BM CM ∵,222BN AN AC ,即222AN BN AC .【点睛】本题考查了勾股定理、三角形的中线;熟练掌握勾股定理,并能进行推理论证是解决问题的关键.9.(2023秋·河南南阳·八年级校考期末)如图,长方形ABCD 中,点E 在边AB 上,将长方形ABCD 沿直线DE 折叠,点A 恰好落在边BC 上的点F 处,若5AE ,3BF ,求CD 的长【答案】9【分析】由折叠的性质可知5EF AE ,再结合勾股定理即可求解.【详解】解:由折叠的性质可知5EF AE .∵四边形ABCD 为长方形,∴90B Ð=°,AB CD ,∴2222534BE EF BF ,∴549CD AB AE BE .即CD 的长为9.【点睛】本题考查折叠的性质,勾股定理,解题的关键是掌握折叠前后对应边相等.10.(2023春·陕西商洛·八年级校考期中)如图,一文物C (看作一点)被探明位于地面A 点垂直往下36米处,由于A 点下有障碍物,考古人员不能垂直下挖,他们从距离A 点15米的B 处斜着挖掘,已知障碍物不在线段BC 上,则要取出文物C 至少要挖()A .39米B .3119米C .42米D .51米【答案】A 【分析】根据题意可知:14,4890AB AC BAC ,,然后根据勾股定理求解即可.【详解】解:∵14,4890AB AC BAC ,,∴2222153639BC AB AC .故选:A .【点睛】本题考查了勾股定理的应用,将实际问题抽象成勾股定理是解题的关键.11.(2023春·河北保定·八年级校考期中)利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图,在用弦图验证勾股定理时,用到的面积相等关系是()A .ABH EFGHS S 正方形△B .ABCD EFGH S S 正方形正方形C .4ABH EFGH ABCDS S S 正方形正方形△D .2ABH ABCD EFGHS S S 正方形正方形△【答案】C 【分析】设DE AH BG CF a ,AE BH CG DF b ,根据题意求出224ABH EFGH S S a b 正方形 ,22ABCD S a b 正方形,进而求解即可.【详解】设DE AH BG CF a ,AE BH CG DF b ,∴ 2221442ABH EFGH S S b a ab a b 正方形 ,22222ABCD S AD DE AE a b 正方形,∴4ABH EFGH ABCD S S S 正方形正方形△.故选:C .【点睛】此题考查了勾股定理的证明,解题的关键是熟练掌握以上知识点.12.(2023秋·全国·八年级专题练习)边长为1的正方形OABC 在数轴上的位置如图所示,点B 表示的数是()A .1B .2C .3D .5【答案】B 【分析】由于正方形OABC 的边长为1,可知OAB 为等腰直角三角形,可利用勾股定理求出OB 的长,即可得到B 点表示的数.【详解】解:∵正方形OABC 的边长为1,∴在等腰直角OAB 中,22112OB =+=.故选:B .【点睛】本题考查了勾股定理,根据四边形OABC 为正方形判断出OAB 为直角三角形是解题的关键.13.(2023春·河南新乡·八年级统考期中)《九章算术》卷九中记载:今有立木,系索其末,委地四尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺,牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽,问绳索长是()A .5尺B .6尺C .8尺D .10尺【答案】D【分析】根据题意得,绳索,木桩形成直角三角形,根据勾股定理,即可求出绳索长.【详解】解:设绳索长为x 尺∴根据题意得: 22248x x 解得10x .∴绳索长为10尺,故选:D .【点睛】本题考查勾股定理的知识,解题的关键是理解题意,运用勾股定理解决实际问题.14.(2023春·重庆忠县·八年级校考阶段练习)如图,这是某种牛奶的长方体包装盒,长、宽、高分别为5cm 、4cm 、12cm ,插吸管处的出口到相邻两边的距离都是1cm ,为了设计配套的直吸管,要求插入碰到底面后,外露的吸管长度要在3cm 至5cm 间(包括3cm 与5cm ,不计吸管粗细及出口的大小),则设计的吸管总长度L 的范围是.【答案】16cm 17cmL 【分析】当吸管与长方体上、下底面垂直时,位于盒体内的长度最短,为12cm ,则15cm 17cm L ;如图,当吸管底端位于点A 时,位于盒体内的长度最长,经过点A ,D ,E 的截面如下图1,根据勾股定理分别求得,5cm DE ,Rt ADE △中,13cm AE ,则16cm 18cm L ;综上,吸管垂直于底面时外露的部分最长,底端底端位于点A 时,外露的部分最短,所以吸管长度范围为16cm 17cm L .【详解】解:当吸管与长方体上、下底面垂直时,位于盒体内的长度最短,为12cm ,外露的吸管长度要在3cm 至5cm 间,则15cm 17cm L ;如图,当吸管底端位于点A 时,位于盒体内的长度最长,经过点A ,D ,E 的截面如下图1,如图2为长方体上底面,5cm DG ,4cm CG ,1cm EH CH JG ,∴4cm DJ DG JG ,3cm JE GH CG CH ,∴225cm DE DJ JE .如图1,Rt ADE △中,222212513(cm)AE AD DE ,外露的吸管长度要在3cm 至5cm 间,则16cm 18cm L ;综上,吸管垂直于底面时外露的部分最长,底端位于点A 时,外露的部分最短,所以吸管长度范围为16cm 17cm L .【点睛】本题考查长方体的截面图,勾股定理;具备一定的空间想象能力,熟练勾股定理的运用是解题的关键.15.(2023春·广东惠州·八年级校考开学考试)直角三角形的斜边长为13,其中一条直角边长为12,把四个相同的直角三角形拼成如图所示的正方形,则阴影部分的面积为.【答案】120【分析】根据勾股定理求出AE 的长度,再根据三角形的面积公式求出AEF △的面积,即可求出阴影部分面积.【详解】解:在Rt AEF 中,222213125AE EF AF ,∴110251232AEF S AE AF ,∴阴影部分的面积430120 .故答案是:120.【点睛】本题主要考查了勾股定理,解题的关键是掌握直角三角形两直角边平方和等于斜边平方.16.(2023春·全国·八年级期末)如图,长方形ABCD 的边AD 在数轴上,若点A 与数轴上表示数1 的点重合,点D 与数轴上表示数4 的点重合,1AB ,以点A 为圆心,对角线AC 的长为半径作弧与数轴负半轴交于一点E ,则点E 表示的数为.【答案】110 /101【分析】根据勾股定理计算出AC 的长度,进而求得该点与点A 的距离,再根据点A 表示的数为1﹣,可得该点表示的数.【详解】解:在长方形ABCD 中,1(4)31AD AB CD ,,∴22223110AC AD CD ,则点A 到该交点的距离为10,∵点A 表示的数为1 ,∴该点表示的数为:110 ,故答案为:110 .【点睛】此题主要考查了勾股定理的应用,解决本题的关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方和一定等于斜边长的平方.17.(2023秋·河南省直辖县级单位·八年级校联考期末)对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.(1)如图1所示的大正方形,是由两个正方形和两个形状大小完全相同的长方形拼成的.用两种不同的方法计算图中空白部分的面积,可以得到的数学等式是_______;(2)将图1中两个阴影的长方形沿着对角线切开,则可以得到四个全等的直角三角形,其中两直角边长分别为,a b ,斜边长为c ,将这四个直角三角形拼成如图2所示的大正方形时,中间空白图形是边长为c 的正方形.试通过两种不同的方法计算中间正方形的面积,并探究a b c 、、之间满足怎样的等量关系.(3)应用:已知直角三角形两条直角边长为6和8,求这个直角三角形斜边上的高.【答案】(1)2222()a b ab a b (2)222c a b(3)245【分析】(1)空白部分是两个正方形的面积和,空白部分也可以看出大正方形的面积减去两个长方形的面积即可得出答案;(2)中间的是边长为c 的正方形,因此面积为2c ,也可以从边长为()a b 正方形面积减去四个直角三角形的面积即可;(3)利用(2)中等式求出斜边,再利用面积法求出结果.【详解】(1)解:方法一:空白部分是两个正方形的面积和,即22a b ;方法二:空白部分也可以看作边长为()a b 的面积,减去两个长为a ,宽为b 的长方形面积,即2()2a b ab ,由两种方法看出2222()a b ab a b ,故答案为:2222()a b ab a b ;(2)中间正方形的边长为c ,因此面积为2c ,也可以看作从边长为()a b 的面积减去四个两条直角边分别a 、b 的面积,即22()2c a b ab ,整理得:222c a b ;(3)∵6a ,8b ,∴斜边226810c ,∴斜边上的高为6824105 ,答:斜边的长为245.【点睛】本题考查完全平方公式的几何背景,勾股定理的证明,解题的关键是结合图形,利用面积得出等量关系.18.(2023春·山西忻州·八年级统考期末)阅读与思考阅读下列材料并完成相应的任务.我国是最早了解和应用勾股定理的国家之一,古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用,古希腊数学家毕达哥拉斯首先证明了勾股定理,在西方,勾股定理又称为“毕达哥拉斯定理”.关于勾股定理的研究还有一个很重要的内容是勾股数组,在课本中我们已经了解到“能够成为直角三角形三条边的三个正整数称为勾股数”.以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:方法1:若m 为奇数 3m ,则a m , 2112b m 和2112c m 是勾股数.方法2:若任取两个正整数m 和 n m n ,则22a m n ,2b mn ,22c m n 是勾股数.任务:(1)在以上两种方法中任选一种,证明以a ,b ,c 为边长的ABC 是直角三角形.(2)学校园林设计师按照如图所示的方式摆放兰花,已知这四个直角三角形全等,且直角三角形的三边是勾股数,较短的直角边长为7m ,要求在每个直角三角形的三个顶点处需要摆放一盆兰花,每个直角三角形的三条边间隔1米摆放一盆兰花,请你计算出总共需要的兰花数量.【答案】(1)见解析(2)总共需要兰花220盆【分析】(1)方法一:21(1)02m c a ,10c b 得c a ,c b ,进行计算得222221=(1)2a b m c,即可得;方法二:先求出a 、b 、c 的平方,即可作答,(2)根据这四个直角三角形全等,且直角三角形的三边是勾股数,较短的直角边长为7m 得角三角形的三边长为7m 24m 25m ,,,则方形AHFD 的边长为31m ,正方形BCEG 的边长为25m ,根据个直角三角形的三个顶点处需要摆放一盆兰花,每个直角三角形的三条边间隔1米摆放一盆兰花,即可得正方形AHFD 上摆放兰花的盆数,方形BCEG 上摆放兰花的盆数,即可得【详解】(1)解:方法一:∵ 222111121(1)0222c m m m c m a m,10c b ,∴c a ,c b ,222224222211(+21)=1(121)42a b m m m m c m ,∴a ,b ,c 为边长的ABC 是直角三角形;方法二:∵22a m n ,2b mn ,22c m n ,∴424222m m a n n ,2224b m n ,422242c m m n n ,∴222 a b c ,∴a ,b ,c 为边长的ABC 是直角三角形;(2)解:∵这四个直角三角形全等,且直角三角形的三边是勾股数,较短的直角边长为7m ,∴直角三角形的三边长为7m 24m 25m ,,,∴正方形AHFD 的边长为:7+24=31(m),正方形BCEG的边长为:25m,∵在每个直角三角形的三个顶点处需要摆放一盆兰花,每个直角三角形的三条边间隔1米摆放一盆兰花,∴正方形AHFD上摆放兰花的盆数为:32+31+31+30=124(盆),正方形BCEG上摆放兰花的盆数为:244=96(盆),∴总共需要的兰花数量为:124+96=220(盆),答:总共需要兰花220盆.【点睛】本题考查了勾股数的应用,解题的关键是理解题意,掌握这些知识点.19.(2023秋·全国·八年级专题练习)问题情境:勾股定理是一个古老的数学定理,它有很多种证明方法.下面利用拼图的方法探究证明勾股定理.定理表述:(1)请你结合图1中的直角三角形,叙述勾股定理(可以选择文字语言或符号语言叙述);尝试证明:(2)利用图1中的直角三角形可以构造出如图2的直角梯形,请你利用图2证明勾股定理.定理应用:(3)某工程队要从点A向点E铺设管道,由于受条件限制无法直接沿着线段AE铺设,需要绕道沿着矩形的边AB和BC铺设管道,经过测量16BE 米,已知铺设每米管道需资金1000元,请你帮助工AB 米,12程队计算绕道后费用增加了多少元?【答案】(1)见解析;(2)见解析;(3)8000元【分析】(1)根据题意可直接进行求解;(2)根据等积法可进行求解;(3)利用勾股定理可进行求解.【详解】解:(1)如果直角三角形的两条直角边长分别为,a b ,斜边长为c ,那么222a b c (2) 21122S a b a b a b 梯形,2ABE ABCS S S 梯形211222c ab 212c ab ,∴221122a b c ab ,∴222 a b c ;(3)在Rt ABE △中,2220AE AB BE ,∴ 16122010008000 (元);答:增加了8000元.【点睛】本题主要考查勾股定理的应用,熟练掌握勾股定理是解题的关键.20.(2023春·浙江台州·八年级统考期末)如图,池塘边有两点A ,B ,点C 是与BA 方向成直角的AC 方向上一点,测得18m,30m AC BC .求A ,B 两点间的距离.【答案】A ,B 两点间的距离是24m【分析】直接由勾股定理求出AB 的长即可.【详解】解:由题意可知,90,18m,30m BAC AC BC ,∴ 2222301824m AB BC AC ,答:A ,B 两点间的距离是24m .【点睛】本题考查了勾股定理的应用,解答本题的关键是明确题意,利用勾股定理求出AB 的长.三、勾股定理的应用21.(2023秋·安徽芜湖·九年级校考开学考试)如图是放在地面上的一个长方体盒子,其中18cm AB ,12cm BC ,10cm BF ,点M 在棱AB 上,且6cm AM ,N 是FG 的中点,一只蚂蚁要沿着长方体盒子的表面从点M 爬行到点N ,它需要爬行的最短路程为()A .20cmB .2106cmC . 12234cmD .18cm【答案】A 【分析】利用平面展开图有两种情况,画出图形利用勾股定理求出MN 的长即可.【详解】解:如图1,∵18cm AB ,12cm BC GF ,N 是FG 的中点,∴16cm 2FN FG ,∴ 18612cm BM , 10616cm BN ,∴ 22121620cm MN ;如图2,∵18cm AB ,12cm BC GF ,N 是FG 的中点,∴16cm 2FN FG ,∴ 186618cm PM ,10cm NP ,∴2218424210610MN .∵202106 ,∴蚂蚁沿长方体表面从点M 爬行到点N 处的最短路程为20cm .故选:A .【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用,利用展开图有两种情况分析得出是解题关键.22.(2023春·山东临沂·八年级校考阶段练习)一艘轮船以16海里/时的速度离开港口向东南方向航行,另一艘轮船同时以12海里/时的速度离开港口向西南方向航行,经过1.5小时后它们相距()A .25海里B .30海里C .40海里D .32海里【答案】B【分析】根据题意,画出图形,且东北和东南的夹角为90 ,根据题目中给出的1.5小时和速度可以计算AC ,BC 的长度,在直角ABC 中,已知AC ,BC 可以求得AB 的长.【详解】解:如图,作出图形,因为东南和西南的夹角为90 ,所以ABC 为直角三角形.在Rt ABC △中,16 1.524(km)AC ,121.518(km)BC ,则2222241830(km)AB AC BC故选:B .【点睛】本题考查了勾股定理在实际生活中的应用,本题中确定ABC 为直角三角形,并且根据勾股定理计算AB 是解题的关键.23.(2023春·河南信阳·八年级校联考阶段练习)某数学兴趣小组开展了关于笔记本电脑的张角大小的实践探究活动.如图,当张角为BAF 时,顶部边缘B 处离桌面的高度BC 为7cm ,此时底部边缘A 处与C 处间的距离AC 为24cm ,小组成员调整张角的大小继续探究,最后发现当张角为DAF 时(点D 是点B 的对应点),顶部边缘D 处到桌面的距离DE 为15cm ,则底部边缘A 处与E 之间的距离AE 为()A .20cmB .18cmC .12cmD .10cm【答案】A 【分析】勾股定理解Rt ABC △得出25cm AB ,勾股定理解Rt ADE △即可求解.【详解】解:依题意,247AC BC ,,在Rt ABC △中, 2225cm AB AC BC ,∵AB AD 25 ,15DE ,在Rt ADE △中, 2222251520cm AE AD DE,故选:A .【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.24.(2023春·四川南充·八年级校考期中)如图由于台风的影响,一棵树在离地面6m 处折断,树顶落在离树干底部8m 处,则这棵在折断前(不包括树根)长度是.【答案】16m /16米【分析】根据大树折断部分、下部、地面恰好构成直角三角形,根据勾股定理解答即可.【详解】解:如图,由题意得m ,8m 6BC AC ,在直角三角形ABC 中,根据勾股定理得:226810AB (米).所以大树的高度是10616 (米).故答案为:16m .【点睛】本题考查了勾股定理的应用,关键是熟练掌握勾股定理:直角三角形中,两直角边的平方和等于斜边的平方.25.(2023春·湖北咸宁·八年级统考期末)如图,一梯子AB 斜靠在竖直的墙AO 上,测得5m AO ,若梯子的顶端沿墙下滑1m ,这时梯子的底端也沿水平方向向外滑动1m ,梯子到CD 的位置,则梯子的长度为m .【答案】41【分析】设m BO x ,利用勾股定理用x 表示出AB 和CD 的长,进而求出x 的值,然后由勾股定理求出AB 的长度.【详解】解:设m BO x ,由题意得:1m AC ,1m BD ,5m AO ,在Rt AOB △中,根据勾股定理得:222225AB AO OB x ,在Rt COD 中,根据勾股定理得: 22222511CD CO OD x ,∴ 22225511x x ,解得:4x ,∴ 22225441m AB AO BO ,即梯子AB 的长为41m .故答案为:41.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理,由勾股定理得出方程是解题的关键.26.(2023秋·八年级课时练习)《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架,其中记载了一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面x 尺,则根据题意列方程为:.【答案】 222310x x 【分析】设折断处离地面x 尺,根据勾股定理建立方程即可求解.【详解】解:如图,设折断处离地面x 尺,根据题意可得:2223(10x)x ,.故答案为:2223(10x)x 【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.27.(2023春·河北保定·八年级统考期末)如图,矩形ABCD 中,8cm AB ,12cm BC ,动点P 从点A 出发沿A B C D A 运动,速度是2cm /秒;点Q 从点C 出发沿C B A D C 运动,速度是4cm /秒,设它们的运动时间为t 秒.(1)当1t 时,连接PQ ,PQcm ;(2)若P 、Q 两点第一次相遇时,t秒;第2次相遇时,t 秒.【答案】1010310【分析】(1)先求得8216BP ,12418BQ ,再利用勾股定理即可求解;(2)根据相遇时间=总路程÷速度和得出第一次相遇的时间,再求出第二次相遇的时间即可.【详解】解:(1)当1t 时,8216BP ,12418BQ ,∴226810PQ ,故答案为:10(2)若P 、Q 两点第一次相遇时,10812243t (秒),从第一次相遇到第二次相遇需要的时间为: 202812243,故P 、Q 两点第2次相遇时,10201033t(秒)故答案为:103;10.【点睛】本题考查了勾股定理的应用、行程问题中的相遇问题.抓住“相遇时间=路程和÷速度和”是解题关键.28.(2023秋·河南郑州·八年级郑州市扶轮外国语学校校考开学考试)如图,长方体的长15cm BE ,宽10cm AB ,高20cm AD ,点M 在CH 上.且5cm CM .(1)求线段DM的长;(2)一只蚂蚁如果耍沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?【答案】(1)55DM(2)蚂蚁爬行的最短距离是25cmCD ,利用勾股定理即可求解;【分析】(1)根据长方体的性质求出10(2)将立体图形展开成平面图形,然后根据两点之间线段距离最短,利用根据勾股定理进行求解,根据立体展开成平面图形情况分类讨论进行进行比较.【详解】(1)解:10CM ,AB CD∵,52222,10555DM CD CM线段DM的长为55.(2)解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm22AM2010525cm要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:22AM20510529cm只要把长方体的上表面剪开与左面所在的平面形成一个长方形,如第个图32220105537cmAM∵25529537∴蚂蚁爬行的最短距离是25cm.【点睛】本题考查了勾股定理的拓展应用,“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.29.(2020秋·广东佛山·八年级校考阶段练习)如图,小巷左右两侧是竖直的墙,巷子宽5米,一架梯子斜靠在左墙时,梯子顶端到地面的距离AC 为3米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离ED 为2米,则CB 的长度为多少?【答案】CB 的长度为2米.【分析】根据勾股定理222AC BC AB ,222BD DE BE ,列方程即可得到结论.【详解】解:根据勾股定理得,222AC BC AB ,222BD DE BE ,∵AB BE ,∴2222AC BC BD DE ,∴ 2222352BC BC ,∴2BC ,答:CB 的长度为2米.【点睛】本题主要考查了勾股定理的应用,解题的关键是掌握勾股定理.30.(2023春·云南昭通·八年级统考期中)如图,四边形ABCD 为某街心花园的平面图,经测量50m AB BC AD ,503m CD ,且90B Ð=°.(1)试判断ACD 的形状,并说明理由;(2)若射线BA 为公园的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点D 处安装一个监控装置来监控道路BA 的车辆通行情况,且被监控的道路长度要超过65m .已知摄像头能监控的最大范围为周围50m (包含50m ),请问该监控装置是否符合要求?并说明理由.(参考数据2 1.4 ,3 1.7 )【答案】(1)直角三角形,见解析(2)符合要求,见解析【分析】(1)根据90B Ð=°,勾股定理求出AC ,再根据勾股定理的逆定理,即可;(2)过点D 作DE BA 于点E ;作A 点关于DE 的对称点A ,连接DA ,根据直角三角形的性质,得45BAC ,根据90DAC ,则45DAE ∠,三角形ADE 是等腰直角三角形,根据勾股定理求出AE ,可推出AA ,即可.【详解】(1)解:(1)ACD 是直角三角形.理由如下:∵90B Ð=°,50m AB BC AD ,∴在Rt ABC △中222AB BC AC ,∵25000AC ,∵22502500AD , 25037500CD ,∴227500AD AC ,∴22AD AC CD ,∴CAD 是直角三角形.(2)符合要求,理由如下:过点D 作DE BA 于点E ;作A 点关于DE 的对称点A ,连接DA ,∴90DEA ,∵90B Ð=°,AB BC ,∴45BAC ,∵90DAC ,∴45DAE ∠,∴DE AE ,∴在Rt DEA V 中222DE EA AD ,∴222500AE ,∴252AE ,∴50270m AA ,∵70m 65m ,∴该监控装置符合要求.。
第1章第1课时 探索勾股定理PPT课件(北师大版)

2.(2018·山东滨州)在直角三角形中,若勾为 3,股
为 4,则弦为( A )
A.5
B.6
C.7
D.8
3.在一个直角三角形中,两直角边长分别为 3 和 4,
下列说法正确的是( C )
A.斜边长为 25
B.该三角形的周长为 25
C.斜边长为 5
D.该三角形的面积为 20
4.如图,在由边长均为 1 个单位长度的小正方形组 成的网格中,点 A,B 都是格点,则线段 AB 的长为( A )
1.下列说法正确的是( D ) A.若 a,b,c 是△ABC 的三边,则 a2+b2=c2 B.若 a,b,c 是 Rt△ABC 的三边,则 a2+b2=c2 C.若 a,b,c 是 Rt△ABC 的三边,∠A=90°, 则 a2+b2=c2 D.若 a,b,c 是 Rt△ABC 的三边,∠C=90°,则 a2+b2=c2
变式 3 飞机在空中水平飞行,某一时刻刚好飞到一 个男孩头顶上方 3 km 处,过了 20 s,飞机距离这个男孩 头顶 5 km(如图).这一过程中飞机飞行的速度是每秒多 少千米?
解:在 Rt△ABC 中,BC2=52-32=16. 因为 BC>0,所以 BC=4(km). 4÷20=0.2(km/s). 答:这一过程中飞机飞行的速度是每秒 0.2 千米.
A.5 C.7
B.6 D.25
5.已知在 Rt△ABC 中,∠C=90°,∠A,∠B, ∠C 的对应边分别为 a,b,c.
(1)若 a=3,b=4,则 c=____5____; (2)若 a=40,b=9,则 c=___4_1____; (3)若 a=6,c=10,则 b=____8____; (4)若 c=25,b=15,则 a=___2_0____.
北师大版七年级上册第一章勾股定理1.1.2 探索勾股定理(共30张PPT)

勾股定理的
在1876年一个周末的傍晚,在美国首都华盛顿 的郊外,有一位中年人正在散步,欣赏黄昏的美 景……他走着走着,突然发现附近的一个小石凳上, 有两个小孩正在聚精会神地谈论着什么,时而大声 争论,时而小声探讨.由于好奇心驱使他循声向两 个小孩走去,想搞清楚两个小孩到底在干什么.只 见一个小男孩正俯着身子用树枝在地上画着一个直 角三角形……
b c
∴a2+b2=c2
方法二
2 (a+b) 大正方形的面积可以表示为 ;
也可以表示为c2 + 2ab. a a2+2ab+b2 = c2 +2ab b a b ∵ (a+b)2 = c2 + 2ab
a a
b
c
c
c
b c
∴a2+b2=c2
方法三 c b 大正方形的面积等于
a
c
2
大正方形面积 也可以表示为
1 4 ab (b a ) 2 2 2ab b 2 a 2 2ab a 2 b2 .
∴a2+b2=c2
方法四
b a c a2
c2
b2
∴ a 2 + b 2 = c2
方法五
④
c
③
⑤
b
a
① ②
∴ c2 = b2 + a2
方法六
a
b
S梯形
c c b
1 a b a b 2
2002 年 的 数 学 家 大 会 ( ICM-2002)在北京召开,这 届大会会标 的中央图案正是经 过艺术处理的弦图,这既标志 着中国古代的数学成就 ,又像 一只转动的风车,欢迎来自世 界各地的数学家们!
(完整版)初中数学知识点思维导图(北师大版)
位置与坐标
确定位置
坐标确定位置
平面直角坐标系
1、点的坐标
2、坐标与图形性质
3、两点间距离公式
4、关于x轴、y轴、原点对称点的坐标
轴对称与坐标变化
轴对称与坐标变化(对称、平移、旋转)
第四章
一次函数
函数
1、常量与变量
2、函数概念、关系式、自变量的取值范围、函数值
3、函数图像
4、函数的表示方法
一次函数与正比例函数
七年级上册
第一章
丰富的图形世界
生活中的立体图形
1、认识立体图形
2、点、线、面、体
3、几何体的表面积
展开与折叠
1、几何体的展开图
2、展开图折叠成几何体
3、正方体相对两个面
截一个几何体
截一个几何体
从三个方向看物体的形状
1、简单几何体的三视图
2、简单组合体的三视图
3、由三视图判断几何体
第二章
有理数及其运算
2、代数式
3、列代数式
4、代数式求值
整式
1、单项式与多项式
整式的加减
1、同类项与合并同类项
2、去口号与添括号
3、整式的加减与化简求值
探索与表达规律
数字的变化规律
第四章
基本平面图形
线段、射线、直线
1、线段、射线、直线
2、直线的性质:两点确定一条直线
比较线段的长短
1、线段的性质:两点之间线段最短
2、两点间的距离
2、方程的解
3、等式的性质
4、一元一次方程的定义
求解一元一次方程
1、一元一次方程的解
2、解一元一次方程
3、含绝对值符号的一元一次方程
4、同解方程
北师大版初中数学各册章节知识点总结

北师大版初中数学各册章节知识点总结第一册:《初二上册》1.直角三角形:直角三角形的定义、直角三角形的性质、勾股定理。
2.平面图形的表示:点、线、线段、射线、角度、平行线、垂直线、相交线等基本概念。
3.二次根式:二次根式的定义、运算法则。
4.初中平面几何基本定理:垂线定理、等腰三角形的性质、三角形中位线定理、角平分线定理等。
5.多边形:多边形的定义、正多边形、变位积分、多边形的内角和、多边形的外角和。
6.梅涅劳斯定理:梅涅劳斯定理的概念、定理的应用。
第二册:《初二下册》1.线性方程:线性方程的定义、解线性方程的常用方法。
2.三角函数的定义和初步认识:三角函数的定义、正弦函数、余弦函数、正切函数等。
3.平行线与相交线:平行线的性质、平行线之间的角对、相交线之间的角对等。
4.二次函数:二次函数的基本性质、二次函数图像的性质与应用。
5.海伦公式:海伦公式的概念、海伦公式的应用。
第三册:《初三上册》1.集合:集合的概念、集合的运算、集合的表示等。
2.图形的相似:图形相似的概念、相似比、相似三角形的性质等。
3.三角形的性质:三角形的角与边的关系、角边关系等。
4.空间几何基本概念:欧几里得空间几何学的基本概念、空间图形与平面图形的关系等。
5.高中数学预修知识:比例与相似、复数等。
第四册:《初三下册》1.数系的扩充:有理数和无理数的概念、实数的分类等。
2.几何体的计算:几何体的表面积、几何体的体积等。
3.空间几何基本定理:角的平分线、角的辅助线等。
4.三角恒等式:三角函数的反函数、三角函数的周期等。
第五册:《九年级上册》1.一次函数:一次函数的定义、一次函数图像的性质、线性规律等。
2.向量几何:向量的定义、向量的运算、向量的平行和垂直等。
3.数的四则运算:整数、有理数、无理数的四则运算等。
4.二次方程与不等式:二次方程的定义、解二次方程的方法等。
5.三角形的面积:三角形的名字、面积的计算公式等。
第六册:《九年级下册》1.指数与对数:指数、对数和底数的概念、指数与对数的性质等。
中考数学考点大串讲(北师大版):勾股定理必刷基础30题(解析版)

专题01勾股定理(基础30题3种题型)一、探索勾股定理1.(2023春·黑龙江佳木斯·八年级校考期中)在Rt ABC △中,90C ,12a ,16b ,则c 的长为()A .26B .18C .20D .21【答案】C【分析】根据勾股定理222 a b c ,即可.【详解】∵在Rt ABC △中,90C ,12a ,16b ∴2222121620c a b 故选:C .【点睛】本题考查勾股定理的知识,解题的关键是掌握勾股定理的运用.2.(2022秋·江苏扬州·八年级仪征市第三中学校考阶段练习)下列各组数中,是勾股数的为()A .1,2,3B .4,5,6C .6,8,10D .7,8,9【答案】C【分析】根据勾股定理的逆定理分别进行分析,从而得到答案.【详解】解:A 、221236 ∵, 这组数不是勾股数;B 、222456+¹Q , 这组数不是勾股数;C 、2226810 ∵, 这组数是勾股数;D 、222789 ∵, 这组数不是勾股数,故选:C .【点睛】此题主要考查了勾股数的定义,解答此题要用到勾股定理的逆定理:已知三角形ABC 的三边满足222 a b c ,则ABC 是直角三角形.3.(2023春·河北廊坊·八年级廊坊市第四中学校考期中)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A 、B 、C 、D 的边长分别是3、5、2、3,则正方形E 的面积是()A .47B .37C .34D .13【答案】A 【分析】根据勾股定理:两条直角边的平方和等于斜边的平方,而正方形的面积等于边长的平方,故可得到以斜边为边长的正方形的面积等于两个以直角边为边长的面积之和.【详解】解:由勾股定理得:正方形F 的面积 正方形A 的面积 正方形B 的面积223534 ,同理,正方形G 的面积 正方形C 的面积 正方形D 的面积222313 ,∴正方形E 的面积 正方形F 的面积 正方形G 的面积341347 .故选:A .【点睛】此题考查的是勾股定理,掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解决此题的关键.4.(2023春·福建福州·八年级统考期中)在ABC 中,90C ,若3AB ,则222AB BC AC .【答案】6【分析】利用勾股定理得222BC AC AB ,再代入计算即可.【详解】解:在ABC 中,90C ∵,222BC AC AB ,2222222(3)6AB BC AC AB ,故答案为:6.【点睛】本题主要考查了勾股定理,熟练掌握勾股定理解题的关键.5.(2023·北京丰台·二模)如图所示,正方形网格中,三个正方形A ,B ,C 的顶点都在格点上,用等式表示三个正方形的面积A B C S S S ,,之间的关系.【答案】A B CS S S 【分析】根据勾股定理以及正方形的面积公式即可得到结论.【详解】解:239A S ,2525B S ,正方形C 的边长为223534 ,∴ 23434C S ,∴A B C S S S ,,之间的关系为A B C S S S ,故答案为:A B C S S S ,【点睛】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.6.(2022秋·七年级单元测试)数组3、4、5;5、12、13;7、24、25;9、40、41;……都是勾股数,若n 为直角三角形的一较长直角边,用含n 的代数式表示斜边为.【答案】1n /1n【分析】首先确定各勾股数中的较长直角边、斜边,认真观察,总结规律,不难得出.【详解】解:因为3、4、5中较长直角边是4、斜边是541 ;5、12、13中较长直角边是12、斜边是13121 ;7、24、25中较长直角边是24、斜边是25241 ;9、40、41中较长直角边是40、斜边是41401 ;…∴若n 为直角三角形的一较长直角边,用含n 的代数式表示斜边为1n .【点睛】此题考查勾股数之间的规律,认真观察是关键.7.(2023春·陕西安康·八年级统考期末)已知在ABC 中,906cm 2cm ACB AC BC ,,,求AB 的长.【答案】210cm【分析】利用勾股定理进行求解即可.【详解】解:∵在ABC 中,906cm 2cm ACB AC BC ,,,∴由勾股定理得222262210cm AB AC BC .【点睛】本题主要考查了勾股定理,熟知勾股定理是解题的关键.8.(2023春·山东聊城·八年级统考期中)如图,某人从A 地到B 地共有三条路可选,第一条路是从A 地沿AB 到达B 地,AB 为10米,第二条路是从A 地沿折线AC CB 到达B 地,AC 为8米,BC 为6米,第三条路是从A 地沿折线AD DB 到达B 地共行走26米,若,,C B D 刚好在一条直线上.(1)求证:90C ;(2)求AD 和BD 的长.【答案】(1)见解析(2)AD 的长为17米,BD 的长为9米【分析】(1)通过计算得出222AC BC AB ,再根据勾股定理的逆定理即可证明.(2)先设一条线段长x ,根据已知条件及勾股定理可列出关于x 的方程,然后求解即可.【详解】(1)证明:∵8AC 米,6BC 米,10AB 米,∴222AC BC AB ,∴ABC 是直角三角形,即90C ;(2)解:设AD x 米,则 26BD x 米,∴ 62632CD BC BD x x (米),在Rt ACD 中,由勾股定理得:2228(32)x x ,解得:17x ,则2626179x .答:AD 的长为17米,BD 的长为9米.【点睛】本题考查了勾股定理及其逆定理的应用,设未知数、运用方程解题是本题的关键所在.9.(2022秋·吉林长春·八年级统考期中)如图①、图②均为43 的正方形网格,每个小正方形的顶点称为格点,边长均为1.在图①、图②中按下列要求各画一个三角形.(1)与ABC 全等,以点B 为一个顶点,另外两个顶点也在格点上.(2)与ABC 全等,且不与ABC 重合.【答案】(1)见解析(2)见解析【分析】(1)根据题意画出符合题意的格点三角形即可;(2)根据题意画出对应的全等三角形即可.【详解】(1)解:如图①中,BCE 即为所求,(2)解:如图②所示,BFK 即为所求;【点睛】本题主要考查了画格点三角形,画全等三角形,正确理解题意是解题的关键.10.(2022春·黑龙江哈尔滨·八年级哈尔滨市虹桥初级中学校校考阶段练习)如图所示,在△ABC 中,CD ⊥AB 于D ,AC =4,BC =3,165AD ,求CD 、BD 的长.【答案】CD 的长为125,BD 的长为95【分析】在Rt △ACD 中,利用勾股定理列式求出CD ,在Rt △BCD 中,利用勾股定理列式计算即可求出BD .【详解】解:∵CD ⊥AB ,∴∠ADC =∠BDC =90°,∴△ADC 和△BDC 是直角三角形,在Rt △ACD 中,222AC AD CD ,∴22221612455CD AC AD ,在Rt △BCD 中,222BC CD BD ,∴2222129355BD BC CD ,答:CD 的长为125,BD 的长为95.【点睛】本题考查了勾股定理,根据图形判断出所求的边所在的直角三角形是解题的关键.11.(2023·山西忻州·统考模拟预测)如图是3世纪我国汉代的赵爽在注解《周髀算经》时给出的“赵爽弦图”.他通过对图形的切割、拼接,巧妙地利用面积关系证明的重要数学定理是()A .三角形内角和定理B .勾股定理C .勾股定理的逆定理D .斜边、直角边定理【答案】B 【分析】“赵爽弦图”通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理.【详解】解:由勾股定理相关的数学背景可知:“赵爽弦图”是对勾股定理的验证故选:B【点睛】本题考查了勾股定理的数学背景.熟知相关数学史即可.12.(2023春·山西吕梁·八年级统考期末)如图,毕达哥拉斯用图1,图2证明了.个重要的数学定理,他的思路是图1中拼成的正方形与图2中拼成的正方形面积相等,通过面积相等可以得到:222114422a b ab c ab ,整理得222 a b c .证明的这个定理是()A .勾股定理B .勾股定理的逆定理C .祖暅原理D .费马定理【答案】A 【分析】根据勾股定理作答即可.【详解】解:由222114422a b ab c ab ,整理得222 a b c .而a 、b 、c 是直角三角形的三边,∴证明的定理是勾股定理,故选:A .【点睛】本题主要考查了勾股定理,熟记勾股定理的内容是解题的关键.13.(2023春·河南驻马店·八年级统考期中)我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于下列哪部著名数学著作中()A .《周髀算经》B .《九章算术》C .《海岛算经》D .《几何原本》【答案】A【分析】加强教材的阅读,熟记相关知识的来源与出处.【详解】解:早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中.故选:A .【点睛】本题考查了勾股定理的历史渊源,仔细阅读教材,熟记知识是解题的关键.14.(2023春·黑龙江绥化·八年级校考期中)如下图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm ,则正方形A ,B ,C ,D 的面积之和为2cm .【答案】49【分析】根据勾股定理计算即可【详解】解:最大的正方形的面积为22749cm ,由勾股定理得,正方形E 、F 的面积之和为249cm ,∴正方形A 、B 、C 、D 的面积之和为249cm ,故答案为49.【点睛】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么222 a b c .15.(2023秋·全国·八年级专题练习)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形密铺构成的大正方形.如图,设勾3a ,弦5c ,则小正方形ABCD 的边长..是.【分析】根据勾股定理计算即可解题.【详解】解:根据勾股定理可得2222534b c a ,∴小正方形ABCD 的边长为431 ,故答案为:1.【点睛】本题考查勾股定理,掌握勾股定理是解题的关键.16.(2023春·湖北宜昌·八年级校考期中)如图,数轴上点A 所表示的数为a ,求 a .【答案】15 /51【分析】根据勾股定理算出斜边长度解题即可,注意是从-1开始.【详解】解:如图,由勾股定理得221115BC CA .∵点C 表示-1,∴点A 表示的数是15a .故答案为:15 .【点睛】本题主要考查了数轴的意义和勾股定理,理解数轴的意义的是解答关键.17.(2023秋·全国·八年级专题练习)如图,将两个全等的直角三角形按照如下的位置摆放,使点A ,E ,D 在同一条直线上,90A D ,AE CD a ,AB ED b ,BE CE c .(1)填空:BEC ______ ,根据三角形面积公式,可得BEC 的面积 ______;根据割补法,由梯形的面积减去阴影部分的面积,可得BEC 的面积 ______.(2)求证:222 a b c .【答案】(1)90,212c ,212c【分析】(1)根据全等三角形的判定和性质以及三角形的面积公式即可得到结论;(2)用两种不同的方法表示梯形ABCD 的面积,计算化简后,即可得出222 a b c .【详解】(1)解:AE CD a ∵,AB ED b ,BE CE c ,BAE ≌ SSS EDC ,ABE DEC ,90ABE AEB ∵,90AEB DEC ,90BEC ,BEC 的面积21122BE CE c,由梯形的面积减去阴影部分的面积,可得BEC 的面积22222111112222222a b a b ab a ab b ab a b ab ab c ,故答案为:90,212c ,212c ;(2)证明:Rt ABE ∵ ≌Rt DEC △,AEB DCE ,BE EC c ,90D ∵,90DCE DEC ,90AEB DEC ,90BEC ,BEC 是等腰直角三角形,Rt ABE Rt CDE Rt BEC ABCD S S S S ∵梯形,2222AB CD AD AE AB ED DC BE EC,即2222a b a b ab ba ca ,2222222a ab bc ab ,222a b c .【点睛】本题考查了梯形,勾股定理的证明,用两种不同的方法表示同一个图形的面积是解决问题的关键.18.(2021秋·黑龙江绥化·八年级校考阶段练习)已知某开发区有一块四边形空地ABCD ,如图所示,现计划在空地上种植草皮,经测量∠A =90°,∠CBD =90°,DB =5m ,CD =13m ,DA =4m ,若每平方米草皮需要200元,问需要多少投入【答案】需要投入资金为7200元【分析】仔细分析题目,需要求得四边形的面积才能求得结果,连接BD,在直角三角形CBD中由勾股定理可求BC的长,在直角三角形ABD中可求得BA的长,由此看,四边形ABCD由Rt△ABD和Rt△DBC 构成,则容易求解.【详解】证明:连接BD∵∠A=90°,∠CBD=90°,∴△CBD,△ABD为直角三角形,在Rt△CBD中,BC2=CD2-BD2∴222213512BC CD BDm在△ABD中,AB2=BD2-AD2∴AB=2222543BD ADm∴四边形ABCD面积=S△BAD十S∆DBC=12∙AD∙AB+12∙DB∙BC=1143+512=6+30=3622m2,36×200=7200(元)所以需要投入资金为7200元.【点睛】此题主要考查了勾股定理的应用,得出△CBD,△ABD为直角三角形,用勾股定理求出BC,AB 的长是解题的关键.19.(2022春·八年级单元测试)洋洋想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多2米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.【答案】214米【分析】因为旗杆、绳子、地面正好构成直角三角形,设旗杆的高度为x米,则绳子的长度为(x+2)米,根据勾股定理即可求得旗杆的高度.【详解】解:设旗杆的高度为x米,则绳子的长度为(x+2)米,根据勾股定理可得:x2+52=(x+2)2,解得,x=21 4.答:旗杆的高度为214米.【点睛】此题考查学生利用勾股定理解决实际问题的能力,关键是利用勾股定理即可求得AB的长.20.(2022秋·全国·八年级专题练习)如图,请在数轴上找到表示17的P点.(保留作图痕迹,不写作法)【答案】见解析【分析】因为17=16+1,则首先作出以1和4为直角边的直角三角形,则其斜边的长即是17,再以原点为圆心,以17为半径画弧,和数轴的正半轴交于一点即可.【详解】解:如图,点P即为所求.【点睛】本题考查运用数轴上的点来表示一个无理数,比较基础.21.(2023春·重庆忠县·八年级统考期末)把5米长的梯子斜靠在墙上,若梯子底端离墙4米,则梯子顶端到离地面()A.2米B.3米C.4米D.4.5米【答案】B【分析】根据勾股定理求解即可.【详解】解:∵梯子的长度为5米,梯子底端离地面4米,将梯子长度看作直角三角形的斜边,梯子底端离地面距离看作一条直角边,梯子顶端到地面的距离为:22543 (米),故选B .【点睛】本题考查勾股定理的实际应用,理解题意将实际问题转化为数字问题是解题的关键.22.(2023·浙江·八年级假期作业)如图,垂直地面的旗杆在离地3m 处断裂,旗杆顶部落地点离旗杆底部4m ,则旗杆折断前的高度为()A .6B .7C .8D .9【答案】C 【分析】根据勾股定理两个直角边的平方和等于斜边的平方.此题要求斜边和直角边的长度,解直角三角形即可.【详解】解:旗杆折断后,落地点与旗杆底部的距离为4m ,旗杆离地面3m 折断,且旗杆与地面是垂直的,所以折断的旗杆与地面形成了一个直角三角形.根据勾股定理,折断的旗杆为 22345m ,所以旗杆折断之前高度为3m 5m 8m .故选:C .【点睛】本题考查了勾股定理在解实际问题中的运用,弄清勾股定理存在的条件是重点,解题的关键是理解文字语言的含义.23.(2023秋·八年级课前预习)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC 为0.7m ,梯子顶端到地面的距离AC 为2.4m .如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A D 为1.5m ,则小巷的宽为().A .2.4mB .2mC .2.5mD .2.7m【答案】D【分析】,ACB A BD △△是直角三角形,根据勾股定理即可求解.【详解】解:根据题意可知,,ACB A BD △△是直角三角形,在Rt ABC △中, 2.4AC ,0.7BC ,∴22222(2.4)(0.7) 5.760.49 6.25AB AC BC , 2.5AB ,在Rt A BD 中, 2.5A B AB , 1.5A D ,则2 2.25A D ,∴22 6.25 2.252BD A B A D,∴小巷的宽为0.72 2.7m CB BD ,故选:D .【点睛】本题主要考查勾股定理的运用,掌握勾股定理的运算方法是解题的关键.24.(2023秋·八年级课前预习)如图,一个圆桶底面直径为5cm ,高12cm ,则桶内所能容下的最长木棒为cm .【答案】13【分析】根据题意画出示意图,再根据勾股定理求解,即可.【详解】解:如图,AC 为圆桶底面直径,BC 为圆桶的高,∵5cm AC ,12cm BC ,∴2222512=13cm AB AC BC ,∴桶内所能容下的最长木棒为:13cm .故答案为:13.【点睛】本题考查勾股定理的运用,解题的关键是将实际问题转化为数学问题,灵活运用勾股定理.25.(2023春·新疆乌鲁木齐·八年级校考期中)已知,一轮船以4海里/时的速度从港口A 出发向东北方向航行,另一轮船以3海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,两船相距海里.【答案】10【分析】根据方位角可知两船所走的方向正好构成了直角,然后根据路程=速度×时间,得两条船分别走了8海里和6海里,再根据勾股定理,即可求得两条船之间的距离.【详解】解:∵两船行驶的方向是东北方向和东南方向,∴90BAC ,两小时后,两艘船分别行驶了428 ,326 海里,根据勾股定理得:228610 (海里).故答案为:10.【点睛】本题考查了勾股定理的应用,熟练运用勾股定理进行计算,基础知识,比较简单.26.(2023秋·全国·八年级专题练习)如图,台阶A 处的蚂蚁要爬到B 处搬运食物,则它爬行的最短距离为.【答案】13m/13米【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【详解】解:如图所示,台阶平面展开图为长方形,5AC ,9312BC ,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.由勾股定理得:222AB AC BC ,13AB ,故答案为:13m .【点睛】本题主要考查了平面展开图—最短路径问题,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.27.(2023秋·全国·八年级专题练习)已知一架5m 长的梯子斜靠在一竖直的墙上,这时梯足距墙脚3m ,若梯子的顶端下滑1m ,则梯足将滑动多远?【答案】1米【分析】根据勾股定理求解即可.【详解】解:在直角三角形ABO 中,根据勾股定理可得,22534m OA ,如果梯子的顶度端下滑1米,则413m OA .在直角三角形A B O 中,根据勾股定理得到:4m OB ,则梯子滑动的距离就是431m OB OB .【点睛】本题考查的知识点是勾股定理的应用,掌握勾股定理是解题的关键.28.(2023春·河北廊坊·八年级统考期末)《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根三尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?【答案】9120尺【分析】设折断处离地的高度为x 尺,利用勾股定理建立方程,解方程即可得.【详解】解:设折断处离地的高度为x 尺,由勾股定理得: 222310x x ,解得9120 x ,答:折断处离地的高度为9120尺.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题关键.29.(2023秋·全国·八年级专题练习)如图,点O是位于东西海岸线的一个港口,A,B两艘客轮从港口O 同时出发,A客轮沿北偏东75°航行,航速是每小时18海里,B客轮沿北偏西15°方向航行,航速是每小时24海里,请计算3小时之后两客轮之间的距离.【答案】90海里【分析】根据题意得:∠AOB=75°+15°=90°,OA=18×3=54(海里),OB=24×3=72(海里),再由勾股定理,即可求解.【详解】解:根据题意得:∠AOB=75°+15°=90°,OA=18×3=54(海里),OB=24×3=72(海里),根据勾股定理得:2222547290AB AO BO海里,即3小时之后两客轮之间的距离90海里.【点睛】本题主要考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.30.(2023秋·全国·八年级专题练习)如图是一个棱长为6cm的正方体的有盖纸盒,一只蚂蚁想从盒底的A 点爬到盒顶的B点,其中BC=2cm,那么蚂蚁爬行的最短行程是多少?【答案】10cm【分析】将正方体侧面展开图展开,由勾股定理计算即可.【详解】解:如图所示.∵BC=2cm,棱长为6cm,∴AD=6+2=8(cm),BD=6cm由勾股定理得,AB=2222=10(cm),BD AD86答:蚂蚁爬行的最短行程是10cm.【点睛】此题考查了平面展开一最短路径问题,利用勾股定理是解题的关键.。
北师大版初中数学公式大全

1北师大版初中数学公式大全1过两点有且只有一条直线过两点有且只有一条直线2两点之间线段最短两点之间线段最短3同角或等角的补角相等同角或等角的补角相等4同角或等角的余角相等同角或等角的余角相等5过一点有且只有一条直线和已知直线垂直过一点有且只有一条直线和已知直线垂直6直线外一点与直线上各点连接的所有线段中,垂线段最短直线外一点与直线上各点连接的所有线段中,垂线段最短7平行公理经过直线外一点,有且只有一条直线与这条直线平行平行公理经过直线外一点,有且只有一条直线与这条直线平行8如果两条直线都和第三条直线平行,这两条直线也互相平行如果两条直线都和第三条直线平行,这两条直线也互相平行 9同位角相等,两直线平行同位角相等,两直线平行10内错角相等,两直线平行内错角相等,两直线平行11同旁内角互补,两直线平行同旁内角互补,两直线平行12两直线平行,同位角相等两直线平行,同位角相等13两直线平行,内错角相等两直线平行,内错角相等 14两直线平行,同旁内角互补两直线平行,同旁内角互补15定理三角形两边的和大于第三边定理三角形两边的和大于第三边16推论三角形两边的差小于第三边推论三角形两边的差小于第三边17三角形内角和定理三角形三个内角的和等于180°180°18推论1直角三角形的两个锐角互余直角三角形的两个锐角互余19推论2三角形的一个外角等于和它不相邻的两个内角的和三角形的一个外角等于和它不相邻的两个内角的和20推论3三角形的一个外角大于任何一个和它不相邻的内角三角形的一个外角大于任何一个和它不相邻的内角21全等三角形的对应边、对应角相等全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等边角边公理有两边和它们的夹角对应相等的两个三角形全等23角边角公理有两角和它们的夹边对应相等的两个三角形全等角边角公理有两角和它们的夹边对应相等的两个三角形全等24推论有两角和其中一角的对边对应相等的两个三角形全等推论有两角和其中一角的对边对应相等的两个三角形全等 25边边边公理有三边对应相等的两个三角形全等边边边公理有三边对应相等的两个三角形全等26斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等 27定理1在角的平分线上的点到这个角的两边的距离相等在角的平分线上的点到这个角的两边的距离相等28定理2在角的内部,到一个角的两边的距离相等的点,在这个角的平分线上在角的内部,到一个角的两边的距离相等的点,在这个角的平分线上 29等腰三角形的性质定理等腰三角形的两个底角相等等腰三角形的性质定理等腰三角形的两个底角相等30推论1等腰三角形顶角的平分线平分底边并且垂直于底边等腰三角形顶角的平分线平分底边并且垂直于底边31等腰三角形的顶角平分线、底边上的中线和高互相重合等腰三角形的顶角平分线、底边上的中线和高互相重合32推论3等边三角形的各角都相等,并且每一个角都等于60°60°33等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)角对等边)34推论1三个角都相等的三角形是等边三角形三个角都相等的三角形是等边三角形 35推论2有一个角等于60°的等腰三角形是等边三角形60°的等腰三角形是等边三角形36在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半30°那么它所对的直角边等于斜边的一半 37直角三角形斜边上的中线等于斜边上的一半直角三角形斜边上的中线等于斜边上的一半38定理线段垂直平分线上的点到这条线段两个端点的距离相等定理线段垂直平分线上的点到这条线段两个端点的距离相等39逆定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上逆定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 40定理1关于某条直线对称的两个图形是全等形关于某条直线对称的两个图形是全等形41定理2如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线42定理3两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上43逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称对称44勾股定理直角三角形两直角边a 、b 的平方和、等于斜边c 的平方的平方45勾股定理的逆定理如果三角形的三边长a 、b 、c 有关系,那么这个三角形是直角三角形有关系,那么这个三角形是直角三角形 46定理四边形的内角和等于360°360° 47四边形的外角和等于360°360°48多边形内角和定理n 边形的内角的和等于(边形的内角的和等于(n-2n-2n-2)×180°)×180°)×180°49推论任意多边的外角和等于360°360°50平行四边形性质定理1平行四边形的两组对角分别相等平行四边形的两组对角分别相等51平行四边形性质定理2平行四边形的两组对边分别相等平行四边形的两组对边分别相等52推论夹在两条平行线间的平行线段相等推论夹在两条平行线间的平行线段相等53平行四边形性质定理3平行四边形的对角线互相平分平行四边形的对角线互相平分54平行四边形判定定理1两组对边分别平行的四边形是平行四边形两组对边分别平行的四边形是平行四边形55平行四边形判定定理2两组对边分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形56平行四边形判定定理3对角线互相平分的四边形是平行四边形对角线互相平分的四边形是平行四边形57平行四边形判定定理4一组对边平行相等的四边形是平行四边形一组对边平行相等的四边形是平行四边形58矩形性质定理1矩形的四个角都是直角矩形的四个角都是直角59矩形性质定理2矩形的对角线相等矩形的对角线相等60矩形判定定理1有三个角是直角的四边形是矩形有三个角是直角的四边形是矩形61矩形判定定理2对角线相等的平行四边形是矩形对角线相等的平行四边形是矩形62菱形性质定理1菱形的四条边都相等菱形的四条边都相等 63菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角菱形的对角线互相垂直,并且每一条对角线平分一组对角64菱形面积菱形面积==对角线乘积的一半,即S=S=(a×b)÷2(a×b)÷2(a×b)÷265菱形判定定理1四边都相等的四边形是菱形四边都相等的四边形是菱形66菱形判定定理2对角线互相垂直的平行四边形是菱形对角线互相垂直的平行四边形是菱形67正方形性质定理1正方形的四个角都是直角,四条边都相等正方形的四个角都是直角,四条边都相等68正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角69定理1关于中心对称的两个图形是全等的关于中心对称的两个图形是全等的70定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分 71逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称于这一点对称 72等腰梯形性质定理等腰梯形在同一底上的两个角相等等腰梯形性质定理等腰梯形在同一底上的两个角相等73等腰梯形的两条对角线相等等腰梯形的两条对角线相等74等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形75对角线相等的梯形是等腰梯形(梯形知识点了解即可)对角线相等的梯形是等腰梯形(梯形知识点了解即可)76平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截那么在其他直线上截得的线段也相等得的线段也相等77推论1经过梯形一腰的中点与底平行的直线,必平分另一腰经过梯形一腰的中点与底平行的直线,必平分另一腰78推论2经过三角形一边的中点与另一边平行的直线,必平分第三边经过三角形一边的中点与另一边平行的直线,必平分第三边79三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半80梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b a+b))÷2S=L×h83(1)比例的基本性质如果a:b=c:d,a:b=c:d,那么那么ad=bc ad=bc。
北师大版初中数学各册章节知识点总结 (超强总结)

新版北师大版初中数学知识点汇总目录七年级上册知识点汇总ﻩ错误!未定义书签。
第一章丰富的图形世界错误!未定义书签。
第二章有理数及其运算ﻩ错误!未定义书签。
第三章字母表示数ﻩ错误!未定义书签。
第四章平面图形及位置关系ﻩ错误!未定义书签。
第五章一元一次方程ﻩ错误!未定义书签。
第六章生活中的数据错误!未定义书签。
七年级下册知识点总结ﻩ错误!未定义书签。
第一章整式的运算错误!未定义书签。
第二章平行线与相交线ﻩ错误!未定义书签。
第三章生活中的数据错误!未定义书签。
第四章概率ﻩ错误!未定义书签。
第五章三角形错误!未定义书签。
第六章变量之间的关系ﻩ错误!未定义书签。
第七章生活中的轴对称ﻩ错误!未定义书签。
八年级上册知识点汇总ﻩ错误!未定义书签。
第一章勾股定理错误!未定义书签。
第二章实数ﻩ错误!未定义书签。
第三章图形的平移与旋转错误!未定义书签。
第四章四平边形性质探索错误!未定义书签。
第五章位置的确定ﻩ错误!未定义书签。
第六章一次函数错误!未定义书签。
第七章二元一次方程组错误!未定义书签。
第八章数据的代表ﻩ错误!未定义书签。
八年级下册知识点汇总ﻩ错误!未定义书签。
第一章一元一次不等式和一元一次不等式组错误!未定义书签。
第二章分解因式错误!未定义书签。
第四章相似图形错误!未定义书签。
第五章数据的收集与处理ﻩ错误!未定义书签。
第六章证明(一)错误!未定义书签。
九年级上册知识点汇总ﻩ错误!未定义书签。
第一章证明(二)ﻩ错误!未定义书签。
第二章一元二次方程ﻩ错误!未定义书签。
第三章证明(三)错误!未定义书签。
第四章视图与投影错误!未定义书签。
第五章反比例函数错误!未定义书签。
第六章频率与概率ﻩ错误!未定义书签。
九年级下册知识点汇总错误!未定义书签。
第一章直角三角形边的关系错误!未定义书签。
第二章二次函数ﻩ错误!未定义书签。
第三章圆错误!未定义书签。
第四章统计与概率错误!未定义书签。
七年级上册知识点汇总(注:※表示重点部分;¤表示了解部分;◎表示仅供参阅部分;)第一章丰富的图形世界¤1。
有关北师大版初中数学知识点总结5篇

有关北师大版初中数学知识点总结5篇北师大版初中数学知识点总结2实数无理数:无限不循环小数叫无理数平方根:①如果一个正数X的平方等于A,那么这个正数X就叫做A的算术平方根。
②如果一个数X的平方等于A,那么这个数X就叫做A的平方根。
③一个正数有2个平方根/0的平方根为0/负数没有平方根。
④求一个数A的平方根运算,叫做开平方,其中A叫做被开方数。
立方根:①如果一个数X的立方等于A,那么这个数X就叫做A的立方根。
②正数的立方根是正数、0的立方根是0、负数的立方根是负数。
③求一个数A 的立方根的运算叫开立方,其中A叫做被开方数。
实数:①实数分有理数和无理数。
②在实数范围内,相反数,倒数,绝对值的意义和有理数范围内的相反数,倒数,绝对值的意义完全一样。
③每一个实数都可以在数轴上的一个点来表示。
相信通过上面的学习,同学们对实数知识点可以很好的掌握了,希望同学们在考试中取得好成绩。
初中数学知识点总结:平面直角坐标系下面是对平面直角坐标系的内容学习,希望同学们很好的掌握下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
初中数学知识点:平面直角坐标系的构成对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
北师大版初中数学知识点思维导图

1、单项式乘单项式
2、单项式乘多项式
3、多项式乘多项式
平方差和完全平方
平方差公式和完全平方公式
整式的除法
1、整式的除法
2、整式的混合运算及化简求值
第一早
两条直线的位置关系
1、相交线(对顶角、邻补角)
2、垂线(垂线段最短、点到直线距离)
相交线与平行
线
3、平行线
探索直线平行的条件
1、同位角、内错角、同旁内角
程
认识分式
1、分式的定义
2、分式有意义的条件
3、分式的值为零的条件
4、分式的值
5、分式的基本性质
6、约分
7、同分
8、最简分式
9、最简公分母
10、列代数式(分式)
分式运算
1、分式乘除法
2、分式加减法
3、分式混合运算
4、分式的化简求值
分式方程
1、分式方程的定义域解
2、解分式方程
3、换元法解分式方程
4、分式方程的增根
3、列表法与树状图法
八年级上册
第一早
勾股定理
探索勾股定理
勾股定理与证明
勾股定理逆定理
1、勾股定理逆定理
2、勾股数
勾股定理的应用
1、勾股定理的应用
2、平面展开--取短路劲问题
第一早
实数
无理数
无理数
平方根
1、平方根
2、算术平方根
3、非负数的性质
立方根
立方根
估算
1、实数大小的比较
2、估算无理数的大小
用计算器开方
元次不等式组
1、一兀一次不等式组的定义
2、解一元一次不等式组
3、一元一次不等式组的整数解
北师大版初中数学知识点总结最新最全

北师大版初中数学知识点总结最新最全北师大版初中数学知识点总结一、数与式1.自然数、零、整数、有理数2.分数、小数的读法、写法及其相互转换3.数的四则运算及其性质:加减乘除4.整数余数定理:被几整除?5.计算含有带分数的算式6.代数式的认识:字母、常数、系数、次数、同类项、多项式7.代数式的计算:加减乘8.利用代数式来解决应用问题:等式、方程9.美元、欧元、人民币、英镑、日元、韩元等外币的汇率及相互换算。
10.银行利息与存款、贷款、信用卡账户余额之间的关系。
二、平面图形1.点、线、面2.直角、等腰、等边三角形3.矩形、正方形、长方形、菱形、梯形、圆、弧4.几何图形的支配性规则及其应用5.相似图形及其性质6.比例、比例关系及其应用7.勾股定理及其应用8.三角形和四边形的性质9.圆心角、中心角、弧、弦、切线、切角、异向角定义及特点10.三角形、四边形及圆的周长和面积的计算三、空间几何1. 全等和相似的三角形2. 空间内常见几何图形(长方体,正方体,棱台,圆柱,圆锥,球)之间的关系3. 空间几何公理及其它性质的应用4. 空间图形体积及表面积的计算4. 三视图及制图5. 空间图形剖分6. 空间图形的对称性及其应用四、单位换算和应用1. 长度、质量、容积、面积、时间、速度、密度、温度等各种物理量的单位换算2. 平均、比例、利率、利益、折扣、增长等问题的计算方法3. 房地产4. 理财5. 道路、桥梁6. 奇妙山7. 建筑物8. 旅游总结:以上是北师大版初中数学的主要知识点,需要注意的是数学知识的学习不是一朝一夕的事,也不是单纯的记忆,需要较长的时间不断练习和总结。
而且,学习数学的时候,应该根据自己的能力和兴趣选择适合自己的学习方法,并注意合理安排时间、多思考多质疑,培养自己的逻辑思维和解决实际问题的能力。
2024年北师大版初一数学知识点总结(二篇)

2024年北师大版初一数学知识点总结一、集合与运算1. 集合的概念与表示- 集合的概念:具有某种特定性质的事物的总称。
- 集合的表示:列举法、描述法、集合关系式。
2. 集合的基本运算- 交集:属于同时属于两个集合的元素所组成的新集合。
- 并集:属于两个集合中至少一个的元素所组成的新集合。
- 差集:属于一个集合而不属于另一个集合的元素所组成的新集合。
- 互斥事件:两个事件不可能同时发生的事件。
- 逆事件:一个事件不发生的事件。
- 交换律、结合律、分配律、对偶律。
二、数与运算1. 自然数与整数- 自然数:正整数及零的集合,用N表示。
- 整数:正整数、负整数和零的集合,用Z表示。
2. 有理数- 有理数:可以表示为两个整数之比的数,有限小数、无限循环小数和无限不循环小数的集合,用Q表示。
- 有理数的运算:加法、减法、乘法、除法。
- 有理数的性质:相等性、大小关系、绝对值。
3. 小数与分数- 小数:有限小数、无限循环小数、无限不循环小数。
- 分数:整数和真分数。
- 分数的化简、比较大小、加法、减法、乘法、除法。
4. 实数- 实数:有理数和无理数的集合,用R表示。
- 实数的性质:有序性、稠密性。
5. 整数的除法- 整数除法的概念与性质。
- 余数与商的关系。
三、代数式与方程式1. 代数式与代数式的值- 代数式:由数和变量以及运算符号组成的式子。
- 代数式的值:当变量取某一确定的值时,代入代数式中计算得到的值。
2. 方程与方程的解- 方程:含有一个或多个未知数的等式。
- 方程的解:是使方程成立的未知数的值。
- 方程与方程组的思想与模型应用。
四、几何图形1. 平面与空间几何- 点、线、面和体。
2. 几何图形与基本图形的性质- 几何图形:点、线和面的集合。
- 基本图形:三角形、四边形、五边形、六边形、圆等。
- 基本图形的性质与分类。
3. 直线与角- 直线:直径、相交、垂直、平行等性质。
- 角:角的概念、角的度量、角的分类。
北师大版初一至初三数学知识点总结

初一上册第一章有理数1.1正数和负数1.3有理数的加减法1.4有理数的乘除法1.5有理数的乘方第二章整式的加减2.1整式2.2整式的加减第三章一元一次方程3.1从算式到方程3.2解一元一次方程(一)——合并同类项与移项3.3解一元一次方程(二)——去括号与去分母3.4实际问题与一元一次方程第四章图形认识初步4.1多姿多彩的图形4.2直线、射线、线段4.3角初一下册第五章相交线与平行线5.1相交线5.2平行线及其判定5.3平行线的性质第六章平面直角坐标系6.1平面直角坐标系6.2坐标方法的简单应用第七章三角形7.1与三角形有关的线段7.2与三角形有关的角7.3多边形及其内角和7.4课题学习镶嵌第八章二元一次方程组8.1二元一次方程组8.2消元——二元一次方程组的解法8.3实际问题与二元一次方程组8.4三元一次方程组解法举例第九章不等式与不等式组9.1不等式用求差法比较大小9.2实际问题与一元一次不等式9.3一元一次不等式组第十章数据的收集、整理与描述10.1统计调查10.2直方图初一数学上下册八年级上册第十一章全等三角形11.1全等三角形11.2三角形全等的判定全等与全等三角形11.3角的平分线的性质第十二章轴对称12.1轴对称12.2作轴对称图形12.3等腰三角形第十三章实数13.1平方根13.2立方根13.3实数第十四章一次函数14.1变量与函数14.2一次函数14.3用函数观点看方程(组)与不等式14.4课题学习选择方案第十五章整式的乘除与因式分解15.1整式的乘法15.2乘法公式15.3整式的除法八年级下册第十六章分式16.1分式16.2分式的运算16.3分式方程第十七章反比例函数17.1反比例函数探索反比例函数的性质17.2实际问题与反比例函数第十八章勾股定理18.1勾股定理勾股定理的证明18.2勾股定理的逆定理第十九章四边形19.1平行四边形19.2特殊的平行四边形19.3梯形平面直角坐标系中的特殊四边形19.4重心第二十章数据的分析20.1数据的代表20.2数据的波动数据波动的几种度量初二数学上下册数学九年级上册第二十一章二次根式21.1 二次根式21.2 二次根式的乘除21.3 二次根式的加减第二十二章一元二次方程22.1 一元二次方程22.2 降次——解一元二次方程22.3 实际问题与一元二次方程三角点阵中前n行的点数计算第二十三章旋转23.1 图形的旋转23.2 中心对称旋转对称性第二十四章圆24.1 圆24.2 点、直线、圆和圆的位置关系24.3 正多边形和圆24.4 弧长和扇形面积第二十五章概率初步25.1 随机事件与概率25.2 用列举法求概率25.3 用频率估计概率实验与探究П的估计数学九年级下册第二十六章二次函数26.1二次函数及其图像26.2用函数观点看一元二次方程函数性质26.3实际问题与二次函数第二十七章相似27.1图形的相似27.2相似三角形27.3位似探索位似的性质第二十八章锐角三角函数28.1锐角三角函数28.2解直角三角形第二十九章投影与视图29.1投影29.2三视图初三数学上下册。
北师大版勾股定理知识点总结

北师大版勾股定理知识点总结嘿,朋友!咱们今天来好好聊聊北师大版的勾股定理。
勾股定理那可是数学世界里的一颗璀璨明珠啊!你想想,它就像一把神奇的钥匙,能帮咱们打开好多几何难题的大门。
先来说说勾股定理到底是啥。
简单说,就是在一个直角三角形中,两条直角边的平方和等于斜边的平方。
这就好比是直角三角形的“身份证”,通过它,咱们能一下子认清这个三角形的真面目。
比如说,一个直角三角形的两条直角边分别是 3 和 4,那斜边是多少呢?这时候勾股定理就派上用场啦!3 的平方是 9,4 的平方是 16,9 加 16 等于 25,那斜边就是 5 呗!是不是很神奇?
再看看勾股定理的证明方法,那也是五花八门,就像一场精彩的魔术表演。
比如说,赵爽弦图,那可是老祖宗留下来的智慧结晶。
还有啊,勾股定理的应用那可太广泛啦!盖房子的时候,工人师傅得靠它保证墙角是直角;测量大树、高楼的高度,它也是个好帮手。
咱们平时做数学题,遇到求直角三角形边长的,第一反应就得想到勾股定理。
这就好像饿了要吃饭,渴了要喝水一样自然。
你说,如果没有勾股定理,这数学世界得少多少乐趣和便利啊?
在考试中,勾股定理可是个重点中的重点。
要是没掌握好,那可就像在黑暗中迷路,找不到方向。
所以啊,咱们可得把勾股定理这宝贝牢牢地抓在手里,让它成为咱们解题的利器,在数学的海洋里畅游无阻。
总之,勾股定理是数学中的重要法宝,学会它,用好它,数学难题都不在话下!。
北师大初中数学中考总复习:勾股定理及其逆定理--知识讲解(基础)-精品
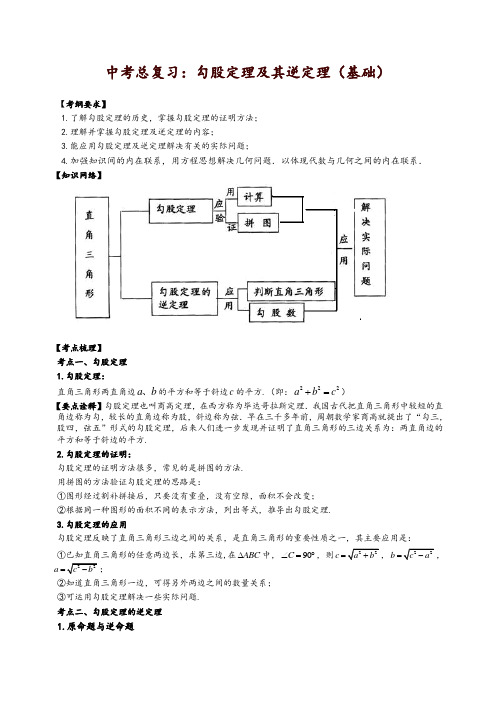
中考总复习:勾股定理及其逆定理(基础)【考纲要求】1.了解勾股定理的历史,掌握勾股定理的证明方法;2.理解并掌握勾股定理及逆定理的内容;3.能应用勾股定理及逆定理解决有关的实际问题;4.加强知识间的内在联系,用方程思想解决几何问题.以体现代数与几何之间的内在联系. 【知识网络】【考点梳理】 考点一、勾股定理 1.勾股定理:直角三角形两直角边a b 、的平方和等于斜边c 的平方.(即:222a b c +=)【要点诠释】勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方. 2.勾股定理的证明:勾股定理的证明方法很多,常见的是拼图的方法. 用拼图的方法验证勾股定理的思路是:①图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变; ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理. 3.勾股定理的应用勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用是: ①已知直角三角形的任意两边长,求第三边,在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-;②知道直角三角形一边,可得另外两边之间的数量关系; ③可运用勾股定理解决一些实际问题. 考点二、勾股定理的逆定理1.原命题与逆命题如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.2.勾股定理的逆定理勾股定理的逆定理:如果三角形的三边长a b c 、、,满足222a b c +=,那么这个三角形是直角三角形. 【要点诠释】①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边;③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形.3.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数;②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等; ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数) 2222,2,m n mn m n -+(,m n >m ,n 为正整数).考点三、勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,两者互为逆定理,都与直角三角形有关. 【典型例题】类型一、勾股定理及其逆定理的综合应用1.(2014春•河西区期末)在正方形ABCD 中,E 是BC 的中点,F 为CD 上一点,且,试判断△AEF 是否是直角三角形?试说明理由.【思路点拨】首先设正方形的边长为4a ,则CF=a ,DF=3a ,CE=BE=2a .根据勾股定理可求出AF ,AE 和EF 的长度.如果它们三个的长度满足勾股定理,△AEF 为直角三角形,否则不是直角三角形. 【答案与解析】解:设正方形的边长为4a , ∵E 是BC 的中点,,∴CF=a,DF=3a ,CE=BE=2a .由勾股定理得:AF2=AD2+DF2=16a2+9a2=25a2,EF2=CE2+CF2=4a2+a2=5a2,AE2=AB2+BE2=16a2+4a2=20a2,∴AF2=EF2+AE2,∴△AEF为直角三角形.【总结升华】勾股定理的应用.在解答此类题时有一个小窍门,题干中各边长都没有给出确定的值,我们已知各边长的比值,这时我们可以将边长设成具体的值.这样解题时用到的都是数字,表达方便.举一反三:【变式】如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为().A.14B.16C.20D.28【答案】D.根据题意可知五个小矩形的周长之和正好能平移到大矩形的四周,故即可得出答案:∵AC=10,BC=8,∴A B=6,图中五个小矩形的周长之和为:6+8+6+8=28.2.如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为().A.14B.15C. 223 D. 3【思路点拨】以A为圆心,AB长为半径作圆,延长BA交⊙A于F,连接DF.在△BDF中,由勾股定理即可求出BD的长.【答案与解析】以A为圆心,AB长为半径作圆,延长BA交⊙A于F,连接DF.可证∠FDB=90°,∠F=∠CBF,∴DF=CB=1,BF=2+2=4,∴BD=2215-=.故选B.BF DF【总结升华】本题考查了勾股定理,解题的关键是作出以A为圆心,AB长为半径的圆,构建直角三角形从而求解.举一反三:【变式】(2015•黄冈模拟)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A.(4+)cm B.5cm C.2cm D.7cm【答案】B.【解析】解:侧面展开图如图所示:∵圆柱的底面周长为6cm,∴AC′=3cm.∵PC′=BC′,∴PC′=×6=4cm.在Rt△ACP中,AP2=AC′2+CP2,∴AP==5.故选:B.类型二、勾股定理及其逆定理与其他知识的结合应用3.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到R t△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是________________.【思路点拨】先根据勾股定理得到AB=2,再根据扇形的面积公式计算出S扇形ABD,由旋转的性质得到Rt△ADE≌Rt△ACB,于是S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD【答案与解析】∵∠ACB=90°,AC=BC=1,∴AB=2,∴S 扇形ABD =6360)2(302ππ=⋅, 又∴Rt△ABC 绕A 点逆时针旋转30°后得到Rt△ADE, ∴Rt△ADE≌Rt△ACB,∴S 阴影部分=S △ADE +S 扇形ABD -S △ABC =S 扇形ABD =6π. 【总结升华】本题考查了扇形的面积公式:3602R n S π=.也考查了勾股定理以及旋转的性质.考点涉及到扇形面积的计算;勾股定理;旋转的性质.4. 如图,矩形纸片ABCD 中,已知AD=8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处, 折痕为AE ,且EF=3,则AB 的长为( ). A. 3 B. 4 C. 5 D. 6【思路点拨】先根据矩形的特点求出BC 的长,再由翻折变换的性质得出△CEF 是直角三角形,利用勾股定理即可求出CF 的长,再在△ABC 中利用勾股定理即可求出AB 的长. 【答案与解析】∵四边形ABCD 是矩形,AD=8, ∴BC=8,∵△AEF 是△AEB 翻折而成,∴BE=EF=3,AB=AF ,△CEF 是直角三角形, ∴CE=8-3=5,在Rt△CEF 中,CF=2222534CE EF -=-= , 设AB=x ,在Rt△ABC 中,AC 2=AB 2+BC 2,即(x+4)2=x 2+82,解得x=6, 故选D .【总结升华】本题考查的是翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键. 举一反三:【变式】(2011台湾)如图为梯形纸片ABCD ,E 点在BC 上,且∠AEC=∠C=∠D=90°,AD =3,BC =9,CD =8.若以AE 为折线,将C 折至BE 上,使得CD 与AB 交于F 点,则BF 长度为何( ).A .4.5B .5C .5.5D .6【答案】B .5.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH 的边长为2米,坡角∠A=30°,∠B=90°,BC =6米.当正方形DEFH 运动到什么位置,即当AE = 米时,有DC 2=AE 2+BC 2.【思路点拨】根据已知得出假设AE =x ,可得EC =12-x ,利用勾股定理得出DC 2=DE 2+EC 2=4+(12-x )2,AE 2+BC 2=x 2+36,即可求出x 的值. 【答案与解析】假设AE =x ,可得EC =12-x ,∵坡角∠A=30°,∠B=90°,BC =6米, ∴AC=12米,∵正方形DEFH 的边长为2米,即DE =2米, ∴DC 2=DE 2+EC 2=4+(12-x )2, AE 2+BC 2=x 2+36, ∵DC 2=AE 2+BC 2,∴4+(12-x )2=x 2+36, 解得:x =314. 故答案为:314.【总结升华】此题主要考查了勾股定理的应用以及一元二次方程的应用,根据已知表示出CE ,AE 的长度是解决问题的关键.6 . 某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6m 、8m .现要将其扩建成等腰三角形,且扩充部分是以8m 为直角边的直角三角形...........求扩建后的等腰三角形花圃的周长. 【思路点拨】原题并没有给出图形,要根据题意画出符合题意的图形,画出图形后,可知本题实际上应三类情况讨论:一是将△ABC 沿直线AC 翻折180°后,得等腰三角形ABD ,如图1;二是延长BC 至点D ,使CD =4,则BD =AB =10,得等腰三角形ABD ,如图2;三是作斜边AB 的中垂线交BC 的延长线于点D ,则DA =DB ,得等腰三角形ABD ,如图3.先作出符合条件的图形后,再根据勾股定理进行求解即可. 【答案与解析】分三类情况讨论如下:(1)如图1所示,原来的花圃为Rt△ABC,其中BC =6m ,AC =8m ,∠ACB=90°.由勾股定理易知AB =10m ,将△ABC 沿直线AC 翻折180°后,得等腰三角形ABD ,此时,AD =10m ,CD =6m .故扩建后的等腰三角形花圃的周长为12+10+10=32(m ). (2)如图2,因为BC =6m ,CD =4m ,所以BD =AB =10m ,在Rt△ACD 中,由勾股定理得AD =2284 =45,此时,扩建后的等腰三角形花圃的周长为45+10+10=20+45.(3)如图3,设△ABD 中DA =DB ,再设CD =xm ,则DA =(x +6)m ,在Rt△ACD 中,由勾股定理得x 2+82=(x +6)2,解得x =37∴扩建后等腰三角形花圃的周长=10+2(x +6)=380(m ). 图1668DC BA图2486BC AD图3x +6x 68BC DA【总结升华】对于无附图几何问题,往往需要根据题意画出图形,结合已知条件及图形分析求解,这样便于寻找解题思路.举一反三:【变式】“希望中学”有一块三角形形状的花圃ABC ,现可直接测量到∠A=30°,AC=40m ,BC=25m ,请求出这块花圃的面积. 【答案】作CD ⊥AB . ∵∠A=30°, ∴CD=12AC=12×40=20(m ), AD=22203AC CD -=(m ), BD=22BC CD -=15(m ).(1)当∠ACB 为钝角时,AB=AD+BD=203+15,∴S △ABC =12AB •CD=12(203+15)×20=(2003+150)(m 2). (2)当∠ACB 为锐角时,AB=AD-BD=203-15.∴S △ABC =12AB •CD=12AB •CD=12(203-15)×20=(2003-150)(m 2).。
勾股定理知识点总结

勾股定理知识点总结一、勾股定理的定义在直角三角形中,两直角边的平方和等于斜边的平方。
如果直角三角形的两条直角边长分别为 a 和 b,斜边长为 c,那么 a²+ b²= c²。
这一定理是数学中非常重要的一个定理,它揭示了直角三角形三条边之间的数量关系。
二、勾股定理的证明勾股定理的证明方法有很多种,以下为大家介绍几种常见的证明方法。
1、赵爽弦图法赵爽弦图是由四个全等的直角三角形拼成一个大正方形,中间是一个小正方形。
大正方形的面积等于四个直角三角形的面积加上小正方形的面积。
设直角三角形的两条直角边分别为 a 和 b,斜边为 c。
大正方形的边长为 c,面积为 c²。
四个直角三角形的面积为 4×(1/2)ab = 2ab,小正方形的边长为(b a),面积为(b a)²= a² 2ab + b²。
所以 c²= 2ab + a² 2ab + b²,即 c²= a²+ b²,证明完毕。
2、毕达哥拉斯证明法以直角三角形的斜边为边长作一个正方形,再以两条直角边为边长分别作两个正方形。
通过计算三个正方形的面积,可以证明勾股定理。
设直角三角形的两条直角边分别为 a 和 b,斜边为 c。
斜边为边长的正方形面积为 c²,两条直角边为边长的正方形面积分别为 a²和 b²。
通过将直角边为边长的两个正方形进行分割和拼接,可以发现它们能够恰好填满斜边为边长的正方形,从而证明 a²+ b²= c²。
三、勾股定理的应用1、已知直角三角形的两条边,求第三条边例如,已知一个直角三角形的两条直角边分别为 3 和 4,求斜边的长度。
根据勾股定理,斜边的长度 c =√(3²+ 4²) = 5 。
2、实际生活中的应用(1)建筑工程中,计算建筑物的高度、跨度等。
2013届北师大版初中数学全程复习方略配套课件第十八讲 勾股定理

【解析】选D.由勾股定理求出 OB = 12 + 22 = 5,根据同弧的 半径相等,因此这个点表示的实数是 5.
3.(2012·荆门中考)如图,△ABC是等边 三角形,P是∠ABC的平分线BD上一点, PE⊥AB于点E,线段BP的垂直平分线交BC 于点F,垂足为点Q.若BF=2,则PE的长为( (A)2 (B) 2 3 (C) 3 ) (D)3
30° 直角边所对的锐角等于_____.
【即时应用】 5 1.如图所示,Rt△ABC中,∠C=90°,AC2=2,BC2=3,则AB2=__.
2.如图所示,Rt△ABC中,∠C=90°,∠A=30°,若BC=6,
12 则AB=___.
3.如图所示,Rt△ABC中,∠ACB=90°,点D是斜边AB的中 8 点,且AB=16,则CD=__.
勾股定理的逆定理的作用是判定一个三角形是否为 特别 直角三角形. 提醒
3.勾股定理的逆定理:如果三角形两边的平方和等于第三边的
平方 ,那么这个三角形是直角三角形. _____
4.如果三角形一边上的_____ 中线 等于这条边的一半,那么这个三
角形是直角三角形.
【即时应用】
1.如图所示,△ABC中,AE,BD为三角形的两条高,则图中共
6 个直角三角形. 有__
90° 2.△ABC中,若AC2+BC2=AB2,则∠A+∠B=____.
【对点训练】 1.(2012·广州中考)在Rt△ABC中,∠C=90°,AC=9,BC=12, 则点C到AB的距离是( )
(A)
36 5
(B) 12 25
(C)
9 4
(D) 3 3 4
【解析】选A.根据勾股定理,得 AB = 92 +122 = 15, 设点C到AB
2024年北师大版七年级数学下册知识点总结(二篇)

2024年北师大版七年级数学下册知识点总结第一章:方程与不等式1.方程的概念:包含未知数的等式称为方程。
方程的解是使得方程成立的数。
2.解方程:通过变量的运算和移项,求出方程的解。
3.解一元一次方程:如ax+b=0,解得x=-b/a。
4.方程的证明:通过逆向思维,将给定的解代入方程,验证等式是否成立。
5.不等式的概念:含有不等于号的等式称为不等式,如ax>b。
6.解不等式:通过移项,求出不等式的解的范围。
7.不等式的证明:将给定的解代入不等式,验证不等式是否成立。
第二章:数据的收集和整理1.数据的表示:通过表格、图表和线段、折线图等图示进行数据的表示,便于观察和分析。
2.数据的整理:对收集到的数据进行整理,包括分类、排序、求最大值、最小值、众数、中位数等。
3.统计的总体与样本:通过抽取一部分数据作为样本,对总体数据进行概括和判断。
第三章:图形的认识1.点、线、面的概念:几何图形由点、线、面组成。
2.平行线与垂直线:平行线的特点是永不相交,垂直线的特点是相交成直角。
3.多边形:具有多个边的几何图形称为多边形,如三角形、四边形、五边形等。
4.正多边形:具有相等边长和相等内角的多边形。
5.对称图形:具有对称性的图形,可以通过某一条线进行折叠重合。
6.图形的相似性:具有相等比例关系的图形称为相似图形。
7.平移、旋转和翻折:运用平移、旋转和翻折等操作,使得图形位置和形态发生变化。
第四章:四边形1.四边形的概念:具有四个边的图形称为四边形,包括梯形、平行四边形、矩形、菱形、正方形等。
2.梯形:有两个底边,两个腰。
3.平行四边形:具有相对边平行的四边形。
4.矩形:具有四个直角的四边形,对角线相等。
5.菱形:具有四个相等边的四边形,对角线互相垂直。
6.正方形:具有四个相等边且具有对称性的四边形。
第五章:比例与相似1.比例的概念:比例是指两个或多个量之间的比值关系。
比值相等时称为成比例。
2.比例的性质:比例的性质包括交换律、放大和缩小、分配律等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理复习
一.知识归纳
1.勾股定理的内容及由来
内容:直角三角形两直角边的平方和等于斜边的平方;
表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c += 2.勾股定理的证明
勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是 ①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见证明方法如下:
c
b
a
H
G F E
D
C
B
A
b
a
c
b
a
c c
a
b
c
a
b a b
c
c b
a
E D C
B
A
方法一:
4EFGH S S S ∆+=正方形正方形ABCD ,221
4()2
ab b a c ⨯+-=,化简可证.
方法二:
四个直角三角形的面积与小正方形面积的和等于大正方形的面积.
四个直角三角形的面积与小正方形面积的和为221
422S ab c ab c =⨯+=+
大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=
方法三:
这1()()2S a b a b =+⋅+梯形,211
2S 222
ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证
勾股定理知识点总结
.勾股定理的适用范
勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形
围
.勾股定理的应用.勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.
勾股定理的逆定理如果三角形三边长a,b,c满足222
a b c
+=,那么这个三角形是直角三角形,其中c为斜边
①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22
a b
+与较长边的平方2c 作比较,若它们相等时,以a,b,c为三边的三角形是直角三角形;若222
a b c
+<,时,以a,b,c为三边的三角形是钝角三角形;若222
a b c
+>,时,以a,b,c为三边的三角形是锐角三角形;
②定理中a,b,c及222
a b c
+=只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足222
a c b
+=,那么以a,b,c为三边的三角形是直角三角形,但是b为斜边
③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形
常见.勾股数及其规律①能够构成直角三角形的三边长的三个正整数称为勾股数,即222
a b c
+=中,a,b,c为正整数时,称a,b,c为一组勾股数
②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等
③用含字母的代数式表示n组勾股数:
22
1,2,1
n n n
-+(2,
n≥n为正整数);
22
21,22,221
n n n n n
++++(n为正整数)
2222
,2,
m n mn m n
-+(,
m n
>m,n为正整数)
勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.
勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.①已知直角三角形的任意两边长,求第三边
在ABC
∆中,90
C
∠=︒,则22
c a b
=+,22
b c a
=-,22
a c b
=-
②知道直角三角形一边,可得另外两边之间的数量关系
③可运用勾股定理解决一些实际问题。
