π值速记表 圆的公式
圆周率快速记忆口诀

圆周率快速记忆口诀
圆周率,又称为弧度常数,是一个圆心角在圆周上代表的弧长与
半径的比值,也代表着循环的永恒。
关于这个神秘的数字,古今学者
们奋斗不息,把它求出了极其精确的值,被称为人类最好的礼物之一。
圆周率的快速记忆口诀代表着每一位学者的勤劳,聪明才智,也
表达了他们对数学的极大的崇敬。
这个口诀只要背下来人生很多场景
都可能会用到,比如数学竞赛、大学入学考试,甚至外围博彩也有可
能会和它打交道,其实非常实用。
一般来讲,快速记忆圆周率的口诀一般会将其拆分成3、4、7这
三个数字,算是它最常用的口诀形式,非常适用。
比如:三个蛤蟆思
故技重演,四舍六入五凑奇数;七上八下九替十把,十四两千五百八
十一。
将这段口诀拆分,分析其本质,就可以看出每一句的意思了,
“三个蛤蟆思故技重演”就表明:圆周率标度精度为3位数,即3.14 ;“四舍六入五凑奇数”背后的想法是:用四舍六入法可以将接近5位
数的圆周率表示为3.141 ;“七上八下九替十把”是指用七以上的数字代替8,以下的数字代替9,那么圆周率的精度就到了5.142 ,最后“十四两千五百八十一”就表明:可以将圆周率精度提升到3.14159 熟练掌握圆周率的快速记忆口诀,可以让你计算圆周率的值变得
更加轻松,更加自如,在上述快速记忆口诀的帮助下,想要在考试过
程中使用圆周率,也可以很快掌握它的必要信息,不断提高它的精确度,向更加极致的完美挑战。
圆周率最简单的公式

圆周率最简单的公式
圆周率最简单的公式是:π=圆周长/直径。
圆周率是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π也等于圆形之面积与半径平方之比。
是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学里,π可以严格地定义为满足sinx=0的最小正实数x。
圆周率是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
而用十位小数便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率倍数表的巧记方法

圆周率倍数表的巧记方法圆周率是数学中的一个重要概念,它是指任何圆的周长与直径的比值,通常用希腊字母π表示。
圆周率的值是一个无限不循环小数,其小数点后的数字是无限的,因此,圆周率的计算一直是数学家们的研究重点。
在数学中,圆周率的值通常取3.1415926……,但是,如果需要更高的精度,就需要更多的小数位数。
在实际应用中,圆周率的精度要求不同,因此,需要掌握一些巧记方法,以便更快地计算圆周率的倍数表。
一、圆周率的定义圆周率是指任何圆的周长与直径的比值,通常用希腊字母π表示。
圆周率的值是一个无限不循环小数,其小数点后的数字是无限的。
圆周率的计算一直是数学家们的研究重点,目前已经计算出了数万亿位的圆周率。
二、圆周率的计算方法圆周率的计算方法有很多种,其中最常用的是无穷级数法和蒙特卡罗法。
无穷级数法是通过一系列无限级数的求和来计算圆周率的值,而蒙特卡罗法则是通过随机模拟的方法来估算圆周率的值。
三、圆周率的巧记方法1. 3.1415926这是圆周率的常用值,可以通过背诵来记忆。
其中,3.14是最常用的近似值,而3.1415926则是更高精度的值。
2. 一句话记忆法“圆周率近似值是三点一四,一五九二六,五三五八九,七九三二三,八四六二六,四三三八三,二六四三三,九五零二八,七一九五九,五九零七二,一九五零二。
”这是一种常用的圆周率记忆方法,通过一句话来记忆圆周率的前几位数字。
这种方法虽然不太容易掌握,但是一旦记住,就可以轻松地计算圆周率的倍数表。
3. 数字图形记忆法这是一种比较有趣的圆周率记忆方法,通过将圆周率的数字转化为图形来记忆。
例如,将数字1看作一根笔直的线段,数字2看作一只天鹅的脖子,数字3看作一个弯曲的钩子,数字4看作一个带有横杠的四角形,数字5看作一个带有斜杠的五角形,数字6看作一个带有弯曲的尾巴的小狗,数字7看作一个带有斜杠的七角形,数字8看作一个带有两个环的腰带,数字9看作一个带有弯曲的尾巴的大狗,数字0看作一个圆形。
圆周率100位与100以内平方速记法2015

圆周率100位与100以内平方速记法2015小学生数学基础能力训练记忆圆周率的作用背圆周率有以下作用:(1)锻炼大脑记忆圆周率对于锻炼大脑的作用很像体育锻炼对于身体各部分机能的发育和健康的作用。
如同疲劳的体力劳动不能代替体育锻炼一样,工作中不断处理“伤脑筋”的事并不能代替对于大脑的锻炼。
有的体育运动项目主要锻炼身体的某一部位,而有的项目则能比较全面地锻炼身体的多个部位。
脑力锻炼也是一样,有的只能锻炼大脑某一部位的功能,有的能锻炼多个部位的功能。
不断地背记几千几百位圆周率,并不只是简单的机械记忆,需要动脑子寻找记忆窍门,所以有助于脑力的发展和保持。
经常锻炼身体的人即使到了老年动作也不迟钝,经常锻炼大脑的人到了老年仍能保持比较好的智力,不少年事很高的脑力劳动者思路清楚的原因就在这里。
据称,曾创背记圆周率世界纪录的日本人友寄英哲在背诵过程中,晚上睡眠情况大为好转,记忆力大大增强,动作反应也变得异常的灵敏。
由此可见背记圆周率确能起到锻炼大脑的作用。
(2)养成背诵的习惯背记数百位、数千位的圆周率的数值,是要下一番工夫的,不是一日之功,背诵多了,就会形成一种背诵的习惯。
(3)学会或自己创造一些记忆数字的方法要记忆上百位、上千位的无理数,完全靠机械记忆是不容易的,在记忆过程中,自觉不自觉地要用一些记忆数字的方法,而且很可能找到一些自己独创的方法。
这种运用和创造记忆方法的能力是有普遍意义的,是脱离圆周率而存在的,会记忆别的内容时表现出来。
所以,从这个意义上讲,即使具体的数字忘记了,但学会的方法和锻炼出来的能力并没有消失,会融入自己的总体知识和能力之中。
(4)提高对于数字的敏感性背诵一段时间圆周率以后,自然而然地会对数字有比较高的敏感性,见到数字就想记忆。
如路遇汽车就想记车牌号,看到或听到广告节目中的电话号码就想记忆等。
(5)增强了记忆数字的自信心自信心强了,记得快、记得牢。
在学习过程中,之所以要订出背几百、上千位的目标就是为了证明自己记忆上的潜力。
圆周率背诵口诀完整版 圆周率100位速记7秒

圆周率背诵口诀完整版圆周率100位速记7秒什幺是圆周率呢,圆周率一共有多少位呢,怎幺背诵圆周率呢,圆周率的记忆方法有什幺呢,下面小编为大家分析一下,仅供大家参考。
什幺是圆周率圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π也等于圆形之面积与半径平方之比。
是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学里,π可以严格地定义为满足sinx= 0的最小正实数x。
圆周率用希腊字母π(读作pài)表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。
它是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
而用十位小数3.141592654便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率的背诵口诀有什幺【中文背圆周率的口诀】 3 .1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 三天一士一壶酒,尔乐苦煞吾,把酒吃,酒杀尔,杀不死,乐尔乐. 4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9 3 7 死珊珊,霸占二妻.救吾灵儿吧!不只要救妻,一路救三舅,救三妻. 5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7 吾一拎我爸,二拎舅(其实就是撕吾舅耳)三拎妻. 8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6 不要溜!司令溜,儿不溜!儿拎爸,久久不溜! 2 8 0 3 4 8 2 5 3 4 2 1 1 7 0 6 7 9 8。
圆周率200位记忆口诀

圆周率的来源和2000位“圆周率”即圆的周长与其直径之间的比率。
关于它的计算问题,历来是中外数学家极感兴趣、孜孜以求的问题。
德国的一位数学家曾经说过:“历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展的一个标志。
”我国古代在圆周率的计算方面长期领先于世界水平,这应当归功于魏晋时期数学家刘徽所创立的新方法——“割圆术”。
所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。
这个方法,是刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。
中国古代从先秦时期开始,一直是取“周三径一”(即)的数值来进行有关圆的计算。
但用这个数值进行计算的结果,往往误差很大。
正如刘徽所说,用“周三径一”计算出来的圆周长,实际上不是圆的周长而是圆内接正六边形的周长,其数值要比实际的圆周长小得多。
东汉的张衡不满足于这个结果,他从研究圆与它的外切正方形的关系着手得到圆周率。
这个数值比“周三径一”要好些,但刘徽认为其计算出来的圆周长必然要大于实际的圆周长,也不精确。
刘徽以极限思想为指导,提出用“割圆术”来求圆周率,既大胆创新,又严密论证,从而为圆周率的计算指出了一条科学的道路。
在刘徽看来,既然用“周三径一”计算出来的圆周长实际上是圆内接正六边形的周长,与圆周长相差很多;那么我们可以在圆内接正六边形把圆周等分为六条弧的基础上,再继续等分,把每段弧再分割为二,做出一个圆内接正十二边形,这个正十二边形的周长不就要比正六边形的周长更接近圆周了吗?如果把圆周再继续分割,做成一个圆内接正二十四边形,那么这个正二十四边形的周长必然又比正十二边形的周长更接近圆周。
这就表明,越是把圆周分割得细,误差就越少,其内接正多边形的周长就越是接近圆周。
如此不断地分割下去,一直到圆周无法再分割为止,也就是到了圆内接正多边形的边数无限多的时候,它的周长就与圆周“合体”而完全一致了。
圆周率——精选推荐

W17,500,“⼭巅3、3⽉14⽇为圆周率⽇圆周率-圆周率⼩数点后10000位3.141 5926 5358 9793 2384 6264 3383 2795 0288 4197 1693 9937 5105 8209 7494 4592 3078 1640 6286 2089 9862 8034 8253 4211 7067 9821 4808 6513 2823 0664 7093 8446 0955 0582 2317 2535 9408 128 5863 1503 0286 1829 7455 5706 7498 3850 5494 5885 8692 6995 6909 2721 0797 5093 0295 5321 1653 4498 7202 7559 6023 6480 6654 9911 9881 8347 9775 3566 3698 0742 6542 5278 6255 1818 4175 7467 3021 8453 1910 4848 1005 3706 1468 0674 9192 7819 1197 9399 5206 1419 6634 2875 4440 6437 4512 3718 1921 7999 8391 0159 1956 1814 6751 4269 1239 7489 4090 7186 4942 3196 1567 9452 0809 5146 6683 0634 3285 8785 6983 0523 5808 9330 6575 7406 7954 5716 3775 2542 0211 4955 7615 8140 0250 1262 2859 4130 2164 7155 0979 2592 3099 0796 5473 7612 5517 6567 5135 7517 8296 6645 4779 1745 7980 6941 1352 8013 1470 1304 7816 4378 8518 5290 9285 4520 1165 8393 4196 5621 3491 4341 5956 2586 5865 5705 5269 0496 5209 8580 3385 0722 4264 8293 9728 5847 8316 3057 7775 6068 8876 4462 6270 8943 8799 3620 1629 5154 1337 1424 8928 3072 2012 6901 4754 6684 7653 5761 6477 3794 6752 0049 0757 1555 2781 9653 6213 2392 6406 1601 3635 8155 9074 2202 0203 1872 7760 5277 2190 0556 4456 2129 6404 3523 1176 0066 5101 2412 0065 9755 8512 7617 8583 8292 0419 7484 4236 0800 7193 0457 6189 3234 9229 2796 5019 8751 8721 2726 7507 9812 5547 0958 9045 5635 7921 2210 3334 6697另有⼀说圆周率:3.14159265358979323846264338327950288419716939937510582097944592307816406286208998628034825342117067982148086513282306764709384460955058223172535940812848111745028410270圆周率已被除尽圆周率是⾃然界最基本的常数之⼀,它代表圆的周长对原得直径之⽐,有着实数实量的根本意义。
快速记忆1π到 100π的数值表
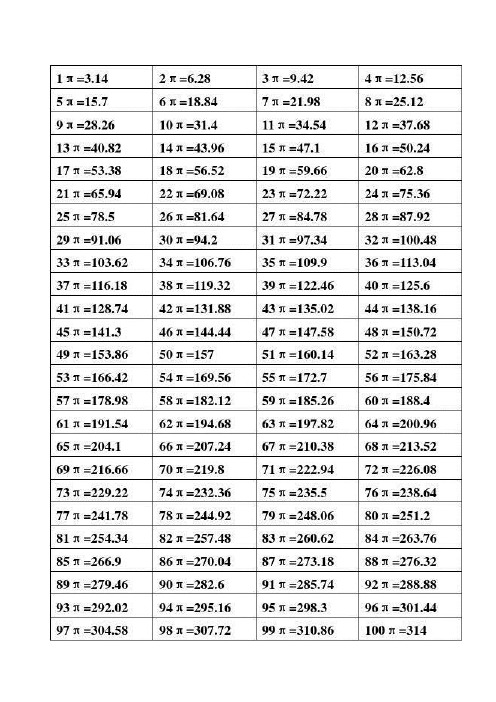
对于这张从1π到100π的数值表,可以通过以下方法帮助快速记忆:1. 分块记忆
将1π~100π的表格划分成较小的区块来逐步记忆。
例如,每10个π为一组:
1π~ 10π:3.14,6.28,9.42,12.56,15.7...
11π~ 20π:34.54,37.68,40.82,43.96...
通过每组固定的模式来分块记忆,先掌握每一组,再合并整张表。
2. 找规律
这张表的数值基本上是等差数列,每增加1个π,其数值增加约为3.14。
例如:
1π= 3.14
2π= 6.28
3π= 9.42
可以记住增加规律,每增加1π,值会增加3.14,从而不用逐个死记硬背。
3. 使用简单标志数字
表中有几个容易记住的关键数字,作为“记忆锚点”,帮助你更快回忆。
例如:
10π= 31.4
20π= 62.8
50π= 157
100π= 314
通过这些标志数字,结合之前的3.14的增量规律,可以帮助你快速推算中
间的值。
4. 运用记忆法则
数字谐音法:用汉字谐音帮助记忆,如3.14对应“山医师”,或编一些有趣的句子帮助联想。
图像联想法:把每个数字转化为具体的图像,并用故事串联,例如34.54可以想象为“三个士兵和一个武士”。
5. 数字计算练习
通过日常多做一些计算π值的练习,加深印象。
每次通过推算来确认自己记住的是否正确。
6. 重复和背诵
每天定期复习和背诵这张表,通过不断的强化记忆,使得这些数字更加牢固。
这些方法结合起来,可以让你更有效地掌握1π~100π的数值。
圆周率口诀

圆周率口诀什么是圆周率圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π也等于圆形之面积与半径平方之比。
是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学里,π可以严格地定义为满足sin x= 0的最小正实数x。
圆周率用希腊字母π(读作pài)表示,是一个常数(约等于3.),是代表圆周长和直径的比值。
它是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
而用十位小数3.便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率的背诵口诀有什么【中文背圆周率的口诀】3 .14 15 9 26 5 3 5 8 97 9 3 2 38 4 6 2 6三天一士一壶酒,尔乐苦煞吾,把酒吃,酒杀尔,杀不死,乐尔乐.4 3 3 8 3 2 7 95 0 2 8 8 4 1 9 7 16 9 3 9 9 3 7死珊珊,霸占二妻.救吾灵儿吧!不只要救妻,一路救三舅,救三妻.5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7吾一拎我爸,二拎舅(其实就是撕吾舅耳)三拎妻.8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6不要溜!司令溜,儿不溜!儿拎爸,久久不溜!2 8 034 8 25 3 4 2 1 1 7 067 9 8饿不拎,闪死爸,而吾真是饿矣!要吃人肉?吃酒吧!【英文背圆周率的口诀】3.1 4 1 5 9Now I,even I,would celebrate2 6 53 5In rhymes inapt,the great8 9 7 9Immortal Syracusan,rivaled nevermore,3 2 3 8 4Who in his wondrous lore,6 2 6Passed on before,4 3 3 8Left men his guidance3 2 7 9How to circles mensurate背圆周率有什么好处1、锻炼大脑记忆圆周率对于锻炼大脑的作用很像体育锻炼对于身体各部分机能的发育和健康的作用。
圆周率前100位顺口溜 圆周率背诵口诀完整版

圆周率前100 位顺口溜圆周率背诵口诀完整版圆周率是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
1 圆周率前一百位速记顺口溜π=3.1415926535 89793 23846 26433 8327950288 41971 69399 37510 58209 74944 5923078164 06286 20899 86280 3482534211 706793 . 14 15 9 26 5 3 5 8 97 9 3 2 38 4 6 2 6山巅一寺一壶酒,尔乐苦煞吾,把酒吃,酒杀尔,杀不死,乐尔乐。
4 3 3 8 3 2 7 95 0 2 8 8 4 1 9 7 16 9 3 9 9 3 7死珊珊,霸占二妻。
救吾灵儿吧!不只要救妻,一路救三舅,救三妻。
5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7吾一拎我爸,二拎舅(其实就是撕吾舅耳)三拎妻。
8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6不要溜!司令溜,儿不溜!儿拎爸,久久不溜!2 8 034 8 25 3 4 2 1 1 7 067 9 8饿不拎,闪死爸,而吾真是饿矣!要吃人肉?吃酒吧!1 圆周率是怎幺算出来的“圆周率”即圆的周长与其直径之间的比率。
关于它的计算问题,历来是中外数学家极感兴趣、孜孜以求的问题。
德国的一位数学家曾经说过:“历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展的一个标志。
”我国古代在圆周率的计算方面长期领先于世界水平,这应当归功于魏晋时。
圆周率位与以内平方速记法5

小学生数学基础能力训练记忆圆周率的作用背圆周率有以下作用:(1)锻炼大脑记忆圆周率对于锻炼大脑的作用很像体育锻炼对于身体各部分机能的发育和健康的作用。
如同疲劳的体力劳动不能代替体育锻炼一样,工作中不断处理“伤脑筋”的事并不能代替对于大脑的锻炼。
有的体育运动项目主要锻炼身体的某一部位,而有的项目则能比较全面地锻炼身体的多个部位。
脑力锻炼也是一样,有的只能锻炼大脑某一部位的功能,有的能锻炼多个部位的功能。
不断地背记几千几百位圆周率,并不只是简单的机械记忆,需要动脑子寻找记忆窍门,所以有助于脑力的发展和保持。
经常锻炼身体的人即使到了老年动作也不迟钝,经常锻炼大脑的人到了老年仍能保持比较好的智力,不少年事很高的脑力劳动者思路清楚的原因就在这里。
据称,曾创背记圆周率世界纪录的日本人友寄英哲在背诵过程中,晚上睡眠情况大为好转,记忆力大大增强,动作反应也变得异常的灵敏。
由此可见背记圆周率确能起到锻炼大脑的作用。
(2)养成背诵的习惯背记数百位、数千位的圆周率的数值,是要下一番工夫的,不是一日之功,背诵多了,就会形成一种背诵的习惯。
(3)学会或自己创造一些记忆数字的方法要记忆上百位、上千位的无理数,完全靠机械记忆是不容易的,在记忆过程中,自觉不自觉地要用一些记忆数字的方法,而且很可能找到一些自己独创的方法。
这种运用和创造记忆方法的能力是有普遍意义的,是脱离圆周率而存在的,会记忆别的内容时表现出来。
所以,从这个意义上讲,即使具体的数字忘记了,但学会的方法和锻炼出来的能力并没有消失,会融入自己的总体知识和能力之中。
(4)提高对于数字的敏感性背诵一段时间圆周率以后,自然而然地会对数字有比较高的敏感性,见到数字就想记忆。
如路遇汽车就想记车牌号,看到或听到广告节目中的电话号码就想记忆等。
(5)增强了记忆数字的自信心自信心强了,记得快、记得牢。
在学习过程中,之所以要订出背几百、上千位的目标就是为了证明自己记忆上的潜力。
记住上百位圆周率以后,再去记忆只有十几位和几位的电话号码一类的数字,觉得容易得很;记住上千位以后,背100位就会觉得轻而易举。
巧记六年级圆的周长和面积常用π值

巧记常用π值圆的周长C=πd=2πr1π≈3.14 1×3=32π≈6.28 2×3=63π≈9.42 3×3=94π≈12.56 4×3=125π≈15.7 5×3=156π≈18.84 6×3=1898酒吧 7π≈21.98 7×3=21 7号二姨开了酒吧1到7π整数部分都乘38π≈25.12 8×3+1=25爸爸两次提到512地震28二爸 9π≈28.26 9×3+1=28这酒二爸的儿子说很牛10π≈31.4 10×3+1=31参考1π11π≈34.54 11×3+1=34双11要三思要无视68溜吧 12π≈37.68 12×3+1=3712个月过去了不管三七二十一溜吧40司令 13π≈40.82 13×3+1=4013姨和司令生了八个儿子14π≈43.96 14×3+1=4314岁翻四座山看九头牛8到14π整数部分都乘3加115π≈47.1 15×3+2=4715岁失去记忆71记忆 16π≈50.24 16×3+2=50石榴遇上502胶水死了17π≈53.38 17×3+2=5317岁我闪闪吧338闪闪吧 18π≈56.52 18×3+2=5618岁我牛我二19π≈59.66 19×3+2=5919岁我就牛牛66牛牛 20π≈62.8 20×3+2=60参考2π21二姨 21π≈65.94 21×3+2=65二姨和刘五酒市进酒去了15到21π整数部分乘3加222尔尔 22π≈69.08 22×3+2=69尔尔说留久点玲爸23尔三 23π≈72.22 23×3+3=72尔三的妻子生了三个儿子24π≈75.36 24×3+3=7524个人跳齐舞三流水平25π≈78.5 25×3+3=7825个人跳骑马舞22到28π整数部分乘3加3 ( 7个一组以此类推)圆的面积S=πr²1²π= 1π≈3.14 25²π= 625π≈1962.5 2²π= 4π≈6.28 35²π= 1225π≈3846.5 3²π= 9π≈9.42 45²π= 2025π≈6358.5 4²π= 16π≈50.245²π= 25π≈78.56²π= 36π≈113.04 2.5²π= 6.25π≈19.625 7²π= 49π≈153.86 3.5²π= 12.25π≈38.465 8²π= 64π≈200.96 4.5²π= 20.25π≈63.585 9²π= 81π≈254.3410²π= 100π≈314备注:来自原创,2020.5.15上传百度文库。
派的计算公式巧记法

派的计算公式巧记法在学习数学的过程中,我们经常需要记忆各种公式和计算方法。
其中,派的计算公式是一个非常重要的内容,它在数学中起着非常重要的作用。
为了帮助大家更好地记忆派的计算公式,我们可以使用一些巧妙的记忆方法,让我们来看看这些方法吧。
首先,我们来看一下派的定义。
派是一个无理数,它的近似值是3.1415926,通常用希腊字母π来表示。
派的计算公式有很多种,其中最常见的是圆的周长和面积的计算公式。
圆的周长公式是2πr,其中r表示圆的半径;圆的面积公式是πr^2,其中r表示圆的半径。
要想记忆这些公式,我们可以使用一些巧妙的方法。
首先,我们可以通过联想来记忆这些公式。
比如,我们可以联想圆的周长公式2πr中的2π,可以看成是两个圆周率π,这样就容易记忆了。
另外,我们也可以通过一些简单的句子或者故事来记忆这些公式。
比如,我们可以用“圆的周长等于2倍的圆周率乘以半径”这样的句子来记忆圆的周长公式。
通过这样的方法,我们可以更加轻松地记忆派的计算公式。
除了圆的周长和面积的计算公式外,派还有很多其他的计算公式。
比如,我们可以通过派的计算公式来计算球的表面积和体积。
球的表面积公式是4πr^2,其中r表示球的半径;球的体积公式是4/3πr^3。
这些公式在数学中也是非常重要的,我们同样可以通过一些巧妙的记忆方法来记忆这些公式。
另外,我们还可以通过一些实际的例子来帮助记忆派的计算公式。
比如,我们可以通过实际测量一个圆的半径和周长,然后通过派的计算公式来计算一下,这样就可以更加直观地理解和记忆这些公式了。
除了记忆派的计算公式外,我们还可以通过一些实际的问题来帮助巩固对这些公式的记忆。
比如,我们可以通过一些实际的问题来应用这些公式,这样就可以更加深刻地理解和记忆这些公式了。
总的来说,派的计算公式是数学中非常重要的内容,它在很多领域都有着广泛的应用。
为了更好地记忆这些公式,我们可以通过一些巧妙的方法来帮助记忆,比如通过联想、句子、故事、实际的例子和实际的问题等。
圆周率公式

圆周率公式
周长C/直径d=3.14159。
π=圆周长/直径=102573/32650=3.141592649310872894333843797856。
圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
圆周率
π也等于圆形之面积与半径平方之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学里,π可以严格地定义为满足sinx=0的最小正实数x。
圆周率用希腊字母π(读作[paɪ])表示,是一个常数(约等于3.141592653),是代表圆周长和直径的比值。
它是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
而用十位小数3.141592653便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率的计算公式

圆周率的计算公式
圆周率π(读作pài)是圆的周长与直径的比值,计算公式: π=圆周长C/直径d≈圆内接正多边形/直径。
当正多边形的边长越多时,其周长就越接近于圆的周长。
圆周率一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数,约等于3.141592653。
它是一个无理数,即无限不循环小数。
在日常生活中,通常都用 3.14代表圆周率去进行近似计算。
而用十位小数3.141592653便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
