口奥题库 - 行程 (2)

合集下载

新疆塔城地区小学数学小学奥数系列3-1-1行程问题(二)

新疆塔城地区小学数学小学奥数系列3-1-1行程问题（二）姓名:________ 班级:________ 成绩:________亲爱的小朋友们，这一段时间的学习，你们收获怎么样呢？今天就让我们来检验一下吧！一、 (共23题；共115分)1. （5分） (2020四上·汉阳期末) 小丽一家周末自驾去某景区游玩，平均每小时行78千米，全程有312千米．他们早上7：30出发，最早什么时候可以到达景区？2. （5分） (2019四上·开福期末) 一辆汽车4小时行480千米．照这样的速度计算，这辆汽车从甲地到乙地要行7小时，甲乙两地相距多少千米？3. （5分）(2020四上·石碣期末)4. （5分） (四上·定海期末) 王叔叔开车从A城出发去B城，行驶2小时后，超过中点40千米，距离B城还有80千米，王叔叔开车每小时行驶多少千米？5. （5分）一条船逆水每小时行12.5千米，42小时到达目的地。

如果返回时顺水每小时行17.5千米，那么需要多少小时返回出发地？6. （5分）在16千米自行车越野赛中，小丽的参赛方法是先以一定速度匀速骑一段时间后，再以另一速度匀速骑完全程．（1）请根据上表，在下面的方格纸上画出他比赛时路程与时间的关系图．（2）从图中观察小丽在出发后变速前速度快还是变速后速度快，你能看出小丽在出发多少分时改变的速度吗？此时她骑了多远的路程？（3）请问小丽用多长时间骑完全程？7. （5分） (2019四上·建邺期末) 小红家离学校有960米，一天她从家出发去学校，前12分钟一共走了720米，照这样的速度，她还要走多少分钟才能到学校？8. （5分） (2020三上·龙华期末) 机器狗和机器猫在广场上沿着不同的长方形运动。

它们都从A点出发，机器狗沿着A→B→E→F→A的路线跑，跑一圈要3分；机器猫沿着A→B→C→D→A的路线跑，跑一圈要4分。

（1）机器猫跑一圈比机器狗多跑多少米？（2）谁跑得快？平均每分快多少米？9. （5分） (2020四上·龙华期末) 涛涛要从艺术楼到教学楼，再到操场。

口奥题库行程

口奥题库行程文件管理序列号：[K8UY-K9IO69-O6M243-OL889-F88688]【基础】【2】从A到B有两条路可走，小王骑车从A过C到B比走另一条路少用3分钟，而从A出发到B，再经过C返回到A要53分钟，小王骑车速度为每小时36千米。

求：小王从A经过C到B所走过的路程。

【答案】15千米【基础】【2】从小明的家到长途汽车站有3千米。

现在从家往车站去，如果用每小时4千米的速度行走，在汽车发车前17分钟到达车站；如果想在汽车发车前2分钟到达车站，那么需用每小时多少千米的速度行走？【答案】每小时3千米【基础】【1】小明以一固定的速度从甲地跑到乙地，上午8时，他离乙地20千米，上午9时半他离乙地8千米，小明几点到达乙地？【答案】十点半【相遇追及】【2】兄弟两人同时从家里出发到学校，路程是1400米。

哥哥骑自行车每分钟行200米，弟弟步行每分钟行80米，在行进中弟弟与刚到学校就立即返回来的哥哥相遇。

从出发到相遇，弟弟走了多少分钟？【答案】10分钟【相遇追及】【3】如图，有两只蜗牛同时一个等腰三角形的顶点A出发，分别沿着两腰爬行。

一只蜗牛每分钟行2.5米，另一只蜗牛每分钟行2米，8分钟后在离C点6米处的P点相遇，则线段BP的长度是多少？【答案】2米(2.5－2)×8=4米，6－4=2米。

则BP长是2米。

【相遇追及】【2】甲、乙二人练习跑歩，若甲让乙先跑10米则甲跑5秒钟可追上乙；若甲让乙先跑2秒钟，则甲跑4秒钟就能追上乙.问：甲、乙二人的速度各是________、________。

【答案】6米/秒，4米/秒【相遇追及】【2】甲走一段路用40分钟，乙走同样一段路用30分钟。

从同一地点出发，甲先走5分钟，乙再开始追，乙________分钟才能追上甲。

【答案】20【多次相遇】【1】甲乙两车同时从A、B两地相向而行，甲车每小时行驶36千米，乙车每小时行驶34千米，两车分别到达目的地后立即返回，第二次相遇时共行驶了12小时，两地相距________米。

六年级下册奥数试题行程问题(二)全国通用(含答案)

第12讲行程问题（二）在四年级的教材中，我们已经对于相遇问题、追及问题、水流问题和车长及桥长等问题，进行了较为细致的研究。

在这一讲中，我们将进一步就环行路上的行程问题以及多次相遇等问题进行研究。

行程问题在小学的应用题中是变化最多的类型之一。

对于行程问题的研究是小学综合运用知识解决问题的一个重要的内容。

因为行程问题的变化可谓是丰富多彩，不仅在小学，而且在中学的数学和物理的学习中，也是极其重要的内容。

一、环行路上的行程问题环行路上的行程问题，有着它独特的方面，由于环行的道路是封闭的，因此，环行路上的运动，计算行程时，通常与环行道路的周长有关。

例1在400米的环行跑道上，A、B两点相距100米，甲、乙两人分别从A、B两点同时出发，按逆时针方向跑步。

甲每秒跑5米，乙每秒跑4米，他们每人跑100米，都要停10秒钟。

求甲追上乙需要多少秒？分析：这道题初看时，由于他们每人跑100米，都要停10秒钟。

似乎不太好解决。

但如果将二人看成不停的跑，就很容易算出甲追上乙的时间，这时再考虑在这期间所停留的时间，问题的解决就比较简单了。

解答：如果甲、乙不停的跑步，甲追上乙共需：100÷（5－4）=100（秒），甲在100秒中共跑：5×100=500（米），而甲在跑100米、200米、300米、400米时共停留了4次，到了500米处恰好追上乙。

不必计算停留的时间。

所以，甲追上乙所需的时间是：100＋4×10=140（秒）说明：甲跑到500米处时，正好是乙跑完400米，并且休息完10秒时。

当甲跑到时，乙恰好要出发，他们两个在这一瞬间正好相遇。

例2 如图，A、B是圆直径的两个端点，小华在点A，小明在点B，他们同时出发，反向而行。

他们在C点第一次相遇，C点离A点100米；在D点第二次相遇，D点离B点80米。

求这个圆的周长。

分析：第一次相遇，两人合起来走了半圈，第二次相遇，两人合起来走了一圈，因此，从开始出发到第二次相遇，两人合起来走了一圈半。

六年级奥林匹克数学讲义八行程问题(二)

八、行程问题（二）1.A、B两地相距150千米.两列火车同时从A地开往B地.快车每小时行60千米.慢车每小时行48千米.当快车到达B地时,慢车离B地还有千米.2.某人沿直线从甲城到乙城去旅行,去的时候以每小时30公里的速度匀速前进.回来时以每小时60公里的速度匀速返回,此人在往返行程中的平均速度是每小时公里.3.某教师每天早上驾车40公里到学校需要用55分钟,某天早上她迟离开家7分钟,那么她的车速每小时为公里时才能和平常一样按时到达学校.4.一辆汽车从甲地开往乙地,每分钟行750米,预计50分钟到达.但汽车行驶到3/5路程时,出了故障,用5分钟修理完毕,如果仍需要在预定时间内到达乙地.汽车行驶余下的路程时,每分钟须比原来快米.5.有甲、乙、丙三辆汽车,各以一定的速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙；甲比乙又晚出发20分钟,出发后1小时40分钟追上丙,那么甲出发后需分钟才能追上乙.6.甲、乙二人相距100米的直路上来回跑步,甲每秒钟跑2.8米,乙每秒钟跑2.2米.他们同时分别在直路两端出发,当他们跑了30分钟时,这段时间内相遇了次.7.甲、乙二人骑自行车从环形公路上同一地点同时出发,背向而行.现在已知甲走一圈的时间是70分钟.如果在出发后第45分钟甲、乙二人相遇,那么乙走一圈的时间是分钟.8.有人沿公路前进,对面来了一辆汽车,他问司机：“后面有自行车吗？”司机回答：“十分钟前我超过一辆自行车”,这人继续走了10分钟,遇到自行车.已知自行车速度是人步行速度的三倍,汽车的速度是步行速度的倍.9.某校和某工厂之间有一条公路,该校下午2点钟派车去该厂接某劳模来校作报告,往返需用1小时.这位劳模在下午1点钟便离厂步行向学校走来,途中遇到接他的汽车,便立刻上车驶向学校,在下午2点40分到达.汽车速度是劳模步行速度的倍.10.游船顺流而下,每小时前进7公里,逆流而上,每小时前进5公里.两条游船同时从同一个地方出发,一条顺水而下,然后返回；一条逆流而上,然后返回.结果,1小时以后它们同时回到出发点.在这1小时内有分钟这两条船的前进方向相同?11.一个圆的周长为1.26米,两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行.这两只蚂蚁每秒分别爬行5.5厘米和3.5厘米.它们每爬行1秒,3秒,5秒……(连续的奇数),就调头爬行.那么,它们相遇时已爬行的时间是多少秒?12.小明和小刚乘火车出外旅行,离开车时间只有2小时,他们家离车站12公里,两人步行每小时只能走4公里,按这个速度非误车不可.恰好小华骑自行车经过,就先将小明带了9公里,让小明继续步行,接着返回原路接小刚.小华在距他们家3公里处遇到小刚,带着小刚追小明.他们提前赶到了车站.你知道他俩在开车前几分钟到达车站的吗?13.有100名少先队员在岸边准备坐船去湖中离岸边600米的甲岛,等最后一人到达甲岛15分钟后,再去离甲岛900米的乙岛,现有机船和木船各1条,机船和木船每分钟各行300米和150米,而机船和木船可各坐10人和25人,问最后一批少先队员到达乙岛,最短需要多长时间?(按小时计算)14.甲乙两地相距很远,每天从甲、乙两地同时相对开出一辆客车,两车速度和路线相同,都要经过整整五天才能到达终点站,然后休整两天,又按原路返回.在这条线路上的每辆客车都这样往返运行.为了保证这条线路上客运任务能正常进行,问这条线路上至少应配备多少辆客车.八、行程问题（二） (答案）第[1]道题答案：30快车到达B地所需时间是:150÷60=2.5(小时),慢车离B地的距离是150-48⨯2.5=30(千米).第[2]道题答案：V =40(公里)设甲乙两城相距S公里,平均速度为每小时V公里,依题意有VSSS26030=+,解得: V =40.第[3]道题答案：5050607605540=⎪⎭⎫⎝⎛-÷(公里/小时).第[4]道题答案：250汽车行驶余下路程需要的时间是100055315053150750=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-⨯÷⎪⎭⎫⎝⎛-⨯⨯(米);故每分钟必须比原来快1000-750=250(米).第[5]道题答案：500根据已知条件得知,乙用40分钟所走的距离与丙用50分钟所走的距离相等;甲用100分钟所走的距离与丙用130分钟所走的距离相等.故丙用130分钟所走的距离,乙用了1045040130=⨯(分钟),即甲用100分钟走A B的距离,乙用104分钟走完.由于甲比乙晚出发20分钟,当甲追上乙时,设甲用了x 分钟,则乙用了(x +20)分钟.依题意得20104100+=x x,解得x =500.第[6]道题答案：45两人一共跑的路程为(2.8+2.2)⨯30⨯60=9000(米),去掉二人第一次相遇时跑的100米,二人每跑200米,就相遇一次,共相遇的次数为(9000-100)÷200=44.5,取整得44次.加上第一次相遇,共44+1=45(次).第[7]道题答案：126设乙骑自行车走一圈要x 分钟,环行公路长为S 米,则有S x S S =⎪⎭⎫⎝⎛+7045,解得x =126(分钟).第[8]道题答案：7设人行速度为每分钟1单位,则自行车速度为每分钟3单位,再设汽车速度为每分钟x 单位,依题意有(x -3)⨯10=(3+1)⨯10,故有x =7.第[9]道题答案：8如下图,A 是学校,C 是工厂,B 是相遇地点.汽车从A 到C 往返需要1小时,从A 到B 往返要40分钟即32小时,这说明AC AB 32=,即也说明汽车从A 到B 要用40÷2=20(分钟).而劳模由C 到B 要用1小时20分,即80分钟.是汽车的4倍,又易知AB =2BC ,即汽车的路程是劳模的2倍,于是汽车的速度是劳模步行速度的4⨯2=8(倍).第[10]道题答案：10设1小时顺流时间为x 分钟,则逆流时间为(60-x )分钟,由于路程一定,行驶时间与速度成反比例,故x :(60-x )=5:7.解得x =25,60-x =35.当两条船同时从同一地方出发,一条顺流走25分钟后,开始返回(逆流行走),这时另一条还在逆流前进,这其间的35-20=10(分钟).两船同时向上游前进. 第[11]道题答案：两只蚂蚁分别从直径AB 的两端同时出发,相向而行,若不调头的话,两只蚂蚁的行程为半个圆的周长,即1.26÷2=0.63(米)=63(厘米).而两只蚂蚁的速度和为每秒5.5+3.5=9(厘米).它们相遇的时间为63÷9=7(秒).即两只蚂蚁需要向前爬的时间是7秒钟.但蚂蚁是按向前,再调头向后,再调头向前……的方式前进.每只蚂蚁向前爬1秒,然后调头反向爬3秒,又调头向前爬5秒,这时相当于又向前爬行了2秒.同理再向后爬7秒,再前爬9秒,再向后爬11秒,再向前爬13秒,就相当于一共向前爬了1+2+2+2=7秒,正好相遇,这时它们用了1+3+5+7+11+13=49(秒).第[12]道题答案：小刚走3公里用的时间是4343=÷(小时);小华骑自行车的速度为()2043939=÷+-(公里/小时);小明到火车站所用时间为()2.14912209=÷-+÷(小时);小刚到火车站用的时间为()2.12031243=÷-+÷(小时);小明、小刚开车前到达火车站的时间为2-1.2=0.8(小时)=48(分).即他俩在开车前48分钟到达车站.第[13]道题答案：机船去甲岛,单程时间为600÷300=2(分).木船去甲岛,单程时间为600÷150=4(分).其中机船在18分钟内,可运5次学生共10⨯5=50(人),到达甲岛时间分别为2、6、10、14、18(分钟);而木船18分钟内,只能运2次学生共25⨯2=50(人),到达甲岛的时间为4、12(分钟),故18分钟内两船可运完学生去甲岛.机船去乙岛,单程时间为:900÷300=3(分),木船去乙岛,单程时间为:900÷150=6(分).其中机船27分钟内,可运5次学生共10⨯5=50(人),到达乙岛的时间为:3、9、15、21、27(分钟),而木船27分钟内,只能运2次学生共25⨯2=50(人),到达乙岛的时间为:6、18(分钟).所以27分钟两船可运光全部学生去乙岛.最短需要时间为18+5+27=50(分)=65(小时). 第[14]道题答案：本题要求每天从甲、乙两地同时相对开出一辆客车,每辆客车运行5天再休整2天,需7天后再往回开,这样为保证每天在线路上有两辆客车在相对开,至少应配备2⨯7=14(辆)客车.A B C。

奥数行程问题归纳总结及部分例题及答案

行程问题是小学奥数中难度系数比较高的一个模块，在小升初考试和各大奥数杯赛中都能见到行程问题的身影。

行程问题中包括：火车过桥、流水行船、沿途数车、猎狗追兔、环形行程、多人行程等等。

每一类问题都有自己的特点，解决方法也有所不同，但是，行程问题无论怎么变化，都离不开“三个量，三个关系”：这三个量是：路程(s)、速度(v)、时间(t)三个关系：1.简单行程：路程=速度×时间2.相遇问题：路程和=速度和×时间3.追击问题：路程差=速度差×时间牢牢把握住这三个量以及它们之间的三种关系，就会发现解决行程问题还是有很多方法可循的。

如“多人行程问题”，实际最常见的是“三人行程”例：有甲、乙、丙三人同时同地出发，绕一个花圃行走，乙、丙二人同方向行走，甲与乙、丙相背而行。

甲每分钟走40米，乙每分钟走38米，丙每分钟走36米。

在途中，甲和乙相遇后3分钟和丙相遇。

问：这个花圃的周长是多少米？分析：这个三人行程的问题由两个相遇、一个追击组成，题目中所给的条件只有三个人的速度，以及一个“3分钟”的时间。

第一个相遇：在3分钟的时间里，甲、丙的路程和为（40+36）×3=228（米）第一个追击：这228米是由于在开始到甲、乙相遇的时间里，乙、丙两人的速度差造成的，是逆向的追击过程，可求出甲、乙相遇的时间为228÷（38-36）=114（分钟）第二个相遇：在114分钟里，甲、乙二人一起走完了全程所以花圃周长为（40+38）×114=8892（米）我们把这样一个抽象的三人行程问题分解为三个简单的问题，使解题思路更加清晰。

总之，行程问题是重点，也是难点，更是锻炼思维的好工具。

只要理解好“三个量”之间的“三个关系”，解决行程问题并非难事！行程问题是小学奥数中难度系数比较高的一个模块，在小升初考试和各大奥数杯赛中都能见到行程问题的身影。

多人行程---这类问题主要涉及的人数为3人，主要考察的问题就是求前两个人相遇或追及的时刻，第三个人的位置，解题的思路就是把三人问题转化为寻找两两人之间的关系。

人教版六年级下册数学奥数行程问题试题

行程问题（一）知识导航行程问题是研究有关物体运动的速度、时间、路程三者之间关系的问题，其基本数量关系是：路程=速度×时间。

行程问题内容繁多，变化无穷，还有一些特殊问题，如“列车过桥”“流水行船”等。

这一讲我们就来学习这些问题。

经典例题1一座桥长350米，一列火车长280米，它以每秒行30米的速度通过这座桥，火车从上桥到离桥需要多长时间？举一反三11、一列火车长300米，每秒钟行20米，要通过一个长300米的山洞，需要多长时间？2、一座桥长1800米，一列火车以每秒25米的速度通过这座桥，车长200米。

火车从上桥到离桥需要用多长时间？3、一列火车由30节车厢组成，每节车厢长20米，每秒钟行25米，要通过一座长1500米的大桥，需要多长时间？（车厢之间的间隙不计）。

经典例题2一列火车长870米，经过铁道边的一个标志牌，用了30秒。

以同样的速度通过一个山洞，从车头进洞到车尾出洞共用了70秒。

这个山洞长多少米？举一反三1、一列火车长800米，从站在铁路边的铁道员旁边经过用了25秒。

以同样的速度通过前方的一个山洞，从车头进洞到车尾出洞共用了50秒。

求这个山洞长多少米？2、一列火车长600米，经过铁道旁边的一个广告牌，用了30秒。

以同样的速度通过一座大桥，从车头上桥到车尾离桥共用了100秒，这座大桥长多少米？3、一列火车长180米，从小明旁边通过，用了10秒钟。

用同样的速度通过一座长990米的大桥，需多少秒？经典例题3一列火车用82秒通过一个长1800米的山洞，以同样的速度用30秒通过一座长500米的隧道。

求这列车的速度和车身的长各是多少？举一反三1、一列火车通过一座长2400米的大桥用了90秒，用同样的速度穿过长1800米的隧道用了70秒，问这列火车的速度和车身长各是多少？2、一列火车通过一个长200米的山洞需要20秒钟，用同样的速度通过一座长500米的大桥需要32秒，求火车的长度和速度。

3、一列火车通过一个长1000米的隧道用了50秒，用同样的速度通过一座长1650米的大桥，用了75秒。

小学的奥数---行程问题

行程问题1、某运动员要跑24里，他先以平均每小时8里的速度跑完这段距离的三分之二，而后他加大速度，问：能否在跑完剩下路程时，使全程的平均速度提高到每小时12里？2、一只小蚂蚁在一根弹性充分好的橡皮筋上的A点，以每秒1厘的速度向前爬行．从小蚂蚁开始爬行的时候算起，橡皮筋在第2秒、第4秒、第6 秒、第8秒、第10秒……时均匀的伸长为原来的2倍．那么，在第9秒时，这只小蚂蚁离A点________厘米.3、狗追狐狸，狗跳一次前进1. 8米，狐狸跳一次前进进1.1米，狗每跳两次时狐狸恰好跳3次．如果开始时狗离狐狸有30米，那么狗跑多少米才能追上狐狸？4、冯老师每天早上做户外运动，第一天他跑步2000米，散步1000米，共用24分钟；第二天他跑步3000米，散步500米，共用22分钟．冯老师跑步时的速度是一样的，散步时的速度也总是一样的．求冯老师跑步的速度．5、老师每天早上晨练，他第一天跑步1000米，散步1600米，共用25分；第二天跑步2000米，散步800米，共用20分钟．假设王老师跑步的速度和散步速度均保持不变．求：(l)王老师跑步的速度；(2)王老师散步800米所用的时间．6、兄弟两人骑白行车同时从甲地到乙地，弟弟在前一半路程每小时行5千米，后一半路程每小时行7千米，哥哥按时间分段行驶，前1/3时间每小时行4千米，中间1/3时间每小时行6千米，后1/3时间每小时行8千米，结果哥哥比弟早到20分，甲、乙两地的路程是________ 千米.7、甲、乙两人从A地到B地，甲前三分之一路程的行走速度是5千米／小时，中间三分之一的路程的行走速度是4。

5千米／小时，最后三分之一的路程的行走速度是4千米／小时；乙前二分之一路程的行走速度是5千米／小时，后二分之一路程的行走速度是4千米／小时．已知甲比乙早到30秒，A地到B地的路程程是______千米．8、张、王两人骑摩托车同时从甲地出发，沿着同一条公路前进，张的速度比王的速度每小时快6千米．张比王早20分钟到达乙地，又继续前进，当王到达乙时，张比王已经多走了20千米，那么，甲、乙两地的距离是______千米。

小学奥数行程专题50道详解(二)

行程专题50道详解二6、小王的步行速度是4.8千米/小时,小张的步行速度是5.4千米/小时,他们两人从甲地到乙地去.小李骑自行车的速度是10.8千米/小时,从乙地到甲地去.他们3人同时出发,在小张与小李相遇后5分钟,小王又与小李相遇.问：小李骑车从乙地到甲地需要多少时间？解：画一张示意图：图中A点是小张与小李相遇的地点,图中再设置一个B点,它是张、李两人相遇时小王到达的地点.5分钟后小王与小李相遇,也就是5分钟的时间,小王和小李共同走了B与A之间这段距离,它等于这段距离也是出发后小张比小王多走的距离,小王与小张的速度差是（5.4-4.8）千米/小时.小张比小王多走这段距离,需要的时间是1.3÷（5.4-4.8）×60=130（分钟）.这也是从出发到张、李相遇时已花费的时间.小李的速度10.8千米/小时是小张速度5.4千米/小时的2倍.因此小李从A到甲地需要130÷2=65（分钟）.从乙地到甲地需要的时间是130＋65=195（分钟）＝3小时15分.答：小李从乙地到甲地需要3小时15分.7、快车和慢车分别从A,B两地同时开出,相向而行.经过5小时两车相遇.已知慢车从B到A用了12.5小时,慢车到A停留半小时后返回.快车到B停留1小时后返回.问：两车从第一次相遇到再相遇共需多少时间？解：画一张示意图：设C点是第一次相遇处.慢车从B到C用了5小时,从C到A用了12.5-5=7.5（小时）.我们把慢车半小时行程作为1个单位.B到C10个单位,C到A15个单位.慢车每小时走2个单位,快车每小时走3个单位.有了上面"取单位"准备后,下面很易计算了.慢车从C到A,再加停留半小时,共8小时.此时快车在何处呢？去掉它在B停留1小时.快车行驶7 小时,共行驶3×7=21（单位）.从B到C再往前一个单位到D点.离A点15-1＝14（单位）.现在慢车从A,快车从D,同时出发共同行走14单位,相遇所需时间是14÷（2＋3）＝2.8（小时）.慢车从C到A返回行驶至与快车相遇共用了7.5＋0.5＋2.8＝10.8（小时）.答：从第一相遇到再相遇共需10小时48分.8、一辆车从甲地开往乙地.如果车速提高20％,可以比原定时间提前一小时到达；如果以原速行驶120千米后,再将速度提高25％,则可提前40分钟到达.那么甲、乙两地相距多少千米？解：设原速度是1.这是具体地反映：距离固定,时间与速度成反比.时间比值：6：5这样可以把原来时间看成6份,后来就是5份,这样就节省1份,节省1个小时.原来时间就是=1×6=6小时.同样道理,车速提高30％,速度比值：1：（1+30%）=1：1.3时间比值：1.3：1这样也节省了0.3份,节省1小时,可以推出行驶一段时间后那段路程的原时间为1.3÷0.3=13/3所以前后的时间比值为（6-13/3）：13/3=5：13.所以总共行驶了全程的5/（5+13）=5/1810、甲、乙两车分别从A,B两地出发,相向而行,出发时,甲、乙的速度比是 5：4,相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B时,乙离A地还有10千米.那么A,B两地相距多少千米？解：相遇后速度比值为[5×（1-20%）]：[4×（1+20%）]=5：6,假设全程为9份,甲走了5份,乙走了4份,之后速度发生变化,这样甲到达B地,甲又走了4份,根据速度变化后的比值,乙应该走了4×6÷5=24/5份,这样距A地还有5-24/5份,所以全程为10÷（1/5）×9=450千米.。

口奥题库 - 行程

口奥题库 - 行程【基础】【2】从A到B有两条路可走，小王骑车从A过C到B比走另一条路少用3分钟，而从A出发到B，再经过C返回到A要53分钟，小王骑车速度为每小时36千米。

求:小王从A经过C到B所走过的路程。

【答案】15千米【基础】【2】从小明的家到长途汽车站有3千米。

现在从家往车站去，如果用每小时4千米的速度行走，在汽车发车前17分钟到达车站;如果想在汽车发车前2分钟到达车站，那么需用每小时多少千米的速度行走,【答案】每小时3千米【基础】【1】小明以一固定的速度从甲地跑到乙地，上午8时，他离乙地20千米，上午9时半他离乙地8千米，小明几点到达乙地,【答案】十点半【相遇追及】【2】兄弟两人同时从家里出发到学校，路程是1400米。

哥哥骑自行车每分钟行200米，弟弟步行每分钟行80米，在行进中弟弟与刚到学校就立即返回来的哥哥相遇。

从出发到相遇，弟弟走了多少分钟,【答案】10分钟【相遇追及】【3】如图，有两只蜗牛同时一个等腰三角形的顶点A出发，分别沿着两腰爬行。

一只蜗牛每分钟行2.5米，另一只蜗牛每分钟行2米，8分钟后在离C点6米处的P点相遇，则线段BP的长度是多少,【答案】2米(2.5,2)×8=4米，6,4=2米。

则BP长是2米。

【相遇追及】【2】甲、乙二人练习跑歩，若甲让乙先跑10米则甲跑5秒钟可追上乙;若甲让乙先跑2秒钟，则甲跑4秒钟就能追上乙.问:甲、乙二人的速度各是________、________。

【答案】6米/秒，4米/秒【相遇追及】【2】甲走一段路用40分钟，乙走同样一段路用30分钟。

从同一地点出发，甲先走5分钟，乙再开始追，乙________分钟才能追上甲。

【答案】280【多次相遇】【2】甲，乙两车分别同时从A,B两地相对开出，第一次在离A地95千米处相遇，相遇后继续前进到达目的地后又立刻返回，第二次在离B地25千米处相遇，AB两地间距离为________。

行程问题奥数题及答案

行程问题奥数题及答案行程问题奥数题及答案1五年级奥数题及答案:行程问题甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行.现在已知甲走一圈的时间是70分钟，如果在出发后45分钟甲、乙二人相遇，那么乙走一圈的时间是____分钟?答案与解析：甲行走45分钟，再行走70-45=25(分钟)即可走完一圈.而甲行走45分钟，乙行走45分钟也能走完一圈.所以甲行走25分钟的路程相当于乙行走45分钟的路程.甲行走一圈需70分钟，所以乙需70÷25×45=126(分钟).即乙走一圈的时间是126分钟.行程问题奥数题及答案2济南小学五年级奥数题及答案：行程问题1.汽车往返于A ，B 两地，去时速度为 40千米／时，要想来回的平均速度为48千米／时，回来时的速度应为多少？2.赵伯伯为锻炼身体，每天步行3小时，他先走平路，然后上山，最后又沿原路返回．假设赵伯伯在平路上每小时行 4千米，上山每小时行 3千米，下山每小时行6千米，在每天锻炼中，他共行走多少米？济南小学五年级奥数题答案1.解答：假设AB两地之间的距离为480÷2=240 (千米)，那么总时间=480÷48=10 (小时)，回来时的速度为240÷（10-240÷4）=60 (千米/时)．2.解答：设赵伯伯每天上山的路程为12千米，那么下山走的路程也是12千米，上山时间为12÷3=4 小时，下山时间为12÷6=2 小时，上山、下山的平均速度为：12×2÷（4+2）=4 （千米/时），由于赵伯伯在平路上的速度也是4 千米/时，所以，在每天锻炼中，赵伯伯的平均速度为 4千米/时，每天锻炼3 小时，共行走了4×3=12 （千米）=12000 （米）．行程问题奥数题及答案31.行程问题甲、乙二人练习跑步，若甲让乙先跑10米，则甲跑5秒钟可追上乙；若甲让乙先跑2秒钟，则甲跑4秒钟就能追上乙.问：甲、乙二人的速度各是多少？解答：分析若甲让乙先跑10米，则10米就是甲、乙二人的路程差，5秒就是追及时间，据此可求出他们的速度差为10÷5=2（米/秒）；若甲让乙先跑2秒，则甲跑4秒可追上乙，在这个过程中，追及时间为4秒，因此路程差就等于2×4=8（米），也即乙在2秒内跑了8米，所以可求出乙的速度，也可求出甲的速度.综合列式计算如下：解：乙的速度为：10÷5×4÷2=4（米/秒）甲的速度为：10÷5+4=6（米/秒）答：甲的速度为6米/秒，乙的速度为4米/秒.2.行程问题上午8点零8分，小明骑自行车从家里出发，8分钟后，爸爸骑摩托车去追他，在离家4千米的地方追上了他.然后爸爸立刻回家，到家后又立刻回头去追小明、再追上他的时候，离家恰好是8千米，问这时是几点几分？解答：从爸爸第一次追上小明到第二次追上这一段时间内，小明走的路程是8-4=4（千米），而爸爸行了4+8=12（千米），因此，摩托车与自行车的速度比是12∶4=3∶1.小明全程骑车行8千米，爸爸来回总共行4+12=16（千米），还因晚出发而少用8分钟，从上面算出的速度比得知，小明骑车行8千米，爸爸如同时出发应该骑24千米.现在少用8分钟，少骑24-16=8（千米），因此推算出摩托车的速度是每分钟1千米.爸爸总共骑了16千米，需16分钟，8+16=24（分钟），这时是8点32分.行程问题奥数题及答案4题型：行程问题难度：李华步行以每小时4千米的速度从学校出发到20.4千米处的冬令营报到。

小学六年级奥数专项行程问题

模块一发车问题【例1】某停车场有10辆出租汽车，第一辆出租汽车出发后，每隔4分钟，有一辆出租汽车开出.在第一辆出租汽车开出2分钟后，有一辆出租汽车进场.以后每隔6分钟有一辆出租汽车回场.回场的出租汽车，在原有的10辆出租汽车之后又依次每隔4分钟开出一辆，问：从第一辆出租汽车开出后，经过多少时间，停车场就没有出租汽车了？【例2】某人沿着电车道旁的便道以每小时4.5千米的速度步行，每7.2分钟有一辆电车迎面开过，每12分钟有一辆电车从后面追过，如果电车按相等的时间间隔以同一速度不停地往返运行．问：电车的速度是多少？电车之间的时间间隔是多少？【巩固】某人以匀速行走在一条公路上,公路的前后两端每隔相同的时间发一辆公共汽车.他发现每隔15分钟有一辆公共汽车追上他；每隔10分钟有一辆公共汽车迎面驶来擦身而过.问公共汽车每隔多少分钟发车一辆?【巩固】某人沿电车线路行走，每12分钟有一辆电车从后面追上，每4分钟有一辆电车迎面开来．假设两个起点站的发车间隔是相同的，求这个发车间隔．【例3】一条公路上，有一个骑车人和一个步行人，骑车人速度是步行人速度的3倍，每隔6分钟有一辆公共汽车超过步行人，每隔10分钟有一辆公共汽车超过骑车人，如果公共汽车始发站发车的时间间隔保持不变，那么间隔几分钟发一辆公共汽车？【巩固】从电车总站每隔一定时间开出一辆电车。

甲与乙两人在一条街上沿着同一方向步行。

甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车。

那么电车总站每隔多少分钟开出一辆电车？【例4】甲城的车站总是以20分钟的时间间隔向乙城发车，甲乙两城之间既有平路又有上坡和下坡，车辆（包括自行车）上坡和下坡的速度分别是平路上的80%和120%，有一名学生从乙城骑车去甲城，已知该学生平路上的骑车速度是汽车在平路上速度的四分之一，那么这位学生骑车的学生在平路、上坡、下坡时每隔多少分钟遇到一辆汽车？【例5】甲、乙两地是电车始发站，每隔一定时间两地同时各发出一辆电车，小张和小王分别骑车从甲、乙两地出发，相向而行．每辆电车都隔4分钟遇到迎面开来的一辆电车；小张每隔5分钟遇到迎面开来的一辆电车；小王每隔6分钟遇到迎面开来的一辆电车．已知电车行驶全程是56分钟，那么小张与小王在途中相遇时他们已行走了分钟．【例6】小峰骑自行车去小宝家聚会，一路上小峰注意到，每隔9分钟就有一辆公交车从后方超越小峰，小峰骑车到半路，车坏了，小峰只好打的去小宝家，这时小峰又发现出租车也是每隔9分钟超越一辆公交车，已知出租车的速度是小峰骑车速度的5倍，那么如果公交车的发车时间间隔和行驶速度固定的话，公交车的发车时间间隔为多少分钟？【例7】某人乘坐观光游船沿顺流方向从A港到B港。

小学五年级奥数行程问题练习题及答案

小学五年级奥数行程问题练习题及答案1.小学五年级奥数行程问题练习题及答案篇一张工程师每天早上8点准时被司机从家接到厂里。

一天，张工程师早上7点就出了门，开始步行去厂里，在路上遇到了接他的汽车，于是，他就上车行完了剩下的路程，到厂时提前20分钟。

这天，张工程师还是早上7点出门，但15分钟后他发现有东西没有带，于是回家去取，再出门后在路上遇到了接他的汽车,那么这次他比平常要提前分钟。

答案解析：第一次提前20分钟是因为张工程师自己走了一段路，从而导致汽车不需要走那段路的来回，所以汽车开那段路的来回应该是20分钟，走一个单程是10分钟，而汽车每天8点到张工程师家里，所以那天早上汽车是7点50接到工程师的，张工程师走了50分钟，这段路如果是汽车开需要10分钟，所以汽车速度和张工程师步行速度比为5：1,第二次，实际上相当于张工程师提前半小时出发，时间按5：1的比例分配，则张工程师走了25分钟时遇到司机，此时提前（30-25）x2=10（分钟）o这道题重要是要求出汽车速度与工程师的速度之比。

2.小学五年级奥数行程问题练习题及答案篇二1、小熊骑自行车出去玩，经过三段长度分别为IOOO米，200米，800米的平路，上坡路和下坡路，包包在这三段路上的速度分别为200米/分，50米/分,400米/分，问小熊走完这三段路程需要多少时间？【分析】简单分段行程平路所需时间：1000÷200=5（分钟）上坡路所需时间：200÷50=4（分钟）下坡路所需时间：800÷400=2（分钟）所以总共需要时间为5+4+2=Π（分钟）2、A、B两地之间是山路，相距60千米，其中一部分是上坡路，其余是下坡路，某人骑电动车从A地到B地，再沿原路返回，去时用了4.5小时，返回时用了3.5小时。

已知下坡路每小时行20千米，那么上坡路每小时行多少千米？【解析】由题意知，去的上坡时间+去的下坡时间二4.5小时回的上坡时间+回的下坡时间二3.5小时则：来回的上坡时间十来回的下坡时间二8小时所以来回的下坡时间=60÷20=3（小时）则：来回的上坡时间二8—3二5（小时）故：上坡速度为60÷5=12（千米/时）3.小学五年级奥数行程问题练习题及答案篇三1、甲放学回家需走10分钟，乙放学回家需走14分钟。

山东省枣庄市数学小学奥数系列3-1-1行程问题(二)

山东省枣庄市数学小学奥数系列3-1-1行程问题（二）姓名:________ 班级:________ 成绩:________亲爱的小朋友们，这一段时间的学习，你们收获怎么样呢？今天就让我们来检验一下吧！一、 (共23题；共115分)1. （5分） A城与B城的距离是560千米。

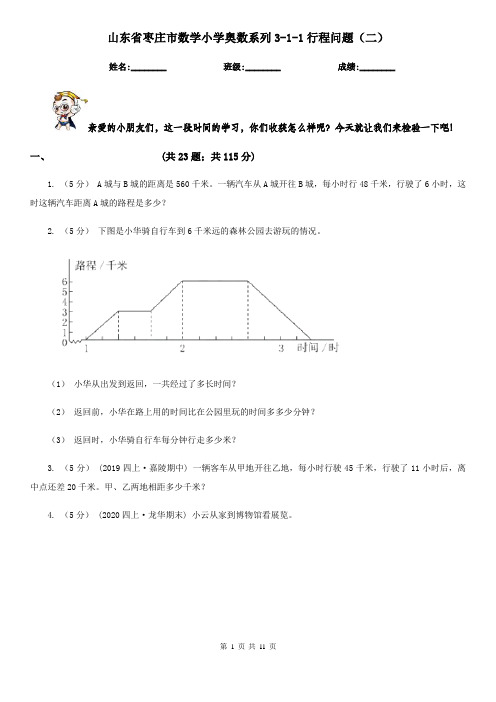
一辆汽车从A城开往B城，每小时行48千米，行驶了6小时，这时这辆汽车距离A城的路程是多少？2. （5分）下图是小华骑自行车到6千米远的森林公园去游玩的情况。

（1）小华从出发到返回，一共经过了多长时间？（2）返回前，小华在路上用的时间比在公园里玩的时间多多少分钟？（3）返回时，小华骑自行车每分钟行走多少米？3. （5分） (2019四上·嘉陵期中) 一辆客车从甲地开往乙地，每小时行驶45千米，行驶了11小时后，离中点还差20千米。

甲、乙两地相距多少千米？4. （5分） (2020四上·龙华期末) 小云从家到博物馆看展览。

（1）说说小云从家到博物馆的行走路线。

（2）若小云以每分钟80米的速度从家出发，小豆豆要以怎样的速度才能在博物馆追上小云？5. （5分） (2019六上·福州期中) 甲、乙两地相距250km，一辆汽车从甲地开往乙地，行了5小时，行了全程的，这辆汽车行完全程一共需要多少小时？6. （5分） (2019五上·山东期中) 在老年运动会上，刘大伯参加了长跑比赛。

全程1.5km。

用了9.7分钟跑完，获得了第一名，李大伯比刘大伯多用了2分钟，李大伯跑了1km平均需要多少分钟？7. （5分）有甲、乙两列货车，甲车长116米，每秒行驶10米；乙车长124米，每秒行驶14米。

两车相遇后，从甲车与乙车车头相遇到车尾分开需要多少秒？8. （5分） (2020三上·西安期末) 爸爸在外地上班，回家的路程是360千米，他上午9时出发坐火车，下午1时下火车，这列火车平均每小时行多少千米？9. （5分） (2019六下·蓝山期中) 父子俩在长400米的环形跑道上散步，他俩同时从同一地点出发，如果相背而行，4分钟相遇：如果同向而行，8分钟父亲可以追上儿子．在跑道上走一圈，父亲和儿子各需要多少分钟？10. （5分）(2018·江苏模拟) 甲、乙两车分别从A、B两地同时出发，甲车匀速由A地前往B地，到达B 地后立即匀速返回A地，返回速度是原速度的1.5倍；乙车匀速由B地前往A地。

小学奥数3-3-2 行程综合问题.专项练习及答案解析-精品

1. 运用各种方法解决行程内综合问题。

2. 发现一些综合问题中，行程与其它模块的联系，并解决奥数综合问题。

行程问题是奥数中的一个难点，内容多而杂。

而在行程问题中，还有一些尤其复杂的综合问题。

它们大致可以分为两类：一、行程内综合，把行程问题中的一些零散的知识点综合在一道题目中，这就是一道行程内综合题目。

例如把环形跑道和猎狗追兔结合在一起，把流水行船和发车间隔结合起来等等。

二、学科内综合，这种问题就不只是行程问题了，把行程问题和其它知识模块里的思想方法结合在一起，这种综合性题目的难度也很大，比如行程与策略综合等等。

本讲内容主要就是针对这种综合性题目。

虽然题目难度偏大，但是这种题目在杯赛和小升初试题中是很受“偏爱”的。

所以很重要。

模块一、行程内综合【例 1】邮递员早晨7时出发送一份邮件到对面山里，从邮局开始要走12千米上坡路，8千米下坡路。

他上坡时每小时走4千米，下坡时每小时走5千米，到达目的地停留1小时以后，又从原路返回，邮递员什么时候可以回到邮局?【考点】变速问题与走停问题【难度】2星【题型】解答【解析】法一：先求出去的时间，再求出返回的时间，最后转化为时刻。

①邮递员到达对面山里需时间：12÷4+8÷5=4.6(小时);②邮递员返回到邮局共用时间：8÷4+12÷5+1+4.6 =2+2.4+1+4.6 = l 0(小时)③邮递员回到邮局时的时刻是：7+10-12=5(时).邮递员是下午5时回到邮局的。

法二：从整体上考虑，邮递员走了（12+8）千米的上坡路，走了（12+8）千米的下坡路，所以共用时间为：（12+8）÷4+（12+8）÷5+1=10(小时)，邮递员是下午7+10-12=5(时) 回到邮局的。

【答案】5时【例 2】小红上山时每走30分钟休息10分钟，下山时每走30分钟休息5分钟．已知小红下山的速度是上山速度的1.5倍，如果上山用了3小时50分，那么下山用了多少时间？【考点】变速问题与走停问题【难度】2星【题型】解答【解析】上山用了3小时50分，即60350230⨯+=(分)，由2303010530÷+=（），得到上山休息了5次，走了230105180-⨯=(分)．因为下山的速度是上山的1.5倍，所行程综合问题知识精讲教学目标以下山走了180 1.5120÷= (分)．由120304÷=知，下山途中休息了3次，所以下山共用12053135+⨯=(分)2=小时15分．【答案】2小时15分【例 3】已知猫跑5步的路程与狗跑3步的路程相同；猫跑7步的路程与兔跑5步的路程相同．而猫跑3步的时间与狗跑5步的时间相同；猫跑5步的时间与兔跑7步的时间相同，猫、狗、兔沿着周长为300米的圆形跑道，同时同向同地出发．问当它们出发后第一次相遇时各跑了多少路程？【考点】环形跑道与猎狗追兔【难度】5星【题型】解答【解析】方法一：由题意，猫与狗的速度之比为9:25，猫与兔的速度之比为25:49．设单位时间内猫跑1米，则狗跑259米，兔跑4925米．狗追上猫一圈需25675300194⎛⎫÷-= ⎪⎝⎭单位时间，兔追上猫一圈需496253001252⎛⎫÷-= ⎪⎝⎭单位时间．猫、狗、兔再次相遇的时间，应既是6754的整数倍，又是6252的整数倍． 6754与6252的最小公倍数等于两个分数中，分子的最小公倍数除以分母的最大公约数，即]()675,62567562516875,8437.5424,22⎡⎡⎤⎣===⎢⎥⎣⎦．上式表明，经过8437.5个单位时间，猫、狗、兔第一次相遇．此时，猫跑了8437.5米，狗跑了258437.523437.59⨯=米，兔跑了498437.516537.525⨯=米．方法二：根据题意，猫跑35步的路程与狗跑21步的路程、兔跑25步的路程相等；而猫跑15步的时间与狗跑25步、兔跑21步的时间相同．所以猫、狗、兔的速度比为152521::352125，它们的最大公约数为 ()[]15,25,211525211,,35212535,21,253557⎛⎫== ⎪⨯⨯⨯⎝⎭，即设猫的速度为151225353557÷=⨯⨯⨯，那么狗的速度为251625213557÷=⨯⨯⨯，则兔的速度为211441253557÷=⨯⨯⨯．于是狗每跑3300(625225)4÷-=单位时追上猫；兔每跑25300(441225)18÷-=单位时追上猫．而[]()3,2532575,4184,182⎡⎤==⎢⎥⎣⎦，所以猫、狗、兔跑了752单位时，三者相遇．猫跑了752258437.52⨯=米，狗跑了7562523437.52⨯=米，兔跑了7544116537.52⨯=米．【答案】16537.5米【例 4】甲、乙两人沿 400 米环形跑道练习跑步，两人同时从跑道的同一地点向相反方向跑去。

小学二年级奥数题《行程问题大全及答案》题库大全

小学二年级奥数题《行程问题大全及答案》题库大全姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分评卷人得分1、操场的一侧插着10面彩旗，每两面彩旗之间的距离是2米，从第1面彩旗到第10面彩旗之间相距多少米？答案与解析：2x（10-1）=18（米）2、小朋友做早操，9个人排成一行，前后两人之间的距离是2米，从第一个小朋友到最后一个小朋友的距离是多少米？答案与解析：（9-1）x2=16（米）3、河岸边有一排柳树，张爷爷每天早晨锻炼，沿河边第1棵树走到第9棵树，一共走了72米。

平均每两棵树之间相隔多少米？答案与解析：72（9-1）=9（米）4、随着神七问天，我国航天员翟志刚成功完成了中国人太空行走第一步。

在19分35秒的时间里，翟志刚与飞船一起飞过了9165千米，约（）千米。

答案与解析：92005、根据图意完成下面各题。

1．小英从家去超市，她应该先向（）走（）米到书店，再向（）走（）米到体育馆，最后向（）走（）米到超市。

2．小东从家去体育馆，要先向（）走（）米到银行，再向（）走（）米到邮局，最后向（）走（）米到体育馆。

3．小丽从家去书店，一共要走（）米；小丰从家去邮局，一共要走（）米。

4．小丰要去小丽家玩，他应该怎样走？他途经哪些地方？他总共要走多远的路程？答案与解析：1．东；350；南；100；东；300；2．西；370；北；330；西；200；3．600；550；4．先向东走150米，再向北走200米，再向东走300米，最后向北走200米到小丽家。

他途经敬老院、体育馆、超市。

总共要走850米。

6、看图回答问题。

（1）文文要从家去医院，先向（）走（）米到超市，再向（）走（）米到医院。

（2）文文从学校出发，向（）走（）米到（），再向（）走（）米到（），再向（）走（）米到（），最后向（）走（）米到自己家，他从学校回家总共要走（）米。