Scilab简明教程
Scilab程序设计教程_v0.02

Scilab程序设计教程内容摘要本书是为适应教学的需要而编写。
全书以Scilab4.1版为基础,介绍Scilab程序设计的方法与应用,主要内容包括:Scilab操作基础、Scilab矩阵及其运算、Scilab程序设计、Scilab 文件操作、Scilab绘图、Scilab数据分析与多项式计算、Scicos图形化仿真环境以及Scilab 常用工具箱。
本书符合教学规律和特点,内容丰富、取材新颖、注重实用、便于教学。
本书可作为高校理工科各专业大学生、研究生学习的教材,也可供广大科技工作者阅读使用。
编者列表:序前言目录1. Scilab基础 (4)1.1. Scilab概述 (4)1.2. Scilab的运行环境与安装 (4)1.3. Scilab集成环境 (6)1.4. Scilab帮助系统 (8)2. Scilab矩阵及其运算 (8)2.1.变量和数据操作 (8)2.2. Scilab矩阵 (11)2.3. Scilab运算 (15)2.4.字符串 (16)2.5.稀疏矩阵 (20)3. Scilab程序设计 (17)3.1. SCI文件 (17)3.2.程序控制结构 (17)3.3.函数文件 (18)3.4.程序举例 (18)3.5.程序调试 (18)4. Scilab文件操作 (19)4.1.文件的打开与关闭 (19)4.2.文件的读写操作 (19)4.3.数据文件定位 (19)5. Scilab绘图 (19)5.1.二维数据曲线图 (19)5.2.其他二维图形 (19)5.3.三维图形 (19)5.4.图形修饰处理 (19)5.5.图像处理及动画制作 (19)6. Scilab数据分析与多项式计算 (20)6.1.数据统计处理 (20)6.2.数据插值 (20)6.3.曲线拟合 (20)6.4.离散傅立叶变换 (20)6.5.多项式计算 (20)7. Scilab解方程与函数极值............................................................................. 错误!未定义书签。
第一讲 Scilab基本操作

-->x=0:0.2:1; -->y=x.*x
// 生成当x=0,0.2,0.4,0.6,0.8,1时, 0.16 0.36 0.64
y=x2函数值序列
y =
0 0.04 1.
>> 表达式 y=x.*x中的“.*”表示对应元素相乘; 另外(./)表示对应元素相除,(.^)表示对应元素求幂.
-->x=0:0.2:1; -->y=x.^2 y =
>> 在Command窗口下进行数学运算,只需将表达式直接输入提示号(--> )之后,并按【Enter】 键即可。Scilab会将计算结果直接存入变量ans,代表Scilab运算后的答案 (Answer),并在 Command窗口下显示其数值。 >> Scilab将所有数值均保存为double形式,故不需要变量声明,Scilab会自动进行变量的创建和 回收。 >> Scilab的基本运算符:加(+)、 减(-)、 乘(*)、 除(/)、指数(^); 上述运算符不仅运用于通常实数之间计算,也可运用于矩阵的运算。
高中数学中的算法初步
Scilab4 简介
一. 基本操作 二. 语言结构 四. 基本绘图 五. 简单应用
三. 程序文件
Scilab是以法国国立信息与自动化研究院(INRIA)的科学家为主开发 的“开放源码”式科学计算自由软件。Scilab一词来源于英文 “Scientific Laboratory”(科学实验室)词头的合并。Scilab与 Matlab非常相似,都是基于矩阵运算的科学计算软件,但它是自由软件,其 指令形式与数学、工程中常用的形式十分相似。 目前国家科技部正大力支持推广和普及Scilab软件,国家教育部同意将其 写入高中数学教材。通过Scilab,一方面可以实践算法实现,另一方面可以进 行数学实验、数学建模活动。
Scilab基本实际操作

Scilab 预定义的一些常数:
i: 基本虚数单位
pi: 圆周率(π=3.1415926...)
e: 欧拉常数(е=2.7182818...)
inf: 表示无限大, 例如1/0
nan或NaN: 表示非数值(Not a number), 例如0/0
>> Scilab将所有数值均保存为double形式,故不需要变量声明,Scilab会自动进行变量的创建和 回收。
>> Scilab的基本运算符:加(+)、 减(-)、 乘(*)、 除(/)、指数(^); 上述运算符不仅运用于通常实数之间计算,也可运用于矩阵的运算。
>> 变量赋值语句一般格式:
变量名 = 数值 或变量组成表达式 或字符串
x= 0 0.2 0.4 0.6 0.8 1.
-->x=0:0.2:1; -->y=x.*x
// 生成当x=0,0.2,0.4,0.6,0.8,1时, y=x2函数值序列
y= 0 0.04 0.16 0.36 0.64 1.
>> 表达式 y=x.*x中的“.*”表示对应元素相乘; 另外(./)表示对应元素相除,(.^)表示对应元素求幂.
-0.0044772
Scilab变量命名规则 1.变量名必须是英文字母,区分大小写 2.字母间不可留空格
>> Scilab显示当前数据格式是10位(含数值符号),如下图:
>> 函数指令format( )的作用是返回当前数据格式的位数. ans=1. 10. (计算结果ans返回的是行列的矩阵形式) 表示当前数据格式是10位(含数值符号“+,-”,正数的符号“+”一般不显示).
SCILAB_Chap4(学习资料)

撰文者:1.中央大氣科學系 楊善文2.(如對本文有貢獻者,記得在此留名。
)程式命令腳本視窗(scipad)的使用:這在第零章已大略說過。
從這章開始到之後的章節,你所需要下的指令行數將會越來越多,主視窗將會逐漸不敷使用。
故筆者建議可以開始去習慣改用scipad來工作了。
在scipad上可以輸入大量行數的語句,存檔後選擇執行鈕後,可以一次執行完。
當寫入的語句如果是系統內定的函式,則自動會以不同顏色顯示,方便使用者閱讀與判斷自己是否有下錯指令語法。
Conférencier : Prénom Nom Date : Transparent 3Scipad語系界面選擇:在[選單]的地方有[語言]可選擇,例如筆者之前的Scipad圖即是法文界面。
執行前一定要存檔。
可從Fichier(檔案)的地方選擇Enregistrer(儲存),如果想要另存新檔,可以選擇Enregistrer sous。
或者也可以直接選擇執行,如果之前沒存,它也會進入存檔界面。
執行程式或是命令腳本:在Exécuter(執行)的地方選擇Charger dans Scilab(讀取進Scilab)。
在edition的地方,有Couper(剪下)、Copier(複製)、Sélectionner tout(全選)、Annuler(取消)等功能。
在Fenêtres(窗戶)的地方,可以切換分頁。
開新分頁在Fichier的地方選擇Nouveau。
在使用Scipad寫程式或命令腳本時,最好在首行加入clear指令,它的功用是清除之前所做的變數宣告。
主要原因是避免之前的宣告影響到腳本中的程式碼,也可以清空記憶體中多餘的變數所佔用的空間。
如果只是想清除之前某個特定的變數,可以在clear後接該變數名即可。
例如:clear x y;如想在行與行之間插入注解語句,可以在該行頭加入:''//'',與C++語法相同。
scilab解带参数方程组

scilab解带参数方程组
Scilab是一种用于数值计算和数据分析的开源软件,它提供了许多工具和函数来解决各种数学问题,包括解带参数方程组。
解带参数方程组通常涉及到多个变量和方程,而Scilab可以通过一些内置的函数和工具来进行求解。
首先,要解带参数方程组,我们需要定义方程组。
假设我们有一个带参数的方程组如下:
x + 2y + z = 5。
2x + y z = 3。
3x y + 2z = 8。
其中,x、y、z为变量,我们可以将这个方程组表示为矩阵形式 Ax = B,其中 A 是系数矩阵,x 是变量矩阵,B 是常数矩阵。
在Scilab中,我们可以使用内置的函数 linsolve 来求解线性方程组。
假设我们定义系数矩阵 A 和常数矩阵 B 如下:
A = [1, 2, 1; 2, 1, -1; 3, -1, 2]
B = [5; 3; 8]
然后,我们可以使用 linsolve 函数来求解方程组:
x = linsolve(A, B)。
这将给出方程组的解 x。
如果我们的方程组是带参数的,比如方程组中含有参数 k,我们可以使用 Scilab 的符号计算工具来处理。
我们可以使用符号变量来表示参数,然后求解方程组得到关于参数的表达式。
总之,Scilab提供了丰富的数值计算工具和符号计算工具,可以帮助我们解决各种数学问题,包括解带参数方程组。
通过合理地利用内置函数和工具,我们可以高效地求解复杂的方程组,并得到我们想要的结果。
希望这个回答能够帮助你更好地理解如何在Scilab中解带参数方程组。
第三讲 Scilab程序文件
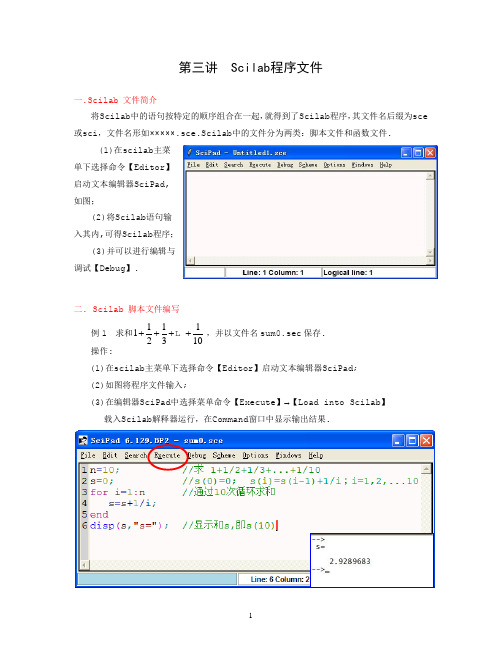
第三讲 Scilab程序文件一.Scilab 文件简介将Scilab中的语句按特定的顺序组合在一起,就得到了Scilab程序,其文件名后缀为sce 或sci,文件名形如×××××.sce.Scilab中的文件分为两类:脚本文件和函数文件.(1)在scilab主菜单下选择命令【Editor】启动文本编辑器SciPad,如图;(2)将Scilab语句输入其内,可得Scilab程序;(3)并可以进行编辑与调试【Debug】.二. Scilab 脚本文件编写例1 求和11112310++++,并以文件名sum0.sec保存.操作:(1)在scilab主菜单下选择命令【Editor】启动文本编辑器SciPad;(2)如图将程序文件输入;(3)在编辑器SciPad中选择菜单命令【Execute】→【Load into Scilab】载入Scilab解释器运行,在Command窗口中显示输出结果.三. Scilab 函数文件编写例2 编写求和111123n++++,并求当10n =的值,并以文件名sum1.sec 保存. 操作如例1,略.函数文件结构函数文件与脚本文件比较1. 脚本文件与函数文件最大的区别是脚本文件内部没有函数,无输入输出变量;2. 脚本文件内的变量不是函数体内部的局部变量,而是基本工作空间内(调用脚本文件的工作空间内)的变量.例3 将上述例子改造成具有多个返回值的情况.四.控制程序流的常用指令return 指令返回到引用函数input 指令请求用户输入pause 指令暂停执行break 指令强行终止其所在for或while循环体error和warning 指令显示出错和警告信息例3 求11a =,21a =的Fibonacci 数组中第一个满足大于10000的元素.例4 输入项数n ,编写求和111123n++++,并求当10n =的值, 并以文件名sum3.sec 保存.。
实验七 用Scilab解常微分方程

实验七用Scilab解常微分方程引言常微分方程是数学中的重要分支,它描述了许多自然现象和工程问题的演化过程。
随着计算机技术的发展,用计算机求解常微分方程的方法得到了广泛应用,其中Scilab是一种功能强大且易于使用的数值计算软件。
本实验将以Scilab为工具,通过实际案例演示如何使用Scilab求解常微分方程问题。
实验内容1. 安装Scilab2. 打开Scilab完成安装后,打开Scilab软件。
在命令窗口中输入以下命令,载入求解常微分方程的相关模块。
// 载入ODE模块load("ode.sci")3. 定义常微分方程在Scilab中,定义常微分方程需要使用函数来描述,例如以下形式的一阶常微分方程:function dydt = myODE(t, y)dydt = -2*t*y;endfunction这个例子中,常微分方程是 dy/dt = -2*t*y。
4. 使用Scilab求解常微分方程在Scilab中,使用`ode`函数来求解常微分方程。
例如,使用以下命令求解初始条件为 y(0) = 1 的常微分方程:t = 0:0.1:10; // 定义求解范围y0 = 1; // 初始条件[t, y] = ode(t, y0, myODE); // 求解常微分方程这个例子中,求解范围是 t=0 到 t=10,初始条件为 y(0) = 1,`ode`函数会返回求解结果。
你可以通过绘图函数绘制出常微分方程的解曲线。
5. 实际案例通过实际案例来演示如何使用Scilab求解常微分方程。
以受阻射击的运动问题为例,其常微分方程为dy/dt = v,dv/dt = -k/m * v,其中y表示位移,v表示速度,k和m分别表示阻力和质量。
function dydt = myODE(t, y)dydt = [y(2);-k/m*y(2)];endfunctiont = 0:0.01:10; // 定义求解范围y0 = [0, 10]; // 初始条件:y(0) = 0, v(0) = 10[t, y] = ode(t, y0, myODE); // 求解常微分方程// 绘制位移随时间的曲线plot(t, y(:,1), "r-")xlabel("时间")ylabel("位移")结论本实验使用了Scilab软件来求解常微分方程问题,通过实际案例的演示,展示了使用Scilab编写常微分方程函数、调用`ode`函数求解常微分方程,并绘制解曲线的步骤和方法。
第1章 SCILAB基础

第一章SCILAB基础本章内容是后续所有内容的基础,读者可以通过本章的学习,了解计算科学软件SCILAB\SCICOS的基本功能和基本操作方法,特别是对SCICOS模块库或工具箱的概念和作用有所了解。
本章需解决的关键问题:SCILAB是什么?可以做什么?如何操作?SCICOS是什么?如何操作?SCICOS和SCILAB之间是什么关系?什么是工具箱?如何安装和加载?本章主要内容:SCILAB基本知识和基本操作;SCICOS基本知识和基本操作;SCICOS工具箱的概念和工具箱的加载方法;本章阅读建议:本章的内容不同于理论知识的学习,建议读者在阅读本章全文的过程中,结合书中讲解,动手在平台上进行操作演练,有助于加深理解和消化本章内容。
本章主要是为初学者提供帮助,已经具备SCILAB\SCICOS基本知识、熟悉其基本操作的读者,可不用学习本章内容。
1.1SCILAB介绍1.1.1 关于SCILAB通用科学软件目前有两大类:进行符号运算的计算机代数系统(Computer Algebra Systems);进行数值计算和专门科学应用设计的通用数值系统(General Purpose Numerical Systems)。
第一类中较为出名的有Maple、Mathematical、Maxima、Axiom和Mupad等,第二类则以MATLAB为代表。
自由开源软件SCILAB就属于第二类。
SCILAB最初是由INRIA 和ENPC 开发,现在由SCILAB 协会维护的开放源代码的科学计算软件。
具有矩阵运算、数值运算、信号处理、程序设计等功能,目前已被广泛应用于教育、科研和工业。
1.1.2 SCILAB基本知识本书内容基于SCILAB 4.1.2版本平台而编写。
此版本软件可以从SCILAB官方主页的链接()下载。
SCILAB中指令和程序的运行可以分为三种情况:命令窗口下的逐句执行、脚本文件的执行、以及SCI函数形式的调用。
《讲Scilab基本操作》课件
通过这个PPT课件,我们将学习Scilab的基本操作,让你在科学计算方面快速 上手。准备好探索Scilab的世界吧!
一、Scilab的介绍
Scilab的概述
了解Scilab是一个开源的数 值计算和数据分析软件, 适用于工程学、科学研究 和教育领域。
Scilab的特点
探讨Scilab在不同领域的应用 前景,如工程学、科学研究 和数据分析。
Scilab的学习建议和 总结
提供学习Scilab的建议和总结, 帮助大家更好地掌握Scilab的 基本操作。
Scilab的数据分析与拟 合
掌握如何使用Scilab进行数 据分析和曲线拟合,以从 数据中获得有用信息。
Scilab与其他编程语言 的集成
了解如何将Scilab与其他编 程语言集成,从ቤተ መጻሕፍቲ ባይዱ扩展其 功能和应用领域。
五、Scilab常见问题解答
1 Scilab的常见错误及解决方法
指导解决常见的Scilab错误,如语法问题、函数调用和脚本调试。
2 Scilab的优化与调试技巧
分享Scilab的性能优化和调试技巧,确保代码的正确性和效率。
3 Scilab的相关资源推荐
为学习Scilab提供相关资源推荐,如文档、教程和论坛。
结束语
Scilab的未来发展
展望Scilab的未来发展方向, 包括新功能、性能改进和社 区贡献。
Scilab的应用前景
掌握Scilab的特性,如多维 数组、函数库、图形显示 和内置编辑器等。
Scilab的优势
了解为什么Scilab是一种强 大的工具,可以用于解决 复杂的数学和工程问题。
二、Scilab的安装与环境配置
scilab指令及应用

18. 图形文件及图形文字
3
xsave 将图形存储为文件 xload 从磁盘中读出图形文件 xbasimp 将图形按PS文件 打印或存储为文件 xs2fig 将图形生成Xfig 格式文件 xbasc 取消图形窗及其相关内 容 xclear 清空图形窗 driver 选择图形驱动器 xinit 图形驱动器初始化 xend 关闭 图形 xbasr 图形刷新 replot 更改显示范围后的图形刷新 xdel 关闭图形 xname 改变当前图形窗名称
17. 图形颜色及图形文字 colormap 应用颜色图 getcolor 交互式选择颜色图 addcolor 增加新色于颜色图 graycolormap 线性灰度图 hotcolormap 热色(红到黄色)颜色图 xset 图形显示方 式设定 xget 读当前图形显示方式设定 getsymbol 交互式选择符号和尺寸
第四讲Scilab基本绘图
//对应的y坐标 //画正弦图象
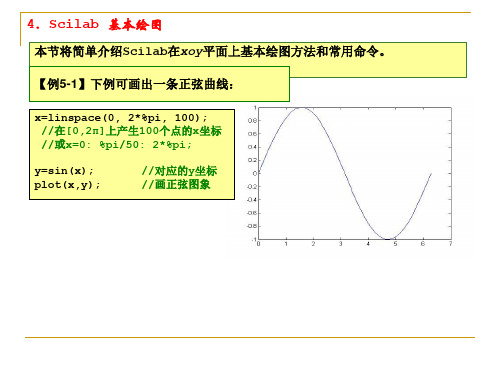
下面简单介绍绘制平面曲线的两个基本函数: plot 与 plot2d
================================================================ (1)函数plot( )基本形式: plot(x,y,<LineSpec> )
函数 plot2d( )基本形式: plot2d(x,y,<opt_args>)
说明: 坐标x,y是实数或向量形式
参数opt_args
形式:key1=value1,key2=value2
• style= [color1, color2, color3, ... ] color1...的值为正数时用相应颜色画实线,0为虚线,负数时用标记画线.
五角形
若要改变颜色,在坐标对后面加上相关控制符即可: y plot(黄x色, sin(kx), 'c黑'色, x,sqcuoasr(ex),正'方g'形); hexagram
六角形
若要同时改变颜色及图线型态,也是在坐标对后面加上相关控制符即可: m plot洋(红x,色sin(x), 'co', xd,iacmoonsd(x),菱'形g*');
// 在布局中的第3个子视图内画图
(2) xtitle('标题','x轴注解', 'y轴注解') (3) xgrid( ) 加入网格线
xgrid([style])以style指定的颜色画网格线 (4) clf( ) 清除或重置视图窗口
位置1
位置2
位置3
位置4
位置5
位置6
scilab 画函数

在Scilab中绘制函数图像的步骤如下:
以下是一个基本的例子,我们将绘制函数y = x^2 的图像:
1. 首先,打开Scilab并创建一个新的脚本文件。
2. 在脚本文件中,首先定义你要绘制的函数。
例如,我们定义函数y = x^2:
scilab代码:
3. 接下来,定义x的取值范围,并计算对应的y值。
例如,我们将x从-10到10,每隔0.1取一个点:
scilab代码:
4. 使用plot2d函数绘制图像:
scilab代码:
5. 如果你想改变线的颜色、样式或者添加网格线,可以使用以下选项:
scilab代码:
6. 运行脚本(可以通过点击菜单栏的“执行”按钮或者直接在命令窗口输入脚本名后按回车键),你将在图形窗口看到所绘制的函数图像。
注意:以上代码适用于Scilab的较新版本。
在不同版本的Scilab中,绘图函数的参数可能会有所不同。
如果你遇到问题,建议查阅Scilab的官方文档或在线帮助。
scilab 使用教程

2.6 向量与矩阵(数组)元素的引用 b(k) 表示向量b的第k个元素 a(i,j) 表示矩阵a的第(i,j)个元素 可以用函数find(条件表达式)来寻找所需的元素。 a($)表示a的最后一个元素。 a($-1) 表示倒数 第二个元素 还可以用逻辑符号来提取矩阵的元素,例如:
2.7 整型数组 采用int8()和int32()把一个数转化为整数。 a=int8(4); b=int8(5); c=a/b 结果为0 2.8 布尔型向量与矩阵的定义及基本运算 逻辑运算:与(&),或(|),非(~); 关系运算:==, >,<,>=,<=,~= 2.9 字符串型数据的定义与运算 2.9.1 字符串的定义 字符串一般用单引号(’)或双引号 (”)括起来。 还可以定义字符串矩阵。 2.9.2 字符串的运算 可采用“+”将两个字符串连起来。
3.5.3 局部变量与全局变量、函数的嵌套定义与递归调用 使用global 定义全局变量。 在scilab中,可以嵌套定义函数,例如:
在scilab中函数还可以递归调用,例如
3.5.4 有关程序调试的几个常用指令 pause, resume, abort
第4章 计算结果可视化
4.1 引言 4.2 二维图形的绘制 4.2.1 plot指令 1、plot指令可以用來绘制一般的曲线图。 例如(对sin函数绘图): t=linspace(0,2*%pi); //取0到2π的范围 y=sin(t); plot(y); 2、多重曲线绘图,例子: x=-2:0.01:2; y1=sin(x); y2=exp(x); y3=sin(x)+cos(x); X=[x;x;x]; Y=[y1,y2,y3]; plot(X',Y');
scilab-使用教程

与MATLAB的互操作性
01
SCILAB可以与MATLAB进行互 操作,允许用户在SCILAB中调 用MATLAB函数或编辑器中的 脚本。
02
互操作性可以通过MATLAB Engine API for Scilab实现, 该API提供了与MATLAB的接 口,以便在SCILAB中执行 MATLAB代码。
图像处理
SCILAB提供了图像处理和分析的功能,可以用 于图像处理和计算机视觉等领域。
ABCD
工程仿真
SCILAB可以用于工程设计和仿真的数值计算和 分析,如流体动力学、结构力学等。
系统控制
SCILAB可以用于控制系统设计和分析,如控制 系统仿真和优化等。
02 SCILAB基础操作
启动与退出SCILAB
易用性
SCILAB的用户界面友好,易于学 习和使用,支持多种编程语言接 口,方便用户进行编程和开发。
开放性
SCILAB是开源软件,用户可以自 由获取和使用源代码,并根据自 己的需求进行定制和开发。
SCILAB的应用领域
科学计算
SCILAB广阵元素
使用单引号或双引号将元素索引括起来,例如 `A(1,1)`或`A"[1,1]"`。
矩阵运算
支持常见的矩阵运算,如加法、减法、乘法 等。
03 SCILAB编程基础
控制流语句
顺序执行
SCILAB中的代码按照从上到下的顺序 执行,无需使用特定的控制流语句。
循环语句
使用`for`循环重复执行特定代码块, 例如`for i=1:10, statements, endfor`。
初值条件
求解常微分方程时需要指定初值条件,可以使用"="指定初值。例如, y(t0)=y0将指定在t0时刻的初值。
scilab中文手册

. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . .
. . . . .
. . . . .
. . . . .
2 Scilab 簡易教學 2.1 啟動 . . . . . . . . . . . . . . . . . . . . 2.2 編輯 . . . . . . . . . . . . . . . . . . . . 2.3 變數宣告、分行、多行連結及註解 . . 2.4 計算環境、系統變數、常數及特殊變數 2.5 矩陣數內容的設定及讀取 . . . . . . . . 2.6 函數呼叫 . . . . . . . . . . . . . . . . . 2.7 使用多項式 . . . . . . . . . . . . . . . . 2.8 多項式矩陣及行列式之符號運算 . . . . 2.9 分式多項式矩陣及其分子及分母多項式 2.10 計算環境之層次 . . . . . . . . . . . . . 2.11 頻率響應及繪圖 . . . . . . . . . . . . . 2.12 合成函數 . . . . . . . . . . . . . . . . . 2.13 動態系統、狀態空間及轉換函數 . . . . 2.14 狀態空間資料的詳細內容 . . . . . . . . 2.15 動態子系統之並聯 . . . . . . . . . . . . 2.16 設計 Scilab 函數 . . . . . . . . . . . . . 2.17 補償器設計範例 . . . . . . . . . . . . . 2.18 執行系統指令 . . . . . . . . . . . . . . 2.19 以 Fortran 或 C 語言提供動態程式庫 . . 2.20 常微分方程組應用範例 . . . . . . . . . 2.21 運算子設計 . . . . . . . . . . . . . . . . 2.22 函數參數的傳遞 . . . . . . . . . . . . . 3 操作環境 3.1 輸入輸出及環境 . . . . . 3.1.1 環境 . . . . . . . 3.1.2 Scilab 之啟動指令 3.1.3 輸入及輸出 . . .
科学计算自由软件SCILAB基础教程

第1章 SCILAB简介 1.1 引言1.2 SCILAB软件的构成1.3 安装SCILAB的系统需求1.4 SCILAB主窗口介绍图1.1 SCILAB 3.0的主窗口图1.2 SCILAB 3.0的文件菜单项图1.3 SCILAB 3.0的编辑菜单项图1.4 SCILAB的选择菜单项图1.5 SCILAB的控制菜单项图1.6 SCILAB的编辑器窗口图1.7 SCILAB的应用窗口图1.8 SCILAB的帮助窗口1.5 SCILAB中的基本操作与预定对象 1.5.1 SCILAB中的文件操作1.5.2 界面层次的控制操作1.5.3 SCILAB主窗口中的快捷键操作1.5.4 SCILAB中预先定义的对象图1.9 who指令后的SCILAB主窗口图1.10 whos指令后的SCILAB主窗口1.6 谈谈如何学习SCILAB图1.11 SCILAB的演示窗口图1.12 SCILAB的选择图形演示窗口图1.13 SCILAB的选择图形演示窗口图1.14 SCILAB的一个图形信息窗口图1.15 SCILAB的一个图形演示窗口第2章 数据类型 2.1 引言2.2 特定符号与常数2.2.1 特定符号2.2.2 特定常数2.3 标量的数值计算2.4 数值型向量与矩阵的定义及基本运算 2.4.1 数值型向量与矩阵的定义2.4.2 数值型向量与矩阵的运算2.5 与数值型矩阵有关的若干常用函数 2.5.1 常用矩阵的生成函数2.5.2 size函数和matrix函数2.5.3 从已知矩阵提取部分元素来构成同阶新矩阵的若干函数2.5.4 与方阵的行列式求值、求逆、线性代数方程组的求解、求矩阵特征值与特征向量等有关的函数2.5.5 与矩阵(数组)或向量有关的数据统计函数2.6 向量与矩阵(数组)元素的引用2.7 整型数组2.8 布尔型向量与矩阵的定义及基本运算2.9 字符串型数据的定义与运算 2.9.1 字符串的定义2.9.2 字符串的运算2.9.3 与处理字符串有关的一些常用函数2.10 多项式类型 2.10.1 多项式的定义2.10.2 多项式运算2.10.3 有关多项式的几个常用函数2.11 表类型2.11.1 表类型的定义2.11.2 表类型数据的引用,域的插入与删除2.11.3 tlist和mlist类型第3章 SCILAB中的程序设计、脚本文件与函数 3.1 引言3.2 顺序结构程序设计3.2.1 赋值语句3.2.2 输入输出语句3.3 选择结构程序设计 3.3.1 if语句图3.1 不完整if语句的框图图3.2 完整if语句的框图3.3.2 select_case语句图3.3 select 语句框图(else缺省情形)3.4 循环结构程序设计 3.4.1 for语句图3.4 for语句的框图3.4.2 while 语句图3.5 while 型循环框图3.4.3 循环语句的嵌套(多重循环语句)3.4.4 continue 语句和break 语句图3.6 循环体内含有continue语句的框图图3.7 循环体内含有break语句的框图3.5 脚本文件与函数3.5.1 脚本文件3.5.2 函数3.5.3 局部变量与全局变量、函数的嵌套定义与递归调用图3.8 用递归调用求 n!示意图(n =4)3.5.4 有关程序调试的几个常用指令3.6 函数的应用3.6.1 函数名作形式参数——二分法求非线性方程的根图3.9 用二分法求方程p(x)=0的根的框图3.6.2 函数的递归调用——求两正整数的最大公因子图3.10 用递归调用求n!示意图3.6.3 多重循环的应用——线性方程组的顺序消元法图3.11 顺序消元法的框图第4章 计算结果可视化 4.1 引言图4.1 图形窗口图4.2 图形窗口的文件菜单图4.3 图形窗口的工具菜单图4.4 图形窗口的编辑菜单4.2 二维图形的绘制4.2.1 plot指令图4.5 利用指令plot(y,'X', 'Y', 'y=f(x)')画图。
scilab 画函数

scilab 画函数使用Scilab 画函数Scilab是一种开源的数值计算软件,可以用于数值分析、数据可视化、模拟和仿真等多种科学计算任务。
在Scilab中,我们可以利用其强大的绘图功能来画出各种函数图形,以更直观地理解函数的特性和行为。
本文将介绍如何使用Scilab画函数,并以一些例子来说明。
我们需要安装Scilab并打开软件。
在Scilab的命令行界面中,我们可以直接输入函数并绘制函数图形。
例如,我们可以输入以下命令来画出函数y = sin(x)的图像:```x = linspace(0, 2*%pi, 100);y = sin(x);plot(x, y);```在上述命令中,我们首先使用linspace函数生成了一个包含100个点的等间隔的x坐标向量。
然后,我们使用sin函数计算了对应的y坐标向量。
最后,我们使用plot函数将x和y的值绘制成曲线图。
除了绘制曲线图外,Scilab还支持绘制散点图、柱状图、面积图等多种类型的图形。
例如,我们可以使用以下命令来画出函数y =x^2的散点图:```x = linspace(-10, 10, 100);y = x.^2;scatter(x, y);```在上述命令中,我们首先生成了一个包含100个点的等间隔的x坐标向量。
然后,我们使用.^操作符对x的每个元素进行平方运算,得到对应的y坐标向量。
最后,我们使用scatter函数将x和y的值绘制成散点图。
除了简单的函数绘制外,Scilab还支持绘制多个函数的图形,并可以对图形进行自定义设置。
例如,我们可以使用以下命令来画出函数y = sin(x)和y = cos(x)的图像,并对图像进行设置:```x = linspace(0, 2*%pi, 100);y1 = sin(x);y2 = cos(x);plot(x, y1, 'r');hold on;plot(x, y2, 'b--');title('Sin and Cos functions');xlabel('x');ylabel('y');legend('sin', 'cos');grid on;```在上述命令中,我们首先分别计算了函数y = sin(x)和y = cos(x)的y坐标向量。
必修3scilab程序

第二个:自然常数 e 的计算(输入一个正整数,输出自然常数 e 的运算值)
n=input('please input a number'); i=1; s=1; t=1; while i<n|i==n s=s+1/t; i=i+1; t=t*i; End disp('s'); disp(s);
第三个:把 k 进制化成十进制
第七个:更相减损术
a=input('please input number a='); b=input('please input number b='); t=1;m=1; if a<b then t=a; a=b; b=t; End while m~=0 m=a-b; a=m; if a<b then t=a; a=b; b=t; End end disp('the highest common factor is'); disp(a);
第十个:秦九Biblioteka 算法n=input('the biggest power number is'); i=1; x=input('x=:'); a=input('first number is :'); b=input('second number is'); u=a*x+b while i<n v=input('next is '); u=u*x+v; i=i+1; End disp(u);
第九个:十进制化 k 进制
n=input('please input a usual number:'); k=input('please input the key number:');
