受力分析和受力图
第三章 物体受力分析及受力图

第三章物体的受力分析及受力图§ 3.1 载荷荷载分类:(1)按作用时间的久暂恒载(dead load):固定载荷,长期作用于结构上的不变荷载,其大小、方向、作用位置是不变的。
例如结构的自重、安装在结构上的设备重量等;活载(live load):建筑物在施工和使用期间可能存在的可变荷载。
例如吊车荷载、结构上的人群、风、雪等荷载。
(2)按荷载的作用范围集中荷载(concentrated load):荷载的作用面积相对于总面积是微小的。
分布荷载(distributed load):分布作用在一定面积或长度上的荷载,如风、雪、自重等荷载。
(3)按荷载作用的性质静荷载(static load):大小、方向和位置不随时间变化或变化极其缓慢,不使结构产生显著的加速度。
例如结构自重、楼面活载等;动荷载(dynamic load):随时间迅速变化或在短暂时间内突然作用或消失的荷载,使结构产生显著的加速度。
注意:车辆荷载、风荷载和地震荷载通常在设计中简化为静力荷载,但在特殊情况下要按动力荷载考虑。
(4)按荷载位置的变化固定荷载(fixed load ):作用位置固定不变的荷载,例如风、雪、结构自重等。
移动荷载(travelling load):可以在结构上自由移动的荷载,例如吊车梁上的吊车荷载、公路桥梁上的汽车荷载就是移动荷载。
常见分布载荷合力作用位置§3.2 工程常见约束与约束力自由物体——空间运动不受任何限制的物体,如飞机、导弹、航天器受约束物体——空间运动受到限制的物体,如汽轮机、车轮。
工程中大部分研究对象都是非自由体,约束(constraint )—— 物体运动过程中所受到的限制。
约束的作用一方面限制物体运动,另一方面表现为约束力。
约束力(reactions)——约束对物体的反作用力,又称约束反力。
是一种被动力,其大小不能预先确定,方向总是与约束力所能阻止的运动方向相反。
主动力-----主动地施加于物体,改变其运动状态的力称为主动力。
受力分析与受力图(精.选)

第 3周(第1、2 讲)【教学过程】:复习导入:在工程实际中,常常需要对结构系统中的某一物体或几个物体进行力学计算。
首先要确定研究对象,然后对它进行受力分析。
即分析研究物体受那些力的作用,并确定每个力的大小、方向和作用点。
即:1、研究对象:我们把所研究的物体称为研究对象。
为了清楚地表示物体的受力情况,需要把所研究的物体从与它相联系的周围物体中分离出来,单独画出该物体的轮廓简图,使之成为分离体,即:2、分离体:解除约束后的自由物体。
3、受力图:在分离体上画上它所受的全部主动力和约束反力,就称为该物体的受力图。
4、内力与外力如果所取的分离体是由某几个物体组成的物体系统时,通常将系统外物体对物体系统的作用力称为外力,而系统内物体间相互作用的力称为内力。
注意:画受力图时一定要分清内力与外力,内力总是以等值、共线、反向的形式存在,故物体系统内力的总和为零。
因此,取物体系统为研究对象画受力图时,只画外力,而不画内力。
5、画受力图是解平衡问题的关键,画受力图的一般步骤为:1)根据题意确定研究对象,并画出研究对象的分离体简图。
2)在分离体上画出全部已知的主动力。
3)在分离体上解除约束的地方画出相应的约束反力。
注意:画受力图时要分清内力与外力,6、下面举例说明受力图的画法。
例1重量为G的均质杆AB,其B端靠在光滑铅垂墙的顶角处,A端放在光滑的水平面上,在点D处用一水平绳索拉住,试画出杆AB的受力图。
解:1、选AB为研究对象2、在C处画主动力G3、画约束反力例2图1-17a所示的三铰拱桥由左、右两拱通过三铰链连接而成。
在拱AC 上作用有载荷FP,两拱自重不计,试分别画出拱AC和拱BC的受力图。
例3、图1-18a是曲柄滑块机构,图1-18c是凸轮机构。
试分别画出两图中滑块及推杆的受力图,并进行比较。
例11、如图1-15a所示,水平梁AB用斜杆CD支承,A、C、D三处均为光滑铰链连接。
匀质梁AB重G1,其上放一重为G2电动机。
物体的受力分析和受力简图
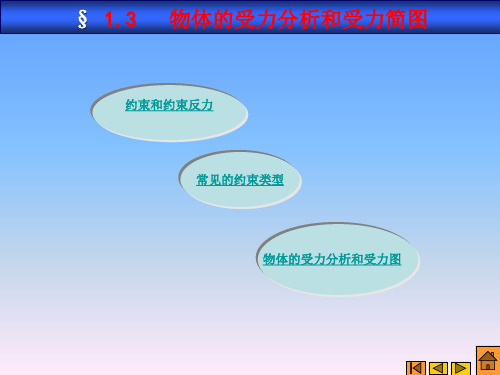
F (2)取左拱AC ,先画主动力, 再画约束力,其受力图如图所示。
F C
F C FAx FAy
F B
三、物体的受力分析与受力图
(3)取整体 ,先画主动力,再画约束力,其受力图如
F C
F B
F C
F D D
F E
E
习题课
讨论题:画杆件AC、BC的受力图。 解(1)取杆AC为研究对象,其受力图如图所示。 (2)取杆BC为研究对象,其受力图如图所示
B
G1
C
A
G2
FAx A
FAy
B FBx
FBy G1
FCy C FCx
FCx
C
FAy
G2
习题课
讨论:改为力G2作用在C点,作AC杆和BC杆的受力图。
F
B
C
FB
FC
习题课
例1-8 图示不计自重的梯子放在光滑水平地面上,画出绳子、梯子左右两部
分与整个系统受力图。 FAy
A
F
H
A
F
H
FAx FAx
A
FAy
A
F
H
D B
E
CB
D
F D
F E E
D CB
E C
F B
解(1)绳子受力图如图所示。
(2)梯子左边部分受力图如图所示 (3)梯子右边部分受力图如图所示 (4)整体受力图如图所示
FT
D FD
B
G
习题课
例1-7 如图a所示刚架由构件AB和CD用铰链C相连, A处是固定铰支座,B 、D
受力分析与受力图

受力分析与受力图
受力分析:分析物体或物体系受到的主动力和约束反力。
受力图是表示物体受力情况的简图,将研究的构件(研究对象)从与它发生联系的周围物体中分离出来,把作用于其上的全部外力都表示出来。
根据计算的要求,全面表示某一物体(或物体系统)受力情况的力学简图,称为该物体(或系统)的受力图。
一个正确的,完整的受力图上,应该明确表示出各力的方向和作用位置(至于力的大小,一般不要求在受力图中按比例表示)。
画好受力图是对物体(或系统)进行受力分析和计算的最基本的步骤。
2-4受力分析和受力图

物体的受力分析与受力图
Hale Waihona Puke 教学目的: 掌握单个物体及物体系统的受力图作法 教学重点: 受力图的画法及注意事项 教学难点: 受力图的画法(约束反力的方向)
画受力图的方法与步骤: 1、取隔离体(研究对象) 2、画出研究对象所受的全部主动力(使物体产生 运动或运动趋势的力) 3、在存在约束的地方,按约束类型逐一画出约束 反力 4、区隔离体时的抛弃部分对分离体的力不能丢。
二、物体系统的受力图
• 与单个物体受力图的区别: • 研究对象---由两个或两个以上的物体联系 在一起的物体系统。 • 作法:将系统当作一个整体。 • 注意:有二力杆时先画二力杆。
7 、正确判断二力构件。
受力分析
• • • • • • 受力分析:分析研究对象的受力情况 1、研究对象与哪些物体有联系? 2、受到哪些力? 3、这些力是什么物体给它的? 4、哪些力已知?哪些力未知? 受力分析前,应先明确对哪一个构件进行 受力分析------选取研究对象。
受力图
脱离体----把研究对象从与它有联系的周围物 体中脱离出来,脱离出来的研究对象即脱 离体。 受力图-----在脱离体上画出周围物体对它的全 部作用力。(主动力、约束反力)
一、单个物体的受力图
• • • • • • • • • 1、一般画法 (1)画脱离体 (2)画已知力 (3)在各相互作用点上画约束反力。 (几处约束?什么约束?约束反力的画法。) 2、注意事项: (1)全部力---主动力、约束反力,按顺序,勿丢落 (2)画反力时,应取消约束,不必画出。 (3)研究对象对约束的作用力或其他物体上受的力不应 画出。
[例1] 画出重物和AB杆的受力图
例2 重量为FW 的小球放置在光滑的斜面上,并 用绳子拉住,画出此球的受力图。 【解】以小球为研究对象,解除小球的约束,画 出分离体,小球受重力(主动力)FW,并画出,同 时小球受到绳子的约束反力(拉力)FTA和斜面的 约束反力(支持力)FNB。
受力分析

一、物体的受力分析与受力图 物体的受力分析 确定物体受了几个力,每个力的作用位置和力的 作用方向。 主动力与被动力 促使物体运动或有运动趋势的力,其大小 主动力: 和方向常常已知,如重力、水压力等。 由主动力引起并随其变化的力,其大小和 被动力: 方向都不知,如约束力。 受力图:将研究对象(物体或物体系统)从周围物体( 约束)中分离出来,画出作用在研究对象上 全部外力(主动力和约束力)的简图。
F
A
G
B
(3)分析并画出约束力FNA和 FNB。
FNA
FNB
例1-2 屋架受均布风力q(N/m),屋架重为 G,画出 屋架的受力图。
解(1)取屋架为研究 对象,并画出分离体图。 (2)画出主动力。 (3)画出约束力。
q
FAx FAy
G
FB
例1-3 杆AB重为G,画出AB 杆的受力图。
C
FAy
CABiblioteka FTGBFAx
A
B
FA
A
C
FT G
B
例1-9 作圆柱体的受力图。
解(1)取圆柱为研究对象, 并画出分离体图。 (2)画出主动力。 (3)画出约束力。
C
A A
FA
B
C
FNB
B
G
G
例1-4 作梁的受力图。 解(1)取梁AB为研究 对象,并画出分离体图。 (2)画出主动力。 (3)画出约束力。
A
F
C B
画受力图时必须清楚:
研究对象是什么? 将研究对象分离出来需要解除哪些约束? 约束限制研究对象的什么运动? 如何正确画出所解除约束处的约束力?
二、单个物体的受力分析 例1-1 碾子重为G,拉力为F,A、B处光滑接触,画出 碾子的受力图。 解 (1)取碾子为研究对象,画 出其分离体图。 (2)分析并画出主动力, 重力 G和拉力F。
物体的受力分析和受力图

(3) 画整个刚架的受力图。 ①以整个刚架为研究对象,取分离体。②在分离体上画出所受的主动力F。
③在分离体上画出其约束反力。 画法1:固定镜支座B的约束反力FB按图2-37b所示方向画出;固定铰支座
A的约束反力用过A点的两个正交分力FAx、FAy表示,其受力图如图2-37d所示。 画法2:根据三力平衡汇交定理可知,主动力F与B端支座反力FB两力的
图2-35
【例2-8】重量为W的圆管放置于图2-36所示的简易构架中,AB杆的自重为G, A端用固定铰支座与墙面连接,B端用绳水平系于墙面的C点上,若所有接触面都 是光滑的,试分别画出圆管和AB 杆的受力图。
解: (1)画圆管的受力图。 ①以圆管为研究对象,取分离体。②在分离体上画出所受的主动力W。③ 在分离体上画出其约束反力。E点和D点的约束反力FNE、FND的作用线均沿其接 触面的公法线,通过圆管横截面的中心,并指向圆管,其受力图如图2。 ①以杆AB为研究对象,取分离体。② 在分离体上画出所受的主动力G。③
在分离体上画出其约束反力。E点的约束反力F 'NE 按与 FNE 等值、反向画
出;B端为绳索约束,约束反力FT 的方向沿绳索中心线背离分离体;A端
固定铰支座的约束反力用两个正交分力 FAx 和 FAy表示,指向可作假定,
其受力图如图2-36c 所示。
图2-36
【例2-9】三铰刚架受力如图2-37a所示,不计各杆自重,试分别画出刚架 AC、BC的受力图和三铰刚架作为整体的受力图。
解: (1)画刚架BC的受力图。 ①以右半刚架BC为研究对象,取分离体。②在分离体上画出所受的主动 力。因在BC上无主动力作用,且自重又不计,故无主动力画出。③在分离体上 画出其约束反力。因BC实为二力构件,其约束反力FB、FC必沿B、C两铰链中 心连线方向,指向可作假定,其受力图如图2-37b 所示。
建筑力学 物体的受力分析和受力图
3. 注意约束反力与约束类型相对应。 每解除一个约束,就有与它相应的约束反
力作用于研究对象;约束反力的方向要依据约 束的类型来画,不能根据主动力的方向来简单 推想。另外,同一约束反力在各受力图中假定 的指向应一致。
普通高等教育“十一五”国家级规划教材
F2
FCy
A
E
FAx FAy
B C FCx FB
F1 CH
F’Cx
D
F’Cy FD
特别注意:
⑴支座A、B、C处的反力,在不同的受力
图中应保持一致。 ⑵铰C处的反力,应符合作用力与反作用
力公理。
普通高等教育“十一五”国家级规划教材
当以若干物体组成的系统为研究对象时,系 统内各物体间的相互作用力称为内力;系统外的 物体作用于该系统中各物体的力称为外力。内力 对系统的作用效果相互抵消,因此可除去,并不 影响整个系统的平衡。
二、物体系统的受力图 物体系统包含多个物体,其受力图画法与
单个物体相同,只是研究对象可能是整个物体 系统或系统的某一部分或某一物体。
⑴画物体系统整体的受力图时,只须把整 体作为单个物体一样对待。
⑵画系统的某一部分或某一物体的受力图 时,只须把研究对象从系统中分离出来,同时 注意被拆开的联系处,有相应的约束反力,并 应符合作用力与反作用力公理。
A端为固定铰支座,B端为可动铰支座,如图所
示。试画出梁AB的受力图。
F
FAx
F
A
B
FAy O
FB
F
FA
FB
普通高等教育“十一五”国家级规划教材
例1-3 一水平梁AB受已知力F作用,A端是固定 端支座,梁AB的自重不计,如图所示。试画出 梁AB的受力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3周(第1、2 讲)
【教学过程】:
复习导入:在工程实际中,常常需要对结构系统中的某一物体或几个物体进行力学计算。
首先要确定研究对象,然后对它进行受力分析。
即分析研究物体受那些力的作用,并确定每个力的大小、方向和作用点。
即:
1、研究对象:我们把所研究的物体称为研究对象。
为了清楚地表示物体的受力情况,需要把所研究的物体从与它相联系的周围物体中分离出来,单独画出该物体的轮廓简图,使之成为分离体,即:
2、分离体:解除约束后的自由物体。
3、受力图:在分离体上画上它所受的全部主动力和约束反力,就称为该物体的受力图。
4、内力与外力
如果所取的分离体是由某几个物体组成的物体系统时,通常将系统外物体对物体系统的
作用力称为外力,而系统内物体间相互作用的力称为内力。
注意:画受力图时一定要分清内力与外力,内力总是以等值、共线、反向的形式存在,故物体系统内力的总和为零。
因此,取物体系统为研究对象画受力图时,只画外力,而不画内力。
5、画受力图是解平衡问题的关键,画受力图的一般步骤为:
1)根据题意确定研究对象,并画出研究对象的分离体简图。
2)在分离体上画出全部已知的主动力.
3)在分离体上解除约束的地方画出相应的约束反力.
注意:画受力图时要分清内力与外力,
6、下面举例说明受力图的画法。
例1 重量为G的均质杆AB,其B端靠在光滑铅垂墙的顶角处,A端放在光滑的
水平面上,在点D处
用一水平绳索拉住,试画出杆AB的受力图。
ﻫ解:1、选AB为研究对象
2、在C处画主动力G
3、画约束反力
例2 图1-17a所示的三铰拱桥由左、右两拱通过三铰链连接而成。
在拱AC
上作用有载荷F P,两拱自重不计,试分别画出拱AC和拱BC的受力图.
例3、图1-18a是曲柄滑块机构,图1-18c是凸轮机构。
试分别画出两图中滑块及推杆的受力图,并进行比较。
例11、如图1-15a所示,水平梁AB用斜杆CD支承,A、C、D三处均为光滑铰链连接。
匀质梁AB重G1,其上放一重为G2电动机。
若不计斜杆CD自重,试分别画出斜杆CD和梁AB(包括电动机)的受力图。
解:(1) 斜杆CD的受力图取斜杆CD为研究对象,由于斜杆CD自重不计,并且只在C、D两处受铰链约束而处于平衡,因此斜杆CD为二力构件。
斜杆CD的约束反力必通过两铰链中心C与D的连线,用F C和F D表示。
如图1-15b所示。
(2) 梁AB的受力图取梁AB(包括电动机)为研究对象,梁AB受主动力G1和G2的作用。
在D处为铰链约束,约束反力F’D与F D是作用与反作用的关系,且F’D=-FD.A处为固定铰链支座约束,约束反力用两个正交的分力F Ax和FA y表示,方向可任意假设。
如图1—15c所示。
小结:受力图在解除约束的分离体简图上,画出它所受的全部外力的简图,称为受力图.
画受力图时应注意:谁是受力物体,谁是施力物体,只画受力,不画施力;只画外力,不画内力;既不要多画力,又不要少画力;解除约束后,才能画上约束反力。
作业:另拟
第 3 周(第3、4 讲)
【教学过程】:
复习导入:各力的作用线汇交于一点的力系称为汇交力系。
用力的平行四边形法则可以求得两力的合力,用此法则也可以求得多个汇交力的合力。
对于包含n 个汇交力的力系F1,F2 ,。
..,F n,所合成的合力FR即为
F R=F1+F2+…+ F n=ΣF
一。
力在直角坐标轴上的投影
1.一次投影法
若已知力F与直角坐标系oxyz三轴间的正向夹角分别为α、β、γ,如图2-1(a)、(b),则力F在这三个轴上的投影可表示为
Fx= Fcosα ﻫFy= Fcosβ (2ﻫFz=Fcosγ
可以看出,力与投影轴正向夹角为锐角时,其投影为正;力与投影轴正向夹角为钝角时,其投影为负。
故力在直角坐标轴上的投影是代数量。
应当注意,在直角坐标系中,分力的大小和投影的绝对值相等,但投影是代数量,分力是失量。
3.合力投影定理
将式(2—1)两边分别向三个直角坐标轴上投影,有
FRx=F1x+F2x +。
.。
+Fnx=ΣFx
FRy=F1y+F2y +。
.+Fny=ΣFy(2-4) FRz=F1z+F2z +...+F nz=ΣFz
即合力在某一轴上的投影,等于各分力在同一轴上投影的代数和。
二、汇交力系的合成与平衡
1.汇交力系合成的解析法
设在刚体上作用有汇交力系F1,F2,..。
,Fn,由合力投影定理可求得合力F R在三个直角坐标轴投影FRx、FRy、FRz,于是合力的大和方向可由下式确定
(2-5)
ﻫ若力系为平面力系,则合力的大小和方向为
(2-6)
2。
汇交力系平衡的解析条件
从前面知道,汇交力系平衡的充要条件是合力等于零,
即F R=ΣF=0
所以ΣFx=0ﻫΣFy=0
(2-7)
ΣFz=0
ﻫ式(2-7)称为汇交力系的平衡方程,它表明汇交力系平衡的解析条件是力系中各力在三个直角坐标轴投影的代数和分别等于零。
利用这三个互相独立的方程,可以求解三个未知数。
若力系为平面汇交力系,则平面汇交力系平衡的解析条件为
ΣFx=0ﻫΣFy=0
当用解析法求解平衡问题时,未知力的指向可以假设,如计算结果为正值,则表示所假设力的指向与实际相同;如为负值,则表示所假设力的指向与实际相反。
例2—1 用解析法求图示汇交力系的合力。
解
图2—2
例2-2 直杆AB、AC铰接于A点,自重不计,在A点挂一物重G=1000N,并用绳子AD吊住,如图2-3所示.已知AB和AC等长且互相垂直,∠OAD=30°,
B、C均为球铰接,求杆AB和AC及绳子AD所受的力。
ﻫ
解取销钉A为研究对象,其受力图,如图2-3所示,是一空间汇交力系。
取直角坐标系Axyz,列平衡方程为
ΣFx=0 -FAC-FTcos30°sin45°=0(1)
ΣFy=0 -FAB-FTcos30°cos45°=0(2)
ΣFz=0 -FTsin30°-G=0 (3)
由式(1)、(2)、(3)解得
FT=2000N,FAB=FAC=-1225N
FAB、FAC均为负值,说明所假设力的指向与实际相反,即两杆均受压力。
小结:
1。
力在坐标轴上的投影
2。
合力投影定理。
即合力在某一轴上的投影,等于各分力在同一轴上投影的代数和。
3.汇交力系合成的解析法
4。
汇交力系的平衡方程
ΣFx=0ﻫΣFy=0ﻫΣFz=0
作业:另拟
【课后记】:本节内容对后续课程的学习很重要,应加强训练。
