数学学院科研基金项目一览表 四川大学数学学院
中南大学2015年基金项目清单
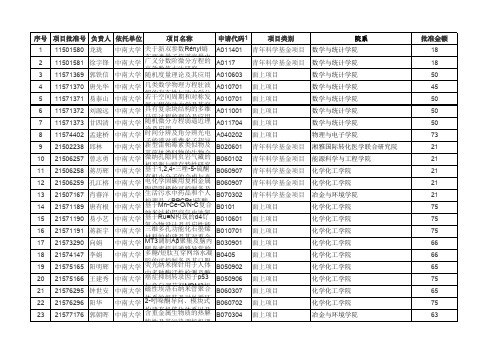
批准金额 18 18 50 45 50 50 50 73 21 21 21 21 21 75 75 75 66 66 65 75 65 75 63
中南大学 关于新双参数Rényi熵 A011401 在两类量子信道容量中 11501581 徐宇锋 中南大学 广义分数阶微分方程的 A0117 高效数值方法研究 11571369 郭铁信 中南大学 随机度量理论及其应用 A010603 11571370 唐先华 中南大学 几类数学物理方程驻波 A010701 解的存在性与动力学分 11571371 易泰山 中南大学 若干空间周期和对称发 A010701 展方程的动力学及其空 11571372 刘源远 中南大学 具有复杂块结构的多维 A011001 马氏过程的理论及应用 11571373 甘四清 中南大学 随机微分方程弱逼近理 A011704 论及应用 11574402 孟建桥 中南大学 时间分辨及角分辨光电 A040202 子能谱对重费米子超导 21502238 邱林 中南大学 新型雷帕霉素类似物及 B020601 其前体类似物的生物合 21506257 曾志勇 中南大学 微纳孔隙间页岩气藏的 B060102 相平衡与赋存特性研究 21506258 蒋历辉 中南大学 基于1,2,4-三唑-5-硫酮 B060907 有机小分子的合成与光 21506259 孔江榕 中南大学 电化学固碳用复相金属 B060907 陶瓷阴极的可控制备及 21507167 肖睿洋 中南大学 生活污水中药品和个人 B070302 护理品(PPCPs)硫酸 21571189 唐有根 中南大学 基于Mn-Ce-O/N-C复合 B0101 纳米结构铝空气电池氧 21571190 易小艺 中南大学 基于Ru≡N构筑的d4钌 B010601 氮合物设计及反应性能 21571191 蒋新宇 中南大学 三维多孔功能化石墨烯 B010701 材料的构建及其对重金 21573290 向娟 中南大学 MT3调制Aβ聚集及脑内 B030901 胰岛素信号通路异常的 21574147 李娟 中南大学 多糖/短肽互穿网络水凝 B0405 胶的可控制备及其口服 21575165 阳明辉 中南大学 荧光纳米探针用于人体 B050902 中多种酶活性检测及酶 21575166 王建秀 中南大学 癌症抑制转录因子p53 B050906 与负向调节剂MDM2相 21576295 钟世安 中南大学 磁性埃洛石纳米管聚合 B060307 体系的组装及对外循环 21576296 阳华 中南大学 2-吲哚酮导向、模块式 B060702 构建有机催化体系以及 21577176 郭朝晖 中南大学 含重金属生物质的热解 B070304 特性及其污染调控机理
国家自然科学基金学科分类

国家自然科学基金学科分类数理科学部A01数学A0101数论A010101解析数论A010102代数数论A010103数论应用A0102代数学A010201群及其表示A010202李群与李代数A010203代数群与量子群A010204同调与K理论A010205环与代数A010206编码与密码A010207代数几何A0103几何学A010301整体微分几何A010302复几何与代数几何A010303几何分析A0104拓扑学A010401代数拓扑与微分拓扑A010402低维流形上的拓扑A010403一般拓扑学A0105函数论A010501多复变函数论A010502复动力系统A010503单复变函数论A010504调和分析与小波分析A010505函数逼近论A0106泛函分析A010601非线性泛函分析A010602算子理论与算子代数A010603空间理论A0107常微分方程与动力系统A010701泛函微分方程A010702定性理论与稳定性理论A010703分支理论与混沌A010704微分动力系统与哈密顿系统A010705拓扑动力系统与遍历论A0108偏微分方程A010801几何、物理和力学中的偏微分方程A010802非线性椭圆和非线性抛物方程A010803混合型、退化型偏微分方程A010804非线性发展方程和无穷维动力系统A0109数学物理A010901规范场论与超弦理论A010902可积系统及其应用A0110概率论与随机分析A011001马氏过程与遍历论A011002随机分析与随机过程A011003随机微分方程A011004极限理论A0111数理统计A011101抽样调查与试验设计A011102时间序列与多元分析A011103数据分析与统计计算A0112运筹学A011201线性与非线性规划A011202组合最优化A011203随机最优化A011204可靠性理论A0113控制论中的数学方法A011301分布参数系统的控制理论A011302随机系统的控制理论A0114应用数学方法A011401信息论A011402经济数学与金融数学A011403生物数学A011404不确定性的数学理论A011405分形论及应用A0115数理逻辑和与计算机相关的数学A011501数理逻辑A011502公理集合论A011503计算复杂性与符号计算A011504机器证明A0116组合数学A011601组合设计A011602图论A011603代数组合与组合矩阵论A0117计算数学与科学工程计算A011701偏微分方程数值计算A011702流体力学中的数值计算A011703一般反问题的计算方法A011704常微分方程数值计算A011705数值代数A011706数值逼近与计算几何A011707谱方法及高精度数值方法A011708有限元和边界元方法A011709多重网格技术及区域分解A011710自适应方法A011711并行算法A02力学A0201力学中的基本问题和方法A020101理性力学与力学中的数学方法A020102物理力学A020103力学中的反问题A0202动力学与控制A020201分析力学A020202动力系统的分岔与混沌A020203运动稳定性及其控制A020204非线性振动及其控制A020205多体系统动力学A020206转子动力学A020207弹道力学与飞行力学A020208载运工具动力学及其控制A020209多场耦合与智能结构动力学A0203 固体力学A020301弹性力学与塑性力学A020302损伤与断裂力学A020303疲劳与可靠性A020304本构关系A020305复合材料力学A020306智能材料与结构力学A020307超常环境下材料和结构的力学行为A020308微纳米力学A020309接触、摩擦与磨损力学A020310表面、界面与薄膜力学A020311岩体力学和土力学A020312结构力学与结构优化A020313结构振动、噪声与控制A020314流固耦合力学A020315制造工艺力学A020316实验固体力学A020317计算固体力学A0204流体力学A020401湍流与流动稳定性A020402水动力学A020403空气动力学A020404非平衡流与稀薄气体流动A020405多相流与渗流A020406非牛顿流与流变学A020407流动噪声与气动声学A020408流动控制和优化A020409环境流体力学A020410工业流体力学A020411微重力流体力学A020412交通流与颗粒流A020413电磁与多场耦合流体力学A020414实验流体力学A020415计算流体力学A0205 生物力学A020501组织与器官系统力学A020502细胞、亚细胞、生物大分子力学A020503仿生、生物材料与运动生物力学A0206 爆炸与冲击动力学A020601爆炸力学A020602冲击动力学A03天文学A0301 宇宙学A030101宇宙学模型和参数、早期宇宙A030102宇宙结构的形成和演化及观测宇宙学A030103宇宙暗物质和暗能量A0302 星系和类星体A030201银河系A030202星系形成、结构和演化A030203星系相互作用和并合;活动星系核A0303 恒星与星际物质A030301恒星结构和演化与恒星大气A030302变星和激变变星、双星和多星系统A030303恒星形成与早期演化、星际介质和星际分子A030304晚期演化和致密天体及其相关高能过程A030305太阳系外行星系统A0304 太阳和太阳系A030401太阳磁场和太阳发电机A030402太阳日冕物质抛射、耀斑、日珥和其他活动A030403日震学和太阳内部结构;太阳黑子和太阳活动周期变化A030404太阳系的起源和演化及太阳系中行星、卫星和其他小天体A030405太阳爆发活动对日地空间天气的影响A0305 天体中基本物理过程的理论和实验A030501天文中基本物理过程和天体辐射过程的理论和实验A030502实验室天体物理A0306 天体测量和天文地球动力学A030601天文参考系及星表A030602相对论天体测量A030603天文地球动力学及天体测量学的应用A030604时间与频率A0307 天体力学和人造卫星动力学A030701人造天体、太阳系小天体、行星系统和恒星系统动力学A030702N体问题、非线性和相对论天体力学A0308 天文技术和方法A030801 光学、紫外和红外天文技术与方法A030802 射电、毫米波和亚毫米波天文技术与方法A030803 高能天体物理技术方法和空间天文技术与方法A030804 海量数据处理及数值模拟天文技术与方法A0309 中、西方天文学史A0310 天文学同其他学科的交叉A04物理学IA0401凝聚态物性I:结构、力学和热学性质A040101固体结构和人工微结构A040102软物质和液体的结构与性质A040103凝聚态物质的力学、热学性质,相变和晶格动力学A040104凝聚态物质的(非电子)输运性质A040105薄膜和纳米结构的形成A040106表面,薄膜和纳米结构的表征和分析A040107表面、界面、介观系统、纳米系统的非电子性质A0402凝聚态物性 II :电子结构、电学、磁学和光学性质A040201块体材料的电子态A040202强关联电子系统A040203电子输运过程:电导、光电导、磁电导A040204表面、界面和低维系统的电子结构及电学性质A040205介观系统和人工微结构的电子结构、光学和电学性质A040206超导电性A040207磁有序系统A040208低维、介观和人工微结构的磁性A040209介电、压电、热电和铁电性质A040210凝聚态物质的光学和波谱学、物质与粒子的相互作用和辐射A040211极端条件下的凝聚态物理A040212量子计算中的凝聚态物理问题A040213软物质、有机和生物材料的电子结构和物理A040214生命现象中的凝聚态物理问题A040215凝聚态物理中的新效应及其他问题A0403原子和分子物理A040301原子和分子结构理论A040302原子、分子、光子相互作用与光谱A040303原子分子碰撞过程及相互作用A040304大分子、团簇与特殊原子分子性质A040305极端条件下的原子分子物理A040306外场中的原子分子性质及其操控A040307量子信息中的原子分子物理问题A040308与原子、分子有关的其他物理问题A0404光学A040401光的传播和成像A040402信息光学中的物理问题A040403光源、光学器件和光学系统中的物理问题A040404纤维光学和集成光学中的物理问题A040405光与物质的相互作用A040406超强、超快光物理A040407微纳光学与光子学A040408量子光学和量子信息A040409非线性光学A040410光学材料中物理问题及固体发光A040411激光光谱学及高分辨高灵敏光谱方法A040412X-射线、红外、THz物理A040413光学在生命科学中的应用A040414与光学有关的其他物理问题和交叉学科A0405声学A040501线性与非线性声学A040502水声和海洋声学及空气动力声学A040503超声学、量子声学和声学效应A040504噪声、噪声效应及其控制A040505生理、心理声学和生物声学A040506语言声学、乐声及声学信号处理A040507声学换能器、声学测量方法和声学材料A040508信息科学中的声学问题A040509 A040510建筑声学与电声学与声学有关的其他物理问题和交叉学科A05物理学IIA0501 基础物理学A050101 物理学中的数学问题与计算方法A050102 经典物理及其唯象学研究A050103 量子物理及其应用A050104 量子信息学A050105 统计物理学与复杂系统A050106 相对论、引力与宇宙学A0502粒子物理学和场论A050201场和粒子的一般理论及方法A050202量子色动力学、强相互作用和强子物理A050203电-弱相互作用及其唯象学A050204非标准模型及其唯象学A050205弦论、膜论及隐藏的空间维度A050206非加速器粒子物理A050207粒子天体物理和宇宙学A0503核物理A050301原子核结构与特性研究A050302原子核高激发态、高自旋态和超形变A050303核裂变、核聚变、核衰变A050304重离子核物理A050305放射性核束物理、超重元素合成及反应机制A050306中高能核物理A050307核天体物理A0504 核技术及其应用A050401 离子束与物质相互作用和辐照损伤A050402 离子束核分析技术A050403 核效应分析技术A050404 中子技术及其应用A050405 加速器质谱技术A050406 离子注入及离子束材料改性A050407 核技术在环境科学、地学和考古中的应用A050408 核技术在工、农业和医学中的应用A050409 新概念、新原理、新方法A0505粒子物理与核物理实验方法与技术A050501 束流物理与加速器技术A050502 荷电粒子源、靶站和预加速装置A050503 束流传输和测量技术A050504 反应堆物理与技术A050505 散裂中子源相关技术A050506 探测技术和谱仪A050507 辐射剂量学和辐射防护A050508 实验数据获取与处理A050509 新原理、新方法、新技术、新应用A0506 等离子体物理A050601 等离子体中的基本过程与特性A050602 等离子体产生、加热与约束A050603 等离子体中的波与不稳定性A050604 等离子体中的非线性现象A050605 等离子体与物质相互作用A050606 等离子体诊断A050607 强粒子束与辐射源A050608 磁约束等离子体A050609 惯性约束等离子体A050610 低温等离子体及其应用A050611 空间和天体等离子体及特殊等离子体A0507 同步辐射技术及其应用A050701 同步辐射光源原理和技术A050702 自由电子激光原理和技术A050703 束线光学技术和实验方法国家自然科学基金学科代码化学科学部B01无机化学B0101无机合成和制备化学B010101合成与制备技术B010102合成化学B0102元素化学B010201稀土化学B010202主族元素化学B010203过渡金属化学B010204丰产元素与多酸化学B0103配位化学B010301固体配位化学B010302溶液配位化学B010303功能配合物化学B0104生物无机化学B010401金属蛋白(酶)化学B010402生物微量元素化学B010403细胞生物无机化学B010404生物矿化及生物界面化学B0105固体无机化学B010501缺陷化学B010502固相反应化学B010503固体表面与界面化学B010504固体结构化学B0106物理无机化学B010601无机化合物结构与性质B010602理论无机化学B010603无机光化学B010604分子磁体B010605无机反应热力学与动力学B0107无机材料化学B010701无机固体功能材料化学B010702仿生材料化学B0108分离化学B010801萃取化学B010802分离技术与方法B010803无机膜化学与分离B0109核放射化学B010901核化学与核燃料化学B010902放射性药物和标记化合物B010903放射分析化学B010904放射性废物处理和综合利用B0110同位素化学B0111无机纳米化学B0112无机药物化学B0113无机超分子化学B0114有机金属化学B0115原子簇化学B0116应用无机化学B02有机化学B0201有机合成有机合成反应与试剂B020101B020102复杂化合物的设计与合成B020103选择性有机反应B020104催化与不对称反应B020105组合合成B0202金属有机化学B020201金属络合物的合成与反应B020202生物金属有机化学B020203金属有机材料化学B0203元素有机化学B020301有机磷化学B020302有机硅化学B020303有机硼化学B020304有机氟化学B0204天然有机化学B020401甾体及萜类化学B020402中草药与植物化学B020403海洋天然产物化学B020404天然产物合成化学B020405微生物与真菌化学B0205物理有机化学B020501活泼中间体化学B020502有机光化学B020503立体化学基础B020504有机分子结构与反应活性B020505理论与计算有机化学B020506有机超分子与聚集体化学B020507生物物理有机化学B0206药物化学B020601药物分子设计与合成B020602药物构效关系B0207化学生物学与生物有机化学B020701多肽化学B020702核酸化学B020703蛋白质化学B020704糖化学B020705仿生模拟酶与酶化学B020706生物催化与生物合成B0208有机分析B020801有机分析方法B020802手性分离化学B020803生物有机分析B0209应用有机化学B020901农用化学品化学B020902食品化学B020903香料与染料化学B0210绿色有机化学B0211有机分子功能材料化学B021101功能有机分子的设计与合成B021102功能有机分子的组装与性质B021103生物有机功能材料B03物理化学B0301结构化学B030101 体相结构B030102 表面结构B030103 溶液结构B030104动态结构B030105光谱与波谱学B030106 纳米及介观结构B030107方法与理论B0302理论和计算化学B030201 量子化学B030202 化学统计力学B030203 化学动力学理论B030204 计算模拟方法与应用B0303 催化化学B030301 多相催化B030302 均相催化B030303 仿生催化B030304 光催化B030305 催化表征方法与技术B0304化学动力学B030401 宏观动力学B030402 分子动态学B030403 超快动力学B030404激发态化学B0305胶体与界面化学B030501 表面活性剂B030502 分散体系与流变性能B030503 表面/界面吸附现象B030504 超细粉和颗粒B030505 分子组装与聚集体B030506 表面/界面表征技术B0306电化学B030601 电极过程动力学B030602 腐蚀电化学B030603 材料电化学B030604 光电化学B030605 界面电化学B030606电催化B030607纳米电化学B030608化学电源B0307光化学和辐射化学B030701 超快光谱学B030702 材料光化学B030703 等离子体化学与应用B030704 辐射化学B030705 感光化学B030706光化学与光物理过程B0308热力学B030801 化学平衡与热力学参数B030802 溶液化学B030803 量热学B030804复杂流体B030805 非平衡态热力学与耗散结构B030806 统计热力学B0309生物物理化学B030901 结构生物物理化学B030902 生物光电化学与热力学B030903 生命过程动力学B030904生物物理化学方法与技术B0310化学信息学B031001 分子信息学B031002 化学反应和化学过程的信息学B031003 化学数据库B031004分子信息处理中的算法B04高分子科学B0401 高分子合成化学B040101高分子设计与合成B040102配位聚合与离子型聚合B040103高分子光化学与辐射化学B040104生物参与的聚合与降解反应B040105缩聚反应B040106自由基聚合B0402 高分子化学反应B040201高分子降解与交联B040202高分子接枝与嵌段B040203高分子改性反应与方法B0403 功能与智能高分子B040301吸附与分离功能高分子B040302高分子催化剂和高分子试剂B040303医用与药用高分子B040304生物活性高分子B040305液晶态高分子B040306光电磁功能高分子B040307储能与换能高分子B040308高分子功能膜B040309仿生高分子B0404 天然高分子与生物高分子B040401基于可再生资源高分子B0405 高分子组装与超分子结构B040501超分子聚合物B040502超支化与树形高分子B0406 高分子物理与高分子物理化学B040601高分子溶液B040602高分子聚集态结构B040603高分子转变与相变B040604高分子形变与取向B040605高分子纳米微结构及尺寸效应B040606高分子表面与界面B040607高分子结构与性能关系B040608高分子测试及表征方法B040609高分子流变学B040610聚电解质与高分子凝胶B040611高分子塑性与黏弹性B040612高分子统计理论B040613高分子理论计算与模拟B0407 应用高分子化学与物理B040701高分子加工原理与新方法B040702高性能聚合物B040703高分子多相与多组分复合体系B040704聚合反应动力学及聚合反应过程控制B040705杂化高分子B040706高分子循环利用B05 分析化学B0501 色谱分析B050101 气相色谱B050102 液相色谱B050103 离子色谱与薄层色谱B050104 毛细管电泳及电色谱B050105 微流控系统与芯片分析B050106色谱柱固定相与填料B0502 电化学分析B050201 伏安法B050202 生物电分析化学B050203 化学修饰电极B050204 微电极与超微电极B050205 光谱电化学分析B050206 电化学传感器B050207 电致化学发光B0503 光谱分析B050301 原子发射与吸收光谱B050302 原子荧光与X-射线荧光光谱B050303 分子荧光与磷光光谱B050304 化学发光与生物发光B050305 紫外与可见光谱B050306 红外与拉曼光谱B050307 光声光谱B050308 共振光谱B0504 波谱分析与成像分析B0505 质谱分析B0506 分析仪器与试剂B050601 联用技术B050602 分析仪器关键部件、配件研制B050603 分析仪器微型化B050604 极端条件下分析技术B0507 热分析与能谱分析B0508 放射分析B0509 生化分析及生物传感B050901 单分子、单细胞分析B050902 纳米生物化学分析方法B050903 药物与临床分析B050904 细胞与病毒分析B050905 免疫分析化学B050906 生物分析芯片B0510 活体与复杂样品分析B0511 样品前处理方法与技术B0512 化学计量学与化学信息学B0513 表面、形态与形貌分析B051301 表面、界面分析B051302 微区分析B051303 形态分析B051304 扫描探针形貌分析B06化学工程及工业化学B0601化工热力学和基础数据B060101状态方程与溶液理论B060102相平衡B060103化学平衡B060104热力学理论及计算机模拟B060105化工基础数据B0602传递过程B060201化工流体力学和传递性质B060202传热过程及设备B060203传质过程B060204颗粒学B060205非常规条件下的传递过程B0603分离过程B060301蒸馏蒸发与结晶B060302干燥与吸收B060303萃取B060304吸附与离子交换B060305机械分离过程B060306膜分离B060307非常规分离技术B0604化学反应工程B060401化学反应动力学B060402反应器原理及传递特性B060403反应器的模型化和优化B060404流态化技术和多相流反应工程B060405固定床反应工程B060406聚合反应工程B060407电化学反应工程B060408生化反应工程B060409催化剂工程B0605化工系统工程B060501化学过程的控制与模拟B060502化工系统的优化B0606无机化工B060601基础无机化工B060602工业电化学B060603精细无机化工B060604核化工与放射化工B0607有机化工B060701基础有机化工B060702精细有机化工B0608生物化工与食品化工B060801生化反应动力学及反应器B060802生化分离工程B060803生化过程的优化与控制B060804生物催化过程B060805天然产物及农产品的化学改性B060806生物医药工程B060807绿色食品工程与技术B0609能源化工B060901煤化工B060902石油化工B060903燃料电池B060904天然气及碳--化工B060905生物质能源化工B0610化工冶金B0611环境化工B061101环境治理中的物理化学原理B061102三废治理技术中的化工过程B061103环境友好的化工过程B061104可持续发展环境化工的新概念B0612资源化工B061201资源有效利用与循环利用B061202材料制备的化工基础B07环境化学B0701 环境分析化学B070101 无机污染物分离分析B070102有机污染物分离分析B070103污染物代谢产物分析B070104污染物形态分离分析B0702 环境污染化学B070201大气污染化学B070202水污染化学B070203土壤污染化学B070204 固体废弃物污染化学B070205 放射污染化学B070206 纳米材料污染化学B070207 复合污染化学B0703 污染控制化学B070301大气污染控制化学B070302水污染控制化学B070303土壤污染控制化学B070304固体废弃物污染控制化学B0704 污染生态化学B070401污染物赋存形态和生物有效性B070402污染物与生物大分子的相互作用B070403污染物的生态毒性和毒理B0705 理论环境化学B070501污染化学动力学B070502 污染物构效关系B070503 化学计量学在环境化学中的应用B070504 环境污染模式与预测B0706 区域环境化学B070601化学污染物的源汇识别B070602污染物的区域环境化学过程B070603污染物输送中的化学机制B0707化学环境污染与健康B070701 环境污染的生物标志物B070702 环境污染与食品安全B070703 人居环境与健康B070704 环境暴露与毒理学国家自然科学基金学科代码生命科学部C01微生物学C0101微生物资源与分类学C010101细菌资源、分类与系统发育C010102放线菌资源、分类与系统发育C010103真菌资源、分类与系统发育C010104病毒资源与分类C0102微生物生理与生物化学C010201微生物生理与代谢C010202微生物生物化学C0103微生物遗传育种学C010301微生物功能基因C010302微生物遗传育种C0104微生物学研究的新技术与新方法C0105环境微生物学C010501陆生环境微生物学C010502水生环境微生物学C010503其他环境微生物学C0106病原细菌与放线菌生物学C010601 植物病原细菌与放线菌生物学C010602 动物病原细菌与放线菌生物学C010603 人类病原细菌与放线菌生物学C0107 病原真菌学C010701 植物病原真菌学C010702 动物病原真菌学C010703 人类病原真菌学C0108 病毒学C010801 植物病毒学C010802 动物病毒学C010803 人类病毒学C010804噬菌体C0109支原体、立克次体与衣原体C010901 支原体C010902 立克次体、衣原体等C02植物学C0201 植物结构学C020101植物形态结构与功能C020102植物形态与发生C0202 植物分类学C020201种子植物分类C020202孢子植物分类C020203植物地理学C0203 植物进化生物学C020301植物系统发育C020302古植物学与孢粉学C020303植物进化与发育C0204 植物生理与生化C020401光合作用C020402生物固氮C020403呼吸作用C020404矿质元素与代谢C020405有机物质合成与运输C020406水分生理C020407抗性生理C020408植物激素与生长发育C020409植物次生代谢与调控C020410种子生理C0205 植物生殖生物学C020501植物配子体发生与受精C020502植物胚胎发生C0206 植物资源学C020601植物资源评价C020602植物引种驯化C020603植物种质C020604植物化学C020605水生植物与资源C0207植物学研究的新技术、新方法C03生态学C0301分子与进化生态学C030101分子生态学C030102进化生态学C0302行为生态学C030201昆虫行为生态学C030202其他动物行为生态学C0303生理生态学C030301植物生理生态学C030302动物生理生态学C0304种群生态学C030401植物种群生态学C030402昆虫种群生态学C030403其他动物种群生态学C0305群落生态学C030501群落结构与动态C030502物种间相互作用C0306生态系统生态学C030601农田生态学C030602森林生态学C030603草地与荒漠生态C030604水域生态学C0307景观与区域生态学C030701景观生态学C030702区域生态学C0308全球变化生态学C030801陆地生态系统与全球变化C030802海洋生态系统与全球变化C0309微生物生态学C0310污染生态学C031001污染生态学C031002毒理生态学C0311土壤生态学C031101土壤生态系统水分、养分循环C031102土壤生物与土壤生态系统C0312保护生物学与恢复生态学C031201生物多样性C031202保护生物学C031203受损生态系统恢复C0313生态安全评价C031301转基因生物的生态安全性评价C031302外来物种的入侵与生态安全性评价C031303生态工程评价C04林学C0401森林资源学C0402森林资源信息学C040201森林资源管理与信息技术C040202森林灾害监测的理论与方法C0403木材物理学C040301材性及其改良C040302木材加工学C040303人工复合木材C0404林产化学C040401树木化学成分分析C040402造纸与制浆C0405森林生物学C040501树木生长发育C040502树木抗逆生理学C040503树木繁殖生物学C0406森林土壤学C0407森林培育学C040701森林植被恢复与保持C040702人工林培育C040703种苗学C040704复合农林业C0408森林经理学C040801森林可持续发展C040802森林分类经营C0409森林健康C040901森林病理C040902森林害虫C040903森林防火C0410林木遗传育种学C041001林木种质资源C041002林木遗传改良C041003林木育种理论与方法C0411经济林学C041101经济林重要形状形成及调控C041102经济林栽培生理C041103林木果实采后生物学C041104茶学C0412园林学C041201园林植物种质资源C041202城市园林与功能C041203园林规划和景观设计C0413荒漠化与水土保持C041301防护林学C041302森林植被与水土保持C041303植被与荒漠化C0414林业研究的新技术与新方法C05生物物理、生物化学与分子生物学C0501生物大分子结构与功能C050101生物大分子结构计算与理论预测C050102生物大分子空间结构测定C050103生物大分子相互作用C0502生物化学C050201蛋白质与多肽生物化学C050202核酸生物化学C050203酶学C050204糖生物学C050205无机生物化学C0503蛋白质组学C0504膜生物化学与膜生物物理学C050401生物膜结构与功能C050402跨膜信号转导C050403物质跨膜转运C050404其他膜生物化学与膜生物物理学C0505系统生物学C0506环境生物物理C050601电磁辐射生物物理C050602声生物物理C050603光生物物理C050604电离辐射生物物理与放射生物学C050605自由基生物学C0507空间生物学C0508生物物理、生物化学与分子生物学研究的新方法与新技术C06遗传学与发育生物学C0601植物遗传学C060101植物分子遗传C060102植物细胞遗传C060103植物数量遗传C0602动物遗传学C060201动物分子遗传C060202动物细胞遗传C060203动物数量遗传C0603微生物遗传学C060301原核微生物遗传C060302真核微生物遗传C0604人类遗传学C060401人类遗传的多样性C060402人类起源与进化C060403人类行为的遗传基础C060404人类表型性状与遗传C0605医学遗传学C060501单基因遗传病的遗传基础C060502多基因遗传病的遗传基础C060503线粒体与疾病C060504染色体异常与疾病C060505肿瘤遗传C060506遗传病模型C0606基因组学C060601基因组结构与分析C060602比较基因组与进化C060603基因组信息学C0607基因表达调控与表观遗传学C060701组蛋白修饰及意义C060702DNA修饰及意义C060703染色体重塑及意义C060704非编码RNA调控与功能C060705转录与调控C0608生物信息学C060801生物数据分析C060802生物信息算法及工具C060803生物信息挖掘C060804生物系统网络模型C0609遗传学研究新方法C0610发育生物学C061001性器官与性细胞发育C061002精卵识别与受精C061003胚胎早期发育C061004组织、器官的形成与发育C061005组织、器官的维持与再生C061006细胞的分化与发育C061007核质互作与重编程C061008干细胞及定向分化基础C061009模式生物与发育C061010发育研究新方法与体系C07细胞生物学C0701细胞、亚细胞结构与功能C0702细胞生长与分裂C0703细胞周期与调控C0704细胞增殖与分化C0705细胞衰老C0706细胞死亡C0707细胞运动C0708细胞外基质。
数学专业的数学科研项目

数学专业的数学科研项目数学科研项目是数学专业学生展示他们在数学领域研究的机会。
这些项目旨在提供给学生一个深入研究数学的平台,培养他们的研究能力和解决问题的能力。
下面我们将介绍数学专业的数学科研项目,并探讨其重要性和益处。
一、数学科研项目的定义和目的数学科研项目是为数学专业的学生提供的一个研究数学的机会。
通过这些项目,学生将深入了解数学的原理和应用,并开展独立的研究工作。
这些科研项目的目的是培养学生的研究和创新能力,帮助他们将理论与实践相结合,提升他们的数学水平和综合素质。
二、数学科研项目的类型数学科研项目的类型多种多样,包括但不限于以下几个方面:1. 纯数学研究项目:这类项目主要关注数学的理论探索和证明,如数论、代数、几何等领域的研究。
学生可以选择一个感兴趣的数学问题进行深入研究,并对其进行证明和解答。
2. 应用数学研究项目:这类项目将数学理论应用于实际问题的解决中。
学生可以选择一个具体的应用领域,如物理学、经济学、计算机科学等,通过数学模型和方法解决相关问题。
3. 数学建模项目:这类项目要求学生在给定的问题下,使用数学建模的方法,构建相应的模型并进行分析。
学生需要在规定的时间内给出解决问题的方案,并对模型的可行性进行评估。
三、数学科研项目的重要性数学科研项目对数学专业学生的学术发展和职业发展都具有重要的意义。
以下是数学科研项目的几个重要方面:1. 提升研究能力:数学科研项目要求学生独立进行研究工作,培养他们的科学研究思维和方法。
通过科研项目,学生将学会提出问题、搜集资料、分析数据、得出结论等一系列研究过程。
2. 培养解决问题的能力:数学科研项目要求学生在实践中将理论应用于实际问题的解决中。
这需要学生具备解决问题的能力,培养他们的创新思维和解决实际问题的能力。
3. 提高学术水平:通过数学科研项目,学生将会深入了解数学的理论和应用,提高自己的数学水平。
同时,学生还可以与导师和同学们进行讨论和交流,拓宽自己的学术视野。
数学学院科研基金项目一览表四川大学数学学院
张伟年
20
3
Deligene-Mumford模空间的拓扑和二维orbifold的弦理论研究
国家自然科学基金
05-07
郑泉
10
省部级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
4
分布式数字图书馆信息快速处理及应用
省攻关项目
05-06
冯民富
10
5
多源信息融合中某些基本问题研究
四川省科技厅
四川大学青年科学基金
H02001022
01-02பைடு நூலகம்
洪绍方
1
22
非牛顿流和牛顿流动问题的无loc
四川大学青年科学基金
H02001023
01-02
穆君
1
2000年
重点项目(国家和省部级):
序号
项目名称
任务来源
编号
起止年月
负责人或
高级人员
总经费
(万)
1
模糊性数学问题的若干研究
教育部
科技司教技00109
00-02
经济模型中数据不确定性分析的比较研究
自然科学科学基金
2001-2002
李竹渝
2
19
迭代函数方程理论及应用
国家自然科学基金
2001
张伟年
0.7
市校级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
20
非光滑优化算法构造与分析
四川大学青年科学基金
H02001021
01-02
谭英谊
1
21
应用数学学科优势

数学与应用数学数学与应用数学专业是三峡大学各专业中历史最悠久的专业之一,经历了宜昌师范专科学校、湖北三峡学院和三峡大学三个发展阶段。
早在1958年宜昌师范专科学校成立之初,就设有数学科,后改为数学系。
1962年专科停办,改办中师。
1975年又恢复高师招生。
1978年4月,经国务院批准,恢复宜昌师范专科学校。
1993年6月,更名为宜昌师范高等专科学校。
专科阶段的数学专业在国内同类学校享有较高声誉,为社会培养了大量优秀的中学数学教师。
1995年3月经国家教委批准,与宜昌医学高等专科学校、宜昌市职业大学合并,组建湖北三峡学院,同年开始招收本科生。
1998年,根据当时国家教委公布的新的本科专业目录,数学教育专业改称“数学与应用数学(师范类)专业”。
2000年6月,湖北三峡学院与武汉水利电力大学(宜昌校区)合并,组建三峡大学。
数学系成为理学院下属的一个系,数学与应用数学(师范类)专业,改变为“数学与应用数学专业”,结束了数学系只有师范教育的历史,得到快速发展。
2001年,应用数学被列为学校重点学科。
2003年获得应用数学硕士学位授予权,并于2004年启动了硕士研究生教育,至今已招收三届硕士研究生。
2005年运筹学与控制论硕士点通过了省学位办的立项建设(鄂学位[2006]13号)。
该专业经过近半个世纪的发展,规模和实力不断壮大,教学水平和科研水平有了大幅度提高,逐步形成了自己的专业优势与办学特色,为国家输送了大量的优秀人才,在湖北省属大学的同类专业内具有一定知名度。
由于本专业有比较突出的成绩,2005年8月被列为三峡大学品牌专业立项建设项目(三峡大教[2005]第20号),2006年,应用数学被批准为省级重点学科(鄂学位[2006]13号)。
(一)教师队伍建设1、专业教师基本情况(1)职称结构:数学与应用数学专业现有教师47人。
其中教授15人,占教师总人数的22.5%;副教授20人,占教师总人数的42.5%;讲师8人,占教师总人数的17.04%,助教7人,占教师总人数的14.89%;高级职称教师占教师总人数的66.6%。
国家自然科学基金 数学 方向

国家自然科学基金是我国科技工作者最为熟悉的一项科研基金,它是由国家自然科学基金委员会负责管理的,旨在支持我国基础科学研究的一项重要资助计划。
在各个学科领域中,都能找到国家自然科学基金的身影,而在数学领域中,国家自然科学基金同样扮演了重要的角色。
让我们来了解一下国家自然科学基金在数学领域中的具体情况。
国家自然科学基金在数学领域,主要资助的是基础数学、概率统计与运筹学、计算数学、应用数学等多个方向的研究项目。
无论是在纯粹的数学理论研究,还是在数学与其他学科的交叉研究中,国家自然科学基金都在为数学领域的发展提供资金支持。
国家自然科学基金对数学领域的资助具有重要意义。
它能够促进我国数学领域的基础研究。
在国家自然科学基金的支持下,大量优秀的数学研究项目得以展开,从而推动了我国数学领域的发展。
国家自然科学基金的资助也有助于促进我国数学与其他学科的交叉研究。
在复杂的现实问题中,数学往往需要与其他学科相结合,国家自然科学基金的资助能够为这种交叉研究提供有力支持。
我个人对国家自然科学基金在数学领域的支持持肯定态度。
作为一项基础科学研究的资助项目,国家自然科学基金为数学领域的发展提供了重要的支持和保障。
我希望未来国家自然科学基金能够继续加大对数学领域的资助力度,推动我国数学科学的蓬勃发展。
在国家自然科学基金的资助下,我国数学领域的基础研究得到了长足发展,同时也为数学与其他学科的交叉研究提供了重要支持。
国家自然科学基金对数学领域的资助意义重大,相信在未来的日子里,国家自然科学基金会继续为我国数学发展做出更大的贡献。
国家自然科学基金是我国科技工作者最为熟悉的一项科研基金,它是由国家自然科学基金委员会负责管理的,旨在支持我国基础科学研究的一项重要资助计划。
在各个学科领域中,都能找到国家自然科学基金的身影,而在数学领域中,国家自然科学基金同样扮演了重要的角色。
国家自然科学基金在数学领域,主要资助的是基础数学、概率统计与运筹学、计算数学、应用数学等多个方向的研究项目。
我国大学内部二级学院治理研究综述及展望

第1期2021年3月中国人民大学教育学刊Renmin University of China Education JournalNo.lMar.2021我国大学内部二级学院治理研究综述及展望吴瑾(中国人民大学科研处,北京1〇〇872)摘要:党的十九届四中全会将国家治理体系和治理能力现代化建设提到了新的高度。
在高等教育领域,二级学院作为大学的基本组成,是以基层治理传导中层大学治理、进一步建立现代大学制度、实现教育领域治理现代化的治理原点。
伴随我国大学治理完善,二级学院治理从理论和实践层面都在不断深化。
为全面客观把握研究现状,本文以CSSC丨期刊论文为分析样本,对我国学院治理相关研究进行梳理,进而探讨未来研究重点方向,以期为二级学院理论研究和治理实践提供参考借鉴。
关键词:学院治理;研究综述;展望中图分类号:G647文献标识号:A文章编号:2095-1760(2021)0丨-0085-15一、文献数据来源与研究方法(一)数据选择本文以中国知网一中国期刊全文数据库(CNKI)为文献数据基础来源,在“高等教育”领域以“学院治理”和“院系治理”为篇名关键词精确筛选 CSSCI和核心期刊,去除掉会议新闻稿、论坛摘要以及论点摘编等非学术论 文以及高职院校和智库治理等与主题无关论文,截止到2019年年底共获得 121篇论文样本。
(二)方法路径为了综合对已有文献经验性回顾和总结,本文首先运用文献计量的方 法技术,对当前研究的论文数量、关键词、研究主题分布、主要作者及发文机 构、受各级各类科研基金资助情况、主要发表刊物以及论文被引用等论文基收稿日期:2020-12-10作者简介:吴瑾,女,中B人民大学科研处、中国人民大学公共管理学院博十研究生。
86中国人民大学教育学刊2021 年本面进行分析,形成对该研究领域的总体呈现。
在此基础上,再通过对文献 内容的综合研究,评述当前主要关注焦点,总结不足并探寻未来研究的主要 方向。
国家自然科学基金项目大数据分析课件

2016年国家自然科学基金项目大数据分析2016年的国家自然科学基金项目评审结果已经出炉。
科学网在已有结果的基础上,结合历史数据,对基金在不同空间尺度的分布情况进行全面考察,多角度探索科学基金分布特征。
(一)按项目类别统计2015-2016年项目数量变化趋势根据国家自然科学基金委8月17日通告显示,共接收项目申请172843项,经初步审查受理169832项,决定资助其中的37409项,约占总数的22%。
和2015年相比,增加202项。
由表可见,一方面,国家正加大力度提升较不发达地区科研机构完成项目的能力和动力,因此增加了地区科学基金项目的数量;另一方面,国家对青年科学项目的水平和要求已经提高.结合历史数据,基金总项数和基金总金额依然呈正相关。
地区科研基金项目多分布在甘肃、广西、贵州、广西、云南等地区,其原因来自制度保护;其他种类基金都分布在高等院校和科研单位比较多的地区,比如北京、上海、广东等经济较发达的城市。
图1 省市项目金额分配(单位:万元)如图1所示,北京市科研机构所获项目资金近38亿元,约占项目金额总数的20.8%,超过末尾18个省市区之和。
分得项目资金10亿元以上的有北京、上海、江苏和广东,总数为86亿余元,约占总额的47。
25%。
(二)大数据分类统计1.单项之最本年度自然科学基金项目单项资助最多的数额是3500万元,该项目研究方向为地球科学,被国家海洋局第一海洋研究所揽。
另外,单项资助1000万元以上的项目37项,总金额42593万元,详情见表2。
表2 单项资助金额1000万以上项目统计表2.数额之最2016年的受自然科学基金资助最多的单位依然是上海交通大学,总项目数901项,单项资助金额从4万元到1050万元不等,平均56。
32万元。
表3按学部对其项目进行分类,可见上海交大在医学科学领域拥有较大优势.3.地区之最从表4中单一机构获得千万元以上资助的地区分类来看,排在前五位的仍旧是北京、江苏、上海、广东、湖北,与总体数据流一致。
四川大学数学学院专业课程介绍范文
in,Functional Analysis,McGraw_Hill Book Company,1973:空间,Banach空间,Hilbert空间(包括有界,紧集,列紧集,完全有界集等)。
Ban 性算子(包括算子范数,有界性,连续性,Hahn-Banach定理,闭图象定理,逆算子定算子Riesz-Schauder理论等)Hilbert空间上的有界线性算子(射影定理、Riesz表示课程名:概率统计名Probability Statistics学分:4:数学分析、线性代数:考试:数学学院各专业概率论基础》(第二版)李贤平高等教育出版社 19971.《概率论》(第一册概率论基础)复旦大学高等教育出版社,1979。
2.《概率论引论》汪仁官北京大学出版社 19943.《概率论及数理统计》(第二版)(上)高等教育出版社 1988:率,条件概率与统计独立性,随机变量与分布函数,数字特征与特征函数,极限定理。
课程名:高等代数-1名:Advanced Algebra-12 学分:5:高中数学:考试:数学数院各专业Linear Algebra》彭国华、李德琅,高等教育出版社,20061。
《高等代数》北京大学数学系几何代数教研空编高等教育出版社2.《高等代数》张禾瑞、郝锅新高等教育出版社3.《Linear Slgebra》B。
Jacob W.H.Freeman Company 1990:高等代数以研究线性方程组为出发点来讨论求解和解的结构和分类等问题,进而研究矩空间,线性映射以及二次型的基本理论。
本课程分两个学期讲授。
高等代数-1的主要和线性映射,线性变换,欧氏空间,线性和双线性型。
课程名:高等代数-2名:Advanced Algebra-22 学分:5:高等代数-1:考试:数学学院各专业Linear Algebra》彭国华、李德琅,高等教育出版社,20061.《高等代数》北京大学数学系几何代数教研空编高等教育出版社2. L.W. Johnson, R.D. Riess J.T. Arnold, Introduction to Linear Algebr , Prentice-Hall Inc. China Machine Press, 2002Lay, Linear Algebra Its Applications (3rd Edition), Pearson Addison Wesley blishing House of Electronics Industry,2003:元多项式、行列式、线性方程组,矩阵代数,二次型,线性空间,线性变换,矩阵法式课程名:解析几何名:Analytic Geometry学分:5:高中数学:考试:数学学院各专业解析几何》廖华奎、王宝富编,科学出版社1.《解析几何》丘维声北京大学出版社。
国家自然基金优秀青年基金项目各个学部

国家自然基金优秀青年基金项目各个学部国家自然基金优秀青年基金项目,是对具备一定科研能力和潜力的青年科研人员的资助,旨在支持他们独立开展科学研究,促进科学技术的进步和创新。
该项目涵盖了各个学部,下面将分别介绍各个学部的项目情况。
在数学学部,国家自然基金优秀青年基金项目主要支持数学基础理论的研究和应用数学的发展。
这些项目包括但不限于纯数学、应用数学、数学教学等方向。
青年学者可以利用该项目的资金开展数学领域的前沿研究,推动数学学科的发展。
在物理学学部,国家自然基金优秀青年基金项目主要资助物理学领域的研究,包括理论物理、实验物理以及物理学在其他学科的应用。
这些项目旨在培养优秀青年科学家,推动物理学的科研创新和发展。
在化学学部,国家自然基金优秀青年基金项目主要资助化学领域的研究,包括有机化学、无机化学、物理化学、生物化学等方向。
这些项目旨在提升青年化学科学家的科研能力,推动化学学科的发展和创新。
科学的研究,包括生物学、生物医学、生物技术等方向。
这些项目旨在支持青年科学家独立开展生命科学研究,促进生命科学的发展和进步。
在地球科学学部,国家自然基金优秀青年基金项目主要资助地球科学领域的研究,包括地质学、地理学、大气科学、海洋科学等方向。
这些项目旨在培养具有扎实地球科学理论和实践能力的青年科学家,推动地球科学的发展和研究。
在信息科学学部,国家自然基金优秀青年基金项目主要资助信息科学与技术领域的研究,包括计算机科学与技术、电子科学与技术、通信与信息系统等方向。
这些项目旨在培养青年科学家在信息领域的研究和创新能力,推动信息科学与技术的发展和进步。
在管理科学与工程学部,国家自然基金优秀青年基金项目主要资助管理科学与工程领域的研究,包括管理学、工程管理、决策科学与工程等方向。
这些项目旨在培养具有良好管理科学与工程理论和实践能力的青年科学家,推动管理科学与工程的发展和应用。
助控制科学与工程领域的研究,包括控制理论与控制工程、系统科学与工程等方向。
四川大学引进人才科研启动经费资助项目

四川大学引进人才科研启动经费资助项目
(中期报告)
结题报告
项目编号:
项目名称:
项目负责人:
所在单位:
资助金额:
起止年月:
填报日期:
四川大学人事处
二〇一〇年二月制表
填表说明
一、本表填写内容必须与事实相符,表达准确,字迹清晰,不得漏项,数字一律填写阿拉伯字。
二、填入表中的各项内容或数据,必须是四川大学引进人才科研启动经费资助期间所取得的结果。
三、填表前,请仔细阅读《四川大学引进人才科研启动经费管理办法》。
四、“主要论著发表情况”中的“期刊级别”,SCI论文按照《四川大学SCI期刊分级方案》(2008年4月讨论稿)的规定填写,哲学社科类文章按照《四川大学哲学社会科学期刊分级方案》(川大社[2009]3号)的规定填写。
填表前,请先阅读《填表说明》
主要成果鉴定及获奖情况
主要论著发表情况
经费使用统计
工作总结。
2023年度国家自然科学基金项目数学

《2023年度国家自然科学基金项目数学》一、前言2023年度国家自然科学基金项目数学,作为科学研究领域的一部分,扮演着重要的角色。
在这篇文章中,我们将深入探讨这一主题,从不同的角度进行全面评估,旨在为读者提供有价值的信息和深刻的理解。
二、概述数学作为一门基础科学,是整个自然科学体系中不可或缺的一部分。
2023年度国家自然科学基金项目数学,将涉及哪些领域和具体的研究内容?这是我们需要探讨的第一个问题。
在数学的广度上,我们将对微分方程、概率论与统计学、数学分析等方面进行全面评估。
我们还将深入了解数学在生物学、物理学、工程学等跨学科领域中的应用,以及数学理论与应用研究的最新进展和关键技术。
三、具体分析1. 微分方程微分方程作为数学的一个重要分支,广泛应用于物理学、化学、生物学等领域。
在2023年度国家自然科学基金项目数学中,微分方程领域的研究将集中在哪些方面?对于非线性微分方程的稳定性和解的存在性问题、微分方程在动力系统中的应用等方面的研究,都将是研究人员关注的重点。
2. 概率论与统计学概率论与统计学作为数学中的重要分支,在2023年度国家自然科学基金项目数学中也将有着重要的地位。
在这一领域,研究人员将关注概率论与统计学在大数据分析、人工智能等领域中的应用,以及概率论与统计学理论的深入研究和发展。
3. 数学分析数学分析是数学的基础,也是其他数学分支如微积分、实分析、复分析等的基础。
在2023年度国家自然科学基金项目数学中,数学分析的研究将主要涉及到哪些方面?对于实变函数、泛函分析、复变函数等方面的研究,以及数学分析在其他学科中的应用等问题。
四、总结与回顾通过对2023年度国家自然科学基金项目数学的全面评估,我们能够更深入地理解数学在科学研究中的重要作用。
数学不仅是一门独立的学科,更是其他学科的基础和工具。
在未来的研究中,我们需要更加注重数学的交叉学科应用,促进不同学科之间的合作与交流,共同推动科学研究的进步和发展。
数学专业的科研项目与资助政策

数学专业的科研项目与资助政策数学是一门博大精深的学科,其研究领域涵盖了许多不同的分支和应用。
作为一名数学专业的研究人员,进行科研项目需要一定的经费和支持。
本文将探讨数学专业的科研项目以及相关的资助政策。
一、科研项目的重要性科研项目对于数学专业的发展至关重要。
通过开展科研项目,研究人员能够深入探索数学领域的问题,并为学科的进一步发展做出贡献。
科研项目还能够促进学者之间的交流与合作,提高研究成果的质量和影响力。
二、科研项目的种类数学专业的科研项目涵盖了各个领域和方向。
常见的科研项目包括基础研究、应用研究和交叉学科研究等。
基础研究主要关注数学理论的推进和证明,探索数学的本质和机理。
应用研究则将数学理论与实际问题相结合,为其他学科或工程领域提供解决方案。
交叉学科研究则将数学与其他学科融合,如数学与计算机科学、数学与物理学等。
三、科研项目的资助政策为了支持数学专业的科研项目,许多机构和组织提供了各种资助政策。
这些资助政策旨在鼓励和支持优秀的科研人员和项目,促进学科的发展。
常见的资助机构包括国家自然科学基金委员会、各地科技部门和学术机构等。
资助政策通常分为项目经费和科研人员的个人资助两个方面。
项目经费主要用于购买实验设备、图书资料、实验室场地等,以支持科研项目的进行。
科研人员的个人资助则包括奖学金、津贴和职称评定等,以激励和保障研究人员的积极性和创造力。
四、资助申请和评审流程申请科研项目的资助通常需要经过一系列的程序和评审过程。
首先,研究人员需要提交项目申请书,详细描述研究内容、预期成果和经费需求等。
然后,申请书会被送至相关机构进行评审。
评审过程通常包括学术评审和经费评审等,以确保项目的科学性、可行性和合理性。
最终,经过评审通过的项目将获得资助,并开始进行科研工作。
五、科研项目的成果与影响科研项目的成果对于学术界和社会的影响不可忽视。
通过科研项目,数学专业的研究人员可以取得新的发现、建立新的理论和解决实际问题。
(项目管理)数学学院科研基金项目一览表四川大学数学学院

(项目管理)数学学院科研基金项目一览表四川大学数学学院数学学院科研基金项目一览表2007年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,弦理论中的几何不变量,国家自然科学基金,,07.1-0.9.12,李安民,130国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,多体问题德的变分方法,国家自然科学基金,,07.1-09.12,张世清,213,非凸和鲁棒向量优化的理论与算法研究,国家自然科学基金,,07.1-09.12,黄南京,244,具有时滞的随机脉冲系统的定性分析,国家自然科学基金,,07.1-09.12,徐道义,255,并行解边界元和有限元的区域分解法与分界外推法,国家自然科学基金,,07.1-09.12,吕涛,246,连续统基数不变量研究,国家自然科学基金,,07.1-09.12,张树果,217,代学曲面上的零圈的模空间,国家数学天元青年基金,,07.1-07.12,李挺,32006年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,分布参数系统的控制理论,国家杰出青年基金,,2006-2009,张旭,70国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,随机动力系统混沌控制与参数估计的稳健性及其在弱信号检测中的作用,国家自然科学基金,,2006-2008,马洪,243,非线性发展方程解的有界性与渐近行为等问题,国家自然科学基金,,2006-2008,穆春来,154,算子半群和李群上的微分算子,国家自然科学基金,,2006-2008,李淼,155,传感器网络中信息压缩与融合理论及算法研究,国家自然科学基金,,2006-2008,周杰,226,仿射流形上的分析,国家自然科学基金,,2006-2008,贾方,157,西部教师培训,国家自然科学基金(天元,,2006.1-12,刘应明,20省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)8,,新世纪优秀人才支持计划,NCET-06-0778,2006-2008,穆春来,509,, 新世纪优秀人才支持计划,NCET-06-0779,2006-2008,张德学,50市校级:序号,项目名称,任务来源,编号,起止,负责人,总经费(万)11,高性能低阶四边形杂交/混合版..壳研究,校青年基金,,2006-2007,罗鲲,212,非线性抛物型方程的区域分解算法,校青年基金,,2006-2007,潘璐,113,我国能源市场化的若干技术问题,成都市科技计划项目,,2006-2008,牛健人,32005年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,动力系统,国家杰出青年科学基金,10428104,05-07,吕克宁,40国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,高阶退化系统的分岔及与不变流形有关的迭代方程,国家自然科学基金,,05-07,张伟年,203,Deligene-Mumford模空间的拓扑和二维orbifold的弦理论研究,国家自然科学基金,,05-07,郑泉,10省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)4,分布式数字图书馆信息快速处理及应用,省攻关项目,,05-06,冯民富,105,多源信息融合中某些基本问题研究,四川省科技厅,,05-07,周杰,36,集值投影动力系统,四川省科技厅,,05-07,黄南京,27,动力系统分岔理论与不变流形,回国启动基金,,2005,杜正东,28,,新世纪人才支持计划,,05-07,张旭,509,素数判定的AKS算法及其改进算法的研究,国防重点实验室,,05-07,孙琦.朱文余.魏齐娇.曹伟,15 10,基于信息融合的超宽带扩频通信信号检测技术研究,教育部博士点基金2,No.20040610004,,2005.1-2007.12,马洪, 6万国际合作:序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费11,非线性变分不等式的理论与算法研究,,,2005-2006,黄南京、方亚平、邓传现、唐亚勇,市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)12,Orbifold的弦理论,校青年基金,200457,2005,陈柏辉,1.513,多源信息融合中的迭代算法及其收斂性分析,校青年基金,200458,2005,何腊梅,114,模糊拓扑空间上的迭代问题,校青年基金,200459,2005,陈丽,115,不确定性条件下的企业预警研究,校科技创新基金,2005cf06,05-07,罗懋康,10.002004年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,环论,国家杰出青年基金,10325107,04-07,彭联刚,70.002,多传感器数据融合问题,国家杰出青年基金(B类),,04-07,李小榕朱允民,40.003,序拓扑及形式语义学的数学基础,国家自然科学基金重点项目,,04-08,罗懋康(负责人)梁基华,80.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)4,多传感器不确定信息决策与估计融合理论与算法,国家自然科学基金,,04-06,朱允民,23.00 5,随机微分差分方程的定性分析,国家自然科学基金,,04-06,徐道义,18.006,区域与流形上的算子与算子代数,国家自然科学基金,,04-06,曹广福,16.007,某些分布参数系统的能控性和长时间行为,国家自然科学基金,,04-06,张旭,16.008,伪概周期性与Banach空间中的微分方程,国家自然科学基金,,04-06,李洪旭,99,扩大仿射李代数及其量子代数,国家自然科学基金,,04-06,谭友军,9省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)10,具有非交换符号代数的Toeplitz代数,教育部博士点基金,,04-06,曹广福,511,基于信息融合的超宽带扩频通信信号检测技术研究,教育部博士点基金,20040610004,04-06,马洪,612,椭圆曲线密码体制中Satoh算法的改进和实现,国防科技重点实验室基金,,04-06,彭国华,15.0013,复杂山地近地表结构模型层次反演方法,省石油管理局,,04-06,冯民富,75市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)13,黎曼面模空间上的对称群作用,校青年基金,200313,2004-2006,陈浩,114,常微分方程分岔理论及平面多项式系统定性理论研究,校青年基金,200314,2004-2006,杜正东,115,迭代方程解的解析性与凹凸性问题,校青年基金,200315,2004-2006,徐冰,12003年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,面向复杂系统实时智能控制与优化的模糊性数学基础研究(973项目“复杂生产制造过程实时、智能控制与优化理论和方法研究”的子课题),科技部973计划,2002CB312206,03-06,刘应明(负责人)李中夫张德学寇辉,300.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,拓扑学中的序代数结构及其在理论计算机科学中的应用,国家自然科学基金,A210201023,03-05,寇辉,9.503,关于非线性发展方程解的一些问题,国家自然科学基金,A210201024,03-05,穆春来,9.504,N-S流动高性能有限元方法研究,国家自然科学基金,A210201025,03-05,谢小平,9.505,分数阶微分方程及模型分数化,国家自然科学基金,A210226030,03-05,李淼,2.506,导出范畴与量子toroidel代数,国家自然科学基金,A210226027,03-05,谭友军,2.507,整体微分几何,国家自然科学基金,A210271083,03-05,赵国松,16省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)8,拓朴与Domain理论的若干问题研究,教育部博士点基金,B120020610057,03-05,梁基华,59,格上拓朴学中的范畴拓朴问题,优秀青年教师资助计划,,,张德学,810,,留学回国人员启动基金,,,张旭,3.0011,微分动力系统,教育部高校青年教师奖,B52003693,03-07,张伟年,5012,中心及退化奇点分岔与不变流形问题,教育部博士点基金,B120020610003,03-05,张伟年,513,多传感器不确定性息决策与估计融合理论与算法,教育部博士点基金,20030610018,03-05,朱允民,5 14,具有非交换符号代数Toeplitz,教育部博士点基金,20030610019,03-05,曹广福,515,Domian理论与格上拓扑学,教育部博士点基金,20030610020,03-05,刘应明,5市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)16,延迟报告数据分析,四川大学青年科学基金,H02003064,03-04,林华珍,0.817,模糊聚合算子研究,四川大学青年科学基金,H02003065,03-04,胡世凯,0.818,仿射李代数的若干问题,四川大学青年科学基金,H02003066,03-04,谭友军,0.819,Bnach空间重的伪概周期微分,四川大学青年科学基金,H02003067,03-04,李洪旭,0.82002年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,有限域上的代数簇的L函数,国家杰出青年基金,A210128103,02-04,万大庆孙琦,402,Domain理论与格上拓扑学,国家杰出青年基金,A210125104,02-06,罗懋康,803,分部参数系统H∞控制理论,教育部优秀博士论文项目,,02-06,张旭,40省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)4,并行解有限元、边界元分裂法与分裂外推法,教育部博士点基金,B120010610005,02-04,吕涛,4 5,基数不变量与极分拆关系研究,教育部优秀青年教师资助计划,B420024003,02-04,张树果,4.006,不分明拓扑空间的范畴论性质,霍英东教育基金会研究基金,B7H200101,02-04,张德学,1.40万美圆7,核截面、吸引子及临界分支曲面,留学回国人员科研启动基金,B2200134510,02-04,周盛凡,2.08,中心及退化奇点分岔与不变流行,博士点基金,20020610001,02-04,张伟年,6 9,拓扑与Domain理论的若干问题,博士点基金,20020610057,02-04,梁基华,510,多体问题,跨世纪人才,,02-04,张世清,2011,严重信道条件客观音质评价信号同步及相关技术研究,十五国防科技预研基金,,02-03,马洪,7市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)12,半群理论及其在控制论中的应用,四川大学青年科学基金,H002067,02-03,顾晓慧,113,模糊推理研究,四川大学青年科学基金,H002065,02-03,黄丽,114,非线性滤波理论及其在信号处理中的应用,四川大学青年科学基金,02066,02-03,周杰,12001年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,数理逻辑及其应用,国家自然科学基金委,A219931020,01-03,张树果,12.42,教育部跨世纪人才培养基金,教育部,,01-03,彭联刚,30.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)3,Domain理论在拓扑学中的应用,国家自然科学基金,A2TY10126022,01-02,寇辉,2.004,高性能有限元方法研究,国家自然科学基金委(天元基金),A2TY10126027,01-02,谢小平,2.005,随机系统多传感器决策与估计融合理论与算法,国家自然科学基金委,A660074016,01-03,朱允民,16.00 6,从范畴拓扑观点看不分明拓扑与Domain理论,国家自然科学基金委,A210071053,01-03,张德学,9.00 7,抽象微分方程理论中的若干问题,国家自然科学基金委,,01-03,黄发伦,11.508,经济、金融模型决策分析中数据不确定性的非参数统计推断,国家社科基金,01BTJ003,01-05,李竹渝,5.2省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)9,DOMAIN理论与拓扑学,教育部博士点基金,B12000061019,01-03,刘应明,610,不分明拓扑中的反射与余反射子范畴,四川省青年科技基金,,01-03,张德学,811,极分拆关系及基数不变量研究,留学回国人员科研启动基金,B2200036707,01-03,张树果,4.0012,非线性分析中某些问题的研究,留学回国人员科研启动基金,B2200047904,01-03,黄南京,3.513,非线性分析中的一些问题,留学回国人员科研启动基金,B2200047905,01-03,陈玉清,514,,留学回国人员启动基金,,,周盛凡,2.0015,模糊性数学问题的若干研究,教育部重点项目,B300109,01-03,刘应明,10国际合作:序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)18,经济模型中数据不确定性分析的比较研究,自然科学科学基金,7010100005,2001-2002,李竹渝,219,迭代函数方程理论及应用,国家自然科学基金,19871058,2001,张伟年,0.7市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)20,非光滑优化算法构造与分析,四川大学青年科学基金,H02001021,01-02,谭英谊,121,关于整数矩阵的研究,四川大学青年科学基金,H02001022,01-02,洪绍方,122,非牛顿流和牛顿流动问题的无loc,四川大学青年科学基金,H02001023,01-02,穆君,12000年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,模糊性数学问题的若干研究,教育部,科技司教技00109,00-02,刘应明,10.00国家基金:省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,理论计算、算法与相关数学问题研究,教育部高校骨干教师资助计划,,00-02,罗懋康,24.003,基础数学的若干问题,教育部高校骨干教师基金(长江教授配套计划),,00-04,梁基华赵国松彭联刚曹广福郑泉,30.004,不可压缩流体的几何与拓扑理论,留学回国人员科研启动基金,B2199936301,00-02,马天,3.00 7,理论计算、算法与相关数学问题研究,高等学校骨干教师资助计划,B820006503,00-02,罗懋康,12 8,基础数学若干前沿问题的研究,高等学校骨干教师资助计划,B820006528,00-02,李安民,309,Domain理论与拓扑学,博士点基金,2000061019,00-02,刘应明,410,公钥密码体制中一些前沿问题的研究,国防科技(重点实验室项目),,00-02,孙琦,15.001999年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)1,格上拓与非经典数理逻辑,国家基金(重点),19831030,99.1-01.12,刘应明,68.002,非线性泛函微分方程的理论及应用,国家基金(重点),19831030,99.1-03.12,徐道义,10.003,迭代方程与动力系统不变性,国家基金(重点),19871058,99.1-01.12,张伟年,8.504,微分几何,国家杰出青年基金B类,19825506,99-01,阮勇斌李安民,30.005,跨世纪优秀人才培养基金,教育部,教技(1998)1号1998JW024,99-0198-01(7),罗懋康,15.0010.00(7)6,核心数学的前沿问题,科技部973计划,G1999075100,99-04,彭联刚,20.007,核心数学的前沿问题,科技部973计划,G1999075100,99-04,李安民,20.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)8,迭代方程与动力系统不变性,国家自然科学基金委,19871058,99-01,张伟年,8.509,格上拓扑与非经典数理逻辑,国家自然科学基金委,198310401999JZ004,99-03,刘应明(负责人)李中夫罗懋康梁基华,68.0010,非线性泛函微分方程的理论及应用,国家自然科学基金委,19831030 1999JZ003,99-03,徐道义,12.00省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)11,法式代数与多参数仿射李代数,教育部博士点基金,19990611999JZ010(7),99-01,彭联刚,4.0012,微分子方程的不变流形及其相交性导致的复杂现象,教育部优秀年轻教师基金,优轻基金教人司1999JW020(7),99-01,张伟年,6.0013,不可压缩流体的几何与拓扑理论,教育部回国基金,教外司留1999JW025(7),99-01,马天,3.0014,关于非线性抛物方程(组)解的几类问题,教育部回国基金,教外司留1999JW026(7),99-01,穆春来,1.5015,非线性抛物方程(组)解的整体存在性和爆破,教育部优秀年轻教师基金,(99年度)优轻基金人司,99-02,穆春来,7.00国际合作:序号,项目名称,任务来源,编号,起止年月,负责人,总经费16,欧盟成员国不同政策对经济研究的影响,欧盟,4040060/99,1999-2000,李竹渝,0.3万欧元市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)17,线丛上的Morse理论与量上上同调,基础研究博士启动基金,1999JX001,1999-2002,李福波,0.50 18,Domain范畴的拓扑结构与Cartesian闭性,基础研究博士启动基金,1999JX002,1999-2002,寇辉,0.50 19,气水单井数值模拟方法的研究,校青年基金,1999JX003,99-00,朱瑞,0.5020,算子半群理论及其应用,校青年基金,1999JX004,99-00,李淼,0.50其他项目:序号,项目名称,任务来源,编号,起止年,负责人,总经费(万)21,迭代映射及方程的动力学,省人事厅,1999JS063,99-00,张伟年,1.5022,格上拓扑,省人事厅,1999JS064,99-00,罗懋康,2.0023,Domain理论与拓扑的几个问题,省人事厅,1999JS065,99-00,梁基华,2.0024,法式李代数,省人事厅,1999JS066,99-00,彭联刚,2.001998年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,新一代空中交通管制系统中关键技术的研究,国家自然科学基金委,,98-01,朱允民马洪,902,复杂系统控制的基础理论研究,攀登计划项目,,98-01,朱允民,国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)3,集值分析中某些问题的理论,算法及应用的研究,国家科学基金,J98047,98-00,张石生,6.004,泛函数分系统的动态行为与控制,国家科学基金,J98048,98-00,徐道义,5.505,丢失数据回归分析的若干问题,国家科学基金,J98051,98-00,秦更生,3.406,多传感器分布统计判决,国家基金,1998JZ005J98023,98.1,朱允民,省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)7,整体微分几何,教育部博士点基金,98061004,98-00,李安民,4.508,数论在数字信号处理号处理中的应用,教育部博士点基金,98061006,98-00,孙琦,4.509,格上拓朴学中的范畴论方法,教育部回国人员基金,(1998)679,98-20,张德学,2.010,国家教委跨世纪优秀人才基金,国家教委科技(1998)1号,59,98—01,罗懋康,10国际合作:序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费11,算子理论与算子代数,基金国际合作,J98019-(4),98-,孙顺华,0.30市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)12,稳定性的机器证明,校青年基金,65,98-20,陆征一,1.0013,Toeplitz代数的结构,校青年基金,61,98-20,严从荃,1.0014,辛拓扑及Seiberg-Witten理论的应用,基础研究,62,98-20,郑泉,1.0015,离散分形几何的研究,基础研究,63,98-20,龙伦海,1.0016,流动问题的数值方法研究,基础研究,64,98-20,谢小平,1.00其他项目:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)17,多传感器分布统计判决,国家自然科学基金委优秀成果出版基金,,98.1,朱允民,1997年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,代数数论,国家重点基金,J971001,97-2000,李德琅,6.0(3)10.0(2)2,整体微分几何及其物理应用,;国家重点基金,J971001(3)J98009(4),97-2000,李安民,6.0(4)10.00(2)3,算子理论与算子代数,国家重点基金,J971001(3),97-01,孙顺华,6.00(4)10.00(2)4,半连续函数空间的无限维拓朴学性质,国家基金(重点),J98056(4)J971003(3),97-99,张德学,3.205,随机系统的多传感器分布决策与估计,攀登计划,G98027,97-01,朱允民,2.006,与微分运算有关的机械问题,攀登计划,,97-01,陆征一,5.007,代数数论,国家重点基金,J98008,97-00,李德琅,6.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)8,模糊性理论中若干基本问题,国家科委,B97102A971002,97-99,刘应明,10.009,快速无损分析谷物种子内碳氮元素的新技术,国家科学基金,J971002,97-98,曹建华,11.0010,半边连续函数空间的无限维拓朴学性质,国家科学基金,J980561997JZ008(7),97-98,张德学,3.2011,连续统的基数特性研究,国家科学基金,J98057(4)J971003,97-98,张树果,4.0012,有限域上的方程和置换多项式,国家科学基金,J98058(4)J971005,97-99,孙琦,4.2013,随机信号检测与估计的多传感器数据融合问题,国家科学基金,J98059(4)J98061(4),97-99,朱允民,7.0014,模糊逻辑中语言值运算的研究,国家科学基金,J98080(4)J9710071997JZ046(7),97-99,李中夫,8.0015,多传感器数据融合的最优化精确解及相应的随机递推算法,国家基金,J9710011997JZ011(7),97-99,朱允民,4.5016,格上拓扑学与DOMAIN理论,教育部博士点基金,97061027,97-99,刘应明,3.5017,结合代数的表示及Kac-Moody李代数,教育部优秀年轻教师基金,B9710011997JW015,97-99,彭联刚,5.50国际合作:序号,项目名称,任务来源,编号,起止年月,负责人,总经费18,辛几何与辛拓扑,国家自然科学基金委国际合作,J971002,97-98,李安民,0.80市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)19,无穷维动系统,基础研究博士启动基金,1997JX014,97-98,周盛凡,1.0020,微分方程稳定性的机器证明,基础研究博士启动基金,X98016(4)1997JX016(7),97-98,陆征一,1.0021,函数空间上的ToepIitz算子与复合算子,基础研究博士启动基金,X98017(4)X971004(2),97-98,曹广福,1.0022,模糊推理系统中属函数的影响及其调整方法,校青年基金,X98001(4)X971001,97-98,汪海波,1.0023,带有撮动位势波动方程解的L估计,博士启动基金,X98015(4)X971003,97-98,穆春来,1.00其他项目:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)24,气水井测井分析方法研究,四川石油管理局(横向),H98036,97-98,熊华鑫,10.001996国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)1,点集拓扑若干新方向,国家自然科学基金委,J961006,1996.9-,刘应明,0.702,有限域上的不定方程和置换多项式,国家自然科学基金委,J961002,1996-,孙琦,0.403,多传感器数据融合的最优化精确解及相应的随即递推算法,国家科学基金,J98054,96-99,朱允民,4.50 4,非线性双曲型守恒律的张驰现象和德尔塔波Deta的研究,国家自然科学基金,19571057,96-98,李才中, 5,狄里克菜特征关于有理由数据的完整和应用,国家自然科学基金,J971002(3)J961006(5),96-98,刘春雷,3.006,子流形的几个问题的研究,国家自然科学基金,J971003(3)J961007(5),96-98,赵国松,6.507,删失数据回归分析的若干问题,国家自然科学基金,J971004(3)J961008(5),96-98,秦更生,3.40 8,代数表示论与李代数的有机联系,国家自然科学基金,J971006(3),96-98,彭联刚,5.509,无穷维动力系统有界解分技,国家自然科学基金,J971008(3),96-98,张伟年,5.00序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)10,无穷维动力系统及其计算机处理,博士后基金,J961002,96-97,,0.50国际合作序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费11,有限域上的不定方程和置换多项式,基金国际合作,J96I002,96-,孙琦,0.4012,点集拓扑若干新生方向,基金国际合作,J961006,96.9-,刘应明,0.7013,大基数及其相关问题,基金国际合作,J961005,96.6-,张树果,0.701995年国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)1,分布参数系统边界反债控制鲁棒稳定化问题,国家科学基金,J961001,95-97,黄发伦,2.002,夸克蜕定试,国家自然科学基金委,J961002,95-97,巫光汉,2.00省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)3,半参数模型和最小束乘理论及应用,教委回国人员基金,B97102(3)J961002(5)J98014(4),95-97,李竹渝,3.004,有界对称域上的Toplitzc-C代数, 教委博士点基金9561017,B97108(3)B98008(4)J961015(5),95-97,孙顺华,3.005,代数表示论与Kac-liodyLle代数及量子群,教委回国人员基金,J961002,95-96,彭联刚,3.00序号,项目名称,任务来源,编号,起止,负责人,总经费(万)6,三维流形的不变量,博士后基金,J961001(5)B97101(3)B98011(4),95-97,韩友发,0.5 7,变分不等式和相补问题的机动研究,校青年基金,X961013(5)X971002(3),95-96,黄南京,0.508,板壳问题的组合稳定化有限元方法及理论研究,校青年基金,X961014(5)X971002(3),95-96,胡兵,0.509,无穷维动力系统及其计算机处理,博士后基金,J961002(5)B98012(4),95-97,周盛凡,0.50 10,多元置换多项式,博士启动费,X971001,95-96,张起帆,1.001994年重点项目(国家和省部级):序号,项目名称,任务来源,编号,起止年月,负责人或高级人员,总经费(万)1,点集拓朴的几个新方向,国家重点基金,J98006(4)J96002(5)J971001(3),94-98,刘应明,16.00国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,大基数及相关问题的研究,国家科学基金,J961005,94-96,张树果,2.203,极大极小不等式变分不等式和相补问题理论及应用研究,国家科学基金,J961003,94-96,张石生,2.00 4,不定方程及应用,国家科学基金,J961004,94-96,孙琦,2.00省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)5,剩余类环Z/p\z上的技术,教委博士点基金,B97701(3)B98001(4)B961008(5),94-97,孙琦,2.56,非线性动力系统的无穷维性态,省青科基金办,U971001,94-96,张伟年,2.807,几类主要无限维拓扑流形的分类,教委优秀青年基金,J961001,94-96,滕辉,3.00市校级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)8,不适定的问题和反问题的样条函数解法,校青年基金,X961002,94-96,向朝进,0.609,非线性增生型映象方程研究中的一些问题,校青年基金,X961001,94-96,陈玉清,0.6010,Sn-i上某些Toeplitz算子及其本质谱的若干问题,博士启动费,,94-96,武洋,0.6011,例摆的模糊控制试验研究,校重点基金,X961001,94-95,李中夫,1.001993年国家基金:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)1,与倾斜理论相关的代数表示问题,国家自然科学基金委(青年基金),19201024,93-95,彭联刚,1.30省部级:序号,项目名称,任务来源,编号,起止年月,负责人,总经费(万)2,格上拓扑学点式处理,教委博士点基金,B961001,93-95,刘应明,3.00。
国家自然科学基金 数学 方向

国家自然科学基金数学方向国家自然科学基金是一个非常重要和具有影响力的科研资助项目,在各个学科领域都有着广泛的支持和应用。
数学方向作为其中的一个重要部分,得到了广大数学学者的关注和积极的参与。
本文将从国家自然科学基金数学方向的重要性、申请流程及要求、数学方向资助的意义和影响力等方面进行探讨和解析。
一、国家自然科学基金数学方向的重要性国家自然科学基金数学方向的重要性是不言而喻的。
作为数学学科的重要支撑和推动力量,国家自然科学基金为广大数学学者提供了宝贵的科研资金和支持,有力地推动了数学学科的发展与进步。
数学作为一门基础学科,对于其他学科的发展起着至关重要的作用。
国家自然科学基金数学方向的资助可以加强数学学科的研究,提高数学学科水平,促进学科交叉和创新,为国家的科技进步和经济发展提供强有力的支撑。
二、国家自然科学基金数学方向的申请流程及要求申请国家自然科学基金数学方向的流程相对来说比较复杂,需要经过严格的审核和评审。
首先,申请者需要根据基金申请的要求准备相关材料,包括研究计划书、研究方案、研究成果等。
其次,申请者需要按照规定的格式和要求填写申请表格,并将材料提交到相关科研机构。
在申请过程中,国家自然科学基金对于申请者的要求也比较严格。
申请者需要具备扎实的数学基础和研究能力,有一定的科研实力和创新潜力。
此外,申请者还需要具备相应的科研条件和环境,能够保证研究项目的顺利进行和取得一定的成果。
三、数学方向资助的意义和影响力国家自然科学基金数学方向的资助具有重要的意义和巨大的影响力。
首先,这种资助可以为广大数学学者提供稳定的科研资金支持,解决经费短缺的问题,有力地推进了数学学科的研究和发展。
其次,这种资助可以促进学科交叉和创新,鼓励数学学者开展前沿性和创新性的研究,推动数学学科不断向前发展。
此外,这种资助还可以加强学术交流与合作,促进国内外数学学者的合作与交流,提高国内数学学术水平和国际竞争力。
最后,数学方向资助还可以培养和支持优秀的人才。
2011年博士点基金名单(新教师类)

申请学校 东南大学 山东大学 中国海洋大学 武汉大学 华中科技大学 中南大学 中山大学 中山大学 华南理工大学 四川大学 四川大学 西南大学 重庆大学
申请人 李铁香 纪广华 岳跃利 吴远山 刘显明 周岳 杨志景 苑占江 张梅 胡文传 张加劲 张双虎 张志民
学科组名称 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学
2011年度高等学校博士学科点专项科研基金资助课题名单(新教师类)
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 课题编号 20110001120111 20110001120112 20110001120113 20110003120003 20110009120025 20110031120001 20110031120002 20110031120003 20110032120074 20110041120038 20110041120039 20110061120003 20110061120004 20110061120005 20110061120006 20110071120001 20110071120002 20110071120023 20110072120008 20110073120068 20110073120069 20110076120002 课题名称 几个带周期边值条件的非线性发展方程的 Cauchy问题 非线性Dirac方程的计算和分析 大规模稀疏模型的快速算法以及高维非凸 稀疏模型的理论分析 树的剪切以及随机树的尺度极限 微分动力系统与奇点相关的大范围性质及 其应用 解析挠率中的几个问题的研究 组合多项式的对数凹与单纯复形 相依风险模型中的渐近理论及其应用 热弹性网络系统的稳定性分析 II1型因子中的若干问题 几类矩阵锥优化问题的增广拉格朗日方法 二阶振动方程的周期解与稳定性 基于秩的稳健经验似然 基于随机矩阵理论的高维典则相关分析 齐次型的华林问题及其对Jacobi猜想的应 多参数正则化方法的理论和计算研究 参数化平行平均曲率子流形的Bernstein 问题和Chern问题的研究 两阶段抽样设计中数据分析的经验似然方 新型网格缩减基与球型解码算法及其应用 关于格路及其均匀分布的研究 正交约束优化问题及其应用 GL(2)的可容许Banach表示研究 申请学校 北京大学 北京大学 北京大学 北京师范大学 北京交通大学 南开大学 南开大学 南开大学 天津大学 大连理工大学 大连理工大学 吉林大学 吉林大学 吉林大学 吉林大学 复旦大学 复旦大学 复旦大学 同济大学 上海交通大学 上海交通大学 华东师范大学 申请人 郭紫华 邵嗣烘 贾金柱 何辉 朱圣芝 苏广想 王星炜 李津竹 韩忠杰 房军生 肖现涛 梁树青 刘天庆 姜丹丹 刘大艳 陆帅 杨翎 郁文 许威 马俊 文再文 谢兵永 学科组名称 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 数学 课题类型 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 新教师类 资助额度 (万元) 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
PTW

行 了讨 论 , 得到了 是P r W 整 环 与 R的 W一全 变 换 、 广 义 变换 是 唧
是 R的 S V一稳 定 极 大理 想 , 则( M: M) 也是 P 哪 整环 .
关键词 :
整 环 ;全 变 换 ;W一全 变换 ;广 义 变换
1 P r I W 整 环 的 W一全 变 换
定义 1 . 1 [
全 变换 .
令R :{ ∈KI 存 在 R 的极 大 理想
一 , , 使 M …M C _R} , 则称 为 的全 变换 . 一, , 使得 …M C _R} , 则称 尺 为 R的
定义 1 . 2 【 均 令R ={ ∈KI 存 在 的极 大 W一理想
收 稿 日期 : 2 0 1 5一o 4— 0 2
整环的扩环进行了研究 , 给出了 P T W 整环与其扩环之间的一些等
基金项 目: 绵阳师范学院科研基 金 自 然科学重点项 目( 2 0 1 4 A 0 4 ) 作者简介 : 万吉湘 ( 1 9 8 1一) , 女, 四川泸州人 , 讲师 , 研究方向 : 交换代数与同调代数
( 1 . 绵阳师范学院数学与计算机科学学院 ,四川绵阳 6 2 1 0 0 0 ; 2 . 西南科技大学理学 院 , 四川绵 阳 6 2 1 0 1 0 ; 四川大学数学学院 , 四川成都
摘 要 :该 文利 用素理想在 星型 算子研 究中的特 殊性 , 对唧
6 1 0 0 6 4 )
整环 的一 类特 殊扩环、 W一全变换、 广义 变换进 Βιβλιοθήκη 中图分类号 :0 1 5 3 .3
文献标 志码 :A
文章编号 :1 6 7 2 - 6 1 2 x ( 2 0 1 5 ) 0 5 - 0 0 1 5 - 0 4
2016年国家自然科学基金项目大数据资料

2016年国家自然科学基金项目大数据分析2016年的国家自然科学基金项目评审结果已经出炉。
科学网在已有结果的基础上,结合历史数据,对基金在不同空间尺度的分布情况进行全面考察,多角度探索科学基金分布特征。
(一)按项目类别统计2015-2016年项目数量变化趋势根据国家自然科学基金委8月17日通告显示,共接收项目申请172843项,经初步审查受理169832项,决定资助其中的37409项,约占总数的22%。
和2015年相比,增加202项。
由表可见,一方面,国家正加大力度提升较不发达地区科研机构完成项目的能力和动力,因此增加了地区科学基金项目的数量;另一方面,国家对青年科学项目的水平和要求已经提高。
结合历史数据,基金总项数和基金总金额依然呈正相关。
地区科研基金项目多分布在甘肃、广西、贵州、广西、云南等地区,其原因来自制度保护;其他种类基金都分布在高等院校和科研单位比较多的地区,比如北京、上海、广东等经济较发达的城市。
图1 省市项目金额分配(单位:万元)如图1所示,北京市科研机构所获项目资金近38亿元,约占项目金额总数的20.8%,超过末尾18个省市区之和。
分得项目资金10亿元以上的有北京、上海、江苏和广东,总数为86亿余元,约占总额的47.25%。
(二)大数据分类统计1.单项之最本年度自然科学基金项目单项资助最多的数额是3500万元,该项目研究方向为地球科学,被国家海洋局第一海洋研究所揽。
另外,单项资助1000万元以上的项目37项,总金额42593万元,详情见表2。
表2 单项资助金额1000万以上项目统计表2.数额之最2016年的受自然科学基金资助最多的单位依然是上海交通大学,总项目数901项,单项资助金额从4万元到1050万元不等,平均56.32万元。
表3按学部对其项目进行分类,可见上海交大在医学科学领域拥有较大优势。
从表4中单一机构获得千万元以上资助的地区分类来看,排在前五位的仍旧是北京、江苏、上海、广东、湖北,与总体数据流一致。
数学与应用数学专业(计算机软件及应用方向)信息与计算科学专业修读指引

数学与应用数学专业(计算机软件及应用方向)信息与计算科学专业修读指引部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑应用数学与信息计算科学系本科修读指引<一)应用数学与信息计算科学系介绍应用数学与信息计算科学系简况:深大应用数学与信息计算科学系建立于1985年, 原名应用数学系,全系有教师27人,其中博导1 名,教授4名,副教授11名,讲师8名,助教1名。
全系教师中计有博士学位者11人,硕士学位者7人,教师队伍年轻化且结构合理。
拥有现代化计算机实验室一个,网络实验室一个。
系资料室有本系及相关专业丰富的图书,资料齐全,近五年来全系老师在国际国内重要刊物上发表论文100余篇,多篇被SCI,EI,CSCI索引,承担国家以及省部级自然科学基金10余项,横向科研基金6项,共获省级科研教案成果奖10余项。
我系现有本科专业2个,在校学生310名;以本系学生为主的深圳大学大学生数学建模队参加全国大学生数学建模竞赛,历四届,共获全国大学生数学建模二等奖一项,广东赛区一等奖4项,二等奖13项,三等奖12项,获奖率平均达79.4%。
b5E2RGbCAP 本系下设两个专业:数学与应用数学<计算机软件及应用)专业和信息与计算科学专业。
1、数学与应用数学<计算机软件及应用)本专业培养掌握数学科学的基本理论与基本方法,具备运用数学知识和较高计算机综合应用技能解决实际问题的能力。
受到科学研究的初步训练,能在科技、教育和经济部门从事实际应用、开发研究和管理工作的高级专门人才。
本专业学生主要学习数学与应用数学的基本理论、基本方法,受到数学模型、计算机和数学软件方面的基本训练,具有较好的科学素养,初步具备科学研究、教案、解决实际问题及开发软件等方面的基本能力。
p1EanqFDPw2、信息与计算科学本专业培养具备良好的数学素养、掌握信息科学和计算科学的基本理论与基本方法,受到科学研究的初步训练,能运用所学知识和较高计算机综合应用技能解决实际问题,能在科技、教育和经济部门从事研究、教案和应用开发和管理工作的高级专门人才。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教育部博士点基金
B12000061019
01-03
刘应明
6
10
不分明拓扑中的反射与余反射子范畴
四川省青年科技基金
01-03
张德学
8
11
极分拆关系及基数不变量研究
留学回国人员科研启动基金
B2200036707
01-03
张树果
4.00
12
非线性分析中某些问题的研究
留学回国人员科研启动基金
B2200047904
01-03
黄南京
3.5
13
非线性分析中的一些问题
留学回国人员科研启动基金
B2200047905
01-03
陈玉清
5
14
留学回国人员启动基金
周盛凡
2.00
15
模糊性数学问题的若干研究
教育部重点项目
B300109
01-03
刘应明
10
国际合作:
序号
项目名称
任务来源
编号
起止年月
负责人或
高级人员
重点项目(国家和省部级):
序号
项目名称
任务来源
编号
起止年月
负责人或
高级人员
总经费
(万)
1
数理逻辑及其应用
国家自然科学基金委
A219931020
01-03
张树果
12.4
2
教育部跨世纪人才培养基金
教育部
01-03
彭联刚
30.00
国家基金:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
3
Domain理论在拓扑学中的应用
国家自然科学基金
A2TY10126022
01-02
寇 辉
2.00
4
高性能有限元方法研究
国家自然科学基金委
(天元基金)
A2TY10126027
01-02
谢小平
2.00
5
随机系统多传感器决策与估计融合理论与算法
国家自然科学基金委
A660074016
01-03
朱允民
16.00
6
从范畴拓扑观点看不分明拓扑与Domain理论
7
市校级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
12
半群理论及其在控制论中的应用
四川大学青年科学基金
H002067
02-03
顾晓慧
1
13
模糊推理研究
四川大学青年科学基金
H002065
02-03
黄丽
1
14
非线性滤波理论及其在信号处理中的应用
四川大学青年科学基金
02066
02-03
周杰
1
2001年
张世清
21
3
非凸和鲁棒向量优化的理论与算法研究
国家自然科学基金
07.1-09.12
黄南京
24
4
具有时滞的随机脉冲系统的定性分析
国家自然科学基金
07.1-09.12
徐道义
25
5
并行解边界元和有限元的区域分解法与分界外推法
国家自然科学基金
07.1-09.12
吕涛
24
6
连续统基数不变量研究
国家自然科学基金
校青年基金
200457
2005
陈柏辉
1.5
13
多源信息融合中的迭代算法及其收斂性分析
校青年基金
200458
2005
何腊梅
1
14
模糊拓扑空间上的迭代问题
校青年基金
200459
2005
陈丽
1
15
不确定性条件下的企业预警研究
校科技创新基金
2005cf06
05-07
罗懋康
10.00
2004年
重点项目(国家和省部级):
数学学院科研基金项目一览表
2007年
重点项目(国家和省部级):
序号
项目名称
任务来源
编号
起止年月
负责人或
高级人员
总经费
(万)
1
弦理论中的几何不变量
国家自然科学基金
07.1-
李安民
130
国家基金:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
2
多体问题德的变分方法
国家自然科学基金
07.1-09.12
9
新世纪优秀人才支持计划
NCET-06-0779
2006-2008
张德学
50
市校级:
序号
项目名称
任务来源编号起止ຫໍສະໝຸດ 负责人总经费(万)
11
高性能低阶四边形杂交/混合版..壳研究
校青年基金
2006-2007
罗鲲
2
12
非线性抛物型方程的区域分解算法
校青年基金
2006-2007
潘璐
1
13
我国能源市场化的若干技术问题
国家自然科学基金
05-07
张伟年
20
3
Deligene-Mumford模空间的拓扑和二维orbifold的弦理论研究
国家自然科学基金
05-07
郑泉
10
省部级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
4
分布式数字图书馆信息快速处理及应用
省攻关项目
05-06
冯民富
10
5
多源信息融合中某些基本问题研究
国家自然科学基金
2006-2008
周杰
22
6
仿射流形上的分析
国家自然科学基金
2006-2008
贾方
15
7
西部教师培训
国家自然科学基金(天元
2006.1-12
刘应明
20
省部级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
8
新世纪优秀人才支持计划
NCET-06-0778
2006-2008
穆春来
50
国家自然科学基金
04-06
张旭
16.00
8
伪概周期性与Banach空间中的微分方程
国家自然科学基金
04-06
李洪旭
9
9
扩大仿射李代数及其量子代数
国家自然科学基金
04-06
谭友军
9
省部级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
10
具有非交换符号代数的Toeplitz代数
教育部博士点基金
04-06
万大庆
孙 琦
40
2
Domain理论与格上拓扑学
国家杰出青年基金
A210125104
02-06
罗懋康
80
3
分部参数系统H∞控制理论
教育部优秀博士论文项目
02-06
张 旭
40
省部级:
序号
项目名称
任务来源
编号
起止年月
负责人
总经费
(万)
4
并行解有限元、边界元分裂法与分裂外推法
教育部博士点基金
B120010610005
负责人
总经费
(万)
2
随机动力系统混沌控制与参数估计的稳健性及其在弱信号检测中的作用
国家自然科学基金
2006-2008
马洪
24
3
非线性发展方程解的有界性与渐近行为等问题
国家自然科学基金
2006-2008
穆春来
15
4
算子半群和李群上的微分算子
国家自然科学基金
2006-2008
李淼
15
5
传感器网络中信息压缩与融合理论及算法研究
编号
起止年月
负责人
总经费
(万)
8
拓朴与Domain理论的若干问题研究
教育部博士点基金
B120020610057
03-05
梁基华
5
9
格上拓朴学中的范畴拓朴问题
优秀青年教师资助计划
张德学
8
10
留学回国人员启动基金
张旭
3.00
11
微分动力系统
教育部高校青年教师奖
B52003693
03-07
张伟年
50
12
中心及退化奇点分岔与不变流形问题
曹广福
5
11
基于信息融合的超宽带扩频通信信号检测技术研究
教育部博士点基金
20040610004
04-06
马 洪
6
12
椭圆曲线密码体制中Satoh算法的改进和实现
国防科技重点实验室基金
04-06
彭国华
15.00
13
复杂山地近地表结构模型层次反演方法
省石油管理局
04-06
冯民富
75
市校级:
序号
项目名称
任务来源
总经费
(万)
18
经济模型中数据不确定性分析的比较研究
自然科学科学基金
7010100005
2001-2002
李竹渝
2
19
迭代函数方程理论及应用
序号
项目名称
任务来源
