简支梁计算示例
简支梁计算表
U.S.A.
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴的惯性 矩:
下翼缘对 Y轴的惯性 矩:
平面外 稳定系数 计算:
截面不 对称影响 系数:
工字形截 面简支梁 的系数
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴下的翼惯缘性对 Y轴的惯性
截面特 性计算:
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
A 0 = 7884 mm 2 重量 61.9 y 0 = 425 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
kg/m
1/7
U.S.A.
JOB No.:__________
即 : 断面
350x6x180x BH 8x180x8
BY________________ DATE______________ CHK'D_____________
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
基本数据 输入:
梁跨度: 梁平面外 计算长度:
l= 18000 mm l'= 3500 mm
H型钢结构简支梁设计计算书

H型钢结构简支梁设计计算书转发评论2011-10-21 11:16-------------------------------| 简支梁设计|| || 构件:BEAM1 || 日期:2011/10/21 || 时间:11:03:20 |------------------------------------ 设计信息-----钢梁钢材:Q235梁跨度(m):15.000梁平面外计算长度(m):6.500钢梁截面:焊接组合H形截面:H*B1*B2*Tw*T1*T2=298*149*149*8*10*10容许挠度限值[υ]: l/400 = 37.500 (mm)强度计算净截面系数:1.000计算梁截面自重作用: 计算简支梁受荷方式: 竖向单向受荷荷载组合分项系数按荷载规范自动取值----- 设计依据-----《建筑结构荷载规范》(GB 50009-2001)《钢结构设计规范》(GB 50017-2003)----- 简支梁作用与验算-----1、截面特性计算A =5.2040e-003; X c =7.4500e-002; Yc =1.4900e-001;Ix =7.6141e-005; Iy =5.5251e-006;ix =1.2096e-001; iy =3.2584e-002;W1x=5.1102e-004; W2x=5.1102e-004;W1y=7.4163e-005; W2y=7.4163e-005;2、简支梁自重作用计算梁自重荷载作用计算:简支梁自重(KN): G =6.1277e+000;自重作用折算梁上均布线荷(KN/m) p=4.0851e-001;3、梁上恒载作用荷载编号荷载类型荷载值1 荷载参数1 荷载参数2 荷载值21 4 1.00 1.00 0.00 0.002 4 1.50 7.50 0.00 0.003 4 1.00 14.00 0.00 0.004、单工况荷载标准值作用支座反力(压为正,单位:KN)△恒载标准值支座反力左支座反力Rd1=4.814, 右支座反力Rd2=4.8145、梁上各断面内力计算结果△组合1:1.2恒+1.4活断面号: 1 2 3 4 5 6 7弯矩(kN.m):0.000 6.538 11.110 14.916 17.955 20.229 21.737 剪力(kN) : 5.777 3.964 3.351 2.738 2.126 1.513 -0.900断面号:8 9 10 11 12 13弯矩(kN.m):20.229 17.955 14.916 11.110 6.538 0.000剪力(kN) :-1.513 -2.126 -2.738 -3.351 -3.964 -5.777△组合2:1.35恒+0.7*1.4活断面号: 1 2 3 4 5 6 7弯矩(kN.m):0.000 7.355 12.498 16.780 20.200 22.758 24.455 剪力(kN) : 6.499 4.459 3.770 3.081 2.391 1.702 -1.013断面号:8 9 10 11 12 13弯矩(kN.m):22.758 20.200 16.780 12.498 7.355 0.000剪力(kN) :-1.702 -2.391 -3.081 -3.770 -4.459 -6.4996、局部稳定验算翼缘宽厚比B/T=7.05 < 容许宽厚比[B/T] =15.0腹板计算高厚比H0/Tw=34.75 < 容许高厚比[H0/Tw]=80.07、简支梁截面强度验算简支梁最大正弯矩(kN.m):24.455 (组合:2; 控制位置:7.500m)强度计算最大应力(N/mm2):45.576 < f=215.000简支梁抗弯强度验算满足。
简支梁计算示例

1.一座五梁式装配钢筋砼简支梁桥的主梁和横隔梁截面如下图1、图2所示,主梁长19.96m ,计算跨径19.5m ,主梁翼缘板刚性连接。
40C 的弹性模量210m N105.23E ⨯=,跨中截面惯性矩4c m 06626.0I =,跨中单位长度质量m kg 1083.51m 3c ⨯=,试计算5号梁5cq m ,50q m 以及在公路-Ⅰ级车道荷载作用下的跨中最大弯矩、最大剪力及支点截面最大剪力。
图1(单位:cm )图2(单位:cm )解:一、5号梁荷载横向分布系数计算1、杠杆原理法(1)绘出5号梁的横向分布影响线:(如图示)10.8751.60.8(2)在5号梁的横向分布影响线上进行最不利加载(如图示)m 50q =1/2(∑ηi )=1/2×0.875=0.4382、刚性横梁法(1)求5号梁的横向分布影响线:(以桥跨中心为坐标原点建立坐标系:如图示)∑a i 2=a 12+ a 22 +a 32 +a 42+ a 52=2×(3.22+1.62)=25.6η51= 1/n-a 5×a 1/∑a i 2=1/5-3.2×3.2/25.6=-0.2η55= 1/n+a 3×a 7/∑a i 2=1/5+3.2×3.2/25.6=0.6绘出5号梁的横向分布影响线(2)在5号梁的横向分布影响线上进行最不利加载:绘出加载图0.875η1=(480-20)/480*0.6=0.575η2=(480-200)/480*0.6=0.35η3=(480-330)/480*0.6=0.1875η4=-30/480*0.6=-0.0375 ?m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575)=0.556m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575-0.0375)=0.538 ?二.内力计算1、恒载内力)(222x l gxx gx x glM x -=⨯-⨯=)2(22x l ggx gl Q x -=-=g=1.583*103kg/m=1.583/9.8*103=16.15kN/m各计算截面的剪力和弯矩值如下表:5号梁恒载内力2、活载内力计算课程设计中要计算简支桥基频,公式为:cc m EI l f 22π=再根据计算基频选择冲击系数。
单跨简支梁一端悬挑计算书
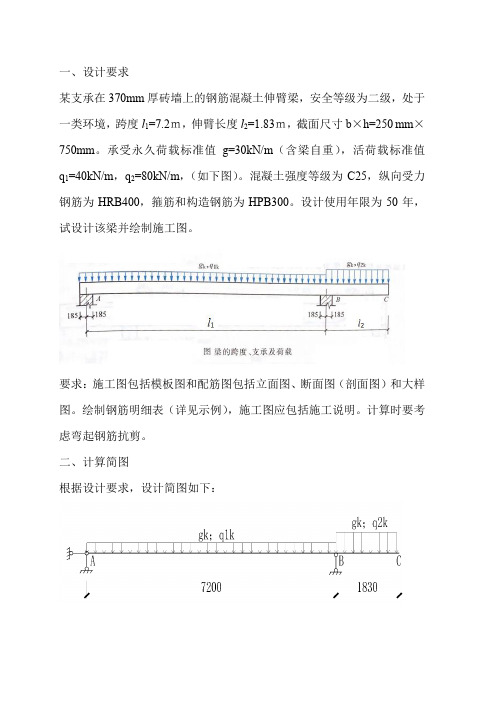
一、设计要求某支承在370mm厚砖墙上的钢筋混凝土伸臂梁,安全等级为二级,处于一类环境,跨度l1=7.2m,伸臂长度l2=1.83m,截面尺寸b×h=250 mm×750mm。
承受永久荷载标准值g=30kN/m(含梁自重),活荷载标准值q1=40kN/m,q2=80kN/m,(如下图)。
混凝土强度等级为C25,纵向受力钢筋为HRB400,箍筋和构造钢筋为HPB300。
设计使用年限为50年,试设计该梁并绘制施工图。
要求:施工图包括模板图和配筋图包括立面图、断面图(剖面图)和大样图。
绘制钢筋明细表(详见示例),施工图应包括施工说明。
计算时要考虑弯起钢筋抗剪。
二、计算简图根据设计要求,设计简图如下:1、恒载标准值gk作用下,构件弯矩图如下:(单位:kN*m)2、活载标准值qk1作用下,构件弯矩图如下:(单位:kN*m)3、活载标准值q k2作用下,构件弯矩图如下:(单位:kN*m)1、恒载标准值g k作用下,构件剪力图如下:(单位:kN)2、活载标准值q k1作用下, 构件剪力图如下:(单位:kN)3、活载标准值q k2作用下, 构件剪力图如下:(单位:kN)五、最不利截面分析根据构件特点,最不利截面分别为A支座右截面(弯矩最小,剪力最大)、第一跨中截面(弯矩最大,剪力最小)、B支座左或右截面(弯矩最大、剪力做大),现将上诉截面各个工况下截面内力列出,详下表:第一跨最不利界面分析时,活荷载g2k对第一跨各截面有利,遂不考虑其作用。
六、截面配筋计算因构件第一跨不承受扭矩荷载,遂采用A支座右截面剪力设计值计算A 支座箍筋配筋面积A svA;采用第一跨跨中弯矩计算第一跨梁底纵向受力钢筋配筋面积A s1 、第一跨跨中梁顶纵向受力钢筋配筋面积A s1’。
因构件第二跨为悬挑梁,不承受扭矩荷载,B支座左右截面弯矩值相等,但左截面剪力设计值大于右截面剪力设计值,遂可采用B支座左截面内力计算第一跨构件梁顶纵向受力钢筋配筋面积A svB及B支座左右截面的箍筋配筋面积A svB、第二跨构件纵向受力钢筋配筋面积A s2、A s2’及箍筋配筋面积A sv2。
有限元例子-简支梁受均布荷载

例1 简支梁受均布荷载计算简图:图1-(a)所示一简支梁,高3 m,长18 m,承受均布荷载10 N/m2,E=2×1010Pa ,μ= 0. 167,取t=1 m,作为平面应力问题。
由于对称,只对右边一半进行有限单元法计算,如图1-(b)所示,而在y轴上的各结点处布置水平连杆支座。
图1 计算简图图2 计算剖分图数据整理1、节点坐标文件91 551 0.750 0.5002 1.500 0.5003 2.250 0.5004 3.000 0.5005 3.750 0.5006 4.500 0.5007 5.250 0.5009 6.750 0.50010 7.500 0.50011 8.250 0.50012 0.750 1.00013 1.500 1.00014 2.250 1.00015 3.000 1.00016 3.750 1.00017 4.500 1.00018 5.250 1.00019 6.000 1.00020 6.750 1.00021 7.500 1.00022 8.250 1.00023 0.750 1.50024 1.500 1.50025 2.250 1.50026 3.000 1.50027 3.750 1.50028 4.500 1.50029 5.250 1.50030 6.000 1.50031 6.750 1.50032 7.500 1.50033 8.250 1.50034 0.750 2.00035 1.500 2.00036 2.250 2.00037 3.000 2.00038 3.750 2.00039 4.500 2.00040 5.250 2.00041 6.000 2.00042 6.750 2.00043 7.500 2.00044 8.250 2.00045 0.750 2.50046 1.500 2.50047 2.250 2.50048 3.000 2.50049 3.750 2.50050 4.500 2.50051 5.250 2.50053 6.750 2.50054 7.500 2.50055 8.250 2.50056 9.000 3.00057 8.250 3.00058 7.500 3.00059 6.750 3.00060 6.000 3.00061 5.250 3.00062 4.500 3.00063 3.750 3.00064 3.000 3.00065 2.250 3.00066 1.500 3.00067 0.750 3.00068 0.000 3.00069 0.000 2.50070 0.000 2.00071 0.000 1.50072 0.000 1.00073 0.000 0.50074 0.000 0.00075 0.750 0.00076 1.500 0.00077 2.250 0.00078 3.000 0.00079 3.750 0.00080 4.500 0.00081 5.250 0.00082 6.000 0.00083 6.750 0.00084 7.500 0.00085 8.250 0.00086 9.000 0.00087 9.000 0.50088 9.000 1.00089 9.000 1.50090 9.000 2.00091 9.000 2.500该文件第1行第1个数据为节点数91,第2个数据为内部节点数55。
例题-简支梁内力计算

ql/2 -ql/2
剪力图
ql2/8
弯矩图
2
2、计算截面内力 距离A支座为x的任一截面上的弯矩和剪 力(内力)分别用Mx、Vx表示。
q R1 A R2 x
Mx Vx
由∑Fy=0,得到R2-Vx- qx=0பைடு நூலகம்
Vx= ql/2-qx
对x截面取矩,由∑Mx=0,得到Mx+ qx×x/2-R2×x=0
3、绘制内力图
Mx= qlx/2-qx2/2
横坐标表示x,纵坐标表示内力(弯矩或剪力,即为内力图。
线分布荷载q的合力为ql力臂合力点到a点的距离为l2荷载对a点的力矩为qlql2qx距离a支座为x的任一截面上的弯矩和剪力内力分别用m表示
简支梁内力计算
已知简支梁跨度为l、分布荷载q。求截面弯矩和剪力分布。
〖解〗
R1
1、求支座约束反力
A
三个约束反力分别用R1、R2、R3表示。 R2
q B
l
R3
由静力平衡条件:∑Fx=0 得到R1=0;
对A点取力矩,力矩等于力×力臂。反力R1、 R2 的力臂为0; 反力R3 的力臂为l,对A点的力矩为-R3 l;线分布荷载q的合力为ql
力臂(合力点到A点的距离)为l/2,荷载对A点的力矩为 ql2/2 。
由∑MA=0,0+0- R3 l+ ql2/2=0
得到R3=ql/2
1
∑Fy=0,得到R2= R3 = ql/2
点载荷简支梁扭矩计算公式

点载荷简支梁扭矩计算公式全文共四篇示例,供读者参考第一篇示例:点载荷简支梁扭矩计算公式是工程力学领域中常用的公式之一,它用来计算简支梁在承受外部载荷作用时产生的扭矩大小。
在工程设计中,扭矩是一个非常重要的参数,能够影响梁的强度、稳定性和耐久性。
准确计算简支梁的扭矩对于工程设计和结构安全具有重要意义。
在工程实践中,简支梁扭矩的计算公式通常采用静力学的原理,结合梁的几何形状和外部载荷的作用来确定。
一般情况下,简支梁的扭矩计算公式可以表示为:M = -M0 + Px – VxM为简支梁的扭矩,单位为N·m;M0为简支梁的固定端的扭矩,单位为N·m;P为梁的外部载荷,单位为N;x为梁的距离离开固定端的距离,单位为m;V为梁的剪力,单位为N。
简支梁是一种常用的结构形式,在实际的工程设计中经常遇到。
简支梁是指在两端支承条件下的梁,通常由一根梁材或梁柱组成,用于支撑和承载外部荷载。
简支梁的设计和计算是工程设计中一个重要的环节,其中扭矩计算公式是不可或缺的一部分。
在实际的工程设计中,工程师通常会根据具体的工程要求和结构形式来选择合适的简支梁扭矩计算公式。
通过合理的计算和分析,可以有效地评估简支梁在承受外部载荷时的受力情况,为工程设计和结构安全提供重要的参考依据。
点载荷简支梁扭矩计算公式是工程设计中的重要工具,在工程实践中具有广泛的应用。
通过准确计算简支梁的扭矩,可以帮助工程师评估结构的强度和稳定性,为工程设计和结构安全提供保障。
在未来的工程实践中,我们需要不断改进和完善简支梁扭矩计算公式,以更好地满足工程设计的需要,促进工程结构的发展和进步。
第二篇示例:点载荷简支梁是工程结构设计中常见的一种构件形式,扭矩是梁在受到外力作用时内部产生的一种重要力学参数。
在设计工程结构时,计算扭矩是十分关键的,可以帮助工程师合理布局结构,确保结构的稳定性和安全性。
本文将介绍点载荷简支梁扭矩的计算公式及其相关知识。
简支梁计算例题

简支梁计算例题设计任务:设计一个简支梁,已知梁的跨度L=6米,梁的截面尺寸为b×h=200×400毫米,承受均布荷载设计值q=70kN/m(包括自重),混凝土强度等级为C25,纵向受拉钢筋采用HRB400级钢筋,箍筋采用HPB300级钢筋。
1. 计算梁所受总弯矩M:M = qL²/ 8 = 70 ×6²/ 8 = 255 kN·m2. 计算梁的截面面积A:A = b ×h = 200 ×400 = 80000 mm²3. 计算梁的截面模量W:W = α×A ×fcm = 1.1 ×80000 ×30 = 2640000 N·mm4. 计算梁的抗弯承载力Mu:Mu = fcmw = 30 ×2640000 = 79200000 N·mm > M = 25500000 N·mm5. 计算梁的纵筋数量:由M/mho²+fyAs/s ≤fcd得出As ≥M/(mho²+ fy/s),其中fy为HRB400级钢筋的抗拉强度设计值,取值为360N/mm²。
通过计算得出As≥8176mm²,选用2Φ28的钢筋,As=12568mm²。
6. 计算箍筋数量:根据构造要求,选用Φ8@200的箍筋,每米长度内布置箍筋数量为n=1×100/200+1=2个。
7. 验算裂缝宽度:根据规范要求,裂缝宽度不应超过Wmax=0.3mm。
根据M/γfW≤Wmax,其中γf为受拉或受压区纵向普通钢筋的配筋率,取值为As/(bho),通过计算得出W≤Wmax。
8. 绘制施工图,标明梁的跨度、截面尺寸、纵向钢筋和箍筋的位置和规格。
结论:根据以上计算和验算,该简支梁的设计满足要求,可以用于实际工程中。
简支梁配筋计算
F(kn/m) 使用系数 F 30 1.4 F(kn/m) 70 1.2
42 84
受力开间计算宽度 使用系数 Q Q(kn/m) 4.2 16.8 1.4 墙面抹灰 P 自重P6 2.1 14 3 0.05 33.179 1筋 面积As (mm2) 2138.38
39717受力点最大弯矩mf112梁配筋计算计算结果均载集中荷载荷载f距支座1的距离2绿色为可输入数据部位2519
梁配筋计算
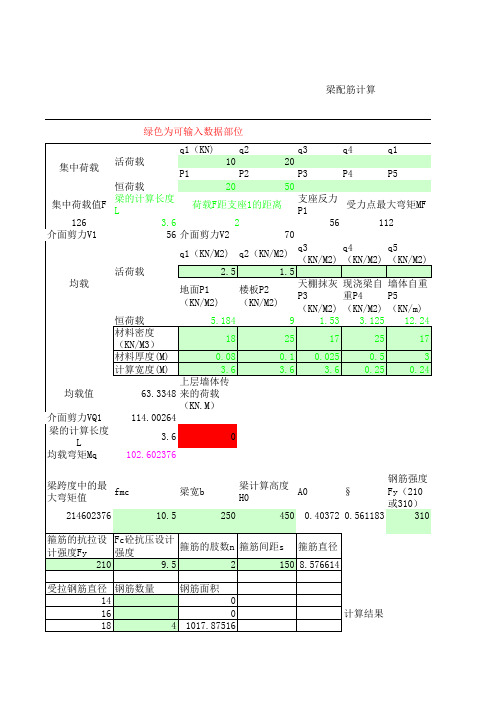
绿色为可输入数据部位 q1(KN) 集中荷载 活荷载 P1 10 P2 q2 20 P3 P4 P5 q3 q4 q1
恒荷载 20 50 梁的计算长度 荷载F距支座1的距离 集中荷载值F 支座反力P 受力点最大弯矩MF L 112 2 126 3.6 56 介面剪力V1 56 介面剪力V2 70 q1(KN/M2) q2(KN/M2) q3(KN/M2q4(KN/M2q5(KN/M2 活荷载 2.5 1.5 天棚抹灰 现浇梁自 墙体自重 均载 地面P1 楼板P2 P3 重P4 P5 (KN/M2) (KN/M2) (KN/M2) (KN/M2) (KN/m) 恒荷载 5.184 9 1.53 3.125 12.24 材料密度 18 25 17 25 17 (KN/M3) 材料厚度(M) 0.08 0.1 0.025 0.5 3 计算宽度(M) 3.6 3.6 3.6 0.25 0.24 上层墙体传 均载值 63.3348 来的荷载 (KN.M) 介面剪力VQ1 114.00264 梁的计算长度L 3.6 0 均载弯矩Mq 102.602376 梁跨度中的最 fmc 大弯矩值 214602376 10.5 梁计算高度 A0 H0 250 450 钢筋强度 § Fy(210 或310) 0.40372 0.561183 310
简支梁计算(双向板)

梁截面:b=0.24m L= 4.6mh=0.4m h 0=0.375m梁自重: 2.592KN/m梁两侧板:Q (面)= 5.2KN/(m*m)板1:跨度:L1(长)= 4.6mL1(短)= 3.3m板2:跨度:L2(长)= 4.6m L2(短)= 3.3m 27KN/m Q1=29.592KN/m fc=14.3放大系数1a1=1fy=360放大系数12、计算配筋:Q2=8.58KN/m Q (总)=Q1+Q2=38.172KN/m100.9649KN*m0.20920.23737905.18mm*mm=14.0824KN/m Q (总)=Q1+Q2=43.67439KN/m115.5188KN*m0.239360.2781060.09mm*mm=11.3312KN/mQ (总)=Q1+Q2=40.9232KN/m108.2419KN*m0.224280.25741981.576mm*mmξ=1-SQRT(1-2*as)=板传给梁的线荷载为:Q2=(2*L1(长)-0.5*L1(短))*L1(短)*Q (面)/4/L1(长)+L2(短)*Q (面)/4as=M/(a1*fc*b*h 0*h 0*1000)=M=Q (总)*L*L/8=梁配筋面积As:As=(a1*fc*b*h*ξ*1000000)/fy=(类型三):当梁一侧板为长垮(板1);一侧板为短垮(板2)时:Q2=(2*L1(长)-0.5*L1(短))*L1(短)*Q (面)/4/L1(长)+(2*L2(长)-0.5*L2(短))*L2(短)*Q (面)/4/L2(长)M=Q (总)*L*L/8=梁配筋面积As:as=M/(a1*fc*b*h 0*h 0*1000)=(L1(短)+L2(短))*Q (面)/4=M=Q (总)*L*L/8=(类型二):当梁两侧板均为其长垮时:作用在梁上的总荷载:类型(一):当梁两侧板均为其短垮时:ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000)/fy=作用在梁上的总荷载:板传给梁的线荷载为:梁配筋面积As:材料数据:ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000)/fy=板传给梁的线荷载为:作用在梁上的总荷载:次梁计算L-1(类型二)1、基本资料:楼板面荷载(包括板自重):作用在梁上墙体线荷载:as=M/(a1*fc*b*h 0*h 0*1000)=需修改计算结果最终结果KN/(m*m)分类。
方钢简支梁受力计算实例

方钢简支梁受力计算实例一、问题描述假设有一根长为L米的方钢简支梁,宽为b米,高为h米,材料为钢,弹性模量为E,横纵向的泊松比分别为μ1和μ2、梁下有一个集中荷载作用,荷载大小为F牛顿,作用位置距离梁端距离为a米。
二、受力分析在进行受力分析之前,需要先确定梁的边界条件。
方钢简支梁是指两端支座固定,并且不受弯矩和剪力的约束,因此可以推断出以下边界条件:梁两端的位移为零,其对应的反力为零。
受力分析主要包括弯矩和剪力的计算。
首先,考虑梁在集中荷载作用下的弯矩分布。
根据梁的几何形状,可知弯矩最大值出现在受力点附近的一侧。
在假设为单纯弯曲的情况下,根据“梁的受力分析方法”,可得弯矩公式:M=F*a*(b*h)/L其中,M为弯矩值,单位为牛顿-米。
接下来,考虑梁在集中荷载作用下的剪力分布。
根据梁的受力平衡条件,可知剪力大小与距离梁端的位置有关,且剪力图形为三角形。
根据“梁的受力分析方法”,可得到剪力公式:V=F*(L-a)/L其中,V为剪力值,单位为牛顿。
三、应力计算根据弯矩和剪力的计算结果,可以进一步计算出梁中心剖面的最大应力。
方钢简支梁是一种对称结构,其应力主要由弯矩和剪力引起。
由于方钢截面为矩形,可以采用莫尔法则进行应力分析。
莫尔法则认为,在弯曲和剪切共同作用下,材料中心剖面上的应力分布满足以下关系:σ=(M*y)/(Iy)+(V*z)/(Iz)其中,σ为应力值,单位为帕斯卡;M为弯矩值,单位为牛顿-米;y为离中性轴距离,单位为米;Iy为关于中性轴的惯性矩,单位为米的四次方;V为剪力值,单位为牛顿;z为截面的高度,单位为米;Iz为关于中性轴的惯性矩,单位为米的四次方。
由于方钢简支梁为矩形截面,其惯性矩的计算公式为:Iy=(1/12)*b*h^3Iz=(1/12)*h*b^3代入之前计算得到的弯矩和剪力值,可以计算出中心剖面的最大应力。
四、位移计算在受力分析中,还需要考虑方钢简支梁的位移。
根据“梁的受力分析方法”,可以得到位移计算公式。
简支梁设计验算-模板

执行规范:《混凝土结构设计规范》(GB 50010-2010), 本文简称《混凝土规范》《建筑结构荷载规范》(GB 50009-2012), 本文简称《荷载规范》钢筋:d - HPB300; D - HRB335; E - HRB400; F - RRB400; G - HRB500; P - HRBF335; Q - HRBF400; R - HRBF500-----------------------------------------------------------------------1 计算简图:2 计算条件:荷载条件:均布恒载标准值: 5.00kN/m 活载准永久值系数: 0.50均布活载标准值: 20.00kN/m 支座弯矩调幅幅度: 0.0%梁容重 : 25.00kN/m3计算时考虑梁自重: 考虑恒载分项系数 : 1.20 活载分项系数 : 1.40活载调整系数 : 1.00配筋条件:抗震等级 : 不设防纵筋级别 : HRB400混凝土等级 : C30 箍筋级别 : HPB300配筋调整系数 : 1.0 上部纵筋保护层厚: 30mm面积归并率 : 30.0% 下部纵筋保护层厚: 30mm最大裂缝限值 : 0.400mm 挠度控制系数C : 200截面配筋方式 : 单筋3 计算结果:单位说明:弯矩:kN.m 剪力:kN纵筋面积:mm2箍筋面积:mm2/m裂缝:mm 挠度:mm-----------------------------------------------------------------------梁号 1: 跨长 = 9700 B×H = 1000 × 500左中右弯矩(-) : 0.000 0.000 0.000弯矩(+) : 0.002 576.301 0.002剪力: 237.650 0.000 -237.650上部as: 40 40 40下部as: 40 40 40上部纵筋: 1000 1000 1000下部纵筋: 1000 3895 1000箍筋Asv: 1271 1271 1271上纵实配: 7E25(3436) 5E18(1272) 7E25(3436)下纵实配: 7E28(4310) 7E28(4310) 7E28(4310)箍筋实配: 4d8@150(1340) 4d8@150(1340) 4d8@150(1340)腰筋实配: 4d18(1018) 4d18(1018) 4d18(1018) 上实配筋率: 0.69% 0.25% 0.69%下实配筋率: 0.86% 0.86% 0.86%箍筋配筋率: 0.13% 0.13% 0.13% 裂缝: 0.000 0.232 0.000挠度: -0.000 32.063 -0.000最大裂缝:0.232mm<0.400mm最大挠度:32.063mm<48.500mm(9700/200)本跨计算通过.-----------------------------------------------------------------------4 所有简图:配筋:支座为7E25,跨中为7E28。
例题-简支梁内力计算

实例三:简支梁的稳定性分析
总结词
简支梁在受到外力作用时,可能会发生失稳现象,导致梁的承载能力下降或完全丧失。
详细描述
简支梁在受到外力作用时,如果外力过大或梁的截面尺寸过小,可能会导致梁的失稳现 象。失稳会使梁的承载能力急剧下降或完全丧失,因此需要进行相应的稳定性分析。稳 定性分析的方法包括静力分析和动力分析,根据不同的工况和要求选择合适的方法进行
弯曲正应力会导致梁发生弯曲变形,因此需要 保证梁的抗弯能力满足设计要求。
剪切应力计算
剪切应力是简支梁在剪力作用 下,截面上产生的应力。
剪切应力的计算公式为: τ=Q/A,其中Q为剪力,A为
截面面积。
剪切应力会导致梁发生剪切变 形,因此需要保证梁的抗剪能
力满足设计要求。
组合应力计算
01
组合应力是简支梁在弯矩和剪力共同作用下,截面上
02 稳定性分析中,需要计算简支梁的临界载荷和屈 曲模态等特性,以确定梁的安全承载能力。
03 稳定性分析的方法包括有限元法和能量法等。
04
CATALOGUE
简支梁的强度计算
弯曲正应力计算
弯曲正应力是简支梁在弯矩作用下,截面上产 生的应力。
弯曲正应力的计算公式为:σ=M/Wz,其中M 为弯矩,Wz为截面对主轴的惯性矩。
3
弯矩图可以用于判断梁的受力状态和变形情况, 以及用于确定梁的承载能力和稳定性等。
03
CATALOGUE
简支梁的受力分析
静力分析
01
静力分析是简支梁内力计算的基础,主要研究简支 梁在恒定载荷和约束力作用下的平衡状态。
02
静力分析中,需要计算简支梁的支反力、剪力和弯 矩等内力,以确定梁的应力和变形。
03
简支梁的内力计算

成绩评定表20 年 月曰学生姓名班级学号专业机械设计制造及其自动化课程设计题目简支梁的内力计算评语组长签字:成绩日期课程设计任务书学院机械工程学院专业机械设计制造及其自动化学生姓名班级学号课程设计题目简支梁的内力计算实践教学要求与任务:1、学习掌握运用ANSYS软件2、运用ANSYS进行有限元分析3、进一步理解有限元分析思想4、运用ANSYS软件进行实际运用,解决实际结构问题工作泗与进度安排:1、上机熟悉ANSYS软件(1天)2、上机操作练习例题,进一步熟悉软件(1天)3、上机操作练习及选定题设题目(1天)4、上机进行ANSYS分析(1天)5、交课程设计报告及答辩(1天)指导教师:201年月日专业负责人:201年月曰学院教学副院长:201年月曰简支粱结构的内力计算问题阐述图示简支梁为】8号工字钢,跨度L=6m,截面高度H=0.5m,截面面积A=0.008m2.惯性矩I=0.m4,弹性模量E=2.06ellN/mm2.集中载荷P=100KN o对该梁进行分析,画出弯矩图和剪力图。
IIH交互式的求解过程1.进入ANSYS在D盘建立一名为的文件夹,工作文件名为jianzhiliang。
然后运行开始---->程---->ANSYS11.0.0---->Ansys Product Launcher—file Management—select Working Directory:D:\,input job namc:jianzhiliang~*Run2.建立几何模型2.1创建关键点(1)选择菜单路径:Main Menu:Preprocessorf Modeling-*Creatc~*Nodcf In Active CS-(2)在创建节点窗口内,在NODE后的编辑椎内输入节点号1,并在X,Y,Z后的编辑框内输入0,0,。
作为节点1的坐标值,按下该窗口内的Apply按钮。
(3)输入节点号2,并在X,Y,Z后的编辑框内输入3,0,。
T梁、简支梁等的配筋计算

b= h= h0=
250 600
mm mm mm 540 mm 3.75 kN/m 14.3 N/㎜2 1.43 N/㎜2 a1= b1= ξ
b=
as= 60 梁自重 混凝土选用
a's= 35
mm
C 30 fc = ft= 1 0.8 0.550
钢筋选用 fy=f'y=
2
其中,1; HPB235级钢 2; HRB335级钢 3; HRB400级钢
3
为充分发挥受压钢筋A's的作用,取As2=A's=
942.48 mm2
AS1 =
a1 fcb
fy
2 (h0 - h0 -
2M )= a1 fcb
-376.55 ㎜2
纵向受拉钢筋总截面面积 As=As1+As2= 受拉钢筋取钢筋直径 实配钢筋面积AS= 2α 's=
565.93 实取
2
㎜2
20
¢=
8
纵向受拉钢筋总截面面积 As=As1+As2= 2399.42 ㎜2 受拉钢筋取钢筋直径
20
¢=
2
实取
9 2
mm ≤
根
实配钢筋面积AS= 2827.43 mm 受压钢筋取钢筋直径 12 ¢= 实取 实配钢筋面积AS= 2α 's= 226.19 mm 70.00 mm
2
OK!
根
OK!
x
验算受压区高度x=fyAs1/(α1fcb)=
AS =
a1 fcb 2M (h0 - h02 )= fy a1 fcb
¢=
取钢筋直径
18
1017.88 mm2
4
实配钢筋面积AS= Asmin=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.一座五梁式装配钢筋砼简支梁桥的主梁和横隔梁截面如下图1、图2所示,主梁长19.96m ,计算跨径19.5m ,主梁翼缘板刚性连接。
40C 的弹性模量2
10m N
105.23E ⨯=,跨中截面惯性矩
4
c m
06626.0I =,跨中单位长度质量m kg 1083.51m 3c
⨯=,试计算5号梁5cq m ,50q m 以
及在公路-Ⅰ级车道荷载作用下的跨中最大弯矩、最大剪力及支点截面最大剪力。
图1(单位:cm )
图2(单位:cm )
解:一、5号梁荷载横向分布系数计算
1、杠杆原理法
(1)绘出5号梁的横向分布影响线:(如图示)
1
0.8751.6
0.8
(2)在5号梁的横向分布影响线上进行最不利加载(如图示)
m 50q =1/2(∑ηi )=1/2×0.875=0.438
2、刚性横梁法
(1)求5号梁的横向分布影响线:
(以桥跨中心为坐标原点建立坐标系:如图示)
∑a i 2=a 12+ a 22 +a 32 +a 42+ a 52=2×(3.22+1.62)=25.6 η51= 1/n-a 5×a 1/∑a i 2=1/5-3.2×3.2/25.6=-0.2 η55= 1/n+a 3×a 7/∑a i 2=1/5+3.2×3.2/25.6=0.6 绘出5号梁的横向分布影响线
(2)在5号梁的横向分布影响线上进行最不利加载:绘出加载图
0.875
η1=(480-20)/480*0.6=0.575 η2=(480-200)/480*0.6=0.35 η3=(480-330)/480*0.6=0.1875 η4=-30/480*0.6=-0.0375 ?
m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575)=0.556
m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575-0.0375)=0.538 ?
二.内力计算 1、恒载内力
)(2
22x l gx x gx x gl M x -=⨯-⨯=
)2(2
2x l g
gx gl Q x -=-=
g=1.583*103kg/m=1.583/9.8*103=16.15kN/m 各计算截面的剪力和弯矩值如下表: 5号梁恒载内力 截面位置x 剪力Q(kN)
弯矩M(kN •m)
x=0 Q=16.15*19.5/2=157.5 M=0 x=l/2
Q=0
M=1/8*16.15*19.5*19.5=767.6
2、活载内力计算
课程设计中要计算简支桥基频,公式为:c
c
m EI l f 2
2π
= 再根据计算基频选择冲击系数。
本题中为计算方便,直接选取冲击系数μ+1=1.3
计算简支梁跨中弯矩时,可以忽略横向分布系数沿跨度方向的变化,即取全梁不变的5cq m 进行计算。
作简支梁跨中弯矩影响线如图:其最大影响线坐标为
875.445.194
=÷=l
,位于跨中。
以车道荷载对该桥进行加载,按照最不利原则,应将集中荷载k p 布置在跨中,均布荷载q k 满布全跨,则有:
()m
kN y p m M k c p ⋅=⨯⨯⨯⨯=⋅⋅⋅⋅+=63.838875.4238556.013.11ξμ ()m
kN q m M k c q ⋅=⨯⨯⨯⨯⨯=Ω⋅⋅⋅⋅+=73.3602/875.45.195.10556.013.11ξμ ∴ 车道荷载在该桥跨中引起的最大弯矩为: (3分)
46P q M M M KN m =+=+=838.63+360.73=1199.46 m kN ⋅
()Ω⋅⋅⋅+=k c q q m Q μ1
总弯矩M=1.2M g +1.4M q =1.2*767.6+1.4*1199.46=2600.36m kN ⋅
跨中最大剪力为:
()kN
q y p m Q k k cq q l 72.121)
6.258.142(7228.0)8/5.195.105.02382.1(556.013.1)2.1(15,2/=+⨯=⨯+⨯⨯⨯⨯⨯=Ω•+••••+=ξμ 支点处最大剪力为:
l
1/2
1/2
+ -
() kN
Q
q
m
y
p
m
Q
q
k
cq
k
q
q
91
. 107
7.
33
76
.2
92
.
56
55
.
62
( 3.1
)1
238
2.1
)
556
.0
438
.0(
5.
19
)
85
.4
3/1
5.
19
(
1
5.
10
)
556
.0
438
.0(
2
85
.4
(
1 3.1
)2/5.
19
5.
10
556
.0
5.0
238
438
.0
2.1(
1 3.1
) 2.1(
1
5
50
=
-
-
+
⨯
=
⨯
⨯
⨯
-
+
⨯
-
⨯
⨯
⨯
-
⨯
⨯
+
⨯
⨯
+
⨯
⨯
⨯
⨯
⨯
=
∆
+
Ω
•
•
+
•
•
•
•
+
=ξ
μ。
