有限元课程实训结课上机参考例题
有限元法基础及应用实验上机报告实例

一,实验描述:1、本作业属于哪类问题在本作业中,根据板的结构特点和受力情况,确定该问题属于平面对称应力问题,定义分析类型为静力学分析。
2、本文采用如何的单位制本题中,长度单位为m,故为方便起见,采用力的单位为N,压强的单位为pa,时间的单位为s,质量的单位为kg。
3、单元类型:对单元描述;材料;实常数单元类型为选取shell Elastic 4node63单元材料:弹性模量为2.1e11pa,泊松比为0.33。
由题意确定时常数,即厚度为0.1m4、划分网格。
网格划分设置。
单元数,节点数。
网格化分设置:设置单元边长值为0.1m,指定单元形状为Areas。
5、加载描述(1)对整体模型,首先对四周固定端加载位移约束,设定其位移值为0;然后,对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
(2)对四分之一模型,首先对两边固定端加载位移约束,设定其位移值为0;然后,对两坐标轴所在的边施加对称载荷,最后对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
6、后处理:最大MISIS应力和最大位移的位置和大小。
绘制结构的应力和变形图。
二,实验步骤(一)绘制整体实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,结果如下:边界条件施加载荷20000N/m求解以后4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图从图中可以看出其中实体边界中点位置的应力最大为0.583e+07pa,最大变形在中间圆弧的位置,0.144e-3m(二)绘制四分之一的实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,注意此处有一个对称载荷的加载,结果如下:4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图三,实验小结这次ANSYS上机实验课是使用shell中的Elastic 4node63单元,这使我对ANSYS软件中的单元有了更深的认识,同时对平面问题的静力分析的基本思路和操作步骤更加熟悉。
有限元上机报告

有限元上机报告模板一、实验目的题目:图示折板上端固定,右侧受力F=1000N,该力均匀分布在边缘各节点上;板厚t=2mm,材料选用低碳钢,弹性模量E=210GPa,u=0.33。
此题属于平面应力问题,采用的单元类型为:Solid Quad-8node单位制:力(N)、弹性模量(MPa)、长度(mm)。
二、实体建模的方法1.定义矩形:Main Menu>Preprocessor>Modeling>Create>Areas>Rectangle>By Dimensions。
输入:X1=0,X2=30,Y1=0,Y2=60。
点击对话框上的Apply按钮创建第一个矩形。
输入X1=30,X2=60,Y1=0,Y2=30。
点击对话框上的OK按钮创建第二个矩形。
2. 面图元的加运算:Main Menu>Preprocessor>Modeling>Operate>Booleans>Add>Areas。
点击对话框上的Pick All按钮,所有的面被加在一起。
点击SAVE_DB保存数据。
三、单元类型1. 此题属于平面应力问题,采用Solid单元的Plane82。
2. 材料属性:弹性模量为21e4MPa,泊松比为0.33。
3. 实常数:板厚2mm。
四、划分网格以边长为2mm的正方形划分单元,总共有675个单元,736个节点。
具体操作如下:1. Main Menu >Preprocessor>Meshing>Mesh Tool.2. 在Mesh Tool面板上点击Size Controls模块内的Global Set 按钮,在弹出的对话框中输入Element edge length为2,按ok完成。
3. 在Mesh下拉框中选Areas。
4. 点击Mesh按钮网格划分,点击Pick All按钮,点击Close关闭Mesh Tool 面板。
有限元ansys上机考试题

如图所示的外伸梁,均布载荷的极度为q = 3kN/m,集中力偶之矩M = 3KNm,梁的截面如图所示,试求梁的内力和变形情况,画出梁的变形图(挠曲线),剪力图和弯矩图。
图示平面梁架,截面为0.1×0.1m2的矩形,弹性模量为2.1×1011Pa,泊松比为0.3。
施加在梁上的集中力F = 10000N。
试求梁架的内力,画出弯矩图与剪力图。
析当在左右臂两侧的突起面上作用以p = 1100Pa的压强时,整个结构的应力分布。
给出最大应力的值。
提示:因该结构几何、载荷均对称,可考虑取一半进行分析并注意对称面上施加合理的约束。
p p料的密度为7830kg/m3,试提取该结构的前10阶固有频率。
如图所示的带孔平板,已知q = 1000Pa,板厚为0.1m,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析平板受力后的变形及应力分布。
提示:单元类型选取带厚度的平面应力单元。
q6m如图所示的涵洞,作用均布载荷7500N/m2,试分析其受力情况。
材料的弹性模量为210GPa,泊松比0.3。
提示:单元类型选择平面应变,可考虑取一半涵洞建立模型。
如图所示的带孔钢制圆盘,已知p = 20MPa,弹性模量为2.1×1011Pa,泊松比为0.3。
若在孔内塞入一个高0.1m,直径为0.1m的铝制圆柱(取铝材的弹性模量为1.2×1011Pa,泊松比为0.3),试分析变形及应力。
p = 20MPa如图所示的带孔平板,已知板厚为1cm,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析平板受力后的变形及应力分布。
提示:单元类型选取带厚度的平面应力单元。
桥梁有关参数如图所示,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析桥面作用向下均布力q=50kN/m时的整个结构变形及应力分布。
提示:单元类型斜拉索用Link单元,其他用梁单元。
或全部采用梁单元,可利用对称性取一半进行分析。
2013有限元上机作业题
有限单元法元上机作业题
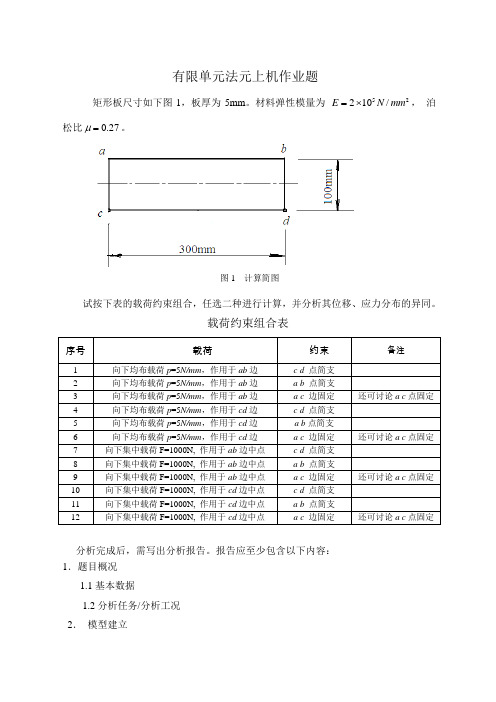
矩形板尺寸如下图1,板厚为5mm 。
材料弹性模量为 25/102mm N E ⨯=, 泊松比27.0=μ。
图1 计算简图
试按下表的载荷约束组合,任选二种进行计算,并分析其位移、应力分布的异同。
载荷约束组合表
分析完成后,需写出分析报告。
报告应至少包含以下内容:
1.题目概况
1.1基本数据
1.2 分析任务/分析工况 2. 模型建立
2.1 单元选择及其分析
2.2 模型建立及网格划分
2.3 载荷处理
3.计算分析
3.1 位移分布及其分析
3.2 应力分布及其分析
4.关于计算分析的体会,意见等
(注:封面上注明题目及其编号、姓名、班级、学号。
)
2013 年16月。
上海大学《有限元》2020年上机考题试题及答案

上海大学2020 ~2021 学年春季学期试卷 A 上机操作题课程名:有限元分析课程号:09A36012 学分: 3应试人声明:我保证遵守《上海大学学生手册》中的《上海大学考场规则》,如有考试违纪、作弊行为,愿意接受《上海大学学生考试违纪、作弊行为界定及处分规定》的纪律处分。
应试人应试人学号应试人所在院系六上机操作题(30分)目标:使用接触预测球(Ball)和窝(Socket)间的球形界面的压力形貌。
模型描述:●球窝连接2D轴对称模型和球窝连接3D四分之一模型●材料:钢对钢●接触:球形界面摩擦区域,摩擦系数=0.25●载荷和边界条件:窝固定在顶部,球的下部在-Y方向施加1000N力上机实验报告要求:1、简要写出主要的分析过程;针对2D轴对称模型和3D四分之一模型,哪些方面需要加以注意(6分);2、针对球窝连接2D轴对称模型,用总体单元尺寸分别为1.0和0.5mm划分网格,给出划分网格后的有限元模型图(4分);3、针对球窝连接2D轴对称模型,分别给出两种网格划分方式下结构的von-Mises应力云图及位移云图,并在云图上标示出最大值所发生的位置;用contact tool给出两种网格划分方式下接触面的接触压力云图。
(12分)。
4、针对球窝连接3D四分之一模型,用总体单元尺寸为0.75mm划分网格,并施加和2D 轴对称模型相同的载荷和边界条件,进行计算,给出划分网格后的有限元模型图,以及von-Mises应力云图及位移云图,并在云图上标示出最大值所发生的位置。
(6分)5、简单描述自己的心得体会。
(2分)上机实验报告:1.2D轴对称模型分析过程:打开workbench15.0,在左侧选择static structurl,材料为钢,在unite菜单中选择单位,然后鼠标右键点击geometry,选择properties,在analysis type中选择2D(在导入前设置为对称界面)如图:在geometry中导入ball-socket2D模型,并打开model,启动Mechanical,将作业单位制改为Metric(mm,Kg,s,mV,mA)改变部件特性为轴对称,选中Geometre,在Details of Geometry中把2D Behavior改为Axisymmetric修改接触行为,在contact of region里面选择Behavior为frictional,将fiction Coefficient修改为0.25执行网格划分,总体单元尺寸分别为1.0和0.5mm划分网格,在element size 填写0.5和1mm,得到以下网格划分:1mm 0.5mm选择static structural,右键选择球窝上边界,插入fixed support,选择球下边界插入load/force,在define by选择component,在y方向输入-1000选中solution,插入deformation total还有stress-equivalent(von mise),再插入contact tool,右键contact tool插入pressure。
有限元例题

q Fx 2 2 F2 Fy 2 0
K 11 K K 21 K 31 K 41
K 12 K 22 K 32 K 42
K 13 K 23 K 33 K 43
K 14 K 24 K 34 K 44
(3)零位移约束的处理,零位移处划行划列
K
K 22 K 32
K 22
K 32
K 23 K 33
线性方程组为:
K 23 2 F2 K 33 3 F3
1 2 1 1 2
(4)计算单元刚度矩阵 单元面积: A1 A2 (5)弹性矩阵:
D
E 1 2
1 0
1 0
0 3 1 0 3E 0 1 3 0 8 1 0 0 1 2
(6)几何矩阵:
B Bi
Bj
Bm
0 ci bi
b i 1 Bi 0 2A ci
2 u 2 q / 2 7 4 4 4 13 2 12 v 0 3Eh 2 7 0 u 3 q / 2 32 4 2 13 v3 0 2 12 0 u 2 1.98 v 2 q 0.36 u 3 Eh 1.79 v3 0.024
计算系数: 对于单元 1:
x1 0, y1 0,
a2 x3 y1 x1 y3 0, a3 x1 y 2 x2 y1 0, E K 332h 74
有限元习题及答案

有限元习题及答案有限元习题及答案有限元方法是一种常用的数值计算方法,用于求解各种工程和科学问题。
在学习有限元方法的过程中,练习习题是非常重要的,可以帮助学生巩固所学的知识,并提高解决实际问题的能力。
本文将介绍一些有限元习题及其答案,希望对学习有限元方法的同学有所帮助。
习题一:一维热传导问题考虑一个长度为L的一维杆,其两端固定,杆上的温度满足以下热传导方程:∂²T/∂x² = 0,其中T为温度,x为位置。
已知杆的两端温度分别为T1和T2,求解杆上的温度分布。
解答一:根据热传导方程,可以得到温度分布的一般解为T(x) = Ax + B,其中A和B为常数。
根据边界条件,可以得到方程组:T(0) = B = T1T(L) = AL + B = T2解方程组可得A = (T2 - T1) / L,B = T1。
因此,温度分布为T(x) = ((T2 - T1) / L) * x + T1。
习题二:二维弹性问题考虑一个矩形薄板,其长为L,宽为W,材料的弹性模量为E,泊松比为ν。
已知薄板的边界上施加了一定的边界条件,求解薄板上的位移场。
解答二:对于二维弹性问题,可以使用平面应力假设,即假设薄板内部的应力只有两个分量σx和σy,并且与z轴无关。
根据平面应力假设和胡克定律,可以得到位移场的偏微分方程:∂²u/∂x² + ν * (∂²u/∂y²) + (1 - ν) * (∂²v/∂x∂y) = 0∂²v/∂y² + ν * (∂²v/∂x²) + (1 - ν) * (∂²u/∂x∂y) = 0其中u和v分别为位移场在x和y方向上的分量。
边界条件根据具体情况给定。
通过数值方法,如有限元方法,可以求解位移场的近似解。
习题三:三维流体力学问题考虑一个三维流体力学问题,流体在一个封闭容器内流动,容器的形状为一个长方体,已知流体的速度场和压力场的初始条件,求解流体的运动状态。
有限元课程实训结课上机参考例题

有限元课程实训结课上机参考例题题 1:图1所示薄板左边固定,右边受均布压力P=100Kn/m 作用,板厚度为0.3cm ;试采用如下方案,对其进行有限元分析,并对结果进行比较。
(1)三节点三角形单元;(2个和200个单元)(2)四节点矩形单元; (1个和50个单元)(3)八节点等参单元。
(1个和20个单元)图 1 题 2:图2所示为一带圆孔的单位厚度(1M )的正方形平板,在x 方向作用均布压力0.25Mpa ,试用三节点常应变单元和六节点三角形单元对平板进行有限元分析,并对以下几种计算方案的计算结果进行比较:(1) 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;注:在y 轴上,孔边应力的精确解为:MPa x 75.0-=σ,在x 轴上,孔边应力的精确解为:MPa y 25.0=σ图 2题 3:图3所示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)图 3题 4:图4所示为一隧道断面,其内受均布水压力q,外受土壤均布压力p;试采用不同单元计算断面内的位移及应力,并分别分析q=0或p=0时的位移和应力分布情况。
(材料为钢,隧道几何尺寸和压力大小自行确定)图 4题 5:图5所示一简化直齿轮轮齿截面,高h=60mm,齿根宽b=60mm,齿顶宽c=25mm,齿顶作用力P=10Kn;试采用不同单元分析轮齿上位移及应力分布,并只指出最大应力位置。
图 5题 6:图6所示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
有限元上机作业

有限元上机作业目录1分布载荷作用下的悬臂梁应力计算 (1)1.1问题描述 (1)1.2计算模型 (1)1.2.1有限元模型及网格划分 (1)1.2.2边界条件 (1)1.2.3材料模型 (2)1.3计算结果 (2)1.4结果检验 (2)1.5小结 (3)2悬臂式连接环的应力与变形分析 (4)2.1问题描述 (4)2.2计算模型 (4)2.2.1有限元模型及网格划分 (4)2.2.2边界条件 (5)2.2.3材料模型 (5)2.3计算结果 (5)2.4结果检验 (6)2.5小结 (7)3具有中心孔的薄壁圆筒受均匀拉伸分析 (7)3.1问题描述 (7)3.2计算模型 (8)3.2.1有限元模型及网格划分 (8)3.2.2边界条件 (8)3.2.3材料模型 (8)3.3计算结果 (9)3.4结果检验 (10)3.5小结 (11)4刚架与弹簧混合建模与分析 (12)4.1问题描述 (12)4.2计算模型 (12)4.2.1有限元模型及网格划分 (12)4.2.2边界条件 (13)4.2.3材料模型 (13)4.3计算结果 (14)4.4结果检验 (15)4.5小结 (17)5过盈配合圆环受力分析 (17)5.1问题描述 (17)5.2计算模型 (18)5.2.1有限元模型及网格划分 (18)5.2.2边界条件 (18)5.2.3材料模型 (18)5.3计算结果 (19)5.4结果检验 (19)5.5小结 (20)6带中心圆孔板的热应力分析 (20)6.1问题描述 (20)6.2计算模型 (21)6.2.1有限元模型及网格划分 (21)6.2.2边界条件 (21)6.2.3材料模型 (22)6.3计算结果 (22)6.4小结 (23)7壳—梁组合结构建模计算 (24)7.1问题描述 (24)7.2计算模型 (24)7.2.1有限元模型及网格划分 (24)7.2.2边界条件 (25)7.2.3材料模型 (25)7.3计算结果 (26)7.4小结 (27)8复杂3D实体建模及受力分析 (27)8.1问题描述 (27)8.2计算模型 (28)8.2.1有限元模型及网格划分 (28)8.2.2边界条件 (28)8.2.3材料模型 (28)8.3计算结果 (29)8.4小结 (29)9含裂缝结构体的应力强度因子 (30)9.1问题描述 (30)9.2计算模型 (30)9.2.1有限元模型及网格划分 (30)9.2.2边界条件 (31)9.2.3材料模型 (31)9.3计算结果 (31)9.4小结 (32)10受热载荷的正方形烟囱建模与温度场求解 (32)10.1问题描述 (32)10.2计算模型 (33)10.2.1有限元模型及网格划分 (33)10.2.2边界条件 (33)10.2.3材料模型 (33)10.3计算结果 (34)11旋转车轮的建模与应力计算 (34)11.1问题描述 (34)11.2计算模型 (34)11.2.1有限元模型及网格划分 (34)11.2.2边界条件 (35)11.2.3材料模型 (35)11.3计算结果 (35)12U型支架的模态分析 (36)12.1问题描述 (36)12.2计算模型 (36)12.2.1有限元模型及网格划分 (36)12.2.2边界条件 (37)12.2.3材料模型 (37)12.3计算结果 (37)13异形截面梁的几何特性和扭转切应力分布 (38)13.1问题描述 (38)13.2计算模型 (39)13.2.1有限元模型及网格划分 (39)13.2.2边界条件 (40)13.2.3材料模型 (40)13.3计算结果 (40)1分布载荷作用下的悬臂梁应力计算1.1 问题描述分析模型如图1-1 所示, 梁的横截面为矩形(长x宽x高= 10x1x2 m2),受到沿长度方向线性分布载荷作用,q=(10000-1000x)N/m。
有限元分析入门实训考题

有限元分析入门实训考题(第1版)李建宇编著天津科技大学机械工程学院2012年4月题目1 选题者:(a) (b) (c)一、题目内容图示平面刚架结构.二、题目要求(1)采用有限元法手工求解;(2)写出完整的求解步骤,包括:a) 离散化:单元编号、节点编号;b) 单元分析:单元刚度矩阵,单元节点等效载荷向量;c) 单元组装:总体刚度矩阵,总体位移向量,总体节点等效载荷; d) 边界条件的引入及总体刚度方程的求解;e) B 点的位移,A 、C 处支撑反力及弯矩图、剪力图和轴力图的计算。
(3)刚度方程的集成与求解可采用Matlab 、Excel 等工具软件辅助完成; (4)利用Ansys 求解,并与手算结果比较.(5)利用A4纸完成题目,打印或手写均可以; (6)简要说明各成员主要负责完成的工作。
一、题目内容图示平面刚架结构。
二、题目要求(1)采用有限元法手工求解;(2)写出完整的求解步骤,包括:a)离散化:单元编号、节点编号;b)单元分析:单元刚度矩阵,单元节点等效载荷向量;c)单元组装:总体刚度矩阵,总体位移向量,总体节点等效载荷;d)边界条件的引入及总体刚度方程的求解;e)B点的位移,A、C处支撑反力及弯矩图、剪力图和轴力图的计算。
(3)刚度方程的集成与求解可采用Matlab、Excel等工具软件辅助完成;(4)利用Ansys求解,并与手算结果比较.(5)利用A4纸完成题目,打印或手写均可以;(6)简要说明各成员主要负责完成的工作。
一、题目内容如图所示的三垮梁,E=30e6 psi,I=305 in4。
(lb,ft,in,psi为英制单位)二、题目要求(1)采用有限元法手工求解;(2)写出完整的求解步骤,包括:a)离散化:单元编号、节点编号;b)单元分析:单元刚度矩阵,单元节点等效载荷向量;c)单元组装:总体刚度矩阵,总体位移向量,总体节点等效载荷;d)边界条件的引入及总体刚度方程的求解;e)求B点的位移,A、C、D、E处支撑反力及弯矩图和剪力图。
有限元试题及答案[1]
![有限元试题及答案[1]](https://img.taocdn.com/s3/m/fd06db80f524ccbff1218440.png)
∴ 又因
证明3、如图所示纯弯梁
梁的厚度很薄,外载沿厚度方向无变化,其中性层为y层,梁长为, 弹性模量为E,基本变量为:
位移(对中性层) 应力(为主应力,其方向很小,不考虑) 应变(为主要应变,中性层取微段莱推导三大方程)
解:根据力得平衡方程(体积力为零时) 知 上两个等式成立,即平衡方程成立,即此情况满足平衡条件。 其边界应力,
, ,
作图如下: 故边界下应力如图2.2所示:
其边界得剪应力如图2.3所示:
四、如图所示 已知,,(平面应力问题)
求:(1)斜面上应力,的表达式 (2)最大主应力,最小主应力及此时斜面的方向余弦。
衡。 (2) 当时,、并不一定为零,此情况下平衡方程并不一定成立,
故此情况下不满足平衡,只有在时,才满足平衡。 (3) 当时,平衡方程成立,故此情况下满足平衡。 (4) 所有均为非零时,只有当,时,平衡方程才成立,才能够满
足平衡,否则不平衡。 三、下列应力分布是否满足平衡条件(体积力为零),(2D平面应力问 题),描述就如图所示平面结构,该应力函数所表示时得边界应力。
解之知 所以: 所以,其形态函数矩阵 又因 所以几何矩阵 又 所以其应力矩阵 单元的势能为: 其刚度矩阵为: 十五、如图所示,为一由两根杆组成的结构(二杆分别沿X,Y)方向, 结构参数 试写成下列FEM分析
(1) 写出各单元的刚度矩阵 (2) 写出总刚度矩阵 (3) 求出节点2的位移 (4) 求各单元应力
如图所示8.4所示力的平衡:
几何方程:由变形后的几何关系可知 其中y为距中性层坐标,为挠度曲率。 即 由虎克定律知物理方程为: 整理上述方程得知下基本方程组 故纯弯梁的应变能: 九、如图所示为1个1D拉压问题 (1)写出描写该问题的所有基本变量 (2)写出所有基本方程,包括BC (3)写出应变能,外力功 (4)写出最小势能原理的一般表达式(1D问题) (5)证明(4)(即该原理与原基本方程的关系) 解(1)基本变量 位移 应力 应变 (2)基本方程 平衡方程 几何方程 物理方程 BC(): BC(p): 由平衡方程得知 (待定) 由几何方程得知 (待定) 由BC()知 由BC(p)知 ∴ (3)应变能 外力功 (4)最小势能一般表达式(1D问题)
有限元例题及答案

例 8-1:E ,A ,L ,s σ 杆I 弹塑性; 杆II 弹性。
求s AF σ3=下2点位移。
解:(1)理论解在荷载s A F σ3=作用下,杆I 屈服而有内力(拉力)S A N σ=1,杆II 内力(压力)为s II A N σ2=,中点2位移δ取决于杆II 的变形,即*===∆=δσσδ22)2(EL AE L A l S S II式中E Ls σδ=*(屈服位移)(2)直接迭代法杆I 和杆II 的刚度分别为⎩⎨⎧=**≤〉)()(δδδδδσL EAAI S k L EA k II =①迭I 迭代步迭代从*=δδ0开始,这时有L EAk k K II I 20=+=*-====δσσδ5.15.123101EL L EA A F K S S②第2迭代步杆I 进入塑性,有L EA A k s I 67.01==δσ杆Ⅱ完全弹性,刚度不变。
因此,总刚为L EAk k K II I 67.11=+=*-====δσσδ8.18.167.13112E L LEA A F k S s 整个迭代过程见表8-1。
表8-1 直接迭代法各次迭代结果(3)切线刚度法杆Ⅰ和杆Ⅱ的切线刚度分别为⎩⎨⎧=**≤〉)()(0δδδδLEAI k L EA k II =①第1迭代步初始状态时,00=δ,杆Ⅰ,Ⅱ中应力、应变均匀为零。
总刚为:L EAk k K T TI T 21=+=由F K T -=δψ,得S A σψ30-=由n Tn n K ψδ1--=∆得,*=--=∆δσδ5.1)3(10S A L由式n n n δδδ∆+=+1得,s δδ5.11=杆中应力:S SI σσσσ5.111-==杆中内力:S SI A N A N σσ5.111-==②第2迭代步由于杆I 已进入塑性,杆Ⅱ仍处弹性,总刚:L EAk k K TIITI T =+=2由F K T -=δψ,得S S S A A A σσσψ5.035.21-=-=由n Tn n K ψδ1--=∆得,*=--=∆δσδ5.0)5.0(11S A LEA由式n n n δδδ∆+=+1得,*=∆+=σδδδ0.2112杆中应力:S II SI A N A N σσ0.222-==检验F K T -=δψ,有030.32=-=S S A A σσψ迭代平衡。
六类有限元上机题

注:题中E表示材料弹性模量,μ表示泊松比,ρ表示密度。
一静力结构分析1 如图1所示为普通订书钉,E=2.1×105MPa,μ=0.3,横截面尺寸为宽B=0.64mm,高H=0.402mm。
当订书钉被压入纸张时,约需要120N的载荷,载荷均匀地分布在订书钉上部。
以下面两种情况进行有限元分析。
(单位:mm)(1)订入时A、B点为铰支条件;(2)订入时A、B点为固定约束。
图1 载荷和尺寸情况2、小型铁路桥由横截面积为3250mm2的钢制杆件组装而成。
一辆火车停在桥上,其载荷施加在桥梁两侧的桁架上,单侧的桁架如图2所示,等效载荷为F1,F2,E=2.1×105MPa,μ=0.3,ρ=7.8×103kg/m3。
试计算位置R处由于载荷作用而沿水平方向移动的距离以及支反力,同时,分析各个节点的位移和非单元应力。
图2 铁路桥单侧桁架及载荷情况3如图3所示,模型参数为:E=3.0×1010Pa,A1=30m,A2=10m,B=80m,t=20m,p=2200Pa。
有关风载的确定,按照海洋井架行业标准,有以下方法:风压(Pa)=0.6115×风速(m/s)×高度系数×形状系数对于一般的海洋井架及建筑物,高度在30m左右,高度系数取为1.1,形状系数取为1.25,风速取为47.8m/s。
换算出来后得到的风压为2200Pa。
图3 高层建筑物及其风载荷4对于含裂纹体的结构及材料,若按照线弹性力学分析,会在裂纹的尖端处产生应力的奇异性,这时需要计算裂纹尖端处的应力强度因子(对于Ⅰ型裂纹,有K1=σ(πa)1/2),并以应力强度因子作为准则来对材料的裂纹是否扩展进行判断。
图4所示为一块矩形平板,其边缘存在长为a的裂纹,板的两端承受拉应作用。
利用结构上下的对成性,取矩形的一半建立有限元模型,完成看一力σ下工作:(1)球裂纹的张角θ(在施加载荷前=0,θ=0)(2)沿直线AO,画出y方向应力σy沿x变化的曲线图。
中南大学有限元习题与答案(Word最新版)

中南大学有限元习题与答案通过整理的中南大学有限元习题与答案相关文档,希望对大家有所帮助,谢谢观看!中南大学有限元习题与答案习题 2.1 解释如下的概念:应力、应变,几何方程、物理方程、虚位移原理。
解应力是某截面上的应力在该处的集度。
应变是指单元体在某一个方向上有一个ΔU的伸长量,其相对变化量就是应变。
表示在x轴的方向上的正应变,其包括正应变和剪应变。
几何方程是表示弹性体内节点的应变分量与位移分量之间的关系,其完整表示如下:物理方程:表示应力和应变关系的方程某一点应力分量与应变分量之间的关系如下:虚位移原理:在弹性有一虚位移情况下,由于作用在每个质点上的力系,在相应的虚位移上虚功总和为零,即为:若弹性体在已知的面力和体力的作用下处于平衡状态,那么使弹性体产生虚位移,所有作用在弹性体上的体力在虚位移上所做的工就等于弹性体所具有的虚位能。
2.2说明弹性体力学中的几个基本假设。
连续性假设:就是假定整个物体的体积都被组成该物体的介质所填满,不存在任何间隙。
完全弹性假设:就是假定物体服从虎克定律。
各向同性假设:就是假定整个物体是由同意材料组成的。
小变形和小位移假设:就是指物体各点的位移都远远小于物体原来的尺寸,并且其应变和转角都小于1。
2.3简述线应变与剪应变的几何含义。
线应变:应变和刚体转动与位移导数的关系,剪应变表示单元体棱边之间夹角的变化。
2.4 推到平面应变平衡微分方程。
解:对于单元体而言其平衡方程:在平面中有代入上式的2.5 如题图2.1所示,被三个表面隔离出来平面应力状态中的一点,求和的值。
解:x方向上:联立二式得:2.6相对于xyz坐标系,一点的应力如下某表面的外法线方向余弦值为,,求该表面的法相和切向应力。
解:该平面的正应力全应力该平面的切应力2.7一点的应力如下MP 求主应力和每一个主应力方向的方向余弦;球该店的最大剪应力。
解:设主平面方向余弦为,由题知将代入得即,。
最大剪应力(1)当时代入式(2.21)(2)当时代入式(2.21)且2.8已知一点P的位移场为,求该点p(1,0,2)的应变分量。
华科有限元上机答案

有限元分析软件ANSYS上机习题姓名郭静班级船海1203班学号 U9目录Project1 简支梁的变形分析 (1)Project2 坝体的有限元建模与受力分析 (3)Project3 受内压作用的球体的应力与变形分析 (5)Project4 受热载荷作用的厚壁圆筒的有限元建模与温度场求解 (7)Project5 超静定桁架的有限元求解 (9)Project6 超静定梁的有限元求解 (11)Project7 平板的有限元建模与变形分析 (13)Project1 梁的有限元建模与变形分析计算分析模型如图1-1 所示, 习题文件名: beam。
NOTE:要求选择不同形状的截面分别进行计算。
梁承受均布载荷:1.0e5 Pa图1-1梁的计算分析模型梁截面分别采用以下三种截面(单位:m):矩形截面:圆截面:工字形截面:B=, H= R= w1=,w2=,w3=,t1=,t2=,t3=进入ANSYS程序→ANSYSED →Interactive →change the working directory into yours →input Initial jobname: beam→Run设置计算类型ANSYS Main Menu: Preferences →select Structural → OK选择单元类型ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete… →Add… →select Beam 2 node 188 →OK (back to Element Types window)→Close (the Element Type window)定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear→Elastic→Isotropic→input EX:, PRXY:→ OK定义截面ANSYS Main Menu: Preprocessor →Sections →Beam →Common Sectns→分别定义矩形截面、圆截面和工字形截面:矩形截面:ID=1,B=,H= →Apply →圆截面:ID=2,R= →Apply →工字形截面:ID=3,w1=,w2=,w3=,t1=,t2=,t3=→OK生成几何模型生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入三个点的坐标:input:1(0,0),2(10,0),3(5,1)→OK生成梁ANSYS Main Menu: Preprocessor →Modeling →Create →Lines →lines →Straight lines →连接两个特征点,1(0,0),2(10,0) →OK网格划分ANSYS Main Menu: Preprocessor →Meshing→Mesh Attributes→Picked lines →OK→选择: SECT:1(根据所计算的梁的截面选择编号);Pick Orientation Keypoint(s):YES →拾取:3#特征点(5,1) →OK→Mesh Tool →Size Controls) lines: Set →Pick All(in Picking Menu) →input NDIV:5→OK (back to Mesh Tool window) → Mesh →Pick All(in Picking Menu) → Close (the Mesh Tool window)模型施加约束最左端节点加约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement → On Nodes→pick the node at (0,0) → OK→select UX, UY,UZ,ROTX → OK最右端节点加约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement → On Nodes→pick the node at (10,0) → OK→select UY,UZ,ROTX → OK施加y方向的载荷ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Pressure→On Beams→Pick All→VALI:100000 → OK分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK结果显示ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape…→select Def + Undeformed→OK (back to Plot Results window) →Contour Plot→Nodal Solu →select: DOF solution, UY, Def + Undeformed , Rotation, ROTZ ,Def + Undeformed →OK退出系统ANSYS Utility Menu: File→ Exit →Save Everything→OKProject2坝体的有限元建模与应力应变分析计算分析模型如图2-1 所示, 习题文件名: dam。
有限元例题(免费)

A1E 1 1 K L1
1 1 4.0 105 1 1 5 4.0 10
4.0 105 5 4.0 10
对单元2来说
Q2 Q Q 3
2
K
2
1 1 2.0 105 AE 1 1 2 L 2.0 105
4.0 105 6.0 105 2.0 105
Q1 2.0 105 Q2 2.0 105 Q3 0
Q1 0
的第一行与第一列均与0相乘,可以在方程中将其划去。
K
K 简化成
6.0 105 5 2.0 10
有
x e x e u x 1 e Q1 e Q2 L L
e Q1 x x u x 1 e , e e L L Q2
进一步写成矩阵形式有
令
u ux
x x N 1 e , e —— 形函数矩阵 L L
x
(2)
e 2
——(1)
e 1
由位移连续性知:
在i点应有
在j点应有
uxi Q
aQ
e 1
e ux j Q2
a bL Q (3)
e
L
e
—— 单元长度
e e Q2 Q1 b Le
联立(2)(3) (4)
解出:
将(2)、(4)代回(1)有
e Q2 Q1e e u x Q1e x 按 Q1e 和 Q2 合并同类项 Le
e
e e
u ( x ) e e N Q N1 , N 2 Q x x x
13-有限元上机实验

5、书写实验报告。
具体要求: 3、采用ANSYS平台作为前后处理器,并使用自主程序进行计算和分析。 (1)要求输出结点与单元的应力、应变和位移结果数据; (2)并对结果导入到ANSYS平台中后处理器。 4、采用ANSYS对该问题进行计算和分析:
(1)要求输出结点与单元的应力、应变和位移结果数据;
(2)要求输出结点与单元的应力和应变等值线图形。
实验及要求如题图所示为一个不计自重的三角形平面应力问题弹性模量e1泊松比025比重0厚度1集中力p10
实验及要求
如题图所示为一个不计自重的三角形平面应力问题,弹性模量E=1,泊松比 μ=0.25,比重γ=0,厚度=1集中力 P=10。试采用ANSYS平台作为前后处理 器,并使用自主程序进行计算和分析。
实验及要求
具体要求: 1、要求使用两种划分单元(三角形单元)方案: (1)如图(b)所示; (2)四边形网格。 2、修改自主程序FEM_Triangle2D3Node.m:
(1)采用“乘极大数”法处理边界条件;
(2)注释程序说明。
实验及要求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元课程实训结课上机参考例题
题 1:图1所示薄板左边固定,右边受均布压力P=100Kn/m 作用,板厚度为0.3cm ;试采用如下方案,对其进行有限元分析,并对结果进行比较。
(1)三节点三角形单元;(2个和200个单元)
(2)四节点矩形单元; (1个和50个单元)
(3)八节点等参单元。
(1个和20个单元)
图 1 题 2:图2所示为一带圆孔的单位厚度(1M )的正方形平板,在x 方向作用均布压力0.25Mpa ,试用三节点常应变单元和六节点三角形单元对平板进行有限元分析,并对以下几种计算方案的计算结果进行比较:
(1) 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;
(2)分别采用不同数量的三节点常应变单元计算;
注:在y 轴上,孔边应力的精确解为:MPa x 75.0-=σ,在x 轴上,孔边应力的精确解为:MPa y 25.0=σ
图 2
题 3:图3所示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)
图 3
题 4:图4所示为一隧道断面,其内受均布水压力q,外受土壤均布压力p;试采用不同单元计算断面内的位移及应力,并分别分析q=0或p=0时的位移和应力分布情况。
(材料为钢,隧道几何尺寸和压力大小自行确定)
图 4
题 5:图5所示一简化直齿轮轮齿截面,高h=60mm,齿根宽b=60mm,齿顶宽c=25mm,齿顶作用力P=10Kn;试采用不同单元分析轮齿上位移及应力分布,并只指出最大应力位置。
图 5
题 6:图6所示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:
(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;
(2)分别采用不同数量的三节点常应变单元计算;
(3)当选常应变三角单元时,分别采用不同划分方案计算。
图 6。
