全等三角形——经典试题汇编 含答案
全等三角形经典题型50题(含答案)
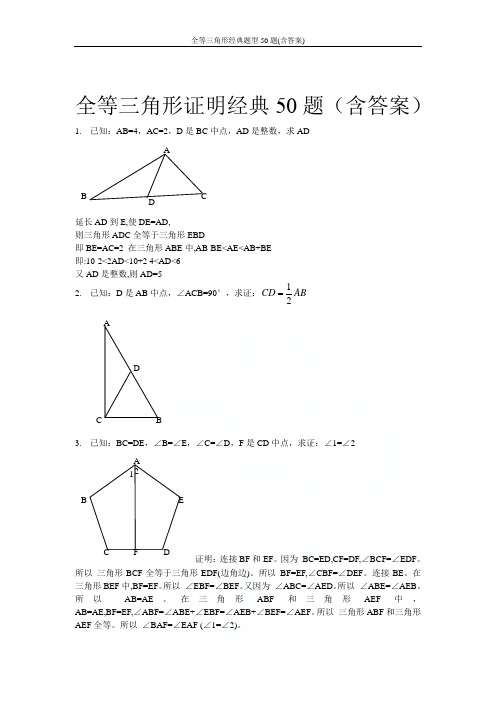
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 。
所,ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形——经典试题汇编含答案

第 1 页 共 11 页北京中考/一模之全等三角形试题精编北京中考16.已知:如图,点E A C ,,在同一条直线上,AB CD ∥,AB CE AC CD ==,.求证:BC ED =.16、△BAC ≌△BCD (SAS ) 所以,BC =ED 海淀一模15. 如图,AC //FE , 点F 、C 在BD 上,AC=DF , BC=EF . 求证:AB=DE .15.证明:∵ AC //EF ,∴ ACB DFE ∠=∠. ………………………………………1分在△ABC 和△DEF 中, ⎪⎩⎪⎨⎧=∠=∠=,,,EF BC DFE ACB DF AC ∴ △ABC ≌△DEF . ………………………………4分∴ AB=DE . ……………………5分 东城一模16. 如图,点B C F E 、、、在同一直线上,12∠=∠,BF EC =,要使ABC ∆≌DEF ∆,还需添加的一个条件是 (只需写出一个即可),并加以证明.ABCDE FABCDEF第 2 页 共 11 页16.(本小题满分5分)解:可添加的条件为:AC DF B E A D =∠=∠∠=∠或或(写出其中一个即可). …1分证明:∵ BF EC =,∴ BF CF EC CF -=-.即 BC EF = . -------2分 在△ABC 和△DEF 中,,12,,AC DF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ △ABC ≌△DEF . --------5分西城一模15.如图,在△ABC 中,AB=CB ,∠ABC=90º,D 为AB 延长线 上一点,点E 在BC 边上,且BE=BD ,连结AE 、DE 、DC . (1) 求证:△ABE ≌△CBD ;(2) 若∠CAE=30º,求∠BCD 的度数.15.(1)证明:如图1.∵ ∠ABC=90º,D 为AB 延长线上一点,∴ ∠A BE=∠CBD=90º . …………………………………………………1分 在△ABE 和△CBD 中,⎪⎩⎪⎨⎧=∠=∠=,,,BD BE CBD ABE CB AB∴ △ABE ≌△CBD. …………………… 2分(2)解:∵ AB=CB ,∠ABC=90º,∴ ∠CAB =45°. …….…………………… 3分 又∵ ∠CAE=30º,∴ ∠BAE =15°. ……………………………………………………………4分∵ △ABE ≌△CBD ,∴ ∠BCD =∠BAE =15°. ……………………………………………………5分图1第 3 页 共 11 页通州一模15.如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BAC DAE ∠=∠求证:△ABD ≌△ACE .15. 解:ΘDAE BAC ∠=∠..........................................................................(3分) ∴DAB EAC ∠=∠ .....................................................................(4分) 在AEC ∆和ADB ∆中⎪⎩⎪⎨⎧=∠=∠=AC AB EAC DAB AE AD∴AEC ∆≌ADB ∆(SAS ) .............................................................(5分)石景山一模16.如图,∠ACB =∠CDE =90°,B 是CE 的中点,∠DCE =30°,AC =CD . 求证:AB ∥DE .16.证明:∵∠CDE=90°,∠DCE=30°∴CE 21DE =………………1分 ∵B 是CE 的中点, ∴CE 21CB =∴DE=CB ………………2分 在△ABC 和△CED 中⎪⎩⎪⎨⎧=∠=∠=DE CB CDE ACB CD AC EDCBA第16题图第 4 页 共 11 页∴△ABC ≌△CED ………………3分 ∴∠ABC=∠E ………………4分 ∴AB ∥DE. ………………5分房山一模15.已知:E 是△ABC 一边BA 延长线上一点,且AE =BC ,过点A 作AD ∥BC ,且使AD =AB ,联结ED .求证:AC =DE .E ADCB15. 证明:∵AD ∥BC∴∠EAD=∠B. …………………………1分 ∵AD=AB. ……………………………2分 AE=BC. ……………………………3分 ∴△ABC ≌△DAE.……………………4分 ∴AC =DE . …………………………5分 昌平一模16.如图,已知△ABC 和△ADE 都是等边三角形,连结CD 、BE .求证:CD =BE .16.证明:∵ △ABC 和△ADE 都是等边三角形,∴ AB =AC ,AE =AD ,∠DAE =∠CAB , ∵ ∠DAE -∠CAE =∠CAB -∠CAE , ∴ ∠DAC =∠EAB ,∴ △ADC ≌△AEB . ……………………… 4分 ∴ CD =BE . ……………………… 5分门头沟一模ED CBAAE ADCB第 5 页 共 11 页FE ACDB16.已知:如图,AB ∥ED ,AE 交BD 于点C ,且BC =DC . 求证:AB =ED .16.证明:∵AB ∥ED ,∴∠ABD=∠EDB. ………………………….1分 ∵BC=DC,∠ACB=∠DCE, ……………3分 ∴△ABC ≌△EDC. ………………….4分 ∴AB=ED . ………………………………5分 丰台一模16.已知:如图,AB ∥CD ,AB =CD ,点E 、F 在线段AD 上,且AF=DE .求证:BE =CF .16.证明: Q AF=DE , ∴ AF-EF=DE –EF . 即 AE=DF .………………1分 Q AB ∥CD ,∴∠A =∠D .……2分 在△ABE 和△DCF 中 ,AB =CD ,∠A =∠D ,AE=DF .∴△ABE ≌△DCF .……….4分∴ BE =CF .…………….5分2012.5丰台一模24.已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是 ; (2)将图1中的△ADE 绕点A 旋转到图2的位置时,判EDCBAB第 6 页 共 11 页断(1)中的结论是否仍然成立,并说明理由.24.解:(1)BM =DM 且BM ⊥DM . ………2分(2)成立. ……………3分理由如下:延长DM 至点F ,使MF =MD ,联结CF 、BF 、BD .易证△EMD ≌△CMF .………4分∴ED =CF ,∠DEM =∠1.∵AB =BC ,AD =DE ,且∠ADE =∠ABC =90°,∴∠2=∠3=45°, ∠4=∠5=45°. ∴∠BAD =∠2+∠4+∠6=90°+∠6.∵∠8=360°-∠5-∠7-∠1,∠7=180°-∠6-∠9,∴∠8=360°-45°-(180°-∠6-∠9)-(∠3+∠9)=360°-45°-180°+∠6+∠9- 45°-∠9 =90°+∠6 . ∴∠8=∠BAD .………5分 又AD =CF . ∴△ABD ≌△CBF . ∴BD =BF ,∠ABD =∠CBF .………6分 ∴∠DBF =∠ABC =90°. ∵MF =MD ,∴BM =DM 且BM ⊥DM ..…………7分 海淀一模22.阅读下面材料:DCBAEM9第 7 页 共 11 页小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形, ∠AOB =∠COD =90︒.若△BOC 的面积为1, 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.图1 图2小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于 . 请你尝试用平移、旋转、翻折的方法,解决下列问题: 如图3,已知△ABC , 分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID .(1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为三边长的三角形的面积等于 .图322. 解:△BCE 的面积等于 2 . …………1分 (1)如图(答案不唯一): ……2分以EG 、FH 、ID 的长度为三边长的 一个三角形是△EGM . …………3分 (2) 以EG 、FH 、ID 的长度为三边长的三角EDCB AGBOCDAIGFABCDE第 8 页 共 11 页形的面积等于 3 . …………5分西城一模24.已知:在如图1所示的锐角三角形ABC 中,CH ⊥AB 于点H ,点B 关于直线CH 的对称点为D ,AC 边上一点E 满足∠EDA =∠A ,直线DE 交直线CH 于点F . (1) 求证:BF ∥AC ;(2) 若AC 边的中点为M ,求证:2DF EM ;(3) 当AB =BC 时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE 相等的线段,并证明你的结论.图1 图2 24.证明:(1)如图6.∵ 点B 关于直线CH 的对称点为D ,CH ⊥AB 于点H ,直线DE 交直线CH 于点F , ∴ BF=DF ,DH=BH .…………………1分 ∴ ∠1=∠2.又∵ ∠EDA =∠A ,∠EDA =∠1, ∴ ∠A =∠2.∴ BF ∥AC (2)取FD 的中点N ,连结HM 、HN . ∵ H 是BD 的中点,N 是FD 的中点,∴ HN ∥BF . 由(1)得BF ∥AC , ∴ HN ∥AC ,即HN ∥EM .第 9 页 共 11 页∵ 在Rt △ACH 中,∠AHC =90°,AC 边的中点为M ,∴ 12HM AC AM ==.∴ ∠A =∠3. ∴ ∠EDA =∠3. ∴ NE ∥HM .∴ 四边形ENHM 是平行四边形.……………………………………… 3分 ∴ HN=EM .∵ 在Rt △DFH 中,∠DHF =90°,DF 的中点为N , ∴ 12HN DF =,即2DF HN =.∴ 2DF EM =. ………………………………………………………… 4分(3)当AB =BC 时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE 相等的线段是EF 和CE . (只猜想结论不给分)证明:连结CD .(如图8)∵ 点B 关于直线CH 的对称点为D ,CH ⊥AB 于点H ,∴ BC=CD ,∠ABC =∠5. ∵ AB =BC ,∴ 1802ABC A ∠=︒-∠,AB =CD .①∵ ∠EDA =∠A ,∴ 61802A ∠=︒-∠,AE =DE .② ∴ ∠ABC =∠6=∠5. ∵ ∠BDE 是△ADE 的外角, ∴ 6BDE A ∠=∠+∠. ∵ 45BDE ∠=∠+∠, ∴ ∠A =∠4.③由①,②,③得 △ABE ≌△DCE .………………………………………5分 ∴ BE = CE . ……………………………………………………………… 6分由(1)中BF=DF 得 ∠CFE=∠BFC .由(1)中所得BF ∥AC 可得 ∠BFC=∠ECF . ∴ ∠CFE=∠ECF . ∴ EF=CE .∴ BE=EF . ……………………………………………………………… 7分 ∴ BE =EF =CE .(阅卷说明:在第3问中,若仅证出BE =EF 或BE =CE 只得2分)北京中考第 10 页 共 11 页24.在ABC △中,BA BC BAC =∠=α,,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ 。
全等三角形证明经典题(含答案)

全等三角形证明经典题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24.5. 证明:连接BF 和EF∵BC=ED,CF=DF,∠BCF=∠EDF ∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴∠EBF=∠BEF 。
∵∠ABC=∠AED 。
∴∠ABE=∠AEB 。
∴AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF 和三角形AEF 全等。
∴∠BAF=∠EAF(∠1=∠2)。
6. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACAD BC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC ∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG ∠CGD =∠EFD 又EF ∥AB ∴∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG 又EF =CG ∴EF =AC7. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS )∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C8. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB ∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC∵AC =AC ∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE9. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题[含答案解析]
![全等三角形经典题型50题[含答案解析]](https://img.taocdn.com/s3/m/6ac3e596960590c69fc3761c.png)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2ADBC证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF和三角形AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE ∴⊿ADC≌⊿GDE(AAS)BACDF2 1 E∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF所以∠B =∠CFE因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD所以∠DAC=∠FAC又因为AC =AC所以△ADC≌△AFC(SAS ) 所以AD =AF 所以AE =AF +FE =CDB AAD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含问题详解)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题带答案

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB从D 做辅助线3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50题(含答案)

1. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
2. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDB ACDF21EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC3.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE4. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC∴∠EAD =∠CAD∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )∴∠E =∠C∵AC =AB+BD∴AE =AB+BD∵AE =AB+BE∴BD =BE∴∠BDE =∠E∵∠ABC =∠E+∠BDE∴∠ABC =2∠E∴∠ABC =2∠C5. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFECD B A∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC又∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
全等三角形证明经典50题(含答案)
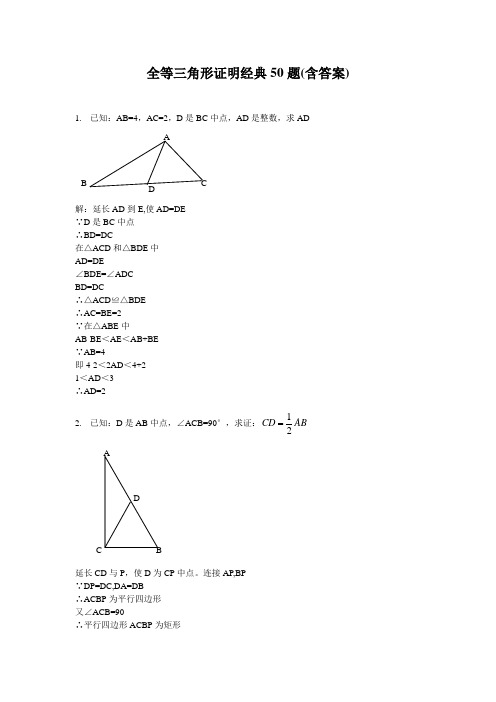
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)B ACDF21 E∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京中考/一模之全等三角形试题精编北京中考16.已知:如图,点E A C ,,在同一条直线上,AB CD ∥,AB CE AC CD ==,.求证:BC ED =.16、△BAC ≌△BCD (SAS ) 所以,BC =ED 海淀一模15. 如图,AC //FE , 点F 、C 在BD 上,AC=DF , BC=EF . 求证:AB=DE .15.证明:∵ AC //EF ,∴ ACB DFE ∠=∠. ………………………………………1分在△ABC 和△DEF 中, ⎪⎩⎪⎨⎧=∠=∠=,,,EF BC DFE ACB DF AC ∴ △ABC ≌△DEF . ………………………………4分∴ AB=DE . ……………………5分 东城一模16. 如图,点B C F E 、、、在同一直线上,12∠=∠,BF EC =,要使ABC ∆≌DEF ∆,还需添加的一个条件是 (只需写出一个即可),并加以证明.ABCDE FABCDEF16.(本小题满分5分)解:可添加的条件为:AC DF B E A D =∠=∠∠=∠或或(写出其中一个即可). …1分证明:∵ BF EC =,∴ BF CF EC CF -=-.即 BC EF = . -------2分 在△ABC 和△DEF 中,,12,,AC DF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ △ABC ≌△DEF . --------5分西城一模15.如图,在△ABC 中,AB=CB ,∠ABC=90º,D 为AB 延长线 上一点,点E 在BC 边上,且BE=BD ,连结AE 、DE 、DC . (1) 求证:△ABE ≌△CBD ;(2) 若∠CAE=30º,求∠BCD 的度数.15.(1)证明:如图1.∵ ∠ABC=90º,D 为AB 延长线上一点,∴ ∠A BE=∠CBD=90º . …………………………………………………1分 在△ABE 和△CBD 中,⎪⎩⎪⎨⎧=∠=∠=,,,BD BE CBD ABE CB AB∴ △ABE ≌△CBD. …………………… 2分(2)解:∵ AB=CB ,∠ABC=90º,∴ ∠CAB =45°. …….…………………… 3分 又∵ ∠CAE=30º,∴ ∠BAE =15°. ……………………………………………………………4分∵ △ABE ≌△CBD ,∴ ∠BCD =∠BAE =15°. ……………………………………………………5分图1通州一模15.如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BAC DAE ∠=∠求证:△ABD ≌△ACE .15. 解:ΘDAE BAC ∠=∠..........................................................................(3分) ∴DAB EAC ∠=∠ .....................................................................(4分) 在AEC ∆和ADB ∆中⎪⎩⎪⎨⎧=∠=∠=AC AB EAC DAB AE AD∴AEC ∆≌ADB ∆(SAS ) .............................................................(5分)石景山一模16.如图,∠ACB =∠CDE =90°,B 是CE 的中点,∠DCE =30°,AC =CD . 求证:AB ∥DE .16.证明:∵∠CDE=90°,∠DCE=30°∴CE 21DE =………………1分 ∵B 是CE 的中点, ∴CE 21CB =∴DE=CB ………………2分 在△ABC 和△CED 中⎪⎩⎪⎨⎧=∠=∠=DE CB CDE ACB CD AC ∴△ABC ≌△CED ………………3分 ∴∠ABC=∠E ………………4分EDCBA第16题图∴AB ∥DE. ………………5分房山一模15.已知:E 是△ABC 一边BA 延长线上一点,且AE =BC ,过点A 作AD ∥BC ,且使AD =AB ,联结ED .求证:AC =DE .E ADCB15. 证明:∵AD ∥BC∴∠EAD=∠B. …………………………1分 ∵AD=AB. ……………………………2分 AE=BC. ……………………………3分 ∴△ABC ≌△DAE.……………………4分 ∴AC =DE . …………………………5分 昌平一模16.如图,已知△ABC 和△ADE 都是等边三角形,连结CD 、BE .求证:CD =BE .16.证明:∵ △ABC 和△ADE 都是等边三角形,∴ AB =AC ,AE =AD ,∠DAE =∠CAB , ∵ ∠DAE -∠CAE =∠CAB -∠CAE , ∴ ∠DAC =∠EAB ,∴ △ADC ≌△AEB . ……………………… 4分 ∴ CD =BE . ……………………… 5分门头沟一模 16.已知:如图,AB ∥ED ,AE 交BD 于点C ,且BC =DC .求证:AB =ED .ED CBADCBAE ADCBFE ACDB16.证明:∵AB ∥ED ,∴∠ABD=∠EDB. ………………………….1分 ∵BC=DC,∠ACB=∠DCE, ……………3分 ∴△ABC ≌△EDC. ………………….4分 ∴AB=ED . ………………………………5分 丰台一模16.已知:如图,AB ∥CD ,AB =CD ,点E 、F 在线段AD 上,且AF=DE .求证:BE =CF .16.证明: Q AF=DE , ∴ AF-EF=DE –EF . 即 AE=DF .………………1分 Q AB ∥CD ,∴∠A =∠D .……2分 在△ABE 和△DCF 中 ,AB =CD ,∠A =∠D ,AE=DF .∴△ABE ≌△DCF .……….4分∴ BE =CF .…………….5分2012.5丰台一模24.已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是 ;(2)将图1中的△ADE 绕点A 旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.EDCBABEMABC24.解:(1)BM =DM 且BM ⊥DM . ………2分(2)成立. ……………3分理由如下:延长DM 至点F ,使MF =MD ,联结CF 、BF 、BD .易证△EMD ≌△CMF .………4分∴ED =CF ,∠DEM =∠1.∵AB =BC ,AD =DE ,且∠ADE =∠ABC =90°,∴∠2=∠3=45°, ∠4=∠5=45°. ∴∠BAD =∠2+∠4+∠6=90°+∠6.∵∠8=360°-∠5-∠7-∠1,∠7=180°-∠6-∠9,∴∠8=360°-45°-(180°-∠6-∠9)-(∠3+∠9)=360°-45°-180°+∠6+∠9- 45°-∠9 =90°+∠6 . ∴∠8=∠BAD .………5分 又AD =CF . ∴△ABD ≌△CBF . ∴BD =BF ,∠ABD =∠CBF .………6分 ∴∠DBF =∠ABC =90°. ∵MF =MD ,∴BM =DM 且BM ⊥DM ..…………7分 海淀一模22.阅读下面材料:小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形, ∠AOB =∠COD =90︒.若△BOC 的面积为1, 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.9ADDA图1 图2小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于 . 请你尝试用平移、旋转、翻折的方法,解决下列问题: 如图3,已知△ABC , 分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID .(1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为三边长的三角形的面积等于 .图322. 解:△BCE 的面积等于 2 . …………1分 (1)如图(答案不唯一): ……2分以EG 、FH 、ID 的长度为三边长的 一个三角形是△EGM . …………3分 (2) 以EG 、FH 、ID 的长度为三边长的三角形的面积等于 3 . …………5分EDCB AGIIGFABCDE西城一模24.已知:在如图1所示的锐角三角形ABC 中,CH ⊥AB 于点H ,点B 关于直线CH 的对称点为D ,AC 边上一点E 满足∠EDA =∠A ,直线DE 交直线CH 于点F . (1) 求证:BF ∥AC ;(2) 若AC 边的中点为M ,求证:2DF EM =;(3) 当AB =BC 时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE 相等的线段,并证明你的结论.图1 图2 24.证明:(1)如图6.∵ 点B 关于直线CH 的对称点为D ,CH ⊥AB 于点H ,直线DE 交直线CH 于点F , ∴ BF=DF ,DH=BH .…………………1分 ∴ ∠1=∠2.又∵ ∠EDA =∠A ,∠EDA =∠1, ∴ ∠A =∠2.∴ BF ∥AC(2)取FD 的中点N ,连结HM 、HN . ∵ H 是BD 的中点,N 是FD 的中点,∴ HN ∥BF . 由(1)得BF ∥AC , ∴ HN ∥AC ,即HN ∥EM. ∵ 在Rt △ACH 中,∠AHC =90°,AC 边的中点为M ,∴ 12HM AC AM ==.∴ ∠A =∠3. ∴ ∠EDA =∠3. ∴ NE ∥HM .∴ 四边形ENHM 是平行四边形.……………………………………… 3分∴ HN=EM .∵ 在Rt △DFH 中,∠DHF =90°,DF 的中点为N , ∴ 12HN DF =,即2DF HN =.∴ 2DF EM =. ………………………………………………………… 4分(3)当AB =BC 时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE 相等的线段是EF 和CE . (只猜想结论不给分)证明:连结CD .(如图8)∵ 点B 关于直线CH 的对称点为D ,CH ⊥AB 于点H ,∴ BC=CD ,∠ABC =∠5. ∵ AB =BC ,∴ 1802ABC A ∠=︒-∠,AB =CD .①∵ ∠EDA =∠A ,∴ 61802A ∠=︒-∠,AE =DE .② ∴ ∠ABC =∠6=∠5. ∵ ∠BDE 是△ADE 的外角, ∴ 6BDE A ∠=∠+∠. ∵ 45BDE ∠=∠+∠, ∴ ∠A =∠4.③由①,②,③得 △ABE ≌△DCE .………………………………………5分 ∴ BE = CE . ……………………………………………………………… 6分由(1)中BF=DF 得 ∠CFE=∠BFC .由(1)中所得BF ∥AC 可得 ∠BFC=∠ECF . ∴ ∠CFE=∠ECF . ∴ EF=CE .∴ BE=EF . ……………………………………………………………… 7分 ∴ BE =EF =CE .(阅卷说明:在第3问中,若仅证出BE =EF 或BE =CE 只得2分)北京中考24.在ABC △中,BA BC BAC =∠=α,,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ 。
