一次函数解析式专题练习
(完整版)函数解析式的练习题兼答案

函数解析式的求法(1)待定系数法:若已知函数的类型(如一次函数、二次函数),可用待定系数法;1.已知f(x)是一次函数,且f[f(x)]=x+2,则f(x)=()A.x+1 B.2x﹣1 C.﹣x+1 D.x+1或﹣x﹣1【解答】解:f(x)是一次函数,设f(x)=kx+b,f[f(x)]=x+2,可得:k(kx+b)+b=x+2.即k2x+kb+b=x+2,k2=1,kb+b=2.解得k=1,b=1.则f(x)=x+1.故选:A.(2)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;9.若函数f(x)满足f(3x+2)=9x+8,则f(x)是()A.f(x)=9x+8 B.f(x)=3x+2C.f(x)=﹣3﹣4 D.f(x)=3x+2或f(x)=﹣3x﹣4【解答】解:令t=3x+2,则x=,所以f(t)=9×+8=3t+2.所以f(x)=3x+2.故选B.(3)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式;18.已知f()=,则()A.f(x)=x2+1(x≠0)B.f(x)=x2+1(x≠1)C.f(x)=x2﹣1(x≠1)D.f(x)=x2﹣1(x≠0)【解答】解:由,得f(x)=x2﹣1,又∵≠1,∴f(x)=x2﹣1的x≠1.故选:C.19.已知f(2x+1)=x2﹣2x﹣5,则f(x)的解析式为()A.f(x)=4x2﹣6 B.f(x)=C.f(x)=D.f(x)=x2﹣2x﹣5【解答】解:方法一:用“凑配法”求解析式,过程如下:;∴.方法二:用“换元法”求解析式,过程如下:令t=2x+1,所以,x=(t﹣1),∴f(t)=(t﹣1)2﹣2×(t﹣1)﹣5=t2﹣t﹣,∴f(x)=x2﹣x﹣,故选:B.(4)消去法:已知f(x)与f 或f(-x)之间的关系式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).21.若f(x)对任意实数x恒有f(x)﹣2f(﹣x)=2x+1,则f(2)=()A.﹣ B.2 C.D.3【解答】解:∵f(x)对任意实数x恒有f(x)﹣2f(﹣x)=2x+1,∴用﹣x代替式中的x可得f(﹣x)﹣2f(x)=﹣2x+1,联立可解得f(x)=x﹣1,∴f(2)=×2﹣1=故选:C函数解析式的求解及常用方法练习题一.选择题(共25小题)2.若幂函数f(x)的图象过点(2,8),则f(3)的值为()A.6 B.9 C.16 D.273.已知指数函数图象过点,则f(﹣2)的值为()A.B.4 C.D.24.已知f(x)是一次函数,且一次项系数为正数,若f[f(x)]=4x+8,则f(x)=()A. B.﹣2x﹣8 C.2x﹣8 D.或﹣2x﹣85.已知函数f(x)=a x(a>0且a≠1),若f(1)=2,则函数f(x)的解析式为()A.f(x)=4x B.f(x)=2x C. D.6.已知函数,则f(0)等于()A.﹣3 B.C.D.37.设函数f(x)=,若存在唯一的x,满足f(f(x))=8a2+2a,则正实数a的最小值是()A.B.C.D.28.已知f(x﹣1)=x2,则f(x)的表达式为()A.f(x)=x2+2x+1 B.f(x)=x2﹣2x+1C.f(x)=x2+2x﹣1 D.f(x)=x2﹣2x﹣110.已知f(x)是奇函数,当x>0时,当x<0时f(x)=()A.B.C.D.11.已知f(x)=lg(x﹣1),则f(x+3)=()A.lg(x+1)B.lg(x+2)C.lg(x+3)D.lg(x+4)12.已知函数f(x)满足f(2x)=x,则f(3)=()A.0 B.1 C.log23 D.313.已知函数f(x+1)=3x+2,则f(x)的解析式是()A.3x﹣1 B.3x+1 C.3x+2 D.3x+414.如果,则当x≠0且x≠1时,f(x)=()A.B.C.D.15.已知,则函数f(x)=()A.x2﹣2(x≠0)B.x2﹣2(x≥2)C.x2﹣2(|x|≥2)D.x2﹣216.已知f(x﹣1)=x2+6x,则f(x)的表达式是()A.x2+4x﹣5 B.x2+8x+7 C.x2+2x﹣3 D.x2+6x﹣1017.若函数f(x)满足+1,则函数f(x)的表达式是()A.x2B.x2+1 C.x2﹣2 D.x2﹣120.若f(x)=2x+3,g(x+2)=f(x﹣1),则g(x)的表达式为()A.g(x)=2x+1 B.g(x)=2x﹣1 C.g(x)=2x﹣3 D.g(x)=2x+7 22.已知f(x)+3f(﹣x)=2x+1,则f(x)的解析式是()A.f(x)=x+ B.f(x)=﹣2x+C.f(x)=﹣x+D.f(x)=﹣x+ 23.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)﹣g(x)=x3+x2+1,则f(1)+g(1)=()A.﹣3 B.﹣1 C.1 D.324.若函数f(x)满足:f(x)﹣4f()=x,则|f(x)|的最小值为()A.B.C.D.25.若f(x)满足关系式f(x)+2f()=3x,则f(2)的值为()A.1 B.﹣1 C.﹣D.二.解答题(共5小题)26.函数f(x)=m+log a x(a>0且a≠1)的图象过点(8,2)和(1,﹣1).(Ⅰ)求函数f(x)的解析式;(Ⅱ)令g(x)=2f(x)﹣f(x﹣1),求g(x)的最小值及取得最小值时x的值.27.已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,求g(x)的解析式.28.已知f(x)=,f[g(x)]=4﹣x,(1)求g(x)的解析式;(2)求g(5)的值.29.已知函数f(x)=x2+mx+n(m,n∈R),f(0)=f(1),且方程x=f(x)有两个相等的实数根.(Ⅰ)求函数f(x)的解析式;(Ⅱ)当x∈[0,3]时,求函数f(x)的值域.30.已知定义在R上的函数g(x)=f(x)﹣x3,且g(x)为奇函数(1)判断函数f(x)的奇偶性;(2)若x>0时,f(x)=2x,求当x<0时,函数g(x)的解析式.函数解析式的求解及常用方法练习题参考答案与试题解析一.选择题(共25小题)2.【解答】解:幂函数f(x)的图象过点(2,8),可得8=2a,解得a=3,幂函数的解析式为:f(x)=x3,可得f(3)=27.故选:D.3.【解答】解:指数函数设为y=a x,图象过点,可得:=a,函数的解析式为:y=2﹣x,则f(﹣2)=22=4.故选:B.4.【解答】解:设f(x)=ax+b,a>0∴f(f(x))=a(ax+b)+b=a2x+ab+b=4x+8,∴,∴,∴f(x)=2x+.故选:A.5.【解答】解:∵f(x)=a x(a>0,a≠1),f(1)=2,∴f(1)=a1=2,即a=2,∴函数f(x)的解析式是f(x)=2x,故选:B.6.【解答】解:令g(x)=1﹣2x=0则x=则f(0)===3 故选D7.【解答】解:由f(f(x))=8a2+2a可化为2x=8a2+2a或log2x=8a2+2a;则由0<2x<1;log2x∈R知,8a2+2a≤0或8a2+2a≥1;又∵a>0;故解8a2+2a≥1得,a≥;故正实数a的最小值是;故选B.8.【解答】解:∵函数f(x﹣1)=x2∴f(x)=f[(x+1)﹣1]=(x+1)2=x2+2x+1 故选A.10.【解答】解:当x<0时,﹣x>0,则f(﹣x)=﹣(1﹣x),又f(x)是奇函数,所以f(x)=﹣f(﹣x)=(1﹣x).故选D.11.【解答】解:f(x)=lg(x﹣1),则f(x+3)=lg(x+2),故选:B.12.【解答】解:函数f(x)满足f(2x)=x,则f(3)=f()=log23.故选:C.13.【解答】∵f(x+1)=3x+2=3(x+1)﹣1 ∴f(x)=3x﹣1故答案是:A 14.【解答】解:令,则x=∵∴f(t)=,化简得:f(t)=即f(x)=故选B15.【解答】解:=,∴f(x)=x2﹣2(|x|≥2).故选:C.16.【解答】解:∵f(x﹣1)=x2+6x,设x﹣1=t,则x=t+1,∴f(t)=(t+1)2+6(t+1)=t2+8t+7,把t与x互换可得:f(x)=x2+8x+7.故选:B.17.【解答】解:函数f(x)满足+1=.函数f(x)的表达式是:f(x)=x2﹣1.(x≥2).故选:D.20.【解答】解:用x﹣1代换函数f(x)=2x+3中的x,则有f(x﹣1)=2x+1,∴g(x+2)=2x+1=2(x+2)﹣3,∴g(x)=2x﹣3,故选:C.22.【解答】解:∵f(x)+3f(﹣x)=2x+1…①,用﹣x代替x,得:f(﹣x)+3f(x)=﹣2x+1…②;①﹣3×②得:﹣8f(x)=8x﹣2,∴f(x)=﹣x+,故选:C.23.【解答】解:由f(x)﹣g(x)=x3+x2+1,将所有x替换成﹣x,得f(﹣x)﹣g(﹣x)=﹣x3+x2+1,根据f(x)=f(﹣x),g(﹣x)=﹣g(x),得f(x)+g(x)=﹣x3+x2+1,再令x=1,计算得,f(1)+g(1)=1.故选:C.24.【解答】解:∵f(x)﹣4f()=x,①∴f()﹣4f(x)=,②联立①②解得:f(x)=﹣(),∴|f(x)|=(),当且仅当|x|=2时取等号,故选B.25.【解答】解:∵f(x)满足关系式f(x)+2f()=3x,∴,①﹣②×2得﹣3f(2)=3,∴f(2)=﹣1,故选:B.二.解答题(共5小题)26.【解答】解:(Ⅰ)由得,解得m=﹣1,a=2,故函数解析式为f(x)=﹣1+log2x,(Ⅱ)g(x)=2f(x)﹣f(x﹣1)=2(﹣1+log2x)﹣[﹣1+log2(x﹣1)]=,其中x>1,因为当且仅当即x=2时,“=”成立,而函数y=log2x﹣1在(0,+∞)上单调递增,则,故当x=2时,函数g(x)取得最小值1.27.【解答】解:设g(x)=ax+b,a≠0;则:f[g(x)]=2ax+b,g[f(x)]=a•2x+b;∴根据已知条件有:;∴解得a=2,b=﹣3;∴g(x)=2x﹣3.28.【解答】解:(1)∵已知f(x)=,f[g(x)]=4﹣x,∴,且g(x)≠﹣3.解得g(x)=(x≠﹣1).(2)由(1)可知:=.29.【解答】解:(Ⅰ)∵f(x)=x2+mx+n,且f(0)=f(1),∴n=1+m+n.…(1分)∴m=﹣1.…(2分)∴f(x)=x2﹣x+n.…(3分)∵方程x=f(x)有两个相等的实数根,∴方程x=x2﹣x+n有两个相等的实数根.即方程x2﹣2x+n=0有两个相等的实数根.…(4分)∴(﹣2)2﹣4n=0.…(5分)∴n=1.…(6分)∴f(x)=x2﹣x+1.…(7分)(Ⅱ)由(Ⅰ),知f(x)=x2﹣x+1.此函数的图象是开口向上,对称轴为的抛物线.…(8分)∴当时,f(x)有最小值.…(9分)而,f(0)=1,f(3)=32﹣3+1=7.…(11分)∴当x∈[0,3]时,函数f(x)的值域是.…(12分)30.【解答】解:(1)∵定义在R上的函数g(x)=f(x)﹣x3,且g(x)为奇函数,∴f(x)=g(x)+x3,故f(﹣x)=g(﹣x)+(﹣x)3=﹣g(x)﹣x3=﹣f(x),∴函数f(x)为奇函数;(2)∵x>0时,f(x)=2x,∴g(x)=2x﹣x3,当x<0时,﹣x>0,故g(﹣x)=2﹣x﹣(﹣x)3,由奇函数可得g(x)=﹣g(﹣x)=﹣2﹣x﹣x3.。
求一次函数的解析式练习题共18页文档

3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
谢谢!
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
一次函数求解析式练习

2014-2015学年度八年级数学同步提高(一次函数解析式求法)1、已知一次函数的图像经过(4、15)、(6、-5)两点,求此一次函数的解析式。
2、已知一次函数的图像平行于直线y=2x-1,且过点(1,3), 求此一次函数的解析式。
3、已知图像经过点(2,-1),且与直线132y x=-+相交于y轴上同一点,求此一次函数的解析式。
4.直线y=kx+b的图像经过(1,2)和直线y=2x-4相交于x轴上一点,求函数解析式5.已知直线y=kx+b与直线y= -2x+4关于y轴对称,求k、b的值。
6.已知直线y=kx+b与直线y= -2x+4关于x轴对称,求k、b的值。
7.已知直线y=kx+6与直线y= -x+4交于A(1,n)点,求k8.若一次函数的图象与直线121y x =-的交点纵坐标是3,且与直线285y x =-无交点.求:这个一次函数解析式.9、已知一次函数y=kx+b 与y=x 平行且在y 轴上的截距为3,求另一条与直线y=kx+b 的图像关于x 对称的直线的解析式.10、已知y-b 与x-a 成正比例,当x=1时y=-2;当x=3时y=2。
求y 与x 的解析式11、若把直线1l 向左平移3个单位,再向下平移2个单位得到直线2l ,2l 的解析式为y=-2x-3,求直线1l 的解析式。
12. 如果一次函数y=kx+b 的自变量x 的取值范围是-2≤x ≤6,相应的函数值范围是-11≤y ≤9,求此函数的解析式13、已知直线l 与直线y=2x+1的交点的横坐标为2,与直线y=-x-8的交点的纵坐标为-7,求直线的解析式。
14.已知一次函数y =kx +b 的图象经过点(-1,-5),且与正比例函数x y 21=的图象相交于点(2,a),求:(1)a 的值。
(2)k 、b 的值。
(3)这两个函数图象与x 轴所围成的三角形面积。
15.已知一次函数y=x+3的图象与x 轴的交点为A 与一次函数y=kx+b 的图象的交点为B ,且B 点横坐标为1,该一次函数与x 轴交于点C (5,0),求y=kx+b 的解析式及△ABC 的面积。
《一次函数》专项练习和中考真题(含答案解析及点睛)

《1.等腰三角形底角与顶角之间的函数关系A .正比例函数 B .一次函数【答案】B【分析】根据一次函数的定义,可得答案【解析】设等腰三角形的底角为y ,顶角为所以,y=﹣12x+90°,即等腰三角形底角与【点睛】本题考查了实际问题与一次函数2.已知y 关于x 成正比例,且当x 时A .3 B .3-【答案】B【分析】先利用待定系数法求出y =【详解】设y kx =,Q 当2x =时,3y x ∴=-,∴当1x =时,3y =-【点睛】本题考查了待定系数法求正比例函点的坐标代入求出k 即可.3. 已知函数y =kx +b 的部分函数值如表所示A .x =2 B .x =3 C 【答案】A【解析】∵当x =0时,y =1,当x =1,y 当y =–3时,–2x +1=–3,解得:x =2,4.如图,直线y=kx+3经过点(2,0,A .x >2B .x <2 《一次函数》专项练习数关系是( ) C .反比例函数D .二次函数答案.顶角为x ,由题意,得x+2y=180, 底角与顶角之间的函数关系是一次函数关系,故选函数,根据题意正确列出函数关系式是解题的关键2=时,6y =-,则当1x =时,y 的值为 C .12D .12-3x -,然后计算1x =对应的函数值. 6y =-,26k ∴=-,解得3k =-,13⨯=-.故选B .比例函数的解析式:设正比例函数解析式为y kx k =表所示,则关于x 的方程kx +b +3=0的解是x … –2 –1 01… y…531 –1….x =–2 D .x =–3 =–1,∴,解得:,∴y =–,故关于x 的方程kx +b +3=0的解是x =2,故选A ),则关于x 的不等式kx+3>0的解集是( )C .x≥2 D .x≤211b k b =+=-⎧⎨⎩21k b =-=⎧⎨⎩故选B . 关键. ()0≠,然后把一个已知2x +1,.【答案】B【分析】直接利用函数图象判断不等式【解析】由一次函数图象可知:关于x的不【点睛】本题考查了一次函数的图象与性质等式之间的内在联系.5.如图,在平面直角坐标系中,直线l与直线l1在第一象限交于点C.若∠BOCAB【答案】B【分析】过C作CD⊥OA于D,利用直线3.依据CD∥BO,可得OD13=AOk的值.【解析】如图,过C作CD⊥OA于D.即A(,0),B(0,1),∴Rt△∵∠BOC=∠BCO,∴CB=BO=1,∵CD∥BO,∴OD13=AO=,得:23=,即k =B式kx+3>0的解集在x轴上方,进而得出结果.的不等式kx+3>0的解集是x<2;故选B.与性质和一元一次不等式及其解法,解题的关键是掌1:y=x+1与x轴,y轴分别交于点A和点BOC=∠BCO,则k的值为( )C D.直线l1:y=+1,即可得到A(,0),B(0=CD23=BO23=,进而得到C23,),.直线l1:y=+1中,令x=0,则y=1,令AOB中,AB==3.AC=2.CD23=BO23=,即C23,),把C23,.键是掌握一次函数与一元一次不B,直线l2:y=kx(k≠0),1),AB==,代入直线l2:y=kx,可得令y=0,则x=,)代入直线l2:y=kx,可【点睛】本题考查了两直线相交或平行问题组成的二元一次方程组的解.6.已知点A (-5,a ),B (4,b )在直线y =-3x 【答案】>【分析】先根据一次函数的解析式判断出函【解析】∵直线y=-3x+2中,k=-3<0,∵-5<4,∴a >b ,故答案为>.【点睛】本题考查了一次函数的性质,根据如果k>0,直线就从左往右上升,y 随7.如图,四边形ABCD 的顶点坐标分别ABCD 分成面积相等的两部分时,直线A .116105y x =+ B .23y =【答案】D【分析】由已知点可求四边形ABCD 分成y=-x+3,设过B 的直线l 为y=kx+b ,并求1125173121k k k k --⎛⎫⎛⎫=⨯-⨯+ ⎪⎪+⎝⎭⎝⎭,即可【解析】解:由()()4,0,2,1,A B ---∴四边形ABCD 分成面积(12AC =⨯设过B 的直线l 为y kx b =+,将点B 代入∴直线CD 与该直线的交点为45,k k -⎛+⎝∴1125173121k k k k --⎛⎫⎛=⨯-⨯+ ⎪ +⎝⎭⎝,∴直线解析式为5342y x =+;故选:【点睛】本题考查一次函数的解析式求法式的方法是解题的关键.行问题,两条直线的交点坐标,就是由这两条直线相+2上,则a ________b .(填“>”“<”或“=”号 断出函数的增减性,再比较出-5与4的大小即可解答,∴此函数是减函数, 根据题意判断出一次函数的增减性是解答此题的关x 的增大而增大,如果k<0,直线就从左往右下降分别()()()()4,0,2,1,3,0,0,3A B C D ---,当过点直线l 所表示的函数表达式为( ) 13x + C .1y x =+ D .54y x =+分成面积()113741422B AC y =⨯⨯+=⨯⨯=;并求出两条直线的交点,直线l 与x 轴的交点坐标即可求k 。
一次函数练习题以及解析解读

【解题方法指导】例1. (1y与x成正比例函数,当时,y=5.求这个正比例函数的解析式.(2已知一次函数的图象经过A(-1,2和B(3,-5两点,求此一次函数的解析式. 解:(1设所求正比例函数的解析式为把,y=5代入上式得,解之,得∴所求正比例函数的解析式为(2设所求一次函数的解析式为∵此图象经过A(-1,2、B(3,-5两点,此两点的坐标必满足,将、y=2和x=3、分别代入上式,得解得∴此一次函数的解析式为点评:(1不能化成带分数.(2所设定的解析式中有几个待定系数,就需根据已知条件列几个方程.例2. 拖拉机开始工作时,油箱中有油20升,如果每小时耗油5升,求油箱中的剩余油量Q(升与工作时间t(时之间的函数关系式,指出自变量x的取值范围,并且画出图象. 分析:拖拉机一小时耗油5升,t小时耗油5t升,以20升减去5t升就是余下的油量.解:图象如下图所示点评:注意函数自变量的取值范围.该图象要根据自变量的取值范围而定,它是一条线段,而不是一条直线.例3. 已知一次函数的图象经过点P(-2,0,且与两坐标轴截得的三角形面积为3,求此一次函数的解析式.分析:从图中可以看出,过点P作一次函数的图象,和y轴的交点可能在y轴正半轴上,也可能在y轴负半轴上,因此应分两种情况进行研究,这就是分类讨论的数学思想方法.解:设所求一次函数解析式为∵点P的坐标为(-2,0∴|OP|=2设函数图象与y轴交于点B(0,m根据题意,SΔPOB=3∴∴|m|=3∴∴一次函数的图象与y轴交于B1(0,3或B2(0,-3将P(-2,0及B1(0,3或P(-2,0及B2(0,-3的坐标代入y=kx+b中,得解得∴所求一次函数的解析式为点评:(1本题用到分类讨论的数学思想方法.涉及过定点作直线和两条坐标轴相交的问题,一定要考虑到方向,是向哪个方向作.可结合图形直观地进行思考,防止丢掉一条直线.(2涉及面积问题,选择直角三角形两条直角边乘积的一半,结果一定要得正值.【综合测试】一、选择题:1. 若正比例函数y=kx的图象经过一、三象限,则k的取值范围是(A. B. C. D.2. 一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的高度y(cm与燃烧时间x (小时的函数关系用图象表示为(3. (北京市一次函数的图象不经过的象限是(A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. (陕西省课改实验区直线与x轴、y轴所围成的三角形的面积为(A. 3B. 6C.D.5. (海南省一次函数的大致图象是(二、填空题:1. 若一次函数y=kx+b的图象经过(0,1和(-1,3两点,则此函数的解析式为_____________.2. (2006年北京市中考题若正比例函数y=kx的图象经过点(1,2,则此函数的解析式为_____________.三、一次函数的图象与y轴的交点为(0,-3,且与坐标轴围成的三角形的面积为6,求这个一次函数的解析式.四、(芜湖市课改实验区某种内燃动力机车在青藏铁路试验运行前,测得该种机车机械效率η和海拔高度h(,单位km的函数关系式如图所示.(1请你根据图象写出机车的机械效率η和海拔高度h(km的函数关系;(2求在海拔3km的高度运行时,该机车的机械效率为多少?五、(浙江省丽水市如图建立羽毛球比赛场景的平面直角坐标系,图中球网高OD为1.55米,双方场地的长OA=OB=6.7(米.羽毛球运动员在离球网5米的点C处起跳直线扣杀,球从球网上端的点E直线飞过,且DE为0.05米,刚好落在对方场地点B处.(1求羽毛球飞行轨迹所在直线的解析式;(2在这次直线扣杀中,羽毛球拍击球点离地面的高度FC为多少米?(结果精确到0.1米【综合测试答案】一、选择题:1. B2. B3. D4. A5. B二、填空题:1. 2.三、分析:一次函数的解析式y=kx+b有两个待定系数,需要利用两个条件建立两个方程.题目中一个条件比较明显,即图象和y轴的交点的纵坐标是-3,另一个条件比较隐蔽,需从“和坐标轴围成的面积为6”确定.解:设一次函数的解析式为,∵函数图象和y轴的交点的纵坐标是-3,∴∴函数的解析式为 .求这个函数图象与x轴的交点,即解方程组:得即交点坐标为(,0由于一次函数图象与两条坐标轴围成的直角三角形的面积为6,由三角形面积公式,得∴∴∴这个一次函数的解析式为四、解:(1由图象可知,与h的函数关系为一次函数设∵此函数图象经过(0,40%,(5,20%两点∴解得∴(2当h=3km时,∴当机车运行在海拔高度为3km的时候,该机车的机械效率为28%五、解:(1依题意,设直线BF为y=kx+b∵OD=1.55,DE=0.05∴即点E的坐标为(0,1.6又∵OA=OB=6.7∴点B的坐标为(-6.7,0由于直线经过点E(0,1.6和点B(-6.7,0,得解得,即(2设点F的坐标为(5,,则当x=5时,则FC=2.8∴在这次直线扣杀中,羽毛球拍击球点离地面的高度是2.8米。
求一次函数的解析式练习题

五、融会贯通——分类与分层
(三)与求函数解析式有关的实际应用题 4、小明将父母给的零用钱按每月相等的数额存放
1.已知正比例函数的图象经过点 (-2,4). 求这个正比例函数的解析式.
Page 1
例1:已知一次函数的图象经过点(3,5)与 (-4,-9).求这个一次函数的解析式. 解:设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点(3,5)与(-4,-9).
∴ 3k+b=5 -4k+b=-9 解得 k=2 b=-1
2 0 b,
b 2.
∴过A,B两点的直线的表达式为y=x-2. ∵当x=4时,y=4-2=2. ∴点C(4,2)在直线y=x-2上. ∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
融会贯通——分类与分层
(一)求函数解析式的综合应用
1. (2011 浙江湖州) 已知:一次函数 y=kx+b的图象经过M(0, 2),(1,3)两点. (l) 求k、b的值; (2) 若一次函数的图象与x轴的交点为A(a,0),求a的值.
Page 6
变式5: 已知弹簧长度y(厘米)在一定限度内 所挂重物质量x(千克)的一次函数,现已测得 不挂重物时弹簧的长度是6厘米,挂4千克质量 的重物时,弹簧的长度是7.2厘米,求这个一次 函数的解析式。
解:设这个一次函数的解析式为:y=kx+b 根据题意,把x=0,y=6和x=4,y=7.2代入,得: b=6 k=0.3 4k+b=7.2 解得 b=6
一次函数的解析式专项练习30题(有答案)

求一次函数解析式专项练习1.已知A(2,﹣1),B(3,﹣2),C(a,a)三点在同一条直线上.(1)求a的值;(2)求直线AB与坐标轴围成的三角形的面积.2.如图,直线l与x轴交于点A(﹣1.5,0),与y轴交于点B(0,3)(1)求直线l的解析式;(2)过点B作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.3.已知一次函数的图象经过(1,2)和(﹣2,﹣1),求这个一次函数解析式及该函数图象与x 轴交点的坐标.4.如图所示,直线l是一次函数y=kx+b的图象.(1)求k、b的值;(2)当x=2时,求y的值;(3)当y=4时,求x的值.5.已知一次函数y=kx+b的图象与x轴交于点A(﹣6,0),与y轴交于点B.若△AOB的面积为12,求一次函数的表达式.6.已知一次函数y=kx+b,当x=﹣4时,y的值为9;当x=6时,y的值为3,求该一次函数的关系式.7.已知y与x+2成正比例,且x=0时,y=2,求:(1)y与x的函数关系式;(2)其图象与坐标轴的交点坐标.8.如果y+3与x+2成正比例,且x=3时,y=7.(1)写出y与x之间的函数关系式;(2)画出该函数图象;并观察当x取什么值时,y<0?9.直线y=kx+b是由直线y=﹣x平移得到的,此直线经过点A(﹣2,6),且与x轴交于点B.(1)求这条直线的解析式;(2)直线y=mx+n经过点B,且y随x的增大而减小.求关于x的不等式mx+n<0的解集.10.已知y与x+2成正比例,且x=1时,y=﹣6.(1)求y与x之间的函数关系式,并建立平面直角坐标系,画出函数图象;(2)结合图象求,当﹣1<y≤0时x的取值范围.11.已知y﹣2与2x+1成正比例,且当x=﹣2时,y=﹣7,求y与x的函数解析式.12.已知y与x﹣1成正比例,且当x=﹣5时,y=2,求y与之间的函数关系式.13.已知一次函数的图象经过点A (,m)和B (,﹣1),其中常量m≠﹣1,求一次函数的解析式,并指出图象特征.14.已知一次函数y=(k﹣1)x+5的图象经过点(1,3).(1)求出k的值;(2)求当y=1时,x的值.15.一次函数y=k1x﹣4与正比例函数y=k2x的图象经过点(2,﹣1).(1)分别求出这两个函数的表达式;(2)求这两个函数的图象与x轴围成的三角形的面积.16.已知y﹣3与4x﹣2成正比例,且x=1时,y=﹣1.(1)求y与x的函数关系式.(2)如果y的取值范围为3≤y≤5时,求x的取值范围.17.若一次函数y=3x+b的图象与两坐标轴围成的三角形面积为24,试求这个一次函数的解析式.18.如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6,相应函数值是﹣11≤y≤9,求此函数解析式.19.某一次函数图象的自变量的取值范围是﹣3≤x≤6,相应的函数值的变化范围是﹣5≤y≤﹣2,求这个函数的解析式.20.已知,直线AB经过A(﹣3,1),B(0,﹣2),将该直线沿y轴向下平移3个单位得到直线MN.(1)求直线AB和直线MN的函数解析式;(2)求直线MN与两坐标轴围成的三角形面积.21.一次函数的图象经过点A(0,﹣2),且与两条坐标轴截得的直角三角形的面积为3,求这个一次函数的解析式.22.如果y+2与x+1成正比例,当x=1时,y=﹣5.(1)求出y与x的函数关系式.(2)自变量x取何值时,函数值为4?23.已知y﹣3与4x﹣2成正比例,且当x=1时,y=5,(1)求y与x的函数关系式;(2)求当x=﹣2时的函数值:(3)如果y的取值范围是0≤y≤5,求x的取值范围;(4)若函数图象与x轴交于A点,与y轴交于B点,求S△AOB.24.已知y﹣3与x成正比例,且x=2时,y=7.(1)求y与x的函数关系式;(2)当时,求y的值;(3)将所得函数图象平移,使它过点(2,﹣1).求平移后直线的解析式.25.已知:一次函数y=kx+b的图象与y轴的交点到原点的距离为3,且过A(2,1)点,求它的解析式.26.已知一次函数y=(3﹣k)x+2k+1.(1)如果图象经过(﹣1,2),求k;(2)若图象经过一、二、四象限,求k的取值范围.27.正比例函数与一次函数y=﹣x+b的图象交于点(2,a),求一次函数的解析式.28.已知y+5与3x+4成正比例,且当x=1时,y=2.(1)求出y与x的函数关系式;(2)设点P(a,﹣2)在这条直线上,求P点的坐标.29.已知一次函数y=kx+b(k≠0)在x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式.30.已知:关于x的一次函数y=(2m﹣1)x+m ﹣2若这个函数的图象与y轴负半轴相交,且不经过第二象限,且m为正整数.(1)求这个函数的解析式.(2)求直线y=﹣x和(1)中函数的图象与x 轴围成的三角形面积.一次函数的解析式30题参考答案:1.(1)设直线AB解析式为y=kx+b,依题意,得,解得∴直线AB解析式为y=﹣x+1∵点C(a,a)在直线AB上,∴a=﹣a+1,解得a=;(2)直线AB与x轴、y轴的交点分别为(1,0),(0,1)∴直线AB 与坐标轴围成的三角形的面积为2.(1)设直线l的解析式为y=kx+b,∵直线l与x轴交于点A(﹣1.5,0),与y轴交于点B (0,3),∴代入得:,解得:k=2,b=3,∴直线l的解析式为y=2x+3;(2)解:分为两种情况:①当P在x轴的负半轴上时,∵A(﹣1.5,0),B(0,3),∴OP=2OA=3,0B=3,∴AP=3﹣1.5=1.5,∴△ABP 的面积是×AP×OB=×1.5×3=2.25;②当P在x轴的正半轴上时,∵A(﹣1.5,0),B(0,3),∴OP=2OA=3,0B=3,∴AP=3+1.5=4.5,∴△ABP 的面积是×AP×OB=×4.5×3=6.25.3.设一次函数的解析式为y=kx+b(k≠0),由已知得:,解得:,∴一次函数的解析式为y=x+1,当y=0时,x+1=0,∴x=﹣1,∴该函数图象与x轴交点的坐标是(﹣1,0)4.(1)由图象可知,直线l过点(1,0)和(0,),则,解得:,即k=,b=;(2)由(1)知,直线l的解析式为y=x+,当x=2时,有y=×2+=;(3)当y=4时,代入y=x+得:4=x+,解得x=﹣5.5.∵图象经过点A(﹣6,0),∴0=﹣6k+b,即b=6k ①,∵图象与y轴的交点是B(0,b),∴•OB=12,即:,∴|b|=4,∴b1=4,b2=﹣4,代入①式,得,,一次函数的表达式是或6.根据题意,得,解得.故该一次函数的关系式是y=﹣x+.7.(1)根据题意,得y=k(x+2)(k≠0);由x=0时,y=2得2=k(0+2),解得k=1,所以y与x的函数关系式是y=x+2;(2)由,得;由,得,所以图象与x轴的交点坐标是:(﹣2,0);与y轴的交点坐标为:(0,2).8.(1)∵y+3与x+2成正比例,∴设y+3=k(x+2)(k≠0),∵当x=3时,y=7,∴7+3=k(3+2),解得,k=2.则y+3=2(x+2),即y=2x+1;(2)由(1)知,y=2x+1.令x=0,则y=1,.令y=0,则x=﹣,所以,该直线经过点(0,1)和(﹣,0),其图象如图所示:由图示知,当x<﹣时,y<09.(1)一次函数y=kx+b的图象经过点(﹣2,6),且与y=﹣x的图象平行,则y=kx+b中k=﹣1,当x=﹣2时,y=6,将其代入y=﹣x+b,解得:b=4.则直线的解析式为:y=﹣x+4;(2)如图所示:∵直线的解析式与x轴交于点B,∴y=0,0=﹣x+4,∴x=4,∴B点坐标为:(4,0),∵直线y=mx+n经过点B,且y随x的增大而减小,∴m<0,此图象与y=﹣x+4增减性相同,∴关于x的不等式mx+n<0的解集为:x>410.(1)设y=k(x+2),∵x=1时,y=﹣6.∴﹣6=k(1+2)k=﹣2.∴y=﹣2(x+2)=﹣2x﹣4.图象过(0,﹣4)和(﹣2,0)点(2)从图上可以知道,当﹣1<y≤0时x的取值范围﹣2≤x<﹣.11.∵y﹣2与2x+1成正比例,∴设y﹣2=k(2x+1)(k≠0),∵当x=﹣2时,y=﹣7,∴﹣7﹣2=k(﹣4+1),∴k=3,∴y=6x+5.12.设y=k(x﹣1),把x=﹣5,y=2代入,得2=(﹣5﹣1)k,解得.所以y与x 之间的函数关系式是13.设过点A,B的一次函数的解析式为y=kx+b,则m=k+b,﹣1=k+b,两式相减,得m+1=k+k,即m+1=(m+1),∵m≠﹣1,则k=2,∴b=m﹣1,则函数的解析式为y=2x+m﹣1(m≠﹣1),其图象是平面内平行于直线y=2x(但不包括直线y=2x﹣2)的一切直线14.(1)∵一次函数y=(k﹣1)x+5的图象经过点(1,3),∴3=(k﹣1)×1+5.∴k=﹣1.(2)∵y=﹣2x+5中,当y=1时,1=﹣2x+5∴x=2.15.(1)把点(2,﹣1)代入y=k1x﹣4得:2k1﹣4=﹣1,解得:k1=,所以解析式为:y=x﹣4;把点(2,﹣1)代入y=k2x得:2k2=﹣1,解得:k2=﹣,所以解析式为:y=﹣x;(2)因为函数y=x﹣4与x 轴的交点是(,0),且两图象都经过点(2,﹣1),所以这两个函数的图象与x轴围成的三角形的面积是:S=××1=.16.(1)设y﹣3=k(4x﹣2),(2分)当x=1时,y=﹣1,∴﹣1﹣3=k(4×1﹣2),∴k=﹣2(4分),∴y﹣3=﹣2(4x﹣2),∴函数解析式为y=﹣8x+7.(5分)(2)当y=3时,﹣8x+7=3,解得:x=,当y=5时,﹣8x+7=5,解得:x=,∴x 的取值范围是≤x ≤.17.当x=0时,y=b,当y=0时,x=﹣,∴一次函数与两坐标轴的交点为(0,b)(﹣,0),∴三角形面积为:×|b|×|﹣|=24,即b2=144,解得b=±12,∴这个一次函数的解析式为y=3x+12或y=3x﹣12 18.根据题意,①当k>0时,y随x增大而增大,∴当x=﹣2时,y=﹣11,x=6时,y=9∴解得,∴函数解析式为y=x﹣6;②当k<0时,函数值随x增大而减小,∴当x=﹣2时,y=9,x=6时,y=﹣11,∴解得,∴函数解析式为y=﹣x+4.因此,函数解析式为y=x﹣6或y=﹣x+4 19.设一次函数解析式为y=kx+b,根据题意①当k>0时,x=﹣3时,y=﹣5,x=6时,y=﹣2,∴解得,∴函数的解析式为:y=x﹣4;②当k<0时,x=﹣3时,y=﹣2,x=6时,y=﹣5,∴解得,∴函数解析式为y=﹣x﹣3;因此这个函数的解析式为y=x﹣4或y=﹣x﹣3.20.设直线AB的解析式为y=kx+b,∵A(﹣3,1),B(0,﹣2),∴,∴k=﹣1,∴直线AB的解析式为:y=﹣x﹣2,∵将该直线沿y轴向下平移3个单位得到直线MN,∴直线MN的函数解析式为:y=﹣x﹣5;(2)∵直线MN与x轴的交点为(﹣5,0),与y轴的交点坐标为(0,﹣5),∴直线MN 与两坐标轴围成的三角形面积为×|﹣5|×||﹣5=12.5.21.设与x轴的交点为B,则与两坐标轴围成的直角三角形的面积=AO•BO,∵AO=2,∴BO=3,∴点B纵坐标的绝对值是3,∴点B横坐标是±3;设一次函数的解析式为:y=kx+b,当点B纵坐标是3时,B(3,0),把A(0,﹣2),B(3,0)代入y=kx+b,得:k=,b=﹣2,所以:y=x﹣2,当点B纵坐标=﹣3时,B(﹣3,0),把A(0,﹣2),B(﹣3,0)代入y=kx+b,得k=﹣,b=﹣2,所以:y=﹣x﹣2.22.(1)依题意,设y+2=k(x+1),将x=1,y=﹣5代入,得k(1+1)=﹣5+2,解得k=﹣1.5,∴y+2=﹣1.5(x+1),即y=﹣1.5x﹣3.5;(2)把y=4代入y=﹣1.5x﹣3.5中,得﹣1.5x﹣3.5=4,解得x=﹣5,即当x=﹣5时,函数值为423.(1)设y﹣3=k(4x﹣2),∵x=1时,y=5,∴5﹣3=k(4﹣2),解得k=1,∴y与x的函数关系式y=4x+1;(2)将x=﹣2代入y=4x+1,得y=﹣7;(3)∵y的取值范围是0≤y≤5,∴0≤4x+1≤5,解得﹣≤x≤1;(4)令x=0,则y=1;令y=0,则x=﹣,∴A(0,1),B(﹣,0),∴S△AOB =××1=.24.(1)∵y﹣3与x成正比例,∴y﹣3=kx(k≠0)成正比例,把x=2时,y=7代入,得7﹣3=2k,k=2;∴y与x的函数关系式为:y=2x+3,(2)把x=﹣代入得:y=2×(﹣)+3=2;(3)设平移后直线的解析式为y=2x+3+b,把点(2,﹣1)代入得:﹣1=2×2+3+b,解得:b=﹣8,故平移后直线的解析式为:y=2x﹣525.根据题意得:当b=3时,y=kx+3,过A(2,1).1=2k+3k=﹣1.∴解析式为:y=﹣x+3.当b=﹣3时,y=kx﹣3,过A(2,1),1=2k﹣3,k=2.故解析式为:y=2x﹣3.26.(1)∵一次函数y=(3﹣k)x+2k+1的图象经过(﹣1,2),∴2=(3﹣k)×(﹣1)+2k+1,即2=3k﹣2,解得k=;(2))∵一次函数y=(3﹣k)x+2k+1的图象经过一、二、四象限,∴,解得,k>3.故k的取值范围是k>3.27.根据题意,得,解得,,所以一次函数的解析式是y=﹣x+3.28.(1)∵y+5与3x+4成正比例,∴设y+5=k(3x+4),即y=3kx+4k﹣5(k是常数,且k≠0).∵当x=1时,y=2,∴2+5=(3×1)k,解得,k=1,故y与x的函数关系式是:y=3x﹣1;(2)∵点P(a,﹣2)在这条直线上,∴﹣2=3a﹣1,解得,a=﹣,∴P 点的坐标是(﹣,﹣2)29.把(1,5)、(6,0)代入y=kx+b中,得,解得,∴一次函数的解析式是y=﹣x+6.30.(1)由题意得:,解得:<m<2,又∵m为正整数,∴m=1,函数解析式为:y=x﹣1.(2)由(1)得,函数图象与x轴交点为(1,0)与y 轴交点为(0,﹣1),∴所围三角形的面积为:×1×1=。
《用待定系数法求一次函数解析式》练习题

=-200x+11 000,当 y=0 时,x=55,∴返回到家的时间为 8:55.
易错点:对图表中的一次函数关系不能作出明确判断
10 .目前,我国大约有 1.3 亿高血压病患者,预防高血压不容忽
视.“千帕(kpa)”和“毫米汞柱(mmHg)”都是表示血压的单位.请
你根据表格提供的信息,判断下列各组换算正确的是( C )
14.(导学号69654150)(2017·苏州)某长途汽车客运公司规定旅客可免费 携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是 行李质量x(kg)的一次函数.已知行李质量为20 kg时需付行李费2元,行 李质量为50 kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数解析式;
1
1 (2)当 y=0 时, x-2=0,得 x=10. 5 答:旅客最多可免费携带行李 10 kg.
15.(导学号69654151)(2016·河北)某商店能通过调低价格的方式促销n
4.已知一次函数 y=kx+b 的图象经过点 A(0,-2),B(1,0),则 b=
2 . -2 ,k=____ ____
5.已知一次函数图象经过A(-2,-3),B(1,3)两点. (1)求这个一次函数的解析式; (2)试判断P(-1,1)是否在这个函数图象上?
解:(1)设一次函数的解析式为 y=kx+b,∵A(-2,-3),B(1,3)
端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点
A运动.已知线段AB长为90 cm,甲的速度为2.5 cm/s.设运动时间为
x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则
图中线段DE所表示的函数解析式为_________________________ .(并 y=4.5k-90(20≤x≤36) 写出自变量的取值范围)
一次函数专项练习(经典题型收集)

一次函数专项练习(经典题型收集)1.自变量x的取值范围为x≠-1.2.自变量x的取值范围为x≠0.3.代入点P(-2,m),得m=2*(-2)+1=-3.4.交点坐标分别为(0,-1)和(1,1)。
5.由于函数经过原点,代入得m=2.6.答案为B,即(-2,1)。
7.底为y,面积为1/2*y*x=8,解得y=16/x。
8.图象为y=x^2,不是一次函数。
9.长度剩余y与时间x成反比例关系,即y=20-5x。
10.代入交点(1,6),解得k=1,b=-3.一次函数练(二)1.n=2.2.解析式为y=(2m-1)/(m^2-3)。
3.m<1/2.4.解得m=4或m=-2.5.y=-6.6.答案为(-2,-4)。
7.根据比例关系,y-2=kx,代入x=-2和y=4,解得k=-3/2,再代入x=6,解得y=7.1.一次函数是指函数的自变量的最高次数为1的函数。
因此,③y=x和④y=-x-1是一次函数。
2.首先将函数展开,得到y=mx^5+10x- m^2+3.由于一次函数的解析式为y=kx+b,因此要求m使得y=mx^5+10x-m^2+3满足一次函数的形式。
因为一次函数的自变量的最高次数为1,因此只有当m=4或m=-4时,y才能写成一次函数的形式。
此时解析式分别为y=4x+3和y=-4x+3.3.当m=1时,y=(m+2)x+m-1变为y=3x,为一次函数;当m=-2时,y=(m+2)x+m-1变为y=-4x-5,为正比例函数。
4.向下平移1个单位后,直线y=-2x的解析式变为y=-2x-1.5.直线y=2x-4与x轴的交点坐标为(2,0),与y轴的交点坐标为(0,-4),三角形的底为2,高为4,因此面积为4.6.当a=-2时,直线经过原点,此时解析式为y=-2x;当a=1时,直线与y轴交于点(0,-2),此时解析式为y=3x-1.7.将点A的坐标代入函数y=2x-1中,得到1-a=2(a+2)-1,解得a=1.8.因为直线与y轴平行,所以斜率为2.又因为过点(-2,1),所以解析式为y=2x+5.9.由于两个函数的图象平行,因此它们的斜率相等。
一次函数解析式的确定练习题
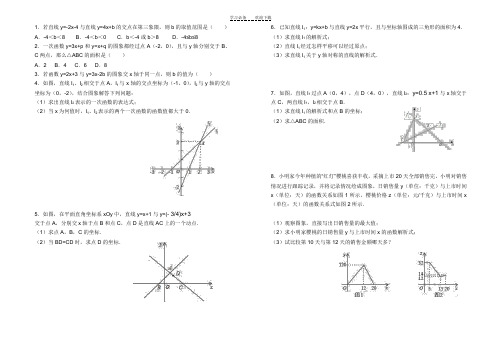
学习必备 欢迎下载1.若直线y=-2x-4与直线y=4x+b 的交点在第三象限,则b 的取值范围是( ) A .-4<b <8 B .-4<b <0 C .b <-4或b >8 D .-4≤b≤82.一次函数y=3x+p 和y=x+q 的图象都经过点A (-2,0),且与y 轴分别交于B 、C 两点,那么△ABC 的面积是( ) A .2 B .4 C .6 D .83.若函数y=2x+3与y=3x-2b 的图象交x 轴于同一点,则b 的值为( ) 4.如图,直线l 1、l 2相交于点A ,l 1与x 轴的交点坐标为(-1,0),l 2与y 轴的交点坐标为(0,-2),结合图象解答下列问题: (1)求出直线l 2表示的一次函数的表达式;(2)当x 为何值时,l 1、l 2表示的两个一次函数的函数值都大于0.5.如图,在平面直角坐标系xOy 中,直线y=x+1与y=(- 3/4)x+3 交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点. (1)求点A ,B ,C 的坐标. (2)当BD=CD 时,求点D 的坐标.6.已知直线l 1:y=kx+b 与直线y=2x 平行,且与坐标轴围成的三角形的面积为4. (1)求直线l 1的解析式;(2)直线l 1经过怎样平移可以经过原点; (3)求直线l 1关于y 轴对称的直线的解析式.7.如图,直线l 1过点A (0,4),点D (4,0),直线l 2:y=0.5 x+1与x 轴交于点C ,两直线l 1,l 2相交于点B . (1)求直线l 1的解析式和点B 的坐标; (2)求△ABC 的面积.8.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y (单位:千克)与上市时间x (单位:天)的函数关系如图1所示,樱桃价格z (单位:元/千克)与上市时间x (单位:天)的函数关系式如图2所示.(1)观察图象,直接写出日销售量的最大值;(2)求小明家樱桃的日销售量y 与上市时间x 的函数解析式; (3)试比较第10天与第12天的销售金额哪天多?。
初中数学求一次函数的表达式15道题题专题训练含答案

(2)求点 的坐标;
4.如图,直线 的表达式为 ,直线 与x轴交于点D,直线 : 与x轴交于点A,且经过点B,直线 、 交于点 .
(1)求m的值;
(2)求直线 的表达式;
(3)根据图象,直接写出 的解集.
5.如图,求图中直线的函数表达式:
6.如图,直线 的表达式为 ,且与 轴交于点 ;直线 经过 , 两点.直线 , ,相交于点 .
6.(1) ;(2)
【解析】
【分析】
(1)设直线 的表达式为 ,将A(4,0),B(3,- )代入得 , 的值,可得一次函数的解析式;
(2)令 ,代入直线 的表达式为 ,可得D点坐标,根据两直线相交可得C点坐标,由三角形的面积公式可得结果.
【详解】
(1)设直线 的解析式为 ,
把A(4,0),B(3,- )代入得 ,
解得:
∴直线 与直线 的交点 的坐标为
【点睛】
此题考查的是求一次函数的表达式和两条直线的交点坐标,掌握用待定系数法求一次函数的表达式和将两个一次函数的表达式联立求交点坐标是解决此题的关键.
4.(1)点C的坐标为 ;(2)直线L2的解析式为y=﹣x+4;(3)
【解析】
试题分析:(1)把点 的坐标代入直线 的解析式求出 的值.
初中数学求一次函数的表达式15道题题专题训练含答案
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.如图,直线l经过点 , ,求直线l的表达式.
2.已知 与 成正比例,当 时, ,求y与x的函数表达式.
3.如图,在平面直角坐标系 中,直线 的表达式为 ,点 , 的坐标分别为 , ,直线 与直线 相交于点 .
一次函数解析式练习题

一次函数解析式练习题一、选择题1. 已知直线y=kx+b经过点(1,2),且斜率为-3,求b的值。
A. 5B. -1C. -5D. 12. 若一次函数y=-2x+1与x轴相交于点(a,0),求a的值。
A. 0.5B. -0.5C. 1D. -13. 直线y=3x+4与y轴的交点坐标是什么?A. (0,7)B. (0,4)C. (1,7)D. (1,4)4. 一次函数y=5x-3的图象不经过第几象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 直线y=-4x+6与直线y=2x-8的交点坐标是什么?A. (1,-2)B. (2,-4)C. (1,2)D. (2,4)二、填空题6. 一次函数y=kx+b的斜率k表示_________。
7. 若一次函数y=kx+b与x轴平行,则k的值为_________。
8. 一次函数y=2x+3与x轴相交点的横坐标为_________。
9. 若一次函数y=kx+b的图象经过第一、二、三象限,则k和b的符号分别为_________。
10. 一次函数y=-3x+5的图象与y轴相交于点(0,5),求当x=-2时,y的值。
三、解答题11. 已知直线l1:y=-2x+4与直线l2:y=3x-1相交于点P,求点P的坐标。
12. 某一次函数的图象经过点A(-1,6)和点B(2,-1),求该一次函数的解析式。
13. 已知一次函数y=kx+b的图象经过点(-2,5)和(1,-1),求k和b的值。
14. 一次函数y=kx+b的图象与x轴相交于点(a,0),与y轴相交于点(0,b),若a=3,b=-2,求k的值。
15. 某工厂生产的产品数量与成本之间存在一次函数关系,设生产x 件产品的成本为y元,已知生产10件产品的成本为100元,生产20件产品的成本为200元,求生产每件产品的平均成本。
四、应用题16. 某商场销售一种商品,其成本为每件20元,销售价格为每件30元。
若该商场希望获得的总利润为600元,求需要销售的商品数量。
求一次函数解析式的专项练习(含答案)

求⼀次函数解析式的专项练习(含答案)⼀次函数的解析式的专项练习⼀次函数的解析式的求法是初中函数的基础。
⼀. ⼀般型例1. 已知函数y m x m =-+-()3328是⼀次函数,求其解析式。
解:由⼀次函数定义知m m 28130-=-≠∴=±≠m m 33∴=-m 3,故⼀次函数的解析式为y x =-+33注意:利⽤定义求⼀次函数y kx b =+解析式时,要保证k ≠0。
如本例中应保证m -≠30⼆. 已知⼀点例2. 已知⼀次函数y kx =-3的图像过点(2,-1),求这个函数的解析式。
解:⼀次函数y kx =-3的图像过点(2,-1)∴-=-123k ,即k =1故这个⼀次函数的解析式为y x =-3变式问法:已知⼀次函数y kx =-3,当x =2时,y =-1,求这个函数的解析式。
三. 已知两点已知某个⼀次函数的图像与x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为_____________。
解:设⼀次函数解析式为y kx b =+由题意得024=-+=k b b ∴==k b 24故这个⼀次函数的解析式为y x =+24四. 已知图象例4. 已知某个⼀次函数的图像如图所⽰,则该函数的解析式为__________。
y2O 1 x解:设⼀次函数解析式为y kx b =+由图可知⼀次函数y kx b =+的图像过点(1,0)、(0,2)∴有020=+=+k b b∴=-=k b 22 故这个⼀次函数的解析式为y x =-+22五. 与座标轴相交例5. 已知直线y kx b =+与直线y x =-2平⾏,且在y 轴上的截距为2,则直线的解析式为___________。
解析:两条直线l 1:y k x b =+11;l 2:y k x b =+22。
当k k 12=,b b 12≠时,l l 12//直线y kx b =+与直线y x =-2平⾏,∴=-k 2。
一次函数的解析式专项练习30题(含答案解析)

∴函数解析式为y= x﹣6;
②当k<0时,函数值随x增大而减小,
∴当x=﹣2时,y=9,x=6时,y=﹣11,
∴ 解得 ,
∴函数解析式为y=﹣ x+4.
因此,函数解析式为y= x﹣6或y=﹣ x+4
19.设一次函数解析式为y=kx+b,根据题意
①当k>0时,x=﹣3时,y=﹣5,x=6时,y=﹣2,
20.已知,直线AB经过A(﹣3,1),B(0,﹣2),将该直线沿y轴向下平移3个单位得到直线MN.
(1)求直线AB和直线MN的函数解析式;
(2)求直线MN与两坐标轴围成的三角形面积.
21.一次函数的图象经过点A(0,﹣2),且与两条坐标轴截得的直角三角形的面积为3,求这个一次函数的解析式.
22.如果y+2与x+1成正比例,当x=1时,y=﹣5.
∴k=3,
∴y=6x+5.
12.设y=k(x﹣1),
把x=﹣5,y=2代入,得2=(﹣5﹣1)k,
解得 .
所以y与x之间的函数关系式是
13.设过点A,B的一次函数的解析式为y=kx+b,
则m= k+b,﹣1= k+b,
两式相减,得m+1= k+ k,即m+1= (m+1),
∵m≠﹣1,则k=2,
∴b=m﹣1,
30.已知:关于x的一次函数y=(2m﹣1)x+m﹣2若这个函数的图象与y轴负半轴相交,且不经过第二象限,且m为正整数.
(1)求这个函数的解析式.
(2)求直线y=﹣x和(1)中函数的图象与x轴围成的三角形面积.
一次函数的解析式30题参考答案:
1.(1)设直线AB解析式为y=kx+b,
2019备战中考数学专题练习(全国通用)-待定系数法求一次函数解析式(含答案)

2019备战中考数学专题练习(全国通用)-待定系数法求一次函数解析式(含答案)一、单选题1.如果P(2,m),A(1,1),B(4,0)三点在同一直线上,则m的值为()A.2B.﹣C.D.12.若点A(2,4)在函数和的图象上,则的值为().A. -5B. -4C. -3D. -23.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B ,则这个一次函数的解析式是().A.y=2x+3B.y=x-3C.y=2x-3D.y=-x+34.正比例函数y=(n+1)x图象经过点(2,4),则n的值是()A. -3B. -C.3D.15.若正比例函数y=kx的图象经过点(-2,6),则的值为()A.-3B.3C. -D.6.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是()A.y=2x+3B.y=-x+2C.y=3x+2D.y=x-17.已知正比例函数y=(2k-3)x的图象过点(-3,5),则k的值为()A. B. C. D.8.若正比例函数的图象经过点(-1,2),则这个图像必经过点()A.(1,2)B.(-1,-2)C.(2,-1)D.(1,-2)9.若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值()A.增加4B.减小4C.增加2D.减小2二、填空题10.如图,在平面直角坐标系中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线将这个图案分成面积相等的两部分,则直线的函数解析式为________.11.已知一次函数的图象经过点(1,2)与(3,5),那么这个函数的表达式为________.12.已知y﹣2与x成正比例,当x=3时,y=1,则y与x的函数表达式是________.13.已知哎平面直角坐标系xOy中,过P(1,1)的直线l与x轴、y轴正半轴交于点A,点B,若三角形AOB的面积等于3,直线l的解析式为________14.一次函数y=kx-3的图象经过点(-1,3),则k=________15.若点(3,1)在一次函数y=kx﹣2(k≠0)的图象上,则k的值是________.16.如图,点A的坐标为(4,2).将点A绕坐标原点O旋转90°后,再向左平移1个单位长度得到点A′,则过点A′的正比例函数的解析式为________.17.如果正比例函数y=kx(k常数,k≠0)的图象经过点(﹣1,2),那么这个函数的解析式是________.三、解答题18.已知y是x的一次函数,下表列出了部分y与x的对应值,求m的值.19.已知一次函数y=kx+b的图象经过点A(0,-1),B(1,0),求这个一次函数的表达式.20.已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点.求该函数关系式.四、综合题21.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.22.已知:y与x﹣3成正比例,且当x=﹣2时,y的值为10.(1)求y与x之间的函数关系式;(2)当x=2时,求y的值.答案解析部分一、单选题1.【答案】C【考点】待定系数法求一次函数解析式【解析】【解答】解:设直线的解析式为y=kx+b(k≠0),△A(1,1),B(4,0),△ ,解得,△直线AB的解析式为y= x+ ,△P(2,m)在直线上,△m=()×2+ = .故选C.【分析】先设直线的解析式为y=kx+b(k≠0),再把A(1,1),B(4,0)代入求出k的值,进而得出直线AB的解析式,把点P(2,m)代入求出m的值即可.2.【答案】B【考点】待定系数法求一次函数解析式【解析】【解答】解:把A(2,4)代入函数y=kx 得,k=2,把A(2,4)代入函数y=5x+b 得,b= -6,△k+b=-6+2=-4.故选B.【分析】把A(2,4)分别代入函数y=kx 和y=5x+b ;求出k、b即可.3.【答案】D【考点】待定系数法求一次函数解析式【解析】【解答】△B点在正比例函数y=2x的图象上,横坐标为1,△y=2×1=2,△B(1,2),设一次函数解析式为:y=kx+b ,△一次函数的图象过点A(0,3),与正比例函数y=2x的图象相交于点B(1,2),△可得出方程组解得则这个一次函数的解析式为y=-x+3选:D.【分析】根据正比例函数图象确定B点坐标再根据图象确定A点的坐标,设出一次函数解析式,代入一次函数解析式.4.【答案】D【考点】待定系数法求一次函数解析式【解析】【解答】解:△正比例函数y=(n+1)x图象经过点(2,4),△4=2(n+1),△n=1.故选D.【分析】本题可直接将点的坐标代入解析式,利用方程解决问题.5.【答案】A【考点】待定系数法求一次函数解析式【解析】【解答】△正比例函数y=kx的图象经过点(-2,6),△把点(-2,6)代入y=kx中,得:6=-2k,△k=-3.故答案为:A.【分析】本题考查待定系数法求正比例函数中k的值,把点(-2,6)代入y=kx中,解关于k的方程求解即可.6.【答案】B【考点】待定系数法求一次函数解析式【解析】【解答】根据一次函数解析式的特点,可得出方程组,解得,那么这个一次函数关系式是y=−x+2 .故选B.【分析】直线y=kx+b经过A(0,2)和B(3,0)两点,代入可求出函数关系式.本题要注意利用一次函数的特点,来列出方程组,求出未知数.7.【答案】D【考点】待定系数法求一次函数解析式【解析】【解答】把点(-3,5)代入正比例函数y=(2k-3)x的解析式得:-3(2k-3)=5,解得:k=.故选D.8.【答案】D【考点】待定系数法求一次函数解析式【解析】【分析】设正比例函数的解析式为y=kx(k≠0),因为正比例函数y=kx的图象经过点(-1,2),所以2=-k,解得:k=-2,所以y=-2x,把这四个选项中的点的坐标分别代入y=-2x中,等号成立的点就在正比例函数y=-2x的图象上,所以这个图象必经过点(1,-2).故选D.9.【答案】A【考点】待定系数法求一次函数解析式【解析】【解答】解:△当x的值减小1,y的值就减小2,△y﹣2=k(x﹣1)+b=kx﹣k+b,y=kx﹣k+b+2.又y=kx+b,△﹣k+b+2=b,即﹣k+2=0,△k=2.当x的值增加2时,△y=(x+2)k+b=kx+b+2k=kx+b+4,当x的值增加2时,y的值增加4.故答案为:A.【分析】根据已知条件分析得出k的值,即可求解。
已知三角形面积求一次函数解析式

《已知三角形面积求解析式》专题
班级姓名
所有欺骗中,自欺是最为严重的.
例:已知一次函数的图像过点B(0,4)且与两坐标轴围成的三角形面积
为4,求此一次函数的解析式?
练习1:已知直线y=kx-4与两坐标轴所围成的三角形面积等于4,求直线解析式;
练习2:已知一次函数的图像经过点A(2,0),且与两坐标轴围成的三角形面积为4,求此一次函数的解析式?
练习3:一次函数y=3x+b的图象与两坐标轴围成的三角形面积是24,求b.
例2:一次函数图像交于x轴于点A(6,0),与正比例函数图像交于点B,且点B在第一象限,其横坐标是4,若△ABO的面积等于12,求这个正比例函数和一次函数的解析式?
练习1:已知已知直线L1经过点A(-1,0)与点B(2,3),另一条直线L2经过点B,且与x轴相交于点p(m,0)若若△APB的面积等于3,求m值和L1、L2的解析式?
直线y=x+3的图像与x轴、y轴交于A、B两点,直线L经过原点,与线段AB交于点C,把△AOB的面积分成1:1两部分,求直线L的解析式;
直线y=x+3的图像与x轴、y轴交于A、B两点,直线L经过原点,与线段AB交于点C,把△AOB的面积分成2:1两部分,求直线L的解析式;
已知一次函数y=kx+b的图像经过M(-1,1)和B(0,2)设该图像与x轴交于点A,问在x轴上是否存在点P,使△ABP为等腰三角形,若存在,求出符
合条件得点P,若不存在说明理由。
确定一次函数解析式专题

确定一次函数解析式专题1. 若一次函数y=kx-3经过点(3,0),则k=_____________,该图像还经过(0,__________),和(1,________________).2. 若一次函数y=kx-2的图像经过点A(-1,2), 则k=_____________,该函数图像经过点B(1,________)和点C(_______________,0).3. 已知直线y=kx+b 平行于直线y=-3x+4,且过点(-2,8)则k=_________,b=_____________.4. 正比例函数的图像经过点(-1,2),则该函数的表达式为______________.5. 已知直线y=2kx-5k+4,当k=_______时,直线经过原点;当k=___________时,直线与y 轴交点为;当k=____________时,直线与x 轴交点为(-1,0).6. 经过(2,-4)和(4,1)两点的直线解析式是______________.7. 已知一次函数y=(m-3)x+2m+4的图像过直线y=-31x+4与y 轴的交点M,则这个一次函数的函数表达式为__________________.8. 已知直线y=kx+b 经过点A(2,0),与y 轴交于点B,且S △AOB =4(O 为原点)则这条直线的函数表达式为__________________.9. 一家小型放映厅的盈利额y/元与售票数x/张之间的关系如图所示.试根据关系图回答下列问题:(1) 当售票数x 满足0<x ≤150时,盈利额y/元与x 之间的函数关系式是___________.(2) 当售票数x 满足150<x ≤200时,盈利额y/元与x 之间的函数关系式是___________. 10小明将RMB1000元存入银行,年利率为2%,利息税为20%,那么x 年后的本息和y (元)与年数x 的函数关系式是 .11.已知一次函数k x k y )1(-=+3,则k = .12已知一次函数1)2(++=x m y ,函数y 的值随x 值的增大而增大,则m 的取值范围是 .13直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k 的值是多少?解析:(1)一次函数的图象与两条坐标轴围成的图形是直角三角形,•两条直角边的长分别是图象与x 轴的交点的横坐标的绝对值和与y 轴的交点的纵坐标的绝对值.(2)确定图象与两条坐标轴的交点坐标可以通过令x=0和y=0解方程求得.14已知一次函数的图象b kx y +=与231-=x y 的图象垂直,且经过点(6,4)求这个函数图象的解析式.一次函数图象和性质专题重点:1. 一次函数关系式:y=kx+b (b ≠0)2. K 决定走向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一次函数解析式的确定练习题
第1题、 如图所示,直线l 就是一次函数y kx b =+的图象,瞧图填空: (1)b = ,k = ; (2)当6x =时,y = ; (3)当6y =时,x = .
第2题、 一次函数2y bx =+的图象经过点(
A -第3题、 正比例函数的图象经过点(23)A --,,第4题、 3y +与1x +成正比例,且当1
x =时,y =则y 与x 之间的函数关系式就是
第5题、 已知直线5y x a =-+与直5y x b =+的交点坐标为(8)m ,, 则a b +的值就是 .
第6题、 若直线1
2
y x n =+与直线1y mx =-相交于(12)-,
,则( ) 第7题、 已知下表就是y 与x 的一次函数,请写出函数表达式,
第8题、 如图所示,直线l 就是一次函数y kx b =+的图象.
(1)图象经过(0),
与(0) ,点; (2)则=k ,=b
第9题、 某一次函数的图象经过点(,请您写第10题、 已知y m -与36x +,当3x =时,7y =,那么y 与x 第11题、 已知一次函数y kx =+21y x =-的图象与y 轴的交点,则这个一次函数的表达式就是 .
第12题、 直线y kx b =+过点(25)-,且与y 轴交于点P ,直线1
32
y x =-
+与y 轴交于Q ,
y
2 点Q 与点P 关于x 轴对称,则这个一次函数的解析式为 .
第13题、 在弹性限度内,弹簧的长度y (cm)就是所挂物体质量x (kg)的一次函数,当所挂物体的质量为1kg 时,弹簧长10cm;当所挂物体的质量为3kg 时,弹簧长12cm.请写出y 与x 之间的函数关系式,并求出所挂物体的质量为6kg 时弹簧时长度.
第14题、 某地长途客运公司规定,旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y (元)就是行李质量x (kg)的一次函数,其图象如图所示. (1)写出y 与x 之间的函数关系式. (2)旅客最多可免费携带多少千克行李?
第15题、 已知直线经过(30)(02)(3)A B C m ,、,、,三点,求这条直线的表达式及m 的值. 第16题、 如图所示,在ABC △中,AB AC =,点A C 、在x 轴正半轴上,点B 在y 轴负半轴上,且A 点横坐标a 与B 点纵坐标b 分别满足34a b ==,.求经过A B 、两点与经过B C 、两点的直线表达式.
第17题、 如图所示,直线l 就是函数y kx b =+
.
第18题、 直线y kx b =+过点(25)-,且与y 轴交于Q ,
点Q 与点P 关于x 轴对称,
第29题、 已知一次函数的图象经过(23)A --,,(1) 求这个一次函数的解析式;
(2) 试判断点(1,1)P -就是否在这个一次函数的图象上?
第19题、 已知直线y kx b =+过点502⎛⎫ ⎪⎝⎭
,
,且与坐标轴所围成的三角形的面积为25
4
,求该直线的函数表达式.
第20题、 若一次函数3y x b =+的图象与两坐标轴所围成的三角形的面积为6,求此函数的表达式.
第21题、 如图所示,一个正比例函数图象与一个一次函数图象相交于点(3),4,且一次函数
的图象与y 轴相交于点B .
(1)求这两个函数的解析式;
(2)求AOB △的面积.
第22题、 已知正比例函数1y k x =与一次函数2y k x b =+
图象与x轴交于点B,且
3
5
OB OA
=,求这两个函数的解析式.
第27题、
直线y kx
=+y轴于点A,与x轴的正半轴交于点B,等边CDO
△的顶点
C D
,分别在线段AB OB
、上,且2
OD DB
=.求k值.
3。
