虚阴极的单电荷层模型
双电层及其结构模型

组织工程
双电层结构在组织工程领 域的应用主要涉及仿生细 胞外基质的设计,以促进 细胞生长和功能化。
生物传感器
双电层理论在生物传感器 设计中发挥关键作用,能 够提高传感器的灵敏度和 选择性。
06
结论与展望
研究结论
总结了双电层的形成机制和影响因素,包括电解质 浓度、表面活性剂和胶体颗粒的存在等。
分析了双电层的结构和性质,包括电位分布、电荷 密度和电导率等,揭示了其与物质传递和化学反应 过程的关系。
实验与理论相结合
应用导向的研究
双电层的研究将更加注重实际应用, 解决能源、环境、生物医学等领域中 的实际问题,推动科技成果转化和应 用。
未来的研究将更加注重实验与理论的 结合,通过实验验证理论预测,同时 通过理论指导实验设计和解释。
双电层研究的挑战与机遇
挑战
双电层的行为和性质受到多种因素的影响,如表面电荷分布、溶液组成、离子 浓度等,如何全面理解和掌握这些因素对双电层的影响是当前研究的难点。
03
双电层的结构模型
结构模型的种类
物理模型
通过物理手段模拟双电层的形成和结构,如电泳、 电聚焦等。
数学模型
通过建立数学方程来描述双电层的性质和行为,如 电位分布、离子浓度等。
计算机模拟模型
利用计算机技术模拟双电层的结构和行为,如分子 动力学模拟、蒙特卡洛模拟等。
结构模型的建立方法
80%
实验测量
深入研究双电层在生物医学领 域的应用,如药物传递、基因 治疗和组织工程等,以提高治 疗效果和降低副作用。
深入研究双电层在生物医学领 域的应用,如药物传递、基因 治疗和组织工程等,以提高治 疗效果和降低副作用。
THANK YOU
感谢聆听
相对论电子束虚阴极静电振荡的粒子模拟

相对论电子束虚阴极静电振荡的粒子模拟
陈德明;王闽
【期刊名称】《计算物理》
【年(卷),期】1990(7)1
【摘要】本文运用有限大小粒子模型,用等离子体粒子模拟方法,对相对论电子束的虚阴极振荡作了一维静电粒子模拟。
结果表明,在注入电流小于空间电荷极限电流时,电子束能稳定传输并能全部通过。
当注入电流超过空间电荷极限电流时,传输是不稳定的,将有部分电子反射,部分通过。
空间电荷形成的虚阴极的位置和电势周期性地振荡。
电流越大,虚阴极位置越靠近注入面且变化范围越小,虚阴极电势越低且振幅越大,振荡频率越高且大于电子束等离子体频率。
【总页数】7页(P24-30)
【关键词】相对论;电子束;虚阴极;振荡;模拟
【作者】陈德明;王闽
【作者单位】国防科技大学应用物理系
【正文语种】中文
【中图分类】O539
【相关文献】
1.具有双电子束结构的双波段相对论返波振荡器粒子模拟研究 [J], 王挺;张建德;钱宝良
2.同轴引出电子束相对论返波振荡器的粒子模拟 [J], 葛行军;钱宝良;钟辉煌
3.一种新型径向三腔同轴虚阴极振荡器全三维粒子模拟研究 [J], 杨超;刘大刚;周俊;廖臣;彭凯;刘盛纲
4.相对论电子束虚阴极振荡的一维粒子模拟 [J], 谢卫平;肖学政
5.低引导磁场下相对论亚纳秒电子束毫米波返波振荡器的粒子模拟 [J], 张运俭;陈洪斌;孟凡宝;范植开
因版权原因,仅展示原文概要,查看原文内容请购买。
电化学双电层理论和模型

双电层双电层的形成:当两相接触时,如果电子或离子等荷电粒子在两相中具有不同的电化学位,荷电粒子就会在两相之间发生转移或交换,界面两侧便形成符号相反的两层电荷,人们把界面上的这两个荷电层称为双电层。
如金属、溶液界面(M/L)两侧,若μM+>μM+(L),则荷电粒子发生转移,金属表面荷负点;反之,则金属表面荷正,这种双电层常称为离子双层。
尽管有时上述的离子双层并不存在,但金属与溶液界面间仍然会存在着电位差,无论是金属表面,还是溶液表面,都存在着偶极层。
由于偶极子正负电荷分隔开而形成的双电层,称为偶极双电层。
对任何一种金属而言,由于金属的电子会“溢出”金属表面形成双极子。
所以即使溶液一侧不存在偶极子层,但对金属与溶液的界面来说,这种偶极双层总是存在的。
此外,溶液中某一种离子有可能被吸附于电极与溶液界面上,形成一层电荷。
这层电荷又借助静电作用吸引溶液中同等数量的带相反电荷的离子而形成双电层,可称之为吸附双层。
这里应当注意:界面上第一层电荷的出现,靠的是静电力以外的其他化学与物理作用,而第二层电荷则是由第一层电荷的静电力引起的。
如果界面上有了吸附双层,当然也会产生一定大小的电位差。
金属与溶液界面的电位差系由上述的三种类型电位差的一部分或全部组成,但其中对电极反应速度有重大影响的,则主要是离子双层的电位差。
离子双层的形成有两种可能的情况。
一是在电极与溶液一旦接触后的瞬间自发形成的。
另一种情况,是在外电源作用下强制形成的双电层。
因为有的时候,当金属与溶液接触时,并不能自发地形成双电层。
如将纯汞(Hg)放入Kill溶液的界面上常常不能自发的形成双电层。
但是,如果将Hg电极与外电源负极连接,外电源就向Hg电极供应电子,在其电位达到K+还原电位之前,电极上不会发生电化学反应,因而此时Hg电极上有了多余的电子而带上负电。
这层负电荷吸引溶液中相同数量的正电荷(如K+),形成双电层。
双电层的结构模型:金属电极和溶液之间界面上形成的双电层,从结构上可以有离子双电层、表面偶极双电层和吸附双电层等三种类型。
双电层及其结构模型

13
结论:
(1)不论电极表面存在正剩余电荷还是负剩余 电荷,界面张力都将随剩余电荷数量的增加而 降低。 (2)根据电毛细曲线的微分方程 ,可以直接通 过电毛细曲线的斜率求出某一电极电位下的电 极表面剩余电荷密度q,也可以方便地判断电 极的零电荷电位值和表面剩余电荷密度的符号。
14
二、双电层的微分电容
4
2、研究电极/溶液界面的思路:
通过使用一些可测的界面参数来研究电极/溶 液界面; 根据一定的界面结构模型来推算界面参数 , 根据实验测量数据来检验模型。 研究的基本方法:充电曲线法 、微分电容曲线 法、电毛细曲线法
5
3、研究电极/溶液界面对研究电极的要求
直流电通过一个电极时,可能 起到以下两种作用:
d /d q
微分电容法是利用Cd~φ 曲线下方的面积求q,
q dq C d 微分电容法更精确和灵敏。 0 d
0
q
微分电容法的应用更广泛 微分电容法和电毛细曲线法都是研究界面结构 与性质的重要实验方法,二者不可偏废。
24
四、零电荷电位
1、零电布和电位分布
双电层的金属一侧,剩 余电荷集中在电极表面。 在双电层的溶液一侧, 剩余电荷的分布有一定 的分散性。 d为紧贴电极表面排列的 水化离子的电荷中心与 电极表面的距。
图4-11金属/溶液界面剩余电荷与电位的分布
37
(1)紧密层电位分布:从x=0点到x=d的范围内 不存在剩余电荷,这一范围即为紧密层。紧密 层厚度为d。如果紧密层内的介电常数是恒定 的,则该层内的电位分布是线性变化的。
34
图4-9 考虑了热运动干扰时的电极/溶液界面双电层结构
35
在金属相中:金属中全部剩余电荷都是紧密 分布,金属内部各点的电位均相等。 在溶液相中: (a)当溶液总浓度较高、电极表面电荷密度较 大时,溶液中剩余电荷倾向于紧密分布,形 成图4-8的紧密双电层。
6双电层理论(共9张)

在电场作用下,带电质点和 反离子分别向相反方向运动。
这模型过于简单,由于离子热 运动,不可能形成平板电容器
第2页,共9页。
扩散(kuòsàn)双电层模型
Gouy和Chapman认为,由于正、负离子静电吸引 和热运动两种效应的结果,溶液中的反离子只有一部 分紧密地排在固体表面附近,相距约一、二个离子厚 度称为紧密层;
他认为吸附在固体表面 的紧密层约有一、二个分子 层的厚度,后被称为Stern层;
由反号离子电性中心
构成的平面称为Stern平面。
第5页,共9页。
Stern模型
由于离子的溶剂化作用,
胶粒在移动时,紧密层会结合 一定数量的溶剂分子一起移动,
所以滑移的切动面由比Stern
层略右的曲线(qūxiàn)表示。
后来Stern又提出了Stern模型。
第1页,共9页。
平板 型模型 (píngbǎn)
Helmholtz认为固体的表面电荷与溶液中的反号 离子构成平行的两层,如同一个平板电容器。
+-
+-
+-
0
+
+ +
-
+-
+-
+-
+-
-
Helmholtz双电层模型
整个双电层厚度为
固体与液体总的电位差即等于热
力学电势0 ,在双电层内,热力学电
从固体表面到Stern平面,
电位从0直线下降为 。
第6页,共9页。
势(diànshì)
带电的固体或胶粒在移动时,移动的切动面与液
体本体之间的电位差称为 电势。
在扩散双电层模型中,切动面AB与溶液本体之间
物理初中电学模型归纳总结

物理初中电学模型归纳总结电学是物理学中的一个重要分支,研究电荷、电场、电流、电阻等与电有关的现象和规律。
初中电学模型是学生初步学习和理解电学知识的基础,对于建立正确的电学思维具有重要意义。
本文将对初中电学模型进行归纳总结,为学生理解和掌握电学知识提供参考。
一、电荷模型在电学中,电荷被视为电现象的基本要素。
电荷模型描述了电荷的特性和作用。
1. 电荷的性质电荷具有两种性质:正电荷和负电荷。
同性电荷相互排斥,异性电荷相互吸引。
2. 电荷守恒定律电荷守恒定律指出,在孤立系统中,电荷的总量是不变的,只能通过相互作用而转移。
3. 电荷分布模型电荷分布模型用于描述电荷在物体上的分布情况,常见的有均匀分布和非均匀分布。
二、电场模型电场是以电荷为源的特殊场,是电荷在空间中产生的影响其他电荷的力的载体。
1. 电场的概念电场是用来描述电荷之间相互作用的力的推送者,用电场线来表示。
电荷产生的电场越靠近电荷越强。
2. 电场的性质电场的性质包括电场强度、电场线和电势。
电场强度表示单位正电荷所受的力,电场线表示电荷在电场中的运动轨迹,电势表示单位正电荷在电场中所具有的能量。
3. 电场分布模型电场分布模型用于描述电荷在空间中产生的电场的分布情况,常见的有均匀电场和非均匀电场。
三、电流模型电流是电荷在导体中的移动引起的现象,也是电能在电路中传输的载体。
1. 电流的概念电流是电荷在单位时间内通过导体截面的数量,用I表示。
单位是安培(A)。
2. 电流的性质电流的性质包括电流强度、电子流和流速。
电流强度表示单位截面上的电荷数量,电子流表示电流的真正载体是电子,流速表示电荷在导体中的移动速率。
3. 电路模型电路模型用于描述电流在电路中的传输方式,包括串联电路和并联电路。
四、电阻模型电阻是导体对电流的阻碍作用,是电路中一个重要的元件。
1. 电阻的概念电阻是用来限制电流通过的元件,用符号R表示。
单位是欧姆(Ω)。
2. 电阻的性质电阻的性质包括电阻值、电阻率和温度系数。
mott-schottky analysis -回复

mott-schottky analysis -回复标题:深入理解Mott-Schottky分析Mott-Schottky分析是一种重要的电化学分析方法,主要用于研究半导体材料的性质和行为。
这种分析方法基于Mott-Schottky理论,该理论描述了半导体与电解质界面的电荷分布情况。
以下我们将一步一步地解析Mott-Schottky分析的基本原理、应用以及实验步骤。
一、Mott-Schottky理论基础Mott-Schottky理论是基于半导体能带理论和空间电荷层理论的一种模型。
在半导体-电解质界面上,由于电子和空穴的迁移,会在半导体一侧形成一个空间电荷层。
在这个区域内,电荷密度不是均匀分布的,而是随着距离半导体表面的距离增加而减小。
根据Mott-Schottky理论,半导体-电解质界面的电势差(也称为平带电势)与空间电荷层的电荷密度之间存在一种线性关系。
这种关系可以通过Mott-Schottky方程来描述:1/(C^2) = (2/q.epsilon.epsilon_0.N_D).(V-V_FB)其中,C是电容,q是电子电荷,ε和ε_0分别是半导体的相对介电常数和真空介电常数,N_D是半导体中的掺杂浓度,V是施加的电压,V_FB 是平带电势。
二、Mott-Schottky分析的应用Mott-Schottky分析在半导体材料的研究中具有广泛的应用。
以下是一些主要的应用领域:1. 掺杂类型和浓度的测定:通过测量Mott-Schottky曲线的斜率和截距,可以确定半导体的掺杂类型(n型或p型)和掺杂浓度。
2. 载流子迁移率的测定:Mott-Schottky分析可以提供关于半导体中载流子迁移率的信息,这对于优化半导体器件的性能非常重要。
3. 表面态和陷阱的分析:Mott-Schottky分析可以揭示半导体-电解质界面处的表面态和陷阱的性质,这对于理解和控制半导体器件的稳定性至关重要。
4. 电化学反应动力学的研究:Mott-Schottky分析也可以用于研究电化学反应的动力学过程,例如氧还原反应和氢析出反应等。
21-第六章-6.1-理想MOS结构的表面空间电荷区解析

Physics of Semiconductor Devices
抱负MOS构造的 外表空间电荷区
前言:
Physics of Semiconductor Devices
金属-氧化物-半导体场效应晶体管〔MOSFET〕是微处理 器、半导体存储器等超大规模集成电路中的核心器件和主 流器件,也是一种重要的功率器件。
Physics of Semiconductor Devices 在栅电压为0的条件下,假设漏、源之间加上电压UDS,则漏端PN结为反 偏,将只有很小的反偏PN结电流从漏极流到源极,但是假设栅极加上确定 的电压时,外表形成了沟道,它将漏区与源区连通,在UDS作用之下就消 逝明显的漏极电流,而且漏极电流的大小依靠于栅极电压。MOSFET的栅 极和半导体之间被氧化硅层阻隔,器件导通时只有从漏极经过沟道到源极 这一条电流通路。
MOSFET: Metal-Oxide-Semiconductor Field-effect transistor
Physics of Semiconductor Devices
场效应晶体管〔Field Effect Transistor,缩写为FET〕 是一种电压把握器件。
其导电过程主要涉及一种载流 子,故也称为“单极”晶体管。
S所分摊,即有:
Physics of Semiconductor Devices
V0
VG
S
空间电荷区半导 体内部边界
金属-氧比物和P型半导体的电位分布图
Physics of Semiconductor Devices
三 载流子的积存、耗尽和反型
空间电荷区静电势φ(x)的消逝转变了空间电荷区中的能带图。 依据VG极性和大小,有可能实现三种不同的外表状况:
电子束激励TM模虚阴极振荡器的分析

图 1 空 心 电子 束 激 励 模 型
图 2 实 心 电 子 柬 激励 模 型
空心 电子 束形 成 虚 阴极 的激 励模 型如 图 1 示 。频 率 为 的 电流元 , 所 激励 TM。主模 的功率 为【 3 ]
G 。 J r) ) f( ) m 。3 h[( +J2 2 ( 2 J + ]
* 收 稿 日期 :0 60— 8 2 0 —72 I 修 订 日期 :0 61一O 2 0—O3 基金项目: 国家 8 3计 划 项 目 资助 课 题 6
作者简介 : 刘
静( 9 2 , , 士研究生 , 事高功率微波器件研究 I o o r ao .o c 。 18 一) 女 硕 从 l f us h o tm.n j y @y
二 二 _
; 一善r (s( 。d z幻 薄 荷 』 Ztir tt ( 是 电 )nr ) ,  ̄
e 一r / √ 2
层 的运动轨 迹 , r R, 分别 为 波导 和空 心 电子 束半 径 ;。 J 为零 阶 B se 函数 ,o为零 阶 B se 函数 的第 n个根 。 esl P esl 实 心 电子 束 形 成 虚 阴 极 的激 励 模 型 如 图 2 示 。 用 完 全 相 同 的 推 导 过 程 , 率 为 的 电 流 元 , 励 所 利 频 激
维普资讯
2 4 0
…
㈤
式 中 :a r 为实心 电子束半 径 。由( )() 1 ,2 两式相 比可 得空心 电子 束和 实 心 电子 束激 励 TM。主模 的功率 之 比
, 一 = = = ㈤
轴向随时间振荡的电场, 通过波导耦合作用 , 激励 T 模 ; M 具有 圆柱轴对称结构 的电子束和波导系统 , 则激励
双电层及其结构模型

双电层及其结构模型双电层是指由正负离子之间形成的电荷层,存在于液体中。
它由紧密吸附在电极表面的正离子层(即化学吸附层)和漂浮在电极表面附近的负离子层(即物理吸附层)组成。
这种双电层的存在是由离子在液体中的溶解度和电离度决定的。
双电层的结构模型可以分为两种,分别是亚布力德双电层模型和海维赛德双电层模型。
亚布力德双电层模型是由瑞士物理学家亚布力德在20世纪30年代提出的。
他认为双电层可以看作由一个内层和一个外层组成。
内层是紧贴电极表面的化学吸附层,包含正离子和一些吸附的溶质分子。
溶质分子与电极表面之间通过共价键或静电相互作用而吸附在一起。
外层则是由溶剂中的负离子组成的物理吸附层,负离子漂浮在电极表面附近,受到电极电场的作用而停留在该位置。
这种模型认为,双电层是稳定的,且在不同电势条件下会有不同的结构。
海维赛德双电层模型是由英国科学家海维赛德在20世纪起提出并发展的。
这个模型认为双电层由内层和外层组成,类似于亚布力德的模型。
但是,海维赛德提出了一种新的概念,即溶剂分子的极化。
他认为,在电极表面附近,溶剂分子会被电场极化,形成一个特定方向的电偶极子,这些电偶极子会受到电场力的作用而定向堆积,形成外层。
因此,海维赛德提出的双电层模型中考虑了电极表面电场对溶剂的影响。
总的来说,双电层的结构模型揭示了离子在液体中的封闭性和电极表面的吸附现象。
根据这些模型,我们可以更好地理解双电层的形成和性质,进一步研究电化学反应、电容和电化学储能等领域的基本原理和应用。
中考物理电学模型总结归纳

中考物理电学模型总结归纳电学模型是物理学中对电现象进行描述和解释的理论模型。
在中考物理考试中,电学模型是重要的考点之一。
本文将对中考物理电学模型进行总结归纳,以帮助同学们更好地理解和掌握相关知识。
一、电荷模型电荷模型是电学中最基本的模型之一。
根据电荷的性质,可以将电荷分为正电荷和负电荷。
同种电荷相互排斥,异种电荷相互吸引。
电荷模型的核心概念是电量,用符号q表示,单位是库仑(C)。
二、电场模型电场模型是描述电荷周围电场分布情况的模型。
电荷周围存在一个电场,电荷在电场中产生力的作用。
电场的强弱用电场强度表示,用符号E表示,单位是牛顿/库仑(N/C)。
电场线是描述电场分布的一种图示方法,它指向正电荷,由负电荷指出。
三、电势模型电势模型是描述电场中点的电势情况的模型。
电势是指单位正电荷在电场中所具有的能量,用符号V表示,单位是伏特(V)。
电势的高低代表了点的电势能的大小,电势随着距离电荷的远近而变化,离电荷越近,电势越高,反之,电势越低。
四、导线模型导线模型是用来描述导体中电荷分布和电流传输情况的模型。
导体内部电荷呈自由移动状态,当导体两端存在电势差时,导体内电荷将发生移动形成电流。
电流的大小用符号I表示,单位是安(A)。
导线中的电流遵循欧姆定律,即电流等于电压与电阻的比值,用公式I=U/R 表示。
五、电阻模型电阻模型是用来描述导体阻碍电流通过的情况的模型。
电阻用符号R表示,单位是欧姆(Ω)。
电阻的大小与导体材料、长度、截面积以及温度等因素有关。
根据欧姆定律,电流和电阻成正比,电压和电阻成正比。
六、电路模型电路模型是用来描述电流在电路中传输和分布的情况的模型。
电路由电源、导线和电器元件组成。
电路中的总电流等于电路中各处电流的代数和。
串联电路中电流相等,电压之和等于总电压;并联电路中电压相等,电流之和等于总电流。
根据基尔霍夫定律,电路中各个节点电流代数和为零,电路中闭合回路沿一定方向电压代数和为零。
通过对中考物理电学模型的总结归纳,我们可以清晰地了解电学模型的基本概念和运用方法。
表面电荷积聚模型

表面电荷积聚模型
表面电荷积聚模型是一种描述物体表面电荷分布的理论模型。
根据这个模型,物体表面上的电荷会积聚在某些地方,形成一个电荷分布图。
我们需要了解一下什么是电荷。
电荷是物质的一种基本属性,它可以分为正电荷和负电荷。
正电荷代表物体失去了电子,而负电荷代表物体获得了电子。
根据库仑定律,相同电荷会互相排斥,不同电荷会互相吸引。
在表面电荷积聚模型中,物体表面的电荷分布是不均匀的。
这是因为物体表面的形状、材料以及周围环境等因素的影响。
例如,当物体表面凹凸不平时,电荷会积聚在凸起的部分,而在凹陷的部分电荷较少。
另外,物体表面的材料也会对电荷的分布产生影响。
某些材料具有更强的吸电性,会使电荷更容易积聚在表面。
通过表面电荷积聚模型,我们可以解释一些现象。
例如,当我们摩擦两个物体时,会发生静电现象。
这是因为摩擦会导致物体表面的电荷重新分布,使得一个物体获得正电荷,另一个物体获得负电荷。
根据表面电荷积聚模型,我们可以预测哪些地方会积聚电荷,进而解释为什么会发生静电现象。
表面电荷积聚模型还可以应用于其他领域。
例如,在电子学中,我们可以利用这个模型来设计电路板的布局,以确保电荷分布均匀,
减少干扰和电磁辐射。
在材料科学中,我们可以通过调控材料表面的电荷分布来改变材料的性质,实现一些特殊的功能。
总的来说,表面电荷积聚模型是描述物体表面电荷分布的一种理论模型。
它可以帮助我们解释和理解一些静电现象,并在其他领域中有一定的应用价值。
通过研究和理解这个模型,我们可以更好地认识电荷的行为规律,为科学研究和工程应用提供指导。
双电层理论的四个模型

双电层(electrical double layer)假设,将一个金属片放进电解液中,那么会发生什么呢?更准确地描述是:在电极与电解液的界面处,物质与电荷的分布状态是怎样的?(1)Helmholtz模型首先,亥姆赫兹(Helmholtz)试图探究这个问题,他建立了一个模型,我们简称其为H模型,其核心思想是:相反的电荷等量分布于界面两侧。
这也是“double layer”的由来。
进而,这个结构可以等效为一个平板电容器,并用如下公式描述单侧的电荷密度(σ)与两层电荷间的电势差(V)的关系,其中,d为正负电荷中心的距离。
σ=εε0 dV而且,该电容器的电容(Cd)可表示为:ðσðV =C d=εε0d至此,H模型成功地将将一个电化学的普遍场景抽象为两个基本公式。
然而,该模型存在一个明显缺陷:由上式可推论出,Cd是一个恒定值,然而实验观测中,Cd是一个变量,相对电位与电解液浓度等都会对其产生影响。
比如,汞电极在NaF电解液中,测得Cd值如下图所示:其中,可以看到明显的两个趋势是:(1)Cd相对于电位成V型的对称分布;(2)电解液的浓度越高,Cd数值越大。
因此,一个良好双电层模型需要解释这两个现象。
(2)Gouy-Chapman模型随后,Gouy和Chapman联手改进了这个模型,我们简称其为G-C模型。
G-C 模型的核心是引入了一个新的概念:扩散层(diffuse layer)让我们回到电极与电解液的界面处,电荷在电极这一侧是严格分布于其表面。
然而,在电解液这一侧却不是这样:由于不同离子间的相互作用,使得很多电荷会扩散到远离界面的体相溶液中。
因此,G-C模型可由下图近似表示:经过G-C模型的改进,原本电容公式中的d就变成了一个变量。
不难想象,当界面两侧电势差较大时,更多的离子会被压缩到靠近电极的位置;当电解液浓度高时,离子也可以在较小的空间上与电极达到电荷平衡。
经过G-C 模型的改进,双电层预测NaF的水溶液作为电解液,其电容与电位及浓度关系如下,可见,经过G-C模型的改进,双电层理论对变化有了很好的解释。
单层模型与多层模型介电常数

单层模型与多层模型介电常数
单层模型和多层模型都是用来描述材料的介电性质的模型,其中介电常数是描述材料电学性质的重要参数。
单层模型指的是将材料视为一个均匀的介质,其内部的介电常数不变,而且整个材料可以被看做是一个连续的单层。
多层模型是将材料视为由多个层组成的结构,在每个层中,介电常数可能不同,因此整个材料被看做是由多个具有不同介电常数的层组成的多层结构。
在单层模型中,如果材料是各向同性的,那么材料中的介电常数是一个标量,可以通过被称为介电恒量的实数来描述。
在多层模型中,由于每种介质都有不同的介电常数,因此材料的介电常数成为一个向量或张量,需要更复杂的数学理论进行描述。
总之,单层模型和多层模型中都需要介电常数作为描述材料电学性质的重要参数。
单层模型可以用于描述均匀介质的介电性质,多层模型可以用于描述复杂材料的介电性质。
原子内部电荷新模型
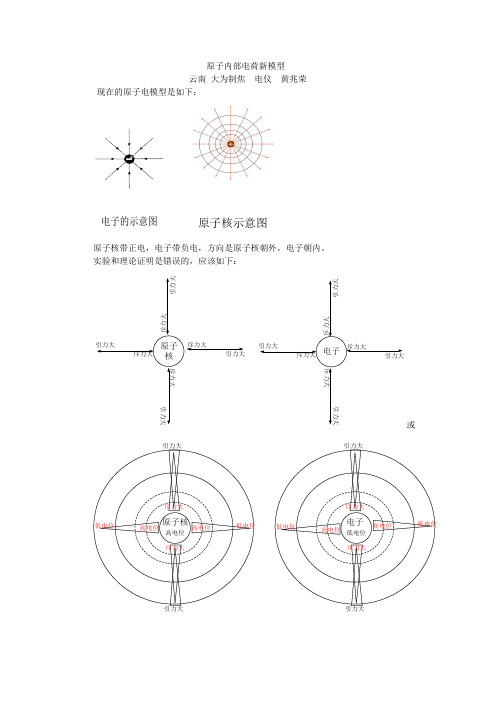
原子内部电荷新模型 云南 大为制焦 电仪 黄兆荣 现在的原子电模型是如下:电子的示意图原子核示意图原子核带正电,电子带负电,方向是原子核朝外,电子朝内。
实验和理论证明是错误的,应该如下:斥力大或原子核引力大斥力大高电位斥力大高电位低电位高电位低电位电子引力大斥力大低电位斥力大高电位低电位高电位低电位若有正、负电荷能抵消,那么大自然和宇宙就没有电荷了。
故原子核、电子它们周围是同一种电荷,越靠近原子核、电子电荷的密度越大,离原子核、电子越远,电荷的密度越小,且是波动的。
引力是电荷密度小,斥力是电荷密度大。
设原子核外的密度为d1….dn,电子的密度为D1…DN依次减少。
1、当电子接近原子核时,有:D1+D2+~+dn+DN 密度增大,它们之间的斥力显现出来,象弹簧、气球一样,你压它,它就排斥你。
2、当电子远离原子核时,也有:D1+D2+~+dn+DN 密度减小,它们之间的引力显现出来,象弹簧、气球一样,你拉它,它就吸引你。
电荷有质量,它们之间有引力和斥力。
理由是:1、除氢原子外,其它原子的原子核的电位都比电子高,2、原子核和电子永远不可能象磁铁那样相吸成为一体,近到到一定距离时,原子核与电子之间显示排斥力,远到到一定距离时,原子核与电子之间显示引力。
原子核与电子之间的距离变化就象弹簧一样变化3、实验任何物体,任何两点都有变化的电参数,电参数是电流、阻抗、电压和频率。
4、任何物体的质量都会发生变化,国际七个一千克标准计量器具的质量都会改变。
5、原子之间即有斥力,也有引力,远到一定距离时,原子之间为引力,近到一定的距离时为斥力,与原子内部一致。
6、星球、星系都是由原子组成,它们之间的距离变化就象弹簧一样变化,就统一起来了不矛盾了。
与原子内部、原子之间运动规律一致。
7、与化工生产、电子电路、高压电气设备、大自然现象、生活常识(用手洗衣服)不矛盾,就能解通了。
8、化学中轨道理论,化学键就能很好地解释。
9、原子核、电子无限远处的电场强度不会为零。
空间电荷模型

空间电荷模型空间电荷模型是一种物理模型,用于描述电荷分布在空间中的情况。
根据这一模型,电荷不再被看作是集中在一个点上的,而是分布在空间中的。
这个模型广泛应用于电磁学和物理学的研究中,能够更准确地描述电荷的分布和电场的作用。
在空间电荷模型中,电荷被认为是连续分布在空间中的。
我们可以将空间中的一小段电荷看作是一个点电荷,然后将所有这些点电荷在空间中连续地分布起来。
这样一来,我们就可以用电荷密度来描述电荷在空间中的分布情况。
电荷密度可以分为体电荷密度和面电荷密度两种情况。
体电荷密度指的是单位体积内的电荷量,通常用符号ρ表示。
面电荷密度则是单位面积内的电荷量,通常用符号σ表示。
在空间电荷模型中,我们可以根据具体情况选择使用体电荷密度或面电荷密度来描述电荷的分布。
根据库仑定律,电荷之间会相互作用,产生电场。
在空间电荷模型中,我们可以通过积分来计算电场的分布。
对于一小段电荷dq,其产生的电场可以表示为dE=k·dq/r²,其中k是电场常数,r是观察点与电荷dq之间的距离。
将所有这些小段电荷的电场矢量叠加起来,就可以得到整个空间中电场的分布情况。
空间电荷模型的应用非常广泛。
在电磁学中,我们可以通过这一模型来描述电荷在导体中的分布情况,从而计算导体表面的电场分布。
在物理学中,我们可以利用空间电荷模型来研究电场对电荷的作用力,进而分析电荷的运动轨迹和能量变化。
空间电荷模型也可以应用于静电场和稳恒电流的研究。
通过对电荷分布的建模,我们可以准确地计算电场和电势的分布情况,从而进一步研究电磁现象的规律和特性。
需要注意的是,空间电荷模型是一个理想化的模型,它假设电荷是连续分布的。
在实际应用中,电荷的分布往往是离散的,这时我们可以通过将离散的电荷离散化地分布起来,近似地使用空间电荷模型。
空间电荷模型是描述电荷在空间中分布的一种理论模型。
通过该模型,我们可以更准确地描述电荷的分布和电场的作用,并在电磁学和物理学的研究中得到广泛应用。
mmff94电荷

mmff94电荷MMFF94电荷是一种用于描述分子的电荷分布的计算方法,它是基于分子力学力场的一种电荷模型。
本文将介绍MMFF94电荷的原理、计算方法以及应用领域。
我们来了解一下MMFF94电荷的原理。
MMFF94电荷是基于分子力学力场的一种电荷模型,它通过计算分子内部原子间的相互作用和分子与外界环境的相互作用来确定分子的电荷分布。
在计算中,MMFF94电荷将分子看作一系列原子和键的组合,通过优化能量函数来确定每个原子的电荷。
接下来,我们来了解一下MMFF94电荷的计算方法。
MMFF94电荷的计算方法主要包括两个步骤:参数化和优化。
在参数化阶段,首先需要收集一系列实验数据,如分子的电荷、键长、键角等信息,然后通过拟合这些实验数据来确定电荷模型的参数。
在优化阶段,根据参数化得到的模型,通过计算分子的能量函数来确定每个原子的电荷。
一般来说,MMFF94电荷的计算需要借助计算机软件进行。
MMFF94电荷在药物设计、材料科学和环境科学等领域有着广泛的应用。
在药物设计中,MMFF94电荷可以用于计算药物分子与受体之间的相互作用,从而预测药物的活性和选择性。
在材料科学中,MMFF94电荷可以用于计算材料的电子结构、光学性质和热力学性质,为新材料的设计和合成提供理论依据。
在环境科学中,MMFF94电荷可以用于计算分子在环境中的溶解度、分布系数和毒性等性质,从而评估分子对环境的影响。
总结起来,MMFF94电荷是一种基于分子力学力场的电荷模型,通过计算分子的能量函数来确定每个原子的电荷。
它的计算方法包括参数化和优化两个步骤,应用领域涵盖药物设计、材料科学和环境科学等。
MMFF94电荷的研究对于深入理解分子的电荷分布和相互作用机制,以及在材料和药物设计中的应用具有重要意义。
希望本文对您对MMFF94电荷有所了解。
Drude模型

D r u d e 模型一. Drude 模型的提出1897年在研究放电管辉光放电实验中的阴极射线时,Thomson 是通过将组成阴极射线的电子当作经典粒子而最先发现了电子的存在。
在发现电子后的最初一段时期内,对原子结构的研究尚处于探索之中,还没有认识到电子等微观粒子运动的独特本质。
因此,在当时还不具备解释金属中的这些传导电子是如何形成以及怎么运动这两个基本问题的理论基础。
1900年受气体分子运动论的启发提出了金属中经典的自由电子理论即Drude 模型,即认为金属中存在有自由电子气体,并用这一理论来解释金属材料的导电、导热等宏观性能。
二. Drude 模型的四个基本假设1.独立电子近似近似认为电子的运动是彼此独立的,就象孤立的单个电子一样,故又称为单电子近似。
2.自由电子近似用经典粒子的碰撞图象来简化电子与离子实之间复杂的相互作用近似认为单个电子在与离子实的相继两次碰撞之间作自由运动,故金属中的传导电子又常称为自由电子3.弛豫时间近似在dt 时间内电子与离子实之间碰撞的几率应为dt/τ。
电子在单位时间内碰撞一次的几率为1/τ,τ称为弛豫时间(即平均自由时间)。
每次碰撞时,电子失去它在电场作用下获得的能量,即电子和周围环境达到热平衡仅仅是通过与原子实的碰撞实现的。
4.经典近似在与离子实的相继两次碰撞之间电子的运动遵循Newton 运动定律碰撞前后电子遵循Boltzmann 统计分布。
三.Drude 模型的成就自由电子气体+波尔兹曼统计欧姆定律○虽然金属至少有两种带电粒子,离子与电子,Drude 假设参与导电作用的仅是其中一种。
○传导电子的来源:价电子与芯电子。
◎首先,来解释金属的导电现象并导出电导率。
电子:平均速度为经典近似假设:热运动遵循Maxwell 速度分布律,故有 ◎若与离子实相继两次碰撞之间的时间间隔为t ,则有 因此有 表明:在外电场作用下金属中的自由电子将形成与外电场方向相反的宏观定向运动,于是就形成了电流◎由此可得到金属材料电导率的微观表达式四.Drude 模型的不足以电子的平均自由程为例,来说明Drude 电子模型所遇到的根本性困难。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
虚阴极的单电荷层模型Ξ叶卫民 李传胪(国防科技大学应用物理系,长沙,410073) 摘 要 通过引入虚阴极振荡的单电荷层模型,得到了虚阴极振荡产生微波的线性色散关系。
同时,分析了入射、反射、透射束流中振荡成份与虚阴极振荡的两本征模式相互作用,得到非线性色散关系,并给出了虚阴极振荡产生微波的机制。
关键词 虚阴极 单电荷层 中图分类号 TN 752 虚阴极振荡产生高功率微波,已被许多实验证实。
在虚阴极理论,尤其是虚阴极自身振荡激励微波方面,仍然有许多工作需要做。
文献[1]用位于两块接地的无限大平行板导体之间的无限薄电荷层模型,给出了虚阴极运动的简单图象;文献[2]用虚阴极的薄电荷层近似,得到了空心束虚阴极激励微波的主模式关系。
但两者的不足之处,均在于没有考虑虚阴极电荷层与微波场的相互作用,因而无法得到虚阴极振荡激励微波的色散关系和模式增长率。
为此,我们利用虚阴极的薄电荷层模型,通过求解虚阴极电荷层在微波场作用下的运动方程,得到了虚阴极振荡激励微波的线性色散关系。
同时,考虑入射、反射、透射束中调制成份,与虚阴极振荡本征模相互作用,得到了非线性色散关系。
1 物理模型通常虚阴极(V C )振荡器中有两种激励微波的机制,即电子在阴极和虚阴极间往返振荡和虚阴极自身振荡。
这里主要分析虚阴极自身振荡机制;同时,在非线性分析时,把电子往返振荡作为入射或反射束流的一个调制成份,用三波相互作用处理方法得出它对虚阴极振荡影响。
模型假设:波导结构和电子束分布均具有圆柱对称,只考虑TM 0n 模;把虚阴极视为一薄电荷层,其电荷数密度为n (r ,z ,t )=N (t )(2Πr )f (r )∆(z -z vc (t ))(1)式中,∫R 0f (r )d r =1,R 为波导半径。
要说明的是:N (t )为虚阴极电荷层所带电荷数。
与以前文献不同的是,我们认为虚阴极电荷层所携带电荷数是变化的。
这与粒子模拟中发现虚阴极附近电荷密度振荡是一致;实际虚阴极应该是一个区域,由于此区域轴向线度相对其振荡产生的电磁波相位因子exp (i Βz )中2Π Β小很多,所以,此处可用∆函数,相当于考虑此区域中心位置振荡;同时,假设入射电子束流强度I i (z ,t ),反射电子束流强度I r (z ,t ),透射电子束流度I t (z ,t ),在瞬态虚阴极位置处z =z vc (t )满足I i -I r -I t =N -1eP (t )=N -1e ∑j =1,2,3∑k A jk (-i Ξjk )exp (-i Ξjk t )+c .c (2)式中,j =1,2,3分别对应入、反、透射束流,Ξjk 对应相应束中不同调制频率。
为简化,不考虑虚阴极电荷层中电子径向运动。
这在强导引磁场下显然成立。
第10卷 第2期强 激 光 与 粒 子 束V o l .10,N o.2 1998年5月H IGH POW ER LA SER AND PA R T I CL E BEAM S M ay,1998 Ξ国家863激光技术领域资助项目1998年1月20日收到原稿,1998年3月31日收到修改稿。
叶卫民,男,1972年2月出生,在读博士 基本物理量:N 0,z 0,v c ,Μ0,v c 分别是为稳态时虚阴极电荷层的携带电荷数、z 向坐标、速度和电场;N 1(t ),z vc (t )分别为虚阴极电荷层携带的扰动电荷数和瞬态虚阴极电荷层z 向坐标;E 0z (z ,r )为稳态时虚阴极振荡器中z 向电场;E _1,R F (z ,r ,t )为虚阴极振荡器中扰动电场;n 1(z ,r ,t )J 1(z ,r ,t ),分别为虚阴极电荷层产生的扰动电荷数密度及z 向扰动电流密度。
定义:稳态时,v 0,vc =0,E 0,z z =z 0,vc =0,d N 0 d t =0;s (t )=∑j ,k A jk exp (-i Ξjk t )+c .c .;一阶小量Ε=N -1 N 0。
本文推导成立条件为Ε<1;若虚阴极电荷数振荡使Ε 1,推导不成立。
由连续性方程和(2)式可知:e d N (t ) d t =e d N 1(t ) d t =N -1eP (t ),则N (t )=N 0+N 1(t )=N 0(1+Εs (t ))。
利用Ε可将各物理量扰动形式写为:z vc (t )=z 0,vc +Εz 1(t ),z .vc =Εz .1(t );N 1=N 0Εs (t ),E 1,R F =ΕE (r ,z ,t );n 1=ΕN 0s (t )f (r ) (2Πr )∆(z -z vc (t ));J 1=-e N 0 (2Πr )f (r )∆(z -z v .c (t ))z .1Ε-Ε2N 0e(2Πr )f (r )∆(z -z vc (t ))z .1s (t )。
由于虚阴极振荡以轴向电流为主,E z ≠0,且简化考虑体系具有圆柱对称性,因此我们可以对E z (r ,z ,t )作贝塞尔-傅立叶展开,只考虑TM 0n 模,则有E 1z ,R F =Ε∑l m E ±l m J 0(Λ0m r R )exp (±i Βz -i Ξl t )+c .c .,Λ0m 是零阶B essel 函数的第m 个根,Ξl 为电磁场的不同频率成份。
进行M axw ell 方程变形,有2E 1z ,R F -(1 c 2)52E 1z ,R F 5t 2=Λ05J 1 5t -(e Ε0)(5n 1 5z )(3) 将上述n 1,J 1及E 1z ,R F 表达式代入(3)可得:Ε∑l m (Ξ2lc 2-Λ20m R 2-Β2)E ±l m J 0(Λ0m r R )exp (±i Βz -i Ξl t )+c .c .=-ΕΛ0N 0e (2Πr )f (r )∆(z -z vc (t ))z ..1-Ε(e N 0 Ε0)f (r )(2Πr )s (t )5∆(z -z vc (t )) 5z +Λ0N 0e (2Πr )f (r )[5∆(z -z vc (t )) 5z z .21-∆(z -z vc (t ))s .z .1-∆(z -z vc (t ))sz ..1]Ε2(4)式中,z vc (t ),z .1可由运动方程得出d (N (t )m z .vc )d t =-e N (t )E z (z vc (t ),r ,t )(5)z v .c (t )处电场E z (z v .c (t ),r ,t )=Ε[∑l m E ±l m J 0(Λ0m r R )exp (±i Βz vc (t )-i Ξl t )+c .c .+(-m e )Αz 1(t )],这里,Α=-e m5E 0z 5z z =z 0vc 。
2 虚阴极电荷层振荡的线性理论线性理论主要指在(4),(5)展开中准确到Ε一次项。
在(5)中展开,只考虑到线性项,则z 1=d 1exp (-Αt )+d 2exp (Αt )+e m ∑l m J 0(Λ0m r R )Ξ2l +Α[E ±l m exp (±i Βz 0,vc -i Ξl t )+c .c .](6) 由于exp (-Αt ),exp (Αt )两项是非稳定项,不能代表虚阴极的振荡效应,故不妨取d 1=d 2=0,将(6)代入(4),两边用1 L ∫L 0d z ∫R 0d rJ 0(Λ0m r R )r exp (-i Βz )作用,L 是腔长,可得∑l Ξ2lc 2-Λ20m R 2-Β2E +l m +1-e -2i ΒL 2i ΒL E -l m e -i Ξl t +E -+l m 1-e -2i ΒL 2i ΒL+E --l m e i Ξl t =-N 0Εe -i Βz 0,vc Λ0em ∑ln c m n (E ±l m e ±i Βz 0vc -i Ξl t +c .c .)-Ξ2l Ξ2l +Α+j Β Ε0B m ∑jk (A jk e -i Ξjk t +c .c )(7)式中B m =∫R 0f (r )J 0(Λ0m r R )d r [J 21(Λ0m )V ]-1;c m n =∫R 0f (r )J 0(Λ0m r R )J 0(Λ0n r R )d r [V J 21(Λ0m )]-1,962第2期叶卫民等:虚阴极的单电荷层模型V为波导体积。
令(7)式两边相同频率项的系数相等,定义行阵F l2m-1=E+l m,F l2m=E-l m,则(I-G l)F l=D l∆jk,l A jk,∆jk,l A jk=∑jkA jk Ξjk=Ξl(8) I为单位矩阵,式中, D l2m-1=-exp(-iΒz0,v.c) [(Ξ2l c2)-(Λ20m R2)-Β2]-1 (iΒN0e Ε0)B m; G l(2m-1)(2n-1)=(Λ0N0e2 m) c m n (Ξ2l c2-Λ20m R2-Β2) Ξ2l (Ξ2l+Α); G l(2m-1)(2n)=[exp(-2iΒL)-1] (2iΒL)∆m n+G l(2m-1)(2n-1)exp(-2iΒz0,v.c); D l2m=-D l2m-1; G l(2m)(2n-1)=G l3(2m-1)(2n); G l(2m)(2n)=G l(2m-1)(2n-1)。
(8)式可看作一非齐次线性方程组,可作如下讨论: 若考虑不同于Ξjk的虚阴极振荡产生电磁场本征频率,即Ξl≠Ξjk,由于(8)式化为齐次,Ξl 必须满足下式,即虚阴极振荡的本征色散关系det(I-G l)=0(9) 若存在Ξjk=Ξl,即微波场中有与入、反、透射束流调制频率一致的成份,则场量有有限解的条件是矩阵(I-G l)与矩阵(G l-I;D l A jk∆jk,l)秩相等,即秩(I-G l)=秩(G l-I;D l A jk∆jk,l)。
这可理解为受迫振荡过程,束流的某一频率调制成份引起虚阴极电荷数相应频率振荡,产生相应频率电磁场。
若存在Ξjk=Ξl,但秩(I-G l)<秩(G l-I;D l A jk∆jk),此时必有det(I-G l)=0,对非齐次线性方程组(8)而言是一无解条件。
它也可以理解为求出解为无穷大量;这就相当于一个“无阻尼”的共振过程;即若束流的某一频率成份与虚阴极振荡本征频率相同,则可产生大幅度的相应频率电磁场。
由此可见,对入射束流进行调制,使它与虚阴极振荡本征频率一致,是提高虚阴极效率,减小虚阴极振荡产生微波频带的有效手段。
在具体实验中,可利用反馈机制,让产生微波场对入射束进行调制;或直接用外部手段对入射束进行预调制。
