2.5 双电层理论和电势
双电层理论

当固体与液体接触时,可以是固体从溶液中选择 性吸附某种离子,也可以是固体分子本身发生电离作 用而使离子进入溶液,以致使固液两相分别带有不同 符号的电荷,在界面上形成了双电层的结构。
早在1879年,Helmholz提出了平板型模型;
1910年Gouy和1913年Chapman修正了平板型模型, 提出了扩散双电层模型;
反离子分别向相反方向运动。
这模型过于简单,由于离子 热运动,不可能形成平板电容器
扩散双电层模型
Gouy和Chapman认为,由于正、负离子静电吸引 和热运动两种效应的结果,溶液中的反离子只有一部 分紧密地排在固体表面附近,相距约一、二个离子厚 度称为紧密层;
另一部分离子按一定的 浓度梯度扩散到本体溶液中, 离子的分布可用Boltzmann 公式表示,称为扩散层。
Stern模型
由于离子的溶剂化作 用,胶粒在移动时,紧密 层会结合一定数量的溶剂 分子一起移动,所以滑移 的切动面由比Stern层略右 的曲线表示。
从固体表面到Stern平面,
电位从0直线下降为 。
电势
带电的固体或胶粒在移动时,移动的切动面与液
体本体之间的电位差称为 电势。
在扩散双电层模型中,切动面AB与溶液本体之间
的电位差为 电势;
在Stern模型中,带有溶剂化层的滑移界面与溶液
之间的电位差称为 电势。
电势总是比热力学电势低,外加电解质会使
电势变小甚至改变符号。
只有在带电质点移动时才显示出 电势,所以它
又被称为电动电势。
电势
a
a
d
d'
d''
b''' b'' b '
扩散双电层理论和Zeta电势(精)

164扩散双电层理论和 Zeta 电势胶体粒子的表面常因解离、吸附、极化、摩擦等原因而带电,分散介质则带反电荷,因此, 在相界面上便形成了双电层。
胶体的这种结构决定了它的电学性质, 并对其稳定性起着十分重要的作用。
本专题便来讨论胶体的双电层结构, 并从中引出一个决定胶体电学性质和稳定性的重要指标——ς(Zeta电势。
1.双电层模型(1 Helmholtz模型1879年, Helmholtz 在研究胶体在电场作用下运动时,最早提出了一个双电层模型。
这个模型如同一个平板电容器, 认为固体表面带有某种电荷, 介质带有另一种电荷, 两者平行, 且相距很近,就像图 64-1所示。
图 64-1 Helmholtz双电层模型按照这个模型,若固体表面的电势为0ψ,正、负电荷的间距为δ,则双电层中的电势随间距直线下降,且表面电荷密度σ与电势0ψ的关系如下式表示δεψσ0= (64-1 式中ε为介质的介电常数。
显然, 这是一个初级双电层模型, 它只考虑到带电固体表面对介质中反离子的静电作用, 而忽视了反离子的热运动。
虽然, 它对胶体的早期研究起过一定的作用, 但无法准确地描述胶体在电场作用下的运动。
(2 Gouy(古依— Chapman (恰普曼模型由于 Helmholtz 模型的不足, 1910和 1913年, Gouy 和 Chapman 先后作出改进,提出了一个扩散双电层模型。
这个模型认为, 介质中的反离子不仅受固体表面离子的静电吸引力, 从而使其整齐地排列在表面附近, 而且还要受热运动的影响, 使其离开表面, 无规则地分散在介质中。
这便形成如图 64-2所示的扩散双电层结构。
2图 64-2 Gouy— Chapman 扩散双电层模型他们还对模型作了定量的处理,提出了如下四点假设:①假设表面是一个无限大的平面,表面上电荷是均匀分布的。
②扩散层中,正、负离子都可视为按 Boltzmanm 分布的点电荷。
③介质是通过介电常数影响双电层的,且它的介电常数各处相同。
双电层理论
双电层理论一.界面与相际一个相的表面叫作“界面”,界面的轮廓清晰,他的范围不会超过一原子层,可以看成是与另一相相互接触的表面。
相际:指两相之间,性质变化的区域,窄宽不等,其范围小之两个分子直径,大到数千个埃以上;其性质与两相中任意一相的本体性质都有所不同。
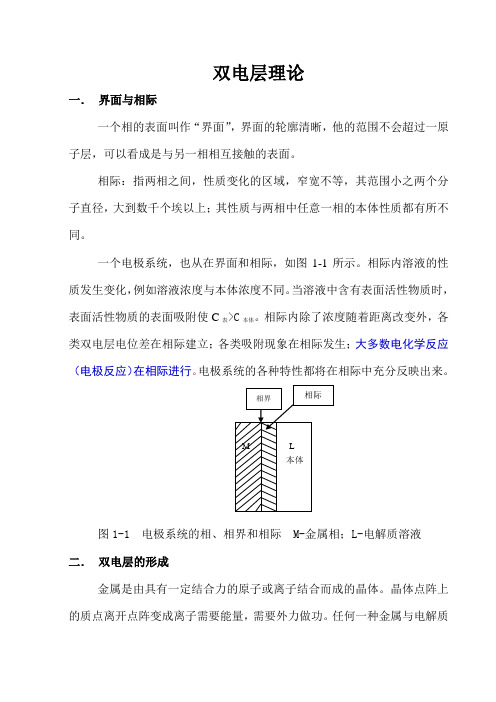
一个电极系统,也从在界面和相际,如图1-1所示。
相际内溶液的性质发生变化,例如溶液浓度与本体浓度不同。
当溶液中含有表面活性物质时,表面活性物质的表面吸附使C表>C本体。
相际内除了浓度随着距离改变外,各类双电层电位差在相际建立;各类吸附现象在相际发生;大多数电化学反应(电极反应)在相际进行。
电极系统的各种特性都将在相际中充分反映出来。
图1-1 电极系统的相、相界和相际 M-金属相;L-电解质溶液二.双电层的形成金属是由具有一定结合力的原子或离子结合而成的晶体。
晶体点阵上的质点离开点阵变成离子需要能量,需要外力做功。
任何一种金属与电解质溶液接触时,其界面上的原子(或离子)之间必然发生相互作用,形成双电层。
1.界面电荷层(1)当性质不同的相接触时,在相界面上形成了不同性质的电势差。
(2)出现电势差的原因是带电粒子或偶极子在界面层中的非均匀分布 双电层:由于电极和溶液界面带有的电荷符号相反,故电极/溶液界面上的荷电物质能部分地定向排列在界面两侧。
2.界面电荷层的形成 (1)自发形成的双电层(a )离子双电层 (b )吸附双电层 (c )偶极双电层 (2)强制形成的双电层金属电极与电解质溶液接触,可以自发形成双电层,也可以在外电源作用下强制形成双电层。
以如下电极反应为例:+++++M M2Hg–2e- = Hg22+ ,φ =0.1 VK+ + e- = K , φ= -1.6V 理想极化电极:在一定的电势范围内,可以借助外电源任意改变双电层的带电状况(因而改变界面区的电势差),而不致引起任何电化学反应的电极。
如KCl溶液中的汞电极。
不极化电极:指有电流通过时,电极与溶液界面间电势差不发生任何变化的电极。
电化学双电层理论和模型

双电层双电层的形成:当两相接触时,如果电子或离子等荷电粒子在两相中具有不同的电化学位,荷电粒子就会在两相之间发生转移或交换,界面两侧便形成符号相反的两层电荷,人们把界面上的这两个荷电层称为双电层。
如金属、溶液界面(M/L)两侧,若μM+>μM+(L),则荷电粒子发生转移,金属表面荷负点;反之,则金属表面荷正,这种双电层常称为离子双层。
尽管有时上述的离子双层并不存在,但金属与溶液界面间仍然会存在着电位差,无论是金属表面,还是溶液表面,都存在着偶极层。
由于偶极子正负电荷分隔开而形成的双电层,称为偶极双电层。
对任何一种金属而言,由于金属的电子会“溢出”金属表面形成双极子。
所以即使溶液一侧不存在偶极子层,但对金属与溶液的界面来说,这种偶极双层总是存在的。
此外,溶液中某一种离子有可能被吸附于电极与溶液界面上,形成一层电荷。
这层电荷又借助静电作用吸引溶液中同等数量的带相反电荷的离子而形成双电层,可称之为吸附双层。
这里应当注意:界面上第一层电荷的出现,靠的是静电力以外的其他化学与物理作用,而第二层电荷则是由第一层电荷的静电力引起的。
如果界面上有了吸附双层,当然也会产生一定大小的电位差。
金属与溶液界面的电位差系由上述的三种类型电位差的一部分或全部组成,但其中对电极反应速度有重大影响的,则主要是离子双层的电位差。
离子双层的形成有两种可能的情况。
一是在电极与溶液一旦接触后的瞬间自发形成的。
另一种情况,是在外电源作用下强制形成的双电层。
因为有的时候,当金属与溶液接触时,并不能自发地形成双电层。
如将纯汞(Hg)放入Kill溶液的界面上常常不能自发的形成双电层。
但是,如果将Hg电极与外电源负极连接,外电源就向Hg电极供应电子,在其电位达到K+还原电位之前,电极上不会发生电化学反应,因而此时Hg电极上有了多余的电子而带上负电。
这层负电荷吸引溶液中相同数量的正电荷(如K+),形成双电层。
双电层的结构模型:金属电极和溶液之间界面上形成的双电层,从结构上可以有离子双电层、表面偶极双电层和吸附双电层等三种类型。
双电层理论——精选推荐

双电层理论表面物理化学所涉及的内容非常宽广,固体在溶液中的荷电性质,实际上影响着固体表面性质和界面区的电荷转移反应及其进行的速度。
由于多种极其重要的表面电化学效应的发现,表面电化学引起了许多种科学家的重视和研究。
第一节 双 电 层2.1.1 双电层的产生在自然界中,固体与液体接触时,固体表面的荷电现象实际上是普遍存在的。
它导致了固—液界面的液体一侧带着相反电荷,这种界面电荷影响界面周围介质中的离子分布,与界面电荷符号相反的介质中的离子被吸向界面(这种离子称为反离子Counter -ions ),而相同符号的离子(称为同离子Co -ions )则被排离界面。
与此同时,离子的热运动又促使它们均匀混合在一起。
因此,在带电界面上形成一个扩散双电层(diffuse double layer )。
所谓扩散,就是界面周围介质中的反离子的过量是以扩散形式分布的,而不是非常整齐地集中排列在带电界面的周围。
例如,人体内与血液接触的动静脉壁和血液中胶粒等界面区都存在双电层结构,致使血液在血管中畅通无阻地流动以输送全身新陈代谢的营养而不产生血栓。
双电层理论研究反离子的扩散分布和带电界面的性质。
固体在溶液中荷电而构成双电层的原因,除了外加电场之外,大致上可归纳为以下几种情况: ① 电离作用固体表面在溶液中产生电离或溶液中的电离成分依靠某种结合力与固体表面结合而使其荷电。
例如,玻璃与水接触时,玻璃中的硅酸盐可电离出钾离子、钠离子或氢离子等,于是使玻璃带负电性而溶液带正电性;蛋白质分子具有的羧基(—COOH)和胺基(—NH 2)官能团,当pH 值降低时(酸性),溶液中电离的H +与胺基以氢键结合,从而使蛋白质带正电,-NH 2+H 2O -NH 3++OH -,而溶液一侧带负电,即在羧酸介质中—COOH 的电离被高氢浓度离子所抑制:—COOH+H 2O -COO -+H 3O+ 当pH 值升高时(碱性),蛋白质的羧基电离而使其带负电。
双电层和电动电势

➢ (3)固定层和可动层是不可分割的整体。
➢ 整个固定层带电量应是电层内正电量与负 电量相互中和后剩余的电量,这个总电量 有一个电重心;可动层也有一个电重心。
4
D
:固定层与可动层两个电重心面
之间的距离。
:固定层与可动层两个电重心面
单位面积上的电量。
➢ 可见任何模型在不断修正过程中得以逐渐 完善。保留正确的,对错误的进行修正。 斯特恩模型显然能解释更多事实,但由于 定量计算上的困难,理论处理仍然采用古 埃—查普曼的处理方法。
➢ P1018图13.16(b)
➢ ②扩散层中离子的分布可用玻兹曼分布式。 ➢ ③扩散电动电势(ξ) ➢ 电解质溶液+,或电解质价型+,或双电层
厚度↓, ξ ↓。
➢ 2、缺点 ➢ ① ξ的物理意义不明确。 ➢ ② ξ与实例不符。
➢ 三、斯特恩修正。(1924年) ➢ 1、思想 ➢ ①动电现象确实是两相界面上存在的反映
➢ ③按电化学性质,贵重金属Po、Au等在 水中应带正电(电解质是正离子)。但是 这些金属的胶体粒子却带正电。
➢ 二、古埃和查普曼扩散双电层模型对其进 行了修正。
➢ 1、思想
➢ ①由于静电引力作用(离子吸附)和热运 动(晶格中某些离子溶解),两种效应的 结果,在溶液中与固体表面离子电荷相反
的离子只有一部分紧密排列在固体表面 (仅有1、2个离子厚度),另一部分离 子与固体表面的距离则可以从紧密层一直 分散到本体溶液之中。双电层实际包括了 紧密层和扩散层两部分。
加,胶体的稳定性增加。如HgS胶体中加
入
K4[F(e,CN)6 ] [F(e C进N)入6 ]4固 定
层中, 离子分布到可动层中。
(整理)表面化学第三章
第三章双电层对离子型溶质,由于电离,吸附在界面的是离子而不是中性分子。
通常液/气,液/液界面的吸附是单分子层的,因而离子型溶质的吸附导致产生一带电单层。
考虑到界面相的电中性,必有等量的相反电荷,即通常所说的反离子,存在于界面相,从而形成所谓的双电层。
双电层的存在是电动电势或ζ-电势产生的基础,而ζ-电势是分散体系的一个重要稳定因素。
因此双电层理论是胶体和界面化学的重要内容。
本章将重点介绍双电层理论,然后讨论电动现象和ζ-电势,最后简单介绍双电层的排斥效应。
3.1双电层理论有机电解质离子吸附在空气/水界面和液/液界面时,其定向排列导致形成带电的吸附单层。
等电荷的反离子分布于界面相。
双电层理论就是要讨论这些反离子的分布规律。
有关双电层模型已经提出了好几种,各模型的不同之处在于不同的反离子的分布规律。
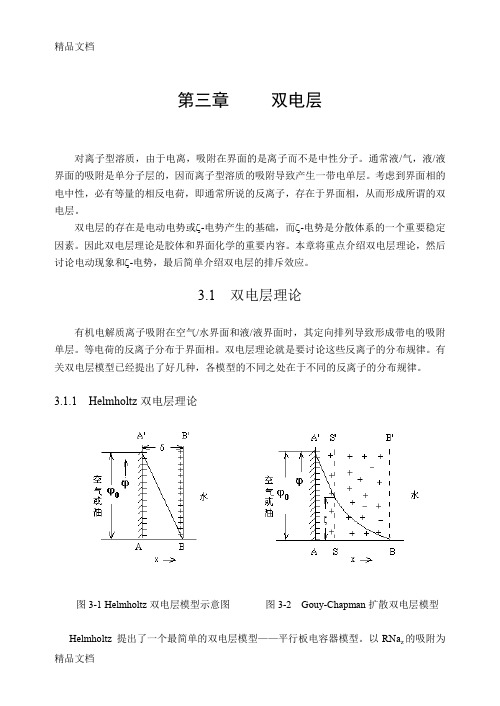
3.1.1 Helmholtz双电层理论图3-1 Helmholtz双电层模型示意图图3-2 Gouy-Chapman扩散双电层模型Helmholtz 提出了一个最简单的双电层模型——平行板电容器模型。
以RNa z的吸附为例, 该模型认为,带负电的R -z 在空气/水界面或油/水界面上定向排列于AA’面,而带相反电荷的反离子定向排列于BB’面,如图3-1所示。
AA’和BB’两平面之间的距离δ即为界面相的厚度,其大小为分子厚度级。
AA’面和BB’面上的电荷密度(单位面积上的电荷)大小相等,但符号相反,类似于平行板电容器。
界面电势ϕ0与AA’面上的电荷密度σ 之间的关系由Helmholtz 公式表达:δπσϕD40= (3-1) 式中D 为区间AA’ BB’的介质的介电常数。
沿x 方向从AA’面到BB’面,界面电势线性地急剧下降,从AA’面上的ϕ0下降到BB’面上的0。
对RNa z 自溶液中的吸附,由于RNa z 是高表面活性的,因此ΓR 和∆n R 之间的差别可忽略,即认为ΓR 等于∆n R ,并且若体系中存在电解质NaCl ,按照Helmholtz 模型,Cl -的吸附量将为零:0=Γ-cl (3-2) 于是Helmholtz 模型的电中性方程为:ΓΓ+=Na R z (3-3) 对带电固/液或液/液界面,电动试验(将在后面详细论述)或其它涉及界面电荷的试验表明,双电层的实际厚度较为宽广。
双电层理论

双电层理论界面与相际一个相的表面叫作“界面”,界面的轮廓清晰,他的范围不会超过一原子层,可以看成是与另一相相互接触的表面。
相际:指两相之间,性质变化的区域,窄宽不等,其范围小之两个分子直径,大到数千个埃以上;其性质与两相中任意一相的本体性质都有所不同。
一个电极系统,也从在界面和相际,如图1-1所示。
相际内溶液的性质发生变化,例如溶液浓度与本体浓度不同。
当溶液中含有表面活性物质时,表面活性物质的表面吸附使C QC本体。
相际内除了浓度随着距离改变外,各类双电层电位差在相际建立;各类吸附现象在相际发生;大多数电化学反应(电极反应)在相际进行。
电极系统的各种特性都将在相际中充分反映出来。
图1-1电极系统的相、相界和相际M-金属相;L-电解质溶液二.双电层的形成金属是由具有一定结合力的原子或离子结合而成的晶体。
晶体点阵上的质点离开点阵变成离子需要能量,需要外力做功。
任何一种金属与电解质溶液接触时,其界面上的原子(或离子)之间必然发生相互作用,形成双电1•界面电荷层(1) 当性质不同的相接触时,在相界面上形成了不同性质的电势差。
(2) 出现电势差的原因是带电粒子或偶极子在界面层中的非均匀分布双电层:由于电极和溶液界面带有的电荷符号相反,故电极 /溶液界面上的荷电物质能部分地定向排列在界面两侧2. 界面电荷层的形成(1)自发形成的双电层(2)强制形成的双电层金属电极与电解质溶液接触,可以自发形成双电层,也可以在外电源作用下强制形成双电层。
以如下电极反应为例:(a )离子双电层 (c )偶极双电层(b )吸附双电层理想极化电极2Hg —2e = Hg22+, 0=0.1 VK+ + e-= K , 忙-1.6V 理想极化电极:在一定的电势范围内,可以借助外电源任意改变双电层的带电状况(因而改变界面区的电势差),而不致引起任何电化学反应的电极。
如KCI溶液中的汞电极。
不极化电极:指有电流通过时,电极与溶液界面间电势差不发生任何变化的电极。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分子层的厚度,后被称为
Stern层; 由反号离子电性中心
构成的平面称为Stern平面。
Stern模型
由于离子的溶剂化作
用,胶粒在移动时,紧密
层会结合一定数量的溶剂 分子一起移动,所以滑移 的切动面由比Stern层略右 的曲线表示。 从固体表面到Stern平面, 电位从0直线下降为 。
电势
§2.5 双电层理论和 电势
当固体与液体接触时,可以是固体从溶液中选择
性吸附某种离子,也可以是固体分子本身发生电离作
用而使离子进入溶液,以致使固液两相分别带有不同 符号的电荷,在界面上形成了双电层的结构。 早在1879年,Helmholz提出了平板型模型; 1910年Gouy和1913年Chapman修正了平板型模型, 提出了扩散双电层模型; 后来Stern又提出了Stern模型。
带电的固体或胶粒在移动时,移动的切动面与液
体本体之间的电位差称为 电势。 在扩散双电层模型中,切动面AB与溶液本体之间
的电位差为 电势; 在Stern模型中,带有溶剂化层的滑移界面与溶液 之间的电位差称为
电势。
电势总是比热力学电势低,外加电解质会使
电势变小甚至改变符号。
只有在带电质点移动时才显示出
又被称为电动电势。
电势,所以它
扩散双电层模型 吸附离子 胶粒表面 紧密层 (离子和溶剂化分子) 反号离子 扩散层
ζ电势: 胶粒表面滑移界面处的电势。 胶粒表面热力学电势φ和电动电势(ζ电势) 的区别: ① 发生在不同的部位; ② 大小不同,一般情况下ζ电势只是热力学 电势的一部分,其绝对值小于φ。
电势
a
d '' d' d
a
b ''' b '' b' b
ቤተ መጻሕፍቲ ባይዱ
'
x
'
c
外加电解质对 电势的影响
胶粒
胶粒表面双电层结构示意图
流动电势示意图
③ φ只取决于被吸附的离子和溶胶中的反号 离子的活度,而ζ电势的值还与溶胶中外加 电解质有关。 当溶胶中有外加电解质存在时,可使紧密 层中反粒子浓度增加,扩散层变薄, ζ电 势的绝对值减小,甚至变为零或相反的值。
④ 胶粒的电泳速率与ζ电势的关系:
E r 4
ε:分散介质的介电常数 η:分散介质的粘度 E : 外加电场强度
这模型过于简单,由于离子热运 动,不可能形成平板电容器
Helmholtz双电层模型
扩散双电层模型
Gouy和Chapman认为,由于正、负离子静电吸引 和热运动两种效应的结果,溶液中的反离子只有一部 分紧密地排在固体表面附近,相距约一、二个离子厚 度称为紧密层; 另一部分离子按一定的 浓度梯度扩散到本体溶液中, 离子的分布可用Boltzmann 公式表示,称为扩散层。 双电层由紧密层和扩散层构 成。移动的切动面为AB面
平板型模型
Helmholtz认为固体的表面电荷与溶液中的反
号离子构成平行的两层,如同一个平板电容器。
+ + + + + + + + + +
0
D 0 4
整个双电层厚度为
固体与液体总的电位差即等于热
力学电势0 ,在双电层内,热力学电 势呈直线下降。
在电场作用下,带电质点和反离
子分别向相反方向运动。
扩散双电层模型
+ + + + + + + + + + + + 紧密层 A 扩散双电层模 型解释了电动 现象,区分了 热力学电位和ζ 电位,并能解 释电解质对ζ电 位的影响,但 它不能解释为 什么ζ电位可以 变号,而有时 还会高于表面 电位的问题。
0
B
扩散层
x
Stern模型
Stern对扩散双电层模 型作进一步修正。 他认为吸附在固体表 面的紧密层约有一、二个
