正切函数的图像
正切函数和余切函数的图像和性质
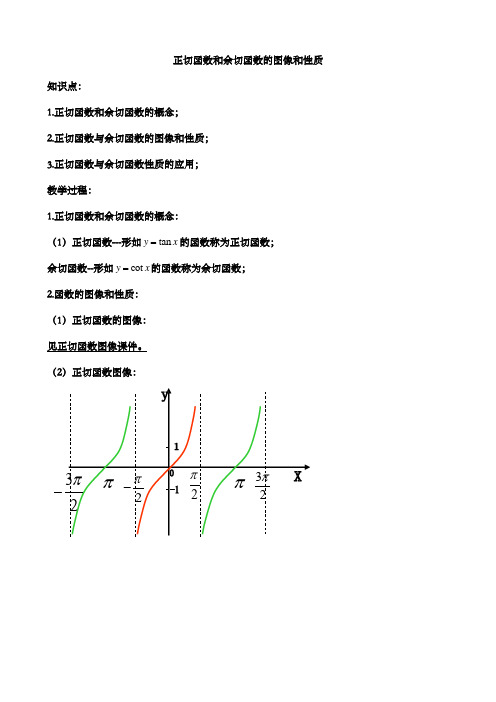
正切函数和余切函数的图像和性质知识点:1.正切函数和余切函数的概念;2.正切函数与余切函数的图像和性质;3.正切函数与余切函数性质的应用;教学过程:1.正切函数和余切函数的概念:(1)正切函数---形如tan=的函数称为正切函数;y x余切函数--形如cot=的函数称为余切函数;y x2.函数的图像和性质:(1)正切函数的图像:见正切函数图像课件。
(2)正切函数图像:-(3)与切函数的图像:归纳填表格:例1.求下列函数的周期: (1)tan(3)3y x π=-+;(2)221tgxy tg x=+;(3)cot tan y x x =-;(4)22tan21tan 2xy x=-; (5)sin 1tan tan 2x y x x ⎛⎫=+ ⎪⎝⎭例2.求下列函数的单调区间: (1)tan(2)24y x π=++;(2)tan()123x y π=-+-;(3)12log cot y x ⎛= ⎝⎭ 例3.求下列函数的定义域:(1)tan 4y x π⎛⎫=- ⎪⎝⎭;(2)y =(3)y = 例4.(1)求函数21)tan tan ]y x x =-的定义域; (2)解不等式:23tan (2)(3tan(2)044x x ππ+-+≤例5.已知2tan tan y x a x =-,当1[0,],[0,]34x a π∈∈时,函数max y =a 的值;例6.已知函数tan ,(0,)2y x x π=∈,若1212,(0,),2x x x x π∈≠。
求证:1212()()()22f x f x x xf ++>。
6.2 正切函数的图像与性质

6.2 正切函数的图像与性质正切函数图像(余切函数的图像)例1.求函数tan(2)3y x π=-的定义域、周期和单调区间。
例2.不通过求值,比较下列各组中两个正切函数值的大小:(1)与;(2) 与.例3. 求函数⎪⎭⎫⎝⎛+=4tan πx y 的定义域.例4 不通过求值,比较下列各组中两个正切函数值的大小:(1)167tan 与173tan ; (2)⎪⎭⎫ ⎝⎛-π411tan 与⎪⎭⎫⎝⎛-π513tan .例5.若tan α=32,借助三角函数定义求角α的正弦函数值和余弦函数值。
例6.化简:()()()()()πααπαπαπαπ---+-+-tan 3tan tan 3tan 2tan【当堂训练】 一、选择题1、下列不等式中,正确的是( )A . tan74π>tan 73πB . tan(-413π)>tan(-512π)C . tan 4<tan3D . tan281°>tan665°2、下列命题中正确的是( ) A . x y tan =在第一象限单调递增. B . 在x y tan =中,x 越大,y 也越大 C . 当x >0时,x tan >0. D . x y tan =的图象关于原点对称3、若βαππβα22tan tan ),23,(,>∈且,则 ( ) A .α<β B .α>β C .α+β>3π D .α+β<2π4、直线y = a (a 为常数)与y = tan ωx (ω>0)的相邻两支的交点距离为 ( )A .πB .ωπ C .ωπ2 D .与a 有关的值5、在下列函数中,同时满足的是( )①在(0,2π)上递增 ②以2π为周期 ③是奇函数 A .y =tan x B .y =cos x C .y =tan 21x D .y =-tan x6、在区间(-π23,π23)内,函数x y tan =与函数x y sin =图象交点的个数为( )A .1B .2C .3D .5二、填空题1、使函数y=tanx 和y=sinx 同时为单调递增函数的区间是 .2、函数y=3tan(21x 4π-)的定义域是 ,值域是 .3、函数y=3tan(2x +3π)的对称中心的坐标是 .4、函数⎪⎭⎫⎝⎛+=42t an πx y 的图象被平行直线 隔开,图象与x 轴交点的横坐标是 ,与y 轴交点的纵坐标是 ,函数的周期是 ,定义域是 ,值域是 ,它的奇偶性是 .5、比较大小:(1)︒222tan ︒223tan ; (2)31)44(tan ︒ 21)44(tan ︒。
正切函数图像及其性质

7
8
(1)求函数y tan2 x tan x 1
(x R且x k , k Z )的值域
2
(2)当函数y
1
2 (tan x
1)2
取得敢大
值时, 自变量x的取值集合.
巩 固 练 习
正弦函数
正切函数
图象 定义域
值域
xR
[-1,1]
正切图象
{x | x k , k Z}
2
(,)
周期性 奇偶性
2π
奇函数
π
奇函数
单调性
[ 2k , 2k ]增
2
2
[ 2k , 3 2k ]减
( k , k ),
2
2
k Z上是增函数
2
2
对称中心
(kπ,0)
(kπ,0)
总结
y
-2π
1 -π
π 32ຫໍສະໝຸດ 2πx 3
0
2
3
2
(2)tCan4(-143
3
)与Dtan(
6
17 5
)
反 馈
训
(2)下列不等式中正确的是( B)
练
A tan 4 tan 3 B tan(-13 ) tan(-12 )
7
7
4
5
C tan 2 tan 3 D tan(-13 ) tan( 15 )
5
5
正切曲线的简图 几何画板
y
回总结
1
-
3 2
-
2
0 -1 2
3
2
x
说出定义域、值域、周期性、奇偶性和 单调性
正切函数图像及性质

(2)tanx <1
y
x
–/2
0
/2
y
1
x
–/2
0 /4 /2
(k,k+/2) kz (k–/2,k+/4)kz
提高练习
直线y=a(a为常数)与正切曲线y=tanx 相交的相 邻两点间的距离是
A、
B、/2
C、2
D、与a值有关
y
a
3 2
0
3
2
2
2
x
五、小结:正切函数的图像和性质
1、正切曲线是先利用平移正切线得y tan x, x ( , )的图象, 22
定义域:{x \ x k ,k z} 36
值域:R
单调递增区间:( k , k),k z 6 36 3
k 对称中心: ( 6 ,0)
例题分析
例3 求函数 y tan 3x 的周期.
解: 因为tan(3x ) tan 3x,
即tan3(x+ )=tan3x,
3
这说明自变量 x ,至少要增加 3 ,函数的值 才能重复取得,所以函数 y tan 3x的周期
再利用周期性把该段图象向左、右扩展得到。
y
2 、y tan x 性质:
⑴
定义域:{x | x
k, k Z} 2
⑵ 值域: R ⑶ 周期性:
⑷ 奇偶性:奇函数,图象关于原点对称。 2
0 x
2
(5) 对称性:对称中心:
, 无对称轴
(6)单调性:在每一个开区间
(-π+ 2
kπ,π+ 2
kπ)
,
(2)tan (
5_) _>__tan
(
第8讲 正切函数图像及其性质(讲义)解析版
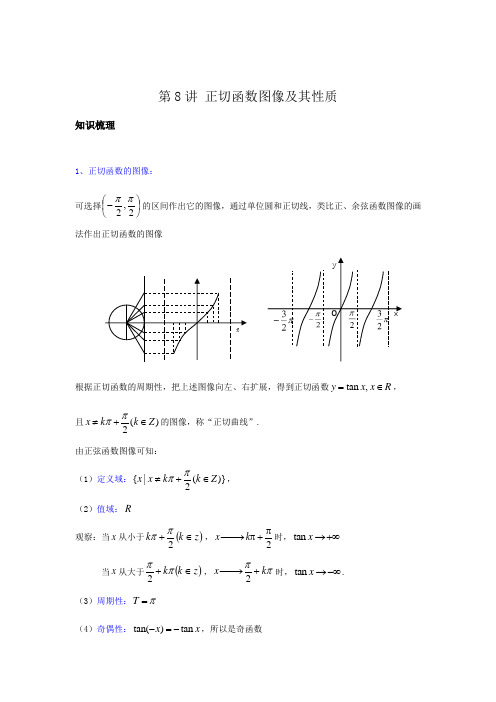
第8讲 正切函数图像及其性质知识梳理1、正切函数的图像:可选择的区间作出它的图像,通过单位圆和正切线,类比正、余弦函数图像的画法作出正切函数的图像根据正切函数的周期性,把上述图像向左、右扩展,得到正切函数tan ,y x x R =∈,且()2x k k Z ππ≠+∈的图像,称“正切曲线”.由正弦函数图像可知: (1)定义域:{|()}2x x k k Z ππ≠+∈,(2)值域:R 观察:当x 从小于,时,tan x →+∞当x 从大于,时,tan x →-∞.(3)周期性:T π=(4)奇偶性:tan()tan x x -=-,所以是奇函数⎪⎭⎫⎝⎛-2,2ππ()z k k ∈+2ππ2π+π−→−k x ()z k k ∈+ππ2ππk x +−→−2x yyx(5)单调性:在开区间(,),22k k k Zππππ-++∈内,函数单调递增.(6)中心对称点:,0,2kk Zπ⎛⎫∈⎪⎝⎭2、余切函数的图象:⎪⎭⎫⎝⎛--=⎪⎭⎫⎝⎛-==2tan2tancotππxxxy即将xy tan=的图象,向左平移2π个单位,再以x轴为对称轴上下翻折,即得xy cot=的图象由余弦函数图像可知:(1)定义域:{|()}x x k k Zπ≠∈,(2)值域:R(3)周期性:Tπ=(4)奇偶性:tan()tanx x-=-,所以是奇函数(5)单调性:在开区间(,),k k k Zπππ+∈内,函数单调递增.(6)中心对称点:,0,2k k Z π⎛⎫∈⎪⎝⎭例题解析一、正切函数的图像例1.(2020·全国高一课时练习)设函数()tan 33x f x π⎛⎫=-⎪⎝⎭. (1)求函数f (x )的最小正周期、对称中心; (2)作出函数f (x )在一个周期内的简图.【答案】(1)最小正周期3π,对称中心是3,02k ππ⎛⎫+⎪⎝⎭()k Z ∈;(2)答案见解析. 【分析】(1)首先根据正切函数的周期公式即可得到函数()f x 的周期,再根据正切函数的对称中心即可得到函数()f x 的对称中心.(2)根据函数的解析式得到()f x 的图象与x 轴的交点坐标为(),0π,图象上的7,14π⎛⎫ ⎪⎝⎭、,14π⎛⎫- ⎪⎝⎭两点,再找到两侧相邻的渐近线方程,画出函数的图象即可. 【详解】(1)()tan 33x f x π⎛⎫=- ⎪⎝⎭,313T ππ==,令332x k ππ-=,k Z ∈,解得32x k ππ=+,k Z ∈, 故对称中心为3,02k ππ⎛⎫+⎪⎝⎭()k Z ∈. (2)令033x π-=,解得x π=,令334x ππ-=,解得74x π=,令334x ππ-=-,解得4x π=, 令332x ππ-=,解得52x π=,令332x ππ-=-,解得2x π=-,所以函数()tan 33x f x π⎛⎫=-⎪⎝⎭的图象与x 轴的一个交点坐标为(),0π, 图象上的点有7,14π⎛⎫⎪⎝⎭、,14π⎛⎫- ⎪⎝⎭两点, 在这个5,22ππ⎛⎫-⎪⎝⎭周期内左右两侧相邻的渐近线方程分别为2x π=-和52x π=, 从而得到函数()f x 在一个周期5,22ππ⎛⎫-⎪⎝⎭内的简图(如图).【点睛】本题主要考查正切函数的周期和对称中心,同时考查了正切函数的图象,关键点是找出图象上的点用描点法画图象,属于中档题.例2.(2020·全国高一课时练习)已知函数()sin cos xf x x=. (1)求函数()f x 的定义域;(2)用定义判断函数()f x 的奇偶性; (3)在[],ππ-上作出函数()f x 的图象.【答案】(1),2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭;(2)奇函数,见解析;(3)见解析 【分析】(1)根据cos 0x ≠,求解即可;(2)由(1)可知()f x 的定义域关于原点对称,判定()f x -和()f x 的关系,从而判定奇偶性;(3)将()f x 写为分段函数,画出图象即可【详解】(1)由cos 0x ≠,得2x k ππ≠+(k Z ∈),所以函数()f x 的定义域是,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭.(2)由(1)知函数()f x 的定义域关于原点对称,因为()()()()sin sin cos cos x xf x f x xx ---===--,所以()f x 是奇函数. (3)()tan ,22tan ,22x x f x x x x ππππππ⎧-<<⎪⎪=⎨⎪--≤<-<≤⎪⎩或,所以()f x 在[],ππ-上的图象如图所示,【点睛】本题考查函数定义域,考查奇偶性的判断,考查函数图象. 例3.作函数||y tan x =的图像. 【难度】★★ 【答案】如图 【解析】||y tan x =等价于 0,2()0,2tanx x x k y k Z tanx x x k ππππ⎧≥≠+⎪⎪=∈⎨⎪-<≠+⎪⎩,图像如图所示.例4.求函数()tan tan f x x x =+的定义域、周期、单调增区间,并画草图. 【难度】★★★【答案】定义域:{|,}2x x k k Z ππ≠+∈ ,周期:T π=,单调增区间:[,)2k k πππ+(1)tan 0x > (2)tan 0x = (3)tan 0x < (4)tan x >【难度】★ 【答案】(1)Z k k k ∈⎪⎭⎫⎝⎛+,2,πππ, (2){}z k k x x ∈=,π (3)Z k k k ∈⎪⎭⎫⎝⎛-,,2πππ, (4)Z k k k ∈⎪⎭⎫ ⎝⎛++,ππππ2,3例6.根据正切函数图像,写出使下列不等式成立的x 值的集合: (1)0tan 1≥+x (2)3tan -x 0≥ 【难度】★★ 【答案】(1) [,),42k k k Z ππππ-+∈(2)[,),32k k k Z ππππ++∈例7.比较下列两数的大小(1)2tan7π与10tan 7π (2)6tan 5π与13tan()5π- (3)81cot 与191cot 【难度】★ 【答案】(1)2tan7π<10tan 7π (2)6tan 5π>13tan()5π- (3)81cot <191cot 例8.函数sin y x =与tan y x =的图像在[2,2]ππ-上的交点有 ( ).A 3个 .B 5个 .C 7个 .D .D 9个【难度】★★【答案】B【巩固训练】1.作出函数|tan |y x =的图象. 【难度】★★ 【答案】如图2.利用图像,不等式tan 21x <≤的解集为____________. 【难度】★★ 【答案】(,],2628k k k Z ππππ-+∈3.比较⎪⎭⎫ ⎝⎛-413tan π与⎪⎭⎫⎝⎛-517tan π的大小 【难度】★【答案】tan413tan -=⎪⎭⎫⎝⎛-π 4π,52tan517tan ππ-=⎪⎭⎫⎝⎛-,⎪⎭⎫⎝⎛=<<2,0tan ,5240πππ在x y内单调递增. ⎝⎛->⎪⎭⎫ ⎝⎛-->-∴<∴ππππππ517tan 413tan ,52tan 4tan ,52tan4tan即 4.若()tan()4f x x π=+,试比较(1),(0),(1)f f f -,并按从小到大的顺序排列:_________. 【难度】★★【答案】(1)(1)(0)f f f <-<5.(2020·全国高一课时练习)设函数()tan 23π⎛⎫=-⎪⎝⎭x f x . (1)求函数f (x )的最小正周期,对称中心; (2)作出函数()f x 在一个周期内的简图.【答案】(1)2T π=,2,03ππ⎛⎫+ ⎪⎝⎭k ()k Z ∈;(2)图象见解析【分析】(1)首先根据正切函数的周期公式即可得到函数()tan 23π⎛⎫=-⎪⎝⎭x f x 的周期,再根据正切函数的对称中心即可得到函数()tan 23π⎛⎫=-⎪⎝⎭x f x 的对称中心. (2)首先根据函数的解析式得到数()tan 23π⎛⎫=-⎪⎝⎭x f x 的图象与x 轴的一个交点坐标为2,03π⎛⎫⎪⎝⎭,在这个交点左右两侧相邻的渐近线方程分别为3x π=-和53x π=,再画出函数的图象即可.【详解】(1)()tan 23π⎛⎫=- ⎪⎝⎭x f x ,212T ππ==.令232ππ-=x k ,k Z ∈,解得23ππ=+x k ,k Z ∈, 故对称中心为2,03ππ⎛⎫+ ⎪⎝⎭k ()k Z ∈.(2)令023x π-=,解得23x π=,令234x ππ-=,解得76x π=, 令234x ππ-=-,解得6x π=,令232x ππ-=,解得53x π=, 令232x ππ-=-,解得3x π=-, 所以函数()tan 23π⎛⎫=-⎪⎝⎭x f x 的图象与x 轴的一个交点坐标为2,03π⎛⎫⎪⎝⎭, 在这个交点左右两侧相邻的渐近线方程分别为3x π=-和53x π=. 故函数在一个周期内的函数图象为:【点睛】本题主要考查正切函数的周期和对称中心,同时考查了正切函数的图象,属于中档题.二、正切函数的定义域及值域1、正切函数的定义域例1.求下列函数的定义域(1)tan 2y x = (2)y = (3)cos tan y x x =⋅ (4)11tan y x=+ 【难度】★ 【答案】(1)⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,24ππ (2)Z k k k ∈⎪⎭⎫ ⎝⎛++-,3,3ππππ (3),2x x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭且 (4),,42x x k x k k Z ππππ⎧⎫≠-≠+∈⎨⎬⎩⎭且例2.(2019·宝山区·上海交大附中高一期末)下列四个函数中,与函数()tan f x x =完全相同的是( )A .22tan21tan 2xy x =- B .1cot y x = C .sin 21cos 2x y x =+ D .1cos 2sin 2x y x -=【答案】C【分析】先判断函数的定义域是否相同,再通过化简判断对应关系是否相同,从而判断出与()f x 相同的函数.【详解】()f x 的定义域为|,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭, A. 22tan 21tan 2x y x =-,因为tan 12,22x x k k Z ππ⎧≠±⎪⎪⎨⎪≠+∈⎪⎩,所以,24,22x k k Z x k k Z ππππ⎧≠±+∈⎪⎪⎨⎪≠+∈⎪⎩, 定义域为{|22x x k ππ≠±或2,}x k k Z ππ≠+∈,与()tan f x x =定义域不相同; B. 1cot y x =,因为cos 0sin 0x x ≠⎧⎨≠⎩,所以,2,x k k Z x k k Zπππ⎧≠+∈⎪⎨⎪≠∈⎩, 所以定义域为,2k x x k Z π⎧⎫≠∈⎨⎬⎩⎭,与()tan f x x =定义域不相同; C. sin 21cos 2x y x =+,因为1cos20x +≠,所以定义域为|,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭, 又因为2sin 22sin cos tan 1cos 22cos x x x y x x x ===+,所以与()tan f x x =相同; D. 1cos 2sin 2x y x-=,因为sin 20x ≠,所以2,x k k Z π≠∈,定义域为|,2k x x k Z π⎧⎫≠∈⎨⎬⎩⎭, 与()tan f x x =定义域不相同.故选:C.【点睛】本题考查与三角函数有关的相同函数的判断,难度一般.判断相同函数时,首先判断定义域是否相同,定义域相同时再去判断对应关系是否相同(函数化简),结合定义域与对应关系即可判断出是否是相同函数.例3.(2019·上海市大同中学高一期中)函数arcsin tan 2y x x =+的定义域是________【答案】[1,)(,)(,1]4444ππππ--- 【分析】解不等式11,2,2x x k k Z ππ-≤≤⎧⎪⎨≠+∈⎪⎩即得解. 【详解】由题得11,2,2x x k k Z ππ-≤≤⎧⎪⎨≠+∈⎪⎩所以x ∈[1,)(,)(,1]4444ππππ---. 故函数的定义域为[1,)(,)(,1]4444ππππ--- 故答案为[1,)(,)(,1]4444ππππ---【点睛】本题主要考查函数定义域的求法,考查反三角函数和正切函数的定义域,意在考查学生对这些知识的理解掌握水平,属于基础题.例4.(2017·上海杨浦区·复旦附中高一期中)已知函数()()lg tan 1f x x =-()f x 的定义域是____.【答案】3,,4242ππππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ 【分析】由意义得出2tan 1090x x ->⎧⎨-≥⎩,解出该不等式组即可得出函数()y f x =的定义域. 【详解】函数()()lg tan 1f x x =-+2tan 1090x x ->⎧∴⎨-≥⎩, ()4233k x k k Z x ππππ⎧+<<+∈⎪∴⎨⎪-≤≤⎩,3,,4242x ππππ⎛⎫⎛⎫∴∈-- ⎪ ⎪⎝⎭⎝⎭,因此,函数()y f x =的定义域为3,,4242ππππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭. 故答案为:3,,4242ππππ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭. 【点睛】本题考查函数定义域的求解, 同时也涉及了正切不等式的求解,考查运算求解能力,属于中等题.例5.求函数y =lg(tan x -+3cos 2+x 的定义域. 【难度】★★【答案】(,),32k k k Z ππππ++∈【解析】tan 2cos 0,2x x x k k Z ππ⎧>⎪⎪≥⎨⎪⎪≠+∈⎩ 由此不等式组作图: ∴(,),32k k k Z ππππ++∈ 【巩固训练】1.函数tan 4y x π⎛⎫=+ ⎪⎝⎭的定义域为__________ 【难度】★【答案】,4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭2.与函数)42tan(π+=x y 的图象不相交的一条直线是 ( ).A 2π=x .B 2π-=x .C 4π=x .D 8π=x【难度】★【答案】D3.求下列函数的定义域(1)1tan y x = ;(2)sin tan()log (2cos 1)4x y x x π=+⋅- . 【难度】★★★【答案】见解析解:等价转化为求一个不等式组的解 (1)sin 0tan 0,()2x x x k k Z ππ⎧⎪≥⎪≠⎨⎪⎪≠+∈⎩(2,2),,()2x k k x k k Z πππππ⇒∈+≠+∈ (2) 2cos 10sin 0,()42x x x k k Z πππ⎧⎪->⎪>⎨⎪⎪+≠+∈⎩⇒(2,2)33(2,2)(2,2)224x k k x k k k k x k πππππππππππππ⎧∈-+⎪⎪⎪∈+++⎨⎪⎪≠=⎪⎩(2,2)(2,2),()443x k k k k k Z πππππππ⇒∈+++∈. 注:转化过程中要注意必须是等价转换,才能保证结果既不扩大也不缩小.在求条件组的解时,常会求角集得交集,可以画数轴,用单位圆或函数的图像,应熟练掌握这种技能.2、正切函数的值域与最值例1.(2016·上海浦东新区·华师大二附中高一期中)设函数()sin 2sin 1cos 2cos x x f x x x-=+-,关于()f x 的性质,下列说法正确的是_________. ①定义域是,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭;②值域是R ;③最小正周期是π; ④()f x 是奇函数;⑤()f x 在定义域上单调递增.【答案】③④【分析】先求定义域,再化简函数解析式,根据正切函数性质求值域、求周期、判断单调性与奇偶性.【详解】()sin 2sin 1cos 2cos 01cos 2cos x x f x x x x x-=∴+-≠+- 22cos cos 0cos 0x x x ∴-≠∴≠且1cos 2x ≠, 定义域是,,23x x k x k k Z ππππ⎧⎫≠+≠±∈⎨⎬⎩⎭; ()sin 2sin sin (2cos 1)tan 1cos 2cos cos (2cos 1)x x x x f x x x x x x --===+--所以()f x ≠()f x 最小正周期是π;()f x 是奇函数;()f x 在定义域上不具有单调性故答案为:③④【点睛】本题考查二倍角余弦公式以及函数综合性质,考查综合分析求解能力,属中档题.例2.(2020·上海高一课时练习)求下列函数的值域:(1)1tan ,,01tan 2+⎛⎫=∈- ⎪-⎝⎭x y x x π; (2)2tan 3tan 1,,34⎡⎤=+-∈-⎢⎥⎣⎦y x x x ππ. 【答案】(1)(1,1)-;(2)13,34⎡⎤-⎢⎥⎣⎦ 【分析】(1)由定义域可得()tan ,0x ∈-∞,令tan t x =则(),0t ∈-∞,所以1211t 1t y t +-==-+--,再根据幂函数的性质计算可得; (2)利用换元法将函数转化为二次函数,根据二次函数的性质计算可得;【详解】解:(1)因为1tan ,,01tan 2+⎛⎫=∈- ⎪-⎝⎭x y x x π,所以()tan ,0x ∈-∞ 令tan t x =则(),0t ∈-∞ 所以1211t 1t y t +-==-+-- 因为(),0t ∈-∞,所以()1,1t -∈-∞-,()11,01t ∈--,()2210,t -∈-, ()211,11t --+∈--,即()1,1y ∈- (2)因为2tan 3tan 1,,34⎡⎤=+-∈-⎢⎥⎣⎦y x x x ππ所以tan x ⎡⎤∈⎣⎦令tan m x =,m ⎡⎤∈⎣⎦所以()223133124y f m m m m ⎛⎫==+-=+- ⎪⎝⎭所以()f m 在3,12⎡⎤-⎢⎥⎣⎦上单调递增,在32⎡⎫-⎪⎢⎣⎭上单调递减, 31324f ⎛⎫-=- ⎪⎝⎭,()13f =,(2f =-所以()13,34f m ⎡⎤∈-⎢⎥⎣⎦即函数的值域为13,34⎡⎤-⎢⎥⎣⎦【点睛】本题考查正切函数的性质的应用,换元法求函数的值域,属于中档题. 例3.(2020·上海高一课时练习)求下列函数的值域:(1)tan ,,626⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦y x x πππ; (2)2tan 1,,1tan 46+⎛⎫=∈- ⎪-⎝⎭x y x x ππ; (3)2sec 2tan 1,,33⎡⎤=++∈-⎢⎥⎣⎦y ππθθθ.【答案】(1)[;(2)12⎛- ⎝⎭;(3)[1,5+ 【分析】(1)首先令6t x π=+,得到tan y t =,再根据tan y t =的单调性即可得到函数的值域.(2)首先令tan t x =,得到213211t y t t+==-+--,再根据函数的单调性即可得到值域.(3)首先将函数化简为2tan 2tan 2y θθ=++,令tan t θ=,得到222y t t =++,再利用二次函数的性质即可求出函数的值域. 【详解】(1)令6t x π=+,因为,26x ππ⎡∈⎤-⎢⎥⎣⎦,所以,33t ππ⎡⎤∈-⎢⎥⎣⎦, 又tan y t =在,33t ππ⎡⎤∈-⎢⎥⎣⎦上为增函数,所以所求函数值域为[. (2)令tan t x =,因为,46⎛⎫∈- ⎪⎝⎭x ππ,所以⎛∈- ⎝⎭t .212(1)332,1,1113⎛+-+===-+∈- ---⎝⎭t t y t t t t . 因为1y t =-为减函数,所以31y t =-在⎛∈- ⎝⎭t 为增函数, 即:321=-+-y t在⎛∈- ⎝⎭t 上为增函数, 所以min 31222y =-+=-,max 522y +=-=.所以函数的值域为12⎛- ⎝⎭. (3)222221sin cos 2tan 1=2tan 1tan 2tan 2cos cos y θθθθθθθθ+=++++=++. 令tan ,,33⎡⎤=∈-⎢⎥⎣⎦t ππθθ,所以[∈t .2222(1)1,[=++=++∈y t t t t .当1t =-时,min 1y =,当t =时,max 5y =+所以函数的值域为[1,5+.【点睛】本题主要考查正切函数的值域问题,利用换元法求值域为解决本题的关键,属于中档题.例4.函数2tan ,0,124y x x ππ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎝⎭⎣⎦的值域为 【难度】★ 【答案】[]32,324- 例5.若⎥⎦⎤⎢⎣⎡-∈4,3ππx ,求函数1tan 2cos 12++=x x y 的最值及相应的x 值;. 【难度】★★ 【答案】4x π=-时,min 1y =; 4x π=时,max 5y =例6.已知2tan tan y x a x =-,当1[0,],[0,]34x a π∈∈时,函数max y =,求实数a 的值. 【难度】★ 【答案】323-=a 例7.求函数252tan 4tan 3y x x =-+的值域. 【难度】★★【答案】(0,5] 【巩固训练】1.求函数sin tan ,[,]44y x x x ππ=+∈-的值域【难度】★★【答案】[1]-+2.求函数2)1(tan 12-+=x y 的最大值,并求当函数取得最大值时,自变量x 的集合. 【难度】★★【答案】2max =y ,此时⎭⎬⎫⎩⎨⎧∈+==Z k k x x x ,4ππ3.已知2tan 2tan 3y x x =-+,求它的最小值【难度】★★【答案】当tan 1x =时,min 2y =4.函数2tan 4tan 1y x x =+-的值域为____________ 【难度】★ 【答案】[)5,-+∞【解析】令tan t x =则转化为t 的二次函数求最值。
正切函数图像.ppt

4.10 正切函数的图像和性质 一、引入
如何用正弦线作正弦函数图象呢? 1、用平移正弦线得y sin x, x [0,2 ]图象. 2、再利用周期性把该段图象向左、右扩展得到.
类 比
用正切线作正切函数y=tanx的图象
4.10 正切函数的图像和性质
二、探究用正切线作正切函数图象
⑷ 奇偶性: 奇函数,图象关于原点对称。
⑸ 单调性: 在每一个开区间
( k , k )
2
2
,k Z 内都是增函数。
(6)渐近线方程:x
k
2
,
kZ
(7)对称中心 (kπ,0) 2
问题讨论
问题:
(1)正切函数是整个定义域上的增函数吗?为什么? (2)正切函数会不会在某一区间内是减函数?为什么?
解: 因为tan(3x ) tan 3x,
即tan3(x+ )=tan3x,
3 这说明自变量 x
,至少要增加
,函数的值
才能重复取得,所以函数
y
3
tan 3x
的周期
是
3
反馈练习:求下列函数的周期:
(1) y 5 tan x
2 2
(2) y tan(4x)
4
例题分析
例 4 解不等式:tan x 3
问题2、如何利用正切线画出函数 的图像?
y
tan
x,x
2
,
2
角 的终边 Y
T3
(
3
,tan
)
3
A
0
X
3
利用正切线画出函数
y
tan
x
,x
2
,
2
的图像:
三角函数正切函数的性质与图像

正切函数的图像向右平移π个单位,可以得 到余弦函数的图像。
左右翻转
正切函数的图像关于$y$轴对称,即$tan( - x) = tan(x)$。 正切函数的图像向左翻转后,可以得到正切函数的图像。
03
正切函数的图像绘制
利用Python绘制正切函数图像
导入matplotlib库
定义正切函数
首先需要导入matplotlib库,该库是 Python中用于绘图的常用库之一。
使用xlabel和ylabel参数可以添加x轴和y轴的标签,例如x轴 标签为“$x$”,y轴标签为“$y$”。
显示网格线
使用grid参数可以显示网格线,以便更好地观察图像的细节 。
04
三角函数的实际应用
物理中的三角函数
简谐振动
简谐振动的位移与时间的关系可以表示为正弦或余弦函数,利用三角函数性 质可以更深入地理解简谐振动的特征。
正切函数的对称性
正切函数图像无对称轴,但在$x = \frac{\pi}{2} + k\pi$ 处,函数图像呈现对称性。
正切函数的奇偶性
$tan( - x) = - tan(x)$,因此正切函数为奇函数。
正切函数的应用
正切函数在解直角三角形、求三角形的面积、研究三角恒 等式等方面具有广泛应用。
对未来研究正切函数的展望
三角函数正切函数的性质与图像
xx年xx月xx日
contents
目录
• 正切函数概述 • 正切函数的性质 • 正切函数的图像绘制 • 三角函数的实际应用 • 总结与展望
01
正切函数概述
正切函数的定义
正切函数:tan(x) = sin(x) / cos(x) 值域:(-∞,∞)
定义域:{x | x ≠ π/2 + kπ,k ∈ Z} 周期:π
正切函数的图像和性质

C.充要条件
4.10 正切函数的图像和性质
小结:
(1)y tan x 的作图是利用平移正切线得到的,当我们获得 , 上图像后,再利用周期性把该段图像向左右延伸、平移。 2 2
(2) y tan x 性质: 定义域 值 周 奇 单调增区间 域 期 偶 性 对 称 中心 渐近线 方程,
y tan x x 利用正切线画出函数 , , 的图像: 2 2
几何画板演示
4.10 正切函数的图像和性质
结合正切函数图像研究正切函数的性质:定义域、值域、周期性、 正切函数的性质: 奇偶性和单调性. ⑤单调性 : R 奇函数.正切曲线关于原点 ②值域: ⑥渐近线: O 对称. ④奇偶性: x x k , k Z ①定义域: 2 tan x x k, k k (k Z ) 内都是增 k(x k Z x 小于 正切函数在每个开区间 当 )且无限接近于 时, k 渐近线方程是: , k Z 正切函数是周期函数,周期是 . 2 Z ),都有 2 2 tan ( k x tan x , k, k ∵任意 x 2 2 2 2 tan x 当 x 大于 k(k Z)且无限接近于 k 时, 函数. 2 2 ∴正切函数是奇函数.
是增函数, 3 3 11 13 ∴ tan tan 即 tan tan . 4 5 4 5
4.10 正切函数的图像和性质
练习:
(1)直线 y a( a 为常数)与正切曲线 y tanx ( 为常数
x x k ,k Z 2
正切函数的图像和性质

是增函数, 3 3 11 13 ∴ tan tan 即 tan tan . 4 5 4 5
4.10 正切函数的图像和性质
练习:
(1)直线 y a( a 为常数)与正切曲线 y tanx ( 为常数
4.10 正切函数的图像和性质
4.10 正切函数的图像和性质
回忆:怎样利用单位圆中的正弦线作出 y sin x图像的. 用正切线作正切函数图像: 正切函数 y tan x是否为周期函数?
sin x sin x f x tan x tan x f x cos x cos x
C.充要条件
4.10 正切函数ቤተ መጻሕፍቲ ባይዱ图像和性质
小结:
(1)y tan x 的作图是利用平移正切线得到的,当我们获得 , 上图像后,再利用周期性把该段图像向左右延伸、平移。 2 2
(2) y tan x 性质: 定义域 值 周 奇 单调增区间 域 期 偶 性 对 称 中心 渐近线 方程
所以函数 y tan x 的定义域是 x x k,k Z 4 4
4.10 正切函数的图像和性质
例2.不通过求值,比较下列各组中两个正切函数值的大小:
13 11 tan 与 tan . tan 167 与 tan 173 ;(2) ( 1) 5 4 3 11 解:( 1 )∵ tan 90 173 180 167 (2)∵ tan 4 4 13 90 3 x , 上是增函数 又 ∵ y tan ,在 270 tan tan 5 5 tan 167 tan 173 3 3 3 ∴ 3 y tan x 又∵ ,函数 ,x , 2 4 5 2 2 2
正切函数的图像和性质

4.10 正切函数的图像和性质
回忆:怎样利用单位圆中的正弦线作出 y sin x图像的. 用正切线作正切函数图像: 正切函数 y tan x是否为周期函数?
sin x sin x f x tan x tan x f x cos x cos x
是它的一个周期. ∴ y tan x 是周期函数,
y tan x x 利用正切线画出函数 , 正切函数的图像和性质
结合正切函数图像研究正切函数的性质:定义域、值域、周期性、 正切函数的性质: 奇偶性和单调性. ⑤单调性 : R 奇函数.正切曲线关于原点 ②值域: ⑥渐近线: O 对称. ④奇偶性: x x k , k Z ①定义域: 2 tan x x k, k k (k Z ) 内都是增 k(x k Z x 小于 正切函数在每个开区间 当 )且无限接近于 时, k 渐近线方程是: , k Z 正切函数是周期函数,周期是 . 2 Z ),都有 2 2 tan ( k x tan x , k, k ∵任意 x 2 2 2 2 tan x 当 x 大于 k(k Z)且无限接近于 k 时, 函数. 2 2 ∴正切函数是奇函数.
且 0 )相交的相邻两点间的距离是( C ) 2 B A. D.与 a 值有关 C . tan x 0是的 x 0 D ) ( 2) (. A.充分不必要条件 B.必要不充分条件
D.既不充分也不必要条件 (3)根据三角函数的图像写出下列不等式成立的角 x 集合 3 tan x 1 ① ② 1 tan x 0 3 x k x k , k Z x k x k , k Z 6 4 4 2
正切函数的图像与性质

1、你已经对正切函数 y tan x 的性质了解多少?
①定义域:{x | x k , k Z}
2
②周 期:T
③奇偶性:奇函数
2、已知的这些性质对作正切函数 y tan x 的图象
有何帮助?
建构数学
一、正切函数y tan x 在 ( , ) 的图象
2
②值 域: R
3 --
2
--
--
2
O
3
x
2
2
③周 期:T
④奇偶性:奇函数
⑤单调性:单调增区间为:( k ,
⑥渐近线: 直线:x
2
k , k Z
2
k )(k
Z)
开区间
2
思考:正切函数在整个定义域内是增函数吗?
数学应用
活动1、求函数
y tan(2x )
4
的定义域。
若求值域、周期、单调区间呢?
整
体
代
练习:P33 , 2
入
数学应用
活动2、比较大小:
(1)tan 138 。与 tan 143 。
(2)tan( 13 )与tan( 17 )
4
y
5
3 --
2
--
--
2
O
3
x
2
2
数学应用
活动3、根据图象求满足下列条件的 x 的取值集合
2
②值 域: R
3 --
2
--
--
2
O
3
x
2
2
正切函数图像

正切函数图像一、正切函数图像定义:。
因此,切线的斜率k=1/x,斜率是一个比值,所以斜率并不等于1,而只是一个表示“角度”的量,用x 表示切线与y轴交点的横坐标,用t表示切线与坐标轴交点的纵坐标。
二、几何意义:定义:。
三、几何关系:切线的斜率k=1/x,即x正切斜率k,斜率就是角度除以弧度。
四、点斜式:1、正切函数的图像是y=ln。
2、切线的斜率k=1/x,即x正切斜率k,斜率就是角度除以弧度。
3、切线斜率k的计算公式为: k=k ( 1)斜率的物理意义:表示单位时间内通过曲线上某一点的切线段长度,即斜率表示通过曲线上某一点的切线的斜率表示通过曲线上某一点的切线的斜率表示通过曲线上某一点的切线的斜率K=arctan (θ/λ)=arctan(θ/λ)( 1)正切值的计算:3、切线斜率k的三种方法:(1)切线和坐标轴互相垂直,此时斜率可取正值;(2)切线与x轴有两个交点,这时斜率是两个不同的角度的正切值的平均值,可取负值;(3)若两条切线与坐标轴互相垂直,且切线分别与坐标轴的交点数之差为n,那么该切线的斜率k=2( n)sinθ/( n-1) cosθ/n五、斜截式: 1、正切函数的图像是y=ln(θ/λ)为一般形式y=sint(θ/λ)。
2、其斜率k的三种方法:(1)切线与坐标轴互相垂直,此时斜率可取正值;(2)切线与x轴有两个交点,这时斜率是两个不同的角度的正切值的平均值,可取负值;(3)若两条切线与坐标轴互相垂直,且切线分别与坐标轴的交点数之差为n,那么该切线的斜率k=2( n) sinθ/( n-1) cosθ/n六、投影式: 1、正切函数的图像是y=ln(θ/λ)的一般式y=sintθ/λ。
8、求斜率k的三种方法:(1)切线和坐标轴互相垂直,此时斜率可取负值;(2)切线与x轴有两个交点,这时斜率是两个不同的角度的正切值的平均值,可取负值;(3)若两条切线与坐标轴互相垂直,且切线分别与坐标轴的交点数之差为n,那么该切线的斜率k=2( n)sinθ/( n-1) cosθ/n七、注意:( 1)不能将斜率看作切线与y 轴交点的横坐标,切线与y轴交点的横坐标必须加上y值再求切线斜率。
正切函数的图像及性质PPT优秀课件

4
24
注意:不要与正弦型函数和余弦型函数的
周期公式混淆了…… 函数y=Asin(ω x+Ф )的周期
T 2
函数y=Acos(ω x+Ф )的周期
T 2
y
1
x
-3/2
- -/2
0 /2
3/2
-1
例3.比较下列各组数的大小
1 . tan1670 与 tan1730
2.tan(11 )与 tan(13 )
3 8
, 4
,
8
,8
,4
3 ,8
o
3 0 3
2 848
84 8 2
由正切函数的周期性,把图象向左、向右 扩展,得到正切函数的图象,称为正切曲线
y
y=tanx
1 x
-3/2 - -/2
0 /2
3/2
-1
从x图中2可k以看,(出k, 正Z切)曲所线隔是的由无被穷相多互支平曲行线的组直成线的.
――[阿萨·赫尔帕斯爵士] 115.旅行的精神在于其自由,完全能够随心所欲地去思考.去感觉.去行动的自由。――[威廉·海兹利特]
116.昨天是张退票的支票,明天是张信用卡,只有今天才是现金;要善加利用。――[凯·里昂] 117.所有的财富都是建立在健康之上。浪费金钱是愚蠢的事,浪费健康则是二级的谋杀罪。――[B·C·福比斯] 118.明知不可而为之的干劲可能会加速走向油尽灯枯的境地,努力挑战自己的极限固然是令人激奋的经验,但适度的休息绝不可少,否则迟早会崩溃。――[迈可·汉默] 119.进步不是一条笔直的过程,而是螺旋形的路径,时而前进,时而折回,停滞后又前进,有失有得,有付出也有收获。――[奥古斯汀] 120.无论那个时代,能量之所以能够带来奇迹,主要源于一股活力,而活力的核心元素乃是意志。无论何处,活力皆是所谓“人格力量”的原动力,也是让一切伟大行动得以持续的力量。――[史迈尔斯] 121.有两种人是没有什么价值可言的:一种人无法做被吩咐去做的事,另一种人只能做被吩咐去做的事。――[C·H·K·寇蒂斯] 122.对于不会利用机会的人而言,机会就像波浪般奔向茫茫的大海,或是成为不会孵化的蛋。――[乔治桑] 123.未来不是固定在那里等你趋近的,而是要靠你创造。未来的路不会静待被发现,而是需要开拓,开路的过程,便同时改变了你和未来。――[约翰·夏尔] 124.一个人的年纪就像他的鞋子的大小那样不重要。如果他对生活的兴趣不受到伤害,如果他很慈悲,如果时间使他成熟而没有了偏见。――[道格拉斯·米尔多] 125.大凡宇宙万物,都存在着正、反两面,所以要养成由后面.里面,甚至是由相反的一面,来观看事物的态度――。[老子]
正切函数的性质与图象

f ( x ) tan( x ) tan( x ) tan[ ( x 2) ] f ( x 2) 2 3 2 3 2 3
因此函数的周期为2.带入正切的单调区间可解得函 数得单调区间
5 1 ( 2k , 2k ), k Z 3 3
(1)1 tan x 0;
y 3
(2) tan x 3 0;
4
3
y 1
小结
正切函数的周期性,奇偶
性,单调性,值域.
作业
课本45页练习
4、值域
正切函数的值域是实数 R. 集
举例
π π 例1 求函数y tan ( x )的定义域, 周 2 3 期和单调区间.
解:
x k 2 3 2
即
所以函数的定义域是 由于
1 { x | x 2k , k Z }. 3
1 x 2k , k Z 3
y A sin( x ), x R.( A 0, 0) y A cos(x ), x R.( A 0, 0)
y A tan( x ).( A 0, 0)
T
2
T
例2 求使下列不等式成立的 的集合: x
§ 1.4.3 正切函数的 性质与图象
引入
正切函数:
y tan x , x k , k Z 2
新课
正切函数图像:
FLASH
1、周期性
正切函数是周期函数, 周期是π.
2、奇偶性
正切函数是奇函数.
3、单调性
π π 在每一个开区间 , kπ ), k Z上都是增函数 (kπ . 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于
f ( x) tan( x ) 4 tan(x )
tan[( x )
f (x )
( 3 k , k ) 4 4
4
4
]
所以函数的周期是
由于 k x k
4
3 k x k 4 4
x
3/2
-1
函数 定义域
值域
周期性 奇偶性 单调性
y=tanx {x | x k , k Z } 2 R T= 奇函数 增区间 (k , k )k Z 2 2
三、应用
例6 求函数
y=tan(x+3 )
的定义域、周期和单调区间.
练习:求函数 y=tan(x+ /4)的定义域,周期,单调 区间。 解:令t=x+ /4,则函数y=tant的定义域是 {t|t k + /2, k z} x+ /4 =t=k + /2 x = k + /2 –/4 = k + /4 所以 ,y=tan(x+ /4)的定义域是 {x|x k + /4, k z}
2
2
k Z
解得
k Z
所以函数的单调增区间是
小结:
3 ( k , k ) 4 4
1.正切曲线的几何画法以及正切函数的性质
2.正切函数性质
3.用数形结合的思想理解和处理有关的问题
.
函数 定义域 值域
y=tanx
{x | x k , k Z } 2
R
周期性
奇偶性 单调性 增区间
2.正弦函数,余弦函数的性质
函数
y
1
y sin x
y
1
y cos x
2
5 2
图象 定义域 值域 周期 奇偶性
2
0
-1
2
3 2
x
0
-1
2
3 2
2
5 2
x
xR
y [1,1]
xR
y [1,1]
2
奇函数
2
偶函数
x[- 2k , 2k ] 增函数 2 2 单调性 x[ 2k , 3 2k ] 减函数 2 2 k Z
∵f x +π = tan x +π = tanx f x
∴ y = tanx 是周期函数, 期.
y = tanx 是否为周期函数?
是它的一个周
y tan x ,x , 的图像: 利用正切线画出函数 2 2 把单位圆右半圆分成8等份。 作法: (1) 等分: 3 3 (2) 作正切线 , , , , , 8 8 4 8 8 4 (3) 平移 (4) 连线
o
3 0 2 8 4 8
8
4
3 8
2
是由通过点(k
2
, 0)(k Z ) 且与 y 轴相互平行的
直线隔开的无穷多支曲线组成
渐 进 线
渐 进 线
3 2
0
正切曲线
三、利用正切函数的图象,讨论它的性质 y
1
-3/2 - -/2
0
/2
1.4.3正切函数的性质与图像
教师:米婷
一、复习回顾
正弦函数图像的绘制
1、用平移正弦线得 sin x, x [0,2 ]图象. y
y
1
_
o1
A
o
-1
_ Βιβλιοθήκη 3 22 35 6
7 6
4 3 5 11 3 2 3 6
2
x
2、再利用周期性把该段 图象向左、右扩展得到 .
x[ 2k , 2k ] 增函数 x[2k , 2k ] 减函数 k Z
二、探究正切函数图象及其性质
问题1、正切函数
y = tanx 的定义域是什么?
y tan x 0 的终边不在y轴上 x k (k z ) 2
问题2、正切函数
T=
奇函数
(k , k )k Z 2 2
作业:P46
6,7
