正切函数的图象与性质(习题)
正切函数的图象和性质练习

正切函数的图象和性质练习根底卷〔15分钟〕 一、选择题1.函数)0)(6tan(≠+=a ax y π的周期为〔 〕A .a π2B .||2a π C .||a πD .aπ 2.以下不等中正确的选项是〔 〕A .73tan74tanππ> B .)512tan()413tan(ππ->-C .cot4<cot3D .cot281°<cot665° 3.如果α,β∈),2(ππ,且tan α<cot β,那么〔 〕A .α<βB .β<αC .23πβα<+ D .23πβα>+4.)4tan(x y +=π的定义域是〔 〕 A .},4|{R x x x ∈≠πB .},4|{R x x x ∈-≠πC .},,4|{Z k R x k x x ∈∈+≠ππ D .},,432|{Z k R x k x x ∈∈+≠ππ 5.以下函数中,周期是2π,且在)12,125(ππ-内是单调递增的函数是〔 〕 A .)3tan(π+=x y B .)32tan(π+=x yC .)3tan(π-=x y D .)32tan(π-=x y二、填空题6.假设函数)52tan(2π-=ax y 的最小正周期是5π,那么a=_____________. 7.tax<-1时,x 的取值集合是______________. 8.)3lg(tan -=y 的定义域是______________.提升卷〔30分钟〕 一、选择题1.以下函数中不是偶函数的是〔 〕 A .y=|tanx| B .y=|cotx| C .tan|x| D .y=tan 〔x-π〕 2.)4sin(π-=x y 与y=-|tanx|在[0,2π]上的交点有〔 〕A .4个B .2个C .1个D .0个3.以下点中函数)5tan(π+=x y 〔x ∈R 且ππk x +≠103,k ∈Z 〕的一个对称中央点是〔 〕A .〔0,0〕B .)0,5(πC .)0,54(πD .〔π,0〕4.函数y=tanx-cotx 是〔 〕A .奇函数B .偶函数C .非奇非偶函数D .既奇且偶函数 5.)3tan(π-=x y ,)3,2()2,3(ππππ---∈ x 的值域是〔 〕 A .]3,0[ B .〔-∞,0〕C .]0,3[-D .),3[]0,(+∞-∞6.要得到y=tan2x 的图象,只需把函数)62tan(π+=x y 的图象〔 〕A .向左平移6π个单位B .向左平移12π个单位 C .向右平移6π个单位D .向右平移12π个单位二、填空题7.函数y=atanx-b 在]4,4[ππ-上的最大值是____________. 8.函数)32tan(π+=x y 的递增区间是____________. 9.函数y=tan 〔cosx 〕的值域是___________. 10.不等式65tantan π≤x 的解集是___________.三、解做题11.求函数y=tanxcosx 的定义域并画出它的图象.12.比拟以下各组数的大小: 〔1〕tanl,tan2,tan3 〔2〕)713cot(π-,89cot π参考答案根底卷一、1.C2.B3.C4.C5.B 二、6.25±=a 7.4222|{ππππ-<<-k x k x 或},43222Z k k x k ∈+<<+ππππ8.2232|{ππππ+<<+k x k x 或},232452Z k k x k ∈+<<+ππππ提升卷一、1.D2.B3.C4.A5.D6.D 二、7.当a ≥0时,a-b ;当a<0时,-a-b 8.)32,352(ππππ+-k k k ∈Z 9. [-tan1, tan1] 10. )62,22(ππππ--k k ⋃)65,22(πππ+k k ∈Z 三、11.略12.〔1〕tan2<tan3<tanl 〔2〕89cot )713cot(ππ<-[解题点拨]2.考查画图水平,注意将图象画在[0,2π]上. 3.)5tan(π+=x y 的一个对称点必须要满足这个x 的值代入式子中使值为0.4.根据函数奇偶性的定义来判断.5.注意把握正切函数在指定区间上的函数图象,现进一步确定其值域.6.注意把握图象变换时,哪一个图象是图象,哪一个是要得到的图象.同时)12(2tan )62tan(ππ+=+=x x y7.注意画图的同时有参数a,就要考虑讨论来明确答案.9.由于|cosx|≤1.即求y=tanx,x ∈[-1,1]上的值域. 10.三角不等式最好利用正切线来处理.可先将65tan π的值化出来. 11.y=tanx ·cosx 可化成y=sinx,但是)(2Z k k x ∈+≠ππ12.通过画图来解,同时注意将)713cot(π-,89cot π转化成正切函数来处理.一般通过诱导公式将其化入到同一个单调区间最为重要!。
正切函数的图像和性质练习题

正切函数图象与性质检测试题一、选择题1、函数4tan xy的定义域是Zk 其中A .4|kxR x B .4|kx R x C .42|kx R x D .42|kx R x 2、函数4,3,tan xx y 的值域是A .1,B .1,3C .,D .,33、函数3tan xy 的单调区间是Zk其中A .kk 65,6B .kk 6,65C .kk 265,26D .kk 26,2654、函数42tan xy 的周期是A .B .2C .2D .45、要得到函数x y 2tan 的图象,只须把32tan xy的图象A .左移3个单位B .右移3个单位C .左移6个单位D .右移6个单位6、观察正切曲线,满足条件1tan x的x 的取值范围是(其中k ∈Z) ()A .(2k π-4,2k π+4)B .(k π,k π+4) C .(k π4,k π+4)D .(k π+4,k π+43)二、填空题7、函数xy tan 11的定义域是.8、函数x ytan 图象的对称中心是.9、函数32tanx y的单调区间是.10、若直线2ax 1a 与函数42tan xy图象不相交,则a.11、观察正切曲线,满足条件3tan x的x 的取值范围是.12、4tan ,3tan ,2tan ,1tan 由小到大排列为.THANKS致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
高一数学必修四课件加习题精选:1.4.3正切函数的图象和性质

利用正切线画出函数y tan x, x ( , )的图象
22
y
•
•1
•
.•
o1
2
4
•
0
4
x
2
•
• 1
•
利用正切函数的周期性,把图象向左,右 扩展,得到正切函数zxxk
y tan x, x R且x k , (k Z )的图象,并把它
6.对称性:对称中心是( k , 0), k Z
2
2
o 2
x 2
对称轴呢?
例1.求函数
y
tan(
x
)
的定义域、
周期和单调区间。 2 3
解:原函数要有意义,自变量x应满足
2
x
3
2
k
,k
Z
即
x
1 3
2k,
k
Z
所以,原函数的定义域是
{x
|
x
1 3
2k ,
k
Z}.
由于tan[2
(
x
2)
3
]
tan(2
7
7
7
7
变式训练:tan 6 tan
5
5
<
tan( 13
5
画出y | tan x | 并讨论它的 单调性,周期性和奇偶性.
3
3
2
2
2
3 2
3
2
2
(1)正切函数的图像
y y tan x
(2)正切函数的性质:
➢定义域:
x
|
x
2
k
,
高中数学-正切函数的性质与图象练习

高中数学-正切函数的性质与图象练习5分钟训练(预习类训练,可用于课前)1.(高考全国卷Ⅰ,文6)函数f(x)=tan(x+4π)的单调区间为( ) A.(kπ-2π,kπ+2π),k∈ZB.(kπ,(k+1)π),k∈ZC.(kπ-43π,kπ+4π),k∈ZD.(kπ-4π,kπ+43π),k∈Z 解析:由kπ-2π<x+4π<kπ+2π,k ∈Z ,解得kπ-43π<x <kπ+4π,k ∈Z . 答案:C2.函数y=tan(πx+4π)的最小正周期是_______________. 解析:T=ππ=1. 答案:13.作出函数y=|tanx |的图象,并根据图象求其单调区间.解:由于y=|tanx|⎪⎪⎩⎪⎪⎨⎧-∈-+∈),2(,tan ),2,[,tan ππππππk k x x k k x x (k ∈Z ), 所以其图象如下图所示,单调增区间为[kπ,kπ+2π)(k ∈Z );单调减区间为(kπ-2π,kπ](k ∈Z ).4.利用函数图象,写出x 的范围:tanx≥-1.解析:在(-2π,2π)内tanx≥-1=tan(-4π),∴-4π≤x<2π. 由周期性可知当tanx≥-1时,kπ-4π≤x<kπ+2π,k ∈Z . 答案:kπ-4π≤x<kπ+2π,k ∈Z . 10分钟训练(强化类训练,可用于课中)1.函数y=tan(21x-3π)在一个周期内的图象是( )图1-4-2解析:函数y=tan(21x-3π)的周期是2π,可排除B 、D ;对于答案C ,图象过点(3π,0),代入解析式不成立,可排除C.答案:A2.已知函数y=tan(2x+φ)的图象过点(12π,0),则φ可以是( ) A.-6π B.6π C.-12π D.12π 解析:将(12π,0)代入原函数可得tan(6π+φ)=0,再将A 、B 、C 、D 代入检验即可. 答案:A3.若f(x)=tan(x+4π),则( ) A.f(0)>f(-1)>f(1) B.f(0)>f(1)>f(-1)C.f(1)>f(0)>f(-1)D.f(-1)>f(0)>f(1)解析:在(-2π,2π)上,y=tanx 为增函数.根据诱导公式把x+4π转化到(-2π,2π)上再比较大小. f(1)=tan(1+4π)=tan(1-43π).又-2π<1-43π<4π-1<4π,所以f(0)>f(-1)>f(1). 答案:A 4.函数y=xtan 11+的定义域是_________________. 解:要使函数y=x tan 11+有意义,则有 ⎪⎩⎪⎨⎧∈+≠≠+),(2,0tan 1Z k k x x ππ 即x≠-4π+kπ且x≠2π+kπ(k∈Z ). ∴函数的定义域为{x|x∈R 且x≠-4π+kπ且x≠2π+kπ,k∈Z . 答案:{x|x∈R 且x≠-4π+kπ且x≠2π+kπ,k∈Z } 5.函数y=x tan 3-的定义域为_______________,值域为_______________.解:∵⎪⎩⎪⎨⎧∈+≠≥-)(2,0tan 3Z k k x x ππ∴tanx≤3. ∴-2π+kπ<x≤3π+kπ(k∈Z ),y≥0. 答案:{x|-2π+kπ<x≤3π+kπ,k∈Z }y≥0 6.求函数y=tan(2x-3π)的单调区间. 解:由y=tanx,x ∈(kπ-2π,kπ+2π)(k ∈Z )是增函数, ∴kπ-2π<2x-3π<kπ+2π,k ∈Z ,即2πk -12π<x <2πk +125π,k ∈Z . 因此,函数的单调递增区间为(2πk -12π,2πk +125π)(k ∈Z ). 7.比较tan1,tan2,tan3的大小.解:∵tan2=tan(2-π),tan3=tan(3-π), 又∵2π<3<π,∴-2π<3-π<0. 显然-2π<2-π<3-π<1<2π. 而y=tanx 在(-2π,2π)内是增函数, ∴tan(2-π)<tan(3-π)<tan1.∴tan2<tan3<tan1.30分钟训练(巩固类训练,可用于课后)1.函数y=tan(4π-x)的定义域是( ) A.{x|x≠4π,x∈R } B.{x|x≠-4π,x∈R } C.{x|x≠kπ+4π,k∈Z ,x∈R } D.{x|x≠kπ+43π,k∈Z ,x∈R } 解析:要使函数有意义,需满足4π-x≠2π+kπ(k∈Z ), ∴x≠-4π+kπ(k∈Z ),也可写成x≠43π+kπ(k∈Z ). 答案:D2.直线y=a(a 为常数)与正切曲线y=tanωx(ω是常数且ω>0)相交,则相邻两交点间的距离是( )A.πB.ωπ2C.ωπ D.与a 的值有关 解析:相邻两交点间的距离恰为该函数的周期,由y=tanωx,ω>0,得T=ωπ. 答案:C3.函数y=2tan(3x-4π)的一个对称中心是( ) A.(3π,0) B.(6π,0) C.(-4π,0) D.(-2π,0) 解析:由y=tanx 的对称中心是(2πk ,0), ∴3x -4π=2πk ,x=12π+6πk (k ∈Z ). 当k=-2时,x=-4π. 答案:C4.(高考全国卷Ⅱ,4)已知函数y=tanωx 在(-2π,2π)内是减函数,则( ) A.0<ω≤1 B.-1≤ω<0 C.ω≥1 D.ω≤-1解析:由||ωπ≥π,∴|ω|≤1.若ω>0,其图象与y=tanx 在(-2π,2π)上有相同的增减性,∵y=tanωx 是(-2π,2π)上的减函数,∴ω<0. 答案:B5.给出下列命题:①正切函数的图象的对称中心是唯一的;②y=|sinx|、y=|tanx|的周期分别为π、2π; ③若x 1>x 2,则sinx 1>sinx 2;④若f(x)是R 上的奇函数,它的最小正周期为T ,则f(2T -)=0. 其中正确命题的序号是_____________________.答案:④6.不通过求值,比较下列各组中两个正切函数值的大小:(1)tan167°与tan173°; (2)tan(411π-)与tan(513π-). 解:(1)∵90°<167°<173°<180°,又∵y=tanx 在(90°,270°)上是增函数, ∴tan167°<tan173°. (2)∵tan(411π-)=tan(-43π),tan(513π-)=tan(53π-), 又∵-23π<-43π<53π-<-2π,函数y=tanx ,x ∈(-23π,-2π)是增函数,∴tan(-43π)<tan(53π-),即tan(411π-)<tan(513π-). 7.若α、β为锐角,且cotα>tanβ,试比较(α+β)与2π的大小. 解:∵α、β∈(0,2π),∴(2π-α)∈(0,2π). 由cotα>tanβ,得tan(2π-α)>tanβ. ∵y=tanx 在x ∈(0,2π)上是增函数, ∴2π-α>β,即α+β<2π. 8.已知函数f(x)=tanx,x∈(0,2π),若x 1、x 2∈(0,2π)且x 1≠x 2,试比较21[f(x 1)+f(x 2)]与f(221x x +)的大小. 解:f(x)=tanx,x ∈(0,2π)的图象如图所示,则f(x 1)=AA 1,f(x 2)=BB 1,f(221x x +)=CC 1,C 1D 是直角梯形AA 1B 1B 的中位线,所以21[f(x 1)+f(x 2)]=21(AA 1+BB 1)=DC 1>CC 1=f(221x x +),即21[f(x 1)+f(x 2)]>f(221x x +).9.有两个函数f(x)=asin(ωx+3π),g(x)=btan(ωx -3π)(其中ω>0).已知它们的周期之和为23π,且f(2π)=g(2π),f(4π)=g 3-(4π)+1,你能确定a 、b 、ω的值吗? 解:∵f(x)的周期为ωπ2,g(x)的周期为ωπ, 由已知ωπ2+ωπ=23π,得ω=2.∴函数式为f(x)=asin(2x+3π),g(x)=btan(2x-3π).由已知,得方程组 ⎪⎪⎩⎪⎪⎨⎧+-⨯-=+⨯-=+,1)342tan(3)342sin(),3tan()3sin(ππππππππb a b a 即⎪⎪⎩⎪⎪⎨⎧+-=-=-.12,323b a b a 解之,得⎪⎩⎪⎨⎧==.21,1b a ∴a=1,b=21,ω=2. 快乐时光相反的例子孙子问当美学教授的爷爷:“爷爷,为什么您说一切假的都是丑的?”“那当然啰,难道你还能举出相反的例子吗?”“能,”孙子爬到美学教授的膝头上,得意地说:“您瞧您自己一装上假牙后又年轻又精神,拿掉假牙,您嘴巴又空又瘪,那才丑呢,这不是相反的例子吗?”教授一时语塞.。
正切函数的图象和性质

4.10 正切函数的图像和性质 问题2、如何利用正切线画出函数 的图像?
y
tan x,x , 2 2
角 的终边 3 T
Y
( , tan )
3 3
A
0
3
X
y tan x x 利用正切线画出函数 , , 的图像: 2 2 把单位圆右半圆分成8等份。 作法: (1) 等分: 3 3 (2) 作正切线 , , , , , 8 8 4 8 8 4 (3) 平移 (4) 连线
在每一个开区间 内都是增函数。
例3、比较下列每组数的大小。
(1)tan167 与 tan173
o
o
13π 11π tan() 与 tan() (2) 4 5
说明:比较两个正切值大小,关键是把相 应的角 化到y=tanx的同一单调区间内,再 利用y=tanx的单调递增性解决。
1、比较大小:
0 < (1)tan1380 _____tan143 。
奇函数,图象关于原点对称。 在每一个开区间
⑸ 单调性:
π π (- + kπ, + kπ), k Z 内都是增函数。 2 2 (6)渐近线方程: x k , k Z两把长条凳,咱们先把它架在上面,以后再慢慢收拾哇!”耿英答应着赶快上前打开南房杂物间的门,秀儿这时候也 进院儿里来了。耿英招呼秀儿帮着从里边搬出两把长条凳来,不远不近地搁在东房的前面。门外边,董家成和二壮、耿憨和青 海、耿老爹和耿正、耿直、李尚武八个男人一起动手,将那个用大红色篷布包裹着的寿棺抬进来架在长条凳上。耿老爹直起腰 来拍拍寿棺,说:“好了,先就这样搁着哇!”耿英说:“两挂大骡车可怎么办啊?”耿老爹说:“是啊,这两挂骡车还真有 点儿没有地方搁呢!”再看一看自家原来的那个驴圈,说:“两骡子拴这个驴圈里也不行啊!”耿憨适才正和董家成在那里仔 细琢磨刚才大家伙儿吃力抬进来的这个大怪物呢!听了耿老爹父女俩的对话,就说:“不碍事,都赶到粉坊院儿里去哇,那儿 的马厩、车棚里宽着呢!”董家成也说:“大壮养的骡子和车一直都在那里呢!让二壮和青海赶去卸了就行了!”耿正说: “俺也去哇,这两头骡子还得伺候呢!”耿憨说:“放心,大壮养骡车都七、八年了,二壮和青海都会伺候着呢!”说着话, 吩咐二壮和青海各赶一挂骡车去粉坊院儿里卸了车,给两头骡子喂上草料照顾好了再回来说话。两个小伙子高兴地答应着出门 去了,其余人都鱼贯进了堂屋。堂屋里,耿兰忙着烧水准备泡茶。热泪高兴地流淌在每一个人的脸上„„耿正、耿英和耿直围 在姥爷的身边,轮番为老人家擦拭着不断涌流出来的眼泪。耿老爹满怀内疚地说:“俺对不起您老人家„„”老岳父摆摆手说: “别说了,都回来了就好啦!好在俺还能看到你们回来„„”耿正兄妹三人几乎同时说:“俺姥娘身体还好哇?俺们一会儿就 去看她!”老人家又摆摆手,嗓音儿沙哑地说:“你们见不着姥娘了!”“怎么,姥娘没了?”兄妹三人都哭了。郭氏和弟弟 也哭了。耿老爹难过地问:“什么时候没的啊?”妻弟妹红着眼圈说:“刚过了三周年。”大家唏嘘感叹了好一会儿„„耿老 爹再次把李尚武介绍给还不认识的亲人们,并且说:“如果没有他和他的哥哥姐姐陪着俺,没有他父母的照顾,俺活不到今天, 更不可能再返回故乡了!”李尚武一一施礼见过姥爷、舅舅、舅母和表弟表妹,以及伯伯大娘叔叔婶子弟弟妹妹,大家伙儿万 分感激地说一些感谢的话,李尚武不好意思地说:“哪里啊,义父不但救了我的命,而且这些年又帮了我们家天大的忙,是我 和全家人应该好好地感谢我的义父呢!”郭氏却只管左一把右一把地擦眼泪,说:“俺倒是不再想说那些个感谢的话了,只高 兴俺又多了一个三儿子!大家伙儿看看,俺这老儿子和他的二哥长得有多像啊,简直就像青山和青海一样,是一对双胞胎呢!” 董家成细细看了,高兴地说:“可不是耶,这不又增加了一对
【2019-2020高一数学试题】人教A版必修4《正切函数的性质与图象》试题 答案解析

正切函数的性质与图象——基础巩固类——一、选择题1.函数y =tan xa 的最小正周期是( ) A .a π B .|a |π C.πaD.π|a |2.下列说法正确的是( )A .正切函数在整个定义域内是增函数B .正切函数在整个定义域内是减函数C .函数y =3tan x 2的图象关于y 轴对称D .若x 是第一象限角,则y =tan x 是增函数3.函数y =tan ⎝⎛⎭⎪⎫π2-x ⎝⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤-π4,π4且x ≠0的值域为( )A .[-1,1]B .(-∞,-1]∪[1,+∞)C .(-∞,1]D .[-1,+∞) .4.函数y =tan ⎝ ⎛⎭⎪⎫x +π5的一个对称中心是( )A .(0,0)B.⎝ ⎛⎭⎪⎫π5,0 C.⎝ ⎛⎭⎪⎫4π5,0 D .(π,0)5.下列各式中正确的是( ) A .tan735°>tan800° B .tan1<tan2 C .tan 5π7<tan 4π7D .tan 9π8<tan π76.函数y =tan ⎝⎛⎭⎪⎫12x -π3在一个周期内的图象是( )二、填空题7.f (x )=tan x +sin x +1,若f (b )=2,则f (-b )= 8.满足tan ⎝ ⎛⎭⎪⎫x +π3≥-3的x 的集合是9.方程x -tan x =0的实根有 个. 三、解答题10.作出函数y =tan|x |的图象,根据图象判断其周期性,并求出单调区间.11.已知x ∈⎣⎢⎡⎦⎥⎤-π3,π4,f (x )=tan 2x +2tan x +2,求f (x )的最大值和最小值,并求出f (x )取最大值和最小值时相应的x 值.——能力提升类——12.函数y =tan(sin x )的值域是( )A.⎣⎢⎡⎦⎥⎤-π4,π4 B.⎣⎢⎡⎦⎥⎤-22,22C .[-tan1,tan1]D .[-1,1]13.下列关于函数y =tan ⎝⎛⎭⎪⎫x +π3的说法正确的是( )A .在区间⎝ ⎛⎭⎪⎫-π6,5π6上单调递增B .最小正周期是πC .图象关于点⎝ ⎛⎭⎪⎫π4,0成中心对称D .图象关于直线x =π6对称14.关于x 的函数f (x )=tan(x +φ)有以下几种说法:①对任意的φ,f (x )都是非奇非偶函数;②f (x )的图象关于⎝ ⎛⎭⎪⎫π2-φ,0对称;③f (x )的图象关于(π-φ,0)对称;④f (x )是以π为最小正周期的周期函数.其中不正确的说法的序号是 .15.已知函数f (x )=x 2+2x tan θ-1,x ∈[-1,3],其中θ∈⎝⎛⎭⎪⎫-π2,π2.(1)当θ=-π6时,求函数的最大值和最小值;(2)求θ的取值范围,使y =f (x )在区间[-1,3]上是单调函数.正切函数的性质与图象(答案解析)——基础巩固类——一、选择题1.函数y =tan xa 的最小正周期是( B ) A .a π B .|a |π C.πaD.π|a |解析:∵y =A tan(ωx +φ)的最小正周期T =π|ω|, ∴T =π|1a |=|a |π.2.下列说法正确的是( C ) A .正切函数在整个定义域内是增函数 B .正切函数在整个定义域内是减函数 C .函数y =3tan x 2的图象关于y 轴对称 D .若x 是第一象限角,则y =tan x 是增函数3.函数y =tan ⎝ ⎛⎭⎪⎫π2-x ⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤-π4,π4且x ≠0的值域为( B ) A .[-1,1]B .(-∞,-1]∪[1,+∞)C .(-∞,1]D .[-1,+∞)解析:∵-π4≤x ≤π4且x ≠0, ∴π4≤π2-x ≤3π4且π2-x ≠π2, ∴值域为(-∞,-1]∪[1,+∞).4.函数y =tan ⎝⎛⎭⎪⎫x +π5的一个对称中心是( C )A .(0,0)B.⎝ ⎛⎭⎪⎫π5,0 C.⎝⎛⎭⎪⎫4π5,0 D .(π,0)解析:令x +π5=k π2(k ∈Z ), 得x =k π2-π5,k ∈Z ,∴函数y =tan ⎝ ⎛⎭⎪⎫x +π5的对称中心是⎝ ⎛⎭⎪⎫k π2-π5,0(k ∈Z ). 令k =2,可得函数的一个对称中心为⎝⎛⎭⎪⎫4π5,0.5.下列各式中正确的是( D ) A .tan735°>tan800° B .tan1<tan2 C .tan 5π7<tan 4π7D .tan 9π8<tan π7解析:tan 9π8=tan ⎝ ⎛⎭⎪⎫π8+π=tan π8<tan π7,故选D.6.函数y =tan ⎝ ⎛⎭⎪⎫12x -π3在一个周期内的图象是( A )解析:由正切函数的定义域得x 2-π3≠π2+k π,k ∈Z ,所以x ≠5π3+2k π,k∈Z ,取k =0和-1,得x ≠5π3且x ≠-π3,选A.二、填空题7.f (x )=tan x +sin x +1,若f (b )=2,则f (-b )=0.解析:f (-b )=tan(-b )+sin(-b )+1=-tan b -sin b +1,f (b )=tan b +sin b +1,∴f (-b )+f (b )=2,∴f (-b )=0.8.满足tan ⎝ ⎛⎭⎪⎫x +π3≥-3的x 的集合是{x |k π-2π3≤x <k π+π6,k ∈Z }.解析:把x +π3看作一个整体,利用正切函数图象可得 k π-π3≤x +π3<k π+π2(k ∈Z ), ∴k π-2π3≤x <k π+π6,k ∈Z .故满足tan ⎝⎛⎭⎪⎫x +π3≥-3的x 的集合是{x |k π-2π3≤x <k π+π6,k ∈Z }. 9.方程x -tan x =0的实根有无数个.解析:利用数形结合的思想,由于y =x 与y =tan x 的图象有无数多个交点,因此方程x -tan x =0有无数个解.三、解答题10.作出函数y =tan|x |的图象,根据图象判断其周期性,并求出单调区间.解:y =tan|x |=⎩⎪⎨⎪⎧tan x ,x ≥0,-tan x ,x <0,根据y =tan x 的图象,可作出y =tan|x |的图象(如图所示).由图可知,函数y =tan|x |不是周期函数,它的单调减区间为⎝⎛⎦⎥⎤-π2,0,⎝ ⎛⎭⎪⎫k π-3π2,k π-π2,k =0,-1,-2,…;单调增区间为⎣⎢⎡⎭⎪⎫0,π2,⎝ ⎛⎭⎪⎫k π+π2,k π+3π2,k =0,1,2,….11.已知x ∈⎣⎢⎡⎦⎥⎤-π3,π4,f (x )=tan 2x +2tan x +2,求f (x )的最大值和最小值,并求出f (x )取最大值和最小值时相应的x 值.解:f (x )=tan 2x +2tan x +2=(tan x +1)2+1,因为x ∈⎣⎢⎡⎦⎥⎤-π3,π4,所以tan x ∈[-3,1].所以当tan x =-1,即x =-π4时, f (x )有最小值,f (x )min =1; 当tan x =1,即x =π4时, f (x )有最大值,f (x )max =5.——能力提升类——12.函数y =tan(sin x )的值域是( C )A.⎣⎢⎡⎦⎥⎤-π4,π4 B.⎣⎢⎡⎦⎥⎤-22,22C .[-tan1,tan1]D .[-1,1]解析:∵-1≤sin x ≤1,而-π2<-1≤sin x ≤1<π2, ∴tan(-1)≤tan(sin x )≤tan1, 即函数值域为[-tan1,tan1].13.下列关于函数y =tan ⎝ ⎛⎭⎪⎫x +π3的说法正确的是( B )A .在区间⎝ ⎛⎭⎪⎫-π6,5π6上单调递增B .最小正周期是πC .图象关于点⎝⎛⎭⎪⎫π4,0成中心对称D .图象关于直线x =π6对称解析:令k π-π2<x +π3<k π+π2,k ∈Z ,解得k π-5π6<x <k π+π6,k ∈Z ,显然(-π6,5π6)不满足上述关系式,故A 错误;易知该函数的最小正周期为π,故B正确;令x +π3=k π2(k ∈Z ),解得x =k π2-π3,k ∈Z ,则函数图象关于点⎝⎛⎭⎪⎫k π2-π3,0(k ∈Z )成中心对称,故C 错误;正切曲线没有对称轴,因此函数y =tan ⎝ ⎛⎭⎪⎫x +π3的图象也没有对称轴,故D 错误.故选B.14.关于x 的函数f (x )=tan(x +φ)有以下几种说法:①对任意的φ,f (x )都是非奇非偶函数;②f (x )的图象关于⎝ ⎛⎭⎪⎫π2-φ,0对称;③f (x )的图象关于(π-φ,0)对称;④f (x )是以π为最小正周期的周期函数.其中不正确的说法的序号是①.解析:①若取φ=k π(k ∈Z ),则f (x )=tan x ,此时,f (x )为奇函数,所以①错;观察正切函数y =tan x 的图象,可知y =tan x 关于⎝ ⎛⎭⎪⎫k π2,0(k ∈Z )对称,令x+φ=k π2得x =k π2-φ,分别令k =1,2知②③正确,④显然正确.15.已知函数f (x )=x 2+2x tan θ-1,x ∈[-1,3],其中θ∈⎝ ⎛⎭⎪⎫-π2,π2.(1)当θ=-π6时,求函数的最大值和最小值;(2)求θ的取值范围,使y =f (x )在区间[-1,3]上是单调函数. 解:(1)当θ=-π6时,f (x )=x 2-233x -1=(x -33)2-43.∵x ∈[-1,3],∴当x =33时,f (x )取得最小值-43,当x =-1时,f (x )取得最大值233.(2)f (x )=(x +tan θ)2-1-tan 2θ是关于x 的二次函数,它的图象的对称轴为x =-tan θ.∵y =f (x )在区间[-1,3]上是单调函数,∴-tan θ≤-1或-tan θ≥3,即tan θ≥1或tan θ≤- 3.又θ∈⎝ ⎛⎭⎪⎫-π2,π2,∴θ的取值范围是⎝ ⎛⎦⎥⎤-π2,-π3∪⎣⎢⎡⎭⎪⎫π4,π2.。
专题1.4.3 正切函数的性质与图象(PPT)含答案

3.
【答案】
xx≠kπ+π3,k∈Z
3
3.(2019 年沙市区期中)函数 y=-tan x 的单调递减区间是________. 【解析】 因为 y=tan x 与 y=-tan x 的单调性相反,所以 y=-tan x 的单 调递减区间为-π2+kπ,2π+kπ(k∈Z). 【答案】 -π2+kπ,2π+kπ(k∈Z)
(2)可按定义法的步骤判断. 【自主解答】 (1)由于 ω=3,故函数的周期为 T=|ωπ |=3π.
【答案】
π 3
(2)①由x≠kπ+π2,k∈Z, tan x≠1,
得 f(x)的定义域为x|x≠kπ+2π且x≠kπ+4π,k∈Z, 不关于原点对称,
所以函数 f(x)既不是偶函数,也不是奇函数.
【解析】 (1)∵tan2x+3π+π=tan2x+3π,即 tan2x+π2+π3=tan2x+π3,
∴f(x)=tan2x+3π的周期是2π.
(2)定义域为xx≠kπ+2π,k∈Z
,关于原点对称,
类型二:正切函数的奇偶性、周期性
例 2、(1)函数 y=4tan 3x+π6 的周期为________. (2)判断下列函数的奇偶性: ①f(x)=tanta2nx-x-ta1n x; ②f(x)=tan x-π4 +tan x+π4 .
【精彩点拨】 (1)可用定义法求,也可用公式法求,也可作出函数图象来 求.
解答本题(2)可先把角化归到同一单调区间内,即利用 tan 2=tan(2-π),tan 3=tan(3-π),最后利用 y=tan x 在-2π,π2上的单调性判断大小关系.
解答本题(3)可先确定 sin x 的范围,然后根据 y=tan x 的单调性求值域.
正切函数的图像与性质(带答案)

正切函数图像及性质 知识点梳理函数y =tan x 的图象与性质 y =tan x π例1、求下列函数的定义域:(1)y =11+tan x;(2)y =lg(3-tan x ).练习、求函数y =tan x +1+lg(1-tan x )的定义域.例3、求下列函数的周期(1)⎪⎭⎫ ⎝⎛+=42tan 3πx y (2)⎪⎭⎫ ⎝⎛+=421tan 3πx y例4、求函数区间,对称中心的定义域、周期和单调⎪⎭⎫ ⎝⎛-=32tan πx y练习1、求函数⎪⎭⎫⎝⎛-=33tan πx y 的定义域、值域,并指出它的单调性、周期性;练习2、求函数的单调区间⎪⎭⎫⎝⎛+-=421tan 3πx y课堂练习1. 函数y =tan ⎝⎛⎭⎫12x -π3在一个周期内的图象是 ( )2.在区间(-3π2,3π2)内,函数y =tan x 与函数y =sin x 的图象的交点个数为( )A.1B.2C.3D.43.函数y =tan x +sin x -|tan x -sin x |在区间⎝⎛⎭⎫π2,3π2内的图象是 ( )4.利用函数图象,解不等式-1≤tan x ≤33.5.下列说法正确的是( )A.y =tan x 是增函数B.y =tan x 在第一象限是增函数C.y =tan x 在每个区间⎝⎛⎭⎫k π-π2,k π+π2(k ∈Z )内是增函数D.y =tan x 在某一区间上是减函数6.函数y =3tan(2x +π4)的定义域是 ( )A .{x |x ≠k π+π2,k ∈Z}B .{x |x ≠k 2π-3π8,k ∈Z}C .{x |x ≠k 2π+π8,k ∈Z}D .{x |x ≠k 2π,k ∈Z}7.直线y =a (a 为常数)与正切曲线y =tan x 相交的相邻两点间的距离是( )A.π2B.2πC.πD.与a 值有关8.下列各式中正确的是( )A.tan 4π7>tan 3π7B.tan ⎝⎛⎭⎫-13π4<tan ⎝⎛⎭⎫-17π5C.tan 4>tan 3D.tan 281°>tan 665°9.函数y =lg(1+tan x )的定义域是( )A.⎝⎛⎭⎫k π-π2,k π+π2(k ∈Z )B.⎝⎛⎭⎫k π-π2,k π+π4(k ∈Z )C.⎝⎛⎭⎫k π-π4,k π+π2(k ∈Z )D.⎝⎛⎭⎫k π-π4,k π+π4(k ∈Z )10.已知函数y =tan ωx 在⎝⎛⎭⎫-π2,π2内是减函数,则ω的取值范围为__________.11.函数y =2tan(3x +φ)⎝⎛⎭⎫-π2<φ<π2的图象的一个对称中心为⎝⎛⎭⎫π4,0,则φ=________.12.若tan ⎝⎛⎭⎫2x -π6≤1,则x 的取值范围是________.13已知函数f (x )=3tan ⎝⎛⎭⎫12x -π3.(1)求f (x )的定义域和值域.(2)讨论f (x )的周期性、奇偶性和单调性.14.求函数y =-tan 2x +10tan x -1,x ∈⎣⎡⎦⎤π4,π3的值域.。
正切函数的图象和性质习题精选

正切函数的图象和性质习题精选一、选择题1.函数的最小正周期是()A.B.C.D.2.函数的定义域是()A.B.C.D.3.函数的值域是()A.B.C.D.4.下列函数中,同时满足①在上是增函数;②为奇函数;③以为最小正周期的函数是()A.B.C.D.5.已知函数,下列判断正确的个数是()①是定义域上的减函数,周期为.②是区间上的减函数,周期为.③是区间上的减函数,周期为.④是区间上的减函数,周期为.A.0 B.1 C.2 D.36.函数的图像对称于()A.原点B.轴C.轴D.直线7.要得到的图像,只需把的图像()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位8.函数的一个对称中心是()A.B.C.D.9.函数的图像相邻的两支截直线所得线段长为,则的值是()A.B.0 C.1 D.-110.在区间范围内,函数与函数的图像交点的个数为()A.1 B.2 C.3 D.411.要得到函数的图像,须将函数的图像()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位12.函数在一个周期内的图像是()二、填空题13.函数的最小正周期是____________.14.函数的定义域是_________.15.函数的值域是__________.16.已知函数是以3为周期的奇函数,且.若,则.三、解答题17.试求函数的定义域,并作出区间上的图像.18.已知.求函数的值域.19.求函数的定义域、值域,并指出它的周期、奇偶性和单调性.20.求证:函数(、)为奇函数的充要条件是.参考答案:一、选择题1.B 2.D 3.B 4.A 5.A 6.B7.C 8.C 9.B 10.C 11.C 12.A二、填空题13.14.15. 16.-1三、解答题17.由得函数的定义域为.又当时,其图像如图所示.18.由已知条件得,解得,∴(),∴(),∴,于是.∴当()时取最小值4,当()时取最大值5.从而函数的值域为[4,5].19.由,得(),∴所求的函数定义域为:;值域为;周期为;它既不是奇函数,也不是偶函数;在区间()上是单调减函数.20.充分性:∵,∴为奇函数,必要性:∵是奇函数.∴,∴,∴,∴,∴,∴,∴,∴().。
高中数学复习:正切函数的图像和性质练习及答案

高中数学复习:正切函数的图像和性质练习及答案1.如下图所示,函数y =cos x |tan x |(0≤x <3π2且x ≠π2)的图象是( )A .B .C .D .2.函数y =tan x +sin x -|tan x -sin x |在区间(π2,3π2)内的图象是( )A .B .C .D .3.函数f (x )=tan x +1tanx ,x ∈{x|−π2<x <0或0<x <π2}的图象为( )A .B .C .D .4.函数y =sin x 与y =tan x 的图象在(-π2,π2)上的交点的个数为( )A .0B .1C .2D .35.已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)等于( )A.2+√3 B.√3 C.√33D.2-√36.下列图象分别是函数①y=|tan x|;②y=tan x;③y=tan(-x);④y=tan|x|在x∈(-3π2,?3π2)内的大致图象.那么图a、b、c、d依次对应的函数关系式应是( )A.①②③④ B.①③④② C.③②④① D.①②④③7.函数y=tan(π4x-π2)的部分图象如图所示,则△AOB的面积等于( )A.1 B.2 C.4 D.928.使不等式tan x≥√3成立的x的集合为( )A.(kπ+π6,kπ+π2)(k∈Z) B.[kπ+π6,kπ+π2)(k∈Z)C.[kπ+π3,kπ+π2)(k∈Z) D.(kπ+π3,kπ+π2)(k∈Z)考点2 正切函数的定义域、值域9.函数y=1tanx的定义域为( )A.{x|x≠0}B.{x|x≠kπ,k∈Z}C.{x|x≠kπ+π2,k∈Z}D.{x|x≠kπ2,k∈Z}10.函数y=√sinx+√tanx的定义域为( )A.{x|2kπ≤x<2kπ+π2,k∈Z}B.{x|2kπ<x≤kπ+π2,k∈Z}C.{x|2kπ≤x<2kπ+π2,k∈Z}∪{x|x=2kπ+π,k∈Z}D.{x|2kπ≤x<2kπ+π2且x≠2kπ+π,k∈Z}11.函数y=tan x(−π4≤x≤π4且x≠0)的值域是( )A.[-1,1] B.[-1,0)∪(0,1] C.(-∞,1] D.[-1,+∞) 12.函数y=tan(sin x)的值域为( )A.[−π4,π4]B.[−√22,√22]C.[-tan1,tan1] D.以上都不对13.(1)求函数y=√tanx−√3的定义域;(2)已知f(x)=tan2x-2tan x(|x|≤π3),求f(x)的值域.14.函数y=tanωx的最小正周期为π2,则实数ω的值为( )A.12B.1 C.2 D.415.已知函数y=tanωx(ω>0)的图象与直线y=a相交于A,B两点,若AB长度的最小值为π,则ω的值为( )A .4B .2C .1D .3 16.函数y =tan 35x 是( )A .周期为π的偶函数B .周期为53π的奇函数 C .周期为53π的偶函数 D .周期为π的奇函数 17.下列函数中,为偶函数的是( ) A .f (x )=sin(2015π2+x ) B .f (x )=cos(2015π2+x ) C .f (x )=tan(2015π2+x ) D .f (x )=sin(2014π2+x )18.函数y =tan (x +π3)图象的对称中心的坐标是( ) A .(k π−π3,0)(k ∈Z ) B .(k 2π-π3,0)(k ∈Z )C .(k π2,0)(k ∈Z ) D .(k π,0)(k ∈Z )19.下列坐标所表示的点不是函数y =tan(x2-π6)的图象的对称中心的是( ) A .(π3,0) B .(−5π3,0) C .(7π3,0) D .(2π3,0)20.下列关于函数y =tan (x +π3)的说法正确的是( ) A .在区间(−π6+5π6)上单调递增 B .最小正周期是πC .图象关于点(π4,0)成中心对称 D .图象关于直线x =π6成轴对称21.若函数f (x )=2cos(4x +π7)-1与函数g (x )=5tan(ax -1)+2的最小正周期相同,则实数a =______.22.给出下列命题:①正切函数的图象的对称中心是唯一的; ②y =|sin x |,y =|tan x |的周期分别为π,π2;③若x1>x2,则sin x1>sin x2;④若f(x)是R上的奇函数,它的最小正周期为T,则f(-T2)=0. 其中正确命题的序号是________.23.试判断下列函数的奇偶性.(1)f(x)=1-2cos x+|tan x|;(2)f(x)=x2tan x-sin2x.24.下列说法正确的是( )A.y=tan x是增函数B.y=tan x在第一象限是增函数C.y=tan x在某一区间上是减函数D.y=tan x在区间(kπ-π2,kπ+π2)(k∈Z)上是增函数25.函数y=tan(x+π5)的单调递增区间是( )A.(−π2+kπ,π2+kπ)(k∈Z)B.(−7π10+kπ,3π10+kπ)(k∈Z)C.(−3π10+kπ,7π10+kπ)(k∈Z)D.(−π5+kπ,π5+kπ)(k∈Z)26.关于函数f(x)=-tan2x,有下列说法:①f(x)的定义域是{x∈R|x≠π2+kπ,k∈Z};②f(x)是奇函数;③在定义域上是增函数;④在每一个区间(-π4+kπ2,π4+kπ2)(k∈Z)上是减函数;⑤最小正周期是π.其中正确的是( )A .①②③B .②④⑤C .②④D .③④⑤ 27.已知函数f (x )=√3tan πxω(ω>0).(1)当ω=4时,求f (x )的最小正周期及单调区间;(2)若|f (x )|≤3在x ∈[-π3,π4]上恒成立,求ω的取值范围.28.对于函数y =tan x2,下列判断正确的是( ) A .周期为2π的奇函数 B .周期为π2的奇函数 C .周期为π的偶函数 D .周期为2π的偶函数29.已知函数f (x )=tan(2x +π4).(1)求该函数的定义域,周期及单调区间; (2)若f (θ)=17,求2cos 2θ2−sinθ−12sin(θ+π4)的值.30.已知函数y =tan(12x -π6).(1)作出此函数在一个周期开区间上的简图; (2)求出此函数的定义域、周期和单调区间;(3)写出此函数图象的渐近线方程和所有对称中心的坐标.31.已知关于实数x的不等式|x−(tanθ+1)22|≤(tanθ−1)22,x2-3(tanθ+1)x+2(3tanθ+1)≤0的解集分别为M,N,且M∩N=∅,则这样的θ存在吗?若存在,求出θ的取值范围. 答案1.如下图所示,函数y=cos x|tan x|(0≤x<3π2且x≠π2)的图象是( )A.B.C.D.【答案】C【解析】∵y=cos x|tan x|={sinx,0≤x<π2,−sinx,π2<x≤πsinx,π<x<3π2.,∴函数y=cos x|tan x|(0≤x<3π2且x≠π2)的图象是C.2.函数y=tan x+sin x-|tan x-sin x|在区间(π2,3π2)内的图象是( )A.B.C.D.【答案】D【解析】当π2<x<π时,tan x<sin x,y=2tan x<0;当x=π时,y=0;当π<x<3π2时,tan x>sin x,y=2sin x.故选D.3.函数f (x )=tan x +1tanx ,x ∈{x|−π2<x <0或0<x <π2}的图象为( )A .B .C .D .【答案】A【解析】因为y =tan x 是奇函数,所以f (x )=tan x +1tanx ,x ∈{x|−π2<x <0或0<x <π2}是奇函数,因此B ,C 不正确,又因为f (x )=tan x +1tanx ,0<x <π2时函数为正数,所以D 不正确,A 正确.4.函数y =sin x 与y =tan x 的图象在(-π2,π2)上的交点的个数为( )A .0B .1C .2D .3 【答案】B【解析】∵sin x <x <tan x ,x ∈(0,π2), ∴在(0,π2)上无交点,又它们都是奇函数,故在(-π2,0)上无交点, 观察图象知两个函数的图象有1个交点.5.已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)等于( )A .2+√3B .√3C .√33D .2-√3【答案】B【解析】由图象知πω=2×(3π8−π8)=π2,ω=2.又由于2×π8+φ=k π+π2(k ∈Z ),φ=k π+π4(k∈Z ),又|φ|<π2,所以φ=π4.这时f (x )=A tan (2x +π4).又图象过(0,1),代入得A =1,故f (x )=tan (2x +π4).所以f (π24)=tan (2×π24+π4)=√3,故选B.6.下列图象分别是函数①y =|tan x |;②y =tan x ;③y =tan(-x );④y =tan|x |在x ∈(-3π2,?3π2)内的大致图象.那么图a 、b 、c 、d 依次对应的函数关系式应是( )A .①②③④B .①③④②C .③②④①D .①②④③ 【答案】D【解析】y =tan(-x )在(-π2,?π2)内是减函数,故选D.7.函数y =tan(π4x -π2)的部分图象如图所示,则△AOB 的面积等于( )A .1B .2C .4D .92【答案】A【解析】函数的周期T=ππ4=4,则A(2,0),∴△AOB的面积S=12×2×1=1.8.使不等式tan x≥√3成立的x的集合为( )A.(kπ+π6,kπ+π2)(k∈Z)B.[kπ+π6,kπ+π2)(k∈Z)C.[kπ+π3,kπ+π2)(k∈Z)D.(kπ+π3,kπ+π2)(k∈Z)【答案】C【解析】∵不等式tan x≥√3,由正切函数的性质可得kπ+π3≤x<kπ+π2,k∈Z,∴使不等式成立的x的集合为{x|kπ+π3≤x<kπ+π2,k∈Z},即x∈[kπ+π3,kπ+π2)(k∈Z).9.函数y=1tanx的定义域为( ) A.{x|x≠0}B.{x|x≠kπ,k∈Z}C.{x|x≠kπ+π2,k∈Z}D.{x|x≠kπ2,k∈Z}【答案】D【解析】函数y=1tanx 有意义,则{x≠kπ,k∈Z,x≠kπ+π2,k∈Z,可得函数的定义域为{x|x ≠k π2,k ∈Z}.10.函数y =√sinx +√tanx 的定义域为( ) A .{x|2k π≤x <2k π+π2,k ∈Z} B .{x|2k π<x ≤k π+π2,k ∈Z}C .{x|2k π≤x <2k π+π2,k ∈Z}∪{x|x =2k π+π,k ∈Z }D .{x|2k π≤x <2k π+π2且x ≠2k π+π,k ∈Z} 【答案】C【解析】由{sinx ≥0tanx ≥0,即{2kπ≤x ≤2kπ+πkπ≤x <kπ+π2(k ∈Z ),得2k π≤x <2k π+π2(k ∈Z )或x =2k π+π(k ∈Z ).所以函数y =√sinx +√tanx 的定义域是{x|2k π≤x <2k π+π2,k ∈Z}∪{x|x =2k π+π,k ∈Z } 11.函数y =tan x (−π4≤x ≤π4且x ≠0)的值域是( )A .[-1,1]B .[-1,0)∪(0,1]C .(-∞,1]D .[-1,+∞) 【答案】B【解析】根据正切函数图象,结合函数的单调性可得. 12.函数y =tan(sin x )的值域为( ) A .[−π4,π4]B .[−√22,√22]C .[-tan1,tan1]D .以上都不对 【答案】C【解析】∵sin x ∈[-1,1],结合函数y =tan x 的图象可知,tan(-1)≤tan(sin x )≤tan1,即y ∈[-tan1,tan1].13.(1)求函数y =√tanx −√3的定义域;(2)已知f (x )=tan 2x -2tan x (|x |≤π3),求f (x )的值域.【答案】(1)要使函数有意义,必须使tan x -√3≥0,即tan x ≥√3, ∴k π+π3≤x <k π+π2,k ∈Z .∴函数y =√tanx −√3的定义域为[k π+π3,k π++π2)(k ∈Z ). (2)令u =tan x ,∵|x |≤π3,∴u ∈[-√3,√3], ∴函数化为y =u 2-2u . 对称轴为u =1∈[-√3,√3]. ∴当u =1时,y min =12-2×1=-1. 当u =-√3时,y max =3+2√3, ∴f (x )的值域为[-1,3+2√3].14.函数y =tan ωx 的最小正周期为π2,则实数ω的值为( ) A .12 B .1 C .2 D .4 【答案】C【解析】因为函数y =tan ωx 的最小正周期为π2,所以π|ω|=π2,考察选项可知,实数ω的值为2. 15.已知函数y =tan ωx (ω>0)的图象与直线y =a 相交于A ,B 两点,若AB 长度的最小值为π,则ω的值为( )A.4 B.2 C.1 D.3【答案】C【解析】根据函数y=tanωx(ω>0)的图象特点可知,两点间的距离必是最小正周期的正整数倍,又由两点间长度的最小值为π,即函数最小正周期为π,所以π|ω|=π.又由ω>0,则ω=1.16.函数y=tan35x是( )A.周期为π的偶函数 B.周期为53π的奇函数C.周期为53π的偶函数 D.周期为π的奇函数【答案】B【解析】正切函数的周期T=π35=53π,函数y=tan35x是奇函数.17.下列函数中,为偶函数的是( )A.f(x)=sin(2015π2+x)B.f(x)=cos(2015π2+x)C.f(x)=tan(2015π2+x)D.f(x)=sin(2014π2+x)【答案】A【解析】对于A,f(x)=sin(2015π2+x)=sin(1007π+π2+x)=sin(3π2+x)=-cos x,为偶函数,则A正确;对于B,f(x)=cos(2015π2+x)=cos(1007π+π2+x)=cos(3π2+x)=sin x,为奇函数,则B错误;对于C ,f (x )=tan(2015π2+x )=tan(1007π+π2+x )=tan(π2+x )=-cot x ,为奇函数,则C 错误;对于D ,f (x )=sin(1007π+x )=sin(π+x )=-sin x ,为奇函数,故D 错误. 故选A.18.函数y =tan (x +π3)图象的对称中心的坐标是( ) A .(k π−π3,0)(k ∈Z )B .(k2π-π3,0)(k ∈Z ) C .(k π2,0)(k ∈Z )D .(k π,0)(k ∈Z )【答案】B【解析】函数y =tan (x +π3)的图象由函数y =tan x 的图象向左平移π3个单位得到, 又由函数y =tan x 的对称中心的坐标是(k π2,0)(k ∈Z ),∴函数y =tan(x +π3)的对称中心的坐标是(k2π-π3,0)(k ∈Z ).19.下列坐标所表示的点不是函数y =tan(x2-π6)的图象的对称中心的是( ) A .(π3,0) B .(−5π3,0) C .(7π3,0) D .(2π3,0)【答案】D 【解析】将π3,-5π3,7π3代入y =tan(x 2-π6)均为0,而2π3代入y =tan(x 2-π6)不为0,所以选D.20.下列关于函数y =tan (x +π3)的说法正确的是( ) A .在区间(−π6+5π6)上单调递增B .最小正周期是πC .图象关于点(π4,0)成中心对称 D .图象关于直线x =π6成轴对称 【答案】B【解析】令k π-π2<x +π3<k π+π2,解得k π-5π6<x <k π+π6,k ∈Z ,显然(−π6,5π6)不满足上述关系式,故A 错误;易知该函数的最小正周期为π,故B 正确;令x +π3=k π2,解得x =k π2-π3,k ∈Z ,任取k 值不能得到x =π4,故C 错误;正切曲线没有对称轴,因此函数y =tan (x +π3)的图象也没有对称轴,故D 错误.故选B.21.若函数f (x )=2cos(4x +π7)-1与函数g (x )=5tan(ax -1)+2的最小正周期相同,则实数a =______. 【答案】±2【解析】函数f (x )=2cos(4x +π7)-1的周期是π2,函数g (x )=5tan(ax -1)+2的最小正周期是π|a|, 因为周期相同,所以π|a|=π2,解得a =±2. 22.给出下列命题:①正切函数的图象的对称中心是唯一的; ②y =|sin x |,y =|tan x |的周期分别为π,π2; ③若x 1>x 2,则sin x 1>sin x 2;④若f (x )是R 上的奇函数,它的最小正周期为T ,则f (-T2)=0. 其中正确命题的序号是________. 【答案】④【解析】①正切函数的图象的对称中心是唯一的,由正切函数的性质可知,①是错误的; ②y =|sin x |,y =|tan x |的周期分别为π,π2,前者正确,后者错误,②是错误的; ③若x 1>x 2,则sin x 1>sin x 2,如果x 1=390°,x 2=90°,sin x 1<sin x 2,③是错误的;④若f(x)是R上的奇函数,它的最小正周期为T,则f(-T2)=0,f(x+T)=f(x),f(-T2+π)=f(-T2)=-f(T2),f(-T2)=0,④是正确的.故答案为④.23.试判断下列函数的奇偶性.(1)f(x)=1-2cos x+|tan x|;(2)f(x)=x2tan x-sin2x.【答案】(1)函数的定义域为{x|x≠π2+kπ,k∈Z},f(-x)=1-2cos(-x)+|tan(-x)|=1-2cos x+|tan x|=f(x),∴函数f(x)是偶函数.(2)函数的定义域为{x|x≠π2+kπ,k∈Z},f(-x)=(-x)2tan(-x)-sin2(-x)=-x2tan x-sin2x,∴函数f(x)是非奇非偶函数.24.下列说法正确的是( )A.y=tan x是增函数B.y=tan x在第一象限是增函数C.y=tan x在某一区间上是减函数D.y=tan x在区间(kπ-π2,kπ+π2)(k∈Z)上是增函数【答案】D【解析】由正切函数的图象可知D正确.25.函数y=tan(x+π5)的单调递增区间是( )A.(−π2+kπ,π2+kπ)(k∈Z)B .(−7π10+k π,3π10+k π)(k ∈Z ) C .(−3π10+k π,7π10+k π)(k ∈Z ) D .(−π5+k π,π5+k π)(k ∈Z )【答案】B【解析】∵y =tan x 的单调递增区间为(−π2+k π,π2+k π)(k ∈Z ), 令k π-π2<x +π5<k π+π2,解得k π-7π10<x <k π+3π10, ∴函数y =tan(x +π5)的单调递增区间是(−7π10+k π,3π10+k π)(k ∈Z ). 26.关于函数f (x )=-tan2x ,有下列说法:①f (x )的定义域是{x ∈R |x ≠π2+k π,k ∈Z };②f (x )是奇函数;③在定义域上是增函数;④在每一个区间(-π4+k π2,π4+k π2)(k ∈Z )上是减函数;⑤最小正周期是π.其中正确的是( )A .①②③B .②④⑤C .②④D .③④⑤ 【答案】C【解析】①由正切函数的定义域可得,2x ≠π2+k π,k ∈Z ,故①错误; ③由正切函数的定义域可知,函数y =-tan2x 在(-π4+k π2,π4+k π2)(k ∈Z )上是减函数,故③错误;⑤根据周期公式可得,T =π2,故⑤错误. 27.已知函数f (x )=√3tan πx ω(ω>0).(1)当ω=4时,求f (x )的最小正周期及单调区间;(2)若|f (x )|≤3在x ∈[-π3,π4]上恒成立,求ω的取值范围. 【答案】(1)当ω=4时,f (x )=√3tan π4x ,则f (x )的最小正周期T =ππ4=4,由k π-π2<π4x <k π+π2,k ∈Z .得4k -2<x <4k +2,k ∈Z ,即函数的单调递增区间为(4k -2,4k +2),k ∈Z . (2)∵ω>0,∴函数f (x )的周期T =ππω=ω,∴若|f (x )|≤3在x ∈[-π3,π4]上恒成立, 则f (x )在x ∈[-π3,π4]上为单调递增函数, 满足-π3>-12T =-ω2, ∴ω>2π3,∵|f (-π3)|>f (π4),此时满足f (-π3)≥-3,即f (-π3)=√3tan(-π3×πω)≥-3, 即tan(-π3×πω)≥-√3,则-π3×πω≥-π3, 则πω≤1,即ω≥π, 综上,ω≥π.28.对于函数y =tan x2,下列判断正确的是( ) A .周期为2π的奇函数 B .周期为π2的奇函数 C .周期为π的偶函数 D .周期为2π的偶函数 【答案】A【解析】函数y =tan x 2的周期T =πω=2π,再由tan(-x 2)=-tan x2可得,此函数为奇函数. 29.已知函数f (x )=tan(2x +π4).(1)求该函数的定义域,周期及单调区间; (2)若f (θ)=17,求2cos 2θ2−sinθ−12sin(θ+π4)的值.【答案】(1)由题意得,T =π2. 由2x +π4≠π2+k π(k ∈Z ),得x ≠k π2+π8,由-π2+k π<2x +π4<π2+k π(k ∈Z ),得k π2-3π8<x <k π2+π8,综上得,函数的周期是π2,定义域是{x |x ≠k π2+π8,k ∈Z },单调增区间是(k π2-3π8,k π2+π8)(k ∈Z ).(2)2cos 2θ2−sinθ−1√2sin(θ+π4)=cosθ-sinθsinθ+cosθ=1-tanθtanθ+1,①∵f (θ)=17,∴tan(2θ+π4)=17, 则tan2θ=tan[(2θ+π4)-π4]=17−11+17=-34,由tan2θ=2tanθ1-tan 2θ=-34,得tan θ=3或-13, 把tan θ=3代入上式①得,2cos 2θ2−sinθ−1√2sin(θ+π4)=-12,把tan θ=-13代入上式①得,2cos 2θ2−sinθ−1√2sin(θ+π4)=2.30.已知函数y =tan(12x -π6).(1)作出此函数在一个周期开区间上的简图; (2)求出此函数的定义域、周期和单调区间;(3)写出此函数图象的渐近线方程和所有对称中心的坐标. 【答案】(1)作出此函数在一个周期开区间上的简图:则对应的图象如图:(2)由12x -π6≠k π+π2,得x ≠2k π+4π3,即函数的定义域为{x |x ≠2k π+4π3,k ∈Z },函数的周期T =π12=2π.由k π-π2<12x -π6<k π+π2,k ∈Z , 得2k π-2π3<x <2k π+4π3,k ∈Z ,即函数的单调递增区间为(2k π-2π3,2k π+4π3),k ∈Z .(3)由12x -π6=k π+π2,得x =2k π+4π3,k ∈Z , 即函数图象的渐近线方程为x =2k π+4π3,k ∈Z ,由12x -π6=k π2,得x =k π+π3,k ∈Z .即所有对称中心的坐标为(k π+π3,0).31.已知关于实数x的不等式|x−(tanθ+1)22|≤(tanθ−1)22,x2-3(tanθ+1)x+2(3tanθ+1)≤0的解集分别为M,N,且M∩N=∅,则这样的θ存在吗?若存在,求出θ的取值范围.【答案】假设θ存在.由|x−(tanθ+1)22|≤(tanθ−1)22,得2tanθ≤x≤tan2θ+1,∴M={x|2tanθ≤x≤tan2θ+1}.∵x2-3(tanθ+1)x+2(3tanθ+1)≤0,∴当tanθ≥13时,2≤x≤3tanθ+1.当tanθ<13时,3tanθ+1≤x≤2.∵M∩N=∅,∴当tanθ≥13时,有3tanθ+1<2tanθ或tan2θ+1<2,即tanθ<-1或-1<tanθ<1,∴13≤tanθ<1.①当tanθ<13时,有2<2tanθ或3tanθ+1>tan2θ+1,即tanθ>1或0<tanθ<3,∴0<tanθ<13.②由①②得0<tanθ<1,∴θ的取值范围是(kπ,kπ+π4),k∈Z.。
第5章5.4.3 正切函数的性质与图象——高一上学期人教A版必修第一册同步新题练习

5.4.3正切函数的性质与图象刷新题夯基础题组一正切(型)函数的定义域、值域1.已知x∈[0,2π],则函数y=√tanx+√-cosx的定义域为()A.[0,π2) B.(π2,π] C.[π,3π2) D.(3π2,2π]2.(2020山东枣庄高一下期末)函数y=tan x2的定义域为.3.函数y=tan(x-π6),x∈(-π12,π2)的值域为.4.已知函数y=-tan2x+4tan x+1,x∈[-π4,π4],则其值域为.题组二正切(型)函数的图象及其应用5.函数y=tan(12x-π3)在一个周期内的图象是()6.函数f(x)=tan 2ωx(ω>0)的图象与直线y=2相交,相邻的两个交点间的距离为π2,则f(π3)的值是()A.-√3B.√33C.1D.√37.(多选)与函数y=tan(2x-π4)的图象不相交的直线是()A.x=3π8 B.x=-π2C.x=π4D.x=-π88.根据正切函数的图象,写出使不等式3+√3tan 2x≥0成立的x的取值集合.题组三正切(型)函数的周期性、奇偶性、单调性、图象的对称性9.(2020河南洛阳高一下质量检测)y=tan 2x的最小正周期是()A.π2B.πC.2πD.3π10.函数f(x)=sin x tan x()A.是奇函数B.是偶函数C.是非奇非偶函数D.既是奇函数又是偶函数11.函数y=2tan3x-π4的图象的对称中心不可能是()A.(π12,0) B.(-13π4,0)C.(5π4,0) D.(7π36,0)12.函数y=2tan(π6-2x)的一个单调递减区间是()A.(-π6,π2) B.(0,π2)C.(π3,5π6) D.(5π6,5π3)13.函数y=tan(3x+π3)的最小正周期是,单调递增区间是.14.已知函数f(x)=3tan(12x-π3).(1)求f(x)的定义域、值域;(2)探究f(x)的周期性、奇偶性、单调性和图象的对称性.刷新题培素养题组一 正切(型)函数的定义域、值域 1.(2020吉林五地六校高一上期末联考,)函数y =√log 12tanx 的定义域是 .2.()函数y =1tanx (-π4<x <π4且x ≠0)的值域为 .题组二 正切(型)函数的图象及其应用 3.(2020北京人大附中高一下阶段检测,)函数y =cos x ·|tan x |(0≤x <3π2且x ≠π2)的大致图象是 ( )4.(2020江西南昌八一中学、洪都中学等六校高一上期末联考,)设函数f (x )={tanx ,x ∈(2kπ-π2,2kπ+π2),|cosx |,x ∈[2kπ+π2,2kπ+3π2](k ∈Z),g (x )=sin|x |,则方程f (x )-g (x )=0在区间[-3π,3π]上的解的个数是 ( ) A.7 B.8 C.9D.105.(多选)()已知函数f (x )={tanx ,tanx >sinx ,sinx ,tanx ≤sinx ,则 ( )A. f (x )的值域为(-1,+∞)B. f (x )的单调递增区间为[kπ,kπ+π2)(k ∈Z) C.当且仅当k π-π2<x ≤k π(k ∈Z)时,f (x )≤0 D. f (x )的最小正周期是2π题组三正切(型)函数性质的综合应用6.(2020山东潍坊高一下期末,)若函数f(x)=tanωx+π4(ω>0)的最小正周期为π,则()A. f(2)>f(0)>f(-π5)B. f(0)>f(2)>f(-π5)C. f(0)>f(-π5)>f(2)D. f(-π5)>f(0)>f(2)7.(2020河南鹤壁高级中学高一月考,)已知函数f(x)=m tan x-k sin x+2(m,k∈R),若f(π3)=1,则f(-π3)= ()A.1B.-1C.3D.-38.(多选)()下列关于函数y=tan(x+π3)的说法正确的是()A.在区间(-π6,5π6)上单调递增B.最小正周期是πC.图象关于点(π6,0)成中心对称D.图象关于直线x=π6成轴对称9.(2020河南南阳高一下期末,)若不等式sin x-tan x+|tan x+sin x|-k≤0在x∈[3π4,π]上恒成立,则k的取值范围是.10.()已知函数f(x)=x2+2x tan θ-1,其中θ≠π2+kπ,k∈Z.(1)当θ=-π6,x∈[-1,√3]时,求函数f(x)的最大值与最小值;(2)若函数g(x)=f(x)x为奇函数,求θ的值;(3)求使y=f(x)在区间[-1,√3]上是单调函数的θ的取值范围.答案全解全析刷新题夯基础1.C由题意知{tanx≥0,-cosx≥0,0≤x≤2π,∴函数的定义域为[π,3π2),故选C.2.答案{x|x≠2kπ+π,k∈Z}解析解不等式x2≠kπ+π2(k∈Z),可得x≠2kπ+π(k∈Z),因此,函数y=tan x2的定义域为{x|x≠2kπ+π,k∈Z}.3.答案(-1,√3)解析∵x∈(-π12,π2 ),∴x-π6∈(-π4,π3),∴tan(x-π6)∈(-1,√3), ∴函数的值域为(-1,√3).4.答案[-4,4]解析∵-π4≤x≤π4,∴-1≤tan x≤1.令tan x=t,则t∈[-1,1].∴y=-t2+4t+1=-(t-2)2+5,t∈[-1,1].易知函数在[-1,1]上单调递增,∴当t=-1,即x=-π4时,y min=-4,当t=1,即x=π4时,y max=4.故所求函数的值域为[-4,4].5.A当x=2π3时,tan(12×2π3-π3)=0,故排除C,D;当x=5π3时,tan(12×5π3-π3)=tan π2,无意义,故排除B.故选A.6.A∵函数f(x)=tan 2ωx(ω>0)的图象与直线y=2相交,相邻的两个交点间的距离为π2,∴该函数的最小正周期为π2ω=π2,∴ω=1,∴f(x)=tan 2x,则f(π3)=tan 2π3=-√3.故选A.7.AD令2x-π4=π2+kπ,k∈Z,得x=3π8+kπ2,k∈Z,∴直线x=3π8+kπ2,k∈Z与函数y=tan2x-π4的图象不相交,结合选项可知A、D符合.故选AD.8.解析如图所示,在同一平面直角坐标系中画出函数y=tan x,x∈(-π2,π2)的图象和直线y=-√3.由图得,在区间(-π2,π2)内,不等式tan x≥-√3的解集是{x|-π3≤x<π2},∴在函数y=tan x的定义域x x≠kπ+π2,k∈Z内,不等式tan x≥-√3的解集是{x|kπ-π3≤x<kπ+π2,k∈Z}.令kπ-π3≤2x<kπ+π2(k∈Z),得kπ2-π6≤x<kπ2+π4(k∈Z),∴使不等式3+√3tan 2x≥0成立的x的取值集合是{x|kπ2-π6≤x<kπ2+π4,k∈Z}.9.A y=tan 2x的最小正周期是T=π2.故选A.10.B f(x)的定义域为x x≠π2+kπ,k∈Z,关于原点对称,又f(-x)=sin(-x)·tan(-x)=sin x·tan x=f(x),∴f(x)为偶函数.11.D对于函数y=2tan(3x-π4),令3x-π4=kπ2,k∈Z,得x=kπ6+π12,k∈Z,所以函数y=2tan(3x-π4)的图象的对称中心为(kπ6+π12,0),k∈Z,取k=0,得对称中心为(π12,0);取k=-20,得对称中心为(-13π4,0);取k=7,得对称中心为(5π4,0).令kπ6+π12=7π36,得k=23∉Z,故对称中心不可能是(7π36,0).12.C y=2tan(π6-2x)=-2tan(2x-π6).令-π2+kπ<2x-π6<π2+kπ,k∈Z,得-π6+kπ2<x <π3+kπ2,k ∈Z . 令k =1,得π3<x <5π6,故选C . 13.答案 π3;(kπ3-5π18,kπ3+π18),k ∈Z解析 因为y =tan (3x +π3),所以T =π3. 令-π2+k π<3x +π3<π2+k π,k ∈Z, 得kπ3-5π18<x <kπ3+π18,k ∈Z,所以函数y =tan (3x +π3)的单调递增区间是(kπ3-5π18,kπ3+π18),k ∈Z .14.解析 (1)令12x -π3≠π2+k π,k ∈Z,得x ≠2k π+5π3,k ∈Z, ∴f (x )的定义域为x x ≠5π3+2k π,k ∈Z ,值域为R .(2)f (x )为周期函数,由于f (x )=3tan (12x -π3)=3tan (12x -π3+π)=3tan [12(x +2π)-π3]=f (x +2π), ∴f (x )的最小正周期T =2π.易知f (x )的定义域不关于原点对称,故f (x )为非奇非偶函数. 令-π2+k π<12x -π3<π2+k π,k ∈Z,得-π3+2k π<x <5π3+2k π,k ∈Z, ∴函数f (x )的单调递增区间为(-π3+2kπ,5π3+2kπ),k ∈Z,无单调递减区间.令12x -π3=kπ2(k ∈Z),得x =k π+2π3(k ∈Z),∴函数f (x )的图象的对称中心是(kπ+2π3,0)(k ∈Z).刷新题培素养1.答案 {x|kπ<x ≤kπ+π4,k ∈Z}解析 要使函数有意义,则lo g 12tan x ≥0,即lo g 12tan x ≥lo g 121,∴0<tan x ≤1,∴k π<x ≤k π+π4,k ∈Z, ∴该函数的定义域是x k π<x ≤k π+π4,k ∈Z . 2.答案 (-∞,-1)∪(1,+∞)解析 当-π4<x <0时,-1<tan x <0,所以1tanx <-1; 当0<x <π4时,0<tan x <1,所以1tanx >1. 即当x ∈(-π4,0)∪(0,π4)时,函数y =1tanx 的值域是(-∞,-1)∪(1,+∞).3.C 依题意,y =cos x ·|tan x |={sinx ,0≤x <π2或π≤x <3π2,-sinx ,π2<x <π.由此判断出正确的选项为C .故选C .4.A 在同一平面直角坐标系中作出函数f (x )与g (x )在区间[-3π,3π]上的图象,如图所示.由图知:f (x )-g (x )=0在[-3π,3π]上解的个数为7,故选A .陷阱分析 作图时要注意到当0<x <π2时,sin x <tan x ,此时正弦曲线与正切曲线没有交点. 5.AD 当tan x >sin x ,即k π<x <k π+π2(k ∈Z)时, f (x )=tan x ∈(0,+∞); 当tan x ≤sin x ,即k π-π2<x ≤k π(k ∈Z)时,f (x )=sin x ∈(-1,1). 综上, f (x )的值域为(-1,+∞),故A 正确;f (x )的单调递增区间是(2kπ-π2,2kπ+π2)和2k π+π,2k π+3π2(k ∈Z),故B 错误; 当x ∈(2kπ+π2,2kπ+π)(k ∈Z)时,f (x )>0,故C 错误; 结合f (x )的图象可知f (x )的最小正周期是2π,故D 正确.故选AD .6.C 由函数f (x )=tan (ωx +π4)(ω>0)的最小正周期为π, 可得πω=π,解得ω=1,即f (x )=tan (x +π4), 令-π2+k π<x +π4<π2+k π,k ∈Z, 得-3π4+k π<x <π4+k π,k ∈Z,当k =1时,π4<x <5π4,即函数f (x )在(π4,5π4)上单调递增,又f (0)=f (π),f (-π5)=f (-π5+π)=f (4π5), 且54π>π>4π5>2>π4,所以f (0)>f (-π5)>f (2).故选C .7.C 解法一:∵f (x )=m tan x -k sin x +2(m ,k ∈R), f (π3)=1,∴f (π3)=m tan π3-k sin π3+2=√3m -√32k +2=1, ∴√3m -√32k =-1,∴f (-π3)=m tan (-π3)-k sin (-π3)+2=-√3m +√32k +2=3.解法二:令g (x )=f (x )-2=m tan x -k sin x ,易知g (x )为奇函数, ∴g (-π3)=-g (π3)=-[f (π3)-2]=-(1-2)=1, 即f (-π3)-2=1,∴f (-π3)=3.8.BC 令k π-π2<x +π3<k π+π2,k ∈Z,得k π-5π6<x <k π+π6,k ∈Z,显然(-π6,5π6)不满足上述关系式,故A 中说法错误;显然该函数的最小正周期为π,故B 中说法正确;令x +π3=kπ2,k ∈Z,得x =kπ2-π3,k ∈Z,当k =1时,得x =π6,故C 中说法正确;正切曲线没有对称轴,因此函数y =tan (x +π3)的图象也没有对称轴,故D 中说法错误.故选BC . 9.答案 [2,+∞)解析 ∵tan x +sin x =sinx cosx +sin x =sinx (1+cosx )cosx,x ∈[3π4,π],∴sin x >0,1+cos x >0,cos x <0, ∴tan x +sin x <0,∴ sin x -tan x +|tan x +sin x |=sin x -tan x -tan x -sin x =-2tan x , ∵不等式sin x -tan x +|tan x +sin x |-k ≤0在x ∈[3π4,π]上恒成立, ∴k ≥-2tan x 在x ∈[3π4,π]上恒成立, ∴k ≥(-2tan x )max =2. 故k 的取值范围是[2,+∞). 10.解析 (1)当θ=-π6时, f (x )=x2-2√33x -1=(x -√33)2-43.∵x ∈[-1,√3],且f (x )的图象开口向上, ∴当x =√33时, f (x )min =-43; 当x =-1时,f (x )max =2√33. (2)由题可知g (x )=x -1x +2tan θ, ∵g (x )为奇函数,∴0=g(-x)+g(x)=-x+1x +2tan θ+x-1x+2tan θ=4tan θ,∴tanθ=0,∴θ=kπ,k∈Z.(3)函数f(x)的图象的对称轴为直线x=-tan θ.∵f(x)在区间[-1,√3]上是单调函数,∴-tan θ≥√3或-tan θ≤-1,即tan θ≤-√3或tan θ≥1,∴-π2+kπ<θ≤-π3+kπ或π4+kπ≤θ<π2+kπ,k∈Z,故θ的取值范围是-π2+kπ,-π3+kπ∪π4+kπ,π2+kπ,k∈Z.。
正切函数的图像与性质 练习(1)(解析版)

第五章 三角函数 5.4.3 正切函数的图像与性质一、选择题1.(2019·重庆一中高一月考)函数tan 2y x =的周期为( ) A .2πB .πC .2πD .4π【答案】A【解析】由题意可知,函数tan 2y x =的周期为2T π=.故选:A.2.(2019·湖北高一月考)函数()2tan()4f x x π=--的定义域为( )A .{3,4x x k k Z ππ⎫≠+∈⎬⎭ B .{3,4x x k k Z ⎫≠+∈⎬⎭C .{3,4x x k k Z ππ⎫=+∈⎬⎭D .{,4x x k k Z ππ⎫≠+∈⎬⎭【答案】A【解析】解不等式42x k πππ-≠+,k Z ∈,得34x k ππ≠+,k Z ∈, 因此,函数()2tan 4f x x π⎛⎫=--⎪⎝⎭的定义域为3,4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭,故选:A. 3.(2019·四川高一期末)已知2a log 3=,121b ()3=,c tan2=,则下列关系中正确的是( )A .a c b >>B .b a c >>C .a b c >>D .c a b >>【答案】C【解析】22a log 3log 21=>=,10211b ()()133=<=,∴b 01∈(,), 又2π2π<<,∴c tan20=<,则下列关系中正确的是:a b c >>.故选:C .4.(2019·辽宁高一课时练)函数()tan()6f x x π=+的图象的一个对称中心是( )A .(,0)3πB .(,0)4πC .(,0)2πD .(,0)6π【答案】A【解析】由正切函数的对称中心(,0),()2k k Z π∈可以推出()f x 对称中心的横坐标满足()6262k k x x k Z ππππ+=⇒=-+∈,带入四个选项中可知,当1k =时,3x π=. 故,03π⎛⎫⎪⎝⎭是图像的一个对称中心,选A. 5.(2019·湖南高一期中)下列函数中,同时满足:①在π0,2⎛⎫⎪⎝⎭上是增函数,②为奇函数,③以π为最小正周期的函数是( ) A .y =tan x B .y =cos x C .y =tan2x D .y =|sin x |【答案】A【解析】正切函数的对称中心为,02k π⎛⎫⎪⎝⎭,正弦函数的对称中心为(),0k π,余弦函数的对称中心为,0()2k k Z ππ⎛⎫+∈ ⎪⎝⎭,解关于对称中心的题目时需要把整个三角函数看成一个整体,从整体性入手求出具体范围.;选项B D ,中所给函数都是偶函数,不符合;选项C 中所给的函数的周期为2π,不符合;故选A6.(2019·河南高一期末)已知函数()()5tan 202f x x πϕϕ⎛⎫=+<<⎪⎝⎭,其函数图像的一个对称中心是,012π⎛⎫⎪⎝⎭,则该函数的单调递增区间可以是( ) A .5,66ππ⎛⎫-⎪⎝⎭ B .,63ππ⎛⎫-⎪⎝⎭ C .,36ππ⎛⎫-⎪⎝⎭ D .5,1212ππ⎛⎫-⎪⎝⎭ 【答案】D【解析】,012π⎛⎫⎪⎝⎭为函数的对称中心 2122k ππϕ∴⨯+=,k Z ∈ 解得:26k ππϕ=-,k Z ∈,0,2πϕ⎛⎫∈ ⎪⎝⎭3πϕ∴=()5tan 23f x x π⎛⎫∴=+⎪⎝⎭当5,66x ππ⎛⎫∈-⎪⎝⎭时,422,333x πππ⎛⎫+∈- ⎪⎝⎭,此时()f x 不单调,A 错误;当,63x ππ⎛⎫∈-⎪⎝⎭时,()20,3x ππ+∈,此时()f x 不单调,B 错误;当,36x ππ⎛⎫∈-⎪⎝⎭时,22,333x πππ⎛⎫+∈- ⎪⎝⎭,此时()f x 不单调,C 错误; 当5,1212x ππ⎛⎫∈-⎪⎝⎭时,2,322x πππ⎛⎫+∈- ⎪⎝⎭,此时()f x 单调递增,D 正确二、填空题7.(2019·上海理工大学附属中学高一期末)方程tan 1x =的解为_________. 【答案】|,4x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭【解析】tan 1x =则,4x k k Z ππ=+∈ 故答案为:|,4x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭8.(2019·河南高一月考)函数()tan f x x =在,34ππ⎡⎤-⎢⎥⎣⎦上的最小值为__________.【答案】【解析】正切函数在给定的定义域内单调递增,则函数的最小值为tan 33f ππ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭.9.(2019·上海市金山中学高一期中)函数2tan()26x y π=-的单调增区间为___________. 【答案】24(2,2),33k k k Z ππππ-+∈ 【解析】令12262k x k πππππ-<-<+,可得242233k x k ππππ-<<+,故函数的单调增区间为2π4π2π,2π33k k ⎛⎫-+ ⎪⎝⎭,k Z ∈.10.(2018·江西高一期末)函数()tan (0)f x x ωω=>的相邻两支截直线4y π=所得线段长4π,则4f π⎛⎫⎪⎝⎭的值________. 【答案】0【解析】∵函数图象的相邻两支截直线y 4π=所得线段长为4π,∴函数f (x )的周期为4π,图象如下:由4ππω=得ω=4,∴f (x )=tan4x ,∴f (4π)=tanπ=0.故答案为:0. 三、解答题11.(2019·黑龙江双鸭山一中高一期末)已知函数()2tan()13f x x π=++.(1)求()f x 的定义域; (2)求()f x 的周期; (3)求()f x 的单调递增区间. 【答案】(1){|,}6x x k k Z ππ≠+∈(2)T π= (3)5,66k k ππππ⎛⎫-++ ⎪⎝⎭,( k Z ∈) 【解析】(1)由()2tan 13f x x π⎛⎫=++ ⎪⎝⎭可得:x 3π+≠k π,2k Z π+∈即,6x k k Z ππ≠+∈,∴()f x 的定义域为{|,}6x x k k Z ππ≠+∈;(2)周期T 1ππ==,∴()f x 的周期为π;(3)由232k x k πππππ-+++<<可得:56k ππ-+<x 6k <ππ+,k Z ∈. ∴单调增区间为5,66k k ππππ⎛⎫-++ ⎪⎝⎭,( k Z ∈). 12.(2019·天水高一期中)已知函数()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π2. (1)求ω的值及函数()f x 的定义域;(2)若328f απ⎛⎫-=⎪⎝⎭,求sin cos αα的值. 【答案】(1)2ω=,()f x 的定义域为1,82x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭;(2)310 【解析】(1)2T ππω== ,2ω∴=, 又因为tan y x =的定义域为,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭,所以242x k ,解得182x k ππ≠+,故()f x 的定义域为1,82x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭。
正切函数知识点与习题附答案
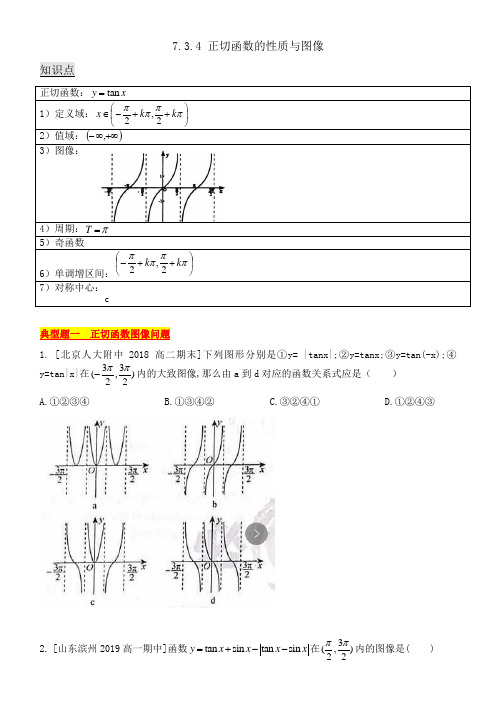
7.3.4 正切函数的性质与图像知识点正切函数:x y tan =1)定义域:⎪⎭⎫⎝⎛++-∈ππππk k x 2,22)值域:()+∞∞-, 3)图像:4)周期:π=T 5)奇函数6)单调增区间:⎪⎭⎫⎝⎛++-ππππk k 2,2 7)对称中心:c典型题一 正切函数图像问题1. [北京人大附中2018高二期末]下列图形分别是①y= |tanx|;②y=tanx;③y=tan(-x);④y=tan|x|在33(,)22ππ-内的大致图像,那么由a 到d 对应的函数关系式应是( )A.①②③④B.①③④②C.③②④①D.①②④③2. [山东滨州2019高一期中]函数tan sin tan sin y x x x x =+--在3(,)22ππ内的图像是( )3.函数1tan()23y x π=-在一个周期内的图像是( )4. 在区间33(,)22ππ-内,函数y=tanx 与y=sinx 的图像交点的个数为( ) A.1 B.2 C.3 D.4 5.函数f(x)=2x-tanx 在(,)22ππ-上的图象大致为( )典型题二 定义域值域问题6.[吉林辽源田家炳高级中学2019高一期末]函数2tan(2)3y x π=+的定义域为( )A. |12x x π⎧⎫≠⎨⎬⎩⎭B.|12x x π⎧⎫≠-⎨⎬⎩⎭C. |,12x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭D. 1|,122x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭ 7.[铜仁2019高一质检]函数f(x)=tan2x 在[,]66ππ-上的最大值与最小值的差为( )A. 3 C. 2 D. 238.函数f(x)=-2tanx+m,x ∈[,]43ππ-有零点,则实数m 的取值范围是 .9.[江西高安中学2018高二期末]函数|2tan |x y =是( )A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数 10.[黑龙江哈尔滨六中2019高一期末]函数)0(tan )(>=ωωx x f 的图像的相邻两支截直线y=4π所得的线段长为4π,则)4(πf 的值是( ) A.0 B.1 C.-1 D.4π11.已知1tan sin )(++=x b x a x f 满足7)5(=πf ,则=)599(πf 。
正切函数的性质与图象 课件(人教版)

又令2x-π3 ≠±π2 ,求得二渐近线方程为 x≠
π -3且
x≠53π,故选
A.
方法二
y=tanx2-π3 的周期
π T= 1 =2π,
2
而由图象 B、D 可知周期为π,故可排除 B、D.
当 x=π3 时,y=tanπ6 -π3 =-tanπ6 ≠0,
故可排除 C,因此应选 A.
方法三 ∵y=tanx2-π3 =tan21x-2π3 ,
π
T=|ω|求解;(2)式应画出函数 y=|tan x|的图象,
利用图象法求解.
π 解析:(1)∵ω= 3 ,∴最小正周期
T=|ωπ |=ππ=3.
Hale Waihona Puke 3(2)函数 y=|tan x|的图象是将函数 y=tan x 的图象
在 x 轴下方的部分沿 x 轴翻折上去,其余不变,因
此函数 y=|tan x|的最小正周期为π.
题型4 正切函数的综合问题
例 4 画出函数 y=|tan x|+tan x 的图象,并指出其定义 域、值域、最小正周期和单调增区间. 分析:本题主要考查正切函数的图象和性质,应先对 tan x 值的符号分类讨论,作出函数 y=|tan x|+tan x 的图象后,再进行研究. 解析:y=|tan x|+tan x=20t,antaxn,xt<a0n. x≥0, 作函数 y=|tan x|+tan x 的图象如下:
观察图象知,其定义域为xx≠kπ+π2 ,k∈Z, 值域为[0,+∞),最小正周期为π,单调增区间为 kπ,kπ+π2 (k∈Z). 点评:含绝对值问题的处理办法,就是讨论去绝对值, 再借助图象解决问题.
解得 2kπ-π2 <x<2kπ+3π2 ,k∈Z. ∵y=tan-21x+π4 的单调减区间就是 u= tan21x-π4 的单调增区间, 而 u=tan12x-π4 的单调增区间为(2kπ-π2 , 2kπ+3π2 ),k∈Z, ∴函数 y=tan-12x+π4 的单调减区间是(2kπ
正切函数的性质与图象期末复习题

正切函数的性质与图象期末复习题一、单选题1.使得不等式1tan x -≤<x 的取值范围是( )A .,43ππ⎡⎫-⎪⎢⎣⎭B .4,43ππ⎡⎫-⎪⎢⎣⎭C .,,43k k k Z ππππ⎡⎫-+∈⎪⎢⎣⎭ D .2,2,43k k k Z ππππ⎡⎫-+∈⎪⎢⎣⎭ 2.直线y a =与函数()()tan 04f x x πωω⎛⎫ ⎪⎝⎭=+>的图象的相邻两个交点的距离为2π,若函数()f x 在区间()(),0m m m ->上是增函数,则实数m 的取值范围是( )A .0,4π⎛⎫ ⎪⎝⎭B .0,2π⎛⎤ ⎥⎝⎦C .0,2π⎛⎫ ⎪⎝⎭D .0,4π⎛⎤ ⎥⎝⎦ 3.下列各组函数中,在区间ππ,22⎛⎫- ⎪⎝⎭上都是增函数的为( ). A .sin y x =,cos y x =B .sin y x =,tan y x =C .cos y x =,tan y x =D .sin y x =-,cos y x =-4.函数()22f x x ππ⎫-<<⎪⎝⎭( ) A .在,22ππ⎛⎫- ⎪⎝⎭上是增函数 B .在,02π⎛⎤- ⎥⎝⎦上是增函数,在0,2π⎛⎫ ⎪⎝⎭上是减函数 C .在,22ππ⎛⎫- ⎪⎝⎭上是减函数 D .在,02π⎛⎤- ⎥⎝⎦上是减函数,在0,2π⎛⎫ ⎪⎝⎭)上是增函数 5.已知tan 2,tan 3,tan 5a b c ===,不通过求值,判断下列大小关系正确的是( ) A .a b c >>B .a b c <<C .b a c >>D .b a c <<6.若02θπ≤<,且不等式cos sin θθ<和tan sin θθ<成立,则角θ的取值范围是( ) A .3,44ππ⎛⎫ ⎪⎝⎭ B .,2ππ⎛⎫ ⎪⎝⎭C .3,2ππ⎛⎫ ⎪⎝⎭D .35,44ππ⎛⎫ ⎪⎝⎭ 7.已知函数()ππ32tan 0242f x x x ⎛⎫⎛⎫=-≤< ⎪⎪⎝⎭⎝⎭,点(),2A x -,()1,B y 为()f x 的图象上两点,O 为坐标原点,则tan AOB ∠=( )A .1B .12C .1-D .12- 8.函数()tan ,(11)f x x x x =⋅-<<的图象可能是( )A .B .C .D .二、多选题9.函数tan(2)6y x π=-的一个对称中心是( ) A .(,0)12π B .2(,0)3π C .(,0)6π D .(,0)3π 10.关于函数()tan 2f x x =,下列说法中正确的是( )A .最小正周期是π2B .图象关于点π,02⎛⎫ ⎪⎝⎭对称C .图象关于直线π4x =对称D .在区间ππ,22⎛⎫- ⎪⎝⎭上单调递增 11.下列说法正确的是A .sin145tan 47︒︒<B .函数tan()(0)y x ωϕω=+≠的最小正周期为πωC .函数2tan 42y x x ππ⎛⎫=≤< ⎪⎝⎭的值域是[2,)+∞ D .函数tan y x =在第一、四象限是增函数 12.已知函数()1212()tan ,,,22f x x x x x x ππ⎛⎫=∈-≠ ⎪⎝⎭,则下列结论中正确的是 A .()()11f x f x π+=B .()()11f x f x -=C .()()12120f x f x x x ->-D .()()()121212022f x f x x x f x x ++⎛⎫>> ⎪⎝⎭三、填空题13.当04x π<<时,函数221sin ()cos sin sin x f x x x x-=⋅-的最小值是________. 14.函数tan ,0244y x x x πππ⎛⎫⎛⎫=--≠ ⎪⎪⎝⎭⎝⎭的值域是__________. 15.函数()lg tan 1x +的定义域是__________. 16.函数2tan 34y x π⎛⎫=+ ⎪⎝⎭的图像是由无穷多支曲线所组成,它们被直线__________隔开.四、解答题17.求下列函数的定义域:(1)y =(2)=y(3)lg cos =+y x18.已知函数sin()(0,0,||)y A x A ωϕωϕπ=+>><的最小正周期为23π,最小值是2,且图像过点5,09π⎛⎫ ⎪⎝⎭,求这个函数的解析式.19.已知函数()tan()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的图像与x 轴相交的两相邻点的坐标分别为,06π⎛⎫ ⎪⎝⎭和5,06π⎛⎫ ⎪⎝⎭,且过点(0,3)-.求: (1)函数()f x 的解析式;(2)满足()f x ≥x 的取值范围.20.已知函数()()0x f x πωω=>. (1)当4ω=时,求()f x 的最小正周期及单调区间;(2)若()3f x 在,34x ππ⎡⎤∈-⎢⎥⎣⎦上恒成立,求ω的取值范围.21.已知定义在区间2,3ππ⎡⎤-⎢⎥⎣⎦上的函数()f x 的图象关于直线6x π=-对称,当2,63x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()sin()(0,0)f x A x ωϕωϕπ=+>的图象如图所示.(1)求()f x 在2,3ππ⎡⎤-⎢⎥⎣⎦上的解析式.(2)求方程()f x =22.设函数f (x )=tan(ωx +φ)0,02πωϕ⎛⎫><< ⎪⎝⎭,已知函数y =f (x )的图象与x 轴相邻两个交点的距离为2π,且图象关于点M ,08π⎛⎫- ⎪⎝⎭对称. (1)求f (x )的解析式;(2)求f (x )的单调区间;(3)求不等式-1≤f (x答案第5页,共1页。
高中数学-正切函数的性质与图象练习

高中数学-正切函数的性质与图象练习一、选择题(每小题3分,共18分)1.下列说法正确的是( )A.正切函数在整个定义域内是增函数B.正切函数在整个定义域内是减函数C.函数y=3tan的图象关于y轴对称D.若x是第一象限角,则y=tanx是增函数【解析】选C.y=3tan=3tan|x|是偶函数,所以图象关于y轴对称.【误区警示】因为正切函数有无数个单调递增区间,很容易误选A,其实正切函数在整个定义域内不是单调函数.2.(·济宁高一检测)函数y=tan(cosx)的值域是( )A. B.C.[-tan1,tan1]D.以上都不对【解析】选C.cosx∈[-1,1],正切函数在[-1,1]上是增函数,所以y=tan(cosx)的值域是[-tan1,tan1].3.与函数y=3tan的图象不相交的一条直线是( )A.x=B.x=-C.x=D.x=【解析】选D.当x=时,2x+=,y=3tan无意义,故选 D.4.(·阜阳高一检测)函数f(x)=tan与函数g(x)=sin的最小正周期相同,则ω= ( )A.±1B.1C.±2D.2【解题指南】先求g(x)的最小正周期,再用正切函数的最小正周期公式求解.【解析】选A.g(x)的最小正周期为=π,则=π,所以ω=±1.5.tan与tan的大小关系为( )A.tanπ>tanB.tanπ=tanC.tanπ<tanD.无法比较【解析】选 C.tan=tan=tan,又y=tanx在上是增函数,而-<-<<,所以tan<tan.6.(2014·海口高一检测)下列函数中,既为偶函数又在(0,π)上单调递增的是( ) A.y=tan|x| B.y=cos(-x)C.y=sinD.y=【解析】选C.四个选项中的函数均为偶函数,但只有选项C中的y=sin=-cosx在(0,π)上单调递增.二、填空题(每小题4分,共12分)7.(·长沙高一检测)函数y=的最小正周期是.【解析】y=的图象是y=tanx的图象保留x轴上方部分,并将下方的部分翻折到x轴上方得到的,所以其最小正周期也为π.答案:π【变式训练】若函数f(x)=2tan的最小正周期T满足1<T<2,则自然数k的值为. 【解析】因为T=,1<<2,<k<π,而k∈N,故k=2或3.答案:2或38.(·宁德高一检测)函数y=tan的递增区间是.【解析】-+kπ<+<+kπ(k∈Z),得-+kπ<<+kπ(k∈Z),即-+2kπ<x<+2kπ(k∈Z),所以递增区间是(k∈Z).答案:(k∈Z)9.函数y=tan,x∈的值域是.【解析】x∈,x+∈,则tan∈,所以值域为.答案:三、解答题(每小题10分,共20分)10.求下列函数的定义域:(1)y=.(2)y=.【解题指南】解答本题(1)可由分母不为零及tanx的定义域求出;(2)可根据被开方数大于等于零,利用对数函数的单调性求出x的取值范围.【解析】(1)要使函数y=有意义,须有所以x≠kπ-,且x≠kπ+(k∈Z),所以函数的定义域为.(2)要使函数y=有意义,须有lo tanx≥0=lo 1.又因为函数y=lo x在(0,+∞)上是减少的,所以0<tanx≤1,所以kπ<x≤kπ+,k∈Z.所以函数y=的定义域为.11.作出函数y=tanx+|tanx|的图象,并求其定义域、值域、单调区间及最小正周期.【解析】y=tanx+|tanx|=其图象如图所示,由图象可知,其定义域是(k∈Z);值域是[0,+∞);单调递增区间是(k∈Z);最小正周期T=π.【拓展提升】巧求三角函数的定义域(1)求三角函数的定义域,既要注意一般函数定义域的规律,又要注意三角函数本身的特有属性.(2)求函数的定义域通常是解不等式组,利用“数形结合”,借助于数轴画线求交集的方法进行.在求解三角函数,特别是综合性较强的三角函数的定义域时,我们同样可以利用“数形结合”,在单位圆中画三角函数线,利用各三角不等式解集的扇形区域的交集来完成.(3)一般地,已知弦函数的取值范围,求角的取值范围用三角函数线简单;已知切函数的取值范围,求角的取值范围用图象比较好.一、选择题(每小题4分,共16分)1.函数y=+的定义域是( )A.B.C.D.【解析】选C.由得.2.要得到y=tan2x的图象,只需把y=tan的图象( )A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【解题指南】找出由y=tan2x的图象如何平移得到y=tan的图象,然后反向移动即可.【解析】选D.将y=tan2x的图象向左平移个单位可以得到y=tan2即y=tan的图象,所以只需把y=tan的图象向右平移个单位,就可得到y=tan2x的图象.3.(·萍乡高一检测)函数y=是( )A.奇函数B.非奇非偶函数C.既是奇函数又是偶函数D.偶函数【解析】选 A.定义域,且y==,f(-x)===-f(x),所以为奇函数.4.下列各式正确的是( )A.tan<tanB.tan>tanC.tan=tanD.大小关系不确定【解析】选B.因为tan=-tan=-tan,tan=-tan=-tan,而tan<tan,所以tan>tan.【变式训练】比较tan与tan大小.【解析】tan=-tan=-tan<0,tan=-tan=tan>0,所以tan<tan.二、填空题(每小题5分,共10分)5.(·金华高一检测)已知函数y=tanωx在上是减函数,则ω的取值范围是 .【解析】由题意知ω<0,且周期≥π,所以≤1,即-ω≤1,即-1≤ω<0.答案:-1≤ω<0【变式训练】函数y=tan的递增区间是.【解析】由kπ-<+<kπ+,k∈Z,解得2kπ-<x<2kπ+,k∈Z.答案:(k∈Z)6.(·黄山高一检测)下列三个说法:①函数y=tan(2x+1)的最小正周期是π;②函数y=tanx的图象关于点(π,0)成中心对称;③函数y=tanx的图象关于点成中心对称.其中正确说法的序号为.【解析】①T=;②③正确,因为y=tanx的对称中心为,k∈Z.答案:②③三、解答题(每小题12分,共24分)7.(·大连高一检测)已知-≤x≤,f(x)=tan2x+2tanx+2,求f(x)的最值及相应的x值.【解析】因为-≤x≤,所以-≤tanx≤1,而f(x)=tan2x+2tanx+2=(tanx+1)2+1,所以当tanx=-1即x=-时,f(x)有最小值1,当tanx=1即x=时,f(x)有最大值 5.【变式训练】求函数y=tan2+tan3x++1的定义域和值域.【解析】由3x+≠kπ+,k∈Z,得x≠+(k∈Z),所以函数的定义域为.设t=tan,则t∈R,y=t2+t+1=+≥,所以原函数的值域是.8.(·揭阳高一检测)已知函数f(x)=2tanωx+(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于2π,求f(x)的单调递增区间.【解析】由题意知,函数f(x)的周期为2π,则=2π,由于ω>0,故ω=,所以f(x)=2tan.再由kπ-<x+<kπ+,k∈Z,得2kπ-<x<2kπ+,k∈Z,即函数f(x)的单调递增区间为,k∈Z.。
高中数学新课程必修第一册《5.4.3正切函数的性质与图象》基础测试答案解析

高中数学新课程必修第一册《5.4.3正切函数的性质与图象》基础测试答案解析1.函数y=3tan的定义域是 ( )A. B.C. D.解析:要使函数有意义,则2x+≠kπ+,k∈Z,即x≠+,k∈Z,所以函数的定义域为,故选C.2.已知x∈[0,2π],则函数y=+的定义域为 ( )A. B. C. D.解析:由题意知∴函数的定义域为,故选C.3.函数y=tan在一个周期内的图象是 ( )解析:当x=时,tan=0,故排除C,D;当x=时,tan=tan,无意义,故排除B.故选A.4.已知函数y=tan(2x+φ)的图象过点,则φ可以是 ( )A.-B.C.-D.解析:因为函数y=tan(2x+φ)的图象过点,所以0=tan,所以tan =0, 所以+φ=kπ(k∈Z),即φ=-+kπ(k∈Z),所以φ可以是-,故选A.5.函数y=tan 是 ( )A.最小正周期为4π的奇函数B.最小正周期为2π的奇函数C.最小正周期为4π的偶函数D.最小正周期为2π的偶函数解析:该函数为奇函数,其最小正周期为2π.故选B.6.函数2tan(3)4y x π=-的图象的对称中心不可能是 ( )A. B. C. D.解析:对于函数y=2tan ,令3x-=,k ∈Z,得x=+,k ∈Z,所以函数y=2tan 的图象的对称中心为,k ∈Z,取k=0,得对称中心为;取k=-20,得对称中心为;取k=7,得对称中心为.故对称中心不可能是.7.函数2tan(2)6y x π=-的一个单调递减区间是 ( )A. B. C. D.解析:y=2tan=-2tan.令-+kπ<2x-<+kπ,k∈Z,得-+<x<+,k∈Z.令k=1,得<x<,故选C.8.下列正切值中,比tan的值大的是 ( )A.tanB.tanC.tan 35°D.tan(-142°)解析:正切函数y=tan x在区间上单调递增,所以tan<tan,tan=tan<tan, tan 35°<tan 36°=tan,tan(-142°)=tan 38°>tan 36°=tan.故选D.9.(多选)下列关于函数y=tan的说法正确的是 ( )A.在区间上单调递增B.最小正周期是πC.图象关于点成中心对称D.图象关于直线x=成轴对称解析:令kπ-<x+<kπ+,k∈Z,得kπ-<x<kπ+,k∈Z,显然不满足上述关系式,故A中说法错误;显然该函数的最小正周期为π,故B中说法正确;令x+=,k∈Z,得x=-,k∈Z,当k=1时,得x=,故C中说法正确;正切曲线没有对称轴,因此函数y=tan 的图象也没有对称轴,故D 中说法错误.故选BC. 10.tan ≥的解集为 .答案 解析 由题可得kπ+≤2x+<kπ+,k ∈Z,所以kπ≤2x<kπ+,k ∈Z,所以≤x<+,k ∈Z.所以不等式的解集为{|,}2212k k x x k Z πππ≤≤+∈. 11.已知函数y=tan,x ∈∪,则其值域为 . 答案:∪[,+∞)解析 ∵x ∈∪,∴+∈∪.令t=+,则y=tan t,t ∈∪,其图象(实线部分)如图所示.由图象可知所求函数的值域为∪[,+∞).12.已知函数f(x)=asin x+btan x-1(a,b∈R),若f(-2)=2 018,则f(2)= .答案-2 020解析根据题意,函数f(x)=asin x+btan x-1,设g(x)=f(x)+1=asin x+btan x,则g(-x)=asin(-x)+btan(-x)=-(asin x+btan x)=-g(x),则函数g(x)为奇函数,则g(2)+g(-2)=f(2)+1+f(-2)+1=0,又由f(-2)=2 018,得f(2)=-2 020.故答案为-2 020.13.若“∀x∈,tan x-1≤m”是真命题,则实数m的最小值为.答案0解析由x∈,可得tan x-1≤0,所以由“∀x∈,tan x-1≤m”是真命题可得m≥0,即m的最小值为0.14.已知函数f(x)=tan(x+φ)的图象的一个对称中心为,则φ的值为.答案-或解析因为是函数f(x)的图象的一个对称中心,所以+φ=,k∈Z,所以φ=-,k∈Z,由于|φ|<,故取k=0或k=1,得φ=-或φ=.15.已知函数y=-tan2x+4tan x+1,x∈,则其值域为.答案[-4,4]解析∵-≤x≤,∴-1≤tan x≤1.令tan x=t,则t∈[-1,1].∴y=-t2+4t+1=-(t-2)2+5,t∈[-1,1].易知函数在[-1,1]上单调递增,∴当t=-1,即x=-时,y min =-4,当t=1,即x=时,y max =4.故所求函数的值域为[-4,4].16.根据正切函数的图象,写出使不等式3+tan 2x≥0成立的x 的取值集合.解析 如图所示,在同一平面直角坐标系中画出函数y=tan x,x ∈的图象和直线y=-.由图得,在区间内,不等式tan x≥-的解集是,∴在函数y=tan x 的定义域{|,}2x x k k Z ππ≠+∈内,不等式tan x≥-的解集是.令kπ-≤2x<kπ+(k ∈Z),得-≤x<+(k ∈Z),∴使不等式3+tan 2x≥0成立的x 的取值集合是.17.已知函数f(x)=3tan.(1)求f(x)的定义域、值域; (2)探究f(x)的周期性、奇偶性、单调性和对称性.解析(1)令x-≠+kπ,k∈Z,得x≠2kπ+,k∈Z,∴f(x)的定义域为5{|2,}3x x k k Zππ≠+∈,值域为R.(2)f(x)为周期函数,由于f(x)=3tan=3tan=3tan=f(x+2π),∴f(x)的最小正周期T=2π.易知f(x)的定义域不关于原点对称,故f(x)为非奇非偶函数. 令-+kπ<x-<+kπ,k∈Z,得-+2kπ<x<+2kπ,k∈Z,∴函数f(x)的单调递增区间为,k∈Z,无单调递减区间.令x-=(k∈Z),得x=kπ+(k∈Z),∴函数f(x)的图象的对称中心是(k∈Z).。
正切函数的性质与图象 作业

一、选择题(每小题5分,共20分)1.函数y =tan ⎝⎛⎭⎫π4-x 的定义域是( ) A .⎩⎨⎧⎭⎬⎫x |x ≠π4,x ∈R B.⎩⎨⎧⎭⎬⎫x |x ≠-π4,x ∈R C.⎩⎨⎧⎭⎬⎫x |x ≠k π+π4,k ∈Z ,x ∈R D.⎩⎨⎧⎭⎬⎫x |x ≠k π+34π,k ∈Z ,x ∈R 解析: y =tan ⎝ ⎛⎭⎪⎫π4-x =-tan ⎝ ⎛⎭⎪⎫x -π4, 所以x -π4≠k π+π2,k ∈Z , 所以x ≠k π+3π4,k ∈Z ,x ∈R . 答案: D2.下列说法正确的是( )A .y =tan x 是增函数B .y =tan x 在第一象限是增函数C .y =tan x 在每个区间⎝⎛⎭⎫k π-π2,k π+π2(k ∈Z )上是增函数 D .y =tan x 在某一区间上是减函数解析: 正切函数在每个区间⎝⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上是增函数.但在整个定义域上不是增函数,另外,正切函数不存在减区间.答案: C3.已知a =tan 2,b =tan 3,c =tan 5,不通过求值,判断下列大小关系正确的是( )A .a >b >cB .a <b <cC .b >a >cD .b <a <c解析: tan 5=tan [π+(5-π)]=tan (5-π),由正切函数在⎝ ⎛⎭⎪⎫π2,π上为增函数可得tan 3>tan 2>tan (5-π).答案: C4.函数y =tan (cos x )的值域是( )A .⎣⎡⎦⎤-π4,π4 B .⎣⎡⎦⎤-22,22 C .[-tan 1,tan 1] D .以上均不对解析: ∵-1≤cos x ≤1,且函数y =tan x 在[-1,1]上为增函数, ∴tan (-1)≤tan x ≤tan 1即-tan 1≤tan x ≤tan 1.答案: C 二、填空题(每小题5分,共15分)5.函数y =1-tan x 的定义域是________.解析: 由1-tan x ≥0即tan x ≤1结合图象可解得.答案: ⎝⎛⎦⎤k π-π2,k π+π4(k ∈Z ) 6.函数y =tan ⎝⎛⎭⎫x 2+π3的单调递增区间是________. 解析: 令k π-π2<x 2+π3<k π+π2,k ∈Z ,解得2k π-5π3<x <2k π+π3,k ∈Z . 答案: ⎝⎛⎭⎫2k π-5π3,2k π+π3,k ∈Z 7.函数y =3tan (π+x ),-π4<x ≤π6的值域为________. 解析: 函数y =3tan (π+x )=3tan x ,因为正切函数在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,所以-3<y ≤3,所以值域为(-3,3].答案: (-3,3]三、解答题(每小题10分,共20分)8.求函数y =tan ⎝⎛⎭⎫12x -π6的定义域、周期及单调区间. 解析: 由12x -π6≠π2+k π,k ∈Z ,得x ≠4π3+2k π,k ∈Z , 所以函数y =tan ⎝ ⎛⎭⎪⎫12x -π6的定义域为 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠4π3+2k π,k ∈Z .T =π12=2π,所以函数y =tan ⎝ ⎛⎭⎪⎫12x -π6的周期为2π. 由-π2+k π<12x -π6<π2+k π,k ∈Z ,得-2π3+2k π<x <4π3+2k π,k ∈Z ,所以函数y =tan ⎝ ⎛⎭⎪⎫12x -π6的单调递增区间为⎝ ⎛⎭⎪⎫-2π3+2k π,4π3+2k π(k ∈Z ).9.求函数y =tan 2x 的定义域、值域和周期,并作出它在区间[-π,π]内的图象. 解析: (1)要使函数y =tan 2x 有意义,必须且只需2x ≠π2+k π,k ∈Z ,即x ≠π4+k π2,k ∈Z ,∴函数y =tan 2x 的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪x ≠π4+k π2,k ∈Z . (2)设t =2x ,由x ≠π4+k π2,k ∈Z 知t ≠π2+k π,k ∈Z ,∴y =tan t 的值域为(-∞,+∞),即y =tan 2x 的值域为(-∞,+∞).(3)由tan 2⎝ ⎛⎭⎪⎫x +π2=tan (2x +π)=tan 2x ,∴y =tan 2x 的周期为π2.(4)函数y =tan 2x 在区间[-π,π]内的图象如图.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
正切函数的图象与性质(习题) ➢ 例题示范 例1:已知sin33cos55tan35a b c =︒=︒=︒,
,,则( )
A .a b c >>
B .b c a >>
C .c b a >>
D .c a b >>
思路分析: 观察33°,55°,35°之间的关系,利用三角函数在区间[090]︒︒,
上的单调性,选择合适的公式化简,转化为可比较的函数值. 由诱导公式可得,
cos55cos(9035)sin35b =︒=︒-︒=︒,
∵sin y x =在区间[090]︒︒,上单调递增,且sin 33a =︒,
∴b a >,
∵sin 35tan 35cos35c ︒=︒=
︒
,且0cos351<︒<, ∴tan35sin35c b =︒>︒=, ∴c b a >>,故选C .
例2:函数23()sin cos 4f x x x =++,2π[0]3
x ∈,的值域是( ) A .[12], B .[]44-, C .[1]4
-, D .[2]4-,
思路分析:
2223()sin cos 4
31cos cos 4
7cos cos 4
f x x x x x x x =++=-++=-++由题意, 设cos t x =,2π[0]3x ∈,,由余弦函数的单调性得,12
1t -≤≤, 则原函数可化为27()4f x t t =-++,12
1t -≤≤, 由二次函数性质得,()[12]f x ∈,,故选A .
➢ 巩固练习
A .2
π B .π C .2π D .4π
C .(1)(0)(1)f f f >>-
D .(0)(1)(1)f f f >->
4. 下列函数属于奇函数的是( )
A .()tan(π)f x x =+
B .π()sin()2f x x =-
C .()cos(3π)f x x =-
D .π()sin()2f x x =+
5. 已知函数()tan f x x x =+,2()=cos g x x x +,则( )
A .()f x 与()g x 都是奇函数
B .()f x 与()g x 都是偶函数
C .()f x 是奇函数,()g x 是偶函数
D .()f x 是偶函数,()g x 是奇函数
6. 函数sin()2
y x π=+在( ) A .[]22
ππ-,上是增函数 B .[0]π,上是减函数 C .[0]-π,上是减函数 D .[]-ππ,上是减函数
7. 函数()cos f x x =的一个单调递减区间是( )
A .[]44
ππ-, B .[]44π3π,
3
C .[]2
3ππ, D .[]2
3π2π, 8. 下列函数中,周期为π,且在[]42
ππ,上为减函数的是( ) A .sin(2)2y x π=+ B .cos(2)2
y x π=+ C .sin()2y x π=+ D .cos()2
y x π=+
9. 若函数()sin 0f x ax a =>()在区间[]3π0,上单调递增,在区间[]32
ππ,上单调递减,则a 的值为( )
A .
32 B .23 C .2 D .3
10. 已知函数()cos 0f x ax a =>(),将()f x 的图象向右平移
3π个单位长度后,若所得图象与原图象重合,则a 的最小值为( )
A .3
1 B .3 C .6 D .9
11. 函数sin =y x 的图象与tan =y x 的图象在()22
ππ-,上的交点有( ) A .4个 B .3个 C .2个 D .1个
12. 若函数1cos()03
y x λλπ=-->()的最大值与最小值之差为2, 则实数λ的值为( )
A .21
B .1
C .32
D .2
13. 函数()cos f x x x =-的部分图象是( )
A .
B .
C .
D .
14. 已知函数()
f x =()4sin 3
g x a =-
15. 求函数23cos 4sin 4[]33
y x x x ππ=+-∈-,,的最大值和最小值.
【参考答案】
➢
巩固练习 1.
C 2.
A 3.
D 4.
A 5.
C 6.
B
7. C
8. A
9. B
10.C
11.D
12.B
13.D
14.最小正周期为2
3
π
,最大值为2,最小值为-2,是奇函数
15.最大值为1
3
,最小值为
13
4
--
5。
