2017年北京高考理科数学真题及答案
2017北京卷高考理数试题及答案

2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷与答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出得四个选项中,选出符合题目要求得一项。
(1)若集合A={x|–2x1},B={x|x–1或x3},则A B=(A){x|–2x–1} (B){x|–2x3}(C){x|–1x1} (D){x|1x3}(2)若复数(1–i)(a+i)在复平面内对应得点在第二象限,则实数a得取值范围就是(A)(–∞,1)(B)(–∞,–1)(C)(1,+∞)(D)(–1,+∞)(3)执行如图所示得程序框图,输出得s值为(A)2(B)3 2(C)53(D )85(4)若x ,y 满足,则x + 2y 得最大值为(A )1 (B )3 (C )5 (D )9(5)已知函数1(x)33xx f ⎛⎫=- ⎪⎝⎭,则(x)f(A )就是奇函数,且在R 上就是增函数 (B )就是偶函数,且在R 上就是增函数 (C )就是奇函数,且在R 上就是减函数(D )就是偶函数,且在R 上就是减函数(6)设m,n 为非零向量,则“存在负数λ,使得m n λ=”就是“m n 0⋅<”得 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(7)某四棱锥得三视图如图所示,则该四棱锥得最长棱得长度为(A )32 (B )23 (C )22 (D )2(8)根据有关资料,围棋状态空间复杂度得上限M 约为,而可观测宇宙中普通物质得原子总数N 约为、则下列各数中与MN最接近得就是 (参考数据:lg3≈0、48)(A )1033 (B )1053 (C )1073 (D )1093第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2017北京高考真题数学理(含解析)

2017年普通高等学校招生全国统一考试(北京卷)理科数学第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分.1.复数().A.B.C.D.2.若,满足,则的最大值为().A.B.C.D.3.执行如图所示的程序框图,输出的结果为().A.B.C.D.4.设,两个不同的平面,是直线且,“”是“”的().A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.某三棱锥的三视图如图所示,则该三棱锥的表面积是().A.B.C.D.6.设是等差数列,下列结论中正确的是().A.若,则B.若,则C.若,则D.若,则7.如图,函数的图像为折线,则不等式的解集是().A.B.C.D.8.汽车的“燃油效率”是指汽车每消耗升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是().A.消耗升汽油,乙车最多可行驶千米B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C.甲车以千米/小时的速度行驶小时,消耗升汽油D.某城市机动车最高限速千米/小时,相同条件下,在该市用丙车比用乙车更省油第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.在的展开式中,的系数为__________.(用数字作答)10.已知双曲线的一条渐近线为,则__________.11.在极坐标中,点到直线的距离为__________.12.在中,,,,则__________.13.在中,点,满足,.若,则__________.__________.14.设函数①若,则的最小值为__________.②若恰有个零点,则实数的取值范围是__________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知函数.(Ⅰ)求的最小正周期;(Ⅱ)求在区间上的最小值.16.(本小题满分13分),两组各有位病人,他们服用某种药物后的康复时间(单位:天)记录如下:组:,,,,,,组:,,,,,,假设所有病人的康复时间互相独立,从,两组随机各选人,组选出的人记为甲,组选出的人记为乙.(Ⅰ)求甲的康复时间不少于天的概率;(Ⅱ)如果,求甲的康复时间比乙的康复时间长的概率;(Ⅲ)当为何值时,,两组病人康复时间的方差相等?(结论不要求证明).17.(本小题满分14分)如图,在四棱锥中,为等边三角形,平面平面,,,,,为的中点.(Ⅰ)求证:;(Ⅱ)求二面角的余弦值;(Ⅲ)若平面,求的值.18.(本小题满分13分)已知函数.(Ⅰ)求曲线在点处的切线方程;(Ⅱ)求证:当时,;(Ⅲ)设实数使得对恒成立,求的最大值.19.(本小题满分14分)已知椭圆:()的离心率为,点,和点都在椭圆上,直线交轴于点..(Ⅰ)求椭圆的方程,并求点的坐标(用,表示);(Ⅱ)设为原点,点与点关于轴对称,直线交轴于点.问:轴上是否存在点,使得若存在,求点的坐标;若不不存在,说明理由.20.(本小题满分13分)已知数列{}满足,,且.记集合.(Ⅰ)若,写出集合的所有元素;(Ⅱ)若集合存在一个元素是的倍数,证明:的所有元素都是的倍数;(Ⅲ)求集合的元素个数的最大值.2017年普通高等学校招生全国统一考试(北京卷)数学答案(理工类)一、选择题题号 1 2 3 4 5 6 7 8答案A D B B C C C D二、填空题题号9 10 11 12 13 14 答案三、解答题15.解:(Ⅰ)周期.(Ⅱ),,,,最小值为.16.解:(Ⅰ)记甲康复时间不小于天为事件.则,答:甲康复时间不小于天的概率为.(Ⅱ)记甲的康复时间比乙的康复时间长为事件.基本事件空间如下表乙甲短短短长长长长短短短短长长长短短短短短长长短短短短短短长短短短短短短短短短短短短短短短短短短短短短所以.(Ⅲ)或,由于组为公差为的等差数列,所以当或时组也为公差为的等差数列,所以方差一定相等,而方差相等的方程是关于的一个一元二次方程,故最多有两个解,所以只有或两个值.17.(Ⅰ)证明:为等边三角形,为中点,又平面平面,平面平面,平面,.(Ⅱ)以为原点建立如图坐标系,,,,平面的法向量;设平面的法向量,则取又二面角为钝角,二面角的余弦值为.(Ⅲ)平面,,,,解得(舍)或.18.解:(Ⅰ)所以又所以切线方程为,即.(Ⅱ)又因为,所以所以在上是增函数又,故所以.(Ⅲ),设,,,,函数是单调递增,显然成立当时,令,得极值,显然不成立,由此可知最大值为.19.解:(Ⅰ)由题意知,,又,解得,,所以的方程为.的斜率,所以方程,令,解得所以.(Ⅱ),同(I)可得,,,因为所以,设则即,又在椭圆上,所以,即,所以,故存在使得.20.解:(Ⅰ),,.(Ⅱ)若存在是的倍数,设,当时,,也是的倍数;当时,,也是的倍数.综上,是的倍数,依次类推,当时,是的倍数;若存在是的倍数,设,当时,,因为,所以也是的倍数;当时,,因为,所以也是的倍数;.综上,是的倍数,依次类推,当时,是的倍数;所以原结论成立.(Ⅲ)当时,将代入,依次得到,,,,,,,,所以当时,,此时,共个元素.由题意,可取的值有,,,共个元素,显然,不论为何值,必为的倍数,所以,①当时,,此时最多有个元素;②当时,,此时最多有个元素;③当时,,此时最多有个元素;所以集合的元素个数的最大值为.2017年普通高等学校招生全国统一考试(北京卷)数学(理工类)选填解析一、选择题1.【答案】A【解析】解:.故选A.2.【答案】D【解析】解:如图,当,.故选D.3.【答案】B【解析】解:结束,输出.故选B.4.【答案】B【解析】解:不能推出,而,,“”是“”的必要不充分条件.故选B.5.【答案】C【解析】解:由三视图知,面ABC,,,,,,.故选C.6.【答案】C【解析】解:,,所以,.故答案为C.7.【答案】C【解析】解:由题可知:,当时,.时,单调递减,单调递增,当时,,的解集为.故答案选C.8.【答案】D【解析】由图可知,对乙车存在一个速度,使燃油效率高于,A错;由图知,当以的速度行驶时,甲车燃油效率最高,行驶相同路程时,耗油最少,B错;甲车以行驶小时耗油升,故C错在限速,相同情况下,丙车燃油效率较乙车高,所以乙车更省油.故答案选D.二、填空题9.【答案】【解析】解:,当时,系数为.故答案为.10.【答案】【解析】解:令,所以.故答案为.11.【答案】【解析】直线方程为,点为,所以点到直线方程的距离为.故答案为.12.【答案】【解析】解:.故答案为13.【答案】,【解析】解:,所以,.故答案为,.14.【答案】,【解析】解:①当时,,时,,时,,所以;②(I)当时,没有两个零点,(Ⅱ)当时,时,,有一个零点;时,;当,即时,恰有两个零点,所以当时,恰有两个零点;(Ⅲ)当时,时,,有一个零点;时,,,有两个零点,此时有三个零点;(Ⅳ)当时,时,无零点;时,有两个零点,此时有两个零点.综上所述.故答案为,.。
2017年高考北京卷理数试题解析(解析版)

绝密★本科目考试启用前 2017年普通高等学校招生全国统一考试数 学(理)(北京卷)第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合A ={x |–2<x <1},B ={x |x <–1或x >3},则A I B =(A ){x |–2<x <–1} (B ){x |–2<x <3} (C ){x |–1<x <1}(D ){x |1<x <3}【答案】A 【解析】试题分析:利用数轴可知{}21A B x x =-<<-I ,故选A. 【考点】集合的运算【点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示;若集合是无限集合就用描述法表示,并注意代表元素是什么.集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.(2)若复数()()1i i a -+在复平面内对应的点在第二象限,则实数a 的取值范围是(A )(–∞,1) (B )(–∞,–1) (C )(1,+∞) (D )(–1,+∞) 【答案】B【解析】 由()()()()1i i i i 111i a a a a a -+=+-+=++-,则1010a a +<⎧⎨->⎩,即1a <-.故选B【考点】复数的运算【点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.复数z =a +b i 复平面内的点Z (a ,b )(a ,b ∈R ).复数z =a +b i(a ,b ∈R ) 平面向量u u u rOZ . (3)执行如图所示的程序框图,输出的s 值为(A )2(B )32(C )53(D )85【答案】C【解析】当0k =时,03<,执行程序1k =,2s =,13<成立,执行程序2k =,32s =,23<,执行程序3k =,53s =,33>,否输出53s =.故选C.【考点】循环结构【点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化;第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.(4)若x ,y 满足32x x y y x ≤⎧⎪+≥⎨⎪≤⎩,,, 则x + 2y 的最大值为(A )1(B )3 (C )5 (D )9【答案】D【解析】如图,画出可行域,2z x y =+表示斜率为12-的一组平行线,当2z x y =+过点()3,3C 时,目标函数取得最大值max 3239z =+⨯=,故选D.【考点】线性规划【点睛】本题主要考查简单的线性规划.解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义.求目标函数的最值的一般步骤为:一画、二移、三求.常见的目标函数类型有:(1)截距型:形如z ax by =+.求这类目标函数的最值时常将函数z ax by =+转化为直线的斜截式:a z y xb b =-+,通过求直线的截距zb的最值间接求出z 的最值;(2)距离型:形如 ()()22z x a y b =-+-;(3)斜率型:形如y b z x a-=-,而本题属于截距形式. (5)已知函数1()3()3xx f x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数【答案】A 【解析】()()113333xx xx f x f x --⎛⎫⎛⎫-=-=-=- ⎪⎪⎝⎭⎝⎭,所以该函数是奇函数,并且3xy =是增函数,13xy ⎛⎫= ⎪⎝⎭是减函数,根据增函数−减函数=增函数,可知该函数是增函数,故选A. 【考点】函数的性质【点睛】本题属于基础题型,根据()f x -与()f x 的关系就可以判断出函数的奇偶性,判断函数单调性的方法:(1)利用平时学习过的基本初等函数的单调性;(2)利用函数图象判断函数的单调性;(3)利用函数的四则运算判断函数的单调性,如:增函数+增函数=增函数,增函数−减函数=增函数;(4)利用导数判断函数的单调性.(6)设m ,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的 (A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件【答案】A【解析】 若0λ∃<,使λ=m n ,即两向量方向相反,夹角为180o ,若0⋅<m n ,也可能夹角为(90,180⎤⎦oo,方向并不一定相反,故不一定存在.故选A.【考点】向量,充分必要条件【点睛】判断充分必要条件的的方法:(1)根据定义,若,p q q p ⇒≠>,那么p 是q 的充分不必要条件,同时q 是p 的必要不充分条件;若p q ⇔,那么p ,q 互为充要条件;若,p q q p ≠>≠>,那么就是既不充分也不必要条件.(2)当命题是以集合形式给出时,那就看包含关系,已知:,p x A ∈:q x B ∈,若A B ≠⊂,那么p 是q 的充分不必要条件,同时q 是p 的必要不充分条件;若A B =,那么p ,q 互为充要条件;若没有包含关系,那么就是既不充分也不必要条件.(3)命题的等价性,根据互为逆否命题的两个命题等价,将p 是q 条件的判断,转化为q ⌝是p ⌝条件的判断. (7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A )2 (B )3(C )2(D )2【答案】B【解析】 几何体四棱锥如图所示,最长棱为正方体的体对角线,即22222223l =++=. 故选B.【考点】三视图【点睛】本题考查了空间想象能力,由三视图还原几何体的方法:或者也可根据三视图的形状,将几何体的顶点放在正方体或长方体里面,便于分析问题.(8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是(参考数据:lg3≈0.48)(A )1033 (B )1053 (C )1073 (D )1093 【答案】D【解析】 设36181010M x N ==,两边取对数36180lg lg 3lg10361lg 380x =-=-,即93.28x =,所以接近9310.故选D.【考点】对数运算【点睛】本题考查了转化与化归能力,本题以实际问题的形式给出,但本质就是对数的运算关系,以及指数与对数运算的关系,难点是令36180310x =,并想到两边同时取对数进行求解,对数运算公式包含log log log a a a M N MN +=,log log log a a aM M N N-=,log log na a M n M =.第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2017年高考真题——数学(理)(北京卷)+Word版含解析(参考版)

y2 = 1 的离心率为 3 m
则实数 m=_________.
1+ m = 3⇒m=2 1
10 若等差数列 {an } 和等比数列 {bn } 满足 a1=b1=–1
a4=b4=8
则
a2 =_______. b2
答案
解析
1
−1 + 3d = − q 3 = 8 ⇒ d = 3, q = −2 ⇒
a2 −1 + 3 = =1 b2 −1× (−2)
解得
因为对
的点在第二象限
所
a + 1 < 0 1 − a > 0
a < −1
故选 B. 输出的 s 值为
3 执行如 所示的程序框
-1-
A 2 答案 C 解析
B
3 2
C
5 3
D
8 5
k = 0 时 0 < 3 成立 第一次进入循环 k = 1, s =
入循环 k = 2, s =
2 +1 3 = 2 2
点 P 的坐标为 1,0
11 在极坐标系中 点 A 在圆 ρ 2 − 2 ρ cos θ − 4 ρ sin θ + 4 = 0 则|AP|的最小值为__________ห้องสมุดไป่ตู้. 答案 1 解 析
C : x 2 + y 2 − 2 x − 4 y + 4 = 0 ⇒ ( x − 1) 2 + ( y − 2) 2 = 1
B {x|–2 D {x|1
A I B = { x −2 < x < −1}
故选 A.
2 若复数 1–i A C –∞ 1 1 +∞
a+i 在复 面内对 的点在第二象限 则实数 a 的取值范围是 B D –∞ –1 –1 +∞
2017年高考真题答案及解析:理科数学(北京卷)

2017年普通高等学校招生全国考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本市卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合{}21A x x =-<<,{}13B x x x =<->或,则A B =( )。
(A ){}21x x -<<- (B ){}23x x -<< (C ){}11x x -<< (D ){}13x x <<【答案】A【难度】容易【点评】本题在高考数学(理)提高班讲座 第一章《集合》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是( )。
(A )(),1-∞i (B )(),1-∞-(C )()1,+∞(D )(1,)-+∞【答案】B【难度】容易【点评】本题在高二数学(理)下学期课程讲座 第四章《复数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(3)执行如图所示的程序框图,输出的s 值为( )。
(A)2(B)3 2(C)5 3(D)8 5【答案】C【难度】容易【点评】本题在高考数学(理)提高班讲座第十三章《算法与统计》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(4)若,x y满足3,2,,xx yy x≤⎧⎪+≥⎨⎪≤⎩则2x y+的最大值为()。
(A)1(B)3(C)5(D)9 【答案】D【难度】容易【点评】本题在高考数学(理)提高班讲座 第二章《函数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(5)已知函数()133xx f x ⎛⎫=- ⎪⎝⎭,则()f x ( )。
(A )是奇函数,且在R 上是增函数(B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数【答案】A【难度】中等【点评】本题在高考数学(理)提高班讲座 第三章《函数的性质及其应用》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
2017年普通高等学校招生全国统一考试数学试题理(北京卷,附解析)

绝密★本科目考试启用前2017年普通高等学校招生全国统一考试数学(理)(北京卷)【试卷点评】2017年北京高考数学试卷,试卷内容上体现新课程理念,贴近中学数学教学,坚持对基础知识、基本技能以及数学思想方法的考查。
我先说一说2017年总体试卷的难度,2017年文科也好、理科也好,整个试卷难度较2015、2016年比较平稳,北京高考应该是从2014年以前和2014年以后,2015、2016年卷子难度都比较低,今年延续了前两年,整体难度比较低。
今天我说卷子简单在于第8题和第14题,难度下降了,相比2014、2015、2016,整体都下降了。
1.体现新课标理念,实现平稳过渡。
试卷紧扣北京考试大纲,新增内容的考查主要是对基本概念、基本公式、基本运算的考查,难度不大。
对传统内容的考查在保持平稳的基础上进行了适度创新,符合北京一贯的风格。
2.关注通性通法,试卷淡化了特殊的技巧,全面考查通性通法,体现了以知识为载体,以方法为依托,题目没有偏怪题,以能力考查为目的的命题要求。
3.体现数学应用,联系实际,例如理科第17 题考查了样本型的概率问题,第三问要求不必证明、直接给出结论(已经连续6年),需注重理解概念的本质原理,第8 题本着创新题的风格,结合生活中的实际模型进行考查,像14 年的成绩评定、15 年的汽车燃油问题,都是由生活中的实际模型转化来的,对推动数学教学中关注身边的数学起到良好的导向。
【试卷解析】本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合A={x|–2<x<1},B={x|x<–1或x>3},则A B=(A){x|–2<x<–1} (B){x|–2<x<3}(C){x|–1<x<1} (D){x|1<x<3}【解析】试题分析:利用数轴可知{}21A B x x =-<<-,故选A.【考点】集合的运算【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示,若集合是无限集合就用描述法表示,注意代表元素是什么,集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.(2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是 (A )(–∞,1) (B )(–∞,–1) (C )(1,+∞) (D )(–1,+∞) 【答案】B【考点】复数的运算【名师点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.复数z =a +b i复平面内的点Z (a ,b )(a ,b ∈R ).复数z =a +b i(a ,b ∈R ) 平面向量OZ .(3)执行如图所示的程序框图,输出的s 值为(A )2 (B )32(C )53(D )85【考点】循环结构【名师点睛】解决此类型时要注意:第一,要明确是当型循环结构,还是直到型循环结构.根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化;第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.(4)若x,y满足32xx yy x≤⎧⎪+≥⎨⎪≤⎩,,,则x + 2y的最大值为(A)1 (B)3 (C)5 (D)9 【答案】D【解析】试题分析:如图,画出可行域,2z x y=+表示斜率为12-的一组平行线,当过点()3,3C时,目标函数取得最大值max3239z=+⨯=,故选D.【考点】线性规划【名师点睛】本题主要考查简单线性规划.解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义;求目标函数的最值的一般步骤为:一画二移三求.其关键是准确作出可行域,理解目标函数的意义.常见的目标函数有:(1)截距型:形如z ax by =+.求这类目标函数的最值常将函数z ax by =+转化为直线的斜截式:a z y x b b =-+,通过求直线的截距zb的最值间接求出z 的最值;(2)距离型:形如()()22z x a y b =-+- ;(3)斜率型:形如y b z x a-=-,而本题属于截距形式. (5)已知函数1()3()3xx f x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数【答案】A 【解析】试题分析:()()113333xx x x f x f x --⎛⎫⎛⎫-=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以函数是奇函数,并且3x 是增函数,13x⎛⎫⎪⎝⎭是减函数,根据增函数-减函数=增函数,所以函数是增函数,故选A. 【考点】函数的性质【名师点睛】本题属于基础题型,根据奇偶性的定义()f x -与()f x 的关系就可以判断函数的奇偶性,判断函数单调性的方法,1.平时学习过的基本初等函数的单调性;2.函数图象判断函数的单调性;3.函数的四则运算判断,增函数+增函数=增函数,增函数-减函数=增函数,判断函数的单调性;4.导数判断函数的单调性. (6)设m ,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件【答案】A【考点】1.向量;2.充分必要条件.【名师点睛】判断充分必要条件的的方法:1.根据定义,若,p q q p ⇒≠>,那么p 是q 的充分不必要 ,同时q 是p 的必要不充分条件,若p q ⇔,那互为充要条件,若p q <≠>,那就是既不充分也不必要条件,2.当命题是以集合形式给出时,那就看包含关系,若:,:p x A q x B ∈∈,若A B ≠⊂,那么p 是q 的充分必要条件,同时q 是p 的必要不充分条件,若A B =,互为充要条件,若没有包含关系,就是既不充分也不必要条件,3.命题的等价性,根据互为逆否命题的两个命题等价,将p 是q 条件的判断,转化为q ⌝是p ⌝条件的判断. (7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A )(B )(C ) (D )2 【答案】B 【解析】试题分析:几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l == B. 【考点】三视图【名师点睛】本题考查了空间想象能力,由三视图还原几何体的方法:或者也可根据三视图的形状,将几何体的顶点放在正方体或长方体里面,便于分析问题.(8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是(参考数据:lg3≈0.48)(A )1033 (B )1053 (C )1073(D )1093【答案】D 【解析】试题分析:设36180310M x N == ,两边取对数,36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,即MN最接近9310,故选D. 【考点】对数运算【名师点睛】本题考查了转化与化归能力,本题以实际问题的形式给出,但本质就是对数的运算关系,以及指数与对数运算的关系,难点是36180310x =时,两边取对数,对数运算公式包含log log log a a a M N MN +=,log log log a a aM M N N-=,log log na a M n M =. 第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2017高考理科数学试题与解析(北京卷)

2017年普通高等学校招生全国考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本市卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合{}21A x x =-<<,{}13B x x x =<->或,则A B =( )。
(A ){}21x x -<<- (B ){}23x x -<< (C ){}11x x -<< (D ){}13x x << 【答案】A【难度】容易(2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是( )。
(A )(),1-∞i (B )(),1-∞-(C )()1,+∞(D )(1,)-+∞ 【答案】B 【难度】容易(3)执行如图所示的程序框图,输出的s 值为( )。
(A)2(B)3 2(C)5 3(D)8 5【答案】C 【难度】容易(4)若,x y满足3,2,,xx yy x≤⎧⎪+≥⎨⎪≤⎩则2x y+的最大值为()。
(A)1(B)3(C)5(D)9 【答案】D【难度】容易(5)已知函数()133xx f x ⎛⎫=- ⎪⎝⎭,则()f x ( )。
(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数 【答案】A 【难度】中等(6)设,m n 为非零向量,则“存在负数λ,使得m n λ=”是“0m n ⋅<”的( )。
(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件 【答案】A 【难度】容易(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )。
2017年高考真题答案及解析:理科数学(北京卷)

2017年普通高等学校招生全国考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本市卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合{}21A x x =-<<,{}13B x x x =<->或,则A B =( )。
(A ){}21x x -<<- (B ){}23x x -<< (C ){}11x x -<< (D ){}13x x <<【答案】A【难度】容易【点评】本题在高考数学(理)提高班讲座 第一章《集合》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是( )。
(A )(),1-∞i (B )(),1-∞-(C )()1,+∞(D )(1,)-+∞【答案】B【难度】容易【点评】本题在高二数学(理)下学期课程讲座 第四章《复数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(3)执行如图所示的程序框图,输出的s 值为( )。
(A)2(B)3 2(C)5 3(D)8 5【答案】C【难度】容易【点评】本题在高考数学(理)提高班讲座第十三章《算法与统计》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(4)若,x y满足3,2,,xx yy x≤⎧⎪+≥⎨⎪≤⎩则2x y+的最大值为()。
(A)1(B)3(C)5(D)9 【答案】D【难度】容易【点评】本题在高考数学(理)提高班讲座 第二章《函数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(5)已知函数()133xx f x ⎛⎫=- ⎪⎝⎭,则()f x ( )。
(A )是奇函数,且在R 上是增函数(B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数【答案】A【难度】中等【点评】本题在高考数学(理)提高班讲座 第三章《函数的性质及其应用》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
2017年高考北京卷理科数学试题及答案解析

解:(I)设 交点为 ,连接 .
因为 平面 ,平面 平面 ,所以 .
因为 是正方形,所以 为 的中点,所以 为 的中点.
(II)取 的中点 ,连接 , .
因为 ,所以 .
又因为平面 平面 ,且 平面 ,所以 平面 .
因为 平面 ,所以 .
因为 是正方形,所以 .
平面 的法向量为 ,所以 .
由题知二面角 为锐角,所以它的大小为 .
(Ⅱ)若a=7,求△ABC的面积.
(16)(本小题14分)
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD= ,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
红色线为三视图还原后的几何体,最长的棱长为正方体的对角线, ,故选B.
(8)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与 最接近的是
(参考数据:lg3≈0.48)
(A)1033(B)1053
(C)1073(D)1093
【答案】D
【答案】A
【解析】
试题分析:若 ,使 ,即两向量反向,夹角是 ,那么 T,若 ,那么两向量的夹角为 ,并不一定反向,即不一定存在负数 ,使得 ,所以是充分不必要条件,故选A.
(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为
(A)3 (B)2 (C)2 (D)2
【答案பைடு நூலகம்B
【解析】
试题分析:几何体是四棱锥,如图
(Ⅰ)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
【数学】2017年高考真题——北京卷(理)(解析版)
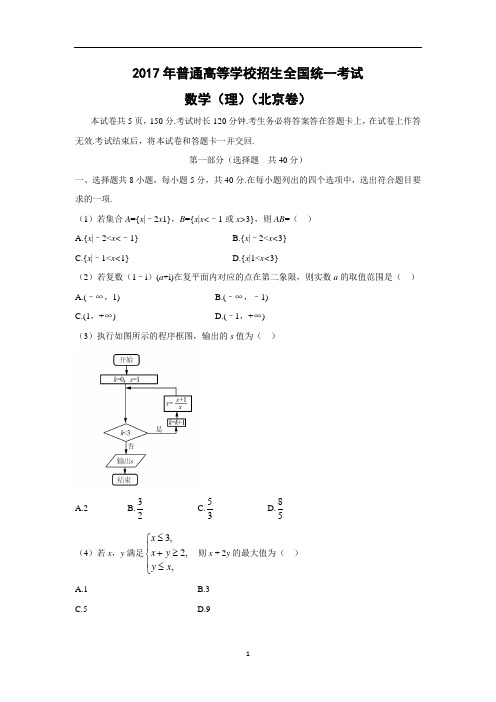
2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)若集合A ={x |–2x 1},B ={x |x<–1或x>3},则AB =( ) A.{x |–2<x<–1} B.{x |–2<x<3} C.{x |–1<x<1}D.{x |1<x<3}(2)若复数(1–i )(a +i)在复平面内对应的点在第二象限,则实数a 的取值范围是( ) A.(–∞,1) B.(–∞,–1) C.(1,+∞)D.(–1,+∞)(3)执行如图所示的程序框图,输出的s 值为( )A.2B.32C.53D.85(4)若x ,y 满足3,2,,x x y y x ≤⎧⎪+≥⎨⎪≤⎩则x + 2y 的最大值为( )A.1B.3C.5D.9(5)已知函数()133xx f x ⎛⎫=- ⎪⎝⎭,则f (x )( )A.是奇函数,且在R 上是增函数B.是偶函数,且在R 上是增函数C.是奇函数,且在R 上是减函数D.是偶函数,且在R 上是减函数(6)设m ,n 为非零向量,则“存在负数λ,使得m =λn ”是“m ·n <0”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )D.2(8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN最接近的是( ) (参考数据:lg3≈0.48)A.1033B.1053C.1073D.1093第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.(9)若双曲线221y x m-=m =_______________. (10)若等差数列{}n a 和等比数列{}n b 满足a 1=b 1=–1,a 4=b 4=8,则22a b =__________. (11)在极坐标系中,点A 在圆22cos 4sin 40ρρθρθ--+=,点P 的坐标为(1,0),则|AP |的最小值为.(12)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若1sin 3α=,cos()αβ-=. (13)能够说明“设a ,b ,c 是任意实数.若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为______________________________.(14)三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点A i 的横、纵坐标分别为第i 名工人上午的工作时间和加工的零件数,点B i 的横、纵坐标分别为第i 名工人下午的工作时间和加工的零件数,i =1,2,3.①记Q 1为第i 名工人在这一天中加工的零件总数,则Q 1,Q 2,Q 3中最大的是_________. ②记p i 为第i 名工人在这一天中平均每小时加工的零件数,则p 1,p 2,p 3中最大的是_________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题13分) 在△ABC 中,A ∠=60°,c =37a . (Ⅰ)求sin C 的值; (Ⅱ)若a =7,求△ABC 的面积.(16)(本小题14分)如图,在四棱锥P-ABCD 中,底面ABCD 为正方形,平面P AD ⊥平面ABCD ,点M 在线段PB 上,PD//平面MAC ,P A =PD AB =4.(I)求证:M为PB的中点;(II)求二面角B-PD-A的大小;(III)求直线MC与平面BDP所成角的正弦值.(17)(本小题13分)为了研究一种新药的疗效,选100名患者随机分成两组,每组个50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“·”表示服药者,“+”表示为服药者.(Ⅰ)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;(Ⅱ)从图中A,B,C,D,四人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);(Ⅲ)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)(18)(本小题14分)已知抛物线C:y2=2px过点P(1,1).过点(0,12)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点. (Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;(Ⅱ)求证:A为线段BM的中点.(19)(本小题13分)已知函数f(x)=e x cos x−x.(Ⅰ)求曲线y= f(x)在点(0,f(0))处的切线方程;(Ⅱ)求函数f (x )在区间[0,2π]上的最大值和最小值.(20)(本小题13分)设{a n }和{b n }是两个等差数列,记c n =max{b 1–a 1n ,b 2–a 2n ,…,b n –a n n }(n =1,2,3,…), 其中max{x 1,x 2,…,x s }表示x 1,x 2,…,x s 这s 个数中最大的数.(Ⅰ)若a n =n ,b n =2n –1,求c 1,c 2,c 3的值,并证明{c n }是等差数列; (Ⅱ)证明:或者对任意正数M ,存在正整数m ,当n ≥m 时,nc M n>;或者存在正整数m ,使得c m ,c m +1,c m +2,…是等差数列.参考答案:一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)【答案】A【解析】{}21A B x x =-<<- ,故选A. (2)【答案】B【解析】()()()()1i i 11i z a a a =-+=++-,因为对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得:1a <-,故选B. (3)【答案】C【解析】0k =时,03<成立,第一次进入循环111,21k s +===,13<成立,第二次进入循环,2132,22k s +===,23<成立,第三次进入循环31523,332k s +===,33<, 否,输出53s =,故选C.(4)【答案】D【解析】如图,画出可行域,2z x y =+表示斜率为12-的一组平行线,当过点()3,3C 时,目标函数取得最大值ma x 3239z =+⨯=,故选D.(5)【答案】A【解析】()()113333x xx x f x f x --⎛⎫⎛⎫-=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以函数是奇函数,并且3x 是增函数,13x⎛⎫ ⎪⎝⎭是减函数,根据增函数-减函数=增函数,所以函数是增函数,故选A. (6)【答案】A【解析】若0λ∃<,使λ=m n ,即两向量反向,夹角是0180, 那么0cos1800⋅==-<m n m n m n ,反过来,若0⋅<m n ,那么两向量的夹角为(0090,180⎤⎦ ,并不一定反向,即不一定存在负数λ,使得λ=m n ,所以是充分不必要条件,故选A. (7)【答案】B【解析】几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l ==,故选B.(8)【答案】D【解析】设36180310M x N == ,两边取对数,36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,即MN最接近9310,故选D. 二、填空题共6小题,每小题5分,共30分. (9)【答案】22m ==. (10)【答案】1【解析】322131383,211(2)a d q d qb -+-+=-=⇒==-⇒==-⨯-. (11)【答案】1【解析】2222:2440(1)(2)1C x y x y x y +--+=⇒-+-= , 所以min ||||211AP AC r =-=-=. (12)【答案】79- 【解析】222sin sin ,cos cos cos()cos cos sin sin cos sin 2sin 179==-∴-=+=-+=-=-βαβααβαβαβααα(13)【答案】-1,-2,-3【解析】123,1(2)3->->--+-=-. (14)【答案】1Q ;2.p三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)解:(1)根据正弦定理×sin 33=sin ==sin60==sin sin 77。
2017年高考真题——北京卷理科标准答案

2017年普通高等学校招生全国统一考试(北京卷)理科数学1. 解析画出数轴图如图所示,则{}21A B x x =-<<-I .故选A.2. 解析 由()()()()1i i i i 111i a a a a a -+=+-+=++-,则1010a a +<⎧⎨->⎩,即1a <-.故选B.3. 解析 当0k =时,03<,执行程序1k =,2s =,13<成立,执行程序2k =,32s =,23<,执行程序3k =,53s =,33>,否输出53s =.故选C. 4. 解析 作出不等式组的可行区域,如图所示,令2z x y =+,则22x zy -=+当过A 点时z ,()3,3A ,故369z =+=.故选D.5. 解析 由题知()133x x f x ⎛⎫=- ⎪⎝⎭,()()113333xx x x f x f x --⎛⎫-=-=-=- ⎪⎝⎭,又因为3x 是增函数,13x⎛⎫- ⎪⎝⎭也是增函数,故()f x 是R 上增函数.故选A. 6. 解析 若0λ∃<,使λ=m n ,即两向量方向相反,夹角为180o ,若0⋅<m n ,也可能夹角为(90,180⎤⎦oo,方向并不一定相反,故不一定存在.故选A.7. 解析几何体四棱锥如图所示,最长棱为正方体的体对角线,即l ==. 故选B.31-1-28. 解析 设36181010M x N ==,两边取对数36180lg lg 3lg10361lg 380x =-=-,即93.28x =,所以接近9310.故选D. 9. 解析由题知1=2m =. 10. 解析 由11a =-,48a =,则21132a a d =+=-+=,由11b =-,48b =,则2q =-,则212b b q ==.故22212a b ==. 11. 解析 由22cos 4sin 40ρρθρθ--+=,化为普通方程为222440x y x y +--+=, 即()()22121x y -+-=,由圆心为()1,2,P 为()1,0,则AP 最小值为1.故选D.12. 解析 由题画出图形,1sin 3α=,则cos 3α=,由于α与β关于y 轴对称, 则()1sin sin 3βα=π-=,cos 3β=-,故()117cos 339αβ⎛-=+⨯=- ⎝⎭.13. 解析 由题知,取一组特殊值,例1a =-,2b =-,3c =-.14. 解析 联结11A B ,22A B ,33A B 比较三者中点终坐标的大小,所以第一位选1Q ,分别作1B ,2B ,3B 关于原点的对称点1B ',2B ',3B ',比较直线11A B ',22A B ',33A B '斜率大小,可得22A B '最大.故填2p . 15. 解析 (1)在ABC △中,因为60A ∠=o ,37c a =,所以由正弦定理得sin 3sin 7c A C a ===. (2)因为7a =,所以3737c =⨯=. 由余弦定理2222cos a b c bc A =+-得222173232b b =+-⨯⨯, 解得8b =或5b =-(舍). 所以ABC △的面积11sin 8322S bc A ==⨯⨯=16.解析 (1)设,AC BD 交点为E ,联结ME .因为PD ∥平面MAC ,平面MAC I 平面PBD ME =,所以PD ME ∥. 因为ABCD 是正方形,所以E 为BD 的中点,所以M 为PB 的中点.(2)取AD 的中点O ,联结OP ,OE . 因为PA PD =,所以OP AD ⊥.又因为平面PAD ⊥平面ABCD ,且OP ⊂平面PAD ,所以OP ⊥平面ABCD . 因为OE ⊂平面ABCD ,所以OP OE ⊥. 因为ABCD 是正方形,所以OE AD ⊥.如图建立空间直角坐标系O xyz -,则P ,(2,0,0)D ,(2,4,0)B -,(4,4,0)BD =-u u u r,(2,0,PD =u u u r.设平面BDP 的法向量为(,,)x y z =n ,则00BD PD ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n,即44020x y x -=⎧⎪⎨=⎪⎩. 令1x =,则1y =,z =于是=n .平面PAD 的法向量为(0,1,0)=p ,所以1cos ,||||2⋅==<>n p n p n p .由题知二面角B PD A --为锐角,所以它的大小为3π.(3)由题意知(1,2,2M -,(2,4,0)D,(3,2,2MC =-u u u u r . 设直线MC 与平面BDP 所成角为α,则sin cos ,9MC MC MCα⋅===u u u u ru u u u ru u u u r <>n n n . 所以直线MC 与平面BDP. 17解析 (1)由图知,在服药的50名患者中,指标y 的值小于60的有15人, 所以从服药的50名患者中随机选出一人,此人指标y 的值小于60的概率为150.350=. (2)由图知,A ,B ,C ,D 四人中,指标x 的值大于1.7的有2人:A 和C .O A BC DEMP所以ξ的所有可能取值为0,1,2.2224C 1(0)C 6P ξ===,112224C C 2(1)C 3P ξ===,2224C 1(2)C 6P ξ===. 所以ξ的分布列为故ξ的期望()0121636E ξ=⨯+⨯+⨯=.(3)在这100名患者中,服药者指标y 数据的方差大于未服药者指标y 数据的方差. 18.解析 (1)由抛物线2:2C y px =过点()1,1P ,得12p =. 所以抛物线C 的方程为2y x =. 抛物线C 的焦点坐标为1,04⎛⎫⎪⎝⎭,准线方程为14x =-.(2)由题意,设直线l 的方程为()102y kx k =+≠,l 与抛物线C 的交点为11(,)M x y ,22(,)N x y . 由212y kx y x⎧=+⎪⎨⎪=⎩,得224(44)10k x k x +-+=.则1221k x x k -+=,12214x x k =.因为点P 的坐标为()1,1,所以直线OP 的方程为y x =,点A 的坐标为11(,)x y . 直线ON 的方程为22y y x x =,点B 的坐标为2112,y x x x ⎛⎫ ⎪⎝⎭. 因为21122112112222y x y x y x x x y x x x +-+-=122112211222kx x kx x x x x ⎛⎫⎛⎫+++- ⎪ ⎪⎝⎭⎝⎭== ()()121221222k x x x x x -++()2221122420k k k k x --⨯+==,所以211122y x y x x +=. 故A 为线段BM 的中点.19.解析 (1)因为()e cos x f x x x =-,所以()e (cos sin )1x f x x x '=--,(0)0f '=. 又因为(0)1f =,所以曲线()y f x =在点(0,(0))f 处的切线方程为1y =.(2)设()e (cos sin )1x h x x x =--,则()e (cos sin sin cos )2e sin x x h x x x x x x '=---=-.当π0,2x ⎛⎫∈ ⎪⎝⎭时,()0h x '<,所以()h x 在区间π0,2⎡⎤⎢⎥⎣⎦上单调递减. 所以对任意π0,2x ⎛⎤∈ ⎥⎝⎦有()(0)0h x h <=,即()0f x '<.所以函数()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上单调递减.因此()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为(0)1f =,最小值为ππ22f ⎛⎫=- ⎪⎝⎭.20.解析 (1)111110c b a =-=-=,{}{}21122max 2,2max 121,3221c b a b a =--=-⨯-⨯=-,{}{}3112233max 3,3,3max 131,332,5332c b a b a b a =---=-⨯-⨯-⨯=-. 当3n …时,()()()()111120k k k k k k k k b na b na b b n a a n ++++---=---=-<, 所以k k b na -关于*k ∈N 单调递减.所以{}112211max ,,,1n n n c b a n b a n b a n b a n n =---=-=-L .所以对任意1n …,1n c n =-,于是11n n c c +-=-, 所以{}n c 是等差数列.(2)设数列{}n a 和{}n b 的公差分别为12,d d ,则()[]()()121111211(1)1k k b na b k d a k d n b a n d nd k -=+--+-=-+--. 所以()()11212111211,,n b a n n d nd d nd c b a n d nd ⎧-+-->⎪=⎨-⎪⎩当时当时„.①当10d >时,取正整数21d m d >,则当n m …时,12nd d >,因此11n c b a n =-. 此时,12,,,m m m c c c ++L 是等差数列.②当10d =时,对任意1n …, (){}(){}()11211211max ,01max ,0n c b a n n d b a n d a =-+-=-+--.此时,123,,,,,n c c c c L L 是等差数列. ③当10d <时, 当21d n d >时,有12nd d <. 所以()()()11211211121n b a n n d nd c b d n d d a d n n n-+---==-+-++… ()111212||n d d a d b d -+-+--.对任意正数M ,取正整数12112211||max ,M b d a d d d m d d ⎧⎫+-+-->⎨⎬-⎩⎭,故当n m …时,nc M n>.。
2017年北京理数高考真题(含答案)

2017年北京理数高考真题(含答案)绝密★本科目考试启用前2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合A={x|–2x1},B={x|x–1或x3},则A B=(A){x|–2x–1} (B){x|–2x3}(C){x|–1x1} (D){x|1x3}(2)若复数(1–i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是(A)(–∞,1)(B)(–∞,–1)(C)(1,+∞)(D)(–1,+∞)(3)执行如图所示的程序框图,输出的s值为(A )2 (B )32(C )53(D )85(4)若x ,y 满足32x x y y x ≤⎧⎪+≥⎨⎪≤⎩,,, 则x + 2y 的最大值为(A ) 1(B )3(C)5(D )9 (5)已知函数1()3()3x xf x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数(6)设m,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的(A )充分而不必要条件 (B )必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A)2(B)3(C)2(D)2(8)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约最接近的是为1080.则下列各数中与MN(参考数据:lg3≈0.48)(A)1033(B)1053(C)1073(D)1093第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
2017年高考北京卷理数试题(Word版含答案)

2017年高考北京卷理数试题(Word版含答案)绝密★本科目考试启用前2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
中/华-资*源%库(1)若集合A={x|-2x1},B={x|x-1或x3},则AB=(A){x|-2x-1} (B){x|-2x3}(C){x|-1x1} (D){x|1x3}(2)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是(A)(-∞,1)(B)(-∞,-1)(C)(1,+∞)(D)(-1,+∞)(3)执行如图所示的程序框图,输出的s值为(A)2 (B)(C)(D)(4)若x,y满足则x + 2y的最大值为(A)1 (B)3(C)5 (D)9(5)已知函数,则(A)是奇函数,且在R上是增函数(B)是偶函数,且在R上是增函数(C)是奇函数,且在R上是减函数(D)是偶函数,且在R上是减函数(6)设m,n为非零向量,则"存在负数,使得"是""的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A)3 (B)2 (C)2 (D)2(8)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg3≈0.48)(A)1033 (B)1053(C)1073 (D)1093第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
(9)若双曲线的离心率为,则实数m=_________.(10)若等差数列和等比数列满足a1=b1=-1,a4=b4=8,则=_______.(11)在极坐标系中,点A在圆上,点P的坐标为(1,0),则|AP|的最小值为___________.(12)在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若,则=___________.(13)能够说明"设a,b,c是任意实数.若a>b>c,则a+b>c"是假命题的一组整数a,b,c的值依次为______________________________.(14)三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.①记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是_________.②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1,p2,p3中最大的是_________.三、解答题共6小题,共80分。
2017年高考北京理科数学试题及答案(word解析版)(完整资料).doc

此文档下载后即可编辑2017年普通高等学校招生全国统一考试(北京卷)数学(理科)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项. (1)【2017年北京,理1,5分】若集合–21{|}A x x =<<,–1{|}3B x x x =<>或,则A B I =( )(A )1|}–2{x x <<- (B )3|}–2{x x << (C )1|}–1{x x << (D )3|}1{x x <<【答案】A【解析】{}21A B x x =-<<-I ,故选A . (2)【2017年北京,理2,5分】若复数()()1i i a -+在复平面内对应的点在第二象限,则实数a 的取值范围是( ) (A )(),1-∞ (B )(),1-∞- (C )()1,+∞ (D )()1,-+∞【答案】B【解析】()()()()1i i 11i z a a a =-+=++-,因为对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得:1a <-,故选B .(3)【2017年北京,理3,5分】执行如图所示的程序框图,输出的s 值为( ) (A )2(B )32(C )53(D )85【答案】C 【解析】0k =时,03<成立,第一次进入循环111,21k s +===,13<成立,第二次进入循环,2132,22k s +===,23<成立,第三次进入循环31523,332k s +===,33< 否,输出53s =,故选C .(4)【2017年北京,理4,5分】若x ,y 满足32x x y y x ≤⎧⎪+≥⎨⎪≤⎩,,, 则2x y +的最大值为( )(A )1 (B )3 (C )5 (D )9 【答案】D【解析】如图,画出可行域,2z x y =+表示斜率为12-的一组平行线,当过点()3,3C 时,目标函数取得最大值max 3239z =+⨯=,故选D .(5)【2017年北京,理5,5分】已知函数1()3()3x x f x =-,则()f x ( )(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数 【答案】A【解析】()()113333xx xx f x f x --⎛⎫⎛⎫-=-=-=- ⎪⎪⎝⎭⎝⎭,所以函数是奇函数,并且3x 是增函数,13x⎛⎫⎪⎝⎭是减函数,根据增函数-减函数=增函数,所以函数是增函数故选A .(6)【2017年北京,理6,5分】设m ,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的( )(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件【答案】A【解析】若0λ∃<,使m n λ=r r,即两向量反向,夹角是0180,那么cos1800m n m n m n ⋅==-<r r r r r r ,反过来,若0m n ⋅<r r,那么两向量的夹角为(0090,180⎤⎦ ,KS5U 并不一定反向,即不一定存在负数λ,使得λ=m n ,所以是充分不必要条件,故选A .(7)【2017年北京,理7,5分】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )(A )32 (B )23 (C )22 (D )2【答案】B【解析】几何体是四棱锥,如图,红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,22222223l =++=,故选B .(8)【2017年北京,理8,5分】根据有关资料,围棋状态空间复杂度的上限M 约为3613,而可观测宇宙中普通物质的原子总数N 约为8010.则下列各数中与MN最接近的是( )(参考数据:30.48lg ≈)(A )3310 (B )5310 (C )7310 (D )9310 【答案】D【解析】设36180310M x N == ,两边取对数,36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,即M N最接近9310,故选D .第二部分(非选择题 共110分)二、填空题:共6小题,每小题5分,共30分。
【数学】2017年高考真题——北京卷(理)(解析版)
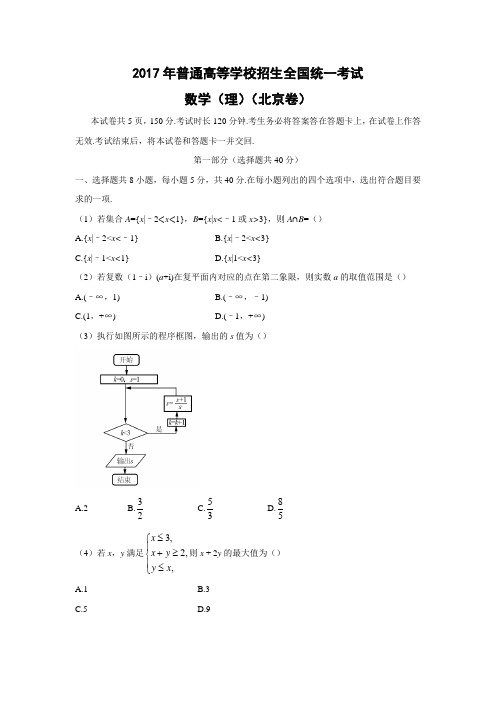
2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)若集合A ={x |–2<x <1},B ={x |x<–1或x>3},则A ∩B =() A.{x |–2<x<–1} B.{x |–2<x<3} C.{x |–1<x<1}D.{x |1<x<3}(2)若复数(1–i )(a +i)在复平面内对应的点在第二象限,则实数a 的取值范围是() A.(–∞,1) B.(–∞,–1) C.(1,+∞)D.(–1,+∞)(3)执行如图所示的程序框图,输出的s 值为()A.2B.32C.53D.85(4)若x ,y 满足3,2,,x x y y x ≤⎧⎪+≥⎨⎪≤⎩则x + 2y 的最大值为()A.1B.3C.5D.9(5)已知函数()1 33x xf x⎛⎫=- ⎪⎝⎭,则f(x)()A.是奇函数,且在R上是增函数B.是偶函数,且在R上是增函数C.是奇函数,且在R上是减函数D.是偶函数,且在R上是减函数(6)设m,n为非零向量,则“存在负数,使得m=λn”是“m·n<0”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()D.2(8)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是()(参考数据:lg3≈0.48)A.1033B.1053C.1073D.1093第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.(9)若双曲线m=_______________.λMN221yxm-=(10)若等差数列和等比数列满足a 1=b 1=–1,a 4=b 4=8,则=__________. (11)在极坐标系中,点A 在圆,点P 的坐标为(1,0),则|AP |的最小值为.(12)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若,=. (13)能够说明“设a ,b ,c 是任意实数.若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为______________________________.(14)三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点A i 的横、纵坐标分别为第i 名工人上午的工作时间和加工的零件数,点B i 的横、纵坐标分别为第i 名工人下午的工作时间和加工的零件数,i =1,2,3.①记Q 1为第i 名工人在这一天中加工的零件总数,则Q 1,Q 2,Q 3中最大的是_________. ②记p i 为第i 名工人在这一天中平均每小时加工的零件数,则p 1,p 2,p 3中最大的是_________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题13分) 在△ABC 中,=60°,c =a . (Ⅰ)求sin C 的值; (Ⅱ)若a =7,求△ABC 的面积.{}n a {}n b 22a b 22cos 4sin 40ρρθρθ--+=1sin 3α=cos()αβ-A ∠37(16)(本小题14分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面P AD⊥平面ABCD,点M在线段PB上,PD//平面MAC,P A=PD,AB=4.(I)求证:M为PB的中点;(II)求二面角B-PD-A的大小;(III)求直线MC与平面BDP所成角的正弦值.(17)(本小题13分)为了研究一种新药的疗效,选100名患者随机分成两组,每组个50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“·”表示服药者,“+”表示为服药者.(Ⅰ)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;(Ⅱ)从图中A ,B ,C ,D ,四人中随机选出两人,记为选出的两人中指标x 的值大于1.7的人数,求的分布列和数学期望E ();(Ⅲ)试判断这100名患者中服药者指标y 数据的方差与未服药者指标y 数据的方差的大小.(只需写出结论)(18)(本小题14分)已知抛物线C :y 2=2px 过点P (1,1).过点(0,)作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线分别与直线OP 、ON 交于点A ,B ,其中O 为原点. (Ⅰ)求抛物线C 的方程,并求其焦点坐标和准线方程; (Ⅱ)求证:A 为线段BM 的中点.(19)(本小题13分)ξξξ12已知函数f (x )=e x cos x −x .(Ⅰ)求曲线y = f (x )在点(0,f (0))处的切线方程; (Ⅱ)求函数f (x )在区间[0,]上的最大值和最小值.(20)(本小题13分)设{a n }和{b n }是两个等差数列,记c n =max{b 1–a 1n ,b 2–a 2n ,…,b n –a n n }(n =1,2,3,…), 其中max{x 1,x 2,…,x s }表示x 1,x 2,…,x s 这s 个数中最大的数.(Ⅰ)若a n =n ,b n =2n –1,求c 1,c 2,c 3的值,并证明{c n }是等差数列; (Ⅱ)证明:或者对任意正数M ,存在正整数m ,当n ≥m 时,;或者存在正整数m ,使得c m ,c m +1,c m +2,…是等差数列.参考答案:2πnc M n>一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. (1)【答案】A【解析】{}21A B x x =-<<- ,故选A. (2)【答案】B【解析】()()()()1i i 11i z a a a =-+=++-,因为对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得:1a <-,故选B.(3)【答案】C【解析】0k =时,03<成立,第一次进入循环111,21k s +===,13<成立,第二次进入循环,2132,22k s +===,23<成立,第三次进入循环31523,332k s +===,33<,否,输出53s =,故选C.(4)【答案】D【解析】如图,画出可行域,2z x y =+表示斜率为12-的一组平行线,当过点()3,3C时,目标函数取得最大值max 3239z =+⨯=,故选D.(5)【答案】A【解析】()()113333x xxx f x f x --⎛⎫⎛⎫-=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以函数是奇函数,并且3x 是增函数,13x⎛⎫ ⎪⎝⎭是减函数,根据增函数-减函数=增函数,所以函数是增函数,故选A.(6)【答案】A【解析】若0λ∃<,使λ=m n ,即两向量反向,夹角是0180, 那么0cos1800⋅==-<m n m n m n ,反过来,若0⋅<m n ,那么两向量的夹角为(0090,180⎤⎦,并不一定反向,即不一定存在负数λ,使得λ=m n ,所以是充分不必要条件,故选A. (7)【答案】B【解析】几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l ==,故选B.(8)【答案】D【解析】设36180310M x N ==,两边取对数,36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,即MN最接近9310,故选D. 二、填空题共6小题,每小题5分,共30分. (9)【答案】22m =⇒=. (10)【答案】1【解析】322131383,211(2)a d q d qb -+-+=-=⇒==-⇒==-⨯-. (11)【答案】1【解析】2222:2440(1)(2)1C x y x y x y +--+=⇒-+-= , 所以min ||||211AP AC r =-=-=. (12)【答案】79- 【解析】222sin sin ,cos cos cos()cos cos sin sin cos sin 2sin 179==-∴-=+=-+=-=-βαβααβαβαβααα(13)【答案】-1,-2,-3【解析】123,1(2)3->->--+-=-. (14)【答案】1Q ;2.p三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)解:(1)根据正弦定理×sin 33=sin ==sin60==sin sin 77214。
【真题】2017年北京市高考理科数学试卷含答案(Word版)

绝密★启封并使用完毕前2017年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合A={x|–2x1},B={x|x–1或x3},则AB=(A){x|–2x–1} (B){x|–2x3}(C){x|–1x1} (D){x|1x3}(2)若复数(1–i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是(A)(–∞,1)(B)(–∞,–1)(C)(1,+∞)(D)(–1,+∞)(3)执行如图所示的程序框图,输出的s值为(A)2(B)3 2(C )53(D )85(4)若x ,y 满足,则x + 2y 的最大值为(A )1 (B )3 (C )5 (D )9(5)已知函数1(x)33xxf ⎛⎫=- ⎪⎝⎭,则(x)f(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数(6)设m,n 为非零向量,则“存在负数λ,使得m n λ=”是“m n 0⋅<”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A )32 (B )23 (C )22 (D )2(8)根据有关资料,围棋状态空间复杂度的上限M 约为,而可观测宇宙中普通物质的原子总数N 约为.则下列各数中与MN最接近的是 (参考数据:lg3≈0.48)(A )1033 (B )1053 (C )1073 (D )1093第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2017年高考北京卷数学(理)试题(word档含答案详细解析)

绝密★本科目考试启用前2017年普通高等学校招生全国统一考试数 学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合A ={x |–2<x <1},B ={x |x <–1或x >3},则AB =(A ){x |–2<x <–1} (B ){x |–2<x <3} (C ){x |–1<x <1}(D ){x |1<x <3}(2)若复数在复平面内对应的点在第二象限,则实数a 的取值范围是(A )(–∞,1) (B )(–∞,–1) (C )(1,+∞) (D )(–1,+∞) (3)执行如图所示的程序框图,输出的s 值为(A )2 (B )(C )(D )()()1i i a -+325385(4)若x ,y 满足 则x + 2y 的最大值为(A )1 (B )3 (C )5(D )9(5)已知函数,则(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数(6)设m ,n 为非零向量,则“存在负数,使得”是“”的 (A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A )(B )(C )(D )2(8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与最接近的是(参考数据:lg3≈0.48)(A )1033 (B )1053(C )1073 (D )1093第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2017高考数学北京卷理(附参考答案及详解)
的 取 值 范 围 是 $! ! %
)%$0 1 #!%
*%$0 1 #0!%
+%$!#/ 1 %
,%$0!#/ 1 %
(!执 行 如 图 所 示 的 程 序 框 图 #输 出 的: 值 为 $! ! %
第2题图
)%(槡$
*%$槡(
+%$槡$
,%$
.!根据有关资料#围棋状态空间 复 杂 度 的 上 限 3 约 为 ((&!#而 可 观
3!若双曲线 #$0-?$ '!的离心率为 槡(#则实数 ?'!!!!!
!#!若 等 差 数 列!+*"和 等 比 数 列!2*"满 足+! '2! ' 0!#+- '2- '.#
则+$ 2$
'
!
!
!
!
!
!!!在极坐标系中#点 " 在 圆$$ 0$$456#0-$678#/-'# 上#点 6
的 坐 标 为 $!##%#则""6"的 最 小 值 为 ! ! ! ! !
C@÷áø $"%& `3Qø 9: 5 @"& =L 9: 9 @(" =L!
"ÐÑ¥*×>K:'*; ' 槡!.E '槡(#
) !.E'(#XB E'"!
!#!!! & | W [ þ !*- "* V W - .#| â [ þ !+- "* V â -G#
, !3 - .
.
4
mI '& -n7tv*,t!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年北京高考理科数学真题及答案本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本市卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若集合{}21A x x =-<<,{}13B x x x =<->或,则A B I =( )。
(A ){}21x x -<<- (B ){}23x x -<< (C ){}11x x -<< (D ){}13x x <<【答案】A【难度】容易【点评】本题在高考数学(理)提高班讲座 第一章《集合》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是( )。
(A )(),1-∞i (B )(),1-∞-(C )()1,+∞(D )(1,)-+∞【答案】B【难度】容易【点评】本题在高二数学(理)下学期课程讲座 第四章《复数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(3)执行如图所示的程序框图,输出的s 值为( )。
(A)2(B)3 2(C)5 3(D)8 5【答案】C【难度】容易【点评】本题在高考数学(理)提高班讲座第十三章《算法与统计》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(4)若,x y满足3,2,,xx yy x≤⎧⎪+≥⎨⎪≤⎩则2x y+的最大值为()。
(A)1(B)3(C)5(D)9 【答案】D【难度】容易【点评】本题在高考数学(理)提高班讲座 第二章《函数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(5)已知函数()133xx f x ⎛⎫=- ⎪⎝⎭,则()f x ( )。
(A )是奇函数,且在R 上是增函数(B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数【答案】A【难度】中等【点评】本题在高考数学(理)提高班讲座 第三章《函数的性质及其应用》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(6)设,m n 为非零向量,则“存在负数λ,使得m n λ=”是“0m n ⋅<”的( )。
(A )充分而不必要条件(B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件【答案】A【难度】容易【点评】本题在高考数学(理)提高班讲座 第九章《平面向量》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )。
(A )32(B )3(C )22(D )2【答案】B【难度】容易【点评】本题在高考数学(理)提高班讲座 第十一章《立体几何》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(8)根据有关资料,围棋状态空间复杂度的上限M 约为3613,而可观测宇宙中普通物质的原子总数N 约为8010,则下列各数中与M N最接近的是( )。
(参考数据:lg30.48≈) (A )3310(B )5310(C )7310(D )9310【答案】D【难度】中等【点评】本题在高考数学(理)提高班讲座 第二章《函数》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
第二部分(非选择题共110分)二、填空题(共6小题,每小题5分,共30分) (9)若双曲线221y x m -=3,则实数m =_________. 【答案】2【难度】容易【点评】本题考查双曲线的计算问题。
在高考数学(理)提高班讲座,第十二章《圆锥曲线的方程与性质》有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(10)若等差数列{}n a 和等比数列{}n b 满足11441,8a b a b ==-==,则22a b =_________. 【答案】1【难度】中等【点评】本题考查数列的计算。
在高考数学(理)提高班讲座,第六章《数列》有详细讲解,在寒假特训班有涉及。
(11)在极坐标系中,点A 在圆22cos 4sin 40ρρθρθ--+= ,点P 的坐标为()1,0,则|AP|的最小值为___________.【答案】1【难度】中等【点评】本题考查直线距离的求解。
在高考数学(理)提高班讲座,第十章《直线与圆》有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(12) 在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称。
若()1sin ,cos 3ααβ=-=_______. 【答案】79-【难度】容易【点评】本题考查平面向量的综合知识。
在高考数学(理)提高班讲座,第九章《平面向量》有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
(13) 能够说明“设,,a b c 是任意实数.若a b c >>,则a b c +>”是假命题的一组整数,,a b c 的值依次为_________.【答案】-1,-2,-3由题意知,,a b c ,均小于0,所以找到任意一组负整数,满足题意即可。
【难度】中等【点评】本题考查不等式的应用。
在高考数学(理)提高班讲座,第七章《不等式》有详细讲解,在高二数学(理)下学期 课程讲座中有涉及。
(14) 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点i A 的横、纵坐标分别为第i 名工人上午的工作时间和加工的零件数,点i B 的横、纵坐标学科&网分别为第i 名工人下午的工作时间和加工的零件数,1,2,3i =。
①记i Q 为第i 名工人在这一天中加工的零件总数,则123Q Q Q ,,中最大的是______。
②记i P 为第i 名工人在这一天中平均每小时加工的零件总数,则123p p p ,,中最大的是_______。
【答案】①1Q ②2p【难度】较难【点评】本题考查直线的相关计算。
在高考数学(理)提高班讲座,第十章《直线与圆》有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
三、解答题(共6题,共80分.解答应写出文字说明,演算步骤或证明过程)(15)(本小题13分)在ABC ∆中,360,7A c a ∠=︒=(Ⅰ)求sin C 的值;(Ⅱ)若7a =,求ABC ∆的面积。
【答案】(1)3314(2)63【难度】中等【点评】本题考查三角函数的应用。
在高考数学(理)提高班讲座,第八章《三角函数》有详细讲解,在百日冲刺班中有涉及。
(16)(本小题14分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD ∥平面,6,4MAC PA PD AB ===。
(Ⅰ)求证:M 为PB 的中点;(Ⅱ)求二面角B PD A --的大小;(III )求直线MC 与平面BDP 所成角的正弦值。
【答案】【难度】较难【点评】本题考查立体几何的应用。
在高考数学(理)提高班讲座,第十一章《立体几何》有详细讲解,在百日冲刺班、寒假特训班、高二数学(理)上学期课程讲座、高二数学(理)下学期课程讲座中均有涉及。
(17)(本小题13分)为了研究一种新药的疗效,选100名患者随机分成两组,每组个50名,一组服药,另一组不服药。
一段时间后,记录了两组患者的生理指标xy和的学科.网数据,并制成下图,其中“·”表示服药者,“+”表示未服药者.(Ⅰ)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;(Ⅱ)从图中A,B,C,D,四人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);(Ⅲ)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)【答案】【难度】较难【点评】本题考查概率的计算。
在高考数学(理)提高班讲座,第十四章《概率》有详细讲解,在高二数学(理)上学期 课程讲座、高二数学(理)下学期 课程讲座中均有涉及。
(18)(本小题14分)已知抛物线C :22y x ρ=过点()1,1P 过点10,2⎛⎫ ⎪⎝⎭作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线分别与直线OP 、ON 交于点A ,B ,其中O 为原点.(I )求抛物线C 的方程,并求其焦点坐标和准线方程;(II )求证:A 为线段BM 的中点。
【答案】【难度】较难【点评】本题考查抛物线的计算。
在高考数学(理)提高班讲座,第十二章《圆锥曲线的方程与性质》有详细讲解,在高二数学(理)上学期 课程讲座、寒假特训班、百日冲刺班中均有涉及。
(19)(本小题13分)已知函数()cos xf x e x x =- (I )求曲线()y f x =在点()()0,0f 处的切线方程;(II )求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值. 【答案】【难度】中等【点评】本题考查曲线的切线方程的计算。
在高考数学(理)提高班讲座,第十二章《圆锥曲线的方程与性质》有详细讲解,在高二数学(理)上学期 课程讲座、寒假特训班、百日冲刺班中均有涉及。
(20)(本小题13分)设{}n a 和{}n b 是两个等差数列,记{}()1122max ,,,,1,2,3,n n n c b a n b a n b a n n =---=…………, 其中{}12max ,,s x x x ……表示12,,s x x x ……这s 个数中最大的数.(I )若,21n n a n b n ==-,求123,,c c c 的值,并证明{}n c 是等差数列;(II )证明:或者对任意正数M ,存在正整数m ,当n m ≥时,n c M n>;或者存在正整数m ,使得12,,m m m c c c ++……是等差数列.【答案】【难度】较难【点评】本题考查等差数列的性质。
在高考数学(理)提高班讲座,第六章《数列》有详细讲解,在寒假特训班有涉及。
