大学物理力学模板
大学物理课件《力学》ch32009-文档资料

Fi
dr
Ai
i
3.1 功
chsling
f静
3. 功是过程量,与路径有关;
4. 作功与参照系有关;
3.1 功
chsling
二 功率 力在单位时间内所作的功,称为功率。
平均功率 瞬时功率
P A
t
P
lim
A
dA
F
v
t0 t dt
P Fvcos
功率的单位 (瓦特)1W 1J s1 1kW 103 W
弹性势能
Ep
1 2
k x2
保守力的功
W (Ep2 Ep1) EP
保守力的功 A 等于质点在始末两位置势能增量的负值
3.4
势能 机械能守恒定律
chsling
等势能 面
重力
Z
万有引力 (无穷远处为势能零点)
等势能面
零势能面 X
M
Fm
r
Y r
3.4
讨论
势能 机械能守恒定律
chsling
rB rA
AG dmAr'2mAddAr
m' r(t dt)
可个以函写数O成 的某 全
rB d ( Gmm)
rA
r
微分
B
r (t)
dr
m'm
m'm
A (G
rB
) (G
rA
)
r(t dt)
3.2 几种常见力的功
chsling
l
l
3.4
势能 机械能守恒定律
大学物理力学PPT课件

即
r
位矢:
r x i y j z k
o
模:
| r| x2y2z2
kz
p
x
i
方向余弦:co s x,co s y,cos z
r
r
r
位矢单位:m
二、位移(displacement)
t时刻,
r1 这r1(称t) 为质点的运动方程,
在运动方程中把t消去可得到质点的轨道方程。
tt r2r2( tt)
dx dl 两边对时间t 求导数, 得 2x 2l
dt dt d l u绞车拉动纤绳的速率, 纤绳随时间在缩
dt
短, 故 d l 0 ; d x v 是小船向岸边移动的速率。
dt
dt
l
22
x h
负号表示小船速
v u
u
x
x 度沿x 轴反方向。
小船向岸边移
d2x dv u2h2
a
动的加速度为
解:(1)由题意可得速度矢量为:
vd rd x(t)id y(t)j i 1tj
d t d t d t
2
所以t =3s时质点的速度为: v(3)i1.5j
(2)由运动方程 x(t) t和2 y(t)(1/4)t22
消去t 可得轨迹方程为: y 1 x2 x 3 4
由此可知该质点的运动轨迹为抛物线。
四、加速度(acceleration)
t
例1:通过绞车拉动湖中小船拉向岸边, 如图。如 果绞车以恒定的速率u拉动纤绳, 绞车定滑轮离水面 的高度为h, 求小船向岸边移动的速度和加速度。
解:以绞车定滑轮处为坐标原点, x 轴水平向
右, y 轴竖直向下, 如图所示。
(完整版)大学物理力学总结

大学物理力学公式总结➢第一章(质点运动学)1.r=r(t)=x(t)i+y(t)j+z(t)kΔr=r(t+Δt)- r(t)一般地|Δr|≠Δr2.v=drdt a=dvdx=d r2dt23.匀加速运动:a=常矢v0=v x+v y+v z r=r0+v0t+12at24.匀加速直线运动:v= v0+at x=v0t+12at2 v2-v02=2ax5.抛体运动:a x=0 a y=-gv x=v0cos v y=v0sinθ-gtx=v0cosθ•t y=v0sinθ•t-12gt26.圆周运动:角速度ω=dθdt =v R角加速度α=dωdt加速度a=a n+a t法相加速度a n=v2R=Rω2,指向圆心切向加速度a t=dvdt=Rα,沿切线方向7.伽利略速度变换:v=v’+u➢第二章(牛顿运动定律)1.牛顿运动定律:第一定律:惯性和力的概念,惯性系的定义, p=m v第二定律:F=dpdt当m为常量时,F=m a第三定律:F12=-F21力的叠加原理:F=F1+F2+……2.常见的几种力:重力:G=m g弹簧弹力:f=-kx3.用牛顿定律解题的基本思路:1)认物体2)看运动3)查受力(画示力图)4)列方程(一般用分量式)➢第三章(动量与角动量)1.动量定理:合外力的冲量等于质点(或质点系)动量的增量,即F dt=d p2.动量守恒定律:系统所受合外力为零时,p=∑p i i =常矢量 3. 质心的概念:质心的位矢 r c =∑m i i r im(离散分布) 或 r c =∫rdmm(连续分布)4. 质心运动定理:质点系所受的合外力等于其总质量乘以质心的加速度,即 F=m a c5. 质心参考系:质心在其中静止的平动参考系,即零动量参考系。
6. 质点的角动量:对于某一点, L=r ×p=m r ×v7. 角动量定理: M =dLdt其中M 为合外力距,M=r ×F ,他和L 都是对同一定点说的。
大学物理力学(全) ppt课件

ppt课件
14
例. 已知质点的运动方程为
x(t) R cost
y(t) R sin t
R和 为常量。(1)求其轨道
形和和态自加和然速特 坐 度征 标a。 系( 中写2)出在质直点角速坐度标v系
ppt课件
15
(1) x2 y2 R2
vx
dx dt
R sin t
lim lim
t0 t
t t 0
ppt课件
dt
3
a dv d (v) dv v d
dt dt
dt dt
如果轨道在点A 的内切圆的曲率半径为 ,
an
v
d
dt
n
v
d
dt
n
v2
n
at
dv
dt
一般情况下, 质点的加速度矢量应表示为
dv dt
R
d
dt
R
v
R
矢量
ppt课件
10
(t) (t) (t)
t 0 (0) 0 (0) 0
(t )
(t)
0 0
t
(t)dt
0 t
(t )dt
0
ppt课件
11
例 质点作匀加速圆周运动, 0 const,
ppt课件
21
牛顿第二定律: F ma
Fx
直角坐标系分量形式Fy
Fz
max may maz
m m m
dvx
大学物理第一篇 力学 综述 第二章
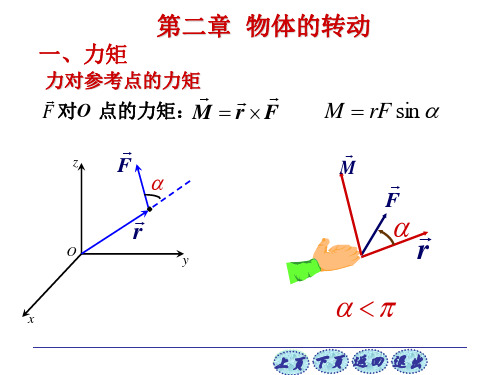
一、力矩
F力 对对O参点考的点力的矩力:矩M
r F
M rF sin
zF
r
O
y
M F
r
x
上页 下页 返回 退出
二、质点的角动量
(1)、质点对点的角动量为
L r p r (mv)
角动量大小 L rmv sin (面积)
L 角动量方向
L
O
r
m
v
v
r
上页 下页 返回 退出
Ft d dr
r
x
上页 下页 返回 退出
4、刚体定轴转动的动能定理
W
2 1
M
zd
W
2 1
M zd
1 2
J22
1 2
J12
对于定轴转动的刚体,外力矩所作的功等
于刚体转动动能的增量 ——刚体绕
dr
1 2
mv22
1 2
mv12
上页 下页 返回 退出
5、 转动定律
上页 下页 返回 退出
(2)、转动惯量
J mjrj2
j
刚体的质量连续分布
J r2dm
➢ 转动惯量的单位:kg·m2 ➢ J 的意义:转动惯性大小的量度 。
上页 下页 返回 退出
3、力矩的功:
dW F dr Ftds
Ftrd
M zd
o
W 0 M zd
比较
W
F
dr
v
F
因为转动惯量
J mjrj2
j
转动定律 M J
z
O rj
Fej
m j
Fij
刚体定轴转动的角加速度与它所受的合 外力矩成正比,与刚体的转动惯量成反比。
大学物理力学(全)ppt课件

之和最小。
05
流体力学基础
流体的性质与分类
流体的定义
流体是指在外力作用下,能够连续变形且不能恢复原 来形状的物质。
流体的性质
流动性、压缩性、黏性。
流体的分类
按物理性质可分为气体和液体;按化学性质可分为纯 净物和混合物。
流体静力学
重力势能
重力做功与路径无关,只与初末 位置的高度差有关。 03
机械能守恒定律
04 只有重力或弹力做功的物体系统 内,动能与势能可以相互转化, 而总的机械能保持不变。
刚体定轴转动动力学
刚体定轴转动的描述
角速度、角加速度和转动惯量等物理量的定义和 计算。
刚体定轴转动的动能定理
刚体定轴转动时,合外力矩对刚体所做的功等于 刚体转动动能的变化。
弹性势能与动能之间的转化
在振动过程中,物体的动能和弹性势能不断相互转化。
弹性碰撞与非弹性碰撞
弹性碰撞
碰撞过程中,物体间无机 械能损失的碰撞。碰撞后 两物体以相同的速度分开
,且动能之和不变。
非弹性碰撞
碰撞过程中,物体间有机 械能损失的碰撞。碰撞后 两物体以不同的速度分开
,且动能之和减小。
完全非弹性碰撞
伯努利方程的应用
伯努利方程在流体力学中有广泛的应用,如计算管道中流体的流速和流量、分析机翼升力原理、解释 喷雾器工作原理等。同时,伯努利方程也是一些工程领域(如水利工程、航空航天工程等)中设计和 分析的重要依据。
06
分析力学基础
约束与自由度
约束的概念
约束是对物体运动的一种限制,它减少了物体的自 由度。
牛顿运动定律
牛顿第一定律(惯性定律)
大学物理公式3篇

大学物理公式第一篇:力学力学是物理学的一个分支,主要研究物体运动的规律和受力情况。
下面是常见的力学公式。
1. 基本运动学公式:v = v₀ + at (速度的变化量)s = s₀ + v₀t + ½at²(位移的变化量)v²– v₀² = 2as (速度和位移的关系)2. 牛顿三定律:F = ma (物体受力与加速度成正比)作用力与反作用力大小相等、方向相反、作用在不同的物体上3. 动力学公式:F = ma (力的大小与加速度成正比)F = Gm₁m₂/r²(万有引力定律)K = ½mv²(动能公式)U = mgh (重力势能公式)E = K + U (机械能公式)4. 动量定理:FΔt = Δp (作用力与动量变化的关系)p = mv (动量公式)5. 碰撞公式:完全弹性碰撞:m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’非完全弹性碰撞:m₁v₁ + m₂v₂ = (m₁ + m₂)V’第二篇:热学热学是物理学的一个分支,主要研究热和温度的现象和规律。
下面是常见的热学公式。
1. 温度计算公式:C = (F – 32) / 1.8 (华氏温度转摄氏温度)F = C × 1.8 + 32 (摄氏度转华氏温度)K = C + 273.15 (摄氏度转开氏温度)2. 热传递公式:Q = mcΔT (热量公式)Q = hAΔT (对流换热公式)Q = kAΔT/d (传导换热公式)3. 热力学公式:Q = ΔU + W (内能变化、热量传递和功的关系)ΔS = Q/T (熵变公式)4. 热力学循环公式:ΔU = W + Q (内能变化、功和热量的关系)η = W/Q₁ = (Q₁– Q₂)/Q₁(热机效率公式)第三篇:电学电学是物理学的一个分支,主要研究电荷和电场的现象和规律。
下面是常见的电学公式。
1. 基本电磁公式:F = kq₁q₂/r²(库仑定律)E = F/q (电场强度公式)U = kq₁q₂/r (电势能公式)V = U/q = kQ/r (电势公式)2. 电流公式:I = Q/t (电流的定义)I = ΔQ/Δt (电流的计算公式)V = IR (欧姆定律)3. 阻抗公式:R = ρl/A (电阻的定义)ρ = RA/l (电阻率公式)Z = R + jX (阻抗的定义)X = 2πfL –1/2πfC (电感和电容的关系)4. 磁场公式:B = μ₀I/2r (安培环形定理)B = μ₀I/4πr²(比奥萨伐尔定律)B = μ₀nI (磁场公式)F = qvBsinθ (洛仑兹力公式)。
大学物理:力学PPT

点P对应的相位:0
( SI )
o
3
x
0 .1
x
t0
练习2:
一质点做简谐振动,其振动周期 T=2s。t=0时的旋转矢量如图所示。 (1)请写出它的振动方程; (2)初始时刻振子的速率;
2
O
3
y / cm
2
(3)第一次到达平衡位置的时间;
同频率简谐振动的相位差比较:
设两个简谐运动的表达式分别为:
x1 A1 cos(t 1 )
相位差:
x2 A2 cos(t 2 )
(t 2 ) (t 1)=2 1
1、2同相
1、2反相 2超前 2落后
2k (2k 1) 0 0
例 4:
两个同周期简谐振动曲线如图所示x1的相位比x2的 相位:( B )
波的干涉: ( interference )
P点: r y1P A1 cos( t 1 2 1 ) 2 r2 2 y2 P A2 cos( t 2 2 ) (2k 1) 相干相消 r2 r1 ( ) 2 相位差: 2 1 相干相长 2k
轨迹方程
运动方程: r (t ) x(t )i y(t ) j
(kinematic equations)
y
y y( x )
x x( t )
y y( t )
轨迹方程:
消去t
y y( x )
o
x
(trajectory equations)
2 已知质点的运动方程为: r 2ti (2 t ) j (SI) 求:(1) t=0及t=2s时质点的位矢; (2) t=0到t=2s内质点的位移; (3) t=2s时质点的速度、加速度; (4) 质点的运动轨迹。 解: r t 2 4i 2 j (1)r t 0 2 j ( 4) x 2 t 2 y 2t (2) r 4 i 4 j 2 x dr y 2 2i 2tj ( 3) v 4 dt dv a 2 j ( SI ) v t 2 2i 4 j dt
2024年大学物理力学ppt课件

弹性力学的基本方程和边界条件
弹性力学的应用举例
平衡方程、几何方程、物理方程及边界条 件的提法
杆件的拉伸与压缩、扭转与弯曲等问题的求 解方法
2024/2/29
12
03
流体力学基础
Chapter
2024/2/29
13
理想流体与粘性流体
1 2
理想流体
无摩擦、无粘性的流体,符合欧拉方程和连续性 方程。
粘性流体
分形几何在物理力学中 的应用
混沌现象与分形几何在 物理力学中的联系与区
别
2024/2/29
39
量子物理力学发展前沿
2024/2/29
量子物理力学的基本概念与原理 量子物理力学的研究对象与方法 量子物理力学的发展前沿与未来趋势
40
生物物理力学研究进展
生物物理力学的基本概念与 原理
生物物理力学的研究对象与 方法
抛体运动、圆周运动、一般曲线运动
9
刚体定轴转动
刚体的基本概念
定义、性质、与实际的联系
刚体定轴转动的描述
角位移、角速度、角加速度
2024/2/29
刚体定轴转动的动力学
转动惯量、转动定律、转动动能定理
刚体定轴转动的实例分析
飞轮转动、陀螺仪原理等
10ห้องสมุดไป่ตู้
刚体平面平行运动
2024/2/29
刚体平面平行运动的描述
5
角动量定理与角动量守恒
角动量定理
质点所受合外力矩等于质点角动量的 变化率,即M=dL/dt。
角动量守恒
在不受外力矩或所受合外力矩为零的 系统中,系统总角动量保持不变。
2024/2/29
6
功、能及能量守恒
《大学物理实验》实验数据记录和处理报告-力学参考模板

孝感学院《大学物理实验》实验数据记录和处理报告日期:2011 年月日天气:__________ 实验室:___________姓名:__________________ 学号:__________ 院系专业:___________ 指导教师:________【实验题目】实验1 用米尺、游标尺、螺旋测径器、读数显微镜测量长度【实验内容和实验数据记录】1.用米尺测量AB间的距离。
2.用游标尺测量铁杯的含铁体积。
表1 用米尺测A、B两点间距离表2 用游标尺测量铁杯的含铁体积3.用螺旋测径器测小钢球的体积。
4.用读数显微器测量挡光片AC、BD 两条边之间的距离。
D ______ mm表3 用螺旋测径器测小钢球的体积表4 用读数显微器测量挡光片AC、BD 两条边之间的距离(单位:mm)实验数据教师核查签字(未签字数据无效):______________【实验数据处理】1.用米尺测量AB 间的距离测量值 __________iX X n==∑A 类不确定度__________A X u S === B 类不确定度_________B u ∆==用方和根求总不确定度__________X u == 测量结果X X =±___________________X u = 2.用游标尺测量铁杯的含铁体积①外圆柱体积_______________D =,_______________H =2____________________________4V D H π==不确定度___________________________V u V ==____________________VV u u V V=⋅= ②内圆柱体积_______________h =,_______________h =,_____________________v =③杯子含铜体积 ______________________________V V v =-=杯______________________________u ==杯测量结果V V =±_______________V u =3.用螺旋测径器测小钢球的体积(不确定度公式的推导及个计算要求实验者自己完成)4.用读数显微器测量挡光片AC 、 BD 两条边之间的距离测量结果AC AC X X =±____________________AC u =BD BD X X =±____________________BD u =孝感学院《大学物理实验》实验数据记录和处理报告日期: 2011 年 月 日 天气:__________ 实 验 室:___________姓名:__________________ 学号:__________ 院系专业:___________ 指导教师:________【实验题目】实验2 随机(偶然)误差的统计分布【实验内容和实验数据记录】测量单摆周期,重复测量120~200次。
大学物理知识点力学ppt课件

dW外 dW非保内 0
E 常数
刚体力学内容总结
刚体定轴转动的角量描述
d
dt
d d 2
dt dt2
线量与角量的关系
si ri
i ri
ai
di
dt
ri
ain
i2
ri
ri2
刚体定轴转动的角动量与转动惯量
L I I m iri2 r 2 d m
刚体定轴转动的角动量定理
3、速度
υ
dr
dx
i
dy
j
dz
k
dt dt dt dt
大小
方向
d d 2r d 2 x d 2 y d 2z
4、加速度 a i j k
大小:
dt
a
dt2
a
dt2 dt2
a2 a2 a2
x
y
z
dt2
方向: cos ax cos ay cos az
a
a
a
5、切向加速度、法向加速度
)若dW外 dW非保内 0 EK EP 常量
解题方法小结
•第一类:求刚体转动某瞬间的角加速度,一般用转动 定律求解。如质点和刚体组成的系统,对质点列牛顿 运动方程,对刚体列转动定律方程,再列角量和线量 的关联方程,并联立求解。
• 第二类:求刚体与质点的碰撞、打击问题。把它们 选作一个系统时,系统所受合外力矩常常等于零, 所以系统角动量守恒。列方程时,注意系统始末状 态的总角动量中各项的正负。
3 ) 已 知 ax ( x),求υx ( x)
4 ) 已 知 υx (t ),求 x(t ) 5) 已 知 υx ( x),求 x(t )
ax ( x)dx υxdυx dx x(t)dt
(完整版)大学物理力学总结

大学物理力学公式总结➢第一章(质点运动学)1.r=r(t)=x(t)i+y(t)j+z(t)kΔr=r(t+Δt)- r(t)一般地|Δr|≠Δr2.v=drdt a=dvdx=d r2dt23.匀加速运动:a=常矢v0=v x+v y+v z r=r0+v0t+12at24.匀加速直线运动:v= v0+at x=v0t+12at2 v2-v02=2ax5.抛体运动:a x=0 a y=-gv x=v0cos v y=v0sinθ-gtx=v0cosθ•t y=v0sinθ•t-12gt26.圆周运动:角速度ω=dθdt =v R角加速度α=dωdt加速度a=a n+a t法相加速度a n=v2R=Rω2,指向圆心切向加速度a t=dvdt=Rα,沿切线方向7.伽利略速度变换:v=v’+u➢第二章(牛顿运动定律)1.牛顿运动定律:第一定律:惯性和力的概念,惯性系的定义, p=m v第二定律:F=dpdt当m为常量时,F=m a第三定律:F12=-F21力的叠加原理:F=F1+F2+……2.常见的几种力:重力:G=m g弹簧弹力:f=-kx3.用牛顿定律解题的基本思路:1)认物体2)看运动3)查受力(画示力图)4)列方程(一般用分量式)➢第三章(动量与角动量)1.动量定理:合外力的冲量等于质点(或质点系)动量的增量,即F dt=d p2.动量守恒定律:系统所受合外力为零时,p=∑p i i =常矢量 3. 质心的概念:质心的位矢 r c =∑m i i r im(离散分布) 或 r c =∫rdmm(连续分布)4. 质心运动定理:质点系所受的合外力等于其总质量乘以质心的加速度,即 F=m a c5. 质心参考系:质心在其中静止的平动参考系,即零动量参考系。
6. 质点的角动量:对于某一点, L=r ×p=m r ×v7. 角动量定理: M =dLdt其中M 为合外力距,M=r ×F ,他和L 都是对同一定点说的。
大学物理PPT(力学部分)

(3)
FN1cos m2 g m2 (a2sin )
(4)
且
FN' 1 FN1
(5)
解以上方程组,可得
a1
m2 m1
gsincos m2sin 2
a2
(m1 m2 )gsin m1 m2sin 2
(2) 设沿水平方向给劈施加力F,且木块与劈以相同的加速 度a沿水平方向运动,方向如图所示。
解 受力如图所示 建立自然坐标
列方程
mgcos m dv (1)
dt
Байду номын сангаас
FN
mgsin
mv 2 R
(2)
R
A
en
FN
mg
et
变量代换
dv dt
dv d d dt
dv d
v dv
R d
分离变量 vdv Rgcos d
利用初始条件,积分
v
0 vdv 0 Rgcos d
即
1v 2 Rgsin
即
v
v
2 0
2gR
2 gR 2 x
所以
v0 2gR 11.2km s1 (第二宇宙速度)
例 如图所示,质量为m的小球与劲度系数为k的轻弹簧构成弹 簧振子系统。开始时,弹簧处于原长,小球静止,现以恒
力F向右拉小球,设小球与水平面间的摩擦系数为。
求 小球向右运动的最大距离。
k
y
mF
x
O
FN
m Fr Fe
2
由此可得
v 2Rgsin
R
A
en
FN
mg
et
由(2)式有
FN
mgsin
m 2Rgsin
大学物理课件质点动力学动量模板

dt
· · ·
F
V1
r1 r
q1 o
r2 V2
q2
F
最接近时: V1=V2
F外 0
动量守恒:
mV0 0 mV1 mV2
A外 A非保内 0
机械能守恒:
1 2
mV02
E p0
1 2
mV12
1 2
mV22
Ep
设:起始时r = r20=∞时为势能零点, 即:Ep0=0
根据定义:
Ep
r
解: 取人 、船为研究系统。由于水的阻力忽略,因此在水平方向
F外 0 ,水平方向动量守恒。
参考位
v
如图设任意时刻船和 人相对于岸的速度为: V, v
取初始静止时船头位置为参考位置
V
则由动量守恒有:
mv MV 0 mv MV
Ss
m0t vdt M 0tVdt
用S、s表示船和人相对参考位置的移动距离,则:
Fy 0
Py Py0
可分别独立使用
⑵ 应用时常采用近似守恒条件:
当外力远小于内力时,可近似认为动量守恒。
⑶ 定理中的各速度指对应于同一参照系的速度。
⑷ 动量定理、动量守恒比牛二律更普遍适用。
⑸ 动能与动量都描述了机械运动,都是状态量,
但两者的描述角度不同:
动能,标量; 其变化:△ Ek = A
求:⑴ 土地的平均阻力;⑵ 重锤与木桩下陷的时间。
解: ⑴ 如图,全过程可分为以下几个分过程:
过程Ⅰ:重锤M自由下落。
初态:V0=0;末态: V 2gh
过程Ⅱ:M、m碰撞过程。
选M、m为系统,作受力分析:
初态:
m: M:
v0 V 2gh
力学受力模型报告模板

力学受力模型报告模板在物理学中,力学是一门研究物体运动和力的关系的学科。
力学的一个重要分支是受力模型,它用来描述物体受到的各种力以及这些力对物体运动的影响。
在本文中,我们将介绍一个力学受力模型的报告模板,用于展示和分析不同受力模型的情况。
受力模型的基本概念在力学受力模型中,我们通常要考虑以下几个方面:•物体的运动状态:物体可能在静止状态、匀速直线运动或做曲线运动。
•受到的力:物体可能受到多个力的作用,这些力可能是接触力、重力、弹性力、摩擦力等。
•受力原理:力学受力模型的基本原理是牛顿第一定律和牛顿第二定律,它们用来描述物体运动状态和受力情况。
报告模板的结构为了更好地展示一个受力模型的情况,我们可以按照以下结构来撰写力学受力模型报告:实验目的在这一部分,我们将介绍实验的目的和研究问题的背景。
例如,我们可能要研究特定条件下物体的运动状态和受力情况,并探究它们的关系。
实验装置和方法在这一部分,我们将介绍实验所使用的装置和实验方法。
例如,我们可能要使用一些测力计、摆锤等仪器来测量物体的受力和运动状态,并通过各种方法来分析和解释实验结果。
实验结果在这一部分,我们将陈述实验的结果和数据。
我们可以使用各种图表和表格来展示实验结果,例如受力分析图、受力与运动状态的关系图等。
实验分析在这一部分,我们将对实验结果进行分析和解释。
我们可以探究不同受力模型的特点,分析它们对物体运动和受力的影响,并推断出可能的物理规律和关系。
结论在这一部分,我们将总结实验的主要结论和研究成果,指出其在实践中的意义和应用。
我们还可以探讨可能存在的不确定性和误差,并提出可能的改进方法。
结论力学受力模型报告模板可以帮助我们更好地展示和分析不同受力模型的情况。
通过遵循上述结构,我们可以以清晰、简明的方式向读者传达实验的过程、结果和分析。
同时,我们还可以在实践中应用这个模板,探索不同实验条件下的物理规律和关系,以推动科学研究的进一步发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.矢量的导数:
dA A(t t ) A(t ) A A lim lim t 0 t 0 t dt t
图4(a)
如图5所示 图4(b)
27
第一章 质点运动学
力学 运动学
机械运动 定量描述物体的运动 相互作用
动力学 运动状态的改变
28
1.1时间与空间
时间的计量 • 一切周期运动都可用来量度时间。
•目前国际通用的时间单位是秒(s).为提高
精度,1967年国际计量大会决定采用原子的
跃迁辐射作为计时标准,并规定铯--133原子
基态的两个超精细能级间跃迁相对应的辐射 的9 912 631 770个周期的持续时间作为1s.
长度的计量
可用物体来计量长度.如古代测量长度常
以人体的某部分作为单位和标准. 近代的测量
第谷去世后,开普勒开始整理他的观察资料,于 1627年《鲁道夫天文表》这份比以往的任何表都精确。 直到18世纪中叶,这份表仍然被看作天文学上的标准 星表,天文学家和航海家们都把它当作指南。 开普勒的研究首先从火星开始,他发现这个行星的 运动与哥白尼的理论出入最大。
开普勒想从火星的观测数据中找出它的运动轨迹, 并用曲线来表示,他经过70次尝试,他找到的最佳方 案还与观测资料相差8角分,即0.133弧度。
32
§1- 2
描述质点运动的物理量
一.时刻和时间间隔 时刻 时间间隔 二.位置矢量 1.参考点O(坐标系原点),质点位置P 从O点到P点的有向线段OP 距离 方位 P O
位置
位置的变动
运动学方程
位置矢量r r t op
33
2.直角坐标系下的表示
z
P(x,y,z)
r xi yj zk r r x2 y 2 z 2 x cos r y cos r z cos r
开普勒(1571-1630)德国
行星运动
定律
3
哥白尼与“天体运行论”
1、地心说与日心说的主要观点 地心说:地球是绝对静止的,一切运动都是相对 于地球而运动的。地心说受到宗教的吹捧与肯定。 日心说:如果是地心说,这样的观点来描述行星 的运动时,行星有无法解释的忽快、忽慢、逆行及z 滞留的现象。 地动日心说可以对天体的运动给予完满的解释。 “天穹的周转是一种视运动,实际是地球运动 的反映。”
2.“天体运行论”于1543年完成,它被誉为自然科学的独立 宣言。所以1543年在科学史上被称为科学革命的一年。
第谷与开普勒 1.丹麦著名天文学家第谷(1546-1601),经过20 年的反复的天文观测,积累了大量准确的星体运动 观测资料,被人誉为“星学之王”。
他的贡献有:
(1)在丹麦国王的支持下,在哥本哈根海峡的一个 小岛上修建了一座完善的天文台。
牛顿的《自然哲学的数学原理》的意义 1.它将个别特殊的情况抽象概括为普遍理论,是当 时力学规律的伟大综合。
2.它成为当时科学上判断正误的准绳。
3.它向后来者提供了一种科学研究的方法。
4.它发挥了科学理论的预言作用,引导人们从已知 的现象去预测未来。
3.物质的相互作用
物质的基本形态 物质的相互作用 强相互作用 源 强子(质子.中子) 1 电磁相互作用 电荷 弱相互作用 基本粒子 引力作用 质量 粒子和场
在1687年,他的《自然哲学的数学原理》的出版, 标志着经典力学体系的建立。 序言:“我把这部著作叫做自然哲学的数学原理,因为 哲学的全部任务看来就在于从各种运动现象来研究各 种自然之力,而后用这些力去论证其他现象……,我 希望能用同样的推理方法,从力学中推导出自然界的 其他现象。” 所谓经典力学体系,简单说来,是以四个绝对化的 概念:空间、时间、质量、力为基础,以三个基本定 律为核心,以万有引力为它的综合,并用微积分来描 述物体运动的因果律。
交叉科学 物理化学 地球物理 生物物理 环境物理 为其他科学提供技术和实验设备
21
力学基本原理及应用
分类 基本规律 基本理论 导出规律 刚体 理论应用 流体 振动 波动 基本原理 万有引力定律 牛顿三定律 质心运动定律 动量、机械能、 角动量定理 角动量守恒; 角动量定理…… 伯努利方程; …… 共振;…… 应用 卫星轨道;超重与失重;汽车中人的前、后 倾;潮涨潮落;表观重力;丢失的重量;地 球的自转;东北信风;台风的形成 物体的运行轨迹;筛选法原理;手抓飞行子 弹;西瓜的威力;机场驱赶小鸟 运动员转速的变化;导航仪;不翻转的子弹; 自行车转弯 轮船的相碰;上旋球;下旋球;香蕉球;机 翼的升力 不敲自响的铜磬;桥梁的坍塌;信号调频
(2)经过二十余年的观察,各个行星的角位置的误 差仅为2’。
(3)1560-1597年邀请开普勒到身边工作,1600年2 月3号收他为助手。 (4)1601.10.24去世,把所有的天文观测资料留给 了开普勒。
2.德国天文学家开普勒(1571-1630) 是第谷的学生与助手,从第谷对火星 的观测资料与他理论计算的8弧分之 差入手,发表了开普勒三定律。写出 “宇宙和谐论”,使我们对天穹星空 的认识,由杂乱到有序。开普勒的一 生,虽多病贫穷,但都未动摇他破解 天体奥秘的决心,他把他的一生都贡 献给了科学事业。
开普勒行星运动定律 第一定律:行星绕太阳作椭圆轨道的运动, 太阳在椭圆的一个焦点上; 第二定律:在相同的时间内,行星和太阳的 连线在椭圆平面内扫过的面积相等;
这两条定律在1609年公布在《新天文学》一书中。
第三定律:行星运动的周期的平方和其距太 阳距离的立方成正比。
这条定律开普勒在1619年出版的《宇宙和谐论》中 公布
多普勒效应…… 变声与变色
22
力学知识逻辑体系
质点运动规律
质点运动学 惯性系 质点动力学
力学理论基础
对称性与守恒律
非惯性系
动量定理与守恒定律 经典时空
定理与守恒
功能原理与守恒定律 角动量定理与守恒定律
时空 结构
特殊质点系 典型问题 普遍运动形式
刚体
流体 波动
振动
现代时空
狭义相对论
广义相对论
宇宙学与天体物理简介
力学
1.力学的研究对象 2 牛顿力学的形成
3. 力学——学习物理学的开始
1
物理学基本知识领域与课程体系
知识领域 机械运动现象与 规律 热运动现象与规 律 研究的对象和内容 研究大到天体、小到颗粒等 宏观物体的空间运动规律 研究大量微观粒子的统计运 动规律 研究包括光波在内的电磁场 的运动、粒子在电磁场中的 运动等规律。 研究物质的微观结构以及微 观粒子的个体运动规律 研究由大量原子所组成的凝 聚态物质的结构、相互作用 及其宏观物理性质 研究时间和空间以及引力场 性质,宇宙的形成、结构及 演化 课程体系 基本课程 后续课程 力学 热学 理论力学 热力学与统 计物理学
Q
∆r r(t+∆t) o r(t) 路程与位移
经典力学
伽利略(1564-1642)意大利
落体和斜面运动 加速度
经 典 物 理 学 体 系
牛顿
(1642-1727)英国
运动三定律 万有引力定律 微积分
11
运动学奠基人 伽利略
一、伽利略捍卫哥白尼学说
伽利略(1564-1642),又是一位献身于哥白尼学说的伟人。 他出生于意大利比萨,17岁入比萨大学学医。1589-1592 年在比萨大学任数学教师,脍炙人口的比萨斜塔实验可能 就在这期间进行的。
长度单位是在法国的米制单位发展起来的 (规定为通过巴黎的自北极至赤道的子午线 的千万分之一为米),目前在国际单位制中长 度的单位是米(m).在1983年国际计量大会
商定以:“1m为光在真空中(1/299792458)s 时间
间隔内所经路径的长度”.
1.2
一.质点 1.定义 2.理想模型
质点和参考系
他和开普勒是同时代的天文学家,哲学家、数学家、物 理学家。他们是好朋友。 就在1609年,伽利略制作成了历史上放大倍数32的天文 望远镜,获得了一系列重大的发现。
二、落体运动的研究
对运动无知,也就对大自然无知。
伽利略对运动的研究主要的贡献: (1)通过相对性原理,提出了 运动与静止的相对性,提出了对 不同参考系运动的不同描述。---伽利略相对性原理 (2)他用数学方法分析了时间 和空间的定量关系。定义了匀速 运动,还明确提出和定义了加速 度的概念。 (3)用实验研究了自由落体的 运动规律。
o
y
x
r t xt i yt j zt k x xt 轨道参量方程 f x, y, z 0 y y t 轨道方程 z z t
运动学方程
34
三.位移
r pQ r t t r t xt t xt i yt t yt j z t t z t k xi yj zk
四、运动叠加原理
伽利略第一个证明抛射体的路径是一条抛物线。 他用运动叠加原理把抛射运动分解为:垂直方向的上 抛运动和水平方向的匀速运动。 他利用公式算出各抛射角时的曲线并证明与实验相符。 他还证明了抛射角为45度射程最大。
牛顿的经典力学体系
一、牛顿简介 1. 牛顿1642年生于英国。 2.1661年考入剑桥大学31 学院。由于学习勤奋,受 到巴罗教授的赏识,1664年成为研究生。 3. 1665年开始研究微分和积分及万有引力定律。 1665年伦敦大瘟疫,一个夏天病逝3万人。牛顿回到家乡, 留下了脍炙人口的“苹果落地”的故事。(据说是法国作 家伏尔泰从牛顿侄女那儿听来的。)
——西方谚语
三、惯性定律
伽利略还发现了惯性定律,他确信,如果一个 物体能够没有摩擦地在一个水平面上滑动的话, 它将能保持自己的速度不变。 他用斜面实验来进行证明。 他虽然得出了惯性定律,但他没有能进行概括 性的描述。以伽利略为代表的惯性观念的改变, 是古代与中世纪自然哲学过渡到经典物理学的最 重要的标志。
