坐标变换总结Clark变换和Park变换
Clark变换与Park变换
当P = 时,坐标变换前后电压空间矢量幅值不变;
当P = 时,坐标变换前后电机功率不变。 推导过程: ①恒功率变换
iα = i − 0.5i − 0.5i
幅值: 1 + + = 倍
√3 √3 iβ = 2 i − 2 i
=>k ∗
= 1 => k =
②等幅值变换 在复平面上的矢量V⃗总能用互差 120 度的 abc 三轴系中的分量 xa、 xb、xc 等效表示(a 轴与复平面实轴重合),如下所示(x⃗和x⃗ 将 合成矢量V⃗)。 x⃗ = k(x + ρx + ρ x )``````````````(1) x⃗ = k (x + x + x )``````````````` (2) 其中,ρ = e = − + j √ 、ρ = e = e = − − j √ ;x⃗ 的 方向与复平面的实轴方向一致。所以有式(2)可以表示为 x = k (x + x + x )````````````````(3) 写出式(1)的实部与虚部如下: R {x⃗} = k x − x − x = k x − (x + x ) ```````(4) I {x⃗} = k √ (x − x )``````````````````````````````````````````(5) 由式(3)可得: x + x = − x ```````````````````````````````````````````````(6) 将(6)代入式(4)中可得: R {x⃗} = k x − − x = 1.5kx − 0.5 ````````` (7) 等幅值变换时,规定x = R {x⃗} + x ,所以有: R {x⃗} = x − x `````````````````````````````````````````````````(8) 将(8)代入式(7)中可得: 1.5kx − 0.5 = x − x ````````````````````````````````````(9)
Clark变换与Park变换

(1.2)
u = V cos(ωt + 120°)
= V cos 120° − V sin 120°
=− V −√ V
u u u
1
0
= − 1⁄2 √3⁄2
− 1⁄2 − √3⁄2
V V
u +u +u =0
(1.3) (1.4)
现在要求的是如何找到一个矩阵 P 使
V V
u
=P u u
(1.5)
书上有两种表达式
设三相交流系统各相电压为: u = V cos ωt u = V cos(ωt − 120°) u = V cos(ωt + 120°)
ua、ub、uc 分别指 ABC 三相电压的瞬时值 Vm 指相电压基波幅值
(1.1)
u = V cos ωt
=V
u = V cos(ωt − 120°)
= V cos 120° + V sin 120° =− V +√ V
1 − 1⁄2 − 1⁄2
P=
与P =
0 √3⁄2 − √3⁄2
为什么有这两种表达式?
1 − 1⁄2 − 1⁄2 (1.6)
0 √3⁄2 − √3⁄2
当P = 时,坐标变换前后电压空间矢量幅值不变;
当P = 时,坐标变换前后电机功率不变。 推导过程: ①恒功率变换
iα = i − 0.5i − 0.5i
两式相减,有:
(1.11)
i = −i sin φ + i cos φ
(1.12)
可得两相静止变两相旋转坐标为:
i i
=
cos φ − sin φ
sin φ cos φ
i i
Matlab_Simulink中Clark变换和Park变换的深度总结教程文件

M a t l a b_S i m u l i n k中C l a r k变换和P a r k变换的深度总结Matlab_Simulink中Clark变换和Park变换的深度总结最近搞三相并网逆变系统,对这个坐标变换产生了很多疑惑。
调模型,排错,最后发现坐标变换这个地方出来的波形总是和我设想的不一样。
以前认为坐标变换都是死的,带公式即可,经过这几天的研究,发现这里面真的有些方法。
基于MATLAB/Simulink中的模块,我也发现了Simulink中和一些书上不一样的地方。
而且现在这个坐标变换每本书上的表示方法都不一样,甚至字母都有好多种。
下面我想基于MATLAB/Simulink深刻的总结一下三相交流控制系统常用的两个变换Clark(3-2)变换和Park(2-2)变换。
首先来搞清楚为什么要用这两个变换,在三相交流系统中,常用的控制器还是经典的PI调节器。
PI调节器可以对直流量进行无净差的调节,而交流量就不行,所以需要将三相交流分量转化为两项直流分量加以控制。
接下来看看Clark变换(3-2)原理。
由于三相分量幅值相等,相位相差120,角速度相等,因此三相分量存在信息冗余,这时,可以去掉一项将其化为两相,这就是Clark变换的作用。
由于两项分量所在的坐标轴是静止的,所以我们把此坐标轴称为两相静止坐标系。
也就是说平面上的原来基于三相静止坐标系的矢量,可以切换到两相静止坐标系表示。
变换的原则是投影原则+等幅值等效原则(DPC时用功率等效原则)。
令A与alfa轴重合,按照变换原则,计算投影ABC分量在alfa、beta上的投影,按照等复制变换原则导出变换矩阵方程如下。
111222 333 0A B Cαβ⎛⎫⎡⎤--⎪⎡⎤⎢⎥⎪=⎢⎥⎢⎥⎪⎣⎦⎢⎥-⎪⎣⎦⎝Simulink中的3/2变换也是基于此变换进行的。
但是,在电气工程中为大家熟知的三相正序的相序是,A为0,B为-120,C为120(也可以是-240).如果按照图中所标注的方向进行坐标变换,那一定要将相序变为负序,也就是说A为0,B为120,C为-120. 如果坚持用传统正序,那么再按上式变换之后的坐标进行变换的话,beta轴就反向了。
坐标变换总结Clark变换和Park变换

坐标变换总结Clark变换和Park变换⼀个坐标系的坐标变换为另⼀种坐标系的坐标的法则。
由于交流异步电动机的电压、电流、磁通和电磁转矩各物理量之间是相互关联的强耦合,并且其转矩正⽐与主磁通与电流,⽽这两个物理量是随时间变化的函数,在异步电机数学模型中将出现两个变量的乘积项,因此,⼜为多变量,⾮线性系统(关键是有⼀个复杂的电感矩阵),这使得建⽴异步电动机的准确数学模型相当困难。
为了简化电机的数学模型,需从简化磁链⼊⼿。
解决的思路与基本分析:1.已知,三相( ABC )异步电动机的定⼦三相绕组空间上互差120度,且通以时间上互差120ω的旋转磁场。
度的三相正弦交流电时,在空间上会建⽴⼀个⾓速度为1⼜知,取空间上互相垂直的(α,β)两相绕组,且在绕组中通以互差90度的两相平衡交流电流时,也能建⽴与三相绕组等效的旋转磁场。
此时的电机数学模型有所简化。
2. 还知, 直流电机的磁链关系为:F---励磁绕组轴线---主磁通的⽅向,即轴线在d轴上,称为直轴(Direct axis)。
A---电枢绕组轴线---由于电枢绕组是旋转的,通过电刷馈⼊的直流电产⽣电枢磁动势,其轴线始终被限定在q轴,即与d轴成90度,称为交轴(Quadrature axis)。
由于q轴磁动势与d轴主磁通成正交,因此电枢磁通对主磁通影响甚微。
换⾔之,主磁通唯⼀地由励磁电流决定,由此建⽴的直流电机的数学模型⼗分简化。
如果能够将三项交流电机的物理模型等效的变换成类似的模型,分析和控制就变得⼤⼤简单了。
电机模型彼此等效的原则:不同坐标系下产⽣的磁动势(⼤⼩、旋转)完全⼀致。
关于旋转磁动势的认识:1) 产⽣旋转磁动势并不⼀定⾮要三相绕组不可。
结论是:除了单相电机之外,两相、三相或四相等任意对称(空间)的多相绕组,若通以平衡的多相电流,都可产⽣旋转磁动势。
根据这⼀道理,利⽤其在空间上互差90度的静⽌绕组,并通以时间上互差90度的平衡交流电流,同样可产⽣旋转磁场(或磁动势F),因⽽可等效代替三相绕组的作⽤。
Clark变换与Park变换详解

Clark 变换与Park 变换详解很多同学对Clark 变换与Park 变换不求甚解,在运用的时候常常感到困惑,本文梳理了这两种变化的详细步骤,希望可以帮到大家。
设三相交流系统各相电压为:cos cos(120)cos(120)a mb mc m u V tu V t u V t ωωω=⎧⎪=-⎨⎪=+⎩ (0.1) a u b u c u 分别指ABC 三相电压的瞬时值,m V 指相电压基波幅值。
cos cos(120)cos120sin120122cos(120)cos120sin120122a m b m c m u V tV u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-+=+=-=--(0.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫ ⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭⎝⎭ (0.3)0a b c u u u ++=(0.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(0.5) 书上有两种表达式11/21/211/21/22302/20/22P P ----⎛⎫⎫== ⎪⎪⎝⎭⎭与 (0.6) 于是有同学开始疑问了,为什么?为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩(0.7) cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.8) 由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ (0.9) 两式相加有:cos sin d u u u αβαα=+ (0.10)22cos sin sin sin cos sin cos cos d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩(0.11)两式相减有:sin cos q u u u αβαα=- (0.12) 可得:cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.13) 将式(1.5)代入(1.13)中可得: cos cos(120)cos(120)23sin sin(120)sin(120)a d b q c u u u u u αααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪ ⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭ (0.14)。
FOCClarke变换和Park变换详解(动图+推导+仿真+附件代码)

FOCClarke变换和Park变换详解(动图+推导+仿真+附件代码)⽂章⽬录1 前⾔永磁同步电机是复杂的⾮线性系统,为了简化其数学模型,实现控制上的解耦,需要建⽴相应的坐标系变换,即Clark变换和Park变换。
2 ⾃然坐标系ABC三相永磁同步电机的驱动电路如下图所⽰;根据图⽰电路可以发现在三相永磁同步电机的驱动电路中,三相逆变输出的三相电压为UAU_{A}UA,UBU_{B}UB,UCU_{C}UC将作⽤于电机,那么在三相平⾯静⽌坐标系ABC中,电压⽅程满⾜以下公式:{UA=UmcosθeUB=Umcos(θe+2π3)UC=Umcos(θe−2π3)\begin{cases}U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \\ U_{C} =U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧U A=Um c osθe U B=Um c os(θe+32π)UC=Um c os(θe−32π)θe\theta_{e}θe为电⾓度UmU_{m}Um为相电压基波峰值所以根据上述公式可以发现,三相电压的⼤⼩是随时间变化的正弦波形,相位依次相差120°,具体如下图所⽰;3 αβ\alpha\betaαβ坐标系由静⽌三相坐标系ABCABCABC变换到静⽌坐标系αβ\alpha\betaαβ的过程称之为Clarke变换;在αβ\alpha\betaαβ静⽌坐标系中,α\alphaα轴和β\betaβ轴的相位差为90°,且αβ\alpha\betaαβ的⼤⼩是随时间变化的正弦波形,具体如下图所⽰;从⾃然坐标系ABCABCABC 变换到静⽌坐标系αβ\alpha\betaαβ,满⾜以下条件:[fαfβf0]=T3s/2s∗[fAfBfC]\begin{bmatrix} f_{\alpha} \\ f_{\beta} \\ f_{0} \end{bmatrix} = T_{3s/2s}*\begin{bmatrix} f_{A} \\ f_{B} \\ f_{C} \end{bmatrix} ⎣⎡fαfβf0⎦⎤=T3s/2s∗⎣⎡f A f B f C⎦⎤其中T3S/2ST_{3S/2S}T3S/2S为变换矩阵:T3S/2S=N∗[1−12−12032−32222222]T_{3S/2S} = N*\begin{bmatrix} 1 &-\cfrac{1}{2} &-\cfrac{1}{2} \\ \\ 0 &\cfrac{\sqrt{3}}{2} &-\cfrac{\sqrt{3}}{2} \\ \\ \cfrac{\sqrt{2}}{2}&\cfrac{\sqrt{2}}{2} &\cfrac{\sqrt{2}}{2} \end{bmatrix} T3S/2S=N∗⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1022−212322−21−2322⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤注意:NNN为系数,做等幅值变换和等功率变换NNN系数不同;等幅值变换 N=23N =\cfrac{2}{3}N=32等功率变换 N=23N =\sqrt\cfrac{2}{3}N=32下⾯均为等幅值变换3.1 Clarke变换三相电流ABCABCABC分别为iAi_{A}iA,iBi_{B}iB,iCi_{C}iC,根据基尔霍夫电流定律满⾜以下公式:iA+iB+iC=0i_{A}+i_{B}+i_{C} = 0iA+iB+iC=0静⽌坐标系αβ\alpha\betaαβ,α\alphaα轴的电流分量为iαi_{\alpha}iα,iβi_{\beta}iβ,则Clark变换满⾜以下公式:iα=iAiβ=13∗iA+23∗iBi_{\alpha} = i_{A} \\ \\ i_{\beta} = \cfrac{1}{\sqrt{3}}*i_{A}+\cfrac{2}{\sqrt{3}}*i_{B}iα=iA iβ=31∗iA+32∗iB在matlab的simulink仿真如下图所⽰;最终得到三相电流iAi_{A}iA,iBi_{B}iB,iCi_{C}iC的仿真结果如下;得到αβ\alpha\betaαβ坐标的 iαi_{\alpha}iα和 iβi_{\beta}iβ的仿真结果如下图所⽰;由上述两张图分析可以得到,等幅值Clark变换前后峰值不变,αβ\alpha\betaαβ坐标系中iαi_{\alpha}iα和iβi_{\beta}iβ相位相差90°。
克拉克(CLARKE)和帕克(PARK)变换

克拉克(CLARKE)和帕克(PARK)变换1918年,Fortescue提出对称分量法,为解决多相(三相)不对称交流系统的分析和计算提供了一个有效方法。
对称分量法是用于线性系统的坐标变换法。
它将不对称多相系统(后面均以三相系统为代表)以同等待定变量的三个三相对称系统来代替,其中正序、负序系统是两个对称、相序相反的三相系统;零序系统是一个三相幅值相同、三相量同相的系统,用来反映三相量之和不为零的不平衡量。
CLARKE 变换首先是将基于3 轴、2 维的定子静止坐标系的各物理量变换到2 轴的定子静止坐标系中。
该过程称为Clarke 变换,PARK 变换此刻,已获得基于αβ 2轴正交坐标系的定子电流矢量。
下一步是将其变换至随转子磁通同步旋转的 2 轴系统中。
该变换称为Park变换在矢量控制中包括以下系统变换从三相变换成二相系统Clarke变换直角坐标系的旋转(αβ静止)到(旋转d q),称为Park 变换反之为Park 反变换关于park变换从数学意义上讲,park变换没有什么,只是一个坐标变换而已,从abc坐标变换到dq0坐标,ua,ub,uc,ia,ib,ic,磁链a,磁链b,磁链c这些量都变换到dq0坐标中,如果有需要可以逆变换回来。
从物理意义上讲,park变换就是将ia,ib,ic电流投影,等效到d,q轴上,将定子上的电流都等效到直轴和交轴上去。
对于稳态来说,这么一等效之后,iq,id正好就是一个常数了。
从观察者的角度来说,我们的观察点已经从定子转移到转子上去,我们不再关心定子三个绕组所产生的旋转磁场,而是关心这个等效之后的直轴和交轴所产生的旋转磁场了。
Clarke变换将原来的三相绕组上的电压回路方程式简化成两相绕组上的电压回路方程式,从三相钉子A-B—C坐标系变换到两相定子α-β坐标系。
也称为3/2变换。
但Clarke变换后,转矩仍然依靠转子通量,为了方便控制和计算,再对其进行Park变换变换后的坐标系以转子相同的速度旋转,且d 轴与转子磁通位置相同,则转矩表达式仅与θ有关。
关于Clark变换与Park变换

错误!未找到引用源。
对Clark 变换与Park 变换的理解设三相交流系统各相电压为:cos cos(120)cos(120)a m b m c m u V t u V t u V t ωωω=⎧⎪=-⎨⎪=+⎩错误!未找到引用源。
a u b u c u 是指ABC 三相电压的瞬时值,m V是指相电压基波幅值。
cos cos(120)cos120sin1201322cos(120)cos120sin1201322a mb mc m u V t V u V t V V V V u V t V V V V ααβαβαβαβωωω===-=+=-+=+=-=-- 错误!未找到引用源。
101/23/21/23/2a b c u V u V u αβ⎛⎫⎛⎫⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪--⎝⎭⎝⎭错误!未找到引用源。
0a b c u u u ++= 错误!未找到引用源。
现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭错误!未找到引用源。
书上有两种表达式11/21/211/21/2223303/23/203/23/2P P ----⎛⎫⎛⎫==⎪⎪--⎝⎭⎝⎭与 错误!未找到引用源。
WHY??为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩ 错误!未找到引用源。
cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪⎪⎪-⎝⎭⎝⎭⎝⎭错误!未找到引用源。
由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ 错误!未找到引用源。
两式相加有:cos sin d u u u αβαα=+ 错误!未找到引用源。
park,clark和ipark浅析

原文地址:park,clark和ipark浅析作者:温暖小屋相信做过电动机矢量控制或者直接转矩控制的朋友们肯定会对park,clark,ipark变换再熟悉不过了,肯定有人认为没有必要写这个东西。
其实我写这个东西只是为了加深自己对上面三种变化的理解,因为今天我在调程序的时候,这三个变换把我弄糊涂了。
好,下面先来介绍这三个变换。
Clark变换。
为什么会有这三个变换呢,从宏观上来讲,三相异步电动机是三相对称的交流供电,那么既然三相对称,我们可以用两相交流电来产生和三相交流相同的磁场效应,这样一来,我们只剩下了两相。
经过变换之后,以前三相对称,相隔120o,而经过变换之后,变成了两相想间隔90o的交流供电。
计算过程如下:变换过程如图1.1所示。
图1.1 clark变换过程我们看到Ia,Ib和Ic都三相对称的交流,而Iq和Id是两相间隔90°的交流电。
那么变换之后的效果如下图1.2所示。
图1.2 clark变换后效果在控制电动的过程中,clark变换的输入输出为图1.3所示。
图1.3 clark变换模块图这里As和Bs是想间隔120°的输入正弦信号,而Alpha和Beta是想间隔90°的输出正弦信号。
所以这的As和Bs分别对应上面的Ia和Ib,而Alpha和Beta分别对应上面的Id和Iq。
Park变换。
我们知道,我们现在讨论的坐标都是在定子角度来看的,也就是静止坐标。
我们知道,三相异步电动机是高耦合,非线性,多变量的系统,控制起来非常困难。
矢量控制的思想就是要实现三相电动机的解耦控制,什么意思呢,就是要像控制直流电动机那样去控制三相电动机,可以分别对励磁电流和转矩电流分别控制,有人问,怎么实现,我回答:马上就可以实现。
我们上面说了,clark变换就是将三相变成两相,但这时候还是静止的,但是相对转子是旋转的,我们要实现解耦控制,就要实现坐标相对转子静止,park变换这个时候可以派上用场了。
Clark变换与Park变换详解

Clark 变换与Park 变换详解很多同学对Clark 变换与Park 变换不求甚解,在运用的时候常常感到困惑,本文梳理了这两种变化的详细步骤,希望可以帮到大家。
设三相交流系统各相电压为:cos cos(120)cos(120)a mb mc m u V tu V t u V t ωωω=⎧⎪=-⎨⎪=+⎩ (0.1) a u b u c u 分别指ABC 三相电压的瞬时值,m V 指相电压基波幅值。
cos cos(120)cos120sin120122cos(120)cos120sin120122a m b m c m u V tV u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-+=+=-=--(0.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫ ⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭⎝⎭ (0.3)0a b c u u u ++=(0.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(0.5) 书上有两种表达式11/21/211/21/22302/20/22P P ----⎛⎫⎫== ⎪⎪⎝⎭⎭与 (0.6) 于是有同学开始疑问了,为什么?为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩(0.7) cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.8) 由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ (0.9) 两式相加有:cos sin d u u u αβαα=+ (0.10)22cos sin sin sin cos sin cos cos d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩(0.11)两式相减有:sin cos q u u u αβαα=- (0.12) 可得:cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.13) 将式(1.5)代入(1.13)中可得: cos cos(120)cos(120)23sin sin(120)sin(120)a d b q c u u u u u αααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪ ⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭ (0.14)。
Clark变换与Park变换详解

Clark 变换与Park 变换详解很多同学对Clark 变换与Park 变换不求甚解,在运用的时候常常感到困惑,本文梳理了这两种变化的详细步骤,希望可以帮到大家。
设三相交流系统各相电压为:cos cos(120)cos(120)a mb mc m u V tu V t u V t ωωω=⎧⎪=-⎨⎪=+⎩ (0.1) a u b u c u 分别指ABC 三相电压的瞬时值,m V 指相电压基波幅值。
cos cos(120)cos120sin120122cos(120)cos120sin120122a m b m c m u V tV u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-+=+=-=--(0.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫ ⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭⎝⎭ (0.3)0a b c u u u ++=(0.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(0.5) 书上有两种表达式11/21/211/21/22302/20/22P P ----⎛⎫⎫== ⎪⎪⎝⎭⎭与 (0.6) 于是有同学开始疑问了,为什么?为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩(0.7) cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.8) 由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ (0.9) 两式相加有:cos sin d u u u αβαα=+ (0.10)22cos sin sin sin cos sin cos cos d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩(0.11)两式相减有:sin cos q u u u αβαα=- (0.12) 可得:cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.13) 将式(1.5)代入(1.13)中可得: cos cos(120)cos(120)23sin sin(120)sin(120)a d b q c u u u u u αααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪ ⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭ (0.14)。
Clark变换Park变换及电机绕组折算的推导

学习中遇到的问题
学习中遇到的问题主要集中在知识点的理解与记忆上, 因为电机课程较难而且长时间没有复习,导致很多知识点都 忘了。其中:
1.变压器原理中频率折算没有找到相关概念与知识点。 2.对“三相不平滑”概念模糊,没有复习到。 3.交流电动机基本理论还没有复习完。
谢谢
i2
N1
k
14
变压器原理
3.功率和阻抗关系 一次和二次绕组瞬时功率关系:
u1i1
N1 N2
u2
N2 N1
i2
u2i2
上式表明一次侧瞬时功率与二次侧瞬时功率相等。设Z •
L
为二次侧负载阻抗,则
ZL
U2
•
,从一次侧看进去的
输入阻抗
Z
' L
为
I2
•
•
•
Z
' L
U1
•
kU2
•
k
2
U2
•
k2ZL
I1 I2 k
d cos sin
q
c
m
sin
cos
2020/3/22
8
Park变换
其中矩阵 c 满足c1 cT,解得m 1 ,因此:
c
cos sin
sin
c
os
9
Park反变换
对矩阵 c 求逆,解得:
c-1
cosБайду номын сангаас s in
- sin
c
os
10
Clark变换
Park变换 变压器原理 学习中遇到的问题
I2
15
变压器原理
4.变压器绕组折算
二次侧对一次侧的影响是通过二次磁动势实现的
foc控制原理——clark变换和park变换

foc控制原理——clark变换和park变换一、导言在现代电力系统中,频繁使用交流电机作为主要动力源。
而在这些电机中,磁场定向控制(Field-Oriented Control,FOC)技术已经成为一种常见的控制策略。
其主要特点是将交流电机分解为两个独立的控制回路,即电流控制回路和转矩控制回路,以实现快速、准确的控制。
本文将重点介绍FOC控制原理中的两个重要变换——clark变换和park变换。
首先会介绍它们的基本概念和原理,然后会详细讨论它们在FOC控制中的应用。
二、clark变换1. 基本概念clark变换也被称为αβ变换,它是一种将三相交流电压或电流转换为两相直流信号的数学变换方法。
通过clark变换,我们可以将三相电流空间矢量转换为两相坐标系中的两个分量。
这两个分量通常被称为α轴和β轴电流。
2. 原理clark变换的原理可以通过公式表达为:α = aβ = (2/√3) * (b - a/2 - c/2)其中,a、b、c分别代表三相电流的幅值。
通过这些公式,我们可以将三相电流转换为两相αβ坐标系。
3. FOC控制中的应用在FOC控制中,clark变换通常用于将三相电流转换为两相电流。
这样一来,我们就可以将三相交流电机的控制问题转化为两相电机的控制问题,从而简化了整个系统的控制难度。
三、park变换1. 基本概念park变换也被称为dq变换,它是一种将αβ坐标系中的两相信号转换为dq坐标系中的信号的数学变换方法。
在FOC控制中,park变换用于将电机状态转换为以磁场和转矩为坐标轴的坐标系中,从而方便进行磁场定向控制。
2. 原理park变换的原理可以通过公式表达为:d = α * cos(θ) + β * sin(θ)q = -α * sin(θ) + β * cos(θ)其中,α、β代表αβ坐标系中的两相信号,θ代表旋转角度。
通过这些公式,我们可以将αβ坐标系中的信号转换为dq坐标系中的信号。
关于Clark变换与Park变换
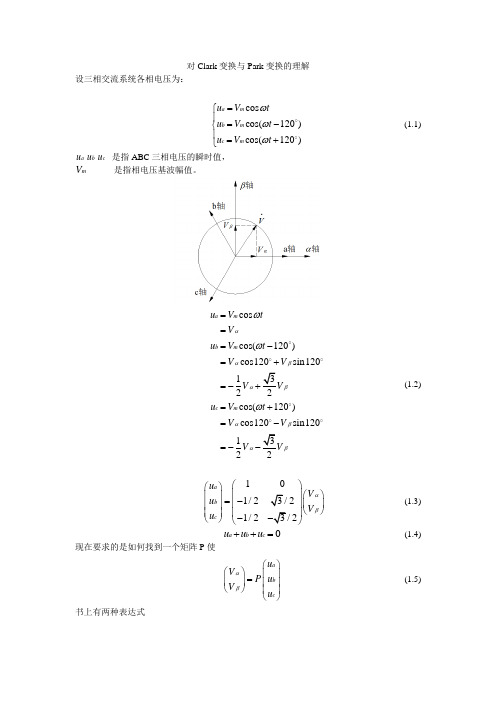
对Clark 变换与Park 变换的理解设三相交流系统各相电压为:cos cos(120)cos(120)a m b m c m u V t u V t u V t ωωω=⎧⎪=-⎨⎪=+⎩(1.1) a u b u c u 是指ABC 三相电压的瞬时值,m V 是指相电压基波幅值。
cos cos(120)cos120sin12012cos(120)cos120sin12012a m b m c m u V t V u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-=+=-=- (1.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪-⎝⎭⎝⎭(1.3)0a b c u u u ++= (1.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(1.5) 书上有两种表达式11/21/211/21/223022022P P----⎛⎫⎫==⎪⎪⎝⎭⎭与(1.6)若为幅值Vm守恒算法,则取系数为2/3;若为功率P守恒算法,则须开根号取系数为后者。
为什么非得是这种表达形式?根据电机的磁动势转变过来的。
由Clark变换推出Park变换cos sinsin cosd qd qu u uu u uαβαααα+=⎧⎨-=⎩(1.7)cos sinsin cosdqu uu uαβαααα⎛⎫⎛⎫⎛⎫=⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(1.8) 由式(1.7)可以得:22cos sin cos cossin sin cos sind qd qu u uu u uαβαααααααα⎧+=⎪⎨-=⎪⎩(1.9)两式相加有:cos sindu u uαβαα=+(1.10)22cos sin sin sincos sin cos cosd qd qu u uu u uαβαααααααα⎧+=⎪⎨-=⎪⎩(1.11)两式相减有:sin cosqu u uαβαα=-(1.12) 可得:cos sinsin cosdqu uu uαβαααα⎛⎫⎛⎫⎛⎫=⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(1.13) 将式(1.5)代入(1.13)中可得:cos cos(120)cos(120)23sin sin(120)sin(120)adbqcuuuuuαααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭(1.14)。
余弦信号经过克拉克变换与帕克变换的意义

余弦信号经过克拉克变换与帕克变换的意义摘要:一、引言二、克拉克变换与帕克变换的定义及原理1.克拉克变换2.帕克变换三、余弦信号经过克拉克变换与帕克变换的意义1.信号参数的提取与分析2.信号处理的便捷性与高效性四、克拉克变换与帕克变换在工程应用中的实例五、总结与展望正文:一、引言在信号处理领域,克拉克变换(Clarke Transformation)与帕克变换(Park Transform)是两种常见的信号变换方法。
它们主要用于将时域信号转换为频域信号,以便于对信号进行更深入的分析。
本文将探讨余弦信号经过这两种变换的意义及其在工程应用中的实例。
二、克拉克变换与帕克变换的定义及原理1.克拉克变换克拉克变换是一种双线性变换,可以将时域信号的幅度和相位信息分离。
对于一个余弦信号,通过克拉克变换,可以得到其频域信号的表达式为:S(jω) = A(ω) * exp(-jφ(ω))其中,A(ω)表示信号的幅度谱,φ(ω)表示信号的相位谱。
2.帕克变换帕克变换是一种单线性变换,也可以将时域信号的幅度和相位信息分离。
与克拉克变换不同的是,帕克变换可以将信号的相位信息转换为频域信号的幅度信息。
对于一个余弦信号,通过帕克变换,可以得到其频域信号的表达式为:S(jω) = A(ω) * exp(-jθ(ω))其中,A(ω)表示信号的幅度谱,θ(ω)表示信号的相位谱。
三、余弦信号经过克拉克变换与帕克变换的意义1.信号参数的提取与分析通过克拉克变换和帕克变换,我们可以将余弦信号的时域参数(幅度和相位)转换为频域参数。
这有助于我们更好地分析信号的频率特性,如幅频特性和相频特性。
2.信号处理的便捷性与高效性将信号转换为频域后,可以利用频域信号进行各种信号处理方法,如滤波、信号调制等。
与直接在时域进行信号处理相比,频域处理具有更高的效率和灵活性。
四、克拉克变换与帕克变换在工程应用中的实例1.通信系统在通信系统中,信号的调制与解调通常采用克拉克变换或帕克变换。
Clark变换与Park变换详解

Clark 变换与Park 变换详解很多同学对Clark 变换与Park 变换不求甚解,在运用的时候常常感到困惑,本文梳理了这两种变化的详细步骤,希望可以帮到大家。
设三相交流系统各相电压为:cos cos(120)cos(120)a mb mc m u V tu V t u V t ωωω=⎧⎪=-⎨⎪=+⎩ (0.1) a u b u c u 分别指ABC 三相电压的瞬时值,m V 指相电压基波幅值。
cos cos(120)cos120sin120122cos(120)cos120sin120122a m b m c m u V tV u V t V V V u V t V V V ααβαβαβαβωωω===-=+=-+=+=-=--(0.2)101/221/22a b c u V u V u αβ⎛⎫⎛⎫ ⎪⎛⎫ ⎪=- ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭⎝⎭ (0.3)0a b c u u u ++=(0.4)现在要求的是如何找到一个矩阵P 使a b c u V P u V u αβ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭(0.5) 书上有两种表达式11/21/211/21/22302/20/22P P ----⎛⎫⎫== ⎪⎪⎝⎭⎭与 (0.6) 于是有同学开始疑问了,为什么?为什么非得是这种表达形式?由Clark 变换推出Park 变换cos sin sin cos d q d q u u u u u u αβαααα+=⎧⎨-=⎩(0.7) cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.8) 由式(1.7)可以得:22cos sin cos cos sin sin cos sin d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩ (0.9) 两式相加有:cos sin d u u u αβαα=+ (0.10)22cos sin sin sin cos sin cos cos d q d q u u u u u u αβαααααααα⎧+=⎪⎨-=⎪⎩(0.11)两式相减有:sin cos q u u u αβαα=- (0.12) 可得:cos sin sin cos d q u u u u αβαααα⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭(0.13) 将式(1.5)代入(1.13)中可得: cos cos(120)cos(120)23sin sin(120)sin(120)a d b q c u u u u u αααααα⎛⎫⎛⎫-+⎛⎫ ⎪= ⎪ ⎪ ⎪-+⎝⎭⎝⎭ ⎪⎝⎭ (0.14)。
三相电感坐标变换

三相电感坐标变换
三相电感坐标变换是指通过适当的线性变换将三相电感坐标系下的物理量转换为两相电感坐标系下的物理量,以便于分析处理。
三相电感坐标变换的基本思路是将三相静止坐标系转换为两相静止坐标系,或者将三相旋转坐标系转换为两相旋转坐标系。
在实际应用中,三相电感坐标变换通常采用Clark变换和Park 变换等算法。
Clark变换是一种将三相静止坐标系转换为两相静止坐标系的方法,它可以消除电压、电流等物理量之间的耦合关系,简化分析过程。
Park变换是一种将三相旋转坐标系转换为两相旋转坐标系的方法,它可以实现三相交流电的矢量控制,提高电力系统的稳定性和动态响应性能。
通过三相电感坐标变换,可以实现对三相电感的解耦控制,提高电力电子系统的稳定性和可靠性。
同时,三相电感坐标变换还可以应用于电机控制、电力系统等领域,为相关领域的发展提供重要的技术支持。
Park-Clark-变换公式及锁相的推导

1 2 3 0
1 2 3 2
1 2 3 2 ,
V 因此: V
或:
1 2 3 0
1 2 3 2
1 Va 2 Vb 3 Vc 2
2 1 1 V (Va Vb Vb) 3 2 2 1 1 2 (Vm * cos t Vm * cos(t 120 ) Vm * cos(t 120 )) 3 2 2 1 2 (Vm * cos t * Vm * 2 * (cos t * cos120 )) 3 2 2 1 * (Vm * cos t Vm * cos t ) 3 2 Vm * cos t
也可由 Vd,Vq 反推 Va,Vb,Vc
1 0 Va 1 3 V Vb 2 V Vc 2 1 3 2 2 0 1 1 3 cos sin Vd Vq 2 sin cos 2 1 3 2 2 cos sin Vd cos( 120 ) sin( 120 ) cos( 120 ) sin( 120 ) Vq
1 | 1 0 0 2 2) (1) /(3) (1) 1 | 0 2 0 ( 1 |0 0 2 0 1)*6 ( 3 ) 0 ( 2 4 2 2 (1) ( 2 ) ( 3) / 3 2 3 6 0 3 3 3 3 3 3 3 3 1 1 3 3 3 3 3 3 2 2 3 3
即:
Vd Vm * cos( t ) Vq Vm * sin( t )
Matlab_Simulink中Clark变换和Park变换的深度总结

Matlab_Simulink中Clark变换和Park变换的深度总结最近搞三相并网逆变系统,对这个坐标变换产生了很多疑惑。
调模型,排错,最后发现坐标变换这个地方出来的波形总是和我设想的不一样。
以前认为坐标变换都是死的,带公式即可,经过这几天的研究,发现这里面真的有些方法。
基于MATLAB/Simulink中的模块,我也发现了Simulink中和一些书上不一样的地方。
而且现在这个坐标变换每本书上的表示方法都不一样,甚至字母都有好多种。
下面我想基于MATLAB/Simulink深刻的总结一下三相交流控制系统常用的两个变换Clark变换和Park变换。
首先来搞清楚为什么要用这两个变换,在三相交流系统中,常用的控制器还是经典的PI调节器。
PI调节器可以对直流量进行无净差的调节,而交流量就不行,所以需要将三相交流分量转化为两项直流分量加以控制。
接下来看看Clark变换(3-2)原理。
于三相分量幅值相等,相位相差120,角速度相等,因此三相分量存在信息冗余,这时,可以去掉一项将其化为两相,这就是Clark变换的作用。
于两项分量所在的坐标轴是静止的,所以我们把此坐标轴称为两相静止坐标系。
也就是说平面上的原来基于三相静止坐标系的矢量,可以切换到两相静止坐标系表示。
变换的原则是投影原则+等幅值等效原则(DPC时用功率等效原则)。
BBetaA(alfa)C令A与alfa轴重合,按照变换原则,计算投影ABC分量在alfa、beta上的投影,按照等复制变换原则导出变换矩阵方程如下。
11A1222B 3330C22Simulink中的3/2变换也是基于此变换进行的。
但是,在电气工程中为大家熟知的三相正序的相序是,A为0,B为-120,C为120(也可以是-240).如果按照图中所标注的方向进行坐标变换,那一定要将相序变为负序,也就是说A为0,B为120,C为-120.如果坚持用传统正序,那么再按上式变换之后的坐标进行变换的话,beta轴就反向了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个坐标系的坐标变换为另一种坐标系的坐标的法则。
由于交流异步电动机的电压、电流、磁通和电磁转矩各物理量之间是相互关联的强耦合,并且其转矩正比与主磁通与电流,而这两个物理量是随时间变化的函数,在异步电机数学模型中将出现两个变量的乘积项,因此,又为多变量,非线性系统(关键是有一个复杂的电感矩阵),这使得建立异步电动机的准确数学模型相当困难。
为了简化电机的数学模型,需从简化磁链入手。
解决的思路与基本分析:1.已知,三相( ABC )异步电动机的定子三相绕组空间上互差120度,且通以时间上互差120ω的旋转磁场。
度的三相正弦交流电时,在空间上会建立一个角速度为1又知,取空间上互相垂直的(α,β)两相绕组,且在绕组中通以互差90度的两相平衡交流电流时,也能建立与三相绕组等效的旋转磁场。
此时的电机数学模型有所简化。
2. 还知, 直流电机的磁链关系为:F---励磁绕组轴线---主磁通的方向,即轴线在d轴上,称为直轴(Direct axis)。
A---电枢绕组轴线---由于电枢绕组是旋转的,通过电刷馈入的直流电产生电枢磁动势,其轴线始终被限定在q轴,即与d轴成90度,称为交轴(Quadrature axis)。
由于q轴磁动势与d轴主磁通成正交,因此电枢磁通对主磁通影响甚微。
换言之,主磁通唯一地由励磁电流决定,由此建立的直流电机的数学模型十分简化。
如果能够将三项交流电机的物理模型等效的变换成类似的模型,分析和控制就变得大大简单了。
电机模型彼此等效的原则:不同坐标系下产生的磁动势(大小、旋转)完全一致。
关于旋转磁动势的认识:1) 产生旋转磁动势并不一定非要三相绕组不可。
结论是:除了单相电机之外,两相、三相或四相等任意对称(空间)的多相绕组,若通以平衡的多相电流,都可产生旋转磁动势。
根据这一道理,利用其在空间上互差90度的静止绕组,并通以时间上互差90度的平衡交流电流,同样可产生旋转磁场(或磁动势F),因而可等效代替三相绕组的作用。
这就是ABC——αβ(3-2)变换的思路。
2)进而认识到,若直流电机电枢绕组以整体同步速度旋转,使其相互正交或垂直的绕组M,T分别通以直流电流,产生的合成磁动势F相对于绕组是固定不变的,但从外部看,它的合成磁动势也是旋转的。
因此还可产生αβ——dq(2-2)变换。
矢量变换控制的基本思想:通过数学上的坐标变换方法,把交流三相绕组中的电流变换为两相静止绕组中的电流。
可以使数学模型的维数降低,参变量之间的耦合因子减少,使系统数学模型简化。
以产生同样的旋转磁动势为准则,可以用以下关系来表示所谓坐标变换的方法就是用一组新的变量来代替原方程中的一组变量,使得原方程(数学模型)得以简化(弱化强耦合或解耦)。
1.变换原则---功率不变约束条件设电压方程为u=Zi新定义的变量为'u、'i设电压变换矩阵为u C ,电流变换矩阵为i C ,则变换前后的电压和电流关系式为'u C u u = 'i C i i =假设变换前后功率不变,即u i P T = '''u i P T = 'P P = ''u i u i T T =经代入整理后,有 E C C u Ti =为简化变换阵,一般取 C C C i u == 代入上式,则有 E C C T= 1-=C C T式中,C 为单元变换矩阵,这种变换属于正交变换。
满足上述功率不变约束条件的正交变换实现了简化的统一变换关系。
2.(3s/2s 变换) 三相静止轴系A-B-C 到两相静止轴系βα-的变换 为便于分析,取三相绕组匝数相等:3N N N N C B A ===并取两相绕组匝数也相等, 2N N N ==βα可得到,两相绕组的旋转磁动势与三相绕组的磁动势等效表达式:οοοο240sin 120sin 0240cos 120cos C C B B C C B B A A i N i N i N i N i N i N i N ++=++=ββαα从而找出3/2磁动势等效下的两种电流间的对应关系及其变换矩阵,(为保证推导的严谨性,在非方阵中引入一个独立变量,称为零轴电流。
当定子绕组为Y 形接线时,可在变换矩阵中消去该独立因子)经推导整理可以得到3/2变换表达式,已知无零线Y 形接线时,0=++C B A i i i ,则有B A c i i i --= 。
代入上式进而可简化为:上式对电压和磁链也成立。
3.(2s/2r 变换) 二相静止轴系α,β到二相旋转轴系 d ,q 的变换假如有两个相互垂直的绕组,在两绕组中分别通以直流电流,并且将此固定磁场以同样的角速度旋转,则两相旋转绕组产生的合成磁场也是一个旋转磁场。
再进一步使两绕组轴线与三相绕组(或与两相静止绕组的轴线同方向)的旋转磁场方向相同。
由此即可用两个直流分量来替代三相交流电。
这可进一步简化参变量间的关系。
设两相静止坐标系与两相旋转坐标系间的夹角为(且随时间变化)01ϕωϕ+=t由两相静止轴系与两相旋转轴系的等效磁动势表达式可 以得到变换关系,⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡βαϕϕϕϕi i i iqdsin cos cos sin当定子三相电流为:代入3/2变换式,有⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡)cos()sin(112φωφωt t I i i m q d其中式说明,从静止三相A-B-C 变换到静止二相d-q ,在D 、Q 绕组中通以互 差90度的与三相同频率的两相平衡正弦交流电流,即可获得与三相静止 绕组等效的磁动势。
又可知,将上式部分(d 轴)展开后有,tI i t I i m dq m dp 1212cos sin sin cos ωφωφ==因此,d 轴分量又可分别定义为瞬时有功电流和瞬时无功电流之和,→→→+=dqdp d i i i因此,d 轴分量又可分别定义为瞬时有功电流和瞬时无功电流之和, →→→+=dqdp d i i i5.3/2变换结果代入2/2变换后有⎥⎦⎤⎢⎣⎡---⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡'')cos()sin(sin cos cos sin 112φωφωϕϕϕϕt t I i i m q d⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''φφsin cos 22m m q dI I i i上式说明,在D-Q 轴上通以两个直流电流,其大小分别为三相绕组中的有功电流和无功电流。
这样也可获得与三相绕组等效的磁动势。
6.由3/2变换的瞬时无功功率理论可以获得与上述同样的结果 已知,⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡βααββαi i e e e e i i e q p q p假定三相瞬时电压为三相平衡电压源,A 相电压为,代入电压3/2变换有代入上式整理后,有⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡βαωωωωi i t t t t i i q p 1111sin cos cos sin可见,上式与2/2变换结果相同。
7.进一步引申还可知道可以看出,经过3/2和2/2变换,三相交流系统中的基波有功分量和基波无功分量在d-q 坐标系表示为直流分量,或者讲,被变换的三相电流中若既含有基波电流,又有高次谐波电流,则经过变换后所获得的直流分量对应原来的基波电流,而变换获得的谐波分量将对应原来的(n-1)次谐波电流(注意到,3/2变换的结果仍保持频率不变,且两变量为正交分量)。
由此启发人们利用这样的变换/反变换结果来获取除了基波成分之外的其它畸变分量。
应注意到,虽然上述对电压的3/2变换代入到瞬时功率表达式中,可以得到与2/2变换同样的结果。
但在实际应用时却属两种检测算法。
例如,它们的低通滤波器设计参数不同;由于w旋转的,它与轴的夹角是随时间变化的,还需从系统电压提取同步相位d-q坐标系是以1信息。
另外,当考虑电压畸变时,2/2变换仍是准确的。
坐标变换由于直流电机的主磁通基本上唯一地由励磁绕组的励磁电流决定,所以这是直流电机的数学模型及其控制系统比较简单的根本原因。
如果能将交流电机的物理模型等效地变换成类似直流电机的模式,分析和控制就可以大大简化。
坐标变换正是按照这条思路进行的。
不同电机模型彼此等效的原则是:在不同坐标下所产生的磁动势完全一致。
1.坐标变换原理交流电机三相对称的静止绕组 A 、B 、C ,通以三相平衡的正弦电流时,产生的合成磁动势是旋转磁动势F,它在空间呈正弦分布,以同步转速ws(即电流的角频率)顺着A-B-C 的相序旋转。
这样的物理模型绘于下图1中。
图1交流电机绕组的等效物理模型图2等效的两相交流电机绕组旋转磁动势并不一定非要三相不可,除单相以外,二相、三相、四相、……等任意对称的多相绕组,通以平衡的多相电流,都能产生旋转磁动势,当然以两相最为简单。
图2中绘出了两相静止绕组a和b它们在空间互差90°,通以时间上互差90°的两相平衡交流电流,也产生旋转磁动势F。
图3旋转的直流绕组当图1和2的两个旋转磁动势大小和转速都相等时,即认为图2的两相绕组与图1的三相绕组等效。
图3两个匝数相等且互相垂直的绕组d 和q,其中分别通以直流电流id和iq,产生合成磁动势F,其位置相对于绕组来说是固定的。
如果让包含两个绕组在内的整个铁心以同步转速旋转,则磁动势F自然也随之旋转起来,成为旋转磁动势。
把这个旋转磁动势的大小和转速也控制成与图1 和图2中的磁动势一样,那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。
由此可见,以产生同样的旋转磁动势为准则,图1的三相交流绕组、图2的两相交流绕组和图3中整体旋转的直流绕组彼此等效。
或者说,在三相坐标系下的iA、iB 、iC,在两相坐标系下的ia、ib和在旋转两相坐标系下的直流id、iq 是等效的,它们能产生相同的旋转磁动势。
坐标变换的任务就是求出iA、iB 、iC 与ia、ib和id、iq 之间准确的等效关系。
2.三相--两相变换(3/2变换)在三相静止绕组A、B、C和两相静止绕组a、b之间的变换,或称三相静止坐标系和两相静止坐标系间的变换,简称3/2 变换。
图4 三相和两相坐标系与绕组磁动势的空间矢量上图绘出了A、B、C和a、b两个坐标系,为方便起见,取A轴和a轴重合。
设三相绕组每相有效匝数为N3,两相绕组每相有效匝数为N2,各相磁动势为有效匝数与电流的乘积,其空间矢量均位于有关相的坐标轴上。
由于交流磁动势的大小随时间在变化着,图中磁动势矢量的长度是随意的。
设磁动势波形是正弦分布的,当三相总磁动势与二相总磁动势相等时,两套绕组瞬时磁动势在a、b轴上的投影都应相等,写成矩阵形式,得考虑变换前后总功率不变,在此前提下匝数比应为代入上式,得三相—两相坐标系的变换矩阵令C3/2 表示从三相坐标系变换到两相坐标系的变换矩阵,则[1]3.两相—两相旋转变换(2s/2r变换)从两相静止坐标系到两相旋转坐标系d、q 变换称作两相—两相旋转变换,简称2s/2r 变换,其中s 表示静止,r 表示旋转。
