线性谐振子相图研究
谐振子-相图_153601860
r = ωd Ae
−(δ / ωd )ϕ
这是一个对数螺旋方程，无论从哪里出发，最后都趋向中心。称中心点 O 为吸 引子（attractor） ，它把相空间里的点都吸引到自己上边。中心点 O 同时又是一 个不动点，它是最简单的一类吸引子，即不动点吸引子。 在相平面中，代表点的矢径值的连续减少，总是表示振子的阻尼运动。
以 y 表示，方程（*6）可写作状态变量的一阶微分方程组 同理，将 x
=y x = − f ( x, y ) y 初始条件改为
（*7）
= t 0= : x(0) x0= , y (0) y0 方程组（*7）的解 x(t ) 和 y (t ) 完全确定系统的运动过程。 将方程组（*7）中两式相除，消去时间微分 dt 后,即得到确定相轨迹族的一 阶微分方程 dy f ( x, y ) = − dx y （*8）
⇒ T0 = ∫
dx 2[ E − U ( x)]
（*5a）
一般情况下， 周期 T0 随初始条件的不同而变化， 只有线性保守系统的周期与初始 条件无关。 例如，对谐振子
T0 = ∫
A
dx kA2 − kx 2
0
例 欠阻尼振子运动的相图 从欠阻尼振子的基本方程出发
x Ae −δ t sin(ωd t + θ ) = −δ t −δ t x = A −δ e sin(ωd t + θ ) + e ωd cos(ωd t + θ ) 做变量代换：
=x ( x) 的一阶微分方程，其解正好是（♣2）式。 这是 x
2 = −ω0 xdx xdx
1 2 2 1 2 = −ω0 ⇒ d x d x 2 2
⇒
3.5 线性谐振子
在自然界中一维谐振子广泛存在,任何体系在平衡位置附近 的小振动,如分子的振动,晶格的振动,原子和表面振动以及辐 射场的振动等都可以分解成若干彼此独立的简谐振动 简谐振动.本节将应 简谐振动 用薛定谔方程来求出谐振子的能量本征值和本征函数. 假设一个一维谐振子,其势能按泰勒级数展开.
T /2
2π
π dx / dt
x=asinωt, 那么
dx = aω cos ωt = ωa 1 ( x / a ) 2 dt a 1 wcl ( x )dx = dx π 1 ( x / a )2
(31) (32)
振幅可以从能量得到 E = 1 mω 2 a 2 , a = 2 E / mω 2 2 相反, 对局域在x+dx中的粒子,量子力学中的几率为
∧ 1 (ξ + ) = a ξ 2
∧+
(48)
从这两个关系, 我们可以估算ψn的相邻函数ψn-1和ψn+1. 为了简便 起见,我们做如下替代
1 (ξ ) = a ξ 2
∧+
(49)
(48)式变为
aψ n = nψ n 1 ,
(6)
k2 k 2 E κ= = = 2 λ 2 m ω ω
为了解方程(6),我们设一个非对称试解
ψ ( y) = e
y/2
( y)
(7)
dψ 1 d y / 2 d 2ψ 1 d d 2 y / 2 = [ ( y ) + ]e and = [ ( y )- + 2 ]e (8) 2 dy 2 dy dy 4 dy dy
λ x, dx =
2
∫ ψ ( x)
4线性谐振子与势垒贯穿
U r r r0处U r 有极小值 0 r r0
2U r 令k r 2 r 0 1 3U r g 2 r 3 r
0
1 1 2 3 U r U r0 k r r0 g r r0 1 2 3
线性谐振子 n=10时的几率密度分布
表明： 当n很大时， 量 迅速振荡，此时其平均值和经典振子
的概率密度已经接近，说明在n很大时即能量很高时， 量子振子的行为可以用经典振子来代替。
1 n x 例：设谐振子的初态为 x,0 A n 0 2
求(a)求归一化常数A；(b) x, t ? 解：(a)
1 2
1 2
(1)、(2)式改写为：
d 2 2 k1 0, 2 dx 2 d k22 0, dx2
x 0, x a 3
0 x a 4
x 0 :1 Aeik x Aeik x
E
1 En n , n 0,1,2,9 2
1 讨论： En n , n 0,1,2, 2
1、量子力学中一维线性谐振子的能量是不连续的，即量子化的。 2、能级的间隔等距，即
U(x)
n=3
En En1 En
/2
舍去！
应有限
方程(4)的渐进解为：
e
2 / 2
设方程(4)的一般解为： e
2
2 / 2
H ( )
2
6
2
代 入
d dH d H 2 2 H 2 H e 2 2 d d d
线性谐振子
• （一）引言
l
（1）何谓谐振子
l
（2）为什么研究线性谐振子
l （二）线性谐振子
l
（1）方程的建立
l
（2）求解
l
（3）应用标准条件
l
（4）厄密多项式
l
（5）求归一化系数
l
（6）讨论
l （三）实例
1
（一）引言
（1）何谓谐振子
在经典力学中，当质量为 的粒子，受弹性力F = - kx作用， 由牛顿第二定律可以写出运动方程为：
ξ2 >> ± 1
d 2 d 2
d
d
[ ]
d d
[ 2 1]
2
所以
c1e 2 / 2 c2e 2 / 2
因整个波函数尚未归一 化，所以c1可以令其等
波函数有 限性条件：
当ξ→±∞ 时， 应有 c2 = 0，
(x
xa
a)
2!
x 2
( x a)2
xa
V (a) V0
V 0 x xa
V(x)
V0
1 2!
2V x 2
( x a)2
xa
V0
1 2
k(x
a)2
a
x
0
V0
其中：k
2V x 2
3
xa
•
取新坐标原点为(a, V0)，则势可表示为标准谐振
d2x dt 2
kx
x 2 x 0
其中 k
其解为 x = Asin(ω t + δ)。这种运动称为简谐振动，作这种运
一维线性谐振子波函数及概率分布的可视演示
一维线性谐振子波函数及概率分布的可视演示1. 引言1.1 介绍一维线性谐振子概念一维线性谐振子是量子力学中常见的模型之一，它是一种简单但非常重要的系统。
在一维线性谐振子中，质点受到一个与位移成正比的恢复力作用，该系统的势能函数可以表示为一个二次函数。
谐振子是一种能永远保持振动的系统，其运动的频率只取决于系统的质量和弹性常数，而与振幅和初相位无关。
一维线性谐振子在物理学和工程学中有着广泛的应用，例如在分子振动、固体声子、原子力显微镜等领域都有着重要作用。
谐振子模型的基本方程是薛定谔方程，通过求解薛定谔方程可以得到谐振子的波函数和能量本征值。
波函数描述了谐振子在不同位置处的可能性振动状态，它可以用来计算系统的物理量，如位置、动量、能量等。
概率分布是描述粒子在不同位置或状态的可能性的函数，对于一维线性谐振子而言，概率分布可以帮助我们了解系统的稳定性和振动行为。
在量子力学中，概率分布是一个非常重要的概念，它反映了粒子在不同态中的出现可能性，是描述微观粒子行为的关键工具。
通过研究一维线性谐振子的波函数和概率分布，我们可以深入理解量子系统的性质和行为，为进一步的物理研究提供基础和指导。
1.2 谐振子波函数的意义谐振子波函数是描述谐振子系统状态的数学函数。
在量子力学中，波函数是描述微观粒子运动及性质的基本工具，而谐振子波函数则是描述谐振子系统可能状态的函数。
谐振子波函数的意义在于通过波函数的数学表达，我们可以揭示谐振子系统的量子性质，如能级结构、态的叠加等。
波函数的意义还在于它可以用来计算系统的物理量，比如位置、动量、能量等的期望值。
谐振子波函数的意义还体现在其具有很强的几何意义。
波函数的模的平方代表了在空间中找到粒子的概率密度，而相位则含有波函数的相对相位信息。
通过波函数的几何意义，我们可以直观理解谐振子系统的量子态分布规律，如波函数的振幅大小和位置分布的关系等。
谐振子波函数的意义在于提供了描述谐振子系统状态的数学工具，揭示了系统的量子性质和几何结构。
第四讲 线性谐振子及应用及算符 ppt 量子力学教学课件
d 2
求渐证解：ξ→±∞时（4）变为 d 2 =ξ2Ψ 上式解
1 2
Ψ（ξ） e 2
e λ取负值 Ψ（ξ）=+
1 2
2 （要求 ξ→-∞时，Ψ（ξ）有限）
可把
Ψ
写成如下形式
Ψ（ξ）=
1 2
e2
H ( ) ，
要求 ξ→∞时，Ψ（ξ）有限，对 Ψ 求=阶微商
d
dH
e d =(-ξH+ d 2 )
1 2
H0=1→Ψ=A e 2 (ξ=ax)
H1=2ξ→Ψ=Aξ
e
1 2
2
H2=4ξ2—2→Ψ=A(4ξ2—2)
1 2
e2
H3=8ξ3—12ξ→Ψ=A(8ξ3—12ξ)
1 2
e2
ξ… Ψn 的通式 Ψn=Nne–ξ1/2Hn（ξ）
∫Ψ*nΨndξ=1,
(ξ=ax)
N=（
a
1
)2
1
2 2n n!
。
Ψn(x)=
(
a
1
1
)2
1 2
e2
Hn(ξ)
一维线性谐阵子波函数
2 2 n n!
四，经典方法处理
在经典力学中，在 ξ→ξ+dξ 之间找到的粒子几率
ω经典（ξ）dξ 与质点在此区域逗留的时间 dt 成比例。
dt
ω经典（ξ）dξ= T ， T 振动周期。
ω经典（ξ）=
1
d
T
=
1 VT
几率密度与质点建度成反比。
dt
力学量与力学量算符的对应关系
力学量
算符
势能 V(r)→ V^ ( ^r)
P2
动能 T= 2
2.7线性谐振子
dH ( ) s 1 s s v sa0 ( s 1)a1 ... (s v 1)av 1 ... d
... av s v ,(a0 0, s 0)
v 0
s(s 1)a0 s 2 (s 1)sa1 s ... (s v 2)(s v 1)av 2 s v ... (2s 1)a0 s ... (2s 2 1)av s v ...
2
由波函数标准条件可知,级数必须在某一项中断:av’+2=0.
(2s 2 1) 0
av2 av4 ... 0, a0 0, v必须是偶数
为了保证奇数项中断,必须取a1=0.
s 0 : 2v 1 2n 1, n 0,1, 2,.... s 1: 2(v 1) 1
Quantum mechanics
§2.7 线性谐振子
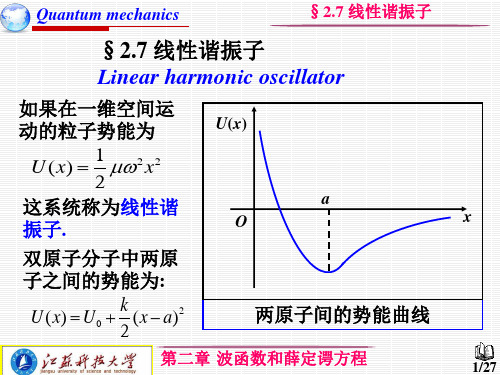
§2.7 线性谐振子 Linear harmonic oscillator
如果在一维空间运 动的粒子势能为
1 U ( x ) 2 x 2 2
U(x)
这系统称为线性谐 振子. 双原子分子中两原 子之间的势能为:
k U ( x) U 0 ( x a) 2 2
2 2 d n n ( x) [ n 1 ( x) dx 2 n 1 n 1 ( x)] 2
9/27
第二章 波函数和薛定谔方程
Quantum mechanics
§2.7 线性谐振子
(4),本征函数
n=0 -4 -2 0 2 4
n=1 -4 -2 0 2 4
n=2 -4 -2 0 2 4
量子力学线性谐振子（精品pdf）
６１§2.7线性谐振子(理想模型)重点：线性谐振子问题的本征解难点：结果讨论及其理解一、参考模型无论在经典物理还是在量子物理中线性谐振子都是很有用的模型。
任何体系在稳定平衡点附近的运动都可以近似地看作一维谐振子。
如双原子分子的振动，晶体结构中原子和离子的振动，核振动等等都使用了谐振子模型，辐射场也可以看作线性谐振子的集合。
以双原子分子为例： 双原子分子中两原子间的势能U 是两原子间距离x 的函数，其形状如图所示。
在a x =处势能有一极小值，这是一个稳定平衡点，在这点附近，)x (U 可以展为)a x (−的幂级数，且注意到 0x Ua x =∂∂= 则：....)a x )(a (''U !21)a (U )x (U 2+−+= 若忽略高次项，且令)a (''U k =， 则有：2)a x (k 21)a (U )x (U −+= 再令0)a (U =；a x 'x −=，则有2'kx 21)'x (U =，可以写成： 2kx 21)x (U =(1) 其中2k μω=。
６２ 凡是在势能为2kx 21)x (U =的场中运动的微观体系都称之为线性谐振子。
二、线性谐振子的本征问题1.体系的哈密顿及本征方程 22222x 21dx d 2H ˆμω+μ−=h )x (E )x (]x 21dx d 2[22222ψ=ψμω+μ−h 2.本征方程的求解 方程两边同乘以ωh 2得： ψω=ψμω+ψμω−h h h E 2x dx d 222 令hμω=α；x α=ξ；ω=λh E 2 (2) 得到：0)()()(d d 222=ξψξ−λ+ξψξ(3) 由于方程0)()()(d d 222=ξψξ−λ+ξψξ不能直接求解，可先求±∞→ξ的渐进解，此时由于λ与2ξ相比可以忽略，则方程退化为： 0d d 222=ψξ−ψξ—渐近方程 (4) 其渐进解为：221e )(ξ±∝ξψ 由波函数的有限性(满足0)(⎯⎯→⎯ξψ∞→ξ)知，只能取2/2e )(ξ−∝ξψ６３ 的解，于是可以令方程0)()()(d d 222=ξψξ−λ+ξψξ的一般解为： )(H e )(2/2ξ=ξψξ− (5) 其中待求函数)(H ξ应满足条件：a. 在ξ有限时)(H ξ应为有限；b. 当±∞→ξ时，)(H ξ也必须保证)(ξψ有限，即0)(→ξψ。
线性谐振子相图研究
文献综述题目：线性谐振子相图研究姓名：学号：系别：物理与电子信息工程系专业：物理学年级：指导教师：2009年2月7 日文献综述一、前言线性谐振子是量子力学中可以精确求解的有限几个事例之一[1]，其中最简单的线性谐振子是简谐振子。
自然界中任何一个力学系统，只要某一个物理量在其稳定平衡点附近作微小振动，便可以用简谐振子模型来描述，例如：复摆的振动、分子的振动、晶格的振动、原子核表面振动以及辐射场的振动等。
在选择适当的坐标系之后，复杂的运动往往可以分解成若干彼此独立的一维简谐振动（simple harmonic vibration ）。
简谐振动作为一种最简单最基本的振动，往往还是复杂运动的初步近似，是研究振动的基础。
因此研究它在理论上和应用上都有重大的意义。
其中从相空间的角度来研究振动系统的力学问题如今已经成为一个研究趋势。
因为相图里包含着完整的力学系统的全部信息，无须去解复杂的运动方程[2]。
计算机技术软硬件的飞速发展，为此研究趋势提供了现实条件。
本论文从简谐振子的基本定义出发，在Fortran 90条件下进行数值模拟并在Origin75 软件下获得简谐振子的相图。
二、主体2.1简谐振动的定义定义一： 物体只在弹性力或准弹性 （线性回复力）作用下发生的运动，即动力学方程为的运动为简谐振动[2]。
定义二： 在无外来强迫力作用下, 物体相对于平衡点的位移随时间按余弦（或正弦）规律变化即 则称物体作简谐振动式即简谐振动的表达式[3]。
—振幅；—角频率；—相位；—初相位。
位移随时间的变化曲线称为振动曲线。
广义定义：某个物理量随时间的变化是按正弦或余弦规律，则可称该物理量做简谐动，可用表示 。
自然界中任何一个力学系统中，只要某一个物理量在其稳定平衡点附近作微小振动，便可以用这种简谐振子模型来描述，例如：复摆的振动、分子的振动、晶格的振动，原子核表面振动、辐射场的振动以及电磁场振动等等。
2.2简谐振动的基本特征及动力学特征简谐振动位移随时间的变化 cos()x A t ωφ=+222d d xx o tω+=()cos()x t A t ωφ=+()cos()x t A t ωφ=+物体作简谐振动时,速度为：物体作简谐振动时，加速度为：可见物体做简谐振动时，其速度、加速度都以同样的角频率作简谐振动，相位依次超前π/2。
线性谐振子量子力学课件
对应的波函数是：
1 2
1 2x2
n (x) Nn H n ( ) e 2 Nn H n (x) e 2 .(
)
(3.2 9)
Nn是归一化常数，利用特殊积分
ex2 dx ,
可得
Nn
2n
n
. !
2.讨论 (1) 能级是等间隔的 ；(2)零点能是
E0
1
2
；(3)能级
的宇称偶奇相间，基态是偶宇称,即ψn(-x)=(-1)ψnn(x) (4)ψn(x)有
当ξ→±∞时，方程变为：
d 2 d 2
2 .
我们发现它有近似解：
12
() ~ e 2 .
但是 e 2 /2 应该舍去。
所以再进行变换：
12
() e 2 H(),
可得关于H(ξ)的如下方程：
d 2 H 2 dH ( 1)H 0. (3.2 4)
d 2
d
二. Hermitian多项式 可以用级数法求解H(ξ)的方程，结果发现：只要H(ξ)是“真”
§ 3.2线性谐振子
一维量子谐振子问题
在经典力学中，一维经典谐振子问题是个基本的问题，它 是物体在势（或势场）的稳定平衡位置附近作小振动这类常见 问题的普遍概括。在量子力学中，情况很类似。一维量子谐振 子问题也是个基本的问题，甚至更为基本。因为它不仅是微观 粒子在势场稳定平衡位置附近作小振动一类常见问题的普遍概 括，而且更是将来场量子化的基础。
d
dt
a
cos(t
)
a
(1
a
2 2
)
1 2
所以几率密度与 (1 2
/
a
2
)
1 2
成比例。
ZJH_2-7_线性谐振子_33p
令k=k’+2
k′
用 k 代替 k’
k
该式对任意ξ 该式对任意ξ都成立， 都成立， 故ξ同次幂前的系数均应为零， 同次幂前的系数均应为零， 2 d H dH bk +2 (k + 1)(k + 2) − bk 2k + bk (λ − 1) = 0 − 2ξ + ( λ − 1) H = 0 2 dξ dξ 2k + 1 − λ bk 方程 P30(2.7-6)式 系数bk的递推公式 bk + 2 = Hermite (k + 1)(k + 2) 9 线性谐振子
(2) ξ→±∞ 需考虑无穷级数H(ξ)的收敛性 H (ξ ) = bkξ k k =0 为此考察相邻两项之比 为此考察相邻两项之比： 两项之比： k +2 2k + 1 − λ bk + 2ξ 2 2 2 2k + 1 − λ bk + 2 = bk → ξ = ξ k→∞ k (k + 1)(k + 2) k ( k + 1)( k + 2) bξ
2 2
±
ξ
ξ
−
ξ
P30(2.7-6)式
线性谐振子
8
ψ (ξ ) = e
H ′′ = ∑bk k (k − 1)ξ
k =0
H (ξ ) P30(2.7-5)式 3). 解H(ξ)——级数解 k k −1 ′ 2ξ H = ∑ 2 bk k ξ H ′ = ∑ bk k ξ
2
k −2
−
ξ2
H(ξ)可表示 H (ξ ) = b ξ k ∑ k 为泰勒级数 k =0
h
α=
mω 2E ,λ = h hω
一维线性谐振子波函数及概率分布的可视演示
一维线性谐振子波函数及概率分布的可视演示1. 引言1.1 引言概述一维线性谐振子是量子力学中的一个经典模型，它的波函数和概率分布是量子态的基本描述。
谐振子模型是许多物理问题的重要近似，可以用来描述原子振动、分子振动、晶格振动等现象。
通过分析谐振子的波函数和概率分布，我们可以更好地理解量子系统的性质和行为。
在本文中，我们将介绍一维线性谐振子模型的基本原理和数学表达，探讨谐振子的波函数和概率分布的性质，以及它们之间的关系。
通过可视化模拟实验，我们将展示谐振子波函数和概率分布在空间中的变化规律，帮助读者更直观地理解量子态的特性。
通过本文的研究，我们希望能够深入探讨一维线性谐振子的波函数和概率分布，为量子力学的学习和研究提供更清晰的视角。
我们也期待通过可视化演示，帮助读者更好地理解量子态的概念和性质。
1.2 研究背景一维线性谐振子是量子力学中一个重要的模型系统，它具有丰富的物理行为和广泛的应用领域。
研究线性谐振子的波函数和概率分布可以帮助我们更好地理解量子力学中的基本概念和原理。
在物理学的发展历程中，谐振子模型一直被广泛应用于描述原子、分子、固体物质、振动系统等多种物理系统，因此对一维线性谐振子的波函数和概率分布进行深入研究具有重要的理论意义和实际应用价值。
通过对谐振子波函数和概率分布的分析，可以揭示量子系统的波动性质和粒子分布规律。
研究一维线性谐振子的波函数及概率分布具有重要的科学意义和应用价值，可以促进量子力学理论的深化和应用技术的发展。
1.3 研究目的我们的研究目的是通过对一维线性谐振子波函数及概率分布的可视演示，帮助读者更直观地理解量子力学中的基本概念和现象。
通过对谐振子模型的介绍，波函数和概率分布的分析，以及它们之间关系的探讨，我们希望能够帮助读者建立起对量子力学中波函数和概率分布之间重要关系的深刻理解。
通过可视化模拟实验，我们将展示不同参数对谐振子波函数和概率分布的影响，帮助读者更好地理解量子态的性质。
量子力学2 波函数-4qz
x 2 0 ( x) e
1/ 2 2
在基态时，经典几率密度和量子几率密度完全 相反，但是量子数很大时量子几率密度将趋于 经典几率密度
n
量子概率分布 经典概率分布
n
能量量子化 能量取连续值
在某些极限的条件下，量子规律可以转化为经典规律。
对应原理
以近似为谐振子势。
k U U 0 ( x a) 2 2
其实很多量子力学问题 简谐运动 合成 复杂振动
分解
量子力学中的简谐运动
一.势函数
1 2 1 2 2 U ( x ) kx m x 2 2
m—振子质量，—固有频率，x—位移
二.哈密顿量
ˆ d 1 2 x 2 H 2 dx2 2
在 x a 处，有一极小 值 V0 。在 x a 附近， 势可以展开成泰勒级数：
V (a) V0
V x 0
xa
V(x) a 0
V0
x
1 V 1 2V V ( x) V (a ) ( x a) 1! x xa 2! x 2 1 V0 k ( x a ) 2 2
当 时级数的渐进行为是
a 2 2 av
这与 e
2
2
的级数展开相同
2 2 e 1 2! 4
! 1! 2 2
b 2 2 ，因此在 时 H ( ) bv
§1.7 一维线性谐振子
一维线性谐振子
1. 一维谐振子经典图像
引言
1.经典谐振子
在经典力学中，当质量为 的粒子，受弹性力 F k x 作 用，由牛顿第二定律可以写出运动方程为： 其解为 x A sin t 。这种运动称为简谐振动，作这种运 动的粒子称为（线性）谐振子。
3.5线性谐振子
38
34
2. H(ξ)满足的方程
将ψ(ξ)表达式代入Schrodinger方程得 关于 待求函数 H(ξ) 所满足的方程：
H 2H ( 1)H 0
如何求解H(ξ) ？级数法求解！
38
35
3.级数解
我们以级数形式来 求解。 为此令：
H bk k k 0
H
bk k k 1
k 0
因此，设能量本征方程的解为：
En1n2n3 En1 En1 En1
n1 ( x) n2 ( y) n3 ( z )
Hˆ Hˆ x Hˆ y Hˆ z
E Ex Ey Ez
( x) ( y) (z)
解得能量本征值为：
则波函数三方向的分量 分别满足如下三个方程：
Eni
(ni
0,
1,
...,
N
→
1
0,
1,
...,
N-1
→
2
0,
1,
...,
N-2
→
...,
...,
...,
...,
...
→
N
0,
→
组合方式数 N+1 N N-1 ... 1
对给定 N ( N= n1 + n2 + n3 ), {n1 , n2, n3 }的组合方式数
(1/2)(N+1)(N+2)
当n1 , n2 确定后， n3 = N－n1－n2，也就确定了，不增加不同组
2
2
d2
dx
2
d2 dy 2
d2 dz 2
1 2
2
(x2
y2
z2)
Hˆ x Hˆ y Hˆ z
线性谐振子
1
1
4
e2x2 / 2
1(x)
211!
e2x2 /2 H1( x)
2
e2x2 / 2 2 x
1
1
2 xe2x2 /2
4
2(x)
222!
e2x2 / 2 H2 ( x)
8
e2x2 /2 4 2 x2 2
其解为 x = Asin(ω t + δ)。这种运动称为 简谐振动,作这种运动的粒子叫谐振子。
因为
F dV dx
所以
因：k m2
V
kxdx
1 2
kx 2
V0
1 2
m 2 x2
V0
若取V0 = 0，即平衡位置处 于势 V = 0 点，则
V 1 m2 x2
2
量子力学中的线性谐振子就是指在该式所描述的势场中 运动的粒子。
e 2 / 2
为了使方程 d 2 d 2
[ 2 ] (x) 0的波函数
在无穷远处有 e 2 / 2渐近形式，我们自然会令：
( ) H( )e 2 / 2
(2.7-5)
• 其中 H(ξ) 必须满足波函数的单值、有限、连续的标准 条件。即：
ω0(ξ)
-1 0 1
ωn(ξ)
n=2
n=1 n=0
-1 1
|10|2
-4 -2
24
求
1
x
0
x
dx
0(x)
1
1
4
e 2x2 / 2
1(x)
9 一维线性谐振子ppt
n
展开系数
m ( x) ( x)dx m ( x) an n ( x)dx an m ( x) n ( x)dx n n
an mn am
n
C.一维谐振子每一个能量的本征值对应有一个本 征函数，即能级是不简并的。 D.坐标算符或动量算符作用于本征函数 上，结果 是 1
2 d 2 1 ˆ H m 2 x 2 2m dx 2 2
ˆ H 不显含时间，是谐振子的能量算符。
• 9.2求解定态Schrodinger方程 ˆ H ( x) E ( x) • 即 • A). 取 B) 定义无量纲能量、无量纲坐标
E
2 d 2 1 ( m 2 x 2 ) ( x) E ( x) 2m dx 2 2 1 d2 ( 2 x 2 ) ( x) E ( x) m 1 得 2 dx
1 1 2 2 7 3 3 3 ( x) 1 4 (2 x 3 x) exp( x ) E3 2 2 3
量子力学概率与经典概率的比较
兰线是经典概率 密度 红线是量子概率密度
谐振子势能曲线和概率密度分布
• 9.4本征值和本征函数的数学性质 • A.能量本征值取分立值，即谐振子的能量是量
n 0,1,2,....
• 本征函数和对应的本征值举例
1 2 2 0 ( x) 1 4 exp( x ), 2 2 1 2 2 1 ( x) 1 4 x exp( x ) 2
1 E0 2 3 E1 2 5 E2 2
1 1 2 2 2 2 2 ( x) 1 4 (2 x 1) exp( x ) 2 2
§3.2线性谐振子
§3.2 线性谐振子重点：谐振子模型的意义能量波函数的特征与经典情况的区别(3.2-1)其中是弹性系数为k的谐振子作简谐振动的角频率。
经典力学中线性谐振子的哈密顿函数为（3.2-2）故在量子力学中，线性谐振子的哈密顿算符为由于U(x)与时间无关，故为定态。
线性谐振子的定态薛定谔方程为（3.2-4）为了简化，引入无量纲的变量（3.2-5）（3.2-6）（3.2-7）则方程（3.2-4）可改写成（3.2-8）我们令方程（3.2-8）的一般解为（3.2-9）所满足的方程得到H（3.2-10）（3.2-11）代入（3.2-7）中，可求得线性谐振子的能级（3.2-12）n=0, 1, 2,…，由此得下面结论：（1）线性谐振子能是只能取分立值（图3.4），好能量是量子化的，，这与普朗（2）谐振子的能级是均匀分布的，相邻两能级间隔克假设一致。
（3）谐振子的基态（n=0）能量为（3.2-13）称为零点能，零点能的存在，是量子力学的一个重要结果，这是旧量子论中所没有的。
对应于不同的n或不同的。
（3.2-14），它可以用下列式子表示方程（3.2-14）的解是厄密多项式（3.2-15）脚标n表示多项式的最高次幂。
下面列出前面n项厄密多项式：（3.2-16）由（3.2-9）式，对应能量E n的波函数是（3.2-17a）或（3.2-14b）这函数称厄密函数，式中N n为归一化常数。
由归一化条件经计算得（见附录1）（3.2-18）归一化后的前三个波函数如下：（3.2-19）等函数是x的偶函数，即从上面各式容易看出，我们称这些波函数具有偶宇称，而我们称这些波函数具有奇宇称。
（三）与经典比较经典和量子谐振子的能级与分布几率上图中横坐标代表振子的位置，抛物线代有势能曲线，En是量子化的能级，虚曲线代表波函数，实曲线代表几率分布，由图可以看出：当n=0时，波函数。
除了有n个节点，即有n个根。
类推，因此波函数只在于绕平均值迅速振荡而已。
第二章 §2.7 线性谐振子_10_22
d 2 2E 2 2 2 2 2 2 2 2 x ( ) 0 d d 2 2 E 2 x ( ) 0 2 d d 2 2E 2 ( ) 0 2 d
( x) 令 x;
2 d2 d2 d2 2 d 2 2 2 1 dx d 2 d d 2
2
2 d 2 2E 2 2 2 2 2 x ( ) 0 2 d
d 2 2 0 2 d
其渐近解为：
~ e
2 / 2
满足束缚态条件：
0,
x
d 2 2 为了使方程 [ ] 0的波函数 2 d 在无穷远处有 ~ e
2 / 2
渐近形式，令：
( ) H ( )e
2 / 2
§2.8 势垒贯穿
按照经典力学，粒子不可能穿过势垒。 但按照量子力学计算，粒子能穿过比它动能更高的势垒， 这种现象称为隧道效应（tunnel effect）。 透射系数：
16 E (V0 E ) 2a |T | exp[ 2m(V0 E ) ] V0
2
经典
隧道 效应
量子
1 V V ( x ) V (a ) 1! x
1 2V V0 2! x 2
1 2V ( x a) 2! x 2 x a
( x a )2
( x a )2
x a
V(x)
x a
1 V0 k ( x a )2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
文献综述题目：线性谐振子相图研究姓名：学号：系别：物理与电子信息工程系专业：物理学年级：指导教师：2009年2月7 日文献综述一、前言线性谐振子是量子力学中可以精确求解的有限几个事例之一[1]，其中最简单的线性谐振子是简谐振子。
自然界中任何一个力学系统，只要某一个物理量在其稳定平衡点附近作微小振动，便可以用简谐振子模型来描述，例如：复摆的振动、分子的振动、晶格的振动、原子核表面振动以及辐射场的振动等。
在选择适当的坐标系之后，复杂的运动往往可以分解成若干彼此独立的一维简谐振动（simple harmonic vibration ）。
简谐振动作为一种最简单最基本的振动，往往还是复杂运动的初步近似，是研究振动的基础。
因此研究它在理论上和应用上都有重大的意义。
其中从相空间的角度来研究振动系统的力学问题如今已经成为一个研究趋势。
因为相图里包含着完整的力学系统的全部信息，无须去解复杂的运动方程[2]。
计算机技术软硬件的飞速发展，为此研究趋势提供了现实条件。
本论文从简谐振子的基本定义出发，在Fortran 90条件下进行数值模拟并在Origin75 软件下获得简谐振子的相图。
二、主体2.1简谐振动的定义定义一： 物体只在弹性力或准弹性 （线性回复力）作用下发生的运动，即动力学方程为的运动为简谐振动[2]。
定义二： 在无外来强迫力作用下, 物体相对于平衡点的位移随时间按余弦（或正弦）规律变化即 则称物体作简谐振动式即简谐振动的表达式[3]。
—振幅；—角频率；—相位；—初相位。
位移随时间的变化曲线称为振动曲线。
广义定义：某个物理量随时间的变化是按正弦或余弦规律，则可称该物理量做简谐动，可用表示 。
自然界中任何一个力学系统中，只要某一个物理量在其稳定平衡点附近作微小振动，便可以用这种简谐振子模型来描述，例如：复摆的振动、分子的振动、晶格的振动，原子核表面振动、辐射场的振动以及电磁场振动等等。
2.2简谐振动的基本特征及动力学特征简谐振动位移随时间的变化 cos()x A t ωφ=+222d d xx o tω+=()cos()x t A t ωφ=+()cos()x t A t ωφ=+物体作简谐振动时,速度为：物体作简谐振动时，加速度为：可见物体做简谐振动时，其速度、加速度都以同样的角频率作简谐振动，相位依次超前π/2。
根据牛顿第二定律Fm a= ，得22cos()F m a m A t m xωωφω==-+=-力与位移大小成正比，符号相反，这样的力就是线性回复力。
这是简谐振动的动力学特征。
2.3相空间和相迹的概念 H q P αα∙∂=∂(1,2,3)s α=H p q αα∙∂=-∂(1,2,3)s α=以上是哈密顿正则方程[4]，其中q α为广义坐标，q α∙为广义速度,p α广义动量。
而正则方程共有 2S 个相互联立的一阶常微分方程组 ，对这 2S 个方程求解，即可完全确定力学系统的运动状态。
在哈密顿方法里，我们引入相空间概念[2]。
相空间：是以S 个广义坐标qα 和 S 个广义动量p α为变数而构成的2S 维抽象空间称为力学系统的相空间。
任一瞬时力学系统的广义坐标和广义动量确定了相空间的一个点，我们称为相点，每个相点对应于系统的一个确定状态，当时间变化时，由于系统运动，这个相点也在相空间中运动，它在相空间中描画出的一条曲线称为相迹。
对于二阶系统，比如要研究简谐振动，它的状态变量只有两个，所以简谐振动的相空间即简化为二维相平面。
相平面：对于以运动物体的位移（x ）和速度(y)作为坐标参量构建的空间，就是的相平面。
相点：相平面每个点对应着系统的一个运动状态，这个点就称为相点，“相”是指物体的运动状态。
d sin()cos()d 2x A t A t tπωωφωωφ==-+=++v 222d d cos()d d x a A t ttωωφ===-+v相轨迹：相点随时间t 的变化在x x ∙- （公式）平面上描绘出的轨迹线，这种轨迹称为相轨迹，它表征了系统运动状态（相）的演变过程。
简而言之，相图上的每一条曲线表示在不同初始条件下，物体在相空间内的运动轨迹，曲线上的任意一点代表物体的某一运动状态。
2.4相轨迹作图方法相轨迹的作图方法可分为：解析法和图解法。
其中解析法主要针对相对比较简单的系统，比如简谐振动系统，可直接由动力学方程求出位移（x）与速度（x ∙）之间的关系的。
用解析法求相轨迹是比较麻烦的，特别是对非线性系统，有时可能无法求出相轨迹的解析表达式。
而图解法则主要针对不能直接由方程求出,x x ∙关系的系统，原则上说，此法对任何非线性系统都适用。
2.4.1用解析法求解简谐振子相图方程[5]广义定义：某个物理量随时间的变化是按正弦或余弦规律，则可称该振动为简谐振动，可用 表示。
速度(y)y x∙=2y x x ω∙∙∙==-2dy y xdxω=-2ydy xdxω=-方程两边积分得：22222yx Cω=-+ 简谐振子相轨迹方程：222x y Cω+=①式中ω为系统初始值，C 是由初始状态决定的常量 法二：cos()x A t ωφ=+cos()x A t ωφ=+d sin()d x A t tωωφ==-+v cos()x A t ωφ=+法一：位移（x ）222221x vAAω+=式中ω为系统初始条件，而常数22020nx x A ω +=，它是由初始状态决定的常量。
由简谐振动系统的相图方程式①②中，可以很显然地看出简谐振动的相轨迹是为闭合的椭圆。
2.5简谐振动能量以弹性系数为k ，质量为m 的弹簧振子为例,圆频率ω 满足2k m ω=2.6计算机辅助获得相图Fortran( Formula Translation System)可谓目前计算机运算中的程序语言之父，它是第一个能将数学公式转换成计算机程序的语言。
Fortran 擅长于数学函数运算，主要应用于数值分析、系统仿真及自动控制等领域。
自1954年，从第一个Fortran 程序诞生到现在接近50年啦，很长一段222211sin ()22k E m m A t υωωφ==+212k p E E E kA=+=消去tcos()x A t ωφ=+d sin()d x A t tωωφ==-+v 22211cos ()22p E kxk A t ωφ==+对于简谐振子系统来说，系统的总能量与振幅A2成正比。
对于系统来说，振动过程中任意时刻机械能守恒②时间内是科学计算语言的唯一选择，期间积累的大量的正确、可靠的程序，尽管Fortran标准改了多次，但由于其向下兼容，很多程序是招值即来，来之能战，并且相比于C语言，Fortran语言的纠错功能更强大，因而可算是个易掌握的好工具。
Origin是有着强大的数据分析和绘图功能的作图软件。
它的数据分析功能包括数据的排序、调整、计算、统计、频谱变换、曲线拟合等各种完善的数学分析功能，而且此软件操作简单，易于掌握。
计算机辅助获得相图的方法本质上是图解法获得相图。
从简谐振子的定义出发，在Fortran 环境下编程，理论上获得无数个模拟数值，然后用这些模拟数值在Origin软件下计算机描点作图。
相比与传统的图解获相图法，计算机辅助画相图效率更高，不仅能任意更改初始条件，而且所作的相图更精确[6]。
2.7用相空间研究完整系统的力学问题[11] [12] [13]每一条相轨迹对应在一段时间内力学系统的状态变化过程。
相轨迹是等能曲线，相应于一定能量的质点运动。
不同相轨迹，对应于不同能量的质点运动，不同能量的相轨迹是不可能相交的。
相空间的每一点称为相点，对应力学系统的一个瞬时状态。
而相图中给定一个相点，实际上等于给定了一组完备的初始定值，即给出完整的动力学系统。
用相空间的概念研究力学问题，实际上是从几何的方法出发研究力学。
它能把力学系统的全部信息在相图上表示出来，而无须去解复杂的运动方程。
三、总结简谐振动系统是一个可以精确求解的模型。
它的动力学系统对我们来说虽然说是完全已知的，但从相图角度研究简谐振动系统，仍展现了它具大的优势——无需解复杂的运动方程，更直观更形象。
本论文在Fortran 90编程环境下对简谐振子进行数值模拟，在Origin75 软件下画出相图。
给定任意的初始条件，画出不同相图。
四、参考文献[1] 刘明.线性谐振子问题研究[J].培训与研究——湖北教育学院学报,2004年9月,21(5)：15-16.[2] 陈建仁.用相空间研究完整系统的力学问题.河南教育学院学报(自然科学版) ,2004年3月,l3(1):25～27[3] 漆安慎.杜婵英.力学[M].高等教育出版社[M].2005年6月第2版[4] 周衍柏.理论力学教程[M].高等教育出版社,1986年3月第2版.282～330[5] 严燕来.叶庆好.大学物理拓展与应用[M].北京：高等教育出版社,2002年12月.49～54.[6] 杨正波.一个非线性力学问题的理论分析和数值模拟研究[J].襄樊学院学,2008年5月，第29卷(5):19～21[7] 丁泽军.Fortran77和90/95编程入门[M].中国科技大学天文与应用物理系,2001年10月[8] 刘卫国.FORTRAN 90 程序设计上机指导与习题选解[M].北京邮电大学出版社,2003年2月.165-18[9] 叶卫平.方安平.于本方.Origin 7.0科技绘图及数据分析[M].机械工业出版社,2004年1月第一版[10] 周建平.精通Origin 7.0[M].北京航空航天大学出版社,2004年3月第一版[11] 许雪芬.巢毅敏倒摆运动稳定性的相空间动力学分析[J].江苏油化学院学报,1999年3月,第11卷(1):43～45[12] 谢利民.弹簧振子运动的实际动力学分析[J].上海师范大学学报(自然科学版),2002年6月,第31卷(2):91～95[13] 克劳斯.迈因策尔.复杂性中的思维[M].中央编译出版社.。