分段线性插值与三次样条插值法

合集下载

几种常用的插值方法

几种常用的插值方法数学系信息与计算科学1班李平指导老师：唐振先摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。

本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。

关键词:任意阶多项式插值,分段多项式插值。

引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。

用多项式建立插值函数的方法主要用两种：一种是任意阶的插值多项式,它主要有三种基本的插值公式：单项式,拉格朗日和牛顿插值；另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。

一．任意阶多项式插值：1.用单项式基本插值公式进行多项式插值：多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点（X,Y ）构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。

虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。

另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。

2.拉格朗日基本插值公式进行插值：先构造一组插值函数L i （x ）=011011()()()()()()()()i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------L L L L ，其中i=0，…n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中i=0，1…n ，令L i （x ）=0()ni i i y l x =∑这就是拉格朗日插值多项式。

Matlab实验报告六(三次样条与分段线性插值)范文

1.分析问题
本题是给出粗略等分点让你插入更多点用双线性插值法来作出更清晰的山区地貌图。
2.问题求解
x=0:400:2800;
y=0:400:2400;
z=[1430 1450 1470 1320 1280 1200 1080 940;
1450 1480 1500 1550 1510 1430 1300 1200;
2.分段线性插值与计算量与n无关;n越大，误差越小.
3.三次样条插值比分段线性插值更光滑。
4.‘linear’：分段线性插值；‘spline’：三次样条值。
【实验环境】
MatlabR2010b
二、实验内容
问题1对函数，x[-5,5]，分别用分段线性插值和三次样条插值作插值（其中插值节点不少于20），并分别作出每种插值方法的误差曲线.
本次实验因为是我们课本没有的内容，心理上给了我很大的压力，幸好我们还能根据老师的课件以及例题去掌握这次实验所需要的各种插值法，但结果还好，两道题都做出来了。
plot(x,y,'*',x1,yl,'r',x1,y2,'b')
y0=1./(1+x1.^2);
y3=yl-y0;
y4=ys-y0;
holdon
plot(x1,y3,'y',x1,y4,'g')
3.结果
4误。
问题2山区地貌图在某山区（平面区域（0，2800）（0，2400）内，单位：米）测得一些地点的高程（单位：米）如表1，试作出该山区的地貌图.
1.分析问题
本题先取出少量的插值节点并作出图形，再用分段线性插值法和三次样条插值法做出更精确的图形，最后在作出误差曲线。

三次样条插值

0)
s(xn 0) s(xn 0)
三弯矩插值法
x xi,
x i+1
s”(x) M i , M i+1
记Mi = s″(xi), f(xi)= yi ,考虑它在任一区间[xi, xi+1]上的形式. 根据三次样条的定义可知 , s(x)的二阶导数 s ″(x)在每一个子区
间[xi, xi+1] ( i=0,1,2,,n-1)上都是线性函数.
2 6
M
i
)(xi1
xi
)
(1)
同理在[xi1, xi ]上讨论得
s(xi )
yi xi
yi1 xi1
(
2 6
M
i
1 6 M i1)(xi
xi1)
(2)
因为s( x)连续，所以（1）（2）即
yi1 yi xi1 xi
1 ( 6 M i1
2 6
M i )(xi1
xi )
yi xi
yi1 xi1
(2) (n 1)内节点处连续及光滑性条件：
s(x s( x
j j
0) 0)
s(x j 0) s(x j 0)
j
1,2,...,n
1
s(x j 0) s(x j 0)
对于待定系数a j ,bj , c j .d j j 1,2,...n,即4n个未知系数，
而插值条件为4n 2个，还缺两个，因此须给出两个条件称为边界条件，有以下三类：
——分段三次插值多项式
分段插值存在着一个缺点,就是会导致插值函数在子区间的端点 (衔接处)不光滑,即导数不连续。
实际应用中，如机翼设计、船体放样等往往要求有二阶光滑度，即二阶连续导数。早期工程师制图时，把富有弹性的细长木条（所谓样条SPLINE ）用压铁固定在样点上，其它地方让其自由弯曲，然后画下曲线（称为样条曲线），它实际上是由分段多项式光滑连接而成，在样点上要求二阶连续可导。

计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )

S
'
(xi

0) S
xi' (
0 )i

S
'
'
x(i

0)S
xi' ' (
0)
1 ,n2, . . . , 1
（1）
这里共有了 3n-3 个条件，再加上条件（2）中的 n+1 个插值条件，共有 4n-2 个条件，
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边

dn1

1
2

Mn

dn

（6）
2 1

2
2
2
1 M1 d1

M2

d2

n 1
2
n
1

M
n
1

dn1
n
n 2 M n dn
由式（1）内点拼接条件，可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
（3）（4）
其中
i

hi 1 hi1
, hi

i

hi hi 1

数值计算方法( 三次样条插值)

u xj hj
分段三次Hermite插值算法
则 v A1 y j 1 A2 y j B1 f j1 B2 f j
算法： 1.输入x j , f j , f j （j 0,1,...,n）； 2.计算插值 (1)输入插值点u; (2)对于j 1,2,...,n做如果u x j 则计算A1 , A2 , B1 , B2 ; v A1 f j 1 A2 f j B1 f j1 B2 f j; 3.输出u , v。
三次样条插值
于是由Taylor展示有 s( x) s( xi ) s( xi )(x xi ) s( xi ) s( xi ) 2 ( x xi ) ( x xi )3 2! 3! M M Mi yi s( xi )(x x j ) i ( x xi ) 2 i 1 ( x xi )3 2! 3!( xi 1 xi )
2M 0 M 1 6 f [ x0 , x0 , x1 ]
三次样条插值
同理(2)式中令i n得 M n 1 2M n 6 f [ xn 1 , xn , xn ] 即有 2M 0 M 1 6 f [ x0 , x0 , x1 ] ） i M i 1 2M i i M i 1 6 f [ xi 1 , xi , xi 1 ] （i 1,2,...,n 1 M 2M 6 f [ x , x , x ] n n 1 n n n 1
三次样条插值
对于待定系数a j , b j , c j .d j j 1,2,...n,即4n个未知系数，
而插值条件为 n 2个，还缺两个，因此须 4 给出两个条件称为边界条件，有以下三类：第一类已知两端点的一阶导数 s( x0 ) f ( x0 ) m0 s( xn ) f ( xn ) mn

三次样条插值

三次样条插值分段线性插值的优点：计算简单、稳定性好、收敛性有保证且易在计算机上实现缺点：它只能保证各小段曲线在连接点的连续性，却无法保证整条曲线的光滑性，这就不能满足某些工程技术的要求。

三次Hermit 插值优点：有较好的光滑性，缺点：要求节点的一阶导数已知。

从２０世纪６０年代开始，首先由于航空、造船等工程设计的需要而发展起来所谓样条(Spline)插值方法，既保留了分段低次插值多项式的各种优点，又提高了插值函数的光滑性。

今天，样条插值方法已成为数值逼近的一个极其重要的分支，在许多领域里得到越来越多广泛应用。

我们介绍应用最广的具二阶连续导数的三次样条插值函数。

一、三次样条插值函数的定义：给定区间],[b a 上的个节点b x x x a n =<<<= 10和这些点上的函数值),,1,0()(n i y x f i i == 若)(x S 满足：（1）),,2,1,0()(n i y x S i i ==；（2）在每个小区间],[b a 上至多是一个三次多项式；（3）)(),(),(x S x S x S '''在],[b a 上连续。

则称)(x S 为函数)(x f 关于节点的n x x x ,,,10 三次样条插值函数。

二、边界问题的提出与类型单靠一个函数表是不能完全构造出一个三次样条插值函数。

我们分析一下其条件个数，条件（2）三次样条插值函数)(x S 是一个分段三次多项式，若用)(x S i 表示它在第i 个子区间],[1i i x x -上的表达式，则)(x S i 形如],[,)(1332210i i i i i i i x x x x a x a x a a x S -∈+++=其中有四个待定系数)3,2,1,0(=j a ij ，子区间共有n 个，所以)(x S 共有n 4个待定系数。

由条件（3）)(),(),(x S x S x S '''在],[b a 上连续，即它们在各个子区间上的连接点110,,,-n x x x 上连续即可，共有)1(4-n 个条件，即⎪⎪⎩⎪⎪⎨⎧==-=+''=-''-=+'=-'-=+=-),2,1,0()()1,,2,1)(0()0()1,,2,1)(0()0()1,,2,1)(0()0(n i y x S n i x S x S n i x S x S n i x S x S i i i i i i i i 共有241)1(3-=++-n n n 个条件，未知量的个数是n 4个。

各种插值法的对比研究

各种插值法的对比研究目录1.引言 (1)2.插值法的历史背景 (1)3.五种插值法的基本思想 (2)3.1拉格朗日插值 (2)3.2牛顿插值 (3)3.3埃尔米特插值 (3)3.4分段线性插值 (4)3.5三次样条插值 (5)4.五种插值法的对比研究 (5)4.1拉格朗日插值与牛顿插值的比较 (5)4.2多项式插值法与埃尔米特插值的比较 (6)4.3多项式插值法与分段线性插值的比较 (6)4.4 分段线性插值与样条插值的比较 (6)5.插值法在实际生活中的应用 (6)6.结束语 (6)致谢 (7)参考文献 (7)各种插值法的对比研究摘要：插值法是一种古老的数学方法,也是数值计算中的一个算法.插值法不仅是微分方程、数值积分、数值微分等计算方法的基础,而且在医学、通讯、精密机械加工等领域都涉及到了它.本文首先介绍了插值的背景以及常用的五种插值法的基本思想,然后通过拉格朗日插值与牛顿插值、多项式插值与埃尔米特插值、多项式插值与分段线性插值、分段线性插值和样条函数插值给出相应的算法与MATLAB 程序,根据已学的知识对五种插值方法与被插函数的逼近程度进行对比研究,找出不同方法间的联系与区别,分析出它们的优缺点,最后在此基础上进一步研究插值法的实际应用,以提高插值法的实用性,从而能让我们在以后的应用中看到一个问题,就知道哪种方法更适合于它,然后大大地快速的提高效率.关键词：多项式插值;样条函数插值;MATLAB 程序;应用1.引言在很多解题以及应用生活中,常常需要用数量关系来反映问题,但是有时没有办法通过数学语言准确地表达出来.已知有些变量之间存在一种函数关系,但没法用函数的表达式表示出来.比如,)(x f 在某个区间上[]b a ,是存在某种数量关系的,但是根据观察和测量或者实验只能得到有限个函数值,我们可以利用这几点来确定函数表达式.或者有一些函数表达式是已经知道的,但是它们的计算是十分繁琐复杂的,不容易发现它的本质,而且它的使用方法也比较局限.函数是表达数与数之间的联系,为了能很好地用数学语言表达出函数的关系,一般通过给定的数据构造一个函数)(x P ,这样既能反映函数)(x f 的特点,又方便计算,用)(x P 近似)(x f .通常选一个简单的函数)(x P ,而且=)(i x P )(i x f ()n i ,...,2,1,0=成立,这个时候的)(x P ,从要表达的函数规律来看,就是我们需要的插值函数[1].所用方法就是插值法,由于所选用的)(x P 的多样化,得到不同的插值法.2.插值法的历史背景插值法的历史源远流长,在很早的时候就涉及到了它.它是数值计算中一个古老的分支,它来源于生产实践.因为牛顿力学的物理理论知识在一千年前没有出现,所以我们的祖先没有办法用很准确的数学解析式来表达日月五星的运行规律.后来,古代的人们有着聪慧的头脑,想出了插值方法,然后发现了日月五星的运行规律.例如唐朝数学家张遂提出了插值法的概念以及不等距节点的插值,并将其应用在天文历法观测中.现代工业革命以后欧洲著名的数学家拉格朗日给出了拉格朗日插值法的概念以及应用.微积分产生后,插值法的基本理论和结果进一步得到改善.3.五种插值法的基本思想如果一个函数)(x f y =在区间[]b a ,上有定义,且已知在点b x x x a n ≤<<<≤...10上的值0y ,1y ,2y , ,n y ,若存在一简单函数)(x P ,使得成立,)(x P 为插值函数,点0x ,1x ,2x , ,n x 称为插值节点,插值节点的区间[]b a ,称为插值区间,求插值函数)(x P 的方法称为插值法.若)(x P 的多项式次数不超过n ,即有)(x P n n x a x a x a a ++++= (2210)3.1拉格朗日插值拉格朗日插值是n 次多项式插值,它是用构造插值基函数的办法来解决n 次多项式插值的问题.拉格朗日插值多项式可以表示为=)(x L n ∑=n k k k x ly 0)(,)(x l k 为插值基函数,表达式为=)(x l k ))...()()...(())...()()...((110110n k k k k k k n k k x x x x x x x x x x x x x x x x --------+-+-,n k ,,1,0 = 截断误差为)()()(x L x f x R n n -=,也是插值余项.关于插值余项,估计有以下定理[2]:设)(x f n 在[]b a ,上连续,)(1x f n +在()b a ,内存在,节点b x x x x a n≤<<<<≤ 210,)(x L n 是满足条件(1.4)的插值多项式,则对任何[]b a x ,∈,插值余项)()!1()()()()(1)1(x n f x L x f x R n n n n +++=-=ωξ 余项表达式的应用有它的局限性,一般只适合于)(x f 高阶导数存在的情况下.若设1)1()(max ++≤≤=n n b x a M x f ,则误差为)()!1()(11x w n M x R n n n +++≤.3.2牛顿插值牛顿插值的基本思想是对n 次插值多项式)(x P n 进行逐次生成,然后用插值条件求出)(x P n 系数[3].因此,提出了均差（即差商）的概念.设称有函数)(x f ,1x ,2x ,3x , ,n x 是一系列不相等的点,则[]=k x x f ,000)()(x x x f x f k k --为函数)(x f 关于点0x ,2x 的一阶均差; []=k x x x f ,,10[]1100],[,x x x x f x x f k k -- 称为)(x f 的二阶均差; []=k x x x f ,...,,10[][]1110210,...,,,,...,,-----k k k k k x x x x x f x x x x f 为)(x f )的k 阶均差. 我们先求出1次多项式,2次多项式,然后类推出n 次多项式,构造出n 次代数插值多项式的另外一种表达形式—牛顿插值多项式=)(x P n +)(0x f []10,x x f +-)(0x x []210,,x x x f )(0x x -+-)(1x x … []n x x x x f ,...,,,210+)(0x x -))...((11---n x x x x ,=)(x R n []n x x x x x f ,...,,,,210)(0x x -))...((1n x x x x --, =)(x f +)(x P n )(x R n . )(x P n 为牛顿插值多项式,)(x R n 为余项.3.3埃尔米特插值有的时候解决函数)(x f 的问题,不仅要在某些点上知道函数值,而且已知在一些点上的导数值.那么这时插值函数)(x P ,它在某些点处的导数值和函数值与原表达式的值相等的.那么我们从几何这个方面来思考这个问题,求出插值多项式的曲线,不但通过已知点组,而且在这些点处与原曲线＂相切＂[4].(一)、泰勒插值定义 [][])(,lim ,0'0000x f x x f x x f x x ==→为一阶重节点均差;[][])(21,,lim ,,0''2100000201x f x x x f x x x f x x x x ==→→为二阶重节点均差; 则n 阶重节点均差为[][])(!1,,,lim ,,,0100000x f n x x x f x x x f n n x x i ==→ . 当0x x i →时,牛顿插值公式的极限为=)(x P n +)(0x f )(0'x f +-)(0x x ...！n x f n )(0)(nx x )(0-. 称为泰勒插值多项式.它满足条件=)(0)(x P k n )(0)(x f k ,),...,2,1,0(n k =（二）、两点三次埃尔米特插值若)(x f 在k x ,1+k x 的函数值为k y ,1+k y ,k k m x f =)(',11')(++=k k m x f ,我们可以构造出一个次数不超过3的多项式,)(3x H 为插值函数.设=)(3x H +k k y x a )(+++11)(k k y x a +k k m x )(β11)(++k k m x β,k a ,1+k a ,k β,1+k β为插值基函数.可得结果 =)(3x H 2111))(21(+++----+k k k k k k x x x x x x x x k y 2111))(21(kk k k k k x x x x x x x x ----+++++++1k y )(k x x -+--++k k k k m x x x x 211)(121)(++--k k k k m x x x x , =)(3x R 2124)())((41+--k k x x x x f ξ！,),(1+∈k k x x ξ. 3.4分段线性插值分段线性插值:一般描述,如给定[]上b a ,1+n 个节点b x x x x a n =<<<<= 210和相应的函数值)(i f f i =),...,2,1,0(n i =,记k k k x x h -=+1,k kh h max =. 构造)(x I h 满足:(1)[]b a C x I h ,)(∈;(2)k k h f x I =)(),,2,1,0(n k =;(3))(x I h 在每个小区间[]1,+k k x x 上是线性函数.由以上条件直接可得)(x I h 在小区间[]1,+k k x x 上的表达式为=)(x I h +--++k k k k f x x x x 1111++--k kk k f x x x x , )1,,2,1,0(-=n k 误差估计 -)(x f =)(x I h ))((!2)(1)(''+--k k k x x x x x f ξ))((max 2121+≤≤--≤+k k x x x x x x x M k k . 当∞→h 时,0)()()(→-=x I x f x R h ,)(x I h 在[]b a ,上一致收敛到)(x f .3.5三次样条插值三次样条插值（Spline 插值）的具体要求是:函数[]b a C x S ,)(2∈,并在每个小区间[]1,+j j x x 上是一个三次多项式,其中b x x x x a n =<<<<=...210是给定节点,如果对给定的节点函数值有j y )(j x f =),...,2,1,0(n j =,并且=)(j x S j y ,),...,2,1,0(n j =成立,这时我们就把)(x S 称为三次样条插值函数.4.五种插值法的对比研究通过讨论插值法的相关内容,可以让我们更好的了解插值法.现在我们先从插值多项式的形式上、用途上、计算方法上、精确度上等进行对比研究,比较各自优缺点,然后再通过实例验证之.4.1拉格朗日插值与牛顿插值的比较（一）拉格朗日插值多项式步骤衔接紧密,条理清晰,在理论中十分重要.但是计算比较复杂,因为每添加一个点,所以的公式都要重新计算,这样计算步骤较多会导致计算量变大,反而会导致出现误差与原来的目的背道而驰.（二）牛顿插值多项式的计算量小,步骤简洁.当添加一个节点时,它仍然可以使用,即具有“承袭性”也叫“继承”,所以此类方法应用灵活.但是我们根据正常的想象和观察插值余项,我们一般局部地总是认为当原函数给出的点是越来越多时,我们借助的辅助函数的次数越高,它就和原函数越来越近,误差越来越小.然而事实并非如此,当遇到插值节点等距分布的情况时,只要求函数点值相等不能够充分反映插值函数的性质[5].4.2多项式插值法与埃尔米特插值的比较多项式插值要求在插值节点上函数值相等,计算简单,条件不怎么苛刻.但是如果有的时候一方面要在节点处函数值相等,另一方面要导数值相等,这时多项式插值否则不满足此类情况.埃尔米特插值不仅算法简单而且它具有强烈收敛性.但是它的光滑度不高,而且它的使用条件,也有局限性.在一些特定的限制条件下,有时函数的导数值在这点是完全没有必要知道的.因此,知道节点处的导数的插值函数成为能否运用Hermite插值的一个重要因素[6].4.3多项式插值法与分段线性插值的比较多项式插计算简单,比较方便,但是节点增加的同时就会出现龙格现象,图形波动较大[7].分段线性插值能够克服龙格现象,有收敛性,但是在区间内有转折点,光滑性不好.4.4 分段线性插值与样条插值的比较样条插值的插值函数算法稳定,而且插值函数光滑,收敛性强,误差小.但是它不能局部确定,常常需要解线性方程组.5.插值法在实际生活中的应用插值法是数值逼近中一个非常重要的部分,其次它在实际生活中起着不容小觑的作用,比如天文学以及数学.6.结束语插值法在解决实际问题中有很大的应用.插值方法是各种各样的,它包含拉格朗日插值法、牛顿插值法、Hermite插值法、分段线性插值法以及三次样条插值法等.我们不论使用哪个插值法,它的原理都是一样的.本课题首先介绍了插值的背景以及各类方法的基本思想;然后通过解题、画图、一道题用几种不同方法来解答,让我们哪种方法适合解答哪种类型的题,再然后进行对比,探讨出它们的优缺点,最后文章举个例子来说明插值法有很大的作用,它和我们是相连的,同时利用MATLAB给出了模拟图,通过这种数与形的结合,更好地了解各类插值法的应用于特征.致谢本论文在苏晓琴老师的悉心指导下完成的，同样也是我第一次写这样的文章。

差值与数值积分

数学实验报告
无 95
苏航
2009011122
实验日期 2011/3/11
数学实验报告
实验一差值与数值积分
班级姓名交报告日期
无 95 苏航
2011/3/19
学号 2009011122
1
数学实验报告
无 95
苏航
2009011122
一、差值
㈠问题描述
选择一些函数，在 n 个节点上用拉格朗日、分段线性、三次样条三种差值方法，计算 m 个插值点的函数值，通过函数和图形输出，将三种插值结果与精确值进行比较，适当增加 n 再作比较，由此作初步分析。
3
数学实验报告
无 95
苏航
2009011122
可以发现，通过增加节点，每一种插值法的结果都比原来更加接近真实值。 dif1 = 0.0015; dif2 = 0.0082; dif3 = 0.0027; (3)10 节点，100 插值点
结果进一步逼近真实值。 dif1 = 0.00062; dif2 = 0.0035; dif3 = 0.0012; (4)简要小结 a.增加节点可以有效地提高插值结果的准确度。 b.在本函数下，拉人格朗日插值法的效果与三次样条插值法的效果相近，两者都好于分段线性插值法。 (5)对比
从结果可以看出，各种积分法的精度都有所提高，其中自适应积分法的精度提高得最多。步长为 0.05，精度要求10−8
11
数学实验报告
无 95
苏航
2009011122
前两种与直接步长相关的积分公式得到的结果的精度进一步提升。由此思考，可以自己编写“以精度为参量”的梯形积分法和 Simpson 积分法，即多次调用现有积分程序，判断精度是否符合要求，若不符则进一步缩小步长，知道满足要求。 (4)对比步长取 0.2，比较自己编写的梯形积分公式以及 Matlab 自带的梯形积分公式。 S[1]为自己所编公式的结果，S[2]为 Matlab 自带公式的结果。

插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。

2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。

3. 分析不同插值方法的优缺点，并比较其精度和效率。

4. 通过实验加深对数值分析理论的理解和应用。

二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。

它广泛应用于科学计算、工程设计和数据分析等领域。

常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。

1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。

其基本思想是：给定一组数据点，构造一个次数不超过n的多项式，使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。

2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。

其基本思想是：给定一组数据点，构造一个次数不超过n的多项式，使得该多项式在这些数据点上的函数值与已知数据点的函数值相等，并且满足一定的差商条件。

三、实验内容1. 拉格朗日插值法（1）给定一组数据点，如：$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$（2）根据拉格朗日插值公式，构造插值多项式：$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$（3）计算插值多项式在不同点的函数值，并与实际值进行比较。

三次样条插值算法详解

局限性
三次样条插值算法要求数据点数量较多，且在某些情况下可能存在数值不稳定性，如数据点过多或数据点分布不均等情况。此外，该算法对于离散数据点的拟合效果可能不如其他插值方法。
对未来研究的展望
01
02
03
改进算法稳定性
针对数值不稳定性问题，未来研究可以探索改进算法的数值稳定性，提高算法的鲁棒性。
3
数据转换
对数据进行必要的转换，如标准化、归一化等，以适应算法需求。
构建插值函数
确定插值节点
根据数据点确定插值节点，确保插值函数在节点处连续且光滑。
构造插值多项式
根据节点和数据点，构造三次多项式作为插值函数。
确定边界条件
根据实际情况确定插值函数的边界条件，如周期性、对称性等。
求解插值函数
求解线性方程组
06
结论
三次样条插值算法总结
适用性
三次样条插值算法适用于各种连续、光滑、可微的分段函数插值问题，尤其在处理具有复杂变化趋势的数据时表现出色。
优点
该算法能够保证插值函数在分段连接处连续且具有二阶导数，从而在插值过程中保持数据的平滑性和连续性。此外，三次样条插值算法具有简单、易实现的特点，且计算效率较高。
根据数据点的数量和分布，合理分段，确保拟合的精度和连续性。
求解线性方程组
使用高效的方法求解线性方程组，如高斯消元法或迭代法。
结果输出
输出拟合得到的插值函数，以及相关的误差分析和图表。
03
三次样条插值算法步骤
数据准备
1 2
数据收集
收集需要插值的原始数据点，确保数据准确可靠。
数据清洗
对数据进行预处理，如去除异常值、缺失值处理等。

不同插值方法绘制断面图效果分析

角，且一阶可导，有一定的光滑性；具分段三次样条插
Ｓｘ＝】・）Ｓ（— ）（— ）ｊＯ１２Ａ）Ｓ（２巧＋＋＋＝，，
…ｎ．ｎ２且＞
值二阶光滑性好、精度高。
根据条件求系数（，，，）的方法是三弯Ｓ，用矩法ｆ－ｌ二阶导数作为参数）８４把（ｌ。。由于上述条件不能
２１分段三次Ｈｒｔ值．ｅｍｉｅ插
段的限制。往往只能获得断面线上的一组有序的离散观测点，而难以获得断面线上任意位置的河底高程，因
此需要点绘大断面图．来获得断面线上任意位置的河底高程。生产中点绘断面图时，就认为在两个观测点
（中国矿业大学资源与地球科学学院，苏徐州２１１）江２１６
摘要：绍了绘制断面图中的各种插值方法，介具体包括线性插值和分段非线性插值；析了目前使用分
的线性插值方法绘制断面图的不足：度一般、精不光滑；出了用分段非线性插值绘制断面图的方法；提分段非线性插值精度高、光滑性好，以分段非线性插值绘制断面图能很好地弥补线性插值的不足，所而且
（）２在每个小区间上，是次数不超过３次的多项式。
克里格法（ｒｉｇ［７艾米特法（ｅｍｉ）样条法ｋｉｎ）－、ｇ５］Ｈｒｔ、ｅ（ｐｉｅ法［“ 。ｓｌ）８ｎ－等

几种常用的插值方法

几种常用的插值方法数学系信息与计算科学1班平指导老师：唐振先摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。

本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。

关键词:任意阶多项式插值,分段多项式插值。

引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。

一．任意阶多项式插值：1.用单项式基本插值公式进行多项式插值：多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A1+A2X+…A n X n-1,它是一个单项式基本函数X0,X1…X n-1的集合来定义多项式,由已知n个点（X,Y）构成的集合,可以使多项式通过没数据点,并为n个未知系数Ai写出n个方程,这n个方程组成的方程组的系数矩阵为Vandermonde 矩阵。

虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde方程组有可能是病态的,这样会导致单项式系数不确定。

另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。

2.拉格朗日基本插值公式进行插值：先构造一组插值函数L i （x ）=011011()()()()()()()()i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------，其中i=0，…n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中i=0，1…n ，令L i （x ）=0()ni i i y l x =∑这就是拉格朗日插值多项式。

数值分析实验报告Hermite插值法、Runge现象,比较Language插值、分段线性插值、分段三次Hermie插值

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度，并画出插值多项式的图像。

1)运用Hermite插值法画出图像，如图4-1，并求质点在时刻1.8时的速度。

>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计（一）Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X，X中第一行每个元素都是插值节点，X中第二行每个元素都是插值节点对应的函数值；%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结运行结果例：给定函数55,11)(2≤≤-+=x xx f ；（1）验证表2-10的误差结果（高次插值的Runge 现象）；（2）以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值，画出三种插值函数以及f(x)的图像，比较三种插值结果。

插值的基本概念

插值的基本概念插值（interpolation）是指在已知有限个数据点的情况下，通过某种数学方法构造出一个函数，使得这个函数在这些数据点上的函数值都与已知的数据相符合。

插值方法常被用于曲线拟合，图像处理，计算机辅助设计，地图制作等领域。

插值方法主要分为三类：多项式插值法、样条插值法和分段线性插值法。

以下分别介绍这三种方法的基本概念。

1. 多项式插值法多项式插值法是指用一个n次多项式来逼近已知的n+1个数据点，从而得到一个插值函数。

插值函数的形式为：f(x) = a0 + a1x + a2x^2 + ... + anxn其中a0, a1, a2, ... , an是n+1个待求系数，取决于已知数据点的值。

为了求得这些系数，需要使用某种算法，如拉格朗日插值法或牛顿插值法。

这两种方法都能够精确地通过已知点，并可方便地计算任意点的函数值。

但是，随着数据点的数量增加，多项式插值方法的计算量将急剧增加，可能导致算法不稳定或数值不可信。

2. 样条插值法样条插值法是一种更为复杂的插值方法，它将插值函数分为若干个小区间，并在每个区间内用一个低次多项式来逼近已知的数据点。

这些局部多项式的系数由已知数据点的值和导数共同决定，使得插值函数在各区间内的函数值和导数连续。

这种连续性和光滑性可以使得插值函数更加符合实际情况，尤其是较大的数据集。

3. 分段线性插值法分段线性插值法是一种简单而有效的插值方法，它在每两个连续的已知数据点间构造一条直线来逼近数据点，并用这些直线段拼接起来形成一个分段线性函数。

虽然这种方法没有样条插值法那么精确，但它计算简单，不需要过多的计算资源。

在实际应用中，分段线性插值法与其他插值方法搭配使用，以提高算法的效率和精度。

总之，插值方法是数学计算和图像处理等领域中不可或缺的工具之一。

通过使用适当方法的插值，可以更加准确和高效地处理数据和图像，从而得到更加可靠的结果。

插值算法——精选推荐

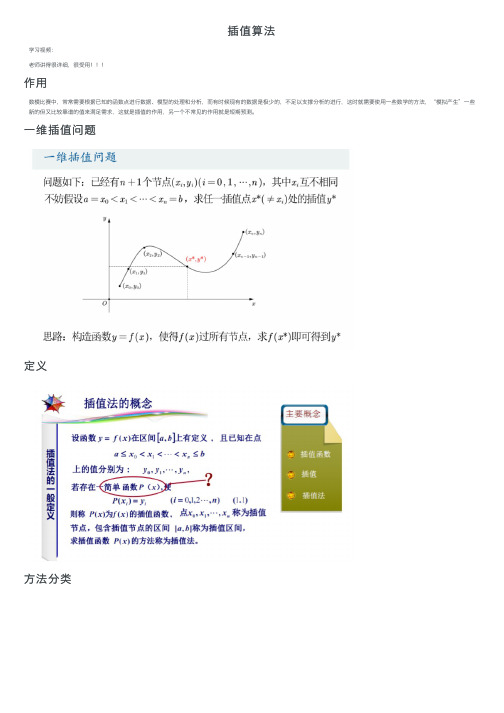
插值算法学习视频：⽼师讲得很详细，很受⽤！！！作⽤数模⽐赛中，常常需要根据已知的函数点进⾏数据、模型的处理和分析，⽽有时候现有的数据是极少的，不⾜以⽀撑分析的进⾏，这时就需要使⽤⼀些数学的⽅法，“模拟产⽣”⼀些新的但⼜⽐较靠谱的值来满⾜需求，这就是插值的作⽤，另⼀个不常见的作⽤就是短期预测。

⼀维插值问题定义⽅法分类本⽂重点介绍数学建模常⽤的两种⽅法：三次样条插值和分段三次埃尔⽶特插值插值多项式原理拉格朗⽇插值法⽅法主要有拉格朗⽇插值法，具体不介绍，它会出现龙波现象（在两端处波动极⼤,产⽣明显的震荡）。

但觉得可以出⼀个ACM题。

分段线性插值插值多项式次数⾼精度未必显著提⾼插值多项式次数越⾼摄⼊误差可能显著增⼤如何提⾼插值精度呢采⽤分段低次插值是⼀种办法概念⽜顿插值法评价与拉格朗⽇插值法相⽐，⽜顿插值法的计算过程具有继承性。

（⽜顿插值法每次插值只和前n项的值有关，这样每次只要在原来的函数上添加新的项，就能够产⽣新的函数）但是⽜顿插值也存在龙格现象的问题。

致命缺点上⾯讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值，⽽这种插值多项式却不能全⾯反映被插值函数的性态。

然⽽在许多实际问题中，不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在⼀个或全部节点上插值多项式与被插函数有相同的低阶甚⾄⾼阶的导数值。

对于这些情况，拉格朗⽇插值和⽜顿插值都不能满⾜埃尔⽶特(Hermite)插值概念保持播值曲线在节点处有切线（光滑），使插值函数和被插函数的密和程度更好。

不但要求在节点上的函数值相等，⽽且还要求对应的导数值也相等,甚⾄要求⾼阶导数也相等，满⾜这种要求的插值多项式就是埃尔⽶特插值多项式。

缺点与改进直接使⽤Hermite插值得到的多项式次数较⾼，也存在着龙格现象，因此在实际应⽤中，往往使⽤分段三次Hermite插值多项式(PCHIP)。

Matlab有内置的函数（实现过程已经帮我们封装好了，会调⽤就⾏了）： p = pchip(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标三次样条插值Matlab有内置的函数： p = spline(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标代码% 分段三次埃尔⽶特插值x = -pi:pi; y = sin(x);new_x = -pi:0.1:pi;p = pchip(x,y,new_x);figure(1); % 在同⼀个脚本⽂件⾥⾯，要想画多个图，需要给每个图编号，否则只会显⽰最后⼀个图哦~plot(x, y, 'o', new_x, p, 'r-')% plot函数⽤法:% plot(x1,y1,x2,y2)% 线⽅式： - 实线 :点线 -. 虚点线 - - 波折线% 点⽅式： . 圆点 +加号 * 星号 x x形 o ⼩圆% 颜⾊： y黄； r红； g绿； b蓝； w⽩； k⿊； m紫； c青% 三次样条插值和分段三次埃尔⽶特插值的对⽐x = -pi:pi;y = sin(x);new_x = -pi:0.1:pi;p1 = pchip(x,y,new_x); %分段三次埃尔⽶特插值p2 = spline(x,y,new_x); %三次样条插值figure(2);plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')legend('样本点','三次埃尔⽶特插值','三次样条插值','Location','SouthEast') %标注显⽰在东南⽅向% 说明：% LEGEND(string1,string2,string3, …)% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。

分段线性插值法求插值-Read

分段线性插值法求插值摘要本文根据题目的要求,利用分段线性插值法对采样点和样本值进行插值计算。

为了更好的评断模型的优化性，我们同时采用了最近点插值，3次多项式插值和3次样条插值法来处理同样的问题，作为分段线性插值方法的参考模型。

根据插值函数计算区间内任意取样点的函数值。

最后再利用所得函数值画出相应的函数图象，并与原函数g(x)的图象进行对比。

通过对本题四个问题的解答，并观察对比函数图象我们得到了如下两个重要的结论：（1）在同一取样点，利用不同的插值方法可能会得到不同的函数值，所得函数值与原函数的标准函数值的误差大小决定了该插值方法的“好坏”。

而最优化的插值方法往往依赖于被插值函数。

本题中，在函数式g(x)对应X,Y的条件下，可以根据对比函数图象明显看出：分段线性插值方法和3次多项式插值方法优于3次样条插值和最近点插值。

（2）在插值计算中，取样点的多少往往会影响所得插值函数优化程度。

一般情况下，取样点越多所得插值函数越优化，对应的函数值与标准函数值越接近。

通过对本题四个问题相应对比函数图象的观察，我们也明显看出：在区间[-6 6]内，当取样点为21，41时，分段线性插值法进行插值计算得到的函数图象基本上与原函数g(x)吻合。

AbstractIn this article ,we use piecewise linear interpolation to compute the sampling point and sample value according to the request of question. In order to judge the model's quality in a better way, we use nearest interpolation, cubic interpolation and spline interpolation regarded as the model reference of piecewise linear interpolation to deal the question in the same way at the same time. Then draw the function picture by function value of any sampling point in the interval of interpolating function. Finally, we make a comparison between the original function g(x) image and the interpolating function image.At the base of analysing the final result and comparing the constrastive image . We can summarize two items of important conclusion as follows:(1)At the same sampling point , different interpolating method canobtain different function value. Usually , the optimizationalgorithm depends on the size of error between the objectfunction value .(2) When processing interpolating compute , the number of thesampling point will make an effect on the quality of a model.Commonly, the more multitudinous the sampling points wereused ,the more precise the interpolation model will be .目录一．问题的重述 (1)二．问题的分析 (1)三．问题的假设 (1)四．分段线性插值原理 (2)五．问题的求解 (2)六．插值方法的优劣性分析 (5)附录 (6)一．问题的重述已知211)(xx g +=,66≤≤-x 用分段线性插值法求插值，绘出插值结果图形，并观察插值误差。

计算方法分段线性三次样条插值专业知识讲座

S(x)在区间45,60上的线性插值为：
S (x x 1 x x x 2 2 ) f1 ) ( x x x 2 x x 1 1 f2 ( ) x 3 3 2 0 x 2 2 3 2 3
S(x)在区间60,9ቤተ መጻሕፍቲ ባይዱ上的线性插值为：
S (x x x 2 x x 3 3 )f2 ( ) x x x 3 x x 2 2 f3 ( ) x 2 63 x 0 3 2 3 2
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不当之处，请联系本人或网站删除。
另外，从舍入误差来看，高次插值误差的传播也较为严重，一个节点上产生的舍入误差会在计算中不断放大，并传播到其它节点上。
因此，次数太高的高次插值多项式往往并不实用，因为节点数增加时，计算量增大了，但插值函数的精度未必能够提高。称为龙格现象。
考察函数 f当(之 x 处，1 请) 联1 x 系2 本,人或网5 站删除x 。 5
右图给出了 P5 (x )
和 P1 0(x)的图像,当n 增大时,Pn ( x ) 在两端
会发生激烈的振荡，
y P 10(x)
f(x)
称为龙格现象。
P 5(x)
-5
0
5x
该现象表明：在大范围内使用高次插值,逼近的效果往往是不理想的。
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不
2.4.1 高次插值当之的处龙，格请联现系象本人或网站删除。
插值多项式余项公式
R( x(f)(n n 1(1 ) ξ)()!xx0)( xx1)(xxn)， ξ(ab,)
例：设函数f(x)定义在区间[0, 1]上，并且满足 |f(4) (x)|<1，xϵ[0, 1]。在4个插值节点 x0=0, x1=1/3, x2=2/3, x3=1, 对f(x)进行插值得多项式P3(x)，估计误差。

常见插值法——精选推荐

常见插值法常见插值法【摘要】插值⽅法在数值分析中起着⾮常重要的作⽤。

在此介绍⼀些常见的插值⽅法及其应⽤范例。

【关键字】数值分析；插值⽅法；应⽤；1. 插值法定义插值法⼜称“内插法”，是利⽤函数f (x)在某区间中插⼊若⼲点的函数值，作出适当的特定函数，在这些表(1) 插值点点上取已知值，在区间的其他点上⽤这特定函数的值作为函数f (x)的近似值，这种⽅法称为插值法。

如果这特定函数是多项式，就称它为插值多项式。

2.常见的插值法及其构造Lagrange 插值法（a).公式推导：表（1）的Lagrange 插值的插值多项式∑==ni i i x l x f x 0n )()()(L ,(j=0,1,2....n)。

其中插值基函数是∏≠=--=nji i j i j x x x x x l 0n )()()(,(i,j=0,1 2...n) 。

其插值余项为其中),b a （∈ξ，∏≠=+--=nji i jij x x x x x 01n )()()(ω(b).matlab 实现⽅法：Matlab 没有直接求解的相关函数，现编译如下： function yi = Lagarange_chazhi(x,y,xi)% 求拉格朗⽇插值,并返回⼀个输⼊为xi 时的函数值 % x 为插值点向量，⾄少有三项 % y 为插值点值的向量，项数与x 相同 m = length(x); %求插值个数 m1 = length(y); if m<=2error('项数不⾜!'); end if m~=m1error('y 的项数应与x 相同'); end %对参数的判断 lag_hanshu = 0; syms X ;for (l = 1:m) %构造插值基函数 la = y(l); for a = (1:l-1)la = la*(X-x(a))/(x(l)-x(a)); endfor a = (l+1:m)la = la*(X-x(a))/(x(l)-x(a)); endformat longlag_hanshu = lag_hanshu+la;%求解出插值函数 endyi = subs( lag_hanshu,'X',xi);%返回插值函数输⼊为xi 时的值 End(c).⽅法缺陷：当插值点个数7n ≥时，将产⽣龙格现象：经典例⼦，对)251(1)(2x x f +=进⾏拉格朗⽇插0x 1x 2x ....... 1-n x n x 0y 1y 2y ....... 1-n y n y),(!)1()()()()(1)1(x n f x L x f x R n n n n +++=-=ωξx a =bx n =1x 2x 1-n x 值图（1）中从左到右，从上到下，n 分别为图(1) Lagarange 插值法的龙格现象4,5...11，可以看出，当7n≥后，它的\插值函数在两个端点处发⽣剧烈的波动，造成较⼤的误差。

三种插值方法比较

17世界后牛顿,拉格朗日分别讨论了等距和非等距的一般插值公式.在近代,插值法仍然是数据处理和编制函数表的常用工具，又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础,许多求解计算公式都是以插值为基础导出的。

三种插值方法的比较：拉格朗日插值、分段线性插值与三次样条插值三种插值法在处理问题时的比较。

插值问题的提法是：已知f(x)(可能未知或非常复杂函数)在彼此不同的n+1个实点 0x ,1x ,…n x 处的函数值是f(0x )，f(1x )，…，f(n x )，这时我们简单的说f(x)有n+1个离散数据对｛（i x ，i y ）｝i n ＝0．要估算f(x)在其它点ｘ处的函数值，最常见的一种办法就是插值，即寻找一个相对简单的函数y(x)，使其满足下列插值条件：y (i x )＝f (i x )，i=0，1，…，n ．并以y (x)作为f (x)的近似值．其中y (x)称为插值函数，f (x)称为被插函数．[1,2,3] 选用不同类型的插值函数，逼近的效果不同，下面给出拉格朗日多项式插值、分段线性插值及三次样条插值在处理问题时的应用比较分析．多项式插值是最常见的一种函数插值．在一般插值问题中，由插值条件可以唯一确定一个次数不超过ｎ的插值多项式满足上述条件．从几何上看可以理解为：已知平面上n+1个不同点，要寻找一条次数不超过ｎ的多项式曲线通过这些点．插值多项式一般有两种常见的表达形式，一个是拉格朗日(Lagrange)插值多项式，另一个是牛顿(Newton)插值多项式．且Ｌａｇｒａｎｇｅ插值公式恒等于Ｎｅｗｔｏｎ插值公式．分段线性插值与三次样条插值可以避免高次插值可能出现的大幅度波动现象(龙格现象)，在实际应用中通常采用分段低次插值来提高近似程度，比如可用分线性插值或分段三次埃尔米特插值来逼近已知函数，但它们的总体光滑性较差．为了克服这一缺点，一种全局化的分段插值方法———三次样条插值成为比较理想的工具。