初中数学九大几何模型解题思路
(完整版)初中数学九大几何模型
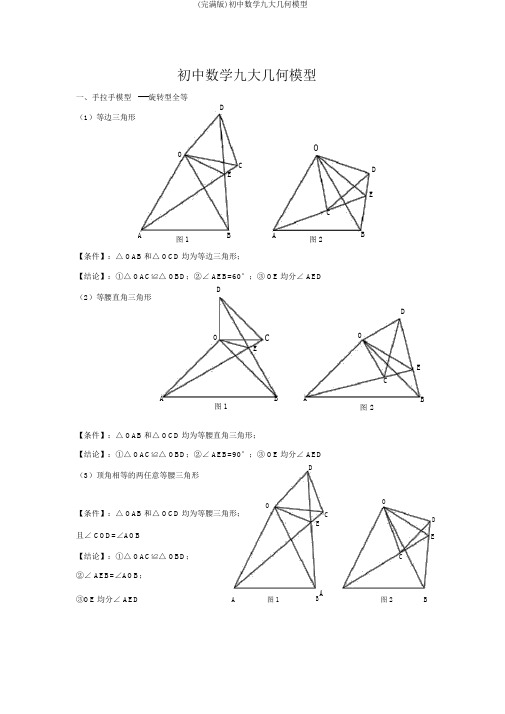
初中数学九大几何模型一、手拉手模型 ----旋转型全等D(1)等边三角形OOC ECA图 1BA图 2【条件】:△ OAB 和△ OCD 均为等边三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 均分∠ AEDD(2)等腰直角三角形OCEABA图 1D EBDOECB图 2【条件】:△ OAB 和△ OCD 均为等腰直角三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 均分∠ AED(3)顶角相等的两任意等腰三角形DOOC【条件】:△ OAB 和△ OCD 均为等腰三角形;DE且∠ COD=∠AOBE【结论】:①△ OAC ≌△ OBD ; C②∠ AEB=∠AOB ;③OE 均分∠ AEDA 图 1BA图 2 BO O二、模型二:手拉手模型----旋转型相似(1)一般情况D【条件】: CD ∥ AB ,CD将△ OCD 旋转至右图的地址A B 【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOAO(2)特别情况C D【条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的地址A B【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ;③ BDOD OB tan ∠ OCD ;④ BD ⊥AC ; ACOC OA⑤连接 AD 、 BC ,必有 AD 2BC222;⑥ S △BCDABCD三、模型三、对角互补模型(1)全等型 -90 °【条件】:①∠ AOB=∠ DCE=90°;② OC 均分∠ AOBECABDOCEA B1AC BD 2 ACDOE B图 1【结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCES△OCDS△OCE1 OC 2A2证明提示:CM①作垂直,如图 2,证明△ CDM ≌△ CEND②过点 C 作 CF ⊥ OC ,如图 3,证明△ ODC ≌△ FEC※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4):ON EB图 2以上三个结论:① CD=CE ;② OE-OD= 2 OC ;A1OC 2AMC③S△OCES△OCD2CDONBEO图 3 EF BD图 4(2)全等型 -120 °【条件】:①∠ AOB=2∠ DCE=120°;② OC均分∠ AOB【结论】:① CD=CE;② OD+OE=OC;③S△DCE S△OCD S△OCE 3 OC24证明提示:①可参照“全等型-90 °”证法一;②如右以下图:在OB上取一点F,使 OF=OC,证明△ OCF为等边三角形。
初中数学几何模型的60种解题技巧

初中数学作为学生学习的基础课程之一,其中的几何模型在数学解题中占据着重要的地位。
掌握几何模型的解题技巧不仅可以帮助学生更好地理解数学知识,还可以提高他们的解题效率。
本文将介绍初中数学几何模型的60种解题技巧,希望能为学生们的学习提供帮助。
1. 角度概念的运用:在几何模型的解题过程中,学生可以通过具体的角度概念来解答问题,例如利用垂直角、平行线、内角和为180度等概念来解题。
2. 图形相似的判断:判断两个图形是否相似是解题的基础,学生可以利用边长比例、角度比例等方法来确定图形的相似性。
3. 平行线相关性质的应用:平行线的性质在几何模型的解题中经常会出现,学生可以通过平行线与角度的关系来解答问题。
4. 圆的相关性质的利用:圆的性质在几何模型中也是常见的,学生需要掌握圆的直径、半径、圆心角等概念,以便解题。
5. 三角形的分类和性质的运用:学生需要掌握等边三角形、等腰三角形、直角三角形等不同类型三角形的性质,并根据题目的要求来进行合理的运用。
6. 应用解题:在学习几何模型的解题过程中,学生需要结合实际的应用场景,将抽象的几何原理与具体的问题相结合来解答问题。
7. 连线问题的求解:对于一些多边形的连线问题,学生可以通过几何模型的知识来进行合理的求解。
8. 几何图形的对称性:对称图形在几何模型中也是常见的,学生可以通过对称性来解答与对称图形相关的问题。
9. 正多边形的性质:正多边形的性质是几何模型解题中的重要内容,学生需要掌握正多边形的内角和为180度、外角的性质等知识。
10. 形状的变换:在几何模型的解题中,学生需要掌握形状的平移、旋转、翻转等变换操作,以便解答形状变换后的问题。
11. 圆的面积和周长的求解:学生需要掌握圆的面积和周长的相关公式,并结合题目要求来进行求解。
12. 三角形的面积和周长的求解:学生需要掌握不同类型三角形的面积和周长的求解方法,并灵活运用到不同的题目中。
13. 平行四边形的面积和周长的求解:平行四边形的面积和周长的求解也是初中数学几何模型解题的重要内容,学生需要掌握相关公式及其应用。
初中数学九大几何模型
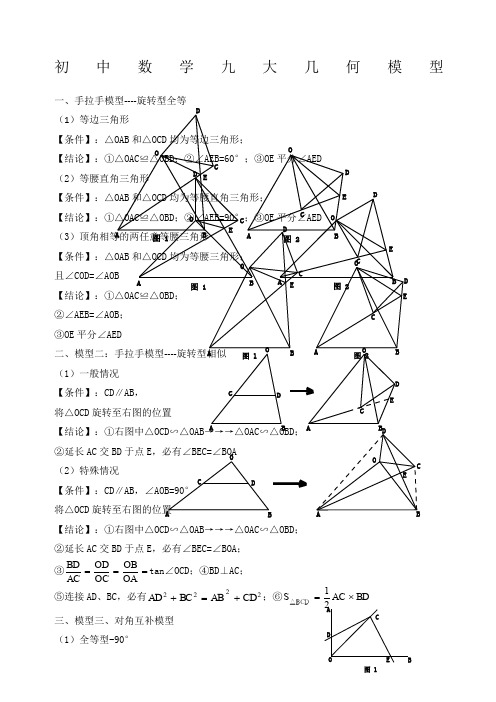
初中数学九大几何模型一、手拉手模型----旋转型全等 (1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形;且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似(1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯= 三、模型三、对角互补模型 (1)全等型-90°OA B CDE图 1OABCD E 图 2O ABC D E图 1OAB C DE图 2OA BCDEOACD E图 1图 2OB COA CDEO B CDEOCDAOBCDE 图 1【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC※当∠DCE 的一边交AO 的延长线于D 时(如图4):以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD△OCE OC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中几何常见九大模型解析(完美版)

初中几何常见九大模型解析(完美版)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何常见九大模型解析模型一:手拉手模型-旋转型全等(1)等边三角形➢条件:均为等边三角形➢结论:①;②;③平分。
(2)等腰➢条件:均为等腰直角三角形➢结论:①;②;➢③平分。
(3)任意等腰三角形➢条件:均为等腰三角形➢结论:①;②;➢③平分模型二:手拉手模型-旋转型相似(1)一般情况➢条件:,将旋转至右图位置➢结论:➢右图中①;➢②延长AC交BD于点E,必有(2)特殊情况➢条件:,,将旋转至右图位置➢结论:右图中①;②延长AC交BD于点E,必有;③;④;⑤连接AD、BC,必有;⑥(对角线互相垂直的四边形)模型三:对角互补模型(1)全等型-90°➢条件:①;②OC平分➢结论:①CD=CE;②;③➢证明提示:①作垂直,如图,证明;②过点C作,如上图(右),证明;➢当的一边交AO的延长线于点D时:以上三个结论:①CD=CE(不变);②;③此结论证明方法与前一种情况一致,可自行尝试。
(2)全等型-120°➢条件:①;➢②平分;➢结论:①;②;➢③➢证明提示:①可参考“全等型-90°”证法一;②如图:在OB上取一点F,使OF=OC,证明为等边三角形。
(3)全等型-任意角➢条件:①;②;➢结论:①平分;②;➢③.➢当的一边交AO的延长线于点D时(如右上图):原结论变成:①;②;③;可参考上述第②种方法进行证明。
请思考初始条件的变化对模型的影响。
➢对角互补模型总结:①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线;②初始条件“角平分线”与“两边相等”的区别;③两种常见的辅助线作法;④注意平分时,相等如何推导?模型四:角含半角模型90°(1)角含半角模型90°-1➢条件:①正方形;②;➢结论:①;②的周长为正方形周长的一半;也可以这样:➢条件:①正方形;②➢结论:(2)角含半角模型90°-2➢条件:①正方形;②;➢结论:➢辅助线如下图所示:(3)角含半角模型90°-3➢条件:①;②;➢结论:若旋转到外部时,结论仍然成立。
初中数学九大几何模型
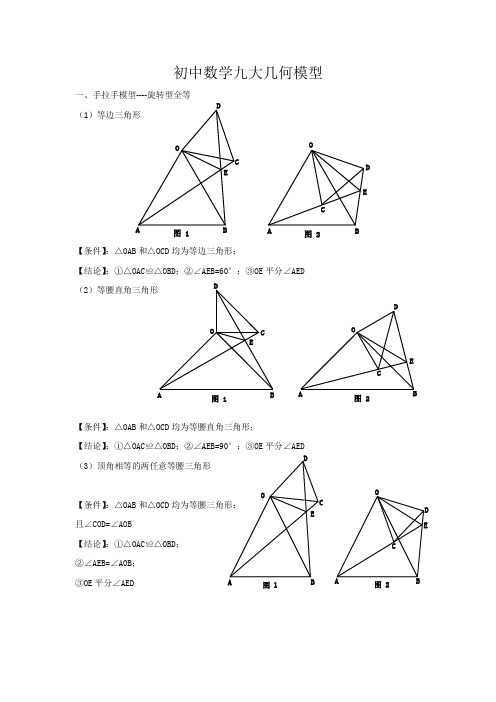
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学九大几何模型解题思路
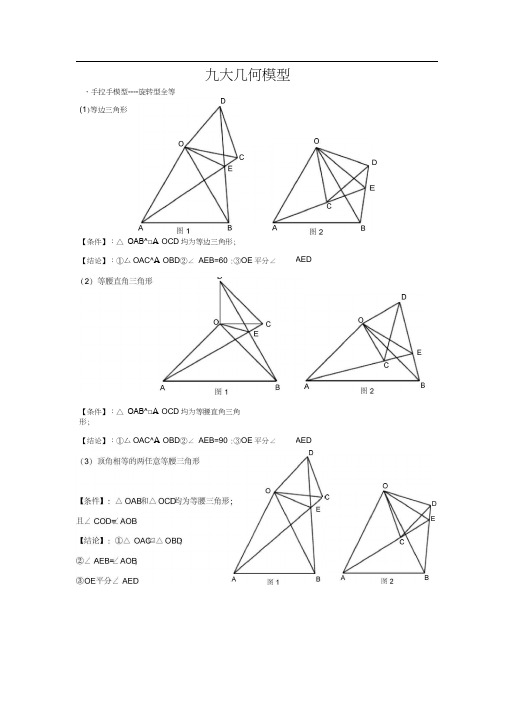
、手拉手模型----旋转型全等【条件】:△ OAB^□A OCD均为等边三角形;【条件】:△ OAB^□A OCD均为等腰直角三角形;九大几何模型(1)等边三角形DAED【结论】:①厶OAC^A OBD②∠ AEB=60 :③OE平分∠【结论】:①厶OAC^A OBD②∠ AEB=90 :③OE平分∠AEDED、模型二:手拉手模型----旋转型相似(1) 一般情况 【条件】:CD// AB, 将厶OCD 旋转至右图的位置 O OJ DEA【结论】:①右图中△ OC 3A OAB÷→→A OAS A OBD ②延长 AC 交BD 于点E ,必有∠ BEC=∠ BOA (2)特殊情况 A 【条件】:CD// AB,∠ AOB=90 将厶OCD 旋转至右图的位置 A 【结论】:①右图中△ OC 3A OAB÷→→A OAS A OBD ②延长 AC 交BD 于点E ,必有∠ BEC=∠ BOA ③ACOD OBtan∠OCD ④BD 丄AC ⑤连接AD BC,必有AD 2 BC 2 AB 2 CD :⑥ SA BCD三、模型三、对角互补模型 (1)全等型-90 ° 【条件】:①∠ AOB ∠ DCE=90 :②OC 平分∠ AOB【结论】:①CD=CE ②OD+OE= 2 OC ③S A DCE证明提示: ①作垂直,如图 2,证明△ CDM ^△ CEN ②过点C 作CF ⊥ OC 如图3,证明△ OD BA FEC ※当∠ DCE 的一边交 Ao 的延长线于 D 时(如图4): SA OCDS以上三个结论:① CD=CE ② OE-ODw 2 OC ③ S A OCE SA OCD(2) 全等型-120 °【条件】:①∠ AOB=∠ DCE=120 :②OC平分∠ AoB【结论】:① CD=CE ②OD+OE=OC③ S MC E S A OC D S^OCE— OC24证明提示:①可参考“全等型-90 ° ”证法一;②如右下图:在OB上取一点F,使OF=OC证明△ OCF为等边三角形。
初中数学九大几何模型
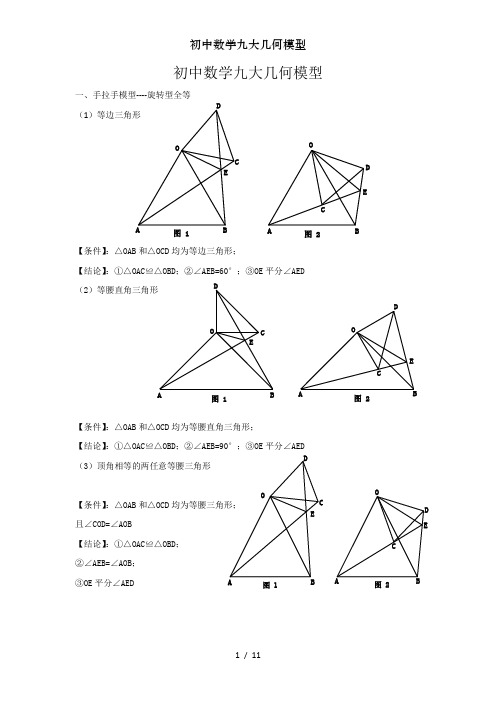
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB COACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中必备的几何模型与解题通法

初中必备的几何模型与解题通法初中的几何学是数学中的一大分支,包括了平面几何和立体几何两个部分。
在学习初中几何学的过程中,掌握几何模型和解题通法是非常重要的。
本文介绍一些初中必备的几何模型和解题通法,帮助初中生更好地掌握几何学。
一、平面几何模型1. 直线段模型:直线段是平面几何中最基本的图形,通常用线段表示。
在解题中,可以利用线段的长度、垂直、平行等性质来推导出答案。
2. 角度模型:角度是指由两条线段或射线共同起点所夹的空间部分。
在解题中,可以利用角度的大小、补角、余角等性质来推导出答案。
3. 三角形模型:三角形是平面几何中最基本的图形之一,由三条线段所组成。
在解题中,可以利用三角形的角度、边长、面积等性质来推导出答案。
4. 四边形模型:四边形是由四条线段所组成的图形,包括了矩形、正方形、平行四边形等。
在解题中,可以利用四边形的对角线、内角和、面积等性质来推导出答案。
5. 圆模型:圆是由一条射线不断绕着一个固定点旋转所形成的图形。
在解题中,可以利用圆的直径、半径、弧度等性质来推导出答案。
二、立体几何模型1. 立方体模型:立方体是由六个正方形所组成的图形,具有六个平面、十二个棱、八个顶点。
在解题中,可以利用立方体的体积、表面积等性质来推导出答案。
2. 圆柱体模型:圆柱体是由一个圆与一个长方形所组成的图形,具有两个平面、两个底面、一个侧面。
在解题中,可以利用圆柱体的体积、表面积等性质来推导出答案。
3. 圆锥体模型:圆锥体是由一个圆锥面与一个圆所组成的图形,具有一个平面、一个底面、一个侧面。
在解题中,可以利用圆锥体的体积、表面积等性质来推导出答案。
4. 球体模型:球体是由一个固定点到平面上所有点的距离相等所形成的图形,具有一个球心、一个半径。
在解题中,可以利用球体的体积、表面积等性质来推导出答案。
三、解题通法1. 分析问题:在解几何题时,首先要明确问题的目标和限制条件,然后根据几何模型的性质进行分析。
2. 画图辅助:画图是解决几何问题的重要手段,可以帮助我们更好地理解问题,从而找到解题的方法。
初中数学九大几何模型
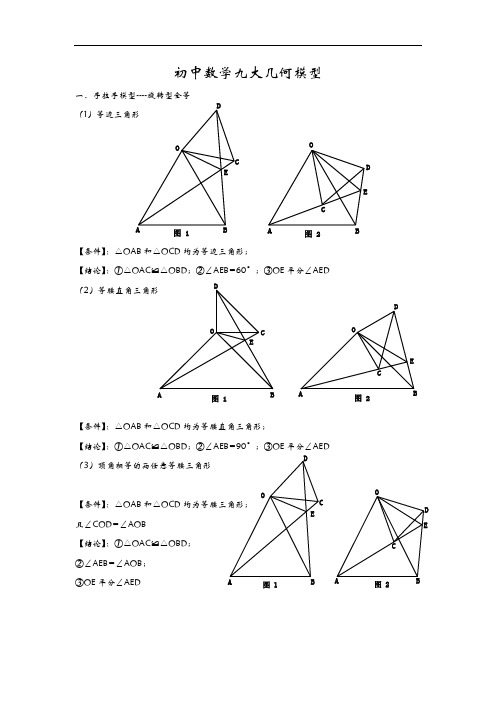
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOBC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OAB CO CDEOB CDEOA C DAO BCDE 图 1A O BCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(2021年整理)初中数学几何9种常见模型解析

初中数学几何9种常见模型解析
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初中数学几何9种常见模型解析)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初中数学几何9种常见模型解析的全部内容。
初中几何9种常见模型解析初中阶段的数学学习中,很多孩子的数学成绩都被一个困难的知识章节给难倒了,那就是几何,在考试中孩子最害怕的就是几何题,一遇到这种题目基本上都是全军覆没,很少能够有孩子把几何题一分不扣的做出来.。
初中必备的几何模型与解题通法

初中必备的几何模型与解题通法
几何模型是指将几何问题转化为具有形质的几何图形,以更直观、更清晰地表达问题,更方便串联知识点、推理方法和解题思路的工具。
以下是初中必备的几何模型与解题通法:
1. 线段与角的模型:将线段及其长度、直线之间的角度转化为几何图形。
2. 三角形的模型:将三角形及其特性(如外角和等于一周、直角三角形和勾股定理)转化为几何图形。
3. 四边形的模型:将四边形及其特性(如平行四边形的对角线互相平分、菱形的对角线互相垂直且平分)转化为几何图形。
4. 圆及其部分的模型:将圆及其半径、直径、弧、扇形、焦点等转化为几何图形。
5. 空间几何模型:将空间几何问题转化为三维立体图形的形式,如平行六面体、正方体等。
解题通法:
1. 画图法:将几何问题转化为几何图形,利用图形特性加以分析。
2. 分类讨论法:根据几何题目的不同条件,将问题分类处理,分别得出不同的结论。
3. 推理法:根据较简单的情况推导出复杂情况的结论。
4. 数学归纳法:通过证明某个结论对于一个特殊情况成立,再从一个情况推导到下一个情况,得出一般性结论。
5. 特殊化方法:将几何问题中涉及到的参数带入到具体数值中进行分析,从而进一步解决问题。
初中数学48个几何模型解题技巧

初中数学48个几何模型解题技巧1.相似三角形定理:两个三角形中,三个对应的角相等,对应的边成比例。
2.相等三角形的性质:两个三角形中,三边分别相等,或者两边分别相等且夹角相等。
3.三角形中,一个内角和一边:根据一个三角形角度和一边的已知信息,可以推导出其他角度和边的关系。
4.三角形的面积计算公式:可以根据底边和高的关系来计算三角形的面积。
5.正方形的性质:四个内角都是直角,四条边相等。
6.正方形的对角线:两条对角线相等且垂直。
7.矩形的性质:四个内角都是直角,对角线相等。
8.矩形的面积:可以通过长和宽的长度相乘计算矩形的面积。
9.菱形的性质:对角线互相垂直,对角线互相平分。
10.菱形的面积:可以通过对角线的乘积除以2来计算菱形的面积。
11.平行四边形的性质:对边平行,对角线互相平分。
12.平行四边形的面积:可以通过底边长度乘以高来计算平行四边形的面积。
13.梯形的性质:有两条平行边。
14.梯形的面积:可以通过上底和下底的和乘以高除以2来计算梯形的面积。
15.直角三角形的性质:有一个内角是直角。
16.直角三角形的勾股定理:直角三角形的两个直角边的平方之和等于斜边的平方。
17.直角三角形的正弦定理:直角三角形的斜边和对应的直角边之间的正弦值成比例。
18.直角三角形的余弦定理:直角三角形的斜边的平方等于两个直角边的平方之和减去两倍直角边的乘积。
19.直角三角形的正切定理:直角三角形的两个直角边的商等于对应的正切值。
20.平行线与横截线的性质:平行线与横截线之间的对应角相等。
21.平面镜映射的性质:物体与其镜像之间的对应角相等。
22.等腰三角形的性质:两个底角相等。
23.等边三角形的性质:三个内角都是60度。
24.角平分线的性质:角平分线可以将一个角分成两个相等的角。
25.外角的性质:外角等于其对应的内角的补角。
26.平面图形的旋转:点、线、图形按一定角度旋转后,与原来的点、线、图形相对应。
27.平行线的判定:两条直线的斜率相等即为平行线。
初中数学九大几何模型.docx

初中数学九大几何模型一、手拉手模型----旋转型全等D(1)等边三角形OOCE DECA图 1B A图 2B【条件】:△ OAB和△ OCD均为等边三角形;【结论】:①△ OAC≌△ OBD;②∠ AEB=60°;③ OE平分∠ AEDD(2)等腰直角三角形DO C OEECA图 1B A B图 2【条件】:△ OAB和△ OCD均为等腰直角三角形;【结论】:①△ OAC≌△ OBD;②∠ AEB=90°;③ OE平分∠AED D(3)顶角相等的两任意等腰三角形OOCEDE【条件】:△ OAB和△ OCD均为等腰三角形;且∠ COD=∠AOB【结论】:①△ OAC≌△ OBD;②∠ AEB=∠AOB;③OE平分∠ AED二、模型二:手拉手模型 ----O O 旋转型相似(1)一般情况DC DE【条件】: CD∥ AB,CA BA B将△ OCD旋转至右图的位置【结论】:①右图中△ OCD∽△ OAB→→→△ OAC∽△ OBD;D②延长 AC交 BD于点 E,必有∠ BEC=∠ BOA O OCC DE (2)特殊情况AB A B【条件】:CD∥ AB,∠ AOB=90°将△ OCD旋转至右图的位置【结论】:①右图中△ OCD∽△ OAB→→→△ OAC∽△ OBD;②延长 AC交 BD于点 E,必有∠ BEC=∠ BOA;③ BD OD OB tan ∠ OCD;④ BD⊥AC;AC OC OA⑤连接 AD、 BC,必有AD2BC 222;⑥ S△BCD 1ABCD AC BD2 AC三、模型三、对角互补模型(1)全等型 -90 °DO E B图1【条件】:①∠ AOB=∠ DCE=90°;② OC平分∠ AOB【结论】:① CD=CE;② OD+OE= 2 OC;③S S S 12OC△DCE△OCD△OCE2AC 证明提示:M①作垂直,如图 2,证明△ CDM≌△ CEND②过点 C 作 CF⊥ OC,如图 3,证明△ ODC≌△ FEC O N E B图 2※当∠ DCE的一边交 AO的延长线于 D 时(如图4):以上三个结论:①CD=CE;② OE-OD= 2 OC;AM C1③ S S2OC△OCE△OCD2ACBOND EOD图 4图 3E F B(2)全等型 -120 °【条件】:①∠ AOB=2∠ DCE=120°;② OC平分∠ AOB【结论】:① CD=CE;② OD+OE=OC;③S S S 32△DCEOC △OCD△OCE4证明提示:①可参考“全等型-90 °”证法一;②如右下图:在OB上取一点F,使 OF=OC,证明△ OCF为等边三角形。
初中数学九大几何模型
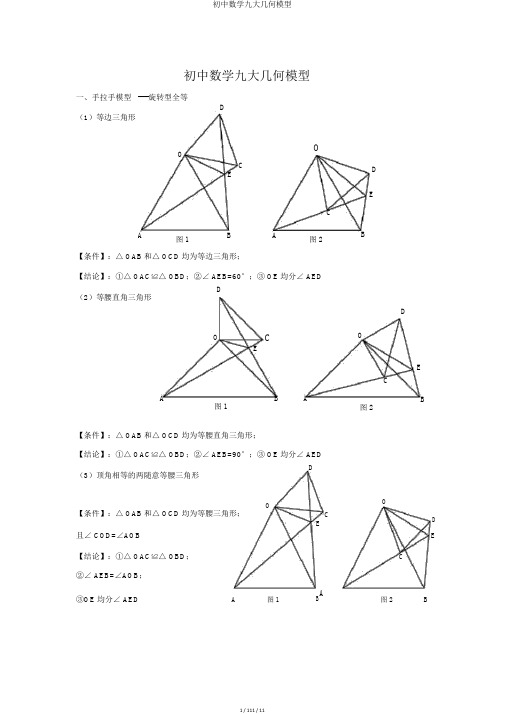
初中数学九大几何模型一、手拉手模型 ----旋转型全等D(1)等边三角形OOC ECA图 1BA图 2【条件】:△ OAB 和△ OCD 均为等边三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 均分∠ AEDD(2)等腰直角三角形OCEABA图 1D EBDOECB图 2【条件】:△ OAB 和△ OCD 均为等腰直角三角形;【结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 均分∠ AED(3)顶角相等的两随意等腰三角形DOOC【条件】:△ OAB 和△ OCD 均为等腰三角形;DE且∠ COD=∠AOBE【结论】:①△ OAC ≌△ OBD ; C②∠ AEB=∠AOB ;③OE 均分∠ AEDA 图 1BA图 2 BO O二、模型二:手拉手模型----旋转型相像(1)一般状况D【条件】: CD ∥ AB ,CD将△ OCD 旋转至右图的地点A B 【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延伸 AC 交 BD 于点 E ,必有∠ BEC=∠ BOAO(2)特别状况C D【条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的地点A B【结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延伸 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ;③ BDOD OB tan ∠ OCD ;④ BD ⊥AC ; ACOC OA⑤连结 AD 、 BC ,必有 AD 2BC222;⑥ S △BCDABCD三、模型三、对角互补模型(1)全等型 -90 °【条件】:①∠ AOB=∠ DCE=90°;② OC 均分∠ AOBECABDOCEA B1AC BD 2 ACDOE B图 1【结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCES△OCDS△OCE1 OC 2A2证明提示:CM①作垂直,如图 2,证明△ CDM ≌△ CEND②过点 C 作 CF ⊥ OC ,如图 3,证明△ ODC ≌△ FEC※当∠ DCE 的一边交 AO 的延伸线于 D 时(如图 4):ON EB图 2以上三个结论:① CD=CE ;② OE-OD= 2 OC ;A1OC 2AMC③S△OCES△OCD2CDONBEO图 3 EF BD图 4(2)全等型 -120 °【条件】:①∠ AOB=2∠ DCE=120°;② OC均分∠ AOB【结论】:① CD=CE;② OD+OE=OC;③S△DCE S△OCD S△OCE 3 OC24证明提示:①可参照“全等型-90 °”证法一;②如右下列图:在OB上取一点F,使 OF=OC,证明△ OCF为等边三角形。
初中数学几何模型大全及解析

初中数学几何模型大全及解析一中点模型【模型1】倍长1、倍长中线;2、倍长类中线;3、中点遇平行延长相交【模型2】遇多个中点,构造中位线1、直接连接中点;2、连对角线取中点再相连【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.二角平分线模型【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为 .三手拉手模型【例】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .四邻边相等的对角互补模型五半角模型六一线三角模型七弦图模型八最短路径模型【两点之间线段最短】1、将军饮马2、费马点【垂线段最短】【两边之差小于第三边】综合练习已知:如图1,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.⑴求证:EG=CG且EG⊥CG;⑵将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.问⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.⑶将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?。
初中数学九大几何模型
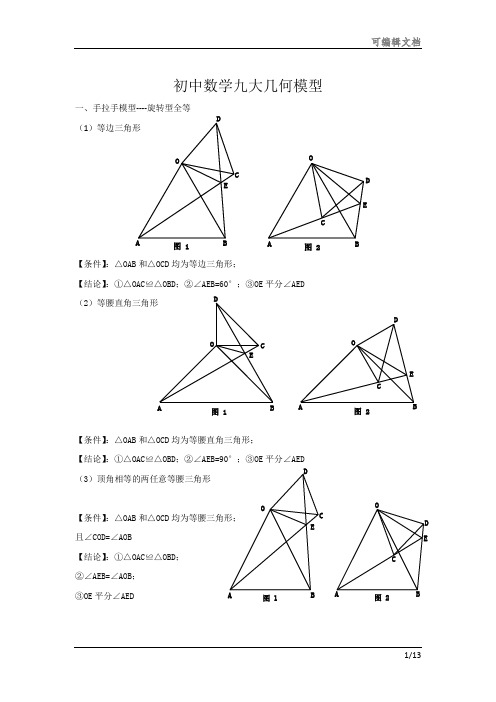
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB COACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OAB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2D【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ;OAB COBCDEOB CDEOCD∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4):以上三个结论:①CD=CE ;②;(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB图 1图 2A O BCDEMN 图 4【结论】:①CD=CE ;②OD+OE=OC 证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(3)全等型-任意角ɑ【条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE ;【结论】:①OC 平分∠AOB ;②OD+OE=2OC ·cos ɑ;※当∠DCE 的一边交AO 的延长线于D 时(如右下图):原结论变成:① ; ② ; ③ 。
可参考上述第②种方法进行证明。
请思考初始条件的变化对模型的影响。
AOBCEFAOBCEFF AOBEDCA对角互补模型总结:①常见初始条件:四边形对角互补,注意两点:四点共圆有直角三角形斜边中线;②初始条件“角平分线”与“两边相等”的区别;③注意OC 平分∠AOB 时,∠CDE=∠CED=∠COA=∠COB 如何引导?四、模型四:角含半角模型90° (1)角含半角模型90°---1【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF+BE ;②△CEF 的周长为正方形ABCD 周长的一半; 也可以这样:【条件】:①正方形ABCD ;②EF=DF+BE ;【结论】:①∠EAF=45°;AO BCDE ADAD(2)角含半角模型90°---2【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF-BE ;(3)角含半角模型90°---3【条件】:①Rt △ABC ;②∠DAE=45°;【结论】1)若∠DAE 旋转到△ABC 2)AB CD EF ABCD E F ABCDE FA AF(4)角含半角模型90°变形【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:△AHE 为等腰直角三角形; 证明:连接AC (方法不唯一) ∵∠DAC=∠EAF=45°,∴∠DAH=∠CAE ,又∵∠ACB=∠ADB=45°;∴△DAH ∽△CAE ∴△AHE ∽△ADC ,∴△AHE 为等腰直角三角形模型五:倍长中线类模型 (1)倍长中线类模型---1 【条件】:①矩形ABCD ;②BD=BE ;ABCDEABCDEFABC D GHFEABCD GHFEABCEF DH ABFDH③DF=EF ; 【结论】:AF ⊥CF模型提取:①有平行线AD ∥BE ;②平行线间线段有中点DF=EF ; 可以构造“8”字全等△ADF ≌△HEF 。
(2)倍长中线类模型---2【条件】:①平行四边形ABCD ;②BC=2AB ;③AM=DM ;④CE ⊥AB ; 【结论】:∠EMD=3∠MEA辅助线:有平行AB ∥CD ,有中点AM=DM ,延长EM ,构造△AME ≌△DMF ,连接CM 构造 等腰△EMC ,等腰△MCF 。
(通过构造8字全等线段数量及位置关系,角的大小转化)模型六:相似三角形360°旋转模型(1)相似三角形(等腰直角)360°旋转模型---倍长中线法 【条件】:①△ADE 、△ABC 均为等腰直角三角形;②EF=CF ; 【结论】:①DF=BF ;②DF ⊥BF辅助线:延长DF 到点G ,使FG=DF ,连接CG 、BG 、BD ,证明△BDG 为等腰直角三角形;突破点:△ABD ≌△CBG ; 难点:证明∠BAO=∠BCGAB C DME AB CDME FDFCDFCG(2)相似三角形(等腰直角)360°旋转模型---补全法 【条件】:①△ADE 、△ABC 均为等腰直角三角形;②EF=CF ; 【结论】:①DF=BF ;②DF ⊥BF 辅助线:构造等腰直角△AEG 、△AHC ;辅助线思路:将DF 与BF 转化到CG 与EF 。
(3)任意相似直角三角形360°旋转模型---补全法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ; 【结论】:①AE=DE ;②∠AED=2∠ABO辅助线:延长BA 到G ,使AG=AB ,延长CD 到点H 使DH=CD ,补全△OGB 、△OCH 构造旋转模型。
转化AE 与DE 到CG 与BH ,难点在转化∠AED 。
A EBDFCA EBDFCHGOABDEOABDG H(4)任意相似直角三角形360°旋转模型---倍长法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ; 【结论】:①AE=DE ;②∠AED=2∠ABO辅助线:延长DE 至M ,使ME=DE ,将结论的两个条件转化为证明△AMD ∽△ABO ,此为难点, 将△AMD ∽△ABC 继续转化为证明△ABM ∽△AOD ,使用两边成比例且夹角相等,此处难点在证明∠ABM=∠AOD模型七:最短路程模型(1)最短路程模型一(将军饮马类)总结:右四图为常见的轴对称类最短路程问题, 最后都转化到:“两点之间,线段最短:解决; 特点:①动点在直线上;②起点,终点固定OABDCEOA BDCEMl(2)最短路程模型二(点到直线类1)【条件】:①OC平分∠AOB;②M为OB上一定点;③P为OC上一动点;④Q为OB上一动点;【问题】:求MP+PQ最小时,P、Q的位置?辅助线:将作Q关于OC对称点Q’,转化PQ’=PQ,过点M作MH⊥OA,则MP+PQ=MP+PQ垂线段最短)(3)最短路程模型二(点到直线类2)【条件】:A(0,4),B(-2,0),P(0,n)l2A A'P QBB'lAl1l2PA+PQ+BQAP O Q M BQ'HPA【问题】:n求解方法:①x 轴上取C(2,0),使sin ∠B 作BD ⊥AC ,交y 轴于点E ,即为所求;③tan∠EBO=tan ∠E (0,1)(4)最短路程模型三(旋转类最值模型)【条件】:①线段OA=4,OB=2;②OB 绕点O 在平面内360°旋转; 【问题】:AB 的最大值,最小值分别为多少?【结论】:以点O 为圆心,OB 为半径作圆,如图所示,将问题转化为“三角形两边之和大于第三边,两边之差小于第三边”。
最大值:OA+OB ;最小值:OA-OBOAB最小值位置最大值位置【条件】:①线段OA=4,OB=2;②以点O为圆心,OB,OC为半径作圆;③点P是两圆所组成圆环内部(含边界)一点;【结论】:若PA的最大值为10,则OC= 6 ;若PA的最小值为1,则OC= 3 ;若PA的最小值为2,则PC的取值范围是 0<PC<2【条件】:①Rt△OBC,∠OBC=30°;②OC=2;③OA=1;④点P为BC上动点(可与端点重合);⑤△OBC绕点O旋转【结论】:PA最大值为PA如下图,圆的最小半径为O到BC垂线段长。
B C模型八:二倍角模型【条件】:在△ABC 中,∠B=2∠C ;辅助线:以BC 的垂直平分线为对称轴,作点A 的对称点A ’,连接AA ’、BA ’、CA ’、 则BA=AA ’=CA ’(注意这个结论)此种辅助线作法是二倍角三角形常见的辅助线作法之一,不是唯一作法。
模型九:相似三角形模型 (1)相似三角形模型--基本型 平行类:DE ∥BC ;A 字型 8字型 A 字型注意对应边要对应)(2)相似三角形模型---斜交型AB C AB CA'AB C DEAD EB C ADECACEADE【条件】:如右图,∠AED=∠ACB=90°; 【结论】:AE ×AB=AC ×AD【条件】:如右图,∠ACE=∠ABC ;【结论】:AC 2=AE ×AB第四个图还存在射影定理:AE ×EC=BC ×AC ;BC 2=BE ×BA ;CE 2=AE ×BE ; (3)相似三角形模型---一线三等角型 【条件】:(1)图:∠ABC=∠ACE=∠CDE=90°; (2)图:∠ABC=∠ACE=∠CDE=60°;(3)图:∠ABC=∠ACE=∠CDE=45°; 【结论】:①△ABC ∽△CDE ;②AB ×DE=BC ×CD ; 一线三等角模型也经常用来建立方程或函数关系。
ABC EABCE斜交型双垂型ABDE图(1)ABCE图(2)AB CDE图(3)(4)相似三角形模型---圆幂定理型【条件】:(2)图:PA 为圆的切线; 【结论】:(1)图:PA ×PB=PC ×PD ;(2)图:PA 2=PC ×PB; (3)图:PA ×PB=PC ×PD ; 以上结论均可以通过相似三角形进行证明。
