2020年高二数学第一学期期中考试模拟试卷附答案(一)
2020-2021高二数学上期中一模试卷带答案

2020-2021高二数学上期中一模试卷带答案一、选择题1.某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是 A .8号学生 B .200号学生C .616号学生D .815号学生2.函数()log a x x f x x=(01a <<)的图象大致形状是( )A .B .C .D .3.甲、乙两人各写一张贺年卡随意送给丙、丁两人中的一人,则甲、乙将贺年卡都送给丁的概率为( )A .12 B .13C .14 D .154.已知变量,x y 之间满足线性相关关系ˆ 1.31yx =-,且,x y 之间的相关数据如下表所示: x 1 2 3 4 y0.1m3.14则实数m =( ) A .0.8 B .0.6C .1.6D .1.85.设a 是甲抛掷一枚骰子得到的点数,则方程220x ax ++=有两个不相等的实数根的概率为( ) A .23B .13C .12D .5126.我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为 ( ) A .45,75,15B .45,45,45C .45,60,30D .30,90,157.某城市2017年的空气质量状况如下表所示: 污染指数T 3060100110130140概率P110 16 13 730 215 130其中污染指数50T ≤时,空气质量为优;50100T <≤时,空气质量为良;100150T <≤时,空气质量为轻微污染,该城市2017年空气质量达到良或优的概率为( )A.35 B .1180 C .119 D .568.执行如图所示的程序框图,则输出的结果是( )A .5B .7C .9D .119.已知不等式501x x -<+的解集为P ,若0x P ∈,则“01x <”的概率为( ). A .14 B .13C .12D .2310.6件产品中有4件合格品,2件次品.为找出2件次品,每次任取一个检验,检验后不放回,则恰好在第四次检验后找出所有次品的概率为( ) A .35B .13C .415D .1511.已知平面区域()20,4y x y y x ⎧⎫≥⎧⎪⎪⎪Ω=⎨⎨⎬≤-⎪⎪⎪⎩⎩⎭,直线2y mx m =+和曲线24y x =-有两个不的交点,它们围成的平面区域为M ,向区域Ω上随机投一点A ,点A 落在区域M 内的概率为()P M .若01m ≤≤,则()P M 的取值范围为( )A .202,π-⎛⎤⎥π⎝⎦B .202,π+⎛⎤⎥π⎝⎦C .212,π+⎡⎤⎢⎥π⎣⎦D .212,π-⎡⎤⎢⎥π⎣⎦12.某产品的广告费用x 与销售额y 的统计数据如下表: 广告费用(万元)4235销售额(万元)49263954根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为 A .63.6万元B .65.5万元C .67.7万元D .72.0万元二、填空题13.已知一组数据:87,,90,89,93x 的平均数为90,则该组数据的方差为______. 14.某人向边长分别为5,12,13的三角形区域内随机丢一粒芝麻,假设芝麻落在区域内的任意一点是等可能的,则其恰落在离三个顶点距离都大于2的地方的概率为__ . 15.在区间[]3,3-上随机取一个数x ,使得11x +≥成立的概率为______. 16.执行如图所示的程序框图,如果输入3n =,则输出的S 为 ________.17.如图所示,程序框图(算法流程图)的输出值x =________.18.某路公共汽车每5分钟发车一次,某乘客到乘车点的时刻是随机的,则他候车时间不超过3分钟的概率是_______.19.如果执行下面的程序框图,那么输出的s =______________.20.已知,x y 之间的一组数据不小心丢失一个,但已知回归直线过点()1.5,4,则丢失的数据是__________.x 0 1 2 3y135三、解答题21.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数, 得到如下资料: 日期1月10日 2月10日 3月10日 4月10日 5月10日 6月10日 昼夜温差()x c o10 11 13 12 8 6 就诊人数y (个) 222529261612该兴趣小组确定的研究方案是:先从这六组数据中选取 2 组,用剩下的 4 组数据求 线性回归方程,再用被选取的 2 组数据进行检验; (Ⅰ)求选取的 2 组数据恰好是相邻两个月的概率;(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出 y 关于x 的线性回归方程 ;(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人, 则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?附:对于一组数据11(,)u v ,2,2)u v ( ,…,(,)n n u v ,其回归直线V u αβ=+ 的斜率和截距的最小二乘估计分别为i1i ii12in()(?)u)ˆ(nu u vuβ==∑-=∑-nn,ˆ-ˆuανβ= .22.如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:(1)79.589.5:这一组的频数、频率分别是多少?(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均数?23.某乡镇为了发展旅游行业,决定加强宣传,据统计,广告支出费x与旅游收入y(单位:万元)之间有如下表对应数据:x24568 y3040605070(1)求旅游收入y对广告支出费x的线性回归方程y bx a=+,若广告支出费12万元,预测旅游收入;(2)在已有的五组数据中任意抽取两组,根据(1)中的线性回归方程,求至少有一组数据,其预测值与实际值之差的绝对值不超过5的概率.(参考公式:1221ni iiniix y nxybx nx==-=-∑∑,a y bx=-,其中,x y为样本平均值,参考数据:521145iix==∑,52113500iiy==∑,511380i iix y==∑)24.高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.25.某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分1000,1500).布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[)3000,3500的频率;(1)求居民收入在[)(2)根据频率分布直方图算出样本数据的中位数;(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按2500,3000的这段应抽取多少人?分层抽样方法抽出100人作进一步分析,则月收入在[)26.甲与乙午觉醒来后,发现自己的手表因故停止转动,于是他们想借助收音机,利用电台整点报时确认时间.(1)求甲等待的时间不多于10分钟的概率;(2)求甲比乙多等待10分钟以上的概率.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】等差数列的性质.渗透了数据分析素养.使用统计思想,逐个选项判断得出答案.详解:由已知将1000名学生分成100个组,每组10名学生,用系统抽样,46号学生被抽到,所以第一组抽到6号,且每组抽到的学生号构成等差数列{}n a ,公差10d =, 所以610n a n=+()n *∈N ,若8610n =+,则15n =,不合题意;若200610n =+,则19.4n =,不合题意; 若616610n =+,则61n =,符合题意;若815610n =+,则80.9n =,不合题意.故选C . 【点睛】本题主要考查系统抽样.2.C解析:C 【解析】 【分析】确定函数是奇函数,图象关于原点对称,x >0时,f (x )=log a x (0<a <1)是单调减函数,即可得出结论. 【详解】由题意,f (﹣x )=﹣f (x ),所以函数是奇函数,图象关于原点对称,排除B 、D ; x >0时,f (x )=log a x (0<a <1)是单调减函数,排除A . 故选C . 【点睛】本题考查函数的图象,考查函数的奇偶性、单调性,正确分析函数的性质是关键.3.C解析:C 【解析】 【分析】甲、乙两人各写一张贺年卡随意送给丙、丁两人中的一人共有4种情况,甲、乙将贺年卡都送给丁有1种情况,利用古典概型求解即可. 【详解】(甲送给丙、乙送给丁)、(甲送给丁,乙送给丙)、(甲、乙都送给丙)、(甲、乙都送给丁)共四种情况,其中甲、乙将贺年卡送给同一人的情况有两种, 所以甲、乙将贺年卡送给同一人丁的情况一种,概率是:14, 故选C . 【点睛】本题主要考查了古典概型的定义及计算,排列,计数原理,属于中档题.4.D【解析】分析:由题意结合线性回归方程的性质整理计算即可求得最终结果. 详解:由题意可得:12345 2.542x +++===,0.1 3.14 1.844m my +++==+, 线性回归方程过样本中心点,则:1.8 1.3 2.514m+=⨯-, 解得:8.1=m . 本题选择D 选项.点睛:本题主要考查线性回归方程的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.5.A解析:A 【解析】分析:可以按照等可能时间的概率来考虑,可以先列举出试验发生包含的事件数,再求出满足条件的事件数,从而根据概率计算公式求解.详解:因为a 是抛掷一枚骰子得到的点数,所以试验发生包含的事件总数为6, 方程220x ax ++=有两个不等实根,所以280a ->, 以为a 为正整数,所以3,4,5,6a =,即满足条件的事件有4种结果,所以所求的概率为4263P ==,故选A. 点睛:本题主要考查的是古典概型及其概率计算公式.,属于基础题.解题时要准确理解题意,先要判断该概率模型是不是古典概型,利用排列组合有关知识,正确找出随机事件A 包含的基本事件的个数和试验中基本事件的总数代入公式()()n A P n =Ω.6.C解析:C 【解析】因为共有学生2700,抽取135,所以抽样比为1352700,故各年级分别应抽取135900452700⨯=,1351200602700⨯=,135600302700⨯=,故选C. 7.A解析:A 【解析】 【分析】根据互斥事件的和的概率公式求解即可. 【详解】由表知空气质量为优的概率是110, 由互斥事件的和的概率公式知,空气质量为良的概率为111632+=, 所以该城市2017年空气质量达到良或优的概率1131025P =+=, 故选:A 【点睛】本题主要考查了互斥事件,互斥事件和的概率公式,属于中档题.8.C解析:C 【解析】循环依次为123,123;S K =+==+=369,325;S K =+==+=91019,527;S K =+==+=191433,729;S K =+==+=结束循环,输出9;K =选C.9.B解析:B 【解析】 【分析】 【详解】分析:解分式不等式得集合P ,再根据几何概型概率公式(测度为长度)求结果.详解:(5)(1)050101x x x x x -+<⎧-<⇒⎨+≠+⎩, ∴{}|15P x x =-<<,||111x x <⇒-<<,∴1(1)15(1)3P --==--.选B .点睛:(1)当试验的结果构成的区域为长度、面积、体积等时,应考虑使用几何概型求解. (2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域.10.C解析:C 【解析】 【分析】题目包含两种情况:第一种是前面三次找出一件次品,第四次找出次品,第二种情况是前面四次都是正品,则剩余的两件是次品,计算概率得到答案. 【详解】题目包含两种情况:第一种是前面三次找出一件次品,第四次找出次品,2314615CpC==;第二种情况是前面四次都是正品,则剩余的两件是次品,44246115CpC==;故12415p p p=+=.故选:C.【点睛】本题考查了概率的计算,忽略掉前面四次都是正品的情况是容易发生的错误.11.D解析:D【解析】【分析】判断平面区域,利用特殊值法排除选项,然后利用特殊法,即可求解相应概率的范围,得到答案.【详解】由题意知,平面区域()2,4yx yy x⎧⎫≥⎧⎪⎪Ω=⎨⎨⎬≤-⎪⎪⎪⎩⎩⎭,表示的图形是半圆是半圆以及内部点的集合,如图所示,又由直线2y mx m=+过半圆24y x=-上一点(2,0)-,当0m=时直线与x轴重合,此时()1P M=,故可排除,A B,若1m=,如图所示,可求得2()2P Mππ-=,所以()P M的取值范围为212,π-⎡⎤⎢⎥π⎣⎦.【点睛】本题主要考查了集合概型的应用,其中解答中判断平面区域,利用特殊值法排除选项,然后利用特殊法,求解相应概率的范围是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.12.B解析:B【解析】【分析】【详解】 试题分析:4235492639543.5,4244x y ++++++====Q , ∵数据的样本中心点在线性回归直线上,回归方程ˆˆˆy bx a =+中的ˆb 为9.4, ∴42=9.4×3.5+a , ∴ˆa=9.1, ∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5 考点:线性回归方程二、填空题13.【解析】该组数据的方差为解析:4【解析】8790899390591x x ++++=⨯∴= 该组数据的方差为222221[(8790)(9190)(9090)(8990)(9390)]45-+-+-+-+-= 14.【解析】由题意可知与三个顶点的距离都小于2的区域的面积恰好为一个半径为2的半圆的面积即所以与三个顶点的距离都大于2的区域的面积由几何概型的概率公式知其恰落在与三个顶点的距离都大于2的地方的概率为答案 解析:1515π- 【解析】由题意可知,与三个顶点的距离都小于2的区域的面积恰好为一个半径为2的半圆的面积,即2π,所以与三个顶点的距离都大于2的区域的面积302π-。
2020年高二数学上期中一模试题含答案
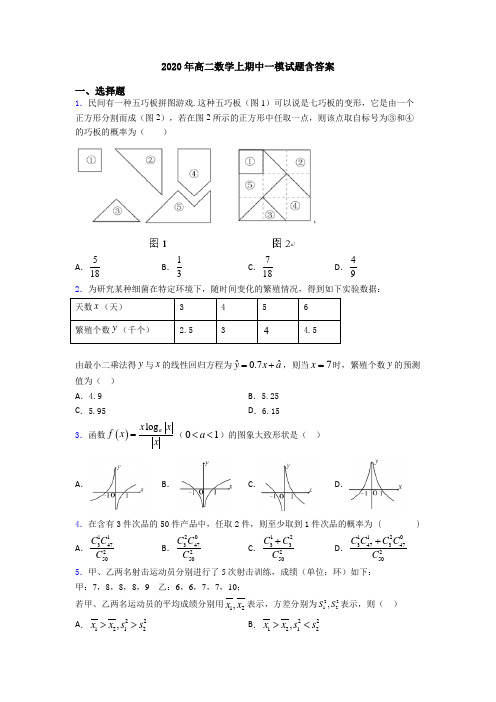
2020年高二数学上期中一模试题含答案一、选择题1.民间有一种五巧板拼图游戏.这种五巧板(图1)可以说是七巧板的变形,它是由一个正方形分割而成(图2),若在图2所示的正方形中任取一点,则该点取自标号为③和④的巧板的概率为( )A .518B .13C .718D .492.为研究某种细菌在特定环境下,随时间变化的繁殖情况,得到如下实验数据: 天数x (天) 3 4 56 繁殖个数y (千个)2.5344.5由最小二乘法得y 与x 的线性回归方程为ˆˆ0.7yx a =+,则当7x =时,繁殖个数y 的预测值为( ) A .4.9 B .5.25 C .5.95 D .6.153.函数()log a x x f x x=(01a <<)的图象大致形状是( )A .B .C .D .4.在含有3件次品的50件产品中,任取2件,则至少取到1件次品的概率为 ( )A .11347250C C C B .20347250C C C C .1233250C C C +D .1120347347250C C C C C + 5.甲、乙两名射击运动员分别进行了5次射击训练,成绩(单位:环)如下: 甲:7,8,8,8,9 乙:6,6,7,7,10;若甲、乙两名运动员的平均成绩分别用12,x x 表示,方差分别为2212,S S 表示,则( )A .221212,x x s s >> B .221212,x x s s ><C .221212,x x s s << D .221212,x x s s <> 6.AQI 即空气质量指数,AQI 越小,表明空气质量越好,当AQI 不大于100时称空气质量为“优良”.如图是某市3月1日到12日AQI 的统计数据.则下列叙述正确的是( )A .这12天的AQI 的中位数是90B .12天中超过7天空气质量为“优良”C .从3月4日到9日,空气质量越来越好D .这12天的AQI 的平均值为1007.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 A .45B .35C .25D .158.执行如图的程序框图,则输出x 的值是 ( )A .2018B .2019C .12D .29.A 地的天气预报显示,A 地在今后的三天中,每一天有强浓雾的概率为30%,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生09-之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:402978191925273842812479569683 231357394027506588730113537779则这三天中至少有两天有强浓雾的概率近似为()A.14B.25C.710D.1510.某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有()①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人;②用简单随机抽样的方法从新生中选出100人;③西部地区学生小刘被选中的概率为150;④中部地区学生小张被选中的概率为15000A.①④B.①③C.②④D.②③11.已知平面区域()2,4yx yy x⎧⎫≥⎧⎪⎪⎪Ω=⎨⎨⎬≤-⎪⎪⎪⎩⎩⎭,直线2y mx m=+和曲线24y x=-有两个不的交点,它们围成的平面区域为M,向区域Ω上随机投一点A,点A落在区域M内的概率为()P M.若01m≤≤,则()P M的取值范围为()A.22,π-⎛⎤⎥π⎝⎦B.22,π+⎛⎤⎥π⎝⎦C.212,π+⎡⎤⎢⎥π⎣⎦D.212,π-⎡⎤⎢⎥π⎣⎦12.已知P是△ABC所在平面内﹣点,20PB PC PA++=u u u r u u u r u u u r r,现将一粒黄豆随机撒在△ABC 内,则黄豆落在△PBC内的概率是()A.23B.12C.13D.14二、填空题13.在区间[-3,5]上随机取一个实数x,则事件“11422x≤≤()”发生的概率为____________.14.某校连续5天对同学们穿校服的情况进行统计,没有穿校服的人数用茎叶图表示,如图,若该组数据的平均数为18,则x=_____________.15.在可行域103x yx yx--≤⎧⎪+≤⎨⎪>⎩,内任取一点(),M x y,则满足20x y->的概率是______.16.某校高一年级有600个学生,高二年级有550个学生,高三年级有650个学生,为调查学生的视力情况,用分层抽样的方法抽取一个样本,若在高二、高三共抽取了48个学生,则应在高一年级抽取学生______个17.执行如图所示的程序框图,则输出S 的结果为________.18.某商家观察发现某种商品的销售量x 与气温y 呈线性相关关系,其中组样本数据如下表:已知该回归直线方程为ˆˆ1.02yx a =+,则实数ˆa =__________. 19.正四面体的4个面上分别写着1、2、3、4,将3个这样均匀的正四面体同时投掷于桌面上,与桌面接触的3个面上的3个数的乘积能被4整除的概率是_____________.20.已知方程0.85 2.1ˆ87yx =-是根据女大学生的身高预报其体重的回归方程, ˆ,x y 的单位是cm 和kg ,则针对某个体()160,53的残差是__________.三、解答题21.国家公安机关为给居民带来全方位的安全感,大力开展智慧警务社区建设.智慧警务建设让警务更智慧,让民生更便利,让社区更安全.下表是某公安分局在建设智慧警务社区活动中所记录的七个月内的该管辖社区的违法事件统计数据: 月份 1 2 3 4 5 6 7 违法案件数196101663421116根据以上数据,绘制了如图所示的散点图.(1)根据散点图判断,用y a bx =+与(0,01)xy c d b d =⋅<<<哪一个更适宜作为违法案件数y 关于月份x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)中的判断结果及表中所给数据,求y 关于x 的回归方程(保留两位有效数字),并预测第8个月该社区出现的违法案件数(取整数). 参考数据:其中i i v lgy =,7117i i v v ==∑.参考公式:对一组数据()11,u v ,()22,u v ,…,(),n n u v ,其回归直线的斜率和截距的最小二乘估计公式分别为:µ1221ni i i ni i u v nuvu nuβ==-=-∑∑,µµv u αβ=-. 22.为了调查某大学学生在周日上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果: 表1:男生上网时间与频数分布表:表2:女生上网时间与频数分布表: (1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;(2)完成表3的22⨯列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?(3)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率.表3:合计附:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++,()20P K k ≥ 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.82823.每年七月份,我国J 地区有25天左右的降雨时间,如图是J 地区S 镇2000-2018年降雨量(单位:mm )的频率分布直方图,试用样本频率估计总体概率,解答下列问题:(1)假设每年的降雨天气相互独立,求S 镇未来三年里至少有两年的降雨量超过350mm 的概率;(2)在S 镇承包了20亩土地种植水果的老李过去种植的甲品种水果,平均每年的总利润为31.1万元.而乙品种水果的亩产量m (kg/亩)与降雨量之间的关系如下面统计表所示,又知乙品种水果的单位利润为32-0.01×m(元/kg ),请帮助老李排解忧愁,他来年应该种植哪个品种的水果可以使利润ξ(万元)的期望更大?(需说明理由); 降雨量[100,200)[200,300)[300,400)[400,500)亩产量 500 700 600 40024.某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.分数段[50,60)[60,70)[70,80)[80,90)x∶y1∶12∶13∶44∶525.随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分,现将评分分为5组,如下表:组别一二三四五满意度评分[0,2)[2,4)[4,6)[6,8)[8,10]频数510a3216频率0.05b0.37c0.16(1)求表格中的a,b,c的值;(2)估计用户的满意度评分的平均数;(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?26.为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.甲班 乙班 合计优秀不优秀合计参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++参考数据:()20P K k ≥0.050 0.010 0.0010k3.841 6.635 10.828【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】分别求出③和④的巧板的面积,根据几何概型的概率关系转化为面积比. 【详解】设巧板①的边长为1,则结合图2可知大正方形的边长为3, 其面积239S ==.其中巧板③是底边长为2的等腰直角三角形,其面积为112112S =⨯⨯=的正方形 与腰长为1的等腰直角三角形的组合图形,其面积为22151122S ⨯⨯+==,故所求的概率12718S S P S +==. 故选:C . 【点睛】本题考查几何概型的概率求法,转化为面积比,属于中档题 .2.B解析:B 【解析】 【分析】根据表格中的数据,求得样本中心为97(,)22,代入回归直线方程,求得ˆ0.35a =,得到回归直线的方程为ˆ0.70.35yx =+,即可作出预测,得到答案. 【详解】由题意,根据表格中的数据,可得34569 2.534 4.57,4242x y ++++++====, 即样本中心为97(,)22,代入回归直线方程ˆˆ0.7yx a =+,即79ˆ0.722a=⨯+, 解得ˆ0.35a=,即回归直线的方程为ˆ0.70.35y x =+, 当7x =时,ˆ0.770.35 5.25y=⨯+=,故选B .【点睛】本题主要考查了回归直线方程的应用,其中解答中熟记回归直线方程的特征,求得回归直线的方程是解答的关键,着重考查了运算与求解能力,属于基础题.3.C解析:C【解析】【分析】确定函数是奇函数,图象关于原点对称,x>0时,f(x)=log a x(0<a<1)是单调减函数,即可得出结论.【详解】由题意,f(﹣x)=﹣f(x),所以函数是奇函数,图象关于原点对称,排除B、D;x>0时,f(x)=log a x(0<a<1)是单调减函数,排除A.故选C.【点睛】本题考查函数的图象,考查函数的奇偶性、单调性,正确分析函数的性质是关键.4.D解析:D【解析】【分析】由题意,恰好两件都是次品,共有23C种不同的取法,恰好两件中一件是次品、一件是正品,共有11347C C种不同的取法,即可求解.【详解】由题意,从含有3件次品的50件产品中,任取2件,共有250C种不同的取法,恰好两件都是次品,共有20347C C种不同的取法,恰好两件中一件是次品、一件是正品,共有11347C C种不同的取法,所以至少取到1件次品的概率为1120347347250C C C CC+,故选D.【点睛】本题主要考查了古典概型及其概率的计算,其中解答中正确理解题意,合理分类讨论,利用组合数的公式是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于基础题.5.B解析:B【解析】【分析】计算18x=,27.2x=,210.4s=,222.16s=得到答案.【详解】17888985x ++++==,26677107.25x ++++==,故12x x >.()()()()()222222178888888980.45s -+-+-+-+-==;()()()()()222222267.267.277.277.2107.2 2.165s -+-+-+-+-==,故2212s s <.故选:B. 【点睛】本题考查了平均值和方差的计算,意在考查学生的计算能力和观察能力.6.C解析:C 【解析】这12天的AQI 指数值的中位数是959293.52+= ,故A 不正确;这12天中,空气质量为“优良”的有95,85,77,67,72,92共6天,故B 不正确;;从4日到9日,空气质量越来越好,,故C 正确;这12天的AQI 指数值的平均值为110,故D 不正确. 故选 C .7.C解析:C 【解析】选取两支彩笔的方法有25C 种,含有红色彩笔的选法为14C 种,由古典概型公式,满足题意的概率值为142542105C p C ===. 本题选择C 选项. 考点:古典概型名师点睛:对于古典概型问题主要把握基本事件的种数和符合要求的事件种数,基本事件的种数要注意区别是排列问题还是组合问题,看抽取时是有、无顺序,本题从这5支彩笔中任取2支不同颜色的彩笔,是组合问题,当然简单问题建议采取列举法更直观一些.8.D解析:D 【解析】 【分析】模拟执行程序框图,依次写出每次循环得到的x ,y 的值,当2019y = 时,不满足条件退出循环,输出x 的值即可得解. 【详解】解:模拟执行程序框图,可得2,0x y ==.满足条件2019y <,执行循环体,1,1x y =-=;满足条件2019y <,执行循环体,1,22x y == ; 满足条件2019y <,执行循环体,2,3x y ==;满足条件2019y <,执行循环体,1,4x y =-= ; …观察规律可知,x 的取值周期为3,由于20196733⨯=,可得: 满足条件2019y <,执行循环体,当2,2019x y == ,不满足条件2019y <,退出循环,输出x 的值为2. 故选D . 【点睛】本题主要考查了循环结构的程序框图,依次写出每次循环得到的x ,y 的值,根据循环的周期,得到跳出循环时x 的值是解题的关键.9.D解析:D 【解析】 【分析】由题意知模拟这三天中至少有两天有强浓雾的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示三天中恰有两天有强浓雾的有可以通过列举得到共4组随机数,根据概率公式,得到结果. 【详解】由题意知模拟这三天中至少有两天有强浓雾的结果,经随机模拟产生了如下20组随机数, 在20组随机数中表示三天中恰有两天有强浓雾的有,可以通过列举得到共5组随机数:978,479、588、779,共4组随机数, 所求概率为41205=, 故选D . 【点睛】本题考查模拟方法估计概率,解题主要依据是等可能事件的概率,注意列举法在本题的应用.10.B解析:B 【解析】分析:由题意逐一考查所给的说法是否正确即可. 详解:逐一考查所给的说法:①由分层抽样的概念可知,取东部地区学生2400100240016001000⨯=++48人、中部地区学生1600100240016001000⨯=++32人、西部地区学生1000100240016001000⨯=++20人,题中的说法正确;②新生的人数较多,不适合用简单随机抽样的方法抽取人数,题中的说法错误;③西部地区学生小刘被选中的概率为100124001600100050=++,题中的说法正确;④中部地区学生小张被选中的概率为100124001600100050=++,题中的说法错误;综上可得,正确的说法是①③.本题选择B选项.点睛:本题主要考查分层抽样的概念,简单随机抽样的特征,古典概型概率公式等知识,意在考查学生的转化能力和计算求解能力.11.D解析:D【解析】【分析】判断平面区域,利用特殊值法排除选项,然后利用特殊法,即可求解相应概率的范围,得到答案.【详解】由题意知,平面区域()2,4yx yy x⎧⎫≥⎧⎪⎪Ω=⎨⎨⎬≤-⎪⎪⎪⎩⎩⎭,表示的图形是半圆是半圆以及内部点的集合,如图所示,又由直线2y mx m=+过半圆24y x=-上一点(2,0)-,当0m=时直线与x轴重合,此时()1P M=,故可排除,A B,若1m=,如图所示,可求得2()2P Mππ-=,所以()P M的取值范围为212,π-⎡⎤⎢⎥π⎣⎦.【点睛】本题主要考查了集合概型的应用,其中解答中判断平面区域,利用特殊值法排除选项,然后利用特殊法,求解相应概率的范围是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.12.B解析:B 【解析】 【分析】推导出点P 到BC 的距离等于A 到BC 的距离的12.从而S △PBC =12S △ABC .由此能求出将一粒黄豆随机撒在△ABC 内,黄豆落在△PBC 内的概率. 【详解】以PB 、PC 为邻边作平行四边形PBDC ,则PB PC +u u u r u u u r =PD u u u r , ∵20PB PC PA ++=u u u r u u u r u u u r r ,∴2PB PC PA +=-u u u r u u u r u u u r , ∴2PD PA =-u u u r u u u r,∴P 是△ABC 边BC 上的中线AO 的中点,∴点P 到BC 的距离等于A 到BC 的距离的12.∴S △PBC =12S △ABC .∴将一粒黄豆随机撒在△ABC 内,黄豆落在△PBC 内的概率为:P=PBC ABC S S V V =12. 故选B . 【点睛】本题考查概率的求法,考查几何概型等基础知识,考运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.二、填空题13.【解析】【分析】解不等式可得出所求事件的区域长度又可求出所有基本事件构成的区域长度由几何概型可求出概率【详解】设事件表示由得则即构成事件的区域的长度为又因为所有的基本事件构成的区域的长度为所以事件的 解析:38【解析】 【分析】解不等式11422x⎛⎫≤≤ ⎪⎝⎭,可得出所求事件的区域长度,又可求出所有基本事件构成的区域长度,由几何概型可求出概率. 【详解】设事件A 表示11|422xx ⎧⎫⎪⎪⎛⎫≤≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,由11422x ⎛⎫≤≤ ⎪⎝⎭得2111222x -⎛⎫⎛⎫≤≤ ⎪ ⎪⎝⎭⎝⎭,则21x -≤≤, 即构成事件A 的区域的长度为12=3+.又因为所有的基本事件构成的区域的长度为53=8+, 所以事件A 的概率3()8P A =. 故答案为38.【点睛】本题考查了几何概型的概率公式,属基础题.14.8【解析】【分析】根据茎叶图计算平均数【详解】由茎叶图得【点睛】本题考查茎叶图以及平均数考查基本运算能力属基础题解析:8 【解析】 【分析】根据茎叶图计算平均数. 【详解】 由茎叶图得1617101920188.5x x +++++=∴=【点睛】本题考查茎叶图以及平均数,考查基本运算能力,属基础题.15.【解析】【分析】画出可行域求出面积满足的区域为图形中的红色直线的下方的四边形其面积为由几何概型的公式可得的概率为:;【详解】约束条件的可行域如图:由解得可行域d 面积为由解得满足的区域为图形中的红色直解析:58【解析】 【分析】画出可行域,求出面积,满足20x y ->的区域为图形中的红色直线的下方的四边形,其面积为1541322-⨯⨯=,由几何概型的公式可得20x y ->的概率为:55248=;【详解】约束条件1030x y x y x --≤⎧⎪+≤⎨⎪>⎩的可行域如图:由103x y x y --=⎧+=⎨⎩解得()2,1A , 可行域d 面积为12442⨯⨯=, 由32x y y x +=⎧=⎨⎩,解得()1.2B . 满足20x y ->的区域为图形中的红色直线的下方的四边形,其面积为1541322-⨯⨯=, 由几何概型的公式可得20x y ->的概率为:55248=;故答案为58.【点睛】本题考查了可行域的画法以及几何概型的概率公式的运用.考查数形结合以及计算能力.在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的,而对于角度而言,则是过角的顶点的一条射线落在Ω的区域(事实也是角)任一位置是等可能的.16.24【解析】【分析】设应在高一年级抽取学生数为n 首先求出高一年级人数占总人数的百分比然后通过分层抽样的性质由此能求出应在高一年级抽取学生数【详解】设应在高一年级抽取学生数为n 因为某校高一年级有600解析:24 【解析】 【分析】设应在高一年级抽取学生数为,首先求出高一年级人数占总人数的百分比,然后通过分层抽样的性质,由此能求出应在高一年级抽取学生数。
2020高二数学上学期期中模拟试题(含解析)

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若,则下列不等式成立的是()A. B. C. D.【答案】C【解析】试题分析:考点:不等式性质2. 若命题,使,则该命题的否定为()A. ,使B.C. ,使D.【答案】D【解析】试题分析:特称命题的否定为:存在改为任意,结论变否定;所以命题,使的否定为:,故答案为D.考点:1、特称命题;2、命题的否定.3. 在等比数列中,是方程的两根,则等于()A. B. C. D. 以上都不对【答案】A【解析】试题分析:由题意得考点:1.二次方程根与系数的关系;2.等比数列4. 已知,则函数的最小值为()A. B. C. D.【答案】C【解析】试题分析:由于,则,所以,当且仅当,由于,即当时,上式取等号,因此函数的最小值为,故选C.考点:基本不等式5. 在中,,则的面积等于()A. B. C. 或 D. 或【答案】D【解析】试题分析:由余弦定理知,整理得,解得或,有三角形面积公式得或.考点:余弦定理及三角形面积的求法.6. 已知变量满足约束条件则的最大值为()A. B. C. D.【答案】B【解析】画出二元一次不等式所示的可行域,目标函数为截距型,,可知截距越大值越大,根据图象得出最优解为,则的最大值为2,选B.【点睛】本题主要考查线性规划问题,首先由不等式组作出相应的可行域,作图时,可将不等式转化为(或),“”取下方,“”取上方,并明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法、值域范围.7. 设等比数列,是数列的前项和,,且依次成等差数列,则等于()A. B. C. D.【答案】C【解析】设等比数列的首项为,公比为,…….①,又依次成等差数列,则,即……②,①②两式相加得:,代入①得:,两式相比:,解得:或,则或,当时,,当时,,选C .8. 设,则的最小值为()A. B. C. D.【答案】A【解析】且,则,,选A.9. 已知等差数列前项和为,若,则在数列中绝对值最小的项为()A. 第项B. 第项C. 第项D. 第项【答案】C10. 已知不等式对一切正整数恒成立,则实数的范围为()A. B. C. D.【答案】B【解析】,不等式对一切正整数恒成立,化为,只需,化为,选B.【点睛】裂项相消法是数列求和最常用的一种方法,本题为不等式恒成立问题,要注意到不等式要求对一切正整数n恒成立,首先把不等式化简后得出,何时恒成立,只需小于左边式子的最小值,其最小值为,其次得出的不等式如何解?可先换元,后利用图象法.11. 在中,是的中点,,则等于()A. B. C. D.【答案】B【解析】设,则选B.点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化.第三步:求结果.12. 已知等差数列的公差,且成等比数列,若是数列的前项和,则的最小值为()A. B. C. D.【答案】A【解析】,成等比数列,,得或(舍去),,,,时原式取得最小值为,故选A.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 在中,,则__________.【答案】【解析】 ,.14. 当实数满足约束条件(其中为小于零的常数)时,的最小值为,则实数的值是__________.【答案】【解析】略15. 已知数列为等比数列,其前项和为,且公比;数列为等差数列,,则__________.(填写“”“”或者“”)【答案】<【解析】比较与的大小,可以用比较法:,数列为等差数列,则 ,因为,即,因此只需研究的正负.由于数列为等比数列,其前项和为,且公比;则=,所以.【点睛】研究不等式的主要方法有比较法、分析法、综合法等,比较两个数的大小常用比较法,比较法又包括差值比较法与商值比较法,差值比较法主要研究差值的正负以说明两个数的大小,本题利用已知条件中等差数列和等比数列的通项公式外,还灵活的运用了等差数列的性质,借助等量代换巧妙的作差解决问题.16. 对于,当非零实数满足且使最大时,的最小值为__________.【答案】【解析】试题分析:设,则,代入到中,得,即……①因为关于的二次方程①有实根,所以,可得,取最大值时,或,当时,,当时,,综上可知当时,的最小值为.考点:1、一元二次方程根的判别式;2、二次函数求值域.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 给定两个命题:对任意实数都有恒成立;.如果为真命题,为假命题,求实数的取值范围.【答案】或【解析】试题分析:根据已知求出两个简单命题中参数的取值范围,命题,命题;再根据复合命题的真假,判断简单命题的真假,分两种情况进行讨论,(1)当真假时;(2)当假真时,从而得到实数的取值范围.试题解析:解:命题:ax2+ax+1>0恒成立当a=0时,不等式恒成立,满足题意)当a≠0时,,解得0<a<4∴0≤a<4命题:a2+8a﹣20<0解得﹣10<a<2∵为真命题,为假命题∴有且只有一个为真,当真假时得当假真时得所以﹣10<a<0或2≤a<4考点:复合命题的真假判断.18. 已知在中,内角的对边分别为.且.(1)求的值;(2)若,求的面积.【答案】(1)(2)【解析】试题分析:(1)已知条件是边角关系,且左边是角的余弦,要求的是,因此可用正弦定理“化边为角”,即,只要交叉相乘,再由两角和与差的正弦公式可得,而在三角形中此式即为,结论有了;(2)由(1)可得,结合余弦定理可求得,由面积公式可得.试题解析:(1)由正弦定理得整理得又∴,即(2)由余弦定理可知①由(1)可知,即②再由③,由①②③联立求得又∴考点:正弦定理,余弦定理,两角和与差的正弦公式,三角形的面积.19. 已知正项数列的前项和为是与的等比中项.(1)求证:数列是等差数列;(2)若,数列的前项和为,求.【答案】(1)见解析(2)【解析】试题分析:已知数列的递推关系中含有前n项和与第n项的关系,求数列的通项公式,一般分两步,第一步n=1时,第二步,常用前n项和减去前n-1项和(两式相减)去处理,化为与的关系后,再求通项公式;错位相减法是数列求和的常用方法,使用错位相减法求和时,要注意末项的符号及等比数列求和的项数,避免失误.试题解析:(1)证明:由是与的等比中项,得 .当时,.当时,,,即.,即.数列是等差数列.(2)数列首项,公差,通项公式为.则,则.①两边同时乘以,得②①-②,得.解得.【点睛】数列的递推关系中为与的关系,求数列的通项公式,一般分两步,第一步n=1时,得出所表达的含义;第二步当时,常用两式相减去处理,化为与的关系后,再求通项公式;数列求和常用方法有错位相减法、倒序相加法、裂项相消法、分组求和法等;要根据数列的特征采用相应的方法准确求和,特别是使用错位相减法要注意运算的准确性.20. 已知函数,其中是自然对数的底数.(1)证明:是上的偶函数.(2)若关于的不等式在上恒成立,求实数的取值范围.【答案】(1)见解析(2)【解析】试题分析:(1)根据函数奇偶性的定义即可证明是R上的偶函数;(2)利用参数分离法,将不等式m≤e-x+m-1在(0,+∞)上恒成立,进行转化对任意恒成立,求最值问题即可求实数m的取值范围.试题解析:(1),,∴是上的偶函数(2)由题意,,即∵,∴,即对恒成立令,则对任意恒成立∵,当且仅当时等号成立∴21. 如图,一辆汽车从市出发沿海岸一条笔直公路以每小时的速度向东均速行驶,汽车开动时,在市南偏东方向距市且与海岸距离为的海上处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与所成的角.【答案】(1)快艇至少以的速度行驶才能把稿件送到司机手中. (2)快艇应向垂直于的方向向北偏东方向行驶.【解析】试题分析:解决三角函数应用问题,首先要审题读懂题意,设出快艇的速度和需要的时间,根据题意利用余弦定理列出关系式,建立函数模型,利用数学知识解决实际问题,本题采用配方法求最值,求出快艇行驶的最小速度后,利用余弦定理求角,得出快艇行驶的方向,给出行驶的方向角.试题解析:(1)如图,设快艇以的速度从处出发,沿方向,后与汽车在处相遇,在中,为边上的高,.设,则.由余弦定理,得,所以.整理,得当,即时,,即快艇至少以的速度行驶才能把稿件送到司机手中.(2)当时,在中,,由余弦定理,得,所以,故快艇应向垂直于的方向向北偏东方向行驶...................22. 在等比数列中,,且的等比中项为.(1)求数列的通项公式;(2)设,数列的前项和为,是否存在正整数,使得对任意恒成立?若存在,求出正整数的最小值;若不存在,请说明理由.【答案】(1)(2)存在满足条件的正整数,正整数的最小值为.【解析】试题分析:根据等比数列的性质,第1项与第5项的等比中项是第3项,利用公差和第三项的值求出首项,从而写出数列的通项公式;根据题意计算,可知为等差数列,利用等差数列前n项和公式写出前n项和,从而得出,而数列求和可以使用裂项相消法,最后根据不等式恒成立条件得出正整数的最小值.试题解析:(1)由的等比中项为,可知,又,则,公比且,.(2),易知数列是首项为,公差为的等差数列,,,则存在满足条件的正整数,且正整数的最小值为.【点睛】根据等比数列的性质,利用已知条件列方程,求出等差数列的公差和首项,从而写出数列的通项公式;根据题意计算,根据通项公式可以判断为等差数列,利用等差数列前n项和公式写出前n项和,从而得出,而数列求和可以使用裂项相消法,最后根据不等式恒成立条件得出正整数的最小值.。
2020年高二数学上期中试卷附答案

22.光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度)
5.B
解析:B
【解析】
【分析】
根据表格中的数据,求得样本中心为 ,代入回归直线方程,求得 ,得到回归直线的方程为 ,即可作出预测,得到答案.
【详解】
由题意,根据表格中的数据,可得 ,
即样本中心为 ,代入回归直线方程 ,即 ,
解得 ,即回归直线的方程为 ,
当 时, ,故选B.
【点睛】
本题主要考查了回归直线方程的应用,其中解答中熟记回归直线方程的特征,求得回归直线的方程是解答的关键,着重考查了运算与求解能力,属于基础题.
(1)求直方图中a的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,若招收学生1200人,请估计所招学生中有多少人可以申请住宿;
(3)求该校学生上学路上所需的平均时间.
26.菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
则甲同学收到李老师或张老师所发活动通知的信息的概率为 .
故选C.
【点睛】
本题考查相互独立事件的概率,考查对立事件的概率.在求两个事件中至少有一个发生的概率时一般先求其对立事件的概率,即两个事件都不发生的概率.这样可减少计算,保证正确.
2024-2025学年高二上学期期中模拟考试数学试题含解析

2024-2025学年高二数学上学期期中模拟卷(考试时间:120分钟试卷满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:沪教版2020必修第三册第十~十一章。
5.难度系数:0.72。
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)1.不重合的两个平面最多有条公共直线【答案】1【解析】根据平面的位置关系可知,不重合两平面平行或相交,当相交时,有且只有一条公共直线.故答案为:12.已知球的表面积是16π,则该球的体积为.3.空间中一个角∠A的两边和另一个角∠B的两边分别平行,若∠A=,则∠B=;【答案】【解析】如图,若角∠A 的两边和角∠B 的两边分别平行,且方向相同,则∠A 与∠B 相等此时70B A ∠=∠=︒;②当角∠A 的两边和角∠B 的两边分别平行,且一边方向相同另一边方向相反,则∠A 与∠B 互补,此时180110B A ∠=︒-∠=︒.故答案为70︒或110︒.4.如图,正三棱柱的底面边长为2,高为1,则直线1B C 与底面ABC 所成的角的大小为(结果用反三角函数值表示).5.在空间中,给出下面四个命题,其中真命题为.(填序号)①过平面α外的两点,有且只有一个平面与平面α垂直;②若平面β内有不共线三点到平面α的距离都相等,则αβ∥;③若直线l 与平面α内的任意一条直线垂直,则l α⊥;④两条异面直线在同一平面内的射影一定是两条相交直线.【答案】③【解析】①过平面α外两点可确定一条直线,当这条直线垂直于平面α时,有无数个平面垂直于平面α,故①错误;②若三点在平面α同侧,则αβ∥;若三点在平面α两侧,则α与β相交,故②错误;③直线l 与平面α内的任意一条直线垂直,则l 垂直于平面α内两条相交直线,由线面垂直的判定定理可得l α⊥,故③正确;④两条异面直线在同一个平面内的射影有可能是两条相交直线,也可能是两条平行直线,还可能是一个点和一条直线,故④错误;故答案为:③6.正四棱锥P -ABCD 的所有棱长均相等,E 是PC 的中点,那么异面直线BE 与P A 所成角的余弦值为.连接AC 交BD 于O 点,连接OE ,则OE 因为⊥PO 面ABCD ,所以PO DB ⊥,又因为所以直在角三角形EOB 中,设PA a =,则故答案为:33.7.如图,有一圆锥形粮堆,其轴截面是边长为6m 的正ABC V ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路程是m .【答案】35【解析】解:由题意得:圆锥的底面周长是6π,则66180n ππ=,解得:180n ︒=可知圆锥侧面展开图的圆心角是180︒,如图所示:则圆锥的侧面展开图中:()3m AP =,6(m)AB =,90BAP ︒∠=所以在圆锥侧面展开图中:()223635m BP =+=故答案为:358.已知一球体刚好和圆台的上、下底面及侧面都相切,且圆台上底面的半径为2,下底面的半径为1,则该圆台的侧面积为.【答案】9π【解析】圆台的轴截面如下图示:截面中圆为内切球的最大圆,且2AF DF AG DH ====,1BE CE BG CH ====,所以3AB CD ==,而上下底面周长分别为4π、2π,故该圆台的侧面积为13(2π4π)9π2⨯⨯+=.故答案为:9π9.如图,已知三棱柱111ABC A B C -的体积为3,P ,Q ,R 分别为侧棱1AA ,1BB ,1CC 上的点,且1AP CR AA +=,则Q ACRP V -=.则111332Q ACRP V d S d -=⋅⋅=⋅⋅⋅设三棱柱111ABC A B C -的体积故答案为:1.10.已知大小为π6的二面角的一个面内有一点,它到二面角的棱的距离为6,则这个点到另一个面的距离为.11.正方形ABCD 中,E ,F 分别为线段AB ,BC 的中点,连接DE ,DF ,EF ,将ADE V ,CDF V ,BEF △分别沿DE ,DF ,EF 折起,使A ,B ,C 三点重合,得到三棱锥O DEF -,则该三棱锥外接球半径R 与内切球半径r 的比值为.【答案】26【解析】在正方形ABCD 中,,AD AE CD ⊥12.空间给定不共面的A,B,C,D四个点,其中任意两点间的距离都不相同,考虑具有如下性质的平面α:A,B,C,D中有三个点到的距离相同,另一个点到α的距离是前三个点到α的距离的2倍,这样的平面α的个数是___________个【答案】32【解析】首先取3个点相等,不相等的那个点由4种取法;然后分3分个点到平面α的距离相等,有以下两种可能性:(1)全同侧,这样的平面有2个;(2)不同侧,必然2个点在一侧,另一个点在一侧,1个点的取法有3种,并且平面过三角形两个点边上的中位线,考虑不相等的点与单侧点是否同侧有两种可能,每种情况下都唯一确定一个平面,故共有6个,⨯=个,所有这两种情况共有8个,综上满足条件的这样的平面共有4832故答案为:32二、选择题(本题共有4题,满分18分,第13-14题每题4分,第15-16题每题5分;每题有且只有一个正确选项)13.下列几何体中,多面体是()A.B.C.D.【答案】B【解析】A选项中的几何体是球,是旋转体;B选项中的几何体是三棱柱,是多面体;C 选项中的几何体是圆柱,旋转体;D 选项中的几何体是圆锥,是旋转体.故选B.14.已知两个平面α、β,在下列条件下,可以判定平面α与平面β平行的是().A .α、β都垂直于一个平面γB .平面α内有无数条直线与平面β平行C .l 、m 是α内两条直线,且l ∥β,m ∥βD .l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β【答案】D【解析】对于A ,如在正方体1111ABCD A B C D -中,平面11AAC C 和平面11AA B B 都与平面ABCD 垂直,但这两个平面不平行,所以A 错误,对于B ,如在正方体1111ABCD A B C D -中,平面11AAC C 和平面11AA B B ,平面11AAC C 中所有平行于交线1AA 的直线都与平面11AA B B 平行,但这两个平面不平行,所以B 错误,对于C ,如在正方体1111ABCD A B C D -中,平面11AAC C 和平面11AA B B ,,M N 分别为11,A B AB 的中点,则1,MN BB 在平面11AA B B 内,且都与平面11AAC C 平行,但这两个平面不平行,所以C 错误.对于D ,因为l 、m 是两条异面直线,所以将这两条直线平移到共面α时,一定在α内形成两条相交直线,由面面平行的判定定理可知,该结论正确.故选:D15.将3个1212⨯的正方形沿邻边的中点剪开分成两部分(如图1);将这6部分接于一个边长为六边形边上(如图2),若拼接后的图形是一个多面体的表面展开图,则该多面体的体积是()A .17282B .864C .576D .2【答案】B【解析】折成的多面体如图①所示,将其补形为正方体,如图②,所求多面体体积为正方体的一半,又依题易求得正方体的边长为12,故3112864,2V =⨯=故选:B.16.如图,在正方体1111ABCD A B C D -中,E 是棱BC 的中点,F 是侧面11BCC B 上的动点,且1A F ∥平面1AD E .设1A F 与平面11BCC B 所成的角为1,A F α与1AD 所成的角为β,那么下列结论正确的是()A .α的最小值为arctan2,β的最小值为arctan3B .α的最小值为arctan3,β的最大值为2πC .α的最小值大于arctan2,β的最小值大于arctan3D .α的最大值小于arctan3,β的最大值小于2π设正方体的棱长为2,因为MN GE ∥,且MN ⊄MN ∴∥平面1AEGD ;同理1A N ∥平面1AEGD ,且∴平面1A MN ∥平面AEGD ∵11A B ⊥面11BB C C ,所以又1AD MN ,所以1A F 与1AD 所成的角为111tan A B B Fα∴=;当F 为MN 中点时,此时当F 与M 或N 重合时,此时2tan 22α∴≤≤,arctan2对于β,当F 为MN 中点时,当F 与M 或N 重合时,β()221252A F ⎛⎫∴=-= ⎪ ⎪⎝⎭tan 3β∴=,tan 3β∴≥,arctan 3β≤≤又arctan3 1.4≈,arctan2故选:A.三、解答题(本大题共有5题,满分78分,第17-19题每题14分,第20、21题每题18分.)17.如图,长方体1111ABCD A B C D -中,1AB AD ==,12AA =,点P 为1DD 的中点.(1)求证:直线1BD //平面PAC ;(2)求异面直线1BD 与AP 所成角的大小.【解析】(1)设AC 和BD 交于点O ,则O 为BD 的中点,连接PO ,(1分)∵P 是1DD 的中点,∴1//PO BD ,(3分)又∵PO ⊂平面PAC ,1⊄BD 平面PAC ,∴直线1BD //平面PAC ;(6分)(2)由(1)知,1//PO BD ,∴APO ∠即为异面直线1BD 与AP 所成的角,(8分)∵PA PC =12AO AC ==且PO AO ⊥,∴1sin2AO APO AP ∠==.又(0,90]APO ∠∈︒︒,∴30APO ∠=︒故异面直线1BD 与AP 所成角的大小为30︒.(14分)18.如图,在圆柱中,底面直径AB 等于母线AD ,点E 在底面的圆周上,且AF D E ⊥,F 是垂足.(1)求证:AF DB ⊥;(2)若圆柱与三棱锥D ABE -的体积的比等于3π,求直线DE 与平面ABD 所成角的大小.【解析】(1)证明:根据圆柱性质,DA ⊥平面ABE ,因为EB ⊂平面ABE ,所以DA EB ⊥,又因为AB 是圆柱底面的直径,点E 在圆周上,所以AE EB ⊥,因为AE DA A ⋂=且,AE DA ⊂平面DAE ,所以EB ⊥平面DAE ,(2分)又因为AF ⊂平面DAE ,所以EB AF ⊥,因为AF D E ⊥,且EB DE E =I ,且,EB DE ⊂平面DEB ,所以AF ⊥平面DEB ,又因为DB ⊂平面DEB ,所以AF DB ⊥.(6分)(2)解:过点E 作EH AB ⊥,H 是垂足,连接DH ,根据圆柱性质,平面ABD ⊥平面ABE ,且平面ABD ⋂平面ABE AB =,且EH ⊂平面ABE ,所以EH ⊥平面ABD ,因为DH ⊂平面ABD ,所以DH 是ED 在平面ABD 上的射影,从而EDH ∠是DE 与平面ABD 所成的角,(8分)设圆柱的底面半径为R ,则2DA AB R ==,所以圆柱的体积为32πV R =,且21233D ABEABE R V AD S EH -=⋅=⋅ ,由:3πD ABE V V -=,可得EH R =,可知H 是圆柱底面的圆心,且AH R =,且DH =,在直角EDH 中,可得tan EH EDH DH ∠==EDH ∠=(14分)19.如图,将边长为2的正方形ABCD 沿对角线BD 折叠,使得平面ABD ⊥平面CBD ,AE ⊥平面ABD ,且2AE(1)求证:直线EC 与平面ABD 没有公共点;(2)求点C 到平面BED 的距离.【解析】(1)取BD 的中点F ,连接CF 、AF ,如图,依题意,在BCD △中,,BC CD BC CD =⊥,则CF BD ⊥,而平面ABD ⊥平面CBD ,平面ABD ⋂平面CBD BD =,CF ⊂平面CBD ,于是得CF ⊥平面ABD ,且2CF =因为AE ⊥平面ABD ,且2AE =//AE CF ,且AE CF =,从而得四边形AFCE 为平行四边形,//EC AF ,(4分)又AF ⊂平面ABD ,EC ⊂/平面ABD ,则//EC 平面ABD ,所以直线EC 与平面ABD 没有公共点;(6分)(2)因为CF ⊥平面ABD ,AF ⊂平面ABD ,所以CF AF ⊥,因为BD AF ⊥,BD CF F = ,,BD CF ⊂平面,CBD 所以AF ⊥平面,CBD 因为//,EC AF ,于是得EC ⊥平面CBD ,因为AE ⊥平面ABD ,,AB AD ⊂平面ABD ,所以,AE AB AE AD ⊥⊥,(8分)因为EC AF ==EB ED =,则等腰BED 底边BD 上的高2h ==,12BED S BD h =⋅= ,而2BCD S =,设点C 到平面BED 的距离为d ,由C BED E BCD V V --=得1133BED BCD S d S EC ⋅=⋅ ,即2=,解得1d =,所以点C 到平面BED 的距离为1(14分)20.如图所示,在四棱锥P ABCD -中,底面四边形ABCD 是菱形,底面,AC BD O PAC = △是边长为2的等边三角形,PB =PD ,AP =4AF(1)求证:PO ⊥底面ABCD (2)求直线CP 与OF 所成角的大小.(3)在线段PB 上是否存在点M ,使得//CM 平面BDF ?如果存在,求BMBP的值;如果不存在,请说明理由.【解析】(1)因为底面ABCD 是菱形,且AC BD O = ,所以O 为AC ,BD 中点,在PBD △中,PB =PD ,可得PO ⊥BD ,因为在PAC 中,PA =PC ,O 为AC ,BD 中点,所以PO ⊥AC ,(3分)又因为AC ⋂BD =O ,所以PO ⊥底面ABCD .(4分)(2)连接OF ,取AP 中点为E ,连接OE ,因为底面ABCD 是菱形,AC ⋂BD =O ,由O 为AC 中点,且E 为AP 中点,AP =4AF ,所以F 为AE 中点,所以CP //OE .,故∠EOF 为直线CP 与OF 所成的角,(8分)又由PAC 为等边三角形,且E 为中点,所以∠EOF =30o .(10分)(3)存在,13BM BP =,连接CE ,ME ,因为AP =4AF ,E 为AP 中点,所以13EF FP =,又因为13BM BP =,所以在PFB △中,EF BMFP BP =,即EM //BF ,(12分)因为EM ⊄平面BDF ,BF ⊂平面BDF ,所以EM //平面BDF ,由(2)知EC //OF ,因为EC ⊄平面BDF ,OF ⊂平面BDF ,所以EC //平面BDF ,因为EC ⋂EM =E ,所以平面EMC //平面BDF ,因为CM ⊂平面EMC ,所以CM //平面BDF .(18分)21.在棱长均为2的正三棱柱111ABC A B C -中,E 为11B C 的中点.过AE 的截面与棱111,BB AC 分别交于点F ,G.(1)若F 为1BB 的中点,试确定点G 的位置,并说明理由;(2)在(1)的条件下,求截面AGEF 与底面ABC 所成锐二面角的正切值;(3)设截面AFEG 的面积为0S ,AEG △面积为1S ,AEF △面积为2S ,当点F 在棱1BB 上变动时,求2012S S S 的取值范围.【解析】(1)在平面11BCC B 内延长1CC ,FE 相交于点P ,则P ∈平面AGEF ,又1P CC ∈⊂平面11ACC A ,则有平面AGEF 平面11ACC A AG =,P AG ∈,即A ,G ,P 三点共线.(2分)因为E 为11B C 的中点,F 为1BB 的中点,所以11112PC B F CC ==,所以113PC PC =,又因为1//GC AC ,所以1113GC PC AC PC ==,所以111112333GC AC A C ===,即点G 为棱11AC 上靠近点1C 的三等分点.(4分)(2)在平面11BCC B 内延长CB ,EF 相交于点Q ,连接AQ ,则平面AGEF 平面ABC AQ =,在平面11ACC A 内作GM AC ⊥于点M ,则GM ⊥平面ABC ,又AQ ⊂平面ABC ,所以G M AQ ⊥,在平面ABC 内作MN AQ ⊥于点N ,连接GN ,又,GM MN ⊂平面GMN ,GM MN M ⋂=,所以AQ ⊥平面GMN ,GN ⊂平面GMN ,所以AQ GN ⊥,所以GNM ∠为截面AGEF 与底面ABC 所成锐二面角的平面角.(6分)在AQC 中,作CH AQ ⊥于点H ,11BQ C E ==,2AC =,3CQ =,60AC B ∠= ,12222ABC S =⨯⨯⨯=△AQC S =由余弦定理2222cos 4967AQ AC CQ AC CQ ACQ =+-⋅⋅∠=+-=,则AQ122AQC S AQ CH ==⋅ ,可得3217CH =,所以237MN CH ==,又22G M AA ==,所以21tan 3GM GNM MN ∠==,故截面AGEF 与底面ABC (10分)(3)设1GC m =,则[]0,1m ∈,2PG mGA m=-.设PGE 的面积为S ,所以12S m S m=-,又因为21S S S =+,所以1222S m S -=,且1221,122S m S -⎡⎤=∈⎢⎥⎣⎦,故()22120121212212S S S S SS S S S S S +==++,令12S t S =,则1,12t ⎡⎤∈⎢⎥⎣⎦,(11分)设()112,12g t t t t ⎛⎫⎡⎤=++∈ ⎪⎢⎥⎣⎦⎝⎭,当12112t t ≤<≤时,()()()()121212121212111t t g t g t t t t t t t t t --=+--=-,120t t -<,120t t >,1210t t -<,则()()120g t g t ->,即()()12g t g t >,所以()12g t t t =++在1,12t ⎡⎤∈⎢⎥⎣⎦上单调递减,所以()()min 14g t g ==,()max 1922g t g ⎛⎫== ⎪,所以()94,2g t ⎡⎤∈⎢⎥,。
2020年高二数学上期中一模试卷及答案

2020年高二数学上期中一模试卷及答案一、选择题1.一组数据的平均数为m ,方差为n ,将这组数据的每个数都乘以()0a a >得到一组新数据,则下列说法正确的是( ) A .这组新数据的平均数为m B .这组新数据的平均数为a m +C .这组新数据的方差为anD .这组新数据的标准差为2.从区间[]0,2随机抽取4n 个数1232,,,...,n x x x x ,1232,,,...,n y y y y 构成2n 个数对()11,x y ,()22,x y ,…,()22,n n x y ,其中两数的平方和小于4的数对有m 个,则用随机模拟的方法得到的圆周率疋的近似值为( ) A .2m nB .2mnC .4m nD .16m n3.在去年的足球甲A 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球. A .1个B .2个C .3个D .4个4.某商场为了了解毛衣的月销售量y (件)与月平均气温x (C ︒)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:由表中数据算出线性回归方程y bx a =+$$$中的2b =-$,气象部门预测下个月的平均气温为6C ︒,据此估计该商场下个月毛衣销售量约为( )A .58件B .40件C .38件D .46件5.从一批产品中取出三件产品,设事件A 为“三件产品全不是次品”,事件B 为“三件产品全是次品”,事件C 为“三件产品不全是次品”,则下列结论正确的是( ) A .事件A 与C 互斥 B .事件B 与C 互斥 C .任何两个事件均互斥D .任何两个事件均不互斥6.执行如图所示的程序框图,则输出的n 值是( )A .5B .7C .9D .117.从甲、乙、丙三人中任选两名代表,甲被选中的概率是( ) . A .12B .13C .23 D .18.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m ,第二次出现的点数为n ,向量p u v =(m ,n),q v =(3,6).则向量p u v与q v共线的概率为( ) A .13B .14C .16D .1129.我国古代名著《庄子g 天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )A .17?,,+1i s s i i i≤=-= B .1128?,,2i s s i i i≤=-= C .17?,,+12i s s i i i ≤=-= D .1128?,,22i s s i i i≤=-= 10.某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有( )①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人;②用简单随机抽样的方法从新生中选出100人; ③西部地区学生小刘被选中的概率为150; ④中部地区学生小张被选中的概率为15000A .①④B .①③C .②④D .②③11.同时掷三枚硬币,至少有1枚正面向上的概率是( ) A .78B .58C .38D .1812.运行如图所示的程序框图,若输出S 的值为129,则判断框内可填入的条件是( )A .4?k <B .5?k <C .6?k <D .7?k <二、填空题13.在5张卡片上分别写有数字1,2,3,4,5,然后将它们混合,再任意排列成一行,则得到的数能被2或5整除的概率是___________.14.执行如图所示的程序框图,则输出的m 的值为____.15.甲乙两人一起去游“西安世园会”,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是________.16.如左下图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是_________。
吉林省2020学年高二数学上学期期中试题理(含解析)

高二数学上学期期中试题 理(含解析)考生注意:1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答.超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.4.本卷命题范围:人教版选修2-1,选修2-2第三章.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数(13)(1)z i i =-+-在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】A 【解析】分析:先化简复数z,再看复数z 在复平面内对应的点所在的象限.详解:由题得13324z i i i =-+++=+,所以复数z 在复平面内对应的点为(2,4),故答案为A.点睛:(1)本题主要考查复数的运算和复数的几何意义,意在考查学生对这些知识的掌握水平.(2) 复数(,)z a bi a b R =+∈对应的点是(a,b ),点(a,b )所在的象限就是复数z a bi =+(),a b ∈R 对应的点所在的象限.复数(,)z a bi a b R =+∈和点(a,b )是一一对应的关系.2.焦点坐标为(1,0)的抛物线的标准方程是( ) A. y 2=-4x B. y 2=4xC. x 2=-4yD. x 2=4y【答案】B 【解析】 【分析】由题意设抛物线方程为y 2=2px (p >0),结合焦点坐标求得p ,则答案可求. 【详解】由题意可设抛物线方程为y 2=2px (p >0),由焦点坐标为(1,0),得P12=,即p=2. ∴抛物的标准方程是y 2=4x . 故选B .【点睛】本题主要考查了抛物线的标准方程及其简单的几何性质的应用,其中解答中熟记抛物线的几何性质是解答的关键,着重考查了推理与运算能力,属于基础题. 3.关于命题,下列判断正确的是( ) A. 命题“每个正方形都是矩形”是特称命题 B. 命题“有一个素数不是奇数”是全称命题C. 命题“x ∀∈R ,4x ∈R ”的否定为“0x ∃∈R ,40x ∉R ”D. 命题“每个整数都是有理数”的否定为“每个整数都不是有理数” 【答案】C 【解析】 【分析】根据特称命题,与全称命题的概念,可判断AB ;根据全称命题的否定,可判断C ,D. 【详解】A 选项,命题“每个正方形都是矩形”含有全称量词“每个”,是全称命题,故A 错; B 选项,命题“有一个素数不是奇数”含有存在量词“有一个”,是特称命题,故B 错;C 选项,命题“x ∀∈R ,4x ∈R ”的否定为“0x ∃∈R ,40x ∉R ”,故C 正确;D 选项,命题“每个整数都是有理数”的否定为“每个整数不都是有理数”,故D 错; 故选:C【点睛】本题主要考查命题真假的判定,熟记全称命题与特称命题的概念,以及含有一个量词的命题的否定即可,属于基础题型. 4.椭圆223530x y +=的离心率为( )A.25B.35【答案】C 【解析】 【分析】先将椭圆方程化为标准形式,得到210a =,26b =,再由离心率的定义,即可得出结果.【详解】因为椭圆方程:223530x y +=可化为221106x y +=,所以210a =,26b =,因此离心率:5c e a ====. 故选:C【点睛】本题主要考查求椭圆的离心率,熟记椭圆的简单性质即可,属于基础题型. 5.“213k =”是“直线y kx =与圆22(2)1x y ++=相切”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】C 【解析】 【分析】直接利用圆心到直线的距离等于半径求得充要条件即可判断.【详解】当直线y kx =与圆22(2)1x y ++=1=,则213k =,故选:C.【点睛】本题考查的知识要点:直线与圆的位置关系的应用,点到直线的距离公式的应用,主要考查充分必要条件的判断,属于基础题型.6.点()00,P x y 是抛物线2:8C x y =上一点,则P 到C 的焦点的距离为( ) A. 02x - B. 02y - C. 02x + D. 02y +【答案】D 【解析】 【分析】先由抛物线方程得到准线方程,再由抛物线的定义,即可得出结果.【详解】因为抛物线2:8C x y =的准线方程为2y =-,点()00,P x y 是抛物线2:8C x y =上一点,由抛物线的定义可得:0||2PF y =+. 故选:D【点睛】本题主要考查求抛物线上的点到到焦点的距离,熟记抛物线的定义即可,属于基础7.当复数2(32)()z x x x i x =-+-∈R 的实部与虚部的差最小时,1zi =-( ) A. 33i -+ B. 33i + C. 13i -D. 13i --【答案】C 【解析】 【分析】实部与虚部的差为242x x -+。
河南省2020年高二数学上学期期中考试卷附答案题库(共7套)

河南省2020年高二数学上学期期中考试卷(一)(理科)(考试时间120分钟满分150分)一.单项选择题:本大题共12小题,每小题5分,共60分.1.已知函数f(x)=x+sinπx﹣3,则的值为()A.4029 B.﹣4029 C.8058 D.﹣80582.如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于()A.B.C.D.3.已知函数f(x)=(ax﹣1)(x+b),如果不等式f(x)>0的解集是(﹣1,3),则不等式f(﹣2x)<0的解集是()A.(﹣∞,﹣)∪(,+∞)B.(﹣,)C.(﹣∞,﹣)∪(,+∞)D.(﹣,)4.已知a,b,c分别是△内角A,B,C的对边,且(b﹣c)(sinB+sinC)=(a﹣)•sinA,则角B的大小为()A.30°B.45°C.60° D.120°5.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+b的取值范围是()A.(4,+∞)B.(2,+∞)C.[2,+∞)D.R6.设x,y满足约束条件,若目标函数的最大值为2,则的图象向右平移后的表达式为()A. B.C.y=sin2x D.7.已知等差数列{a n}的前n项和为S n,a2=4,S10=110,则的最小值为()A.7 B.8 C. D.8.设x,y∈R,a>1,b>1,若a x=b y=2.2a+b=8,则的最大值为()A.2 B.3 C.4 D.log239.若目标函数z=ax+by(a>0,b>0)满足约束条件且最大值为40,则的最小值为()A. B.C.1 D.410.设数列{a n}的前n项和为S n,且a1=1,{S n+na n}为常数列,则a n=()A.B. C.D.11.设等差数列{a n}的前n项和为S n,且满足S19>0,S20<0,则,,,…,中最大项为()A. B. C.D.12.已知等差数列{a n}的前n项和为S n,向量=(n,),=(m,),=(k,)(n,m,k∈N*),且=λ•+μ•,则用n、m、k表示μ=()A.B.C.D.二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卷中横线上.13.若关于x的不等式|ax﹣2|<3的解集为{x|﹣<x<},则a=.14.设S n是数列{a n}的前n项和(n∈N*),若a1=1,S n﹣1+S n=3n2+2(n≥2),则S101=.15.设S n为数列{a n}的前n项之和,若不等式n2a n2+4S n2≥λn2a12对任何等差数列{a n}及任何正整数n恒成立,则λ的最大值为.16.△ABC中,角A,B,C所对的边分别为a,b,c,下列命题正确的是(写出正确命题的编号).①总存在某内角α,使cosα≥;②若AsinB>BsinA,则B>A.③存在某钝角△ABC,有tanA+tanB+tanC>0;④若2a+b+c=,则△ABC的最小角小于;⑤若a<tb(0<t≤1),则A<tB.三.解答题:本大题共6小题,共70分.17.(10分)设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a,b∈M.(Ⅰ)证明:|a+b|<;(Ⅱ)比较|1﹣4ab|与2|a﹣b|的大小.18.(12分)在△ABC中,内角A,B,C所对的边长分别为a,b,c,tan.(Ⅰ)求角C的大小;(Ⅱ)已知△ABC不是钝角三角形,且c=2,sinC+sin(B﹣A)=2sin2A,求△ABC的面积.19.(12分)已知a>0,b>0,a+b=1.(Ⅰ)求的最小值.(Ⅱ)求证:.20.(12分)已知数列{a n},{b n},{c n}满足(a n+1﹣a n)(b n+1﹣b n)=c n(n∈N*).(1)若{b n]为等差数列,b1=c1=2,a n=2n,求数列{b n}的前n项和S n;(2)设c n=2n+n,a n=.当b1=1时,求数列{b n]的通项公式.21.(12分)f(x)=ax2+bx+c(a≠0).(Ⅰ)f(﹣1)=0且任意x∈R,x≤f(x)≤,求f(x);(Ⅱ)若|f(x)|<1的解集(﹣1,3),求a的范围.22.(12分)已知数列{a n}、{b n}中,对任何正整数n都有:a1b n+a2b n+a3b n﹣2…+a n﹣1b2+a n b1=2n+1﹣n﹣2.﹣1(1)若数列{a n}是首项和公差都是1的等差数列,求b1,b2,并证明数列{b n}是等比数列;(2)若数列{b n}是等比数列,数列{a n}是否是等差数列,若是请求出通项公式,若不是请说明理由;(3)若数列{a n}是等差数列,数列{b n}是等比数列,求证: + +…+<.参考答案一.单项选择题:1.D2.A3.A.4.A.5.B.6.C.7.D8.B.9.B.10.B.11.C12.C.二.填空题:13.答案为:﹣3.14.答案为:15451.15.答案为:.16.答案为:①④⑤三.解答题:17.解:(Ⅰ)记f(x)=|x﹣1|﹣|x+2|=,由﹣2<﹣2x﹣1<0解得﹣<x<,则M=(﹣,).…(3分)∵a、b∈M,∴|a|<,|b|<,∴|a+b|≤|a|+|b|<.…(6分)(Ⅱ)由(Ⅰ)得a2<,b2<.因为|1﹣4ab|2﹣4|a﹣b|2=(1﹣8ab+16a2b2)﹣4(a2﹣2ab+b2)=(4a2﹣1)(4b2﹣1)>0,…(9分)所以|1﹣4ab|2>4|a﹣b|2,故|1﹣4ab|>2|a﹣b|.…(10分)18.解:(Ⅰ)在△ABC中,内角A,B,C所对的边长分别为a,b,c,tan,得到,所以,所以sinC=,又C∈(0,π),所以C=或者;(Ⅱ)∵sinC+sin(B﹣A)=sin(B+A)+sin(B﹣A)=2sinBcosA,而2sin2A=4sinAcosA∴由sinC+sin(B﹣A)=2sin2A,得sinBcosA=2sinAcosA当cosA=0时,∠A=,可得b==2,可得三角△ABC的面积S=bc=;当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a…①,∵c=2,∠C=60°,c2=a2+b2﹣2abcosC∴a2+b2﹣ab=12…②,联解①②得a=2,b=4;∴△ABC的面积S=absinC=×2×4×sin60°=2.19.证明:(Ⅰ)∵.∵,∵=,令,∵,;{t1<t2t1<t2,,∵t1﹣t2<0,t1t2﹣2<0,∴y1﹣y2>0,∴y在上是减函数,∴;(Ⅱ)∵由(Ⅰ)20.解:(1)记数列{b n]的公差为d,依题意,(a2﹣a1)(b2﹣b1)=c1,∴(4﹣2)d=2,即d=1,∴b n=2+(n﹣1)=n+1,∴S n==;(2)∵a n=,∴a n+1﹣a n=﹣=(﹣1)n+1,∵c n=2n+n,∴b n+1﹣b n==(﹣1)n+1•(2n+n),∴b n﹣b n﹣1=(﹣1)n•(2n﹣1+n﹣1)(n≥2),b n﹣1﹣b n﹣2=(﹣1)n﹣1•(2n﹣2+n﹣2),b3﹣b2=(﹣1)3•(22+2),b2﹣b1=(﹣1)2•(21+1),当n=2k时,以上各式相加得:b n﹣b1=(2﹣22+23﹣…﹣2n﹣2+2n﹣1)+[1﹣2+3﹣…﹣(n﹣2)+(n﹣1)]=+=+,∴b n=b1++=++;当n=2k﹣1时,b n=b n+1﹣(﹣1)n+1(2n+n)=++﹣2n﹣n=﹣﹣+;综上所述,b n=.21.解:(Ⅰ)f(﹣1)=0,a﹣b+c=0,又x=1,1≤f(1)≤1,∴f(1)=1即a+b+c=1∴又∵x≤ax2+bx+c恒成立,∴…(4分)(Ⅱ)①a>0,ax2+bx+c<1解集(﹣1,3)且f(x)min>﹣1,∴,∴f(x)=ax2﹣2ax+1﹣3a,∴f(x)min=a﹣2a+1﹣3a>﹣1,∴…(8分)②若a<0,则﹣ax2﹣bx﹣c<1解集(﹣1,3)且f max(x)<1,∴,∴f(x)=ax2﹣2ax﹣3a﹣1,∴f(x)max=a﹣2a﹣3a﹣1<1,∴综上述或…(12分)22.解:(1)b1=1,b2=2,依题意数列{a n}的通项公式是a n=n,故等式即为b n+2b n﹣1+3b n﹣2+…+(n﹣1)b2+nb1=2n+1﹣n﹣2,b n﹣1+2b n﹣2+3b n﹣3+…+(n﹣2)b2+(n﹣1)b1=2n﹣n﹣1,(n≥2),两式相减可得b n+b n﹣1+…+b2+b1=2n﹣1,得b n=2n﹣1,数列{b n}是首项为1,公比为2的等比数列.(2)设等比数列{b n}的首项为b,公比为q,则b n=bq n﹣1,从而有:bq n﹣1a1+bq n﹣2a2+bq n﹣3a3+…+bqa n﹣1+ba n=2n+1﹣n﹣2,又bq n﹣2a1+bq n﹣3a2+bq n﹣4a3+…+ba n﹣1=2n﹣n﹣1(n≥2),故(2n﹣n﹣1)q+ba n=2n+1﹣n﹣2,a n=×2n×n,要使a n+1﹣a n是与n无关的常数,必需q=2,即①当等比数列{b n}的公比q=2时,数列{a n}是等差数列,其通项公式是a n=;②当等比数列{b n}的公比不是2时,数列{a n}不是等差数列.(3)由(2)知a n b n=n•2n﹣1,显然n=1,2时++…+<,当n≥3时++…+=+…+<++…+=1=.河南省2020年高二数学上学期期中考试卷(二)(文科)(考试时间120分钟满分150分)一.单项选择题:本大题共12小题,每小题5分,共60分.1.已知函数f(x)=x+sinπx﹣3,则的值为()A.4029 B.﹣4029 C.8058 D.﹣80582.如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于()A.B.C.D.3.已知函数f(x)=(ax﹣1)(x+b),如果不等式f(x)>0的解集是(﹣1,3),则不等式f(﹣2x)<0的解集是()A.(﹣∞,﹣)∪(,+∞)B.(﹣,)C.(﹣∞,﹣)∪(,+∞)D.(﹣,)4.已知a,b,c分别是△内角A,B,C的对边,且(b﹣c)(sinB+sinC)=(a﹣)•sinA,则角B的大小为()A.30°B.45°C.60° D.120°5.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+b的取值范围是()A.(4,+∞)B.(2,+∞)C.[2,+∞)D.R6.设x,y满足约束条件,若目标函数的最大值为2,则的图象向右平移后的表达式为()A. B.C.y=sin2x D.7.已知等差数列{a n}的前n项和为S n,a2=4,S10=110,则的最小值为()A.7 B.8 C. D.8.设x,y∈R,a>1,b>1,若a x=b y=2.2a+b=8,则的最大值为()A.2 B.3 C.4 D.log239.若目标函数z=ax+by(a>0,b>0)满足约束条件且最大值为40,则的最小值为()A. B.C.1 D.410.设数列{a n}的前n项和为S n,且a1=1,{S n+na n}为常数列,则a n=()A.B. C.D.11.设等差数列{a n}的前n项和为S n,且满足S19>0,S20<0,则,,,…,中最大项为()A. B. C.D.12.已知等差数列{a n}的前n项和为S n,向量=(n,),=(m,),=(k,)(n,m,k∈N*),且=λ•+μ•,则用n、m、k表示μ=()A.B.C.D.二.填空题:本大题共4小题,每小题5分,共20分.13.若关于x的不等式|ax﹣2|<3的解集为{x|﹣<x<},则a=.14.设S n是数列{a n}的前n项和(n∈N*),若a1=1,S n﹣1+S n=3n2+2(n ≥2),则S101=.15.已知点G是斜△ABC的重心,且AG⊥BG, +=,则实数λ的值为.16.已知点A(a,b)与点B(1,0)在直线3x﹣4y+10=0的两侧,给出下列说法:①3a﹣4b+10>0;②当a>0时,a+b有最小值,无最大值;③>2;④当a>0且a≠1,b>0时,的取值范围为(﹣∞,﹣)∪(,+∞).其中,所有正确说法的序号是.三.解答题:本大题共6小题,共70分.17.设函数f(x)=|x﹣1|+|x﹣a|.(1)若a=﹣1,解不等式f(x)≥3(2)如果∀x∈R,f(x)≥2,求a的取值范围.18.已知向量=(sinx,),=(cosx,﹣1).(1)当∥时,求cos2x﹣sin2x的值;(2)设函数f(x)=2()•,已知在△ABC中,内角A、B、C 的对边分别为a、b、c,若a=,b=2,sinB=,求f(x)+4cos(2A+)(x∈[0,])的取值范围.19.已知a>0,b>0,a+b=1,则的最小值是.20.已知数列{a n},{b n},{c n}满足(a n+1﹣a n)(b n+1﹣b n)=c n(n∈N*).(1)若{b n]为等差数列,b1=c1=2,a n=2n,求数列{b n}的前n项和S n;(2)设c n=2n+n,a n=.当b1=1时,求数列{b n]的通项公式.21.f(x)=ax2+bx+c(a≠0).(Ⅰ)f(x)=x的二实根x1,x2,且0<x1<x2<对x∈(0,x1),比较f(x)与x1的大小;(Ⅱ)若|f(x)|<1的解集(﹣1,3),求a的范围.22.已知数列{a n}、{b n}中,对任何正整数n都有:a1b n+a2b n﹣1+a3b n+…+a n﹣1b2+a n b1=2n+1﹣n﹣2.﹣2(1)若数列{a n}是首项和公差都是1的等差数列,求b1,b2,并证明数列{b n}是等比数列;(2)若数列{b n}是等比数列,数列{a n}是否是等差数列,若是请求出通项公式,若不是请说明理由.参考答案一.单项选择题:1.D2.A3.A.4.A.5.B.6.C.7.D8.B.9.B.10.B.11.C12.C.二.填空题:13.答案为:﹣3.14.答案为:15451.15.答案为:16.答案为:③④三.解答题:17.解:(1)若a=﹣1,函数f(x)=|x﹣1|+|x﹣a|=|x﹣1|+|x+1|,表示数轴上的x对应点到1、﹣1对应点的距离之和,而﹣1.2和1.5 对应点到1、﹣1对应点的距离之和正好等于3,故不等式f(x)≥3的解集为{x|≤﹣1.5,或x≥1.5}.(2)由于∀x∈R,f(x)≥2,故函数f(x)的最小值为2.函数f(x)=|x﹣1|+|x﹣a|表示数轴上的x对应点到1、a对应点的距离之和,它的最小值为|a﹣1|,即|a﹣1|=2,求得a=3 或a=﹣1.18.解:(1)∵∴∴(2)由正弦定理得,(a<b,即A<B),所以A=∵∴所以19.解:由已知,∴.∴由于f(t)=t+﹣2在上单调递减,∴当且仅当时,取最小值.故答案为:.20.解:(1)记数列{b n]的公差为d,依题意,(a2﹣a1)(b2﹣b1)=c1,∴(4﹣2)d=2,即d=1,∴b n=2+(n﹣1)=n+1,∴S n==;(2)∵a n=,∴a n+1﹣a n=﹣=(﹣1)n+1,∵c n=2n+n,∴b n+1﹣b n==(﹣1)n+1•(2n+n),∴b n﹣b n﹣1=(﹣1)n•(2n﹣1+n﹣1)(n≥2),b n﹣1﹣b n﹣2=(﹣1)n﹣1•(2n﹣2+n﹣2),b3﹣b2=(﹣1)3•(22+2),b2﹣b1=(﹣1)2•(21+1),当n=2k时,以上各式相加得:b n﹣b1=(2﹣22+23﹣…﹣2n﹣2+2n﹣1)+[1﹣2+3﹣…﹣(n﹣2)+(n﹣1)]=+=+,∴b n=b1++=++;当n=2k﹣1时,b n=b n+1﹣(﹣1)n+1(2n+n)=++﹣2n﹣n=﹣﹣+;综上所述,b n=.21.解:(Ⅰ)∵f(x)﹣x=a(x﹣x1)(x﹣x2),∴f(x)=a(x﹣x1)(x﹣x2)+x,∴f(x)﹣x1=a(x﹣x1)(x﹣x2)+(x﹣x1)=(x﹣x1)[a(x﹣x2)+1],∵,∵a>0∴a(x﹣x1)+1>0x﹣x1<0,∴f(x)﹣x1<0∴f(x)<x1…(Ⅱ)①a>0,ax2+bx+c<1,解集(﹣1,3)且f(x)min>﹣1,∴,∴f(x)=ax2﹣2ax+1﹣3a,∴f(x)min=a﹣2a+1﹣3a>﹣1,∴…②若a<0,则﹣ax2﹣bx﹣c<1解集(﹣1,3)且f max(x)<1,∴,∴f(x)=ax2﹣2ax﹣3a﹣1,∴f(x)max=a﹣2a﹣3a﹣1<1,∴综上述或…22.解:(1)证明:依题意数列a n的通项公式是a n=n,n=1时,a1b1=4﹣1﹣2=1;n=2时,a1b2+a2b1=8﹣2﹣2=4,则b1=1,b2=2,故等式即为b n+2b n﹣1+3b n﹣2+…+(n﹣1)b2+nb1=2n+1﹣n﹣2,b n﹣1+2b n﹣2+3b n﹣3+…+(n﹣2)b2+(n﹣1)b1=2n﹣n﹣1(n≥2),两式相减可得b n+b n﹣1+…+b2+b1=2n﹣1,得b n=2n﹣1,对n=1也成立.则数列{b n}是首项为1,公比为2的等比数列.(2)设等比数列{b n}的首项为b,公比为q,则b n=bq n﹣1,从而有:bq n﹣1a1+bq n﹣2a2+bq n﹣3a3+…+bqa n﹣1+ba n=2n+1﹣n ﹣2,又bq n﹣2a1+bq n﹣3a2+bq n﹣4a3+…+ba n﹣1=2n﹣n﹣1(n≥2),故(2n﹣n﹣1)q+ba n=2n+1﹣n﹣2,a n=•2n+•n+,要使a n+1﹣a n是与n无关的常数,必需q=2.即①当等比数列b n的公比q=2时,数列{a n}是等差数列,其通项公式是a n=;②当等比数列b n的公比不是2时,数列{a n}不是等差数列.河南省2020年高二数学上学期期中考试卷(三)(文科)(考试时间120分钟满分150分)一、单项选择题(本大题共12小题,每小题5分,共60分)1.设,是向量,命题“若,则”的逆命题是()A.若,则B.若,则C.若,则 D.若,则2.已知命题p:∀x∈R,sinx≤1,则¬p为()A.∃x∈R,sinx≥1 B.∀x∈R,sinx≥1 C.∃x∈R,sinx>1 D.∀x ∈R,sinx>13.要从已编号(1~60)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是()A.5、10、15、20、25、30 B.3、13、23、33、43、53C.1、2、3、4、5、6 D.2、4、8、16、32、484.抛物线x=﹣2y2的准线方程是()A.B.C.D.5.如下图,在半径为1的半圆内,放置一个边长为的正方形ABCD,向半圆内任投一点,该点落在正方形内的概率是()A.πB. C.D.2π6.已知双曲线的离心率为2,焦点是(﹣4,0),(4,0),则双曲线方程为()A. B. C. D.7.执行如图所示的程序框图,运行的结果是4,则输入的x的值可以是()A.2,4或16 B.﹣2,2或4 C.﹣2,2或16 D.﹣2,4或16 8.等轴双曲线C的中心在原点,右焦点与抛物线的焦点重合,则C的实轴长为()A.B.2C.4 D.89.设F1、F2是椭圆E: +=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.10.过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是原点,若|AF|=3,则△AOF的面积为()A. B.C.D.211.现有五个球分别记为A,C,J,K,S,随机放进三个盒子,每个盒子只能放一个球,则K或S在盒中的概率是()A. B.C. D.12.已知椭圆C: +=1(a>b>0)的离心率为,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为()A. +=1 B. +=1 C. +=1 D. +=1二、填空题(每小题5分,共20分)13.已知某公司准备投资一个项目,为慎重起见,该公司提前制定了两套方案,并召集了各部门的经理对这两套方案进行研讨,并对认为合理的方案进行了投票表决,统计结果如茎叶图所示,试说明方案比较稳妥的是.14.若抛物线y2=2px的焦点与椭圆+=1的右焦点重合,则p的值为.15.命题“∀x∈R,ax2﹣2ax+3>0恒成立”是假命题,则a的取值范围是.16.双曲线=1(a>0,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则该双曲线的离心率e=.三、解答题:(本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.)17.已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.(I)从中任取1个球,求取得红球或黑球的概率;(II)列出一次任取2个球的所有基本事件.(III)从中取2个球,求至少有一个红球的概率.18.(1)已知命题p:(x+2)(x﹣10)≤0,命题q:1﹣m≤x≤1+m,m>0,若q是p的充分不必要条件,求实数m的取值范围.(2)已知命题p:|a|<2,命题q:一次函数f(x)=(2﹣2a)x+1是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.19.已知三点P(5,2)、F1(﹣6,0)、F2(6,0).(Ⅰ)求以F1、F2为焦点且过点P的椭圆标准方程;(Ⅱ)设点P、F1、F2关于直线y=x的对称点分别为P′、F1′、F2′,求以F1′、F2′为焦点且过点P′的双曲线的标准方程.20.某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a,b),(a,),(a,b),(,b),(,),(a,b),(a,b),(a,),(,b),(a,),(,),(a,b),(a,),(,b)(a,b)其中a,分别表示甲组研发成功和失败,b,分别表示乙组研发成功和失败.(Ⅰ)若某组成功研发一种新产品,则给该组记1分,否则记0分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;(Ⅱ)若该企业安排甲、乙两组各自研发一样的产品,试估计恰有一组研发成功的概率.21.如图,已知圆,Q是圆上一动点,AQ 的垂直平分线交直线CQ于点M,设点M的轨迹为E.(Ⅰ)求轨迹E的方程;(Ⅱ)过点A作倾斜角为的直线l交轨迹E于B,D两点,求|BD|的值.22.在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为.(Ⅰ)求抛物线C的方程;(Ⅱ)过点F的直线交轨迹C于A,B两点,交抛物线C的准线l于点M,已知,,求λ1+λ2的值.参考答案一、单项选择题1.D2.C3.B4.D.5.C.6.A.7.C.8.C.9.C.10.B.11.D12.D.二、填空题13.解:首先将茎叶图的数据还原:第一套方案:8 25 20 24 38 41 55 58 64 67 66 73 72 70,第二套方案:6 5 12 14 19 19 21 36 37 42 42 45 54 61,第一套方案在14个部门的经理得票数为681票,第二套方案在14个部门的经理得票数为413票,第一套方案要比第二套方案得票率高得多,故第一套方案比较稳妥,故答案为:第一套方案14.解:由椭圆+=1,可得a2=6,b2=2,∴c==2,∴右焦点F(2,0).由抛物线y2=2px可得焦点.∴=2,解得p=4.故答案为:4.15.解:命题“ax2﹣2ax+3>0恒成立”是假命题,即“∃x∈R,ax2﹣2ax+3≤0成立”是真命题①.当a=0时,①不成立,当a≠0 时,要使①成立,必须a<0或,∴a<0或a≥3故答案为:(﹣∞,0)∪[3,+∞).16.解:∵双曲线的虚轴两端点为B1、B2,两焦点为F1,F2.∴F1(﹣c,0),B1(0,b),可得直线F1B1的方程为y=(x+c),即bx﹣cy+bc=0.∵双曲线的两顶点为A1、A2,以A1A2为直径的圆内切于菱形F1B1F2B2,∴点O到直线F1B1的距离等于半径,即=a,化简得b2c2=a2(b2+c2),∵b2=c2﹣a2,∴上式化简为(c2﹣a2)c2=a2(2c2﹣a2),整理得c4﹣3a2c2+a4=0.两边都除以a4,得e4﹣3e2+1=0,解之得e2=∵双曲线的离心率e>1,∴e2=,可得e==故答案为:三、解答题:17.解:(Ⅰ)从6只球中任取1球得红球有2种取法,得黑球有3种取法,得红球或黑球的共有2+3=5种不同取法,任取一球有6种取法,所以任取1球得红球或黑球的概率得,(II)将红球编号为红1,红2,黑球编号为黑1,黑2,黑3,则一次任取2个球的所有基本事件为:红1红2红1黑1红1黑2红1黑3红1白红2白红2黑1红2黑2红2黑3黑1黑2黑1黑3黑1白黑2黑3黑2白黑3白(III)由(II)知从6只球中任取两球一共有15种取法,其中至少有一个红球的取法共有9种,所以其中至少有一个红球概率为.18.解:(1)命题p:(x+2)(x﹣10)≤0,∴﹣2≤x≤10,命题q:1﹣m≤x≤1+m,m>0∴1﹣m≤x≤1+m,∵q是p的充分不必要条件,p:x∈[﹣2,10],q:x∈[1﹣m,1+m]∴[1﹣m,1+m]⊂[﹣2,10],∴,解得:,当1﹣m=﹣2时,m=3,[﹣2,4]⊂[﹣2,10],∴m=3成立,∴实数m的取值范围是[3,+∞);(2)若命题p:|a|<2,则﹣2<a<2,命题q:一次函数f(x)=(2﹣2a)x+1是增函数,则2﹣2a>0,解得:a<1,若p∨q为真,p∧q为假,则p,q一真一假,p真q假时:,解得:1≤a<2,p假q真时:,解得:a≤﹣2,综上:a∈(﹣∞,﹣2]∪[1,2).19.解:(1)由题意可设所求椭圆的标准方程为(a>b>0),其半焦距c=6∴,b2=a2﹣c2=9.所以所求椭圆的标准方程为(2)点P(5,2)、F1(﹣6,0)、F2(6,0)关于直线y=x的对称点分别为点P′(2,5)、F1′(0,﹣6)、F2′(0,6).设所求双曲线的标准方程为由题意知,半焦距c1=6,,b12=c12﹣a12=36﹣20=16.所以所求双曲线的标准方程为.20.解:(Ⅰ)甲组研发新产品的成绩为1,1,1,0,0,1,1,1,0,1,0,1,1,0,1,则=,==乙组研发新产品的成绩为1,0,1,1,0,1,1,0,1,0,0,1,0,1,1则=,==.因为所以甲的研发水平高于乙的研发水平.(Ⅱ)记E={恰有一组研发成功},在所抽到的15个结果中,恰有一组研发成功的结果是(a,),(,b),(a,),(,b),(a,),(a,),(,b)共7个,故事件E发生的频率为,将频率视为概率,即恰有一组研发成功的概率为P(E)=.21.解:(Ⅰ)由题意得|MC|﹣|MA|=|MC|﹣|MQ|=|CQ|=2<2,∴轨迹E是以A,C为焦点,实轴长为2的双曲线的左支…∴轨迹E的方程为=1(x)…(Ⅱ)设切线l的方程为y=x﹣,代入=1,消元得x2﹣4x ﹣8=0.设B,D两点的坐标分别为(x1,y1),(x2,y2),则x1+x2=4,x1x2=﹣8所以|BD|==4.22.解:(Ⅰ)∵⊙Q过M、F、O三点,∴Q一定在线段FO的中垂线上,∵抛物线x2=2py的焦点F(0,),O(0,0)∴FO的中垂线为:y=,设Q(x Q,y Q),得y Q=,结合抛物线的定义,得Q到抛物线C的准线的距离为﹣(﹣)=,解之得p=2由此可得,抛物线C的方程为x2=4y;(Ⅱ)由已知得直线l的斜率一定存在,由抛物线x2=4y的焦点F为(0,1),准线方程为y=﹣1,所以可设l:y=kx+1,则M点坐标为(﹣,﹣1),设直线l交抛物线于A(x1,y1),B(x2,y2),由直线与抛物线方程联立,可得x2﹣4kx﹣4=0∴x1+x2=4k,x1•x2=﹣4,又由,,∴(x1+,y1+1)=λ1(﹣x1,1﹣y1),∴x1+=﹣λ1x1,∴λ1=﹣﹣1,同理λ2=﹣﹣1,∴λ1+λ2=﹣﹣1﹣﹣1=﹣﹣2=0.河南省2020年高二数学上学期期中考试卷(四)(文科)(考试时间120分钟满分150分)一、单项选择题:(本大题共12小题,每小题5分,满分60分)1.△ABC中,A=45°,B=30°,a=10,则b=()A.5B.10C.10D.52.下列命题中,正确的是()A.若a>b,c>d,则a>c B.若ac>bc,则a>bC.若<,则a<b D.若a>b,c>d,则ac>bd3.设x,y∈R,则“x≥2且y≥2”是“x2+y2≥4”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.已知{a n}为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=()A.7 B.5 C.﹣5 D.﹣75.若a,b∈R,且ab>0,则下列不等式中,恒成立的是()A.a2+b2>2ab B. C.D.6.数列{a n}中,a1=1,a2=2,a n+2=a n+1﹣a n,则{a n}的前51项和S51=()A.1 B.2 C.3 D.47.在△ABC中,b=3,c=3,B=30°,则a的值为()A.3 B.23 C.3D.28.已知0<x<1,a=2,b=1+x,c=,则其中最大的是()A.a B.b C.c D.不确定9.在△ABC中,cos2B>cos2A是A>B的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件10.实数x,y满足不等式组,则ω=的取值范围是()A.[﹣,]B.[﹣1,] C.[﹣1,1)D.[﹣,1)11.已知等差数列{a n}的前n项和为S n,若,且A、B、C三点共线(该直线不过原点O),则S200=()A.100 B.101 C.200 D.20112.设a>0,b>0,且不等式++≥0恒成立.则实数k的最小值等于()A.4 B.0 C.﹣2 D.﹣4二、填空题:(共4小题,每小题5分,共20分)13.在等比数列{a n}中,若a4=5,a8=6,则a2a10=.14.不等式﹣6x2﹣x+2≤0的解集是.15.已知x>0,y>0,x+2y=16,则xy的最大值为.16.设x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为6,则的最小值为.三、解答题:(本题共6小题,共70分.)17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA (Ⅰ)求B的大小;(Ⅱ)若,c=5,求b.18.在△ABC中,角A、B、C所对的边分别为a、b、c,且a=2,cosB=.(1)若b=4,求sinA的值;(2)若△ABC的面积S△ABC=4,求b、c的值.19.设等差数列{a n}第10项为24,第25项为﹣21.(1)求这个数列的通项公式;(2)设S n为其前n项和,求使S n取最大值时的n值.20.关于x的不等式:x2﹣(1+a)x+a>0.(1)当a=2时,求不等式的解集;(2)当a∈R时,解不等式.21.在△ABC中,角A、B、C的对边分别为a、b、c,面积为S,已知acos2+ccos2=b(1)求证:a、b、c成等差数列;(2)若B=,S=4求b.22.已知{a n}是公比为q的等比数列,且a1,a3,a2成等差数列.(Ⅰ)求q的值;(Ⅱ)设{b n}是以2为首项,q为公差的等差数列,其前n项和为S n,当n≥2时,比较S n与b n的大小,并说明理由.参考答案一、单项选择题1.A.2.C3.A.4.D5.D6.D7.C.8.C.9.C10.D.11.A12.D.二、填空题13.答案为:30.14.答案为:{x|x≥,或x≤﹣}.15.答案为32.16.答案为:三、解答题17.解:(Ⅰ)由a=2bsinA,根据正弦定理得sinA=2sinBsinA,所以,由△ABC为锐角三角形得.(Ⅱ)根据余弦定理,得b2=a2+c2﹣2accosB=27+25﹣45=7.所以,.18.解:(1)∵cosB=>0,且0<B<π,∴sinB==.由正弦定理得=,∴sinA===.(2)∵S△ABC=acsinB=×=4,∴c=5.由余弦定理得b2=a2+c2﹣2accosB=22+52﹣2×2×5×=17,∴b=.19.解:(1)∵等差数列{a n}第10项为24,第25项为﹣21,∴,解得a1=51,d=﹣3,∴a n=51+(n﹣1)×(﹣3)=﹣3n+54.(2)∵a1=51,d=﹣3,∴S n=51n+=﹣+=﹣(n﹣)2+,∴n=16,或n=17时,S n取最大值.20.解:(1)当a=2时,原不等式化为x2﹣3x+2>0,即(x﹣1)(x ﹣2)>0,解得x>2或x<1.∴原不等式的解集为{x|x>2或x<1}.(2)原式等价于(x﹣a)(x﹣1)>0,当a>1时,解得x>a或x<1,故解集是{x|x>a或x<1};当a=1时,不等式化为(x﹣1)2>0,故其解集是{x|x≠1};当a<1时,解得x>1或x<a,故解集是{x|x>1或x<a}.21.解:(1)由正弦定理得:sinAcos2+sinCcos2=sinB,即sinA•+sinC•=sinB,∴sinA+sinC+sinAcosC+cosAsinC=3sinB,即sinA+sinC+sin(A+C)=3sinB,∵sin(A+C)=sinB,∴sinA+sinC=2sinB,由正弦定理化简得:a+c=2b,∴a,b,c成等差数列;(2)∵S=acsinB=ac=4,∴ac=16,又b2=a2+c2﹣2accosB=a2+c2﹣ac=(a+c)2﹣3ac,由(1)得:a+c=2b,∴b2=4b2﹣48,即b2=16,解得:b=4.22.解:(1)由题意可知,2a3=a1+a2,即a(2q2﹣q﹣1)=0,∴q=1或q=﹣;(II)q=1时,S n=2n+=,∵n≥2,∴S n﹣b n=S n﹣1=>0当n≥2时,S n>b n.若q=﹣,则S n=,同理S n﹣b n=.∴2≤n≤9时,S n>b n,n=10时,S n=b n,n≥11时,S n<b n.河南省2020年高二数学上学期期中考试卷(五)(文科)(考试时间120分钟满分150分)一、单项选择题:本大题共12小题,每小题5分,共60分.1.不等式≥0的解集为()A.(﹣1,2]B.[﹣1,2]C.(﹣∞,﹣1)∪(2,+∞)D.(﹣∞,﹣1]∪(2,+∞)2.已知命题p:“∀x∈R,x+1≥0”的否定是“∀x∈R,x+1<0”;命题q:函数y=x﹣3是幂函数,则下列命题为真命题的是()A.p且q B.p或q C.¬q D.p且(¬q)3.已知在等差数列{a n}中,a2=6,a4=14,则数列{a n}前10项的和为()A.100 B.400 C.380 D.2004.若△ABC的三个内角满足sinA:sinB:sinC=5:11:13,则△ABC()A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.可能是锐角三角形,也可能是钝角三角形5.“a=﹣5”是“直线y=x+4与圆(x﹣a)2+(y﹣3)2=8相切”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.函数f(x)=(x2﹣1)2+2的极值点是()A.x=1 B.x=﹣1C.x=1或x=﹣1或x=0 D.x=07.已知数列{a n}满足log3a n+2=log3a n+1(n∈N*)且a2+a4+a6=9,则log(a5+a7+a9)的值是()A.﹣8 B.﹣ C.8 D.8.已知曲线+=1(k∈R)表示焦点在y轴上的椭圆,则k的取值范围是()A.(﹣∞,1)∪(3,+∞)B.(﹣∞,3)C.(1,+∞)D.(1,3)9.若变量x,y满足约束条件,且z=2x+y的最大值和最小值分别为m和n,则n﹣m=()A.﹣5 B.﹣6 C.5 D.610.抛物线y2=4x的焦点为F,准线为l,经过F且斜率为的直线与抛物线在x轴上方的部分相交于点A,AK⊥l,垂足为K,则△AKF的面积是()A.4 B.C.D.811.已知实数4,m,9构成一个等比数列,则圆锥曲线的离心率为()A.B.C.或D.或712.已知定义在R上的函数f(x)、g(x)满足f(x)=a x g(x),且f′(x)g(x)<f (x)g′(x),且+=,若有穷数列{}(n∈N*)的前n项和等于,则n等于()A.3 B.4 C.5 D.6二、填空题:本大题共4个小题,每小题5分.、共20分.13.已知函数f(x)=lnx﹣f′(﹣1)x2+3x﹣4,则f′()=______.14.若点(2,1)是抛物线y2=2px(p>0)的一条弦的中点,且这条弦所在的直线的斜率为1,则p的值是______.15.若双曲线﹣=1(a>0,b>0)的一条渐近线的倾斜角为,离心率为e,最小值为______.16.已知函数f(x)=x3+ax2+2bx+c,函数f(x)在区间(0,1)内取极大值,在区间(1,2)内取极小值,则u=的取值范围是______.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.等差数列{a n}中,a7=4,a19=2a9,(Ⅰ)求{a n}的通项公式;(Ⅱ)设b n=,求数列{b n}的前n项和S n.18.在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.(Ⅰ)求角A的大小;(Ⅱ)若△ABC的面积S=5,b=5,求sinBsinC的值.19.已知函数f(x)=﹣2x2+lnx,其中a为正常数.(1)若a=1,求函数f(x)的单调区间;(2)若函数f(x)在区间[2,4]上为单调递增函数,求实数a的取值范围.20.设抛物线C:y2=4x,F为C的焦点,过F的直线L与C相交于A、B两点.(1)设L的斜率为2,求|AB|的大小;(2)求证:•是一个定值.21.已知函数f(x)=x3﹣3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为﹣2.(Ⅰ)求a;(Ⅱ)证明:当k<1时,曲线y=f(x)与直线y=kx﹣2只有一个交点.22.如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且,.(1)求椭圆的标准方程;(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F 恰为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.参考答案一、单项选择题1.A.2.B 3.D.4.C 5.A.6.C.7.A.8.D.9.B.10.C.11.C.12.C.二、填空题13.解:∵f(x)=lnx﹣f′(﹣1)x2+3x﹣4,∴f′(x)=﹣2f′(﹣1)x+3∴f′(﹣1)=﹣1+2f′(﹣1)+3,∴f′(﹣1)=﹣2,∴f′()=2﹣2×(﹣2)×+3=7,故答案为:7.14.解:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,两式相减,得(y1﹣y2)(y1+y2)=2p(x1﹣x2),依题意x1≠x2,∴k AB==1,于是y1+y2=2p=2,因此p=1.故答案为:1.15.解:双曲线﹣=1的渐近线方程为y=±x,由题意可得﹣=tan=﹣,即有b=a,c=2a,e==2,则==(a+)≥•2=.当且仅当a=2时,取得最小值.故答案为:.16.解:f(x)=x3+ax2+2bx+c,∴f′(x)=x2+ax+2b,∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根f′(0)>0,f′(1)<0,f′(2)>0即,画出满足条件的平面区域,如图示:,由,解得:A(﹣3,1),则u=的几何意义表示平面区域内的点与(1,2)的直线的斜率,而K AB=,K BC=1,故u∈,故答案为:.三、解答题17.解:(I)设等差数列{a n}的公差为d∵a7=4,a19=2a9,∴解得,a1=1,d=∴=(II)∵==∴s n===18.解:(Ⅰ)由cos2A﹣3cos(B+C)=1,得2cos2A+3cosA﹣2=0,即(2cosA﹣1)(cosA+2)=0,解得(舍去).因为0<A<π,所以.(Ⅱ)由S===,得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故.又由正弦定理得.19.解:(1)若a=1,则f(x)=3x﹣2x2+ln x,该函数的定义域为(0,+∞),f′(x)=﹣4x+3==(x>0).…当x∈(0,1),f′(x)>0时,函数f(x)=3x﹣2x2+ln x单调递增.当x∈(1,+∞),f′(x)<0时,函数f(x)=3x﹣2x2+ln x单调递减.故函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).…(2)f′(x)=﹣4x+,若函数f(x)在区间[2,4]上为单调递增函数,即在区间[2,4]上,f′(x)=﹣4x+≥0,即﹣4x+≥0在[2,4]上恒成立.…即≥4x﹣.令h(x)=4x﹣,因为函数h(x)在[2,4]上单调递增,所以,即≥,…解之得,∴实数a的取值范围为.…20.解:(1)依题意得F(1,0),∴直线L的方程为y=2(x﹣1),设直线L与抛物线的交点A(x1,y1),B(x2,y2),联立消去y整理得x2﹣3x+1=0,∴x1+x2=3,x1x2=1.法一:|AB|==•=.法二:|AB|=|AF|+|BF|=x1+x2+p=3+2=5.(2)证明:设直线L的方程为x=ky+1,设直线L与抛物线的交点A(x1,y1),B(x2,y2),由消去x整理得y2﹣4ky﹣4=0.∴y1+y2=4k,y1y2=﹣4,∵═(x1,y1)•(x2,y2)=x1x2+y1y2=(ky1+1)(ky2+1)+y1y2=k2y1y2+k(y1+y2)+1+y1y2=﹣4k2+4k2+1﹣4=﹣3.∴是一个定值为﹣3.21.解:(Ⅰ)函数的导数f′(x)=3x2﹣6x+a;f′(0)=a;则y=f(x)在点(0,2)处的切线方程为y=ax+2,∵切线与x轴交点的横坐标为﹣2,∴f(﹣2)=﹣2a+2=0,解得a=1.(Ⅱ)当a=1时,f(x)=x3﹣3x2+x+2,设g(x)=f(x)﹣kx+2=x3﹣3x2+(1﹣k)x+4,由题设知1﹣k>0,当x≤0时,g′(x)=3x2﹣6x+1﹣k>0,g(x)单调递增,g(﹣1)=k﹣1,g(0)=4,当x>0时,令h(x)=x3﹣3x2+4,则g(x)=h(x)+(1﹣k)x>h(x).则h′(x)=3x2﹣6x=3x(x﹣2)在(0,2)上单调递减,在(2,+∞)单调递增,∴在x=2时,h(x)取得极小值h(2)=0,g(﹣1)=k﹣1,g(0)=4,则g(x)=0在(﹣∞,0]有唯一实根.∴g(x)>h(x)≥h(2)=0,∴g(x)=0在(0,+∞)上没有实根.综上当k<1时,曲线y=f(x)与直线y=kx﹣2只有一个交点.22.解.(1)如图建系,设椭圆方程为,则c=1又∵即(a+c)•(a﹣c)=1=a2﹣c2,∴a2=2故椭圆方程为(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,则设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),故k PQ=1,于是设直线l为y=x+m,由得3x2+4mx+2m2﹣2=0,又F为△PQM的垂心,则MP⊥FQ,故又y i=x i+m(i=1,2)得x1(x2﹣1)+(x2+m)(x1+m﹣1)=0即2x1x2+(x1+x2)(m﹣1)+m2﹣m=0由韦达定理得解得或m=1(舍)经检验符合条件,此时直线l的方程为y=x﹣.河南省2020年高二数学上学期期中考试卷(六)(考试时间120分钟满分150分)一、单项选择题:本大题共12小题,每小题5分,共60分.1.已知集合M={x|﹣4≤x≤7},N={x|x2﹣x﹣12>0},则M∩N为()A.{x|﹣4≤x<﹣3或4<x≤7} B.{x|﹣4<x≤﹣3或4≤x<7}C.{x|x≤﹣3或x>4} D.{x|x<﹣3或x≥4}2.已知等比数列{a n}的公比为正数,且a3•a9=2a52,a2=1,则a1=()A.B.C.D.23.设等差数列{a n}的前n项和为S n,若S3=9,S6=36,则a7+a8+a9=()A.63 B.45 C.36 D.274.有下列四个命题:①“若x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q≤1,则x2+2x+q=0有实根”的逆否命题;④“不等边三角形的三个内角相等”逆命题;其中真命题为()A.①②B.①③ C.②③ D.③④5.在△ABC中,“A>30°”是“sinA>”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也必要条件6.设命题P:∃n∈N,n2>2n,则¬P为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2n C.∀n∈N,n2≤2n D.∃n∈N,n2=2n7.在△ABC中,a=2,b=2,B=,则A等于()A.B.C.或D.或8.若x、y满足条件,则z=﹣2x+y的最大值为()A.1 B.﹣C.2 D.﹣59.已知椭圆+=1(m>0 )的左焦点为F1(﹣4,0),则m=()A.2 B.3 C.4 D.910.已知双曲线C:﹣=1的离心率e=,且其右焦点为F2(5,0),则双曲线C 的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=111.已知点F1、F2分别是椭圆的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率e是()A.B.C.D.12.若x,y∈R+,且2x+8y﹣xy=0,则x+y的最小值为()A.12 B.14 C.16 D.18二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上。
高二数学第一学期期中试卷参考答案

淮安市高中校协作体2020~2021学年第一学期高二年级期中考试数学试卷参考★答案★考试时间:120分钟 总分:150分 命题人:蒋法宝一、单项选择题(本大题共有8小题,每题5分,共40分)”1. “0a =”是“函数221y ax x =++与x 轴只有一个交点”的( )A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件 【★答案★】C2.已知等差数列{}n a 中,161,11a a ==,则数列{}n a 的公差为( ) A .53B .2C .8D .13【★答案★】B3.椭圆2214x y m +=的焦距为2,则m 的值等于( )A .3B .5C .8D . 5或3【★答案★】D 4.已知0x <,函数4y x x=+的最大值是( ) A .4B .-4C .-6D .-8【★答案★】B5.双曲线mx 2+y 2=1的虚轴长是实轴长的3倍,则m 的值为( ) A .9B .-9C .19D .-19【★答案★】D6.已知等比数列{}n a 中,17a =,435a a a =,则7a =( ) A .19B .17C .13D .7【★答案★】B7.一元二次不等式2201920200x x --<的解集为( ) A .(2020,1)- B .(1,2020)- C .(,1)(2020,)-∞-+∞ D .(,2020)(1,)-∞-+∞【★答案★】B8.设等差数列{}n a 的公差10,4d a d ≠=,若k a 是1a 与2k a 的等比中项,则k=( )A .3或6B .3 或-1C .6D .3【★答案★】D二、多项选择题(本大题共有4小题,每题5分,共20分。
在每小题给出的选项中,有多项符合要求.全部选对的得5分,部分选对的得3分,有选错的得0分.) 9.下列说法正确的是( )A .命题“(2,)x ∃∈-+∞,24x ≤”的否定是“(2,)x ∀∈-+∞,24x >”B .命题“x ∀∈R ,22x >-”的否定是“x ∃∈R ,22x <-”C .“22x y >”是“x y >”的必要而不充分条件D .“0m >”是“关于x 的方程2x 2x m 0--=有一正一负根”的充要条件 【★答案★】AD10.下列说法正确的有( ) A .若a b >,则22ac bc >B .若22a bc c>,则a b > C .若a b >,则22a b > D .若a b >,则22a b > 【★答案★】BD11.设等差数列{}n a 的前n 项和为n S .若30S =,46a =,则( ) A .23n S n n =- B . 2392n n nS -= C .36n a n =-D .2n a n =【★答案★】BC12.若正实数a ,b 满足1a b +=,则下列说法正确的是( ) A .14ab ≥B .114a b+≥ C . 2a b +≤D .2212a b +≥【★答案★】BCD三、填空题(本大题共有4小题,每题5分,共20分) 13.已知{}n a 为等差数列,a 3+a 8=25,a 6=11,则a 5= _______ 【★答案★】1414.已知点P 为双曲线C :2213664x y -=上的动点,点()10,0A -,点()10,0B .若16PA =,则PB =_______【★答案★】28或4 15.计算:111113355720192021++++=⨯⨯⨯⨯__________.【★答案★】1010202116.设a ,b 为正数,若22a b +=,当a 取值为__________时12a b+取最小值为________ 【★答案★】12,4 四、解答题(本大题共有6小题,第17题10分,其余每题12分,共70分) 17.已知命题p :“方程210x mx -+=有两个不相等的实根”,命题p 是真命题. (1)求实数m 的取值集合M ;(2)设不等式()(4)0x a x a ---<的解集为N ,若x ∈N 是x ∈M 的充分条件,求a 的取值范围. 解:(1) 命题p :方程210x mx +=-有两个不相等的实根,240m ∴∆=->,解得2m >,或2m <-.M={m|2m >,或2m <-}. ………………………………5分 (2) 因为x ∈N 是x ∈M 的充分条件,所以N M ⊆ N={|4}x a x a <<+42a +≤-或2,a ≥综上,6a ≤-或2a ≥ ………………………………10分 18.已知在等差数列{}n a 中,1344,3a a a +==;{}n b 是各项都为正数的等比数列,1113b a =,3141b a =.(1)求数列{}n a ,{}n b 的通项公式; (2)求数列{}n n a b 的前n 项和n T .解:(1)由134a a +=,得224a =即22a =, 所以等差数列{}n a 的公差42321222a a d --=== 则数列{}n a 的通项公式为211(2)2(2)122n a a n d n n =+-=+-=+ …………3分所以1111313322b a ==⨯= 由3141b a =,得381b ⨯=,即318b =, 由0q >所以等比数列{}n b 的公比3112b q b ==, 所以数列{}n b 的通项公式为1112nn n b b q-⎛⎫== ⎪⎝⎭.………………………………6分 (2)由数列{}n n a b 的前n 项和为n T =112233n n a b a b a b a b ++++ ①得12n T =1223341n n a b a b a b a b +++++ ②由①-②得12n T =11231n n n a b db db db a b +++++-=1111[1()]311142(1)12222212n n n -+-⨯+⨯-+-=113111[1()](1)44222n n n -++--+ =2412n n ++-所以n T =1422n n ++- ………………………………12分19.(1)求焦点在x 轴上,长轴长为8,焦距为4的椭圆标准方程; (2)求一个焦点为()5,0,渐近线方程为43yx 的双曲线标准方程. 解:(1)设椭圆标准方程为:()222210x y a b a b+=>>由长轴长知:28a =4a ∴=由焦距知:24c =222162c a b b ∴=-=-=,解得:212b =∴椭圆标准方程为:2211612x y += ………………………………6分 (2)双曲线焦点在x 轴上 ∴可设双曲线标准方程为()222210,0x ya b a b-=>>∴双曲线渐近线方程为:43b y x x a =±=±43b a ∴= 又焦点为()5,022221659a b a a ∴+=+=,解得:29a =216b ∴= ∴双曲线标准方程为:229116x y -= ………………………………12分20.已知函数9()(1)1f x x x x =+>- (I )求函数()f x 的最小值; (II )若不等式()71tf x t ≥++恒成立,求实数t 的取值范围. 解:(I )110x x >∴-> 99()1111f x x x x x ∴=+=-++-- 92(1)171x x ≥-⋅+=- 当且仅当911x x -=-即4x =时上式取得等号 当4x =时,函数()f x 的最小值是7. ………………………………6分 (II )由(I )知,当1x >时,()f x 的最小值是7, 要使不等式()71t f x t ≥++恒成立,只需771t t ≥++ 01tt ∴≤+ 解得10t -<≤实数的取值范围是(1,0]- ………………………………12分 21.已知数列{}n a 的前n 项和n S 满足:2n n S a =-. (1)求{}n a 的通项公式;(2)设41n n c a =+,求数列{}n c 的前n 项和n T .解:(1)当1n =时,112S a =-,得11a =. 当2n ≥时,由2n n S a =-,① 得112n n S a --=-,②①—②,得12n n a a -=,又110a =≠,∴0n a ≠,∴()1122n n a n a -=≥, ∴{}n a 是等比数列,∴112n n a -⎛⎫= ⎪⎝⎭ ………………………………6分(2)由112n n a -⎛⎫= ⎪⎝⎭,则1141412n n n c a -⎛⎫=+=⨯+ ⎪⎝⎭,则123n n T c c c c =++++()1234n a a a a n =+++++31112481212n n n n -=⨯+=+---………………………………12分 22.已知不等式2364ax x -+>的解集为{1x x <或}x b >. (1)求,a b(2)解不等式2()0ax at b x bt -++<.解:(1)因为不等式2364ax x -+>的解集为{1x x <或}x b >, 所以x 1=1与x 2=b 是方程2320ax x -+=的两个实数根,且b >1.由根与系数的关系,得3121b ab a ⎧+=⎪⎪⎨⎪⋅=⎪⎩,解得12a b =⎧⎨=⎩; ……………………………6分(2)原不等式化为:2(t 2)20x x t -++<,即(2)()0x x t --<,①当2t >时,不等式的解集为{}2x x t <<,……………………………8分 ②当2t <时,不等式的解集为{}2x t x <<,……………………………10分t=时,不等式的解集为∅.……………………………12分③当2感谢您的下载!快乐分享,知识无限!。
2020-2021高二数学上期中模拟试卷(及答案)

2020-2021高二数学上期中模拟试卷(及答案)一、选择题1.民间有一种五巧板拼图游戏.这种五巧板(图1)可以说是七巧板的变形,它是由一个正方形分割而成(图2),若在图2所示的正方形中任取一点,则该点取自标号为③和④的巧板的概率为()A.518B.13C.718D.492.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b分别为14,18,则输出的a ()A.0B.2C.4D.143.在本次数学考试中,第二大题为多项选择题.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分,小明因某原因网课没有学习,导致题目均不会做,那么小明做一道多选题得5分的概率为()A.115B.112C.111D.144.阅读下边的程序框图,运行相应的程序,则输出s的值为( )A .1B .0C .1D .35.已知变量,x y 之间满足线性相关关系ˆ 1.31yx =-,且,x y 之间的相关数据如下表所示: x 12 3 4 y0.1m3.14则实数m =( ) A .0.8B .0.6C .1.6D .1.86.某商场为了了解毛衣的月销售量y (件)与月平均气温x (C ︒)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表: 月平均气温x C ︒171382月销售量y (件)24334055由表中数据算出线性回归方程y bx a =+$$$中的2b =-$,气象部门预测下个月的平均气温为6C ︒,据此估计该商场下个月毛衣销售量约为( )A .58件B .40件C .38件D .46件7.已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )A .100,20B .200,20C .100,10D .200,108.6件产品中有4件合格品,2件次品.为找出2件次品,每次任取一个检验,检验后不放回,则恰好在第四次检验后找出所有次品的概率为( ) A .35B .13C .415D .159.将三枚质地均匀的骰子各掷一次,设事件A =“三个点数之和等于15”,B =“至少出现一个5点”,则概率()|P A B 等于( ) A .5108B .113C .17D .71010.如图所示是为了求出满足122222018n +++>L 的最小整数n ,和两个空白框中,可以分别填入( )A .2018S >?,输出1n -B .2018S >?,输出nC .2018S ≤?,输出1n -D .2018S ≤?,输出n11.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x (万8.28.610.0 11.3 11.9元)支出y(万元)6.27.58.08.59.8根据上表可得回归直线方程ˆˆˆy bx a=+,其中ˆˆˆ0.76,b a y bx==-,据此估计,该社区一户收入为15万元家庭年支出为()A.11.4万元B.11.8万元C.12.0万元D.12.2万元12.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,...,960,分组后某组抽到的号码为41.抽到的32人中,编号落入区间[]401,755的人数为()A.10B.11C.12D.13二、填空题13.在区间[2,4]-上随机地取一个实数x,若实数x满足||x m≤的概率为23,则m=_______.14.连续抛掷一颗骰子2次,则掷出的点数之和不超过9的概率为______.15.某校连续5天对同学们穿校服的情况进行统计,没有穿校服的人数用茎叶图表示,如图,若该组数据的平均数为18,则x=_____________.16.在可行域103x yx yx--≤⎧⎪+≤⎨⎪>⎩,内任取一点(),M x y,则满足20x y->的概率是______.17.某单位为了了解用电量y(度)与气温x(℃之间的关系,随机统计了某4天的用电量与当天气温(如表),并求得线性回归方程ˆ360y x=-为:x c914-1y184830d不小心丢失表中数据c,d,那么由现有数据知3c d-____________.18.三位同学参加跳高、跳远、铅球项目的比赛.若每人只选择一个项目,则有且仅有两人选择的项目完全相同的概率是 (结果用最简分数表示).19.课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应的城市的个数分别为4、12、8.若用分层抽样的方法抽取6个城市,则乙组中应抽取的城市数为_________.20.已知方程0.85 2.1ˆ87yx =-是根据女大学生的身高预报其体重的回归方程, ˆ,x y 的单位是cm 和kg ,则针对某个体()160,53的残差是__________.三、解答题21.随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入y (单位:千元)的数据如下表: 年份 2014 2015 2016 2017 2018 年份代号t 1 2 3 4 5 人均纯收入y547810(1)求y 关于t 的线性回归方程;(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?附:回归直线的斜率和截距的最小二乘估计公式分别为()()()121niii nii tty y b tt==--=-∑∑$,a y bt =-$$.22.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4 组[45,55),第5组[55,65],得到的频率分布直方图如图所示(1) 求a 的值(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取12人,再从这12人中随机抽取3人进行问卷调查,求在第1组已被抽到1人的前提下,第3组被抽到2人的概率; (3)若从所有参与调查的人中任意选出3人,记关注“生态文明”的人数为X ,求X 的分布列与期望.23.“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.共生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据(),(1,2,,6)i i x y i =L ,如表所示:已知611806i i y y ===∑,613050i i i x y ==∑.(1)已知变量,x y ,只有线性相关关系,求产品销量y (件)关于试销单价x (元)的线性回方程y bx a =+$$$;(2)用µi y 表示用(Ⅱ)中所求的线性回归方程得到的与i x 对应的产品销量的估计值.当销售数据(),i i x y 对应的差的绝对值µ||1i i y y -≤时,则将售数数(),i i x y 称为一个“好数据”.现从6小销售数据中任取2个;求“好数据”至少有一个的概率.(参考公式:线性回归方程中,b a 的最小二乘估计分别为1221ni ii nii x y nx ybxnx==-=-∑∑$,a y bx =-$$)24.某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(]195,210内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数; (2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?(3)根据已知条件完成下面22⨯列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?甲流水线 乙流水线 合计合格品 不合格品 合计附:()()()()22()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.临界值表:()20P K k ≥ 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0k2.0722.7063.8415.0246.6357.87910.82825.为了调查教师对教育改革认识水平,现从某市年龄在[]20,45的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在[)[)[]30,35,35,40,40,45中用分层抽样的方法选取6名教师代表.(1)求年龄在[)35,40中的教师代表人数;(2)在这6名教师代表中随机选取2名教师,求在[)35,40中至少有一名教师被选中的概率.26.某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试.现从这些学生的成绩中随机抽取了50名学生的成绩,按照[)[)[]50,60,60,70,,90,100⋅⋅⋅分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).(1)求频率分布直方图中x 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);(2)用样本估计总体,若该校共有2000名学生,试估计该校这次测试成绩不低于70分的人数;(3)若利用分层抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人,试求成绩在[]80,100的学生至少有1人被抽到的概率.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】【分析】分别求出③和④的巧板的面积,根据几何概型的概率关系转化为面积比. 【详解】设巧板①的边长为1,则结合图2可知大正方形的边长为3, 其面积239S ==.其中巧板③是底边长为2的等腰直角三角形,其面积为112112S =⨯⨯=的正方形 与腰长为1的等腰直角三角形的组合图形,其面积为22151122S ⨯⨯+==, 故所求的概率12718S S P S +==. 故选:C . 【点睛】本题考查几何概型的概率求法,转化为面积比,属于中档题 .2.B解析:B 【解析】 【分析】 【详解】由a=14,b=18,a <b , 则b 变为18﹣14=4, 由a >b ,则a 变为14﹣4=10, 由a >b ,则a 变为10﹣4=6, 由a >b ,则a 变为6﹣4=2, 由a <b ,则b 变为4﹣2=2, 由a=b=2, 则输出的a=2. 故选B .3.C解析:C 【解析】 【分析】根据题意结合组合的知识可知,总的答案的个数为11个,而正确的答案只有1个,根据古典概型的计算公式,即可求得结果. 【详解】总的可选答案有:AB ,AC ,AD ,BC ,BD ,CD , ABC ,ABD ,ACD ,BCD ,ABCD ,共11个,而正确的答案只有1个, 即得5分的概率为111p =. 故选:C. 【点睛】本题考查了古典概型的基本知识,关键是弄清一共有多少个备选答案,属于中档题.4.B解析:B 【解析】经过第一次循环得到32s i ==,,不满足4i >, 执行第二次循环得到43s i ==,, 不满足4i >,, 执行第三次循环得到s=1,i=4,不满足4i >,, 经过第四次循环得到05s i ==,, 满足判断框的条件 执行“是”输出0S =.故选B . 5.D解析:D 【解析】分析:由题意结合线性回归方程的性质整理计算即可求得最终结果. 详解:由题意可得:12345 2.542x +++===,0.1 3.14 1.844m m y +++==+, 线性回归方程过样本中心点,则:1.8 1.3 2.514m+=⨯-, 解得:8.1=m . 本题选择D 选项.点睛:本题主要考查线性回归方程的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.6.D解析:D 【解析】试题分析:由表格得(),x y 为:()10,38,因为(),x y 在回归方程y bx a =+$$$上且2b =-$,()38102a ∴=⨯-+,解得58a =∴2ˆ58y x =-+,当6x =时,26ˆ5846y=-⨯+=,故选D. 考点:1、线性回归方程的性质;2、回归方程的应用.7.B解析:B 【解析】 【分析】 【详解】试题分析:由题意知,样本容量为()3500450020002%200++⨯=,其中高中生人数为20002%40⨯=,高中生的近视人数为4050%20⨯=,故选B. 【考点定位】本题考查分层抽样与统计图,属于中等题.8.C解析:C 【解析】 【分析】题目包含两种情况:第一种是前面三次找出一件次品,第四次找出次品,第二种情况是前面四次都是正品,则剩余的两件是次品,计算概率得到答案. 【详解】题目包含两种情况:第一种是前面三次找出一件次品,第四次找出次品,2314615C p C ==;第二种情况是前面四次都是正品,则剩余的两件是次品,44246115C p C ==;故12415p p p =+=. 故选:C . 【点睛】本题考查了概率的计算,忽略掉前面四次都是正品的情况是容易发生的错误.9.B解析:B 【解析】 【分析】根据条件概率的计算公式即可得出答案. 【详解】3311166617()216A P AB C C C +==Q ,11155561116691()1216C C C P B C C C =-=()()()72161|2169113P AB P A B P B ∴==⨯= 故选:B 【点睛】本题主要考查了利用条件概率计算公式计算概率,属于中档题.10.A解析:A【解析】 【分析】通过要求122222018n +++>L 时输出且框图中在“是”时输出确定“”内应填内容;再通过循环体确定输出框的内容. 【详解】因为要求122222018n +++>L 时输出,且框图中在“是”时输出, 所以“”内输入“2018S >?”,又要求n 为最小整数, 所以“”中可以填入输出1n -,故选:A . 【点睛】本题考查了程序框图的应用问题,是基础题.11.B解析:B 【解析】 试题分析:由题,,所以.试题解析:由已知,又因为ˆˆˆybx a =+,ˆˆˆ0.76,b a y bx ==- 所以,即该家庭支出为万元.考点:线性回归与变量间的关系.12.C解析:C 【解析】 【分析】由题意可得抽到的号码构成以11为首项、以30为公差的等差数列,求得此等差数列的通项公式为a n =30n ﹣19,由401≤30n ﹣21≤755,求得正整数n 的个数,即可得出结论. 【详解】∵960÷32=30,∴每组30人,∴由题意可得抽到的号码构成以30为公差的等差数列, 又某组抽到的号码为41,可知第一组抽到的号码为11,∴由题意可得抽到的号码构成以11为首项、以30为公差的等差数列,∴等差数列的通项公式为a n =11+(n ﹣1)30=30n ﹣19, 由401≤30n ﹣19≤755,n 为正整数可得14≤n ≤25, ∴做问卷C 的人数为25﹣14+1=12, 故选C . 【点睛】本题主要考查等差数列的通项公式,系统抽样的定义和方法,根据系统抽样的定义转化为等差数列是解决本题的关键,比较基础.二、填空题13.2【解析】【分析】画出数轴利用满足的概率可以求出的值即可【详解】如图所示区间的长度是6在区间上随机地取一个数若满足的概率为则有解得故答案是:2【点睛】该题考查的是有关长度型几何概型的问题涉及到的知识解析:2 【解析】 【分析】画出数轴,利用x 满足||x m ≤的概率,可以求出m 的值即可. 【详解】 如图所示,区间[2,4]-的长度是6,在区间[2,4]-上随机地取一个数x , 若x 满足||x m ≤的概率为23, 则有2263m =,解得2m =, 故答案是:2. 【点睛】该题考查的是有关长度型几何概型的问题,涉及到的知识点有长度型几何概型的概率公式,属于简单题目.14.【解析】【分析】根据古典概型概率公式求解【详解】连续抛掷一颗骰子2次共有36种基本事件其中掷出的点数之和不超过9的事件有种故所求概率为【点睛】本题考查古典概型概率考查基本分析与运算能力属基础题解析:56【解析】【分析】根据古典概型概率公式求解. 【详解】连续抛掷一颗骰子2次,共有36种基本事件,其中掷出的点数之和不超过9的事件有66654330+++++=种,故所求概率为305366=. 【点睛】本题考查古典概型概率,考查基本分析与运算能力,属基础题.15.8【解析】【分析】根据茎叶图计算平均数【详解】由茎叶图得【点睛】本题考查茎叶图以及平均数考查基本运算能力属基础题解析:8 【解析】 【分析】根据茎叶图计算平均数. 【详解】 由茎叶图得1617101920188.5x x +++++=∴=【点睛】本题考查茎叶图以及平均数,考查基本运算能力,属基础题.16.【解析】【分析】画出可行域求出面积满足的区域为图形中的红色直线的下方的四边形其面积为由几何概型的公式可得的概率为:;【详解】约束条件的可行域如图:由解得可行域d 面积为由解得满足的区域为图形中的红色直解析:58【解析】 【分析】画出可行域,求出面积,满足20x y ->的区域为图形中的红色直线的下方的四边形,其面积为1541322-⨯⨯=,由几何概型的公式可得20x y ->的概率为:55248=;【详解】约束条件1030x y x y x --≤⎧⎪+≤⎨⎪>⎩的可行域如图:由103x y x y --=⎧+=⎨⎩解得()2,1A , 可行域d 面积为12442⨯⨯=, 由32x y y x +=⎧=⎨⎩,解得()1.2B . 满足20x y ->的区域为图形中的红色直线的下方的四边形,其面积为1541322-⨯⨯=, 由几何概型的公式可得20x y ->的概率为:55248=;故答案为58.【点睛】本题考查了可行域的画法以及几何概型的概率公式的运用.考查数形结合以及计算能力.在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的,而对于角度而言,则是过角的顶点的一条射线落在Ω的区域(事实也是角)任一位置是等可能的.17.【解析】分析:由题意首先确定样本中心点然后结合回归方程过样本中心点整理计算即可求得最终结果详解:由题意可得:回归方程过样本中心点则:即:整理可得:故答案为:270点睛:(1)正确理解计算的公式和准确解析:【解析】分析:由题意首先确定样本中心点,然后结合回归方程过样本中心点整理计算即可求得最终结果.详解:由题意可得:91412244c c x ++-+==,1848309644d dy ++++==, 回归方程过样本中心点,则:962236044d c ++=⨯-,即:()96322240d c +=+-, 整理可得:3270c d -=. 故答案为:270.点睛:(1)正确理解计算$,ba $的公式和准确的计算是求线性回归方程的关键. (2)回归直线方程y bx a =+$$$必过样本点中心(),x y .(3)在分析两个变量的相关关系时,可根据样本数据作出散点图来确定两个变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程来估计和预测.18.【解析】【分析】【详解】每个同学都有三种选择:跳高与跳远;跳高与铅球;跳远与铅球三个同学共有3×3×3=27种有且仅有两人选择的项目完全相同有种其中表示3个同学中选2个同学选择的项目表示从三种组合中解析:23【解析】 【分析】 【详解】每个同学都有三种选择:跳高与跳远;跳高与铅球;跳远与铅球三个同学共有3×3×3=27种,有且仅有两人选择的项目完全相同有21133218C C C ⨯⨯=种,其中23C 表示3个同学中选2个同学选择的项目,13C 表示从三种组合中选一个,12C 表示剩下的一个同学有2中选择,故有且仅有两人选择的项目完全相同的概率是182273=. 考点:古典概型及其概率计算公式.19.3【解析】分析:根据分层抽样的方法各组抽取数按比例分配详解:根据分层抽样的方法乙组中应抽取的城市数为点睛:本题考查分层抽样概念并会根据比例关系确定各组抽取数解析:3 【解析】分析:根据分层抽样的方法,各组抽取数按比例分配. 详解:根据分层抽样的方法,乙组中应抽取的城市数为126=34+12+8⨯. 点睛:本题考查分层抽样概念,并会根据比例关系确定各组抽取数.20.-029【解析】所以残差是解析:-0.29【解析】0.8516082.71ˆ53.29y=⨯-= ,所以残差是5353.290.29.-=- 三、解答题21.(1)$1.2 3.6y t =+ (2)2014年至2018年该地区农村居民家庭人均纯收入逐年增加,平均每年增加1.2千元;10.8千元 【解析】 【分析】(1)根据所给数据利用公式计算,t ,y ,()51=-∑ii tt ,()()51=--∑i ii t ty y ,然后代入()()()1211==--=-∑∑$niii ni tty y btt,a y bt =-$$求解,再写出回归方程.(2)根据(1)的结果,由b$的正负来判断,将6t =,代入回归方程,预测该地区2019年农村居民家庭人均纯收入. 【详解】(1)由所给数据计算得()11234535t =⨯++++=, ()15678107.25y =⨯++++=,()514101410ii tt =-=++++=∑, ()()()()()()()512 2.21 1.200.210.82 2.812iii tty y =--=-⨯-+-⨯-+⨯-+⨯+⨯=∑()()()1211121.210niii ni tty y bt t==--===-∑∑$, $7.2 1.23 3.6ay bt =-=-⨯=$, 所求回归方程为$1.2 3.6y t =+.(2)由(1)知, 1.20b=>$,故2014年至2018年该地区农村居民家庭人均纯收入逐年增加,平均每年增加1.2千元.2019年时6t =,$1.26 3.610.8y =⨯+=,故预测该地区2019年农村居民家庭人均纯收入约为10.8千元. 【点睛】本题主要考查线性回归分析,还考查了运算求解的能力,属于中档题. 22.(1) 0.035a = (2) 2150(3)()12.5E X =【解析】试题分析:(1)由频率分布直方图求出a 的值;(2)设从12人中随机抽取3人,第1组已被抽到1人为事件A ,第3组抽到2人为事件B ,由条件概率公式得到所求概率;(3)X 的可能取值为0,1,2,3,求出相应的概率值,从而得到X 的分布列与期望. 试题解析:(1)由()100.0100.0150.0300.0101a ⨯++++=,得0.035a =,(2)第1,2,3组的人数分别为20人,30人,70人,从第1,2,3组中用分层抽样的方法抽取12人,则第1,2,3组抽取的人数分别为2人,3人,7人.设从12人中随机抽取3人,第1组已被抽到1人为事件A ,第3组抽到2人为事件B ,则()()()1227312122121021031221|.50C C P AB C P B A C C C C P A C ===+ (3)从所有参与调查的人中任意选出1人,关注“生态文明”的 概率为4,5P =X 的可能取值为0,1,2,3. ()30341015125P X C ⎛⎫∴==-= ⎪⎝⎭,()121344121155125P X C ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭ ()212344482155125P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭,()33346435125P X C ⎛⎫=== ⎪⎝⎭所以X 的分布列为4~3,5X B ⎛⎫⎪⎝⎭Q ,()4123.55E X np ==⨯=23.(1)$4106y x =-+;(2)45. 【解析】 【分析】(1)根据所给数据计算回归方程中的系数,得回归方程;(2)由回归方程计算每个销量的估计值,确定“好数据”的个数,然后确定基本事件的个数后可求得概率. 【详解】 (1)由已知4567896.56x +++++==,1221ni ii ni i x y nx ybx nx==-=-∑∑$222222230506 6.5804(456789)6 6.5-⨯⨯==-+++++-⨯,$80(4) 6.5106a=--⨯=, ∴所求回归直线方程为$4106y x =-+.(2)由(1)4x =时,µ190y =,25x =时,µ286y =,36x =时,µ382y =,47x =时,µ478y =,58x =时,µ574y =,69x =时,µ670y =, 与销售数据比较,“好数据”有3个,(4,90),(6,82),(8,74), 从6个数据中任取2个的所有可能结果共有652⨯=15种,其中2个数据中至少有一个是“好数据”的结果有33312⨯+=种, 所求概率为124155P ==. 【点睛】本题考查线性回归直线方程,考查古典概型.解题时根据所给数据计算回归方程的系数,考查了学生的运算求解能力与数据处理能力. 24.(1)390019;(2)答案见解析;(3)答案见解析. 【解析】 【分析】(1)由题意得到关于中位数的方程,解方程可得乙流水线生产产品该质量指标值的中位数;(2)求出甲,乙两条流水线生产的不合格的概率,即可得出结论; (3)计算可得2K 的近似值,结合参考数值可得结论. 【详解】(1)设乙流水线生产产品的该项质量指标值的中位数为x , 因为()()0.480.0120.0320.05250.50.0120.0320.0520.07650.86=++⨯<<+++⨯=,则()()0.0120.0320.05250.0762050.5x ++⨯+⨯-=, 解得390019x =. (2)由甲,乙两条流水线各抽取的50件产品可得,甲流水线生产的不合格品有15件, 则甲流水线生产的产品为不合格品的概率为1535010P ==甲, 乙流水线生产的产品为不合格品的概率为()10.0120.02855P =+⨯=乙,于是,若某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线生产的不合格品件数分别为315000150050001000105⨯=⨯=,; (3)2×2列联表:则2100(350600)41.3505075253K ⨯-==≈⨯⨯⨯,因为1.3<2.072,所以没有85%的把握认为“该企业生产的这种产品的该项质量指标值与甲,乙两条流水线的选择有关”. 【点睛】本题主要考查频率分布直方图计算中位数的方法,独立性检验的应用,古典概型计算公式及其应用等知识,意在考查学生的转化能力和计算求解能力. 25.(1)2名;(2)35【解析】 【分析】(1)根据分层抽样的比例关系计算得到答案.(2)记在[)35,40中选取2名教师代表为a ,b ,其余的4名代表为A 、B 、C 、D ,列出所有情况和满足条件的情况,相除得到答案. 【详解】(1)由频率分布直方图得:年龄在[)30,35的教师有1000.06530⨯⨯=, 年龄在[)35,40的教师有1000.04520⨯⨯=, 年龄在[]40,45的教师有1000.02510⨯⨯=, 设年龄在[)35,40的教师代表人数为x ,则66020x =,∴2x = ∴从年龄在[)35,40中选取教师代表人数为2名;(2)记在[)35,40中选取2名教师代表为a ,b ,其余的4名代表为A 、B 、C 、D 从这6名教师中选2名教师的选法为: ab ,aA ,aB ,aC ,aD , bA ,bB ,bC ,bD ,AB ,AC ,AD ,BC ,BD ,CD以上共15种在[)35,40中至少有一名教师被选中的选法为:ab ,aA ,aB ,aC ,aD ,bA ,bB ,bC ,bD以上9种在[)35,40中至少有一名教师被选中为事件A ,则()93155P A ==. ∴在[35,40)中至少有一名教师被选中的概率为35. 【点睛】本题考查了频率直方图,分层抽样,概率的计算,意在考查学生的综合应用能力.26.(1)0.02x =,74,2203;(2)1200;(3)1920. 【解析】【分析】(1)根据频率和为1可求得第第4组的频率,由此求得x 的值;根据频率分布直方图中平均数和中位数的估计方法可计算得到结果;(2)计算得到50名学生中成绩不低于70分的频率,根据样本估计总体的方法,利用总数⨯频率可得所求人数;(3)根据分层抽样原则确定[)70,80、[)80,90和[]90,100种分别抽取的人数,采用列举法列出所有结果,从而可知成绩在[]80,100的学生没人被抽到的概率;根据对立事件概率公式可求得结果.【详解】(1)由频率分布直方图可得第4组的频率为:()10.010.030.030.01100.2-+++⨯= 0.2100.02x ∴=÷=估计所抽取的50名学生成绩的平均数为:()550.01650.03750.03850.02950.011074⨯+⨯+⨯+⨯+⨯⨯=由于前两组的频率之和为0.10.30.4+=,前三组的频率之和为0.10.30.30.7++= ∴中位数在第3组中设中位数为t ,则有:()700.030.1t -⨯=,解得:2203t =即所求的中位数为2203(2)由(1)知:50名学生中成绩不低于70分的频率为:0.30.20.10.6++=用样本估计总体,可以估计高三年级2000名学生中成绩不低于70分的人数为:20000.61200⨯=(3)由(1)可知,后三组中的人数分别为15,10,5∴这三组中所抽取的人数分别为3,2,1记成绩在[)70,80的3名学生分别为,,a b c ,成绩在[)80,90的2名学生分别为,d e ,成绩在[]90,100的1名学生为f ,则从中随机抽取3人的所有可能结果为:(),,a b c ,(),,a b d ,(),,a b e ,(),,a b f ,(),,a c d ,(),,a c e ,(),,a c f ,(),,a d e ,(),,a d f ,(),,a e f ,(),,b c d ,(),,b c e ,(),,b c f ,(),,b d e ,(),,b d f ,(),,b e f ,(),,c d e ,(),,c d f ,(),,c e f ,(),,d e f ,共20种其中成绩在[]80,100的学生没人被抽到的可能结果为(),,a b c ,只有1种,故成绩在[]80,100的学生至少有1人被抽到的概率:11912020P =-= 【点睛】本题考查利用频率分布直方图计算频率、频数、估计平均数、中位数的问题,分层抽样、古典概型概率问题的求解;考查学生对于统计和概率部分知识的综合掌握情况,属于常考题型.。
湖北省部分中学2020年秋高二数学上学期期中联考试卷附答案解析

D.
0,1 2
二、选择题:本题共 4 小题,每小题 5 分,共 20 分,在每小题给出的选项中有多项符合题目要求,全部选 对的得 5 分,有选错的得 0 分,部分选对的得 3 分
9.下列说法正确的是( )
A.命题“ x R , x2 1 ”的否定是“ x0 R , x02 1”
B.命题“ x0 (3, ) , x02 9 ”的否定是“ x (3, ) , x2 9 ” C.“ m 0 ”是“关于 x 的方程 x2 2x m 0 有一正一负根”的充分不必要条件 D.“ a 5 ”是命题“ x R, x2 ax a 0 ”为假命题的充分不必要条件
湖北省部分中学 2020 年秋高二数学上学期期中联考试卷
第 I 卷(选择题)
一、选择题:本题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中只有一项是符合题目要 求的
1.已知点 A(-3, 2) , B(0, 1) ,则直线 AB 的倾斜角为( )
A. 300
B. 450
C.1350
10.抛掷一枚骰子 1 次,记“向上的点数是 4,5,6”为事件 A,“向上的点数是 1,2”为事件 B,“向上的点 数是 1,2,3”为事件 C,“向上的点数是 1,2,3,4”为事件 D,则下列关于事件 A,B,C,D 判断正确的是 ()
A.A 与 B 是互斥事件但不是对立事件
B.A 与 C 是互斥事件也是对立事件
所以“ m ”是“ m l ”的充要条件 故选 C
5.【答案】B
【解析】由圆的几何性质两圆在点 A 处的切线互相垂直,且过对方圆心 O2O1.则
在 Rt△O2AO1 中,|O1A|= 5 |O2A|= 20 ,斜边上的高为半弦,用等积法易 得: AB 5 5 20 ⇒|AB|=4.故答案为:B
福建师范大学附属中学2020-2021学年上学期期中考模拟试卷高二数学(实验班)试题及答案

绝密★启用前福建师大附中2020-2021 学年上学期期中考模拟试卷高二数学(实验班)第I 卷(选择题,共64 分)一、单项选择题:每小题6 分,共48 分.在每小题给出的选项中,只有一个选项是正确的.1. 已知α, β∈ (0, π),则“sin α + sin β < 1”是“sin(α + β) < 1”的( ▲)3 3A. 充分不必要条件B. 必要不充分条件C. 充分且必要条件D. 既不充分也不必要条件2. 已知直线l: x sin α + y cos α = 1 (0 ≤ α < 2π) 与圆C: (x− 2)2 + (y− √5)2 = 4 相切,则满足条件的α的个数为( ▲)A. 1B. 2C. 3D. 43. 已知圆C : (x + 2a)2+ y2 = 4 与圆C : x2 + (y− b)2= 1 有且仅有1 条公切线,则 1 + 1的最小1 2值为( ▲)a2b2A. 6B. 7C. 8D. 94. 已知点M(x, y) 在曲线C: x2 + y2− 4x− 21 = 0 上运动,设t = x2 + y2 + 12x− 12y− 150 − a,且t的最大值为b,若a, b > 0,则 1 + 1a+1 b的最小值为( ▲)A. 1B. 2C. 3D. 45. 如图所示,两半径相等的圆A, B相交,CD为它们的公切线段,且两块阴影部分面积相等,在线段AB上任取一点M,则M在线段EF上的概率为( ▲)A. 1 −π4 B. 2 − π2C. 2− 1D. 4− 1ππx + y− 2 ≤ 06. 已知区域D = {(x, y)| { x− y + 2 ≤ 0 },给定下列四个命题:3x− y + 6 ≥ 0p1: ∀(x, y) ∈ D, x + y + 1 ≥ 0 p2: ∀(x, y) ∈ D, 2x− y + 2 ≤ 0 p : ∃(x, y) ∈ D, y+1 ≤−4 p : ∃(x, y) ∈ D, x2 + y2≤ 23 x−1 4则下列选项中是真命题的为( ▲)A. p1 ∧p3B. p2 ∧p4C. p1 ∧p4D. p2 ∧p37. 已知在△ ABC内有一点O满足∠OAB = ∠OAC = ∠OBC = ∠OCA = α,给定下列两个命题:p: 存在点O使得α≥ 36°q: 对于任意的点O总有c, a, b成等比数列则下列选项中是真命题的为( ▲)A. p∧qB. p∧(¬q)C. (¬p) ∧qD. (¬p) ∧(¬q)8. 在平面直角坐标系中,定义d(A, B) = max{|x1 −x2|, |y1 −y2|} 为两点A(x1, y1), B(x2, y2) 的“切比雪夫距离”,并对于点P与直线l上任意一点Q,称d(P, Q) 的最小值为点P与直线l间的“切比雪夫距离”,记作d(P, l),给定下列四个命题:p1: 对于任意的三点A, B, C,总有d(C, A) + d(C, B) ≥ d(A, B)p : 若点P(3, 1),直线l: 2x− y− 1 = 0,则d(P, l) = 42 3p3: 满足d(O, M) = C(C > 0) 的点M的轨迹为正方形p4: 若点F1(−c, 0), F2(c, 0),则满足|d(P, F1) −d(P, F2)| = 2a(2c > 2a > 0) 的点M的轨迹与直线y = k (k为常数) 有且仅有2 个公共点则下列选项中真命题的个数为( ▲)A. 1B. 2C. 3D. 4二、多项选择题:每小题6 分,共12 分.在每小题给出的选项中,正确选项不少于2 个,全部选对得6 分,选对但不全得3 分,有选错得0 分.9.在平面直角坐标系中,直线l: y = k(x− 2) + 3 与坐标轴分别交于点A, B,则下列选项中是真命题的有( ▲ )A.存在正实数m使得△ OAB面积为m的直线l恰有一条B.存在正实数m使得△ OAB面积为m的直线l恰有二条C.存在正实数m使得△ OAB面积为m的直线l恰有三条D.存在正实数m使得△ OAB面积为m的直线l恰有四条10.下列选项中说法正确的有( ▲ )A. “若点(2, 1) 在圆x2 + y2 + kx + 2y + k2− 15 = 0 外,则k < −4 或k > 2”的否命题B. 已知直线y = kx与圆(x + cos θ)2+ (y− sin θ)2= 1,∀θ∈ ℝ,总有k使得直线与圆恒相切C. 已知直线y = kx与圆(x + cos θ)2+ (y− sin θ)2= 1,∀k∈ ℝ,总有θ使得直线与圆恒相切D. 过直线2x + y + 4 = 0 上的动点P引圆C: x2 + y2− 2y = 1 的两条切线,A, B为切点,则四边形PACB面积的最小值为2√2第II 卷(非选择题,共86 分)三、填空题:每小题 6 分,共24 分.11.已知五个互不相等的样本x1, x2, x3, x4, x5 ∈ℕ,它们的平均数为7,标准差为2,则样本数据中最大值为▲.12. 已知点A(x1, y1), B(x2, y2) 是曲线x2 + y2− 2x + 4y = 0 上的两点,则|x1y2 −x2y1| 的最大值为▲.13. 已知区域D表示不在直线(1 − m2)x + 2my = 2 + 2√3m(m∈ ℝ) 上的点构成的集合,在区域D内任取一点P(x, y),则√x+的取值范围为▲.√x2+y214. 已知在平面内有P1, P2, … , P n共n个点,若在该平面内有点P到P1, P2, … , P n的距离之和最小,则称点P为点P1, P2, … , P n的一个“中位点”,给定下列四个命题:p1: 若三点A, B, C共线,且C在线段AB上,则C是A, B, C的“中位点”p2: 若四点A, B, C, D共线,则它们的“中位点”存在且唯一p3: 直角三角形的斜边中点是该直角三角形三个顶点的“中位点”p4: 梯形对角线交点是梯形四个顶点的唯一“中位点”则上述命题中真命题有▲.(写出所有真命题的序号)四、解答题:4 小题,共66 分.解答应写出文字说明、证明过程或演算步骤.15. (16 分)已知圆M: (x− 2)2+ y2 = 1,过直线l: x = −1 上一动点P作圆的两条切线,切点分别为A, B.(I)当有一条切线于坐标轴平行时,求另一条切线的方程;(II)当圆切点弦所对的圆心角最小时,求|AB| 的值;(III) 记切线PA, PB分别交y轴于点S, T,求|ST| 的最小值.16. (16 分)若过点P的两直线l1, l2斜率之积为λ(λ≠ 0),则称直线l1, l2是一组“Pλ共轭线对”.(I) 若直线l1, l2是一组“O−3共轭线对”,当两直线夹角最小时,求两直线倾斜角;(II) 若点A(0, 1), B(−1, 0), C(1, 0) 分别是直线PQ, QR, RP上的点(A, B, C, P, Q, R均不重合),且直线PR, PQ是一组“P1 共轭线对”,直线QP, QR是一组“Q4 共轭线对”,直线RP, RQ是一组“R9 共轭线对”,求点P的坐标;(III) 若直线l1, l2是一组“M−2共轭线对”,其中点M(−1, −√2),当两直线旋转时,求原点到两直线距离之积的取值范围.17. (18 分)疫苗能够使人体获得对病毒的免疫力,是保护健康人群最有效的手段.新冠肺炎疫情发生以来, 军事医学科学院陈薇院土领衔的团队开展应急科研攻关,研制的重组新型冠状病毒疫苗(腺病毒载体),于 4 月 12 日开始招募志愿者,进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体, 人体中检测到抗体,说明有抵御病毒的能力.科研人员要定期从接种疫苗的志愿者身上采集血液样本, 检测人体中抗体含量水平(单位:miu /mL ,百万国际单位/毫升).(I) IgM 作为人体中首先快速产生的抗体,是人体抗感染免疫的“先头部队”.经采样分折,志愿者身体中 IgM 含量水平 y (miu /mL ) 与接种天数 x (接种后每满 24 小时为一天,x ∈ ℕ∗)近似满足函数 关系:y = { 0.1x , x ≤ 10.经研究表明,IgM 含量水平不低于 0.2miu /mL 时是免疫的有效时段,试e 10−x , x > 10 估计接种一次后IgM 含量水平有效时段可经历的时间(向下取整).(参考数据:e ≈ 2.718) (II) IgG 虽然是接种后产生比较慢的抗体,却是血清和体液中含量最高的抗体,也是亲和力最强、人体内分布最广泛、具有免疫效应的抗感染“主力军”.科研人员每间隔 3 天检测一次(检测次数依次记为 t i , i = 1, 2, 3, 4, 5, 6, 7)某志愿者人体中 IgG 的含量水平,记作 z i (miu /mL ) (i = 1, 2, 3, 4, 5, 6, 7),得到相关数据如下表:(i) 请画出散点图,并根据散点图判断,线性拟合模型 z = a + bt 与指数拟合模型 z = c ∙ d t 哪种更适合拟合 z 与 t 的关系(不必说明理由);(ii) 研究人员发现,上述数据中存在一组异常数据应当予以剔除.试根据余下的六组数据,利用(i)中选择的拟合模型计算回归方程,并估计原异常数据对应的 z i 值.(回归系数与估计值均保留两位小数,由七组数据计算出的参考数据见下表,其中 u = ln z )参考公式:线性回归直线 y = a + bx 的斜率和截距的最小二乘估计分别为 b= ∑(x i − x̅)(y i − y ),a = y − bx̅ ∑(x i − x̅)218. (16 分)某科研团队发现了一种新型单细胞生物,在长时间观测后,科研团队发现每个活细胞在每一分钟内都会独立且等可能地发生以下四件事中的一件:①死亡;②保持原状;③分裂成两个活细胞;④分裂成三个活细胞.若初始时在一条件适宜的孤立系统中放置两个活细胞,试计算理论上在无限长时间后该系统中仍有活细胞存活的概率.( )绝密★启用前福建师大附中 2020-2021 学年上学期期中考模拟试卷高二数学(实验班)答案第 I 卷(选择题,共 64 分)一、单项选择题:每小题 6 分,共 48 分.在每小题给出的选项中,只有一个选项是正确的.二、多项选择题:每小题 6 分,共 12 分.在每小题给出的选项中,正确选项不少于 2 个,全部选对得 6 分,选对但不全得 3 分,有选错得 0 分.第 II 卷(非选择题,共 86 分)三、填空题:每小题 6 分,共 24 分.四、解答题:4 小题,共 66 分.解答应写出文字说明、证明过程或演算步骤.15. 解:(I) 3x + 4y − 1 = 0 或 3x − 4y − 1 = 0(II) |AB |min =4√23(III) |ST |min =√2216. 解:(I)π , 2π(II) P (3, 3) 或 P 3 ,3(III) d d∈ [0, √2)3 35 51 217. 解:(I) 9 天(II) (i) 指数拟合模型 z = c ∙ d t(ii) ẑ = 0.06 × 2.27t ;z 4 = 1.5518. 解:2√2 − 2。
浙江省9 1高中联盟2020-2021学年高二上学期期中考试数学试题 Word版含答案

2020学年第一学期9+1高中联盟期中考试高二年级数学学科试题第Ⅰ卷(选择题 共40分)一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.直线3y =+的倾斜角为( )A . 30°B . 60°C . 120°D .150°2. 已知直线1:10l mx y +-=,()2:2310l m x my ++-=,m R ∈,则“2m =-”是“12l l ⊥”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件3.椭圆2241x y +=的离心率为 ( )A .34 B C . 23D .4. 在空间直角坐标系中,已知()()1,0,2,3,2,4M N --,则MN 的中点Q 关于平面xOy 的对称点坐标是( )A .()1,1,1-B .()1,1,1--C . ()1,1,1--D .()1,1,1 5. 已知m 为空间的一条直线,,αβ为两个不同的平面,则下列说法正确的是( ) A .若//,//m ααβ,则//m β B .若,m αβα⊥⊥,则//m β C . 若//,m ααβ⊥,则m β⊥ D .若,//m ααβ⊥,则m β⊥6. 方程2x =所表示的曲线大致形状为( )A .B .C .D .7. 已知点F 为椭圆221:+184x y C =的右焦点,点P 为椭圆1C 与圆()222:218C x y ++=的一个交点,则PF =( )A . 1BC . 2D .8. 设有一组圆()()()224*:1k C x y k k k N -+-=∈,给出下列四个命题:①存在k ,使圆与x 轴相切 ②存在一条直线与所有的圆均相交 ③存在一条直线与所有的圆均不相交 ④所有的圆均不经过原点 其中正确的命题序号是( )A .①②③B .②③④C .①②④D .①③④9. 若三棱锥P ABC -满足,,,PA BC PB AC PC AB ===,则该三棱锥可能是( ) A .2,3,4AB BC CA === B .3,4,5AB BC CA === C . 4,5,6AB BC CA === D .以上选项都不可能10. 如图,在棱长为1的正方体中1111ABCD A B C D -,若点,M N 分别为线段1BD ,1CB 上的动点,点P 为底面ABCD 上的动点,则MN MP +的最小值为( )A .23B .CD .1第Ⅱ卷(非选择题 共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.已知直线():10l mx y m m R ++-=∈过定点P ,则点P 的坐标是___________,点P 关于直线20x y +-=的对称点Q 的坐标是__________.12.某几何体的三视图如图所示,其中俯视图中的圆弧为14圆周,则该几何体的体积为__________,表面积为___________.13.已知(),P m n 是椭圆2214x y +=上的动点,则23m n +的最大值是 ,点P 到直线:20l x y -+=的最小距离是___________.14.如图,在三棱锥P ABC -中,点B 在以AC 为直径的圆上运动,PA ⊥平面ABC ,AD PB ⊥,垂足为D ,DE PC ⊥,垂足为E ,若2PA AC ==,则PEEC= ,三棱锥P ADE -体积的最大值是__________.15.经过点()2,1M -作圆22:5O x y +=的切线,则切线的方程为 .16.已知正三棱柱111ABC A B C -的棱长均为2,则异面直线AB 与1A C 所成角的余弦值为 .17.已知O 为坐标原点,12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左右焦点,A 为椭圆的右顶点,P为C 上一点,且2PF x ⊥轴,过点A 的直线l 与线段2PF 交于点M ,与y 轴交于点N ,若直线1F M 与y 轴交于点Q ,且3ON OQ =,则C 的离心率为___________.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18. 已知m R ∈,命题:p 方程22119x y m m+=+-表示焦点在y 轴上的椭圆;命题:q 函数()2f x x x m =-+在[]2,2-上有零点.(1)若命题p 是真命题,求实数的取值范围;(2)若命题,p q 中有且只有一个真命题,求实数m 的取值范围. 19. 如图,三棱柱111ABC A B C -的棱长均相等,113CC B π∠=,平面ABC ⊥平面11BCC B ,,E F 分别为棱11A B 、BC 的中点.(1)求证://BE 平面11A FC ; (2)求二面角111F AC B --的大小.20. 如图,已知三棱锥A BCD -中,点M 在BD 上,2BAD BDC π∠=∠=,BM MD DC ==,且ACD∆为正三角形.(1)证明:CM AD ⊥;(2)求直线CM 与平面ACD 所成角的正弦值.21.如图,已知圆()()221:112C x y -++=,圆()()222:215C x y +++=,过原点O 的直线l 与圆1C ,2C 的交点依次是,,P O Q .(1)若2OQ OP =,求直线l 的方程;(2)若线段PQ 的中点为M ,求点M 的轨迹方程.22.如图,已知椭圆22:143x y Γ+=,斜率为k 的直线l 与椭圆Γ交于,A B 两点,过线段AB 的中点M 作AB 的垂线交y 轴于点C .(1)设直线,OA OB 的斜率分别为12,k k ,若1k =,直线l 经过椭圆Γ的左焦点,求1211k k +的值; (2)若AB =23,14k ⎡⎤∈⎢⎥⎣⎦,求OMC ∆面积的取值范围.试卷答案一、选择题1-5:CABDD 6-10:DBCCA 二、填空题11. ()()1,1,1,3- 12. 26π+,)144π+13. 5,5 14. 3,3415. 250x y -+=16. 4 17. 13三、解答题18.解:(1)命题:91014p m m m ->+>⇒-<<, 即实数m 的取值范围为()1,4-;(2)命题p 真:[]2,2x ∈-时,216,4m x x ⎡⎤=-∈-⎢⎥⎣⎦,p 真q 假时1,44m ⎛⎫∈ ⎪⎝⎭,p 假q 真时[]6,1m ∈--,∴[]16,1,44m ⎛⎫∈--⋃ ⎪⎝⎭. 19.证明:(1)取11A C 的中点G ,连接,EG FG , 于是111//2EG B C ,又111//2BF B C , 所以//BF EG ,所以四边形BFGE 是平行四边形,所以//BE FG ,而BE ⊄面11A FC ,FG ⊆面11A FC , 所以直线//BE 平面11A FC ;(2)连接11,FB B G ,∵ 四边形11BCC B 为菱形,01160CC B ∠=,F 为BC 的中点,∴111FB B C ⊥,∵平面ABC ⊥平面11BCC B ,∴1FB ⊥平面111A B C ,又111B G AC ⊥,∴11FG A C ⊥, ∴1FGB ∠就是二面角11F A C B --的平面角,设棱长为2,则11FB BG ==14FGB π∠=,∴二面角11F A C B --的大小为4π. 20.解:(1)取AD 中点P ,连结,MP CP ,由条件CP AD ⊥, 又由,//2BAD MP AB π∠=得MP AD ⊥,∴AD ⊥面CMP ,又∵CM ⊂面MPC ,∴CM AD ⊥;(2)过M 作MH CP ⊥于点H ,由(1)可知,AD MH ⊥,∴MH ⊥面ACD , ∴MCP ∠即为直线CM 与面ACD 所成的角, 不妨设1CD =,则CM MP CP ===,∴cos MCP ∠==∴sin 3MCP ∠=所以直线CM 与平面ACD21.解:(1)设直线l 的方程为:y kx =,12,C C 到直线l 的距离为12,d d .由条件=221243d d -=,所以2243⨯-=,整理,得240k k -=,解得0k =或4k =, 所以直线l 的方程为:0y =或4y x =;(2)设:l y kx =;则由()()22215y kx x y =⎧⎪⎨+++=⎪⎩消去y ,得()()221240k x k x +++=, 解得122240,1k x x k+==-+.其中2k ≠-, 所以()222424,11k k k Q k k +⎛⎫+-- ⎪++⎝⎭, 由()()22112y kx x y =⎧⎪⎨-++=⎪⎩消去y ,得()()221220k x k x ++-=, 解得342220,1kx x k -==+,其中1k ≠,所以()222222,11k k k P k k -⎛⎫- ⎪++⎝⎭, 设(),M x y ,则()22211211k x k k k y k +⎧=-⎪+⎪⎨+⎪=-⎪+⎩消去k ,得:2220x y x y +++=,(挖去点33,22⎛⎫-- ⎪⎝⎭和36,55⎛⎫- ⎪⎝⎭). 22.解:(1)由已知可得直线l 的方程为:1y x =+,设()()1122,,,A x y B x y ,由221143y x x y =+⎧⎪⎨+=⎪⎩得:27880x x +-=,且121288,77x x x x +=-=-,所以12121212121212121221181113x x x x x x x x k k y y x x x x x x +++=+=+==+++++;(2)设直线l 的方程为:y kx m =+,()()1122,,,A x y B x y ,由22143y kx m x y =+⎧⎪⎨+=⎪⎩,得:()2224384120k x kmx m +++-=,由韦达定理可知21212228412,4343km m x x x x k k -+=-=++, 所以2443M kmx k =-+, 线段AB 的中垂线方程为:221434343km m y x k k k ⎛⎫=-++ ⎪++⎝⎭,整理得2143my x k m =--+, 所以243C my k =-+.又由()222221212228412414234343km m AB x x x x k k k -⎛⎫=+-=+--= ⎪++⎝⎭, 整理可得:2224343k k +-=+,即()222224314341k m k k +=+-+①, 所以()22222411222434343OMD M km m k S OC x m k k k ∆===+++将①代入整理可得:2211112231432124OMC kk S k k k k k k∆=-=-++++, 因为23,14k ⎡⎤∈⎢⎥⎣⎦,所以2k ⎤∈⎥⎣⎦,而我们知道,1112,3124y y k k kk==-++都是关于k 在2⎤⎥⎣⎦上的单调递减函数,所以当1k =时,OMC S ∆有最小值128,当k =时,OMC S ∆所以1,2842OMC S ∆⎡∈⎢⎣⎦.。
湖北省2020学年高二数学上学期期中试题(含解析)

高二数学上学期期中试题(含解析)一、选择题(本大题共12小题)1.已知命题:0P x ∀>,总有(1)1xx e +>,则p ⌝为( )A. 00x ∃≤ 使得00(1)xx e +1≤B. 00x ∃> 使得00(1)xx e +1≤C. 0x ∀> 总有(1)1xx e +≤ D. 0x ∀≤,总有(1)1xx e +≤【答案】B 【解析】 【分析】利用全称命题的否定解答即得解.【详解】根据全称命题的否定为特称命题可知,¬p 为∃x 0>0,使得(x 0+1)0e x ≤1, 故选B .【点睛】本题主要考查全称命题的否定,意在考查学生对该知识的理解掌握水平.2.一直平面内的定点A ,B 和动点P ,则“动点P 到两定点A ,B 的距离之和为为一定值”是动点P 的轨迹是以A ,B 为焦点的椭圆的( ) A. 必要不充分条件 B. 充分不必要条件 C. 充要条件 D. 既不充分也不必要【答案】A 【解析】 【分析】结合椭圆的定义,利用充分条件和必要条件的定义进行判断.【详解】若点P 的轨迹是以A 、B 为焦点的椭圆,则根据椭圆的定义可知动点P 到两定点A ,B 的距离之和2PA PB a += (0a >,且a 为常数)成立是定值.若动点P 到两定点A ,B 的距离之和2PA PB a += (0a >,且a 为常数),当2a AB ≤,此时的轨迹不是椭圆.∴“动点P 到两定点A ,B 的距离之和为为一定值”是动点P 的轨迹是以A ,B 为焦点的椭圆的必要不充分条件. 故选:A【点睛】本题主要考查充分条件和必要条件的判断,结合椭圆的定义是解决本题的关键. 3.直线l 经过2(2,1),(3,)()A B t t R ∈两点,则直线l 的倾斜角的取值范围是( )A. π[0,)2∪3[,)4ππ B. [0,π) C. [0,]4πD. [0,]4π∪(,)2ππ【答案】A 【解析】 【分析】 先通过2121y y k x x -=-求出两点的斜率,再通过tan k α=求出倾斜角α的值取值范围.【详解】2213tan 1,,tan [1,[0,)2)[,)324t k t t R παααππ-===-∈⇒∈-+∞⋃⇒∈-故选A.【点睛】已知直线上两点求斜率利用公式2121tan y y x x α-=-.需要注意的是斜率不存在的情况.4.已知直线y kx b =+沿x 轴负方向平移3个单位长度,再沿y 轴正方向平移1个单位长度后,又回到原位置,则斜率k =( ). A. 13- B. 3-C.13D. 3【答案】A 【解析】 【分析】由函数图像的平移,求平移后的解析式,再求参数的值即可.【详解】解:将直线y kx b =+沿x 轴负方向平移3个单位长度,再沿y 轴正方向平移1个单位长度后,所得直线方程为(3)131y k x b kx b k =+++=+++ , 由题意可知310k +=,解得13k =-, 故选A.【点睛】本题考查了函数图像的平移,属基础题.5.已知椭圆22221(0)x y a b a b+=>>的短轴长为4,上顶点A ,左顶点B ,焦点1F ,2F 分别是椭圆左右焦点,且1F AB的面积为4- )B.C.D.【答案】C 【解析】 【分析】由题意可知2b =,且()142S a c b =-=-,列方程组求2c . 【详解】解:椭圆22221(0)x y a b a b+=>>的短轴长为4,可得2b =,上顶点A ,左顶点B ,焦点1F ,2F 分别是椭圆左右焦点,且1F AB的面积为4-, 可得()142a c b -=-()1242a c -⨯=-4a c -=-224a c -=,可得4a =,c =,椭圆的焦距为: 故选:C【点睛】本题考查椭圆的简单性质的应用,是基本知识的考查,是基础题.6.已知实数,x y 满足{0134x y x y≥≥+≤,则231x y x +++的取值范围是( )A. 2[,11]3B. [3,11]C. 3[,11]2D. [1,11]【答案】C 【解析】232(1)1.11x y y x x +++=+++其中11y x ++表示两点(,)x y 与(1,1)--所确定直线的斜率,由图知,min max 10114,5,13410PB PA k k k k ----======----所以11y x ++的取值范围是1[,5],4231x y x +++的取值范围是3[,11].2选C.7.过点作圆224x y +=的两条切线,切点分别为A 、B ,O 为坐标原点,则OAB ∆的外接圆方程是A. 22(2)(1)5x y -+-= B. 22(4)(2)20x y -+-= C. 22(2)(1)5x y +++= D. 22(4)(2)20x y +++=【答案】A 【解析】【详解】由题意知,OA⊥PA,BO⊥PB, ∴四边形AOBP 有一组对角都等于90°, ∴四边形AOBP 的四个顶点在同一个圆上,所以此圆的直径是OP ,OP 的中点为(2,1),5, ∴四边形AOBP 的外接圆的方程为22(2)(1)5x y -+-=, ∴△AOB 外接圆的方程为22(2)(1)5x y -+-=, 故选 A .8.椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ,以2F 为圆心的圆过椭圆的中心,且与椭圆交于点P ,若直线1PF 恰好与圆2F 相切于点P ,则椭圆的离心率为( )31+ 31C.2251- 【答案】B 【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=,又1PF 恰好与圆2F 相切于点P ,可知2||PF c =且12PF PF ⊥,即可列出方程求椭圆的离心率.【详解】由1PF 恰好与圆2F 相切于点P ,可知2||PF c =,且 12PF PF ⊥, 又12||||2PF PF a +=,可知1||2PF a c =-, 在12Rt PF F ∆中,222(2)4a c c c -+=, 即2222a ac c -= 所以2220,(0,1)e e e +-=∈,解得212e -+==, 故选:B【点睛】本题主要考查了椭圆的定义,椭圆的简单几何性质,圆的切线的性质,属于中档题. 9.唐代诗人李欣的是《古从军行》开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为221x y +≤,若将军从()2,0A 出发,河岸线所在直线方程40x y +-=,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )B. 1C.1【答案】B 【解析】 【分析】先求出点A 关于直线4x y +=的对称点'A ,点'A 到圆心的距离减去半径即为最短. 【详解】设点A 关于直线4x y +=对称点(,)A a b ','2AA bk a =-, AA '的中点为2,22a b +⎛⎫⎪⎝⎭,故122422b a a b ⎧=⎪⎪-⎨+⎪+=⎪⎩解得4a =,2b =,要使从点A 到军营总路程最短,即为点f A 到军营最短的距离, 即为点'A 和圆上的点连线的最小值,为点'A 和圆心的距离减半径, “将军饮马”的最短总路程为4161251+-=-,故选:B【点睛】本题考查了数学文化问题、点关于直线的对称问题、点与圆的位置关系等等,解决问题的关键是将实际问题转化为数学问题,建立出数学模型,从而解决问题.10.设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ,(点P 与点,A B 不重合),则PAB △的面积最大值是( ).A. 25B.52C. 55【答案】B 【解析】 【分析】先求出0m =时,交点(0,3)P ,131322PABS =⨯⨯=;当0m ≠时,利用基本不等式求PAB △的面积最大值,综合得解.【详解】动直线0x my +=,令0y =,解得0x =, 因此此直线过定点(0,0)A .动直线30mx y m --+=,即()130m x y -+-=, 令10x -=,30y -=, 解得1x =,3y =, 因此此直线过定点()1,3B .0m =时,两条直线分别为0x =,3y =,交点(0,3)P ,131322PABS=⨯⨯=. 0m ≠时,两条直线的斜率分别为:1m-,m , 则11m m-⨯=-, 因此两条直线相互垂直.22211115()1024442PAB S PA PB PA PB AB ∆=⋅⋅≤+=⋅=⋅=当PA PB ==PAB △的面积取得最大值52. 综上可得:PAB △的面积最大值是52. 故选B .【点睛】本题主要考查直线的位置关系,考查利用基本不等式求最值,意在考查学生对这些知识的理解掌握水平和分析推理能力.11.设椭圆C :2211612x y +=上的一点P 到两条直线4y =和8x =的距离分别是1d ,2d ,则122d d +的最小值( )A. 5B. 6C. 7D. 8【答案】D 【解析】 【分析】设()4P cos θθ,02θπ≤<,由题意可得:1222484d d cos θθ+=-+-,利用三角函数的单调性、和差公式即可得出结论.【详解】解:设()4P cos θθ,02θπ≤<, 由题意可得:122248416416816886d d cos cos sin πθθθθθ⎛⎫+=-+-=--=-+≥-= ⎪⎝⎭.当且仅当816sin πθ⎛⎫+= ⎪⎝⎭时取等号. 122d d ∴+的最小值为8.故选:D【点睛】本题考查了椭圆的标准方程及其参数方程、三角函数的单调性、和差公式,考查了推理能力与计算能力,属于中档题.12.已知椭圆C :22221(0)x y a b a b+=>>的左、右焦点分别为1F ,2F ,点P 是椭圆C 上一点,椭圆C 内一点Q 满足:点Q 在2PF 的延长线上1.QF QP ⊥若13sin 5F PQ ∠=,则该椭圆离心率的取值范围是( )A. 1,32⎛ ⎝⎭B. 1,13⎛⎫⎪⎝⎭C. ⎫⎪⎪⎝⎭D.2⎝⎭【答案】A 【解析】 【分析】由1QF QP ⊥,可得点Q 在以12F F 为直径,原点为圆心的圆上,由点Q 在椭圆的内部,可得以12F F 为直径的圆在椭圆内,可得c b <;于是e <,再根据临界值,由点P 的位置建立不等式,确定即可得出e 的范围. 【详解】解:1QF QP ⊥,∴点Q 在以12F F 为直径,原点为圆心的圆上,点Q 在椭圆的内部,∴以12F F 为直径的圆在椭圆内,c b ∴<;222c a c ∴<-,222c a ∴<,故202e <<. 13sin 5F PQ ∠=,14cos 5F PQ ∠=,设1PF m =,2PF n =,222142cos c m n mn F PQ ∴=+-⋅∠,()2222818424455c m n mn mn c a mn ∴=+--⇒=- ,222184445mn a c b ∴=-=,① 12113sin 210PF F S mn F PQ mn ∆=⋅∠=,由已知可知,点Q 在以12F F 为直径的圆上,不包含1F ,2F 两个点,当点Q 与2F 重合时,此时22b PF a =,12PF F S ∆的最大值是1222122PF F b b cS c a a ∆=⋅⋅= 由图象可知其他满足条件的Q 满足条件时,需满足2310b cmn a < ②由①②可知2109mn b = ,2103b cmn a<⋅ 22101093b c b a∴<⋅,解得:13ca>,综上可知:1232e<<.故选:A【点睛】本题考查了椭圆的标准方程及其性质、数形结合方法,考查了推理能力与计算能力,属于中档题,本题的关键是根据满足条件的点P的位置确定,建立面积条件的12PF F∆的不等关系,求出离心率的范围.二、填空题(本大题共4小题)13.已知直线l过点(1,2),且原点到直线l的距离为1,则直线l方程为__________.【答案】x=1或3x﹣4y+5=0【解析】【分析】分两种情况,当斜率不存在时,验证是否满足题意;当斜率存在时,设出点斜式方程,再由点到直线的距离公式求出斜率即可求解.【详解】直线l的斜率不存在时,可得直线l的方程为:x=1,满足题意;直线l的斜率存在时,可设直线l的方程为:y﹣2=k(x﹣1),化为:kx﹣y+2﹣k=0.2211kk-=+,解得:k34=,∴直线l的方程为:y﹣234=(x﹣1),化为:3x﹣4y+5=0,综上可得:直线l的方程为:x=1或3x﹣4y+5=0,故答案为:x=1或3x﹣4y+5=0.【点睛】本题主要考查直线的点斜式方程、点到直线的距离公式,注意斜率不存在的情况,考查分类讨论的思想,属于基础题14.若椭圆2214x y m+=的焦距为1,则m =______.【答案】154或174【解析】 【分析】讨论焦点的位置,然后利用21c =,求m 的值.【详解】解:椭圆2214x y m+=的焦距为1,当焦点在x 轴时,24a =,2b m =21c ∴=== ,解得:154m =当焦点在y 轴时,2a m =,24b =,21c ∴===,解得:174m =. 故答案为:154或174. 【点睛】本题考查根据椭圆方程的形式求参数,是基础题,解题时要认真审题,注意椭圆的性质的合理运用.15.已知O 为坐标原点,椭圆T :22221x y a b +=()0,1B ,过椭圆上一点P 的两条直线PA ,PC 分别与椭圆交于A ,C ,设PA ,PC 的中点分别为D ,E ,直线PA ,PC 的斜率分别是1k ,212(,0)k k k <,若直线OD ,OE 的斜率之和为2,则124k k +的最大值为______. 【答案】94- 【解析】 【分析】首先根据待定系数法求椭圆方程,再利用点差法求OD k 和OE k 与12,k k 的斜率关系,最后利用基本不等式求最值.【详解】不妨设a b >,根据题意可知22221c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩,解得:1,1a b c ===∴椭圆方程是2212x y +=设()()()112233,,,,,P x y A x y B x y221122221212x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ ,两式相减得()2222121202x x y y -+-= 整理为:()()()()1212121202x x x x y y y y +-++-=当120x x +≠,且120x x -≠时,12121212102y y y y x x x x +-+⨯=+-, 1102OD k k ∴+⋅=,即112OD k k =-,同理:212OE k k =-, 1211222k k ∴--=,即12114k k +=- ,()21121212124111144544k k k k k k k k k k ⎛⎫⎛⎫⎛⎫∴+=-⨯++=-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭211245144k k k k ⎛⎫=--+ ⎪⎝⎭12,0k k <,122140,0k kk k ∴>>,211244k k k k ∴+≥= ,21124114k k k k ⎛⎫∴-+≤- ⎪⎝⎭21124515914444k k k k ⎛⎫∴--+≤--=- ⎪⎝⎭.当且仅当21124k kk k=时等号成立,即212k k=时,故124k k+的最大值是94-.故答案为:94-【点睛】考查点差法求斜率关系式,和利用基本不等式求最值,意在考查推理能力和计算能力,属于中档题型,本题的关键是利用点差法求斜率间的关系.16.已知直线0x y b-+=与圆229x y+=交于两点A,B,若24OA OB AB+≥(其中O 为坐标原点),则实数b的取值范围______【答案】(32,22,32--⋃【解析】【分析】利用平行四边形法则,转化为224OD AB≥,借助于弦长公式22194OD AB+=,求得219OD≤<,利用点到直线的距离求b的取值范围.【详解】解:设AB中点为D,则OD AB⊥,2OA OB AB+≥,224OD AB∴≥,42.AB OD∴≤221||94OD AB+=,2||1OD∴≥.直线0x y b-+=与圆229x y+=交于不同的两点A、B,2||9OD ∴<. 21||9OD ∴≤<,则219≤<.b ∴-≤b ≤<即实数b的取值范围是(.-⋃故答案为:(.-⋃【点睛】本题考查向量知识的运用,考查直线与圆的位置关系,考查学生的推理和计算能力,属于中档题.三、解答题(本大题共6小题)17.已知1:210l x y -+=和2:20l x y +-=的交点为P . (1)求经过点P 且与直线3:3450x l y -+=垂直的直线的方程(2)直线l '经过点P 与x 轴、y 轴交于A 、B 两点,且P 为线段AB 的中点,求OAB ∆的面积.【答案】(1)4370x y +-=;(2)2 【解析】 【分析】(1)联立两条直线的方程,解方程组求得P 点坐标,根据3l 的斜率求得与其垂直直线的斜率,根据点斜式求得所求直线方程.(2)根据(1)中P 点的坐标以及P 为AB 中点这一条件,求得,A B 两点的坐标,进而求得三角形OAB 的面积.【详解】解:(1)联立21020x y x y -+=⎧⎨+-=⎩,解得交点P 的坐标为()1,1,∵l 与3l 垂直, ∴l 的斜率3143k k =-=-, ∴l 的方程为()4113y x -=--,即4370x y +-=. (2)∵P 为AB 的中点,已知(2,0)A ,(0,2)B ,即2OA OB ==,∴1122222OAB S OA OB ∆=⋅⋅=⨯⨯= 【点睛】本小题主要考查两条直线交点坐标的求法,考查两条直线垂直斜率的关系,考查直线的点斜式方程,考查三角形的面积公式以及中点坐标,属于基础题.18.已知P :方程2222220x y x my m m +++-++=表示圆心在第三象限的圆,q :方程2231x my +=表示焦点在y 轴上的椭圆.()1若p ⌝为真命题,求实数m 的取值范围;()2若“p q ∧”为假,“p q ∨为真”,求m 的取值范围.【答案】(1)(] ,1-∞;(2)][()0,13,⋃+∞. 【解析】 【分析】(1)首先求p 为真命题时,m 的取值范围,再求其补集,就是p ⌝为真时,m 的取值范围; (2)求出命题q 为真时m 的取值范围,利用“p q ∧”为假,“p q ∨为真”时p 、q 一真一假;从而列不等式求得实数m 的取值范围.【详解】解:()1方程2222220x y x my m m +++-++=可化为222(1)()21x y m m m +++=--;若P 为真命题,则20210m m m -<⎧⎨-->⎩,解得1m >;所以p ⌝为真命题时,实数m 的取值范围是(],1-∞;()2命题q :方程2231x my +=表示焦点在y 轴上的椭圆,若q 为真命题时,03m <<;由“p q ∧”为假,“p q ∨为真”,则p 、q 一真一假; 当p 真q 假时,103m m m >⎧⎨≤≥⎩或,即3m ≥;当p 假q 真时,103m m ≤⎧⎨<<⎩,即01m <≤;综上知,实数m 的取值范围是][()0,13,⋃+∞.【点睛】本题考查了圆的方程与椭圆的标准方程应用问题,也考查了简单的复合命题真假性判断问题,是基础题.19.若直线34120x y -+=与x 轴,y 轴的交点分别为,A B ,圆C 以线段AB 为直径. (Ⅰ)求圆C 的标准方程;(Ⅱ)若直线l 过点3,44⎛⎫- ⎪⎝⎭,与圆C 交于点,M N ,且120MCN ∠=,求直线l 的方程.【答案】(Ⅰ)()22325224x y ⎛⎫++-= ⎪⎝⎭;(Ⅱ)34x =-或1216730x y -+=.【解析】 【分析】(1)本题首先根据直线方程确定A 、B 两点坐标,然后根据线段AB 为直径确定圆心与半径,即可得出圆C 的标准方程;(2)首先可根据题意得出圆心C 到直线l 的距离为54,然后根据直线l 的斜率是否存在分别设出直线方程,最后根据圆心到直线距离公式即可得出结果.【详解】(1)令方程34120x y -+=中的0x =,得3y =,令0y =,得4x =-. 所以点,A B 的坐标分别为()()4,0,0,3A B -.所以圆C 的圆心是32,2⎛⎫- ⎪⎝⎭,半径是52r , 所以圆C 的标准方程为()22325224x y ⎛⎫++-= ⎪⎝⎭.(2)因为120MCN ∠=,圆C 的半径为52,所以圆心C 到直线l 的距离为54.若直线l 的斜率不存在,直线l 的方程为34x =-,符合题意. 若直线l 的斜率存在,设其直线方程为344y k x ⎛⎫=++ ⎪⎝⎭,即3404kx y k -++=.圆C 的圆心到直线l的距离54d ==,解得34k =. 则直线l 的方程为33444y x ⎛⎫=++ ⎪⎝⎭,即1216730x y -+=.综上,直线l 的方程为34x =-或1216730x y -+=.【点睛】本题考查圆的标准方程与几何性质,考查直线和圆的位置关系,当直线与圆相交时,半径、弦长的一半以及圆心到直线距离可构成直角三角形,考查计算能力,在计算过程中要注意讨论直线l 的斜率是否存在,是中档题.20.如图,1l ,2l 是通过某城市开发区中心O 的两条南北和东西走向的街道,链接M ,N 两地之间的铁路是圆心在2l 上的一段圆弧,若点M 在O 正北方向,且3MO km =,点N 到1l ,2l 距离分别为4km 和5km .()1建立适当的坐标系,求铁路线所在圆弧的方程;()2若该城市的某中学拟在O 点正东方向选址建分校,考虑环境问题,要求校址到点O 的距离大于4km ,并且铁路线上任意一点到校址的距离不能少于29km ,求该校址距离点O 的最近距离.(注:校址视为一个点)【答案】(1)()22(4)2504,53x y x y -+=≤≤≥≥ (2)距O 最近6km 的地方. 【解析】 【分析】()1建立坐标系,利用圆心在弦的垂直平分线上求圆心坐标,再求半径,进而写出圆的方程. ()2据条件列出不等式,运用函数单调性解决恒成立问题.【详解】解:()1分别以2l 、1l 为x 轴,y 轴建立如图坐标系.据题意得()0,3M ,()4,5N ,531402MN k -∴==-, MN 中点为()2,4,∴线段MN 的垂直平分线方程为:()422)y x -=--,故圆心A 的坐标为()4,0,半径5R ==.∴弧MN 的方程为:()22(4)2504,53x y x y -+=≤≤≥≥()2设校址选在(),0(4)B a a >,04x ≤≤恒成立.04x ≤≤恒成立()﹡ 整理得:()282200a x a -+-≥,对04x ≤≤恒成立().﹡令()()28220f x a x a =-+-.4a >,820a ∴-<,()f x ∴在[]0,4上为减函数.()()244824200a f a a >⎧⎨=-⨯+-≥⎩, 解得6a ≥,即校址选在距O 最近6km 的地方.【点睛】本题主要考查求圆的方程的方法,函数的恒成立问题,利用二次函数在闭区间上的单调性求函数的值域,意在考查抽象和概括,将实际问题转化为数学问题,属于中档题.21.已知椭圆C :22221(0)x y a b a b +=>>的离心率3,连接椭圆的四个顶点得到的菱形的面积为.()1求椭圆C 的方程;()2如图所示,该椭圆C 的左、右焦点1F ,2F 作两条平行的直线分别交椭圆于A ,B ,C ,D 四个点,试求平行四边形ABCD 面积的最大值.【答案】(1)22 132x y +=;(2) 最大值为33. 【解析】 【分析】()1由题意离心率可得6a =,再结合面积求解a ,b 的值,则椭圆方程可求; ()2由()1知,()11,0F -,且直线AB 的斜率不为0,设直线AB 的方程为1x ty =-,联立直线方程与椭圆方程,把平行四边形ABCD 的面积用三角形OAB 的面积表示,然后利用换元法结合单调性求最值.【详解】解:()1由题意,3c e a ==,则22213a b a -=,即6a =. 又122262a b ⋅⋅=3a ∴=2b = ∴椭圆C 的方程为22132x y +=;()2由()1知,()11,0F -,且直线AB 的斜率不为0,设直线AB 的方程为1x ty =-,()11,A x y ,()22,B x y ,联立221132x ty x y =-⎧⎪⎨+=⎪⎩,消去x 得:()2223440t y ty +--=.得122423t y y t +=+,122423y y t -=+. 四边形ABCD 是平行四边形,根据对称性可知,A C 和,B D 关于点O 对称,∴1121442OABABCD S SOF y y ==⋅⋅-=四边形== 令21m t =+,则1m ≥,ABCD S ∴==四边形 1m ≥,且函数144y m m=++在[)1,+∞上单调递增, ∴当1m =,即0t =时,平行四边形ABCD .【点睛】本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,训练了利用换元法与函数的单调性求最值,是中档题.22.已知ABC 的两个顶点为()0,2B -,()0,2C ,平面内P ,Q 同时满足0PA PB PC ++=①;QA QB QC ==②;//PQ BC ③.()1求顶点A 的轨迹E 的方程;()2过点()F 作两条互相垂直的直线1l ,2l ,直线1l ,2l 被点A 的轨迹E 截得的弦分别为11A B ,22A B ,设弦11A B ,22A B 的中点分别为M ,.N 试问:直线MN 是否恒过一个顶点?若过定点,请求出该顶点,若不过定点,请说明理由.【答案】(1)()2210124x y x +=≠;(2)直线MN 过定点,0.2⎛⎫ ⎪ ⎪⎝⎭【解析】 【分析】()1由已知向量等式可知P 为三角形ABC 的重心,设(),A x y ,则,33x y P ⎛⎫⎪⎝⎭,再由QA QB QC ==,知Q 是三角形ABC 的外心,结合//PQ BC 得,03x Q ⎛⎫ ⎪⎝⎭, 由QC QA =列式求解顶点A 的轨迹E 的方程;()2设出直线1l 的方程,与椭圆方程联立求得M 的坐标,同理求得N 的坐标,求得MN 的斜率,写出直线方程的点斜式,整理后利用线系方程说明直线MN 过定点.⎫⎪⎪⎝⎭【详解】解:()10PA PB PC ++=,P ∴为三角形ABC 的重心,设(),A x y ,则,33x y P ⎛⎫ ⎪⎝⎭, 由QA QB QC ==,知Q 是三角形ABC 的外心,Q ∴在x 轴上, 又//PQ BC ,,0.3x Q ⎛⎫∴ ⎪⎝⎭由QC QA=,得=221124x y +=. A ,B ,C 三点不共线,∴顶点A 的轨迹方程为()2210124x y x +=≠; ()2由()1知,()F 为A 的轨迹E 的右焦点, 设()111,A x y ,()122,B xy , 由221124x ty x y ⎧=+⎪⎨+=⎪⎩,得()22340t y ++-=.则12y y +=,12243y y t -=+, ()1212x x t y y ∴+=++=由中点坐标公式得22,33M t t ⎛⎫- ⎪ ⎪++⎝⎭,同理可求得222,.3131N t t ⎛⎫ ⎪ ⎪++⎝⎭则当21t ≠时,()2431MN t k t ==-. ∴直线MN的方程为()2431t y x t ⎛= -⎝⎭. 即()()22244431)3131t t t y x x t t t ⎛⎛==- ---⎝⎭⎝⎭. ∴直线MN过定点.2⎛⎫ ⎪ ⎪⎝⎭【点睛】本题考查圆锥曲线方程的求法,考查平面向量的应用,考查直线与圆锥曲线位置关系的应用,考查计算能力,是中档题.1、在最软入的时候,你会想起谁。
2020学年高二(上)期中数学试卷带答案

2020学年高二(上)期中数学试卷一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5分)数列{n+2n}中的第4项是.2.(5分)抛物线x2=4y的准线方程为.3.(5分)若原点(0,0)和点(1,1)在直线x+y﹣a=0的两侧,则a的取值范围是.4.(5分)已知等差数列{a n},其中a1=,a2+a5=4,a n=33,则n的值为.5.(5分)若x,y满足,则目标函数z=x+2y的最大值为.6.(5分)设等比数列{a n}的前n项和为S n,若27a3﹣a6=0,则=.7.(5分)若正数x,y满足x+3y=5xy,则3x+4y的最小值是.8.(5分)已知双曲线﹣y2=1(a>0)的一条渐近线为x+y=0,则a=.9.(5分)已知数列{a n}是等比数列,S n是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为,求S5.10.(5分)已知椭圆:的焦距为4,则m为.11.(5分)若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则的取值范围是.12.(5分)椭圆+=1(a>b>0)的右焦点F(c,0)关于直线y=x的对称点Q在椭圆上,则椭圆的离心率是.13.(5分)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第100项,即a100=.14.(5分)若实数a,b满足a=+2,则a的最大值是.二.解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)求适合下列条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点(2,﹣6);(2)在x轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6.16.(14分)已知数列{a n}的通项公式是a n=n2+kn+4(1)若k=﹣5,则数列中有多少项是负数?n为何值时,a n有最小值.并求出最小值,(2)对于n∈N*,都有a n>a n,求实数k的取值范围.+117.(14分)某厂家计划在2016年举行商品促销活动,经调查测算,该商品的年销售量m万件与年促销费用x万元满足:m=3﹣,已知2016年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).(1)将2016年该产品的利润y万元表示为年促销费用x万元的函数;(2)该厂2016年的促销费用投入多少万元时,厂家的利润最大?18.(16分)(1)解关于x的不等式:(a2+a﹣1)x>a2(1+x)+a﹣2(a∈R);(2)如果x=a2﹣4在上述不等式的解集中,求实数a的取值范围.19.(16分)在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的焦距为2.(1)若椭圆C经过点(,1),求椭圆C的标准方程;(2)设A(﹣2,0),F为椭圆C的左焦点,若椭圆C上存在点P,满足=,求椭圆C的离心率的取值范围.20.(16分)已知递增数列{a n}的前n项和为S n,且满足a1=1,4S n﹣4n+1=a n2.设b n=,n∈N*,且数列{b n}的前n项和为T n.(1)求证:数列{a n}为等差数列;(2)试求所有的正整数m,使得为整数;(3)若对任意的n∈N*,不等式λT n<n+18(﹣1)n+1恒成立,求实数λ的取值范围.二.高二数学试题(第二卷)21.(5分)为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有辆.22.(5分)若随机安排甲乙丙三人在3天节日中值班,每人值班1天,则甲与丙都不在第一天的概率为.23.(5分)已知命题甲是“{x|≥0}”,命题乙是“{x|log3(2x+1)≤0}”,则甲是乙的条件.(从充分不必要、必要不充分、充要、既不充分也不必要中选填)24.(5分)下列四个命题:①命题“若a=0,则ab=0”的否命题是“若a=0,则ab≠0”;②若命题P:∃x∈R,x2+x+1<0,则﹁p:∀x∈R,x2+x+1≥0;③若命题“﹁p”与命题“p或q”都是真命题,则命题q一定是真命题;④命题“若0<a<1则log a(a+1)<”是真命题.其中正确命题的序号是.(把所有正确命题序号都填上)25.(10分)设命题p:函数y=kx+1在R上是增函数,命题q:∃x∈R,x2+(2k﹣3)x+1=0,如果p∧q是假命题,p∨q是真命题,求k的取值范围.26.(10分)将扑克牌4种花色的A,K,Q共12张洗匀.(1)甲从中任意抽取2张,求抽出的2张都为A的概率;(2)若甲已抽到了2张K后未放回,求乙抽到2张A的概率.参考答案与试题解析一.填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5分)数列{n+2n}中的第4项是20.【分析】根据题意,可得数列的通项a n=n+2n,将n=4代入通项计算可得答案.【解答】解:根据题意,数列{n+2n}的通项a n=n+2n,则其第4项a4=4+24=20;故答案为:20.【点评】本题考查数列的通项公式,涉及数列的表示方法,关键是理解数列通项公式的定义.2.(5分)抛物线x2=4y的准线方程为y=﹣1.【分析】由抛物线x2=2py(p>0)的准线方程为y=﹣即可求得抛物线x2=4y的准线方程.【解答】解:∵抛物线方程为x2=4y,∴其准线方程为:y=﹣1.故答案为:y=﹣1.【点评】本题考查抛物线的简单性质,掌握其几何性质是关键,属于基础题.3.(5分)若原点(0,0)和点(1,1)在直线x+y﹣a=0的两侧,则a的取值范围是(0,2).【分析】因为原点O和点P(1,1)在直线x+y﹣a=0的两侧,所以(﹣a)•(1+1﹣a)<0,由此能求出a的取值范围.【解答】解:因为原点O和点P(1,1)在直线x+y﹣a=0的两侧,所以(﹣a)•(1+1﹣a)<0,解得0<a<2,故答案为:(0,2).【点评】本题考查二元一次不等式的几何意义,解题时要认真审题,注意公式的灵活运用.4.(5分)已知等差数列{a n},其中a1=,a2+a5=4,a n=33,则n的值为50.【分析】由已知求得等差数列的公差,代入a n=33可求n的值.【解答】解:在等差数列{a n},由a1=,a2+a5=4,得2a1+5d=4,即,.∴,由a n=33,得,解得:n=50.故答案为:50.【点评】本题考查了等差数列的通项公式,是基础的计算题.5.(5分)若x,y满足,则目标函数z=x+2y的最大值为3.【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z 的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由z=x+2y得y=﹣x+z,平移直线y=﹣x+z,由图象可知当直线y=﹣x+z经过点B时,直线y=﹣x+z的截距最大,此时z最大.由,解得,即B(1,1),代入目标函数z=x+2y得z=2×1+1=3故答案为:3.【点评】本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值和最小值,利用数形结合是解决线性规划问题中的基本方法.6.(5分)设等比数列{a n}的前n项和为S n,若27a3﹣a6=0,则=28.【分析】设出等比数列的首项和公比,由已知求出公比,代入等比数列的前n 项和得答案.【解答】解:设等比数列{a n}的首项为a1,公比为q,由27a3﹣a6=0,得27a3﹣a3q3=0,即q=3,∴=.故答案为:28.【点评】本题考查了等比数列的通项公式,考查了等比数列的前n项和,是基础的计算题.7.(5分)若正数x,y满足x+3y=5xy,则3x+4y的最小值是5.【分析】将方程变形,代入可得3x+4y=(3x+4y)()=×3,然后利用基本不等式即可求解.【解答】解:∵x+3y=5xy,x>0,y>0∴∴3x+4y=(3x+4y)()=×3=5当且仅当即x=2y=1时取等号故答案为:5【点评】本题主要考查了利用基本不等式求解最值问题,解题的关键是基本不等式的应用条件的配凑8.(5分)已知双曲线﹣y2=1(a>0)的一条渐近线为x+y=0,则a=.【分析】运用双曲线的渐近线方程为y=±,结合条件可得=,即可得到a 的值.【解答】解:双曲线﹣y2=1的渐近线方程为y=±,由题意可得=,解得a=.故答案为:.【点评】本题考查双曲线的方程和性质,主要考查双曲线的渐近线方程的求法,属于基础题.9.(5分)已知数列{a n}是等比数列,S n是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为,求S5.【分析】由a2•a3=2a1=a1•a4,可得a4=2,再由a4与2a7的等差中项为,得a4 +2a7 =,故有a7 =.求出首项和公比,再利用等比数列的前n项和公式求出s5.【解答】解:数列{a n}是等比数列,S n是它的前n项和,若a2•a3=2a1=a1•a4,可得a4=2.再由a4与2a7的等差中项为,可得a4 +2a7 =,故有a7 =.∴q3==,∴q=,∴a1=16.∴s5==31.【点评】本题主要考查等差数列的定义和性质,等比数列的通项公式,等比数列的前n项和公式,属于中档题.10.(5分)已知椭圆:的焦距为4,则m为4或8.【分析】分焦点在x,y轴上讨论,结合焦距为4,可求m的值.【解答】解:由题意,焦点在x轴上,10﹣m﹣m+2=4,所以m=4;焦点在y轴上,m﹣2﹣10+m=4,所以m=8,综上,m=4或8.故答案为:m=4或8.【点评】本题考查椭圆的性质,考查学生对椭圆方程的理解,属于基础题.11.(5分)若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则的取值范围是[4,+∞)或(﹣∞,0] .【分析】由题意可知===++2.由此可知的取值范围.【解答】解:在等差数列中,a1+a2=x+y;在等比数列中,xy=b1•b2.∴===++2.当x•y>0时,+≥2,故≥4;当x•y<0时,+≤﹣2,故≤0.答案:[4,+∞)或(﹣∞,0]【点评】本题考查数列的性质和应用,解题时要认真审题,仔细思考.12.(5分)椭圆+=1(a>b>0)的右焦点F(c,0)关于直线y=x的对称点Q在椭圆上,则椭圆的离心率是.【分析】设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.【解答】解:设Q(m,n),由题意可得,由①②可得:m=,n=,代入③可得:,可得,4e6+e2﹣1=0.即4e6﹣2e4+2e4﹣e2+2e2﹣1=0,可得(2e2﹣1)(2e4+e2+1)=0解得e=.故答案为:.【点评】本题考查椭圆的方程简单性质的应用,考查对称知识以及计算能力.13.(5分)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第100项,即a100=5252.【分析】根据题意,分析所给的图形可得a n﹣a n﹣1=n+2(n≥2),结合a1的值,可得a100=a1+(a2﹣a1)+(a3﹣a2)+…+(a100﹣a99),代入数据计算可得答案.【解答】解:根据题意,分析相邻两个图形的点数之间的关系:a2﹣a1=4,a3﹣a2=5,…由此我们可以推断:a n﹣a n﹣1=n+2(n≥2),又由a1=5,所以a100=a1+(a2﹣a1)+(a3﹣a2)+…+(a100﹣a99)=5+4+5+…+102=5+=5252;即a100=5252;故答案为:5252.【点评】本题考查数列的表示方法,涉及归纳推理的运用,关键是依据图形,发现变化的规律.14.(5分)若实数a,b满足a=+2,则a的最大值是20.【分析】用换元法,设=x,=y,则x≥0,y≥0;求出b与a的解析式,由a=+2得出y与x的关系式,再根据其几何意义求出a的最大值.【解答】解:设=x,=y,且x≥0,y≥0;∴b=x2,4a﹣b=y2,即a==;∴a=+2可化为=y+2x,即(x﹣4)2+(y﹣2)2=20,其中x≥0,y≥0;又(x﹣4)2+(y﹣2)2=20表示以(4,2)为圆心,以2为半径的圆的一部分;∴a==表示圆上点到原点距离平方的,如图所示;∴a的最大值是×(2r)2=r2=20故答案为:20.【点评】本题考查了给出条件求最值的应用问题,主要考查了换元法和圆的方程的运用问题,考查了数形结合和运算能力,属于中档题.二.解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)求适合下列条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点(2,﹣6);(2)在x轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6.【分析】(1)设椭圆的标准方程为=1,或,a>b>0,由已知得a=2b,且椭圆过点(2,﹣6),由此能求出椭圆的标准的方程.(2)设椭圆的标准方程为=1,a>b>0,由已知条件推导出c=b=3,由此能求出椭圆的标准方程.【解答】解:(1)设椭圆的标准方程为=1,或,a>b>0,∵长轴长是短轴长的2倍,∴a=2b,①∵椭圆过点(2,﹣6),∴=1,或=1,②由①②,得a2=148,b2=37或a2=52,b2=13,故所求的方程为或.(2)设椭圆的标准方程为=1,a>b>0,∵在x轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6,如图所示,∴△A1FA2为一等腰直角三角形,OF为斜边A1A2的中线(高),且OF=c,A1A2=2b,∴c=b=3.∴a2=b2+c2=18.故所求椭圆的方程为.【点评】本题考查椭圆的标准方程的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.16.(14分)已知数列{a n}的通项公式是a n=n2+kn+4(1)若k=﹣5,则数列中有多少项是负数?n为何值时,a n有最小值.并求出最小值,>a n,求实数k的取值范围.(2)对于n∈N*,都有a n+1【分析】(1)将k=﹣5代入可知a n=(n﹣1)(n﹣4),进而令a n<0可得负数项,通过配方可得最小值;>a n化简得k>﹣2n﹣1,进而可知k>﹣2﹣1=﹣3.(2)通过a n+1【解答】解:(1)若k=﹣5,则a n=n2﹣5n+4=(n﹣1)(n﹣4),令a n<0,则1<n<4,∴数列中第2、3项共2项为负数,∵f(x)=x2﹣5x+4是开口向上,对称轴x=的抛物线,∴当n=2或3时,a n有最小值22﹣5×2+4=﹣2;(2)依题意,a n>a n,即(n+1)2+k(n+1)+4>n2+kn+4,+1整理得:k>﹣2n﹣1,>a n,又∵对于n∈N*,都有a n+1∴k大于﹣2n﹣1的最大值,∴k>﹣2﹣1=﹣3.【点评】本题考查数列的递推式,考查运算求解能力,注意解题方法的积累,属于基础题.17.(14分)某厂家计划在2016年举行商品促销活动,经调查测算,该商品的年销售量m万件与年促销费用x万元满足:m=3﹣,已知2016年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).(1)将2016年该产品的利润y万元表示为年促销费用x万元的函数;(2)该厂2016年的促销费用投入多少万元时,厂家的利润最大?【分析】(1)由题目中,每件产品的销售价格为 1.5×(万元),则利润y=m[1.5×]﹣(8+16m+x),整理即可.(2)对(1)利润函数y=﹣[+(x+1)]+29(x≥0),利用基本不等式求最大值即可.【解答】解:(1)由题意知,每件产品的销售价格为1.5×(万元),∴利润函数y=m[1.5×]﹣(8+16m+x)=4+8m﹣x=﹣[+(x+1)]+29(x≥0).(2)因为利润函数y=﹣[+(x+1)]+29(x≥0),所以,当x≥0时,+(x+1)≥8,∴y≤﹣8+29=21,当且仅当=x+1,即x=3(万元)时,y max=21(万元).所以,该厂家2016年的促销费用投入3万元时,厂家的利润最大,最大为21万元.【点评】本题考查了商品利润函数模型的应用,也考查了基本不等式a+b≥2(a>0,b>0)的灵活运用,是中档题.目.18.(16分)(1)解关于x的不等式:(a2+a﹣1)x>a2(1+x)+a﹣2(a∈R);(2)如果x=a2﹣4在上述不等式的解集中,求实数a的取值范围.【分析】(1)把原不等式右边的未知项移项到左边进行合并,同时右边的式子分解因式,然后根据a﹣1大于0,a﹣1等于0及a﹣1小于0三种情况,根据不等式的基本性质把x的系数化为1,分别求出原不等式相应的解集即可;(2)解法一:分两种情况:a大于1时,根据相应的解集列出关于a的不等式组;同理a小于1时列出相应的不等式组,求出两不等式组解集的并集即可得到a的范围;解法二:把x=a2﹣4代入原不等式中化简,得到关于a的不等式,画出相应的图形,根据图形即可得到满足题意的a的取值范围.【解答】解:(1)(a2+a﹣1)x>a2(1+x)+a﹣2,(a2+a﹣1)x﹣a2x>a2+a﹣2,(a﹣1)x>a2+a﹣2,(a﹣1)x>(a﹣1)(a+2),当a>1时,解集为{x|x>a+2};当a=1时,解集为∅;当a<1时,解集为{x|x<a+2};(2)解法一:由题意,或,分别化为:或,解得:a>3或﹣2<a<1,则实数a的取值范围为(﹣2,1)∪(3,+∞);解法二:将x=a2﹣4代入原不等式,并整理得:(a+2)(a﹣1)(a﹣3)>0,根据题意画出图形,如图所示:根据图形得:实数a的取值范围为(﹣2,1)∪(3,+∞).【点评】此题考查了其他不等式的解法,利用了分类讨论及数形结合的思想,第二小题有两种解法:一种是利用转化的思想,讨论a大于1和a小于1,根据第一问求出的解集列出相应的不等式组;另一种是直接把x的值代入原不等式,借助图形来求解.19.(16分)在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的焦距为2.(1)若椭圆C经过点(,1),求椭圆C的标准方程;(2)设A(﹣2,0),F为椭圆C的左焦点,若椭圆C上存在点P,满足=,求椭圆C的离心率的取值范围.【分析】(1)由题意可得a2﹣b2=1,代入已知点,可得a,b的方程,解方程即可得到所求椭圆方程;(2)设P(x,y),运用两点的距离公式,化简整理,即可得到P的轨迹方程,由题意和圆相交的条件,结合离心率公式,即可得到所求范围.【解答】解:(1)由题意可得c=1,即a2﹣b2=1,又代入点(,1),可得+=1,解方程可得a=,b=,即有椭圆的方程为+=1;(2)由题意方程可得F(﹣1,0),设P(x,y),由PA=PF,可得=•,化简可得x2+y2=2,由c=1,即a2﹣b2=1,由椭圆+=1和圆x2+y2=2有交点,可得b2≤2≤a2,又b=,可得≤a≤,即有离心率e=∈[,].【点评】本题考查椭圆的方程的求法,注意运用方程的思想,考查轨迹方程的求法,以及椭圆和圆相交的关系,考查运算能力,属于中档题.20.(16分)已知递增数列{a n}的前n项和为S n,且满足a1=1,4S n﹣4n+1=a n2.设b n=,n∈N*,且数列{b n}的前n项和为T n.(1)求证:数列{a n}为等差数列;(2)试求所有的正整数m,使得为整数;(3)若对任意的n∈N*,不等式λT n<n+18(﹣1)n+1恒成立,求实数λ的取值范围.【分析】(1)由已知条件推导出a n﹣2=a n﹣1(n≥2)或a n﹣2=﹣a n﹣1(n≥2),由此能证明数列{a n}为等差数列.(2)由a n=2n﹣1,知=1﹣,由此能求出所有的正整数m,使得为整数.(3)由a n=2n﹣1,知,由此利用裂项求和法结合已知条件能求出实数λ的取值范围.【解答】(1)证明:由,得,…(2分)所以,即,即(n≥2),所以a n﹣2=a n﹣1(n≥2)或a n﹣2=﹣a n﹣1(n≥2),即a n﹣a n﹣1=2(n≥2)或a n+a n﹣1=2(n≥2),…(4分)若a n+a n﹣1=2(n≥2),则有a2+a1=2,又a1=1,所以a2=1,则a1=a2,这与数列{a n}递增矛盾,所以a n﹣a n﹣1=2(n≥2),故数列{a n}为等差数列.…(6分)(2)解:由(1)知a n=2n﹣1,所以==,…(8分)因为,所以,又2m﹣1≥1且2m﹣1为奇数,所以2m﹣1=1或2m﹣1=3,故m的值为1或2.…(10分)(3)解:由(1)知a n=2n﹣1,则,所以T n=b1+b2+…+b n==,…(12分)从而对任意n∈N*恒成立等价于:当n为奇数时,恒成立,记,则≥49,当n=3时取等号,所以λ<49,当n为偶数时,恒成立.记,因为递增,所以g(n)min=g(2)=﹣40,所以λ<﹣40.综上,实数λ的取值范围为λ<﹣40.…(16分)【点评】本题考查等差数列的证明,考查满足条件的所有的正整数的求法,考查实数的取值范围的求法,解题时要注意裂项求和法的合理运用.二.高二数学试题(第二卷)21.(5分)为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.【分析】由频率分布直方图先求出时速在区间[40,60)内的汽车的频率,由此能求出时速在区间[40,60)内的汽车数量.【解答】解:由频率分布直方图得:时速在区间[40,60)内的汽车的频率为(0.01+0.03)×10=0.4.∴时速在区间[40,60)内的汽车有0.4×200=80(辆).故答案为:80.【点评】本题考查频数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.22.(5分)若随机安排甲乙丙三人在3天节日中值班,每人值班1天,则甲与丙都不在第一天的概率为.【分析】由甲与丙都不在第一天值班,得乙在第一天值班,由此能求出甲与丙都不在第一天值班的概率.【解答】解:随机安排甲乙丙三人在3天节日中值班,每人值班1天,∵甲与丙都不在第一天值班,∴乙在第一天值班,∵第一天值班一共有3种不同安排,∴甲与丙都不在第一天值班的概率p=.故答案为:.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.23.(5分)已知命题甲是“{x|≥0}”,命题乙是“{x|log3(2x+1)≤0}”,则甲是乙的必要不充分条件.(从充分不必要、必要不充分、充要、既不充分也不必要中选填)【分析】利用不等式的解法分别化简甲乙命题,进而判断出结论.【解答】解:命题甲:≥0,化为x(x﹣1)(x+1)≥0,且x≠1,解得:﹣1≤x≤0,或x>1.命题乙:log3(2x+1)≤0,化为0<2x+1≤1,解得:0.则甲是乙的必要不充分条件.故答案为:必要不充分.【点评】本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.24.(5分)下列四个命题:①命题“若a=0,则ab=0”的否命题是“若a=0,则ab≠0”;②若命题P:∃x∈R,x2+x+1<0,则﹁p:∀x∈R,x2+x+1≥0;③若命题“﹁p”与命题“p或q”都是真命题,则命题q一定是真命题;④命题“若0<a<1则log a(a+1)<”是真命题.其中正确命题的序号是②、③.(把所有正确命题序号都填上)【分析】利用命题的否定的形式判断出①错;利用含量词的命题的否定形式判断出②对;利用复合命题的真假与构成其简单命题的真假的关系判断出③对;利用对数函数的单调性判断出④错.【解答】解:对于①,由于否命题是对命题的条件、结论同时否定,①只否定了结论,条件没否定,故①错;对于②,由于含量词的命题有否定公式是:量词交换,结论否定,故②对;对于③,因为”¬p“为真,故p假;因为“p或q”为真,所以p,q有真,所以q 一定为真,故③对;对于④,因为0<a<1,y=log a x是减函数,∵∴,故④错.故答案为:②③【点评】本题考查命题的否定与命题的否命题的区别:命题的否定是将命题全盘否定,一般只将结论否定即可;二否命题是条件、结论同时否定.注意对数函数的单调性与底数的范围有关.25.(10分)设命题p:函数y=kx+1在R上是增函数,命题q:∃x∈R,x2+(2k ﹣3)x+1=0,如果p∧q是假命题,p∨q是真命题,求k的取值范围.【分析】分别求出p,q为真时的k的范围,根据p,q一真一假,得到关于k 的不等式组,解出即可.【解答】解:∵y=kx+1在R递增,∴k>0,由∃x∈R,x2+(2k﹣3)x+1=0,得方程x2+(2k﹣3)x+1=0有根,∴△=(2k﹣3)2﹣4≥0,解得:k≤或k≥,∵p∧q是假命题,p∨q是真命题,∴命题p,q一真一假,①若p真q假,则,∴<k<;②若p假q真,则,∴k≤0;综上k的范围是(﹣∞,0]∪(,).【点评】本题考查了复合命题的判断,考查一次函数以及二次函数的性质,是一道中档题.26.(10分)将扑克牌4种花色的A,K,Q共12张洗匀.(1)甲从中任意抽取2张,求抽出的2张都为A的概率;(2)若甲已抽到了2张K后未放回,求乙抽到2张A的概率.【分析】(1)甲从中任意抽取2张,基本事件总数n==66,抽出的2张都为A包含的基本事件个数m=,由此能求出抽出的2张都为A的概率.(2)甲已抽到了2张K后未放回,余下10张中抽出2张的方法有=45,抽出的两张都是A的方法有,由此能求出乙抽到2张A的概率.【解答】解:(1)将扑克牌4种花色的A,K,Q共12张洗匀.甲从中任意抽取2张,基本事件总数n==66,抽出的2张都为A包含的基本事件个数m=,∴抽出的2张都为A的概率p==.(2)甲已抽到了2张K后未放回,余下10张中抽出2张的方法有=45,抽出的两长都是A的方法有,∴乙抽到2张A的概率p==.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.。
2020-2021高二数学上期中一模试题带答案

2020-2021高二数学上期中一模试题带答案一、选择题1.如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是A.1 4B.8πC.12D.4π2.如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为2a的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是()A.18π-B.4πC.14π-D.与a的值有关联3.一个盒子里装有大小相同的10个黑球、12个红球、4个白球,从中任取2个,其中白球的个数记为X,则下列概率等于11222422226C C CC+的是 ( )A.P(0<X≤2)B.P(X≤1)C.P(X=1)D.P(X=2)4.为研究某种细菌在特定环境下,随时间变化的繁殖情况,得到如下实验数据:天数x(天)3456繁殖个数y(千个) 2.534 4.5由最小二乘法得y与x的线性回归方程为ˆˆ0.7y x a=+,则当7x=时,繁殖个数y的预测值为()A.4.9B.5.25C.5.95D.6.155.在区间上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“12x y -≤”的概率,3p 为事件“12xy ≤”的概率,则 ( ) A .123p p p << B .231p p p << C .312p p p <<D .321p p p <<6.阅读下边的程序框图,运行相应的程序,则输出s 的值为( )A .1B .0C .1D .37.从区间[]0,2随机抽取4n 个数1232,,,...,n x x x x ,1232,,,...,n y y y y 构成2n 个数对()11,x y ,()22,x y ,…,()22,n n x y ,其中两数的平方和小于4的数对有m 个,则用随机模拟的方法得到的圆周率疋的近似值为( )A .2m n B .2m n C .4m n D .16m n8.AQI 即空气质量指数,AQI 越小,表明空气质量越好,当AQI 不大于100时称空气质量为“优良”.如图是某市3月1日到12日AQI 的统计数据.则下列叙述正确的是( )A .这12天的AQI 的中位数是90B .12天中超过7天空气质量为“优良”C .从3月4日到9日,空气质量越来越好D .这12天的AQI 的平均值为1009.执行如图所示的程序框图,则输出的结果是( )A .5B .7C .9D .1110.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m ,第二次出现的点数为n ,向量p u v =(m ,n),q v =(3,6).则向量p u v 与q v共线的概率为( )A .13B .14C .16D .11211.某程序框图如图所示,该程序运行后输出的k 的值是( )A .4B .5C .6D .712.设点(a,b)为区域4000x y x y +-≤⎧⎪>⎨⎪>⎩内任意一点,则使函数f(x)=2ax 2bx 3-+在区间[12,+∞)上是增函数的概率为A .13B .2 3C .1 2D .1 4二、填空题13.在5张卡片上分别写有数字1,2,3,4,5,然后将它们混合,再任意排列成一行,则得到的数能被2或5整除的概率是___________. 14.下列说法正确的个数有_________(1)已知变量x 和y 满足关系23y x =-+,则x 与y 正相关;(2)线性回归直线必过点(),x y ;(3)对于分类变量A 与B 的随机变量2k ,2k 越大说明“A 与B 有关系”的可信度越大 (4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数2R 的值越大,说明拟合的效果越好.15.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为_________16.已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边,若3b =,三内角A ,B ,C 成等差数列,则该三角形的外接圆半径等于______________;17.如左下图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是_________。
2020-2021高二数学上期中第一次模拟试题(含答案)
2020-2021高二数学上期中第一次模拟试题(含答案)一、选择题1.用电脑每次可以从区间()0,1内自动生成一个实数,且每次生成每个实数都是等可能性的,若用该电脑连续生成3个实数,则这3个实数都大于13的概率为( ) A .127B .23C .827D .492.设样本数据1210,,,x x x L 的均值和方差分别为1和4,若(i i y x a a =+为非零常数,1,2,,10)i =L ,则1210,,,y y y L 的均值和方差分别为( )A .1,4a +B .1,4a a ++C .1,4D .1,4a +3.设a 是甲抛掷一枚骰子得到的点数,则方程220x ax ++=有两个不相等的实数根的概率为( ) A .23B .13C .12D .5124.执行如图所示的程序框图,则输出的n 值是( )A .5B .7C .9D .115.微信中有个“微信运动”,记录一天行走的步数,小王的“微信步数排行榜”里有120个人,今天,他发现步数最少的有0.85万步,最多的有1.79万步.于是,他做了个统计,作出下表,请问这天大家平均走了多少万步?( )A.1.19B.1.23C.1.26D.1.316.如图,是民航部门统计的某年春运期间12个城市出售的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是()A.深圳的变化幅度最小,北京的平均价格最高.B.深圳和厦门的平均价格同去年相比有所下降.C.平均价格从高到低居于前三位的城市为北京、深圳、广州.D.平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门.7.执行如图所示的程序框图,则输出的结果是()A.5B.7C.9D.118.已知不等式51xx-<+的解集为P,若x P∈,则“1x<”的概率为().A.14B.13C.12D.239.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量pu v=(m,n),qv=(3,6).则向量pu v与qv共线的概率为( )A.13B.14C.16D.11210.如图所示是为了求出满足122222018n+++>L的最小整数n,和两个空白框中,可以分别填入()A.2018S>?,输出1n-B.2018S>?,输出nC.2018S≤?,输出1n-D.2018S≤?,输出n11.已知函数()cos3xf xπ=,根据下列框图,输出S的值为()A.670B.16702C.671D.67212.设点(a,b)为区域40x yxy+-≤⎧⎪>⎨⎪>⎩内任意一点,则使函数f(x)=2ax2bx3-+在区间[12,+∞)上是增函数的概率为 A .13B .2 3C .1 2D .1 4二、填空题13.已知一组数据4.8,4.9,5.2,5.5,5.6,则该组数据的方差是______. 14.从某居民区随机抽取10个家庭,获得第i 个家庭的月收入x i (单位:千元)与月储蓄y i (单位:千元)的数据资料,算得101ii x =∑=80, 101ii y =∑=20, 110i i i x y =∑=184, 1210i ix =∑=720.则家庭的月储蓄y 对月收入x 的线性回归方程为__________. 附:线性回归方程y =bx +a 中, 1221ni i i n i i x y nxy b x nx==-=-∑∑,a =y -b x ,其中x , y 为样本平均值.线性回归方程也可写为ˆy=ˆb x +ˆa . 15.以下四个命题错误的序号为_______(1) 样本频率分布直方图中小矩形的高就是对应组的频率.(2) 过点P(2,-2)且与曲线33y x x =-相切的直线方程是9160x y +-=.(3) 若样本1210,,x x x L 的平均数是5,方差是3,则数据121021,21,,21x x x +++L 的平均数是11,方差是12.(4) 抛掷一颗质地均匀的骰子,事件“向上点数不大于4”和事件“向上点数不小于3”是对立事件.16.某单位为了了解用电量y (度)与气温x (℃之间的关系,随机统计了某4天的用电量与当天气温(如表),并求得线性回归方程ˆ360yx =-为:不小心丢失表中数据c ,d ,那么由现有数据知3c d -____________.17.已知多项式32256f x x x x =--+(),用秦九韶算法,当10x =时多项式的值为__________.18.以下说法正确的是_____________ . ①类比推理属于演绎推理.②设有一个回归方程ˆ23yx =- ,当变量每增加1个单位,y 平均增加3个单位. ③样本相关系数r 满足以下性质:1r ≤,并且r 越接近1,线性相关程度越强;r 越接近0,线性相关程度越弱.④对复数12,z z 和自然数n 有()1212nn n z z z z ⋅=⋅.19.若按右上图所示的程序框图运行后,输出的结果是63,则判断框中的整数M 的值是__________。
陕西省2020年高二数学上学期期中考试卷附答案题库(共八套)

范文陕西省2020年高二数学上学期期中考试卷附答案1/ 8题库(共八套)陕西省 2020 年高二数学上学期期中考试卷(一)(考试时间120 分钟满分 150 分)一.单项选择题(每小题 5 分,共 60 分)1.不等式<0 的解集为() A.{x|﹣2<x<3} B.{x|x<﹣2} C . {x|x <﹣ 2 或 x > 3} D.{x|x>3} 2.等差数列{an}中,a7+a9=16,a4=1,则 a12=() A.15 B.30 C.31 D.64 3.已知点 P(x0,y0)和点 A(1,2)在直线 l:3x+2y﹣8=0 的异侧,则() A.3x0+2y0>0 B.3x0+2y0<0 C.3x0+2y0<8 D.3x0+2y0>8 4.已知等差数列{an}的前 n 项和为 Sn,a2=﹣2,S4=﹣4,若Sn 取得最小值,则 n 的值为() A.n=2 B.n=3 C.n=2 或 n=3 D.n=4 5.在△ABC 中,a= ,b= ,A=30°,则角 B 等于()A.90°B.60°或120° C.120° D.60° 6.设 0<a<b,则下列不等式中正确的是() A.a<b<< B.a<<<b C.a<<b< D.<a<<b 7.在△ABC 中,a=2,b=3,,则其外接圆的半径为() A. B. C. D.9 8.不等式 ax2+5x+c>0 的解集为{x| <x< },则 a,c 的值为()A.a=6,c=1 B.a=﹣6,c=﹣1C.a=1,c=6 D.a=﹣1,c=﹣6 9.设△ABC,bcosC+ccosB=asinA,则△ABC 的形状为() A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定 10.数列 1 ,3 ,5 ,7 ,…,(2n﹣1)+ ,…的前 n 项和 Sn 的值为() A.n2+1﹣ B.2n2﹣n+1﹣ C.n2+1﹣ D.n2﹣n+1﹣ 11.若不等式(a ﹣2)x2+2(a﹣2)x﹣4<0 对一切x∈R 恒成立,则实数 a 取值的集合() A.{a|a≤2} B.{a|﹣2<a<2} C.{a|﹣2<a≤2} D.{a|a≤﹣ 2} 12.已知 f(x)=log2(x﹣2),若实数 m,n 满足 f(m)+f(n)=3,则 m+n 的最小值为() A.5 B.7 C.4+4 D.9 二.填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.在等差数列{an}中,S10=10,S20=30,则 S30= . 14.在△ABC 中,若∠B=30°,,AC=2,求S△ABC. 15.设 x,y 满足约束条件,则目标函数 z=3x﹣y 的最大值为. 16.已知二次函数 f(x)=ax2﹣x+c(x∈R)的值域为[0,+∞),则 + 的最小值为.3/ 8三.解答题(共 70 分) 17.求下列不等式的解集.(1)(2)x2+(2﹣a)x﹣2a≥0. 18.等差数列{an}的前 n 项和记为 Sn,已知 a10=30,a20=50.(1)求通项{an};(2)令 Sn=242,求 n. 19.如图所示,我艇在 A 处发现一走私船在方位角45°且距离为 12 海里的 B 处正以每小时 10 海里的速度向方位角105°的方向逃窜,我艇立即以 14 海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 20 .已知 a , b , c 分别为△ ABC 内角 A ,B , C 的对边,且.(1)求 A 的值.(2)若 a=2,△ABC 的面积为,求 b,c 的值. 21.已知等差数列{an}满足 an+1>an,a1=1,且该数列的前三项分别加上 1,1,3 后顺次成为等比数列{bn}的前三项.(1)求数列{an},{bn}的通项公式;(2)令 cn=an?bn,求数列{cn}的前 n 项和 Sn.22.已知函数,数列{an}满足.(1)求证:数列{ }是等差数列;(2)求数列{an}的通项公式;(3)记Sn=a1a2+a2a3+…+anan+1,求 Sn.5/ 8参考答案一.单项选择题 1. A 2. A.3. D.4. C.5. B 6. B 7. C.8. B.9. B.10. A 11. C.12. C.二.填空题 13.解:若数列{an}为等差数列则 Sm,S2m﹣Sm,S3m﹣S2m 仍然成等差数列.所以 S10,S20﹣S10,S30﹣S20 仍然成等差数列.因为在等差数列{an}中有S10=10,S20=30,所以S30=60.故答案为60. 14.解:∵∠B=30°,>AC=2,∴由正弦定理可得:sinC= = =,∴由 0<C<π 及大边对大角可得:∠C= .∴∠A=π﹣∠B﹣∠C= ,∴S△ABC= AB?AC= =2 . 15.解:由约束条件作出可行域如图,联立,解得:B(2,1),化 z=3x﹣y 为 y=3x﹣z,由图可知,当直线 y=3x﹣z 过 B(2,1)时 z 有最大值为3×2﹣1=5.故答案为:5. 16.解:∵二次函数 f(x)=ax2﹣x+c 的值域为[0,+∞),∴ ,解得 a>0,c>0,ac= .∴ + ≥2 =8,当且仅当 a=c= 时取等号,∴ + 的最小值为 8,故答案为:8 三.解答题 17.解:(1)由得,,化简得,,等价于(x+1)(x﹣1)<0,解得﹣1<x<1,∴不等式的解集是(﹣1,1);7/ 8(2)由 x2+(2﹣a)x﹣2a≥0 得,(x+2)(x﹣a)≥0,①当 a=﹣2 时,不等式的解集是 R;②当 a>﹣2 时,不等式的解集是(﹣∞,﹣2]∪[a,+∞);③当 a<﹣2 时,不等式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高二数学第一学期期中考试模拟试卷(一)(文科)(考试时间120分钟满分150分)一.单项选择题(本大题共12小题,每小题5分,满分60分)1.若直线的倾斜角为120°,则直线的斜率为()A.B.C.D.2.设m,n是自然数,条件甲:m3+n3是偶数;条件乙:m﹣n是偶数,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充分且必要条件D.既不充分也不必要条件3.点P(a,3)到直线4x﹣3y+1=0的距离等于4,则P点的坐标是()A.(7,3)B.(3,3)C.(7,3)或(﹣3,3)D.(﹣7,3)或(3,3)4.如图,正方体ABCD﹣A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线()A.AD上B.B1C1上C.A1D1上D.BC上5.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图()A.B.C.D.6.已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是()A.6:5 B.5:4 C.4:3 D.3:27.设l、m、n表示不同的直线,α、β、γ表示不同的平面,给出下列4个命题:①若m∥l,且m⊥α,则l⊥α;②若m∥l,且m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,α∩γ=n,且n∥β,则m∥l.其中正确命题的个数是()A.1 B.2 C.3 D.48.在圆x2+y2﹣2x﹣6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.B.C.D.9.直线x﹣y+m=0与圆x2+y2+2y﹣1=0有两个不同交点的一个必要而不充分条件是()A.﹣3<m<1 B.﹣2<m<0 C.﹣4<m<2 D.﹣2<m<110.如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是()A.①②B.③④C.②③D.①④11.已知正方体ABCD﹣A1B1C1D1,过A1点可作条直线与直线AC和BC1都成60°角()A.1 B.2 C.3 D.412.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B﹣AC ﹣D,则四面体ABCD的外接球的体积为()A.πB.πC.πD.π二.填空题(每小题5分,共20分)13.命题“若实数a满足a≤2,则a2<4”的否命题是命题(填“真”、“假”之一).14.对于一个底边在x轴上的正三角形ABC,边长AB=2,采用斜二测画法做出其直观图,则其直观图的面积是.15.一条直线经过P(1,2),且与A(2,3)、B(4,﹣5)距离相等,则直线l为.16.一个等腰直角三角形的顶点分别在底边长为4的正三棱柱的三条侧棱上,则此直角三角形的斜边长是.三.解答题(本大题共6小题,满分70分,第17题10分,其余各题每题12分.解答应写出文字说明,证明过程或演算步骤)17.已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,分别求满足下列条件的a,b 值(1)l1⊥l2,且直线l1过点(﹣3,﹣1);(2)l1∥l2,且直线l1在两坐标轴上的截距相等.18.如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E、F分别为PC、BD的中点.(1)求证:EF∥平面PAD;(2)求证:面PAB⊥平面PDC.19.已知圆M:x2+y2﹣4y+3=0,Q是x轴上动点,QA、QB分别切圆M于A、B两点,(1)若|AB|=,求直线MQ的方程;(2)求四边形QAMB面积的最小值.20.已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x﹣3y+16=0,CA:2x+y ﹣2=0,求:(1)∠ABC的平分线所在的直线方程;(2)AB与AC边上的中位线所在直线方程.21.已知三棱柱ABC﹣A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.(Ⅰ)求证:BB′⊥底面ABC;(Ⅱ)在棱A′B′上找一点M,使得C′M∥面BEF,并给出证明.22.已知圆C:x2+(y﹣3)2=4,一动直线l过A(﹣1,0)与圆C相交于P、Q两点,M是PQ中点,l与直线m:x+3y+6=0相交于N.(Ⅰ)求证:当l与m垂直时,l必过圆心C;(Ⅱ)当时,求直线l的方程;(Ⅲ)探索是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.参考答案一.单项选择题1.B 2.C 3.C.4.B.5.D.6.D.7.B.8.B.9.C 10.D.11.C.12.C.二.填空题13.解:命题的否命题为:“若实数a满足a>2,则a2≥4”∵a>2∴a2>4∴a2≥4∴否命题为真命题故答案为:真14.解:如图所示,A′B′=AB=2,O′C′==,作C′D′⊥x′,则C′D′==.∴其直观图的面积===.故答案为:.15.解:①当所求直线与AB平行时,k AB==﹣4,可得y﹣2=﹣4(x﹣1),化为4x+y﹣6=0;②当所求直线经过线段AB的中点M(3,﹣1)时,k==﹣,可得y﹣2=﹣(x ﹣1),化为3x+2y﹣7=0.综上可得所求直线方程为:4x+y﹣6=0;或3x+2y﹣7=0.故答案为:4x+y﹣6=0;或3x+2y﹣7=0.16.解:如图,正三棱柱ABC﹣A1B1C1中,△ABC为正三角形,边长为4,△DEF为等腰直角三角形,DF为斜边,设DF长为x,则DE=EF=,作DG⊥BB1,HG⊥CC1,EI⊥CC1,则EG==,FI==,FH=FI+HI=FI+EG=2,在Rt△DHF中,DF2=DH2+FH2,即x2=16+(2)2,解得x=4.即该三角形的斜边长为4.故答案为:4.三.解答题17.解:(1)∵两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0且l1⊥l2,∴a(a﹣1)+(﹣b)×1=0,即a2﹣a﹣b=0,又∵直线l1过点(﹣3,﹣1),∴﹣3a+b+4=0,联立解得a=2,b=2;(2)由l1∥l2可得a×1﹣(﹣b)(a﹣1)=0,即a+ab﹣b=0,在方程ax﹣by+4=0中令x=0可得y=,令y=0可得x=﹣,∴=﹣,即b=﹣a,联立解得a=2,b=﹣2.18.证明:(1)连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.所以在△CPA中,EF∥PA,又PA⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD;(2)平面PAD⊥平面ABCD平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA正方形ABCD中CD⊥ADPA⊂平面PADCD⊂平面ABCD又,所以PA2+PD2=AD2所以△PAD是等腰直角三角形,且,即PA⊥PD.因为CD∩PD=D,且CD、PD⊂面PDC所以PA⊥面PDC又PA⊂面PAB,所以面PAB⊥面PDC.19.解:(1)圆M:x2+y2﹣4y+3=0,即x2+(y﹣2)2=1,圆心M(0,2),半径r=1.由+MN2=r2=1,求得:MN=.由BM2=MNMQ,求得MQ=3.设Q(x0,0),则=3,即x0=±.所以直线MQ的方程为2x+y﹣2=0 或2x﹣y+2=0.(2)易知,当MQ取得最短时,四边形QAMB面积的最小值,即Q与O重合,此时,QA=,即四边形QAMB面积的最小值为1×=.20.解:(1)由求得,可得点B的坐标为(﹣4,0).设∠ABC的内角平分线所在直线的斜率为k,则=,即=.求得k=,或k=﹣7.由题意可得,∠ABC的内角平分线所在直线的斜率k应在BA、BC的斜率之间,故取k=,故∠ABC的平分线所在的直线方程为y﹣0=(x+4),即x﹣7y+4=0.(2)由,求得,可得点A的坐标为(4,﹣6),故线段AB的中点D的坐标为(0,﹣3),再根据AB与AC边上的中位线所在直线的斜率等于BC的斜率,故AB与AC边上的中位线所在直线方程为y+3=(x﹣0),即4x﹣3y﹣9=0.21.(Ⅰ)证明:取BC中点O,因为三角形ABC是等边三角形,所以AO⊥BC,又因为面BCC'B'⊥底面ABC,AO⊂面ABC,面BCC'B'∩面ABC=BC,所以AO⊥面BCC'B',又BB'⊂面BCC'B',所以AO⊥BB'.又BB'⊥AC,AO∩AC=A,AO⊂面ABC,AC⊂面ABC,所以BB'⊥底面ABC.(Ⅱ)显然M不是A',B',当M为A'B'的中点,使得C'M∥面BEF.证明:过M作MN∥AA'交BE于N,则N为中点,则MN=(A'E+B'B)=2,则MN=C'F,MN∥C'F,所以四边形C'MNF为平行四边形,所以C'M∥FN,C'M⊄平面BEF,NF⊂平面BEF,所以C'M∥面BEF.22.解:(Ⅰ)∵直线l与直线m垂直,且,∴k l=3,又k AC=3,所以当直线l与m垂直时,直线l必过圆心C;(Ⅱ)①当直线l与x轴垂直时,易知x=﹣1符合题意,②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),即kx﹣y+k=0,因为,所以,则由CM==1,得,∴直线l:4x﹣3y+4=0.从而所求的直线l的方程为x=﹣1或4x﹣3y+4=0;(Ⅲ)因为CM⊥MN,∴,当直线l与x轴垂直时,易得,则,又,∴,当直线l的斜率存在时,设直线l的方程为y=k(x+1),则由,得N(,),则,∴=,综上,与直线l的斜率无关,且.。
