插值与曲线拟合实验报告
曲线拟合与插值实验报告

东南大学《数学实验》报告学号姓名成绩实验内容:曲线拟合与插值一实验目的用最小二乘法实现多项式拟合;3次样条函数的应用二预备知识(1)熟悉一般的曲线拟合的最小二乘法原则(2)熟悉正规方程、差分表、均差表的概念(3)熟悉“\”、polyfit、polyval、interp1、spline等Matlab命令三实验内容与要求O氨下表给出了氨蒸汽的一组温度和压力数据。
那么能否从所列的数据中计算75C蒸汽的压力?表氨蒸汽的压力和温度O) 20 25 30 35 40 45 50 55 60 温度(C压力(kN/m2) 805 985 1170 1365 1570 1790 2030 2300 2610(1)用p o l y f i t、p o l y v a l命令求解氨蒸汽问题(2)用解正规方程的方法令求解氨蒸汽问题(3)已知某平原地区的一条公路经过如下坐标点,请用不同的插值方法绘出这条公路(不考虑公路的宽度)。
对于上表给出的数据,编程计算三次样条插值估计的公路长度。
X(m) 0 30 50 70 80 90 120 148 170 180Y(m) 80 64 47 42 48 66 80 120 121 138X(m) 202 212 230 248 268 271 280 290 300 312Y(m) 160 182 200 208 212 210 200 196 188 186X(m) 320 340 360 372 382 390 416 430 478 440Y(m) 200 184 188 200 202 240 246 280 296 308X(m) 420 380 360 340 320 314 280 240 200Y(m)334 328 334 346 356 360 392 390 400。
matlab插值与曲线拟合实验报告

湖南大学电气与信息工程学院 《数值计算》课程 上机实验报告姓名: 班级: 学号: 日期:指导老师:本次实验题号:第 3 次实验1) 实验目的:1) 用MATLAB 实现拉格朗日插值和分段线性插值。
2) 了解matlab 实现曲线拟合方法的实际应用。
二. 实验内容:1) 插值算法的应用:题目:用拉格朗日插值程序,分段线形插值函数分别研究f (X )的数据表,计算f(0.472) X 0.46 0.47 0.48 0.49 Y0.48465550.49375420.50274980.51166832) 曲线拟合方法的实际应用用电压V=10V 的电池给电容器充电,电容器上t 时刻的电压v(t)=V-(V-V0)e^(-t/T),其中V0是电容器的初始电压,T 是充电常数。
实验测量了一组数据如下,请根据数据表确定V0和T 的大小。
t 0.5 1 2 3 4 5 7 9 V(t) 6.366.487.268.228.668.999.439.63三. 算法介绍或方法基础1.1 拉格朗日插值法对于已给定的点 00(,),...,(,)k k x y x y 和待估计的点的横坐标x ,如上述理论,将其值代入1100,011()()()()():......()()()()kj j i k j i i j j i j j j j j j kx x x x x x x x x x l x x x x x x x x x x x -+=≠-+-----==-----∏计算出插值基函数的值,然后根据公式:():()ki i j L x y l x ==∑计算出纵坐标的估计值,由此完成对该点的插值过程,其中k 为该点插值的阶数。
1.2 线性分段插值利用已给定的点 00(,),...,(,)k k x y x y 对插值区间分为1k -段,将每段的端点(,)i i x y 与 11(,)i i x y ++作为数据点利用公式100010()()()()()f x f x p x f x x x x x -=+--在所构成的区间进行线性插值。
插值与拟合试验

实验:插值与拟合实验目的1.掌握用MATLAB计算拉格朗日、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值的结果进行初步的分析。
2.掌握用MATLAB作线性最小二乘的方法。
3.通过实例学习如何用插值方法与拟合方法解决实际问题,注意二者的联系和区别。
实验内容选择一些函数,在n个节点上(n不要太大,如5~11)用拉格朗日、分段线性、三次样条三种插值方法,计算m个插值点的函数值(m要适中,如50~100)。
通过数值和图形输出,将三种插值结果与精确值进行比较。
适当增加n,再作比较,由此作初步分析。
y=exp(-x2),-2≤x≤2.取n=5,m=80用MATLAB计算插值数据比较如下:y是精确值,y1是分段线性值,y2是三次样条法插值,y3是拉格朗日插值由于对称性,只给出x>0的值程序:function y=lagr(x0,y0,x)%函数输入:n个节点以数组x0,y0输入,m个插值点以数组x输入?%函数输出:输出数组y为m个插值?n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); endends=p*y0(k)+s;endy(i)=s;end结果:x0=-2:0.5:2;y0=exp(-1*x0.^2);x=-2:0.05:2y=exp(-1*x.^2);y1=lagr(x0,y0,x);y2=interp1(x0,y0,x);y3=spline(x0,y0,x);[x;y;y1;y2;y3]'plot(x,y,'k--',x,y1,'r'),xlabel('x')ylabel('y/y1')title('拉格朗日插值(n=9,m=21)'),legend('原函数曲线','拉格朗日插值曲线'), pause,plot(x,y,'k--',x,y2,'r'),xlabel('x')ylabel('y/y2')title('分段线性插值(n=9,m=21)'),legend('原函数曲线','分段线性插值曲线'), pause,plot(x,y,'k--',x,y3,'r'),xlabel('x')ylabel('y/y1')title('三次样条插值(n=9,m=21)'),legend('原函数曲线','三次样条插值曲线'), x =Columns 1 through 9-2.0000 -1.9500 -1.9000 -1.8500 -1.8000 -1.7500 -1.7000 -1.6500 -1.6000Columns 10 through 18-1.5500 -1.5000 -1.4500 -1.4000 -1.3500 -1.3000 -1.2500 -1.2000 -1.1500Columns 19 through 27-1.1000 -1.0500 -1.0000 -0.9500 -0.9000 -0.8500 -0.8000 -0.7500 -0.7000Columns 28 through 36-0.6500 -0.6000 -0.5500 -0.5000 -0.4500 -0.4000 -0.3500 -0.3000 -0.2500Columns 37 through 45-0.2000 -0.1500 -0.1000 -0.0500 0 0.0500 0.1000 0.1500 0.2000Columns 46 through 540.2500 0.3000 0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500Columns 55 through 630.7000 0.7500 0.8000 0.8500 0.9000 0.9500 1.0000 1.0500 1.1000Columns 64 through 721.1500 1.2000 1.2500 1.3000 1.3500 1.4000 1.4500 1.5000 1.5500Columns 73 through 811.6000 1.6500 1.7000 1.7500 1.8000 1.8500 1.9000 1.95002.0000ans =-2.0000 0.0183 0.0183 0.0183 0.0183 -1.9500 0.0223 0.0048 0.0270 0.0207 -1.9000 0.0271 0.0011 0.0357 0.0243 -1.8500 0.0326 0.0044 0.0444 0.0292 -1.8000 0.0392 0.0127 0.0531 0.0355 -1.7500 0.0468 0.0243 0.0619 0.0433 -1.7000 0.0556 0.0381 0.0706 0.0525 -1.6500 0.0657 0.0535 0.0793 0.0633 -1.6000 0.0773 0.0700 0.0880 0.0757 -1.5500 0.0905 0.0873 0.0967 0.0897 -1.5000 0.1054 0.1054 0.1054 0.1054 -1.4500 0.1222 0.1244 0.1316 0.1229 -1.4000 0.1409 0.1446 0.1579 0.1421 -1.3500 0.1616 0.1660 0.1841 0.1633 -1.3000 0.1845 0.1889 0.2104 0.1863 -1.2500 0.2096 0.2136 0.2366 0.2114 -1.2000 0.2369 0.2402 0.2629 0.2384 -1.1500 0.2665 0.2689 0.2891 0.2675-1.1000 0.2982 0.2998 0.3154 0.2988 -1.0500 0.3320 0.3328 0.3416 0.3322 -1.0000 0.3679 0.3679 0.3679 0.3679 -0.9500 0.4056 0.4050 0.4090 0.4058 -0.9000 0.4449 0.4439 0.4501 0.4455 -0.8500 0.4855 0.4844 0.4912 0.4867 -0.8000 0.5273 0.5261 0.5322 0.5288 -0.7500 0.5698 0.5687 0.5733 0.5716 -0.7000 0.6126 0.6117 0.6144 0.6145 -0.6500 0.6554 0.6547 0.6555 0.6571 -0.6000 0.6977 0.6972 0.6966 0.6989 -0.5500 0.7390 0.7388 0.7377 0.7397 -0.5000 0.7788 0.7788 0.7788 0.7788 -0.4500 0.8167 0.8168 0.8009 0.8159 -0.4000 0.8521 0.8524 0.8230 0.8507 -0.3500 0.8847 0.8850 0.8452 0.8827 -0.3000 0.9139 0.9142 0.8673 0.9117 -0.2500 0.9394 0.9397 0.8894 0.9372 -0.2000 0.9608 0.9610 0.9115 0.9588 -0.1500 0.9778 0.9779 0.9336 0.9763 -0.1000 0.9900 0.9901 0.9558 0.9892 -0.0500 0.9975 0.9975 0.9779 0.99720 1.0000 1.0000 1.0000 1.0000 0.0500 0.9975 0.9975 0.9779 0.9972 0.1000 0.9900 0.9901 0.9558 0.9892 0.1500 0.9778 0.9779 0.9336 0.9763 0.2000 0.9608 0.9610 0.9115 0.9588 0.2500 0.9394 0.9397 0.8894 0.9372 0.3000 0.9139 0.9142 0.8673 0.9117 0.3500 0.8847 0.8850 0.8452 0.8827 0.4000 0.8521 0.8524 0.8230 0.8507 0.4500 0.8167 0.8168 0.8009 0.8159 0.5000 0.7788 0.7788 0.7788 0.7788 0.5500 0.7390 0.7388 0.7377 0.7397 0.6000 0.6977 0.6972 0.6966 0.6989 0.6500 0.6554 0.6547 0.6555 0.6571 0.7000 0.6126 0.6117 0.6144 0.6145 0.7500 0.5698 0.5687 0.5733 0.5716 0.8000 0.5273 0.5261 0.5322 0.5288 0.8500 0.4855 0.4844 0.4912 0.4867 0.9000 0.4449 0.4439 0.4501 0.44550.9500 0.4056 0.4050 0.4090 0.40581.0000 0.3679 0.3679 0.3679 0.3679 1.0500 0.3320 0.3328 0.3416 0.33221.1000 0.2982 0.2998 0.3154 0.2988 1.1500 0.2665 0.2689 0.2891 0.2675 1.2000 0.2369 0.2402 0.2629 0.2384 1.2500 0.2096 0.2136 0.2366 0.2114 1.3000 0.1845 0.1889 0.2104 0.1863 1.3500 0.1616 0.1660 0.1841 0.1633 1.4000 0.1409 0.1446 0.1579 0.1421 1.4500 0.1222 0.1244 0.1316 0.1229 1.5000 0.1054 0.1054 0.1054 0.1054 1.5500 0.0905 0.0873 0.0967 0.0897 1.6000 0.0773 0.0700 0.0880 0.0757 1.6500 0.0657 0.0535 0.0793 0.0633 1.7000 0.0556 0.0381 0.0706 0.0525 1.7500 0.0468 0.0243 0.0619 0.0433 1.8000 0.0392 0.0127 0.0531 0.0355 1.8500 0.0326 0.0044 0.0444 0.0292 1.9000 0.0271 0.0011 0.0357 0.02431.9500 0.0223 0.0048 0.0270 0.02072.0000 0.0183 0.0183 0.0183 0.0183上图是根据插值数据作出的曲线。
数值分析实验报告--插值与拟合及其并行算法

《数值分析》实验报告实验五、插值与拟合及其并行算法一.实验目的:1.学会拉格朗日插值, 分段线性插值或三次样条插值以及曲 线拟合等数值分析问题,通过 MATLAB 编程解决这些数 值分析问题,并且加深对此次实验内容的理解。
2.加强编程能力和编程技巧,练习从数值分析角度看问题, 同时用 MATLAB 编写代码。
二.实验要求:学会在计算机上实现拉格朗日插值,分段线性插值或三次 样条插值以及曲线拟合等数值分析问题,分析几种插值方法的异 同。
三.实验内容:分别用下列题目完成①:拉格朗日插值及其误 差分析 ②:三次样条 ③: 曲线拟合及其误差分析,实验要求。
四.实验题目: (1)已知 sin 30 D = 0.5 , sin 45D = 0.707 1 ,sin 60 D = 0.866 0 ,用拉格朗日插值及其误差估计的MATLAB主程序求 sin 20D 的近似值,并估计其误差。
(2)观测得出函数 y=f(x)在若干点处的值为 f(0)=0, f(2)=16, f(4)=36, f(6)=54, f(10)=82 和 f'(0)=8, f'(10)=7, 试求 f(x)的三次样条函数,并计算 f(3)和 f(8)的近似值. ( 3 ) t=[2.1 7.9 10.1 13 14.5 15.3];r=[13.5 36.9 45.7 求出 r 与 t 之间的关系, 及三 57.3 62.78 74.9];根据给出数据, 种误差,并作出拟合曲线。
五.实验原理:(1)拉格朗日插值公式:P5 ( x) = ∑ y i l i ( x)i =05li ( x) =( x − x 0 ) " ( x − xi −1 )( x − xi +1 ) " ( x − x n ) ( xi − x0 ) " ( xi − xi −1 )( xi − xi +1 ) " ( xi − x n )(2)三次样条插值公式:Sn(x)={Si(x)=a i x +b i x +c i x+d i , x ∈ [x i −1 ,x i ] ,i=1,2,….,n}32(3)曲线拟合: 最小二乘法并不只限于多项式,也可以用于任何具体给出的函数 形式。
插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点,并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等,并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法(1)给定一组数据点,如:$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$(2)根据拉格朗日插值公式,构造插值多项式:$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$(3)计算插值多项式在不同点的函数值,并与实际值进行比较。
数值计算插值法与拟合实验

dy0=-10.*(1-5.^4)./(1+5.^4).^2;dyn=10.*(1-5.^4)./(1+5.^4).^2;
m=maspline(x1,y1,dy0,dyn,xx);
plot(xx,m,'ok')
2、
程序:
x=[-1.5 -1.0 -0.5 0.0 0.5 1.0 1.5]';
plot(xx,m,'ok')
第二个方程
程序
x=-5:0.2:5;
y=atan(x);
plot(x,y,'r');
hold on
x1=-5:1:5;
y1=atan(x1);
xx=-4.5:0.5:4.5;
yy=malagr(x1,y1,xx);
plot(xx,yy,'+')
dy0=1./(1+25);dyn=1./(1+25);
实验报告三
一、实验目的
通过本实验的学习,各种插值法的效果,如多项式插值法,牛顿插值法,样条插值法,最小二乘法拟合(即拟合插值),了解它们各自的优缺点及插值。
二、实验题目
1、插值效果比较
实验题目:将区间 10等份,对下列函数分别计算插值节点 的值,进行不同类型的插值,作出插值函数的图形并与 的图形进行比较:
y=[-4.45 -0.45 0.55 0.05 -0.44 0.54 4.55]';
plot(x,y,'or');hold on
%三.2:1.5;
y1=p1(1)*x1.^3+p1(2)*x1.^2+p1(3)*x1+p1(4);
插值与拟合实验报告

学生实验报告了解插值与拟合的基本原理和方法;掌握用MATLAB计算插值与作最小二乘多项式拟合和曲线拟合的方法;通过范例展现求解实际问题的初步建模过程;通过动手作实验学习如何用插值与拟合方法解决实际问题,提高探索和解决问题的能力。
这对于学生深入理解数学概念,掌握数学的思维方法,熟悉处理大量的工程计算问题的方法具有十分重要的意义。
二、实验仪器、设备或软件:电脑,MATLAB软件三、实验内容1.编写插值方法的函数M文件;2.用MATLAB中的函数作函数的拟合图形;3.针对实际问题,试建立数学模型,并求解。
四、实验步骤1.开启软件平台——MATLAB,开启MATLAB编辑窗口;2.根据各种数值解法步骤编写M文件;3.保存文件并运行;4.观察运行结果(数值或图形);5.写出实验报告,并浅谈学习心得体会。
五、实验要求与任务根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会)。
1.天文学家在1914年8月的7次观测中,测得地球与金星之间距离(单位:米),并取得常用对数值,与日期的一组历史数据如下表:由此推断何时金星与地球的距离(米)的对数值为9.93518?解:输入命令days=[18 20 22 24 26 28 30];distancelogs=[9.96177 9.95436 9.94681 9.93910 9.93122 9.92319 9.91499]; t1=interp1(distancelogs,days,9.93518) %线性插值t2=interp1(distancelogs,days,9.93518,'nearest') %最近邻点插值t3=interp1(distancelogs,days,9.93518,'spline') %三次样条插值t4=interp1(distancelogs,days,9.93518,'cubic') %三次插值计算结果:t1 =24.9949t2 =24t3 =25.0000t4 =25.0000综上所得,可推断25日金星与地球的距离(米)的对数值为9.93518。
插值与曲线拟合实验报告

数值计算方法插值与拟合实验报告摘要:通过实验介绍插值方法中常见的拉格朗日插值,线性分段插值和牛顿前插公式,分析计算各种方法的插值余项。
在曲线拟合方面使用两种不同类型的曲线来拟合同一组数据,并计算残差向量范数,比较不同曲线拟合的效果,在此例上给出优劣的判断。
关键词:拉格朗日插值;线性分段插值;牛顿前插公式;曲线拟合引言在工程和科学计算中经常碰到只知道离散的数据测量点而需要匹配其变量之间的数学函数表达式的情况,这就需要插值和拟合的数值方法来解决这些问题。
插值法是在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点,也是离散函数逼近的重要方法,利用它可通过函数在有限点处的取值状况,估算出函数在其他点处的近似值。
曲线拟合则是用连续曲线近似地刻画或比拟平面上离散点所表示的坐标之间的函数关系,在各个方面也有着愈加广泛的应用。
1 算法介绍1.1 拉格朗日插值法 1.1.1 算法理论对某个多项式函数,已知有给定的k +1个取值点:00(,),...,(,)k k x y x y其中i x 对应着自变量的位置,而i y 对应着函数在这个位置的取值。
假设任意两个不同的x j 都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:():()ki i j L x y l x ==∑其中每个()j l x 为拉格朗日基本多项式(或称插值基函数),其表达式为:1100,011()()()()():......()()()()kj j i k j i i j j ij j j j j j k x x x x x x x x x x l x x x x x x x x x x x -+=≠-+-----==-----∏拉格朗日基本多项式 ()j l x 的特点是在 j x 上取值为1,在其它的点 ,i x ij ≠上取值为0。
对于给定的 1k +个点:00(,),...,(,)k k x y x y ,拉格朗日插值法的思路是找到一个在一点j x 取值为1,而在其他点取值都是0的多项式()j l x 。
插值法和拟合实验报告

插值法和拟合实验报告一、实验目的1.通过实验了解插值法和拟合法在数值计算中的应用;2.掌握拉格朗日插值法、牛顿插值法和分段线性插值法的原理和使用方法;3.学会使用最小二乘法进行数据拟合。
二、实验仪器和材料1.一台计算机;2. Matlab或其他适合的计算软件。
三、实验原理1.插值法插值法是一种在给定的数据点之间“插值”的方法,即根据已知的数据点,求一些点的函数值。
常用的插值法有拉格朗日插值法、牛顿插值法和分段线性插值法。
-拉格朗日插值法:通过一个n次多项式,将给定的n+1个数据点连起来,构造出一个插值函数。
-牛顿插值法:通过递推公式,将给定的n+1个数据点连起来,构造出一个插值函数。
-分段线性插值法:通过将给定的n+1个数据点的连线延长,将整个区间分为多个小区间,在每个小区间上进行线性插值,构造出一个插值函数。
2.拟合法拟合法是一种通过一个函数,逼近已知的数据点的方法。
常用的拟合法有最小二乘法。
-最小二乘法:通过最小化实际观测值与拟合函数的差距,找到最优的参数,使得拟合函数与数据点尽可能接近。
四、实验步骤1.插值法的实验步骤:-根据实验提供的数据点,利用拉格朗日插值法、牛顿插值法、分段线性插值法,分别求出要插值的点的函数值;-比较三种插值法的插值结果,评价其精度和适用性。
2.拟合法的实验步骤:-根据实验提供的数据点,利用最小二乘法,拟合出一个合适的函数;-比较拟合函数与实际数据点的差距,评价拟合效果。
五、实验结果与分析1.插值法的结果分析:-比较三种插值法的插值结果,评价其精度和适用性。
根据实验数据和插值函数的图形,可以判断插值函数是否能较好地逼近实际的曲线。
-比较不同插值方法的计算时间和计算复杂度,评价其使用的效率和适用范围。
2.拟合法的结果分析:-比较拟合函数与实际数据点的差距,评价拟合效果。
可以使用均方根误差(RMSE)等指标来进行评价。
-根据实际数据点和拟合函数的图形,可以判断拟合函数是否能较好地描述实际的数据趋势。
matlab实验报告 插值和拟合
建模中数据处理和分析班级 学号 姓名 实验地点 完成日期 成绩(一)实验目的与要求应用matlab 处理数据并分析,主要学会并熟练掌握数据拟合和插值。
(二)实验内容1. 用下面一组数据拟合ktbea t c 02.0)(-+=中的参数a ,b ,k2.在某山区测得一些地点的高程如下表。
平面区域为 1200<=x<=4000,1200<=y<=3600) 试作出该山区的地貌图X Y 120016002000240028003200360040001200 1130 1250 1280 1230 1040 900 500 700 1600 1320 1450 1420 1400 1300 700 900 850 2000 1390 1500 1500 1400 900 1100 1060 950 2400 1500 1200 1100 1350 1450 1200 1150 1010 2800 1500 1200 1100 1550 1600 1550 1380 1070 3200 1500 1550 1600 1550 1600 1600 1600 1550 36001480 1500 1550 1510 1430 1300 1200 980(三)实验具体步骤 实验1要先建立一个M 文件,文件中代码如下: function F=myfun(x,xdata) F=x(1)+x(2)*exp(-0.02*x(3)*xdata) 接下来在command window 中输入如下代码: Clc Clearxdata=[100:100:1000];ydata=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59]/1000; x0=[0.2 0.05 0.05];[x,resnorm]=lsqcurvefit(@myfun,x0,xdata,ydata) 接着MATLAB 会进行若干次运算,并给出结果:所以拟合的结果是a=0.0063,b=-0.0034,c=0.2542 然后,我们作图看看拟合的结果,输入代码plot(xdata,0.0063-0.0034*exp(-0.02*0.2542*xdata),xdata,ydata,'o') 得到图像如下:实验二建立一个m 文件,在其中输入代码如下: x=1200:400:4000;y=1200:400:3600;100200300400500600700800900100044.555.566.57x 10-3temps=[1130 1250 1280 1230 1040 900 500 700;1320 1450 1420 1400 1300 700 900 850;1390 1500 1500 1400 900 1100 1060 950;1500 1200 1100 1350 1450 1200 1150 1010;1500 1200 1100 1550 1600 1550 1380 1070;1500 1550 1600 1550 1600 1600 1600 1550;1480 1500 1550 1510 1430 1300 1200 980];mesh(x,y,temps)xi=1200:30:4000;yi=1200:30:3600;zi=interp2(x,y,temps,xi',yi,'cubic');mesh(xi,yi,zi)meshz(xi,yi,zi)colordef black运行后打开图形窗口的属性设置对话框,对背景,颜色等属性进行设置,得到下图:(四)实验结果实验中顺利得到拟合结果以及一个三维图像,虽然过程艰辛,但结果十分美好。
插值法和拟合实验报告(数值计算)

插值法和拟合实验报告一、实验目的1.通过进行不同类型的插值,比较各种插值的效果,明确各种插值的优越性;2.通过比较不同次数的多项式拟合效果,了解多项式拟合的原理;3.利用matlab 编程,学会matlab 命令;4.掌握拉格朗日插值法;5.掌握多项式拟合的特点和方法。
二、实验题目1.、插值法实验将区间[-5,5]10等分,对下列函数分别计算插值节点kx 的值,进行不同类型的插值,作出插值函数的图形并与)(x f y =的图形进行比较:;11)(2x x f += ;arctan )(x x f = .1)(42x x x f +=(1) 做拉格朗日插值; (2) 做分段线性插值; (3) 做三次样条插值.2、拟合实验给定数据点如下表所示:分别对上述数据作三次多项式和五次多项式拟合,并求平方误差,作出离散函数),(i i y x 和拟合函数的图形。
三、实验原理1.、插值法实验∏∑∏∏∏∑∑≠==≠=≠=≠=+-==--==-===-=-=----==++==ji j ji i i i i ni i n nji j jnji j ji i nji j jn i i i ni i n nn o i ni i n x x x x x y x l x L x x c ni x x c x x x cx x x x x x x x c y x l x L y x l y x l y x l x L ,00,0,0,0110000)(l )()()(1,1,0,1)()(l )()())(()()()()()()()(,故,得再由,设2、拟合实验四、实验内容1.、插值法实验1.1实验步骤:打开matlab软件,新建一个名为chazhi.m的M文件,编写程序(见1.2实验程序),运行程序,记录结果。
1.2实验程序:x=-5:1:5;xx=-5:0.05:5;y1=1./(1+x.^2);L=malagr(x,y1,xx);L1=interp1(x,y1,x,'linear');S=maspline(x,y1,0.0148,-0.0148,xx);hold on;plot(x,y1,'b*');plot(xx,L,'r');plot(x,L1,'g');plot(xx,S,'k');figurex=-5:1:5;xx=-5:0.05:5;y2=atan(x);L=malagr(x,y2,xx);L1=interp1(x,y2,x,'linear');S=maspline(x,y2,0.0385,0.0385,xx);hold on;plot(x,y2,'b*');plot(xx,L,'r');plot(x,L1,'g');plot(xx,S,'k');figurex=-5:1:5;xx=-5:0.05:5;y3=x.^2./(1+x.^4);L=malagr(x,y3,xx);L1=interp1(x,y3,x,'linear');S=maspline(x,y3,0.0159,-0.0159,xx);hold on;plot(x,y3,'b*');plot(xx,L,'r');plot(x,L1,'g');plot(xx,S,'k');1.3实验设备:matlab软件。
实验一 插值与拟合

实验一、数据插值与曲线拟合【实验目的】1.了解数据插值、曲线拟合的概念和原理。
2.掌握一维、二维的数据插值方法。
3.掌握多项式拟合方法和一般曲线拟合方法。
【实验内容】把题目和相应的完整命令写在实验报告上。
1.数据插值有什么插值方式?曲线拟合依据的基本原理是什么?数据插值与曲线拟合有什么不同点?2.某实验室对一根长10米的钢轨进行热源的温度在60秒内传播测试。
x:表示测量点,h:测量时间,t:测量得到的(1)用线性插值求出在25秒时3.6米处钢轨的温度。
(2)用样条插值求出在这60秒内每隔20秒,钢轨每隔1米处的温度。
3.用命令polyfit来验证课本《数学模型》第10页中“参数估计”部分式子(4)的各参数。
【相关知识说明】1.数据插值问题1:某气温测量站,在某一天的早上6时至傍晚5时内,每隔1小时测量一次气温,得到下表试估计在h=8.2,11.5,12.1,16.7时的气温值。
类似上面,在工程测量和科学实验中,往往测量出一批数据,例如n 个数据1122(,),(,),,(,)n n x y x y x y ,这些数据点反映了一个函数关系()y F x =,然而我们并不知道()F x 的表达式是怎么样的。
数据插值的任务就是根据已测得的数据构造一个函数()y f x =,使得在(1,2,,)i x i n =处,有()()i i f x F x =,且在两个相邻的采样点之间,()f x 光滑过度。
数据插值的基本思路是构造一个相对简单的函数()y f x =,通过全部的数据点1122(,),(,),,(,)n n x y x y x y ,即(),1,2,,i i y f x i n ==。
再用()f x 来计算要插值的点。
(1)一维数据插值的命令(MATLAB 语言,下同)cx是需要插值的数据。
method为可选参数,表示要用什么方式来插值:注意:x的数据必须单调,cx不能超出x的范围。
(2)二维数据插值的命令现在我们来看怎么回答问题1,这是一维插值问题。
插值与曲线拟合实验报告

插值与曲线拟合实验报告实验目的:1. 了解插值和曲线拟合的原理和方法;2. 掌握梯形公式的应用;3. 掌握拉格朗日插值多项式和牛顿插值多项式的构造方法;4. 掌握用MATLAB进行数据拟合的方法。
实验仪器:1. 计算机;2. MATLAB软件。
实验原理:插值:给定一组数据点,插值就是在这些数据点之间插入某些值,以尽量接近原函数的方式得到一个新的函数。
插值方法有很多种,其中比较常用的是拉格朗日插值多项式和牛顿插值多项式。
拉格朗日插值多项式:以一种通用的方式构造多项式,使其通过给定的一组数据点。
构造方法是依据n个数据点(x1,y1),(x2,y2),…,(xn,yn)构造n-1次函数L(x),使得L(xi)=yi且有L(xj)=0(j不等于i)。
该多项式的形式为:L(x)=y1*L1(x)+y2*L2(x)+…+yn*Ln(x)其中,Lk(x)的构造方法是:Lk(x)=(x-x1)(x-x2)…(x-xk-1)(x-xk+1)…(x-xn) /(xk-x1)(xk-x2)…(xk-xk-1)(xk-xk+1)…(xk-xn)牛顿插值多项式:采用递推公式构造,其形式为:其中,f(x0,x1)表示在x0和x1之间的斜率,f(x0,x1,x2)表示在x0、x1和x2之间的曲率,以此类推。
曲线拟合:给定一组数据点,拟合就是寻找一个函数或者曲线,以最优化的方式拟合这些数据点,从而对未知的数据点进行预测。
拟合方法有很多种,其中比较常用的是线性方程、最小二乘法和多项式拟合。
最小二乘法:使用这种方法时,需要有一个数学模型,以此作为拟合函数。
当给定输入-输出数据时,使用最小二乘法以最小化误差平方和的方式来确定函数中未知的参数。
在MATLAB中使用polyfit函数实现多项式拟合。
实验结果:选择数据点如下:x = [1,2,3,4,5];y = [0.7652, 0.6347, 0.4496, 0.2499, 0.0621];使用梯形公式计算插值结果为 0.3865;使用拉格朗日插值多项式计算插值结果为 0.3865;使用牛顿插值多项式计算插值结果为 0.3865。
数学实验8-曲线拟合及插值

23
a =1.0e+006 *
-0.00000000000014
0.00000000107892 -0.00000304878595
0.00381927346813
-1.79012132225427
仿真结果表明, 人口增加的模型用多项式拟合能 比较准确地反映人口自然增长的规律,对长期预 测具有指导意义。
8
7 0 2 4 6 8 10 12 14 16 18 20
The length of the label is
L= 26.3809 (m)
% prog45.m This program is to fit the data by polynomial %
format long t=linspace(0,20,21); x=linspace(0,20,100); P=[9.01,8.96,7.96,7.97,8.02,9.05,10.13,11.18,12.26,13.2 8,13.32,12.61,11.29,10.22,9.15,7.90,7.95,8.86,9.81,10.8 0,10.93]; [a,s]=polyfit(t,P,12); yy=polyval(a,x); plot(x,yy,'r*--',t,P,'b+-'); L=0; for i=2:100 L=L+sqrt((x(i)-x(i-1))^2+(yy(i)-yy(i-1))^2); end disp('The length of the label is L=');disp(L);
实验13 人口数量预测模型实验
实验目的
1、学会用MATLAB软件 进行数据拟合 2、掌握在最小二乘意 义下数据拟合的理论和 方法. 3、通过对实际问题的 分析和研究,初步掌 握建立数据拟合数学 模型的方法
插值与拟合的实验报告心得

插值与拟合的实验报告心得1.引言1.1 概述插值与拟合是数值分析和数据处理领域中常见的重要技术方法,通过对已知数据点进行插值计算,得到未知点的数值估计。
插值方法可以帮助我们填补数据间的空缺、平滑曲线和预测未来趋势,因此在科学研究、工程建模和数据分析中具有广泛的应用价值。
本实验报告将对插值的基本概念进行介绍,探讨插值方法的分类和在实际应用中的意义。
同时,我们将总结实验结果,评述插值与拟合的优缺点,并提出对进一步研究的建议,希望通过本报告对插值与拟合的方法和应用有一个全面的了解。
1.2文章结构文章结构部分的内容可以包括:在本报告中,将包括以下几个部分的内容:1. 引言:介绍插值与拟合的基本概念,以及本实验的目的和意义。
2. 正文:包括插值的基本概念、插值方法的分类以及插值在实际应用中的意义。
我们将深入探讨这些内容,并解释它们在实验中的具体应用。
3. 结论:总结本次实验的结果,分析插值与拟合的优缺点,并提出对进一步研究的建议。
通过以上内容的分析和探讨,我们希望能够全面地了解插值与拟合的理论基础和实际应用,为进一步的研究和实践提供一定的参考和启发。
1.3 目的本实验的目的在于通过对插值和拟合的实验研究,探索和了解这两种数学方法在现实生活中的应用。
通过实验,我们将深入了解插值的基本概念和分类方法,以及插值在实际应用中的意义。
同时,我们还将对插值和拟合的优缺点进行分析,为进一步的研究提供建议和启示。
通过本实验,我们的目的是掌握插值与拟合方法的应用和特点,为实际问题的求解提供更多的数学工具和思路。
2.正文2.1 插值的基本概念插值是指通过已知数据点构建出一个函数,该函数经过这些数据点,并且在每个数据点上都有相应的函数值。
换句话说,插值是一种通过已知离散数据点来推断未知数据点的方法。
在数学上,插值可以用于近似未知函数的值,或者用于填补数据间的空隙。
在插值过程中,我们通常会选择一个合适的插值函数,比如多项式函数、三角函数或者样条函数等,来拟合已知的数据点。
实验报告—拟合与插值
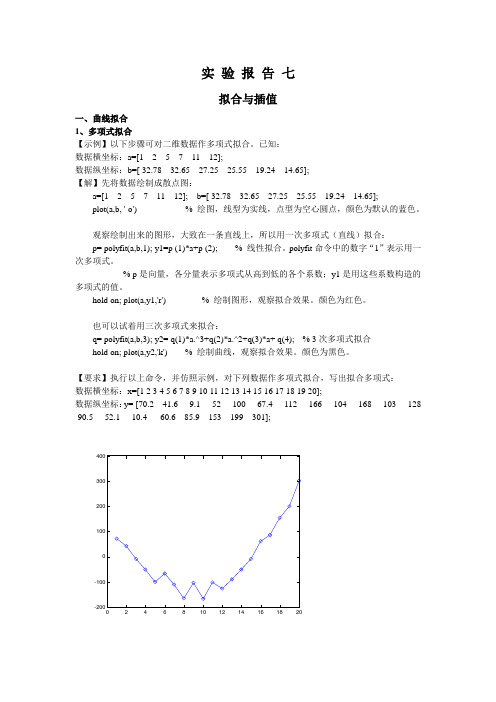
实验报告七拟合与插值一、曲线拟合1、多项式拟合【示例】以下步骤可对二维数据作多项式拟合。
已知:数据横坐标:a=[1 2 5 7 11 12];数据纵坐标:b=[ 32.78 32.65 27.25 25.55 19.24 14.65];【解】先将数据绘制成散点图:a=[1 2 5 7 11 12]; b=[ 32.78 32.65 27.25 25.55 19.24 14.65];plot(a,b, '-o') % 绘图,线型为实线,点型为空心圆点,颜色为默认的蓝色。
观察绘制出来的图形,大致在一条直线上,所以用一次多项式(直线)拟合:p= polyfit(a,b,1); y1=p (1)*a+p (2); % 线性拟合。
polyfit命令中的数字“1”表示用一次多项式。
% p是向量,各分量表示多项式从高到低的各个系数;y1是用这些系数构造的多项式的值。
hold on; plot(a,y1,'r') % 绘制图形,观察拟合效果。
颜色为红色。
也可以试着用三次多项式来拟合:q= polyfit(a,b,3); y2= q(1)*a.^3+q(2)*a.^2+q(3)*a+ q(4); % 3次多项式拟合hold on; plot(a,y2,'k') % 绘制曲线,观察拟合效果。
颜色为黑色。
【要求】执行以上命令,并仿照示例,对下列数据作多项式拟合,写出拟合多项式:数据横坐标:x=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20];数据纵坐标:y= [70.2 41.6 -9.1 -52 -100 -67.4 -112 -166 -104 -168 -103 -128 -90.5 -52.1 -10.4 60.6 85.9 153 199 301];024681012141618202、一般的最小二乘拟合【示例1】已知数据横、纵坐标分别为x =1:0.5:10; y=[0.84 2.24 3.64 3.74 1.2701 -4.29 -12.11 -19.79 -23.97 -21.34 -10.06 9.09 32.19 52.76 63.32 57.69 33.38 -6.78 -54.40];并已知该组数据满足 12sin()ay x a x =,其中12,a a 为待定系数。
计算方法上机作业插值与拟合实验报告

计算方法实验题目:班级:学号:姓名:目录计算方法实验 (1)1 实验目的 (3)2 实验步骤 (3)2.1环境配置: (3)2.2添加头文件 (3)2.3主要模块 (3)3 代码 (4)3.1主程序部分 (4)3.2多项式方程部分 (4)3.3核心算法部分 (8)3.4数据结构部分 (13)4运行结果 (19)4.1拉格朗日插值法运行结果 (19)4.2牛顿插值法运行结果 (20)4.3多项式拟合运行结果 (20)5总结 (21)拉格朗日插值法 (21)牛顿插值法 (21)多项式拟合 (21)6参考资料 (22)1 实验目的1.通过编程对拉格朗日插值法、牛顿插值法以及多项式拟合数据的理解2.观察上述方法的计算稳定性和求解精度并比较各种方法利弊2 实验步骤2.1环境配置:VS2013,C++控制台程序2.2添加头文件#include "stdio.h"#include "stdlib.h"#include "stdafx.h"2.3主要模块程序一共分成三层,最底层是数据结构部分,负责存储数据,第二层是交互部分,即多项式方程部分,负责输入输出获得数据,最上层是核心的算法部分,负责处理已获得的数据。
具体功能如下:●数据结构部分数据结构部分是整个程序的最底层,负责存储部分。
因方程系数作为数据元素插入和删除操作较少,而顺序表空间利用率大且查看方便,故此程序选用顺序表保存系数。
数据结构文件中写的是有关顺序表的所有基本操作以供其他文件调用。
本次实验使用列主元高斯消元法作为求解方程组的方法,所以也用了二维顺序表存储数组。
综上,数据结构部分文件是前两个试验的文件内容和,稍作修改。
●常系数微分方程部分多项式方程部分是程序的第二层,内容主要是常系数微分方程导数的计算和显示菜单部分。
●算法部分算法部分分为两个文件,一个是插值部分,一个是拟合部分。
插值部分文件负责有关插值的核心算法,处于整个程序最上层部分,负责拉格朗日插值法和牛顿插值法的具体实现过程。
数值分析拟合实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析方法对一组已知数据点进行拟合,掌握线性插值、多项式插值、样条插值等方法的基本原理和实现过程,并学会使用MATLAB进行数值拟合。
二、实验内容1. 线性插值线性插值是一种简单的插值方法,适用于数据点分布较为均匀的情况。
其基本原理是通过两个相邻的数据点,利用线性关系拟合出一条直线,然后通过该直线来估算未知的值。
2. 多项式插值多项式插值是一种较为精确的插值方法,通过构造一个多项式函数来逼近已知数据点。
其基本原理是利用最小二乘法求解多项式的系数,使得多项式在已知数据点上的误差最小。
3. 样条插值样条插值是一种更灵活的插值方法,通过构造一系列样条曲线来逼近已知数据点。
其基本原理是利用最小二乘法求解样条曲线的系数,使得样条曲线在已知数据点上的误差最小。
三、实验步骤1. 线性插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`linspace`生成插值点:xi = linspace(1, 5, 100);(3)使用MATLAB内置函数`interp1`进行线性插值:yi = interp1(x, y, xi, 'linear');(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');2. 多项式插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`polyfit`求解多项式系数:p = polyfit(x, y, 3);(3)使用MATLAB内置函数`polyval`进行多项式插值:yi = polyval(p, xi);(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');3. 样条插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`spline`进行样条插值:yi = spline(x, y, xi);(3)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');四、实验结果与分析1. 线性插值线性插值方法简单易行,但精度较低,适用于数据点分布较为均匀的情况。
工程数值分析实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析的方法,对工程实际问题进行建模、求解和分析。
通过学习数值方法的基本原理和算法,提高解决实际工程问题的能力。
二、实验内容1. 线性方程组的求解2. 矩阵特征值与特征向量的计算3. 函数插值与曲线拟合4. 数值微分与积分三、实验步骤1. 线性方程组的求解(1)编写程序实现高斯消元法、克劳斯消元法和列主元素法(2)设计输入界面,用户输入增广矩阵的行和列,填写系数及常数项(3)分别运用三种方法求解线性方程组,比较求解结果的正确性、数值稳定性和计算效率2. 矩阵特征值与特征向量的计算(1)编写程序实现幂法、QR算法和逆幂法(2)设计输入界面,用户输入矩阵的行和列,填写矩阵元素(3)分别运用三种方法计算矩阵的特征值与特征向量,比较求解结果的准确性和计算效率3. 函数插值与曲线拟合(1)编写程序实现拉格朗日插值、牛顿插值和样条插值(2)设计输入界面,用户输入函数的自变量和函数值,选择插值方法(3)分别运用三种方法进行函数插值,比较插值结果的准确性和光滑性4. 数值微分与积分(1)编写程序实现有限差分法、龙格-库塔法和辛普森法(2)设计输入界面,用户输入函数的导数或积分的上下限,选择数值方法(3)分别运用三种方法进行数值微分和积分,比较求解结果的准确性和计算效率四、实验结果与分析1. 线性方程组的求解通过实验,我们发现列主元素法在求解线性方程组时具有较好的数值稳定性,计算效率也较高。
而高斯消元法和克劳斯消元法在处理大型稀疏矩阵时存在一定的困难。
2. 矩阵特征值与特征向量的计算实验结果表明,QR算法和逆幂法在计算矩阵特征值与特征向量时具有较高的准确性和计算效率。
幂法在处理大型稀疏矩阵时表现出较好的性能。
3. 函数插值与曲线拟合在函数插值和曲线拟合实验中,样条插值方法具有较好的准确性和光滑性。
拉格朗日插值和牛顿插值方法在处理简单函数时表现良好,但在处理复杂函数时可能存在精度问题。
