人教新课标版数学高一- 数学必修三练习第2课时条件结构

合集下载

必修三第2课时程序框图、顺序结构和条件结构

学生练习：学案3、1
小结
顺序结构的程序框图的基本特征： (1) 必须有两个起止框，穿插输入、输出框和处理框，没有判断框. (2) 各程序框从上到下用流程线依次连接. (3) 处理框按计算机执行顺序沿流程线依次排列.
顺序结构无法对描述对象进行判断，并根据判断结果的不同进行处理，因此需要条件结构条件结构的两种形式：
程序框图、顺序结构和条件结构
8/3/2024
复习引入：
设计一个算法，判断n是否是偶数？
程序框图：（流பைடு நூலகம்图）
它是一种用程序框、流程线和文字说明来表示算法的图形。程序框图的基本符号及其功能P6 2
画程序框图的规则：
① 使用标准的图形符号 ② 程序框图一般按从上到下、从左到
右画 ③ 程序框图都是一个进入点、一个退
学生练习：能力测试 P6 互动探究
设计一个算法求解一元二次方程并画出程序框图
程序框图：
学生练习：能力测试 P6 例2
小结：
① 解决分段函数的函数值问题时，一般采用条件结构，如果含有n个解析式，则需n-1 个判断框
② 凡是必须先根据条件作出判断，再决定进行哪一个步骤的问题，在画流程图时，必须引入判断框，用条件结构
练习巩固
１看下面的程序框图，分析算法的作用
（1）
开始输入x y=3*x*x+4*x+5 输出y
（2）
开始输入a,b
a<b? 是
输出a,b
结束
结束
否输出b,a
学生练习： 1、能力测试P6 P3-4 2、学案知识运用和当堂检测
课堂作业： P20 A3
家庭作业：课时作业本60-61页
判断“以任意给定的3个正实数为三条边边长的三角形是否存在”的算法步骤如何设计？

人教A版高中数学必修3课后习题 1.1.2 第2课时条件结构

第2课时条件结构课后篇巩固提升1.给出以下四个问题:①输入一个数x,输出它的绝对值; ②求面积为6的正方形的周长; ③求三个数a,b,c 中的最大数; ④求函数f(x)={x -1,x ≥0,x +2,x <0的函数值.其中需要用条件结构来描述其算法的程序框图的有( ) A.1个B.2个C.3个D.4个,并根据判断的结果进行不同的处理.所给的四个问题中,只有②只需计算求值,不需要判断.故选C.2.执行右面的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]t∈[-1,1),则执行s=3t,故s∈[-3,3).若t∈[1,3],则执行s=4t-t2,其对称轴为t=2.故当t=2时,s取得最大值4.当t=1或3时,s取得最小值3,则s∈[3,4].综上可知,输出的s∈[-3,4].故选A.3.阅读如图所示的程序框图,运行相应的程序.若输入x的值为1,则输出y 的值为( )A.2B.7C.8D.128x=1,因为1≥2不成立,所以y=9-1=8,输出y=8.(第3题图)(第4题图)4.执行如图所示的程序框图,若输出的结果是8,则输入的数是( )A.2或-2√2B.2√2或-2√2C.-2或-2√2D.2或2√2x3=8时,x=2,a=4,b=8,b>a,输出8;当x2=8时,x=±2√2,a=8,b=±16√2,又a>b时输出8,所以x=-2√2.故选A.5.如图所示的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A.c>x? B.x>c? C.c>b? D.b>c?x的作用是保留3个数中的最大值,所以第二个条件结构的判断框内语句为“c>x?”,满足“是”则交换两个变量的数值,输出x的值后结束程序,满足“否”直接输出x的值后结束程序.故选A.(第5题图)(第6题图)6.对任意非零实数a,b,若a*b 的运算原理如图所示,则(log 28)*(12)-2= .log 28=3,(12)-2=4,∴a=3,b=4.∵a≤b,∴输出b -1a =4-13=1.7.如图所示的程序框图,若输出y 的值为54,则输入的x 值为 .y={2x +1,x ≤0,2x +1,x >0.当x≤0时,则y=2x +1=54,整理得2x =14,解得x=-2;当x>0时,则y=2x+1=54,整理得2x=14,解得x=18.所以x=-2或x=18.或18(第7题图)(第8题图)8.已知函数y={log 2x (x ≥2),2-x (x <2),如图所示的是给定x 的值,求其对应的函数值y 的程序框图.①处应填写 ;②处应填写 .y=2-x,∴①处应填“x<2?”,不满足x<2,即x≥2时,y=log 2x,故②处应填“y=log 2x”.y=log 2x9.如图,是判断“美数”的程序框图,在[30,40]内的所有整数中“美数”的个数是多少?3整除,不能被6整除或能被12整除的数.在[30,40]内的所有整数中,所有能被3整除的数有30,33,36,39,共4个数,在这四个数中能被12整除的有36,在这四个数中不能被6整除的有33,39,所以在[30,40]内的所有整数中“美数”的个数是3个.。

2020-2021人教版数学3课时1.1.2第2课时条件结构含解析

2020-2021学年人教A版数学必修3课时分层作业：1.1.2第2课时条件结构含解析课时分层作业（三)条件结构（建议用时：60分钟）一、选择题1．下列问题的算法中，需要条件结构的是(）A．求三个数的和B．求某个正实数的常用对数C．求半径为r的圆的面积D．解关于x的一元二次不等式ax2＋bx＋c＞0D[A，B，C中均不对变量进行讨论，只有D中需要讨论，因此需要条件结构．］2．若f(x)＝x2，g(x）＝log2x，则如图所示的程序框图中,输入x ＝0。

25，输出h（x）＝（）A．0.25B．2C．－2D．－0。

25C[当x＝0。

25时，f（0。

25)＝错误!〉g（0。

25)＝－2,故执行“是”路径，即h（x）＝log2x,h（0.25）＝log20.25＝－2.］3．已知函数y＝错误!图中表示的是给定x的值，求其对应的函数值y的程序框图①处应为(）A．x〈2? B．x〉2?C．x≠2？D．x＝2？A［框图“是”出口对应的是y＝2－x，结合分段函数的解析式知，①处应填x<2？]4．执行如图所示的程序框图，若输出结果为2，则输入的实数x的值是()A．3 B。

14C．4 D．2C［由题意，若x〉1,则令y＝log2x＝2，得x＝4>1；若x≤1,则令y＝x－1＝2，得x＝3,但3〉1，应舍去．］5．计算函数y＝错误!的值的程序框图如图所示，则对①②③的填空完全正确的是（)A．①y＝0；②x＝0？；③y＝x＋6B．①y＝0;②x＜0?；③y＝x＋6C．①y＝x2＋1;②x＞0？；③y＝0D．①y＝x2＋1；②x＝0？;③y＝0D［由分段函数的表达式知，当x＞0时，y＝x2＋1，故①处填“y＝x2＋1"；由②的条件不满足则执行y＝x＋6知②处填“x＝0？”；由当x＝0时,y＝0知,③处填“y＝0”．]二、填空题6．判断正整数x的奇偶性的程序框图如图，则①处应为________(只要写出一种正确答案即可)．r＝1？［框图的功能是判断一个正整数是奇数还是偶数，关键看能否被2整除,当满足条件时为奇数，所以余数为1,即①处可填r＝1？。

2019-2020学年度最新高中数学新人教版必修3教案：第1章 1-1-2 第2课时条件结构-含答案

2019-2020学年度最新高中数学新人教版必修3教案：第1章1-1-2 第2课时条件结构-含答案1．了解条件结构的概念，并明确其执行过程．(重点)2．理解条件结构在程序框图中的作用．(难点)3．会用条件结构设计程序框图解决有关问题．(易错易混点)[基础·初探]教材整理1条件结构的概念阅读教材P10例4前面的内容，完成下列问题．在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向．条件结构就是处理这种过程的结构．判断(正确的打“√”，错误的打“×”)(1)条件结构是一种重要的基本逻辑结构，任何算法都离不开它．()(2)条件结构的条件需要放在判断框内，判断框有两个出口，根据条件的成立与否，要走不同的出口．()(3)条件结构的判断框有两个出口，所以执行条件结构后的结果不唯一．()【答案】 (1)× (2)√ (3)×教材整理2 条件结构程序框图的形式与特征阅读教材P 10例4前面的内容，完成下列问题．是否成立，选择不同的执行框(步骤A 、步骤B )，无论条件是否成立，都要执行步骤A 和步骤B 之一，但不可能既执行步骤A 又执行步骤B ，也不可能步骤A 和步骤B 都不执行．(2)在单条件结构中，步骤A 和步骤B 可以有一个是空的，即不执行任何操作．1．判断给出的整数n 是否为偶数，设计程序框图时所含有的基本逻辑结构是( )A ．顺序结构B ．条件结构C ．顺序结构、条件结构D ．以上都不正确【解析】任何程序框图中都有顺序结构．当n 能被2整除时，n 是偶数；否则，n 不是偶数，所以必须用条件结构来解决．故选C.【答案】 C2．如图1-1-15所示，若输入x ＝－1，则输出y ＝________.图1-1-15【解析】 ∵－1<3，∴y ＝4－(－1)＝5.【答案】 5[小组合作型](1)( )图1-1-16A ．顺序结构B ．条件结构C ．判断结构D ．以上都不对 (2)给出以下四个问题：①输入一个数x ，输出它的相反数；②求面积为6的正方形的周长；③求三个数a ，b ，c 中的最大数；④求函数f (x )＝⎩⎨⎧x －1，x ≥0，x ＋2，x <0的函数值．其中不需要用条件结构来描述其算法的有( )A．1个B．2个C．3个D．4个【精彩点拨】根据顺序结构与条件结构的特点判断．【尝试解答】(1)此逻辑结构是条件结构．(2)语句①不需要对x进行判断，所以不需要用条件结构来描述算法；语句②不需要进行判断，不需要使用条件语句；语句③要比较两个数的大小，需要用到条件结构；语句④为分段函数，需要判断x的范围，所以需要用到条件结构来描述算法．【答案】(1)B(2)B条件结构不同于顺序结构的地方：它不是依次执行操作指令进行运算，而是依据条件作出逻辑判断，选择执行不同指令中的一个.一般地，这里的判断主要是判断“是”或“否”，即判断是否符合条件的要求，因而它有一个入口和两个出口，但最后还是只有一个终结口.[再练一题]1．条件结构不同于顺序结构的特征是含有()A．处理框B．判断框C．输入、输出框D．起止框【解析】由于顺序结构中不含判断框，而条件结构中必须含有判断框，故选B.【答案】 B111222画出程序框图.【精彩点拨】先对x1，x2是否相等进行判断，然后利用斜率公式．【尝试解答】算法如下：第一步，输入x1，y1，x2，y2.第二步，如果x1＝x2，输出“斜率不存在”；否则，k＝y2－y1x2－x1.第三步，输出k.程序框图如图所示：1．已知两点求直线斜率，若条件中已知x1≠x2，则只用顺序结构即可解决问题；若无限制条件，必须分类讨论应用条件结构解决问题．2．程序框图中的判断框内的内容x1＝x2，也可改为x1≠x2，此时相应地与“是”、“否”相连的图框必须对换．3．解决这类问题时，首先对问题设置的条件作出判断，设置好判断框内的条件，然后根据条件是否成立选择不同的流向．[再练一题]2．设计求一个数的绝对值的算法并画出程序框图．【解】算法如下：第一步，输入实数x.第二步，若x≥0，则y＝x；若x<0，则y＝－x.第三步，输出y.程序框图如图所示：1，c＝5，则输出结果为________．图1-1-17【精彩点拨】该程序框图的功能是找出三个数中最小的数，所以逐一比较两数的大小即可．【尝试解答】因为a＝2，b＝－1，c＝5，所以根据程序框图可知，先令x ＝a，即x＝2.再比较x与b的大小，因为x＞b，所以令x＝b，即x＝－1，然后比较x与c的大小，因为x＜c，所以直接输出x，故输出结果为－1.【答案】－1条件结构读图要注意：(1)理清所要实现的算法的结构特点和流程规则，分析其功能.(2)结合框图判断所要填入的内容或计算所要输出或输入的值.[再练一题]3．某市出租车的起步价为8元(含3千米)，超过3千米的里程每千米收2.6元，另外每车次超过3千米收燃油附加费1元(不考虑其他因素)．相应的收费系统的程序框图如图1-1-18所示，则(1)处应填________，(2)处应填________.图1-1-18【解析】当x＞3时，y＝8＋2.6(x－3)＋1＝9＋2.6(x－3)＝2.6x＋1.2；当x≤3时，y＝8.【答案】y＝2.6x＋1.2y＝8[探究共研型]探究1【提示】 1.条件结构是依据指定条件选择执行不同指令的控制结构．2．条件结构主要用在需要根据条件进行判断的算法中，如分段函数的求值、比较数据的大小关系等．探究2 一个判断框有两条流出线，能说条件结构执行的结果不唯一吗？【提示】一个判断框有两个退出点，但根据判断条件是否成立，选择的退出点是确定的，所以条件结构执行的结果是唯一的，即条件结构只有一个退出点，不能将判断框的退出点和条件结构的退出点混为一谈．探究3 在条件结构中，“条件”可以改变吗？【提示】求分段函数的函数值的程序框图画法不唯一，判断框内的内容可以改变，但相应处理框的内容也要发生改变．“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式．某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：f ＝⎩⎨⎧0.53ω， ω≤50，50×0.53＋(ω－50)×0.85， ω＞50. 其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)．试设计计算费用f 的算法并画出程序框图．【精彩点拨】在计算费用f 时，需要讨论ω与50的大小．所以要用条件结构画程序框图．【尝试解答】算法步骤如下：第一步，输入物品的重量ω.第二步，如果ω≤50，则令f ＝0.53ω，否则执行第三步．第三步，f ＝50×0.53＋(ω－50)×0.85.第四步，输出托运费f .程序框图如下：[再练一题]4．设火车托运质量为w (kg)的行李时，每千米的费用(单位：元)标准为： f ＝⎩⎨⎧0.4w ， w ≤30，0.4×30＋0.5(w －30)， w >30，试画出路程为s 千米时，行李托运费用M 的程序框图．【解】算法如下：第一步：输入物品质量w 、路程s ，第二步：若w >30.那么f ＝0.4×30＋0.5(w －30)；否则，f ＝0.4w .第三步：计算M ＝s ×f .第四步：输出M .程序框图如图所示：探究4 什么是条件结构的嵌套？有哪些特征？【提示】所谓嵌套，是指条件结构内，又套有小的分支，对条件进行二次或更多次的判断．常用于一些分段函数的求值问题．一般地，如果是分三段的函数，则需要引入两个判断框；如果是分四段的函数，则需要引入三个判断框；以此类推．探究5 在条件结构的嵌套中，判断框中的条件是唯一的吗？【提示】不是．在具体的程序设计中，这里的条件可以不同，但相应的条件下对应的结果是相同的．因此对于一个具体问题，编写的程序可以是不一样的．已知函数y ＝f (x )＝⎩⎨⎧ 1， x >0，0， x ＝0，－1， x <0，试写出求该函数的函数值的算法，并画出程序框图.【精彩点拨】解答本题可先对x 的值进行判断，然后根据不同情况y 取不同的值．【尝试解答】算法如下：第一步，输入x .第二步，判断x >0是否成立，若成立，则y ＝1，转执行第四步；若不成立，则执行第三步．第三步，判断x ＝0是否成立，若成立，则y ＝0，转执行第四步；否则y ＝－1，执行第四步．第四步，输出y .程序框图：1．下列关于条件结构的说法中正确的是()A．条件结构的程序框图有一个入口和两个出口B．无论条件结构中的条件是否满足，都只能执行路径之一C．条件结构中两条路径可以同时执行D．对于一个算法来说，判断框中条件是唯一的【解析】根据条件结构的特征可知，选B.【答案】 B2．如图1-1-19所示的程序框图，其功能是()图1-1-19A．输入a，b的值，按从小到大的顺序输出它们的值B．输入a，b的值，按从大到小的顺序输出它们的值C．求a，b的最大值D．求a，b的最小值【解析】取a＝1，b＝2知，该程序框图输出b＝2，因此是求a，b的最大值．【答案】 C3．如图1-1-20所示的程序框图，输入x ＝2，则输出的结果是________．图1-1-20【解析】通过程序框图可知本题是求函数y ＝⎩⎪⎨⎪⎧x ＋2，x ＞1，x ＋1，x ≤1的函数值，根据x ＝2可知y ＝2＋2＝2.【答案】 24．已知函数y ＝⎩⎨⎧log 2x ，x ≥2，2－x ，x <2.如图1-1-21表示的是给定x 的值，求其对应的函数值y 的程序框图．图1-1-21①处应填写________；②处应填写________．【解析】由框图可知只要满足①中的条件则对应的函数解析式为y ＝2－x ，故此处应填写x <2？，则②处应填写y ＝log 2x .【答案】 x <2？ y ＝log 2x5．某居民区的物业管理部门每月向居民收取卫生费，计费方法是：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出一人加收1.2元．设计一个算法，根据住户的人数，计算应收取的卫生费，并画出程序框图.【解】算法如下：第一步，输入x.第二步，若x≤3，则y＝5；否则，y＝5＋1.2(x－3)．第三步，输出y.程序框图如图所示：学业分层测评(三)条件结构(建议用时：45分钟)[学业达标]一、选择题1．下列算法中含有条件结构的是()A．求点到直线的距离B．已知三角形三边长求面积C．解一元二次方程x2＋bx＋4＝0(b∈R)D．求两个数的平方和【解析】A、B、D均为顺序结构，由于解一元二次方程时需判断判别式值的符号，故C选项要用条件结构来描述．【答案】 C2．下列关于条件结构的描述，不正确的是()A．条件结构的出口有两个，但在执行时，只有一个出口是有效的B．条件结构的判断条件要写在判断框内C．条件结构只有一个出口D．条件结构根据条件是否成立，选择不同的分支执行【解析】条件结构的出口有两个，算法的流程根据条件是否成立有不同的流向．【答案】 C3．若f(x)＝x2，g(x)＝log2x，则如图1-1-22所示的程序框图中，输入x＝0.25，输出h(x)＝()图1-1-22A．0.25B．2C．－2D．－0.25【解析】h(x)取f(x)和g(x)中的较小者．g(0.25)＝log20.25＝－2，f(0.25)＝0.252＝1 16.【答案】 C4．若输入－5，按图1-1-23中所示程序框图运行后，输出的结果是()图1-1-23A．－5 B．0C．－1 D．1【解析】因为x＝－5，不满足x＞0，所以在第一个判断框中执行“否”，在第2个判断框中，由于－5＜0，执行“是”，所以得y＝1.【答案】 D5．下列算法中，含有条件结构的是()A．求两个数的积B．求点到直线的距离C．解一元二次方程D．已知梯形两底和高求面积【解析】解一元二次方程时，当判别式Δ<0时，方程无解，当Δ≥0时，方程有解，由于分情况，故用到条件结构．【答案】 C二、填空题6．如图1-1-24所示，是求函数y＝|x－3|的函数值的程序框图，则①处应填________，②处应填________．图1-1-24【解析】 ∵y ＝|x －3|＝⎩⎪⎨⎪⎧x －3， x ≥3，3－x ， x ＜3.∴①中应填x ＜3? 又∵若x ≥3，则y ＝x －3. ∴②中应填y ＝x －3. 【答案】 x ＜3？ y ＝x －37．如图1-1-25所示的算法功能是________．图1-1-25【解析】根据条件结构的定义，当a ≥b 时，输出a －b ；当a ＜b 时，输出b －a . 故输出|b －a |的值．【答案】计算|b －a |8．如图1-1-26是求某个函数的函数值的程序框图，则满足该程序的函数的解析式为________．图1-1-26【解析】由框图可知f (x )＝⎩⎪⎨⎪⎧2x －3，x ＜0，5－4x ，x ≥0.【答案】 f (x )＝⎩⎨⎧2x －3，x ＜0，5－4x ，x ≥0三、解答题9．写出输入一个数x ，求分段函数y ＝⎩⎨⎧ x ，e x，x ≥0，x <0的函数值的程序框图.【解】程序框图如图所示：10．设计一个程序框图，使之能判断任意输入的数x 是奇数还是偶数．【解】程序框图如下：[能力提升]1．根据图1-1-27中的流程图操作，使得当成绩不低于60分时，输出“及格”，当成绩低于60分时，输出“不及格”，则()图1-1-27A．①框中填“是”，②框中填“否”B．①框中填“否”，②框中填“是”C．①框中填“是”，②框中可填可不填D．①框中填“否”，②框中可填可不填【解析】当x≥60时，应输出“及格”；当x＜60时，应输出“不及格”．故①中应填“是”，②中应填“否”．【答案】 A2．执行如图1-1-28所示的程序框图，如果输入t∈[－1,3]，则输出的s属于()图1-1-28A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]【解析】因为t ∈[－1,3]，当t ∈[－1,1)时，s ＝3t ∈[－3,3)；当t ∈[1,3]时，s ＝4t －t 2＝－(t 2－4t )＝－(t －2)2＋4∈[3,4]，所以s ∈[－3,4]．【答案】 A3．某程序框图如图1-1-29所示，若输出的结果是8，则输入的数是________．图1-1-29【解析】由程序框图知，⎩⎪⎨⎪⎧ x 2≥x 3，x 2＝8或⎩⎪⎨⎪⎧x 2<x 3，x 3＝8，解得x ＝－22或x ＝2. 【答案】－22或24．如图1-1-30所示是某函数f (x )给出x 的值，求相应函数值y 的程序框图．图1-1-30(1)写出函数f (x )的解析式；(2)若输入的x 取x 1和x 2(|x 1|<|x 2|)时，输出的y 值相同，试简要分析x 1与x 2的取值范围．【解】 (1)f (x )＝⎩⎪⎨⎪⎧x 2－1，|x |≥1，1－x 2，|x |<1.(2)画出y ＝f (x )的图象：由图象及y ＝f (x )为偶函数，且|x 1|<|x 2|时，f (x 1)＝f (x 2)知x 1∈(－1,1)，x 2∈[－2，－1)∪(1，2]．21 / 21。

数学人教A版必修3课件：1.1.2 第2课时条件结构1

1.1.2 第 2 课时条件结构
课前热身在一个算法中，经常会遇到一些________的判断，算法的流程根据 ________有不同的流向，条件结构就是________这种过程的结构.
自我条件条件是否成立处理
校对
名师讲解 1.条件结构算法中经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向，这种先根据条件作出判断再决定执行哪一种操作的结构称为条件结构．如图①所示．
【答案】 B
随堂训练
1.如图所示的程序框图，输入的 x＝2，则输出的结果是( )
A．1 C．3
B．2 D．4
【解析】该程序框图的功能是求分段函数
y＝x＋x＋1 2
(x≤1)， (x>1)
的函数值，
∴当 x＝2 时，y＝ 2＋2＝2，输出 2. 【答案】 B
2．某算法的程序框图如图所示，则输出量 y 与输入量 x 满足的关系式是 ________．
函数值 y 的程序框图，①处应填写________．②处应填写________．
【解析】由框图可知，只要满足①中的条件，则对应的函数解析式为 y＝ 2－x，故此处应填 x<2？，则②处应填写 y＝log2x.
【答案】 x<2？ y＝log2x
4．设计一个求一个数 x 的绝对值的算法，并画出相应的程序框图．解：算法如下：
程序框图：
三条件结构的实际应用【例 3】设火车托运行李，当行李重量为 m kg 时，每千米的费用(单位：元)标准为 y＝00..33×m30＋当0m.5≤m3－0 k3g0时，当m＞30 kg时，画出求行李托运费的程序框图．
解：程序框图如图：
四
识图
【例 4】如图所示的流程图中，如果输入的 x＝1π2，那么输出的 y 值为( )

人教新课标版数学高一-必修3导学案第2课时条件结构

1.1.2程序框图与算法的基本逻辑结构第2课时条件结构（配合配套的课件、练习使用效果更佳）周；使用时间17 年月日；使用班级；姓名【学习目标】1.掌握条件结构的程序框图的画法；2.能用条件结构框图描述分类讨论问题的算法；3.进一步熟悉程序框图的画法.重点：掌握条件结构的程序框图的画法难点：能用条件结构框图描述分类讨论问题的算法【检查预习】预习课本，完成导学案“自主学习”部分，准备上课回答.【自主学习】知识点一条件结构思考我们经常需要处理分类讨论的问题，顺序结构能否完成这一任务？为什么？在一个算法中，经常会遇到一些条件的判断，算法的流程根据是否成立有不同的流向.处理这种过程的结构叫条件结构.知识点二条件结构的两种形式结构形式特征两个步骤A、B根据选择一个执行根据条件选择是否执行步骤A类型一用程序框图表示条件结构例1 下面给出了一个问题的算法：第一步，输入x .第二步，若x >1，则y ＝x 2＋3，否则y ＝2x －1.第三步，输出y .试用程序框图表示该算法.跟踪训练1 任意给定3个正实数，设计一个算法，判断以这3个正实数为三条边边长的三角形是否存在，并画出这个算法的程序框图.类型二用条件结构框图描述分类讨论问题的算法例2 “特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式.某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：f ＝⎩⎪⎨⎪⎧0.53ω， ω≤50，50×0.53＋(ω－50)×0.85， ω>50. 其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克).试设计计算费用f 的算法并画出程序框图.跟踪训练2 设计算法判断一元二次方程ax 2＋bx ＋c ＝0是否有实数根，并画出相应的程序框图.类型三涉及三类以上的分类讨论问题例3 解关于x 的方程ax ＋b ＝0的算法的程序框图如何表示？跟踪训练3 设计一个求解一元二次方程ax 2＋bx ＋c ＝0的算法，并画出程序框图.【学生展示】探究点一、二【教师点评】探究点三及【学生展示】出现的问题【当堂检测】1.条件结构不同于顺序结构的特征是含有( )A.处理框B.判断框C.输入、输出框D.起止框2.下列说法：①条件结构是最简单的算法结构；②顺序结构就是按照程序语句的自然顺序，依次地执行顺序；③条件结构中的判断框中的条件是与流程走向相关联的；④条件结构可以根据设定的条件，控制语句流程，有选择地执行不同的语句序列.其中正确的说法是( )A.①②③B.①③④C.②③④D.①②③④ 3.下列算法中，含有条件结构的是( )A.求两个数的积B.求点到直线的距离C.解一元二次方程D.已知梯形两底和高求面积4.求下列函数的函数值的算法中需要用到条件结构的是( )A.f (x )＝x 2－1B.f (x )＝2x ＋1C.f (x )＝⎩⎪⎨⎪⎧ x 2＋1，x >1，x 2－1，x ≤1D.f (x )＝2x5.如图所示的程序框图，其功能是( )A.输入a ，b 的值，按从小到大的顺序输出它们的值B.输入a ，b 的值，按从大到小的顺序输出它们的值C.求a ，b 的最大值D.求a ，b 的最小值【小结作业】小结：作业：对应限时练。

高中数学必修三 1.1.2 第2课时条件结构习题新人教A版必修3

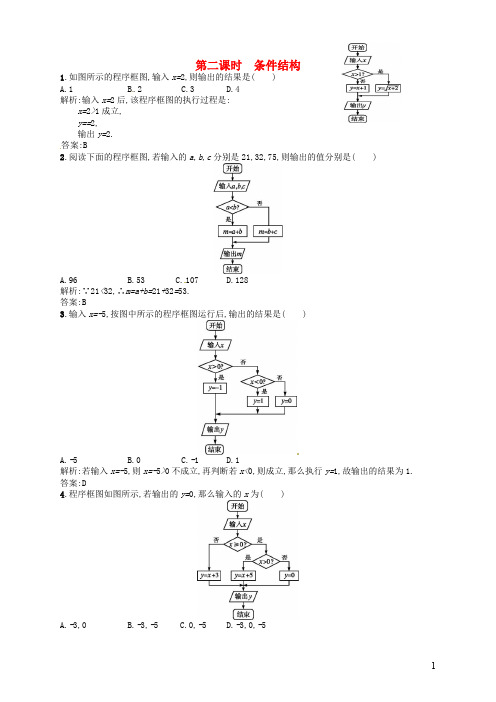
第二课时条件结构1.如图所示的程序框图,输入x=2,则输出的结果是( )A.1B.2C.3D.4解析:输入x=2后,该程序框图的执行过程是:x=2>1成立,y==2,输出y=2.答案:B2.阅读下面的程序框图,若输入的a,b,c分别是21,32,75,则输出的值分别是( )A.96B.53C.107D.128解析:∵21<32,∴m=a+b=21+32=53.答案:B3.输入x=-5,按图中所示的程序框图运行后,输出的结果是( )A.-5B.0C.-1D.1解析:若输入x=-5,则x=-5>0不成立,再判断若x<0,则成立,那么执行y=1,故输出的结果为1.答案:D4.程序框图如图所示,若输出的y=0,那么输入的x为( )A.-3,0B.-3,-5C.0,-5D.-3,0,-5解析:当x<0时,由x+3=0,得x=-3;当x>0时,由x+5=0,得x=-5,不合条件;当x=0时,y=0.故选A.答案:A5.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )A.f(x)=x2B.f(x)=C.f(x)=e xD.f(x)=sin x解析:由程序框图知,输出的函数是奇函数,且存在零点,函数f(x)=x2,f(x)=e x不是奇函数,而函数f(x)=是奇函数,但不存在零点,而函数f(x)=sin x是奇函数,且存在零点,故选D.答案:D6.对任意非零实数a,b,若a⊗b的运算原理如图所示,则(log28)⊗=.解析:∵log28=3,=4,即a=3,b=4,∴a<b,∴输出=1.答案:17.已知函数y=|x-3|,程序框图表示的是给定x值,求其相应函数值的算法,请将该程序框图补充完整.其中①处应填,②处应填.解析:y=|x-3|=所以①处填x<3?(或x≤3?),②处填y=x-3.答案:x<3?(或x≤3?) y=x-38.如图所示的程序框图的功能是.解析:该程序框图表示的算法步骤是:第一步,输入a,b,c三个数.第二步,判断a与b,a与c的大小,如果a同时大于b,c,则输出a,结束算法;否则执行第三步.第三步,判断b与c的大小,因为a已小于b或c,则只需比较b与c的大小就能看出a,b,c中谁是最大的了,如果b>c,则输出b,否则输出c.即求a,b,c的最大值.答案:求a,b,c的最大值9.画出解关于x的不等式ax+b<0的程序框图.解:程序框图为:10.儿童乘坐火车时,若身高h不超过1.2m,则无需购票;若身高h超过1.2m,但不超过1.5m,则可买半票;身高h超过1.5m应买全票.请设计一个算法,输入儿童的身高,输出购票情况,并画出程序框图.解:算法如下:第一步,输入身高h.第二步,判断h≤1.2是否成立,若成立,则输出“免费”,结束算法;若不成立,则执行第三步.第三步,判断h≤1.5是否成立,若成立,则输出“半票”,若不成立,则输出“全票”.程序框图如下:。

高中数学必修三课时作业14：1.1.2 第2课时条件结构

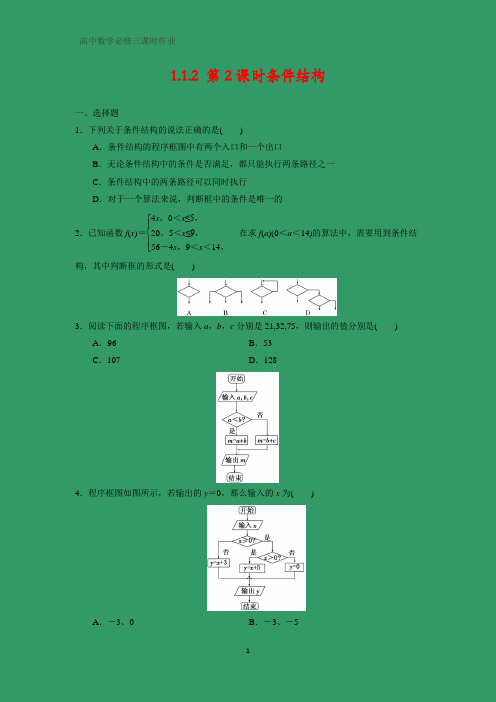
1.1.2 第2课时条件结构一、选择题1．下列关于条件结构的说法正确的是( )A ．条件结构的程序框图中有两个入口和一个出口B ．无论条件结构中的条件是否满足，都只能执行两条路径之一C ．条件结构中的两条路径可以同时执行D ．对于一个算法来说，判断框中的条件是唯一的 2．已知函数f (x )＝⎩⎪⎨⎪⎧4x ，0＜x ≤5，20，5＜x ≤9，56－4x ，9＜x ＜14，在求f (a )(0＜a ＜14)的算法中，需要用到条件结构，其中判断框的形式是( )3．阅读下面的程序框图，若输入a ，b ，c 分别是21,32,75，则输出的值分别是( )A ．96B ．53C ．107D ．1284．程序框图如图所示，若输出的y ＝0，那么输入的x 为( )A ．－3、0B ．－3、－5C ．0、－5D ．－3、0、－55．某程序框图如图所示，现输入如下四个函数，则可以输出的函数是( )A ．f (x )＝x 2B ．f (x )＝1xC ．f (x )＝ln x ＋2x －6D ．f (x )＝x 3＋x 二、填空题6．任给一个x 值计算y ＝⎩⎪⎨⎪⎧1x ＜0，2x ＝0，3x ＞0中的y 值的算法的程序框图如图所示，其中图框中的①②③分别为________，________，________.7．如图是某种算法的程序框图，当输出的y 的值大于2时，则输入的x 的取值范围为________．8．如图所示的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入________．三、解答题9．如图所示的程序框图，其作用是：输入x的值，输出相应的y值．若要使输入的x值与输出的y值相等，求这样的x值有多少个？10．在新华书店里，《三维设计》每本售价14.80元，书店为促销，规定：如果顾客购买5本或5本以上，10本以下则按九折(即13.32元)出售；如果顾客购买10本或10本以上，则按八折(即11.84元)出售．请设计一个完成计费工作的程序框图．参考[答案]1.【[解析]】选B 条件结构只有一个入口，故A 错；条件结构的两条路径只能由判断框内条件选择其一执行，故C 错，判断框内条件可适当变化，只需其后步骤相应调整即可，故D 错．【[答案]】B2.【[解析]】选D 本题给定的分段函数有三个选择，所以要在条件结构内嵌套条件结构，符合这一条件的只有D. 【[答案]】D3.【[解析]】选B ∵21＜32，∴m ＝21＋32＝53，即输出53. 【[答案]】B4.【[解析]】选A 由框图知，当x ＝－3、0时，输出的y 值均为0. 【[答案]】A5.【[解析]】选D 由框图可知，当输入的函数f (x )为奇函数且存在零点时，才可输出f (x )，由选项可知，仅f (x )＝x 3＋x 同时满足这两个条件，故选D. 【[答案]】D6.【[解析]】由于第一个判断框“是”执行y ＝1，故①填“x ＜0？”，再由y ＝1，y ＝2知③填“y ＝3”，故②填“x ＞0？”．【[答案]】x ＜0？ x ＞0？ y ＝37.【[解析]】由题知，此算法的程序框图是求分段函数f (x )＝⎩⎨⎧3－x－1， x ≤0，x ， x ＞0的值．若f (x )＞2，①当x ≤0时，3－x －1＞2，即3－x ＞3，所以－x ＞1，即x ＜－1； ②当x ＞0时，x ＞2，即x ＞4.综上所述，x 的取值范围为(－∞，－1)∪(4，＋∞)．【[答案]】(－∞，－1)∪(4，＋∞)8.【[解析]】由框图知将a ，b ，c 中较大的用x 表示，先令x ＝a ，再比较x 与b 的大小，若b ＞x ，则令x ＝b ，否则判断x 与c 的大小，若x ＞c ，则输出x ，否则令x ＝c ，再输出x . 【[答案]】c ＞x ?9.解：由题可知算法的功能是求分段函数y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2＜x ≤5，1x ，x ＞5的函数值，要满足题意，则需要⎩⎪⎨⎪⎧ x ≤2，x 2＝x 或⎩⎪⎨⎪⎧2＜x ≤5，2x －3＝x 或⎩⎪⎨⎪⎧x ＞5，1x＝x解得x ＝0或x ＝1或x ＝3，共3个值．10.解：程序框图：。

(新)人教版高中数学必修三1.2.2《条件语句》精品课件(共22张PPT)

转化。
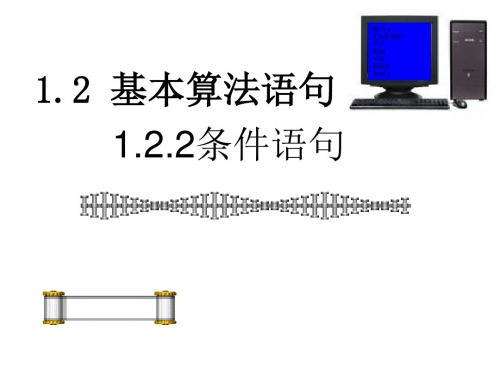
INPUT “a，b，c=”；a，b，c d=b∧2-4*a*c IF d>=0 THEN p= -b/(2*a) q=SQR(d)/(2*a) IF d=0 THEN PRINT “x1=x2=”；p ELSE PRINT “x1，x2=”；p+q，p-q END IF ELSE PRINT “No real root.” END IF END
1.2 基本算法语句 1.2.2条件语句
输入:x If x>0 then Y=1 Else Y=0 End if 输出 y
知识再现
1.输入语句、输出语句和赋值语句的一般格式分别是什么？输入语句： INPUT “提示内容”；变量输出语句： PRINT “提示内容”；表达式赋值语句：变量=表达式
IF
条件 THEN 语句体1 ELSE 语句体2 END IF
满足条件？
否
是
语句体1
语句体2
IF
条件 THEN 语句体1 ELSE 语句体2 END IF
满足条件？
否
是
语句体1 语句体2
当计算机执行上述语句时，首先对IF 后的条件进行判断，如果（IF）条件符合，那么（THEN）执行语句体1，否则（ELSE）执行语句体2.
两种语句的区别与联系
区别：第一种语句只有一个语句体，是满足条件时执行的语句体：而第二种语句含有两个语句体，满足条件时执行语句体1，不满足条件时执行语句体2. 联系：两种语句首先都要对条件进行判断，然后才执行相应的语句体；执行语句体以后，程序都交汇于一点完成条件语句；都以IF开始，以END结束。
满足条？
否
是
语句体
IF
条件 THEN 语句体 END IF

人教A版高中数学必修三第一章1.1-1.1.2第2课时条件结构同步练习(I)卷

人教A版高中数学必修三第一章1.1-1.1.2第2课时条件结构同步练习（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题；共12分)1. （2分） (2018高二下·磁县期末) 在如图所示的计算的值的程序框图中，判断框内应填入A .B .C .D .2. （2分）根据给出的算法框图，计算f(-1)+f(2)=（）A . 0B . 1C . 2D . 43. （2分）按右面的程序框图运行后,输出的S应为（）A . 26B . 35C . 40D . 574. （2分） (2018高三上·大连期末) 执行如图程序，输出的值为（）A .B .C .D .5. （2分）(2017·石家庄模拟) 执行如图的程序框图，如果输入的a=6，b=4，那么输出的s的值为（）A . 17B . 22C . 18D . 206. （2分）执行如图所示的程序框图，若输入的x的值为2，则输出的x的值为（）A . 3B . 126C . 127D . 128二、填空题 (共4题；共4分)7. （1分） (2017高一下·淮安期末) 如图是一个算法的流程图，则输出的a的值是________．8. （1分） (2015高三上·如东期末) 如图是一个算法的流程图，则输出的k的值是________ ．9. （1分）(2019·新宁模拟) 某程序框图如图所示，若输入x的值为0，则输出y的值是________ .10. （1分） (2016高二下·姜堰期中) 如图所示的算法语句中，输出的结果是x=________．三、解答题 (共4题；共20分)11. （5分）画出输入一个数x ，求分段函数y＝的函数值的程序框图.12. （5分）编写程序，要求输入任意3个实数，输出它们的最小值．13. （5分）某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．（1）求n的值；（2）把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖．求a和b 至少有一人上台抽奖的概率．（3）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．14. （5分）学习优秀奖的条件如下：⑴五门课的成绩总分不低于500分．⑵每门课成绩都不低于90分．⑶三门主课每门的成绩都不低于100分，其他两门课的成绩都不低于90分．输入某学生的五门课的成绩，问他是否够优秀条件．画出程序框图．参考答案一、单选题 (共6题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共4题；共4分)7-1、8-1、9-1、10-1、三、解答题 (共4题；共20分)11-1、12-1、13-1、14-1、。

高一数学必修3课件：1-1-2-2条件结构

[答案] D
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
[解析]
1 因为a＝ 2 >b＝＝ 4
1 ，所以a>b成立，所以 16
1 2 输出a· b＝ 2×4＝ 4 .
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
5．某市的出租车收费办法如下：不超过2千米收7元(即起步价7元)，超过2千米的里程每千米收2.6元，另每车次超过2千米收燃油附加费1元(不考虑其他因素)．相应收费系统的程序框图如图所示，则①处应填( )
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
[解析]
算法如下：
第一步，输入x1，y1，x2，y2. 第二步，如果x1＝x2，输出“斜率不存在”； y2－y1 否则，k＝ . x2－x1 第三步，输出k.
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
程序框图如下．
第一章
1.1
1.1.2 第2课时
成才之路 ·数学 ·人教A版 · 必修3
命题方向2
嵌套式条件结构
凡是必须先根据条件作出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，根据题目条件，选择简单条件结构或嵌套式条件结构．如求分段函数的函数值的程序框图的画法，如果是分两段的函数，只需引入一个判断框；如果是分三段的函数，需引入两个判断框；分四段的函数需引入三个判断框，依此类推．判断框内的内容是没有固定顺序的．

数学人教A版必修3课件：1.1.2 第2课时条件结构2

第四步，输出 y. 程序框图如图所示：
变式训练
已知函数 y＝10＋，xx，＝x0>，0，－x－3，x<0，
设计一个算法，输入自变量 x 的值，
输出对应的函数值．请写出算法步骤，并画出程序框图．
解：算法如下：
第一步，输入自变量 x 的值．第二步，判断 x>0 是否成立，若成立，计算 y＝1＋x，否则，执行下一步．第三步，判断 x＝0 是否成立，若成立，令 y＝0，否则，计算 y＝－x－3. 第四步，输入 y.
程序框图如下图所示：
变式训练设计求一个数的绝对值的算法并画出程序框图． [分析] 根据绝对值的意义，要讨论一个数 x 的正负，故使用条件结构．解：算法如下：第一步，输入实数 x. 第二步，若 x≥0，则 y＝x；若 x<0，则 y＝－x. 第三步，输入 y.
程序框图如下:
命题方向 2 嵌套式条件结构
对条件结构的理解剖析:可以从以下几方面来理解: (1)条件结构有一个入口和两个出口; (2)每执行一次条件结构,只能执行两个出口中的一个,不能同时执行两个
出口; (3)根据是否满足条件来确定执行哪个出口,满足条件执行一个出口,不满
足条件执行另一个出口. (4)对于算法中含有分类讨论的步骤,在设计程序框图时,通常用条件结构
1.1.2 第 2 课时条件结构
条件结构 (1)概念:算法的流程根据条件是否成立有不同的流向,这种处理判断条件的结构称为条件结构. (2)程序框图:如图①②所示.
(1)条件结构是程序框图的重要组成部分.其特点是先判断后执行. (2)在利用条件结构画程序框图时要注意两点:一是需要判断的条件是什么, 二是条件判断后分别对应着什么样的结果. (3)判断框虽然有两个出口,但根据条件是否成立,选择的出口是确定的,故执行结果也是唯一的.如上面图①中,若条件成立,则执行步骤 A,若条件不成立,则执行步骤 B;图②中,若条件成立,则执行步骤 A,若条件不成立,则不执行任何步骤. (4)凡是必须先根据条件作出判断然后再进行哪一个步骤的问题,在画程序框图时,必须引入一个判断框并应用条件结构.

人教新课标版数学高一-必修3训练 1. 条件结构

第2课时条件结构一、基础达标1．下列算法中，含有条件结构的是() A．求两个数的积B．求点到直线的距离C．解一元二次方程D．已知梯形两底和高求面积答案 C解析解一元二次方程时，当判别式Δ<0时，方程无解，当Δ≥0时，方程有解，由于分情况，故用到条件结构．2．下列关于条件结构的描述，不正确的是() A．条件结构的出口有两个，但在执行时，只有一个出口是有效的B．条件结构的判断条件要写在判断框内C．双选择条件结构有两个出口，单选择条件结构只有一个出口D．条件结构根据条件是否成立，选择不同的分支执行答案 C解析C中单选择条件结构中的出口有两个，故C错．3．若输入－5，按图中所示程序框图运行后，输出的结果是()A．－5 B．0 C．－1 D．1答案 D解析因x ＝－5，不满足x ＞0，所以在第一个判断框中执行“否”，在第2个判断框中，由于－5＜0，执行“是”，所以得y ＝1. 4．求下列函数的函数值的算法中需要用到条件结构的是( )A ．f (x )＝x 2－1B ．f (x )＝2x ＋1C ．f (x )＝⎩⎨⎧x 2＋1（x >1）x 2－1（x ≤1）D ．f (x )＝2x答案 C解析 C 项中函数f (x )是分段函数，需分类讨论x 的取值范围，要用条件结构来设计算法，A 、B 、D 项中均不需要用条件结构．5．(2013·太原高二检测)如图所示的程序框图运行后输出结果为12，则输入的x 值为( )A ．－1B.22C.12D ．－1或22答案 D解析程序框图表示的是求分段函数f (x )＝⎩⎪⎨⎪⎧x 2，x ≥14，2x，x ≤0，log 12x ，0<x <14的函数值，由⎩⎪⎨⎪⎧x 2＝12x ≥14得，x ＝22；由⎩⎪⎨⎪⎧2x ＝12x ≤0得，x ＝－1.又⎩⎪⎨⎪⎧log 12x ＝120<x <4无解，故选D. 6．如图所示的程序框图，若a ＝5，则输出b ＝________．答案 26解析这是一个分段函数b ＝⎩⎪⎨⎪⎧a 2＋1，a ≤5，2a ，a ＞5的求值问题，根据条件易知b ＝52＋1＝26.7．如果学生的数学成绩大于或等于120分，则输出“良好”，否则输出“一般”．用程序框图表示这一算法过程．解二、能力提升8．如图所示，给出一个程序框图，其作用是输入x的值，输出相应的y的值．若要使输入的x的值与输出的y的值相等，则输入的这样的x的值有()A．1个B．2个C．3个D．4个答案 C解析当x≤2时，x＝1或x＝0，则x＝y；不成立，所当2＜x≤5时，若x＝y，则x＝2x－3，∴x＝3；当x＞5时，x＝1x以满足题意的x的值有1，0，3.9．(2013·课标全国Ⅰ)执行下面的程序框图，如果输入t∈[－1，3]，则输出的s 属于()A．[－3，4] B．[－5，2] C．[－4，3] D．[－2，5] 答案 A解析因为t∈[－1，3]，当t∈[－1，1)时，s＝3t∈[－3，3)；当t∈[1，3]时，s＝4t－t2＝－(t2－4t)＝－(t－2)2＋4∈[3，4]，所以s∈[－3，4]．10．如图中，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分，当x1＝6，x2＝9，p＝8.5时，x3等于()A ．10B ．7C ．8D ．11答案 C解析 x 1＝6，x 2＝9，|x 1－x 2|＝3<2不成立，即为“否”，所以再输入x 3；由绝对值的意义(一个点到另一个点的距离)和不等式|x 3－x 1|<|x 3－x 2|知，点x 3到点x 1的距离小于点x 3到x 2的距离，所以当x 3<7.5时，|x 3－x 1|<|x 3－x 2|成立，即为“是”，此时x 2＝x 3，所以p ＝x 1＋x 32，即6＋x 32＝8.5，解得x 3＝11>7.5，不合题意；当x 3>7.5时，|x 3－x 1|<|x 3－x 2|不成立，即为“否”，此时x 1＝x 3，所以p ＝x 3＋x 22，即x 3＋92＝8.5，解得x 3＝8>7.5，符合题意，故选C. 11．已知函数y ＝⎩⎨⎧log 2x ，x ≥22－x ，x <2，如图表示的是给定x 的值，求其对应的函数值y的程序框图．①处应填写________；②处应填写________．答案 x <2？ y ＝log 2x解析 ∵满足判断框中的条件执行y ＝2－x ， ∴①处应填x <2？.不满足x <2即x ≥2时，y ＝log 2x ，故②处应填y ＝log 2x .12．画出解不等式ax>b(b≥0)的程序框图．解程序框图如图：三、探究与创新13．到银行办理个人异地汇款(不超过100万)时，银行要收取一定的手续费．汇款额不超过100元，收取1元手续费；超过100元但不超过5 000元，按汇款额的1%收取；超过5 000元但不超过100万时，一律收取50元手续费，其他情况不予办理．试设计一个算法描述汇款额为x元时，银行收取手续费为y元的过程，并画出程序框图．解由题意知本题是一个分段函数问题，分段函数解析式为y＝⎩⎪⎨⎪⎧10.01x50（0＜x≤100），（100＜x≤5 000），（5 000＜x≤1 000 000）.其算法如下：第一步：输入汇款额x；第二步：判断x≤100是否成立；若成立，则y＝1，若不成立，则执行第三步；第三步：判断x≤5 000是否成立；若成立，则y＝x×1%，若不成立，则执行第四步；第四步：判断x≤1 000 000是否成立；若成立，则y＝50，若不成立，则输出“不予办理”；第五步：输出y.程序框图如图：。

高中数学必修三 1.1.2 第2课时条件结构导学案新人教A版必修3

1.1.2.2条件结构课前预习案【知识链接】2015年元旦期间，某商品进行团购优惠活动：购买5件或5件以下，每件88元；超过5件，超过的部分按每件8折优惠．1．若某人购买x件，试写出购物总费用y与购买件数x的关系式．2．设计上述问题的算法时，应注意什么？3．上述问题若画程序框图，只用顺序结构能完成吗？【知识梳理】条件结构(1)概念：算法的流程根据条件是否成立有不同的____，这种处理________的结构称为条件结构．(2)程序框图：如图①②所示．小结：(1)条件结构是程序框图的重要组成部分．其特点是先判断后执行．在利用条件结构画程序框图时要注意两点：一是需要判断的条件是什么，二是条件判断后分别对应着什么样的结果.判断框虽然有两个出口，但根据条件是否成立，选择的出口是确定的，故执行结果也是唯一的.如上面图①中，若条件成立，则执行步骤A，若条件不成立，则执行步骤B；图②中，若条件成立，则执行步骤A，若条件不成立，则不执行任何步骤.凡是必须先根据条件作出判断然后再进行哪一个步骤的问题，在画程序框图时，必须引入一个判断框并应用条件结构.对条件结构的理解说明：可以从以下几方面来理解：(1)条件结构有一个入口和两个出口；(2)每执行一次条件结构，只能执行两个出口中的一个，不能同时执行两个出口；(3)根据是否满足条件来确定执行哪个出口，满足条件执行一个出口，不满足条件执行另一个出口．(4)对于算法中含有分类讨论的步骤，在设计程序框图时，通常用条件结构来解决．例如，给出如图所示的程序框图，若输入m＝－2，则m＞0不成立，此时执行ω＝－2－1＝－3，则输出－3.若输入m＝3，则m＞0成立，此时执行ω＝3＋1＝4，则输出4.自主小测1、判断整数n是否是偶数，设计程序框图时所含有的基本逻辑结构是( ) A．顺序结构B．条件结构C．顺序结构、条件结构D．以上都不正确2、知ab＝14，运算原理如图所示，则输出的值为()A．14+B．4+C．D．3．某市的出租车收费办法如下：不超过2千米收7元(即起步价7元)，超过2千米的里程每千米收2.6元，另每车次超过2千米收燃油附加费1元(不考虑其他因素)．相应收费系统的程序框图如图所示，则①处应填( )A．y＝7＋2.6x B．y＝8＋2.6xC．y＝7＋2.6(x－2) D．y＝8＋2.6(x－2)课上导学案【例题讲解】【例题1】任意给定3个整实数，设计一个算法，判断以这3个正实数为三边边长的三角形是否存在，并画出这个算法的程序框图.【例题2】设计一个求解一元二次方程02=++c bx ax 的算法，并画出程序框图表示.【当堂检测】1．如图是计算函数y ＝ln(),2,0,23,2,3x x x x x ⎧--⎪-<⎨⎪>⎩≤≤的值的程序框图，在①②③处应分别填入的是()A ．y ＝ln(－x)，y ＝0，y ＝2xB ．y ＝ln(－x)，y ＝2x ，y ＝0C ．y ＝0，y ＝2x ，y ＝ln(－x)D ．y ＝0，y ＝ln(－x)，y ＝2x2．如图是求某个函数的函数值的程序框图，则满足该程序框图的函数的解析式为__________．【问题与收获】【知识链接】答案：1、【提示】 y ＝⎩⎪⎨⎪⎧ 88x ，440＋－， x≤5，x>5.2、【提示】注意判断购买的件数对购物费用的影响．3、【提示】不能．知识梳理答案：(1)流向判断条件【做一做】 C 任何程序框图中都有顺序结构．当n 能被2整除时，n 是偶数；否则，n 不是偶数，所以必须用条件结构来解决．自主小测答案：1．D 因为ab ＝14a ＞b 成立，所以输出14＝4. 2．D 当x ＞2时，y ＝7＋2.6(x －2)＋1＝8＋2.6(x －2)，所以①处应填y ＝8＋2.6(x －2)．3．B 当x ＞－2不成立时，有x≤－2，则y ＝ln(－x)，则①处填入y ＝ln(－x)；当x ＞－2成立时，若x ＞3成立，则y ＝2x ，则②处填入y ＝2x ；若x ＞3不成立，即－2＜x≤3，则y ＝0，则③处填入y ＝0. 例题答案：见教材（略）当堂检测答案：1．f(x)＝23,0,54,0x x x x -<⎧⎨-⎩≥ 当满足x ＜0时，f(x)＝2x －3；当不满足x ＜0，即x≥0时，f(x)＝5－4x ，所以满足该程序的函数解析式为f(x)＝23,0,54,0.x x x x -<⎧⎨-⎩≥ 2．分析：题中当n 是奇数和n 是偶数时的计算方式不同，所以需对n 的奇偶性加以判断，然后计算结果．解：算法步骤如下：第一步，输入n 的值．第二步，若n 为奇数，计算w ＝3n ＋1的值；否则，计算w ＝2n的值．第三步，输出w.程序框图如图所示．。

人教版高中数学必修三第一章1.1-1.1.2第2课时条件结构

第一章算法初步 1.1 算法与程序框图1.1.2 程序框图与算法的基本逻辑结构第2课时条件结构A 级基础巩固一、选择题1．下列算法中含有条件结构的是( ) A ．求点到直线的距离 B ．已知三角形三边长求面积C ．解一元二次方程x 2＋bx ＋4＝0(b ∈R)D ．求两个数的平方和解析：A 、B 、D 均为顺序结构，由于解一元二次方程时需判断判别式值的符号，故C 选项要用条件结构来描述．答案：C2．已知函数f (x )＝⎩⎪⎨⎪⎧4x ，0<x ≤5，20，5<x ≤9，56－4x ，9<x <14，在求f (a )(0<a <14)的算法中，需要用到条件结构，其中判断框的形式是()解析：本题给定的分段函数有三个选择，所以要在条件结构内嵌套条件结构，符合这一条件的只有D.答案：D3．已知如图所示的程序框图，若输入x＝3，则输出y的值为()A．－2B．0C．2D．3答案：C4．阅读下面的程序框图，若输入a，b，c分别是21，32，75，则输出的值是()A．96 B．53 C．107 D．128解析：因为21<32，所以m＝21＋32＝53，即输出的值为53.答案：B5．如图所示的程序框图，其功能是()A．输入a，b的值，按从小到大的顺序输出它们的值B．输入a，b的值，按从大到小的顺序输出它们的值C ．求a ，b 的最大值D ．求a ，b 的最小值解析：取a ＝1，b ＝2知，该程序框图输出b ＝2，因此是求a ，b 的最大值．答案：C 二、填空题6．已知函数y ＝|x －3|，如图所示程序框图表示的是给定x 值，求其相应函数值的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．解析：由f (x )＝|x －3|＝⎩⎪⎨⎪⎧x －3，x ≥3，3－x ，x <3及程序框图知，①处应填x <3？，②处应填y ＝x －3.答案：x <3？ y ＝x －37．如图的程序框图的功能是计算函数________的函数值．答案：y ＝|2x －3|8．对任意非零实数a ，b ，若a ⊗b 的运算原理的程序框图如图所示．则3⊗2＝________．解析：由程序框图知，当a ≤b 时，输出b －1a ；当a >b 时，输出a ＋1b.因为3>2，所以输出3＋12＝2.答案：2 三、解答题9．写出输入一个数x ，求分段函数y ＝⎩⎪⎨⎪⎧x ，（x ≥0），e x ，（x <0）的函数值的程序框图．解：程序框图如下图所示：10．设计算法判断一元二次方程ax 2＋bx ＋c ＝0是否有实数根，并画出相应的程序框图．解：算法步骤如下：第一步，输入3个系数a ，b ，c . 第二步，计算Δ＝b 2－4ac .第三步，判断Δ≥0是否成立．若是，则输出“方程有实数根”；否则，输出“方程无实数根”．结束算法．相应的程序框图如下图：B 级能力提升1．若输入－5，按图中所示程序框图运行后，输出的结果是( )A ．－5B ．0C ．－1D ．1解析：因x ＝－5，不满足x >0，所以在第一个判断框中执行“否”，在第2个判断框中，由于－5<0，执行“是”，所以y ＝1.答案：D2．已知函数y ＝⎩⎪⎨⎪⎧log 2x ，x ≥2，2－x ，x ＜2，如图表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写__________；②处应填写________．解析：因为满足判断框中的条件执行y ＝2－x ，所以①处应填x ＜2？.不满足x ＜2即x ≥2时，y ＝log 2x ，故②处应填y ＝log 2x . 答案：x ＜2？ y ＝log 2x3．某居民区的物业部门每月向居民收取卫生费，计费方法如下：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费，并画出程序框图．解：设费用用y (元)表示，人数用x 表示，则y ＝⎩⎪⎨⎪⎧5（x ≤3），5＋1.2（x －3）（x >3）.算法如下：第一步，输入x .第二步，若x ≤3，则y ＝5，否则执行第三步．第三步，y ＝5＋1.2(x －3)．第四步，输出y . 程序框图如下图所示．。

高中数学必修三课时作业13：1.1.2 第2课时条件结构

1.1.2 第2课时条件结构1．下列图形符号属于处理框(执行框)的是()2．下列关于程序框图的说法正确的有()①用程序框图表示算法直观、形象，容易理解；②程序框图能清楚地展现算法的逻辑结构，也就是通常所说的一图胜万言；③在程序框图中，起止框是任何流程图不可少的；④输入和输出框可用在算法中任何需要输入、输出的位置．A．1个B．2个C．3个D．4个3．给出下面的程序框图：若输出的结果为2，则①处的执行框内应填的是()A．x＝2 B．b＝2C．x＝1 D．a＝54．如图是一个算法的程序框图，已知a1＝3，输出的b＝7，则a2等于()A．9 B．10C．11 D．125.如图所示的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的()A．c>x?B．x>c?C．c>b?D．b>c?6．如图所示程序框图表示的算法的运行结果是________．7．写出如图所示程序框图的运行结果：S＝________．8．如图所示的程序框图，若a ＝5，则输出b ＝________．9．已知函数f (x )＝⎩⎪⎨⎪⎧－x ＋1，x >0，0，x ＝0，x ＋3，x <0，请设计程序框图，要求输入自变量，输出函数值．10．尺规作图，确定线段AB 的一个5等分点，请你设计一个算法，并画出程序框图．11．在新华书店里，某教辅材料每本售价14.80元，书店为促销，规定：如果顾客购买5本或5本以上，10本以下则按九折(即13.32元)出售；如果顾客购买10本或10本以上，则按八折(即11.84元)出售．请设计一个完成计费工作的程序框图．参考[答案]1.【[解析]】选D.处理框用矩形表示．【[答案]】D2.【[解析]】选D.由程序框图可知：①②③④都正确．【[答案]】D3.【[解析]】选C.∵b ＝2，∴2＝a －3，即a ＝5. ∴2x ＋3＝5时，得x ＝1. 【[答案]】C4.【[解析]】选C.由题意知该算法是计算a 1＋a 22的值．∴3＋a 22＝7，得a 2＝11，故选C.【[答案]】C5.【[解析]】选A.变量x 的作用是保留3个数中的最大值，所以第二个判断框内语句为“c >x ？”，满足“是”则交换两个变量的数值，输出x 的值后结束程序，满足“否”直接输出x 的值后结束程序，故选A. 【[答案]】A6.【[解析]】由题意P ＝5＋6＋72＝9，S ＝9×4×3×2＝216＝6 6. 【[答案]】6 67.【[解析]】S ＝24＋42＝2.5.【[答案]】2.58.【[解析]】根据题意a ＝5，所以执行判断框后的“否”步骤，即b ＝a 2＋1，所以输出26. 【[答案]】269.解：程序框图如图所示：10.解：算法如下：第一步，如图，从已知线段的左端点A出发，作一条射线AP；第二步，在射线上任取一点C，得线段AC；第三步，在射线上作线段CE＝AC；第四步，在射线上作线段EF＝AC；第五步，在射线上作线段FG＝AC；第六步，在射线上作线段GD＝AC，那么线段AD＝5AC；第七步，连接DB；第八步，过C作BD的平行线，交线段AB于M，这样点M就是线段AB的一个5等分点．程序框图如图：11.解：程序框图：。

2020-2021学年人教版数学必修3配套训练：1.1.2 第2课时条件结构

第一章算法初步1．1算法与程序框图1．1.2程序框图与算法的基本逻辑结构第2课时条件结构[A组学业达标]1．下列关于条件结构的描述，正确的是() A．条件结构的出口有两个，这两个出口有时可以同时执行B．条件结构的判断框内的条件是惟一的C．条件结构根据条件是否成立选择不同的分支执行D．在条件结构的任何一个分支中，只能执行一个语句，而不能是多个答案：C2．如图所示的程序框图中，输入x＝2，则输出的结果是()A．1B．2C．3 D．4解析：输入x＝2后，该程序框图的执行过程是：输入x＝2，x＝2>1成立，y ＝2＋2＝2，输出y＝2.答案：B3．下列程序框图的运算结果为()A．5 B．10C．15 D．20解析：运行程序：a＝5≥4成立，则S＝1×5＝5，故选A. 答案：A4．某算法的程序框图如图所示，若输出结果为12，则输入的实数x的值是__________．解析：当x≤1时，y＝x－1≤0，∵输出结果为12，∴x>1，∴log2x＝12，∴x＝ 2.答案： 25．阅读如图所示的程序框图，写出它表示的函数是__________．解析：由程序框图知，当x ＞3时，y ＝2x －8；当x ≤3时，y ＝x 2，故本题框图的功能是输入x 的值，求分段函数y ＝⎩⎨⎧2x －8（x ＞3），x 2（x ≤3）的函数值．答案：y ＝⎩⎨⎧2x －8（x ＞3）x 2（x ≤3）6．如图是求实数x 的绝对值的算法程序框图，则判断框①处可填__________．解析：由程序框图可知，满足判断框①时，输出实数x 本身，所以判断框①中可填x ≥0？或x >0? 答案：x ≥0？(或x >0？)7．某次考试，为了统计成绩情况，设计了如图所示的程序框图．当输入一个同学的成绩x ＝75时，输出结果为__________．解析：由于75<80，在程序框图中的第一个判断框中，将按“否”的指向进入第二个判断框，又因75≥60，将按“是”的指向，所以输出的是“及格”．答案：及格8．设计一个算法：输入一个实数，输出它的绝对值，并画出程序框图．解析：设输入数为x ，绝对值为y . 则y ＝|x |＝⎩⎨⎧x （x ≥0），－x （x ＜0）.算法如下：第一步，输入x .第二步，若x ≥0，则y ＝x ，否则执行第三步．第三步，y ＝－x . 第四步，输出y . 程序框图如图：9．已知关于x的一元二次方程ax2＋bx＋c＝0(a≠0)，设计一个算法，判断方程是否有实数根．写出算法步骤，并画出程序框图．解析：算法如下：第一步，输入a，b，c.第二步，计算ω＝b2－4ac.第三步，判断ω≥0是否成立，若成立，输出方程有实数根；若不成立，输出方程无实数根．程序框图如下：[B组能力提升]10．如图中，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分．当x1＝6，x2＝9，p＝8.5时，x3等于()A ．10B ．7C ．8D ．11解析：∵x 1＝6，x 2＝9， ∴|x 2－x 1|＝3>2，输入x 3，假设|x 3－x 1|<|x 3－x 2|成立，即|x 3－6|<|x 3－9|，解得x 3<7.5，把x 3赋值给x 2，p ＝x 1＋x 22＝x 1＋x 32＝8.5，解得x 3＝11，与x 3<7.5矛盾，舍去；假设|x 3－x 1|≥|x 3－x 2|成立，即|x 3－6|≥|x 3－9|，解得x 3≥7.5，把x 3赋值给x 1，p ＝x 1＋x 22＝x 2＋x 32＝8.5，解得x 3＝8，符合要求．答案：C 11．如图所示，给出一个程序框图，其作用是输入x 的值，输出相应的y 的值．若要使输入的x 的值与输出的y 的值相等，则输入的这样的x 的值有 ( )A ．1个B ．2个C ．3个D ．4个解析：当x ≤2时，x ＝1或x ＝0，则x ＝y ；当2＜x ≤5时，若x ＝y ，则x ＝2x －3，∴x ＝3；当x ＞5时，x ＝1x 不成立，所以满足题意的x 的值有1，0，3. 答案：C12．已知函数y ＝⎩⎨⎧log 2x ，x ≥22－x ，x <2，如图表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写__________；②处应填写__________．解析：∵满足判断框中的条件执行y ＝2－x ， ∴①处应填x <2？.不满足x <2即x ≥2时，y ＝log 2x ，故②处应填y ＝log 2x . 答案：x <2？ y ＝log 2x13．某程序框图如图所示，若输出的结果是8，则输入的数是__________．解析：由程序框图知⎩⎨⎧x 2≥x 3x 2＝8或⎩⎨⎧x 2＜x 3x 3＝8，解得x ＝－22或x ＝2. 答案：－22或214．儿童乘坐高铁时，若身高h 不超过1.2 m ，则无需购票；若身高h 超过1.2 m ，但不超过1.5 m ，可买半票；若身高h 超过1.5 m 应买全票．请设计一个算法，输入儿童的身高，输出购票情况，并画出程序框图．解析：算法如下：第一步，输入h .第二步，判断h ≤1.2是否成立，若成立，则输出“免费”；若不成立，则执行第三步．第三步，判断h ≤1.5是否成立，若成立，则输出“半票”，若不成立，则输出“全票”．程序框图如下：15.如图所示是某函数f(x)给出x的值时，求相应函数值y的程序框图．(1)写出函数f(x)的解析式；(2)若输入的x取x1和x2(|x1|<|x2|)时，输出的y值相同，试简要分析x1与x2的取值范围．解析：(1)由程序框图知该程序框图执行的功能是求函数f(x)＝|x2－1|的值，故f(x)的解析式为f(x)＝|x2－1|.(2)画出f(x)＝|x2－1|的草图如下图．由图象的对称性知：要使f(x1)＝f(x2)且|x1|<|x2|，需－1<x1<1，同时2≥x2>1或－2≤x2<－1，∴x1的取值范围是{x|－1<x<1}，x2的取值范围是{x|1<x≤2或－2≤x<－1}．。

高中数学必修三课时作业16：1.1.2 第2课时条件结构

第2课时条件结构1.下列关于条件结构的描述，正确的是()A.条件结构的出口有两个，这两个出口有时可以同时执行B.条件结构的判断框内的条件是唯一的C.条件结构根据条件是否成立选择不同的分支执行D.在条件结构的任何一个分支中，只能执行一个语句，而不能是多个[解析]条件结构的两个出口不能同时执行，故A不正确；条件结构的判断框内的条件可能有多个，不是唯一的，故B不正确；在条件结构的任何一个分支中，可以执行多个语句，故D不正确，故选C.[答案] C2.已知程序框图如图所示，则程序框图中含有的基本结构有()A.顺序结构B.模块结构C.条件结构D.顺序结构和条件结构[解析]由图知其中有判断框，故含有条件结构，所有的程序框图都含有顺序结构，故选D.[答案] D3.如图所示的程序框图，输入x ＝2，则输出的结果是( )A.1B.2C.3D.4[解析] x ＝2满足条件x >1，故y ＝2＋2＝2，即输出的结果是2.[答案] B4.阅读如图所示的程序框图，写出它表示的函数是________.[解析] 由程序框图可知，当x >3时，y ＝2x －8；当x ≤3时，y ＝x 2，故本题框图的功能是输入x 的值，求分段函数y ＝⎩⎪⎨⎪⎧2x －8（x >3）x 2（x ≤3）的函数值.[答案] y ＝⎩⎨⎧2x －8 （x ＞3）x 2（x ≤3）5.对任意非零实数a ，b ，若a ⊗b 的运算原理如图所示，则(log 28)⊗4＝________.[解析] 因为log 28＝3，且满足3≤4，所以(log 28)⊗4＝3⊗4＝4－13＝1. [答案] 16.设计程序框图，输入x 的值，求函数y ＝⎩⎨⎧x 2（x ≥0），－x 2（x <0）的值.解算法如下：第一步，输入x 的值.第二步，判断x 的大小，若x ≥0，则y ＝x 2；否则，y ＝－x 2. 第三步，输出y 的值. 程序框图如图：7.求过两点P1(x1，y1)，P2(x2，y2)的直线的斜率.设计该问题的算法并画出程序框图.解算法如下：第一步，输入x1，y1，x2，y2.第二步，如果x1＝x2，输出“斜率不存在”；否则，k＝y2－y1x2－x1.第三步，输出k.程序框图如下图所示：能力提升8.某市的士收费办法如下：不超过2公里收7元(即起步价7元)，超过2公里的里程每公里收2.6元，另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示，则①处应填()A.y＝7＋2.6xB.y＝8＋2.6xC.y＝7＋2.6(x－2)D.y＝8＋2.6(x－2)[解析]当x>2时，2公里内的收费为7元，2公里外的收费为(x－2)×2.6，另外燃油附加费为1元，所以y＝7＋2.6(x－2)＋1＝8＋2.6(x－2).[答案] D9.2008年3月1日开始实施的《个人所得税》规定：全月总收入不超过2 000元的免征个人工资、薪金所得税，超过2 000元的部分需征税.设全月总收入金额为x元，前三级税率如下表所示：当工资薪金所得不超过4 000元时，计算个人所得税的一个程序框图如图，则输出①、输出②分别为()A.0.05x0.1xB.0.05x0.15x－250C.0.05x－1000.1x－200D.0.05x－1000.1x－225[解析]当2 000<x≤2 500时，税收y＝(x－2 000)×5%＝0.05x－100，当2 500<x≤4 000时，税收y＝500×5%＋(x－2 500)×10%＝0.1x－225.[答案] D10.阅读如图所示的程序框图.如果输入a＝log312，b＝⎝⎛⎭⎪⎫1213，c＝213，那么输出的是________.[解析] 该程序框图的算法功能是输出a ，b ，c 中的最大值.因为a ＝log 3 12＜0，0＜b ＝⎝ ⎛⎭⎪⎫1213＜1，c ＝213＞1，所以a ＜b ＜c ，因此最后输出的为c .[答案] c11.如图，若f (x )＝x 2，g (x )＝log 2x ，输入x 的值为0.25，则输出的结果为________.[解析] 当x ＝0.25时，f (0.25)＝116，g (0.25)＝－2，则f (0.25)>g (0.25)，所以h (0.25)＝g (0.25)＝－2. [答案] －212.如图所示的程序框图，其作用是：输入x 的值，输出相应的y 值.若要使输入的x 值与输出的y 值相等，求这样的x 值有多少个. 解由题可知算法的功能是求分段函数y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2＜x ≤5，1x ，x ＞5的函数值，要满足题意，则需要⎩⎪⎨⎪⎧x ≤2，x 2＝x 或⎩⎪⎨⎪⎧2＜x ≤5，2x －3＝x 或⎩⎨⎧x ＞5，1x ＝x ，解得x ＝0或x ＝1或x ＝3，共3个值.13.(选做题)有一城市，市区是半径为15 km 的圆形区域，近郊区为距市中心15～25 km 的范围内的环形地带，距市中心25 km 以外的为远郊区，坐标原点O 为市中心，如图所示.市区地价为每公顷100万元，近郊区地价为每公顷60万元，远郊区地价为每公顷20万元.请画出输入坐标为(x ，y )的点处的地价的算法的程序框图. 解程序框图如下图所示.。

人教A版高中数学必修三第一章1.1-1.1.2第2课时条件结构同步训练(II)卷

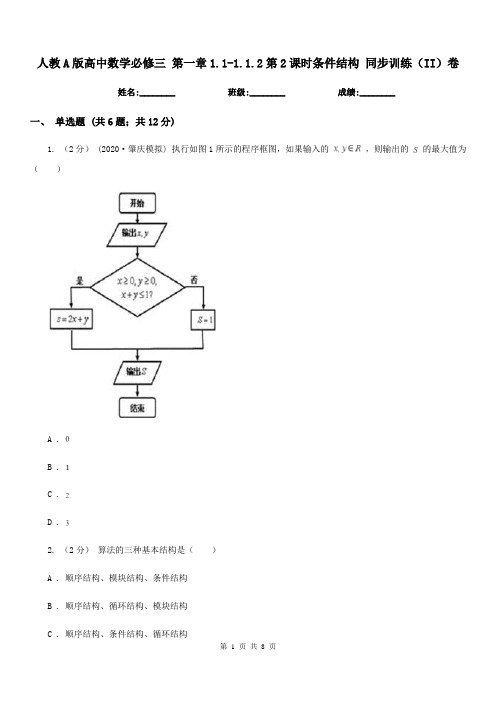
人教A版高中数学必修三第一章1.1-1.1.2第2课时条件结构同步训练（II）卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题；共12分)1. （2分）(2020·肇庆模拟) 执行如图1所示的程序框图，如果输入的，则输出的的最大值为（）A .B .C .D .2. （2分）算法的三种基本结构是（）A . 顺序结构、模块结构、条件结构B . 顺序结构、循环结构、模块结构C . 顺序结构、条件结构、循环结构D . 模块结构、条件结构、循环结构3. （2分）(2017·肇庆模拟) 图是计算函数的值的程度框图，在①、②、③处应分别填入的是（）A . y=ln（﹣x），y=0，y=2xB . y=ln（﹣x），y=2x ， y=0C . y=0，y=2x ， y=ln（﹣x）D . y=0，y=ln（﹣x），y=2x4. （2分）程序框图，如图所示，已知曲线E的方程为ax2+by2=ab (a，b∈R)，若该程序输出的结果为s，则（）A . 当s＝1时，E是椭圆B . 当s＝0时，E是一个点C . 当s＝0时，E是抛物线D . 当s＝－1时，E是双曲线5. （2分）任何一种算法都离不开的基本结构为（）A . 逻辑结构B . 条件结构C . 循环结构D . 顺序结构6. （2分）(2017·天津) 阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（）A . 0B . 1C . 2D . 3二、填空题 (共5题；共5分)7. （1分）给出以下四个问题，①x，输出它的相反数．②求面积为6的正方形的周长．③求三个数a，b，c 中输入一个数的最大数．④求函数的函数值．其中不需要用条件语句来描述其算法的有________ 个．8. （1分） (2019高二下·吉林月考) 对任意非零实数，若的运算原理如程序框图所示，则________．9. （1分）对任意非零实数a ， b ，若a⊗b的运算原理的程序框图如图所示．则3⊗2＝________．10. （1分）执行右边的程序框图，输出的T的值为________ .11. （1分） INPUT xIF 9＜x AND x＜100 THENa=x\10b=x MOD 10x=10*b+aPRINT xEND IFEND若输入的x为61，则输出是________ ．三、解答题 (共2题；共10分)12. （5分）在边长为4的正方形ABCD的边上有一点P沿着折线BCDA由点B（起点）向点A（终点）运动．设点P运动的路程为x，△APB的面积为y，且y与x之间的函数关系式用如图所示的程序框图给出．（1）写出框图中①、②、③处应填充的式子；（2）若输出的面积y值为6，则路程x的值为多少？并指出此时点P的在正方形的什么位置上？13. （5分）已知一个程序语句如图：（1）若输入X的值为0，求输出Y的值？（2）若输出Y的值为3，求输入X的值？参考答案一、单选题 (共6题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共5题；共5分)7-1、8-1、9-1、10-1、11-1、三、解答题 (共2题；共10分)12-1、13-1、。

人教新课标版数学高一- 数学必修三练习 第2课时条件结构

必修三 第2课时 程序框图、顺序结构和条件结构

人教A版高中数学必修3课后习题 1.1.2 第2课时 条件结构

2020-2021人教版数学3课时1.1.2第2课时 条件结构含解析

2019-2020学年度最新高中数学新人教版必修3教案：第1章 1-1-2 第2课时 条件结构-含答案

数学人教A版必修3课件：1.1.2 第2课时 条件结构1

人教新课标版数学高一-必修3导学案 第2课时 条件结构

高中数学 必修三 1.1.2 第2课时 条件结构习题 新人教A版必修3

高中数学必修三课时作业14：1.1.2 第2课时 条件结构