时序逻辑电路课后习题答案
(完整版)时序逻辑电路习题与答案

第12章时序逻辑电路自测题一、填空题1.时序逻辑电路按状态转换情况可分为时序电路和时序电路两大类。
2.按计数进制的不同,可将计数器分为、和N进制计数器等类型。
3.用来累计和寄存输入脉冲个数的电路称为。
4.时序逻辑电路在结构方面的特点是:由具有控制作用的电路和具记忆作用电路组成。
、5.、寄存器的作用是用于、、数码指令等信息。
6.按计数过程中数值的增减来分,可将计数器分为为、和三种。
二、选择题1.如题图12.1所示电路为某寄存器的一位,该寄存器为。
A、单拍接收数码寄存器;B、双拍接收数码寄存器;C、单向移位寄存器;D、双向移位寄存器。
2.下列电路不属于时序逻辑电路的是。
A、数码寄存器;B、编码器;C、触发器;D、可逆计数器。
3.下列逻辑电路不具有记忆功能的是。
A、译码器;B、RS触发器;C、寄存器;D、计数器。
4.时序逻辑电路特点中,下列叙述正确的是。
A、电路任一时刻的输出只与当时输入信号有关;B、电路任一时刻的输出只与电路原来状态有关;C、电路任一时刻的输出与输入信号和电路原来状态均有关;D、电路任一时刻的输出与输入信号和电路原来状态均无关。
5.具有记忆功能的逻辑电路是。
A、加法器;B、显示器;C、译码器;D、计数器。
6.数码寄存器采用的输入输出方式为。
A、并行输入、并行输出;B、串行输入、串行输出;C、并行输入、串行输出;D、并行输出、串行输入。
三、判断下面说法是否正确,用“√"或“×"表示在括号1.寄存器具有存储数码和信号的功能。
( )2.构成计数电路的器件必须有记忆能力。
( )3.移位寄存器只能串行输出。
( )4.移位寄存器就是数码寄存器,它们没有区别。
( )5.同步时序电路的工作速度高于异步时序电路。
( )6.移位寄存器有接收、暂存、清除和数码移位等作用。
()思考与练习题12.1.1 时序逻辑电路的特点是什么?12.1.2 时序逻辑电路与组合电路有何区别?12.3.1 在图12.1电路作用下,数码寄存器的原始状态Q3Q2Q1Q0=1001,而输入数码D3D2D1D0=0110时,在CP的作用下,Q3Q2Q1Q0状态如何变化?12.3.2 题图12.2所示移位寄存器的初始状态为111,画出连续3个C P脉冲作用下Q2Q1Q0各端的波形和状态表。
第6章_时序逻辑电路 课后答案

第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。
状态转换图如图A6.3【题 6.5】分析图P6.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQQ A Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能,画出电路的状态转换图,检查电路能否自启动,说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。
A =0时作二进制加法计数,A =1时作二进制减法计数。
01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=•=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000,由状态方程可得:状态转换图如图A6.7。
(完整版)触发器时序逻辑电路习题答案

第4章 触发器4.3 若在图4.5电路中的CP 、S 、R 输入端,加入如图4.27所示波形的信号,试画出其Q 和Q 端波形,设初态Q =0。
SRCP图4.27 题4.3图解:图4.5电路为同步RS 触发器,分析作图如下:S RQ4.5 设图4.28中各触发器的初始状态皆为Q =0,画出在CP 脉冲连续作用下个各触发器输出端的波形图。
Q 11CPQ 3CPCPQ 2Q 6Q 4Q 5CP图4.28 题4.5图解:Q Q nn 111=+ Q Q n n 212=+ Q Q nn 313=+Q Q n n 414=+ Q Q n n 515=+ Q Q nn 616=+Q 1CP Q 2Q 3Q 4Q 5Q64.6 试写出 图4.29(a)中各触发器的次态函数(即Q 1 n+1 、 Q 2 n+1与现态和输入变量之间的函数式),并画出在图4.29(b )给定信号的作用下Q 1 、Q 2的波形。
假定各触发器的初始状态均为Q =0。
1A BCP>1D C1=1A BQ 1Q 2Q 2(a)BA(b)图4.29题4.6图解:由图可见:Q B A AB Q n n 111)(++=+ B A Q n ⊕=+12B A Q 2Q 14.7 图4.30(a )、(b )分别示出了触发器和逻辑门构成的脉冲分频电路,CP 脉冲如图4.30(c )所示,设各触发器的初始状态均为0。
(1)试画出图(a )中的Q 1、Q 2和F 的波形。
(2)试画出图(b )中的Q 3、Q 4和Y 的波形。
Y(b )(c )CPQ 1Q 2(a )图4.30 题4.7图解: (a )Q Q nn 211=+ QQ nn 112=+ Q F 1CP ⊕= R 2 = Q 1 低电平有效CPQ 1Q 2F(b )Q Q Q n n n 4313=+ Q Q Q n n n 4314=+ Q Q Y nn43=CP 3= CP 上降沿触发 CP 4= CP 下降沿触发CPQ 3Q 4Y4.8 电路如图4.31所示,设各触发器的初始状态均为0。
电工与电子技术习题参考答案第9章

第9章时序逻辑电路习题解答9.1 d R端和d S端的输入信号如题9.1图所示,设基本RS触发器的初始状态分别为1和0两种情况,试画出Q端的输出波形。
题9.1图解:9.2 同步RS触发器的CP、R、S端的状态波形如题9.2图所示。
设初始状态为0和1两种情况,试画出Q端的状态波形。
题9.2图解:9.3 设主从型JK触发器的初始状态为0,J、K、CP端的输入波形如题9.3图所示。
试画出Q端的输出波形(下降沿触发翻转)。
解:如题9.3图所示红色为其输出波形。
第9章时序逻辑电路225题9.3图9.4 设主从型JK触发器的初始状态为0,J、K、CP端输入波形如题9.4图所示。
试画出Q端的输出波形(下降沿触发翻转)。
如初始状态为1态,Q端的波形又如何?解:如题9.4图所示红色为其输出波形。
题9.4图9.5 设维持阻塞型D触发器的初始状态为0,D端和CP端的输入波形如题9.5图所示,试画出Q端的输出波形(上升沿触发翻转)。
如初始状态为1态,Q端的波形又如何?解:如题9.5图所示红色为其输出波形。
第9章时序逻辑电路226题9.5图9.6 根据CP时钟脉冲,画出题9.6图所示各触发器Q端的波形。
(1)设初始状态为0;(2)设初始状态为1。
(各输入端悬空时相当于“1”)题9.6图解:第9章时序逻辑电路2279.7 题9.7图所示的逻辑电路中,有J和K两个输入端,试分析其逻辑功能,并说明它是何种触发器。
题9.7图=⋅⋅⋅=⋅+⋅解:由图得D Q F J Q Q F J QJ K Q n D Q n+10 0 0 0 00 0 1 1 10 1 0 0 00 1 1 0 01 0 0 1 11 0 1 1 11 1 0 1 11 1 1 0 0此电路为D触发器和与非门组成的上升沿触发的JK触发器。
9.8 根据题9.8图所示的逻辑图和相应的CP、d R、D的波形,试画出Q1和Q2端的输出波形。
设初始状态Q1=Q2=0。
题9.8图解:第9章时序逻辑电路2289.9 试用4个D触发器组成一个四位右移移位寄存器。
电子技术——几种常用的时序逻辑电路参考答案

第七章几种常用的时序逻辑电路参考答案一、选择题1.当时的输入信号,电路原来状态,a2.a3.b4.b5.JK6.基本RS,1R S+=(RS=0)7.T8.1,1n nQ Q+=9.J=K=T;J=K=T=1;J=D,K=D10.n nD TQ TQ=+;nD Q=11.并行,串行;并行输出,串行输出12.数码,移位13.清零14.同步计数器,异步计数器。
15.a,清零,置数,保持16.b17.异步,同步。
18.a,M*N19.2,双稳态触发器20.双向移位二、判断题1. B2. C3. C4. D5. B6. A7. C8. C9. A10. B11. C12. D13. D14. B15. D16. D17. A18. C19. C20. D三、判断题1.错2.对3.对4.错5.对6.错7.对8.对9.错10.错11.对12.对13.对14.错15.对四、简答题1.(9-1易)图示是用与非门组成的基本RS触发器试根据其特性表,并写出特性方程和约束条件。
R SnQ1n Q+功能0 0 0 0 01不定不定不允许0 1 0 1 01置010 1 0 011置11 1 1 1 011保持参考答案:特征方程:1n nQ S RQ+=+,约束条件:1R S+=2.(9-1中) 用JK 触发器(特性方程1n n n Q JQ KQ +=+)可以转换成其他逻辑功能触发器,适当连接给出的JK 触发器的输入端分别将其转换成: 1).T 触发器(1n n n Q TQ TQ +=+) 2).T ’触发器(1n n Q Q +=) 3).D 触发器(1n Q D +=)参考答案:3.(9-1中)写出JK 触发器,T 触发器,T ’触发器,D 触发器的特性方程。
参考答案:JK 触发器特性方程:1n n n Q JQ KQ +=+T 触发器特性方程:1n n n Q TQ TQ +=+ T ’触发器特性方程:1n n Q Q += D 触发器特性方程:1n QD +=4.(9-3中)同步计数器的同步是指什么? 参考答案:所谓同步指组成计数器的所有触发器共用一个时钟脉冲,使应该翻转的触发器在时钟脉冲作用下同时翻转,并且该时钟脉冲即输入的计数脉冲。
时序逻辑电路习题集答案

第六章时序逻辑电路6.1 基本要求1. 正确理解组合逻辑电路、时序逻辑电路、寄存器、计数器、同步和异步、计数和分频等概念。
2. 掌握时序逻辑电路的分析方法,包括同步时序逻辑电路和异步时序逻辑电路。
3. 熟悉寄存器的工作原理、逻辑功能和使用。
4. 掌握二进制、十进制计数器的构成原理。
能熟练应用集成计数器构成任意进制计数器。
5. 掌握同步时序逻辑电路的设计方法。
6.2自测题一、填空题1.数字电路按照是否有记忆功能通常可分为两类:、。
2.由四位移位寄存器构成的顺序脉冲发生器可产生个顺序脉冲。
3.时序逻辑电路按照其触发器是否有统一的时钟控制分为时序电路和时序电路。
4. 用D触发器来构成12进制计数器,需要个D触发器。
二、选择题1.同步计数器和异步计数器比较,同步计数器的显著优点是。
A.工作速度高B.触发器利用率高C.电路简单D.不受时钟CP控制。
2.把一个五进制计数器与一个四进制计数器串联可得到进制计数器。
A.4B.5C.9D.203. N个触发器可以构成最大计数长度(进制数)为的计数器。
A.NB.2NC.N2D.2N4. N个触发器可以构成能寄存位二进制数码的寄存器。
A.N-1B.NC.N+1D.2N5.五个D触发器构成环形计数器,其计数长度为。
A.5B.10C.25D.326.同步时序电路和异步时序电路比较,其差异在于后者。
A.没有触发器B.没有统一的时钟脉冲控制C.没有稳定状态D.输出只与内部状态有关7.一位8421BCD码计数器至少需要个触发器。
A.3B.4C.5D.108.欲设计0,1,2,3,4,5,6,7这几个数的计数器,如果设计合理,采用同步二进制计数器,最少应使用级触发器。
A.2B.3C.4D.89.8位移位寄存器,串行输入时经个脉冲后,8位数码全部移入寄存器中。
A.1B.2C.4D.810.用二进制异步计数器从0做加法,计到十进制数178,则最少需要个触发器。
A.2B.6C.7D.8E.1011.某电视机水平-垂直扫描发生器需要一个分频器将31500H Z的脉冲转换为60H Z的脉冲,欲构成此分频器至少需要个触发器。
第6章 时序逻辑电路-习题答案
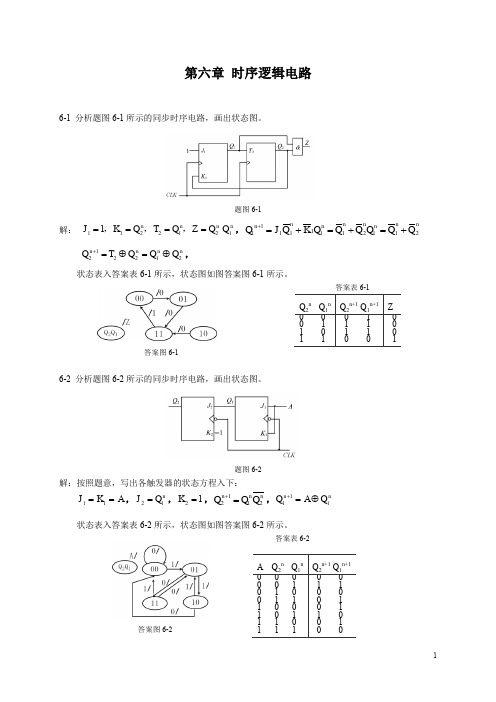
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路,画出状态图。
题图6-1解: 11221211n n n n J K Q T Q Z Q Q ====,,,,11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕,状态表入答案表6-1所示,状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路,画出状态图。
题图6-2 解:按照题意,写出各触发器的状态方程入下:11J K A ==,21n J Q =,21K =,1212n n nQ Q Q +=,111n n Q A Q +=⊕状态表入答案表6-2所示,状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路,画出状态图。
题图6-3解:按照题意,写出各触发器的状态方程入下:1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1,,, 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中,已知寄存器的初始状态Q 1Q 2Q 3=111。
时序逻辑电路习题解答
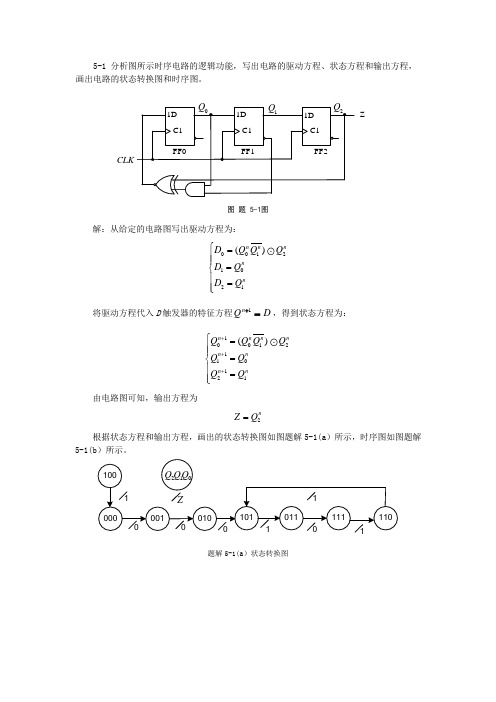
5-1 分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
CLKZ图 题 5-1图解:从给定的电路图写出驱动方程为:00121021()n n nn n D Q Q Q D Q D Q ⎧=⎪⎪=⎨⎪=⎪⎩将驱动方程代入D 触发器的特征方程D Qn =+1,得到状态方程为:10012110121()n n n n n n n n Q Q Q Q Q Q Q Q +++⎧=⎪⎪=⎨⎪=⎪⎩由电路图可知,输出方程为2nZ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-1(a )所示,时序图如图题解5-1(b )所示。
题解5-1(a )状态转换图1Q 2/Q ZQ题解5-1(b )时序图综上分析可知,该电路是一个四进制计数器。
5-2 分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
YA图 题 5-2图解:首先从电路图写出驱动方程为:()0110101()n n n n nD AQ D A Q Q A Q Q ⎧=⎪⎨==+⎪⎩将上式代入触发器的特征方程后得到状态方程()101110101()n n n n n n nQ AQ Q A Q Q A Q Q ++⎧=⎪⎨==+⎪⎩电路的输出方程为:01n nY AQ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-2所示YA题解5-2 状态转换图综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态“00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3 已知同步时序电路如图(a)所示,其输入波形如图 (b)所示。
试写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
X(a) 电路图1234CLK5678X(b)输入波形 图 题 5-3图解:电路的驱动方程、状态方程和输出方程分别为:00101100011011011, ,n n n n n n n n n nJ X K X J XQ K XQ X Q XQ XQ XQ Q XQ XQ XQ Y XQ ++⎧==⎪⎨==⎪⎩⎧=+=⎪⎨⎪=+=+⎩= 根据状态方程和输出方程,可分别做出1110,n n Q Q ++和Y 的卡诺图,如表5-1所示。
数字电路与数字逻辑4时序逻辑电路习题解答
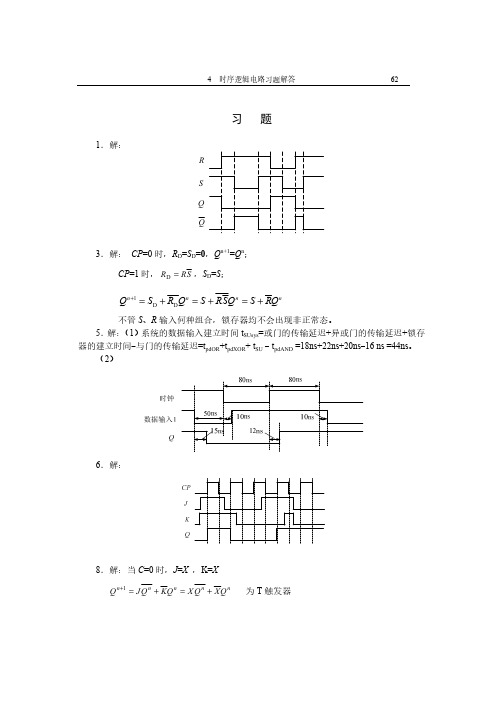
4 62习 题1.解:QQRS3.解: CP =0时,R D =S D =0,Q n+1=Q n ; CP =1时,S R R =D ,S D =S ;1D D n n n n Q S R Q S RSQ S RQ +=+=+=+不管S 、R 输入何种组合,锁存器均不会出现非正常态。
5.解:(1)系统的数据输入建立时间t SUsys =或门的传输延迟+异或门的传输延迟+锁存器的建立时间-与门的传输延迟=t pdOR +t pdXOR + t SU - t pdAND =18ns+22ns+20ns -16 ns =44ns 。
(2)4 63当C =1时, J =X X K = X Q K Q J Q n n n =+=+1 为D 触发器9. 解:当EN =0 ,Q n+1=Q n ;当EN =1,Q n+1=D ,则D EN Q EN Q n n ⋅+⋅=+11,令D EN Q EN D n ⋅+⋅=1即可。
10.解:根据电路波形,它是一个单发脉冲发生器,A 可以为随机信号,每一个A 信号的下降沿后;Q 1端输出一个脉宽周期的脉冲。
12.解:(1)(2)4 6415. 解:X =0时,计至9时置0000:03Q Q LD =,D 3D 2D 1D 0=0000X =1时,计至4时置1011:23Q Q LD =,D 3D 2D 1D 0=10112303Q Q X Q Q X LD +=,D 2=0,D 3=D 1=D 0=X16.解:当片1计数到1001时,置数信号LD 为低电平,这时,再来一个CP 脉冲,下一个状态就进入0000。
应该等到片0和片1的状态同时为1001时,片1的下一个状态才能进入0000。
改进后电路为:对改进后电路的仿真结果:17.解:4 6518.解:19. 解:从图所示电路图可知,S 1S 0=01,根据表4.8-3所示的74LS194功能表,电路处于右移功能。
右移数据输入端的逻辑表达式为:32IR Q Q D =。
21章 题库——时序逻辑电路+答案

第21章 触发器和时序逻辑电路一、填空题1、JK 触发器的特性方程为:=+1n Q ________________________。
2、时钟触发器按照结构和触发方式不同可分为:_________、__________、_________和主从式触发器四种。
3、T 触发器的特性方程为=+1n Q _________________。
4、4个触发器组成的寄存器可以存储__________位二进制数。
5、将JK 触发器的J 端连在Q 端上,K 端接高电平。
假设)(t Q =0,则经过50个CP 脉冲作用后,它的状态)50(+t Q =_____。
6、对于时钟RS 触发器,若要求其输出“0”状态保持不变,则输入的RS 信号应为________。
7、组成计数器的各个触发器的状态能在时钟信号到达时同时翻转,它属于__________ 计数器。
(填“同步”或“异步”)8、当JK 触发器的输入J=1,K=0时,触发器的次态Q n+1=____________。
9、若要构成十二进制计数器,最少要用__________个触发器。
10、构成一个模6的同步计数器最少要________个触发器。
11、一个 JK 触发器有____个稳态,它可存储____位二进制数。
二、选择题1、下列触发器中有空翻现象的是_________。
A 、同步式触发器B 、维持阻塞式触发器C 、主从式触发器D 、边沿式触发器 2、在以下各种电路中,属于时序电路的有__________。
A 、译码器B 、计数器C 、数据选择器D 、编码器 3、JK 触发器当J=K=1时,Q n+1=__________。
A 、0B 、1C 、Q nD 、 Q n4、下列触发器中逻辑功能最多是_______。
A 、J-K 触发器B 、D 触发器C 、T 触发器D 、T ′触发器 5、在CP 有效的情况下,当输入端D=0时,则D 触发器的输出端=+1n Q ________。
电子技术习题解答触发器和时序逻辑电路及其实际应用习题解答
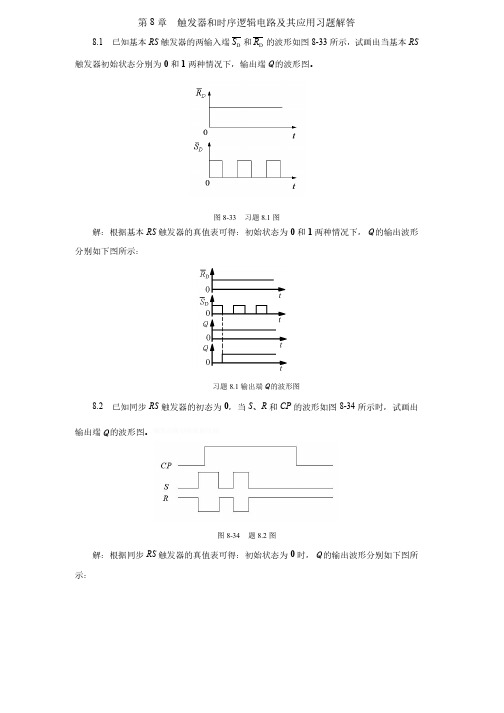
第8章触发器和时序逻辑电路及其应用习题解答8.1 已知基本RS 触发器的两输入端D S 和D R 的波形如图8-33所示,试画出当基本RS 触发器初始状态分别为0和1两种情况下,输出端Q的波形图。
图8-33 习题8.1图解:根据基本RS 触发器的真值表可得:初始状态为0和1两种情况下,Q的输出波形分别如下图所示:习题8.1输出端Q的波形图8.2 已知同步RS 触发器的初态为0,当S 、R 和CP 的波形如图8-34所示时,试画出输出端Q的波形图。
矚慫润厲钐瘗睞枥庑赖。
图8-34 题8.2图解:根据同步RS 触发器的真值表可得:初始状态为0时,Q的输出波形分别如下图所示:习题8.2输出端Q的波形图8.3 已知主从JK 触发器的输入端CP 、J 和K 的波形如图8-35所示,试画出触发器初始状态分别为0时,输出端Q的波形图。
聞創沟燴鐺險爱氇谴净。
图8-35 习题8.3图解:根据主从JK 触发器的真值表可得:初始状态为0情况下,Q的输出波形分别如下图所示:图所示:习题8.3输出端Q的波形图的波形图8.4 已知各触发器和它的输入脉冲CP 的波形如图8-36所示,当各触发器初始状态均为1时,试画出各触发器输出Q端和Q 端的波形。
残骛楼諍锩瀨濟溆塹籟。
图8-36 习题8.4图解:根据逻辑图及触发器的真值表或特性方程,且将驱动方程代入特性方程可得状态方程。
即:(a )J =K =1;Qn +1=n Q,上升沿触发酽锕极額閉镇桧猪訣锥。
(b)J =K =1;Qn +1=n Q, 下降沿触发下降沿触发(c)K =0,J =1;Qn +1=J n Q+K Qn =1,上升沿触发,上升沿触发 (d)K =1,J =n Q;Qn +1=J nQ+K Qn =n Qn Q+0·Qn =n Q,上升沿触发,上升沿触发 (e)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,上升沿触发,上升沿触发(f)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=nQ,下降沿触发,,下降沿触发, 再根据边沿触发器的触发翻转时刻,可得当初始状态为1时,各个电路输出端Q的波形分别如图(a )、(b )、(c )、(d )、(e )和(f )所示,其中具有计数功能的是:(a )、(b )、(d )、(e )和(f )。
电子技术习题解答.第8章.触发器和时序逻辑电路及其应用习题解答

第8章 触发器和时序逻辑电路及其应用习题解答8.1 已知基本RS 触发器的两输入端D S 和D R 的波形如图8-33所示,试画出当基本RS 触发器初始状态分别为0和1两种情况下,输出端Q的波形图。
图8-33 习题8.1图解:根据基本RS 触发器的真值表可得:初始状态为0和1两种情况下,Q的输出波形分别如下图所示:习题8.1输出端Q的波形图8.2 已知同步RS 触发器的初态为0,当S 、R 和CP 的波形如图8-34所示时,试画出输出端Q的波形图。
图8-34 题8.2图解:根据同步RS 触发器的真值表可得:初始状态为0时,Q的输出波形分别如下图所示:习题8.2输出端Q的波形图8.3 已知主从JK触发器的输入端CP、J和K的波形如图8-35所示,试画出触发器初始状态分别为0时,输出端Q的波形图。
图8-35 习题8.3图解:根据主从JK触发器的真值表可得:初始状态为0情况下,Q的输出波形分别如下图所示:习题8.3输出端Q的波形图8.4 已知各触发器和它的输入脉冲CP的波形如图8-36所示,当各触发器初始状态均为1时,试画出各触发器输出Q端和Q端的波形。
图8-36 习题8.4图解:根据逻辑图及触发器的真值表或特性方程,且将驱动方程代入特性方程可得状态方程。
即:(a )J =K =1;Qn +1=n Q,上升沿触发 (b)J =K =1;Qn +1=n Q, 下降沿触发 (c)K =0,J =1;Qn +1=J n Q+K Qn =1,上升沿触发 (d)K =1,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0·Qn =n Q,上升沿触发 (e)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,上升沿触发 (f)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,下降沿触发, 再根据边沿触发器的触发翻转时刻,可得当初始状态为1时,各个电路输出端Q的波形分别如图(a )、(b )、(c )、(d )、(e )和(f )所示,其中具有计数功能的是:(a )、(b )、(d )、(e )和(f )。
第9章 时序逻辑电路 习题解答

1 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
1 0 0 0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0101
011 0
0101
01 0 0
0011
001 0
0001
9
10
11
12
13
14
15
16
0 0 0 0
0(借位)
9-19图9-69所示电路。试画出在图中时钟脉冲CP作用下Q0、 、Q1、 和输出ф1、ф2的波形图,并说明ф1和ф2波形的相位差(时间关系)。
图9-69题9-19图
解图中各触发器均接成 触发器,每来一个计数脉冲,触发器的状态改变一次。
输出ф1、ф2的逻辑表达式为
可得到各输出的波形如题9-19解图所示。由此波形可见, 和 的相位差为1/4个周期。
9-20试列出图9-70所示计数器的真值表,从而说明它是几进制计数器。设初始状态为000。
图9-70题9-20图
图9-68题9-17图
解各触发器使用同一个计数脉冲,所以该计数器为同步计数器。由图可写出各触发器输入端的激励方程
,
,
,
将以上各式代入JK触发器的特征方程即得计数器状态方程
设初始状态为000,则可得到计数器的状态转换表如表9-5所示,其工作波形如题9-17解图所示,可见该计数器为同步六进制加法计数器。
a) b)
图9-63题9-10图
解图中 和 是触发器的置0和置1端,低电平有效。 的状态根据D触发器的输入端D的状态而变化,CP脉冲上升沿触发。JK触发器的输入端 , ,CP脉冲下降沿触发。依此画出的Q1端和Q2端波形如题9-10解图所示。
数字电子技术(第三版)课后习题答案XT6

第六章时序逻辑电路1.解:状态迁移图计数器的计数模为六。
2.(1)由所给方程画出逻辑图(2)该电路是异步电路,对异步电路的分析,主要注意每一级触发器的时钟。
对Q2、Q3而言,因为其J=K=1,每一时钟下降沿必翻转,即在Q1由1→0时,Q2翻转一次;同样,Q2由1→0时,Q3翻转一次。
为了判断电路的计数模,应先作出状态迁移表。
该电路为一个具有自启动能力的异步模九计数器(3) 由上述状态迁移表,可画出状态迁移图,如图所示。
2. 解 由波形图直接得状态迁移关系。
由此可看出该计数器是一个同步模六递减计数器。
由状态迁移表、作出卡诺图,从而求得各级触发器的特征方程,再与JK 触发器特征方程n nn Q K Q J Q+=+1相比较,即可得激励方程:nAn B nC A nAB nAC A n Cn A B nB n AC nAn A nB n A nB nC nA nB n Cn A nC nB nA n C Q Q Q C K Q K Q K J Q Q J Q Q J Q Q Q Q Q Q Q Q Q Q Q Q Q Q ========+=+=+++11111迁移表卡诺图 如选D 触发器,则激励方程为:nAn B nC nAA n CnA nB n A B nCn A nC nB nA C nAn A n C nA nB n A n B n Cn A nC n B n A n C Q Q Q C QD Q Q Q Q D Q Q Q Q Q D Q Q Q Q Q Q Q Q Q Q Q Q Q ==+=+==+=+=+++111由激励方程画出逻辑图。
D 触发器电路图。
最后还应检验自启动能力: 110→011; 111→110 显然该电路具有自启动能力。
3. 解:写出方程 激励方程:nnn Q Q D Q D 21211⊕==特征方程:nnn n n Q Q QQ Q 2112111⊕==++状态真值表状态迁移图该电路为同步四进制加法计数器。
时序逻辑电路习题解答

5-1分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图和时序图。
解:从给定的电路图写出驱动方程为:D o (Q 0Q i n)e Q 2D i Q 01D 2 Q i nQ 01 1(Q 0Q n)eQ ;Q i n 1Q 0Q 21Q ;由电路图可知,输出方程为Z Q ;CLK将驱动方程代入D 触发器的特征方程Q n 1D ,得到状态方程为:5-1(a )所示,时序图如图题解Z图题5-1图根据状态方程和输出方程,画出的状态转换图如图题解题解5-1(a )状态转换图综上分析可知,该电路是一个四进制计数器。
5-2分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
解:首先从电路图写出驱动方程为:D o A& D i A Qg :A (Q : Q i n)将上式代入触发器的特征方程后得到状态方程Q 0 1AQ :Q :1 AQ 0Q :A (Q nQ :)电路的输出方程为:CLKQ i12345——-A1 11 t----------- 1------------ 1|| 1 » 1 1 1----------- 1 ---------- 1 --------------►CLK0 Q 2/Z 仝题解5-1(b )时序图0 Q o 胃AY图题5-2图丫AQoQ;根据状态方程和输出方程,画出的状态转换图如图题解5-2 所示综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态" 00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3已知同步时序电路如图(a )所示,其输入波形如图 (b )所示。
试写出电路的驱动方 程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
CLK 1 2345678(b )输入波形 图题5-3图解:电路的驱动方程、状态方程和输出方程分别为:J 。
第十三章 时序逻辑电路习题及答案

第十三章时序逻辑电路习题及答案一、填空题1、数字逻辑电路常分为组合逻辑电路和两种类型。
2、时序逻辑电路是指任何时刻电路的稳定输出信号不仅与当时的输入信号有关,而且与有关。
3、时序逻辑电路由两大部分组成。
4、时序逻辑电路按状态转换来分,可分为两大类。
5、时序逻辑电路按输出的依从关系来分,可分为两种类型。
6、同步时序电路有两种分析方法,一种是另一种是。
7、同步时序电路的设计过程,实为同步时序电路分析过程的过程。
8、计数器种类繁多,若按计数脉冲的输入方式不同,可分两大类。
9、按计数器进制不同,可将计数器分为。
10、按计数器增减情况不同,可将计数器分。
11、二进制计数器是逢二进一的,如果把n个触发器按一定的方式链接起来,可枸成。
12、一个十进制加法计数器需要由 J-K触发器组成。
13、三个二进制计数器累计脉冲个数为;四个二进制计数器累计脉冲个数为。
14、寄存器可暂存各种数据和信息,从功能分类,通常将寄存器分为。
15、数码输入寄存器的方式有;从寄存器输出数码的方式有。
16、异步时序逻辑电路可分为和。
17、移位寄存器中,数码逐位输入的方式称为。
18、计数器可以从三个方面进行分类:按__ _ _方式,按_________________方式,按______________方式。
19、三位二进制加法计数器最多能累计__个脉冲。
若要记录12个脉冲需要___个触发器。
20、一个四位二进制异步加法计数器,若输入的频率为6400H Z,在3200个计数脉冲到来后,并行输出的频率分别为______H Z,_____ H Z,____ H Z,_____ H Z。
一个四位二进制加法计数器起始状态为1001,当最低位接收到4个脉冲时,各触发器的输出状态是:Q0为__;Q1为__;Q2为__;Q3为__。
21、时序逻辑电路的特点是:任意时刻的输出不仅取决于______________,而且与电路的______有关。
22、寄存器一般都是借助有________功能的触发器组合起来构成的,一个触发器存储____二进制信号,寄存N位二进制数码,就需要__个触发器。
时序逻辑电路练习题及答案
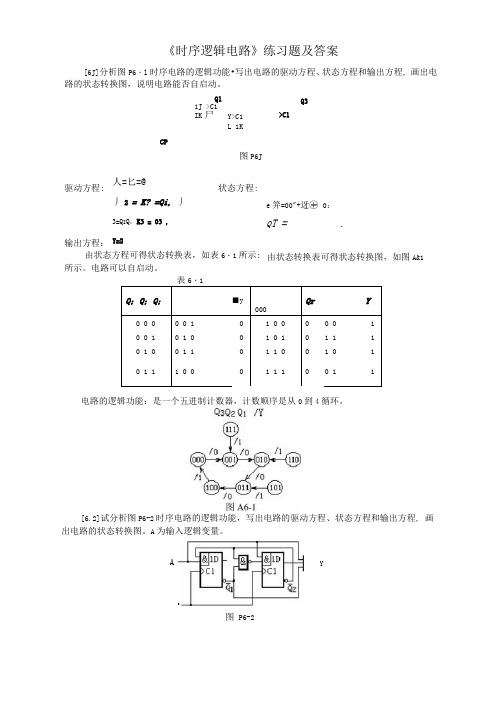
《时序逻辑电路》练习题及答案CP图P6J6・1Q;Q;Q;■y000Qr Y0 0 0 0 0 1 0 1 0 0 0 0 0 10 0 1 0 1 0 0 1 0 1 0 1 1 10 1 0 0 1 1 0 1 1 0 0 1 0 10 1 1 1 0 0 0 1 1 1 0 0 1 1电路的逻辑功能:是一个五进制计数器,计数顺序是从0到4循环。
[6.2]试分析图P6-2时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图。
A为输入逻辑变量。
[6J]分析图P6・l时序电路的逻辑功能•写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图,说明电路能否自启动。
Q11J >C1IK尸Y>C1L 1K>C1Q3驱动方程:人=匕=@丿2 = K? =Qi, 丿3=Q I Q,K3 = 03 ,Y=2状态方程:e笄=00"+迓㊉0:Q T= .输出方程:由状态方程可得状态转换表,如表6・1所示:所示。
电路可以自启动。
由状态转换表可得状态转换图,如图A&1A Y图P6-2CP图P6・3【解]___人=223, K] =1 ;丿2 =01,心=0仪3; Q 置=瓯・a : er* =aa+aaQ ; y= Q2Q3电路的状态转换图如图A6・3所示,电路能够自启动。
Q3Q2Q1 /¥/0/O 图 A6-3[64] 分析图P6・4给出的时序电路,画出电路的状态转换图.检査电路能否自启动, 说明电路实现的功能。
A 为输入变量。
【解1 驱动方程:A =.状态方程:QT = A© , 输出方程:丫 =辺2餌=A^©=A(@+0)由状态方程可得状态转换表,如表6-2所示:由状态转换表 可得状态转换图,如图A&2所示0电路的逻辑功能是:判断A 是否连续输入四个和四个以上“T' 信号,是则YH,否则Y=0,Q2Q1 A/YA00 Q70 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 00 1 0 1 0 10 0[6.3] 试分析图P6・3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,检査电路能否自启动0r°>ci一 IKr°t>ci丿3 = 2121* K3 = Q](2r' = aaa+aa1/1表6・YrHhCl L IK101/oZo□0Dll/O□IZo/I LIO100D007 r4>cirvci °2f >C1 -IKf=>Cl L-I IKCP图P64【解]__丿广K| = 1,代入到特性方程刖=W+K Q :.得:er' =:A=K2=A + a,代入到特性方程2賈=厶02" +斤20;,得: y== A ae,+AQQ由状态办程可得H 状态转换表,如髮6・4所示,状态转换图如图A6・4所示。
时序逻辑电路课后答案

第六章 时序逻辑电路【题 】 分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.3【解】驱动方程: 11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩e 电路能自启动。
状态转换图如图【题】 分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQQ A Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图1图A6.5【题 】 分析图时序电路的逻辑功能,画出电路的状态转换图,检查电路能否自启动,说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212Q Q Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图。
A =0时作二进制加法计数,A =1时作二进制减法计数。
01图A6.6【题 】 分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=•=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000,由状态方程可得:状态转换图如图。
数字电路答案第四章 时序逻辑电路2

解:分析习题4.3图(a )所示的锁存器逻辑图,当锁存命令CP =1,输入信号D 被封锁,锁存器的输出状态保持不变;当锁存命令CP =0,锁存器输出D Q =,Q=D ;当锁存命令CP 出现上升沿,输入信号D 被封锁。
根据上述分析,画出锁存器输出Q 及Q 的波形如习题4.3图(c )所示。
习题4.4 习题图4.4是作用于某主从JK 触发器CP 、J 、K 、R D 及S D 端的信号波形图,试绘出Q 端的波形图。
解:主从JK 触发器的R D 、S D 端为异步清零和复位端,且为低有效。
只有当1==D D S R 时,在CP 下降沿的作用下,J 、K 决定输出Q 状态的变化。
Q 端的波形如习题4.4图所示。
习题4.5 习题4.5图(a )是由一个主从JK 触发器及三个非门构成的“冲息电路”, 习题4.5图(b )是时钟CP 的波形,假定触发器及各个门的平均延迟时间都是10ns ,试绘出输出F 的波形。
解:由习题4.5图(a )所示的电路连接可知:1D ===K J S ,F R =D 。
当1D =R 时,在CP 下降沿的作用下,且经过10 ns ,状态Q 发生翻转,再经过30ns ,F 发生状态的改变,Q F =。
0D =R 时,经过10ns ,状态Q =0。
根据上述对电路功能的分析,得到Q 和F 的波形如习题4.5图(c )所示。
习题4.6 习题4.6图(a )是一个1检出电路,图(b )是CP 及J 端的输入波形图,试绘出R D 端及Q 端的波形图(注:触发器是主从触发器,分析时序逻辑图时,要注意CP =1时主触发器的存储作用)。
解:分析习题4.6图(a )的电路连接:Q CP R K S ⋅===D D ,0,1;分段分析习题习题4.6图(a )(b )CP J(c )CP JQR D(a )(b ) 100nsCP习题4.5图10ns100nsCPQF(c )F 10ns30ns30ns4.6图(b )所示CP 及J 端信号波形。
(完整版)第21章触发器和时序逻辑电路习题答案
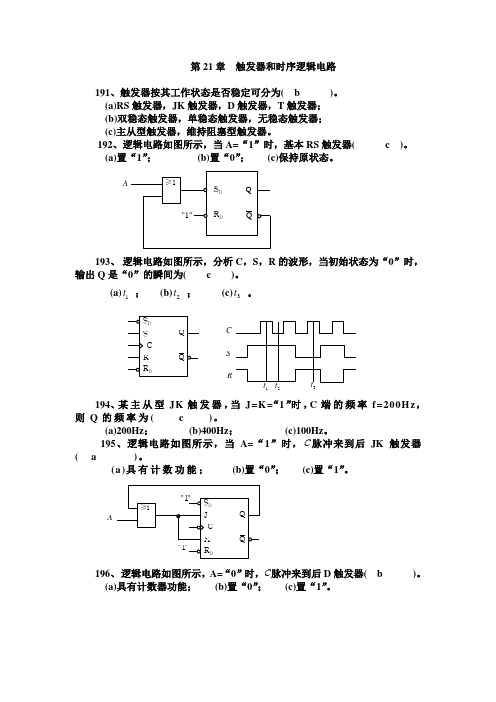
第21章 触发器和时序逻辑电路191、触发器按其工作状态是否稳定可分为( b )。
(a)RS 触发器,JK 触发器,D 触发器,T 触发器;(b)双稳态触发器,单稳态触发器,无稳态触发器;(c)主从型触发器,维持阻塞型触发器。
192、逻辑电路如图所示,当A=“1”时,基本RS 触发器( c )。
(a)置“1”; (b)置“0”; (c)保持原状态。
A193、 逻辑电路如图所示,分析C ,S ,R 的波形,当初始状态为“0”时,输出Q 是“0”的瞬间为( c )。
(a)1t ; (b)2t ; (c)3t 。
C S Rt 1t 2t3194、 某主从型JK 触发器,当J=K=“1”时,C 端的频率f=200Hz ,则Q 的频率为( c )。
(a)200Hz ; (b)400Hz ; (c)100Hz 。
195、逻辑电路如图所示,当A=“1”时,C 脉冲来到后JK 触发器( a )。
(a)具有计数功能; (b)置“0”; (c)置“1”。
A196、 逻辑电路如图所示,A=“0”时,C 脉冲来到后D 触发器( b )。
(a)具有计数器功能; (b)置“0”; (c)置“1”。
A 197、逻辑电路如图所示,分析C 的波形,当初始状态为“0”时,输出Q是“0”的瞬间为( a )。
(a) 1t ; (b)2t ; (c)3t 。
C t 1t 2t 3198、逻辑电路如图所示,它具有( a )。
(a)D 触发器功能; (b)T 触发器功能; (c)T'触发器功能。
199、逻辑电路如图所示,它具有( b )。
(a)D 触发器功能; (b)T 触发器功能;(c)T'触发器功能。
200、时序逻辑电路与组合逻辑电路的主要区别是( c )。
(a)时序电路只能计数,而组合电路只能寄存;(b)时序电路没有记忆功能,组合电路则有;(c)时序电路具有记忆功能,组合电路则没有。
201、寄存器与计数器的主要区别是( b )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章
习题解答
9.1 题9.1图所示电路由D 触发器构成的计数器,试说明其功能,并画出与CP 脉冲对应的各输出端波形。
Q CP
题9.1图
解:(1)写方程
时钟方程:0CP CP =;10CP
Q =;21CP Q = 驱动方程:00n D Q =;11n D Q =;22n D Q =
状态方程:0100n n Q D Q CP +==↑;11110n n Q D Q Q +==↑;2122
1n n
Q D Q Q +==↑
(2)列状态转换表 (3)画状态转换图
111
210210n n n n n n CP Q Q Q Q Q Q +++0 0 0 0 1 1 11 1 1 1 1 1 02 1 1 0 1 0 13 1 0 1 1 0 04 1 0 0 0 1 15 0 1 1 0 1 06 0 1 0 0 0 17 0 0 1 0 0 0
(4)画波形图
CP 2Q 1Q 0
Q
(5)分析功能
该电路为异步三位二进制减法计数器。
9.6 已知题9.6图电路中时钟脉冲CP 的频率为1MHz 。
假设触发器初状态均为0,试分析电路的逻辑功能,画出Q 1、Q 2、Q 3的波形图,输出端Z 波形的频率是多少?
CP
题9.6图
解:(1)写方程
时钟方程:123CP CP CP CP ===
驱动方程:113n n D Q Q =;212n n D Q Q =⊕;312n n D Q Q =
状态方程:
11113n n n Q D Q Q CP +==↑;12212n n n Q D Q Q CP +==⊕↑;13312n n n Q D Q Q CP +==↑ 输出方程:3n Z Q =
(2)列状态转换表 (3)画状态转换图
111321321n n n n n n CP Q Q Q Q
Q Q Z
+++0 0 0 0 0 0 1 01 0 0 1 0 1 0 02 0 1 0 0 1 1 03 0 1 1 1 0 0 04 1 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 0 1 1 1 0 0 1 0 1
(4)画波形图
(5)分析功能
该电路为能够自启动的同步5进制加法计数器。
Z 波形的频率为200K.
CP
2Q 1
Q
0Q Z
9.10 同步十进制计数吕74LS160的功能表如表题9.10所示,分析由74LS160芯片构
成的题9.10图所示计数器的计数器长度。
题9.10图
(a)
(b)
解:(a )由图可得状态转换表为:
该计数器的计数长度为8.
(b )由图可得状态转换表为:
该计数器的计数长度为7.
9.12 应用同步四位二进制计数器74LS161实现模11计数。
试分别用清除端复位法与预置数控制法实现。
74LS161功能表见表题9.8。
表题9.8
解:(1)清除端复位法
因为是异步清零,所以实现11进制共需12个状态。
状态转换表为:
310CR Q QQ =
”
(2) 预置数控制法
因为是同步置数,所以实现11进制共需11个状态。
设初始状态为32100000D D D D =, 则状态转换表为:
”
9.14 试用两片74LS210构成一个模25计数器,要求用二种方法实现。
74LS210的功能表见表题9.13。
解:(1)将两片74LS210先接成100进制,再实现25进制。
(2)由5×5实现
9.20 已知逻辑图和时钟脉冲CP波形如图9.20所示,移位寄存器A和B均由维持阻塞D 触发器组成。
A寄存器的初态Q4A Q3A Q2A Q1A=1010,B寄存器的初态Q4B Q3B Q2B Q1B=1011,主从JK的初态为0,试画出在CP作用下的Q4A、Q4B、C和Q D端的波形图。
CP
题9.20图
解:各端波形如图所示:
CP
Q
4A
Q
4B
C
Q
D
9.26 试求101序列信号检测器的状态图,检测器的功能是当收到序列101时输出为1,并规定检测的101序列不重迭,即:
X:010*******
Z:0001000001
S,
解:设初始状态为
0 Array
S:表示接收到一个“1”时的状态
1
S:表示接收到一个“0”时的状态
2
S:表示接收到第二个“1”时的状态
3
状态图为:
9.35 用JK 触发器设计具有以下特点的计数器:
(1)计数器有两个控制输入C 1和C 2,C 1用以控制计数器的模数,C 2用以控制计数的增减;
(2)若C 1=0,计数器模=3;如果C 1=1,则计数器模为4; (3)若C 2=0,则为加法计数;若C 2=1则为减法计数。
作出状态图与状态表,并画出计数器逻辑图。
解:由题意可知共需4个状态,状态图为:
状态表为:
×
11121010000010011000100010101110110010011111100110001110011
1
01
n n n n C C Q Q Q Q ++⨯
⨯⨯⨯得次态卡诺图为:
则状态方程为:1120201201201()()n n n n n n
n Q C Q C Q Q C Q C C Q Q +=+++ 10110
()n n n
Q Q C Q +=+ 驱动方程为:
12020120
120
n n n n J C Q C Q K C Q C C Q
=+=+;
01101
n J Q C K =+=
逻辑图为:
C C。
