2020年全国初中数学竞赛历年竞赛试题以及参考答案：一

合集下载

2020-2021学年全国初中数学竞赛试题(多份)及答案

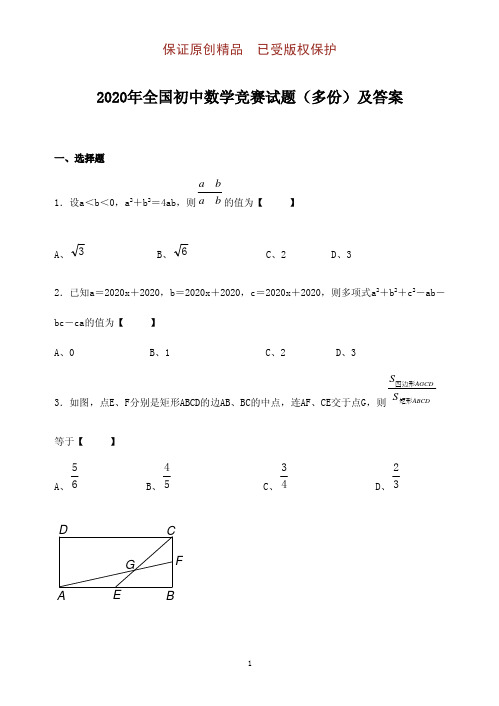
保证原创精品　已受版权保护2020年全国初中数学竞赛试题（多份）及答案一、选择题1．设a ＜b ＜0，a 2＋b 2＝4ab ，则b a ba 的值为【】A 、3B 、6C 、2D 、32．已知a ＝2020x ＋2020，b ＝2020x ＋2020，c ＝2020x ＋2020，则多项式a 2＋b 2＋c 2－ab －bc －ca 的值为【】A 、0B 、1C 、2D 、33．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则ABCDAGCDS S 矩形四边形等于【】A 、65B 、54C 、43D 、32ABC DEF G保证原创精品　已受版权保护4．设a 、b 、c 为实数，x ＝a 2－2b ＋3，y ＝b 2－2c ＋3，z ＝c 2－2a ＋3，则x 、y 、z 中至少有一个值【】A 、大于0B 、等于0C 、不大于0D 、小于05．设关于x 的方程ax 2＋(a ＋2)x ＋9a ＝0，有两个不等的实数根x 1、x 2，且x 1＜1＜x 2，那么a 的取值范围是【】A 、72＜a ＜52 B 、a ＞52 C 、a ＜72 D 、112＜a ＜06．A 1A 2A 3…A 9是一个正九边形，A 1A 2＝a ，A 1A 3＝b ，则A 1A 5等于【】A 、22b a B 、22b ab a C 、b a 21D 、a ＋b二、填空题7．设x 1、x 2是关于x 的一元二次方程x 2＋ax ＋a ＝2的两个实数根，则(x 1－2x 2)(x 2－2x 1)的最大值为。

8．已知a 、b 为抛物线y ＝(x －c)(x －c －d)－2与x 轴交点的横坐标，a ＜b ，则bc c a 的值为。

9．如图，在△ABC 中，∠ABC ＝600，点P 是△ABC 内的一点，使得∠APB ＝∠BPC ＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝。

2020年全国初中数学联赛决赛试题(江西卷)详细解题答案

2020年全国初中数学联赛决赛试题（江西卷）详细解题答案〔2008年4月１９日上午９：00—１１：３０〕－、选择题〔每题7分，共42分〕1 、解：由1114123+=，而1111,236++=故删去11810与后，可使剩下的数之和为1.应选C212+=====12.应选A . 3、解：555=5×545=5×18125，因125被8除余l ，因此18125被8除余l ，故知555被8除余5，而在125、375、625、875四数中，只有125被8除余5，应选A4 、解：由〔1〕、〔3〕得2x y x =-，63x z x =-,故x ≠0，代人〔2〕解得2710x =，因此277y =， z =-54.检验知此组解满足原方程组.因此10X ＋7y ＋Z ＝0．应选D5、解：图中只有边长为1或2的两种菱形，每个菱形恰有一条与其边长相等的对角线，原正三角形内部每条长为1的线段，恰是一个边长为1的菱形的对角线；这种线段有18条，对应着18个边长为1的菱形；原正三角形的每条中位线恰是一个边长为2的菱形的对角线，三条中位线对应着3个边长为2的菱形；共得21个菱形. 选C6、解：设28abcd =3()xy ，那么据末位数字特点得y ＝2，进而确定xy ：因360＝216000， 370＝343000，因此60＜xy ＜70，故只有，xy =62，而262＝238328，那么ab ＝38，cd ＝32，ab ＋cd =70. 应选D二．填空题〔每题7分，共28分〕7、解：据条件式9........1xy +=（）令z ，那么〔1〕式化为：z xy ++9，即有9-z ＝xy81-18z ＋2z ＝2222(1)(4)2x y x y xy ++++……(2),又由2z =2(=2222(4)(1)2x y y x xy++++代入〔2〕得，81-18z=4,因此7718z =. 8、解：l ＋2＋…＋61＝1891，2018—1891＝117，由于形如ab 的页码被当成ba 后，加得的和数将相差9a b -，因为,a b 只能在1，2，…，9中取值，a b -≤8，得9a b -≤72，由于117＝72＋45＝63＋54，设弄错的两位数是ab 和cd ，假设9a b -=72，9c d -=45，只有ab ＝19，而cd 能够取l6，27，38，49；这时ab +cd 的最大值是68；假设9a b -=63，9c d -=54，那么ab 能够取18，29，而cd 能够取17，28，39，ab +cd 的最大值也是68．9、解：如右图，连OA ，OB ，OC ，线段 OA 将阴影的上方部分剖分成两个弓形，将这两个弓形分不按顺时针及反时针绕点O 旋转0120后，阴影部分便合并成△OBC ，它的面积等于△A BC 310、解：653)=3(8215)+，令 815+a ，815-b ，得 a ＋b ＝16，ab=4，a,b 是方程21640x x -+=的两个根，故得2a ＝16a －4，2b ＝16b －4；3a ＝162a －4a ，32164b b b =-；因此3a +3b ＝16〔2a +2b 〕-4〔a+b 〕＝16〔16〔a+b 〕一8〕－4〔a+b 〕=252〔a+b 〕-128=3904.∵0＜b ＜1，∴0＜3b ＜1，∴3a 的最大整数值不超过3903.三.解答题〔共70分〕11、解：当a ＝0时，方程的有理根为75x =； ……5分以下考虑a ≠0的情形，现在原方程为一元二次方程，由判不式2(5)4(7)0,a a a +-+≥即32a ＋18a －25≤091569156a ---+≤≤整数 a 只能在其中的非零整数1，－1，－2，－3，－4，－5，－6，－7中取值，…… 10 分由方程得25523(3)a a x +±-+=……〔1〕当a ＝1，由〔1〕得x ＝2和4；当a=－1时，方程无有理根；当a ＝－2，由〔1〕得x ＝1和－52；当a=－3时，方程无有理根； ……15分当a ＝－4，由〔1〕得x ＝－1和34；当a=－5时，方程无有理根；当a ＝－6，由〔1〕得x ＝12和－13；当a ＝－7时，由〔1〕得x ＝37和17-；…… 20分A P 12、证明：EF 截△PMN ，那么.. 1..........(1)NK MF PE KM FP EN=……5分 BC 截 △PAE ，那么.. 1...........(2)EB AC PN BA CP NE =，即有2,PN CP NE AC = 因此2..............(3)PE CP AC EN AC+=, ……10分AD 截△PCF ，那么..1,FD CA PM DC AP MF=即22,............(4)PM AP PF AP AC MF AC MF AC-=∴=……15分因AP ＝AC ＋CP ，得2CP ＋ AC ＝2AP －AC ，由(3),(4)得，,........20PE FP EN MF=分 — 即.1,MF PE FP EN =因此由(1)得 NK ＝KM ，即K 是线段 AM 的中点 ……25分 13、解：将这120人分不编号为12120,,....,P P P ，并视为数轴上的120个点，用k A 表示这120人之中未答对第k 题的人所成的组,k A 为该组人数, k=l ，2，3，4，5，那么1A =24,234537,46,54,85,A A A A ==== ……5分将以上五个组分不给予五种颜色，假如某人未做对第k 题，那么将表示该人点染第k 色，k=l ，2，3，4，5，咨询题转化为，求出至少染有三色的点最多有几个？由于1A +2345A A A A +++＝246，故至少染有三色的点不多于2463=82个，……10分右上图是满足条件的一个最正确染法，即点1285,,....,P P P 这85 个点染第五色；点1237,,....,P P P 这37个点染第二色；点383983,,....,P P P 这46个点染第四色；点1224,,....,P P P 这24 个点染第一色；点252678,,....,P P P 这54个点染第三色；因此染有三色的点最多有78个. …20分因此染色数不多于两种的点至少有42个，即获奖人数至少有42个人〔他们每人至多答错两题，而至少答对三题，例如7980120,,...,P P P 这 42 个人) …… 25分陈永华录入 cryzcyh@ 85 46 5437 24。

2020-2021学年全国初中数学竞赛试题(含答案)

2020年全国初中数学竞赛试题（含答案）考试时间 2020年4月2日上午 9∶30－11∶30 满分120分一、选择题（共5小题，每小题6分，满分30分。

以下每道小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的。

请将正确选项的代号填入题后的括号里。

不填、多填或错填均得0分）1．在高速公路上，从3千米处开始，每隔4千米经过一个限速标志牌；并且从10千米处开始，每隔9千米经过一个速度监控仪．刚好在19千米处第一次同时经过这两种设施，那么第二次同时经过这两种设施的千米数是（）（A ）36 （B ）37 （C ）55 （D ）902．已知21 m ，21 n ，且)763)(147(22 n n a m m =8，则a 的值等于（）（A ）－5 （B ）5 （C ）－9 （D ）93．Rt △ABC 的三个顶点A ，B ，C 均在抛物线2x y 上，并且斜边AB 平行于x 轴．若斜边上的高为h ，则（）（A ）h <1 （B ）h =1 （C ）1<h <2（D ）h >24．一个正方形纸片，用剪刀沿一条不过任何顶点的直线将其剪成两部分；拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分；又从得到的三部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分……如此下去，最后得到了34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）（A ）2020 （B ）2020 （C ）2020 （D ）20205．如图，正方形ABCD 内接于⊙O ，点P 在劣弧AB 上，连结DP ，交AC 于点Q ．若QP=QO ，则QA QC的值为（）（A ）132 （B ）32（C ）23 （D ）23 二、填空题（共5小题，每小题6分，满分30分）6．已知a ，b ，c 为整数，且a ＋b=2020，c －a =2020．若a <b ，则a ＋b ＋c 的最大值为．7．如图，面积为c b a 的正方形DEFG 内接于面积为1的正三角形ABC ，其中a ，b ，c 为整数，且b 不能被任何质数的平方整除，则b ca 的值等于．8．正五边形广场ABCDE 的周长为2020米．甲、乙两人分别从A 、C 两点同时出发，沿A !’B !’C !’D !’E !’A !’…方向绕广场行走，甲的速度为50米/分，乙的速度为46米/分．那么出发后经过分钟，甲、乙两人第一次行走在同一条边上．9．已知0<a <1，且满足183029302301 a a a ，则 a 10的值等于．( x 表示不超过x 的最大整数)10．小明家电话号码原为六位数，第一次升位是在首位号码和第二位号码之间加上数字8，成为一个七位数的电话号码；第二次升位是在首位号码前加上数字2，成为一个八位数的电话号码．小明发现，他家两次升位后的电话号码的八位数，恰是原来电话号码的六位数的81倍，则小明家原来的电话号码是．三、解答题（共4题，每小题15分，满分60分）11．已知a bx，a ，b 为互质的正整数（即a ，b 是正整数，且它们的最大公约数为1），且a ≤8，1312 x ．试写出一个满足条件的x ；（1）（第7题图）ABCDGFE求所有满足条件的x ．（2）12．设a ，b ，c 为互不相等的实数，且满足关系式14162222 a a c b ①542 a a bc ②求a 的取值范围．13．如图，点P 为⊙O 外一点，过点P 作⊙O 的两条切线，切点分别为A ，B ．过点A 作PB 的平行线，交⊙O 于点C ．连结PC ，交⊙O 于点E ；连结AE ，并延长AE 交PB 于点K ．求证：PE·AC=CE·KB ．A14．10个学生参加n个课外小组，每一个小组至多5个人，每两个学生至少参加某一个小组，任意两个课外小组，至少可以找到两个学生，他们都不在这两个课外小组中．求n的最小值．2020年全国初中数学竞赛试题参考答案一、选择题（共5小题，每小题6分，满分30分。

2020年全国初中数学联合竞赛试题参考答案第1试

2020年全国初中数学联合竞赛试题参考答案第第一试求符合条件且周长不超过解由等式可得30的三角形的个数.令a b m,b c n ,那么a c m n ，其中m,n 均为自然数、选择题：〔此题总分值42分，每题 7分〕1.假设a,b,c 均为整数且满足(a b)10(a c)101，那么 |a b| |b c| |c a |1.B . 2.C . 3.4.2. 假设实数a,b,c 满足等式 2、一5 3|b|4、,5 9|b|6c , 那么c 可能取的最大值为0.B . 1.假设a,b 是两个正数，且C . 2.a 1~b~ 1 .B . a b33.0, 那么假设方程x 2 3x 1. D . - a b32.1 0的两根也是方程ax 2 bx0的根，那么a b 2c 的值为—13.B . — 9.C . 6.在厶ABC 中， CAB 60 , D , E 分不是边AB ,A . 5 . CDB 2 CDE ,那么 DCBD . 0.15 °B . 20° .C . 25° . AC 上的点，且 AED(30° .60 , ED DB CE, B )关于自然数n ，将其各位数字之和记为a n ,如a 2009 2 0 0 9 11 , a 2010 2 3，那么a 3Il la2009a201028062. 二、填空题: B . 28065. 〔此题总分值28 分, C . 28067. 每题7分〕 D . 28068.1 .实数X, y 满足方程组19,x y 1,那么x 2132.二次函数ybx c 的图象与x 轴正方向交于 A , B 两点，与y 轴正方向交于点 C . AB、3AC ,CAO 30，那么 3.在等腰直角△ ABC 中，AB = BC = 5, P 是厶 ABC 内一点，且 PA = ,PC = 5,那么 PB = _ . 10 4.将假设干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要显现，且任意中间夹有球的两个球必为同一种颜色的球 .按这种要求摆放，最多能够摆放 _______ 15_个球. 5个或10个第二试〔A 〕.〔此题总分值20分〕设整数a,b,c 〔 a b c 〕为三角形的三边长，满足a 2 b 2 2c ab ac bc 13,(a b)2 (b c)2 (a c)2 26因此，等式①变为m 2 n 2 (m n)226，即1)(2)设m,n 是方程的两个整数根，且m n .(c (c 2n mn 13由于m,n 均为自然数，判定易知，使得等式②成立的〔1〕当 m 3,n 1 时，b c 1 , a b 3 c1) c c 4，解得c 3.又因为三角形的周长不超过号.因此3m,n 只有两组：m 3,和m 1,n 1 n 3.4 .又a,b,c 为三角形的三边长，因此30,即 a b c (c 4) (cc 25，因此c 能够取值4, 5, 6, 7 8,对应可得到5个符合条件的三角形 3〔2〕当m 1,n3时，b c 3, a b 1 c 4.又a,b,c 为三角形的三边长，因此3) c c 解得c 1•又因为三角形的周长不超过30,即a b c (c 4) (c3)c a ，即30,解得c a ，即30，解得23 •因此1 3综合可知：符合条件且周长不超过30的三角形的个数为 5+ 6= 11.二.〔此题总分值 25分〕等腰三角形△ ABC 中，AB = AC , 的内切圆OI 与BC 边的切点，作MD//AC ，交O I 于点D.证明： PD 是O I 的切线. 证明过点P 作O I 的切线PQ 〔切点为Q 〕并延长，交 BC 于点N.因为CP 为/ ACB 的平分线，因此/ ACP = / BCP. 又因为PA 、PQ 均为O I 的切线，因此/ APC = / NPC. 又 CP 公共，因此△ ACP ◎△ NCP ，因此/ PAC =Z PNC. 由 NM = QN , BA = BC ,因此△ QNM BAC ,故/ NMQ =Z ACB ，因此 MQ//AC. 又因为 MD//AC ，因此 MD 和MQ 为同一条直线. 又点Q 、D 均在O I 上，因此点Q 和点 23，因此c 能够取值2, 3, 4, 5, 6, 7,对应可得到6个符合条件的三角形3/ C 的平分线与AB 边交于点P , M ABCD 重合，故PD 是O 的切线• 三.〔此题总分值25分〕二次函数y x 2 bx c 的图象通过两点 P (1,a), Q (2,10a). 〔1〕假如a, b, c 差不多上整数，且c 8a ，求a, b,c 的值. 〔2〕设二次函数 2 y x bx c 的图象与x 轴的交点为 A 、B ,与y 轴的交点为 x 2 bx c 0的两个根差不多上整数，求△ ABC 的面积. bx c 的图象上，故1 b c 解得b 9a 3, c8a 2.8a 2 9a 3,. 口〔1〕由 c b 8a 知解得19a 3 8a,又a 为整数，因此a2, b 9a 3 15, c解点P (1,a)、Q (2,10a)在二次函数 2a 3. 8a 2 14.C.假如关于x 的方程a , 4 2a c 10a ,由根与系数的关系可得 m n b 3 9a , mn c 2 8a ，消去a ，得9mn 8(m n) 6,10 2 1/ m —, m —, m ——, 解得m 1，或 9或 9或 93n 2, 13 7 2n —, n -, n -,9 9 3又m,n 是整数，因此后面三组解舍去，故 m 1,n 2.号.因此3 c 25，因此c 能够取值4，5，6, 7, 8,对应可得到5个符合条件的三角形〔2〕当m 1,n3时，b c 3， a b 1 c 4.又a,b,c 为三角形的三边长，因此(c 3) c c 4，解得c 1.又因为三角形的周长不超过30,即a b c (c 4) (c 3) c 30，解得23 23c .因此1 c ，因此c 能够取值2，3，4，5，6，7,对应可得到6个符合条件的三角形.3 3综合可知：符合条件且周长不超过30的三角形的个数为 5+ 6= 11.54，分解因式，得(9m 8)(9n 8) 10.—9m8 1,亠 9m 8 2,亠 9m 8 因此或或 9n 8 10, 9n 8 5, 9n 8 因此，b (m n) 3， c mn2，二次函数的解析式为 y x 2 3x 2 .(c 1易求得点A 、B 的坐标为〔1,0〕和〔2,0〕，点C 的坐标为〔0,2〕，因此△ ABC 的面积为一2第二试〔B 〕a 2b 2c 2 ab ac bc解不妨设a bc ，由等式可得2 2(a b) (b c)(a 2c)226①令 a b m,b cn ，那么a c m n ，其中m,n 均为自然数.因此，等式①变为 2m 2 2n (m n)26，即2 2m n mn 13②由于m,n 均为自然数，判定易知，使得等式②成立的〔1〕当 m 3,n 1 时，b c 1， a b 3 c1) c c 4，解得c 3.又因为三角形的周长不超过m, n 只有两组: m 3,和n 1m 1, n 3.4 .又a,b,c 为三角形的三边长，因此30，即卩 a b c (c 4) (c1)(2 1) 2 1 .13，求符合条c a ，即30，解得c a ，即两边同时乘以9,得81mn 72(m n)10,亠 9m 8 5, 或1, 9n 8 2,〔此题总分值20分〕设整数a,b,c 为三角形的三边长，满足件且周长不超过 30的三角形的个数〔全等的三角形只运算1次〕第二试〔C 〕〔此题总分值20分〕题目和解答与〔B 〕卷第一题相同• 〔此题总分值25分〕题目和解答与〔A 〕卷第二题相同•〔此题总分值25分〕设p 是大于2的质数，k 为正整数.假设函数y x 2 px (k 1)p 4的图象与x 轴的两个交点的横坐标至少有一个为整数，求k 的值.解由题意知，方程x 2 px (k 1)p 4 0的两根x 1, x 2中至少有 '个为整数.由根与系数的关系可得 x 1X2p, x 1x 2 (k 1)p 4，从而有(X 1 2)(X 2 2) X 1X 22(x 1X 2) 4 (k 1)p①〔1〕假设k 1，那么方程为: x 2 px 2( p2) 0，它有两个整数根2和2 p〔2〕假设k 1，那么k 1 0.因为x 1 x 2p 为整数，假如 X 1,X 2中至少有-个为整数，那么 X 1,X 2差不多上整数k 1k 1假如m 为负整数，那么(m 1)p 0 , 0，从而(m 1)p0 ,与②式矛盾mm综上所述，k 1 .二. 〔此题总分值三. 〔此题总分25分〕题目和解答与〔 25分〕题目和解答与〔 A 〕卷第二题相同 A 〕卷第三题相同又因为 p 为质数，由①式知 p 1X 1 2 或 p|X 22 .不妨设 p 1 X 1 2 ，那么可设 x 1 2mp 〔其中m 为非零整数〕，那么由①式可得c k 1 X 2 2 -m故(X2) (X 2 2) mp k 1 即X x 2 4 mpk 1mm又X-i X 2p , 因此 p 4 mp ——1，即mk 1 (m 1)p4②m假如m 为正整数，那么 (m 1)p(1 1) 3 6 , k 1k 0,从而(m 1)p - 16，与②式矛盾mm 因此，k 1时，方程x 2px (k 1) p 4不可能有整数根.。

2020年全国初中数学竞赛试题及答案

１nm L F HK DE OAB C全国初中数学竞赛试题及答案一、选择题：（共5小题，每小题6分，满分30分．以下每小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的．请将正确选项的代号填入题后括号里．不填、多填或错填都得0分）1．方程组⎪⎩⎪⎨⎧=+=+612y x y x 的实数解的个数为（）（A ）1 （B ）2 （C ）3 （D ）4解：选（A ）。

当x ≥0时，则有y －|y|=6,无解；当x<0时，则y ＋|y|=18,解得：y=9,此时x=－3. 2．口袋中有20个球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么上述取法的种数是（）（A ）14 （B ）16 （C ）18 （D ）20解：选（B ）。

只用考虑红球与黑球各有4种选择：红球（2,3,4,5），黑球（0,1,2,3）共4×4＝16种 3．已知a 、b 、c 是三个互不相等的实数，且三个关于x 的一元二次方程02=++c bx ax ，02=++a cx bx ，02=++b ax cx 恰有一个公共实数根，则abc ca b bc a 222++的值为（）（A ）0 （B ）1 （C ）2 （D ）3解：选（D ）。

设这三条方程唯一公共实数根为t ，则20at bt c ++=，20bt ct a ++=，20ct at b ++=三式相加得：2()(1)0a b c t t ++++=，因为210t t ++≠，所以有a+b+c=0,从而有3333a b c abc ++=，所以ab c ca b bc a 222++＝333a b c abc ++＝33abcabc= 4．已知△ABC 为锐角三角形，⊙O 经过点B ，C ，且与边AB ，AC 分别相交于点D ，E ．若⊙O 的半径与△ADE 的外接圆的半径相等，则⊙O 一定经过△ABC 的（）（A ）内心（B ）外心（C ）重心（D ）垂心解：选（B ）。

2020年初三学科竞赛考试数学试题(含答案)

（1）求证:△AEF≌△BEC；
（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，如图2，求sin∠ACH的值．
24．（本题满分13分）在Rt△ABC中，BC=9， CA=12，∠ABC的平分线BD交AC与点D， DE⊥DB交AB于点E．
（1）设⊙O是△BDE的外接圆，求证：AC是⊙O的切线；
3．第Ⅰ卷每题选出答案后，请用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，先用橡皮擦干净，再改涂其他答案。
第 Ⅰ 卷（选择题共36分）
1、选择题（本题共12个小题，在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,每小题3分,满分36分）
1．计算下列各式，结果为负数的是
试卷类型：A
2020年初三学科竞赛考试
数学试题
温馨提示：
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷1－2页为选择题，共36分；第Ⅱ卷3－8页为非选择题，共114分。满分为150分，考试时间为120分钟。
2．答第Ⅰ卷前务必将自己的姓名、考号、考试科目、试卷类型涂写在答题卡上。考试结束，试题和答题卡一并上交。
（1）本次抽样调查的养殖户的总户数是；把图2条形统计图补充完整．
（2）若该地区建档的养殖户有1500户，求非常严重与严重的养殖户一共有多少户？
（3）某调研单位想从5户建档养殖户（分别记为a，b，c，d，e）中随机选取两户，进一步跟踪监测病毒传播情况，请用列表或画树状图的方法求出选中养殖户e的概率．
23.（本题满分12分）如图1，△ABC中，∠ACB=90°,∠CAB=30°，△ABD是等边角形，过点C作CF//BD,交AB于点E，交AD于点F。
A．3 B．4 C．5 D．6
10．阅读理解：我们知道，引进了无理数后，有理数集就扩展到实数集：同样，如果引进“虚数”实数集就扩展到“复数集”现在我们定义：“虚数单位”，其运算规则是：il＝i，i2＝﹣1，i3＝﹣i，i4＝1，i5＝i，i6＝﹣1，i7＝﹣i，则i2020＝（）

2020版七年级数学竞赛试卷(含答案)

2020七年级数学竞赛试卷一、选择题（每小题3分，共24分） 1、已知实数c b a ,,在数轴的对应位置如图，则|c －1|+|a －c |+|a －b |化简后的结果是（）A 、1－2c +bB 、2a －b －1C 、1+2a －b －2cD 、b －12、把两个整数平方得到的数“拼”起来（即按一定顺序写在一起）后仍然得到一个平方数，则称最后得到的这个数为“拼方数”。

如把整数4，3分别平方后得到16，9，拼成的数“169”是13的平方，称“169”是“拼方数”在下列数中，属于“拼方数”的是（） A 、225 B 、494 C 、361 D 、12193、据报道，日本福岛核电站发生泄漏事故后，在我市环境空气中检测出一种微量的放射性核素“碘－131”，含量为每立方米0.4毫贝克(这种元素的半衰期是8天,即每8天含量减少一半,如8天后减少到0.2毫贝克),那么要使含量降至每立方米0.0004毫贝克以下,下列天数中,能达到目标的最少天数是（）A 、64B 、71C 、82D 、1044、三角形三边的长a ，b ，c 都是整数，且[a ，b ，c ]＝60，（a ，b ）＝4，（b ，c ）＝3．（注：[a ，b ，c ]表示a ，b ，c 的最小公倍数，（a ，b ）表示a ，b 的最大公约数），则a ＋b ＋c 的最小值是（）（A ）30 （B ）31 （C ）32 （D ）33 5、方程6|3||2|=++-x x 的解的个数是（） A ．1 B ．2 C ．3 D ．46、把四张大小相同的长方形卡片（如图①按图②、图③两种放在一个底面为长方形（长比宽多6cm ）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长C 2，图③中阴影部分的周长为C 3，则（）A 、C 2 = C 3B 、C 2 比C 3 大12 cm C 、C 2 比C 3 小6 cmD 、C 2 比C 3 大3 cm7、如图，直线上有三个不同的点A ，B ，C ，且AB =10，BC =5，在直线上找一点D ，使得AD +BD +CD 最小，这个最小值是（）A 、15B 、14C 、10D 、7.58、将1，2，3，4，…，12，13这13个整数分为两组，使得一组中所有数的和比另一组中所有数的和大10，这样的分组方法（）A 、只有一种B 、恰有两种C 、多于三种D 、不存在二、填空题(每小题3分,共24分)9、若正整数x ，y 满足2010x =15y ，则x +y 的最小值是___________；10、数列1，1，2，3，5，8，13，21，34，55，…的排列规律：前两个数是1，从第3个数开始，每一个数都是它前两个数的和，这个数列叫做斐波契数列，在斐波契数列前2010个数中共有___________个偶数 11、小聪沿街匀速行走，发现每隔6分钟从背后驶过一辆18路公交车，每隔3分钟从迎面驶来一辆18路公交车。

(2020年整理)全国初中数学竞赛试题及答案.doc

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题（共5小题，每小题6分，共30分.）1（甲）．如果实数a，b，c22||()||a abc a b c-++-+可以化简为（）．（A）2c a-（B）22a b-（C）a-（D）a1（乙）．如果22a=-11123a+++的值为（）．（A）2-（B2（C）2 （D）22（甲）．如果正比例函数y = ax（a ≠ 0）与反比例函数y =xb（b ≠0 ）的图象有两个交点，其中一个交点的坐标为（－3，－2），那么另一个交点的坐标为（）．（A）（2，3）（B）（3，－2）（C）（－2，3）（D）（3，2）2（乙）．在平面直角坐标系xOy中，满足不等式x2＋y2≤2x＋2y的整数点坐标（x，y）的个数为（）．（A）10 （B）9 （C）7 （D）53（甲）．如果a b，为给定的实数，且1a b<<，那么1121a ab a b++++，，，这四个数据的平均数与中位数之差的绝对值是（）．（A）1 （B）214a-（C）12（D）143（乙）．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．30ADC∠=︒，AD = 3，BD = 5，则CD的长为（）．（A）23（B）4（C）52（D）4.54（甲）．小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱数将是你的n倍”；小玲对小倩说：“你若给我n元，我的钱数将是你的2倍”，其中n为正整数，则n的可能值的个数是（）．OAB CED（A ）1 （B ）2 （C ）3 （D ）44（乙）．如果关于x 的方程 20x px q p q --=（，是正整数）的正根小于3，那么这样的方程的个数是（）．（A ） 5 （B ） 6 （C ） 7 （D ） 85（甲）．一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，3，4，5，6．掷两次骰子，设其朝上的面上的两个数字之和除以4的余数分别是0，1，2，3的概率为0123p p p p ，，，，则0123p p p p ，，，中最大的是（）．（A ）0p （B ）1p （C ）2p （D ）3p5（乙）．黑板上写有111123100L ，　，，，　共100个数字．每次操作先从黑板上的数中选取2个数a b ，，然后删去a b ，，并在黑板上写上数a b ab ++，则经过99次操作后，黑板上剩下的数是（）．（A ）XXXX （B ）101 （C ）100 （D ）99二、填空题（共5小题，每小题6分，共30分）6（甲）．按如图的程序进行操作，规定：程序运行从“输入一个值x ”到“结果是否>487？”为一次操作. 如果操作进行四次才停止，那么x 的取值范围是 .6（乙）.如果a ，b ，c 是正数，且满足9a b c ++=，111109a b b c c a ++=+++，那么a b cb c c a a b+++++的值为．7（甲）．如图，正方形ABCD 的边长为215， E ，F 分别是AB ，BC 的中点，AF 与DE ，DB 分别交于点M ，N ，则△DMN 的面积是 . 7（乙）.如图所示，点A 在半径为20的圆O 上，以OA 为一条对角线作矩形OBAC ，设直线BC 交圆O 于D 、E 两点，若12OC =，则线段CE 、BD 的长度差是。

2020年全国初中数学竞赛试题(多份)及答案

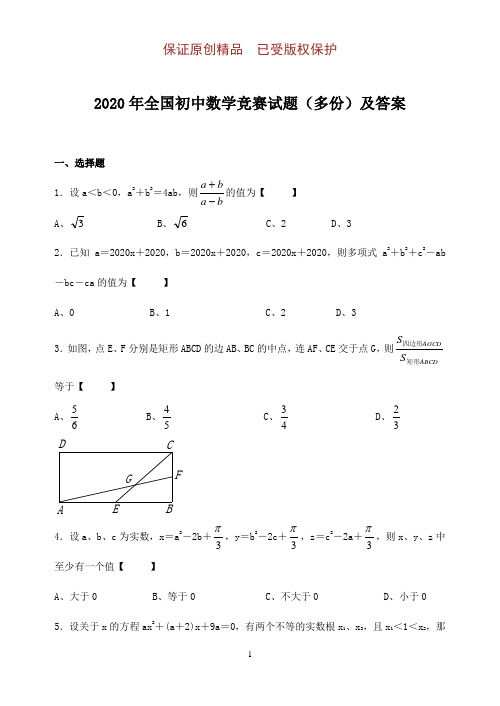
2020年全国初中数学竞赛试题（多份）及答案一、选择题1．设a ＜b ＜0，a 2＋b 2＝4ab ，则ba b a -+的值为【】 A 、3 B 、6 C 、2 D 、32．已知a ＝2020x ＋2020，b ＝2020x ＋2020，c ＝2020x ＋2020，则多项式a 2＋b 2＋c 2－ab －bc －ca 的值为【】A 、0B 、1C 、2D 、3 3．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则ABCDAGCDS S 矩形四边形等于【】A 、65B 、54C 、43D 、32 A BC DE F G4．设a 、b 、c 为实数，x ＝a 2－2b ＋3π，y ＝b 2－2c ＋3π，z ＝c 2－2a ＋3π，则x 、y 、z 中至少有一个值【】 A 、大于0 B 、等于0 C 、不大于0 D 、小于05．设关于x 的方程ax 2＋(a ＋2)x ＋9a ＝0，有两个不等的实数根x 1、x 2，且x 1＜1＜x 2，那么a 的取值范围是【】A 、72-＜a ＜52B 、a ＞52C 、a ＜72-D 、112-＜a ＜0 6．A 1A 2A 3…A 9是一个正九边形，A 1A 2＝a ，A 1A 3＝b ，则A 1A 5等于【】A 、22b a +B 、22b ab a ++C 、()b a +21 D 、a ＋b 二、填空题7．设x 1、x 2是关于x 的一元二次方程x 2＋ax ＋a ＝2的两个实数根，则(x 1－2x 2)(x 2－2x 1)的最大值为。

8．已知a 、b 为抛物线y ＝(x －c)(x －c －d)－2与x 轴交点的横坐标，a ＜b ，则b c c a -+-的值为。

9．如图，在△ABC 中，∠ABC ＝600，点P 是△ABC 内的一点，使得∠APB ＝∠BPC ＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝。

2020年七年级数学竞赛初赛试卷及答案解析

第 1 页共 8 页2020年七年级数学竞赛初赛试卷一．填空题（共11小题）1．我们知道：1+2+3=3×(3+1)2=6，1+2+3+4=4×(4+1)2=10，那么1+2+3+…+100＝． 2．计算：(−2007)5×(−3.25)5×(−23)5×(−1446)5×(−413)5= ．3．设四位数abcd 满足a 3+b 3+c 3+d 3+1＝10c +d ，则这样的四位数的个数为．4．一商店在某一时间以每件a 元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，若卖出这两件衣服商店共亏损8元，则a 的值为．5．现有145颗棒棒糖，分给若干小朋友，不管怎样分，都至少有1个小朋友分到5颗或5颗以上，这些小朋友的人数最多有个．6．已知关于x 的方程（a ﹣1）x 2+2x ﹣a ﹣1＝0的根都是一整数，那么符合条件的整数a 有个．7．如图，在一个4×4的方格棋盘的A 格里放一枚棋子，如果规定棋子每步只能向上、下或左、右走一格，那么这枚棋子走28步后到达B 处．（填“一定能”或“一定不能”或“可能”）8．观察下列各等式：第一个等式：22−12−12=1，第二个等式：32−22−12=2，第三个等式：42−32−12=3…根据上述等式反映出的规律直接写出第四个等式为；猜想第n 个等式（用含n 的代数式表示）为．9．观察下列一组数，按规律在横线上填写适当的数，−12，36，−512，720，……，第7个数是．10．满足25{x }+[x ]＝25的所有实数x 的和是（其中[x ]表示不大于x 的最大整数，{x }＝x ﹣[x ]表示x 的小数部分）．11．两个多位正整数，若它们各数位上的数字之和相等，则称这两个多位数互为调和数”例如：49与76，因为4+9＝7+6＝13，所以49与76互为“调和数”；又如：225与18，因。

2020年全国初中数学联合竞赛试题参考答案第1试

2020年全国初中数学联合竞赛试题参考答案第1试第一试一、选择题：〔此题总分值42分，每题7分〕1. 假设,,a b c 均为整数且满足1010()()1a b a c -+-=，那么||||||a b b c c a -+-+-= 〔 B 〕A ．1.B ．2.C ．3.D ．4.2．假设实数,,a b c 满足等式3||6b =，9||6b c =，那么c 可能取的最大值为〔 C 〕A ．0.B ．1.C ．2.D ．3. 3．假设b a ,是两个正数，且,0111=+-+-ab b a 那么〔 C 〕 A ．103a b <+≤. B ．113a b <+≤. C ．413a b <+≤. D ．423a b <+≤. 4．假设方程2310x x --=的两根也是方程420x ax bxc +++=的根，那么2a b c +-的值为〔 A 〕A ．－13.B ．－9.C ．6.D ． 0.5．在△ABC 中，︒=∠60CAB ，D ，E 分不是边AB ，AC 上的点，且︒=∠60AED ，CE DB ED =+，CDE CDB ∠=∠2,那么=∠DCB ( B )A ．15°.B ．20°.C ．25°.D ．30°.6．关于自然数n ，将其各位数字之和记为n a ，如2009200911a =+++=，201020103a =+++=，那么12320092010a a a a a +++++= 〔 D 〕A ．28062.B ．28065.C ．28067.D ．28068.二、填空题：〔此题总分值28分，每题7分〕1．实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩那么22x y += 13 .2．二次函数c bx x y ++=2的图象与x 轴正方向交于A ，B 两点，与y 轴正方向交于点C ．AC AB 3=，︒=∠30CAO ，那么c = 19．3．在等腰直角△ABC 中，AB ＝BC ＝5，P 是△ABC 内一点，且PA PC ＝5，那么PB ＝．4．将假设干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要显现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放，最多能够摆放____15___个球.第二试〔A 〕一．〔此题总分值20分〕设整数,,a b c 〔a b c ≥≥〕为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长不超过30的三角形的个数.解由等式可得 222()()()26a b b c a c -+-+-= ①令,a b m b c n -=-=，那么a c m n -=+，其中,m n 均为自然数.因此，等式①变为222()26m n m n +++=，即 2213m n mn ++= ②由于,m n 均为自然数，判定易知，使得等式②成立的,m n 只有两组：3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ 〔1〕当3,1m n ==时，1b c =+，34a b c =+=+.又,,a b c 为三角形的三边长，因此b c a +>，即(1)4c c c ++>+，解得3c >.又因为三角形的周长不超过30，即(4)(1)30a b c c c c ++=++++≤，解得253c ≤.因此2533c <≤，因此c 能够取值4，5，6，7，8，对应可得到5个符合条件的三角形. 〔2〕当1,3m n ==时，3b c =+，14a b c =+=+.又,,a b c 为三角形的三边长，因此b c a +>，即(3)4c c c ++>+，解得1c >.又因为三角形的周长不超过30，即(4)(3)30a b c c c c ++=++++≤，解得233c ≤.因此2313c <≤，因此c 能够取值2，3，4，5，6，7，对应可得到6个符合条件的三角形. 综合可知：符合条件且周长不超过30的三角形的个数为5＋6＝11.二．〔此题总分值25分〕等腰三角形△ABC 中，AB ＝AC ，∠C 的平分线与AB 边交于点P ，M 为△ABC 的内切圆⊙I 与BC 边的切点，作MD//AC ，交⊙I 于点D.证明：PD 是⊙I 的切线. 证明过点P 作⊙I 的切线PQ 〔切点为Q 〕并延长，交BC 于点N. 因为CP 为∠ACB 的平分线，因此∠ACP ＝∠BCP. 又因为PA 、PQ 均为⊙I 的切线，因此∠APC ＝∠NPC. 又CP 公共，因此△ACP ≌△NCP ，因此∠PAC ＝∠PNC.由NM ＝QN ，BA ＝BC ，因此△QNM ∽△BAC ，故∠NMQ ＝∠ACB ，因此MQ//AC.又因为MD//AC ，因此MD 和MQ 为同一条直线.又点Q 、D 均在⊙I 上，因此点Q 和点D 重合，故PD 是⊙I 的切线.三．〔此题总分值25分〕二次函数2y x bx c =+-的图象通过两点P (1,)a ，Q (2,10)a .〔1〕假如,,a b c 差不多上整数，且8c b a <<，求,,a b c 的值.〔2〕设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ，与y 轴的交点为 C.假如关于x 的方程20x bx c +-=的两个根差不多上整数，求△ABC 的面积.解点P (1,)a 、Q (2,10)a 在二次函数2y x bx c =+-的图象上，故1b c a +-=，4210a c a +-=，解得93b a =-，82c a =-.〔1〕由8c b a <<知8293,938,a a a a -<-⎧⎨-<⎩解得13a <<. 又a 为整数，因此2a =，9315b a =-=，8214c a =-=.(2) 设,m n 是方程的两个整数根，且m n ≤.NC A由根与系数的关系可得39m n b a +=-=-，28mn c a =-=-，消去a ，得98()6mn m n -+=-，两边同时乘以9，得8172()54mn m n -+=-，分解因式，得(98)(98)10m n --=.因此981,9810,m n -=⎧⎨-=⎩或982,985,m n -=⎧⎨-=⎩或9810,981,m n -=-⎧⎨-=-⎩或985,982,m n -=-⎧⎨-=-⎩ 解得1,2,m n =⎧⎨=⎩或10,913,9m n ⎧=⎪⎪⎨⎪=⎪⎩或2,97,9m n ⎧=-⎪⎪⎨⎪=⎪⎩或1,932,3m n ⎧=⎪⎪⎨⎪=⎪⎩又,m n 是整数，因此后面三组解舍去，故1,2m n ==.因此，()3b m n =-+=-，2c mn =-=-，二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为〔1,0〕和〔2,0〕，点C 的坐标为〔0,2〕，因此△ABC 的面积为1(21)212⨯-⨯=. 第二试〔B 〕一．〔此题总分值20分〕设整数,,a b c 为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长不超过30的三角形的个数〔全等的三角形只运算1次〕.解不妨设a b c ≥≥，由等式可得 222()()()26a b b c a c -+-+-= ①令,a b m b c n -=-=，那么a c m n -=+，其中,m n 均为自然数.因此，等式①变为222()26m n m n +++=，即 2213m n mn ++= ②由于,m n 均为自然数，判定易知，使得等式②成立的,m n 只有两组：3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ 〔1〕当3,1m n ==时，1b c =+，34a b c =+=+.又,,a b c 为三角形的三边长，因此b c a +>，即(1)4c c c ++>+，解得3c >.又因为三角形的周长不超过30，即(4)(1)30a b c c c c ++=++++≤，解得253c ≤.因此2533c <≤，因此c 能够取值4，5，6，7，8，对应可得到5个符合条件的三角形. 〔2〕当1,3m n ==时，3b c =+，14a b c =+=+.又,,a b c 为三角形的三边长，因此b c a +>，即(3)4c c c ++>+，解得1c >.又因为三角形的周长不超过30，即(4)(3)30a b c c c c ++=++++≤，解得233c ≤.因此2313c <≤，因此c 能够取值2，3，4，5，6，7，对应可得到6个符合条件的三角形. 综合可知：符合条件且周长不超过30的三角形的个数为5＋6＝11.二．〔此题总分值25分〕题目和解答与〔A 〕卷第二题相同.三．〔此题总分值25分〕题目和解答与〔A 〕卷第三题相同.第二试〔C 〕一．〔此题总分值20分〕题目和解答与〔B 〕卷第一题相同.二．〔此题总分值25分〕题目和解答与〔A 〕卷第二题相同.三．〔此题总分值25分〕设p 是大于2的质数，k 为正整数．假设函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数，求k 的值．解由题意知，方程04)1(2=-+++p k px x 的两根21,x x 中至少有一个为整数．由根与系数的关系可得4)1(,2121-+=-=+p k x x p x x ，从而有p k x x x x x x )1(4)(2)2)(2(212121-=+++=++ ①〔1〕假设1k =，那么方程为0)2(22=-++p px x ，它有两个整数根2-和2p -．〔2〕假设1k >，那么01>-k .因为12x x p +=-为整数，假如21,x x 中至少有一个为整数，那么21,x x 差不多上整数.又因为p 为质数，由①式知2|1+x p 或2|2+x p ．不妨设2|1+x p ，那么可设12x mp +=〔其中m 为非零整数〕，那么由①式可得212k x m -+=，故121(2)(2)k x x mp m -+++=+，即1214k x x mp m-++=+．又12x x p +=-，因此14k p mp m--+=+，即 41)1(=-++mk p m ② 假如m 为正整数，那么(1)(11)36m p +≥+⨯=，10k m ->，从而1(1)6k m p m-++>，与②式矛盾. 假如m 为负整数，那么(1)0m p +<，10k m -<，从而1(1)0k m p m-++<，与②式矛盾. 因此，1>k 时，方程04)1(2=-+++p k px x 不可能有整数根．综上所述，1=k ．。

2020年全国初中数学联合竞赛试题参考答案

2020年全国初中数学联合竞赛试题参考答案讲明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.假如考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题〔此题总分值42分，每题7分〕此题共有6小题，每题均给出了代号为D C B A ,,,的四个答案，其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每题选对得7分；不选、选错或选出的代号字母超过一个〔不论是否写在括号内〕，一律得0分.1．设213a a +=，213b b +=，且a b ≠，那么代数式2211a b +的值为〔〕 )(A 5. )(B 7. )(C 9. )(D 11.【答】B .解由题设条件可知2310a a -+=，2310b b -+=，且a b ≠，因此,a b 是一元二次方程2310x x -+=的两根，故3a b +=，1ab =，因此222222222211()23217()1a b a b ab a b a b ab ++--⨯+====. 应选B . 2．如图，设AD ，BE ，CF 为三角形ABC 的三条高，假设6AB =，5BC =，3EF =，那么线段BE 的长为〔〕 )(A 185. )(B 4. )(C 215. )(D 245. 【答】D . 解因为AD ，BE ，CF 为三角形ABC 的三条高，易知,,,B C E F 四点共圆，因此△AEF ∽△ABC ，故35AF EF AC BC ==，即3cos 5BAC ∠=，因此4sin 5BAC ∠=. 在Rt △ABE 中，424sin 655BE AB BAC =∠=⨯=. 应选D . 3．从分不写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，那么所组成的数是3的倍数的概率是〔〕)(A 15. )(B 310. )(C 25. )(D 12. 【答】C . 解能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个. 因此所组成的数是3的倍数的概率是82205=. 应选C .4．在△ABC 中，12ABC ∠=︒，132ACB ∠=︒，BM 和CN 分不是这两个角的外角平分线，且点,M N 分不在直线AC 和直线AB 上，那么〔〕)(A BM CN >. )(B BM CN =.)(C BM CN <. )(D BM 和CN 的大小关系不确定.【答】B .解 ∵12ABC ∠=︒，BM 为ABC ∠的外角平分线，∴1(18012)842MBC ∠=︒-︒=︒. 又180********BCM ACB ∠=︒-∠=︒-︒=︒，∴180844848BMC ∠=︒-︒-︒=︒，∴BM BC =. 又11(180)(180132)2422ACN ACB ∠=︒-∠=︒-︒=︒， ∴18018012()BNC ABC BCN ACB ACN ∠=︒-∠-∠=︒-︒-∠+∠168(13224)=︒-︒+︒12ABC =︒=∠，∴CN CB =. 因此，BM BC CN ==.应选B .5．现有价格相同的5种不同商品，从今天开始每天分不降价10％或20％，假设干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r ，那么r 的最小值为〔〕)(A 39()8. )(B 49()8. )(C 59()8. )(D 98. 【答】 B .解容易明白，4天之后就能够显现5种商品的价格互不相同的情形.设5种商品降价前的价格为a ，过了n 天. n 天后每种商品的价格一定能够表示为98(110%)(120%)()()1010k n k k n k a a --⋅-⋅-=⋅⋅，其中k 为自然数，且0k n ≤≤. 要使r 的值最小，五种商品的价格应该分不为：98()()1010i n i a -⋅⋅，1198()()1010i n i a +--⋅⋅， 2298()()1010i n i a +--⋅⋅，3398()()1010i n i a +--⋅⋅，4498()()1010i n i a +--⋅⋅，其中i 为不超过n 的自然数. 因此r 的最小值为44498()()91010()988()()1010i n i i n ia a +---⋅⋅=⋅⋅. 应选B . 6．实数,x y满足(2008x y =，那么223233x y x y -+-2007-的值为〔〕 )(A 2008-. )(B 2018. )(C 1-. )(D 1.【答】D .解 ∵22(2008)(2008)2008x x y y ----=， ∴2222008200820082008x x y y y y --==+---， 2222008200820082008y y x x x x --==+---，由以上两式可得x y =. 因此22(2008)2008x x --=，解得22008x =，因此22222323320073233200720071x y x y x x x x x -+--=-+--=-=.应选D .二、填空题〔此题总分值28分，每题7分〕1．设512a -=，那么5432322a a a a a a a+---+=-2-. 解 ∵225135()122a a --===-，∴21a a +=， ∴543232323222()2()2a a a a a a a a a a a a a a a a+---++--++=-⋅- 33332221211(1)(11)2(1)1a a a a a a a a a a a--+--===-=-++=-+=-⋅----. 2．如图，正方形ABCD 的边长为1，,M N 为BD 所在直线上的两点，且5AM =，135MAN ∠=︒，那么四边形AMCN 的面积为52解设正方形ABCD 的中心为O ，连AO ，那么AO BD ⊥，22AO OB ==, 2222232(5)()22MO AM AO =-=-=, ∴2MB MO OB =-=. 又135ABM NDA ∠=∠=︒， 13590NAD MAN DAB MAB MAB ∠=∠-∠-∠=︒-︒-∠45=︒-MAB AMB ∠=∠，因此△ADN ∽△MBA ，故AD DNMB BA =，从而12AD DN BA MB =⋅==. 依照对称性可知，四边形AMCN 的面积115222(22222MAN S S MN AO ==⨯⨯⨯=⨯⨯⨯=△. 3．二次函数2y x ax b =++的图象与x 轴的两个交点的横坐标分不为m ，n ，且1m n +≤.设满足上述要求的b 的最大值和最小值分不为p ，q ，那么p q +=12解依照题意，,m n 是一元二次方程20x ax b ++=的两根，因此m n a +=-，mn b =. ∵1m n +≤，∴1m n m n +≤+≤，1m n m n -≤+≤. ∵方程20x ax b ++=的判不式240a b ∆=-≥，∴22()1444a m n b +≤=≤. 22244()()()11b mn m n m n m n ==+--≥+-≥-，故14b ≥-，等号当且仅当12m n =-=时取得； 22244()()1()1b mn m n m n m n ==+--≤--≤，故14b ≤，等号当且仅当12m n ==时取得. 因此14p =，14q =-，因此12p q +=. 4．依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2018个位置的数字是 1 .解 21到23，结果都只各占1个数位，共占133⨯=个数位； 24到29，结果都只各占2个数位，共占2612⨯=个数位；210到231，结果都只各占3个数位，共占32266⨯=个数位；232到299，结果都只各占4个数位，共占468272⨯=个数位；2100到2316，结果都只各占5个数位，共占52171085⨯=个数位；现在还差2008(312662721085)570-++++=个数位.2317到2411，结果都只各占6个数位，共占695570⨯=个数位.因此，排在第2018个位置的数字恰好应该是2的个位数字，即为1.第二试〔A 〕一．〔此题总分值20分〕 221a b +=，关于满足条件01x ≤≤的一切实数x ，不等式 (1)(1)()0a x x ax bx b x bx ------≥ 〔1〕恒成立.当乘积ab 取最小值时，求,a b 的值.解整理不等式〔1〕并将221a b +=代入，得 2(1)(21)0a b x a x a ++-++≥ 〔2〕在不等式〔2〕中，令0x =，得0a ≥；令1x =，得0b ≥.易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象〔抛物线〕的开口向上，且顶点的横坐标在0和1之间.由题设知，不等式〔2〕关于满足条件01x ≤≤的一切实数x 恒成立，因此它的判不式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥. 由方程组 221,14a b ab ⎧+=⎪⎨=⎪⎩ 〔3〕消去b ，得42161610a a -+=，因此2a =2a =又因为0a ≥，因此a =a =，因此方程组〔3〕的解为a b ⎧=⎪⎪⎨⎪=⎪⎩或a b ⎧=⎪⎪⎨⎪=⎪⎩因此ab 的最小值为14，现在,a b 的值有两组，分不为a b ==a b ==二．〔此题总分值25分〕如图，圆O 与圆D 相交于,A B 两点，BC 为圆D 的切线，点C 在圆O 上，且AB BC =.〔1〕证明：点O 在圆D 的圆周上.〔2〕设△ABC 的面积为S ，求圆D 的的半径r 的最小值.解〔1〕连,,,OA OB OC AC ，因为O 为圆心，AB BC =，因此△OBA ∽△OBC ，从而OBA OBC ∠=∠.因为,OD AB DB BC ⊥⊥，因此9090DOB OBA OBC DBO ∠=︒-∠=︒-∠=∠，因此DB DO =，因此点O 在圆D 的圆周上.〔2〕设圆O 的半径为a ，BO 的延长线交AC 于点E ，易知BE AC ⊥.设2AC y =(0)y a <≤，OE x =，AB l =，那么222a x y =+，()S y a x =+，22222222()2222()aS l y a x y a ax x a ax a a x y=++=+++=+=+=. 因为22ABC OBA OAB BDO ∠=∠=∠=∠,AB BC =,DB DO =，因此△BDO ∽△ABC ，因此BD BO AB AC=，即2r a l y =，故2al r y =. 因此22223222()4422a l a aS S a S r y y y y ==⋅=⋅≥，即22S r ≥，其中等号当a y =时成立，这时AC 是圆O 的直径.因此圆D 的的半径r 的最小值为22S . 三．〔此题总分值25分〕设a 为质数，b 为正整数，且29(2)509(4511)a b a b +=+ 〔1〕求a ，b 的值.解〔1〕式即2634511()509509a b a b ++=，设634511,509509a b a b m n ++==，那么 509650943511m a n a b --== 〔2〕故351160n m a -+=，又2n m =，因此2351160m m a -+= 〔3〕由〔1〕式可知，2(2)a b +能被509整除，而509是质数，因此2a b +能被509整除，故m 为整数，即关于m 的一元二次方程〔3〕有整数根，因此它的判不式251172a ∆=-为完全平方数.不妨设2251172a t ∆=-=〔t 为自然数〕，那么2272511(511)(511)a t t t =-=+-. 由于511t +和511t -的奇偶性相同，且511511t +≥，因此只可能有以下几种情形：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解. ②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解.③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解. ④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解.⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =.⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去. 综合可知251a =.现在方程〔3〕的解为3m =或5023m =〔舍去〕. 把251a =，3m =代入〔2〕式，得5093625173b ⨯-⨯==. 第二试〔B 〕一．〔此题总分值20分〕221a b +=，关于满足条件1,0x y xy +=≥的一切实数对(,)x y ，不等式 220ay xy bx -+≥ 〔1〕恒成立.当乘积ab 取最小值时，求,a b 的值.解由1,0x y xy +=≥可知01,01x y ≤≤≤≤.在〔1〕式中，令0,1x y ==，得0a ≥；令1,0x y ==，得0b ≥.将1y x =-代入〔1〕式，得22(1)(1)0a x x x bx ---+≥，即2(1)(21)0a b x a x a ++-++≥ 〔2〕易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象〔抛物线〕的开口向上，且顶点的横坐标在0和1之间.由题设知，不等式〔2〕关于满足条件01x ≤≤的一切实数x 恒成立，因此它的判不式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥. 由方程组 221,14a b ab ⎧+=⎪⎨=⎪⎩ 〔3〕消去b ，得42161610a a -+=，因此224a -=或224a +=，又因为0a ≥，因此4a =或4a =. 因此方程组〔3〕的解为4,4a b ⎧=⎪⎪⎨⎪=⎪⎩或,44a b ⎧=⎪⎪⎨⎪=⎪⎩因此满足条件的,a b 的值有两组，分不为a b ==a b == 二．〔此题总分值25分〕题目和解答与〔A 〕卷第二题相同.三．〔此题总分值25分〕题目和解答与〔A 〕卷第三题相同.第二试〔C 〕一．〔此题总分值20分〕题目和解答与〔B 〕卷第一题相同.二．〔此题总分值25分〕题目和解答与〔A 〕卷第二题相同.三．〔此题总分值25分〕设a 为质数，,b c 为正整数，且满足29(22)509(41022511)2a b c a b c b c ⎧+-=+-⎨-=⎩ (1)(2) 求()a b c +的值.解〔1〕式即266341022511()509509a b c a b c +-+-=，设66341022511,509509a b c a b c m n +-+-==，那么 5096509423511m a n a b c ---== 〔3〕故351160n m a -+=，又2n m =，因此 2351160m m a -+= 〔4〕由〔1〕式可知，2(22)a b c +-能被509整除，而509是质数，因此22a b c +-能被509整除，故m 为整数，即关于m 的一元二次方程〔4〕有整数根，因此它的判不式251172a ∆=-为完全平方数.不妨设2251172a t ∆=-=〔t 为自然数〕，那么2272511(511)(511)a t t t =-=+-. 由于511t +和511t -的奇偶性相同，且511511t +≥，因此只可能有以下几种情形：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解.②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解. ③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解.④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解. ⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =.⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去.综合可知251a =，现在方程〔4〕的解为3m =或5023m =〔舍去〕. 把251a =，3m =代入〔3〕式，得50936251273b c ⨯-⨯-==，即27c b =-. 代入〔2〕式得(27)2b b --=，因此5b =，3c =，因此()251(53)2008a b c +=⨯+=.。

2020年八年级全国初中数学竞赛试题及答案

2020年八年级全国初中数学竞赛试题及答案2020年全国初中数学竞赛试题一、选择题1.设 $a<b$，$a+b=4ab$，则 $\frac{22}{a-b}$ 的值为【】。

A。

3 B。

6 C。

2 D。

32.已知 $a=1999x+2000$，$b=1999x+2001$，$c=1999x+2002$，则多项式 $a+b+c-ab-bc-ca$ 的值为【】。

A。

0 B。

1 C。

2 D。

33.如图，点 $E$、$F$ 分别是矩形 $ABCD$ 的边 $AB$、$BC$ 的中点，连 $AF$、$CE$ 交于点 $G$，则四边形$AGCD$ 的面积等于【】。

A。

5432 B。

C。

D。

65434.设 $a$、$b$、$c$ 为实数，$x=a-2b+\frac{2}{3}\pi$，$y=b-2c+\frac{2}{3}\pi$，$z=c-2a+\frac{2}{3}\pi$，则 $x$、$y$、$z$ 中至少有一个值【】。

A。

大于 0 B。

等于 0 C。

不大于 0 D。

小于 05.设关于 $x$ 的方程 $ax+(a+2)x+9a=\frac{1}{2}$ 有两个不等的实数根 $x_1$、$x_2$，且 $x_1<1<x_2$，那么 $a$ 的取值范围是【】。

A。

$-\frac{2}{22}0$ C。

$a<-\frac{2}{22}$ D。

$-\frac{5}{77}<a<\frac{2}{22}$6.$A_1A_2A_3\cdots A_9$ 是一个正九边形，$A_1A_2=a$，$A_1A_3=b$，则 $A_1A_5$ 等于【】。

A。

$a^2+b^2$ B。

$a^2+ab+b^2$ C。

D。

$2a^2+2b^2$二、填空题7.设 $x_1$、$x_2$ 是关于 $x$ 的一元二次方程$x+ax+a=2$ 的两个实数根，则 $(x_1-2x_2)(x_2-2x_1)$ 的最大值为【】。

2019-2020年初中数学竞赛初赛试题(一,含详解)

及 x 轴围成的三角形面积为 sk ，则 s1 s2 s3 ... s2006 的值是
。
13．如图，正方形 ABCD和正方形 CGEF的边长分别是 2 和 3，且
点 B、 C、 G 在同一直线上， M 是线段 AE 的中点，连结 MF，则 MF
的长为
。
14．边长为整数的等腰三角形一腰上的中线将其周长分为
心 DEF 的各边与 ABC 的对应边平行，且各对应边的距离都是
1cm,
那么 DEF 的周长是（
）
(A)5cm (B)6cm (C)
( 6 3 )cm (D) ( 3 3 )cm
3．将长为 15cm 的木棒截成长度为整数的三段，使它们构成一个三角形的三边，则不同的截法有 ( ) (A)5 种 (B) 6 种 (C)7 种 (D)8 种
（ 1）随着 m 的变化，该二次函数图象的顶点 P 是否都在某条抛物线上？如果是，请求出该抛物线的表达式；如果不是，请说明理由；
（ 2）如果直线 y x 1 经过二次函数 y x 2 2( m 1 ) x m 1 图象的顶点 P，求
此时 m的值。
全国初中数学竞赛初赛试题（一）参考答案
一、选择题 1．答案 D
4．作抛物线 A 关于 x 轴对称的抛物线 B，再将抛物线 B 向左平移 2 个单位，向上平移 1 个单位，得到的抛物线 C 的函数解析式是 y 2( x 1 ) 2 1，则抛物线 A 所对应的函数表达
式是 ( )
(A) y 2( x 3 )2 2 (B) y 2( x 3) 2 2
(C) y 2( x 1 )2 2 (D) y 2( x 3 )2 2
顶点，棋子停在顶点 D。依这样的规则，在这 10 次移动的过程