材料力学复习汇总
材料力学总复习

一、基本变形
外力
拉伸与压缩
扭转
弯曲
内力
FN F
应力 强度条件
变形
FN
A
max [ ]
l FNl EA
刚度条件
T Me
T
IP
max [ ]
Mnl
GI P
FS 外力
M 外力对形心之矩
My
,
FS
S
* z
Iz
bI z
, max [ ] max [ ]
1、积分法
2、叠加法
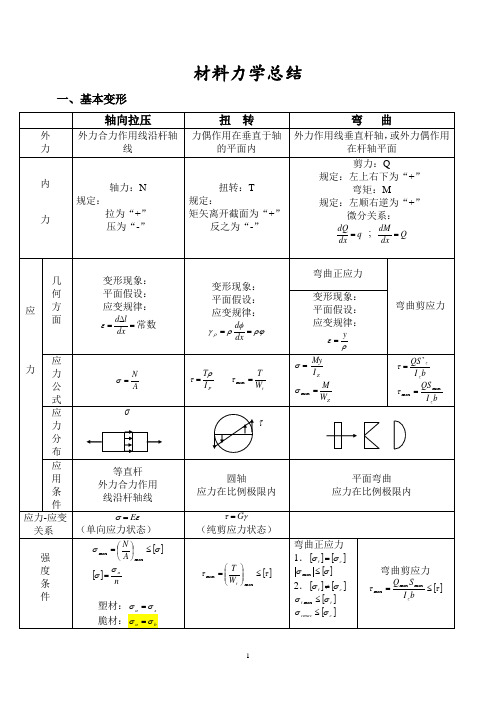
∑Fix= 0, FN1 cos30°+FN2=0 (1)
(2)画节点A的位移图(见图c) (3)建立变形方程
△L1=△L2cos30°
(4)建立补充方程
△L1=△LN1+△LT,
即杆①的伸长△l1由两部份组成,△l N1表示由轴力FN1引起的变形, △lT表示温度升高引起的变形,因为△T 升温,故△lT 是正值。
因为AB 杆受的是拉力,所以沿AB 延
长线量取BB1等于△L1;同理,CB 杆受
的也是拉力,所以沿杆CB 的延长线量取
BB2 等于△L。
分别在点B1 和B2 处作BB1 和BB2 的垂
线,两垂线的交点B′为结构变形后节点
B应有的新位置。即结构变形后成为
ABˊC 的形状。图c称为结构的变形图。
为了求节点B的位置,也可以单独作出节点B的位移图。位移图的作 法和结构变形图的作法相似,如图d所示。
C1 5、求应力并校核强度:
A1
1
FN 1 A
66 .7 MPa ,
2
FN 2 A
133 .2MPa ,
剪切
F AB A1
F BC A2
材料力学性能总复习-知识归纳整理

知识归纳整理《材料力学性能》课程期末总复习一、名词解释刚度、形变强化、弹性极限、应力腐蚀开裂、韧性、等温强度、缺口效应、磨损、腐蚀疲劳、脆性断裂、等强温度、应力松弛、Bauschinger效应、粘着磨损、缺口敏感度、冲击韧度、滞弹性、韧脆转变温度、应力腐蚀、抗拉强度、蠕变、高温疲劳、低应力脆断、氢脆、弹性变形、应力状态软性系数、应力幅、应力场强度因子、变动载荷、抗热震性、弹性比功、残余应力、比强度、高周疲劳、约比温度、滑移、应变时效、内耗、断面收缩率、腐蚀磨损二、挑选题1、Bauschinger效应是指经过预先加载变形,然后再反向加载变形时材料的弹性极限()的现象。
A.升高B.降低C.不变D.无规律可循2、橡胶在室温下处于:()A.硬玻璃态B.软玻璃态C.高弹态D.粘流态3、下列金属中,拉伸曲线上有明显屈服平台的是:()A.低碳钢B.高碳钢C.白口铸铁D.陶瓷4、HBS所用压头为()。
A.硬质合金球B.淬火钢球C.正四棱金刚石锥D.金刚石圆锥体5、对称循环交变应力的应力比r为()。
A.-1 B.0 C.-∞D.+∞6、Griffith强度理论适用于()。
A.金属B.陶瓷C.有机高分子D.晶须7、疲劳裂纹最易在材料的什么部位产生()。
A.表面B.次表面C.内部D.不一定8、⊿Kth表示材料的()。
A.断裂韧性B.疲劳裂纹扩展门槛值求知若饥,虚心若愚。
C.应力腐蚀破碎门槛值D.应力场强度因子9、拉伸试样的直径一定,标距越长则测出的断面收缩率会()。
A.越高B.越低C.不变D.无规律可循10、下述断口哪一种是延性断口()。
A.穿晶断口B.沿晶断口C.河流花样D.韧窝断口11、与维氏硬度可以相互比较的是()。
A.布氏硬度B.洛氏硬度C.莫氏硬度D.肖氏硬度12、为提高材料的疲劳寿命可采取如下措施()。
A.引入表面拉应力B.引入表面压应力C.引入内部压应力D.引入内部拉应力13、材料的断裂韧性随板材厚度或构件截面尺寸的增加而()。
材料力学复习

第一章 绪论1. 承载能力:强度:构件在外力作用下抵抗破坏的能力刚度:构件在外力作用下抵抗变形的能力稳定性:构件在外力作用下保持其原有平衡状态的能力2. 变形体的基本假设:连续性假设、均匀性假设、各向同性假设3. 求内力的方法:截面法4. 杆件变形的基本形式:拉伸或压缩、剪切、扭转、弯曲第二章 拉伸、压缩1. 轴力图必须会画:轴力N F 拉为正、压为负2. 横截面上应力:均匀分布 AF N =σ 3. 斜截面上既有正应力,又有切应力,且应力为均匀分布。
ασσα2cos =αστα2sin 21=σ为横截面上的应力。
横截面上的正应力为杆内正应力的最大值,而切应力为零。
与杆件成45°的斜截面上切应力达到最大值,而正应力不为零。
纵截面上的应力为零,因此在纵截面不会破坏。
4. 低碳钢、灰铸铁拉伸时的力学性能、压缩时的力学性能低碳钢拉伸在应力应变图:图的形状、四个极限、四个阶段、各阶段的特点、伸长率(脆性材料、塑性材料如何区分)5. 强度计算脆性材料、塑性材料的极限应力分别是 拉压时的强度条件:][max max σσ≤=AF N 强度条件可以解决三类问题:强度校核、确定许可载荷、确定截面尺寸 6.杆件轴向变形量的计算 EA l F l N =∆ EA :抗拉压刚度 7. 剪切和挤压:剪切面,挤压面的判断第三章 扭转1.外力偶矩的计算公式: 2.扭矩图T 必须会画:扭矩正负的规定3.切应力互等定理、剪切胡克定律4.圆轴扭转横截面的应力分布规律:切应力的大小、作用线、方向的确定sb σσ,min /::)(9549r n kW P m N n P M ⋅=5.横截面上任一点切应力的求解公式:ρI ρT τP ρ=——点到圆心的距离6. 扭转时的强度条件:][max max ττ≤=tW T 7.实心圆截面、空心圆截面的极惯性矩、抗扭截面模量的计算公式 实心圆截面:极惯性矩432D πI p =,抗扭截面模量316D πW t = 空心圆截面:极惯性矩)1(3244αD πI P -=,抗扭截面模量)1(1643αD πW t -==, 8.圆轴扭转时扭转角:pI G l T =ϕ p I G :抗扭刚度 第四章 弯曲内力1.纵向对称面、对称弯曲的概念2. 剪力图和弯矩图必须会画:剪力、弯矩正负的规定3.载荷集度、剪力和弯矩间的关系4. 平面曲杆的弯矩方程5.平面刚架的弯矩方程、弯矩图第五章 弯曲应力1. 纯弯曲、中性层、中性轴的概念2.弯曲时横截面上正应力的分布规律:正应力的大小、方向的确定3. 横截面上任一点正应力的计算公式:zI My =σ 4. 弯曲正应力的强度校核][max max σσ≤=zW M 或][max max max σI y M σz ≤= 对于抗拉压强度不同的材料,最大拉压应力都要校核5. 矩形截面、圆截面的惯性矩和抗弯截面模量的计算 矩形截面:惯性矩,1213bh I z =抗弯截面模量:261bh W z = 实心圆截面:惯性矩464D πI z =,抗弯截面模量:332D πW z = 空心圆截面:惯性矩)1(6444αD πI z -=,抗弯截面模量:)1(3243αD πW z -=, 第七章 应力和应变分析、强度理论1. 主应力、主平面、应力状态的概念及应力状态的分类2. 二向应力状态分析的解析法:应力正负的规定:正应力以拉应力为正,压应力为负;切应力对单元体内任意点的矩顺时针转向为正;α角以逆时针转向为正D d α=D d α=任意斜截面上的应力计算最大最小正应力的计算公式最大最小正应力平面位置的确定 最大切应力的计算公式主应力、主平面的确定3. 了解应力圆的做法,辅助判断主平面4. 广义胡克定律5.四种强度理论内容及适用范围第八章 组合变形1. 组合变形的判断2. 圆截面轴弯扭组合变形强度条件 第三强度理论:[]σσ≤+=WT M r 223 第四强度理论:[]σσ≤+=W T M r 22375.0 W ——抗弯截面模量323d W π=第九章 压杆稳定1. 压杆稳定校核的计算步骤(1)计算λ1和λ2(2)计算柔度λ,根据λ 选择公式计算临界应(压)力(3)根据稳定性条件,判断压杆的稳定性2. P 1σπλE = ba s 2σλ-= ⎪⎪⎩⎪⎪⎨⎧+-=--++=ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy y x xy y x y x 22min max 22xy y x y x τσσσσσσ+⎪⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫y x xy σστα--=22tan 0231max σστ-=柔度i lμλ= AI i = I ——惯性矩 μ——长度系数;两端铰支μ=1;一端铰支,一段固定μ=0.7;两端固定μ=0.5; 一端固定,一端自由μ=23. 大柔度杆1λλ≥ 22cr λπσE = 中柔度杆12λλλ<≤ λσb a -=cr小柔度杆 2λλ< s cr σσ=4. 稳定校核条件st cr n n FF ≥= F ——工作压力 cr F =cr σ A 第十章 动载荷1. 冲击动荷因数冲击物做自由落体 冲击开始瞬间冲击物与被冲击物接触时的速度为 v水平冲击时 Δst 是冲击点的静变形。
“材料力学”重点归纳

“材料力学”重点归纳
第一章静力学基础
掌握:静力学基本概念和定理:力、力偶、平衡力系、等效力系、合力投影定理、合力矩定理、力线平移定理、静力学的基本任务等。
重点掌握:掌握各种力系的简化和平衡方程应用。
了解材料力学的发展沿革,理解本课程的任务、内容、目的。
第二章材料力学绪论
掌握:了解材料力学的基本任务和杆件的基本变形。
重点掌握:材料力学的基本概念:弹性变形、塑性变形、破坏、强度、刚度、稳定性、内力、应力、应变等。
第三章应力分析和应变分析理论
掌握:应力状态、应力张量、应力张量不变量、空间应力圆、等效应力、八面体应力、变形位移、应变状态、应变张量、偏斜应力张量、偏斜应变张量等概念。
应力分析理论、应变分析理论。
重点掌握:应力状态、应力张量、应力张量不变量、空间应力圆、等效应力、八面体应力、变形位移、应变状态、应力分析理论。
第四章固体材料的弹性本构关系和塑性本构关系
掌握:固体材料弹性变形和塑性变形的主要特点、弹性本构关系(广义胡克定律)、主应力空间、屈服函数、常用屈服条件、常用强度理论等。
重点掌握:固体材料弹性变形和塑性变形的主要特点、弹性本构关系(广义胡克定律)、常用屈服条件和强度理论等。
第五章材料力学实验
了解和掌握金属材料单轴拉伸和压缩力学实验的原理和方法。
(完整版)材料力学复习重点汇总

6.有效裂纹长度:将原有的裂纹长度与松弛后的塑性区相重合并得到的裂纹长度【新P74;旧P86】。
五、试述应力场强度因子的意义及典型裂纹 的表达式
答:应力场强度因子 :表示应力场的强弱程度。 在裂纹尖端区域各点的应力分量除了决定于位置外,尚与强度因子 有关,对于某一确定的点,其应力分量由 确定, 越大,则应力场各点应力分量也越大,这样 就可以表示应力场的强弱程度,称 为应力场强度因子。 “I”表示I型裂纹。 几种裂纹的 表达式,无限大板穿透裂纹: ;有限宽板穿透裂纹: ;有限宽板单边直裂纹: 当b a时, ;受弯单边裂纹梁: ;无限大物体内部有椭圆片裂纹,远处受均匀拉伸: ;无限大物体表面有半椭圆裂纹,远处均匀受拉伸:A点的 。
六、试述冲击载荷作用下金属变形和断裂的特点。
冲击载荷下,瞬时作用于位错的应力相当高,结果使位错运动速率增加,因为位错宽度及其能量与位错运动速率有关,运动速率越大,则能量越大,宽度越小,故派纳力越大。结果滑移临界切应力增大,金属产生附加强化。
由于冲击载荷下应力水平比较高,将使许多位错源同时开动,增加了位错密度和滑移系数目,出现孪晶,减少了位错运动自由行程的平均长度,增加了点缺陷的浓度。这些原因导致金属材料在冲击载荷作用下塑性变形极不均匀且难以充分进行,使材料屈服强度和抗拉强度提高,塑性和韧性下降,导致脆性断裂。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
材料力学复习资料全

材料力学复习资料全材料力学复习资料一、填空题K为了保证机器或结构物正常地工作,要求每个构件都有足够的抵抗破坏的能力,即要求它们有足够的强度:冋时要求他们有足够的抵抗变形的能力?即要求它们有足够的刚度:另外,对于受压的细长直杆,还要求它们工作时能保持原有的平衡状态,即要求其有足够的稳定性「2、材料力学是研究构件强度、刚度、稳定性的学科。
3、强度是指构件抵抗破坏的能力:冈帔是指构件抵抗变形的能力:稳左性是指构件维持其原有的平衡状态的能力。
4、在材料力学中,对变形固体的基本假设是连续性假设、均匀性假设、各向同性假设5、随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫舉性变形。
6、截面法是计算力的基本方法。
7、应立是分析构件强度问题的重要依据。
8、线应变和切应变是分析构件变形程度的基本量。
9、轴向尺寸远大于横向尺寸,称此构件为枉。
10、构件每单位长度的伸长或缩短,称为线应变°11、单元体上相互垂直的两根棱边夹角的改变量.称为切应变-12、轴向拉伸与压缩时直杆横截而上的力,称为轴力,13、应力与应变保持线性关系时的最大应力,称为比例极限14、材料只产生弹性变形的最大应力,称为弹性极根:材料能承受的最大应力,称为强度极限。
15、弹性模量E是衡量材料抵抗弹性变形能力的指标。
16、延伸率6是衡量材料的塑性指标。
6 M5%的材料称为塑性材料:§ V5%的材料称为脆性材料。
17、应力变化不大,而应变显著增加的现象,称为屈服或流动18、材料在卸载过程中,应力与应变成线性关系。
19、在常温下把材料冷拉到强化阶段,然后卸载,当再次加载时,材料的比例极限提高,而塑性降低,这种现象称为冷作硬化20、使材料丧失正常工作能力的应力,称为极限应力,21、在工程计算中允许材料承受的最大应力,称为许用应力。
22、当应力不超过比例极限时,横向应变与纵向应变之比的绝对值,称为泊松比一23、胡克定律的应力适用恫是应力不超过材料的比例极限。
完整版材料力学复习总结

1、材料力学的任务:强度、刚度和稳定性;应力单位面积上的内力。
平均应力P m F(1.1)A全应力p lim p m lim —dF(1.2)A A 0 A dA正应力垂直于截面的应力分量,用符号表示。
切应力相切于截面的应力分量,用符号表示。
应力的量纲:国际单位制:Pa(N/m2)、MPa、GPa工程单位制:kgf/m2、kgf/cm2线应变单位长度上的变形量,无量纲,其物理意义是构件上一点沿某一方向变形量的大小。
外力偶矩传动轴所受的外力偶矩通常不是直接给出,而是根据轴的转速n与传递的功率P来计算当功率P单位为千瓦(kW),转速为n (r/min )时,外力偶矩为PM e 9549 (N .m)n当功率P单位为马力(PS),转速为n (r/min)时,外力偶矩为PM e 7024 (N .m)n拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力,且为平均分布,其计算公式为甩(3-1)A式中F N为该横截面的轴力,A为横截面面积。
正负号规定拉应力为正,压应力为负。
公式(3-1)的适用条件:(1 )杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件;(2)适用于离杆件受力区域稍远处的横截面;(3)杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角200时拉压杆件任意斜截面(a图)上的应力为平均分布,其计算公式为全应力p cos(3-2)正应力 2 cos(3-3)切应力1sin 22(3-4)式中为横截面上的应力。
正负号规定:由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
拉应力为正,压应力为负。
图1.2对脱离体内一点产生顺时针力矩的为正,反之为负。
两点结论:(2)当45时,即与杆轴成450的斜截面上,达到最大值,即()max 乙1 . 2拉(压)杆的应变和胡克定律(1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
材料力学复习总结

D 3
32
1
4
矩形截面
hb 3 Iy 12
bh 3 Iz 12
I z bh 2 Wz h 12
实心圆截面 I
d 4
32
W
d 3
16
W
空心圆截面 I
D 4 1 4
32
d , D
D 3 1 4
16
,
Mx W
第6章精华
ω
ω
x
M 0
x
M 0
d 2 w( x) 0 2 dx
d w( x) w'' ( x) 0 dx2
x
2
x ω
M 0
d w( x) 0 dx2
2
ω
d 2 w( x) M 0 w'' ( x) 0 dx2
小结
y
z
dA
附录A的精华
面积:
A dA
2
x y
2
cos 2 xy sin 2
x y
' '
x y
2
sin 2 xy cos 2
求出过危险点任意斜截面上的正应力和切 应力
max x y y 2 x xy 2 2 min
惯性半径
A
yzdA
2 A
I P r dA
iy
Iy A
iz
Iz A
附录A的精华
圆形截面 环形截面
64 D 4 I y Iz I 1 4 64 Iy Iz I
d 4
Wy Wz W
材料力学复习资料汇总

材料力学复习一一、选择题1. 图中所示三角形微单元体,已知两个直角截面上的切应力为0τ,则斜边截面上的正应力σ和切应力τ分别为 。
A 、00,στττ==;B 、0,0σττ==;C 、00,στττ=-=;D 、0,0σττ=-=。
2. 构件中危险点的应力状态如图所示,材料为低碳钢,许用应力为[]σ,正确的强度条件是 。
A 、[]σσ≤;B 、[]στσ+≤;C 、[],[][]/2σσττσ≤≤=;D 、224[]στσ+≤。
3. 受扭圆轴,当横截面上的扭矩不变而直径减小一半时,该横截面上的最大切应力原来的最大切应力是 。
A 、2倍B 、4倍C 、6倍D 、8倍4. 两根材料相同、抗弯刚度相同的悬臂梁I 、II 如图示,下列结论中正确的是 。
A.I 梁和II 梁的最大挠度相同 B.II 梁的最大挠度是I 梁的2倍 C.II 梁的最大挠度是I 梁的4倍 D.II 梁的最大挠度是I 梁的1/2倍2PPlI2lII题1-4 图5. 现有两种压杆,一为中长杆,另一为细长杆。
在计算压杆临界载荷时,如中长杆误用细长杆公式,而细长杆误用中长杆公式,其后果是 。
A 、两杆都安全;B 、两杆都不安全;C 、中长杆不安全,细长杆安全;D 、中长杆安全,细长杆不安全。
6. 关于压杆临界力的大小,说法正确的答案是 A 与压杆所承受的轴向压力大小有关; B 与压杆的柔度大小有关;C 与压杆所承受的轴向压力大小有关;D 与压杆的柔度大小无关。
二、填空0τ0ττσ4545题 1-1 图στ题 2-2 图σεO1.结构构件应该具有足够的 、 和 。
2.低碳钢拉伸破坏经历了四个典型阶段: 阶段、 阶段、 阶段和 阶段。
衡量材料强度的指标是 、 。
3.在其他条件不变的前提下,压杆的柔度越大,则临界应力越 、临界力越 ;材料的临界柔度只与 有关。
4.两圆截面杆直径关系为:123D D =, 则12Z Z I I =;12Z Z W W =;12P P I I =;12P P W W =;5.图中所示的T 形截面梁,若已知A-A 截面上、下表面沿x 方向的线应变分别为0.00040.0002εε=-=下上,,则此截面的中性轴位置y c 与截面高h 之间的关系为c y = 2/3 h 。
材料力学复习资料汇总

12材料力学一、填空1、图所示桁架中,水平杆看作刚性,三根竖杆长度相同,横截面积均为A ,材料相同,屈服极限为σy .当三杆均处于弹性阶段时,各杆轴力之比为N 1: N 2: N 3=5:2:-1.当三杆中有一杆开始屈服时,荷载P 的值为(1.5σy A ).2、一等截面圆直杆,长度为l ,直径为d ,材料的弹性模量为E ,轴向受压力P ,在弹性范围内,其最大切应力为(2P /πd 2),受载后的长度为(l -4lP /πEd 2),受载后的直径为( d +4μP /πEd ),杆件内的应变能为(2P 2l /πE d 2 )。
3、外径 D = 55 mm ,内径 d = 45 mm 的钢管,两端铰支,材料为 Q235钢,承受轴向压力 F 。
则能使用欧拉公式时压杆的最小长度是(1.78m ),当压杆长度为上述最小长度的4/5时,压杆的临界应力为(188.5kN )。
已知:E = 200 GPa ,σ p = 200 MPa ,σs = 240 MPa ,用直线公式时,a = 304 MPa , b =1.12 MPa 。
4、一等直圆杆,直径为d ,长度为l ,两端各作用一扭矩T ,材料的泊松比为μ,弹性模量为E 。
则两端面的相对转角为(64(1+μ)Tl /πEd 4),杆件内储存的应变能为(32(1+μ)T 2l /πEd 4 );又若两端各作用一弯矩M ,则按第三强度理论时,其危险点的相当应力为(22332M T d+π),按第四强度理论时,其危险点的相当应力为(22375.032M T d +π)。
6、矩形截面梁,材料的抗弯许用应力[σ]=8MPa ,梁内最大弯矩M max =24kNm ,梁截面的高宽比h /b =1.5.则梁宽b 应取( 20cm ).7、圆柱形蒸汽锅炉的外径为D ,内径为d ,壁厚为t ,若材料的许用应力为[σ].则锅炉能承受的最大内压力(工作压力)为(p=2[σ]t/d)。
(完整版)材料力学知识点总结
材料力学总结一、基本变形二、还有:(1)外力偶矩:)(9549m N nNm •= N —千瓦;n —转/分 (2)薄壁圆管扭转剪应力:tr T22πτ=(3)矩形截面杆扭转剪应力:hb G Th b T 32max ;βϕατ==三、截面几何性质(1)平行移轴公式:;2A a I I ZC Z += abA I I c c Y Z YZ += (2)组合截面: 1.形 心:∑∑===ni ini cii c AyA y 11; ∑∑===ni ini cii c AzA z 112.静 矩:∑=ci i Z y A S ; ∑=ci i y z A S 3. 惯性矩:∑=i Z Z I I )( ;∑=i y y I I )(四、应力分析:(1)二向应力状态(解析法、图解法)a . 解析法: b.应力圆:σ:拉为“+”,压为“-” τ:使单元体顺时针转动为“+”α:从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c :适用条件:平衡状态(2)三向应力圆:1max σσ=; 3min σσ=;231max σστ-=x(3)广义虎克定律:[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态 1.纯剪切应力状态:τσ=1 ,02=σ,τσ-=32.一种常见的二向应力状态:223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力:r σ11σσ=r ,313σσσ-=r ,()()()][212132322214σσσσσσσ-+-+-=r σxσ六、材料的力学性质脆性材料 δ<5% 塑性材料 δ≥5%低碳钢四阶段: (1)弹性阶段(2)屈服阶段 (3)强化阶段 (4)局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七.组合变形ε八、压杆稳定欧拉公式:2min2)(l EI P cr μπ=,22λπσE cr =,应用范围:线弹性范围,σcr <σp ,λ>λp柔度:iul =λ;ρρσπλE=;ba s σλ-=0,柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:22λπσE cr =λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σs稳定校核:安全系数法:w I cr n P P n ≥=,折减系数法:][σϕσ≤=AP提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
材料力学复习重点

1、杆件变形的基本形式有哪些的?
2、轴向拉伸、压缩时杆件的内力、应力及变形的求法?
3、温度变化和构件制造误差对静定结构和超静定结构的影响
4、剪切和挤压的实用计算
5、切应力、切应变的计算方法
6、圆轴受扭时横截面上任一点且应力求法?
7、常见界面的抗扭截面系数是什么?(圆形、圆环形)
8、脆性材料圆杆扭转破坏的形式及原因?
9、什么是材料的屈服极限,什么是材料的
?
0.2
10、应力应变曲线及曲线各部分的意义?
11、剪力方程、弯矩方程、剪力图、弯矩图的做法?
12、荷载集度、剪力和弯矩的关系?
13、弯曲正应力的求法?(公式5.2及公式各参数的意义)
14、变性固体的基本假设,及其意义?
15、许用应力的确定?
16、高宽比h/b=2的矩形截面梁,若将梁的横截面由竖放改成平放,则梁的最大挠度是原来的多少倍?
17、积分法求弯曲变形中积分常数怎么确定?
18、例7.4
19、二向应力状态下,任意斜截面上正应力、切应力、主应力及主应力方位求法?
20、各个公式的使用范围?(如扭转切应力公式、弯曲正应力公式、胡克定律、欧拉公式等)
21、利用欧拉公式时压杆的最小长度和压杆的临界应力。
材料力学总复习

求支反力一定要校核。 求支反力一定要校核。 法一:列剪力方程、弯矩方程。 法一:列剪力方程、弯矩方程。 求控制截面的内力值。 求控制截面的内力值。 法二:简易法。 法二:简易法。
9
例题2 矩形截面梁, 例题2 矩形截面梁,已知 q = 2kN⋅ m,[σ ] =10MPa 反力( (1)反力(2’) q 。(6 (2)作FS图,M图。(6’) B 校核梁的正应力强度。( A 。(7 (3)校核梁的正应力强度。(7’)
材料力学 总复习
第一章:绪论 第一章: 材料力学:变形固体基本假设 ,弹性, 塑性, 研究对象 第二章~ 第二章~第五章 基本变形
1
第二章 拉压
1、横截面上的内力与应力 轴力:拉为正,压为负。 轴力:拉为正,压为负。 内力、应力的概念;单位:MPa, 内力、应力的概念;单位:MPa,GPa FN σ= A 2、强度条件及许用应力
N N
∫
L
EA(x)
3
4、材料的力学性质 塑性材料——低碳钢 塑性材料——低碳钢 脆性材料——铸铁 脆性材料——铸铁 (1)低碳钢的拉伸图 变形的四个阶段: 四个强度(极限)指标 σP < σe < σs < σb 两个塑性指标: 两个塑性指标:σs , σ0.2
名义屈服极限
(2)铸铁的压缩实验— σb 铸铁的压缩实验—
2
2
4、、剪切计算 、、剪切计算 单剪: 单剪:
P FS = n
抗弯截 面模量
M2 + 0.75T 2 σr 4 = Wz
双剪: 双剪: FS = P
2n
剪切面积 Q 强度条件: 强度条件: τ = A ≤ [τ ]
s
5、挤压实用计算
材料力学总复习

基本概念 第一部分 基本变形部分 第二部分 复杂变形部分 压杆稳定 平面图形几何性质
基本概念
• 强度,刚度,稳定性 • 连续性,均匀性,各向同性 • 基本变形形式:拉压,剪,扭、弯 • 塑性,脆性材料的区别 • 截面法
σ(MPa)
材料试验
b
a
s e p
σp σe σs
εp εt
f
σb
ε
εe
第二部分
复杂变形部分
平面应力分析
σy
σx
y
ቤተ መጻሕፍቲ ባይዱ
τxy
Ox
σα
α
σx
y
σy
ττxαy
n
Ox
τ
⎪⎪⎩⎪⎪⎨⎧τσαα==σσxx−2+2σσyys+inσ2xα−2+στyxcycoos2s2αα−τ xysin2α
平面内的主应力
σy
σ 2′
⎩⎨⎧σσmm´´ainx
σ
=x
+σ
σ
y ±( x
2
−σ y
例题
下列四种截面梁均是边长为a的正方形截面,若载荷均
作用在纵向对称面内,计算四种截面梁的抗弯截面系数
WZ=
。(b、c两种截面未经粘合)
例题
正方形截面分别按图示中的两种情形放置,则两者间
的抗弯刚度之间的关系为 。
A:(a)>(b)
B:(a)<(b)
√C:(a)=(b)
D:不一定
正方形截面对于过形心的任何轴的惯性矩相等,固两种放 置方式中的抗弯刚度相同。
对象,对中间铰取矩,得到活动铰的约束反力也为零。固对于 固定端一侧的梁相当于自由端受集中力F作用的悬臂梁,二者 的内力图相同。
材料力学复习总结

• 主平面剪:应力为零的面.
主单元体:各侧面上只有正应力作用,而无剪应 力作用的单元体.
平面应力状态:两个主应力不等于零的应力状态. 三向应力状态:三个主应力不等于零的应力状态.
梁上的力既有外力也有内力( Fs 、M),利
用平衡条件即可求得截面上的剪力和弯矩。
2.内力的正负号是根据变形规定的:使梁产生 顺时针转动的剪力规定为正,反之为负;使梁 下部产生拉伸而上部产生压缩的弯矩规定为正, 反之为负。
3.画剪力、弯矩图的方法可以分为二种:根据
剪力、弯矩方程作图和利用q、Fs、M间的微分
• 叠加法的主要步骤为: 1)将组合变形按基本变形的加载条件或
相应内力分量分解为几种基本变形;
2)根据各基本变形情况下的内力分布, 确定可能危险面;根据危险面上相应内力分 量画出应力分布图,由此找出可能的危险点; 根据叠加原理,得出危险点应力状态;
3)根据构件的材料选取强度理论,由危 险点的应力状态,写出构件在组合变形情况 下的强度条件,进而进行强度计算。
若梁的弯矩分了n段,每段积分有两个常数,共有 2n个常数;而梁有2个边界条件;n段,(n-1)个内 点,每一内点有两个光滑连续条件,又有2(n-1) 个光滑连续条件,这样一共有2n定常数的条件。
由以上运算可以看出,梁的挠度曲线取决于两个 因素:受力(弯矩)和边界条件。
3.在小变形和弹性范围内,梁的位移与载荷为 线性关系,可以用叠加法求梁的位移:将梁 的载荷分为若干种简单载荷,分别求出各简 单载荷的位移,将它们叠加起来即为原载荷 产生的位移。
(第一强度理论) (第二强度理论) (第三强度理论) (第四强度理论)
(完整版)材料力学知识点总结

以家为家,以乡为乡,以国为国,以天下为天下。——《管子·牧民》
六、材料的力学性质
脆性材料 <5%
塑性材料 ≥5% 低碳钢四阶段: (1)弹性阶段
(2) 屈服阶段 (3) 强化阶段 (4) 局部收缩阶段
强度指标 s , b
e
塑性指标 ,
拉
压
α
s
tg
b
E 扭
45
低
碳
钢
滑移线与轴线 45,剪
只有s,无b
( l)2
cr
2
cr p
p
柔度:
ul
;
i
E
;
0
a s b
,
柔度是一个与杆件长度、约束、截面尺寸、形 状有关的数据,λ↑Pcr↓σcr↓
>p——大柔度杆:
cr
2E
2
临界应力
o<<p——中柔度杆:cr=a-b
cr cr=s o
cr=a-b
2E
cr
2
P
<0——小柔度杆:cr=s
P 稳定校核:安全系数法: n cr n ,折减系数法:
材料疲劳极限:材料经无限次应力循环而不发生疲劳破坏的应力极限值——N=107:
1
条件疲劳极限:(有色金属)无水平渐近线:N=(5-7)107 对应的
1
构件疲劳极限:考虑各种因素 0
;
1
0 1
1 k
1 k
6
谋事在人,成事在天!——《增广贤文》
我尽一杯,与君发三愿:一愿世清平,二愿身强健,三愿临老头,数与君相见。——《白居易》
P
[]
P
w
A
I
提高杆件稳定性的措施有:
材料力学性能复习总结

绪论弹性:指材料在外力作用下保持和恢复固有形状和尺寸的能力。
塑性:材料在外力作用下发生不可逆的永久变形的能力。
刚度:材料在受力时抵抗弹性变形的能力。
强度:材料对变形和断裂的抗力。
韧性:指材料在断裂前吸收塑性变形和断裂功的能力。
硬度:材料的软硬程度。
耐磨性:材料抵抗磨损的能力。
寿命:指材料在外力的长期或重复作用下抵抗损伤和失效的能。
材料的力学性能的取决因素:内因——化学成分、组织结构、残余应力、表面和内部的缺陷等;外因——载荷的性质、应力状态、工作温度、环境介质等条件的变化。
第一章 材料在单向静拉伸载荷下的力学性能1.1 拉伸力—伸长曲线和应力—应变曲线应力—应变曲线退火低碳钢在拉伸力作用下的力学行为可分为弹性变形、不均匀屈服塑性变形、均匀塑性变形和不均匀集中塑性变形和断裂几个阶段。
弹性变形阶段:曲线的起始部分,图中的oa 段。
多数情况下呈直线形式,符合虎克定律。
屈服阶段:超出弹性变形范围之后,有的材料在塑性变形初期产生明显的塑性流动。
此时,在外力不增加或增加很小或略有降低的情况下,变形继续产生,拉伸图上出现平台或呈锯齿状,如图中的ab 段。
均匀塑性变形阶段:屈服后,欲继续变形,必须不断增加载荷,此阶段的变形是均匀的,直到曲线达到最高点,均匀变形结束,如图中的bc 段。
不均匀塑性变形阶段:从试样承受的最大应力点开始直到断裂点为止,如图中的cd 段。
在此阶段,随变形增大,载荷不断下降,产生大量不均匀变形,且集中在颈缩处,最后载荷达到断裂载荷时,试样断裂。
弹性模量E :应力—应变曲线与横轴夹角的大小表示材料对弹性变形的抗力,用弹性模量E退火低碳钢应力—应变曲线表示。
塑性材料应力—应变曲线(a)弹性—弹塑性型:Oa为弹性变形阶段,在a点偏离直线关系,进入弹—塑性阶段,开始发生塑性变形,开始发生塑性变形的应力称为屈服点,屈服点以后的变形包括弹性变形和塑性变形。
在m点卸载,应力沿mn降至零,发生加工硬化。
(b)弹性-不均匀塑性-均匀塑性型:与前者不同在于出现了明显的屈服点aa′,有时呈屈服平台状,有时呈齿状。
材料力学总复习
mB
mC
A
0.7m
C B
1m
mB
mC
A
0.7m
C
B
1m
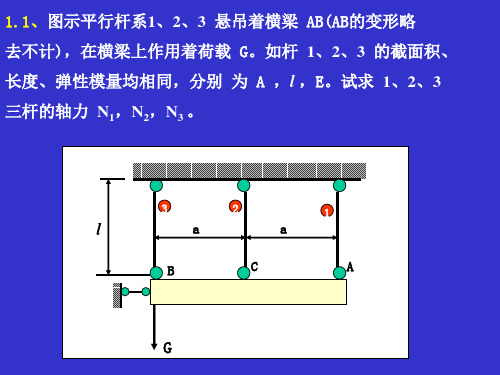
解:由截面法得知
T AB 2.53KN .m
T BC 1.27 KN .m
需分段计算相对扭转角
BA
T AB l AB GI P ,
CB
T BC l BC GI P
IP
d
4
32
mB
mC
T AB 2.53KN .m T BC 1.27 KN .m
(3) 物理方程
N1l l 1 EA
N2l l 2 EA
N3l l 3 EA
3 3 2 1
2
1
l
B
a
a
C
B
l 2
B
A
l1
A
C
A
l3
C
G 补充方程
N1 N 3 2N 2
3 3 2 1
2
1
l
B
a
a
C
B
l 2
B
A
l1
A
C
A
l3
C
G (4) 联立平衡方程与补充方程求解
补充方程
2 N 2l2 N1l1 N3l3 (1)
2Δ2 Δ1 Δ3 l l l
静力方程
N1
1
2
3
A P
N2
B
N3
C
M
c
(F ) 0
Δ1 l
120 P 160 N1 80 N 2 0(2)
Δ2 l
Δ3 l
M
A
(F ) 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学一、填空题1.为保证构件能正常的工作,要求其具有足够的承载能力,与承载能力有关的是( )A.构件的强度,刚度和稳定性B.构件的强度,应力和稳定性C.构件的变形,刚度和稳定性D.构件的强度,刚度和变形2.在常温静载下衡量塑性材料是否失效的重要指标是( )A.比例极限B.弹性极限C.屈服极限D.强度极限3.切应力互等定理是指两垂直于截面交线的切应力必定成对出现,且( )A.大小相等,方向均指向或背离此交线B.大小相等,方向平行此交线c.大小不等,方向均指向或背离此交线 D.大小不等,方向平行此交线4.梁上有分布载荷作用受弯曲变形时,其内力图的特征是( )A.剪力图无变化,弯矩图有突变B.剪力图有突变,弯矩图无变化C.剪力图是斜直线,弯矩图是抛物线D.剪力图是抛物线,弯矩图是斜直线5.细长压杆的柔度对临界应力有很大的影响,与它有关的是( )A.杆端约束,截面的形状和尺寸,压杆的长度B.杆端约束,截面的形状和尺寸,许用应力C.压杆的长度,截面的形状和尺寸,许用应力D.杆端约束,截面的形状和尺寸,许用应力6.脉动循环的交变应力,如果=0,其循环特征( )A.r=-lB.r=0C.r=1/2D.r=15.塑性材料的极限应力是( )1 / 232 / 23A.比例极限p σB.弹性极限e σC.屈服极限s σD.强度极限b σ7.轴向拉伸时,杆的伸长量( )A.与轴力和抗拉刚度均成正比B.与轴力和抗拉刚度均成反比C.与轴力成反比,与抗拉刚度成正比D.与轴力成正比,与抗拉刚度成反比8.两个材料不同的受扭转作用的轴,其载荷、约束、截面形状、尺寸及其长度均相同,则其( )A.变形相同,应力不同B.变形和应力均相同C.变形不同,应力相同D.变形和应力均不相同9.圆形截面梁剪切弯曲时,横截面上最大切应力发生在( )A.中性轴上,方向平行于剪力B.中性轴上,方向垂直于剪力C.距中性轴最远处,方向平行于剪力D.距中性轴最远处,方向垂直于剪力10.图示弯曲梁的BC 段A.有变形,无位移B.有位移,无变形C.既有变形,又有位移D.既无变形,又无位移11.材料的持久极限是指材料能经受无限次应力循环而不发生疲劳破坏的( )A.最低应力B.平均应力C.最高应力D.应力幅度12、截面外径为D 、内径为d ,其抗弯截面系数为( ) 5.材料的塑性指标有( )A.δ和ψB.s σ和ψC.s σ和δD. s σ、δ和ψ13.二受拉杆材料、横截面及受力均相同,但长度不同,则二杆不同的是( )A.轴向正应力σB.轴向伸长l ∆C.轴向线应变εD.横向线应变ε', A.)d D (6433-π B. )d D (3233-π C.])D d (1[D 6443-π D.])Dd (1[D 3243-π 14.在压杆稳定计算中,如果用细长杆的公式计算中长杆的临界压力,或是用中长杆的公式计算细长杆的临3 / 23界压力,则( )A.二者的结果都偏于安全B.二者的结果都偏于危险C.前者的结果偏于安全,后者的结果偏于危险D.前者的结果偏于危险,后者的结果偏于安全15.构件受冲击载荷,若要降低其动应力,可以采取措施( )A.增加构件的强度B.减小构件的强度C.增加构件的刚度D.减小构件的刚度16.对称循环交变应力的循环特征r=( )A.-1B.0C.0.5D.1 17.常用的应力单位是兆帕(MPa ),1Mpa =( )A .103N /m 2B .106 N /m 2C .109 N /m 2D .1012 N /m 218.题7图示螺钉在拉力P 作用下,挤压面积A jy =( )A .2d 4πB .dh 4π C .2D 4π D .)d (D 422-π 19.长度为l 的简支梁上作用了均布载荷q ,根据剪力、弯矩和分布载荷间的微分关系,可以确定( )A .剪力图为水平直线,弯矩图是抛物线B .剪力图是抛物线,弯矩图是水平直线C .剪力图是斜直线,弯矩图是抛物线D .剪力图是抛物线,弯矩图是斜直线20.如题9图示,平面应力状态( )A .σx >0, τx >0, τy <0B .σx <0, τx <0, τy >0C .σx <0, τx >0, τy <0D .σx >0, τx <0, τy >021.当具有一定速度的物体作用到静止构件上时,物体的速度发生急剧改变,由于惯性,使构件受到很大的作用力,这种现象称为冲击,例如( )A.电梯上升B.压杆受压C.齿轮啮合D.落锤打桩22.脆性材料的许用应力[σ]小于()A.σe B.σpC.σs D.σb7.圆轴受扭时,内力偶矩称为扭矩,表示为()A.F N B.F QC.T D.M23.一等截面铸铁梁的弯矩图如图所示,设计梁的截面时,最合理的截面应该是图()24.图示超静定梁的超静定次数是()A.1次B.2次C.3次D.4次25.对于一个单元体,下列结论中错误的是()A.正应力最大的面上切应力必为零B.切应力最大的面上正应力必为零C.正应力最大的面与切应力最大的面相交成45°角D.正应力最大的面与正应力最小的面相互垂直26.使材料丧失正常工作能力的应力称为极限应力,低碳钢的极限应力是()A.比例极限σPB.弹性极限σeC.屈服极限σsD.强度极限σb27.题7图示空心圆轴扭转时,受扭矩T作用,其横截面切应力分布的正确表达应为()4 / 235 /2328.题8图示两外伸梁的尺寸和支座均相同,受力的方向有所不同,根据叠加法,挠度最大处可能是( )A.(a )图的D 截面或C 截面B.(a )图的C 截面或(b )图的C 截面C.(b )图的D 截面D.(b )图的C 截面29.用单元体表示点的应力状态,在主平面上( )A.正应力一定最大B.正应力一定为零C.切应力一定最大D.切应力一定为零10.汽车在平坦大道或崎岖山路上行驶时,其车轮轴上作用的是( )A.弯曲正应力B.扭转切应力C.交变应力D.拉压正应力30.当轴传递的功率不变时,该轴所承受的外力偶矩M 0与其转速成( )A .正比B .反比C .二次函数关系D .三次函数关系31.当水平梁上某横截面的弯矩为负值时,则该横截面上正应力的正确分布图是()32.图示悬臂梁自由端的( )A .挠度和转角均为正B .挠度为正,转角为负C .挠度为负,转角为正6 / 23D .挠度和转角均为负33.判断压杆属于细长杆、中长杆、还是短粗杆的依据是( )A .柔度B .长度C .横截面尺寸D .临界应力5.工程上区分塑性材料和脆性材料的标准是看其延伸率δ大于等于还是小于( )A .1%B .3%C .5%D .10%34.直径和长度相同而材料不同的圆轴,在相同扭矩作用下,它们的( )A .最大切应力相同,而扭转角不同B .最大切应力相同,扭转角也相同C .最大切应力不同,而扭转角相同D .最大切应力不同,扭转角也不同35.梁在弯曲变形时,其中性层的曲率( )A .与弯矩成反比,与抗弯刚度成正比B .与弯矩成正比,与抗弯刚度成反比C .与弯矩及抗弯刚度均成正比D .与弯矩及抗弯刚度均成反比36.图示矩形截面对z 、y 两形心轴的惯性矩分别为( )A .22121,121hb I bh I y z ==B .22121,121bh I hb I y z ==C .33121,121bh I hb I y z ==D .33121,121hb I bh I y z == 37.用积分法求一悬臂梁受力后的变形时,边界条件为:在梁的固定端处( )A .挠度为零,转角也为零B .挠度为零,转角不为零C .挠度不为零,转角为零D .挠度不为零,转角也不为零38.影响构件疲劳强度的三个主要因素是:构件的( )A .外形、尺寸大小、残余应力B .残余应力、尺寸大小、表面加工质量C .外形、残余应力、表面加工质量D .外形、尺寸大小、表面加工质量39.一般情况下题5图所示结构中二杆的合理选材方案是( )A. 1杆用钢材,2杆用铸铁B. 1杆用铸铁,2杆用钢材C. 二杆均用钢材D. 二杆均用铸铁40.连接件切应力计算的基础是假设( )A. 剪切面不超过1个7 / 23B. 切应力不超过材料的比例极限C. 剪切面为圆形或矩形D.切应力在剪切面上均匀分布41.在下列4种情况中,截面上弯矩M 为正、剪力F S 为负的是( )42.题8图所示悬臂梁,若已知截面B 的挠度和转角分别为υB 和θB ,则C 端挠度与转角分别为( )A. υC =2υB ,θC =θBB. υC =θB a,θC =θBC. υC =υB +θBa ,θC =θBD. υC =υB +θBa ,θC =043.用动能定理解冲击问题的方法,是( )A. 精确方法,所得结果偏于安全B. 精确方法,所得结果偏于危险C. 近似方法,所得结果偏于安全D. 近似方法,所得结果偏于危险44.脉动循环交变应力的循环特征r=( )A. –1B. 0C. 0.5D. 145.设ε和ε′分别表示杆件轴向拉压时的轴向线应变和横向线应变,μ为材料的泊松比,则下列公式中正确的是( )A.εεμ/'=B.εεμ/'-=C.εεμ'=/D.εεμ'-=/46.连接件切应力计算的基础是假设( )A.构件沿剪切面被剪断B.剪切面与作用力平行C.切应力在剪切面上均匀分布D.切应力不超过材料的剪切比例极限47.图示悬臂梁,若已知截面B 的挠度和转角分别为v B 和B θ,则C 端挠度为( )A.B C v v 2=B.a v B C θ=C.a v v B B C θ+=D.B C v v =48.圆截面细长压杆的材料和杆端约束保持不变,若将其直径缩小一半,则压杆的临界压力为原压杆的( )A.1/2B.1/4C.1/8D.1/168 / 2349.构件受冲击载荷,若要降低其动应力,可以采取的措施是( )A.增加构件的刚度B.增加构件的强度C.减少构件的刚度D.减少构件的强度50.交变应力的变化特点可用循环特征r 来表示,其公式为( ) A.max min σσ=r B. mr σσmin = C. a m r σσ= D. ma r σσ=51.各向同性假设认为,材料沿各个方向具有相同的( )A .应力B .变形C .位移D .力学性质52.关于截面法下列叙述中正确的是( )A .截面法是分析杆件变形的基本方法B .截面法是分析杆件应力的基本方法C .截面法是分析杆件内力的基本方法D .截面法是分析杆件内力与应力关系的基本方法53.在下列关于梁转角的说法中,错误的是( )A .转角是横截面绕中性轴转过的角度B .转角是横截面绕梁轴线转过的角度C .转角变形前后同一横截面间的夹角D .转角是挠曲线之切线与轴向坐标轴间的夹角54.某机轴为Q235钢制,工作时发生弯扭组合变形。
