传送带和滑块模型(完整资料).doc
(完整版)高中物理传送带模型(解析版)
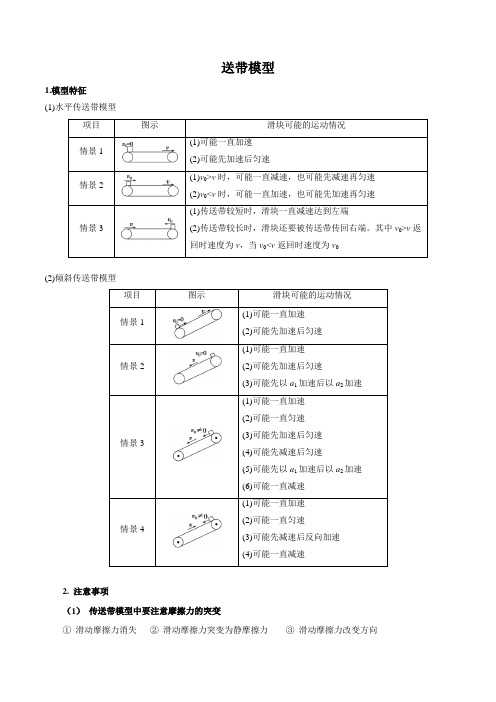
送带模型1.模型特征(1)水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v返回时速度为v,当v0<v返回时速度为v0(2)倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速情景3(1)可能一直加速(2)可能一直匀速(3)可能先加速后匀速(4)可能先减速后匀速(5)可能先以a1加速后以a2加速(6)可能一直减速情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速(4)可能一直减速2. 注意事项(1)传送带模型中要注意摩擦力的突变①滑动摩擦力消失②滑动摩擦力突变为静摩擦力③滑动摩擦力改变方向(2)传送带与物体运动的牵制。
牛顿第二定律中a 是物体对地加速度,运动学公式中S 是物体对地的位移,这一点必须明确。
(3) 分析问题的思路:初始条件→相对运动→判断滑动摩擦力的大小和方向→分析出物体受的合外力和加速度大小和方向→由物体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【典例1】如图所示,传送带的水平部分长为L ,运动速率恒为v ,在其左端无初速放上木块,若木块与传送带间的动摩擦因数为μ,则木块从左到右的运动时间可能是( )A.L v +v 2μgB.L vC.2L μgD.2L v【答案】 ACD【典例2】如图所示,倾角为37°,长为l =16 m 的传送带,转动速度为v =10 m/s ,动摩擦因数μ=0.5,在传送带顶端A 处无初速度地释放一个质量为m =0.5 kg 的物体.已知sin 37°=0.6,cos 37°=0.8,g =10 m/s 2.求:(1)传送带顺时针转动时,物体从顶端A 滑到底端B 的时间; (2)传送带逆时针转动时,物体从顶端A 滑到底端B 的时间. 【答案】 (1)4 s (2)2 s【典例3】如图所示,与水平面成θ=30°的传送带正以v =3 m/s 的速度匀速运行,A 、B 两端相距l =13.5 m 。
(完整版)高中物理传送带模型

一、水平传送带:情景图示滑块可能的运动情况情景1 ⑴可能一直加速⑵可能先加速后匀速情景2 ⑴vv=,一直匀速⑵vv>,一直减速或先减速后匀速⑶vv<,一直加速或先加速后匀速情景3 ⑴传送带较短,一直减速到左端⑵传送带足够长,滑块还要被传回右端:①vv>,返回时速度为v②vv<,返回时速度为v二、倾斜传送带:情景图示滑块可能的运动情况情景1 ⑴可能一直加速⑵可能先加速后匀速⑶可能从左端滑落情景21.可能一直加速⑵可能先加速后匀速⑶可能先以1a加速,后以2a加速情景31可能一直加速⑵可能一直匀速⑶可能先加速后匀速⑷可能先减速后匀速⑸可能先以1a加速,后以2a加速情景4 ⑴可能一直加速⑵可能一直减速⑶可能先减速到0,后反向加速1、如图所示为火车站使用的传送带示意图,绷紧的传送带水平部分长度L =4 m ,并以s m v /10=的速度向右匀速运动。
现将一个可视为质点的旅行包无初速度地轻放在传送带的左端,已知旅行包与传送带之间的动摩擦因数μ=0.2,取2/10s m g =。
(1)求旅行包经过多长时间到达传送带的右端。
(2)若要旅行包从左端运动到右端所用时间最短,传送带速度的大小应满足什么条件?2、如图所示,绷紧的传送带,始终以2 m/s 的速度匀速斜向上运行,传送带与水平方向间的夹角︒=30θ. 现把质量为10 kg 的工件轻轻地放在传送带底端P 处,由传送带传送至顶端Q 处.已知P 、Q 之间的距离为4 m ,工件与传送带间的动摩擦因数23=μ,取2/10s m g = (1)通过计算说明工件在传送带上做什么运动;(2)求工件从P 点运动到Q 点所用的时间.3、(讲逆时针)如图所示,倾角为37°、长为L=16m 的传送带,转动速度为s m v /10=,在传送带顶端A 处无初速地释放一个质量为kg m 5.0=的物体,已知物体与传送带间的动摩擦因数5.0=μ,取2/10s m g =。
传送带模型和滑块模型

专题:传送带模型和滑块模型1、板块模型此类问题通常是一个小滑块在木板上运动,小物块与长木板是靠一对滑动摩擦力或静摩擦力联系在一起的。
分别隔离选取研究对象,均选地面为参照系,应用牛顿第二定律及运动学知识,求出木板对地的位移等,解决此类问题的关键在于深入分析的基础上,头脑中建立一幅清晰的动态的物理图景,为此要认真画好草图。
在木板与木块发生相对运动的过程中,作用于木块上的滑动摩擦力f 为动力,作用于木板上的滑动摩擦力f为阻力,由于相对运动造成木板的位移恰等于物块在木板左端离开木板时的位移Sm 与木板长度L 之和,而它们各自的匀加速运动均在相同时间t 内完成。
例2 如图3所示,质量M=8kg的小车放在光滑的水平面上,在小车右端加一水平恒力F,F=8N,当小车速度达到1.5m/s时,在小车的前端轻轻放上一大小不计、质量m=2kg的物体,物体与小车间的动摩擦因数μ=0.2,小车足够长,求物体从放在小车上开始经t=1.5s通过的位移大小。
(g取10m/s2)?解答:物体放上后先加速:a1=μg=2m/s2,此时小车的加速度为:??????? ,当小车与物体达到共同速度时:v共=a1t1=v0+a2t1,解得:t1=1s?? ,v共=2m/s,以后物体与小车相对静止:(∵,物体不会落后于小车)物体在t=1.5s内通过的位移为:s=a1t12+v共(t-t1)+ a3(t-t1)2=2.1m解决这类问题的方法是:①研究物块和木板的加速度;②画出各自运动过程示意图;③找出物体运动的时间关系、速度关系、相对位移关系等;④建立方程,求解结果,必要时进行讨论。
要求学生分析木板、木块各自的加速度,要写位移、速度表达式,还要寻找达到共同速度的时间等等在这三个模型中尤其板块模型最为复杂。
其次是传送带模型,一般情况下只需要分析物体的加速度和运动情况,而传送带一般是匀速运动不需另加分析。
最后是追及相遇问题,它只是一个运动学问题并没有牵扯受力分析问题,相对是最简单的,只要位移关系速度公式就可以问题。
传送带和滑块模型(完整资料).doc

【最新整理,下载后即可编辑】传送带模型专题传送带模型是一个经典的力学模型,也是实际生活中广泛应用的一种机械装置,以其为背景的问题都具有过程复杂、条件隐蔽性强的特点,传送带问题也是高考中的常青树,从动力学角度、功能角度进行过多次考查,它自然成为师生关注的热点。
一、难点形成的原因:1、对于物体与传送带之间是否存在摩擦力、是滑动摩擦力还是静摩擦力、摩擦力的方向如何,等等,这些关于摩擦力的产生条件、方向的判断等基础知识模糊不清;2、对于物体相对地面、相对传送带分别做什么样的运动,判断错误;3、对于物体在传送带上运动过程中的能量转化情况考虑不全面,出现能量转化不守恒的错误过程。
二、难点突破策略:在以上三个难点中,第1个难点应属于易错点,突破方法是先正确理解摩擦力产生的条件、方向的判断方法、大小的决定因素等等。
通过对不同类型题目的分析练习,做到准确灵活地分析摩擦力的有无、大小和方向。
第2个难点是对于物体相对地面、相对传送带分别做什么样的运动,判断错误。
该难点应属于思维上有难度的知识点,突破方法是灵活运用“力是改变物体运动状态的原因”这个理论依据,对物体的运动性质做出正确分析,判断好物体和传送带的加速度、速度关系,画好草图分析,找准物体和传送带的位移及两者之间的关系。
如图甲所示,A、B分别是传送带上和物体上的一点,刚放上物体时,两点重合。
设皮带的速度为V0,物体做初速为零的匀加速直线运动,末速为V0,其平均速度为V0/2,所以物体的对地位移x物=20tV,传送带对地位移x传送带=V0t,所以A、B 两点分别运动到如图乙所示的A'、B'位置,物体相对传送带的位移也就显而易见了,x物=2传送带x,就是图乙中的A'、B'间的距离,即传送带比物体多运动的距离,也就是物体在传送带上所留下的划痕的长度。
第3个难点也应属于思维上有难度的知识点。
对于匀速运动的传送带传送初速为零的物体,传送带应提供两方面的能量,一是物体动能的增加,二是物体与传送带间的摩擦所生成的热(即内能),有不少同学容易漏掉内能的转化,因为该知识点具有隐蔽性,往往是漏掉了,也不能在计算过程中很容易地显示出来,尤其是在综合性题目中更容易疏忽。
传送带模型和滑块长木板模型word版
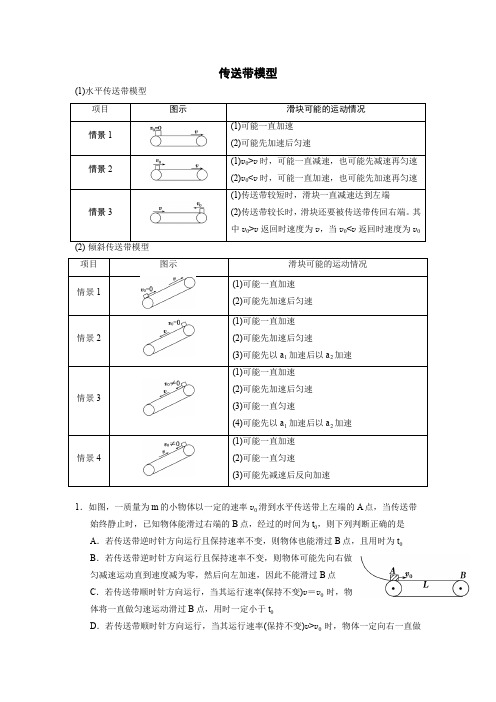
传送带模型(1)水平传送带模型 (1)(2)(1)(2)(1)(2)中(1)(2)(1)(2)(3)(1)(2)(3)(4)(1)(2)(3)1.如图,一质量为m 的小物体以一定的速率v 0滑到水平传送带上左端的A 点,当传送带始终静止时,已知物体能滑过右端的B 点,经过的时间为t 0,则下列判断正确的是A .若传送带逆时针方向运行且保持速率不变,则物体也能滑过B 点,且用时为t 0B .若传送带逆时针方向运行且保持速率不变,则物体可能先向右做匀减速运动直到速度减为零,然后向左加速,因此不能滑过B 点C .若传送带顺时针方向运行,当其运行速率(保持不变)v =v 0时,物体将一直做匀速运动滑过B 点,用时一定小于t 0D .若传送带顺时针方向运行,当其运行速率(保持不变)v >v 0时,物体一定向右一直做匀加速运动滑过B点,用时一定小于t02.如图所示,绷紧的长为6m的水平传送带,沿顺时针方向以恒定速率v1=4m/s运行.一小物块从与传送带等高的光滑水平台面滑上传送带,其速度大小为v2=5m/s.若小物块与传送带间动摩擦因数μ=0.3,重力加速度g=10m/s2,下列说法中正确的是()A.小物块在传送带上先向左做匀减速直线运动,然后向右做匀加速直线运动B.小物块将从传送带左端滑出C.若传送带的速度为6m/s,小物块将从传送带右端滑出,滑出的速度为6m/sD.若传送带的速度为6m/s,小物块将从传送带右端滑出,滑出的速度为5m/s4.物块m在静止的传送带上匀速下滑时,传送带突然转动,传送带转动的方向如图中箭头所示。
则传送带转动后()A.物块将减速下滑B.物块仍匀速下滑C.物块受到的摩擦力变小D.物块受到的摩擦力变大5.如图为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时其运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力) ().A.粮袋到达B点的速度与v比较,可能大,也可能相等或小B.粮袋开始运动的加速度为g(sin θ-μcos θ),若L足够大,则以后将一定以速度v做匀速运动C.若μ≥tan θ,则粮袋从A到B一定一直是做加速运动D.不论μ大小如何,粮袋从A到B一直做匀加速运动,且a>g sin θ2.如图3-2-24所示,传送带两轮A、B的距离L=11 m,皮带以恒定速度v=2 m/s运动,现将一质量为m的物块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,传送带的倾角为α=37°,那么物块m从A端运到B端所需的时间是多少?(g取10 m/s2,cos37°=0.8)滑块木板模型1.如图所示,质量为1 k g的木块A与质量为2 kg的木块B叠放在水平地面上,A、B间的最大静摩擦力2 N,B与地面间的动摩擦因数为0.2.用水平力F作用于B,则A、B保持相对静止的条件是(g=10 m/s2)( )A.F≤12 N B.F≤10 N C.F≤9 N D.F≤6 N2. 物体A叠放在物体B上,B置于光滑水平面上。
(完整word版)高考物理滑块和传送带问题及答案

一、滑块问题1.以下图,有一块木板静止在圆滑且足够长的水平面上,木板质量为M=4kg,长为L=1.4m;木板右端放着一小滑块,小滑块质量为 m=1kg ,其尺寸远小于 L 。
小滑块与木板之间的动摩擦因数为0.4 (g 10m / s2 )(1)现用恒力 F作用在木板 M 上,为了使得 m能从 M 上边滑落下来,问: F大小的范围是什么?(2)其余条件不变,若恒力F=22.8 牛顿,且一直作用在 M 上,最终使得 m能从 M 上边滑落下来。
问:m在M 上边滑动的时间是多大?分析:( 1)小滑块与木板间的滑动摩擦力f Nmg小滑块在滑动摩擦力f作用下向右匀加快运动的加快度a1 f / m g4m / s2木板在拉力 F和滑动摩擦力 f作用下向右匀加快运动的加快度a2( F f ) / M 使 m能从 M 上边滑落下来的条件是a2a1即 (F f ) / M f / m 解得 F( M m) g20N( 2)设 m在 M 上滑动的时间为 t,当恒力 F=22.8N ,木板的加快度a2( F f ) / M 4.7m / s2)小滑块在时间 t内运动位移S1a1t 2/ 2木板在时间 t内运动位移S2a2t 2/ 2因S2S1L即 4.7t 2 / 24t 2 / 2 1.4解得 t2s2.长为 1.5m 的长木板 B 静止放在水平冰面上,小物块 A 以某一初速度从木板 B 的左端滑上长木板 B,直到 A、B 的速度达到同样,此时 A、B 的速度为 0.4m/s,而后 A、B 又一起在水平冰面上滑行了8.0cm 后停下.若小物块 A 可视为质点,它与长木板 B 的质量同样, A、 B 间的动摩擦因数μ1.求:(取 g=10m/s2)v=0.25( 1)木块与冰面的动摩擦因数.A B (2)小物块相关于长木板滑行的距离.(3)为了保证小物块不从木板的右端滑落,小物块滑上长木板的初速度应为多大?分析:( 1) A、 B 一同运动时,受冰面对它的滑动摩擦力,做匀减速运动,加快度v222a g 1.0m/s解得木板与冰面的动摩擦因数μ=0.102s( 2)小物块 A 在长木板上受木板对它的滑动摩擦力,做匀减速运动,加快度a1=μ1g=2.5m/s2小物块 A 在木板上滑动,木块 B 受小物块 A 的滑动摩擦力和冰面的滑动摩擦力,做匀加快运动,有μ1mg-μ2(2m)g=ma2解得加快度 a2=0.50m/s2设小物块滑上木板时的初速度为v10,经时间 t 后 A、 B 的速度同样为 v由长木板的运动得 v=a2t ,解得滑行时间tv0.8s a2小物块滑上木板的初速度v10=v+a t=2.4m/s1小物块 A 在长木板 B 上滑动的距离为s s s v t 1 a t21a t2 0.96m12012122( 3)小物块 A 滑上长木板的初速度越大,它在长木板 B 上相对木板滑动的距离越大,当滑动距离等于木板长时,物块 A 达到木板 B 的最右端,二者的速度相等(设为v′),这类状况下 A 的初速度为保证不从木板上滑落的最大初速度,设为v0.有 v0 t 1a1t 21a2t 2L 22v0 v a1t v a2t由以上三式解得,为了保证小物块不从木板的右端滑落,小物块滑上长木板的初速度不大于最大初速度v02( a1a2 ) L 3.0m/s动力学中的传递带问题一、传递带模型中要注意摩擦力的突变①滑动摩擦力消逝②滑动摩擦力突变成静摩擦力③滑动摩擦力改变方向二、传递带模型的一般解法①确立研究对象;②剖析其受力状况和运动状况,(画出受力剖析图和运动情况图),注意摩擦力突变对物体运动的影响;③分清楚研究过程,利用牛顿运动定律和运动学规律求解未知量。
统考版高考物理总复习 专题三 动力学中的“传送带”和“滑块—滑板”模型

系为xB=xA+L
物块A带动长为L的木板B,物块恰好不
从木板上掉下的临界条件是物块恰好滑
到木板右端时二者速度相等,则位移关
系为xB+L=xA
例2. [2021·全国乙卷,21](多选)水平地面上有一质量为m1的长木板,
木板的左端上有一质量为m2的物块,如图(a)所示.用水平向右的拉力
专题三
动力学中的“传送带”和“滑块—滑板”模型
关键能力·分层突破
关键能力·分层突破
模型一
“传送带”模型
1.模型特点
传送带在运动过程中,会涉及很多的力,是传送带模型难点的原因,
例如物体与传送带之间是否存在摩擦力,是滑动摩擦力还是静摩擦力
等;该模型还涉及物体相对地面的运动以及相对传送带的运动等;该
F作用在物块上,F随时间t的变化关系如图(b)所示,其中F1、F2分别
为t1 、t2 时刻F的大小.木板的加速度a1 随时间t的变化关系如图(c)所
示.已知木板与地面间的动摩擦因数为μ1,物块与木板间的动摩擦因
数为μ2.假设最大静摩擦力均与相应的滑动摩擦力相等,重力加速度大
小为g.则(
)
A.F1=μ1m1g
央.空香皂盒的质量为m=20 g,香皂及香皂盒的总质量为M=100 g,香皂盒与
传送带之间的动摩擦因数为μ=0.4,风洞区域的宽度为L=0.6 m,风可以对香皂
盒产生水平方向上与传送带速度垂直的恒定作用力F=0.24 N,假设最大静摩擦
力等于滑动摩擦力,香皂盒可看作质点,取重力加速度g=10 2 ,试求:
跟进训练
1.如图所示,物块M在静止的足够长的传送带上以速度v0匀速下滑时,传送带突
然启动,方向如图中箭头所示,在此传送带的速度由0逐渐增加到2v0后匀速运动
第4讲传送带模型和滑块—滑板模型 高考物理(北京版)一轮复习

得tmin=
vmin a
=2
1
s=2
s。
1-2 如图所示,倾角为37°、长为l=16 m的传送带,转动速度为v=10 m/s, 在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的物体,物体与 传送带间的动摩擦因数μ=0.5。已知sin 37°=0.6,cos 37°=0.8,g=10 m/s2。 求:
(1)B运动的时间; (2)力F的大小。 答案 (1)3 s (2)26 N
解析 (1)对于B,在未离开A时,其加速度为
aB1=
μ1mg m
=1
m/s2
设经过时间t1后B离开A,离开A后B的加速度为
aB2=-
μ2mg m
=-2
m/s2
设物体B离开A时的速度为vB,有vB=aB1t1和
1 2
a t2 B1 1
1.如图所示,传送带保持1 m/s的速度顺时针转动。现将一质量m=0.5 kg 的物体轻轻地放在传送带的a点上,设物体与传送带间的动摩擦因数μ= 0.1,a、b间的距离L=2.5 m,则物体从a点运动到b点所经历的时间为 (g取
10 m/s2) ( C )
A. 5 s
B.( 6 -1)s
C.3 s
2
得t=4 s (2)传送带逆时针转动,当物体下滑速度小于传送带转动速度时,物体相
对传送带向上运动,则物体所受滑动摩擦力沿传送带向下,设物体的加
速度大小为a1,由牛顿第二定律得
mg sin 37°+μmg cos 37°=ma1
则有a1=
mg
sin
37
μmg m
cos
37
=10
m/s2
设当物体运动速度等于传送带转动速度时经历的时间为t1,位移为x1,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【最新整理,下载后即可编辑】传送带模型专题传送带模型是一个经典的力学模型,也是实际生活中广泛应用的一种机械装置,以其为背景的问题都具有过程复杂、条件隐蔽性强的特点,传送带问题也是高考中的常青树,从动力学角度、功能角度进行过多次考查,它自然成为师生关注的热点。
一、难点形成的原因:1、对于物体与传送带之间是否存在摩擦力、是滑动摩擦力还是静摩擦力、摩擦力的方向如何,等等,这些关于摩擦力的产生条件、方向的判断等基础知识模糊不清;2、对于物体相对地面、相对传送带分别做什么样的运动,判断错误;3、对于物体在传送带上运动过程中的能量转化情况考虑不全面,出现能量转化不守恒的错误过程。
二、难点突破策略:在以上三个难点中,第1个难点应属于易错点,突破方法是先正确理解摩擦力产生的条件、方向的判断方法、大小的决定因素等等。
通过对不同类型题目的分析练习,做到准确灵活地分析摩擦力的有无、大小和方向。
第2个难点是对于物体相对地面、相对传送带分别做什么样的运动,判断错误。
该难点应属于思维上有难度的知识点,突破方法是灵活运用“力是改变物体运动状态的原因”这个理论依据,对物体的运动性质做出正确分析,判断好物体和传送带的加速度、速度关系,画好草图分析,找准物体和传送带的位移及两者之间的关系。
如图甲所示,A、B分别是传送带上和物体上的一点,刚放上物体时,两点重合。
设皮带的速度为V0,物体做初速为零的匀加速直线运动,末速为V0,其平均速度为V0/2,所以物体的对地位移x物=20tV,传送带对地位移x传送带=V0t,所以A、B 两点分别运动到如图乙所示的A'、B'位置,物体相对传送带的位移也就显而易见了,x物=2传送带x,就是图乙中的A'、B'间的距离,即传送带比物体多运动的距离,也就是物体在传送带上所留下的划痕的长度。
第3个难点也应属于思维上有难度的知识点。
对于匀速运动的传送带传送初速为零的物体,传送带应提供两方面的能量,一是物体动能的增加,二是物体与传送带间的摩擦所生成的热(即内能),有不少同学容易漏掉内能的转化,因为该知识点具有隐蔽性,往往是漏掉了,也不能在计算过程中很容易地显示出来,尤其是在综合性题目中更容易疏忽。
突破方法是分析有滑动摩擦力做功转化为内能的物理过程,使“只要有滑动摩擦力做功的过程,必有内能转化”的知识点在头脑中形成深刻印象。
三.传送带模型是高中物理中比较成熟的模型,典型的有水平和倾斜两种情况.一般设问的角度有两个:(1)动力学角度:首先要正确分析物体的运动过程,做好受力情况分析,然后利用运动学公式结合牛顿第二定律,求物体及传送带在相应时间内的位移,找出物体和传送带之间的位移关系.(2)能量角度:求传送带对物体所做的功、物体和传送带由于相对滑动而产生的热量、因放上物体而使电动机多消耗的电能等,常依据功能关系或能量守恒定律求解.传送带模型问题中的功能关系分析(1)功能关系分析:W F=ΔE k+ΔE p+Q.(2)对W F和Q的理解:①传送带的功:W F=Fx传;②产生的内能Q=F f x相对.三.传送带问题类析1.水平传送带上的力与运动情况分析例1.水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查。
如图所示为一水平传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行。
一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动。
设行李与传送带间的动摩擦因数μ=0.1,AB间的距离=2m,g取10 m/ s2。
(1)求行李刚开始运动时所受的滑动摩擦力大小与加速度大小;(2)求行李做匀加速直线运动的时间;(3)如果提高传送带的运行速率,行李就能被较快地传送到B处。
求行李从A处传送到B处的最短时间和传送带对应的最小运行速率。
解析:水平传送带问题研究时,注意物体先在皮带的带动下做匀加速运动,当物体的速度增到与传送带速度相等时,与皮带一起做匀速运动,要想传送时间最短,需使物体一直从A处匀加速到B处。
(1)行李刚开始运动时所受的滑动摩擦力F=μmg以题给数据代入,得F=4N由牛顿第二定律,得F=ma代入数值,得a=1 m / s2(2)设行李做匀加速直线运动的时间为t,行李加速运动的末速度为v=1 m / s,则v=at 代入数据,得t=1 s。
(3)行李从A 处匀加速运动到B 处时,传送时间最短,则代入数据,得t min =2 s 。
传送带对应的最小运行速率v min =at min代入数据,解得v min =2 m / s针对训练1 如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为,传送带的皮带轮的半径为,传送带的上部距地面的高度为,现有一个旅行包(视为质点)以的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为,。
试讨论下列问题:(1)若传送带静止,旅行包滑到B 端时,人若没有及时取下,旅行包将从B 端滑落,则包的落地点距B 端的水平距离为多少?(2)设皮带轮顺时针匀速转动,并设水平传送带长度仍为,旅行包滑上传送带的初速度恒为。
当皮带的角速度值在什么范围内,旅行包落地点距B 端的水平距离始终为(1)中所求的距离?若皮带的角速度,旅行包落地点距B 端的水平距离又是多少?2。
倾斜传送带上的力与运动情况分析传送带沿逆时针转动,与物体接触处的速度方向斜向下,物体初速度为零,所以物体相对传送带向上滑动(相对地面是斜向下运动的),因此受到沿斜面向下的滑动摩擦力作用,这样物体在沿斜面方向上所受的合力为重力的下滑分力和向下的滑动摩擦力,因此物体要做匀加速运动。
当物体加速到与传送带有相同速度时,摩擦力情况要发生变化,同速的瞬间可以看成二者间相对静止,无滑动摩擦力,但物体此时还受到重力的下滑分力作用,因此相对于传送带有向下的运动趋势,若重力的下滑分力大于物体和传送带之间的最大静摩擦力,此时有μ<tan θ,则物体将向下加速,所受摩擦力为沿斜面向上的滑动摩擦力;若重力的下滑分力小于或等于物体和传送带之间的最大静摩擦力,此时有μ≥tan θ,则物体将和传送带相对静止一起向下匀速运动,所受静摩擦力沿斜面向上,大小等于重力的下滑分力。
也可能出现的情况是传送带比较短,物体还没有加速到与传送带同速就已经滑到了底端,这样物体全过程都是受沿斜面向上的滑动摩擦力作用。
例2.如图所示,传送带与水平方向夹37°角,AB 长为L =16m 的传送带以恒定速度v =10m/s 运动,在传送带上端A 处无初速释放质量为m =0.5kg 的物块,物块与带面间的动摩擦因数μ=0.5,求: (1)当传送带顺时针转动时,物块从A 到B 所经历的时间为多少?(2)当传送带逆时针转动时,物块从A 到B 所经历的时间为多少?解析 (1) 当传送带顺时针转动时,设物块的加速度为a ,物块受到传送带给予的滑动摩擦力μmgcos37°方向沿斜面向上且小于物块重力的分力mg sin37°,根据牛顿第二定律,有:mg sin37°- μmgcos37°=ma 代入数据可得: a =2 m/s 2物块在传送带上做加速度为a =2 m/s 2的匀加速运动,设运动时间为t ,t = 代入数据可得:t =4s(2)物块放上传送带的开始的一段时间受力情况如图甲所示,前一阶段物块作初速为0的匀加速运动,设加速度为a 1 ,由牛顿第二定律,有mgsin37°+μmgcos37°=ma 1 , 解得:a 1 =10m/s 2,设物块加速时间为t 1 ,则t 1 =, 解得:t 1=1sa L21a v370 A B因位移s 1==5m <16m ,说明物块仍然在传送带上.设后一阶段物块的加速度为a 2, 当物块速度大于传送带速度时,其受力情况如图乙所示.由牛顿第二定律,有:mg sin37°- μmgcos37°=ma 2 ,解得a 2=2m/s 2 ,设后阶段物块下滑到底端所用的时间为t 2.由L -s =v t 2+a 2t 22/2,解得t 2=1s 另一解-11s 不合题意舍去.所以物块从A 到B 的时间为:t =t 1+t 2=2s针对训练2如图所示,皮带轮带动传送带沿逆时针方向以速度v 0=2 m / s 匀速运动,两皮带轮之间的距离L=3.2 m ,皮带绷紧与水平方向的夹角θ=37°。
将一可视为质点的小物块无初速地从上端放到传送带上,已知物块与传送带间的动摩擦因数μ=0.5,物块在皮带上滑过时能在皮带上留下白色痕迹。
求物体从下端离开传送带后,传送带上留下的痕迹的长度。
(sin37°=0.6,cos37°=0.8,取g=10 m / s 2)3、传送带问题中能量转化情况的分析例3如图所示,水平长传送带始终以速度v=3m/s 匀速运动。
现将一质量为m=1kg 的物块放于左端(无初速度)。
最终物体与传送带一起以3m/s 的速度运动,在物块由速度为零增加至v=3m/s21121t a的过程中,求:(1)由于摩擦而产生的热量。
(2)由于放了物块,带动传送带的电动机消耗多少电能?解析:(1)小物块刚放到传送带上时其速度为零,将相对于传送带向左滑动,受到一个向右的滑动摩擦力,使物块加速,最终与传送带达到相同速度v。
=μmg物块所受的滑动摩擦力为Ff物块加速度加速至v的时间物块对地面位移这段时间传送带向右的位移则物块相对传送带向后滑动的位移根据能量守恒定律知(2)电动机多消耗的电能即物块获得的动能及产生的热量之和,即。
针对训练3如图所示,绷紧的传送带与水平面的夹角θ=30°,=2m/s的速率皮带在电动机的带动下,始终保持v运行。
现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。
求:(1)工件与皮带间的动摩擦因数;(2)电动机由于传送工件多消耗的电能。
4、依托传送带的临界、极值问题例4如图2所示为粮店常用的皮带传输装置,它由两台皮带传输机组成,一台水平传送,AB两端相距3m;另一台倾斜,传送带与地面倾角;CD两端相距4.45m,B、C相距很近.水平部分AB以的速率顺时针转动,将质量为10kg的一袋米匀速传到倾斜的CD部分,米袋与传送带间动摩擦因数为0.5.求:(1)若CD部分不运转,求米袋沿传输带所能上升的最大距离;(2)若要米袋能被送到D端,CD部分运转速度应满足的条件及米袋从C到D所用时间的取值范围。
解析:(1)米袋沿CD上滑时,由牛顿第二定律得:由运动学公式得:代入数值解得:(2)设CD部分运转速度为时,米袋恰能达D点,则:米袋速度减为之前:加速度;位移米袋速度小于之后:加速度;位移又因,解得:即要把米袋送到D点,CD部分速度,且应沿顺时针方向转动。
