迭代法求平方根 - 360文档中心

开平方根的算法

开平方根的算法是一种常用的数学运算方法，可以用于求一个数的平方根。

常见的开平方根算法有以下几种：
1. 迭代法：迭代法是一种基于逐步逼近的方法，即通过对取平方根的数进行逐步逼近，直至误差足够小。

迭代公式为：X(n+1) = (X(n) + S/X(n)) / 2，其中X(n)为第n次逼近的平方根，S为待开平方根的数。

通过多次迭代计算，逼近的结果即为待开平方根的平方根。

2. 牛顿迭代法：牛顿迭代法也是一种逐步逼近的方法，但由于使用了函数的导数，因此迭代速度更快。

迭代公式为：X(n+1) = (X(n) + S/X(n)) / 2，其中X(n)为第n次逼近的平方根，S为待开平方根的数。

通过多次迭代计算，逼近的结果即为待开平方根的平方根。

3. 二分法：二分法是将待开平方根的值按照大小平分为两部分，然后判断目标数属于哪部分，再将该部分继续平分，直至误差足够小。

二分公式为：X(n+1) = (a + b)/2，其中a为待开平方根数的下限，b为待开平方根数的上限，X(n)为第n次逼近的平方根。

通过多次二分计算，逼近的结果即为待开平方根的平方根。

这些算法均可用于开平方根运算，具体使用哪种算法，需要根据具体情况而定。

迭代法求平方根C语言实验报告

实验五: 迭代法求平方根
物理学416班赵增月F12 2011412194 日期: 2013年10月31日
一·实验目的
1.熟练掌握程序编写步骤；
2.学习使用循环结构。

二·实验器材
1.电子计算机；
2.VC6.0
三·实验内容与流程
1.流程图
2.输入以下程序#include<stdio.h>
#include<math.h>
void main()
{
float x2,x1,a;
printf("请输入实数a=");
scanf("%f",&a);
x2=a*0.5;
do
{ x1=x2;
x2=0.5*(x1+a/x1);
}while(fabs(x2-x1)>1e-5);
printf("a 的平方根是: %f\n",x2);
}
四·实验结果
运行显示如下:
请输入实数a=4
a 的平方根是: 2.000000
Press any key to continue
五·实验总结与反思
1.注意循环的初始值的设定, 要保证循环可以进行；
2.循环必须有结束的条件, do while结构中, 不满足循环条件跳出循环。

3.。

平方根的计算方法

平方根的计算方法导言：平方根（square root）是数学中常见的运算，用于求一个数的平方根。

计算平方根可以帮助我们解决很多实际问题，例如在几何学、物理学和工程学中的应用。

本文将介绍几种计算平方根的方法，并探讨它们的优缺点。

一、牛顿法（Newton's Method）牛顿法是一种迭代法，通过不断逼近平方根的值来得到更加精确的结果。

该方法基于牛顿-拉夫逊法则，其迭代公式如下：x_(x+1) = x_x - (x_x^2 - x)/(2x_x)其中，x为需要求平方根的数，x为迭代次数，x_x为迭代过程中的近似值。

通过迭代计算，x_x将逐渐逼近平方根。

牛顿法的优点是收敛速度快、迭代次数较少，适用于求解大部分整数和实数的平方根。

但是，牛顿法需要选择一个合适的初始值，否则可能导致结果偏离真实值。

二、二分法（Bisection Method）二分法是一种基于区间划分的方法，通过不断将区间缩小，逐渐逼近平方根的值。

该方法的思路是，如果一个数的平方大于待求平方根的数，那么这个数的平方根必然在该数左侧；反之，如果一个数的平方小于待求平方根的数，那么这个数的平方根必然在该数右侧。

通过不断将区间一分为二，可以逐步缩小范围。

二分法的优点是简单易实现，并且收敛性较好。

然而，与牛顿法相比，二分法的收敛速度较慢，需要更多的迭代次数。

三、连分数（Continued Fraction）法连分数法是一种将平方根表示为连分数的方法，通过截断连分数的展开式，可以近似计算平方根的值。

以求解正整数的平方根为例，设平方根为一个无限连分数：√x = x_0 + 1/(x_1 + 1/(x_2 + 1/(x_3 + 1/(x_4 + ...))))其中，x_x为连分数的系数。

通过不断截断、逼近连分数的展开，可以得到近似的平方根。

连分数法的优点是可以提供较为准确的结果，并且在计算机实现时能够保持高精度。

然而，连分数法的计算步骤繁琐，对于非整数的平方根计算较为复杂。

用迭代法求a的平方根的原理

用迭代法求a的平方根的原理
迭代法是一种通过反复逐步逼近的方法，用于求解一个方程的近似解。

对于求平方根的问题，迭代法的原理可以描述如下：
1. 假设我们要求一个数a 的平方根，我们可以猜测一个初始的近似解x0。

2. 我们利用这个近似解x0 来更新我们的猜测，并得到一个更好的近似解x1。

这个更新的过程可以使用如下的迭代公式来进行：
x_{k+1} = (x_k + a / x_k) / 2
其中，x_{k+1} 表示新的近似解，x_k 表示上一次的近似解。

3. 我们不断地重复上述的更新过程，直到我们得到一个满足我们要求的精度或近似解为止。

可以通过设定一个迭代次数或者定义一个收敛准则来判断何时停止迭代。

4. 当满足停止条件后，我们得到的近似解x_k 可以作为a 的平方根的近似值。

迭代法的原理在不断逼近的过程中，通过近似解的不断更新，逐渐靠近真实解。

这样的方法常用于求解无法直接求解的方程或函数，包括求解平方根、方程根、最优解等，并且具有广泛的应用。

平方根和立方根的计算

平方根和立方根的计算计算平方根和立方根是数学中常见的运算，它们在各个领域都有重要的应用。

本文将介绍如何计算平方根和立方根，并提供一些实际问题中的应用示例。

一、平方根的计算平方根是指一个数的二次方等于该数的非负实数解。

计算平方根有多种方法，下面将介绍两种常用的方法：试位法和牛顿迭代法。

1. 试位法试位法是通过不断逼近目标值来计算平方根的方法。

以计算一个数a的平方根为例，首先选择一个初始的近似值x0，然后通过迭代的方式逐步逼近真实的平方根。

假设x0是a的一个近似平方根，将x0代入方程x^2 = a，得到x1 = (x0 + a / x0) / 2。

再将x1代入方程，得到x2，以此类推，直到得到满足精度要求的近似平方根。

2. 牛顿迭代法牛顿迭代法也是一种常用的计算平方根的方法。

该方法通过不断求导和迭代来逼近平方根的值。

以计算一个数a的平方根为例，假设初始近似值x0，通过迭代的方式更新近似值，即x1 = (x0 + a / x0) / 2，再将x1代入得到x2，以此类推，直到满足精度要求的近似平方根。

二、立方根的计算立方根是指一个数的三次方等于该数的实数解。

计算立方根也有多种方法，下面介绍两种常用的方法：试位法和二分法。

1. 试位法试位法计算立方根的步骤与计算平方根类似。

假设x0是一个近似值，将x0代入方程x^3 = a，得到x1 = (2 * x0 + a / (x0^2)) / 3。

再将x1代入得到x2，以此类推，直到满足精度要求的近似立方根。

2. 二分法二分法是一种通过不断二分区间来逼近立方根的方法。

假设a是待求的数，选择一个区间[x, y]，使得x^3 <= a <= y^3。

然后计算区间的中点m = (x + y) / 2，如果m^3与a的差值足够小，则可以认为m就是近似的立方根。

否则，根据与a的大小关系调整区间，并重复以上步骤，直到满足精度要求的近似立方根。

三、应用示例平方根和立方根的计算在实际问题中有广泛的应用，下面列举一些例子：1. 几何学中的应用：计算物体的体积、表面积等需要用到平方根和立方根的问题。

牛顿迭代法求平方根

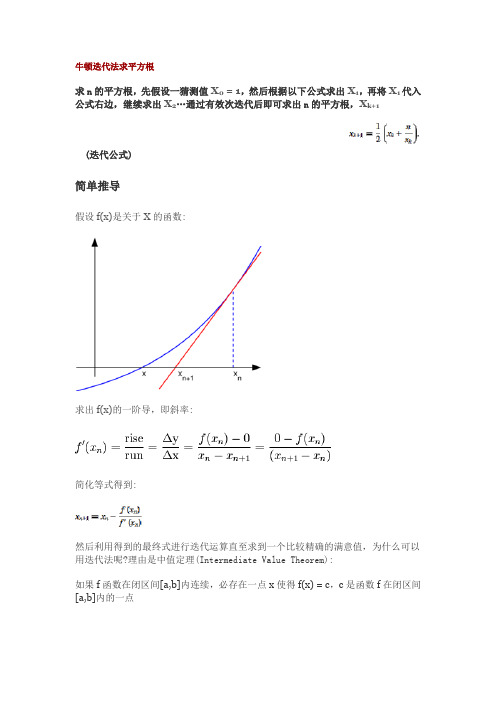
牛顿迭代法求平方根求n的平方根，先假设一猜测值X0 = 1，然后根据以下公式求出X1，再将X1代入公式右边，继续求出X2…通过有效次迭代后即可求出n的平方根，X k+1(迭代公式)简单推导假设f(x)是关于X的函数:求出f(x)的一阶导，即斜率:简化等式得到:然后利用得到的最终式进行迭代运算直至求到一个比较精确的满意值，为什么可以用迭代法呢?理由是中值定理(Intermediate Value Theorem):如果f函数在闭区间[a,b]内连续，必存在一点x使得f(x) = c，c是函数f在闭区间[a,b]内的一点我们先猜测一X初始值，例如1，当然地球人都知道除了1本身之外任何数的平方根都不会是1。

然后代入初始值，通过迭代运算不断推进，逐步靠近精确值，直到得到我们主观认为比较满意的值为止。

例如要求768的平方根，因为252 = 625，而302 = 900，我们可先代入一猜测值26，然后迭代运算，得到较精确值:27.7128。

回到我们最开始的那个”莫名其妙”的公式，我们要求的是N的平方根，令x2 = n，假设一关于X的函数f(x)为:f(X) = X2 - n求f(X)的一阶导为:f'(X) = 2X代入前面求到的最终式中:X k+1 = X k - (X k2 - n)/2X k化简即得到我们最初提到的那个求平方根的神奇公式了:用泰勒公式推导我之前介绍过在The Art and Science of C一书中有用到泰勒公式求平方根的算法，其实牛顿迭代法也可以看作是泰勒公式(Taylor Series)的简化，先回顾下泰勒公式:仅保留等式右边前两项:令f(X0+ε) = 0，得到:再令X1 = X0+ ε0，得到ε1…依此类推可知:转化为:引申从推导来看，其实牛顿迭代法不仅可以用来求平方根，还可以求立方根，甚至更复杂的运算。

同样，我们还可以利用pascal语言来实现下那个最简单的求平方根的公式(尽管我们可以直接用sqrt()完成)program asd (input,output);vara,x,n,i:real;beginwriteln('Please input a!');read(a);x:=1;n:=1000;i:=1;while i<=n dobeginx:=(x+(a/x))/2;i:=i+1;end;writeln(x:10:3);readln;end.2007年赣州市信息学奥赛高中组上机测试题第2题：编程求平方根（15分）任给常数b，编程求b的算术平方根，要求准确到小数点后3位，注意不能调用高级语言系统的开平方根函数。

C语言复习---迭代法，牛顿迭代法，二分法求根

C语⾔复习---迭代法，⽜顿迭代法，⼆分法求根⼀：⽤迭代法求 x=√a。

求平⽅根的迭代公式为：X(n+1)= (Xn+a/Xn) /2。

#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆：⽤求⽅程在1.5附近的根（2x3-4x2+3x-6=0）例：⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三：⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0（这是前提，选取的区间必须满⾜这个条件）,给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。

平方根和立方根的计算方法

平方根和立方根的计算方法在数学中，平方根和立方根是基本的运算之一。

计算平方根和立方根的方法有多种，下面将介绍几种常见的计算方法。

一、平方根的计算方法：1. 牛顿迭代法牛顿迭代法是一种常用的求解方程近似解的方法，也可以用来计算平方根。

设要计算的数为x，初始估计值为a，根据迭代公式：a = (a + x / a) / 2反复迭代，直到a的平方与x的差小于预设的误差范围，即可得到x的平方根。

2. 二分法二分法是一种逐步逼近的方法。

设要计算的数为x，初始估计值为a，设区间左端点为low，右端点为high，mid为区间中点，计算mid 的平方与x的差，若差小于预设的误差范围，则mid即为所求的平方根；若差大于0，则将区间缩小至low和mid之间，否则将区间缩小至mid和high之间。

反复迭代，直到满足条件的mid被找到。

二、立方根的计算方法：1. 二分法与计算平方根的二分法类似，设要计算的数为x，初始估计值为a，设区间左端点为low，右端点为high，mid为区间中点，计算mid的立方与x的差，若差小于预设的误差范围，则mid即为所求的立方根；若差大于0，则将区间缩小至low和mid之间，否则将区间缩小至mid和high之间。

反复迭代，直到满足条件的mid被找到。

2. 牛顿迭代法与计算平方根的牛顿迭代法类似，设要计算的数为x，初始估计值为a，根据迭代公式：a = (2 * a + x / (a * a)) / 3反复迭代，直到a的立方与x的差小于预设的误差范围，即可得到x的立方根。

三、总结：平方根和立方根的计算方法可以通过牛顿迭代法和二分法来实现。

牛顿迭代法通过逐步逼近求解方程的近似解，而二分法则通过逐步缩小区间来逼近方程的解。

选择适当的方法，根据需要的精度和效率来计算平方根和立方根，可以得到准确的结果。

以上就是关于平方根和立方根的计算方法的介绍。

通过牛顿迭代法和二分法，我们可以方便地计算平方根和立方根，为数学和科学研究提供了便利。

求平方根的算法公式

求平方根的算法公式平方根这玩意儿，在数学里可是个挺重要的角色。

咱们先来说说啥是平方根。

比如说，4 的平方根是啥？咱知道 2×2 = 4，还有 -2× -2 也等于 4，所以 4 的平方根就是 ±2 。

那怎么求一个数的平方根呢？这就得靠算法公式啦！求平方根的算法公式，常见的有牛顿迭代法。

这名字听着挺高大上，其实原理没那么复杂。

咱来一步步拆解。

假设咱要求一个数 a 的平方根，先随便猜一个数 x₀作为初始值。

然后按照下面这个公式来不断更新 x 的值：x₁ = (x₀ + a / x₀) / 2 。

一直重复这个过程，x 的值就会越来越接近 a 的平方根。

就像我之前教过的一个学生，叫小李。

这孩子一开始对这个公式那是一头雾水。

我就跟他说：“小李啊，你就把这当成是一个解谜的游戏，咱们要一步步找到那个正确的答案。

”小李瞪着大眼睛，一脸迷茫。

我就拿 9 这个数给他举例。

咱先猜x₀ = 3 ，然后按照公式算：x₁ = (3 + 9 / 3) / 2 = 3 。

哟呵，一次就猜对啦，不过这是运气好。

那再试试 10 。

咱还是先猜 x₀ = 3 ，x₁ = (3 + 10 / 3) / 2 ≈ 3.1667 。

再算一次 x₂ = (3.1667 + 10 / 3.1667) / 2 ≈ 3.1623 。

就这样一直算下去，就能越来越接近 10 的平方根啦。

小李跟着我一步一步算，慢慢地好像有点开窍了。

后来他自己做题的时候，一开始还是会出错，不是计算粗心，就是公式用错。

但这孩子有股子倔劲儿，不停地练习。

经过一段时间，小李已经能熟练运用这个公式求平方根了。

有一次课堂小测验，有道求平方根的难题，好多同学都没做出来，小李不仅做出来了，答案还全对！所以说啊，这个求平方根的算法公式，只要多练习，多琢磨，就没那么难。

就像咱们做其他事情一样，一开始可能觉得困难重重，但只要坚持下去，总能找到解决的办法。

在数学的世界里，平方根的算法公式就像是一把神奇的钥匙，能帮我们打开很多难题的大门。

牛顿迭代法平方根fpga

牛顿迭代法平方根fpga
牛顿迭代法是一种逼近算法，可以用来求解函数的零点或函数的解，其原理是通过不断逼近函数的根，直到找到根的近似值。

在本文中，我们将介绍如何使用牛顿迭代法来计算平方根，并将其应用于FPGA实现中。

平方根是一个重要的数学运算，广泛应用于科学、工
程和计算机科学等领域。

虽然计算平方根的方法有很多种，但牛顿迭代法是其中一种最常用的方法之一。

在本文中，我们将介绍如何使用牛顿迭代法来计算平方根的方法，并将其应用于FPGA实现中。

使用牛顿迭代法计算平方根的基本思路是，选择一个初始值x0，并通过不断迭代逼近函数的根，直到满足
一定的精度要求为止。

对于平方根函数f(x) = x^2 - a，其迭代公
式可以写成：
xn+1 = 1/2(xn + a/xn )
其中，xn 表示第n次迭代的近似值，xn+1 表示第n+1次迭代的近似值，a表示待求平方根的数。

在FPGA实现中，我们可以使用Verilog HDL来描述牛顿迭代法
的运算逻辑，并将其实现在FPGA上。

具体实现过程包括：
1. 定义输入输出端口：定义输入端口a和输出端口x。

2. 初始化寄存器：定义一个寄存器，用于存储迭代计算过程中
的中间值，并将其初始化为输入寄存器a的值。

3. 迭代计算：使用上述公式进行迭代计算，并将每次计算的结
果存储到寄存器中。

4. 输出计算结果：将最终计算得到的平方根值输出到输出端口x。

通过将牛顿迭代法实现在FPGA上，可以实现高效的计算平方根的功能。

这种实现方式具有低延迟、高并行度和可重构性等优点，可广泛应用于数字信号处理、图像处理和机器学习等领域。

sqrt方法(一)

sqrt方法(一)sqrt相关方法简介在数学和编程中，sqrt用于计算一个数的平方根。

计算平方根的方法有多种，本文将介绍几种常用的方法。

方法一：牛顿迭代法1.初始化一个猜测值x作为平方根的近似值。

2.使用迭代公式x = (x + n / x) / 2来更新猜测值x，其中n是待求平方根的数字。

3.重复步骤2，直到x的平方接近于n。

方法二：二分查找法1.初始化左边界left为0，右边界right为n。

2.当左边界小于等于右边界时，执行以下步骤：–计算中间值mid，mid = (left + right) / 2。

–如果mid的平方接近于n，则返回mid作为平方根。

–如果mid的平方大于n，则将右边界更新为mid-1。

–如果mid的平方小于n，则将左边界更新为mid+1。

3.返回left作为平方根。

方法三：使用数学库函数1.在许多编程语言中，都提供了sqrt函数来计算平方根。

只需要调用该函数，并传入待求平方根的数字作为参数，即可得到结果。

方法四：二进制近似法1.将n转换为二进制表示。

2.初始化一个近似值x为1。

3.对每一位的二进制数字进行迭代处理：–x的平方不断逼近n。

–如果该位为1，则将x更新为x = (x + n / x) / 2，否则保持不变。

4.重复步骤3，直到迭代收敛。

5.返回x作为平方根。

方法五：插值法1.将平方根的求解问题转化为多项式的求解问题。

2.构造一个具有稀疏系数的多项式。

3.使用插值法来求解多项式的根，即可得到平方根。

结论根据不同的场景和需求，选择合适的方法来计算平方根。

牛顿迭代法和二分查找法是比较常用的方法，而使用数学库函数则是最简单快速的方式。

二进制近似法和插值法则是更为复杂的求解方式，适用于特定的问题。

在实际应用中，可以根据具体情况进行选择。

方法一：牛顿迭代法1.初始化一个猜测值x作为平方根的近似值。

2.使用迭代公式x = (x + n / x) / 2来更新猜测值x，其中n是待求平方根的数字。

如何求解平方根和立方根

如何求解平方根和立方根平方根和立方根是数学中常见的运算操作。

在解决实际问题或进行数学计算时，求解平方根和立方根是很常见的需求。

本文将介绍如何求解平方根和立方根，并提供一些实用的计算方法。

一、求解平方根平方根指的是一个数的平方等于给定数的算术根。

求解平方根有多种方法，下面将介绍其中的两种常见方法。

1. 牛顿迭代法牛顿迭代法是一种用于逼近函数零点的方法，可以用来计算平方根。

设我们要求解一个非负数x的平方根，首先猜测一个近似值y，然后通过以下迭代公式不断改进y的值，直到满足精度要求：y = (y + x / y) / 2其中，x是被开方的数，y是近似的平方根。

2. 二分查找法二分查找法是一种常用的搜索算法，也可以用来求解平方根。

对于非负数x，我们将其平方根的范围定在0到x之间。

假设l和r分别是这个范围的左右边界，我们可以通过不断用中间值m取代l或r，并判断m的平方与x的大小关系，来逐渐逼近平方根的值：当m的平方小于x时，将l更新为m；当m的平方大于x时，将r更新为m；当m的平方等于x时，m即为x的平方根。

二、求解立方根立方根指的是一个数的立方等于给定数的算术根。

求解立方根也有多种方法，下面将介绍一种常见的方法。

1. 牛顿迭代法利用牛顿迭代法我们同样可以求解立方根。

假设我们要求解一个非负数x的立方根，首先猜测一个近似值y，然后通过以下迭代公式不断改进y的值，直到满足精度要求：y = (2 * y + x / (y * y)) / 3其中，x是被开立方的数，y是近似的立方根。

不断迭代直到y的值不再发生显著变化。

除了牛顿迭代法，还可以通过二分查找法以及其他数值方法来求解立方根。

不同的方法适合不同的问题和精度要求。

总结求解平方根和立方根是数学中常见的运算操作。

本文介绍了两种常用的方法来求解平方根：牛顿迭代法和二分查找法，以及一种常用的方法来求解立方根：牛顿迭代法。

根据实际问题和精度要求，可以选择合适的方法来求解平方根和立方根。

开平方根的计算方法

开平方根的计算方法开平方根是数学中一个常用的计算方法，用来求一个非负数的平方根。

开平方根的计算方法主要有两种，一种是通过数学运算推导，另一种是通过数值近似计算。

1.通过数学运算推导的方法：(1)数学定理法：比如利用牛顿迭代法、二分法等数学定理来计算平方根。

以下是其中较为常用的方法：-牛顿迭代法：设f(x)=x^2-n，其中n是需要开平方根的数。

根据泰勒公式，可得f(x)在x=a点附近的近似表达式为f(a)+f'(a)(x-a)，将其求根可以近似表示为x-f(a)/f'(a)=x-(x^2-n)/(2x)=(x+n/x)/2、通过迭代计算，可以得到平方根的近似值。

-二分法：设f(x)=x^2-n，其中n是需要开平方根的数。

在区间[0,n]内，不断取中点判断f(x)的正负性，逐渐缩小区间直到找到平方根的近似值。

(2)泰勒级数法：利用泰勒级数展开来计算平方根。

设函数f(x)=x^2-n，其中n是需要开平方根的数。

若将f(x)在x=a处展开为泰勒级数，可以得到f(x)的一个逼近公式，将其反解即可得到平方根的近似值。

(3)其他方法：除了上述方法外，还有一些使用特殊函数（如函数幂级数）或变形等数学运算的方法。

例如，可以通过利用欧拉恒等式公式，将开平方根的计算转化为对复数的求解，进而得到结果。

2.通过数值近似计算的方法：(1)迭代法：通过不断迭代计算，逼近原数的平方根。

常用的迭代方法有牛顿迭代法和二分法，即前文提到的通过数学运算推导的方法。

(2)逼近算法：通过设定初始值和精度要求，利用逼近算法不断逼近原数的平方根。

常用的逼近算法有泛化平方根算法、二次逼近算法等。

这些开平方根的计算方法都是在数学理论的基础上推导和运用而成的，可以根据实际需要选择适合的方法。

当然，对于计算机来说，还可以利用编程语言中提供的内置函数来计算平方根，如C语言中的sqrt(函数、Python语言中的math.sqrt(函数等。

平方根计算方法

平方根计算方法平方根是数学中常见的一个概念，它代表了一个数的平方根。

在日常生活和工作中，我们经常会用到平方根，比如在测量、计算等方面。

那么，如何准确地计算一个数的平方根呢？接下来，我将向大家介绍几种常见的平方根计算方法。

首先，我们来介绍一种简单的方法——牛顿迭代法。

牛顿迭代法是一种通过不断逼近的方法来求解方程的数值近似解的算法。

对于求一个数a的平方根，我们可以将其转化为求解方程f(x)=x^2-a=0的正实根。

然后，通过不断迭代计算x的值，最终得到a的平方根。

这种方法在计算机程序中应用广泛，具有较高的精度和稳定性。

其次，我们可以使用二分法来计算平方根。

二分法是一种不断将区间二等分的方法来逼近方程的根。

对于求一个数a的平方根，我们可以将其转化为求解方程f(x)=x^2-a=0的正实根。

然后，我们可以选取一个初始的区间[a, b]，不断将区间二等分，直到得到一个足够精确的解。

这种方法简单直观，适用于手工计算和简单程序设计。

另外，我们还可以利用泰勒展开来计算平方根。

泰勒展开是一种将一个函数在某点附近展开成无穷级数的方法。

对于求一个数a的平方根，我们可以利用泰勒展开将平方根函数在某一点附近展开成无穷级数，然后通过截断级数来近似计算平方根的值。

这种方法在数学分析和科学计算中有着广泛的应用。

最后，我们还可以使用牛顿-拉弗森方法来计算平方根。

牛顿-拉弗森方法是一种通过不断迭代的方法来逼近方程的根的算法。

对于求一个数a的平方根，我们可以将其转化为求解方程f(x)=x^2-a=0的正实根。

然后，通过不断迭代计算x的值，最终得到a的平方根。

这种方法在实际计算中具有较高的效率和精度。

综上所述，平方根是数学中常见的一个概念，我们可以通过多种方法来计算一个数的平方根。

不同的方法适用于不同的场景，我们可以根据实际需求选择合适的方法来计算平方根。

希望以上介绍的几种方法能够对大家有所帮助，谢谢阅读！。

求平方根算法

求平方根算法求平方根是数学中常见的计算问题。

我们都知道，平方根就是一个数的二次方等于它，例如，4的平方根就是2，因为2的平方等于4。

在计算机科学中，求平方根也是一个经典的问题。

那么，如何实现一个高效的平方根算法呢？本文将深入探讨这个问题。

首先，我们需要明确一个概念，就是牛顿迭代法。

牛顿迭代法是一种用于求解方程的数值方法，其基本思想是通过不断迭代，逐步逼近方程的根。

在求平方根的问题中，我们可以将方程f(x) = x^2 - a转换为求解f(x) = 0的问题，其中a是待求解的数。

然后，我们可以使用牛顿迭代法来逼近方程f(x) = 0的根。

具体地，我们可以设初始值x0为a的一半，即x0 = a/2。

然后，我们可以通过以下公式来迭代计算下一个值x1：x1 = (x0 + a/x0)/2接着，我们可以用同样的公式来计算x2，x3，x4，以此类推，直到计算出一个足够精确的平方根。

具体来说，我们可以通过比较相邻两个值的差的绝对值是否小于一个给定的精度值来判断是否达到了目标精度。

当然，牛顿迭代法并不是求平方根的唯一方法。

还有一些其他的算法，例如二分法、泰勒展开法等等。

但是，相比之下，牛顿迭代法具有更快的收敛速度和更高的精度。

最后，我们需要注意一个问题，就是在计算过程中可能会出现除以零的情况。

为了避免这种情况，我们可以在迭代之前先进行一些特判，例如判断a是否为负数或零，或者直接返回a本身作为其平方根。

综上所述，求平方根是一个经典的计算问题，牛顿迭代法是其中一种高效的解决方法。

在实际应用中，我们需要根据具体情况选择合适的算法，并注意算法的实现细节，以保证计算的精度和效率。

牛顿迭代法求平方根原理

牛顿迭代法求平方根原理牛顿迭代法，听起来挺高大上的，但其实它就像是在教你怎么用小聪明来解决问题。

想象一下，你要找一个数字的平方根，就像在找藏在沙子里的宝藏，千辛万苦就是想挖到它。

别担心，牛顿大叔来了，带着他的智慧，告诉我们其实这事儿并没有那么复杂。

你只需要一开始有个粗略的猜测，就像你去餐馆点菜，随便选了道菜，结果发现味道意外地不错。

牛顿迭代法的核心就是不断调整你的猜测，让它越来越接近那个真正的平方根。

具体是怎么操作的呢？你得有个初始值，随便找个接近的数字。

比如说你想找16的平方根，随便说个4就行，虽然心里知道可能还差得远。

接下来呢，牛顿就教你一个公式，这个公式像是你找到的那把钥匙，能帮你打开通往答案的大门。

公式里有分子和分母，但别担心，这可不是高深的数学，简单的说就是用你的初始值和目标值来做个小算式。

慢慢地，你的猜测会变得更准确，就像你练习游泳，开始时在水里扑腾，久而久之就能自如地游来游去。

接下来你可能会问，这个过程到底要重复几次呢？重复的次数就像你找美食的过程，越多越能发现好东西。

每一次计算都让你离目标更近，就像是在一条漫长的路上行驶，你的导航系统在不断更新。

没错，牛顿迭代法就像是你身边那个爱纠正你方向的朋友，总是提醒你，哎，别走错了，往左一点，再往右一点，直到你找到那个隐藏的“宝藏”。

说到这里，有的人可能会觉得这种方法太复杂，算来算去的，容易搞混。

其实不然，牛顿法就像是在打怪升级，刚开始可能会遇到各种小怪，稍微用点力就能干掉。

等你掌握了窍门，每次的调整就像是轻松击败敌人一样简单。

要是中途遇到难关，别着急，换个角度想想，可能答案就在眼前，只是你没有看到而已。

牛顿迭代法不仅仅适用于平方根，它的应用范围可广了去了。

很多数学问题都能用这个思路去解决，像是解方程、优化问题，甚至在科学和工程领域也是个大杀器。

想象一下，科学家们在实验室里，面对复杂的数据，他们可能也在使用这样的算法来寻找最佳解法，简直就是数学界的瑞士军刀，处处可用。

迭代法求平方根公式

迭代法求平方根公式
平方根是在数学中经常使用的基本概念，而求平方根的方法也有很多种。

其中一种较为常用的方法是迭代法。

迭代法求平方根的公式如下：
设一个数a的平方根为x，则可以得到以下迭代公式：
x1 = (x0 + a/x0)/2
x2 = (x1 + a/x1)/2
……
xn+1 = (xn + a/xn)/2
通过迭代，取得的值逐渐逼近平方根的实际值。

当取得的值与实际值相差足够小时，即可停止迭代，得到近似值。

这种方法的优点在于简单易实现，同时可以通过迭代次数来控制精度。

当然，迭代法求平方根也存在一些缺点，比如可能会出现无限循环或者收敛速度较慢等问题。

因此，在具体使用时需要结合实际情况进行判断和调整。

平方根计算方法

平方根计算方法有许多数学问题都需要计算平方根，无论是为了求解几何问题，还是算术问题，或者是为了量化某一概念。

平方根计算在数学和科学领域都扮演着很重要的角色，而且在工程领域也有着相当重要的作用。

因此，本文将讨论如何计算平方根。

一般来说，平方根的计算可以通过两种方法完成，即解方程法和迭代法。

首先，我们来看看解方程法。

在解方程法中，我们需要将求平方根的问题转换为一个方程，然后根据这个方程的条件来求解。

重要的是，这个方程要求求解的数据要满足一定的特征，否则求解就会出现问题。

其次，我们来看看迭代法。

迭代法是一种使用计算机程序来计算平方根的方法，它通过重复运行程序来自动计算。

这种方法比解方程法更容易，但是计算准确度可能会下降。

这种方法通常采用牛顿-拉夫逊迭代法，它指出，当一个近似值可以不断迭代求出更加精确的结果时，数值计算的精度就可以不断提高。

此外，还有一些其他的方法可以用来计算平方根，比如二分法，梯度下降法以及折半法。

二分法是指将要求求解的数据从1到n之间划分成几份，然后求解这几份数据中各自的平方根。

梯度下降法则是通过不断减小一个变量来计算平方根。

而折半法则是将待求的数据的平方根的值猜测为比实际值小的一个字，并判断其误差值，然后根据误差值不断调整平方根的值，直到误差值为零为止。

上述的方法都可以用来计算平方根，但是，每一种方法都有各自的优缺点，因此，我们在实际应用时，要根据具体需求来选择不同的方法。

总之，平方根是一种很重要的数学运算，可以通过解方程法、迭代法、二分法、梯度下降法以及折半法等不同的方法来计算。

但无论使用何种方法，都必须确保结果的准确性。