图论与网络优化课程设计_Matlab实现
超全图论matlab程序-可解决图论方面的绝大多数问题

程序三:有向图关联矩阵和邻接矩阵互换算法
function W=mattransf(F,f) if f==0 m=sum(sum(F)); n=size(F,1); W=zeros(n,m); k=1; for i=1:n for j=i:n if F(i,j)~=0 W(i,k)=1; W(j,k)=-1; k=k+1; end end end elseif f==1 m=size(F,2); n=size(F,1); W=zeros(n,n); for i=1:m a=find(F(:,i)~=0); if F(a(1),i)==1 W(a(1),a(2))=1; else W(a(2),a(1))=1; end end else fprint('Please imput the right value of f'); end W;
第二讲:最短路问题
程序一:Dijkstra算法(计算两点间的最短路)
图论与网络优化-刘彬农庆琴

图与网 2 络基本
概念
连通性?
图的连通度、边连通度、块的概念 络进行建模的实
2 与基本性质
际问题 (包括工
图的搜索与连通性判定算法
件排序问题)
最短路 (SP)?
2
最短路问题、Dijkstra 算法和 Floyd 用数学软件求解
算法
最短路问题
3
树
什么是树 (Tree)?
最小支撑树 (MCST)?
2 树的定义与基本性质、割边、割点 1.MCST 其他算 法;
2. 主要参考书: [1] 图论与网络流理论,高随祥,高等教育出版社,2009.01. [2] Introduction to Graph Theory (Second Edition), Douglas B. West, Prentice Hall,
2001.(中译本:图论导引,李建中、骆吉周译,机械工业出版社,2006)
图论与网络优化以图和网络为研究对象,通过对事物间的联系、相互影响进行网 络建模,对网络结构以及建立在网络结构上行为决策进行研究。本课程主要介绍图论 与网络优化的基本概念、重要理论和算法以及理论的应用,主要包括以下三部分内容:
1)图的概念与结构:树、连通度、Euler 环游与 Hamilton 圈、匹配、独立集与团、 平面图染色等;
-2-
四、教材与主要参考书
1. 教材: [1] Graph theory with applications, J.A. Bondy and U.S.R. Murty, The Macmillan Press
Ltd, New York, 1976.(中译本:图论及其应用,科学出版社,1984) [2] 运筹学(第 4 版),运筹学教材编写组,清华大学出版社,2012.09。
图论与网络优化问题的解决方法研究与教学设计

优化网络
遗传算法可用于优化网络 结构 有效解决网络优化问题
总结
网络优化算法包括贪心算法、动态规划算法、模 拟退火算法和遗传算法。这些算法在解决网络优 化问题时各具特点,能够有效地寻找最优解。学 习和掌握这些算法,对于解决实际的网络优化问 题具有重要的意义。
● 05
第五章 应用案例分析
物流配送优化
人工智能 大数据
研究深入
图论算法 解决实际问题
应用领域
多领域应用 产生更多成果
技术创新
推动学术研究 促进技术发展
感谢
01 导师支持
学术指导
02 同事帮助
团队合作
03 专家学者
学术引领
感谢观看
最小生成树算法
Prim算法 Kruskal算法
最大流算法
Ford-Fulkerson算法 Edmonds-Karp算法
最小费用最大流算法
Zkw费用流算法 Successive Shortest Path算法
图的应用
网络优化
通过图论解决网 络流、最短路径
等问题
物流路径规 划
利用图算法规划 最优的物流路径
图论与网络优化问题的解决 方法研究与教学设计
汇报人:XX
2024年X月
第1章 简介 第2章 图的基本概念 第3章 网络流问题 第4章 网络优化算法 第5章 应用案例分析 第6章 总结与展望
目录
● 01
第1章 简介
图论与网络优化 问题的重要性
图论与网络优化问题 是数学领域中的重要 分支,研究的内容涵 盖图的性质、网络的 优化和算法设计等方 面。通过对实际生活 中的物流规划、通信 网络设计等问题进行 研究,可以有效提高 资源利用率,降低成 本,提高效率。
matlab课程设计完整版

matlab课程设计完整版一、教学目标本节课的教学目标是让学生掌握MATLAB的基本语法和操作,能够利用MATLAB进行简单的数学计算和数据分析。
具体来说,知识目标包括:了解MATLAB的历史和发展,掌握MATLAB的基本语法和数据类型,熟悉MATLAB的工作环境。
技能目标包括:能够使用MATLAB进行矩阵运算,编写简单的MATLAB脚本程序,进行数学计算和数据分析。
情感态度价值观目标包括:培养学生对科学计算软件的兴趣,增强学生的动手能力和团队协作能力。
二、教学内容本节课的教学内容主要包括MATLAB的基本语法和操作。
首先,介绍MATLAB的历史和发展,使学生对MATLAB有一个整体的认识。
然后,讲解MATLAB的基本语法和数据类型,如矩阵的创建和操作,数据的输入和输出等。
接着,介绍MATLAB的工作环境,包括命令窗口、变量浏览器和脚本文件等。
最后,通过实例演示和练习,使学生能够熟练使用MATLAB进行简单的数学计算和数据分析。
三、教学方法为了达到本节课的教学目标,将采用讲授法、实践法和讨论法等多种教学方法。
首先,通过讲授法向学生介绍MATLAB的基本概念和语法。
然后,通过实践法,让学生动手操作MATLAB软件,进行实际的数学计算和数据分析。
在实践过程中,引导学生进行讨论,分享自己的心得和经验,互相学习和进步。
最后,通过讨论法,对学生的学习情况进行总结和评价,及时调整教学策略。
四、教学资源为了保证本节课的教学质量,将准备教材、多媒体资料和实验设备等多种教学资源。
教材是学生学习的基础,多媒体资料可以丰富教学手段,实验设备则是学生进行实践操作的重要工具。
此外,还将利用网络资源,如在线教程和讨论区,为学生提供更多的学习资料和实践机会。
五、教学评估本节课的教学评估将采用多元化的评价方式,以全面、客观、公正地评估学生的学习成果。
评估方式包括平时表现、作业和考试等。
平时表现主要考察学生的课堂参与度和团队合作能力,通过观察和记录学生在课堂上的表现来进行评估。
matlab的教学课程设计

matlab 的教学课程设计一、课程目标知识目标:1. 掌握MATLAB的基础知识,包括数据类型、矩阵运算、程序流程控制等;2. 学会使用MATLAB进行数据可视化、图像处理、数值计算等操作;3. 了解MATLAB在工程领域的应用,并能结合所学专业进行简单的数据分析。
技能目标:1. 能够熟练运用MATLAB编写程序,解决实际问题;2. 学会使用MATLAB进行数据导入、导出,以及与Excel、Word等软件的数据交互;3. 培养学生运用MATLAB进行科学计算和工程问题求解的能力。
情感态度价值观目标:1. 培养学生对MATLAB编程的兴趣和热情,激发学生主动探索精神;2. 培养学生严谨的科学态度,提高学生的团队协作能力;3. 引导学生认识到MATLAB在现代工程技术中的重要性,树立正确的价值观。
课程性质:本课程为实践性较强的课程,旨在培养学生的编程能力和实际应用能力。
学生特点:学生具备一定的数学基础和编程兴趣,但对MATLAB编程可能较为陌生。
教学要求:结合学生特点和课程性质,注重理论与实践相结合,以案例教学为主,培养学生的实际操作能力。
在教学过程中,关注学生的个体差异,鼓励学生提问、讨论,提高学生的参与度和积极性。
通过课程学习,使学生能够独立完成MATLAB程序编写,解决实际问题。
二、教学内容1. MATLAB基础知识:数据类型、矩阵运算、程序流程控制等;教材章节:第一章 MATLAB概述,第二章 MATLAB基础知识。
2. 数据可视化与图像处理:绘图函数、图像处理基本操作等;教材章节:第三章 数据可视化,第四章 图像处理。
3. 数值计算:线性方程组求解、数值积分、插值等;教材章节:第五章 数值计算。
4. MATLAB在实际工程中的应用:结合所学专业,进行数据分析与处理;教材章节:第六章 MATLAB在工程中的应用。
5. MATLAB与其他软件的数据交互:数据导入、导出,与Excel、Word等软件的数据交互;教材章节:第七章 MATLAB与其他软件的数据交互。
网络优化matlab课程设计

网络优化matlab课程设计一、课程目标知识目标:1. 理解网络优化的基本概念和原理,掌握运用MATLAB进行网络优化的基本方法。
2. 学会使用MATLAB软件构建网络模型,分析网络性能指标,并针对问题提出优化策略。
3. 掌握运用MATLAB进行网络优化求解的算法和步骤,能够独立完成网络优化问题的求解。
技能目标:1. 培养学生运用MATLAB软件解决实际网络优化问题的能力。
2. 培养学生分析问题、提出解决方案的能力,提高逻辑思维和解决问题的技巧。
3. 培养学生的团队协作和沟通能力,通过小组讨论和实践,共同完成网络优化项目。
情感态度价值观目标:1. 激发学生对网络优化和网络科学研究的兴趣,培养积极的学习态度。
2. 培养学生面对复杂问题时的耐心和毅力,增强克服困难的信心。
3. 引导学生关注网络优化技术在现实生活中的应用,提高社会责任感和创新意识。
课程性质:本课程为实践性较强的选修课程,旨在让学生在掌握网络优化基本原理的基础上,运用MATLAB软件进行实际操作,培养解决实际问题的能力。
学生特点:学生具备一定的数学基础和网络知识,对MATLAB软件有一定了解,具有较强的学习能力和动手能力。
教学要求:注重理论与实践相结合,强调学生的主体地位,鼓励学生积极参与课堂讨论和实践活动,培养创新精神和实践能力。
通过本课程的学习,使学生能够独立完成网络优化问题的建模、求解和优化。
二、教学内容1. 网络优化基本概念:介绍网络优化定义、类型及其应用场景,重点讲解网络优化问题的数学模型。
2. MATLAB基础知识:回顾MATLAB软件的基本操作、矩阵运算和编程语法,为后续网络优化建模打下基础。
3. 网络优化建模:讲解如何利用MATLAB构建网络优化模型,包括图论、线性规划、非线性规划等基本方法。
- 图论基础:节点、边、路径、连通图等概念及其在MATLAB中的表示方法。
- 线性规划:线性规划模型及其求解方法,使用MATLAB求解线性规划问题。
图论与网络优化课程设计_Matlab实现

1
四种基本网络(NCN、ER、WS、BA) 的构造及其性质比较
1. 概述
1. 网络科学的概述 网络科学(Network Science)是专门研究复杂网络系统的定性和定量规律的一门崭新 的交叉科学,研究涉及到复杂网络的各种拓扑结构及其性质,与动力学特性(或功能)之间 相互关系,包括时空斑图的涌现、动力学同步及其产生机制,网络上各种动力学行为和信息 的传播、预测(搜索)与控制,以及工程实际所需的网络设计原理及其应用研究,其交叉研 究内容十分广泛而丰富。网络科学中被广泛研究的基本网络主要有四种,即:规则网络之最 近邻耦合网络 (Nearest-neighbor coupled network) ,本文中简称 NCN; ER 随机网络 G(N,p); WS 小世界网络;BA 无标度网络。本文着重研究这几种网络的构造算法程序。计算各种规模 下(例如不同节点数、不同重连概率或者连边概率)各自的网络属性(包括边数、度分布、 平均路径长度、聚类系数),给出图、表和图示,并进行比较和分析。 2. 最近邻耦合网络的概述 如果在一个网络中, 每一个节点只和它周围的邻居节点相连, 那么就称该网络为最近邻 耦合网络。这是一个得到大量研究的稀疏的规则网络模型。 常见的一种具有周期边界条件的最近邻耦合网络包含围成一个环的 N 个节点,其中每 个节点都与它左右各 K / 2 个邻居节点相连,这里 K 是一个偶数。这类网络的一个重要特征 就是网络的拓扑结构是由节点之间的相对位置决定的, 随着节点位置的变化网络拓扑结构也 可能发生切换。 NCN 的 Matlab 实现: %function b = ncn(N,K) %此函数生成一个有 N 个节点,每个节点与它左右各 K/2 个节点都相连的最近邻耦合网络 %返回结果 b 为该最近邻耦合网络对应的邻接矩阵 function b = ncn(N,K) b=zeros(N); for i = 1:N for j = (i+1):(i+K/2) if j<=N b(i,j)=1; b(j,i)=1; else b(i,j-N)=1;
图论算法及matlab程序的三个案例

图论实验三个案例单源最短路径问题 1.1 Dijkstra 算法Dijkstra 算法是解单源最短路径问题的一个贪心算法。
其基本思想是,设置 一个顶点集合S 并不断地作贪心选择来扩充这个集合。
一个顶点属于集合S 当且 仅当从源到该顶点的最短路径长度已知。
设 v 是图中的一个顶点,记l(v)为顶点 v 到源点V 1的最短距离,V i,V jV ,若(V i,V j)E ,记“到百的权w 。
Dijkstra 算法:① S {V J I(V J 0 ; V V {可 1(V ) i i S V {V J ;J7JJJ7②S,停止,否则转③;l(v) min{ l(v) , d(V j ,v)}V j S④ 存在Vi 1,使l (V i l) min{l(V)},V S ;⑤SSU{v i 1}S S {v i 1}i i 1实际上,Dijkstra 算法也是最优化原理的应用:如果V 1V 2LV n1Vn是从V1到Vn的最短路径,贝UV 1V 2L Vn1也必然是从V1到Vn 1的最优路径。
在下面的MATLA 实现代码中,我们用到了距离矩阵,矩阵第 i 行第j 行元 素表示顶点Vi到Vj的权Wj,若v 到V j无边,则W ijrealmax,其中realmax 是 MATLA 常量,表示最大的实数(1.7977e+308)function re=Dijkstra(ma)%用Dijkstra 算法求单源最短路径%俞入参量ma是距离矩阵%输出参量是一个三行n 列矩阵,每列表示顶点号及顶点到源的最短距离和前顶点n=size(ma,1);% 得到距离矩阵的维数s=ones(1,n);s(1)=0;% 标记集合S和S 的补r=zeros(3,n);r(1,:)=1:n;r(2,2:end)=realmax;% 初始化for i=2:n;% 控制循环次数mm=realmax;for j=find(s==0);% 集合S中的顶点for k=find(s==1);% 集合S补中的顶点if(r(2,j)+ma(j,k)<r(2,k))r(2,k)=r(2,j)+ma(j,k);r(3,k)=j;endif(mm>r(2,k))mm=r(2,k);t=k;endendends(1,t)=0;%找到最小的顶点加入集合Send re=r;1.2动态规划求解最短路径动态规划是美国数学家 Richard Bellman 在1951年提出来的分析一类多阶 段决策过程的最优化方法,在工程技术、工业生产、经济管理、军事及现代化控 制工程等方面均有着广泛的应用。
Matlab中的复杂网络与图论分析方法

Matlab中的复杂网络与图论分析方法在当今数字时代,数据网络正在成为各行各业的核心,这就给研究网络结构和分析网络行为提供了前所未有的机会。
而复杂网络和图论分析方法则成为了研究数据网络的一种重要手段。
本文将介绍在Matlab中应用的复杂网络和图论分析方法,探讨其原理和应用。
一、复杂网络:拓扑结构的研究复杂网络是指由大量节点和链接组成的网络,其中节点代表实体,链接代表实体之间的关系。
通过研究复杂网络的拓扑结构,我们可以揭示数据网络中的规律和性质,了解网络中节点的连接模式和信息传播机制。
1.1 网络拓扑结构的描述在复杂网络研究中,一种常用的描述方法是邻接矩阵和度矩阵。
邻接矩阵是一个由0和1组成的矩阵,其中的元素表示节点之间的连接关系,1表示连接,0表示未连接。
度矩阵是一个对角矩阵,用于描述每个节点的度数,即与该节点相连的链接数。
1.2 网络节点的度分布节点的度数是指与该节点相连的链接数,而节点的度分布则是指不同度数的节点在网络中的分布情况。
在复杂网络中,节点的度分布往往符合幂律分布,即少数节点的度数非常大,而大部分节点的度数相对较小。
通过分析节点的度分布,可以了解网络中的核心节点和边缘节点,以及网络的鲁棒性和可靠性。
1.3 网络中的社区结构社区结构是指网络中节点的聚集现象,即节点之间的连接更密集,而与其他社区的联系较弱。
通过识别和研究网络中的社区结构,可以帮助我们揭示网络中的隐含规律、发现重要节点和子网络,并理解网络的分层结构和功能。
二、图论分析:探索网络行为的机制图论是研究网络结构和图形模型的数学理论,主要关注网络中节点和链接之间的关系。
通过图论分析,我们可以量化和描述网络中的节点和链接的特性,揭示网络的演化机制和行为规律。
2.1 网络中的中心性度量中心性是衡量网络中节点重要性的指标,可以帮助我们识别重要节点和影响网络动态行为的因素。
在复杂网络中,常用的中心性度量包括度中心性、接近中心性和介数中心性等。
matlab期末简单的课程设计

matlab期末简单的课程设计一、课程目标知识目标:1. 理解并掌握MATLAB基本语法和编程规范;2. 学会使用MATLAB进行数据可视化、矩阵运算和简单算法实现;3. 掌握MATLAB在工程领域的应用,如信号处理、控制系统等。
技能目标:1. 能够运用MATLAB编写程序,解决实际问题;2. 培养学生利用MATLAB进行数据处理和分析的能力;3. 提高学生运用MATLAB进行团队协作和沟通表达的能力。
情感态度价值观目标:1. 培养学生对MATLAB编程的兴趣,激发学生主动探索的精神;2. 培养学生严谨、认真的科学态度,提高学生的自主学习能力;3. 引导学生认识到MATLAB在工程领域的实用价值,增强学生的职业认同感。
本课程针对高年级学生,课程性质为实践性较强的专业选修课。
结合学生特点,课程目标注重培养学生的实际操作能力和团队协作能力。
在教学过程中,要求教师关注学生的个体差异,充分调动学生的积极性,引导学生运用MATLAB解决实际问题。
通过本课程的学习,期望学生能够掌握MATLAB的基本使用方法,为后续专业课程学习和工程实践打下坚实基础。
二、教学内容1. MATLAB基础知识:介绍MATLAB的安装与界面,基本语法和编程规范,数值、字符串和结构体等数据类型,矩阵的创建和运算,流程控制语句,函数编写与调用等。
教材章节:第1章 MATLAB概述,第2章 MATLAB编程基础。
2. 数据可视化:学习使用MATLAB绘制二维、三维图形,包括线图、散点图、柱状图等,以及图形的修饰和布局。
教材章节:第3章 数据可视化。
3. 算法实现与应用:介绍MATLAB在数值计算、信号处理、控制系统等领域的应用,通过实例讲解常见算法的实现。
教材章节:第4章 矩阵计算,第5章 算法实现与应用。
4. MATLAB高级应用:学习MATLAB在图像处理、优化算法、神经网络等领域的应用,提高学生解决复杂工程问题的能力。
教材章节:第6章 高级应用。
图论算法及Matlab程序代码

图论算法及其MATLAB 程序代码求赋权图G = (V , E , F )中任意两点间的最短路的Warshall-Floyd 算法:设A = (a ij )n ×n 为赋权图G = (V , E , F )的矩阵, 当v i v j ∈E 时a ij = F (v i v j ), 否则取a ii =0, a ij = +∞(i ≠j ), d ij 表示从v i 到v j 点的距离, r ij 表示从v i 到v j 点的最短路中一个点的编号.① 赋初值. 对所有i , j , d ij = a ij , r ij = j . k = 1. 转向②② 更新d ij , r ij . 对所有i , j , 若d ik + d k j <d ij , 则令d ij = d ik + d k j , r ij = k , 转向③.③ 终止判断. 若d ii <0, 则存在一条含有顶点v i 的负回路, 终止; 或者k = n 终止; 否则令k = k + 1, 转向②.最短路线可由r ij 得到.例1 求图6-4中任意两点间的最短路.解:用Warshall-Floyd 算法, MATLAB 程序代码如下:n=8;A=[0 2 8 1 Inf Inf Inf Inf2 0 6 Inf 1 Inf Inf Inf8 6 0 7 5 1 2 Inf1 Inf 7 0 Inf Inf 9 InfInf 1 5 Inf 0 3 Inf 8Inf Inf 1 Inf 3 0 4 6Inf Inf 2 9 Inf 4 0 3Inf Inf Inf Inf 8 6 3 0]; % MATLAB 中, Inf 表示∞D=A; %赋初值for (i=1:n)for (j=1:n)R(i,j)=j;end ;end %赋路径初值for (k=1:n)for (i=1:n)for (j=1:n)if (D(i,k)+D(k,j)<D(i,j))D(i,j)=D(i,k)+D(k,j); %更新dijR(i,j)=k;end ;end ;end %更新rijk %显示迭代步数D %显示每步迭代后的路长R %显示每步迭代后的路径pd=0;for i=1:n %含有负权时if (D(i,i)<0)pd=1;break ;end ;end %存在一条含有顶点vi 的负回路if (pd)break ;end %存在一条负回路, 终止程序end %程序结束图6-4Kruskal避圈法:将图G中的边按权数从小到大逐条考察, 按不构成圈的原则加入到T 中(若有选择时, 不同的选择可能会导致最后生成树的权数不同), 直到q (T ) = p (G ) − 1为止, 即T的边数= G的顶点数− 1为止.Kruskal避圈法的MATLAB程序代码如下:n=8;A=[0 2 8 1 0 0 0 02 0 6 0 1 0 0 08 6 0 7 5 1 2 01 0 7 0 0 0 9 00 1 5 0 0 3 0 80 0 1 0 3 0 4 60 0 2 9 0 4 0 30 0 0 0 8 6 3 0];k=1; %记录A中不同正数的个数for(i=1:n-1)for(j=i+1:n) %此循环是查找A中所有不同的正数if(A(i,j)>0)x(k)=A(i,j); %数组x记录A中不同的正数kk=1; %临时变量for(s=1:k-1)if(x(k)==x(s))kk=0;break;end;end%排除相同的正数k=k+kk;end;end;endk=k-1 %显示A中所有不同正数的个数for(i=1:k-1)for(j=i+1:k) %将x中不同的正数从小到大排序if(x(j)<x(i))xx=x(j);x(j)=x(i);x(i)=xx;end;end;endT(n,n)=0; %将矩阵T中所有的元素赋值为0q=0; %记录加入到树T中的边数for(s=1:k)if(q==n)break;end%获得最小生成树T, 算法终止for(i=1:n-1)for(j=i+1:n)if (A(i,j)==x(s))T(i,j)=x(s);T(j,i)=x(s); %加入边到树T中TT=T; %临时记录Twhile(1)pd=1;%砍掉TT中所有的树枝for(y=1:n)kk=0;for(z=1:n)if(TT(y,z)>0)kk=kk+1;zz=z;end;end%寻找TT中的树枝if(kk==1)TT(y,zz)=0;TT(zz,y)=0;pd=0;end;end%砍掉TT中的树枝if(pd)break;end;end%已砍掉了TT中所有的树枝pd=0;%判断TT中是否有圈for(y=1:n-1)for(z=y+1:n)if(TT(y,z)>0)pd=1;break;end;end;endif(pd)T(i,j)=0;T(j,i)=0;%假如TT中有圈else q=q+1;end;end;end;end;endT %显示近似最小生成树T, 程序结束求二部图G的最大匹配的算法(匈牙利算法), 其基本思想是:从G的任意匹配M开始, 对X中所有M的非饱和点, 寻找M−增广路. 若不存在M−增广路, 则M为最大匹配; 若存在M−增广路P, 则将P中M与非M的边互换得到比M多一边的匹配M1 , 再对M1重复上述过程.设G = ( X, Y, E )为二部图, 其中X = {x1, x2, … , x n }, Y = { y1, y2, … , y n}. 任取G的一初始匹配M (如任取e∈E, 则M = {e}是一个匹配).①令S = φ , T = φ , 转向②.②若M饱和X \S的所有点, 则M是二部图G的最大匹配. 否则, 任取M的非饱和点u∈X \ S , 令S = S ∪{ u }, 转向③.③记N (S ) = {v | u∈S, uv∈E}. 若N (S ) = T, 转向②. 否则取y∈N (S ) \T. 若y是M 的饱和点, 转向④, 否则转向⑤.④设x y∈M, 则令S = S ∪{ x }, T = T ∪{ y }, 转向③.⑤u −y路是M−增广路, 设为P, 并令M = M⊕P, 转向①. 这里M⊕P = M∪P \M∩P, 是对称差.由于计算M−增广路P比较麻烦, 因此将迭代步骤改为:①将X中M的所有非饱和点(不是M中某条边的端点)都给以标号0和标记*, 转向②.②若X中所有有标号的点都已去掉了标记*, 则M是G的最大匹配. 否则任取X中一个既有标号又有标记*的点x i , 去掉x i的标记*, 转向③.③找出在G中所有与x i邻接的点y j (即x i y j∈E ), 若所有这样的y j都已有标号, 则转向②, 否则转向④.④对与x i邻接且尚未给标号的y j都给定标号i. 若所有的y j都是M的饱和点, 则转向⑤, 否则逆向返回. 即由其中M的任一个非饱和点y j的标号i找到x i, 再由x i的标号k找到y k , … , 最后由y t的标号s找到标号为0的x s时结束, 获得M−增广路x s y t…x i y j, 记P = {x s y t, …, x i y j }, 重新记M为M⊕P, 转向①.⑤将y j在M中与之邻接的点x k (即x k y j∈M), 给以标号j和标记*, 转向②.例1求图6-9中所示的二部图G的最大匹配.图6-9匈牙利算法的MATLAB程序代码如下:m=5;n=5;A=[0 1 1 0 01 1 0 1 10 1 1 0 00 1 1 0 00 0 0 1 1];M(m,n)=0;for(i=1:m)for(j=1:n)if(A(i,j))M(i,j)=1;break;end;end%求初始匹配Mif(M(i,j))break;end;end%获得仅含一条边的初始匹配Mwhile(1)for(i=1:m)x(i)=0;end%将记录X中点的标号和标记*for(i=1:n)y(i)=0;end%将记录Y中点的标号和标记*for(i=1:m)pd=1;%寻找X中M的所有非饱和点for(j=1:n)if(M(i,j))pd=0;end;endif(pd)x(i)=-n-1;end;end%将X中M的所有非饱和点都给以标号0和标记*, 程序中用n+1表示0标号, 标号为负数时表示标记*pd=0;while(1)xi=0;for(i=1:m)if(x(i)<0)xi=i;break;end;end%假如X中存在一个既有标号又有标记*的点, 则任取X中一个既有标号又有标记*的点xiif(xi==0)pd=1;break;end%假如X中所有有标号的点都已去掉了标记*, 算法终止x(xi)=x(xi)*(-1); %去掉xi的标记*k=1;for(j=1:n)if(A(xi,j)&y(j)==0)y(j)=xi;yy(k)=j;k=k+1;end;end%对与xi邻接且尚未给标号的yj都给以标号iif(k>1)k=k-1;for(j=1:k)pdd=1;for(i=1:m)if(M(i,yy(j)))x(i)=-yy(j);pdd=0;break;end;end%将yj在M中与之邻接的点xk (即xkyj∈M), 给以标号j和标记*if(pdd)break;end;endif(pdd)k=1;j=yy(j); %yj不是M的饱和点while(1)P(k,2)=j;P(k,1)=y(j);j=abs(x(y(j))); %任取M的一个非饱和点yj, 逆向返回if(j==n+1)break;end%找到X中标号为0的点时结束, 获得M-增广路Pk=k+1;endfor(i=1:k)if(M(P(i,1),P(i,2)))M(P(i,1),P(i,2))=0; %将匹配M在增广路P中出现的边去掉else M(P(i,1),P(i,2))=1;end;end%将增广路P中没有在匹配M中出现的边加入到匹配M中break;end;end;endif(pd)break;end;end%假如X中所有有标号的点都已去掉了标记*, 算法终止M %显示最大匹配M, 程序结束利用可行点标记求最佳匹配的算法步骤如下:设G = ( X , Y , E , F )为完备的二部赋权图, L 是其一个初始可行点标记, 通常取.,,0)(},|)(max{)(Y y X x y L Y y xy F x L ∈∈ =∈= M 是G L 的一个匹配. ① 若X 的每个点都是M 的饱和点, 则M 是最佳匹配. 否则取M 的非饱和点u ∈X , 令S = {u }, T = φ , 转向②.② 记N L (S ) = {v | u ∈S , uv ∈E L }. 若N L ( S ) = T , 则G L 没有完美匹配, 转向③. 否则转向④.③ 调整可行点标记, 计算a L = min { L ( x ) + L ( y ) − F (x y ) | x ∈S , y ∈Y \T }.由此得新的可行顶点标记H (v ) =,,),(,)(,)(T v S v v L a v L a v L L L ∈∈+−令L = H , G L = G H , 重新给出G L 的一个匹配M , 转向①.④ 取y ∈N L ( S ) \T , 若y 是M 的饱和点, 转向⑤. 否则, 转向⑥.⑤ 设x y ∈M , 则令S = S ∪{ x }, T = T ∪{ y }, 转向②.⑥ 在G L 中的u − y 路是M −增广路, 记为P , 并令 M = M ⊕P , 转向①.利用可行点标记求最佳匹配算法的MATLAB 程序代码如下:n=4;A=[4 5 5 12 2 4 64 2 3 35 0 2 1];for (i=1:n)L(i,1)=0;L(i,2)=0;endfor (i=1:n)for (j=1:n)if (L(i,1)<A(i,j))L(i,1)=A(i,j);end ; %初始可行点标记LM(i,j)=0;end ;endfor (i=1:n)for (j=1:n) %生成子图Glif (L(i,1)+L(j,2)==A(i,j))Gl(i,j)=1;else Gl(i,j)=0;end ;end ;endii=0;jj=0;for (i=1:n)for (j=1:n)if (Gl(i,j))ii=i;jj=j;break ;end ;endif (ii)break ;end ;end %获得仅含Gl 的一条边的初始匹配MM(ii,jj)=1;for (i=1:n)S(i)=0;T(i)=0;NlS(i)=0;endwhile (1)for (i=1:n)k=1;否则.for(j=1:n)if(M(i,j))k=0;break;end;endif(k)break;end;endif(k==0)break;end%获得最佳匹配M, 算法终止S(1)=i;jss=1;jst=0;%S={xi}, T=φwhile(1)jsn=0;for(i=1:jss)for(j=1:n)if(Gl(S(i),j))jsn=jsn+1;NlS(jsn)=j;%NL(S)={v|u∈S,uv∈EL}for(k=1:jsn-1)if(NlS(k)==j)jsn=jsn-1;end;end;end;end;endif(jsn==jst)pd=1; %判断NL(S)=T?for(j=1:jsn)if(NlS(j)~=T(j))pd=0;break;end;end;endif(jsn==jst&pd)al=Inf; %如果NL(S)=T, 计算al, Inf为∞for(i=1:jss)for(j=1:n)pd=1;for(k=1:jst)if(T(k)==j)pd=0;break;end;endif(pd&al>L(S(i),1)+L(j,2)-A(S(i),j))al=L(S(i),1)+L(j,2)-A(S(i),j);end;end;end for(i=1:jss)L(S(i),1)=L(S(i),1)-al;end%调整可行点标记for(j=1:jst)L(T(j),2)=L(T(j),2)+al;end%调整可行点标记for(i=1:n)for(j=1:n) %生成子图GLif(L(i,1)+L(j,2)==A(i,j))Gl(i,j)=1;else Gl(i,j)=0;endM(i,j)=0;k=0;end;endii=0;jj=0;for(i=1:n)for(j=1:n)if(Gl(i,j))ii=i;jj=j;break;end;endif(ii)break;end;end%获得仅含Gl的一条边的初始匹配MM(ii,jj)=1;breakelse%NL(S)≠Tfor(j=1:jsn)pd=1;%取y∈NL(S)\Tfor(k=1:jst)if(T(k)==NlS(j))pd=0;break;end;endif(pd)jj=j;break;end;endpd=0;%判断y是否为M的饱和点for(i=1:n)if(M(i,NlS(jj)))pd=1;ii=i;break;end;endif(pd)jss=jss+1;S(jss)=ii;jst=jst+1;T(jst)=NlS(jj); %S=S∪{x}, T=T∪{y}else%获得Gl的一条M-增广路, 调整匹配Mfor(k=1:jst)M(S(k),T(k))=1;M(S(k+1),T(k))=0;endif(jst==0)k=0;endM(S(k+1),NlS(jj))=1;break;end;end;end;endMaxZjpp=0;for(i=1:n)for(j=1:n)if(M(i,j))MaxZjpp=MaxZjpp+A(i,j);end;end;endM %显示最佳匹配MMaxZjpp %显示最佳匹配M的权, 程序结束从一个可行流f 开始, 求最大流的Ford--Fulkerson 标号算法的基本步骤:⑴ 标号过程① 给发点v s 以标号(+, +∞) , δ s = +∞.② 选择一个已标号的点x , 对于x 的所有未给标号的邻接点y , 按下列规则处理:当yx ∈E , 且f yx >0时, 令δ y = min { f yx , δ x }, 并给y 以标号 ( x − , δ y ).当xy ∈E , 且f xy <C xy 时, 令δ y = min {C xy − f xy , δ x }, 并给y 以标号 ( x + , δ y ). ③ 重复②直到收点v t 被标号或不再有点可标号时为止. 若v t 得到标号, 说明存在一条可增广链, 转⑵调整过程; 若v t 未得到标号, 标号过程已无法进行时, 说明f 已经是最大流.⑵ 调整过程④ 决定调整量δ =δ vt , 令u = v t .⑤ 若u 点标号为( v +, δ u ), 则以f vu + δ 代替f vu ; 若u 点标号为( v −, δ u ), 则以 f vu − δ 代替f vu .⑥ 若v = v s , 则去掉所有标号转⑴重新标号; 否则令u = v , 转⑤.算法终止后, 令已有标号的点集为S , 则割集(S , S c )为最小割, 从而W f = C (S , S c ). 例1 求图6-19所示网络的最大流.利用Ford--Fulkerson 标号法求最大流算法的MATLAB 程序代码如下:n=8;C=[0 5 4 3 0 0 0 00 0 0 0 5 3 0 00 0 0 0 0 3 2 00 0 0 0 0 0 2 00 0 0 0 0 0 0 40 0 0 0 0 0 0 30 0 0 0 0 0 0 50 0 0 0 0 0 0 0]; %弧容量for (i=1:n)for (j=1:n)f(i,j)=0;end ;end %取初始可行流f 为零流for (i=1:n)No(i)=0;d(i)=0;end %No,d 记录标号图6-19while(1)No(1)=n+1;d(1)=Inf; %给发点vs标号while(1)pd=1;%标号过程for(i=1:n)if(No(i)) %选择一个已标号的点vifor(j=1:n)if(No(j)==0&f(i,j)<C(i,j)) %对于未给标号的点vj, 当vivj为非饱和弧时No(j)=i;d(j)=C(i,j)-f(i,j);pd=0;if(d(j)>d(i))d(j)=d(i);endelseif(No(j)==0&f(j,i)>0) %对于未给标号的点vj, 当vjvi为非零流弧时No(j)=-i;d(j)=f(j,i);pd=0;if(d(j)>d(i))d(j)=d(i);end;end;end;end;endif(No(n)|pd)break;end;end%若收点vt得到标号或者无法标号, 终止标号过程if(pd)break;end%vt未得到标号, f已是最大流, 算法终止dvt=d(n);t=n; %进入调整过程, dvt表示调整量while(1)if(No(t)>0)f(No(t),t)=f(No(t),t)+dvt; %前向弧调整elseif(No(t)<0)f(No(t),t)=f(No(t),t)-dvt;end%后向弧调整if(No(t)==1)for(i=1:n)No(i)=0;d(i)=0; end;break;end%当t的标号为vs时, 终止调整过程t=No(t);end;end; %继续调整前一段弧上的流fwf=0;for(j=1:n)wf=wf+f(1,j);end%计算最大流量f %显示最大流wf %显示最大流量No %显示标号, 由此可得最小割, 程序结束设网络G = ( V , E , C ), 取初始可行流 f 为零流, 求解最小费用流问题的迭代步骤: ① 构造有向赋权图 G f = ( V , E f , F ), 对于任意的v i v j ∈E , E f , F 的定义如下:当f ij = 0时, v i v j ∈E f , F ( v i v j ) = b ij ;当f ij = C ij 时, v j v i ∈E f , F ( v j v i ) = −b ij ;当0< f ij <C ij 时, v i v j ∈E f , F ( v i v j ) = b ij , v j v i ∈E f , F ( v j v i ) = −b ij .转向②.② 求出有向赋权图G f = (V , E f , F )中发点v s 到收点v t 的最短路µ , 若最短路µ存在转向③; 否则f 是所求的最小费用最大流, 停止.③ 增流. 同求最大流的方法一样, 重述如下:令.,,,−+∈∈ −=µµδj i j i ij ij ij ij v v v v f f C δ = min {δ ij | v i v j ∈µ}, 重新定义流f = { f ij }为 f ij =,,,,−+∈∈ −+µµδδj i j i ijij ij v v v v f f f如果W f 大于或等于预定的流量值, 则适当减少δ 值, 使W f 等于预定的流量值, 那么 f 是所求的最小费用流, 停止; 否则转向①.求解含有负权的有向赋权图G = ( V , E , F )中某一点到其它各点最短路的Ford 算法. 当v i v j ∈E 时记w ij = F (v i v j ), 否则取w ii =0, w ij = +∞(i ≠j ). v 1到v i 的最短路长记为π ( i ), v 1到v i 的最短路中v i 的前一个点记为θ ( i ). Ford 算法的迭代步骤:① 赋初值π (1) = 0, π ( i ) = +∞, θ ( i ) = i , i = 2, 3, … , n .② 更新π ( i ), θ ( i ). 对于i = 2, 3, … , n 和j = 1, 2, … , n , 如果π ( i )<π ( j ) + w ji , 则令π ( i ) = π ( j ) , θ ( i ) = j . ③ 终止判断:若所有的π ( i )都无变化, 停止; 否则转向②. 在算法的每一步中, π ( i )都是从v 1到v i 的最短路长度的上界. 若不存在负长回路, 则从v 1到v i 的最短路长度是π ( i )的下界, 经过n −1次迭代后π ( i )将保持不变. 若在第n 次迭代后π ( i )仍在变化时, 说明存在负长回路.其它.例2 在图6-22所示运输网络上, 求s 到t 的最小费用最大流, 括号内为(C ij , b ij ).求最小费用最大流算法的MATLAB 程序代码如下:n=5;C=[0 15 16 0 00 0 0 13 140 11 0 17 00 0 0 0 80 0 0 0 0]; %弧容量b=[0 4 1 0 00 0 0 6 10 2 0 3 00 0 0 0 20 0 0 0 0]; %弧上单位流量的费用wf=0;wf0=Inf; %wf 表示最大流量, wf0表示预定的流量值for (i=1:n)for (j=1:n)f(i,j)=0;end ;end %取初始可行流f 为零流while (1)for (i=1:n)for (j=1:n)if (j~=i)a(i,j)=Inf;end ;end ;end %构造有向赋权图for (i=1:n)for (j=1:n)if (C(i,j)>0&f(i,j)==0)a(i,j)=b(i,j);elseif (C(i,j)>0&f(i,j)==C(i,j))a(j,i)=-b(i,j);elseif (C(i,j)>0)a(i,j)=b(i,j);a(j,i)=-b(i,j);end ;end ;endfor (i=2:n)p(i)=Inf;s(i)=i;end %用Ford 算法求最短路, 赋初值for (k=1:n)pd=1; %求有向赋权图中vs 到vt 的最短路for (i=2:n)for (j=1:n)if (p(i)>p(j)+a(j,i))p(i)=p(j)+a(j,i);s(i)=j;pd=0;end ;end ;endif (pd)break ;end ;end %求最短路的Ford 算法结束if (p(n)==Inf)break ;end %不存在vs 到vt 的最短路, 算法终止. 注意在求最小费用最大流时构造有向赋权图中不会含负权回路, 所以不会出现k=ndvt=Inf;t=n; %进入调整过程, dvt 表示调整量while (1) %计算调整量if (a(s(t),t)>0)dvtt=C(s(t),t)-f(s(t),t); %前向弧调整量elseif (a(s(t),t)<0)dvtt=f(t,s(t));end %后向弧调整量if (dvt>dvtt)dvt=dvtt;endif (s(t)==1)break ;end %当t 的标号为vs 时, 终止计算调整量t=s(t);end %继续调整前一段弧上的流fpd=0;if (wf+dvt>=wf0)dvt=wf0-wf;pd=1;end %如果最大流量大于或等于预定的流量值t=n;while (1) %调整过程if (a(s(t),t)>0)f(s(t),t)=f(s(t),t)+dvt; %前向弧调整elseif (a(s(t),t)<0)f(t,s(t))=f(t,s(t))-dvt;end %后向弧调整if (s(t)==1)break ;end %当t 的标号为vs 时, 终止调整过程t=s(t);endif (pd)break ;end %如果最大流量达到预定的流量值wf=0; for (j=1:n)wf=wf+f(1,j);end ;end %计算最大流量zwf=0;for (i=1:n)for (j=1:n)zwf=zwf+b(i,j)*f(i,j);end ;end %计算最小费用f %显示最小费用最大流图6-22wf %显示最小费用最大流量zwf %显示最小费用, 程序结束。
应用篇-第14章-图论算法及其MATLAB实现

对每个图G=(V,E),均有
d(v)=2|E|
vV
证明:根据顶点度的定义,在计算点度时每条边对于它所关联的顶点被计 算了两次。因此,图G 中点度的总和恰为边数|V|的2倍。证毕。 推论14.1 在任何图G=(V,E)中,奇点的个数为偶数。
定理14.4对任意有向图D=(V,A)均有
14.8 Dijkstra 算法及其MATLAB实现
14.8.1 问题描述与算法思想
Dijkstra算法是解单源最短路径问题的一个贪心算法。其基本思想是,设置 一个顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当 且仅当从源到该顶点的最短路径长度已知。设v是图中的一个顶点,记L(v) 为顶点v到源点v1的最短距离, vi , v j V 若 (vi , v j ) E ,记vi到vj的权。
① A(G)为对称矩阵;
② 若G 为无环图,则A(G)中第i行(列)的元素之和等于顶点vi的度; ③ 两图G 和H 同构的充分必要条件是存在置换矩阵P 使得A(G)=PTA(H)P。
类似地,有向图D 的邻接矩阵A(D)=(aij)n×n的元素aij定义为:元素aij表示从始点vi到 终点vj的有向边的条,,其中vi和vj为D 的顶点。
14.3.2 关联矩=(V,E),其中顶点集V={v1,v2,…,vn},边集E={e1,e2,…,eε}。 用 mij表示顶点vi与边ej关联的次数,可能取值为0,1,2,称所得矩阵M(G)=(mij)n×ε为 图G 的关联矩阵。 类似地,有向图D 的关联矩阵M(D)=(mij)n×ε的元素mij定义为:
14.2.4 路
在图论理论中,路具有特殊的重要性,古往今来,许多学者均对它进行过深入研究。本 节主要介绍简单图G=(V,E)中有关路和连通性的简单性质。 定理14.1 若图G 中有一条(u,v)途径,则G 中也存在一条(u,v)路。
数学实验 实验图与网络优化
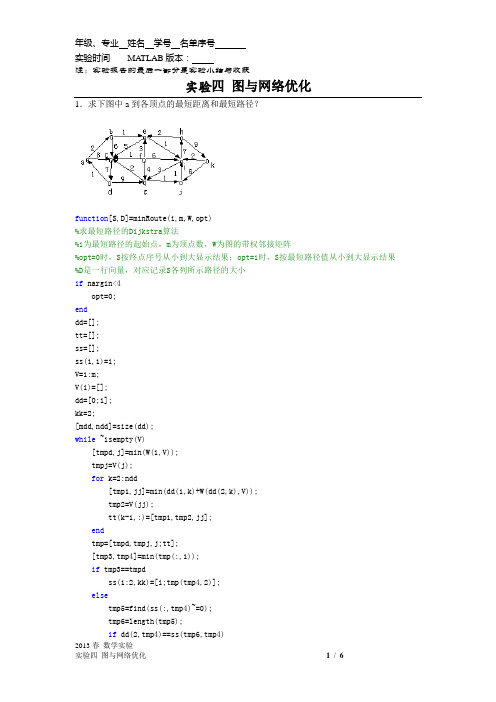
实验四图与网络优化1.求下图中a到各顶点的最短距离和最短路径?function[S,D]=minRoute(i,m,W,opt)%求最短路径的Dijkstra算法%i为最短路径的起始点,m为顶点数,W为图的带权邻接矩阵%opt=0时,S按终点序号从小到大显示结果;opt=1时,S按最短路径值从小到大显示结果%D是一行向量,对应记录S各列所示路径的大小if nargin<4opt=0;enddd=[];tt=[];ss=[];ss(1,1)=i;V=1:m;V(i)=[];dd=[0;i];kk=2;[mdd,ndd]=size(dd);while ~isempty(V)[tmpd,j]=min(W(i,V));tmpj=V(j);for k=2:ndd[tmp1,jj]=min(dd(1,k)+W(dd(2,k),V));tmp2=V(jj);tt(k-1,:)=[tmp1,tmp2,jj];endtmp=[tmpd,tmpj,j;tt];[tmp3,tmp4]=min(tmp(:,1));if tmp3==tmpdss(1:2,kk)=[i;tmp(tmp4,2)];elsetmp5=find(ss(:,tmp4)~=0);tmp6=length(tmp5);if dd(2,tmp4)==ss(tmp6,tmp4)实验四图与网络优化 ss(1:tmp6+1,kk)=[ss(tmp5,tmp4);tmp(tmp4,2)];elsess(1:3,kk)=[i;dd(2,tmp4);tmp(tmp4,2)];endenddd=[dd,[tmp3;tmp(tmp4,2)]];V(tmp(tmp4,3))=[];[mdd,ndd]=size(dd);kk=kk+1;endif opt==1[tmp,t]=sort(dd(2,:));S=ss(:,t);D=dd(1,t);elseS=ss;D=dd(1,:);end>> clear all>> w=inf*ones(11);>> w(1,[2,3])=[2,8];>> w(2,[3,5])=[6,1];>> w(3,[4])=[7];>> w(4,[1,7])=[1,9];>> w(5,[3,9])=[5,1];>> w(6,[3,5,7,9])=[1,3,4,6];>> w(7,[3,10])=[2,1];>> w(8,[5,11])=[2,9];>> w(9,[7,8])=[3,7];>> w(10,[9])=[1];实验四图与网络优化>> w(11,[9,10])=[2,6];>> [s,d]=minRoute(1,11,w)s =1 1 1 1 1 1 1 1 1 1 10 2 2 2 2 3 2 2 3 2 60 0 5 5 5 0 5 5 4 5 00 0 0 9 9 0 9 9 0 9 00 0 0 0 7 0 7 8 0 8 00 0 0 0 0 0 10 0 0 11 0d =0 2 3 4 7 8 8 11 15 20 Inf因此,按顶点序号a-b; a-b-e; a-b-e-i; a-b-e-i-g; a-c; a-b-e-i-g-j; a-b-e-i-h; a-c-d; a-b-e-i-h-k; a-f; 按上面次序最短距离分别是0 2 3 4 7 8 8 11 15 20 Inf2.一辆货车从水泥厂运水泥至某建筑工地。
matlab图与网络分析模型选讲ppt课件

20
对规模不大的TSP问题可将其转化为数学规划问题:
引入0-1变量:xij=
1,由第i城市进入第j城市,且i ≠ j
0,其它
nn
目标函数:z min
3)端点重合为一点的边称为环. e5
e1 v1
4) 若一对顶点之间有两条以上的边联结,则这些边 称为重边.
5)既没有环也没有重边的图,称为简单图.
2
6) 若图G的每一条边e 都赋以一个实数w(e),
称w(e)为边e的权,G连同边上的权称为赋权图 ,
记为:G(V,E,W), W={w(e)| e∈E}
18
clc,clear x=[1,1,1,2,2,3,4,4,5,5,5,6,6,6,7,7,8,9]; y=[2,4,5,3,6,8,5,7,2,6,7,3,8,9,6,9,9,9]; z=[2.5,5.6,6.1,7.1,3.6,3.4,4.9,7.4,2.4,7.2,5.7,3.8,5.3,4.5,3.8,6. 7,7.4,0]; f=sparse(x,y,z) [flow,flowmat]=graphmaxflow(f,1,9) name1([1:9],1)='v'; name2=int2str([1:9]'); name=cellstr(strcat(name1,name2)); view(biograph(flowmat,name,'ShowWeights','on'))
maxV ( f )
s.t
.
u jV
0
图论和网络的教学设计方案

添加标题
添加标题
添加标题
添加标题
感谢您的观看
汇报人:XX
图论在网络分析、 计算机科学、交通 运输、社交网络等 领域有广泛应用。
图论和网络的基本 概念包括图、路径 、连通性、树等。
图论和网络的应用场景
推荐系统:通过分析用户行为 和网络结构,利用图论和网络 进行个性化推荐。
社交网络分析:利用图论和网 络分析社交网络中的关系和影 响力。
生物信息学:利用图论和网络 对基因、蛋白质等生物分子进
01
0 2
03
04
图论和网络的扩展知识
最小生成树算法:用于在加权连 通图中找到一棵包含所有顶点的 树,使得所有边的权值之和最小
最短路径算法:用于在加权图中找 到两个顶点之间的最短路径,通常 用于路由和交通规划
图的着色问题:将图的顶点染上颜 色,使得相邻顶点颜色不同,且用 色最少的染色方案
网络流算法:用于解决诸如最大流、 最小截、二分匹配等网络流问题, 常用于优化资源分配和路径规划
01
0 2
03
04
能力目标
能够理解和掌握图论的基 本概念和原理
能够运用图论的方法解决 实际网络问题
能够设计和实施有效的网 络优化算法
能够培养学生的逻辑思维 和问题解决能力
情感态度与价值观目标
培养学生对图论和 网络的兴趣和好奇 心,激发探索欲望。
培养学生的合作精 神和沟通能力,提 高团队协作能力。
高
添加标题
添加标题
添加标题
添加标题
学生反馈与改进措施
学生参与度:评价 学生在课堂上的表 现和参与度,以及 他们在图论和网络 学习中的兴趣和投
入程度。
添加标题
matlab课程设计

mat lab课程设计一、课程目标知识目标:1. 学生能理解MATLAB的基本概念,掌握MATLAB的基本语法和编程环境。
2. 学生能够运用MATLAB进行基本的数据处理、数学运算和图形绘制。
3. 学生掌握MATLAB在工程领域的应用,如信号处理、控制系统分析等。
技能目标:1. 学生能够熟练使用MATLAB软件,进行数据输入、编辑和调试程序。
2. 学生能够运用MATLAB解决实际问题,设计简单的算法和程序。
3. 学生通过MATLAB实践,提高逻辑思维和问题解决能力。
情感态度价值观目标:1. 培养学生对MATLAB编程的兴趣,激发学生主动探索精神。
2. 培养学生严谨、细致的学术态度,养成良好的编程习惯。
3. 增强学生的团队合作意识,提高沟通与协作能力。
课程性质:本课程为实用技能型课程,旨在让学生掌握MATLAB软件的使用,培养实际应用能力。
学生特点:学生具备一定的数学基础和编程兴趣,但对MATLAB软件的了解程度不一。
教学要求:教师需根据学生特点,采用案例教学、任务驱动等方法,引导学生主动参与实践,提高综合运用能力。
在教学过程中,注重个体差异,关注学生成长,及时调整教学策略。
二、教学内容1. MATLAB基础知识:介绍MATLAB软件的安装与配置,界面及基本操作,变量与数据类型,矩阵的创建与运算。
教材章节:第一章 MATLAB概述,第二章 MATLAB基础知识。
2. MATLAB编程:讲解MATLAB控制语句,函数与脚本,调试与优化技巧。
教材章节:第三章 MATLAB编程,第四章 程序调试与优化。
3. 数据可视化:教授MATLAB绘图功能,包括二维图形、三维图形、图像处理等。
教材章节:第五章 数据可视化。
4. MATLAB应用案例分析:介绍MATLAB在信号处理、控制系统分析、数值计算等领域的应用。
教材章节:第六章 MATLAB应用案例分析。
5. MATLAB实践项目:设计具有实际背景的MATLAB编程项目,培养学生解决实际问题的能力。
matlab小课程设计

matlab小课程设计一、课程目标知识目标:1. 学生能理解MATLAB软件的基本操作,掌握数据类型、变量、矩阵等基础知识;2. 学生能运用MATLAB进行简单的数学运算、数据可视化及编程;3. 学生了解MATLAB在工程领域的应用,如信号处理、控制系统等。
技能目标:1. 学生能熟练使用MATLAB软件,完成数据输入、输出,进行基本的数据分析;2. 学生能运用MATLAB编写简单的程序,解决实际问题;3. 学生能通过MATLAB实现课程相关实验,提高实践操作能力。
情感态度价值观目标:1. 培养学生对MATLAB编程的兴趣,激发学生主动探索新知识的热情;2. 培养学生团队协作意识,提高沟通与表达能力;3. 培养学生严谨的科学态度,养成良好的编程习惯。
课程性质:本课程为选修课程,旨在帮助学生掌握MATLAB软件的使用,提高编程能力和实践操作能力。
学生特点:学生具有一定的数学基础,对计算机编程有一定兴趣,但编程经验不足。
教学要求:结合学生特点,注重理论与实践相结合,通过案例教学,使学生能够学以致用,提高解决实际问题的能力。
将课程目标分解为具体的学习成果,以便进行教学设计和评估。
二、教学内容1. MATLAB软件概述- 软件安装与界面认识- 基本操作与功能介绍2. MATLAB基础知识- 数据类型与变量- 矩阵与数组操作- 数学运算与函数3. MATLAB编程基础- 控制流(条件语句、循环语句)- 函数编写与调试- 文件操作与数据存储4. MATLAB数据可视化- 二维图形绘制- 三维图形绘制- 图形修饰与动画制作5. MATLAB应用案例分析- 信号处理- 控制系统设计- 优化问题求解6. MATLAB实验操作- 基本操作练习- 程序编写与调试- 综合应用案例实践教学内容安排与进度:第一周:MATLAB软件概述与基本操作第二周:MATLAB基础知识第三周:MATLAB编程基础第四周:MATLAB数据可视化第五周:MATLAB应用案例分析第六周:MATLAB实验操作教材关联:教学内容与教材相关章节紧密联系,涵盖教材中MATLAB基础与应用部分的核心内容,确保学生能够系统地学习并掌握MATLAB相关知识。
图论和网络分析算法及Matlab实现(Graph-and-Network-Analysis)PPT课

如图,现要在六个城镇间架设通讯网络(均沿道路架
设),每段道路上的架设费用如图。求能保证各城镇均
能通话且总架设费用最少的架设方案。
C
5 10
8
9
5
A 8
7
3
B
6
9
E 3
F
2
4
D
二. 最短路问题
1. 问题:求网络D中一定点v1到其它点的最短路。
例3 求如图网络中v1至v7的最短路,图中数字 为两点间距离。
.
7
问题的两个共同特点
(1)目的都是从若干可能的安排或方案中寻求 某种意义下的最优安排或方案,数学问题称 为最优化或优化问题。
(2)它们都可用图形形式直观描述,数学上把这 种与图相关的结构称为网络。图和网络相关 的最优化问题就是网络最优化。 网络优化问题是以网络流为研究的对象,常 常被称为网络流或网络流规划等。
图在计算机中的表示:
关 联 矩 阵 : n*m或 者 是 m*n
1 1 1 0 1 0 0
1
1
0
0
0
1
0
0 0 1 1 0 1 0
0
0
01
1
0
1
邻 接 矩 阵 : n*n
0 1 1 1
1
01
0
1 1 0 1
1
01
1
邻接矩阵为对称阵,
简单图对角线元素为0
3 . 链与圈
链 : 由 G 中 的 某 些 点 与 边 相 间 构 成 的 序 列 v 1 e 1 v2 e2 ek 1 vk,
v2 v3
v5 v4
树的性质:(1)树的任2点间有且仅有1链; (2)在树中任去掉1边,则不连通; (3)在树中不相邻2点间添1边,恰成1圈; (4)若树T有n个顶点,则T有n-1条边。
图论在matlab中的实现

用 index2×n 存放各边端点的信息, 当选中某一边之后,就将此边对 应的顶点序号中较大序号改记为 此边的另一序号,同时把后面边 中所有序号为的改记为。此方法 的几何意义是:将序号的这个顶 点收缩到顶点,顶点不复存在。 后面继续寻查时,发现某边的两 个顶点序号相同时,认为已被收 缩掉,失去了被选取的资格。
while length(result)<loop temp=min(data(3,:)); flag=find(data(3,:)==temp); flag=flag(1); v1=data(1,flag);v2=data(2,flag); if index(1,flag)~=index(2,flag) result=[result,data(:,flag)]; end if v1>v2 index(find(index==v1))=v2; else index(find(index==v2))=v1; end data(:,flag)=[]; index(:,flag)=[]; end result
Kruskal算法如下 Kruskal算法如下 : clc;clear; M=1000; a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40; a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;a(4,7)=42; a(5,6)=70; [i,j]=find((a~=0)&(a~=M)); b=a(find((a~=0)&(a~=M))); data=[i';j';b'];index=data(1:2,:); loop=max(size(a))loop=max(size(a))-1; result=[];
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论与网络优化课程设计四种基本网络(NCN、ER、WS、BA)的构造及其性质比较摘要:网络科学中被广泛研究的基本网络主要有四种,即:规则网络之最近邻耦合网络(Nearest-neighbor coupled network),本文中简称NCN;ER随机网络G(N,p);WS小世界网络;BA无标度网络。
本文着重研究这几种网络的构造算法程序。
通过运用Matlab软件和NodeXL网络分析软件,计算各种规模下(例如不同节点数、不同重连概率或者连边概率)各自的网络属性(包括边数、度分布、平均路径长度、聚类系数),给出图、表和图示,并进行比较和分析。
关键字:最近邻耦合网络;ER随机网络;WS小世界网络;BA无标度网络;Matlab;NodeXL。
四种基本网络(NCN、ER、WS、BA)的构造及其性质比较1.概述1.网络科学的概述网络科学(Network Science)是专门研究复杂网络系统的定性和定量规律的一门崭新的交叉科学,研究涉及到复杂网络的各种拓扑结构及其性质,与动力学特性(或功能)之间相互关系,包括时空斑图的涌现、动力学同步及其产生机制,网络上各种动力学行为和信息的传播、预测(搜索)与控制,以及工程实际所需的网络设计原理及其应用研究,其交叉研究内容十分广泛而丰富。
网络科学中被广泛研究的基本网络主要有四种,即:规则网络之最近邻耦合网络(Nearest-neighbor coupled network),本文中简称NCN;ER随机网络G(N,p);WS小世界网络;BA无标度网络。
本文着重研究这几种网络的构造算法程序。
计算各种规模下(例如不同节点数、不同重连概率或者连边概率)各自的网络属性(包括边数、度分布、平均路径长度、聚类系数),给出图、表和图示,并进行比较和分析。
2.最近邻耦合网络的概述如果在一个网络中,每一个节点只和它周围的邻居节点相连,那么就称该网络为最近邻耦合网络。
这是一个得到大量研究的稀疏的规则网络模型。
常见的一种具有周期边界条件的最近邻耦合网络包含围成一个环的N个节点,其中每K个邻居节点相连,这里K是一个偶数。
这类网络的一个重要特征个节点都与它左右各/2就是网络的拓扑结构是由节点之间的相对位置决定的,随着节点位置的变化网络拓扑结构也可能发生切换。
NCN的Matlab实现:%function b = ncn(N,K)%此函数生成一个有N个节点,每个节点与它左右各K/2个节点都相连的最近邻耦合网络%返回结果b为该最近邻耦合网络对应的邻接矩阵function b = ncn(N,K)b=zeros(N);for i = 1:Nfor j = (i+1):(i+K/2)if j<=Nb(i,j)=1;b(j,i)=1;elseb(i,j-N)=1;b(j-N,i)=1; end end end end图-1即为20N =,6K =时的最近邻耦合网络的节点图。
图- 1:最近邻耦合网络3. ER 随机网络的概述与完全规则网络相对应的是完全随机网络,最为经典的模型是Erdos 和Reny i 于20世纪50年代末开始研究的现在称为ER 随机图的模型。
该模型既易于描述又可通过解析方法研究。
在20世纪的后40年中,ER 随机图理论一直是研究复杂网络拓扑的基本理论。
关于随机图的理论较为全面的数学论述可参考Bollobas 的著作[1]。
ER 随机图(,)G N p 的构造算法:(1). 初始化:给定N 个节点以及连边概率[0,1]p ∈。
(2). 随机连边:a) 选择一对没有边相连的不同节点。
b) 生成一个随机数(0,1)r ∈。
c) 如果r p <,那么在这对节点之间添加一条边;否则就不添加边。
d) 重复步骤a) ~c),直到所有的节点对都被选择过一次。
ER 算法的Matlab 实现: %function b = er(N,p)%此函数生成一个有N 个节点,节点连边概率p ∈[0,1]的ER 随机图 %返回结果b 为该ER 随机图对应的邻接矩阵function b = er(N,p) b = zeros(N);for i = 1:N-1for j = (i+1):N r=rand; if r<pb(i,j)=1; b(j,i)=1; end end end end图-2即为20N =,0.3158p =时的完全随机网络的节点图。
图- 2:完全随机网络4. WS 小世界网络的概述顾名思义,小世界网络具有明显聚类和小世界特征。
从直观上看,毕竟大部分实际网络既不是完全规则也不是完全随机的:在现实生活中,人们通常认识他们的邻居和同事,但也可能有一些朋友远在异国他乡。
WS 小世界网络的工作1998年6月在《Nature 》[2]上发表,作者是美国Cornell 大学的博士生Watts 及其导师、非线性动力学专家Strogatz 教授。
Watts 和Strogatz 发现:作为从完全规则网络向完全随机网络的过渡,只要在规则网络中引入少许的随机性就可以产生具有小世界特征的网络模型,现在称为WS 小世界网络模型。
WS 小世界模型构造算法: (1). 从规则网络开始:给定一个含有N 个节点的环状最近邻耦合网络,其中每个节点都与它左右相邻的/2K 个节点相连,K 是偶数。
(2). 随机化重连:以概率p 随机地重新连接网络中原有的每条边,即把每条边的一个端点保持不变,另一个端点改取为网络中随机选择的一个节点。
其中规定不得有重边和自环。
WS 算法的Matlab 实现代码: %function b = ws(N,K,p)%此函数生成一个具有N 个节点的WS 小世界网络。
%返回结果b 为该小世界网络对应的邻接矩阵。
%由于WS 小世界网络都是首先由规则的最近邻耦合网络生成的,故需要先调用ncn.mfunction b = ws(N,K,p) b = ncn(N,K); for i = 1:N-1 for j = i+1:N if b(i,j)~=0 if rand<pb(i,j) = 0;b(j,i) = 0; %随机重连,遍历原规则网络中的每一条边 c = 1:N-1;c = c'; %保持其一端的节点不变,产生一个随机数 for h = N-1:(-1):i %若该随机数小于p ,则随机选取除该端点 c(h,1) = h+1; %之外的另一个节点作为另一端的节点。
endd = ceil((N-1)*rand); s = c(d,1); b(i,s) = 1; b(s,i) = 1; end end end end end图-3即为20,6N K ==,0.5p =时的WS 小世界网络的节点图。
图- 3:WS 小世界网络5. BA 无标度网络的概述20世纪末网络科学研究上有两个重要发现,一个是上面提到的W S 小世界网络,另一个就是BA 无标度网络。
这类网络的节点的度没有明显的特征长度,其度分布都可以用适当的幂律形式来较好地描述。
现实生活中的Internet 、WWW 、科研合作网络以及蛋白质交互网络等众多不同领域的网络都是是某种形式上的BA 无标度网络。
BA 无标度网络的工作于1999年10月发表在《Science 》上[3],由美国Notre Dam e 大学物理系的Barabas i 教授及其博士生Albert 合作完成。
BA 无标度网络模型构造算法: (1). 增长:从一个具有M 个节点的连通网络开始,每次引入一个新的节点并且连接到m 个已经存在的节点上,这里m ≤M 。
(2). 优先连接:一个新节点与一个已经存在的节点i 连接的概率i ∏与节点i 的度ik 之间满足如下关系ii jjk k ∏=∑。
BA 算法的Matlab 实现代码: %function b = ba(M,m,N)%此函数生成一个具有N 个节点的BA 无标度网络%M 为初始代连通网络的节点数、m 为每次引入的新节点连接到已存在的节点的个数 %其中m ≤M%返回结果b 为所求BA 无标度网络对应的邻接矩阵function b = ba(M,m,N) b = zeros(N);if M==1 M=2; endfor i = 1:M-1 %这里为简便起见,假使初始网络为完全连通网络 for j = (i+1):M b(i,j) = 1; b(j,i) = 1; end endd = zeros(N,1); %建立一个存储每个节点度值的矩阵 for i = 1:Md(i,1) = M-1; endfor i = M+1:Nmm = 0; %mm 为当前步已经和新节点连接的旧节点个数 dd = d(1:i-1,1); %dd 为d 的副本 while mm<m mm = mm+1;dn = 0; %dn 为节点度之和 for j = 1:i-1dn = dn+dd(j,1); endp = zeros(i-1,1); %p 为节点累积度值占总度值百分比的矩阵 p(1,1) = dd(1,1)/dn; for j = 2:i-1p(j,1) = p(j-1,1)+dd(j,1)/dn; endr = rand;for j = 1:i-1 %进行m 次轮盘赌方法选择与新节点相连的节点 if r<p(j,1) b(i,j)=1; b(j,i)=1;d(i,1)=d(i,1)+1; d(j,1)=d(j,1)+1; dd(j,1) = 0; break; end end end end示例:图-4即为3,2,20M m N ===时的BA 无标度网络的节点图图- 4:BA 无标度网络从以上四种网络的构造算法出发,很容易得出其边数、度分布、平均路径长度、聚类系数的理论值,如下表:表- 1ln ln ln NN2(ln )N N通过拓扑性质的表达式得出有意义的结论。
例如:小世界网络的平均路径长度(记比同等规模的随机网运用以上四个算法的Matlab代码生成规模为1000的4种网络模型,再用NodeXL分析其拓扑性质,通过比较得出结论。
表- 2NCN(1000,6)ER(1000,0.006)WS(1000,6,0.5)BA(3,3,1000)图像边数3000 3015 2992 2994度分布平均度6 6.030 5.984 5.998平均路径长度83.667 4.029739 4.280806 3.451422聚类系数0.6 0.006 0.089 0.04比较和分析(1)、在同等网络规模下,小世界网络的平均路径长度介于规则网络与随机网络之间,这也是小世界网络所以为“小世界”最为显著的特征;(2)、由表中度分布图可以看出:规则网络有规则的度分布、无标度网络明显倾向于幂律分布,即网络中绝大多数节点的度集中于某一值,但始终有少数节点的度在较远的其他值,这有点类似于现实生活中的“二八法则”、而随机网络和小世界网络的度分布都倾向于二项分布、正态分布或者泊松分布;(3)、从四个网络的聚类系数可以看出,规则网络、小世界网络和无标度具有相对较大的聚类系数。
