最新小学数学常见几何模型典型例题及解题思路
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型一一很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图S i : = a :b⑶夹在一组平行线之间的等积变形,如下图S^ ACD = S^ BCD 反之,如果S A ACD =S A BCD,则可知直线AB平行于CD⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:(第四届”迎春杯欄试题)如图‘三角形A眈的面积为1 ,其中AE = 3AB ,,三角形册肉的面积是多少?解析:连接CE,如图。
AE=3AB,所以S A AEC =3S △ABC=3所以S A BCE =2又因为:BD=2BC,所以S A BDE=2S A BCE=4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在△ ABC中,D,E分别是AB,AC上的点(如图1)或D在BA的延长线上,E 在AC 上( 女口图2) ,则S A ABC:ADE二(AB AC): (AD AE)此模型的结论可以用将来初中学到的正弦定理进行证明!因为S^ABC=AB >ACsinA,S^ADE=AD >AEsinA所以:S A ABC: S A ADE= (AB/CsSA): (AD >AEsinA) = (AB 0C):(AD >AE)经典例题:已知MEF的面积为7平方厘米,BE = CE、AD = 2BD*CF=3AF,求心眈的面积・三、蝴蝶定理模型任意四边形中的比例关系(蝴蝶定理”:① S i: S 2 = S 4 : S3 或者S S^ = S2 S 4②AO:OC 二 $ S 2 : S 4 S 3蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径•通过构造模型,一方面可以使不规则四边形的面积关系 与四边形内的三角形相联系;另一方面,也可以得到与面积对应 的对角线的比例关系。
小学小学数学几何五大模型使用方法(含考试典型例题)

小学小学数学几何五大模型使用方法(含考试典型例题)展开全文•在学习小学数学的时候,几何模型算是比较新颖的一个模块,学生们熟练掌握五大面积模型,并掌握五大面积模型的各种变形,今天康康老师就为大家推荐一篇小学数学几何五大模型的内容,第二页还有例题分享,大家可以参考一下。
知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如下图:③夹在一组平行线之间的等积变形,如右图;反之,如果,则可知直线AB平行于CD.④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在中,D、E分别是AB、AC上的点如图⑴(或D在BA 的延长线上,E在AC上),则三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①或者②蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”):四、相似模型(一)金字塔模型 (二) 沙漏模型所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学小学数学里,出现最多的情况是因为两条平行线而出现的相似三角形.五、燕尾定理在三角形ABC中,AD,BE,CF相交于同一点O,那么.上述定理给出了一个新的转化面积比与线段比的手段,因为和的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.。
小学平面几何常考题型总结(含解题套路)

小学平面几何常考题型总结(含解题套路)小学曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
规则图形的面积及周长都有相应的公式直接计算,家长应确保孩子对这些计算公式烂熟于心。
实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算,一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下:例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米. 解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积. 例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
小学数学几何图形九大解法

或 S 阴=7×4-4×4÷2=20(平方厘米) 例 2:已知下列两个等腰直角三角形,直角边分别是 10 厘米和 6 厘米。求 阴影部分的面积。
解:10-6=4(厘米) 6-4=2(厘米)S 阴=(6+2)×4÷2=16(厘米) 例 3:下图长方形长 9 厘米,宽 6 厘米,求阴影部分面积。
例 2:下图是一个等腰三角形,它的腰长是 20 厘米,面积是 144 平方厘米。 在底边上任取一点向两腰作垂线,得 a 和 b, 求 a+b 的和。
解:过顶点连接 a、b 的交点。 20b÷2+20a÷2=14410a+10b=144 a+b=14.4
九、看外高 例 1:下图两个正方形的边长分别是 6 厘米和 3 厘米,求阴影部分的面积。
八、代数法 例 1:图中三角形甲的面积比乙的面积少 8 平方厘米,AB=8cm,CE=6cm。 求三角形甲和三角形乙的面积各是多少?
解:设 AD 长为 Xcm。再设 DF 长为 Ycm。 8X+8=8(6+X)÷2X=44Y÷2+8=6(8-Y)÷2Y=3.2S 甲=4×3.2÷2=6.4 (c ㎡)S 乙=6.4+8=14.4(c ㎡)
数学 几何图形的九大解法
ห้องสมุดไป่ตู้五、等量代换 例 1:已知 AB 平行于 EC,求阴影部分面积。
解:因为 AB//EC 所以 S△AOE=S△BOC 则 S 阴=0.5S 长方形=10×8÷2=40 (㎡) 例 2:下图两个正方形边长分别是 6 分米、4 分米。求阴影部分面积。
解:因为 S1+S2=S3+S2=6×4÷2 所以 S1=S3 则 S 阴=6×6÷2=18(平方分米) 六、等腰直角三角形 例 1:已知长方形周长为 22 厘米,长 7 厘米,求阴影部分面积。
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
小学数学常见几何模型典型例题解题思路

小学数学常见几何模型典型例题及解题思路(1)巧求面积常用方法:直接求;整体减空白;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏斗等模型);差不变1、ABCG 是边长为12厘米的正方形,右上角是一个边长为6厘米的正方形FGDE ,求阴影部分的面积。
答案:72AHFECB I DG思路:1)直接求,但是阴影部分的三角形和四边形面积都无法直接求;2)整体减空白。
关键在于如何找到整体,发现梯形BCEF 可求,且空白分别两个矩形面积的一半。
2、在长方形ABCD 中,BE=5,EC=4,CF=4,FD=1。
△AEF 的面积是多少?答案:20ADB FCE思路:1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求3、如图所示的长方形中,E 、F 分别是AD 和DC 的中点。
(1)如果已知AB=10厘米,BC=6厘米,那么阴影部分面积是多少平方厘米?答案:22.5(2)如果已知长方形ABCD 的面积是64平方厘米,那么阴影部分的面积是多少平方厘米?答案:24B CD FE思路(1)直接求,无法直接求;2)已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型4、正方形ABCD 边长是6厘米,△AFD (甲)是正方形的一部分,△CEF (乙)的面积比△AFD (甲)大6平方厘米。
请问CE 的长是多少厘米。
答案:8ABD CF思路:差不变5、把长为15厘米,宽为12厘米的长方形,分割成4个三角形,其面积分别为S 1、S 2、S 3、S 4,且S 1=S 2=S 3+S 4。
求S 4。
答案:10DCF S 1S 2S 3S 4思路:求S4需要知道FC 和EC 的长度;FC 不能直接求,但是DF 可求,DF 可以由三分之一矩形面积S1÷AD ×2得到,同理EC 也求。
最后一句三角形面积公式得到结果。
6、长方形ABCD 内的阴影部分面积之和为70,AB=8,AD=15。
小学数学常见几何模型典型例题及解题思路

小学数学常见几何模型典型例题及解题思路(1)巧求面积常用方法:直接求;整体减空白;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏斗等模型);差不变1、ABCG 是边长为12厘米的正方形,右上角是一个边长为6厘米的正方形FGDE ,求阴影部分的面积。
.答案:72AHFECB I DG思路:1)直接求,但是阴影部分的三角形和四边形面积都无法直接求;2)整体减空白。
.关键在于如何找到整体,发现梯形BCEF 可求,且空白分别两个矩形面积的一半。
.2、在长方形ABCD 中,BE=5,EC=4,CF=4,FD=1。
△AEF 的面积是多少?答案:20ADB FCE思路:1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求3、如图所示的长方形中,E 、F 分别是AD 和DC 的中点。
(1)如果已知AB=10厘米,BC=6厘米,那么阴影部分面积是多少平方厘米?答案:22.5(2)如果已知长方形ABCD 的面积是64平方厘米,那么阴影部分的面积是多少平方厘米?答案:24B CD FE思路(1)直接求,无法直接求;2)已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型4、正方形ABCD 边长是6厘米,△AFD (甲)是正方形的一部分,△CEF (乙)的面积比△AFD (甲)大6平方厘米。
请问CE 的长是多少厘米。
答案:8ABD CF思路:差不变5、把长为15厘米,宽为12厘米的长方形,分割成4个三角形,其面积分别为S 1、S 2、S 3、S 4,且S 1=S 2=S 3+S 4。
求S 4。
答案:10DCEF S 1S 2S 3S 4思路:求S4需要知道FC 和EC 的长度;FC 不能直接求,但是DF 可求,DF 可以由三分之一矩形面积S1÷AD ×2得到,同理EC 也求。
最后一句三角形面积公式得到结果。
6、长方形ABCD 内的阴影部分面积之和为70,AB=8,AD=15。
八大类几何模型+60种解题技巧

一、常见的八大类几何模型在解决几何题目时,我们经常会遇到一些常见的几何模型。
这些模型包括但不限于:直角三角形、等腰三角形、等边三角形、直接相似三角形、等腰梯形、菱形、正方形和矩形。
1. 直角三角形直角三角形是一个内角为90度的三角形。
在求解直角三角形题目时,可以运用勾股定理、正弦定理、余弦定理等方法。
2. 等腰三角形等腰三角形是指两边相等的三角形。
在解决等腰三角形问题时,可以利用等角定理、等边角定理等。
3. 等边三角形等边三角形是指三边相等的三角形。
解决等边三角形问题时,可以利用等边三角形的性质,如高、中线等。
4. 直接相似三角形直接相似三角形是指对应角相等的两个三角形。
在对直接相似三角形进行解题时,可以利用相似三角形的性质,如边比例定理等。
5. 等腰梯形等腰梯形是指有两对对边相等的梯形。
解决等腰梯形问题时,可以运用梯形的性质以及各边的关系。
6. 菱形菱形是指四条边都相等的四边形。
在解决菱形问题时,可以利用菱形的性质,如对角线垂直平分、对角相等等。
7. 正方形正方形是指四条边相等且四个角均为直角的四边形。
解决正方形问题时,可以利用正方形的性质,如对角线相等、对角线垂直等。
8. 矩形矩形是指四边均为直角的四边形。
在解决矩形问题时,可以利用矩形的性质,如对角线相等、邻边互相垂直等。
二、60种解题技巧在解决几何题目时,我们还可以运用一些解题技巧来更快更准确地得出答案。
下面列举了60种解题技巧,以供参考。
1. 勾股定理2. 余弦定理3. 正弦定理4. 度角关系5. 弧度制下的两点间弧长相关关系6. 三角恒等变形7. 各角平分线8. 高度定理9. 中线定理10. 角平分线定理11. 等角定理12. 外角定理13. 内角定理14. 中位线定理15. 等腰三角形的性质16. 等边三角形的性质17. 相似三角形的三边对应比例关系18. 相似三角形的高度关系19. 相似三角形的边对应比例关系20. 相似三角形的面积关系21. 三角形高到底关系22. 三角形高乘底除以2的面积公式23. 三角形内切圆24. 三角形外接圆25. 正方形的性质26. 矩形的对角线关系27. 矩形的邻边互相垂直关系28. 长方形的面积公式29. 长方形的周长公式30. 菱形的性质31. 菱形对角线垂直平分32. 平行四边形的性质33. 平行四边形的对角线相等关系34. 平行四边形的对角互补35. 梯形的中位线关系36. 梯形的对角线垂直关系37. 梯形的高关系38. 圆的性质39. 圆周角的关系40. 圆心角的关系41. 切线关系42. 切线长定理43. 余弦定理的推广44. 余角关系45. 同位角关系46. 交叉线定理47. 锐角三角函数的关系48. 平行线夹角关系49. 余切函数的关系50. 同义形的面积公式51. 直角三角形斜边上的高52. 各角平分线角度关系53. 三角形中位线长度关系54. 三角形中位线平行长的关系55. 等角三角形三角函数的关系56. 三角形半周长乘外切圆内切圆面积关系57. 圆相关不等式58. 反证法59. 斜率性质60. 坐标系下平移关系解决几何问题时,首先要熟练掌握常见的八大类几何模型,然后灵活运用各种解题技巧,以便更加高效地解决问题。
小学奥数几何五大模型
(4)相似模型1、相似三角形:形状相同、大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论:因为DE BC ∥,所以ADE ABC △∽△,则①AD AE DE==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?GFE D CBA解析:把另外三个三等分点标出之后,正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接,这样就把整个正方形分割成了9个形状各不相同的三角形,同时我们把空白部分的6个三角形按顺时针标记1~6。
这9个三角形的底边都是正方形边长的三分之一;阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知,CD 边上的阴影三角形的面积与第1、2个三角形相等;BC 边上的阴影三角形与第3、4个三角形相等;AB 边上的阴影三角形与第5、6个三角形相等。
因此,阴影面积是空白面积的二分之一,是正方形面积的三分之一,即:12×12÷3=48。
例2、如图所示,Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点,且DQ CP ME 、、彼此平行,已知5753AD BC AE EB ====、、、,求阴影部分三角形PQM 的面积。
小升初奥数几何五大模型经典例题

【奥数】小升初几何五大模型经典例题二、五大模型经典例题详解(1)等积变换模型例1、图中的E、F、G分别是正方形ABCD三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?例2、如图所示,Q、E、P、M分别为直角梯形ABCD两边AB、CD上的点,且DQ、CP、ME彼此平行,已知AD=5、BC=7、AE=5、EB=3,求阴影部分三角形PQM的面积。
(2)鸟头(共角)定理模型例1、如图所示,平行四边形ABCD,BE=AB、CF=2CB、GD=3DC、HA=4AD,平行四边形ABCD的面积为2,求平行四边形ABCD与四边形EFGH的面积比。
例2、如图所示,△ABC的面积为1,BC=5BD、AC=4EC、DG=GS=SE、AF=FG,求△FGS的面积。
(3)蝴蝶模型例1、如图,正六边形面积为1,那么阴影部分面积为多少?例2、如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,求余下的四边形OFBC的面积。
例3、如图,已知正方形ABCD的边长为10厘米,E为AD的中点,F为CE的中点,G 为BF的中点,求三角形BDG的面积。
例1、如图,正方形的面积为1,E、F分别为AB、BD的中点,GC=1/3FC,求阴影部分的面积。
例2、如图,长方形ABCD,E为AD的中点,AF与BD、BE分别交于G和H,OE垂直于AD,交AD于E点,交AF于O点,已知AH=5,HF=3,求AG的长。
例1、如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,求四边形BGHF的面积。
例2、如图,在△ABC中,BD=2DA、CE=2EB、AF=2FC,那么△ABC的面积是阴影△GHI 面积的几倍?例3、如图,在△ABC中,点D是AC的中点,点E、F是BC的三等分点,若△ABC的面积是1,求四边形CDMF的面积。
小学数学常见几何模型典型例题及解题思路

小学数学常见几何模型典型例题及解题思路( 1 )巧求面积常用方法:直接求;整体减空白;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏斗等模型);差不变1、ABCG 是边长为 12 厘米的正方形,右上角是一个边长为 6 厘米的正方形 FGDE,求阴影部分的面积。
答案: 72F EA HDI GB C思路: 1)直接求,但是阴影部分的三角形和四边形面积都无法直接求;2 )整体减空白。
关键在于如何找到整体,发现梯形 BCEF可求,且空白分别两个矩形面积的一半。
2、在长方形 ABCD 中,BE=5 ,EC=4 ,CF=4 ,FD=1 。
△AEF 的面积是多少?答案: 20A DFB E C思路: 1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求3、如图所示的长方形中,E、F 分别是 AD 和 DC 的中点。
(1)如果已知 AB=10 厘米, BC=6 厘米,那么阴影部分面积是多少平方厘米?答案:22.5(2)如果已知长方形 ABCD 的面积是 64 平方厘米,那么阴影部分的面积是多少平方厘米?答案:24D F CEA B思路( 1)直接求,无法直接求; 2 )已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型4、正方形 ABCD 边长是 6 厘米,△AFD(甲)是正方形的一部分,△CEF(乙)的面积比△AFD(甲)大 6 平方厘米。
请问 CE 的长是多少厘米。
答案: 8A DFB C E思路:差不变5、把长为 15 厘米,宽为 12 厘米的长方形,分割成 4 个三角形,其面积分别为 S1 、S2 、S3 、S4 ,且 S1=S 2=S 3 +S 4。
求 S4。
答案: 10AS1DS2 S3FS4B E C思路:求 S4 需要知道 FC 和 EC 的长度; FC 不能直接求,但是 DF可求,DF 可以由三分之一矩形面积S1÷AD ×2 得到,同理 EC 也求。
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
小学数学《几何图形题9大解法归纳》含例题

小学数学《几何图形题9大解法归纳》含例题分割法▌例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)解:将图形分割成两个全等的梯形。
S组=(7-2+7)×2÷2×2=24(平方厘米)▌例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
解:将图形分割成3个三角形。
S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米)▌例3:左图中两个正方形边长分别为8厘米和6厘米。
求阴影部分面积。
解:将阴影部分分割成两个三角形。
S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米)添辅助线▌例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。
S阴=4×4÷2=8(平方厘米)▌例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?解:因为添一条辅助线平行于三角形一条边,发现40平方厘米是一个平行四边形。
所以梯形下底:40÷8=5(厘米)▌例3:平行四边形的面积是48平方厘米,BC分别是这个平行四边形相邻两条边的中点,连接A、B、C得到4个三角形。
求阴影部分的面积。
解:如果连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。
S阴=48÷8×3=18(平方厘米)倍比法▌例1:已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。
解:因为OC=2AO,所以SBOC=2×2=4(㎡)SDOC=4×2=8(㎡)SABCD=2+4×2+8=18(㎡)▌例2:已知S阴=8.75㎡,求下图梯形的面积。
小学数学五大经典几何图形模型及解题思路精讲

小学数学五大经典几何图形模型及解题思路精讲1、等积变换模型(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积之比等于底之比;(3)两个三角形底相等,面积在之比等于高之比;(4)在一组平行线之间的等积变形。
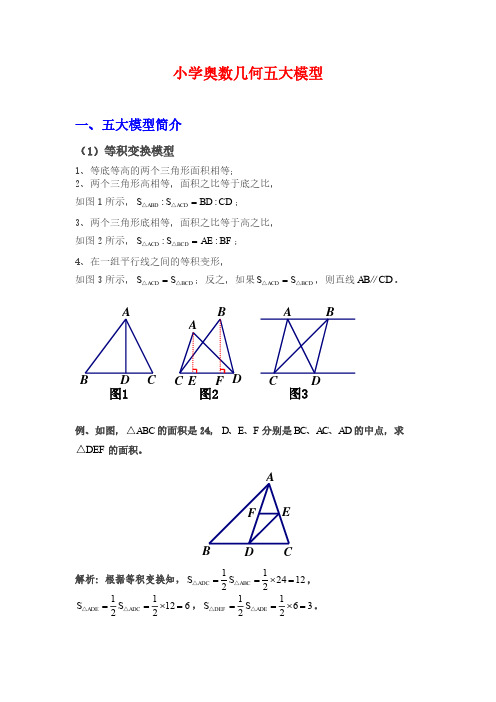
【例题】如图,三角形A B C的面积是24,D、E、F分别是B C、A C、A D的中点,求三角形DE F的面积。
2、鸟头(共角)定理模型(1)两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;(2)共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
【例题】如图在△A B C中,D在B A的延长线上,E在AC上,且A B:A D=5:2,AE:E C=3:2,△A D E的面积为12平方厘米,求△ABC的面积。
3、蝴蝶模型(1)梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(因为S△ABC= S△DBC,所以S△ABC-S△OBC= S△DBC-S△OBC)S1:S3=a2:b2②S1:S3:S2:S4= a2:b2:ab:ab③梯形S的对应份数为(a+b)2。
(2)任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3或者S1×S3=S4×S2;②AO:OC=(S1+S2):(S4+S3)蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径,通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例题】如图,己知正方形AB C D的边长为10厘米,E为AD的中点,F为CE的中点,G为B F的中点,求三角形BD G的面积。
4、相似模型(1)相似三角形:形状相同,大小不相等的两个三角形相似。
(2)寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
(3)相似三角形性质①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
(完整版)小学数学常见几何模型典型例题及解题思路

小学数学常见几何模型典型例题及解题思路(1)巧求面积常用方法:直接求;整体减空白;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏斗等模型);差不变1、ABCG 是边长为12厘米的正方形,右上角是一个边长为6厘米的正方形FGDE ,求阴影部分的面积。
答案:72AHFECB I DG思路:1)直接求,但是阴影部分的三角形和四边形面积都无法直接求;2)整体减空白。
关键在于如何找到整体,发现梯形BCEF 可求,且空白分别两个矩形面积的一半。
2、在长方形ABCD 中,BE=5,EC=4,CF=4,FD=1。
△AEF 的面积是多少?答案:20ADB FCE思路:1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求3、如图所示的长方形中,E 、F 分别是AD 和DC 的中点。
(1)如果已知AB=10厘米,BC=6厘米,那么阴影部分面积是多少平方厘米?答案:22.5(2)如果已知长方形ABCD 的面积是64平方厘米,那么阴影部分的面积是多少平方厘米?答案:24B CD FE思路(1)直接求,无法直接求;2)已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型4、正方形ABCD 边长是6厘米,△AFD (甲)是正方形的一部分,△CEF (乙)的面积比△AFD (甲)大6平方厘米。
请问CE 的长是多少厘米。
答案:8ABD CF思路:差不变5、把长为15厘米,宽为12厘米的长方形,分割成4个三角形,其面积分别为S 1、S 2、S 3、S 4,且S 1=S 2=S 3+S 4。
求S 4。
答案:10DCEF S 1S 2S 3S 4思路:求S4需要知道FC 和EC 的长度;FC 不能直接求,但是DF 可求,DF 可以由三分之一矩形面积S1÷AD ×2得到,同理EC 也求。
最后一句三角形面积公式得到结果。
6、长方形ABCD 内的阴影部分面积之和为70,AB=8,AD=15。
(完整版)小学数学常见几何模型典型例题及解题思路

(完整版)⼩学数学常见⼏何模型典型例题及解题思路⼩学数学常见⼏何模型典型例题及解题思路(1)巧求⾯积常⽤⽅法:直接求;整体减空⽩;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏⽃等模型);差不变1、ABCG 是边长为12厘⽶的正⽅形,右上⾓是⼀个边长为6厘⽶的正⽅形FGDE ,求阴影部分的⾯积。
答案:72AHFECB I DG思路:1)直接求,但是阴影部分的三⾓形和四边形⾯积都⽆法直接求;2)整体减空⽩。
关键在于如何找到整体,发现梯形BCEF 可求,且空⽩分别两个矩形⾯积的⼀半。
2、在长⽅形ABCD 中,BE=5,EC=4,CF=4,FD=1。
△AEF 的⾯积是多少?答案:20ADB FCE思路:1)直接求,⽆法直接求;2)由于知道了各个边的数据,因此空⽩部分的⾯积都可求3、如图所⽰的长⽅形中,E 、F 分别是AD 和DC 的中点。
(1)如果已知AB=10厘⽶,BC=6厘⽶,那么阴影部分⾯积是多少平⽅厘⽶?答案:22.5(2)如果已知长⽅形ABCD 的⾯积是64平⽅厘⽶,那么阴影部分的⾯积是多少平⽅厘⽶?答案:24B CD FE思路(1)直接求,⽆法直接求;2)已经知道了各个边的数据,因此可以求出空⽩的位置;3)也可以利⽤鸟头模型4、正⽅形ABCD 边长是6厘⽶,△AFD (甲)是正⽅形的⼀部分,△CEF (⼄)的⾯积⽐△AFD (甲)⼤6平⽅厘⽶。
请问CE 的长是多少厘⽶。
答案:8ABD CF思路:差不变5、把长为15厘⽶,宽为12厘⽶的长⽅形,分割成4个三⾓形,其⾯积分别为S 1、S 2、S 3、S 4,且S 1=S 2=S 3+S 4。
求S4。
答案:10DCEF S 1S 2S 3S 4思路:求S4需要知道FC 和EC 的长度;FC 不能直接求,但是DF 可求,DF 可以由三分之⼀矩形⾯积S1÷AD ×2得到,同理EC 也求。
最后⼀句三⾓形⾯积公式得到结果。
6、长⽅形ABCD 内的阴影部分⾯积之和为70,AB=8,AD=15。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学常见几何模型典型例题及解题思路(1)巧求面积常用方法:直接求;整体减空白;不规则转规则(平移、旋转等);模型(鸟头、蝴蝶、漏斗等模型);差不变1、ABCG 是边长为12厘米的正方形,右上角是一个边长为6厘米的正方形FGDE ,求阴影部分的面积。
答案:72AHFECB I DG思路:1)直接求,但是阴影部分的三角形和四边形面积都无法直接求;2)整体减空白。
关键在于如何找到整体,发现梯形BCEF 可求,且空白分别两个矩形面积的一半。
2、在长方形ABCD 中,BE=5,EC=4,CF=4,FD=1。
△AEF 的面积是多少?答案:20ADB FCE思路:1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求3、如图所示的长方形中,E 、F 分别是AD 和DC 的中点。
(1)如果已知AB=10厘米,BC=6厘米,那么阴影部分面积是多少平方厘米?答案:22.5(2)如果已知长方形ABCD 的面积是64平方厘米,那么阴影部分的面积是多少平方厘米?答案:24B CD FE思路(1)直接求,无法直接求;2)已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型4、正方形ABCD 边长是6厘米,△AFD (甲)是正方形的一部分,△CEF (乙)的面积比△AFD (甲)大6平方厘米。
请问CE 的长是多少厘米。
答案:8ABD CF思路:差不变5、把长为15厘米,宽为12厘米的长方形,分割成4个三角形,其面积分别为S 1、S 2、S 3、S 4,且S 1=S 2=S 3+S 4。
求S 4。
答案:10DCEF S 1S 2S 3S 4思路:求S4需要知道FC 和EC 的长度;FC 不能直接求,但是DF 可求,DF 可以由三分之一矩形面积S1÷AD ×2得到,同理EC 也求。
最后一句三角形面积公式得到结果。
6、长方形ABCD 内的阴影部分面积之和为70,AB=8,AD=15。
求四边形EFGO 的面积。
答案10。
ABCDFOEG思路:看到长方形和平行四边形,只要有对角线,就知道里面四个三角形面积相等。
然后依据常规思路可以得到答案。
思路2:从整体看,四边形EFGO的面积=△AFC的面积+△BFD的面积-空白部分的面积。
而△ACF的面积+△BFD的面积=长方形面积的一半,即60。
空白部分的面积等于长方形面积减去阴影部分的面积,即120-70=50 。
所以四边形的面积EFGO的面积为60-50=10。
比例模型1、如图,AD=DB,AE=EF=FC。
已知阴影部分面积为5平方厘米,△ABC的面积是多少平方厘米?答案30平方厘米。
A DBE FC思路:由阴影面积求整个三角形的面积,因此需要构造已知三角的面积和其它三角形的面积比例关系,而题目中已经给了边的比,因此依据等高模型或者鸟头模型即可得到答案。
2、△ABC的面积是180平方厘米,D是BC的中点,AD的长是AE的3倍,EF的长是BF的3倍,那么△AEF的面积是多少平方厘米?答案22.5平方厘米ABCDFE思路:仅仅告诉三角形面积和边的关系,需要依据比例关系进行构造各个三角形之间的关系,从而得出答案 3、在四边形ABCD 中,E ,F 为AB 的三等分点,G ,H 为CD 的三等分点。
四边形EFHG 的面积占总面积的几分之几?答案是1/3ABCDEFG HABCDEFG H思路:仅仅告诉边的关系,求四边形之间的关系,需要首先考虑如何分解为三角形,然后再依次求解。
4、在四边形ABCD 中,ED :EF :FC=3:2:1,BG :GH :AH=3:2:1,已知四边形ABCD 的面积等于4,则四边形EHGF 的面积是多少?答案4/3ABCDGH FEABCDGH FE5、 在△ABC 中,已知△ADE 、△DCE、△BCD 的面积分别是89,28,26,那么三角形DBE 的面积是多少?答案178/9ACB DE思路:需要记住反向分解三角形,从而求面积。
6、在角MON 的两边上分别有A 、C 、E 及B 、D 六个点,并且△OAB 、△ABC 、△BCD 、△CDE 、△DEF 的面积都等于1,则△DCF 的面积等于多少?答案3/47、四边形ABCD的面积是1,M、N是对角线AC的三等分点,P、Q是对角线BD的三等分点,求阴影部分的面积?答案1/9A BDCPQM N一半模型比例模型---共高模型一半模型蝴蝶模型(漏斗,金字塔)鸟头模型燕尾模型风筝模型切记梯形的一半模型(沿着中线变化)切记任意四边形的一半模型1、在梯形ABCD中,AB与CD平行,点E、F分别是AD和BC的中点。
△AMB 的面积是3平方厘米,△DNC 的面积是7平方厘米。
1)△AMB 和△DNC 的面积和等于四边形EMFN 的面积; 2)阴影部分的面积是多少平方厘米。
DC思路:一种应用重叠=未覆盖思路:将各个三角形标记,应用两个一半模型=整体梯形 2、任意四边形ABCD ,E 、F 、G 、H 分别为各边的中点。
证明四边形EFGH 的面积为四边形ABCD 面积的一半。
A BDCEGFHA BDCA BDCEGFHEGFH3、四边形ABCD 中,E 、F 、G 、H 分别是各边的中点。
求阴影部分与四边形PQRS 的面积比。
答案相等C思路:依次应用一半模型和重叠等于未覆盖。
证明需要分别连接BD 和AC 。
4、已知M 、N 分别为梯形两腰的中点,E 、F 为M 、N 上任意两点。
已知梯形ABCD 的面积是30平方厘米,求阴影部分的面积。
答案:15ABD CMNEF5、已知梯形ABCD 的面积是160,点E 为AB 的中点,DF :FC=3:5。
阴影部分的面积为多少。
答案:30A B CE F鸟头模型1、 已知△ABC 面积为1,延长AB 至D ,使BD=AB ;延长BC 至E ,使CE=2BC ,延长CA 至F ,使AF=3AC 。
求△DEF 的面积。
答案:18FEDA BC思路:依次使用鸟头模型,别忘了最终还需要加上△ABC 的面积。
2、 在平行四边形ABCD 中,BE=AB ,CF=2CB ,GD=3DC ,HA=4AD ,平行四边形的面积是2,四边形EFGH 的面积是多少?答案:36AB CDGHEF3、 四边形EFGH 的面积是66平方米,EA=AB ,CB=BF ,DC=CG ,HD=DA ,求四边形ABCD 的面积?答案:13.2AB C DGHEF4、5、 将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延伸两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是多少?答案:60GHEFB ACD思路:依次使用两类不同鸟头模型,别忘了最终还需要减去一个四边形ABCD 的面积。
6、7、 在三角形ABC 中,延长AB 至D ,使BD=AB ,延长BC 至E ,使CE=1/2BC ,F 是AC 的中点,若三角形ABC 的面积是2,则三角形DEF 的面积是多少?答案:3.5ABFCED ABFCED思路:分割所求三角形,分别应用比例模型和鸟头模型。
8、9、 △ABC 中,延长BA 到D ,使DA=AB ,延长CA 到E ,使EA=2AC ,延长CB 到F ,使FB=3BC ,如果△ABC 的面积是1,那么△DEF 的面积是多少?答案:7ACDFE思路:△ABC 和△EFC 是鸟头模型,从而求出四边形ABEF 的面积,△ABC 和△AED 是鸟头模型,从而求出△AED 面积,从而 解题小技巧:1,答案为5ABDCO104?22、总面积为52,其中两个分别为6,7,另外两个分别是多少?答案18,21ABDCOX 6Y 73、在△ABC 中,已知M ,N 分别在AC 、BC 上,BM 与AN 相交于点O 。
若△AOM ,△ABO 和△BON 的面积分别是3,2,1,则△MNC 的面积是多少?答案22.5。
ABCNMO风筝模型求出△MON=1.5;△ANM :△MNC=△ABM :△BMC (3+1.5):x=(3+2):(1+1.5+x )。
