第3讲-主应力及主切应力
材料力学 主应力

材料力学主应力主应力是材料力学中的一个重要概念,它是指在一个物体内部某一点上的一个力对应的应力。
主应力的研究对于了解材料的力学性能和变形行为具有重要意义。
本文将从主应力的定义、计算以及应用等方面进行阐述。
我们来了解一下主应力的定义。
主应力是指在一个点上的一个力对应的应力,它是力对应的作用面上的单位面积上的力的大小。
主应力可以分为正应力和负应力,正应力是指某一面上的应力向外作用,而负应力则是指某一面上的应力向内作用。
主应力的大小可以通过实验或计算来得到,它是材料力学中的一个重要参数,可以用来描述材料受力情况下的变形行为。
我们来介绍一下主应力的计算方法。
主应力的计算可以通过应力分析或应力变换的方法来进行。
在应力分析中,可以通过测量力的大小和作用面积的大小来计算主应力的大小。
在应力变换中,可以通过施加不同方向的力来计算主应力的大小。
主应力的计算方法较为复杂,需要具备一定的数学和力学基础。
然后,我们来讨论一下主应力的应用。
主应力的应用非常广泛,它可以用来分析材料的强度和变形性能。
在工程设计中,主应力可以用来评估材料的承载能力和安全性。
在材料加工中,主应力可以用来控制材料的变形和裂纹的产生。
在材料测试中,主应力可以用来评估材料的力学性能和耐久性。
总之,主应力在材料力学中具有重要的应用价值。
我们来总结一下主应力的重要性。
主应力是材料力学中的一个重要概念,它是描述材料受力情况下的变形行为的重要参数。
主应力的计算和应用对于了解材料的力学性能和变形行为具有重要意义。
研究主应力可以帮助我们更好地理解材料的力学行为,为工程设计和材料加工提供科学依据。
因此,主应力的研究具有重要的理论和实际意义。
主应力是材料力学中的一个重要概念,它是描述材料受力情况下的变形行为的重要参数。
主应力的计算和应用对于了解材料的力学性能和变形行为具有重要意义。
通过研究主应力,我们可以更好地理解材料的力学行为,为工程设计和材料加工提供科学依据。
希望本文能够帮助读者对主应力有更深入的了解。
三向应力状态求主应力和最大切应力

三向应力状态求主应力和最大切应力咱们来一起了解一个特别有趣的东西,就像在玩一个超级有挑战性的游戏一样。
这个东西就是三向应力状态下求主应力和最大切应力。
先来说说应力是什么吧。
想象一下,你有一块小橡皮,你用手捏它、拉它或者压它,橡皮里面就会有那种抵抗你用力的感觉,这个就是应力啦。
就像你拉一个弹簧,弹簧会有一股劲儿想恢复原来的样子,这个劲儿就有点像应力。
那三向应力状态呢?咱们把这个小橡皮放在一个小盒子里,这个盒子从三个方向都对橡皮有作用,就好像上下左右前后都在给它压力或者拉力,这就是三向应力状态啦。
现在咱们来求主应力。
主应力就像是一群小伙伴里的小队长。
比如说在一个班级里,大家做游戏分组的时候,每个小组都有一个组长。
主应力就是在应力这个大家庭里比较特殊的“组长”。
怎么找到这个“组长”呢?咱们可以想象一个小正方体的泥巴块,这个泥巴块各个面都受到不同的力。
我们要找到这样的力,当这个泥巴块按照这个力的方向变形的时候,它不会歪着变形,而是直直地变形。
这个时候的力就是主应力啦。
我给你们讲个小故事哦。
有一个小木偶,它的身体就像我们说的那个泥巴块。
小木偶的胳膊、腿和身体各个部分都被不同的小绳子拉着或者推着,就像泥巴块各个面受力一样。
小木偶想要直直地站着或者动起来,它就需要找到那些主要的力量方向,就像我们找主应力一样。
再来说最大切应力。
切应力就像是你拿一把小刀去切一块软软的蛋糕时,蛋糕抵抗你切它的那种力。
最大切应力呢,就是这些切应力里最大的那个。
还是说那个小泥巴块,在它受到不同方向的力的时候,它的里面就会有切应力。
就像你把泥巴块想象成是一个装满水的小盒子,你要是扭这个盒子,水就会晃来晃去,这个晃的感觉就有点像切应力。
比如说,咱们有一块软软的豆腐,你用不同的板子从不同的方向去压豆腐,豆腐里面就会有应力。
豆腐可能会被压得变形,这个变形就和应力有关系。
而在这些应力里,我们就能找到主应力和最大切应力。
知道了三向应力状态下的主应力和最大切应力有什么用呢?这就像我们知道了怎么让小木偶更好地动起来,或者怎么让豆腐被压的时候按照我们想要的方式变形一样。
第三章 应力分析

σx τxy τxz σy yx τ τyz Sx τzy σz τzx By Sz S= σ Sy N
A x
主平面上的应力
S x = σ l , S y = σ m, S z = σ n S x = σl = σ x l + τ yx m + τ zx n ⎫
⎪ S y = σm = τ xy l + σ y m + τ zy n⎬ ⎪ S z = σn = τ xz l + τ yzx m + σ z n ⎭
S y dF − σ y mdF − τ xy ldF − τ zy ndF = 0
写成矩阵形式:
z C σ τx
y x
dF N σ Sz S Sy Sx O τz
y z
斜面上全应力为: 斜面上切应力为:
S = Sx + S y + Sz
2 2 2
2
σ
y z
τx τy
x z
σ = S xl + S y m + S z n
F0
P
N θ
σ0
σθ C F1 C1 Q Q
P P ⎧ C ⎪ Sθ = F = F cos θ = σ 0 cos θ 1 0 ⎪ ⎪ 2 ⎨σ θ = Sθ cos θ = σ 0 cos θ ⎪ 1 ⎪τ θ = Sθ sin θ = σ 0 cos θ sin θ = σ 0 sin 2θ 2 ⎪ ⎩
SN = σ N +τ N
2 2
2
3.2 点应力状态
点应力状态:点的应力状态,是指物体内任意一点附近不同方位上所承 受的应力情况,必须了解物体内任意一点的应力状态,才可推断整个变 形物体的应力状态。 1、一点应力状态的两种描述方法 第一种方法:应力状态图 在变形区内某点附近取一无限小的单元六面体,在其每个界面上都 作用着一个全应力,设单元体很小,可视为一点,故对称面上的应力是 相等的,只需在三个可见的面上画出全应力:
应力不变量,主应力,最大切应力

主题:应力不变量、主应力和最大切应力的意义和计算方法摘要:本文将介绍应力不变量、主应力和最大切应力的概念及其在工程实践中的重要性,同时分析其计算方法和影响因素,旨在帮助读者更深入地理解应力分析的相关概念。
一、概述在工程实践中,应力分析是非常重要的一项工作。
而应力不变量、主应力和最大切应力则是应力分析中的一些重要概念,对工程结构的强度和稳定性有着重要的影响。
本文将对这些概念进行深入探讨,介绍其计算方法和作用机理。
二、应力不变量的意义和计算方法应力不变量是描述应力状态的一个重要参数。
它是应力张量的三个主应力的平均值,代表了系统中应力的均匀分布程度。
应力不变量的计算方法是将应力张量表示成矩阵形式,然后利用矩阵运算求得其不变量。
在工程实践中,应力不变量的大小直接影响着材料的变形和破坏行为,因此对于工程设计来说具有重要意义。
三、主应力的概念及其作用主应力是应力张量的三个特征值,代表了应力状态的主要特征。
主应力的大小和方向决定了材料在受力时的变形和破坏模式,因此对于工程结构的强度分析非常重要。
在实际工程中,通过对主应力的计算和分析,工程师可以更好地预测材料的破坏行为,从而有针对性地进行结构设计和改进。
四、最大切应力的意义和计算最大切应力是应力张量中剪应力分量的最大值,代表了材料在受力时的最大切应力情况。
在材料变形和破坏过程中,最大切应力往往是导致材料失效的主要因素之一。
对最大切应力的计算和分析对于工程设计来说至关重要,能够有效地预测材料的破坏情况,从而指导工程实践中的结构设计和材料选择。
五、应力不变量、主应力和最大切应力的影响因素除了介绍这些概念的意义和计算方法之外,本文还将分析应力不变量、主应力和最大切应力的影响因素。
材料的物理性质、载荷的作用方式以及结构的几何形状等都会对这些应力参数产生影响。
了解这些影响因素有助于工程师更好地进行应力分析和结构设计。
六、结论通过对应力不变量、主应力和最大切应力的深入探讨,我们可以更好地理解这些应力参数在工程实践中的重要性和作用机理。
主切应力和最大切应力--材料成型原理
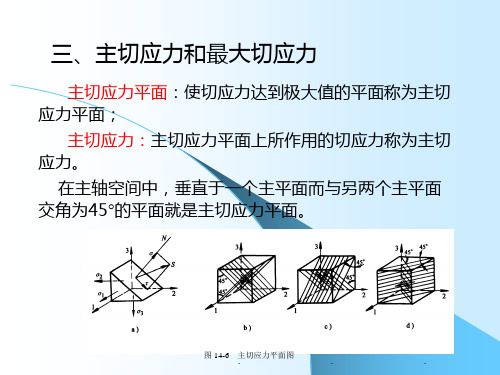
主切应力平面:使切应力达到极大值的平面称为主切 应力平面;
主切应力:主切应力平面上所作用的切应力称为主切 应力。
在主轴空间中,垂直于一个主平面而与另两个主平面 交角为45的平面就是主切应力平面。
图 14-6 主切应力平面图
22
1
1
1
a ) l 0, m2 n2 1 b )l 0, m n 1 c )m 0,l n 1 d )
表示。 设三个主应力的关系为 1 2 3 ,则
max
1 3
2
(14-19)
主切应力平面上的正应力值和主切应力值
12
1
2
2
;
23
2
3
2
;
31
3
2
1
;
12 23 31
1 2 3
2
2
3
2
1
2
(14-20)
主切应力的性质:
• 若1=2=3=,即变形体处于三向等拉或三向等压 的应力状态(即球应力状态)时,主切应力为零: 12=23=31=0
由此得
( x
x x
dx)dydz
x dydz
(
yx
yx y
dy)dzdx
y xdzdx
( zx
zx z
dz)dxdy zx dxdy 0
x yx zx 0
x y z
得质点的应力平衡微分方程
x
x
yx
y
zx
z
0
xy
x
y
y
zy
z
0
xz
x
yz
• 若三个主应力同时增加或减少一个相同的值时,主切 应力值将保持不变。
第3讲-主应力及主切应力

2020/8/15
21
Lesson 5
同理可求得2、3的方向余弦
2
z
l 0
l 0
m 1 或
n 0
m 1 n 0
3
1
3
x
l 0.862
l 0.862
m 0 或 m 0
n 0.507
n 0.507
2020/8/15
22
2020/8/15
11
Lesson 5
主应力的特点
三个主应力所作用的主微分面是相互垂直的
将主应力1代入(*)式中的任何两个方程, 并与(**)式联立,可以求解出主应力1的
方向余弦l1、m1、n1,同理,可以求解出主
应力2及3的方向余弦l2、m2、n2及l3、m3、
n3 。 每两个主应力的方向余弦之间满足以下关系
第五讲 Lesson Five
张贵杰
Zhang Guijie
Tel:0315-2592155 E-Mail: zhguijie@
河北理工大学金属材料与加工工程系 Department of Metal Material and Process Engineering Hebei Polytechnic University, Tangshan 063009
2020/8/15
17
Lesson 5
对此方程组求解分不同情况
当1≠2≠3时,
1)l m 0, n 1 ,此解指主微分面上切应力为零
2)l 0, m 0 时, l 1 m 0 n 1
2
2
3)l 0, m 0 时, l 0 m 1 n 1
2
2
4)l 0, m 0 时,此种情况不可能成立。
第三章力学基础(应力分析)

主应力
4 2 3
例题:已知点的应力状态 ij 2 6 1 ,求其
3 1 5
的主应力、主方向。(应力单位:MPa)
解:
J1 x y z 4 6 5 15
J2
(
x
y
y
z
z
x)
2 xy
2 yz
2 zx
(24 30 20) 4 1 9 60
x xy xz 4 2 3 J3 xy y yz 2 6 1 120 6 6 20 4 54
)l ( y
yxm )m
zxn zyn
0 0
xzl yz m ( z )n 0
主应力
➢ 由于 l 2 m2 n2 1 ,因此l、m、n不同时为零 则三元齐次方程组的系数矩阵一定等于零
x xy xz
yx y
yz
yz zy 0 z
展开方程组系数矩阵,可得
3 J1 2 J2 J3 0
主应力
➢应力状态特征方程
3 J1 2 J2 J3 0
式中 J1 x y z
J2
( x y
y z
z
x
)
2 xy
2 yz
2 zx
J3
x y z
2 xy yz zx
x
2 yz
y
2 zx
z
2 xy
主应力
➢ 应力状态特征方程 3 J1 2 J2 J3 0 的三
xl2 ym2 zn2 2( xylm yzmn zxnl) 即 ijlil j
2 n
S2
2 n
如何求解斜面上的应力
例题说明
➢ 已知某点应力张量为
ij yxx
xy y
xz yz
材料力学主应力知识点总结

材料力学主应力知识点总结材料力学是研究物质在外力作用下变形和破坏的学科,主应力是材料受力引起的应变状态中所表现出来的应力。
主应力是材料力学中的重要知识点,本文将对主应力的概念、计算方法以及其应用进行总结。
一、主应力的概念主应力指的是在某个特定方向上的最大和最小应力。
根据材料在不同应力状态下的表现,主应力可分为拉应力和压应力。
拉应力是指某一方向上的应力值为正值,而压应力则是指某一方向上的应力值为负值。
二、主应力的计算方法主应力的计算可以通过应力转换公式来实现。
对于平面应力状态下的主应力计算,我们可以使用著名的Mohr圆方法。
该方法通过绘制Mohr圆图来确定主应力的数值。
绘制Mohr圆图的步骤如下:1. 根据给定的平面应力状态下的两个主应力值,构建一个坐标系。
2. 在坐标系中找到两个主应力值所对应的坐标点,分别标记为A和B。
3. 以点A和B为圆心,AB的长度为半径作圆弧,确定一个圆。
根据圆的性质,圆弧与横轴和纵轴相交的两点分别为两个主应力值的坐标点。
4. 连接圆心和两个主应力值的坐标点,得到两条线段,分别表示两个主应力的方向。
5. 从圆心开始,沿着圆弧方向的逆时针方向旋转90度,该方向所对应的弧度为斜面上的剪应力最大值。
三、主应力的应用主应力是材料力学中常用的计算参数,具有广泛的应用价值。
下面介绍几个主应力的应用场景:1. 设计材料和结构:在工程设计过程中,了解主应力及其分布情况对材料的选择和结构的设计至关重要。
通过对主应力的计算和分析,可以确定材料的最大承载能力,从而确保结构的安全性和耐久性。
2. 破坏分析:主应力可以用于破坏分析,即通过判断主应力是否超过材料的极限强度来预测材料的破坏。
如果主应力超过了材料的极限强度,则材料可能发生破坏或变形。
3. 应力集中分析:在实际工程中,往往存在应力集中的情况,即某一点或某一区域的应力值明显高于周围区域。
主应力可以用于分析应力集中的位置和程度,进而指导设计和加强工艺。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/8/15
11
Lesson 5
主应力的特点
三个主应力所作用的主微分面是相互垂直的
将主应力1代入(*)式中的任何两个方程, 并与(**)式联立,可以求解出主应力1的
方向余弦l1、m1、n1,同理,可以求解出主
应力2及3的方向余弦l2、m2、n2及l3、m3、
n3 。 每两个主应力的方向余弦之间满足以下关系
l1l2 m1m2 n1n2 0
l2l3 m2m3 n2n3 0
l3l1 m3m1 n3n1 0
2020/8/15
12
Lesson 5
三个主应力均为实根 主应力具有极值性质
三个主应力中的最大值赋给1,最小值赋给 3,并按大小顺序排列1≥2≥3,则过该 点任意微分斜面上的正应力中,1为最大值, 3为最小值。
1 0 0 T 0 2 0
0 0 3
为主应力张量
正应力 n 1l 2 2m2 3n2
2020/8/15
15
Lesson 5
10.4.2 主切应力和最大切应力
主切应力
任意微分斜面上的切应力也有极大值和最大值。 极值切应力又称为主切应力。
在主坐标系下,任意微分斜面上的切应力
展开后得
1 2 3 0
3 1 2 3 2 1 2 2 3 31 1 2 3 0
由代数学可知,具有相同的根的方程是全等方 程,因此该式与应力状态特征方程全等。有
2020/8/15
10
应力张量不变量
Lesson 5
I1 x y z 1 2 3
2 n
1
2 2 l 2m2
2
3 2 m2n2
3
1 2 n2l 2
上式中消去n,得到n与l、m的函数关系
2 n
12
2 3
l2
2 2
2 3
m2
2 3
1 3
l2 2 3
m2 3
2
2020/8/15
16
Lesson 5
当微分面转动时,切应力随之变化。我们所求 的是,当l、m、n为何值时,微分面上的切应 力取极值。由二元函数f(x,y)求极值的方法可求 得微分面上的切应力的极值。
I2 x y y z z x
2 xy
2 yz
2 zx
1 2 2 3 3 1
I3
x y z
2 xy yz zx
x
2 yz
y
2 zx
z
2 xy
1 2 3
对同一点应力状态,三个主应力的数值是一定的,而
与过该点的坐标系的选择无关,不管应力分量怎样随坐 标系改变。那么I1、I2、I3 是不随坐标系改变的,分别称 为一次、二次和三次应力常量,或称为应力张量不变量。
f
(l,
m)
2 n
2 1
2 3
l2
2 2
z x
(
2 xy
2 yz
zx2 )
I3
x y z
2 xy yz zx
x
2 yz
y zx2
z
2 xy
则有
3 I1 2 I2 I3 0
2020/8/15
9
Lesson 5
三次方程式称为应力状态特征方程。此方程 的三个根就是三个主应力,而这三个主应力 均为实根。由因式分解可知
2020/8/15
Lesson 5
6
Lesson 5
代入到斜面应力方程中有
Snx Sny
l m
xxyllyxymmzxzynn
Snz
n
xzl
yzm
z
n
整理后可得
x
xyl
l
y
y
xm m
zx zy
n n
0 0
xzl yzm z n 0
又有
l2 m2 n2 1esson 5
4
2020/8/15
Lesson 5
5
主应力的求解
如果取微分面ABC为主 微分面,即该微分面上 只有主应力而没有切应 力。这时,作用在此面 上的全应力就是主应力。
用 表示主应力,则它
在各坐标轴上的投影为
Snx l Sny m Snz n
zy 0
z
2020/8/15
8
展开此行列式,得
Lesson 5
3 ( x y z ) 2
x
y
y z
z x
(
2 xy
2 yz
zx2 )
x y z
2 xy yz zx
x yz2
y zx2
z
2 xy
0
令
I1 ( x y z )
I2
x
y
y z
2020/8/15
13
Lesson 5
主坐标系
因为三个主应力两两相互垂直,若取坐标轴 与主应力方向一致,则构成主坐标系,其坐 标轴称为主轴。
3(z)
3
2020/8/15
1
1(x)
2
2(y)
14
Lesson 5
在主坐标系下斜面上的应力为
Sn1 1l 0 m 0 n 1l Sn2 0 l 2m 0 n 2m Sn3 0 l 0 m 3n 3n 或 Sn1 1 0 0 l Sn2 0 2 0 m Sn3 0 0 3 n
(*) (**)
2020/8/15
7
Lesson 5
由上面四个方程可求出主应力及其方向余
弦l、m、n。显然,前三个方程构成一个齐 次方程组,显然不能有l = m = n = 0这样的
解。如要方程组有其他解时,必须取该方程 组的系数行列式为零,即
x
xy xz
yx
y
yz
zx
金属塑性变形理论
Theory of metal plastic deformation
第五讲 Lesson Five
张贵杰
Zhang Guijie
Tel:0315-2592155 E-Mail: zhguijie@
河北理工大学金属材料与加工工程系 Department of Metal Material and Process Engineering Hebei Polytechnic University, Tangshan 063009
第十章 应力状态分析
主要内容
Main Content
应力状态基本概念 斜面上任一点应力状态分析 求和约定和应力张量 主应力及主切应力 球应力及偏差应力
2020/8/15
Lesson 5
2
10.4 主应力及主切应力
Lesson 5
10.4.1 主应力的概念
通过坐标变换可以找到只有正应力的 坐标面,此坐标轴称为主轴,此应力 称为主应力,该坐标面为主平面。
