数学建模Matlab作业
数学建模Matlab练习4

MATLAB练习四1. 绘制两个一元函数的曲线图(例如y=sin(x)、y=cos(x)),加上标注说明,包括坐标、抬头、曲线说明等。
%lianxi41.mx=0:pi/30:2*pi;y=sin(x);plot(x,y,'-ob','markersize',10);hold ony1=cos(x);plot(x,y1,'-.dm','markersize',10);legend('sinx','cosx');title('sin和cos函数的曲线图')xlabel('x');ylabel('y');2. 寻找一组数据拟合多项式,写出M文件,包括拟合的次数,数值的计算,数学表达式的呈现,图形的呈现等。
%lianxi42x=0:pi/20:pi;y=sin(x);n=input('n=');p=polyfit(x,y,n);x1=0:pi/20:pi*2;y1=sin(x1);y2=polyval(p,x1)plot(x1,y1,'-ob',x1,y2,':dm');legend('原曲线','拟合曲线');xlabel('x');ylabel('y');title('sin的拟合曲线和原曲线');axis([-0.2,6.5,-1.2,1.2])3. 求解一个代数方程,写出M文件,应该包括函数式M文件和命令式M文件。
%fc3.mfunction f=fc3(x)f='3*x-1=0';%lianxi43clc;clear;close;sprintf('原方程和其解析解的结果为:')s=solve(fc3)sprintf('保留10位有效数字的结果为:')digits(10)sprintf('数值解的结果为:')x=vpa(s)4. 求解一个代数方程组,写出M文件,应该包括函数式M文件和命令式M文件。
Matlab与数学建模综合练习(1)

《Matlab与数学建模》综合练习1.按顺序进行如下的操作:(1)产生一个5阶魔术方阵A;并计算A'与A-1(即inv(A));>> A=magic(5)A =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9 >> B=A'B =17 23 4 10 1124 5 6 12 181 7 13 19 258 14 20 21 215 16 22 3 9 >> inv(A)ans =-77/15600 133/2600 -23/650 3/2600 53/15600 89/2063 -97/2600 -3/650 33/2600 23/15600 -59/1950 1/325 1/325 1/325 71/1950 73/15600 -17/2600 7/650 113/2600 -577/15600 43/15600 1/200 27/650 -9/200 98/8837 (2)求A的特征值;>> eig(A)ans =65-2383/112-3846/2932383/1123846/293(3)计算A 的各列的总和与平均值; (4)计算A 的各行的总和与平均值;(5)若b=[1 2 3 4 5] ',求方程组 Ax=b 的解; (6)验证你的结论的正确性.2.产生行向量S =[1.0, 1.2, 1.4, …, 20],并计算S * S' 与 S' * S ,你有何“发现”?3.设A=⎪⎪⎭⎫ ⎝⎛4321;B=⎪⎪⎭⎫⎝⎛5055;求C=A * B – B * A ,你有何“发现”?4.若设矩阵A=⎪⎪⎭⎫⎝⎛4321;B=⎪⎪⎭⎫⎝⎛5005;求C=A * B – B * A ,你又有何“发现”? 5.如何建立如下的矩阵(命令方式和程序方式)?(1)1010200400020040002004⨯⎪⎪⎪⎪⎪⎭⎫⎝⎛; (2)1010010101001010100⨯⎛⎫⎪ ⎪⎪ ⎪ ⎪⎝⎭;>> a=ones(10,1)a =1 1 1 1 1 1 1 1 1 1>> A=0*a A =0 0 0 0 0 0 0>> b=diag(A)b =Columns 1 through 70 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0Columns 8 through 100 0 00 0 00 0 00 0 00 0 00 0 00 0 00 0 00 0 00 0 0>> c=ones(10)c =Columns 1 through 71 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 1Columns 8 through 101 1 11 1 11 1 11 1 11 1 11 1 11 1 11 1 11 1 11 1 1>> C=10*cC =Columns 1 through 710 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 10Columns 8 through 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 10>> m=triu(C,1)m =Columns 1 through 70 10 10 10 10 10 100 0 10 10 10 10 100 0 0 10 10 10 100 0 0 0 10 10 100 0 0 0 0 10 100 0 0 0 0 0 100 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0Columns 8 through 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 1010 10 100 10 100 0 100 0 0>> n=tril(C,-1)n =Columns 1 through 70 0 0 0 0 0 010 0 0 0 0 0 010 10 0 0 0 0 010 10 10 0 0 0 00 010 10 10 10 10 0 010 10 10 10 10 10 010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 10Columns 8 through 100 0 00 0 00 0 00 0 00 0 00 0 00 0 00 0 010 0 010 10 0>> K=m+n+bK =Columns 1 through 70 10 10 10 10 10 1010 0 10 10 10 10 1010 10 0 10 10 10 1010 10 10 0 10 10 1010 10 10 10 0 10 1010 10 10 10 10 0 1010 010 10 10 10 10 10 1010 10 10 10 10 10 1010 10 10 10 10 10 10Columns 8 through 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 10 10 10 0 10 10 10 0(3)1010200411120041112004⨯⎪⎪⎪⎪⎪⎭⎫⎝⎛;>> c=ones(10,1)c =1 1 1 1 1 1 1 1 1 1>> C=1024*c C =1024102410241024102410241024102410241024>> F=diag(C)F =Columns 1 through 61024 0 0 0 0 00 1024 0 0 0 00 0 1024 0 0 00 0 0 1024 0 00 0 0 0 1024 00 0 0 0 0 10240 0 0 0 0 00 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0Columns 7 through 100 0 0 00 0 0 00 0 0 00 0 0 00 0 0 00 0 0 01024 0 0 00 1024 0 00 0 1024 00 0 0 1024>> a=ones(10)a =Columns 1 through 61 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 1Columns 7 through 101 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 1>> U=triu(a,1)U =Columns 1 through 60 1 1 1 1 10 0 1 1 1 10 0 0 1 1 10 0 0 0 1 10 0 0 0 0 10 0 0 0 0 00 0 0 0 0 00 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0Columns 7 through 101 1 1 11 1 1 11 1 1 11 1 1 11 1 1 11 1 1 10 1 1 10 0 1 10 0 0 10 0 0 0>> D=tril(A,-1)D =Columns 1 through 60 0 0 0 0 01 0 0 0 0 01 1 0 0 0 01 1 1 0 0 01 1 1 1 0 01 1 1 1 1 01 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 1Columns 7 through 100 0 0 00 0 0 00 0 0 00 0 0 00 0 0 00 0 0 00 0 0 01 0 0 01 1 0 01 1 1 0>> Q=D+U+FQ =Columns 1 through 61024 1 1 1 1 11 1024 1 1 1 11 1 1024 1 1 11 1 1 1024 1 11 1 1 1 1024 11 1 1 1 1 10241 1 1 1 1 11 1 1 1 1 11 1 1 1 1 11 1 1 1 1 1Columns 7 through 101 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1024 1 1 1 1 1024 1 1 1 1 1024 1 1 1 1 1024(4)1010101010101010101010⨯--⎛⎫⎪-- ⎪⎪ ⎪ ⎪--⎝⎭(5)1000120011100⎛⎫⎪⎪⎪⎪⎪⎝⎭a=10:10:100a =Columns 1 through 710 20 30 40 50 60 70Columns 8 through 1080 90 100>> A=diag(a)A =Columns 1 through 710 0 0 0 0 0 00 20 0 0 0 0 00 0 30 0 0 0 00 0 0 40 0 0 00 0 0 0 50 0 00 0 0 0 0 60 00 0 0 0 0 0 700 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0Columns 8 through 100 0 00 0 00 0 00 0 00 0 00 0 00 0 080 0 00 90 00 0 100>> a=ones(10)a =Columns 1 through 71 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 1Columns 8 through 101 1 11 1 11 1 11 1 11 1 11 1 11 1 11 1 11 1 1>> D=tril(a,-1)D =Columns 1 through 70 0 0 0 00 01 0 0 0 00 01 1 0 0 00 01 1 1 0 00 01 1 1 1 00 01 1 1 1 10 01 1 1 1 1 1 01 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 1Columns 8 through 100 0 00 0 00 0 00 0 00 0 00 0 00 0 00 0 01 1 0>> W=A+DW =Columns 1 through 710 0 0 0 00 01 20 0 0 00 01 1 30 0 00 01 1 1 40 00 01 1 1 1 500 01 1 1 1 1 60 01 1 1 1 1 1 701 1 1 1 1 1 11 1 1 1 1 1 11 1 1 1 1 1 1Columns 8 through 100 0 00 0 00 0 00 0 00 0 00 0 00 0 080 0 01 90 01 1 100 (6)11123111113412111111220⎛⎫ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭(7)20042000002004300000200440000020045000002004⎛⎫ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭6.绘制下列曲线的图形(散点图与折线图):]2,1[,1323-∈+--=x x x x y7.绘制下列曲面的图形:2222yx z +=(提示:曲面由两部分构成)8.在同一个图形上作下列两个函数的图象:(1)]2,0[),(sin 2π∈=x x y ; (2)]2,0[),(cos 2π∈=x x y9.假如你有一组实测数据,例如:x=[53 56 60 67.5 75 90 110]; y=[109 120.5 130 141.1 157.5 180 185]; 求其回归直线,画回归直线图形并计算最小误差平方和. 10.假如你有一组实测数据,例如:x=[75 86 95 108 112 116 135 151 155 160 163 167 171 178 185]; y=[10 12 15 17 20 22 35 41 48 50 51 54 59 66 75]; 求其回归直线,画回归直线图形并计算最小误差平方和.11.随机产生500个0到100的整数FS 作为学生的考试分数.(1) 画出FS 的简单直方图;(2) 画出每个分数段(0~10、10~20、…,90~100)的统计频数直方图; 12.求下列各结果:(1)用Matlab 因式分解:1001x-.(2)用Matlab 求极限:xx L xx e-+=→10)1(lim.(3)用Matlab 求积分:⎰+∞2sin x x d .(4)用Matlab 求幂级数:∑∞=+---1212114)1(n n n n x 的和函数(化简结果).13.非线性回归尝试说明:用线性回归方法将得到:x y 5961.00089.11+-=,但当18=x 时,2794.0-=y ,这是非常荒唐的结果!显然,一个基本要求是当0=x 时0=y .试尝试使用非线性回归模型: bax y =.请尝试以下的命令:ezplot3('sin(t)', ' cos(t)', 't', [0,6*pi]) ezcontour('x*exp(-x^2 - y^2)') ezcontourf('x*exp(-x^2 - y^2)')ezmesh('(s-sin(s))*cos(t)','(1-cos(s))*sin(t)','s',[-2*pi,2*pi]) ezmeshc('(s-sin(s))*cos(t)','(1-cos(s))*sin(t)','s',[-2*pi,2*pi]) ezsurf('x*exp(-x^2 - y^2)') ezsurfc('x*exp(-x^2 - y^2)')。
数学建模题目2道 解答 matlab
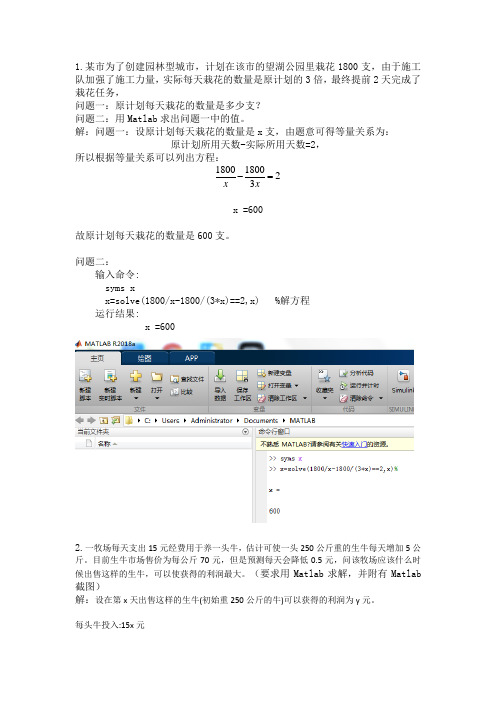
1.某市为了创建园林型城市,计划在该市的望湖公园里栽花1800支,由于施工队加强了施工力量,实际每天栽花的数量是原计划的3倍,最终提前2天完成了栽花任务,
问题一:原计划每天栽花的数量是多少支?
问题二:用Matlab求出问题一中的值。
解:问题一:设原计划每天栽花的数量是x支,由题意可得等量关系为:
原计划所用天数-实际所用天数=2,
所以根据等量关系可以列出方程:
18001800
-=
2
3
x x
x =600
故原计划每天栽花的数量是600支。
问题二:
输入命令:
syms x
x=solve(1800/x-1800/(3*x)==2,x) %解方程
运行结果:
x =600
2.一牧场每天支出15元经费用于养一头牛,估计可使一头250公斤重的生牛每天增加5公斤。
目前生牛市场售价为每公斤70元,但是预测每天会降低0.5元,问该牧场应该什么时候出售这样的生牛,可以使获得的利润最大。
(要求用Matlab求解,并附有Matlab 截图)
解:设在第x天出售这样的生牛(初始重250公斤的牛)可以获得的利润为y元。
每头牛投入:15x元
产出:(70-0.5x)(250+5x)元
利润:y=(70-0.5x)(250+5x)-15x=-2.5x^2+210x+17500
使用Matlab软件计算,得
当天数x=42时,利润y取得最大值21910(元)。
故该牧场应该在第42天时候出售这样的生牛,可以使获得的利润最大。
附Matlab计算截图:
①利润y取得最大值的Matlab计算截图
②天数x=42天的Matlab计算截图。
数学建模作业题+答案

数学建模MATLAB 语言及应用上机作业11. 在matlab 中建立一个矩阵135792468101234501234A ⎡⎤⎢⎥⎢⎥=⎢⎥-----⎢⎥⎣⎦答案:A = [1,3,5,7,9;2,4,6,8,10;-1,-2,-3,-4,-5;0,1,2,3,4]2. 试着利用matlab 求解出下列方程的解(线性代数22页例14)123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩ 答案:A=[2 ,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6]; B=[8;9;-5;0]; X=A\B 或A=[2,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6] b=[8,9,-5,0]' X=inv(A)*b3. 生成一个5阶服从标准正态分布的随机方阵,并计算出其行列式的值,逆矩阵以及转置矩阵。
答案:A=randn(5) det(A) inv(A) A'4. 利用matlab 求解出110430002A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的特征值和特征向量。
答案:A=[-1,1,0;-4,3,0;0,0,2] [V,D]=eig(A)5.画出衰减振荡曲线3sin3t y et -=在[0,4]π上的图像。
要求,画线颜色调整为黑色,画布底面为白色。
(在实际中,很多打印机时黑白的,因此大多数作图要考虑黑白打印机的效果。
) 给出恰当的x ,y 坐标轴标题,图像x 轴的最大值为4π。
6. 生成一个0-1分布的具有10个元素的随机向量,试着编写程序挑选出向量中大于0.5的元素。
数学建模和Matlab 上机作业2(2016-9-20)跟老师做(不用整合进作业中):上机演示讲解:函数,递归的两个例子的写法。
附:1. Fibonacci Sequence (斐波那契数列)在数学上,费波那西数列是以递归的方法来定义: F1= 1;F2= 1;F (n )=F (n-1)+F (n-2) 2. 阶乘举例:数学描述:n!=1×2×……×n ;计算机描述:n!=n*(n-1)!自己做(需要整合进作业中,提交到系统中):1. 写一个m 文件完成分值百分制到5分制的转换(即输入一个百分制,转换后输出一个5级对应的得分,联系条件控制语句)。
三峡大学数学建模matlab题目

1.在4×4的棋盘上安置4个皇后,要求任意两个皇后不在同一行、不在同一列、不在同一对角线上,输出所有的方案。
for i1=1:4 %i1.。
表示皇后的位置for i2=1:4for i3=1:4for i4=1:4hh=zeros(4,4);%用于模拟棋盘hh(1,i1)=1; % 1表示此处有皇后由于分列,所以不再同一列hh(2,i2)=1;hh(3,i3)=1;hh(4,i4)=1;if i1==i2 || i1==i3 || i1==i4 || i2==i3 || i2==i4 || i3==i4 % 判断是否在同一行continue;endif abs(i1-i2)==1 || abs(i1-i3)==2 || abs(i1-i4)==3 || abs(i2-i3)==1 || abs(i2-i4)==2 ...|| abs(i3-i4)==1 % 判断是否在一条对角线上continue;enddisp(hh);%打印棋盘,1为皇后endendendend2.问题描述:有形如下图所示的数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的数值的和最接近零。
n=input('输入数塔的层数n(正整数n<=20) ');st=zeros(n);for i1=1:nfor j1=1:i1fprintf('输入第%d行第%d个数据(且数字的绝对值不超过1000000) ',i1,j1);st(i1,j1)=input(' ');endendsz=inf;ls=zeros(1,n(1)-1);lj=zeros(1,n(1)-1);for i1=0:2^n-1ss=st(1,1);for j1=1:n(1)-1ls(j1)=mod(i1,2);i1=floor(i1/2);endk=1;for j1=1:n(1)-1k=k+ls(j1);ss=ss+st(j1+1,k);endif ss<szsz=ss;lj=ls;endendfprintf(' %d ',st(1,1));for i1=1:n(1)-1if lj(i1)==1fprintf(' 向右选择');elsefprintf(' 向左选择');endfprintf('%3d ',st(i1+1));endfprintf(' 最终的最小值是%d \n',sz);3. 现有21根火柴,两人轮流取,每人每次可取走1- 4根,不可多取,也不能不取,谁取最后一根火柴则谁输。
Matlab与数学建模综合练习3

Matlab与数学建模综合练习31、画sin(6x)的图,x ∈[0,68×Pi];>> x=0:1:68*pi; >> plot(x,sin(6*x))2、画],0[],,0[),sin()sin(2Pi p Pi t p t ∈∈?的三维图; >> t=0:0.1:pi;p=t; >> [T,P]=meshgrid(t,p); >> Z=sin(T).*sin(P.^2); >> surf(T,P,Z)>> mesh(T,P,Z)3、画图]6,6[],6,6[,222-∈-∈+y x e y x 和]6,6[],6,6[),sin(22-∈-∈+y x y x ,并合并这两个图。
>> x=-6:0.3:6;y=x; >> [X,Y]=meshgrid(x,y); >> Z1=2.*exp(sqrt(X.^2+Y.^2)); >> surf(X,Y,Z1) >> hold on >> Z2=sin(sqrt(X.^2+Y.^2)); >> surf(X,Y,Z2)>> x=-6:0.3:6;y=x;>> [X,Y]=meshgrid(x,y);>> Z1=2.*exp(sqrt(X.^2+Y.^2)); >> mesh(X,Y,Z1)>> hold on>> Z2=sin(sqrt(X.^2+Y.^2)); >> mesh(X,Y,Z2)4、设=+=+32/)7(11x x x x n n n ,数列}{n x 是否收敛?若收敛,其值为多少?精确到6位有效数字。
5、设 ,131211p p p n nx ++++= }{n x 是否收敛?若收敛,其值为多少?精确到17位有效数字。
数学建模中30道经典MATLAB程序

编程1、编写一程序,要求输入五个整数,然后由小到大排序再输出。
%输入n个数,然后由小到大输出a=input('输入数据:')n=length(a); %输入数据的长度i=1;j=1; %赋初值for i=1:n %需要进行n次比较for j=2:n %与相邻的进行n-1次比较if a(j-1)>a(j)b=a(j-1);a(j-1)=a(j);a(j)=b; %比较前者是否比后者大,大的就互换endendendfprintf(' %d',a) ;2、将一个整型数组的元素按逆序重新存放(如原序为:8,6,5,4改为4,5,6,8)。
function lin5a=input('输入数据:')n=length(a);%求输入a的长度for i=1:n/2b=a(i);a(i)=a(n+1-i);a(n+1-i)=b;endfprintf(' %d',a)3、输入一个字符,如果是大写字母,则将其转换成小写并输出,若是小写,则直接输出;若是非字母字符则打印:‘datarror’.function xin2a=input('输入数据:','s')if a>=65&a<=90fprintf('shuchu is %c\n',a+32);elseif a>=97&a<=122fprintf('shuchu is %c\n',a);elsea='dataerror';fprintf('shuchu is %s',a);end4、输入一个整数,写一程序输出它是几位数。
function lin6a=input('输入数据:','s')n=length(a)%求输入a的长度b=n;fprintf('weishu %d',b);end5、写一程序求1!+2!+ (10)function wi=1;j=1;s=0; %赋初值while i<=10j=j*i;s=s+j;i=i+1;endfprintf('s is %d\n',s);6、从键盘上输入a与n的值,计算sum=a+aa+aaa+aaaa+……(共n项)的和。
数学建模matlab例题参考及练习

数学建模matlab例题参考及练习数学实验与数学建模实验报告学院:专业班级:姓名:学号:完成时间:年⽉⽇承诺书本⼈承诺所呈交的数学实验与数学建模作业都是本⼈通过学习⾃⾏进⾏编程独⽴完成,所有结果都通过上机验证,⽆转载或抄袭他⼈,也未经他⼈转载或抄袭。
若承诺不实,本⼈愿意承担⼀切责任。
承诺⼈:年⽉⽇数学实验学习体会(每个⼈必须要写字数1200字以上,占总成绩的20%)练习1 ⼀元函数的图形 1.画出x y arcsin =的图象.2.画出x y sec =在],0[π之间的图象. 3.在同⼀坐标系中画出x y =,2x y =,3x y =,3x y =,x y =的图象.4.画出3232)1()1()(x x x f ++-=的图象,并根据图象特点指出函数)(x f 的奇偶性.5.画出)2ln(1++=x y 及其反函数的图象.6.画出321+=x y 及其反函数的图象.练习2 函数极限1.计算下列函数的极限.(1)xxx1lim4-+π→.程序:sym x;f=(1+sin(2*x))/(1-cos(4*x)); limit(f,x,pi/4)运⾏结果:lx21ans =1(2).程序:sym x;f=(1+cos(x))^(3*sec(x)); limit(f,x,pi/2)运⾏结果:lx22ans =exp(3)(3)22)2xx-ππ→.程序:sym x;f=log(sin(x))/(pi-2*x)^2; limit(f,x,pi/2)运⾏结果:lx23ans =-1/8(4)212lim xxex→.程序:x xx sec32)sym x ;f=x^2*exp(1/x); limit(f,x,0) limit(f,x,0,'right') limit(f,x,0,'left')运⾏结果:lx24ans = NaNans = Infans = 0%左极限为零,存在,右极限为⽆穷⼤,在x 趋近于零时函数没有极限(5))215(lim 122x x x x +-∞→.程序:sym x ;f=5*x^2/(1-x^2)+2^(1/x); limit(f,x,inf)运⾏结果:>> lx25ans = -4(6)x x x x x -+-→32112lim .程序:sym x ;f=(x^2-2*x+1)/(x^3-x); limit(f,x,1)运⾏结果:>> lx26ans = 0(7)x x x 11lim 20-+→.程序:sym x ;f=(sqrt(1+x^2)-1)/x; limit(f,x,0))3sin(cos 21lim 3π--π→x x x . 程序:sym x ;f=(1-2*cos(x))/sin(x-pi/3); limit(f,x,pi/3)运⾏结果:>> lx28ans = 3^(1/2)(9)tgxx x )1(lim 0+→.程序:sym x ;f=(1/x)^tan(x); limit(f,x,0,'right')运⾏结果:>> lx29ans =(10)xx arctgx )2(lim π+∞→.程序:sym x ;f=(2/pi*atan(x))^x; limit(f,x,inf,'left')运⾏结果:>> lx210ans =Inf2.解⽅程012=-?x x . 程序:sym x ;X=solve(x*2^x-1)运⾏结果:>> lx202 X =lambertw(0, log(2))/log(2)%⽅程有两个解X=solve(3*sin(x)+1-x)运⾏结果:>> lx203 X =-0.53847936154.解⽅程03=++q px x .(p 、q 为实数) 程序:X=solve('x^3+p*x+q=0','x')运⾏结果: X =((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3) - p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) -((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)/2 - (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) -q/2)^(1/3)))/2 p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) - ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)/2 + (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)))/2练习 3 导数及偏导数计算1.求下列函数的导数.(1))11)(1(-+=x x y程序:sym x ;f=(sqrt(x)+1)*(1/sqrt(x)-1); diff(f)运⾏结果:>> lx31ans =(1/x^(1/2) - 1)/(2*x^(1/2)) - (x^(1/2) + 1)/(2*x^(3/2))(2)x x x y ln sin =程序:sym x ;f=x*sin(x)*log(x); diff(f)运⾏结果:>> lx32ans =sin(x) + log(x)*sin(x) + x*cos(x)*log(x)2.求下列参数⽅程所确定的函数的导数.(1)??==t y t x 44程序:ans =1/t^3(2)??-=+=arctgt t y t x )1ln(2程序:sym t ;f1=log(1+t^2);f2=t-atan(t); diff(f2)/diff(f1)运⾏结果:>> lx322ans =-((t^2 + 1)*(1/(t^2 + 1) - 1))/(2*t) 3.求下列隐函数的导数.(1)22ln y x xyarctg+=程序:syms x y ;f=atan(y/x)-log(sqrt(x^2+y^2));yx=-diff(f,x)/diff(f,y)运⾏结果;>> lx331 yx =(x/(x^2 + y^2) + y/(x^2*(y^2/x^2 + 1)))/(1/(x*(y^2/x^2 + 1)) - y/(x^2 + y^2)) (2)x y y x=程序:syms x y ; f=x^y-y^xyx=-diff(f,x)/diff(f,y)运⾏结果:>> lx332 f =x^y - y^x yx =f=exp(x)*sin(x); diff(f,x,4)运⾏结果:>> lx34 ans =(-4)*exp(x)*sin(x)5.验证x e y xsin =满⾜关系式:022=+'-''y y y程序:sym x ;f=exp(x)*sin(x); y2=diff(f,x,2); y1=diff(f,x,1); y=f;y2-y1*2+2*y=='0' 运⾏结果:>> lx35ans =1%运⾏结果为1表⽰y2-y1*2+2*y=='0'成⽴6.设)ln(y x x u +=,求22x u ??,22y u,y x u 2. 程序:syms x y ; f=x*log(x+y); uxx=diff(f,x,2) uyy=diff(f,y,2) f1=diff(f,x); uxy=diff(f1,y)运⾏结果: >> lx36uxx =2/(x + y) - x/(x + y)^2uyy =-x/(x + y)^2uxy =1/(x + y) - x/(x + y)^27.求下列多元隐函数的偏导数y zx z ,.(1)1cos cos cos 222=++z y x程序:syms x y z ;-(cos(x)*sin(x))/(cos(z)*sin(z)) zy =-(cos(y)*sin(y))/(cos(z)*sin(z))(2)xyz e z= 程序:syms x y z ; f=exp(z)-x*y*zzx=-diff(f,x)/diff(f,z) zy=-diff(f,y)/diff(f,z)运⾏结果:>> lx372 f =exp(z) - x*y*z zx =(y*z)/(exp(z) - x*y) zy =(x*z)/(exp(z) - x*y) 8.证明函数22)()(lnb y a x u -+-=(b a ,为常数)满⾜拉普拉斯⽅程:02222=??+??y u x u (提⽰:对结果⽤simplify 化简)练习4 积分计算1.计算下列不定积分.(1)?+dxx x 12 (2)+x xdx 2sin 12sin2.计算下列定积分.(1)?exdxx 1ln (2)ππ342sin dxxx3.求?+tdx x x x4.求摆线)cos 1(),sin (t a y t t a x -=-=的⼀拱(π≤≤20t )与x 轴所围成的图形的⾯积.5.计算⼆重积分 (1)??≤++122)(y x dxdyy x (2)??≤++xy x dxdyy x 22)(226.计算?+Ldsy x 22 L 为圆周)0(22>=+a ax y x7.计算?++-L dy y x dx y x )()(2222,其中L 为抛物线2x y =上从点(0,0)到点(2,4)的⼀段弧.练习5 matlab ⾃定义函数与导数应⽤1.建⽴函数x x a a x f 3sin 31sin ),(+=,当a 为何值时,该函数在3π=x 处取得极值,它是极⼤值还是极⼩值,并求此极值.2.确定下列函数的单调区间.(1)7186223---=x x x y (2))0(82>+=x xx y3.求下列函数的最⼤值、最⼩值.(1)2332x x y -=41≤≤-x(2)312824≤≤-+-=x x x y练习6 matab 矩阵运算与数组运算1.计算(1)???--521111204321+???21(2)??-01301213?03010*******????? ??-205101(3)52422??- 2.设????? ??-=243121013A ,??-=112111201B ,求满⾜关系B X A =-23的X .练习7 矩阵与线性⽅程组1.求下列矩阵的秩.(1)???-321110021 (2)4820322513454947513253947543173125 2.求下列矩阵的⾏列式,如可逆,试⽤不同的⽅法求其逆矩阵.(1)??--285421122 (2)??---6201111121324321 3.设X ????? ?-111012111==--+=+-+=+-+=+-+6223312433862344224221432143214321x x x x x x x x x x x x x x x x (2)-=+--=+--=-+-212201432143214321x x x x x x x x x x x x练习8 常微分⽅程与级数求1-6题微分⽅程的通解1.1222+='y y y x 2.x y x y dx dy -+= 3.x xx y y +='cos 4.1)2sin cos (='+y y y x 5.x e y y y x2cos 3=-'+'' 6.x x y y sin 14++=+'' 求7、8题初值问题的解7.==-++-+=10)2(212222x y dx dy x xy y y xy x8.===++==0000222,02V dt dx x x x a dt dxn dtx d t t9.给出函数x x e x f xx cos 2sin )(+=在点0=x 的7阶taylor 展开式以及在x=1处的 5阶taylor 展开式.10.判别下列级数的敛散性,若收敛求其和.(1)+++311(2)∑∞=+112n nntgπ11.求幂级数∑∞=--22)1(nnnnnx的和函数.12.求函数项级数∑∞=-1nnnn xπ的和函数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x=[-3:.1:3]; %确定x的值
y1=2.*x+5;
y2=x.^2-3.*x+1;
subplot(1,2,1); %建立二个窗口,并在第一个编辑
plot(x,y1);
axis([-4 4 -5 20]); %划定坐标范围
subplot(1,2,2); %建立二个窗口,并在第一个编辑
plot(x,y2);
axis([-4 4 -5 20]); %可省略,因为坐标范围就是以第二幅图为准的程序效果图:
x=[190 33 45 42 45];
explode = [0 1 0 0 0]; %输入分离切面向量
pie(x,explode,{'生活费','资料费','电话费','购买衣服费','其它费用'}); %绘图程序效果图:
第三题代码:(这一题我是按照点乘来做的,而且精度调的比较大,如果是按矩阵做,只需要把z的表达式一改就行了)
[x,y]=meshgrid(-5:.01:5); %x的精度为0.01
z=x.^2+y.^2+sin(x.*y);
meshc(x,y,z) %绘制等高图
执行效果图:
第四题代码:
x=0:pi/5:4*pi;
y=sin(x).*exp(-x/10);
xx=0:.1:4*pi; %取间隔为0.1
yy=spline(x,y,xx) %三次样条插值
plot(x,y,'o',xx,yy) %绘图,并用’o’标记执行效果图:。
