第八届小机灵杯三年级初赛
小学奥数习题版三年级三大原理最短路线学生版

知识要点快乐热身【例 1】 如下图所示,小虎家在A 地,姥姥家在B 地。
一天,他要去看望姥姥,但不知有几条路可走,走哪条路最短,热心的小朋友们快帮帮他吧?最短路线【例2】如下图所示,从甲地到乙地一共有两条路可走,请问哪条路长?哪条路短?【例3】观察下图,若黑猫与白猫奔跑速度相同,那么哪只猫先捉到老鼠?白猫黑猫鼠【例4】直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线之和最短,问汽车站建在哪儿最好?乙甲BA走格子边【例5】一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们你能给它找到几条这样的最短路线呢?BA【例6】如果A、B 两点变成下面两图这样的位置关系,那么从A到B的最短路线有几条呢?BA【例7】方格纸上取一点A作为起点,再在A的右上方任取一点B作为终点,画一条由A到B的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?【例8】小明和小强到少年宫参加2010上海世博会志愿者培训,少年宫和学校之间的地图如下。
如果他们从学校出发,共有多少种不同的最短路线?学校少年宫【例9】小虎和小羊是好朋友,它们居住的小区的平面图如下。
星期天,两人相约去博物馆看展览,现在小虎要先去小羊家和小羊会和,请问小虎去小羊家的最短路线有多少条?【例10】小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!北村南村【例11】如图,从F点出发到G点,走最短的路程,有多少种不同的走法?GF【例12】“五一”长假就要到了,小新和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?北京黄山【例13】下图是小明家和学校的示意图,亲爱的同学们,你们觉得小明从家到学校共有几条最短路线呢?学校小明家【例14】小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?游乐场小猪家【例15】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图)。
四年级几何图形剪拼学生版

知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形(不要求大小相等)将一个正方形分割成若干个正方形(不要求大小相等)n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何(本讲)一、 三角形面积公式:三角形面积=底⨯高2÷,即S 三角形2a h =⨯÷。
二、 平行四边形面积公式:平行四边形面积=底⨯高,即S 平行四边形a h =⨯。
三、 梯形面积公式:梯形面积=(上底+下底)⨯高2÷,即S 梯形()2a b h =+⨯÷。
四、 菱形面积公式:菱形面积=两条对角线乘积的一半,即S 菱形2m n =⨯÷ 五、n 边形的内角和公式:n 边形的内角和(2)180n =-⨯o 。
图形面积【例 1】如图所示,已知三角形的一条边为a,这条边上的高为h。
请用图形剪拼的方法,求出这个三角形的面积S三角形。
hahaha【例 2】如图所示,已知平行四边形的一条边为a,这条边上的高位h。
请用图形剪拼的方法,求出这个平行四边形的面积S平行四边形。
ha【例 3】如图所示,已知梯形的两条平行的边分别为a、b,梯形的高为h。
请用图形剪拼的方法,求出这个梯形的面积S梯形。
hab【例 4】如图所示,已知菱形的两条对角线分别为m、n。
请用图形剪拼的方法,求出这个平行四边形的面积S菱形。
(提示:菱形的两条对角线相互垂直)mn图形分割【例 5】 (2005年12月第六届“中环杯”小学生思维能力训练活动四年级复赛第二(5)题)将一个长方形分成形状完全一样的四块,至少画出8种分法,请用图表示。
(形状一样,排列方向不一样,只能看作一种分法)【例 6】 如图所示为一个34⨯的长方形方格纸,请用5种不同的方法将它分割成完全相同的两部分(保持每个小方格的完整)。
【例 7】 如图所示,请将44⨯的正方形分成形状相同、大小相等的四个图形,并且使其中每个图形都含有“上海世博”这四个字。
小学奥数习题版三年级几何巧求面积教师版

知识要点简单求面积【例 1】 4个相同的长方形和一个小正方形拼成一个面积是100平方厘米的大正方形,已知小正方形的面积是36平方厘米,问长方形的长和宽各是多少厘米?【分析】 1001010=⨯,3666=⨯,大正方形的边长为10厘米,小正方形的边长为6厘米,长方形的宽为:(106)22-÷=(厘米),长为:628+=(厘米)【例 2】 如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?我们已经学会了计算正方形、长方形的周长和面积,运用这些基础的知识,可以解决一些较复杂的面积计算.由长方形、正方形引出的问题形式多样,要解决这些问题,关键要能够合理地切拼,要做到这一点,就需要我们开动脑筋,细心观察,掌握图形特点,找出分割与切拼的方法,达到解决问题的目的.1. 掌握巧妙的解题方法.2. 了解“等量代换”的思想.3. 培养学生灵活运用的能力.巧求面积75【分析】 阴影部分的宽是752-= (厘米),长是523-= (厘米),面积是236⨯= (平方厘米).【例 3】 一个长方形周长是80厘米,它是由3个完全相同的小正方形拼成的,那么每个小正方形的面积是多少平方厘米?【分析】 小正方形的边长:80810÷=厘米,每个小正方形的面积:1010100⨯=平方厘米。
面积增减【例 4】 一块长方形铁板,长15分米,宽l2分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【分析】 如图,铁板面积比原来减少多少平方分米,就是求阴影部分的面积,用原长方形的面积减去空白部分的面积.1512(152)(122)⨯--⨯-=180130- =50(平方分米)2221512【例 5】 一块长方形地长是80米,宽是45米,如果把宽增加5米,要使原来的面积不变,长应减少多少米?【分析】 808045(455)8-⨯÷+= (米).【例 6】 人民路小学操场原来长80米,宽55米,改造后长增加20米,宽减少5米.现在操场的面积比原来增加多少?【分析】 (8020)(555)8055600+⨯--⨯= (平方米).【例 7】 有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?【分析】 根据题意,可以用下图表示增减变化的情况,从图中可以看出,原来长方形的长为(2720680)(6050)340+÷-= (米),宽为6803405052÷+= (米)。
第8届小机灵3年级初赛解析

第八届“小机灵杯”小学数学竞赛三年级初赛全方位解析1、666+666-666×666÷666 = ( )。
【考点】速算与巧算——抵消法【解析】原式=666+666-666×1=6662、如果10 – 9 + 8 ×□÷ 7 + 6 -5 + 4 – 3× 2 =0,那么□=( )。
【考点】速算与巧算——带符号搬家【解析】原式=8×□÷7+(10-9+6-5+4-3×2)=8×□÷7+0=0,即8×□÷7=0,也就是8×□=0。
所以□=03、观察表中各数的排列规律,A是( )。
【考点】找规律【解析】横向看:第一行依次加1=1×1第二行依次加4=2×2第三行依次加9=3×3第四行依次加16=4×4所以A=20+16=364 、一个正方形,如果边长增加5厘米,这个正方形的周长增加( )厘米。
【考点】巧求周长【解析】一条边增加了5厘米,则四条边一共增加了5×4=20(厘米)。
5 、两个正整数的和是18,其中一个数是另一个数的5倍.这两个数分别是( )和( )。
【考点】和差倍问题——小数=和÷(倍数+1)【解析】利用和倍公式:小数:18÷(5+1)=3,大数:3×5=156 、如图,网格中的小正方形的面积都是1平方厘米,那么,阴影部分的面积是( )平方厘米。
【考点】巧求面积【解析】方法1:如下图,图形被分为红色和紫色两部分,利用三角形面积公式:红色三角形的面积为:4×1÷2=2(平方厘米);紫色三角形的面积为:4×2÷2=4(平方厘米)。
总面积为:2+4=6(平方厘米)方法2:割补法,如下图,大直角三角形的面积为所在长方形的一半。
所以总面积为2×1÷2+5×2÷2=6(平方厘米)7、从1-10这10个正整数中,每次取出两个不同的数,使它们的和是4的倍数.共有( )种不同的取法。
2和差倍问题(学生)

1. 和差问题是已知大小两个数的和与这两个数的差,求大小两个数各是多少的应用题。
解决和差问题我们可画线段图来分析,结论如下:1) 方法一:(和+差)2÷=大数 和-大数=小数 或 大数-差=小数2) 方法二:(和-差)2÷=小数 和-小数=大数 或 小数+差=大数2. 和倍问题就是已知两个数的和以及它们之间的倍数关系,求这两个数各是多少的问题。
解答此类应用题时要根据题目中所给的条件和问题,画出线段图,使数量关系一目了然,从而找出解题规律,正确迅速地列式解答。
和倍问题的数量关系式是:1) 和÷(倍数1+)=小数2) 小数⨯倍数=大数 或 和-小数=大数3. 差倍问题就是已知大小两数的差,以及大小两数的倍数关系,求大小两数的问题。
差倍问题的特点与和倍问题类似。
解答差倍问题的关键是要确定两个数量的差及相对应的倍数差,一般情况下,在题目中不直接给出,需要经过调整和计算才能得到。
解题思路:首先要在题目中找到1倍量,然后画图确定解题方法。
被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量。
基本关系式:1) 差÷(倍数1-)=小数2) 小数⨯倍数=大数 或 小数+差=大数【例1】 文具店有钢笔和圆珠笔共850支,当两种笔卖出同样多的支数后,还剩下钢笔123支,圆珠笔87支。
原来文具店有钢笔多少支?第二讲和差倍问题知识概述例题精讲【拓展】(2009年第八届“小机灵杯”三年级初赛)在6~26之间插入三个数,使它们每相邻的两个数的差相等,这些数的和是()。
【例2】(2006年第五届“小机灵杯”三年级初赛)把27米长的一根绳子分成三段,使后一段都比前一段多3米。
那么,这三段绳子分别()米、()米、()米。
【拓展】(2009年第八届“小机灵杯”三年级初赛)王强,李刚是哥哥,小丽,小红是妹妹,四人的年龄和为90,哥哥都比妹妹大4岁,小红比王强小5岁。
小红多少岁?【例3】(2009年第八届“小机灵杯”三年级初赛)两正整数的和是18,其中一个数是另一个数的5倍,这两数分别是()和()。
第九届小机灵杯初赛(三年级)— 含答案

第九届小机智杯初赛(三班级)—含答案第九届“小机智杯”学校数学竞赛三班级组初赛试题1.计算:210+209-208+207-206+…+3-2+1=()。
315 2.如图所示,从上往下,每个方格中的数都等于它下方两个方格中所填数之和,最上层方格中两个数之和是()。
20103.如图所示,a 、b 、c 、d 、e 、f 、g 、h 、i 、j 表示10个各不相同的数,表中的数为所在行与列对应字母的差,例如“b -h =6”,图中“九宫格”中九个数的和是()。
45 4.小胖比他的表姐小12岁,再过4年小胖的年龄是他表姐年龄的一半,他俩今年的年龄总和是()岁。
285.如图所示,从A 点走到B 点,沿线段走最短路线,共有()种不同走法。
186.五位打工者一天的辛苦劳动后共获得330元工资,由于工种不同,获得最高工资者比其他四位分别多得12、14、21和28元,获得最低工资者的工资是()元。
537.如图所示的图形的周长是()厘米。
2008.在数20468204682046820468中划去10个数字(不能转变原来数字的挨次),得到一个最小的十位数,这个最小的十位数是()。
20004204689.右边的乘法算式中,只知道一个数字“8”,请你补全,那么这个算式的积最小是()。
106810.在1、2、3、4、5、6六个数中,选三个数,使它们的和能被3整除,那么,不同的选取共有()种。
811.有四袋糖,每袋糖的块数都不相同,任意三袋糖的块数总和都不少于60块,那么,这四袋糖的块数总和至少有()块。
8212.3根火柴可以摆成一个小三角形,用许多根火柴摆成了一个如图那样的大三角形,假如大三角形外沿的每条边都增加到10根火柴,那么摆成这样外形的大三角形需要用()根火柴。
30013.一次测验中,小胖答错了6道题,小亚答错了7道题,小丁丁答对的题的数量等于小胖和小亚答对题数量的总和,小丁丁答对了17道题,这次测验共有()道题。
相遇问题竞赛真题训练

相遇问题相遇问题竞赛真题训练竞赛真题训练真题博览:1、(第十三届小机灵杯(第十三届小机灵杯三年级三年级三年级决赛)决赛)甲、乙两地相距3千米。
明明和亮亮同时从两地出发同向而行,行了20分钟两人还未相遇且相距2900米。
已知明明每分钟行80米,亮亮每分钟行________米。
2、(第十三十三届小机灵杯三年级初赛届小机灵杯三年级初赛届小机灵杯三年级初赛))AB两地相距1000米,甲从A地出发,1小时后到达B地。
乙在甲出发后20分钟从B地出发,40分钟到达A地。
甲、乙二人相遇点距A地________米。
3、(第(第121212届届“走美杯走美杯””四年级初赛)甲、乙两市相距55千米。
小王同学从甲市出发去乙市,先骑车行了25千米,接着改乘大客车,速度提高了1倍。
到达乙市后,他发现骑车所用的时间比乘车所用的时间多了1小时。
小王同学骑车的速度是________千米/小时。
4、(2013(2013年亚太选拔赛四年级年亚太选拔赛四年级年亚太选拔赛四年级))甲、乙两地相距600千米,快车和慢车分别从甲、乙两地同时出发相向而行,10小时相遇,快车的速度是慢车的两倍。
试问:如果慢车比快车早出发3小时,当两车相遇时快车离甲乙两地中点相距多少千米?答案解析:1、【答案】85或75【解答】20分钟后,两个人的距离减少了3000-2900=100米;因此速度差每分钟100÷20=5米;因此亮亮的速度是每分钟80+5=85米或80-5=75米。
2、【答案】600米。
【解答】由乙40分钟可走1000米,得到乙的速度为1000÷40=25米/分钟;甲60分钟可走1000米,而乙60分钟可走25×60=1500米;由1000与1500的关系不难看出,相同时间内若甲走2份路程,则乙可走3份;现在甲比乙早出发20分钟,即为乙比甲晚出发20分钟;可构造一种情形:乙先向后退20分钟甲再出发,即为乙后退25×20=500米;此时甲、乙二人的实际距离为1000+500=1500米;甲、乙二人相遇点与A地的距离即为相遇时甲所走的路程;在二人的路程和1500米当中,甲所走的路程为1500÷(2+3)×2=600米;所以甲、乙二人相遇点距A地600米。
上海小升初息息相关的杯赛

上海小升初息息相关的杯赛近几年上海各大重点中学对各种杯赛都很重视,特别是在小升择校的过程中,有一张杯赛的证书如同应聘的时候有名牌大学的毕业证书一样。
参加杯赛可以锻炼学生的考试能力,培养学生在考场上应试能力,熟能生巧,让孩子在以后的大考中处变不惊。
参加杯赛培训能扩大学生的知识面,培养好的学习方法。
在杯赛中取的好的成绩,学生能建立强大的自信心。
数学竞赛能提高中小学生学习数学的兴趣,培养数学的思维品质,增强在实际学习中运用数学的能力,同时为学生学好数学创造条件。
1、“读写新天地杯”小学生语文现场阅读活动“读写新天地杯”语文现场阅读活动结合课程标准,紧贴现行教材,邀请市小学语文界专家、一线优秀的骨干教师根据各年段阅读要求分别命题。
各年级现场阅读的内容绝大部分采自《小学语文同步阅读写作》一书中的相关内容。
为体现活动的公正、公平和公开,题目全部为客观性命题,主要形式为是非题、判断题、选择题。
2-3年级的选择题以单项为主,4-5年级的选择题以多项为主。
参加对象:小学2—5年级学生。
2、“读写新天地杯”小学生英语现场阅读活动“读写新天地杯”英语现场阅读活动结合课程标准,紧贴现行教材,邀请市小学英语界专家、一线优秀的英语骨干教师根据各年段阅读要求分别命题。
为体现活动的公正、公平和公开,题目全部为客观性命题,主要形式为完形填空、是非题、判断题、选择题。
参加对象:小学2—5年级学生。
3、七彩杯现场写作主办单位《七彩读写》编委会,邀请全国语文学习科学专业委员会和上海市语言文字工作者协会、上海演讲学研究会、上海文学发展基金会儿童读物基金委员会为指导单位。
参加对象:2—5年级小学生。
活动形式:写作活动题型包括看图作文、想象作文、命题作文、半命题作文等。
报名方式:学生可根据自己的特长自由选择参加写作活动或演讲活动,亦可两项活动同时参加。
得奖率:一等奖5%;二等奖10%;三等奖15%;鼓励奖20%。
两个活动均获得一等奖者获评特等奖。
【第01讲】三年级几何巧求面积教师版

知识要点简单求面积【例 1】 4个相同的长方形和一个小正方形拼成一个面积是100平方厘米的大正方形,已知小正方形的面积是36平方厘米,问长方形的长和宽各是多少厘米?【分析】 1001010=⨯,3666=⨯,大正方形的边长为10厘米,小正方形的边长为6厘米,长方形的宽为:(106)22-÷=(厘米),长为:628+=(厘米)【例 2】 如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?5【分析】 阴影部分的宽是752-= (厘米),长是523-= (厘米),面积是236⨯= (平方厘米).【例 3】 一个长方形周长是80厘米,它是由3个完全相同的小正方形拼成的,那么每个小正方形的面积是多少平方厘米?【分析】 小正方形的边长:80810÷=厘米,每个小正方形的面积:1010100⨯=平方厘米。
巧求面积面积增减【例 4】 一块长方形铁板,长15分米,宽l2分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【分析】 如图,铁板面积比原来减少多少平方分米,就是求阴影部分的面积,用原长方形的面积减去空白部分的面积.1512(152)(122)⨯--⨯-=180130- =50(平方分米)1512【例 5】 一块长方形地长是80米,宽是45米,如果把宽增加5米,要使原来的面积不变,长应减少多少米?【分析】 808045(455)8-⨯÷+= (米).【例 6】 人民路小学操场原来长80米,宽55米,改造后长增加20米,宽减少5米.现在操场的面积比原来增加多少?【分析】 (8020)(555)8055600+⨯--⨯= (平方米).【例 7】 有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?【分析】 根据题意,可以用下图表示增减变化的情况,从图中可以看出,原来长方形的长为(2720680)(6050)340+÷-= (米),宽为6803405052÷+= (米)。
小学奥数习题版三年级几何巧求面积学生版

巧求面积知识要点我们已经学会了计算正方形、长方形的周长和面积,运用这些基础的知识,可以解决一些较复杂的面积计算.由长方形、正方形引出的问题形式多样,要解决这些问题,关键要能够合理地切拼,要做到这一点,就需要我们开动脑筋,细心观察,掌握图形特点,找出分割与切拼的方法,达到解决问题的目的.1.掌握巧妙的解题方法.2.了解“等量代换”的思想.3.培养学生灵活运用的能力.简单求面积【例 1】4个相同的长方形和一个小正方形拼成一个面积是100平方厘米的大正方形,已知小正方形的面积是36平方厘米,问长方形的长和宽各是多少厘米?【例 2】如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?75【例 3】一个长方形周长是80厘米,它是由3个完全相同的小正方形拼成的,那么每个小正方形的面积是多少平方厘米?面积增减【例 4】一块长方形铁板,长15分米,宽l2分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【例 5】一块长方形地长是80米,宽是45米,如果把宽增加5米,要使原来的面积不变,长应减少多少米?【例 6】人民路小学操场原来长80米,宽55米,改造后长增加20米,宽减少5米.现在操场的面积比原来增加多少?【例 7】有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?【例 8】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【例 9】一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?等量代换【例 10】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?24【例 11】若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例 12】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)366找规律【例 13】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?… …平移【例 14】有一块菜地长37米,宽25米,菜地中间留了1米宽的路,把菜地平均分成四块,每一块地的面积是多少?37米25米1米1米【例 15】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,红条宽都是2厘米,这条手帕白色部分的面积是多少?【例 16】(第六届小机灵杯决赛第七题)图中由若干个相同的正方形拼成,图形的周长是68厘米,这个图形的面积是多少平方厘米?【例 17】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?翻折【例 18】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?旋转【例 19】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【例 20】(第七届小机灵杯决赛第六题)图中是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是多少?第6题【例 21】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积。
第八届小机灵数学竞赛三年级初赛

第八届小机灵三年级初赛1、666+666-666*666/6662、如果10-9+8*□/7+6-5+4-3*2=0,那么□=()。
3、观察表中各数的排列规律,A是()。
4、一个正方形,如果边长增加5厘米,这个正方形的周长增加()厘米。
5、两个正整数的和是18,其中一个数是另一个数的5倍。
这两个数分别是()和()。
6、如图,网格中的小正方形的面积都是1平方厘米,那么,阴影部分的面积是()平方厘米。
7、从1-10这10个正整数中,每次取出两个不同的数,使它们的和是4的倍数。
共有()种不同的取法。
8、3只橘子的价格与4只苹果和1只梨的价格相同,4只梨的价格与6只橘子的价格相同。
()只苹果的价格与1只梨的价格相同。
9、在6和26之间插入三个数,使它们每相邻的两个数的差相等,这些数的和是()。
10、64位同学都面向主席台,排成8行8列的方阵。
小胖在方阵中,它的正左方有3位同学,正前方有2位同学。
若整个方阵的同学向右转,则小胖的正左方有()位同学,正前方有()位同学。
11、一个三位数除以37,商和余数相同,这个数最小是()。
12、在方框中添加适当的运算符号(不能添加括号),使算式成立。
17□3□4□9□7□6□4=2013、用数字1,2,3,4组成各位数字都不相同的两位数,并按从小到大的顺序排列,第10个数比第7个数多()。
14、学生问数学老师的年龄。
老师说:“由三个相同数字组成的三位数除以这三个数字的和,所得的结果就是我的年龄”,老师的年龄是()岁。
15、在图中的每个方格中各放1枚围棋(黑子或白子),有()种放法。
16、51518……共210个数字,其中1有()个,8有()个,5有()个;这些数字的和是()。
17、王强、李刚是哥哥,小丽、小红是妹妹,四人的年龄和为90,哥哥都比妹妹大4岁,小红比王强小5岁。
小红()岁。
18、给定三种重量的砝码5g,13g,19g,(每种砝码的数量足够的多),将它们组合凑成100g,(每种砝码至少用一个)有()中不同的方法。
小学五年级奥数竞赛培训试题 (3)

第八届“小机灵杯”小学生数学竞赛(初赛)1.计算: 3.9 5.5 6.3 3.613570.9 1.1 1.3()。
【考点】速算与巧算。
【分析】3.9 5.5 6.3 3.613570.9 1.1 1.33.9 5.5 6.3 3.65 1.170.93 1.33.62.在一位整数中,任取一个质数和一个合数相乘,所有乘积的总和是()。
【考点】乘法原理。
【分析】乘积总和是23574689459。
3.两个正整数的最大公约数是12,最小公倍数是240,这两个数的差最大是()。
【考点】最大公约数和最小公倍数,短除法。
【分析】由短除法知道,这两个正整数可以表示成A12a和B12b,a,b1且ab20,要使这两个数的差最大,有a20,b1,差是24012228。
注:关于最大公约数和最小公倍数还有一个性质:两个数的乘积等于它们的最大公约数和最小公倍数的乘积。
4.986261004除以13的余数是()。
【考点】余数的乘法定理。
【分析】余数的乘法定理告诉我们,乘积的余数等于余数的乘积的余数。
987mod13,6262mod13,10043mod13,则986261004723423mod13。
5.一个正整数与1470的积是一个完全平方数,那么这个数最小是()。
【考点】质因数分解与完全平方数。
【分析】147023572,完全平方数分解质因数后每个质因数的次数都是偶数,所以这个数最小是23530。
6.1~100这100个数除以7,余数不为0的数的和是()。
【考点】等差数列求和。
【分析】1~100中除以7余数为0的有7、14、⋯⋯98,所以除以7,余数不为0的数的和是12100714984315。
上海学而思教材研发中心7.一个农夫看见池塘里有一群鹅,他自言自语地说:“我如果有这些鹅,再加上这些鹅,然后再加上这些鹅的一半,又加上这些鹅的一半的一半,最后再加上我家里的5只,就正好是93只鹅。
”池塘里有鹅()只。
【考点】分数应用题。
4最短路线(教师)

第四讲最短路线知识概述从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:⑴两点之间线段最短。
⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力。
例题精讲【例1】如下图所示,小虎家在A地,姥姥家在B地。
一天,他要去看望姥姥,但不知有几条路可走,走哪条路最短,热心的小朋友们快帮帮他吧?【分析】两点之间,线段最短。
【拓展】如下图所示,从甲地到乙地一共有两条路可走,请问哪条路长?哪条路短?【分析】一样。
【拓展】观察下图,若黑猫与白猫奔跑速度相同,那么哪只猫先捉到老鼠?白猫黑猫鼠【分析】黑猫。
【拓展】有一只蜗牛从A点出发,要沿长方形的边或对角线爬到C点,中间不许爬回A点,也不能走重复的路,那么它有多少条不同的爬行路线?最短的是哪条呢?ODCBA【分析】共有9种:A O C→→、A O D C A O B C→→→→→→、、A B C→→、A B O C→→→、A B O D C→→→→、A D C→→、A D O C→→→、A D OB C→→→→,最短的路是:A O C→→。
【例2】直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线之和最短,问汽车站建在哪儿最好?乙甲BA【拓展】(2010年第十一届“中环杯”三年级初赛)如图,一个牧童从甲地出发,赶着羊群先到河边饮水,再将羊群赶到乙地吃草。
已知从甲地到河边饮水点,以及从饮水点到乙地都是直线路程,请问应该怎么选择河边饮水点的位置,使这群羊所走的路线为最短?请在图上表示出来并作文字说明。
【分析】轴对称知识的运用。
【拓展】 如图,在河里有A 、B 两岛,一次划船比赛从A 岛出发划向B 岛,赛程规定必须先划到北岸,然后再划到南岸,最后再划向B 岛,问应该怎样选择路线,才能使路程最短?【分析】 路线如右图所示。
三年级小机灵杯1-12届初赛7-8届决赛真题及答案

小机灵杯1-12届复赛真题试卷小机灵杯1-11届复赛真题答案小机灵杯7届决赛真题小机灵杯8届决赛真题第一届小机灵杯邀请赛1、按规律填数:901 812 723 634 545 ( ) ( )2、在一个减法算式中,把被减数,减数,差这三个数相加,所得的和除以被减数(不等于0),商等于( ).3、右式中,不同的字母表示不同的数字,那么ABC表示的三位数是( ).4、如果2只白兔2天吃白菜2千克,照这样计算,那么8只白兔8天吃白菜()千克.5、右面算式中的被除数是( )6、甲,乙两人今年的年龄和是33岁,4年后,甲比乙大3岁,问甲今年( )岁.7、把边长分别为10厘米,9厘米,8厘米和7厘米的4个正方形按照从大到小的顺序排成一行(如图)排成的图形的周长是( )厘米.8、有一堆围棋子,白子的个数是黑子个数的2倍,拿走96个白子后,黑子的个数是白子个数的2倍,原来黑子有( )个.9、有1张伍元币,4张贰元币,8张壹元币.要拿出8元钱可以有( )种不同的方法.10、亮亮和聪聪玩“石头、剪刀、布”的游戏,两人用同样多的石子做记录,输一次就给对方一颗石子,结果亮亮胜了3次,聪聪比原来多了9颗石子,他们共做了( )次游戏.11、任取自然数2,3,4,5,6,7中的三个数(不能重复)组成一个和,那么不相同的和共有( )个.12、新华小学的电表显示的用电量是61111,要使电表显示的用电量的五位数中有四个数码相同,学校至少再用( )度.13、黑、白两种颜色的珠子,一层黑,一层白,排成正三角形的形状(如图),当白珠子比黑珠子多10颗时,共用了( )颗白珠子.14、公园里有一排彩旗,按3面黄旗,2面红旗,4面绿旗的顺序排列,小明看到这排彩旗的尽头是一面绿旗,已知这排彩旗不超过200面,这排旗子最多有( )面.15、将写有数码的纸片倒过来看,0、1、8三个数字不变,6倒过来是9,9倒过来是6,而其余的数字倒过来则没有意义,某种游戏卡片是从001,002,003,004,……,998,999共有999张,那么,所有的卡片倒过来看,与原卡片数值保持不变的共有( )张.第二届小机灵杯邀请赛1.在右面竖式的各个方框中填上适当的数字,使竖式成立.2.推算是24,是28,那么是( )3.按下面的规律摆五角星,第82个五角星是( )色的.在这种颜色的五角星中,它是第( )个.★★★☆☆★☆★★★☆☆★☆★★4.学校有60人要参加“金孔雀”舞蹈比赛,比赛时要求每排人数即不能少于4人,也不能多于16人,问共有( )中排法.5.根据前面三个算式的启发,括号里面应当填上( )4.5.6.7.8.9.6.一个电影院的第一排有15个座位,以后每一排都比前一排多2个座位,最后一排有73个座位,这个电影院一共有( )个座位.7.下图中不含“★”的三角形比含“★”的三角形多( )个.8.把21分拆成两个自然数之和,且使这两个自然数的乘积最大,这个最大的乘积是( ).9.如图,在长方形ABCD 中,EFGH 是正方形.如果AF=11厘米,HC=14厘米,那么长方形ABCD 的周长是()厘米.10.将不大于12且互不相同八个自然数天使右图八个放个中,使九宫格图中的每一行,每一列以及对角线上的三个数的和都等于21.11.在一道减法算式里,被减数、减数与差的和是360,而差比减数的4倍还多20.被减数是 (),减数是(),差是().12.有两个完全一样的长方形,拼成两种长方形,一种长方形的周长是100厘米,另一种长方形的周长是140厘米,原来长方形的长是()厘米,宽是()厘米.13.某商场里面花布的米数是白布的3倍,如果每天卖20米白布和45米花布.()天以后,白布全部卖完,而花布还剩下180米,原来有花布()米.14.1996年爸爸的年龄是姐姐和妹妹年龄和的4倍,2004年爸爸的年龄是姐姐和妹妹年龄和的2倍,爸爸是()年出生的.15.书架上、下两层摆放着若干本书.如果从上层拿10本放到下层,则下层的本数是上层的2倍,如果从下层拿到10本放到上层,则上层的本数是下层的3倍,上层原来有图书()本,下层原来有图书()本.第三届小机灵杯邀请赛1、用简便方法计算下面的题目:100+99989796959465432-+-+-+-+-+-2、不同的余数有多少个?24? ①余数共有()个;②不同的余数共有()个.3、用40米的铁丝围成一个长和宽不相等的而且是整米的长方形,一共有( )种不同的围法.4、时钟现在是整点,再过112小时,钟面上恰好是1点整.请你判断,现在是()整.5、把一张正方形的纸对折,再对折,这样连续几次,写出对折了4次时长方形的块数是()块.6、在下面一列数中,第12个数是:()123654789121110131415,,,,,7、右图中有()几个长方形8、小华和小强的体重是84千克,小华和小玲的体重是80千克,小强和小玲的体重是82千克小华比小玲重()千克.9、如图,在长方形ABCD 中,EFGH 是正方形.如果16AF =厘米,21HC =厘米,那么长方形ABCD 的周长是()厘米.10、从小到大的连续10个自然数,如果最小的数与最大的数之和是99,那么最小的数是().11、有四种不同面值的硬币如下图所示,假若你恰好有着四种硬币各一枚.一共能组成()种不同的钱数.请你用加法算式一个一个的列举出来.12、如下图,李明从A 走到B 再到C 再到D,走了38米.玛丽从B 到C 再到D 再到A,走了31米.这个长方形池ABCD 的周长是()米.第四届小机灵杯邀请赛1、699999+69999+6999+699+69=().2、一列数15791317,,,,,,从第二项起,后项减去它的前一项的差都相等,从左向右数起, 第()个数是197.3、观察下面三角形中的各数的规律,并按照这个规律求m 的值.m =().4、在一条直线上有四个点,,,A B C D ,点B 不在,,A C 之间,点D 是AC 的中点,从B 到D 的距离是20cm ,从B 到C 的距离是12cm ,从A 到B 的距离是多少?5、将一张正方形纸片对折成长方形后,在此长方形纸上画两条直线,然后沿着两条直线各剪一刀,最多能将这张正方形纸分成()块.6、一个长方形的长是40cm ,宽是25cm ,如果将此长方形剪两刀,得到3个或4个长方形,那么被剪两道后得到的那些长方形的周长之和最多是()cm .7、2个男孩和2个女孩参加歌咏比赛,他们一个接一个地唱,假定两女孩不能连着唱,必须隔开,能排成()种不同的顺序.8、假如20只兔子可换2只羊,9只羊可换3头猪,8头猪可换2头牛,那么用5头牛可换()只兔子.9、哥哥给了弟弟84分之后,弟弟反而比哥哥多36分,哥哥原来比弟弟多()分.10、用一只茶杯将水倒入一只空水瓶里,如果2杯水倒入这个水瓶里,这个水瓶的和水的重量是540克,如果5杯水倒入这个水瓶里,这个水瓶的和水的重量是600克,空水瓶的重量是( ). 11、在某一个月中,有三个星期日的日期刚好是偶数号,那么这一个月的8号是星期().12、小平和小丽到新华书店去买书,她们选中了同一本书,可是她们带的钱不够,小平差15元,小丽差2元,只好先合买一本,还多1元.每本书()元.13、一本字典共有199也,在这本字典的页码上,数字1共出现了()次.14、口袋里装有红、黄、蓝、绿4种颜色的球各5个.小华闭着眼睛从口袋里往外摸球,每次摸出1个球.他至少要摸出()个球才能保证摸出的球中每种颜色的球都有.15、10名乒乓球运动员分成三队,每队若干个队员进行单打比赛.规定同队的运动员彼此之间不用比赛,不同队的运动员两两比赛一场,那么比赛的总场数最少是( )场,最多是( )场.第五届小机灵杯邀请赛复赛1、199+298+397+496+595+20=().2、9937+4599+83=创( ).3、小明去同学家玩.走进了弄堂,但记不起门牌号码了.怎么办呢?他忽然想起,这个门牌号码挺有意思,曾经研究过一次.它是一个三位数,个位数字比百位数字大4,是位数字比个位也大4.根据这点记忆,你能帮助小明找到同学家吗?如果想到了,就写在下面.门牌号码是().4、企鹅出版社出版了一套《天才智慧》丛书,出版社为这套丛书设计了一个漂亮的书盒,这套丛书连同书盒售价280元,书店允许顾客只买书而不买书盒.如果书价比书盒贵230元,那么书盒价为()元.5、波特有6只狗,如果他每次遛2只狗,那么狗的搭配情况总共有()种.6、请把图中①~⑨号小正方形的标号填入右图中九个小方格 中,使这九块小正方形刚好拼成中间的图形.7、一批图书,本数在50~60之间,平均分给9名同学,结果余下的书和每人分到的书的本数相同,那么这批图书共有多().8、园林工人在一条马路的一边栽树(包括端点),,每2棵树之间的距离是4米,一共栽树86棵,这条马路长()米.9、下图是用17根火柴棒摆成的,图中共有8个正方形.从图中至少拿掉()根火柴棒,才能将这8个正方形全部破坏(构不成正方形),请在图中表示出来.10、图10,线段10,8,3,a cm b cm c cm ===图形的周长是()cm .11、一位妇人,人到中年,很不愿提起自己的年龄,但她又不愿说谎.一天,有人问及她的年龄,她只好实话实说:“我4年后的年龄的6倍减去我3年前的年龄的6倍,就是我现在的年龄.”这位妇人今年( )岁.12、有5个袋子.A袋和B袋的重量之和是120千克,B袋和C袋的重量之和是135千克,C袋和D袋的重量之和是115千克,D袋和E袋重量之和是80千克,A袋、C袋、E袋子的重量之和是160千克.A袋的重量是( )千克,B袋的重量是( )千克,C袋的重量是( )千克,D袋的重量是( )千克,E袋的重量是( )千克.c g h k u,背面分别写着1,2,3,4,5,但是顺序不同.把13、有5张扑克牌,表面分别写着字母,,,,c k u,第二次出现了如下情况这些扑克牌随意散放,第一次出现了如下情况25k c g,那么字母u背面的数字是( ).2414、数一数下面图形共有( )个正方形.15、把27米长的一根绳子分成三段,使后一段比前一段多三米.那么这三段绳子分别长()米,( )米,( )米.第六届小机灵杯邀请赛复赛A 卷1、()()1+4+7+10++4047101337-+++++=.2、左式中,不同的符号表示不同的数字,那么○+△+◇=.3、下面的一列数是按一定的规律排列的,那么括号中的数是.1,4,10,22,46,(),190,4、在图中,从甲点出发沿逆时针方向绕五边形走,到乙点拐第一个弯,拐第101个弯在点.5、一本故事书的页码共用了192个数字,这本书一共有页.6、5位选手进行象棋比赛,每两个人之间都要进行比赛一盘,规定选手胜一盘得2分,平均一盘各得一分,输一盘不得分.已知比赛后,其中4位选手总共得16分,则第5位选手得了分.7、某年的三月份正好有4个星期二和星期五,那么这年的3月1日是星期.8、有十个连续自然数,前五个数的和为60,后五个数的和是?9、有一桶水,一只小鸭可饮用25天,如果和一只小鸡同饮,那么可以饮用20天,如果给一只小鸡饮用,可以饮用天?10、一个正方形队列,如果减少一横行和一竖行,要减少21人,问原正方形队列有人?11、如图所示的病房区共有五间单人病房,住着,,,A B C D 四位病人,根据不同的病情要求让A 与D 交换病房,C 与B 交换病房,每一次交换只能将一位病人搬入另一间无人的病房,那么需要完成交换,至少要为病人搬次家?54321DCB A D走廊走廊12、解放军某部赶往受灾地区志愿抗洪,原计划每辆汽车乘30人,还多3人任意分乘到各辆车上,但是由于有另外的紧急任务调走了一辆车,这时只好改为每辆汽车乘34人,还多5人任意分乘到各辆车上.原来准备辆车,共派出人去抗洪.1、()()6+8+10+12++368101214+34-++++=.2、左式中,不同的符号表示不同的数字,那么○+△+◇=. 3、下面的一列数是按一定的规律排列的,那么括号中的数是.1,3,7,15,31,(),127,4、把1到500号卡片依次发给甲、乙、丙、丁四个小朋友,1234567891011121314151617那么,119号卡片发给5、一本故事书共有185页,那么编这一本书的页码一共要个数字.6、右图共有个长方形.7、某月内有三个星期六是偶数,这个月的18日是星期.8、用3,4,5,6四个数字卡片排两位数乘两位数的竖式,乘积最大与乘积最小的两个积的差是?9、市里举行足球比赛,有15个区各派出1个代表队,每个队都要与其他各队比赛一场,这些比赛分别在15个区的区体育场进行,平均每个体育场要举行场比赛?10、用5张长2分米、宽1分米的长方形不干胶,贴在一块长5分米、宽2分米的木板上,将其盖住.你能设计出种不同方案.(通过旋转或翻转后形成相同图案的算一种)11、经纬小学有10名同学参加区数学比赛,平均分为90分,其中2名同学分别获得第一名和第二名,他们的得分都是整数,另外有五个人都得了92分,有3人都得了84分.获得第二名的同学得分.12、小军用一张正方形的纸片做剪纸练习,先把它从中间剪开得到两个长方形,再把其中一个长方形从中间剪开得到两个正方形,再把其中一个正方形从中间剪开得到两个长方形……那么这样剪了21次,一共剪成 长方形, 正方形.1、()()7+9+11+13++379111315+35-++++=.2、左式中,不同的符号表示不同的数字,那么○+△+◇=. 3、下面的一列数是按一定的规律排列的,那么括号中的数是.2,3,5,9,17,33,(),129,4、在图中,从A 点出发沿顺时针方向绕五角星走,到B 点拐第一个弯,拐第95个弯在点.5、小刚从一本书的54页阅读到67页,苏明从95页阅读到135页,小强从180页阅读到237页,他们总共阅读了页. 6、右图共有个长方形.7、希望小学的操场上有150名学生在跳绳和打球.其中女生54名,如果有63名学生在跳绳,有42名男生在打球,那么有名女生在跳绳.8、用2,3,4,5四个数字卡片排两位数乘两位数的竖式,乘积最大与乘积最小的两个积的和是?9、有15只甲A 足球队,进行双循环比赛(每两支队赛两场),共要举行场比赛?10、有很多张长2分米、宽1分米的长方形不干胶,和边长为1分米的正方形不干胶,用这些不干胶贴在一块长3分米、宽2分米的木板上,将其盖住.你能设计出种不同方案.(通过旋转或翻转后形成相同图案的算一种)11、继红小学有10名学生参加小机灵杯数学比赛,平均分为90分,平均分和每个同学的得分都是正整数,前9名的分数各不相同,其中一名同学得满分,第十名同学得分的最低分是分.12、小军用一张正方形的纸片做剪纸练习,先把它从中间剪开得到两个长方形,再把其中一个长方形从中间剪开得到两个正方形,再把其中一个正方形从中间剪开得到两个长方形……那么这样剪了36次,一共剪成长方形,正方形.第七届小机灵杯邀请赛复赛1、如果*a b a ba b =?-,例如4*3434313=?-=,那么13*8=2、用0~9十个数字填写下面的竖式,已经用了三个数字,剩下的七个数字,每个只能用一次,要使算式成立,减数是3、一个长方形队列,如果增加一横行和一竖行,就要增加13人,这个长方形的队列原来最少有人4、桌上有8张扑克牌,点数分别是2,3,5,6,7,8,9,10.甲、乙、丙三人各取两张牌,两张牌的点数分别是:甲是9,乙是15,丙是17,那么甲取出的两张点数是5、甲校原来比乙校多48人,为了方便就近入学甲校有若干人转入乙校,这是甲校反而比乙校少12人.甲校有人转入乙校6、将1,4,7,10,13,16,19,22,25这9个数分别填入下图中的9个圆圈中,使三条边上的四个数字和都想等,每条边上四个数字的和最大是7、如果三本书的价钱等于四本笔记本的价钱,而买四本书要比三本笔记本多花5角6分,那么买一本书和一本笔记本共需元8、下面两种那个途中,周长较大的是.(在横线上填写表示图名的字母)9、某三位数是7的倍数,且在400到500之间,它的百位数字与个位数字的和是9,那么这个三位数是10、下图中有10个编好号码的房间,你可以从小号码的房间周到相邻的大号码的房间,但是不能从大号码的房间走到小号码的房间,从1号房间走到10号房间共有种不同的走法11、有若干根长度相等的火柴棒,把这些火柴棒摆成如下面的图形,照这样摆下去,到第10行为止,一共用了根火柴棒12、在一块长5米,宽4米的长方形地上铺80块边长为5分米的小正方形地砖,现在把每相邻的两个小正方形的边界用细玻璃条隔开,并在长方形地的边界上用细金属条围上.如果嵌1米长的细玻璃条需3元,围1米长的细金属条需5元,那么共需元(接缝处长度忽略不计)第八届小机灵杯邀请赛复赛1、666666666666666+-锤=( )2、如果10987654320-+⨯÷+-+-⨯=,那么□=( ).3、观察表中各数的排列规律,A是( ).4、一个正方形,如果边长增加5厘米,这个正方形的周长增加( )厘米.5、两个正整数的和是18,其中一个数是另一个数的5倍.这两个数分别是( )和( ).6、如图,网格中的小正方形的面积都是1平方厘米,那么,阴影部分的面积是( )平方厘米.7、从1-10这10个正整数中,每次取出两个不同的数,使它们的和是4的倍数.共有( )种不同的取法.8、3只橘子的价格与4只苹果和1只梨的价格相同,4只梨的价格与6只橘子的价格相同.( )只苹果的价格与1只梨的价格相同.9、在6和26之间插入三个数,使它们每相邻的两个数的差相等,这些数的和是( ).10、64位同学都面向主席台,排成8行8列的方阵.小胖在方阵中,它的正左方有3位同学,正前方有2位同学.若整个方阵的同学向右转,则小胖的正左方有( )位同学,正前方有( )位同学.11、一个三位数除以37,商和余数相同,这个数最小是( ).12、在方框中添加适当的运算符号(不能添加括号),使算式成立.17□3□4□9□7□6□4=2013、用数字1,2,3,4组成各位数字都不相同的两位数,并按从小到大的顺序排列,第10个数比第7个数多( ).14、学生问数学老师的年龄.老师说:“由三个相同数字组成的三位数除以这三个数字的和,所得的结果就是我的年龄”,老师的年龄是( )岁.15、在图中的每个方格中各放1枚围棋(黑子或白子),有( )种放法.16、1881515188151518……共210个数字,其中1有( )个,8有( )个,5有( )个;这些数字的和是( ).17、王强、李刚是哥哥,小丽、小红是妹妹,四人的年龄和为90,哥哥都比妹妹大4岁,小红比王强小5岁.小红( )岁.18、给定三种重量的砝码5g,13g,19g,(每种砝码的数量足够的多),将它们组合凑成100g,(每种砝码至少用一个)有( )中不同的方法.19、有两个正整数,把这两个正整数相乘,再加上这两个正整数的和,结果正好等于34,这两个正整数中较大的数是( ).20、写出所有数字的和为13,积为24,这样的四位数的偶数是( ).第九届小机灵杯邀请赛复赛下面每题6分1、计算2102092082072062052047654321+-+-+-++-+-+-+=.2、如右图所示,从上往下,每个方框中的数都等于它下方两个方框中所填的数的和.最上层方框中两个数的和是.3、如右图所示,,,,,,,,,,a b c d e f g h i j 表示10个各不相同的数.表中的数为所在行与列对应字母的差,例如“6b h -=”.图中“九宫格”中就个数的和是.4、小胖比他的表姐小12岁,再过4年小胖的年龄是他表姐年龄的一般,他俩今年的年龄总和是岁.5、如下图所示,从A 点走到B 点,沿线段走最短路线,共有种不同的走法.6、五位打工者一天的辛苦劳动后共获得330元工资.由于工种不同,获得最高工资者比其他四位分别多的12,14,21和28元,获得最低工资者的工资是元.7、右边图形的周长是厘米.8、在数20468204682046820468中划去10个数字(不能改变原来数字的顺序),得到一个最小的十位数,这个最小的十位数是 .AB下面每题9分9、下边的乘法算式中,只知道一个数字“8”.请补全.那么这个算式的最小值是.⨯810、在1,2,3,4,5,6六个数中,选三个数,使它们的和能被3整除.那么,不同的选法共有种.11、有四袋糖,每袋糖的块数都不相同,任意三袋糖的块数总和都不少于60快.那么,这四袋糖的块数总和至少有块.12、3根火柴可以摆成一个小三角形.用很多根火柴摆成了如右图那样的一个大三角形.如果大三角形外沿的每条边都增加10根火柴,那么摆成这样形状的大三角形共需要根火柴.下面每题12分13、一次测验中,小胖答错了6道题,小亚答错了7道题,小丁丁答对的题目的数量等于小胖和小亚答对题数量的总和,小丁丁大队了17道题,这次测验共有道题.+++=,小于2000的四位数中,数字和等于26的四位数共有14、1997的数字和是199726个.15、小刚在一个长方形中任取三条边相加,所得的和是78厘米,小亚在同一个长方形中任取三条边相加,所得的和是66厘米.这个长方形的周长是厘米.第十一届“小机灵杯”数学竞赛初赛试卷(三年级组)时间:60分钟总分:120分第一项:每题8分1.已知1+2+3+….+49+50=1275,那么1+2+3+….+49+50+49+48+….+3+2+1=_______。
三年级下册数学讲义-竞赛专题:第三讲-间隔问题(含答案解析)人教版

知识概述植树问题:植树问题关键在于段数与棵树的相互转换。
段数=总距离÷棵距一、不封闭路线:(1)在一段距离中,两端都植树, 棵数=段数+1;(2)在一段距离中,两端都不植树, 棵数=段数-1;(3)在一段距离中,一端不植树, 棵数=段数.二、封闭路线:如环湖栽树、游泳池等在封闭曲线上植树,棵数=段数=周长÷棵距爬楼问题:爬楼层数=楼的层数-1(第一层楼不用爬)锯木头问题:锯木头的段数=锯的次数+1 (锯第一次得两段)间隔问题主要包括植物问题、锯木头问题、爬楼问题、敲钟问题等,是一类有多种实际背景的问题,问题的关键是一条线(封闭与不封闭)上分点数与点与点之间的间隔之间的关系,有时还涉及到总长度,间隔数及一个间隔的长度的计算。
植树问题是典型的间隔问题,掌握了植物问题其它类型也就迎刃而解了。
名师点题间隔问题植树节那天,三年级的小朋友打算在30米长的路一边栽树,从一端起,每隔5米栽一棵,(1)两端都要栽。
小鸥说:“一共要栽6棵。
”小雅说:“一共要栽7棵。
”谁说得对呢?(2)如果两端都不栽树,一共要栽几棵?(3)如果一端栽树,另一端不栽树,一共要栽几棵?【解析】每隔5米栽一棵,那也就是说,30米里有几个5米就是栽了几棵树,所以用3056÷=(棵)。
看起来,小鸥的想法是对的,但是不符合实际。
我们画一条直线段表示30米长的路,然后在线段上按照要求画上小树苗,如图所示。
5米5米5米5米5米5米可以看到一共栽了7棵树。
那也就是说,用305÷求到的是有几个间隔,也就是这条路被分成几段,但是因为两端都栽了树,所以棵数应该比间隔数多1。
(1)11=+=÷+棵数段数总距离棵距=30517÷+=(棵)。
因此小雅说得对,一共要栽树7棵。
(2)两端都不栽树,段数-1=6-1=5棵(3)一端栽一端不栽,棵树=段数=6棵600米长的马路一侧装了一排路灯,起点和终点都装了,一共16盏,相邻两盏之间的距离相等,求相邻两盏路灯之间相距多少米?【解析】在马路的一侧装了16盏路灯,16盏路灯减去起点处的一盏,就有16115-=个间距。
小学奥数习题版三年级其他等量代换学生版

知识要点重量上的等量代换【例 1】 如下图所示,一个菠萝的重量等于多少个苹果的重量?生活中有很多相等的量,如平衡的天平、平衡的跷跷板两边的重量相等。
根据这些相等的关系进行推理,进而可以等量代换,找到答案。
1.两个相等的量可以相互代换(包括重量相等、价格相等)。
2.将不同等式中相同种类的物品通过加、减、乘、除转化成相同个数,这样可以形成新的等式。
3.将两个不同等式中,左边物品相加,右边物品相加。
这样可以形成新的等式。
4.如果天平不平衡,先求出天平左、右两端的物品在重量上相差多少,然后得出使天平平衡的方法。
等量代换【例2】如下图,1头猪的重量等于几只公鸡的重量?【例3】观察下图,看看谁最重?【例4】根据下图,试求出1只袋鼠的重量相当于多少只小鸡的重量?【例5】下图中第三个天平右边的盘子应放几个小正方体才能保持平衡?【例6】根据下图,试求出1串葡萄重多少克?【例7】1只狗重9千克,根据下面的图,你能求出1只猫与1只鸭各重多少千克?【例8】如下图所示,1瓶可乐相当于多少杯牛奶的重量?【例9】算一算1只小熊的重量与几只鸭的重量一样重?【例10】如下图所示,一个西瓜的重量等于多少个苹果的重量?【例11】已知买1个汉堡包的钱可以买2个冰激凌;买1个冰激凌的钱可以买3杯牛奶。
求:(1)买60杯牛奶的钱可以买几个汉堡包?(2)买60个汉堡包的钱可以买多少杯牛奶?【例12】已知1个排球和1个足球共重5千克;1个排球和1个篮球共重6千克;1个足球和1个篮球共重7千克。
求篮球、足球、排球各重多少千克?【例13】在下图中的“?”处放上几个小,才能使天平保持左右平衡?【例14】1个西瓜的重量等于2个哈密瓜的重量,1个哈密瓜的重量等于8个苹果的重量,2个苹果的重量等于3个柿子的重量,那么1个西瓜的重量等于几个柿子的重量?【例15】1头大象的重量等于4头牛的重量,l头牛的重量等于3匹马的重量,则1头大象的重量等于多少匹马的重量?【例16】玩具店运来一批卡通猫,如果2个纸箱同1个木箱装的一样多,4个木箱同1个大箱装的一样多,那么装在16个纸箱里的这批卡通猫要装几个大箱?【例17】1只兔子的重量+2只猴子的重量=11只鸡的重量;3只兔子的重量=9只鸡的重量;1只猴子的重量=几只鸡的重量?【例18】1个菠萝加1个梨的重量等于7个桃子的重量,2个梨的重量等于4个桃子的重量。
三年级计算数字问题教师版

知识要点四、数的分析 1、采用枚举法2、从低位向高位依次分析五、数的变化1、数字0、1、6、8、9倒过来看分别是0、1、9、8、6。
2、数字0、1、8在镜子里看分别是0、1、8。
一、数的拆分1、把数拆分时,按从大到小的顺序排列。
例:5分成两个数的分法,54132=+=+。
二、数的分组1、把数分组时,先求所有数的总和,把这些数分成若干组,每组数的和=所有数的和÷组数。
例:1~6分成三组,和为21,每一组的和为2137÷=,所以7162534=+=+=+。
三、数的在数位上的排列1、认识基本数字:0、1、2、3、4、5、6、7、8、9。
2、在计数器上,个位、十位、百位、千位上的珠子分别表示几个一、几个十、几个百、几个千。
3、在读位数不高于五的自然数时,末尾所有的0都不读,中间连续的0只念一次。
例:10002读作:一万零二;96000读作:九万六千;3050读作:三千零五十。
和倍问题数的拆分【例 1】把10拆分成3个不同的自然数相加的形式(0除外)共有多少种不同的分拆方法?【分析】分拆时,可以按从大到小的顺序排列,根据题意,两个不同的非零自然数相加和最小为123+=分拆成的数不可能大于1037-=。
最大数是7:10721=++,最大数是6:10631=++,最大数是5:10541=++,=++、10532所以,一共有4种不同的分拆方法:【例 2】把15分拆成四个不同的自然数相加的形式(0除外)共有多少种不同的分拆方法?【分析】分拆时,可以按从大到小的顺序排列,根据题意,分拆成的数不可能大于151239---=。
最大数是9:159321=+++,最大数是8:158421=+++,最大数是7:157521=+++,=+++、157431最大数是6:156531=+++。
=+++、156432把15分拆成四个不同的自然数相加的形式(0除外)共有6种不同的分拆方法:【例 3】(第六届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛三年级试卷)用若干个1分、2分、5分的硬币组成1角钱(不要求每种硬币都有),共有多少种不同的方法?【分析】1角10=分,考虑5分的个数来拼凑。
巧算速算练习题

巧算速算练习题巧算速算练习题1.计算2011×990+2011×11=_____。
(第九届走美杯三年级初赛)★2.2012×9+2012×8-2012×7=_____。
(第十届走美杯三年级初赛A卷)★3.计算23×98-37×23+23×38+23=_____。
(第十一届走美杯四年级决赛)★4.计算25×13×2+15×13×7=_____。
(第十五届中环杯三年级决赛)★5.算式5×13×(1+2+4+8+16)的计算结果是_____。
(2015年数学花园探秘中年级组决赛)★6.计算2011-(9×11×11+9×9×11-9×11)=_____。
(2011年数学解题能力展示中年级复赛)★★7.在下面的□中填入一个相同的数字,使算式成立。
97+□×(19+91÷□)=321, □=_____。
(第十三届小机灵杯三年级决赛)★★8.计算2×(999999+5×379×4789)=_____。
(第十三届走美杯上海赛区三年级决赛)★★9.计算13+73+132+145+255+274+326+368+427=_____。
(第十四届中环杯三年级选拔赛)★★10.计算2015-123-125-127-129-131=_____。
(第十三届小机灵杯三年级初赛)★★11.计算1+3+5+7+…+97+99-2014=_____。
(第十三届走美杯三年级初赛)★★12.101-99+97-…-7+5-3+1=_____。
(第十一届走美杯三年级决赛)★★13.计算2014-37×13-39×21=_____。
(第十四届中环杯三年级决赛)★★★14.123×8+82×9+41×7-2009=_____。
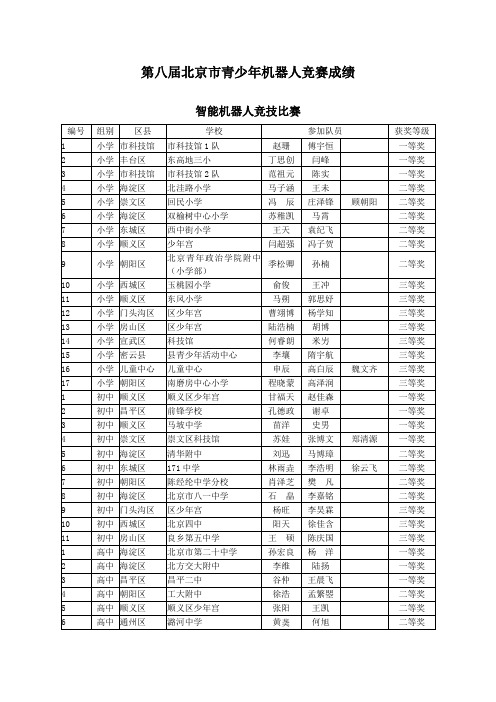
第八届北京市青少年机器人竞赛成绩
3
高中
海淀区
北京市八一中学
林乐祺
郭佳玮
吴昊
张皓辰
二等奖
4
高中
海淀区
北方交大附中
李逍然
郝运
王翊坤
陈斯末
三等奖
5
高中
朝阳区
工大附中
周天一
陈昊
张野
张宝頔
三等奖
2008年4月13日
宣武区回民学校
佀传伊森
王安
周春粟
康灵祺
杨帆
三等奖
1
高中
东城区
北京市第二中学
邓谨睿
赵鹏
孙继源
吕景瀚
刘晨阳
一等奖
2
高中
顺义区
牛山一中
靖凯旋
李丹
郝颖琨
张亚军
李晨龙
一等奖
3
高中
海淀区
北方交大附中
那超
李望松
臧潜
王典
胡琪唯
二等奖
4
高中
通州区
潞河中学
闫承稽
李魁姣
任雪
苏春阳
陈紫薇
二等奖
5
高中
朝阳区
北京市陈经纶中学
金 鑫
第八届北京市青少年机器人竞赛成绩
智能机器人竞技比赛
编号
组别
区县
学校
参加队员
获奖等级
1
小学
市科技馆
市科技馆1队
赵珊
傅宇恒
一等奖
2
小学
丰台区
东高地三小
丁思创
闫峰
一等奖
3
小学
市科技馆
市科技馆2队
范祖元
陈实
一等奖
4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
D
C
三年级
颜明老师 整理
【分析】巧求面积。 将阴影部分看成两部分三角形 ABD 和三角形 BCD 。小正方形的面积是1 平方厘米, 每个小正方形的边长是1厘米。三角形 ABD 的面积 412 2 (平方厘米), 三角形 BCD 的面积是 42 2 4 (平方厘米), 阴影部分的面积是6 (平方厘米)。
没有19g 砝码, 63 135 10
只有一个19g 砝码, 63 19 44 , 44 313 5
有两个19g 砝码, 63 19 2 25 , 25 5 5
有三个19g 砝码, 63 3 19 6 ,没有符合条件的组合方式
一共有 3种不同的方法。
【19】有两个正整数,把这两个正整数相乘,再加上这两个正整数的和,结果正好等于34 , 这两个正整数中较大的数是( )
4 13
8 1 7 2 6 3 5 ,
12 10 2 9 3 8 4 7 5 ,
16 10 6Leabharlann 9 7 , 所以一共有13 4 2 10 (种)。
方法二:用 1~10 这 10 个数分别除以 4,观察余数的情况: 1、2、3、0、1、2、3、0、1、2,如果两个数的和是 4 的倍数,可能的情况有 3
【分析】考点:等量代换。
4 只梨的价格与 6 只橘子的价格相同,那么 2 只梨的价格与 3 只橘子的价格相同,
而 3只橘子的价格与 4 只苹果和1 只梨的价格相同,所以 2 只梨的价格与 4 只苹果和
1只梨的价格相同,那么1只梨的价格与 4 只苹果的价格相同。
【9】在 6与26 之间插入三个数,使它们每相邻的两个数的差相等,这些数的和是(
)岁
因为小红比王强小5 岁,所以比小红大4 岁的是李刚,比小丽大4 岁的是王强。
三年级
颜明老师 整理
哥哥总共比妹妹大4 4 8 岁,所以妹妹的年龄和是 (90 8) 2 41, 哥哥的年龄和是 49 岁,王强比李刚大1岁,所以王强的年龄是 (49 1) 2 25(岁), 小红的年龄是25 5 20 (岁)。
【7】从 1 ~ 10 这 10 个正整数中,每次取出两个不同的数,使它们的和是 4 的倍数,共有
(
)种不同的取法。
【分析】考点:数论:余数性质、整除。枚举法的应用、加乘原理。
方法一:1 ~ 10 这10 个正整数中,两个不同的数相加最小为1 2 3 , 最大的为9 10 19 ,所以两数相加是 4 的倍数,这样的倍数可能是 4 、8 、12 、16 。
【分析】数字问题,枚举法。
令较大的数为a ,较小的数为 b 方法一:枚举。若 b 1 ,那么 a a 1 34 ,没有符合条件的 a ; 若 b 2 ,那么2a a 2 34 ,没有符合条件的 a ; 若 b 3 ,那么3a a 3 34 ,没有符合条件的 a ; 若 b 4 ,那么4a a 4 34 , a 6 ,符合条件, 46 4 6 34 。 方法二: a b a b 34 ,两边都加上1, a b a b 1 35 , 整理得 (a 1)(b 1) 35 5 7 ,所以a 7 1 6 。
类:第一类:余 1+余 3:共 32=6 个;
第二类:余 0+余 0:共 21 2=1 个; 第三类:余 2+余 2:共 32 2=3 个;
所以,共有 6+1+3=10 种不同的取法。
【8】3只橘子的价格与 4 只苹果和1只梨的价格相同,4 只梨的价格与6 只橘子的价格相同。
(
)只苹果的价格与 1只梨的价格相同
)。
【分析】考点:数论:带余除法性质。
这个三位数除以 37 ,商和余数相同,说明这个数是 37 1 38 的倍数,
所以这个数最小是38 3 114 。
【12】在方框中填适当的运算符号(不能填括号),使算式成立: 17349764 20
【分析】考点:巧填算符。17 3 4 9 7 6 4 50 , 50 20 30 ,而 9 6 15 , 所以只要将 9 、 5 之前的加号改为减号即可,即17 3 4 9 7 6 4 20 。
)。
【分析】考点:等差数列。
插入三个数后一共五个数,第三个数等于(26 6) 2 16 ,
根据中项定理:所以这些数的和是16 5 80 。
【10】 64 位同学都面向主席台,排成8 行8 列的方阵,小胖在方阵中,他的正左方有3 位同
学,正前方有 2 位同学,若整个方阵的同学向右转,则小胖正左方有( 学,正前方有( )位同学
【4】一个正方形,如果边长增加5 厘米,这个正方形的周长增加( 【分析】考点:巧求周长。
周长增加54 20 (厘米)。
)厘米。
【5】两个正整数的和是 18,其中一个数是另一个数的 5 倍,这两个数分别是(
)
和(
)。
【分析】考点:和倍问题。
较小的数是18 (5 1) 3 ,另一个数是 35 15 。
【6】如图,网格中的小正方形的面积都是1平方厘米,那么阴影部分的面积是( )平 方厘米。
【分析】分步计数原理。 因为每个方格都与其他的方格不完全相同,所以共有 2 2 2 2 16 (种)方法。
【16】1881515188151518...... 共有 210 个数字,其中1有(
)个,8 有(
)个,
5 有(
)个;这些数字的和是(
)。
【分析】周期问题。
我们发现每 7 个数字1881515 是一次重复, 210 个数字一共重复了210 7 30 次。
)位同
【分析】间隔与方阵。
面向主席台是,小胖的正右方还有 8 3 1 4 位同学。当整个方阵的同学向右转时, 原来在小胖正前方的同学变成了小胖的正左方,原来在小胖正左方的同学变成了小
胖的正后方。所以转向后,小胖正左方有2 位同学,正前方有4 位同学。
三年级
颜明老师 整理
【11】一个三位数除以 37 ,商和余数相同这个数最小是(
【14】学生问数学老师的年龄。老师说:“由三个相同的数字组成的 三位数除以这三个数的
和,所得的结果就是我的年龄”,老师的年龄是(
)岁
【分析】年龄问题、数字问题。
三个相同的数字组成的三位数肯定是111 的倍数,111 37 3 ,
三个数的和在 3 ~ 27 之间,所以老师的年龄只可能是 37 。
【15】在右边的每个方格中各放 1 枚围棋(黑子或白子),有( )种方法
【20】写出所有数字的和为13 ,积为 24 ,这样的四位数的偶数是( ) 【分析】数字问题。
乘积为 24 ,所以这样的四位偶数中没有0 。 24 2 2 2 3 4 6 83 , 所以这样的四位偶数组成的数字只可能是3 、8 、1 、1, 有:1138 、1318 、 3118 ,这三个。
三年级
颜明老师 整理
【3】观察表中各数的规律, A 是(
)。
1234 2 6 10 14 3 12 21 30 4 20 A 52
【分析】考点:数表规律。 第1 行,右边的数等于左边的数加上 1 ; 第 2 行,右边的数等于左边的数加上 4 ; 第 3行,右边的数等于左边的数加上 9 ; 第 4 行, 20 14 16 , 按规律, A 20 16 36 , 52 36 16 ,符合规律。
二、填空题。 【13】用数字1, 2, 3, 4 组成各位数字都不相同的两位数,并按从小到大的顺序排列,第10 个
数比第 7 个数多( ) 【分析】考点:分类与分步。
十位数字是1,共有3 个;十位数字是 2 ,共有3 个; 十位数字是 3,共有3 个;十位数字是 4 ,共有3 个。 那么第10 个数是 41 ,第 7 个数是 31, 41 31 10 。
【18】给定三种重量的砝码 5g ,13g ,19g ,(每种砝码的数量足够多),将它们组合凑成100 g ,
(每种砝码至少有一个)有(
)种不同的方法。
【分析】戥称与砝码问题。
5 13 19 37 , 100 37 63 ,显然63 不可能用同种砝码组合而成,
所以只可能由几种组合而成。我们来考虑 63g 的组合情况:
那么1有 330 90 (个), 8有 230 60(个), 5 有 2 30 60 (个),这些数字
的和是 90 860 560 90 480 300 870
三、填空题。
【17】王强,李刚是哥哥,小丽,小红是妹妹,四人的年龄和为 90 ,哥哥都比妹妹大 4 岁,
小红比王强小 5 岁。小红( 【分析】年龄问题。
2009 年第八届“聪明小机灵”智力冲浪展示活动
三年级初赛分析
一、填空题。
【1】 666 666 666 666 666 =(
)。
【分析】考点:速算巧算。
原式666 666 666 666 。
【2】如果10 9 8 □7 6 5 4 32 0 ,那么□=(
)。
【分析】考点:巧填算符。
等式左边1 8 □7 1 4 6 8 □7 ,所以□= 0
